The Role of Water Compartments in the Material Properties of Cortical Bone

Abstract

Comprising ~20% of the volume, water is a key determinant of the mechanical behavior of cortical bone. It essentially exists in 2 general compartments: within pores and bound to the matrix. The amount of pore water – residing in vascular-lacunar-canalicular space – primarily reflects intracortical porosity (i.e., open spaces within the matrix largely due to Haversian canals and resorption sites), and as such, is inversely proportional to most mechanical properties of bone. Movement of water according to pressure gradients generated during dynamic loading likely confers hydraulic stiffening to the bone as well. Nonetheless, bound water is a primary contributor to mechanical behavior of bone in that it is responsible for giving collagen the ability to confer ductility or plasticity to bone (i.e., allows deformation to continue once permanent damage begins to form in the matrix) and decreases with age along with fracture resistance. Thus, dehydration by air-drying or by solvents with less hydrogen bonding capacity causes bone to become brittle, but interestingly, it also increases stiffness and strength across the hierarchical levels of organization. Despite the importance of matrix hydration to fracture resistance, little is known about why bound water decreases with age in hydrated human bone. Using ¹H nuclear magnetic resonance (NMR), both bound and pore water concentrations in bone can be measured ex vivo because the proton relaxation times differ between the two water compartments giving rise to two distinct signals. There are also emerging techniques to measure bound and pore water in vivo with magnetic resonance imaging (MRI). NMR/MRI-derived bound water concentration is positively correlated with both strength and toughness of hydrated bone, and may become a useful clinical marker of fracture risk.

Introduction: Water compartments of bone

The three primary constituents of bone are i) fribrillar type 1 collagen (~35–45% by volume) with enzymatic and non-enzymatic crosslinks, ii) calcium (Ca²⁺)-phosphate (PO₄³⁻) (~35–45% by volume) in the form of semi-crystalline hydroxyapatite with carbonate substitutions and various vacancies, and iii) water (~15–25% by volume) [1, 2]. Arguably, water is the least studied constituent, even less than the non-collagenous proteins and growth factors within the matrix of bone (~ 1% by volume). As part of the bone anatomy, extracellular water occupies the intra-cortical porosity, which includes the vascular space comprising Haversian and Volkmann’s canals (5–20%), and the lacuno-canalicular network (~ 1%) (Fig. 1A) [3, 4]. This is commonly referred to as free, mobile, or pore water and can move according to pressure gradients that develop during movement of skeleton. Since certain residues of the collagen molecule are hydrophilic (e.g., lysine, arginine, and hydroxyproline), water molecules naturally associate themselves with the matrix. The osteoid secreted by osteoblasts is essentially hydrated collagen, and as the collagen mineralizes, water is displaced [5] though not completely. Recent evidence strongly suggests that water bound to the crystal surface actually helps orient apatite crystals during biomineralization [6]. Water can either be loosely or tightly bound to the matrix (Fig. 1B, 1C), and the amount of bound water occupying absorption sites has been estimated to be about 45 mg of H₂O per gram of human bone [7] and 40 mg of H₂O per gram of bovine bone [8] as determined by dielectric measurements. Bound water similarly exists in other mineralized tissues such as dentin – a bone-like substance with type 1 collagen, calcium-phosphate mineral, and water – that exists below the enamel of teeth.

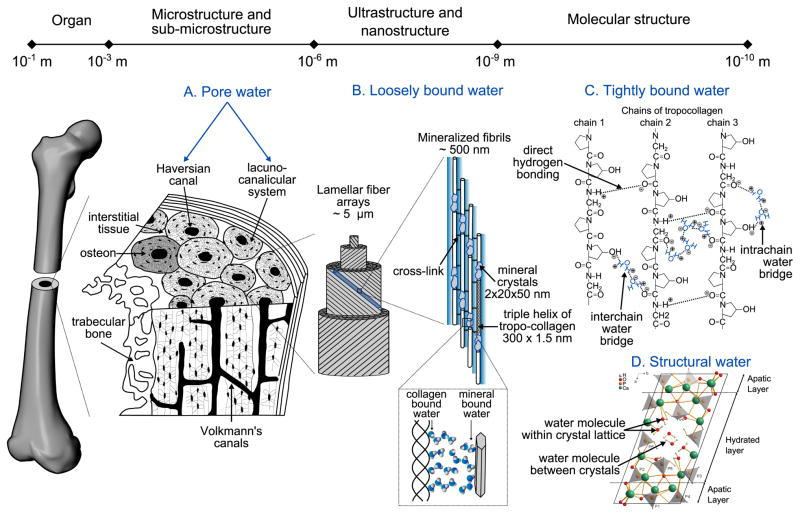
Fig. 1.

Schematic of the presence of water in bone at each hierarchical level of organization. Cortical tissue has a network of pores comprising vascular porosity (Haversian and Volkman's canals) and the lacuno-canalicular network. The bone matrix is arranged in arrays of lamellar fibers that are made up of collagen fibrils mineralized by apatite crystals. In this highly organized structure, water exists at different energy levels: free as liquid, loosely bound, tightly bound, and part of the mineral lattice. (A) At the microscale, free (or pore) water occupies the vascular-lacunar-canalicular space. (B) Loosely bound water is found at the surface of the collagen fibrils and between the collagen and the mineral phase. (C) At the molecular scale, tightly bound water refers to water molecules trapped inside the collagen triple helix. Examples of water bridges within a chain or between the chains of a tropocollagen molecule are illustrated on a small sequence of collagen (GLY-PRO-HYP) where hydrogen bonds are represented with dotted lines, and plus and minus signs indicate the polarity of the bonded atoms (adapted from Bella et al. [17] and Brodsky et al. [16]). (D) Structural water refers to the water molecules found within the core of the apatite structure (reprinted with the permission of PNAS from Davies et al. [28]).

The classic way to determine free and bound water is to perform calorimetry on frozen tissues to quantify the amount of free water (that which freezes) and then quantify the total water by drying the sample [9]. This approach is not without its limitations (dependent on freezing temperature and drying does not remove all water). Nonetheless, using this principle of non-freezable water in tissues, dynamic mechanical spectroscopy was performed on human dura mater [10] and rat tail tendons [11] as a function of increasing temperature (well below freezing from 80 K to 300 K) with the collagen samples having different levels of re-hydration (<0.01 g/g to 0.61 g/g of collagen) in order to deduce water-collagen interactions. This involves i) twisting collagen ~2° while under constant stress within a cryostat, ii) releasing the torque to monitor the free oscillation of the collagen as it returns to equilibrium while still under tensile stress, and iii) repeating the twist and oscillation monitoring after increasing temperature by 2 K [12]. In doing so, the logarithmic change in amplitude over the nth oscillation increases (faster decay) as temperature increases with several relaxation peaks indicating that different compartments of water within the collagen thaw at different temperatures below 273 K (0 °C). Coupled with other observations from low temperature X-ray diffraction, Nomura et al. [10] proposed that these changes in oscillation behavior (or rigidity) corresponded to i) non-freezable, ‘hidden’ water (0–0.07 g/g of collagen) existing within the tropocollagen molecule, ii) non-freezable, tightly bound water (0.07–0.25 g/g) associated with hydrophilic residues among the collagen helices (Fig. 1C), iii) transition water or loosely bound water that is partially freezable (0.25–0.45 g/g) and interacts with polysaccharides, and iv) freezable, free water (>0.45 g/g) that exists in gaps between microfibrils (Fig. 1). Pineri et al. [11] proposed a similar model refining tightly bound water as either triple hydrogen bonding within the helix involving hydroxyproline or double hydrogen bonding with other hydrophilic sites of the collagen molecule. Additional X-ray diffraction studies of tendon [13] and synthetic collagen-like polypeptides [14] support the presence of at least two water molecules forming an interchain hydrogen-bonded bridge between polar groups of amino acids (Fig. 1C), and this bound water contributes to the highly ordered structure of collagen [15–17]. Taken together, these studies suggest the existence of water interacting with collagen with varying degrees of entrapment: water molecules trapped inside the collagen triple helix require a greater drop in temperature to freeze than those located between neighboring collagen molecules, which in turn require an even less of a temperature drop to freeze than water molecules present between the fibers (Fig. 1).

In the case of mineralized collagen, bound water also exists as an organized layer between mineral crystals and collagen molecules with an initial estimated thickness of 0.160 nm [18] and later measured to be ~0.230–0.255 nm (distance between water protons and surface phosphorus atoms) [19]. This water-mineral interaction presumably arises as the surfaces of mineral crystals are charged [20]. However, recent work indicates that there are multiple compartments of water in the mineral phase. Coupling thermogravimetric analyzer to a mass spectrometer in tandem, Mkukuma and co-workers [21, 22] observed the removal of water peaked around 100 °C (~63% of water in bone) and again around 350 °C with the latter peak corresponding to a carbon dioxide peak (i.e., collagen removal). The water that is eliminated before bone reaches 200 °C is the aforementioned loosely to tightly bound water within collagen but also water absorbed to mineral crystals (water remaining after centrifuging hydroxyapatite at 40,000 g [23]). The water that is entirely eliminated by raising the temperature to 540 °C (after collagen removal) is likely trapped in the mineral phase and is referred here as structural water (Fig. 1D).

The evidence of this structural water comes from nuclear magnetic resonance (NMR) studies of mineralized tissue and synthetic hydroxyapatite. Analyzing dentine, enamel, cementum, and bone with broad-line proton (¹H) NMR, Casciani detected a loss of proton resonance of hydrate water when heating bone from 215 °C to 540 °C [24]. Using solid-state NMR (magic-angle spinning) and cross-polarization techniques (¹H-³¹P), Wilson et al. [19] identified structural water occupying vacancies in the mineral crystals of deproteinated bone and identified hydroxide ions (OH⁻) in unmodified bone that participated in hydrogen bonding with neighboring water molecules within the mineral crystal. As a side note, the hydroxyl content of bone is about 21% of the stoichiometric-indicated amount in hydroxyapatite [25]. Also, the actual distance between collagen and mineral decreases with a reduction in the level of hydration [26]. More recently, analyzing synthetic hydroxyapatites with variable carbonate content by ²H NMR after heating (150 °C and 500 °C) confirmed the existence of water deep in the crystal lattice of mineral [27]. Then, using multinuclear solid-state NMR (including ¹⁷O NMR), Davis et al. [28] deduced that a hydrate layer involving octacalcium-phosphate-citrate bridges mineral platelets. Thus, water is a part of the crystal lattice of mineral in bone (Fig. 1D). The functional significance of this structural water is not entirely clear, but may play a role in mineral crystal aggregation that forms a continuum and is present after the removal of collagen [28] and may provide stability to imperfections (i.e., vacancies) that are inherent in the crystals [19]. In addition to these roles in mineralization, bound water and pore water appear to be important attributes in the ability of mineralized tissues like bone and teeth to resist fracture as described below.

Effect of thermal dehydration on the mechanical properties of bone

Water influences the mechanical behavior of bone and is a primary determinant of fracture resistance. Along with collagen, it confers ductility or plasticity to bone (i.e., deformation beyond the elastic limit or yield point). In this section, we address the effect of removing water through thermal dehydration (e.g., air drying at room temperature or drying in a vacuum oven at elevated temperatures below 115°C) on bone mechanical properties at different hierarchical levels of organization (Table 1).

Table 1.

Effect of dehydration on bone mechanical properties at different length scales

Tissue	Dehydration treatment	Mechanical test	Effect of dehydration*	Ref
At the mineralized fibril scale
Equine cortical	Air dried	AFM	↑ stiffness parallel to the fibril (+83%) and orthogonal to the fibril (+54%)	[29]
Elephant dentin	Acetone, ethanol	AFM	↑ stiffness of collagen fibers: water: E~40 MPa; ethanol: E~1000 MPa; acetone:E~1500 MPa ↓ viscoelasticity of collagen fibers in water > in ethanol > in acetone	[65]
At the lamellar scale
Porcine cortical	Air dried (24h)	Nanoindentation	↑stiffness (+42% in osteons and +26% in interstitial bone)	[33]
Bovine cortical	Air dried	Nanoindentation	↑ stiffness (+40%)	[34]
Human cortical and trabecular	50°C (24h)	Nanoindentation	↑ stiffness (dry state: E = [11.1–31.6 GPa]; wet state: E = [7.0–18.5 GPa])	[35]
Mouse tibia	Air dried (1h)	Nanoindentation	↑ stiffness and ↑ hardness (Edry /Ewet ~ 1.3; Hdry/Hwet ~ 4.1)	[36]
Bovine cortical	Air dried (14 days)	Nanoindentation	↑ stiffness (+15% in osteons, +10% in interstitial bone) ↑ hardness (+18% in osteons, +12% in interstitial bone)	[37]
Canine cortical		Nanoindentation	↑ stiffness and ↑ hardness (Edry /Ewet ~ 1.6 and Hdry /Hwet ~ 1.4)	[38]
Equine cortical	Air dried (24h)	Nanoindentation	↑ stiffness and ↑ hardness (Edry /Ewet ~ 1.7; Hdry/Hwet ~ 1.5)	[29]
Mouse femora	Dehydrated in ethanol + embedded inPMMA	Dynamic nanoindentation	↓viscoelasticity (tan δ) from wet to dry conditions	[42]
Fibrolamellar bovine bone		Micromechanical tensile tests	↑ stiffness and ↑ hardness Tensile test parallel to the collagenfiber: strengthdry/Strengthwet ~ 1.7 Tensile test perpendicular to the collagen fiber: Edry/Ewet ~ 3.3	[39]
Equine cortical	100% ethanol	Nanoindentation	↑ stiffness (Edry /Ewet ~ 1.3)	[67]
Equine cortical	50%, 70%, 100% Ethanol (24h)	Nanoindentation	↑ stiffness (increase dependent on the ethanol concentration) 50% EtOH: E = 8.5 GPa; 70% EtOH: E = 13.1 GPa; 100% EtOH: E = 15.8 GPa	[66]
At the scale of an osteon
Human vertebrae	Air dried (overnight)	Microindentation	↑ stiffness, ↑ anisotropy ratio (Eaxial/Etransverse), ↑ elastic energy, ↑ dissipated energy	[41]
Equine cortical	Air dried (24h)	Microindentation	↑ stiffness (Edry /Ewet ~ 1.25)	[29]
Lamb cortical	42°C (48h)	Microindentation	↑ Vickers hardness	[45]
Human femur	Air dried	Microindentation	↑ hardness (+54%)	[44]
Human trabecular	70% ethanol	Microindentation	↑ hardness (+10%)	[68]
At the material level
Human femur, tibia, humerus	Air dried	Tensile and compression test	↑ stiffness in compression (Edry /Ewet ~ 1.25) and tension (Edry /Ewet ~ 1.6) ↑ ultimate stress in compression (σdry /σwet ~ 1.63) and tension (σdry /σwet ~ 1.50)	[46]
Human femur	Air drying	Tensile test	↑ modulus of elasticity (+18%) ↓ percentage elongation under tension (−45%) ↑ ultimate tensile strength (+31%)	[44]
Human tibia,horse radius, dog femur, sheep metacarpus	Air dried (5h)	Tensile test	↑ stiffness (+7%)	[47]
Human femur	Drying in a vacuum at 21, 50, 70, and 110°C for 4h	3-point bending test	↑ stiffness (p<0.0001) ↓ strength (p<0.0001) ↓ toughness (p<0.0001)	[48]
Mouse femur	Air dried (21°C, 48h)	3-point bending test	↑ stiffness (+40%), ↓ ductility (ultimate deflection: −57%)	[49]
Human femur	Air drying, 62°, and 103°C	Tensile test	no changes in stiffness and yield strength: ↓ toughness and ↓ post-yield strain	[50]
Bovine cortical	60°C (24h) or 110°C (2h)	Fracture toughness	↓ fracture toughness (Kdry / Kwet ~ 0.69) ↓ work to fracture (Wfdry /Wfwet ~ 0.16)	[51]
Bovine cortical		Fracture toughness	↓ fracture toughness (Kwet 60% greater than Kdry)	[52]
Bovine cortical		Fracture toughness	↓ fracture toughness (Kwet 2 to 3 times higher than Kdry depending on the strain rate)	[53]
Bovine dentin	Air dried (22°C, 7 days)	Fracture toughness	↓ fracture energy (wet = 554 J/m2; dry = 114 J/m2)	[54]
Bovine cortical	70% ethanol	Fracture toughness	↑ fracture toughness (Kdry 25–45% greater than Kwet) ↓ work to fracture (Wfdry 28–56% lower than Wfwet)	[64]
Bovine cortical	ethanol	Fracture toughness	↑ fracture toughness (Kdry 17% greater than Kwet)	[63]
Elephant dentin	86-proof Scotch whisky	Bending test Fracture toughness	↑ stiffness (75–100%) ↑ strength (40–50%) ↑ growth toughness	[61]
Elephant dentin	Methanol, ethanol, acetone	Bending test Fracture toughness	↑ stiffness, bending strength ↓ ductility/deformation prior to fracture ↑ initiation toughness ↑ growth toughness	[65]

^*The following abbreviations have been used: Young modulus (E), hardness (H), stress (σ), stress intensity factor (K), work to fracture (W_f)

Mineralized fibril level (~100 nm)

Using atomic force microscopy to perform quasi-static indentations to a 120 nm depth on equine cortical bone (mineralized), Faingold et al. [29] showed that a small decrease in water content (from 12% by wt to 9% by wt of water) drastically increased the stiffness of bundles of mineralized fibrils, and this occurred for indentations parallel (+83%) or orthogonal (+54%) to the fibril. The stiffening of the mineralized fibrils is most likely due to the stiffening of the collagen phase upon dehydration, as found experimentally with AFM experiments on rat tail tendon [30] and predicted by a model of the nanomechanics of a collagen microfibril [31]. Along with an increase in stiffness, tighter molecular packing of the collagen relative to the mineral phase occurs with dehydration [18, 32].

Lamellar level (~1–10 μm)

Moving up to the scale of the lamella, Young’s modulus and hardness, as determined by nanoindentation, are consistently found to be lower by 30–50% in hydrated bone samples compared to the dehydrated ones [29, 33–38]. Performing nanoindentation experiments on bovine plexiform bone, Seto et al. [39] found that the ratio of mean elastic moduli measured along the direction of the fiber to those measured perpendicular to the fiber (anisotropy) is greater under wet conditions than compared to the dry tissue. This suggests that the extent of stiffening upon dehydration is not isotropic but greater in the direction perpendicular to the fiber. Comparable results were obtained using microindentation (2.5 μm depth) on mineralized tendon [40] and human trabecular vertebrae [41] with the anisotropy ratio (axial to transverse indentation direction) being higher for wet than for dry indentations. Interestingly, Faingold et al. [29] reported the opposite behavior (i.e., a slight increase in the anisotropy ratio with dehydration). An explanation could be that the average fibril orientation in their samples (metacarpal equine bone) was ~45° to the long axis of the osteon (rotated plywood arrangement) and had an anisotropy ratio close to one for wet bone. The dehydration may have affected the collagen orientation away from 45°, thereby imparting some anisotropic elastic behavior in the dry tissue. Presumably, the anisotropic changes in elasticity noticed in previous studies occurred because the collagen fibrils were oriented parallel to the direction of indentation. Water content in bone also influences relaxation phenomena. This was assessed at the tissue level in mouse femora using dynamic nanoindentation (200 nm depth). The viscous damping characterized by the loss factor or tan δ, in which δ is the phase shift between the imparted stress and the strain response, dropped to zero in the dry bones, confirming the loss of viscoelasticity upon dehydration to purely elastic behavior [42]. To date, the contribution of the different water compartments to fatigue resistance has not been investigated, though the expectation is that dehydration would increase microdamage accumulation, thereby reducing fatigue life. Pore water was observed to increase as a consequence of the increase in fatigue-induced microdamage in cortical bone due to cyclic loading [43].

Osteonal level (~50–100 μm)

At the scale of the osteon level, microindentation measurements reveal the same trend as the one observed at the smaller length scales. That is, dehydration causes an increase in hardness and modulus [29, 38, 41, 44, 45]. Viewing microindents with confocal laser scanning microscopy revealed the formation of indentation-induced microcracks in the dehydrated bones only, possibly as an alternate energy dissipation mechanism to viscous damping [45].

Material level (~1 mm)

At the apparent-level, removal of water leads to a significant increase in bone stiffness or modulus [44, 46–49] and a decrease in bone toughness or post-yield toughness [48–51] suggesting that water influences both the pre and post-yield behaviors of bone, respectively. Dehydration affects post-yield properties more so than elastic properties as shown by Nyman et al. [50] where a minimal amount of water loss (<3% wt) had no effect on modulus or yield strength but produced a significant decrease in post-yield strain of bone from both young (<50 years) and elderly (>70 years) donors. Dehydration also significantly impairs fracture toughness, i.e. the ability of bone to resist crack initiation [51–53]. Analyzing the resistance to fracture in notched bovine teeth, work to fracture was reduced by 80% in dehydrated specimens [54]. Crack growth resistance of a material manifests itself through intrinsic toughening mechanisms (e.g., formation of microcracks ahead of the crack tip and debonding between lamellae), and extrinsic toughening mechanisms that operate behind the crack tip (e.g. crack deflection and ligament bridging) [55]. Optical observations on both hydrated and dehydrated dentin [54] revealed that loss of fracture toughness upon dehydration essentially results from the loss of extrinsic toughening mechanisms, precisely the inability of dehydrated tissue to form fibrous bridges in the wake of the crack. Finally, dynamic mechanical analyses indicate that bone viscoelastic behavior is most likely governed by water content rather than by collagen morphology as denaturing collagen by heat did not affect the storage modulus per loss modulus (i.e., tan δ is the viscous damping behavior under dynamic loading) of hydrated bone but water removal profoundly reduced tan δ, whether or not the collagen was denatured [56]. The larger viscoelasticity in wet bones compared to dry bones was also reported in human tibia [57] and bovine cortical bone [58]. Also, pore water present in wet bone, but not dry, contributes to hydraulic stiffening of bone as suggested by fluid flow constitutive models of cortical bone [59]. In an analytical model of cortical bone, loss of creep upon partial dehydration was attributed to the loss of bound water residing between mineral crystals, which facilitated ductile sliding (and thereby energy dissipation) between mineral crystals [60].

Effect of dehydration with solvents on the mechanical properties of bone

To further establish the importance of hydration to mechanical behavior of bone, chemical dehydration can be used to remove water while maintaining hydrogen-hydrogen bonding with collagen. The specimen is placed in a non-aqueous solution that is miscible with water, allowing the water to diffuse from the collagen and pores into the other solvent, which is present in great excess. This removal of water is reversible by simple rehydration in saline solution [61–64]. The effect of solvents on bone properties has been addressed in a number of studies (Table 1) because solvents are generally used as part of the sterilization process to manufacture bone allografts as well as in dentistry.

Relative to water, ethanol increases tissue stiffness at several length scales: increased elastic modulus as measured by AFM [65] and nanoindentation [66, 67], increased microhardness with increasing ethanol concentrations [68], and increased stiffness at the millimeter scale [61, 65]. The increased stiffness of tissues dehydrated in polar solvents presumably originates from the shrinkage of the tissue, the latter being inversely related to the hydrogen bonding capability of the solvent [69]. In the hydrated state, water-mediated hydrogen bonds (also called water bridges) link adjacent tropocollagen molecules (Fig. 1C) [70]. Removal of water from the collagen microfibril permits additional hydrogen bonds to form between collagen molecules (direct collagen-collagen bonding) and thereby may participate in strengthening the fibrils [62, 71] as well as embrittling the collagen phase. Deep ultra-violet Raman analyses of bone revealed changes in the Amide I band when ethanol replaced water [65], indicating changes in the protein conformation in the organic matrix as direct collagen-collagen bonding increases with dehydration.

The extent to which a solvent can replace water depends on its polarity (potential difference between positive and negative electrical charges across the molecule that arises because two covalently bonded atoms do not share electrons equally), molecular size (dependent on the number of atoms and their size), and hydrogen bonding capability (the ability of an electronegative atom like oxygen to share a proton with another electronegative atom in which the strength of the hydrogen bond increases as the electronegativity of sharing atoms increases) [72]. When dehydrated bone (70 °C for ~4 hours) was soaked in ethylene glycol (similar polarity as water but larger molecular size), dimethylformamide (acceptor of proton), or carbon tetrachloride (non-polar), a significant volume fraction of the original matrix water was not replaced (at least 15% not replaced depending on the solvent). The specimens immersed in these solvents had significantly higher Young’s modulus, higher strength, and lower post-yield deformation at the apparent level than the rehydrated bone specimens, illustrating the same brittleness behavior as bones that were air- or heat-dehydrated. In a study on the effect of fixation techniques on mechanical properties of bone, specimens of human and bovine cortical bone were stored for 6 months in ethyl alcohol-glycerine-phenol (96%-3%-1% by volume), which primarily dehydrates the bone (though some fixation may occur), and then subjected to a three point bending test. Compared to fresh-frozen control samples, the alcohol-soaked bone samples had higher strength and lower post-yield toughness [73].

Conversely to what is observed with thermal dehydration of cortical bone (Table 1), ethanol dehydration actually causes an increase in fracture toughness, i.e. crack initiation toughness [63, 64] and growth toughness [61] of dentin (elephant tusk). Using acetone, methanol, and ethanol, Nalla et al. [65] found that both crack initiation and growth toughness significantly increased with decreasing hydrogen bonding energy. As previously mentioned, water forms hydrogen-bond bridges connecting adjacent chains of collagen (Fig. 1C). Because organic solvents have weaker hydrogen-bonding capability than water, these solvents form fewer bridges across the chains. Thereupon, more hydrogen bonding sites are available on the collagen chains, allowing for an increase in direct collagen-collagen hydrogen-bonding (i.e., sharing a proton between oxygen and nitrogen on two different residues of the polypeptide). The latter is thought to explain the presence of more uncracked-ligament bridges in the wake of the crack, thereby improving one of the extrinsic toughening mechanisms of bone [61]. Ultimately though, fewer hydrogen-bonded bridges in collagen translate to less plastic or more brittle bone. There are no studies reporting whether these polar solvents increase the fracture toughness properties of human cortical bone. Presumably, with thermal dehydration, there are no water or solvent bridges, and this toughening mechanism is absent. Given the known effects of solvents on post-yield properties and the higher critical stress intensity factor but lower work-to-fracture of notched bovine cortical bone stored in 70% ethanol (reversible when rehydrated) [64], ethanol would likely decrease the non-linear strain energy dissipation of bone (J-integral) even if it increased the crack initiation toughness of human bone.

While the dehydration studies (Table 1) demonstrate that water influences mechanical behavior, bones in vivo do not dry out. Thus, to connect the importance of bound water and pore water to fracture resistance of bone, we need a method to quantify these water compartments both ex vivo and in vivo.

Assessing water in bone with magnetic resonance techniques

Magnetic resonance imaging (MRI) is a common medical imaging modality that generates tomographic maps of the NMR signal from the hydrogen (¹H) nucleus (i.e., a proton). As such, MRI primarily visualizes water and fat, and the image contrast is largely dictated by a combination of i) proton density, ii) the longitudinal relaxation time constant (T₁, which is the time constant of proton magnet moments’ return to thermal equilibrium), and iii) the transverse relaxation time constant (T₂ or T₂*, which are, simply put, the time constants of the decay of the observable NMR signal, with or without removing the effects of spatial variations in the magnetic field, respectively). Because conventional MRI requires a finite time delay (> 1 ms) between signal excitation and acquisition in order to spatially encode the NMR signal, cortical bone, with its relatively low proton density (≈ ¼ that of soft tissues) and short T₂ (< 1 ms), generally provides no signal. However, specialized MRI methods for measuring signal from cortical bone have now been established (see Imaging bound water and pore water in the bones of humans, below) and are currently being investigated as a clinical approach for evaluating bone fracture risk. To understand the challenges of imaging bound water and pore water in bone, we first describe the underlying ¹H NMR signal characteristics from cortical bone with respect to magnetic field strength (B₀). The ability to distinguish proton signals from different sources depends on B₀.

The history of quantitative measures of the ¹H NMR signal from cortical bone is relatively short, beginning with measures of T₁ (≈ 300 ms) and T₂ (≈ 250 μs) made at a magnetic field strength (B₀ = 2T) in the range typical of clinical MRI systems [74]. In a subsequent study by the same group [75], quantitative measures of water content with ¹H NMR at B₀ = 9.4T were shown to negatively correlate with mineral content, as measured with ³¹P NMR, indicating the potential for MRI to provide an indirect measure of the amount of mineral in bone. In this latter study, bone was collected from a rabbit model of osteomalacia (hypomineralization induced by low phosphorus diet vs. normal diet).

Meanwhile, two groups with backgrounds in NMR characterization of porous media also began studying the ¹H NMR signal from cortical bone. Fantazzini and colleagues applied ¹H NMR relaxometry methods to bovine and porcine cortical bone samples at low-field (B₀ = 0.47 T) [76]. Free induction decay (FID) signals as a function of T₂* were found to exhibit a rapidly-decaying Gaussian-shaped component, reasoned to be from the relatively immobile collagen protons, and a longer-lived “liquid like” component from water inside the solid material of bone. Further, these short and long-lived signals were observed to have similar longitudinal relaxation time constants (T₁), which was argued to reflect cross-relaxation between the collagen and water protons suggesting the source of signal was bound water. Spin-echo signals, analyzed as a distribution T₂ values, showed a dominant component with T₂ ≈ 400 μs and a small tail of more slowly relaxing signals. This latter distribution of signal with T₂’s > 400 μs likely reflected pore water signal, but it was not further investigated in that study.

Independently and around the same time, Wang and Ni [77, 78], also following the methods of NMR studies of porous media, performed more detailed analyses of the distribution of T₂ times of ¹H NMR signals in cortical bone. These measures were performed at very low magnetic field strength (B₀ = 0.047 T) and revealed signal components with intermediate (T₂ = 1–10 ms) and longer (T₂ = 10–100 ms) relaxation times, which correlated strongly with independent measures of smaller (osteocytic lacunae) and larger (Harversian) pore volumes, respectively. These observations were consistent with the model that relaxation rates of water in porous media are proportional to the surface to volume ratio of the pores. Subsequent work from the same group [79], performed at B₀ = 0.63 T (closer to clinical MRI field strengths), also looked at FID signals (similar to the work by Fantazzini et al. [76]) and identified two sub-millisecond components reasoned to be derived from solid and bound-water protons. Also, as discussed below, this signal characterization was later shown to correlate with mechanical properties in cortical bone specimens [80].

This series of papers provided the essential foundation for much of the current application of MRI to characterize the bound and pore water compartments of cortical bone; however, most of the work was not done at clinical MRI magnetic field strengths (typically B₀ = 1.5 – 3.0 T), and the assignment of signal components to anatomical origins was logical but not rigorously evaluated.

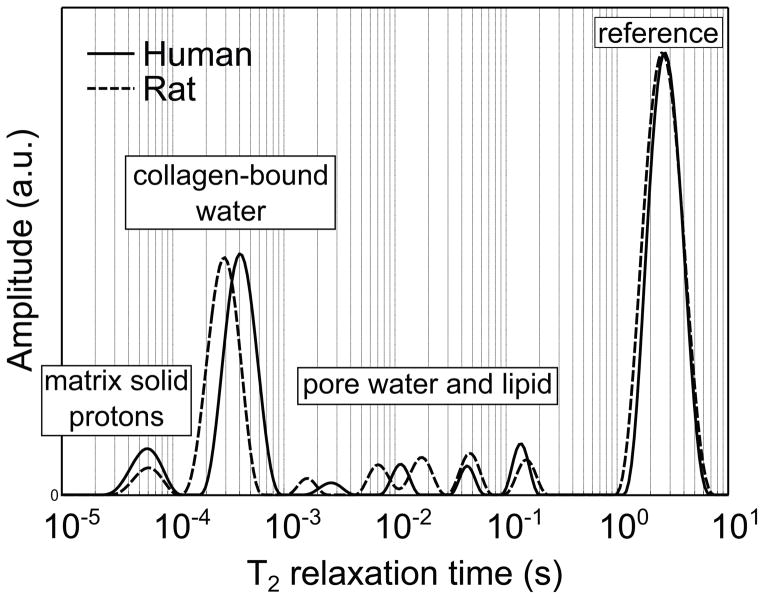
Building from these previous studies, Horch et al. presented more comprehensive ¹H NMR studies of human (cadaveric) cortical bone specimens [81]. These experiments included T₂ relaxometry, (similar to the aforementioned studies by Wang and colleagues, but spanning a broader T₂ domain), removing water and exchangeable proton signals by sample preparation with deuterated buffer (similar to the previous studies of Fernandez-Seara et al.[75, 82]), and relaxation-exchange spectroscopy to identify physical relationships between signals with different T₂ time constants. Collectively, these measures identified the dominant proton signal source from three domains of T₂: matrix solid protons (T₂ < 100 μs), collagen-bound water (T₂ ≈ 400 μs), and pore water (T₂ > 1 ms) (see Fig. 2). Exchangeable protons on collagen and lipid methylene protons were identified as secondary contributors to the signals in the intermediate and long T₂ domains, respectively. The assignments of the bound and pore water signals, which are the most relevant to clinical MRI measures, were supported by independent studies by Ong et al. using deuterated samples and direct observation of the ²H NMR signal [83]. Thus, the ability to distinguish bound and pore water based on T₂ was well established, but the works of Horch et al. [81] and Ong et al. [83] were done at B₀ = 4.7T and 9.4T, respectively, so the relaxation characteristics of bound and pore water signals at common clinical MRI fields strengths remained somewhat unclear.

Fig. 2.

T₂ relaxation spectra were generated for a human (solid line) and a rat (dotted line) cortical bone specimens by fitting 10,000 Carr-Purcell-Meiboom-Gill echoes collected at 100 μs echo spacing to a sum of 128 decaying exponential functions. The area under each peak or peaks in the case of the pore water pool is normalized to the area under the reference peak (microsphere with a known proton content placed next to the bone specimen during the measurement) to convert signals in arbitrary units into water volume (or mol of water). Bound and pore water can further be expressed as proton concentration in the bulk bone specimen (mol ¹H/L_bone) or volume fraction of the apparent volume of the specimen (original data).

Imaging bound water and pore water in the bones of humans

Translation of this cortical bone ¹H NMR signal characterization into a clinically practical MRI method for quantitative imaging of bound and/or pore water required overcoming multiple challenges and remains in development. First, since the bound water signal decays quite rapidly (T₂ ≈ 400 μs), little signal is observed in conventional MRI methods which typically involve a delay time (known as the echo time, TE) of 1 ms or greater between signal excitation and observation. This limitation has been largely overcome through ultra-short echo time (UTE) methods [84, 85], which involve signal acquisition as short as 8 μs after the end of signal excitation, although typically closer to 100 μs. Much of the signal with T₂ < 100 μs is lost during signal excitation and acquisition, regardless. Thus, UTE MRI is able to measure signals from both bound water (T₂ ≈ 400 μs) and pore water (T₂ > 1 ms) in cortical bone, and the use of a signal reference with known water density and relaxation rates can be used to convert image intensity into quantitative measures of water density (Fig. 3) [86]. However, the methods used to measure the distribution of T₂ times with ¹H NMR are not directly applicable to UTE MRI, so an alternate strategy is needed to distinguish the bound and pore water signals when imaging.

Fig. 3.

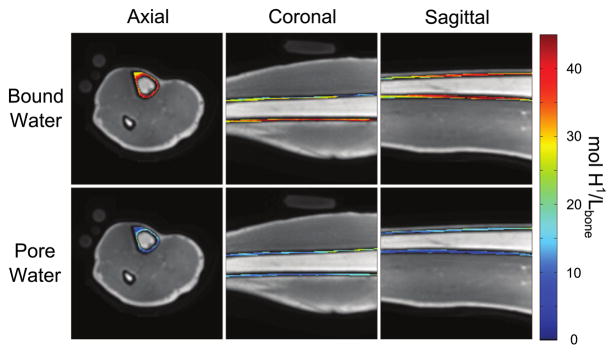
Pore and bound water maps are overlaid conventional UTE images in three cardinal planes, acquired from a human tibia in vivo using a clinical MRI (3T) scanner. Details of imaging acquisition and processing are similar to those in Manhard et al. [92]. The circular markers outside the limb are CuSO₄ doped, 10% H₂O/ 90% D₂O that are used to convert proton signal into absolute units of proton density, while the larger phantoms are used to aid in B₁-mapping.

To date, two approaches show promise for quantitative in vivo measurement of bound and pore water in individuals using MRI. One approach involves the acquisition of multiple UTE images with different echo times (TEs) between 8 μs and 20 ms. Then, the signal decay from any given cortical bone image voxel is fitted with a bi-exponential model, where the fast relaxing component is presumed to be from bound water and the slow relaxing component from pore water [87]. One potential challenge of this method is that the acquisition of multiple images is, generally, time-consuming, requiring the subject to remain in the magnet for an extended period of time. There is, however, a fast two-dimensional (2D) implementation of this approach which shares NMR signal across acquisitions with different TEs, permitting scan times of a few minutes [88]. The trade-off is that water is only assessed for one slice of bone, and the signal sharing may impart error on the signal analysis. Another challenge of this approach is that the magnetic field perturbation in the porous regions of cortical bone broadens the pore water line width thereby accelerating its apparent transverse relaxation rate (1/T₂*) as measured by UTE. That is, the time constants of signal decay with this method are characterized as T₂*, as opposed to T₂, values. This may make it difficult to distinguish signals of pore water from bound water, particularly at increasing magnetic field strengths. Also, the presence of lipid signal, which oscillates relative to the water signal, will complicate the analysis. Nonetheless, experimental studies show promise for this approach at current clinical field strengths but indicate that it may not work well at higher field strengths (e.g., B₀ = 7T) [89].

An alternative approach to distinguishing bound and pore water signals in UTE is through T₂ and/or T₁ selective magnetization preparation prior to UTE acquisition. In other words, pore water signal is nulled or suppressed during acquisition of the bound water signal and vice versa. With this approach, a bound or pore water image is formed and converted to a quantitative measure of water equivalent proton concentration by comparison to a known reference (as described above) [90]. This approach is largely insensitive to the line broadening effects on pore water with increasing magnetic field — that is, the method is distinguishing bound and pore water based on their T₂ as opposed to T₂* values. Also, it is not confounded by an oscillating lipid signal — the lipid signal will show up as a pore water signal. The primary drawback to this approach though is that it requires two independent acquisitions to measure both bound and pore water concentrations. Recent studies on a clinical 3.0T MRI system show promise for this approach as well [91, 92].

Relationships between water compartments and the material properties of bone

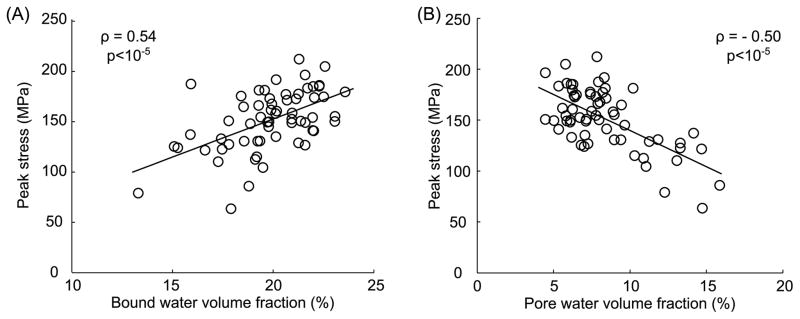
The development of ¹H NMR spectroscopy and UTE MRI over the past 10 years has facilitated investigations into whether the different water compartments (i.e., bound and pore water) are related to the mechanical properties of hydrated bone. Because there is an age-related decrease in bound water [80] (Fig. 4) but also an age-related increase in porosity [93, 94] or bone water concentration [89], these two magnetic resonance outcomes should be considered independently when making comparisons between water compartments and bone mechanical properties. As demonstrated by Horch and coworkers [95], the total amount of proton signal from human cortical bone did not explain the age-related changes in peak stress assessed via a three-point bending test, whereas bound and pore water per bone volume significantly explained the variance in strength and flexural modulus (R² = [0.48–0.68]). As described in the previous section, this total signal included solid protons of the matrix, bound water, and pore water as determined by the T₂ spectrum of the three proton pools from high field ¹H NMR (Fig. 2). Similar correlations between peak stress of human cortical bone and bound water or peak stress and pore water were obtained using the same NMR technique but for the peak stress at the notch of single-edge notched beam specimens (Fig. 5). Based on the same principle (i.e., distinguishing the protons pools among matrix, bound water and pore or mobile water) but using spectra of T₂* relaxation times from low-field ¹H NMR (free induction decay signals), Nyman et al. [80] also found that bound water per wet bone mass was positively associated with both peak bending strength (R² = 0.36) and toughness (R² = 0.40), while pore water per bone mass negatively correlated with modulus of elasticity (R² = 0.25). Recently, we found that bound water and pore water correlated to fracture toughness properties to a greater extent than age [96]. Thus, bound water appears to be more important to post-yield properties as it gives collagen ductility [48], whereas pore water is more important to elastic properties as porosity contributes to stiffness [97].

Fig. 4.

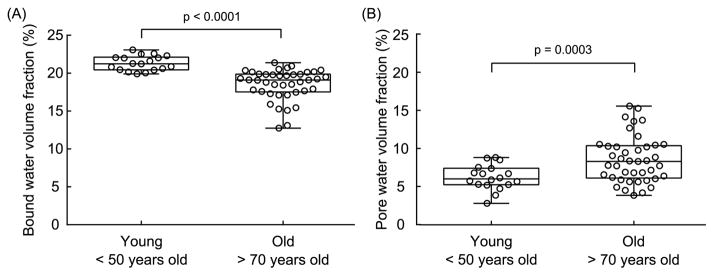
(A) Bound water per apparent bone volume significantly decreased with age in a set of cortical bone specimens (femur mid-shaft) from young (n=18, 21 – 50 years old) and old (n=41, 70–105 years old) donors. (B) Pore water per apparent bone volume slightly increased with age. The same trend was observed for porosity as measured by μCT (voxel size of 5 μm) (original data).

Fig. 5.

Strength of cortical bone, assessed as peak stress endured by a notched beam specimen subjected to three-point bending, (A) increased with an increase in bound water per apparent bone volume and (B) decreased with an increase in pore water apparent bone volume (n=62, human femoral samples). Correlation coefficient (ρ) was determined using Spearman’s rank correlation (original data).

In a recent study, Bae et al. [98] implemented three-dimensional (3D) and 2D UTE MRI sequences to measure total bone water content and to distinguish bound (short T₂* ~ 200–400 μs) from pore water (longer T₂*~ 1–4 ms) using a T₂* bi-component analysis of human cortical bone, respectively. In such an approach, bound and free water components are not independent measures but inversely related to each other (the T₂* short and long fractions sum to 100%). Determining mechanical properties from monotonic load-to-failure tests in four point bending, they found that the long T₂* relaxation time (i.e. how fast the free water relaxes) was directly associated with energy-to-failure (R² = 0.17), while the long T₂* fraction (presumably related to the signal from pore water) was inversely correlated with failure strain (R² = 0.14). There was also direct correlation between the short T₂* relaxation time (i.e., how fast the bound water relaxes) and energy-to-failure (R² = 0.30) as well as failure strain (R² = 0.29). In contrast, there were no significant correlations with the modulus, yield strain, and yield stress of cortical bone among any of the NMR properties indicating that bi-component analysis of water signals is partially sensitive to the variance in post-yield mechanical properties.

To the best of our knowledge, there is only one study correlating the mechanical properties of trabecular bone to bound water. Using ¹H NMR to investigate changes in trabecular bone water content in rats between normal, bone loss (osteopenia induced by lactation or ovariectomy), and bone restoration (PTH administration after ovariectomy), Rai et al. [99] found that bound water decreased significantly in both osteopenic and bone restoration groups compared to control. The absence of changes in bound water after a gain of bone mass (restoration group) likely explains why, in this study, bound water did not correlate with compression parameters (stiffness and energy to failure). Further studies are still necessary to determine the contribution of bound water to the apparent mechanical behavior of trabecular bone. Further development and application of high resolution MRI to trabecular bone is however crucial as it can image trabecular bone architecture as an alternative, non-irradiation method to peripheral quantitative computed tomography [100].

Drug effects on hydration

Although not widely prescribed for osteoporosis relative to bisphosphonates, raloxifene – a selective estrogen receptor modulator - decreases fracture risk without much of an increase in areal bone mineral density [101]. In pre-clinical models of estrogen withdrawal (ovariectomy in rats), raloxifene affected tissue properties of bone as determined by nanoindentation [102] and increased estimated material strength and toughness as determined by three-point bending, albeit the effect was greater when combined with estrogen [103]. In addition, raloxifene treatment of intact, mature female dogs also improved bone mechanical properties in ways that appear to be independent of aBMD [104, 105]. Thus, a non-cellular, matrix-based mechanism of action has been proposed for the effect of raloxifene on fracture risk. Gallant and coworkers [106] measured bound water via 3D UTE MRI in human and canine bone samples incubated in raloxifene (dissolved in dimethyl sulfoxide) for two weeks. Material-level properties derived from four-point bending indicated that raloxifene induced changes predominantly in the post-yield properties with a greater energy to failure (+34% in canine), post-yield energy (+38% in canine), and higher toughness (+22% in human). Part of this improvement in bone toughness was attributed to the significantly increased matrix-bound water content (+17%), independent of porosity. This was supported by the significant correlation in the raloxifene-treated specimens between bound water and post-yield properties (post-yield energy to failure: R² = 0.54).

In an ovariectomized (OVX) rat model [107], bisphosphonate treatment (alendronate at 0.025 mg/kg/day) decreased total water content assessed with UTE MRI of the femur (−19% relative to OVX animals). Total water did not correlate with elastic modulus and strength across specimens but did so for the mean of each experimental group. In this study, a decrease in mean water content was systematically paralleled with an increase in the mean degree of mineralization, which likely explains the negative correlation between water content and mechanical properties across group means.

Possible mechanisms by which water contributes to fracture resistance

Pore water derived from NMR or MRI techniques undoubtedly provides a surrogate measure of intracortical porosity, as depicted through the significant correlations in human cortical bone between pore water measured from a clinical 3T scanner and the porosity assessed with micro-computed tomography (μCT) (R² = 0.77 in [89], R² = 0.83 in [108], R² = 0.31 in [98]) and between porosity derived from NMR analysis of the long T₂ (or T₂*) component and porosity assessed by histomorphometry (R² = 0.72 in [77], R² = 0.64 in [80]). As such, an increase in pore water should translate in a loss of bone stiffness and strength as porosity weakens the tissue [109]. In addition, porosity is a major determinant of fracture toughness, as an increase porosity produces more stress concentrators in the tissue and a reduction of the net loading area [110]. This was also observed in a dataset of 62 human cortical specimens where pore water (derived from ¹H NMR) significantly correlated with crack initiation toughness (ρ=−0.53) [96].

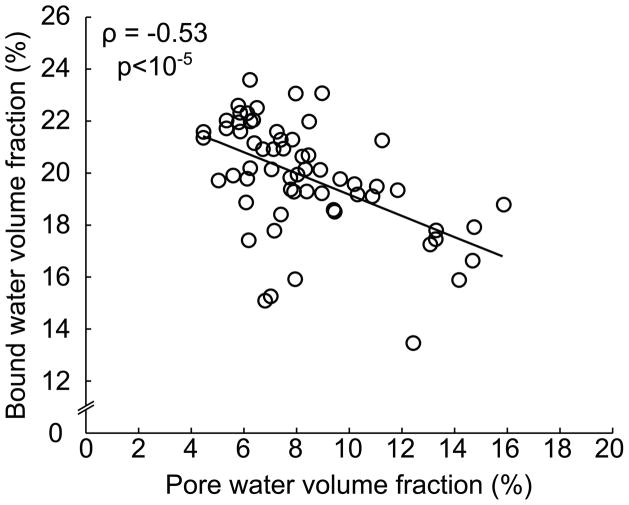
The role of bound water in the mechanical behavior of bone is less clear. In so far as bound water requires matrix, then it is inversely proportional to pore water (more porosity translates to less matrix). While this is true, we have yet to observe a correlation coefficient (ρ) between the two compartments near 1 with considerable scatter though slope is significantly different than 0 (Fig. 6). Thus, bound water is not simply another surrogate of porosity. As previously discussed, mineralization displaces water from osteoid. In rodents, the degree of mineralization within cortical bone tissue of the diaphysis increases throughout life, and we observe that tissue mineral density (TMD), as determined by μCT, increases, while bound water fraction per bone matrix volume decreases (Fig. 7). This implies that bound water is a surrogate of mineralization or ash fraction of bone, at least for rodents whose bones do not undergo intracortical remodeling. However, bound water in human cortical bone decreases with age, despite bone turnover or osteonal remodeling throughout life with only modest changes in TMD or ash fraction, if at all, with age after skeletal maturation [111]. Also, bound water [95] and bone density [112] are both directly correlated with material strength of human cortical bone.

Fig. 6.

Bound water and pore water, each normalized to apparent bone volume, are not simply surrogates of one another (n=62, human femoral samples) as pore water weakly correlates with bound water with considerably scatter between the two water compartments. There are other factors besides matrix density that influence the amount of bound water in bone. Correlation coefficient (ρ) was determined using Spearman’s rank correlation (original data).

Fig. 7.

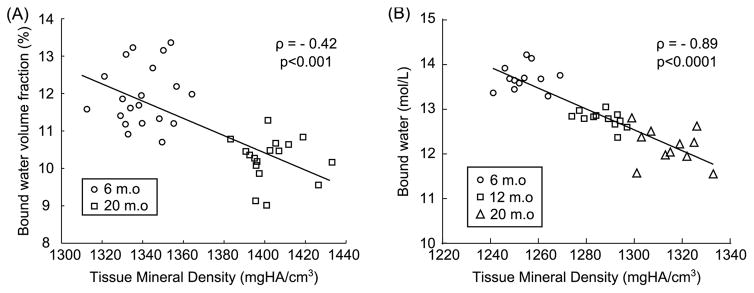
In rodents, bound water decreases as mineralization increases throughout life. Illustration in (A) mice and (B) rats. Bound water can be expressed as the volume fraction of the bone tissue volume (%) or as the concentration of protons (mol/L) in the bone tissue volume in which the latter was determined by μCT (voxel size of 6 μm). Correlation coefficient (ρ) was determined using Spearman’s rank correlation (original data).

Bound water likely has multiple determinants, all interrelated, and this could explain why bound water correlates with multiple material properties (strength, toughness, and resistance to crack propagation). Other than primary or secondary mineralization, there is little known about what attributes of bone influence bound water. We can speculate nonetheless that collagen crosslinking, non-collagenous proteins (NCPs), and proteoglycans influence bound water as they are present in the extracellular matrix of bone and can affect hydrogen bonding sites. There are two general types of collagen crosslinks: enzymatic and non-enzymatic. Enzymatic crosslinking participates in the fibrillation of collagen. There is the possibility that if the function of lysyl oxidase, the main crosslinking enzyme, is disrupted (e.g., copper deficiency or osteolathyrism), the packing of collagen fibrils is abnormal. Whether this leads to a decrease in bound water (or increase for that matter) is not known, but disrupting lysyl oxidase with a toxin does decrease toughness and fracture toughness of mouse bone without affecting TMD [113]. Through reactions with sugar, non-enzymatic collagen crosslinks accumulate over time and can occur at multiple sites (e.g., lysine and arginine) along the collagen molecule. They stiffen the collagen [114, 115] much like dehydration does. Again, there is no evidence that the accumulation of non-enzymatic collagen crosslinks (e.g., pentosidine or glucosepane) in mineralized tissues affects the way water binds to the matrix, but at least in soft tissues, collagen with fewer crosslinks seems to participate in more hydrogen-hydrogen bonding with water [116]. Inducing crosslinks with glutaraldehyde induces tighter packing of the collagen fibrils, thereby causing a dehydration effect [117]. Bone has NCPs such as osteopontin, osteocalclin, and osteonectin and proteoglycans such as biglycan and decorin. While each of these factors has multiple biological functions in bone, they are highly polar and thus could attract water into the bone matrix.

Future Directions

Given the importance of water compartments to the mechanical behavior of bone, finding ways to manipulate water distribution to promote fracture resistance could lead to new therapies that lower fracture risk. This requires experimental studies establishing what in the bone matrix causes greater or less bound water per bone tissue volume. The aforementioned findings from the study involving ex vivo exposure of bone to raloxifene [106] point to hydroxyl groups, which facilitate hydrogen-hydrogen bonding, as being one possible path to explore. There is also the availability of genetic models to identify signaling pathways that favor higher bound water and lower pore water and rodent models of disease to identify changes in bone matrix that decrease bound water. With respect to fully realizing the use of water compartments to improve clinical assessment of fracture risk, technical advances include: optimizing data analysis to improve precision and accuracy, speeding up scan time, and increasing the signal-to-noise ratio. Ultimately, the ability of MRI-derived measurements of bound water and pore water to predict fracture needs to be established first in cross-sectional (fracture vs. non-fracture cases) and then in longitudinal studies. Such evidence would provide the impetus to use MRI for assessing the effect of drugs and diseases such as diabetes on bound water and pore water in bone.

In summary, water is an integral constituent that influences the mechanical properties of bone. The fundamental role of water lies in its existence within different compartments at different hierarchical levels of organization. Structural or tightly bound water (i.e., water molecules located inside the tropocollagen triple helix) stabilize the collagen conformation and assembly. Water molecules bound to the collagen surface confer bone its ductility (capacity to endure large plastic strain without catastrophic failure). Free water residing in pores likely participates in the hydraulic stiffening of bone. Each compartment of water contributes to different properties of bone mechanical behavior, which justifies the development of techniques able to separate bound from pore water to better predict fracture risk and prevent the decline of bone health.