Efficient Saccade Planning Requires Time and Clear Choices

Abstract

We use eye movements constantly to gather information. Saccades are efficient when they maximize the information required for the task, however there is controversy regarding the efficiency of eye movement planning. For example, saccades are efficient when searching for a single target (Nature, 434 (2005) 387–91), but are inefficient when searching for an unknown number of targets in noise, particularly under time pressure (Vision Research 74 (2012), 61–71). In this study, we used a multiple-target search paradigm and explored whether altering the noise level or increasing saccadic latency improved efficiency. Experiments used stimuli with two levels of discriminability such that saccades to the less discriminable stimuli provided more information. When these two noise levels corresponded to low and moderate visibility, most observers did not preferentially select informative locations, but looked at uncertain and probable target locations equally often. We then examined whether eye movements could be made more efficient by increasing the discriminability of the two stimulus levels and by delaying the first saccade so that there was more time for decision processes to influence the saccade choices. Some observers did indeed increase the proportion of their saccades to informative locations under these conditions. Others, however, made as many saccades as they could during the limited time and were unselective about the saccade goal. A clear trend that emerges across all experiments is that conditions with a greater proportion of efficient saccades are associated with a longer latency to initiate saccades, suggesting that the choice of informative locations requires deliberate planning.

Introduction

Our eyes are moving constantly at the rate of approximately three times per second to gather information from our dynamic surroundings. We know from Yarbus (1967) that we move our eyes to different parts of the image depending on the task. Recently there has been an interest in determining if these eye movements gather information efficiently for the task at hand, i.e., whether each saccade maximizes task-relevant information. Studies to date provide mixed results, depending on the task. Some studies indicate that saccadic targeting is efficient. For instance, eye movements executed during search for a single target appear to be efficient (Najemnik & Geisler, 2005, 2008) and appear to incorporate knowledge about where the target is most likely to occur (Chukoskie, Snider, Mozer, Krauzlis & Sejnowski, 2013, but see Araujo, Pavel & Kowler, 2001). On the other hand, other studies show that saccades are not always directed to maximize expected gain in a reward/penalty paradigm (Strizke, Trommershauser & Gegenfertner, 2009; Ackermann & Landy, 2013; Schutz, Trommershauser & Gegenfurtner, 2012), nor do they fully incorporate the decrease in visibility with target eccentricity (Zhang, Morvan & Maloney, 2010). Furthermore, saccades are grossly inefficient in tasks requiring a sequence of eye movements to gather information about multiple targets (Verghese, 2012). Here we investigate conditions that may lead to improvements in the efficiency of active visual search for an unknown number of targets.

The current study is based on the Verghese (2012) study that used 6 potential target locations and a limited time for active visual search. Here, the observer’s task is to find an unknown number of targets embedded in noise. As trial duration is limited and there is not sufficient time to examine all potential target locations, an efficient strategy within a Bayesian information-maximization framework is to saccade to a location that maximizes the information gained across all target locations (Najemnik & Geisler, 2005, Renninger et al, 2007). For instance, a saccade directed midway between 2 uncertain locations increases the information at both locations, compared to a saccade that goes directly toward one of the target locations. However, our studies (Verghese, 2012) show that human saccades are not directed at locations that maximize global information, but are directed at potential target locations. But even this local strategy is not efficient; observers make saccades to locations where the posterior probability is high (probable locations), rather than to informative locations where the uncertainty (entropy) is high. Thus saccade strategy does not appear to be efficient at either a global or a local level. But why are observers not able to implement a local strategy that selects informative locations over probable target locations, where there is little information to be gained?

Does this occur because the noise level was so high, that it is hard to distinguish the more probable target locations from uncertain locations? Here, we investigate whether making the probable target locations clearly visible minimizes the need to examine them and therefore helps the observer direct saccades to more uncertain locations. In this study, the targets and distractors were horizontal and vertical Gabor patches respectively, embedded in noise. Because of the large orientation difference, the stimuli were clearly discriminable at high signal-to-noise ratios (SNR). We used two levels of SNR in our experiment: low, and moderate or high. The low level was set so that observers were uncertain about the orientation of the patch and needed to make a saccade to the patch to determine the orientation. The “moderate” level was set so that observers were reasonably confident about target identity (>80%) without having to make a saccade. The first experiment indicated that most observers did not look preferentially at uncertain locations.

We wondered whether increasing the discriminability between the two SNR levels (as in Hooge & Erkelens, 1999) would make it easier to ignore the more discriminable stimuli and select the more uncertain stimuli. Accordingly, in subsequent experiments we set the “high” SNR to near infinity by removing all the noise. This manipulation increased the number of saccades to the uncertain targets. However some observers still tended to make short-latency saccades to the clearly visible horizontal targets. To determine whether delaying saccades would give observers the time necessary to determine the most uncertain locations we asked observers to hold fixation briefly after display onset. Delaying saccades helped some observers make more efficient saccades. Others, however, still attempted to make saccades to as many locations as possible without selecting uncertain locations.

Methods

Participants

Five (4 female, 1 male) individuals, ranging in age from 27 to 50 voluntarily took part in our experiments. Two observers were authors (O1 and O2); the other three were naive as to the purpose of the experiment. Observer O3 had participated previously in psychophysical experiments, observers (O4 and O5) were practiced at psychophysical and eye movement experiments. All observers had normal vision or vision corrected to normal, and provided informed consent, in writing, to participate in the experiments. The Smith-Kettlewell Institutional Review Board approved the experimental protocol. All experiments were carried out in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

Stimuli

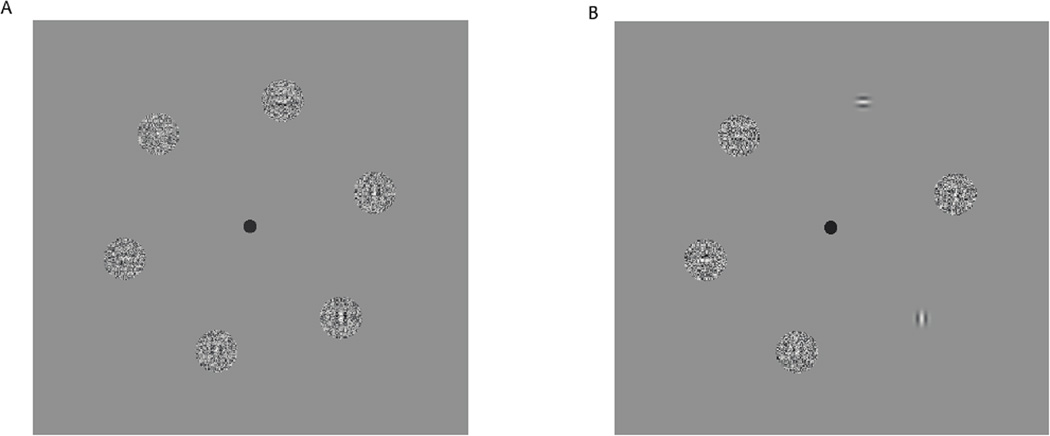
The basic design of the experiment was similar to Verghese (2012). Stimuli were presented on 21” ViewSonic G225f monitor that was gamma-corrected. Observers viewed the display binocularly at a distance of 1m, such that a pixel subtended 0.02°. In this study the stimuli were made up of six Gabor patches equally spaced on an invisible circle centered at fixation with a radius of 3 deg (see Figure 1). To avoid placement of targets along cardinal axes, stimuli were placed at 60° angular intervals starting at 15° counter clockwise from right horizontal (i.e., at 15, 75, 135, 195, 255 and 315 degrees around the circle). Targets were horizontal Gabors, and distractors were vertical Gabor patches. The spatial frequency of the sine wave in the Gabor was 5 c/deg and the standard deviation of the Gabor envelope was set to spatial period/√2, or 0.14 °. This resulted in about 1.5 cycles of the grating being visible. Random noise of contrast 0.38 was added to the patches at each location. Each patch was 1° in diameter. The Gabors were displayed in cosine (even) phase and the contrast of the sinusoid was randomly set to one of two values— 0.19 and 0.38 in Experiment 1, corresponding to low and moderate SNR values of 0.5 and 1 respectively. In Experiments 2 and 3 the noise was removed from the higher-contrast patch, taking the signal-to-noise ratio towards infinity. Each of the six locations had equal probability of being assigned a lower or higher SNR signal, regardless of whether it was a target or distractor.

Figure 1.

Stimulus configuration. A. Stimuli used in Experiment 1. Horizontal Gabor targets and vertical Gabor distractors were embedded in noise. The noise contrast was fixed but the Gabor contrast was set to 0.19 and 0.38 resulting in stimuli of low and moderate visibility stimuli. B. In Experiments 2 & 3, the moderate visibility stimuli were replaced by high-contrast Gabor patches with no added noise.

Design

Each location had an independent probability of having a horizontal target. This probability was held fixed within a block of 100 trials and was set to one of three values: 0.17, 0.5, or 0.83. Participants were informed about the value of the prior before each block. Viewing was binocular. Monocular (left) eye movements were monitored with an Eyelink 1000. A block of experiments began with an eye-tracker calibration using a 5-point grid. At the start of each trial, the observer was required to fixate a central fixation dot and press the space bar to initiate the trial. The trial was initiated only if eye position was within 1° of the fixation dot. Observers were free to move their eyes once the trial started. Display duration was limited to 900 ms. The central fixation dot remained visible throughout the trial except in Experiment 3, where it disappeared 200 ms into the trial. At the end of the trial observers were presented with a report screen with gray discs marking the location of the six stimuli and had to indicate all target locations by clicking on them. A trial was scored correct only if all targets and no distractors were selected. The observer had the option to click a “Forgot” button if he/she could not remember the location of the targets. These trials were rare (<5%) and were not analyzed further. Auditory feedback was provided.

Before the main search experiments, we determined the ability of observers to discriminate horizontal from vertical Gabor patches. Observers were asked to identify the orientation (horizontal/vertical) of single Gabor patch presented at one of 5 SNR values. The patch was presented for 100 ms followed by a mask, in a known location at an eccentricity of 0, 1, 2 or 3 degrees to the right of fixation, along the horizontal meridian. This measurement also provided a visibility map for the target as a function of eccentricity, We chose SNR values of 0.5 and 1 for Experiment 1 because these values satisfied our criterion for a pair of SNR values for which visibility at an eccentricity of 3° was poor at the lower SNR, and was good at the higher SNR. Figure S2 in Supplementary Materials shows the visibility plots for these two SNR values: visibility declines considerably at 3° for an SNR of 0.5, but is high and declines only slightly with eccentricity for an SNR of 1. Because we measured visibility only along the horizontal meridian, it could be argued that our measurements don’t take in to account horizontal-vertical asymmetries or enhanced visibility in the lower visual field (Carrasco, Talgar, Cameron, 2001). However, Carrasco et al (2001) showed that these anisotropies are not significant at the small eccentricity (3°) and low spatial frequency (5 c/degree) used in our study.

Experiment 1 and 2 consisted of two parts. The first part determined the visibility of the peripheral patches in the absence of eye movements, while the observer fixated the central spot for 900ms. This no-saccade condition was repeated in separate blocks for each of the three target priors. These data provided a realistic estimate of the visibility of these patches in the context of the actual experiment using multiple patches, as opposed to visibility measured with a single patch. In addition, measuring these values for different priors provided an indication of how the probability of correctly discriminating the different stimulus types is affected by the prior. The second part of the experiment allowed active search with eye movements, and used the same sequence of trials as the no-saccade condition, for a particular value of target prior. Thus the two parts of the experiment used identical stimuli, without and with saccades, allowing us to determine how saccades improved the visibility of stimuli. As mentioned before, Experiments 2 and 3 were similar to Experiment 1, except that noise was removed from the higher contrast patch, and that a 200ms delay was introduced in Experiment 3 before the saccade-go signal. Observers were asked to wait until fixation offset to initiate saccades. In all experiments, the value of the target prior was kept fixed for a block of 100 trials.

A given patch was considered fixated if the saccade landed within 1.5° of the center of the patch, i.e., the saccade was closer to that patch than to any other patch or to central fixation. Saccades were defined as eye movements with a velocity of at least 30 °/s and fixations were required to have a dwell time of at least 50 ms.

Model

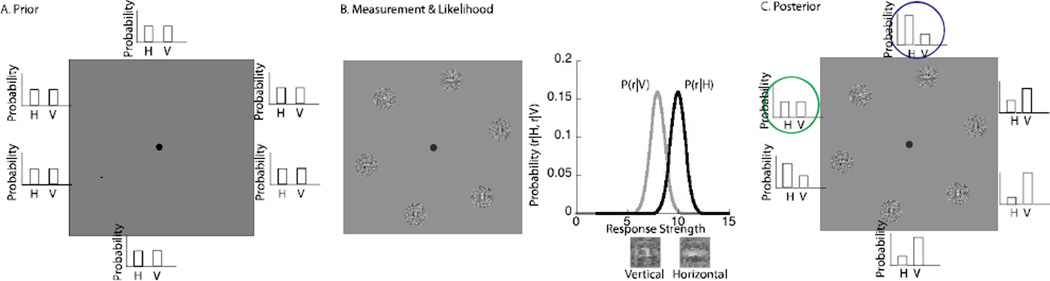
We analyzed performance in our experiments within a Bayesian information theoretic framework as in Verghese (2012), but we restricted our analysis to two sub-ideal models—a local entropy model and a maximum a posteriori (MAP) model. To summarize briefly, for every trial, we computed the likelihood of a target at each location, and used Bayes rule to combine it with the prior probability of a target for that block, to calculate the posterior probability of the target at that location. We then determined the accuracy of the trial when saccades targeted (i) locations with the highest entropy (largest uncertainty as in Legge et al, 1997, Lee & Yu, 2000; Renninger et al, 2007), or (ii) locations with the highest posterior probability of signal (Beutter et al 2003, Najemnik & Geisler, 2005, Verghese 2012).

Specifically at each location i, we defined the posterior probability of the horizontal target P(H|r_i), and the vertical distractor P(H|r_i), in the following manner:

$$p_i(H|r_i)=\frac{p(H)p_i(r_i|H)}{p(H)p_i(r_i|H)+p(V)p_i(r_i|V)}$$

$$p_i(V|r_i)=\frac{p(V)p_i(r_i|V)}{p(H)p_i(r_i|H)+p(V)p_i(r_i|V)}$$ (1)

The prior probability of the target P(H) and distractor P(V), sum to 1; i.e. P(H) + P(V) =1. As in Verghese, (2012), we assumed that each location generated a response r_i to a filter matched to the target properties (orientation, spatial frequency and position centered on the target location)¹. The likelihoods, P(r_i|H), P(r_i|V) were computed by comparing the measured response r_i to the distribution of target and distractor, generated over 10,000 samples of noise at that particular SNR (see Figure 2). These template response distributions were Gaussian, with a standard deviation of 1. The mean of the target distribution depended on SNR and was 10.3 and 15.2 at SNR values of 0.5 and 1 respectively. The mean of the distractor distribution was 8.2 regardless of SNR. The distractor has a non-zero mean because the stimulus defined as gamma-corrected luminance values and the template was cosine phase and hence contained a DC term.

Figure 2.

Model stages: A. Before the trial begins, the probability of a target at each location is equal to the prior probability, set to prior=0.5 in this case. The two-bar histograms at stimulus locations thus show equal probability for target and distractor. B. The measurement stage computes the response of a filter matched to the horizontal target at each location and estimates the likelihood of the target by comparing the response to the corresponding distributions to the target and distractor at the corresponding SNR. C. The posterior is the product of prior and the likelihood at each location. The locations marked in blue and green indicate the maximum a posteriori probability (MAP) and the highest entropy location, respectively.

Consistent with (Cover & Thomas, 1991), the entropy at a location i was defined:

$${\mathit{\text{entropy}}}_i=-(p_i(H|r_i)\text{ln}(p_i(H|r_i))+p_i(V|r_i)\text{ln}(p_i(V|r_i))$$ (2)

In this study, we compare the observer’s performance to model strategies that direct saccades to stimulus locations. This choice is a “local” model motivated by the fact that observed saccade distributions in our previous work and in this study are typically clustered around stimulus locations rather than a global model that considers all potential fixation locations in the display (as in Najemnik & Geisler, 2005; Renninger et al, 2007). Figure S1 plots the saccade distribution of 5 observers and shows that observers’ saccades are directed towards target locations.

Before the trial was initiated, the probability of a target at each location was set to the value of the prior. After the display came on, the likelihood of a target at each location was calculated by comparing the response of a matched horizontal filter to the distribution of responses to target and distractor. The posterior was updated by multiplying the likelihood by the prior. The model then chose saccade locations according to the Maximum a posteriori (MAP), local entropy, or random strategy. When the model followed the MAP strategy, it selected locations in descending order based on the posterior probability, starting with the location with the highest posterior probability, and fixated these locations in turn. Thus, this model selected locations on the basis of how probable the target was at that location. When the model implemented an entropy strategy, it chose locations in the order of decreasing entropy. Entropy is maximum when uncertainty is maximum, i.e., when the posterior probability of target and distractor at a location are equal. Conversely, entropy is zero when the posterior probability of either target or distractor is 1. We also considered the predictions of a model that selected locations at random, with the constraint that each location was selected only once. For the comparison between models in Figure 3, we ignored the observer’s internal noise, but for comparison between model and observer in Figure 5, we incorporated internal noise estimated from the measured discriminability between target and distractor into the response distributions.

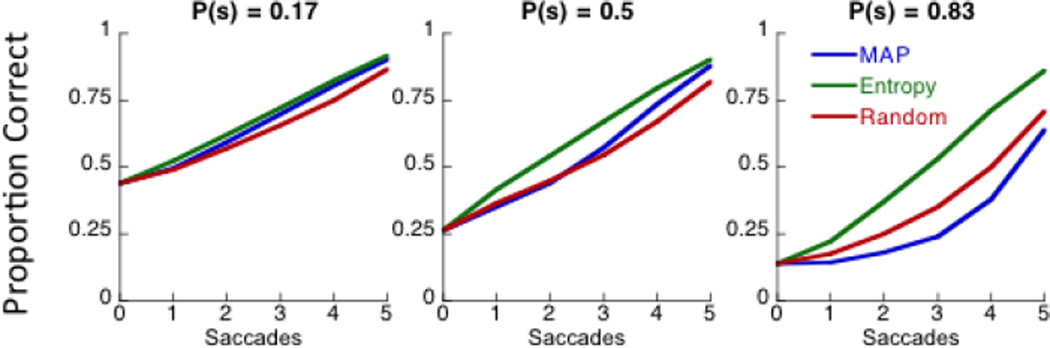
Figure 3.

Model performance (proportion of trials correct) as a function of the number of saccades for different prior probabilities of the target. The model predictions are based on the assumption that locations with saccades are discriminated perfectly and locations without saccades are discriminated based on the response to a filter selective to the target.

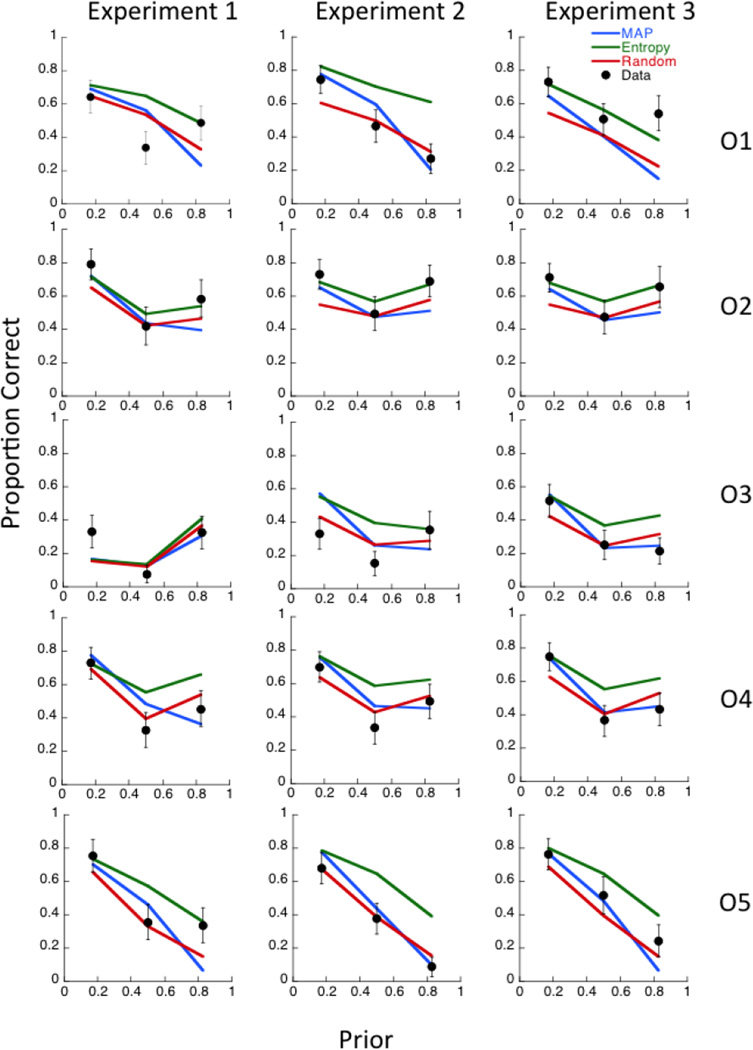
Figure 5.

Proportion correct versus target prior. Each column plots data for a particular Experiment, with Experiment 1 on the left, Experiment 2 in the middle and Experiment 3 on the right. The rows plot data for individual observers. The black symbols represent accuracy in a block of 100 trials with error bars showing the binomial 95% confidence intervals. The green, blue and red lines represent the predictions of the entropy, MAP and Random models.

To generate model predictions to compare the performance of the three models, we made a few simplifying assumptions. Ideally the posterior should be updated after each saccade. But previous work suggested that observers did not incorporate knowledge from one saccade before planning the next saccade (Renninger et al, 2007, Figure 8B) particularly when the intersaccadic interval is short as in Caspi, Beutter, Eckstein, (2004). The average intersaccadic interval in our study was much shorter than the typical 200 to 300 ms between saccades—the interval between the first and second saccade was 177 ± 8 ms and that between second and third saccades was 156 ± 2 ms. We therefore assumed that locations for potential saccades are selected based on initial posteriors estimated from central fixation and that all saccades are planned before the execution of the first saccade. We also made a further assumption regarding unsaccaded locations. Because each stimulus location was 3° away from its nearest neighbor and from the central fixation dot, and because observers typically made saccades towards these locations rather than between them, we assumed that a saccade to a particular location only improved the visibility at that location and not at any other location. We assumed that the model discriminated the stimuli perfectly at saccaded locations (This aspect of the model applies only to the model predictions in Figure 3 and not to version of the model based on individual observers’ discriminability in Figure 5). At the end of the trial, the model selected all locations where the posterior probability of the target was greater than 0.5. Proportion correct for a trial was computed by comparing model choices to the true target locations in that trial. A trial was deemed correct if the model correctly selected all target locations and discarded all distractor locations.

Figure 8.

Comparison of accuracy and number of saccades. A. Accuracy (proportion of trials in which all targets were detected) is plotted versus the prior probability of the target. Data are averaged across the three experiments. B. The average number of saccades is plotted as a function of target prior. The error bars plot the standard error of the mean across experiments.

Figure 3 compares model predictions of the three strategies. Proportion correct at identifying all the targets in a trial are plotted as a function of the number of saccades, for different values of prior probability. For each strategy, the model chose saccade locations based on the Bayesian framework outlined above. The left, middle, and right panels show performance for prior target probability set to 0.17, 0.5 or 0.83, respectively. In each panel the green, red and blue curves show the predicted accuracy of the Entropy, MAP and Random strategies. Clearly the probability of correctly identifying all the targets in a trial depends both on the number of saccades, and on the prior probability of the target. In general, proportion correct increases with the number of saccades. If we focus on performance with 2–3 saccades (the average number of saccades in a trial across our observers), the prior probability of the target has a profound effect on performance for each of the strategies. For all values of target prior, the entropy strategy produces the highest proportion correct. When the prior is low (0.17) and targets are relatively rare, the MAP strategy (blue) does almost as well as the Entropy strategy (green). However, as the prior increases the MAP strategy becomes increasingly inefficient. When the prior probability of the target is 0.83, the MAP model performs worse than the random model (red). Thus the Entropy strategy is clearly more efficient than the MAP strategy when targets are frequent. Do our observers incorporate this more efficient saccade strategy?

To generate trial-by-trial model predictions for each observer, the model made the same number of saccades as the observer did on a trial, but selected locations based the MAP, Entropy, or Random strategy. To compare model and human performance, we incorporated each observer’s visibility map (internal noise) into the model prediction. (See S2 in Supplementary Materials. As we do not have a visibility map for O5, we used the average visibility map from the other 4 observers to predict her data.) To incorporate the observer’s internal noise, we increased the standard deviation of the templatebased target and distractor distributions to match the observer’s d’ at 3° eccentricity, for that SNR. We drew a sample from the modified target distribution at target locations, and from the modified distractor distribution at distractor locations. We then calculated the likelihood of target and distractor based on this sample. After multiplying the likelihood by the prior, we used the posterior probabilities at each location to determine which locations to fixate. At the start of the trial, locations were chosen in the order of decreasing entropy in the uncertainty reduction model and in the order of decreasing posterior probability of target for the MAP model. No updates occurred during the trial. At the end of the trial, the actual discriminability at each location was determined by individual observer discriminability at saccaded and non-saccaded locations. The d’ at saccaded locations was set to the d’ at the eccentricity of the nearest fixation; at non-saccaded locations we substituted the average discriminability measured in the no-saccade version of the experiment, at the corresponding value of SNR and prior. We did not take the particular location of the target into account, because we do not find strong evidence for anisotropy: the discriminability difference between the upper and lower visual field was marginally significant (p=0.058) at an SNR of 0.5, but not significant for SNR of 1. There was no significant difference between locations near the horizontal and vertical meridians for either SNR. We believe the use of each observer’s discriminability estimated from identical stimuli in the no-saccade condition is a significant improvement over the hypothetical distributions used to generate model predictions in Verghese (2012).

Experiment 1: Multiple-target search with noisy targets

The first part of the experiment measured observers’ performance in the absence of saccades. Observers fixated the central fixation spot for the duration of the trial (900 ms) and then selected locations that contained the target. Fixation was monitored and trials where eye position deviated by more than 1° were discarded. The no-saccade condition was repeated for all three values of stimulus prior, in separate blocks. These measurements provided baseline visibility for all the 4 stimulus types (low/moderate SNR for target/distractor) in the context of the experiment with multiple stimuli, for each observer, and were used in the model predictions to determine presence/absence of the target at un-saccaded locations.

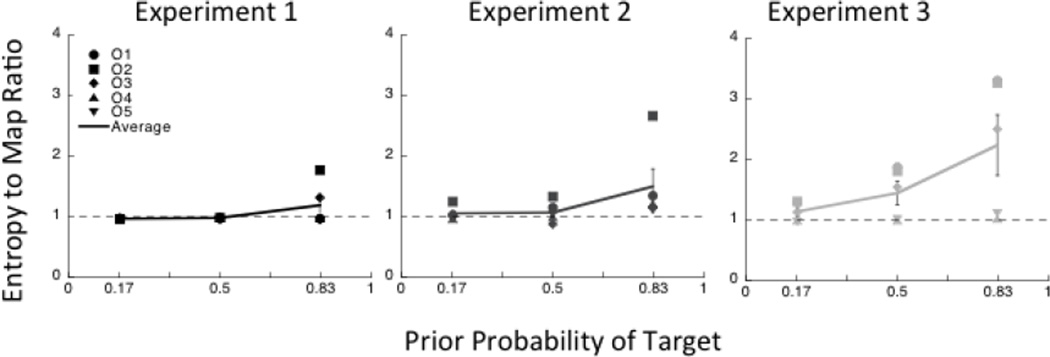
The second part of the experiment measured performance following active visual search for 900 ms on stimuli identical to those presented in the no-saccade condition, presented in the same sequence. We first analyzed these data is to determine whether saccades select probable (MAP) or uncertain (entropy) locations. We compared how many observed saccades in a block of trials were compatible with model predictions that included internal noise. For example, if the observer made 3 saccades in a trial, we compared the fixated locations to the 3 most uncertain (highest entropy) locations and to the 3 most probable (highest posterior probability) locations selected by the models. The number of entropy (MAP) saccades the observer made in a trial corresponded to how many of the observer’s fixated locations matched the respective model choices. The leftmost panel of Figure 4 shows saccade strategy in Experiment 1 as a ratio of saccades that selected uncertain versus probable locations as a function of target prior. If observers were efficient they would direct their saccades to more uncertain locations when the target was more frequent. Considerable variability among observers is evident. One experienced observer (and author) O2 shows a greater ratio of Entropy to MAP saccades when the target prior is 0.83. Others have the same proportion of Entropy to MAP saccades for all target priors, with a ratio close to 1 (dashed line). On average (thick line) the ratio was not significantly different than 1 (F(2,8) = 1.96, p = 0.203), suggesting that observers use these two strategies equally often. Importantly in this Experiment, the ratio is not less than 1 as it was in Verghese (2012) where observers made saccades preferentially to probable target locations when the prior probability of target was higher. One possible reason for this difference is that half the stimuli (on average) had higher SNR, making them more visible. Another possible reason is that it was easier to identify stimulus locations in this study because noise was not uniformly distributed within the central display region, but confined to distinct stimulus patches.

Figure 4.

The ratio of Entropy to MAP saccades is plotted as a function of prior probability for Experiments 1, 2 and 3. The dashed line represents a ratio of 1. Different symbols show data for different observers and the continuous line shows the average with error bars representing the standard error across the 5 observers.

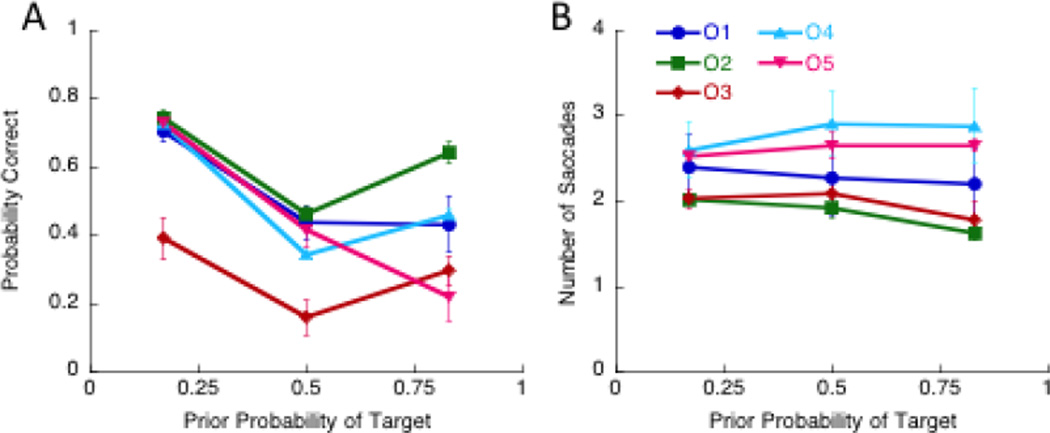
We also analyzed individual accuracy on the task and compared it to a model that makes the same number of saccades on a trial and uses discriminability measured in the nosaccade condition (for that observer) to judge the presence of a target at non-saccaded locations. The data for Experiment 1 are shown in the leftmost column of Figure 5 where each of the five rows shows data for one observer. The black symbols show observed performance (error bars show 95% binomial confidence intervals), and the green, blue, and red lines show the model predictions for the Entropy, MAP, and Random strategies, respectively. We first compare the data at different prior levels to model predictions and then compare overall performance across all priors to the model. The Entropy and MAP model predictions are similar for low priors, but diverge as prior increases, with the entropy strategy predicting significantly better performance at a prior of 0.83. The Random strategy is worse than these two strategies at low values of prior, but is better than the MAP strategy at a prior of 0.83.

If we look at the data across all observers, we see that trial accuracy is best when targets are rare at a prior of 0.17, declines considerably when targets and distractors are equally probable at a prior of 0.5, and improves slightly when targets are frequent at a prior of 0.83. If we look at the data of individual observers and compare these to model predictions based on each person’s individual visibility, it is clear that observers differ considerably. Observers 1 and 2 (authors and most practiced observers) have performance consistent with the entropy strategy (green) when targets are rare and frequent (priors of 0.17 and 0.83). When targets and distractors are equally likely at a location (prior=0.5), their performance falls short of the entropy prediction. Across all values of prior, only O2’s data are well fit by the entropy model. Table 1 shows χ² values for the fit of each model to observer data, with models that are not rejected shown in bold. Models with a χ²>5.99, the critical value for p=0.95 and 2 degrees of freedom, are rejected.

Table 1.

χ² values for the fits of each of the three models to each observer’s data in Experiment 1. Models that are not rejected (p≥0.95) are indicated in bold. For observer O4, the AIC strongly favors the Random model over the MAP.

Observer/Model	O1	O2	O3	O4	O5
MAP	3.69	9.44	17.8	4.26	111
Entropy	15.8	2.15	22.4	17.3	8.51
Random	14.8	6.07	22.7	2.77	25.0

In general, observers 3, 4, and 5 perform worse than the entropy model. Their performance is close to the entropy/MAP prediction when targets are rare (prior=0.17)², and lie between the MAP and entropy predictions when targets are most frequent (prior=0.83), consistent with their saccades selecting probable and uncertain locations equally often. For these three observers, performance is closest to the prediction of a random model) when targets and distractors are equally likely at each location (prior=0.5). One possibility is that this condition is susceptible to memory demands because observers have to remember which three of the six patches (on average) are targets. This is perhaps more demanding than remembering the few locations that have targets when the prior is low, or the few locations that don’t have targets when the prior is high. Table 1 shows that in the case of O4, both the Random and MAP models are not rejected. We used the Akaike Information Criterion (Burnham & Anderson, 2002) to calculate the relative likelihood of each model and determine which is a better fit to the data (see Supplementary materials). In this case, the AIC strongly favors the Random model.

It is possible that observers could not readily determine which patches had lower SNR, and were therefore not able to direct saccades to these more uncertain patches. To examine this possibility, we conducted a control experiment to measure the discriminability of the patches with lower SNR from patches with higher SNR. Two SNR values were chosen for each trial, with one of them always set to the lower SNR value used in Experiment 1. The display duration was brief (100 ms) with the two patches presented to the left and right of fixation at an eccentricity of 3°. Observers were asked to ignore the orientation of the Gabors, which were equally likely to be horizontal or vertical, and simply judge whether the patch on the left or the right contained the low-SNR target. Fixation was monitored and trials where eye position deviated by more than 1° were discarded. Four of our 5 observers participated in this control experiment.

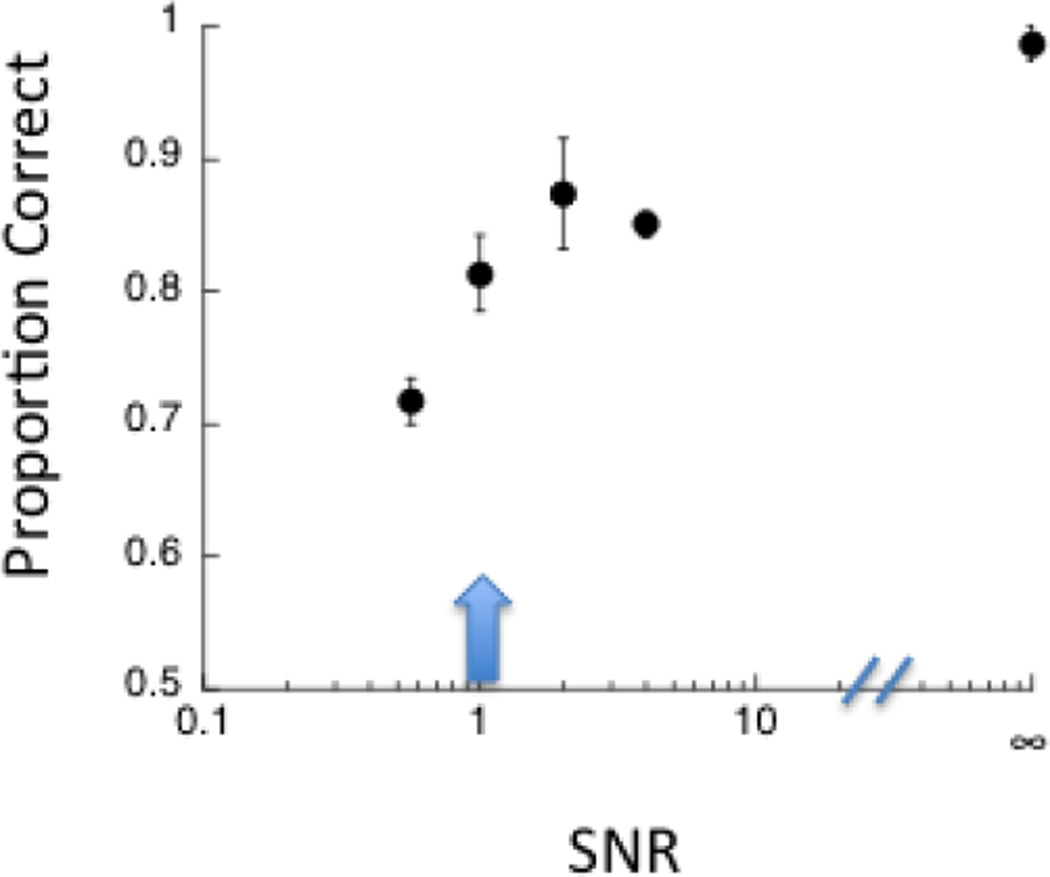
Figure 6 plots the average discriminability across observers as a function of the higher SNR value. It is clear that the two SNR values used in Experiment 1 were discriminated only about 82% of the time. We wondered whether saccades would consistently select the more uncertain (lower SNR) target if we made the pair of SNR values in the experiment perfectly discriminable, by removing all the noise from the higher SNR stimuli (rightmost point in the Figure 6).

Figure 6.

Proportion correct versus the signal-to noise ratio of the higher SNR value in each trial. The arrow represents the higher SNR value used in Experiment 1.

Experiment 2: Multiple-target search with clear and noisy stimuli

The goal of this experiment was to determine whether presenting observers with two classes of clearly discriminable stimuli (with and without noise) would help direct saccades to the noisy, uncertain stimuli. This experiment was identical to Experiment 1 except that the higher SNR patches had no added noise. As before, we first measured performance in a no-saccade version to obtain an estimate of visibility of the 4 stimulus types when they were at a distance of 3° from fixation and no saccade was made to them.

We then measured performance when eye movements were allowed to the same stimuli. The middle panel of Figure 4 shows saccade strategy as the ratio of saccades that selected entropy locations relative to MAP locations. The ratio is close to 1 when targets are rare, consistent with the similarity of the model predictions for a target prior of 0.17. When targets and distractors are equally likely (prior =0.5), most observers still make a similar number of entropy and MAP saccades, but when targets are frequent (prior = 0.83), most observers now show a slight preference for entropy locations. Thus, increasing the discriminability between clear and noisy targets did not significantly increase the proportion of saccades to uncertain locations.

If we examine the overall trial accuracy (probability of finding all the targets) in this Experiment, the panels in the middle column of Figure 5 show that overall accuracy is roughly similar to that in Experiment 1 even though the orientation of the Gabor is now clearly visible in half the stimuli. This result indicates that it is the discriminability of the lower SNR patches that is driving the overall accuracy; the average d’ across observers at the lower SNR was 1.28±0.40, and for the higher SNR was 2.73±0.58. The crucial question is whether making the noisy stimuli clearly discriminable from the clear stimuli causes performance to be closer to the entropy model. The answer depends on the observer. Table 2 shows that across all values of prior, the performance of O2 is consistent with the entropy prediction, that of O1 and O4 with the random model, and that of O5 with the MAP prediction.

Table 2.

χ² values for the fits of each of the three models to the data in Experiment 2. Models that cannot be rejected at the 0.95 level are indicated in bold. If more than one model satisfies this criterion, we calculate the AIC to determine which model is a better fit to the data (see Supplementary materials). For O1, the AIC positively favors the random model, and for O4, it strongly favors the random model. For O5, the AIC positively favors the MAP model.

Observer/Model	O1	O2	O3	O4	O5
MAP	4.97	7.38	22.15	5.58	2.19
Entropy	34.39	1.37	30.38	17.99	36.35
Random	4.01	8.51	11.85	3.96	2.99

In related studies (Verghese & Ghahghaei, 2012; Janssen & Verghese, 2015) we looked at choice of saccade goal vs. saccade latency and noted that longer latency to the first saccade was correlated with a greater proportion of saccades to uncertain locations. This outcome indicates that planning saccades to uncertain locations takes time, compared to making saccades to locations that look most like the target. We wondered whether delaying the first saccade would improve saccade efficiency in this study.

Experiment 3: Search with Delayed Saccades

This experiment examined the effect of delaying the first saccade on the choice of saccade goal. The experiment was identical to Experiment 2, except that the fixation spot was on only for the first 200 ms. Offset of the fixation spot was a saccade-go signal. Observers were allowed to move their eyes freely for the next 700 ms, resulting in a total display duration of 900 ms, as before. Although observers were asked to wait until the fixation spot disappeared before initiating saccades, we analyzed all trials even if the first saccade was made before the central fixation spot disappeared.

As the SNR levels were identical to Experiment 2, we did not conduct a no-saccade version of Experiment 3. As expected, introducing a fixation delay increased saccade latency for 4 out of 5 observers. O5 seems to have ignored the instructions to hold fixation for the first 200 ms. The latency of the first saccade, averaged over prior, was 505ms, 310ms, 375 ms, 388ms and 155ms for O1, O2, O3, O4 and O5, respectively. An analysis of fixation choice shows that some observers made a greater proportion of entropy saccades in Experiment 4 (Figure 2, rightmost panel). Observers 1, 2, and 3 consistently made entropy saccades at all target priors, and increased the proportion of entropy saccades with target prior. Observers 4 and 5 did not change their saccade strategy.

Individual observer accuracy in this experiment (Figure 5) shows that when targets were frequent (prior=0.83) and saccades to uncertain locations would have conferred the greatest advantage over saccades to probable locations, observers O1 and O2 did as well as the entropy model prediction, whereas observers O3, O4 performed close to the prediction of the MAP model, and observer 05’s performance was in between the entropy and random models. Table 3 shows that performance in the task was consistent with individual saccade strategy for all observers except O3. Her saccades selected entropy locations, but her accuracy was not consistent with the Entropy model. We investigated whether the discrepancy was because she could not remember the exact target locations when there were many targets. But this was not the case. Her accuracy is poor when targets are rare and when targets are frequent. Overall it appears that each observer uses a specific strategy to perform the task. We examine these strategies in the section Further Analyses, below.

Table 3.

χ² values for the fits of each of the three models to the data in Experiment 3. Models that cannot be rejected at the 0.95 level are indicated in bold. If more than one model satisfies this criterion, we calculate the AIC to determine which model is a better fit to the data (see Supplementary materials). For O2, the AIC strongly favors the Entropy model. The AIC positively favors the MAP model for O3 and compellingly favors it for O4.

Observer/Model	O1	O2	O3	O4	O5
MAP	109.22	5.28	1.82	1.95	46.00
Entropy	6.64	1.76	18.32	15.45	8.49
Random	53.23	6.01	5.22	4.67	10.85

Further Analyses

Relation between efficient saccades and prior

Figure 3 shows that when 2 or 3 saccades are made per trial, the predicted model accuracy based on an Entropy strategy is better than that based on a MAP strategy, particularly when the target is more frequent. How well did observers incorporate the prior probability of the target into their saccade strategy? Did our experimental manipulations across experiments 1, 2 and 3 affect observer’s strategy? A 3 (Experiments: 1, 2 and 3) × 3 (prior: 0.17, 0.5 and 0.83) repeated-measures ANOVA on the Entropy-to-MAP saccade ratio revealed an interaction between experiment and prior (F(2,8) = 5.34, p = 0.034). Breaking down this interaction across different experiments revealed that the effect of prior was significant only in Experiment 3 (F(2,8) = 5.73, p = 0.029): the ratio increased significantly with prior in Experiment 3. This significant effect is mostly driven by the results of O1, O2 and O3 who showed an increase in the ratio with prior (Figure 4). For these observers, when the choices were clear and the first saccade was delayed, the prior significantly affected their saccade strategy with a greater proportion of saccades made towards uncertain than probable locations at higher values of the prior.

Relation between efficient saccades and saccade latency

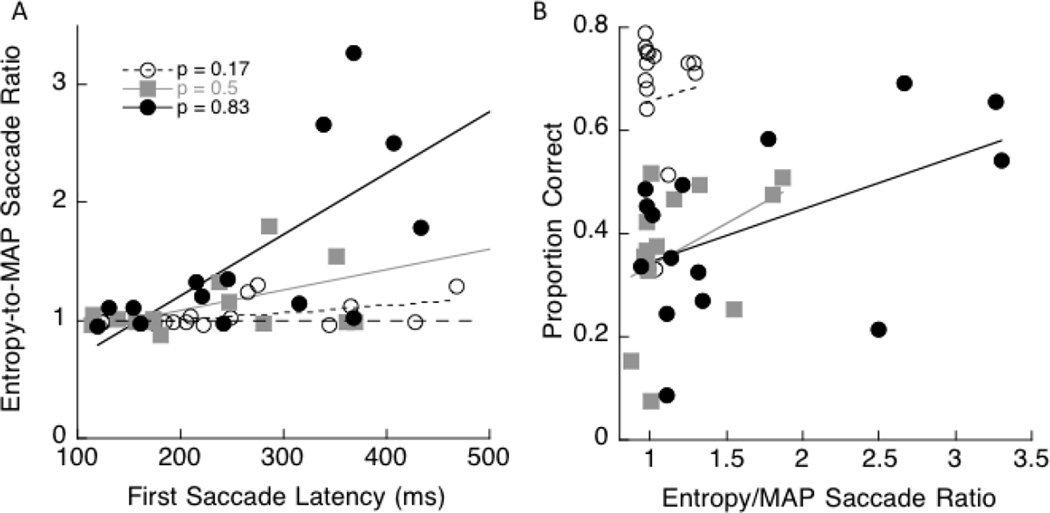
The most consistent result in our study, across observers and experimental conditions, is that a longer latency for the first saccade is associated with a greater proportion of saccades to uncertain locations. Figure 7A plots the ratio of saccades to uncertain locations relative to those to probable target locations versus the latency of the first saccade. For each prior, we show data for all 5 observers across 3 experiments (15 points in all). The slope of the regression line is positive and significantly different from zero for target priors of 0.5 and 0. 83 (p<.01 and p< 0.001, respectively). When targets are rare (prior=0.17), the slope is positive but only marginally significant (p=0.06). Thus, it is clear that when observers took longer to initiate saccades, those saccades preferentially selected uncertain locations. This is consistent with the choice of uncertain locations being a more deliberate strategy. The longer latencies associated with more efficient saccade strategies is consistent with the relative “neural computing time” required by the various saccade strategies. The MAP strategy perhaps requires less computation than the entropy strategy, which is a less complex computation than the full Bayesian model (Najemnik & Geisler, 2005, 2008, 2009).

Figure 7.

The relation of saccade strategy to latency and accuracy. A. The ratio of saccades to uncertain locations relative to probable target locations is plotted versus latency of the first saccade. The dashed line represents a ratio of 1. The open, gray and black symbols represent data for target priors of 0.17, 0.5 and 0.83 respectively, and the corresponding lines are the regression lines through the data. The lines have a slope significantly different from zero for priors of 0.5 and 0.83. Each symbol represents the data of one observer for the 3 experiments. B. Accuracy vs. entropy-to-MAP saccade ratio. Accuracy is positively correlated with a greater number of entropy saccades. The regression line has a positive slope that is marginally significant for a target prior of 0.83.

Relation between efficient saccades and accuracy

The predictions in Figure 3 indicate that overall accuracy in a condition should increase when observers make saccades to higher entropy locations. The relation between efficient saccades and accuracy is not apparent in the individual data panels in Figure 5. We therefore plotted each observer’s accuracy with respect to their Entropy-to-MAP saccade ratio, as shown in Figure 7B. We plot the data for each value of prior separately. Accuracy is positively correlated with making more entropy saccades. The slopes for target priors of 0.17 and 0.5 are not significantly different from zero, but the slope for a target prior of 0.83 is marginally significant (p=0.053). A within-subject ANOVA shows that there is an effect of prior on proportion correct (F(2,8)=13.82, p=0.003). Pairwise comparisons with Bonferroni correction showed accuracy was significantly different between priors of 0.17 and 0.5 (p<0.001) and marginally different between priors of 0.17 and 0.83 (p=0.09). There was no difference in accuracy between priors of 0.5 and 0.83. If we combine the data across priors of 0.5 and 0.83, there is a significant correlation between accuracy and Entropy-to-MAP Saccade ratio (R=0.475, p<0.01), indicating that saccades to uncertain locations improve accuracy when there are multiple targets.

Another very clear trend is that each observer has a consistent saccade strategy. Observers 4 and 5 made as many saccades as possible, with the shortest latency to initiate saccades (see Figure 8B), and were less selective about target location, resulting in Entropy-to-MAP saccade ratios close to 1. In fact 05 had a stereotyped pattern of saccades, starting at the top or top left, and moving counter-clockwise to fixate as many locations as possible. This tendency was undiminished across the three experiments (see supplementary figure S1). Observer 2 consistently made longer-latency saccades that selected uncertain locations, while Observer 1 and 3 tended to make more uncertain saccades in Experiments 2 and 3. The trend for saccades to have longer latency when they select informative locations is consistent with other studies that show that shorter latency saccades are dominated by salience and that it takes longer for saccades to be directed to a less salient target or to incorporate reward (Donk & Van Zoest, 2011; Schutz et al, 2012; Janssen & Verghese, 2015). It is important to note the difference between the results of the current study and those of Verghese (2012) where none of the observers, even non-naive observers with considerable practice, made saccades preferentially to uncertain locations. Here we see that the authors (O1 and O2) and to some extent naive observer O3 are able to direct saccades to uncertain locations because these locations are easier to identify. Thus, in this less demanding situation, it is possible with deliberation to plan an efficient course of action.

Tradeoff between number of locations visited and a selective saccade strategy

Setting aside all of the theory behind informative saccades, are there multiple strategies that achieve equivalent performance on the task? Given that selecting informative locations is time-consuming, can observers do as well or better by being less selective and visiting as many locations as possible? To address these questions we replot the data from Figure 5 averaging each observer’s accuracy across the three experiments for each value of prior (Figure 8A). Alongside, we plot the average number of saccades as a function of target prior (Figure 8B). The same symbols refer to specific observers as in Figure 3 and 7 (the colors are added to more easily identify observers). It is clear that O4 and O5 who tend to make the most number of saccades (Figure 8B) perform quite well when the target prior is low. We also know from Figure 3 that O4 and O5 have an Entropy-to-MAP saccade ratio close to 1, which means that they have no preference for uncertain over probable locations. Thus it appears they are making as many non-selective saccades as possible during the 900 ms display. Furthermore, the distribution of their saccades shows a preference for locations in the upper field. As the targets are randomly distributed, their preference for these locations makes their saccade choice only as good as a strategy that selects locations randomly. This strategy does have an impact on performance when targets are frequent (prior=0.83), because they do not make enough saccades to cover both clear and noisy targets. In comparison O2, who consistently makes the fewest saccades and selects uncertain locations, has high trial accuracy at all values of the prior, including when targets are frequent. The cost of unselective saccades is most apparent at high values of target prior. Thus, making many saccades does not improve performance over making more deliberate saccades to obtain information.

Observer’s goal: foraging or finding all targets?

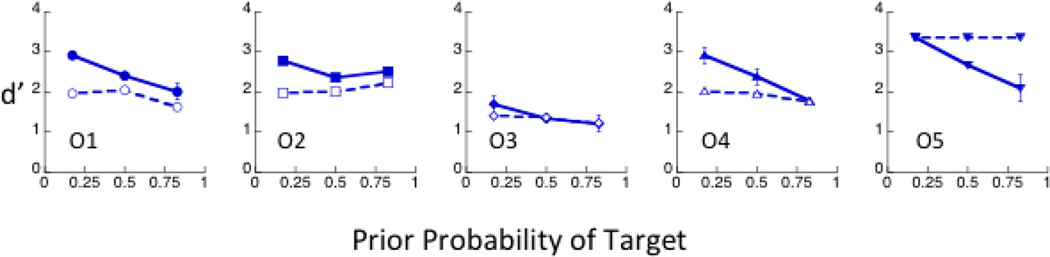
There is another possibility — observers who do not select informative locations may be making saccades to confirm the presence of a target. As in foraging for food, they might want to reach likely targets first, before trying to find all the targets. To investigate this possibility we compared average discriminabiliity in the saccade version of Experiments 2 and 3 to the discriminability in the no-saccade condition. Our objective here is to determine whether overall discriminability improved in the saccade condition. If observers made saccades to MAP locations, where the discriminability was high even without a saccade, then there would not be a significant increase in d’, compared to the no-saccade condition. However, if the observer made a saccade to high entropy (informative) locations, then the increase in d’ would be higher. We calculated d’, the ability to discriminate horizontal target from vertical distractor from the average number of hits and false alarms (across all six locations for all 100 trials in the block) for each value of target prior. Because we used identical trials in the saccade and no-saccade conditions, there are no differences in orientation, contrast or placement of stimuli. Therefore the only changes in discriminability are due to the saccade. Figure 9 plots the data from the saccade and no-saccade conditions as filled and open symbols, respectively, in separate panels for each observer. For 4 out of 5 observers, saccades improve discriminability when targets are rare (prior=0.17). However only observers O1 and O2 show increased d’ in the saccade condition when targets are frequent (prior=0.83). This result is consistent with the previous comparison of overall accuracy to the entropy model prediction showing that these two observers direct saccades to informative locations. Observers O3, and O4 direct their saccades to higher-visibility target locations, resulting in no improvement in d’ when targets were frequent. Observer O5 has a very conservative criterion in the no-saccade condition and has no false alarms. Because of this strategy, her d’ is pegged at the maximum for the no-saccade condition. Thus it appears that naive observers adopt a saccade strategy directed at confirming target presence at probable locations, rather than finding all the targets in the display.

Figure 9.

Average d’ for the saccade and no-saccade conditions as a function of the prior probability of the target. The filled and open symbols represent data for the saccade and no-saccade conditions, respectively.

Discussion

We set out to determine how observers selected saccade targets in a visual search task with an unknown number of targets. The time for active search was limited and correct performance depended on finding all the targets, so efficient search required directing saccades to locations where more information could be gained. This strategy was particularly important when the probability of targets was high. In the context of our experiments, efficient visual search involved saccades towards uncertain stimuli but observers differed in their ability to direct saccades to these stimuli. The most practiced observer, O2, consistently made saccades to uncertain locations, but two naive observers seemed to choose equally between uncertain and MAP locations and generate as many saccades as they could within the 900 ms interval.

Comparison to single-target search

Even though most observers do not select uncertain locations, they perform as well as the Entropy model when targets are rare (prior=0.17). This condition is the closest to single-target search although there is a difference. When the prior probability of the target at a location is set to 0.17, the frequency of 1-target trials is the highest, although there could be anywhere from 0 to 6 targets on any given trial. Therefore our results are consistent with other studies showing that accuracy in visual search for single targets is efficient. Of course it is difficult to distinguish the MAP and entropy models for single/rare targets, because the locations selected by the models often overlap. Our fixation analysis suggests that observers on average did not select uncertain locations when targets were rare, but Najemnik and Geisler (2008) show that the pattern of fixations for a single target in 1/f noise is indeed consistent with an entropy model that chooses local regions of high entropy. On the other hand, Rao et al (2002) and Beutter et al (2003) show that saccades in a single-target search targeted MAP locations.

Saccade efficiency

While searching for an unknown number of targets, observers show biases in eye movement behavior consistent with maximizing information. For example, saccades are biased to upper visual field locations to compensate for the poorer sensitivity in this region (Najemnik & Geisler, 2009). In addition, saccades tend to be hypometric, so that the parafovea is not wasted on the edges of the display (Renninger et al, 2007). But beyond these general adaptations, naive observers in our task do not make saccades to locations where they will gain the most information. This is perhaps because observers have had little experience with situations where they need to gather visual information from multiple locations under time pressure. In the real world, moving the eyes toward salient targets (Itti & Koch, 2005, Itti & Baldi, 2009), or probable target locations (Zelinsky, 2008) is adequate for many tasks. Practice with multiple-target search seems to make saccades more efficient as the most practiced observer is the only one who consistently made saccades consistent with the entropy strategy. It is possible that individuals who are experts at monitoring multiple targets including action video game players, quality control inspectors on an assembly line, recycling plant workers who sort mixed recycling streams, and subsistence hunters, will make more efficient saccades.

While there are several studies that show that maximizing the information gained with every fixation is an optimal way to gathering information with a foveated system, (Legge, Klitz, and Tjan 1997; Lee & Yu, 2000; Raj, Frazor, Geisler & Bovik, 2005; Butko and Movellan, 2010), fewer studies have compared these models to human performance. One counter-example is reading where Legge, Hooven, Klitz, Mansfield, and Tjan (2002) showed that that the characteristic eye movement patterns such as skipping small words, fixating the center of words, and backward saccades were consistent with the eyes moving to informative locations. In their case the specific task was to identify the upcoming word from a fixed lexicon of words. However they did not perform a saccade-by saccade analysis of eye-movement patterns, so it is not clear that each fixation was optimized to gather maximum information.

Another example of a task that benefits from selecting informative locations is object recognition (Renninger, Verghese and Coughlan, 2007). In their study Renninger et al (2007) had observers examine a novel silhouette with eye movements in a limited time, and then had them distinguish this silhouette from a similar silhouette. The fixation locations of observers in this task appeared equally consistent with two models: a model that selected salient locations, and a model that selected local regions with high entropy, but with a bias toward the centroid of the shape. The authors argued in favor of the local entropy model because the distribution of model fixations across all shapes in the experiment resembled observers’ fixation distributions more than did the salience model.

Finally, there is the example of face recognition. Peterson & Eckstein (2012) showed that in a task where observers were asked to make a single saccade to a face to determine the identity, gender or emotional state, they chose a location that maximized the information necessary to make the judgment. It is interesting to note that the tasks in which humans make saccades that are consistent with maximizing information are highly practiced tasks that are ecologically relevant (face recognition and reading). For tasks such as visual search, observers are typically searching for a single target, so they tend to direct saccades to the most probable target location. They simply extend this search behavior, which is effective for single targets, to the case of finding multiple unknown targets. They do so even when the targets are quite visible, suggesting that there might be a confirmation bias in visual search.

Saccade planning is deliberate

Other studies have shown that short-latency saccades go to the salient stimuli, even if they are distractors (Donk & van Zoest, 2011) and when they are not rewarded (Schutz et al, 2012). Thus it appears that the saccadic system might have evolved to respond quickly to salient targets because they signal ecologically important stimuli such as ripe fruit through salient color, or a predator through salient motion in the periphery. It is also clear that saccades that incorporate task-relevant information take longer—whether the task is to find the less salient target, to ignore the salient stimulus and find the rewarded stimulus, or to find the most informative locations (Donk & Van Zoest, Schutz et al, 2012, Janssen & Verghese, 2015). The current study shows that a strategy that preferentially selects informative entropy locations is correlated with a longer latency for the first saccade. More importantly, we were able to show that deliberately delaying the first saccade caused observers to make a greater proportion of entropy saccades. Therefore it appears that it takes time for saccades to incorporate task-relevant information, and to overcome the reflexive tendency for saccades to target salient locations.

Conclusion

In the context of active visual search for an unknown number of targets in a limited time, we investigated whether the choice of saccades locations combines bottom-up image-based factors with the specific demands of a task. As there was only enough time to make eye movements to a subset of possible target locations, we examined whether saccades adapt to choose locations where the most information can be gained. In a sequence of three experiments that made it progressively easier to identify informative locations, we found that observers differed considerably in their saccadic strategy. Some made as many saccades as possible without consideration as to whether these were to informative locations; others made more informative saccades, particularly when the informative locations were easier to identify and when targets were frequent. Less selective saccades were associated with shorter latency and a greater number of saccades whereas saccades to more informative locations were correlated with a longer saccade latency suggesting that the latter is a deliberate strategy. Thus we show that efficient saccade planning takes time.

Highlights.

• Saccade strategy in multiple-target search can adapt to the probability of the target

• Saccade planning is more efficient when choices are clear

• Delaying the first saccade improves saccade efficiency