Regularization Paths for Conditional Logistic Regression: The clogitL1 Package

Abstract

We apply the cyclic coordinate descent algorithm of Friedman, Hastie, and Tibshirani (2010) to the fitting of a conditional logistic regression model with lasso $\left({\ell }_1\right)$ and elastic net penalties. The sequential strong rules of Tibshirani, Bien, Hastie, Friedman, Taylor, Simon, and Tibshirani (2012) are also used in the algorithm and it is shown that these offer a considerable speed up over the standard coordinate descent algorithm with warm starts.

Once implemented, the algorithm is used in simulation studies to compare the variable selection and prediction performance of the conditional logistic regression model against that of its unconditional (standard) counterpart. We find that the conditional model performs admirably on datasets drawn from a suitable conditional distribution, outperforming its unconditional counterpart at variable selection. The conditional model is also fit to a small real world dataset, demonstrating how we obtain regularization paths for the parameters of the model and how we apply cross validation for this method where natural unconditional prediction rules are hard to come by.

1. Introduction

Suppose we have K independent strata, each with n_k independent observations, (Y_ki, X_ki), k = 1, 2, . . . , K; i = 1, 2, . . . , n_k, where each Y_ki is a dichotomous random variable taking on values 0 or 1 and each X_ki is a p-vector of fixed regressors or exposure variables. The quantities are related via the logistic regression model:

$$\mathrm{logit}(\mathsf{P}\left(Y_{ki}\right)=1\mid X_{ki})\doteq \log \left(\frac{\mathsf{P}(Y_{ki}=1\mid X_{ki})}{1-\mathsf{P}(Y_{ki}=1\mid X_{ki})}\right)={\beta }_{0k}+{\beta }^{\mathsf{T}}{X}_{ki}.$$ (1)

Note that each observation has two indices: the first identifying its stratum; the second, its number within the stratum. The stratum e ect is incorporated by giving each stratum its own intercept β_0k (with β the same for all strata). The logistic regression model has been studied extensively and its properties are well established and widely known.

Furthermore, consider a retrospective (case-control) study design where the number of cases (Y_ki = 1) and controls (Y_ki = 0) in each stratum k are fixed beforehand at m_k and n_k − m_k respectively. We may assume, without loss of generality, that the observations at indices i = 1, 2, . . . , m_k in stratum k are the cases and those at indices i = m_k + 1, m_k + 2, . . . , n_k are the controls. These types of studies are more feasible in practice when prospective studies are too costly, time consuming or simply unethical. Examples abound in epidemiology, economics and the actuarial sciences.

Now the core assumption of model Equation 1 – Y random; X fixed – is exactly reversed and the likelihood that stems from that equation is no longer valid for the probability mechanism generating the data. In the conditional logistic likelihood literature, this problem is dealt with by treating the intercepts β_0k as nuisance parameters and making a conditional argument to derive a new quantity, called the “conditional logistic likelihood”:

$$\begin{array}{cc}\hfill L\left(\beta \right)=& \prod _{k=1}^K{L}_k\left(\beta \right)\hfill \\ \hfill =& \prod _{k=1}^K\frac{\exp \left({\beta }^{\mathsf{T}}{\sum }_{i=1}^{m_k}{X}_{ki}\right)}{{\sum }_{u\in S_{m_k},n_k}\exp \left({\beta }^{\mathsf{T}}{\sum }_{i\in u}{X}_{ki}\right)}\hfill \end{array}$$ (2)

See Breslow and Day (1980) for further details. The set S_m,n is defined in Section 2.

We maximize Equation 2 to obtain estimates for β. The advantage of using the conditional likelihood is twofold:

1. All nuisance parameters are eliminated, possibly reducing the standard error and bias of the estimates of β.

2. This conditional probability (and hence the likelihood) remains valid regardless of study type (prospective or retrospective).

This method is used in a variety of application areas to study the effect of exposure variables on some dichotomous event of interest. An example is in epidemiology where we have data on K patients (our strata) and tissue characteristics for different tissue samples from each patient. For each patient, some tissue samples are cancerous, while others are healthy. The goal would be to find those tissue characteristics most related to the development of cancer. It seems natural to have some principled, automatic method for selecting the relevant exposure variables. Here we propose a penalized conditional logistic regression model where we minimize:

$$-\log L\left(\beta \right)+\lambda P_{\alpha }\left(\beta \right),$$ (3)

where

$$\lambda P_{\alpha }\left(\beta \right)=\lambda \left(\alpha \sum _{j=1}^p\mid {\beta }_j\mid +\frac{1}{2}(1-\alpha )\sum _{j=1}^p{\beta }_j^2\right)$$ (4)

is the elastic net penalty proposed by Zou and Hastie (2005).

In this paper, we apply the cyclic coordinate descent algorithm of Friedman et al. (2010) and Wu and Lange (2008) to obtain a path of penalized solutions. Having a path of solutions facilitates cross validation when determining the optimal λ value. A recursive formula proposed by Gail, Lubin, and Rubenstein (1981) is used to compute the likelihood and its derivatives exactly. The cyclic coordinate descent algorithm is stable and reasonably efficient.

Section 2 discusses the model rationale and algorithm implementation: how we compute the normalizing constant in the denominator of Equation 2 and how we apply cyclic coordinate descent to obtain the solution path. Section 3 shows how sequential strong rules drastically improve the e ciency with which we can compute the solutions. Section 4 looks at the time taken to arrive at solutions for datasets of different sizes. A comparison is made between the conditional and unconditional models in Section 5, looking at the difference in variable selection performance and predictive power. Finally, Section 6 briefly addresses the implementation of cross validation for a method that does not immediately present us with a convenient way of making predictions.

We provide a publicly available R (R Core Team 2014) implementation in the package clogitL1 (Reid and Tibshirani 2014), available from the Comprehensive R Archive Network (CRAN) at http://CRAN.R-project.org/package=clogitL1.

2. Rationale and algorithm

Breslow and Day (1980) suggest three approaches to adapt the standard logistic model to the case-control design. The first involves some assumptions on the effect of regressors X_ki on the probability of being selected to the sample (some of which are unlikely to be borne out in practice). It can be shown that the standard logistic model (with slightly different values for the intercepts) can be applied with impunity in this case.

Their second suggestion uses Bayes’ rule to justify the use of the standard logistic model. However, one still has to contend with many nuisance parameters (intercepts and marginal distributions of X and Y ).

The approach adopted here is to use a suitable conditional probability to eliminate the intercepts and finesse the need to estimate fully general marginal distributions. Attention focuses, in each stratum k, on the conditional probability:

$$\mathsf{P}\left(\phantom{\mid }{Y}_{k1}=Y_{k2}=\cdots =Y_{k{m}_k}=1\mid \sum _{i=1}^{n_k}{Y}_{ki}=m_k\right)=\frac{\exp \left({\beta }^{\mathsf{T}}{\sum }_{i=1}^{m_k}{X}_{ki}\right)}{{\sum }_{u\in S_{m_k,n_k}}\exp \left({\beta }^{\mathsf{T}}{\sum }_{i\in u}{X}_{ki}\right)},$$ (5)

where S_m,n is the collection of $\left(\begin{array}{c}\hfill n\hfill \\ \hfill m\hfill \end{array}\right)$ sets {i₁, i₂, . . . , i_m} where 1 ≤ i₁ < i₂ < < . . . < i_m ≤ n. This is the conditional probability that the case indices are as observed given that exactly m_k cases were observed.

Assuming that observations are independent across strata, the conditional likelihood is as in Equation 2.

We wish to find β that minimizes a penalized version of the (negative) log conditional likelihood:

$$-l\left(\beta \right)=-{\beta }^{\mathsf{T}}\sum _{i=1}^{m_k}{X}_{ki}+\log \left(\sum _{u\in S_{m_k,n_k}}\exp \left({\beta }^{\mathsf{T}}\sum _{i\in u}{X}_{ki}\right)\right).$$ (6)

The Lagrangian formulation of the problem becomes:

$$\widehat{\beta }={\mathrm{argmin}}_{\beta }\left[-{\beta }^{\mathsf{T}}\sum _{i=1}^{m_k}{X}_{ki}+\log \left(\sum _{u\in S_{m_k,n_k}}\exp \left({\beta }^{\mathsf{T}}\sum _{i\in u}{X}_{ki}\right)\right)+\lambda P_{\alpha }\left(\beta \right)\right],$$ (7)

where P_α (β) is as in Equation 4.

The α parameter trades o between the ${\ell }_1$ and ${\ell }_2$-penalties, the former encouraging sparsity (setting individual β_j estimates to 0), while the latter merely shrinks estimates toward 0. The default is α = 1, which corresponds to a pure ${\ell }_1$-penalty. As we decrease α toward 0, we retain the variable selecting behavior of an ${\ell }_1$-penalty while improving stability of β estimates.

The parameter λ controls the extent of regularization. As λ → ∞, $\widehat{\beta }$ is eventually set to 0, while the maximum conditional likelihood estimate is obtained when λ = 0. As λ increases from 0, we obtain solutions with progressively fewer non-zero parameter estimates.

2.1. A small example

Before delving into the technical details, let us consider a small real world example. The dataset under consideration is from Breslow and Day (1980) to be found in the R (R Core Team 2014) package Epi (Carstensen, Plummer, Laara, and Hills 2013). It comprises of 315 observations divided into 63 strata of size 5. Each stratum contains one case (a patient with endometrical cancer) and 4 controls (non-cancer patients), matched by date of birth, marital status and residence. Since observations come in matched sets, conditional logistic likelihood maximization is ideally suited here.

Predictor variables are rife with missing values and we selected only 5 out of a possible 11 predictors for this small study. Predictors included in this example are:

• gall: Indicator of gall bladder disease.

• hyp: Indicator of hypertension.

• est: Indicator of use of estrogen drugs.

• non: Indicator of use of non-estrogen drugs.

• age: Age in years.

The age variable was centered and standardized to ensure that the scale of this variable is comparable to that of the indicator variables. The scale of predictors affect their ${\ell }_1$-penalized parameter estimates.

Figure 1 plots the profile of parameter estimates against the value of the penalty parameter λ (we set α = 1). We start at λ for which all parameter estimates are 0 (far right), decreasing λ and recomputing estimates until we reach the unconstrained maximum conditional likelihood estimates (λ = 0; far left).

Figure 1.

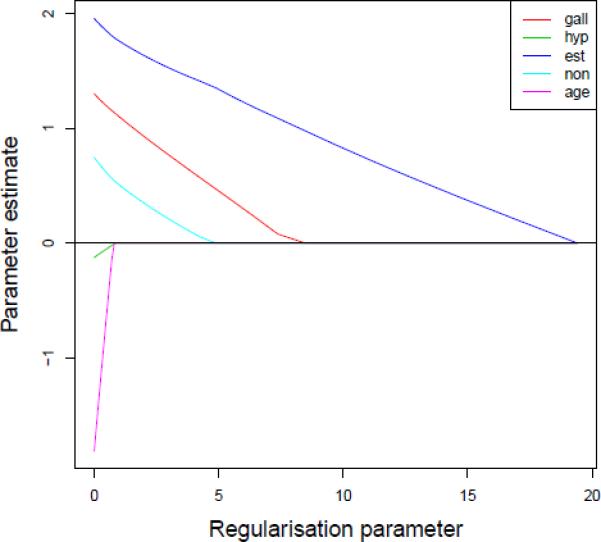
Parameter profile for endometrical cancer dataset. β estimates are plotted against the regularization parameter λ.

Gall bladder disease and the taking of estrogen and non-estrogen drugs all seem to have a positive effect on the probability of developing cancer. The estrogen drug indicator is the first predictor to have a non-zero parameter estimate and seems to have a significant effect on cancer development. Age and hypertension seem to have modest negative effects on cancer development, but both of these predictors enter late and are probably not significant.

Now let us discuss the technical details behind the computation of a parameter profile as in Figure 1.

2.2. Penalized least squares

We employ a strategy very similar to the standard Newton-Raphson algorithm for solving Equation 7. At each iteration, rather than solving a standard least squares problem, we solve a penalized one.

The quadratic approximation of the log conditional likelihood centered at a point $\tilde{\beta }$ is

$$\begin{array}{cc}\hfill l\left(\beta \right)=& l\left(\tilde{\beta }\right)+{(\beta -\tilde{\beta })}^{\mathsf{T}}\stackrel{.}{l}\left(\tilde{\beta }\right)+\frac{1}{2}{(\beta -\tilde{\beta })}^{\mathsf{T}}\ddot{l}\left(\tilde{\beta }\right)(\beta -\tilde{\beta })\hfill \\ \hfill =& l\left(\tilde{\beta }\right)+{(\beta -\tilde{\beta })}^{\mathsf{T}}s-\frac{1}{2}{(\beta -\tilde{\beta })}^{\mathsf{T}}H(\beta -\tilde{\beta }),\hfill \end{array}$$

where $s=\stackrel{.}{l}\left(\tilde{\beta }\right)$ is the p-vector of first derivatives (score vector) and $H=-\ddot{l}\left(\tilde{\beta }\right)$ is the (negative) Hessian. The form and computation of these quantities are discussed later.

The algorithm becomes:

1. Initialize $\tilde{\beta }$.

2. Compute s and H.

3. Find $\widehat{\beta }$ minimizing $-{(\beta -\tilde{\beta })}^{\mathsf{T}}s+\frac{1}{2}{(\beta -\tilde{\beta })}^{\mathsf{T}}H(\beta -\tilde{\beta })+\lambda P_{\alpha }\left(\beta \right)$.

4. Set $\tilde{\beta }=\widehat{\beta }$.

5. Repeat Steps 2 through 4 until convergence.

In principle, this algorithm could be implemented with the solver of one's choice. The criterion in Step 3 is convex in the optimization variable and any effective convex optimization solver (with the necessary tweaks required of these) would converge to the global optimum of the objective. We, however, implement a different algorithm. Section 2.3 describes the minimization in Step 3, which is done via cyclic coordinate descent.

2.3. Cyclic coordinate descent

The minimization in Step 3 above is done one coordinate at a time, rather than in a batch as in the standard Newton-Raphson update step. Letting M(β) denote the objective in Step 3, we obtain the derivative:

$$\frac{\partial M}{\partial {\beta }_j}=-s_j+({\beta }_j-{\tilde{\beta }}_j)H_{jj}+\sum _{l\ne j}({\beta }_l-{\tilde{\beta }}_l)H_{lj}+\lambda \alpha \cdot \mathrm{sign}\left({\beta }_j\right)+\lambda (1-\alpha )\cdot {\beta }_j.$$

Setting each of these equations to 0, we obtain the following update:

$${\widehat{\beta }}_j=\frac{S\left({\tilde{\beta }}_j{H}_{jj}+s_j+{\sum }_{l\ne j}({\tilde{\beta }}_l-{\widehat{\beta }}_l)H_{lj},\lambda \alpha \right)}{H_{jj}+\lambda (1-\alpha )},$$ (8)

where

$$S(x,t)=\mathrm{sign}\left(x\right)\cdot {(\mid x\mid -t)}_{+}$$

is the soft thresholding operator.

These are cycled over j = 1, 2 . . . , p, 1, 2, . . . , p, . . . until convergence, each time updating the value of $\widehat{\beta }$ for use in subsequent updating equations. Note that $\tilde{\beta }$ s and H remain fixed throughout this cyclic coordinate descent epoch.

Convergence of this algorithm is discussed in Friedman et al. (2010). Their sentiments will largely be reiterated in Section 2.6, once we have discussed the pathwise algorithm.

2.4. Computing the likelihood and its derivatives

Our cyclic coordinate descent updates require computation of the entire score vector, the diagonal of the Hessian and o diagonal Hessian entries for those j such that ${\tilde{\beta }}_j$ and ${\widehat{\beta }}_j$ become unequal during the descent phase.

Taking first and second derivatives of the likelihood in Equation 2, we obtain the following expressions for the score vector and (negative) Hessian:

$$\begin{array}{cc}\hfill s=& \sum _{k=1}^K\left(\sum _{i=1}^m{X}_{ki}-{\mu }_k\right),\hfill \\ \hfill H=& \sum _{k=1}^K\sum _{u\in S_{m,n}}{p}_{ku}\left(\sum _{i\in u}{X}_{ki}-{\mu }_k\right){\left(\sum _{i\in u}{X}_{ki}-{\mu }_k\right)}^{\mathsf{T}},\hfill \end{array}$$

where

$${\mu }_k=\sum _{u\in S_{m,n}}{p}_{ku}\sum _{i\in u}{X}_{ki}$$

and

$$p_{ku}=\frac{\exp \left({\beta }^{\mathsf{T}}{\sum }_{i\in u}{X}_{ki}\right)}{{\sum }_{v\in S_{m,n}}\exp \left({\beta }^{\mathsf{T}}{\sum }_{i\in v}{X}_{ki}\right)}.$$

Brute force computation of s and H requires enumeration of at least $\left(\begin{array}{c}\hfill n_k\hfill \\ \hfill m_k\hfill \end{array}\right)$ terms in each stratum, leading to an $O\left(\left(\begin{array}{c}\hfill n_k\hfill \\ \hfill m_k\hfill \end{array}\right)\right)$ computation time in each stratum k for every entry of s and H (of which there are O(p²)). Computation increases rather rapidly as n_k and m_k increase. For example, $\left(\begin{array}{c}\hfill 20\hfill \\ \hfill 10\hfill \end{array}\right)=184756$ and $\left(\begin{array}{c}\hfill 40\hfill \\ \hfill 20\hfill \end{array}\right)=1.378\times {10}^{11}$. It does not seem implausible that strata should contain as many as 40 (or more) observations. A particular medical application could allow for measuring many tissue samples per patient.

Even though Breslow and Day (1980) suggest that β estimates and their standard errors from the conditional likelihood are almost certain to be numerically close to those from the standard unconditional likelihood for large n_k and m_k, the arguments are asymptotic. What is large enough to ensure this numerical similarity is often to be judged for each application separately and then one needs a method to compute the conditional likelihood estimates. A more amenable method for computing these quantities is required.

2.5. The normalizing constant and its derivatives

The major computation bottleneck occurs because the normalizing constant in each stratum comprises of $\left(\begin{array}{c}\hfill n_k\hfill \\ \hfill m_k\hfill \end{array}\right)$ terms. These are carried over into the first and second derivatives, because the derivative operator commutes with finite sums.

Consider the normalizing constant for a single stratum k, omitting subscripts for ease of exposition:

$$B_k(m,n)=\sum _{u\in S_{m,n}}\exp \left({\beta }^{\mathsf{T}}\sum _{i\in u}{X}_{ki}\right).$$ (9)

Gail et al. (1981) propose a recursive formula for the computation of Equation 9:

$$B_k(m,n)=B_k(m,n-1)+e^{{\beta }^{\mathsf{T}}{X}_{kn}}{B}_k(m-1,n-1)$$ (10)

with base case conditions: B_k(0, n) = 1 ∀n and B_k(m, n) = 0 for m > n.

The intuition is that, to compute the normalizing constant for a stratum with n observations of which m are cases, we can fix attention on the last observation (numbered n). The overall sum can be split into one which does not contain a term relating to observation n and one which does. The former sum is simply the normalizing constant of a stratum with n − 1 observations from which we still require m cases (see first term of Equation 9). The second is the normalizing constant for a stratum with n − 1 observations from which we require only m − 1 cases, because we have already kept one observation aside as a case. We must multiply this second normalizing constant by the contribution of this kept out observation, hence the second term.

Using the recursive formula allows us to compute the normalizing constant in O(m(n − m)) time, suggesting that the entire likelihood can be computed in $O\left({\sum }_{k=1}^K{m}_k(n_k-m_k)\right)$ time.

Taking first and second derivatives of Equation 10 on both sides yields recursive expressions for the first and second derivatives of the normalizing constant:

$${\stackrel{.}{B}}_k(m,n)={\stackrel{.}{B}}_k(m,n-1)+e^{{\beta }^{\mathsf{T}}{X}_{kn}}{\stackrel{.}{B}}_k(m-1,n-1)+X_{kn}{e}^{{\beta }^{\mathsf{T}}{X}_{kn}}{B}_k(m-1,n-1)$$

and

$${\ddot{B}}_k(m,n)={\ddot{B}}_k(m,n-1)+e^{{\beta }^{\mathsf{T}}{X}_{kn}}{\ddot{B}}_k(m-1,n-1)+X_{kn}{e}^{{\beta }^{\mathsf{T}}{X}_{kn}}{\stackrel{.}{B}}_k{(m-1,n-1)}^{\mathsf{T}}+e^{{\beta }^{\mathsf{T}}{X}_{kn}}{\stackrel{.}{B}}_k(m-1,n-1)X_{kn}^{\mathsf{T}}+X_{kn}{X}_{kn}^{\mathsf{T}}{e}^{{\beta }^{\mathsf{T}}{X}_{kn}}{B}_k(m-1,n-1).$$

The score vector and Hessian can be computed fairly directly once we have these quantities:

$$\begin{array}{cc}\hfill s=& \sum _{k=1}^K\left(\sum _{i=1}^m{X}_{ki}-\frac{{\stackrel{.}{B}}_k(m_k,n_k)}{B_k(m_k,n_k)}\right),\hfill \\ \hfill H=& \sum _{k=1}^K\left[\frac{{\ddot{B}}_k(m_k,n_k)}{B_k{(m_k,n_k)}^2}-\left(\frac{{\stackrel{.}{B}}_k(m_k,n_k)}{B_k(m_k,n_k)}\right){\left(\frac{{\stackrel{.}{B}}_k(m_k,n_k)}{B_k(m_k,n_k)}\right)}^{\mathsf{T}}\right].\hfill \end{array}$$

Each entry of s and H can how also be computed in $O\left({\sum }_{k=1}^K{m}_k(n_k-m_k)\right)$ time. Notice that the recursive calculations depend on those obtained during the computation of lower order derivatives. This has interesting implications for the implementation of the algorithm.

Consider Equation 8. Without any prior knowledge of which parameter estimates are to become non-zero in the subsequent cyclic coordinate descent epoch, we are forced to compute s and the diagonal elements of H. We can postpone the computation of the o diagonal elements until such time that ${\widehat{\beta }}_j$ differs from ${\tilde{\beta }}_j$ at which point we compute all the o diagonal Hessian elements involving variable j. To implement this strategy, we would need to keep persistent copies of all the intermediate recursive computations obtained while computing the normalizing constant and its first derivatives – a memory burden of $O\left({\sum }_{k=1}^K{m}_k(n_k-m_k)\right)$. For large p, n_k and m_k this could amount to an unacceptable use of memory.

Alternatively, all entries of s and H could be computed before we begin our cyclic descent epoch. Computing these quantities at the same time would allow for intermediate computations to be discarded as soon as we have the final values. This, on the other hand, would lead to excessive computation time, with much time being spend wastefully, computing Hessian entries of many variables that are unlikely to become non-zero over the current cyclic descent epoch.

Ideally, we would like some heuristic that could help predict which elements of $\widehat{\beta }$ are likely to become non-zero in the next epoch (hopefully far fewer than p of them) and perform the whole batch of likelihood computations for only this comparatively small set of variables. We discuss this later.

2.6. Pathwise algorithm

We are interested in computing parameter estimates not at one particular value of λ, but rather a grid of, say, 100 of them. To this end, we begin with the smallest λ such that all parameter estimates are 0. From Equation 8, this is easily seen to be:

$${\lambda }_{max}=\frac{{\max }_j\mid s_j\mid }{\alpha }.$$

We then find the optimal β for each λ along a grid of 100 values spaced between λ_max and λ_min = ελ_max where ε = 0.00001. Notice that we do not run down to the unregularized solution. For $p>{\sum }_{k=1}^K{n}_k$ this solution is undefined anyway and for $p\le {\sum }_{k=1}^K{n}_k$, solutions can be numerically unstable at λ = 0.

Each solution at the current λ value is used as a warm start for the algorithm when computing the solution at the next λ value. This lends stability to an algorithm that is not guaranteed to converge without step size optimization (which we do not do here). No problems of such ilk have been encountered yet. Warm starting on previous solutions gives us a good chance of starting in the zone of quadratic convergence of the Newton-Raphson algorithm, where quadratic approximations to the objective are good and convergence is rapid and guaranteed.

Friedman et al. (2010) suggest that λ values should be spaced uniformly on the log scale, suggesting that successive λ values are related via:

$${\lambda }_{k+1}={\lambda }_k{\left(\frac{{\lambda }_{min}}{{\lambda }_{max}}\right)}^{\frac{1}{100}}.$$

It was found that the nature of the grid has significant influence on the overall computation time. This is discussed further in the next section.

For the case where ${\sum }_{k=1}^K{n}_k<p$, one cannot estimate more than ${\sum }_{k=1}^K{n}_k$ parameters. We would like to terminate the algorithm early should we explain almost all of the variability in the observations. Following Simon, Friedman, Hastie, and Tibshirani (2011), we use a deviance cuto .

The deviance of a model with parameter β is defined to be:

$$D\left(B\right)=2(l_{saturated}-l\left(\beta \right)),$$

where l_saturated is the maximum log-likelihood value achieved when the exponents in the likelihood are allowed to vary freely and not just over linear combinations of β. Fairly simple arguments suggest that in this case l_saturated = 0.

The algorithm terminates when

$$D_{null}-D\left({\beta }_{current}\right)\ge 0.99D_{null},$$

where $D_{null}=2(0-l\left(0\right))=-2{\sum }_{k=1}^K\log \left(\begin{array}{c}\hfill n_k\hfill \\ \hfill m_k\hfill \end{array}\right)$.

3. Strong rules

It has been intimated in the previous section that the recursive structure of the computation of the likelihood and its derivatives encourages a search for a heuristic for reducing the number of score and Hessian entries to be computed in each iteration of our algorithm. Should we find a good heuristic, we could reduce the computation burden and simultaneously reduce the memory overhead by computing all related quantities in a batch. Obviously we would still like to obtain the exact penalized maximum conditional likelihood estimates after its application.

Tibshirani et al. (2012) propose a heuristic for screening variables immediately after the most recent decrement of λ. Suppose we have just computed the solution at ${\lambda }_{k-1}:\widehat{\beta }\left({\lambda }_{k-1}\right)$ and the associated score vector s. Their sequential strong rule suggests that, when solving for the current λ_k, we may ignore all variables such that:

$$\mid s_j\mid \le \alpha (2{\lambda }_k-{\lambda }_{k-1}).$$ (11)

Steps 2–6 in Section 2.2 may then proceed with only those variables that pass this test. Those that do not pass the test are simply left at 0.

The authors show that this rule is not safe and some parameter estimates that should be non-zero at the end of the iteration could be screened at the start of it. However, they also show that such errors are rare. Either way, one need only check the KKT conditions at the end of each iteration and rerun Steps 2–6 should a violation be detected, using the current solution as a warm start. These KKT conditions are:

$$\mid s_j-{\lambda }_k(1-\alpha ){\widehat{\beta }}_j\left({\lambda }_k\right)\mid \le {\lambda }_k$$

for j = 1, 2, . . . , p, where the score vector s is computed at the proposed solution at λ_k. Should all variables satisfy the KKT conditions, we have found the exact penalized maximum conditional likelihood parameter estimates.

The sequential strong rule is shown to discard many variables over the course of the algorithm and reduces overall computation time considerably. For the current application, it has the additional benefit of precluding the need for persistent copies of intermediate recursive computations, reducing memory overhead.

3.1. Efficiency gains of sequential strong rules

The sequential strong rule provides a significant speed up (often by a factor of 2–5 over the non-strong-rule case). Not only does it allow the computation of fewer Hessian entries per iteration, but it also allows a reordering of the score and Hessian computations, making the code more amenable to compiler optimization.

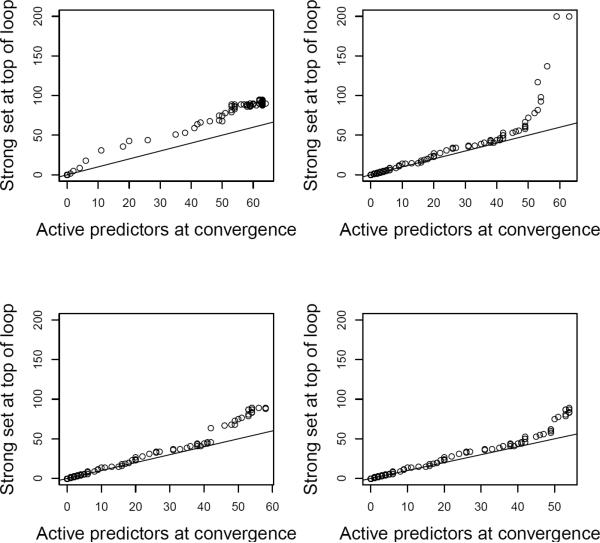
Figure 2 shows the screening performance of the strong rule. The actual number of nonzero predictors comprising the solution at each λ value is plotted on the horizontal axis. The number of predictors selected to the strong set (those on which we solely focus for that iteration) is plotted on the vertical axis. The unit slope line through the origin is plotted for reference. If the strong rule worked perfectly, points would lie along the reference line. We see that the strong rule is somewhat conservative, always selecting more variables for consideration than those that turn out to be active at the end of the iteration.

Figure 2.

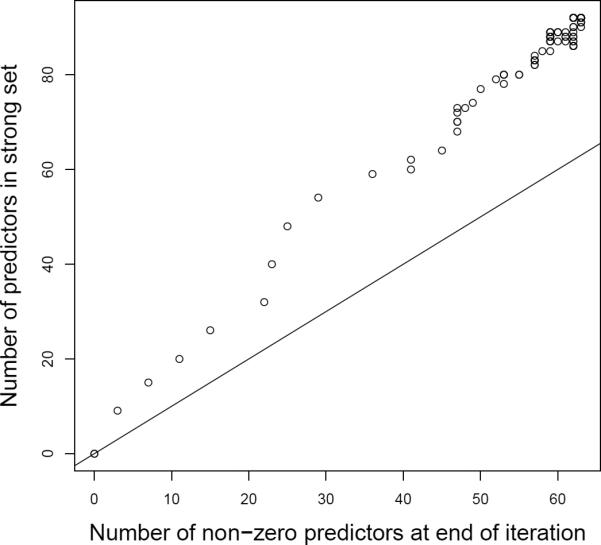
Screening performance of sequential strong rule. K = 10, n = 10, m = 5, p = 200.

A matter not addressed by Tibshirani et al. (2012) is the cost of this conservatism. In their applications, score and Hessian computations are comparatively cheap. Here they are quite expensive and any savings on the number of these quantities computed is welcome. Perhaps then there is a way to choose the grid of λ visited so that the sequential strong rule chooses smaller strong sets in each iteration. This is discussed in the next section.

3.2. Choosing different grids

We experimented with different ways of choosing the grid of 100 λ values. One obvious alternative to the uniform logarithmic grid is the uniform linear grid:

$${\lambda }_{k+1}={\lambda }_k-\frac{{\lambda }_{max}-{\lambda }_{min}}{100}.$$

This grid has the unwelcome property that the strong rule threshold Equation 11 becomes negative for small λ, forcing all predictors into the strong set, considerably slowing down the algorithm in the final iterations.

Perhaps a compromise between the two grids could be tried, starting with linear jumps between successive λ values and then transitioning to logarithmic jumps at later iterations.

A simulation study comparing the performance of the different grid choices was run. Fixing α = 1 and the number of strata at K = 10, as well as the number of observations and cases per stratum at n = 10 and m = 5, respectively, regressors X_kij, k = 1, 2, . . . , K, i = 1, 2, . . . , n, j = 1, 2, . . . , p were generated independently from a N(0, 1) distribution. The number of predictors was set to p = 100, 200, 500, 1000, 2000 in turn. q = ⌊ 0.25p ⌋ of the regression parameters chosen randomly, assigned a sign uniformly at random and these comprised the non-zero predictors (with absolute value |β_j| = 2). For each stratum, m cases were selected (without replacement) based on the logistic success probabilities implied by the generated regressors and coefficients.

B = 3 of these datasets were generated for each p and the algorithm was put to work at computing a path of β solutions over 4 different grids of 100 λ values. All simulations were done on an Intel Dual Core 2.5GHz processor.

Table 1 shows the average running times for each of 4 different grid types.

Table 1.

Speed in seconds for strong rules with different grid types.

Jumps	p = 100	p = 200	p = 500	p = 1000	p = 2000
Logarithmic	0.50	0.77	2.19	3.93	7.65
Linear	0.90	1.75	13.04	27.10	166.90
80 Linear; 20 Logarithmic	0.46	0.70	2.00	3.65	7.05
90 Linear; 10 Logarithmic	0.40	0.57	1.47	2.48	4.96

Notice the considerable speed up provided by the hybrid grids and the very poor performance of the linear grid at higher values of p. Figure 3 demonstrates the screening performance of the sequential strong rule under each of the four grids. From the figure we see that the poor performance of the linear grid stems from its tendency to include nearly all of the predictors in the strong set at later iterations. Nearly all of the computation time is spent at these last one or two iterations.

Figure 3.

Screening performance of sequential strong rule for different grid choices. Top left panel: logarithmic jumps, top right: linear jumps, bottom left: 80 linear jumps followed by 20 logarithmic jumps, bottom right: 90 linear jumps followed by 10 logarithmic jumps. p = 200.

Speed ups in the hybrid grids stem from at least three sources:

1. Strong sets are smaller and fewer score and Hessian entries are computed at each iteration. This is demonstrated by the string of points in the third and fourth panels hugging the reference line more tightly than do those in the first panel.

2. λ values in the grid decrease more slowly under linear jumps, allowing the algorithm to spend more time where solutions are naturally sparse.

3. λ is not allowed to become as small as in the logarithmic case, so we never reach λ values that would require a large number of non-zero parameters.

No strong set violations were encountered for any of the grid choices over any of the simulations.

4. Timings

Having settled on the 90–10 linear-log grid, we ran further simulations in the same vein of Section 3, studying the performance of the algorithm over changes in the parameters.

4.1. Fixed K

Consider the case where the number of strata K = 10 is fixed. B = 3 simulation runs were made over a grid of parameters defined by:

• n = 10, 20, 40.

• $m=1,5,\frac{n}{2}$.

• p = 100, 200, 500, 1000, 2000.

Table 2 summarizes the results. Evidently the $m=\frac{n}{2}$ case is most computationally intensive. This is as expected, since the normalizing constant has the largest number of terms when m has this relationship to n. Broad intuition about these numbers seems to be borne out: running time seems to grow roughly linearly in p, linearly in n for fixed m and quadratically in n if $m=\frac{n}{2}$.

Table 2.

Speed in seconds with fixed K.

	p = 100	p = 200	p = 500	p = 1000	p = 2000
n = 10; m = 5	0.33	0.70	1.25	2.49	4.65
n = 20; m = 10	0.83	1.78	3.97	8.38	27.71
n = 40; m = 20	3.87	9.94	41.35	180.28	433.76
n = 10; m = 1	0.07	0.12	0.16	0.35	0.55
n = 20; m = 1	0.18	0.26	0.48	0.97	1.35
n = 40; m = 1	0.38	0.69	1.02	1.80	3.41
n = 10; m = 5	0.33	0.70	1.25	2.49	4.84
n = 20; m = 5	1.48	2.80	6.71	13.64	20.19
n = 40; m = 5	10.84	7.27	19.83	41.27	73.69

4.2. Fixed sample size

Since the total sample size K × n comprises of the number of strata multiplied by the number of observations within a stratum, we can run simulations wherein we keep the sample size fixed, but trade off between the two components. This provides a deeper understanding of how K and n affect the running time.

Table 3 shows the results for two fixed sample sizes (100 and 200) with rows showing how we trade off between K and n. The number of cases within each stratum is taken to be $m=\lceil \frac{n}{2}\rceil$.

Table 3.

Speed in seconds with fixed sample size.

Sample size = 100	p = 100	p = 200	p = 500	p = 1000	p = 2000
K = 50; n = 2	0.06	0.12	0.25	0.34	0.58
K = 20; n = 5	0.07	0.39	0.36	0.58	1.13
K = 10; n = 10	0.14	0.25	0.63	0.87	1.53
K = 5; n = 20	0.26	0.57	1.13	2.09	4.32
K = 2; n = 50	0.47	1.05	2.17	5.69	13.36

Sample size = 200	p = 100	p = 200	p = 500	p = 1000	p = 2000
K = 100; n = 2	0.22	0.35	0.79	1.41	2.62
K = 50; n = 4	0.22	0.51	1.26	1.92	3.74
K = 20; n = 10	0.44	0.89	2.43	4.97	13.26
K = 10; n = 20	0.66	1.97	4.78	9.75	28.37
K = 5; n = 40	1.36	3.42	14.54	35.12	62.98

Looking down the rows of the table, we see that running time seems to increase roughly linearly in p, while down the columns we see an increase in running time with a decrease in the number of strata K and an increase in the number of observations per stratum n. The larger the n, the more effort required to compute the normalization constant within a stratum. The additional computation required per stratum seems to outweigh the effect of decreasing the number of strata.

4.3. Comparison to package penalized

Avalos, Grandvalet, Duran Adroher, Orriols, and Lagarde (2012) note the equivalence of the conditional logistic likelihood Equation 2 to the discrete partial likelihood of a Cox proportional hazards model with tied death times. In particular, for each stratum we associate cases with deaths and controls with censorings. All deaths occur at the same time (say time 1) and all censorings at some later time. The Cox discrete partial likelihood is exactly the same as the conditional probability contribution for a stratum in this case. Multiplying K partial likelihoods together allows us to use software for the Cox likelihood to compute parameter estimates for the conditional likelihood. They suggest that the R package penalized (Goeman 2010; Goeman, Meijer, and Chaturvedi 2012) be used to fit the conditional logistic model.

However, this package uses Breslow's approximation to deal with tied death times. Although a reasonable approximation for few ties, it quickly becomes poor if the number of ties grows relative to the total number of observations. So this method does not provide estimates gleaned from the exact likelihood. Furthermore, these estimates can differ quite dramatically from those gleaned from the exact likelihood even for moderate values of m. Opportunities for comparison between the method implemented in penalized and our method are thus limited, except when we have only 1 case in each stratum. Then the partial and conditional likelihoods are the same. See also Hastie and Pregibon (1988) for an algorithm for fitting generalized linear models in this case.

Table 4 shows the performance of the two methods (ours and the one using penalized) for a simulation run as in Section 3. The number of strata is fixed at K = 10, each containing m = 1 case. Running times are quoted over a grid of different n–p combinations.

Table 4.

Speed in seconds for different algorithms: K = 10.

clogitL1	p = 100	p = 200	p = 500	p = 1000	p = 2000
n = 10	0.07	0.10	0.20	0.39	0.77
n = 20	0.16	0.28	0.43	0.81	1.33
n = 30	0.23	0.37	0.78	1.40	2.41
n = 40	0.43	0.61	1.07	2.18	3.38

penalized	p = 100	p = 200	p = 500	p = 1000	p = 2000
n = 10	1.03	1.18	1.43	2.23	3.87
n = 20	1.19	1.47	1.93	3.13	5.35
n = 30	1.39	1.59	2.52	3.94	7.00
n = 40	1.83	1.99	2.78	5.22	8.90

Our method seems to run more efficiently than does the penalized equivalent. This provides some comparison between the two algorithms for the (limited) case where both yield the same result.

5. Comparison to unconditional model

The conditional logistic regression model was initially promulgated to find estimates of β in the logistic regression setup of Equation 1 where we have an intercept for each stratum. The conditioning argument eliminates nuisance intercept parameters from the objective, allowing the optimization algorithm to focus attention only on estimating β , perhaps reducing bias and variance of these estimates. One could, of course, simply apply the unconditional (standard) logistic regression model, including dummy variables for each stratum to allow for estimation of the β_0k.

The question arises then about how these two methods compare, both in their variable selection performance and their ultimate predictive ability. This section seeks to address these via an appropriate simulation study.

5.1. Simulation setup

Datasets for each simulation run were generated as in the rest of the paper. We used the sample function in R, which allows the selection of m case indices from {1, 2, . . . , n} without replacement. It has a prob argument which allows one to stipulate the weights with which this sample should be selected.

Regressors X_kij were generated i.i.d. from a N(0, 1) distribution for k = 1, 2, . . . , K; i = 1, 2, . . . , n and j = 1, 2, . . . , p for a prespecified number of strata, K, observations per stratum, n, and regressors, p. Of these regressors, q = ⌊ 0.1 × p ⌋ had non-zero predictors with β_j = ±2, the sign being selected uniformly at random. Intercepts β_0k – one for each stratum – were generated i.i.d. from N(0, 2). Individual success probabilities were then obtained as in Equation 1 and fed to our sampling function to deliver m case indices within each stratum.

For each of B = 100 simulated datasets, 4 models were fit, obtaining estimates of β at a grid of 100 λ values:

1. Conditional logistic (using our software).

2. Unconditional logistic without intercept.

3. Unconditional logistic with a single intercept for all strata.

4. Unconditional logistic with different intercept for each stratum.

The latter three models were all fit using the glmnet package (Friedman et al. 2010; Friedman, Hastie, and Tibshirani 2014).

5.2. Variable selection

Although the conditional and unconditional models both seek to estimate β, they do so by maximizing different criteria. Estimates will differ between the two types of model, with different numbers of non-zero parameters at similar levels of regularization.

For each λ value, we can compute, for each method 1–4 above, a sensitivity (proportion of true non-zero β correctly detected) and a specificity (proportion of true zero β correctly left undetected). Ranging over the 100 λ values for each method traces out a receiver operating characteristic (ROC) curve. Since there are only a finite number of sensitivity values that can be achieved, an average ROC curve can be obtained by averaging the specificity values at each unique sensitivity value. These curves could provide some insight into the variable selection ability of each of the models. Data was generated in a way that clearly favors the conditional and multi-intercept unconditional models.

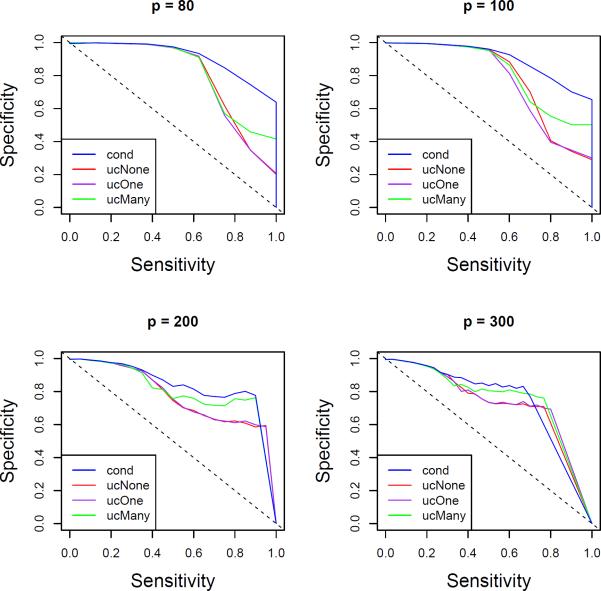
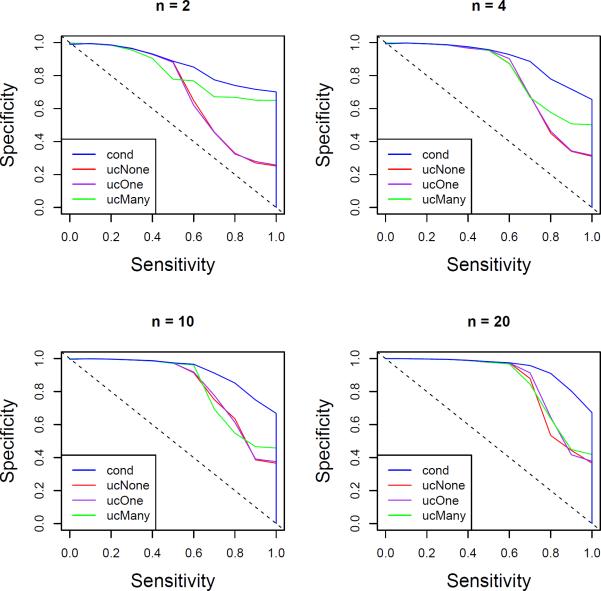
Figures 4 and 5 show the ROC curves obtained in our simulations. Sensitivity is on the horizontal axis; specificity on the vertical. The former figure fixes the number of observations n within each stratum and varies the number of regressors p, while the latter fixes p and allows n to vary. Sample sizes are kept fixed at 150 and $m=\lfloor \frac{n}{2}\rfloor$.

Figure 4.

ROC curves for fixed n. Average ROC curves are plotted for conditional model (blue), unconditional model with no intercept (red), unconditional model with single intercept (purple) and unconditional model with intercept for every stratum (green). n = 2, m = 1, K = 75, p ranges over 80 (top left), 100 (top right), 200 (bottom left) and 300 (bottom right).

Figure 5.

ROC curves for fixed p. Average ROC curves are plotted for conditional model (blue), unconditional model with no intercept (red), unconditional model with single intercept (purple) and unconditional model with intercept for every stratum (green). p = 100, n ranges over 2 (top left), 4 (top right), 10 (bottom left) and 20 (bottom right). Sample sizes are kept as close to 150 as possible, $m=\frac{n}{2}$.

It seems as though the conditional and multi-intercept unconditional models do indeed off er better variable selection performance. Perhaps the conditional model, in turn, has an edge over the multi-intercept unconditional one. The difference between the conditional and unconditional models is greatest when strata are large and regressors are few and disappears quite quickly in p. Notice that the difference is quite significant for large n.

5.3. Prediction

One could ask how the superior variable selection performance is translated into predictive power. The trouble is that the conditional logistic model is not geared toward prediction. We make conditional arguments to eliminate intercepts as nuisance parameters, but these are crucial for predicting the class membership of new data points.

Even the unconditional model struggles here, because every new observation will come from a new stratum with a different intercept and we cannot learn these from the training data directly. At least this method provides estimates of the intercepts (either a single one or one for each stratum).

In order for the conditional model to provide predictions, we need to finesse the intercept problem. To this end, we propose two heuristically motivated methods. Both rely on computing a threshold t_k for each stratum in the training set. All observations with linear predictor $\left({\widehat{\beta }}_{\lambda }^{\mathsf{T}}{X}_{ki}\right)$ greater than the threshold are deemed cases; the rest controls. Thresholds are selected within each stratum to minimize the misclassification rate. A simple grid search over each of the observed linear predictors is sufficient to find the appropriate threshold.

Prediction of a new point proceeds by comparing its linear predictor to the average of the thresholds over all the training set strata (called the mean method) or using each threshold to provide a prediction for the new test point and then taking a majority vote over all these predictions (called the committee method).

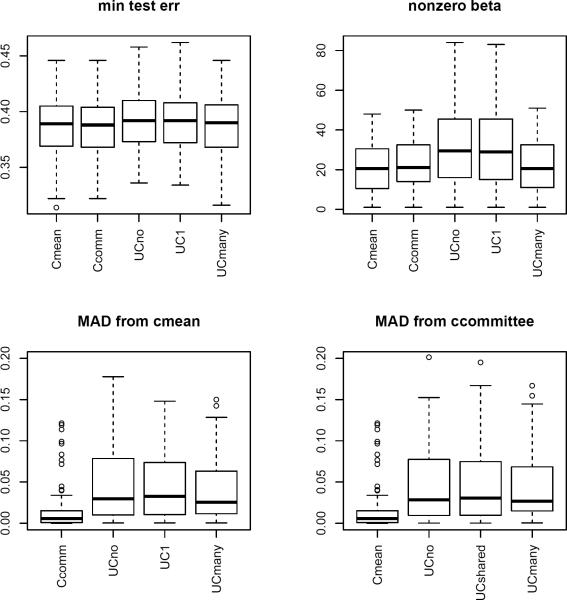
We ran a simulation comparing the prediction performance of each of the methods. A training sample of size 150 was generated as above and a test set of size 750. The 4 models from the previous section were fit to the training set and used to predict the test set. For each simulated dataset, we could find λ minimizing test misclassification error for each method. This also gives us the β profile of the test error minimizing model. B = 100 simulations were run. Figure 6 shows boxplots summarizing the results of these simulations.

Figure 6.

Boxplots summarizing minimum test error parameter profiles for different methods. Top left: minimum test error. Top right: number of non-zero parameters at minimum test error. Bottom: mean absolute difference from conditional mean method (left) and committee method (right) at minimum test error. p = 100, n = 2, m = 1.

The top left panel shows the minimum test error for each of the methods. Notice how both conditional and the multi-intercept unconditional methods outperform (slightly) the other two unconditional methods. The top right panel shows the number of non-zero β in the test error minimizing profile for each method. Notice how the conditional methods seem to select slightly fewer variables.

The bottom two panels show the mean absolute difference from the mean method β profile (left) and the committee method profile (right). It would seem that the two conditional methods produce very similar profiles, while conditional profiles differ somewhat from unconditional ones.

It should be noted that this is a difficult prediction problem:

• Each stratum has its own intercept. Test points then have intercepts unrelated to those in the training set and it is difficult to obtain good estimates for them from the training set.

• Even if we knew the intercept of a test point exactly, we force each stratum of size n to have $m=\lfloor \frac{n}{2}\rfloor$ cases. This means that even observations with small unconditional success probabilities (say below 0.5) could be forced to be cases. This makes it even more difficult for these methods to predict, because they tend to predict cases when the unconditional success probability computed from the parameter estimates is above 0.5.

Even though the prediction performance of the conditional methods and the multi-intercept unconditional method seems very similar, this may not speak to the quality of the β estimates of each, but rather to both methods’ inability to estimate intercepts well.

5.4. Pathological solutions

It is well known that the (unconstrained) unconditional logistic regression model produces pathological solutions when the data is perfectly separable. In particular, suppose that we have N data points (y_i, x_i) of which M are successes (cases). Also suppose we have only one regressor (so each $x_i\in \Re$). If max_yi=1 x_i < min_yi=0 x_i or max_yi=0 x_i < min_yi=1 x_i, the maximum likelihood estimate of β is driven to ±∞. There are 2×M! × (N − M)! arrangements of the x_i values that would lead to such a solution.

The problem is more severe for the conditional logistic model. Suppose that $N={\sum }_{k=1}^K{n}_k$ and $M={\sum }_{k=1}^K{m}_k$ so that we have K strata with n_k observations and m_k cases apiece. Now the pathology occurs when we have separation (in the same direction) in each stratum, i.e., max_yki=0 x_ki < min_yki=1 x_ki for all k or max_yki=1 x_ki < min_yki=0 x_ki for all k. The 2 × M! × (N − M)! arrangements above all satisfy these constraints and hence also lead to pathological solutions in the conditional model. There are, however, many more configurations that lead to separation (in the same direction) in each stratum.

Very large parameter estimates play havoc with optimization algorithms, leading to instability and rounding errors. More care needs to be taken in the conditional case and the final solution will probably need to be regularized more severely than for the unconditional case.

6. Cross validation

Since intercepts are conditioned away in the conditional likelihood, we cannot use standard cross validation (CV) techniques to estimate prediction error. These standard techniques leave out some data, find parameter estimates and then predict the left out data. The average error over all the left out data serves as an estimate of the prediction error of the model. We choose the λ that minimizes this prediction error.

Here we follow the approach of van Houwelingen, Bruinsma, Hart, van't Veer, and Wessels (2006) and estimate the CV error of the ith left out fold to be:

$${\widehat{CV}}_i\left(\lambda \right)=l\left({\beta }_{-i}\left(\lambda \right)\right)-l_{-i}\left({\beta }_{-i}\left(\lambda \right)\right),$$

where l_−i is the log-likelihood excluding part i of the data and β_−i(λ) is obtained by maximizing l_−i + λ∥β∥₁.

Data should be split by leaving out entire strata at a time. These seem to be the most appropriate sampling units. Note that the above formula then has a very simple form: merely the sum over the left out strata of each stratum's log conditional likelihood contribution. We choose the λ that maximizes ${\sum }_i{\widehat{CV}}_i\left(\lambda \right)$.

As illustration, consider the small dataset of Section 2.1. This CV method was applied to it, using 10 folds. Figure 7 shows the CV curve (multiplied by −1 so we look for a minimum). Two vertical lines are drawn: the leftmost is at the minimizing (log) λ , while the other is drawn at the smallest with CV value one standard deviation away from the minimum CV error. The method seems to select 3 predictors if the minimum is used.

Figure 7.

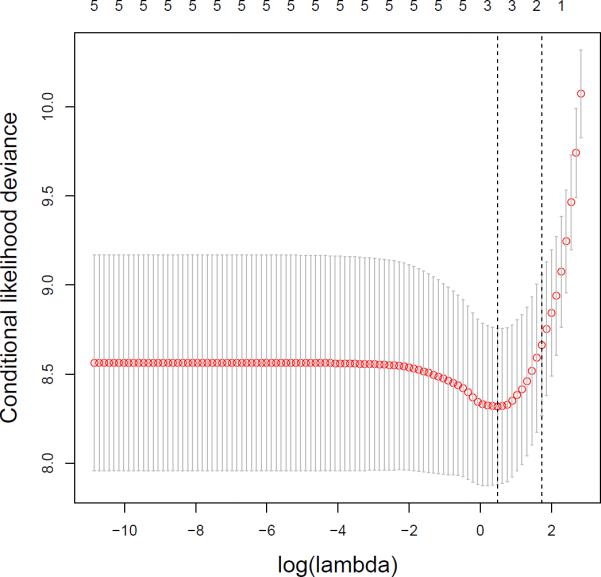
CV deviance curve (with standard error bands) for the endometrical cancer dataset. CV error seems to be minimized for a model with 3 predictors.

7. Discussion

We have applied the cyclic coordinate descent machinery to the fitting of conditional logistic regression models with lasso and elastic net penalties. Relatively efficient recursive algorithms were used to perform the computationally intensive task of computing normalizing constants, gradients and Hessians for the likelihood within strata.

Sequential strong rules greatly improve e ciency by allowing us to compute fewer score and Hessian entries at every iteration and streamlining the computation of these dependent quantities.

A comparison was made between the conditional and unconditional models on a simulated dataset favoring the conditional model. The conditional model seems to perform admirably both in variable selection and predictive performance, outperforming the unconditional model in the former, while doing at least as well as the unconditional model at the latter.