Ascertaining regions affected by GC-biased gene conversion through weak-to-strong mutational hotspots

Abstract

A major objective for evolutionary biology is to identify regions affected by positive selection. High d_N/d_S values for proteins and accelerated lineage-specific substitution rates for non-coding regions are considered classic signatures of positive selection. However, these could also be the result of non-adaptive phenomena, such as GC-biased gene conversion (gBGC), which favors the fixation of strong (C/G) over weak (A/T) nucleotides. Recent estimates indicate that gBGC affected up to 20% of regions with signatures of positive selection. Here we evaluate the impact of gBGC through its molecular signature of weak-to-strong mutational hotspots. We implemented specific modifications to the test proposed by Tang and Lewontin (1999) for identifying regions of differential variability and applied it to regions previously investigated for the influence of gBGC. While we found significant agreement with previous reports, our results suggest a smaller influence of gBGC than previously estimated, warranting further development of methods for its detection.

1. Introduction

1.1. Inference of positive selection

One of the main objectives in evolutionary molecular biology is the detection of selective forces and their genomic targets. This is particularly important for the human species, because it can reveal functionally important genomic regions as well as historical events that occurred during the emergence and evolution of humans. One major selection force is purifying, or negative, selection, which acts by removing from populations alleles that negatively impact the reproductive fitness of individuals. Additionally, genetic drift and positive selection are both acknowledged to significantly contribute to evolutionary change. In the case of genetic drift, allele frequencies increase or decrease due to chance, a process thought to apply to most genetic variants in human populations [1]. In the case of positive selection, the main driver for adaptive evolution, alleles with beneficial impact on individual fitness are preferentially retained in populations, and consequently their frequency increases. Well known examples of positive selection events identified in human include the increased prevalence of sickle-cell anemia as an adaptation to the threat of malaria [2], increased lactose tolerance as an adaptation to a milk-based diet [3, 4], lighter pigmentation as an adaptation for more efficient vitamin D synthesis [5–7], and altered metabolic rates as an adaptation to cooler climates [8].

Traditionally, adaptive evolution was identified in protein coding regions [9, 10] through increased rates of substitution at non-synonymous sites (d_N) relative to rates of substitution at synonymous sites (d_S), denoted by d_N/d_S. Values of d_N/d_S > 1 are considered by many as evidence of adaptive forces acting on corresponding genes because the rate at which mutations that change the amino acids occur at frequencies higher than the neutral rate (measured at synonymous sites). The availability of polymorphism data has allowed the development of new tests that make use of both population-based and comparative data by comparing levels of polymorphism and inter-species divergence, such as the McDonald-Kreitman test [11]. Moreover, the increasing number of complete genomes has further allowed the development of phylogeny-based tests on a genome-wide scale [12–14]. With the advent of next generation sequencing platforms, vast population data have become available, supporting the development and application of additional tests to detect adaptive forces (for a review of such tests see [15]). Recent years have seen an explosion in the number of reports of regions in the human genome being subject to adaptive forces, with more than one hundred such publications being currently recorded in dbPSHP, a database of recent positive selection in human populations [16].

The interest in finding protein-coding genes evolving under the influence of positive selection remains high, as such findings could provide intriguing insights into human development [17–19]. However, the idea that modification of regulatory elements may be responsible for many morphological differences between closely related species, such as human and chimpanzees [20], has motivated a search for non-coding regions that exhibit signs of positive selection [21]. Concentrating on putatively functional regulatory regions displaying deep conservation across many species, several studies have identified regions with accelerated rates of evolution both in the human lineage and other lineages [22–25]. These reports led to further fascinating discoveries, with some of these elements being documented in non-coding RNA genes with brain-specific activity [26], or as human-specific developmental enhancers [27].

1.2. The role of gBGC in confounding positive selection signatures

The finding of accelerated human-specific mutation rates is highly suggestive of the influence of positive selection with consequent evolutionary implications. Upon closer inspection, however, some of these regions have revealed unexpected mutational biases that favor changes from weak (A or T) to strong (C or G) nucleotides. For example, the 118-bp human accelerated region 1 (HAR1) contains 18 human-specific changes (HAR1 corresponds to hg18 coordinates chr20:61,203,939–61,204,056 here, but in other publications, e.g. [28], it corresponds to 106 bps at chr20:61,203,966–61,204,071, with 13 out of 14 human-specific changes shared between the two HAR1 definitions), all of them being of the weak-to-strong (W→S) type [26]. The ADCYAP1 gene accumulated a total of 20 human-specific mutations, all W→S, across the 231 bps that make exons 2 and 3 [29]. It becomes therefore problematic to interpret such findings as the result of adaptive forces, since there is no a priori mechanistic or functional reason for which positive selection should favor W→S mutations. An alternative explanation for the observed mutational bias is provided by a recombination-associated process, in which the mismatch repair machinery favors strong over weak alleles [30]. The phenomenon has been observed to occur preferentially in regions with high recombination rates [31–34] where it leads to a gene conversion bias favoring GC-alleles, known as GC-biased gene conversion (gBGC) [35]. A consequence of this recombination-associated phenomenon is a higher frequency or fixation of deleterious mutations [36, 37], supporting the hypothesis that excessive fixation of weak-to-strong mutations is not due to adaptive forces. However, because gBGC can lead to a burst in the lineage-specific mutation-rates, it could lead to the false discovery of positively selected regions [38]. This alternative explanation for some regions with human-specific accelerated mutation rates has fueled heated debate over the role of positive selection. For example, the human-specific mutations accumulated in the region of HACNS1 (also known as HAR2) were argued to be the combined result of both adaptive evolutionary forces and gBGC [27, 39], while evolutionary models incorporating the effect of gBGC could explain the same mutation pattern without the influence of adaptive forces [29, 35, 36, 40].

To help disentangle the effects of gBGC and positive selection, Ratnakumar et al. [29] have outlined three main distinctive features of the two phenomena: a) biased patterns of W→S mutations are only favored by gBGC; b) gBGC affects both neutral and functional sites, whereas positive selection affects functional sites only; c) gBGC is associated with regions of high male recombination. The second among these features is nicely illustrated by the example of the ADCYAP1 gene, where the d_N/d_S for exons 2 and 3 in the human lineage is estimated at 2.05 [29]. Although such a high value would normally be associated with positive selection, Ratnakumar and colleagues argued that the observed mutations could be explained within the context of gBGC alone. This argument is supported by the unusual high density of W→S mutations that extends in regions well beyond the limits of exons 2 and 3 (see Fig. 2 in [29]), consistent with the influence of gBGC and further supported by theoretical modeling. Here we propose that the property of gBGC to affect both functional and non-functional regions could be used in a specific test to evaluate its mutational impact. Specifically, a significant impact of gBGC would be assigned to genomic regions characterized by W→S mutational hotspots that contrast with their surroundings in terms of their density of W→S mutations.

2. Methods

2.1. Identification of mutational hotspots

Detection of mutational hotspots has been previously addressed by Tang and Lewontin [41], who proposed a test for detecting regions of differential variability (e.g. mutational hotspots or coldspots) based on empirical cumulative distribution function (ECDF) statistics [42]. In the context of DNA or protein sequences, the problem can be formulated with a given a number of n mutations in a sequence of size N, and their positions denoted by x_k, where k = 1, …, n and 1 ≤ x₁ < x₂ < … < x_n ≤ N. Positional deviations from the uniform distribution can be measured with the G function as follows:

$$G(x_k)=\frac{k}{n}-\frac{x_k}{N}.$$

Finding regions of differential variability involves finding regions bound by two mutations, i and j, where the G function is monotonically increasing or decreasing. For such regions, an overall deviation from a uniform distribution, ΔG_i,j, can be simply computed as the difference between the values of the G function at the two positions:

$$\mathrm{\Delta }{G}_{i,j}=G(x_j)-G(x_i),\text{where}1\le i<j\le n.$$

A statistical test, denoted here as TLW test for Tang-Lewontin test, can be applied to find whether any such region deviates significantly from what can be expected in the case of the null hypothesis of random mutation occurrence (i.e. probability of mutation is uniform across all sites). The T statistic for this test is defined as the ΔG_i,j with the highest absolute value among ΔG_i,j values computed for all regions where the G function is monotonically increasing or decreasing, and can be formalized as follows:

$$\begin{array}{c}T=\underset{\mathrm{\Delta }{G}_{i,j}\in \mathrm{\Gamma }}{\text{argmax}}\left|\mathrm{\Delta }{G}_{i,j}\right|,\text{where}\mathrm{\Gamma }={\mathrm{\Gamma }}_{+}\cup {\mathrm{\Gamma }}_{-},\\ {\mathrm{\Gamma }}_{+}=\left\{\mathrm{\Delta }{G}_{i,j};G(x_k)-G(x_{k-1})\ge -s,\forall 1\le i<k\le j\le n\right\},\\ {\mathrm{\Gamma }}_{-}=\left\{\mathrm{\Delta }{G}_{i,j};G(x_k)-G(x_{k-1})\le s,\forall 1\le i<k\le j\le n\right\},\text{and}s=\frac{0.3}{n}.\end{array}$$

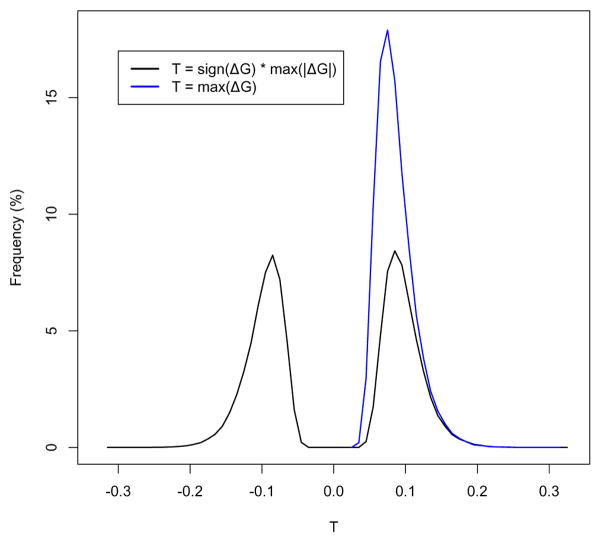
A null distribution for T can be constructed using Monte Carlo simulations, in which the x_k values are obtained by assigning to the n mutations random positions (without replacement) across the N space. The bimodal distribution in Figure 1 represents the null distribution of T for the case of N = 5000 and n = 60, also exemplified in [41]. The null distribution of T can be further used to find critical T* values for desired α levels of type I error.

Figure 1.

Distribution of the T statistic for the case of N = 5000 and n = 60 (these correspond to values used in Figure 2 in [41]). The modified TLW test makes use of the unimodal distribution (blue).

In the expressions above, s represents a smoothing parameter that allows a slight relaxation in the monotony of G to account for atypical random spacing [41]. In other words, in a region where G is to be considered almost monotonically increasing, ΔG_k,k+1 is allowed to be negative, but not with values smaller than −s. This is a simple smoothing procedure employed by Tang and Lewontin, who used a value of s = 0.005 for the case of N = 5000 and n = 60 [41]. This value corresponds to allowing two mutations to be located at a distance 30% greater than the average expected distance between two mutations (N/n). It also has the nice property that it determines the null bimodal distribution of T to be symmetrical around 0 (Figure 1), while no smoothing (s = 0) determines an asymmetrical distribution skewed toward positive values (data not shown).

2.2. Modifications of the TLW test for detecting hotspots of human-specific W→S mutations

Notably, the TLW test was originally proposed to identify regions of differential variability in the context of uniform background and mutational processes. The application of this test for identifying hotspots of human-specific W→S mutations requires several specific modifications of the test.

First, the null distribution of the T statistic needs only consider the case of mutational hotspots, but not coldspots. Specifically, we are interested in detecting hotspots of human-specific W→S mutations, the molecular signature of gBGC. Therefore the T statistic could be defined as the maximum among ΔG values computed for all intervals of monotonically increasing G (i.e. among values included in the Γ₊ set), or simply

$$T=max(\mathrm{\Delta }G).$$

Consequently, while the null distribution of the original T statistic is bimodal and centered around 0, the modified test statistic can only take positive values and its null distribution becomes unimodal (Figure 1).

Secondly, identifying regions affected by gBGC implies specifically finding hotspots of human-specific W→S mutations, a subset of all possible mutation types. Consequently, applying the TLW specifically to W→S mutations ignores all the other mutations types at the risk of identifying regions not specifically associated with gBGC. This is because other phenomena, including bona fide positive selection, can increase the W→S mutation rate relative to surrounding regions by virtue of higher unbiased fixation rates for all substitution types. To account for the influence of other mutational phenomena, we compute an adjusted function, denoted G^a, based on the number of human-specific mutations that are not of the W→S type. Specifically, we first compute two G functions, Gⁿ corresponding to the number of human-specific W→S substitutions (n), and G^h corresponding to the entire set of human-specific substitutions (h, where n ≤ h ≤ N):

$$\begin{array}{c}{G}^n(x_k)=\frac{k}{n}-\frac{x_k}{N},\text{where}k=1,\dots ,n,\text{and}\\ G^h(x_k)=\frac{k}{h}-\frac{x_k}{N},\text{where}k=1,\dots ,h.\end{array}$$

We then compute two sets of corresponding ΔG values between consecutive W→S mutations:

$$\begin{array}{l}\mathrm{\Delta }{G^n}_k=G^n(x_k)-G^n(x_{k-\mathit{1}}),\text{where}k=1,\dots ,n\text{and}{G}^n(x_{\mathit{0}})=0;\\ \mathrm{\Delta }{G^h}_k=G^h(x_k)-G^h(x_{k-\mathit{1}}),\text{where}k=1,\dots ,n\text{and}{G}^h(x_{\mathit{0}})=0.\end{array}$$

The G^a function is then computed using adjusted ΔG^a values between consecutive W→S mutations:

$$\begin{array}{c}{G}^a(x_k)=G^a(x_{k-\mathit{1}})+\mathrm{\Delta }{G^a}_k,\text{where}k=1,\dots ,n,G^a(x_{\mathit{0}})=0,\text{and}\\ \mathrm{\Delta }{G^a}_k=\mathrm{\Delta }{G^n}_k-\mathrm{\Delta }{G^h}_k·\frac{h-n}{h}.\end{array}$$

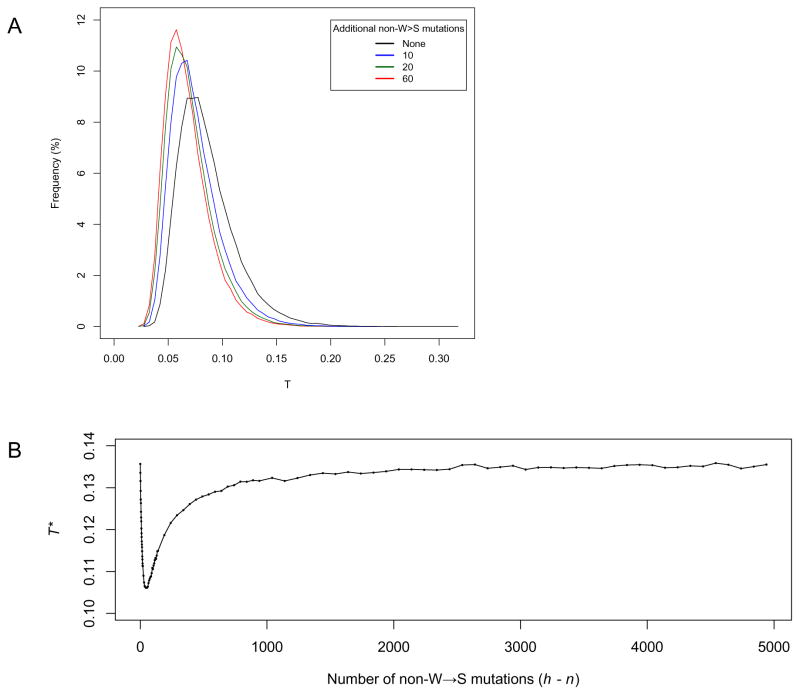
In order to compute the T null distribution, as well as T* critical values, we replaced the original G function with G^a. We also adjusted the smoothing parameter proportionally with the number of non-W→S human-specific mutations (s^a = sⁿ − s^h · (h − n)/h ). To illustrate how non-W→S mutations influence the distribution of T, and consequently of T* critical values, we use the same numerical example with 60 mutations (n = 60) in a 5 kb sequence (N = 5000). If we consider n to be the number of W→S mutations, the number of other mutation types can vary between 0 (h = n) and 4940 (h = N − n, or 5000 – 60). When h = n, the term h − n in the expression of ΔG^a_k becomes 0, and therefore no correction is applied (ΔG^a_k = ΔGⁿ_k). Also, when h = N − n, all positions along the sequence are occupied with a mutation, resulting in a uniform distribution of all mutations and consequently in ΔG^h values of 0. This leads again to no correction being applied because ΔG^a_k = ΔGⁿ_k. In between these two extremes, for n < h < N − n, all correction values for monotonically increasing intervals are positive, resulting in smaller values of T and shifted T distributions (Fig. 2A). The critical T* values mirror this aspect, taking highest values when h = n and h = N − n, and lower values in between these extremes (Fig. 2B). One can see that T* values decrease sharply for h values immediately above n, with minimum values occurring when the number of other mutation types is comparable to the number of W→S mutations (e.g. n = 60, h − n = 20, …, 120). This amount of relative occurrence for different mutation types is commonly found among cases investigated in this study, underscoring the importance of this correction.

Figure 2.

The influence of non-W→S substitutions on the T statistic and its critical values. A) Examples of T distributions for N = 5000, n = 60, and G adjusted for the presence of additional non-W→S human-specific substitutions (h − n): 0 (black), 10 (blue), 20 (green), 60 (red). B) Variation of the critical T* value (defined as the 95^th percentile of the T distribution) relative to the number of non-W→S mutations, when N = 5000, n = 60.

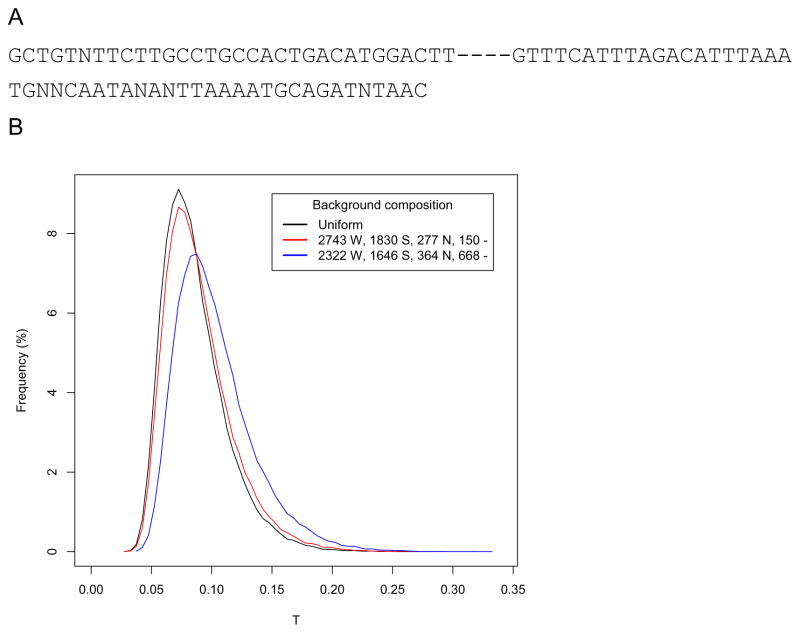
Thirdly, the original TLW test was developed for the general case where the probability of mutations was uniform across the region investigated. In contrast, the detection of human-specific mutations does not have uniform probability across all sites, being largely dependent on the ability of unambiguously defining the ancestral alleles for each site. For example, in the case of human-chimp-macaque three species alignments, positions where human-specific mutations can be defined are those where the outgroup sequence of macaque is identical to the chimp sequence. Moreover, the detection of a W→S mutation in human requires that ancestral sites must contain a consensus A or T nucleotide (Fig. 3A). Given these restrictions, it becomes clear that the probability of detecting W→S mutations is not uniform and that the background alignment is specific to each investigated region. Consequently, the null distribution of T needs to be constructed with respect to the corresponding consensus chimp-macaque sequence. In Figure 3B we show how the distribution of T constructed with specific non-uniform backgrounds varies relative to the case of uniform background where all mutations can occur at any position with equal probability. We notice that the number of gaps, where neither W→S nor other human-specific substitutions can occur, has a large impact on the distribution of T. This effect is particularly large when the gaps form long stretches, because they cause all mutations to be artificially agglomerated in non-gap regions. This positional bias artificially inflates ΔG and, consequently, T values. However, computing the null distribution of T specifically on this gapped background sequence leads to distributions shifted toward higher T values (Fig. 3B), and consequently higher T*, effectively controlling for the gap-induced bias.

Figure 3.

The influence of the chimp-macaque consensus sequence on the distribution of T. A) Example of chimp-macaque consensus sequence (corresponds to chr16:76918109–76918194 in hg18). For simulation purposes, W→S mutations are randomly placed at weak consensus nucleotides (A or T, green), other mutation types can be placed at both weak and strong consensus nucleotides (C or G, orange), while no mutation can be placed at discordant positions (N, black) and gaps (“-”). B) Null distributions of T for the case of N = 5000 and n= 60 under the null with uniform background (black) and two specific consensus sequences (red and blue). W – number of weak (A or T) nucleotides, S – number of strong nucleotides (C or G), N – number of discordant positions, “-” – number of gaps.

We applied our modified TLW test to the case of ADCYAP1, and found that exons 2 and 3 reside in a significant (P < 10⁻⁴) hotspot comprising 69 W→S mutations (Fig. 4). This finding not only replicates, but also quantifies the previously described high incidence of W→S substitutions at ADCYAP1 and confirms the capacity of our approach to detect gBGC documented at this locus [29].

Figure 4.

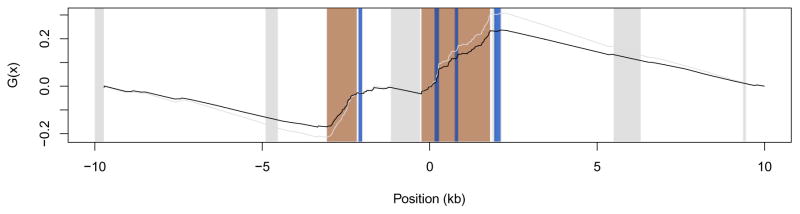
Graph of the G functions computed with human-specific substitutions in the ADCYAP1 genomic region. The black line represents the adjusted G^a function, the grey line corresponds to the original G function, and dots correspond to positions of human-specific W→S mutations. Blue bars correspond to ADCYAP1 coding region, regions in orange correspond to significant hotspots of W→S mutations, and gray bars correspond to alignment gaps longer than 50 bps.

2.3. Identification of human-specific mutations and sequence background

For the purpose of identifying human-specific mutations and determining the background sequence necessary for computing region-specific null distributions of the T statistic we used three sets of multiple sequence alignments. For the analysis of HARs we used human – chimpanzee – macaque (hg18 – panTro2 – rheMac2) alignments extracted from 28-way vertebrate alignments that are available at the UCSC Genome Browser (http://hgdownload.soe.ucsc.edu/goldenPath/hg18/multiz28way/), which were the same set of alignments used by Kostka et al. [28]. Specifically, we extracted the rows containing the human, chimpanzee, and macaque sequences, and retained only the alignment blocks that contained all three species. We further stitched together contiguous alignment blocks (i.e. alignment blocks with consecutive coordinates for all three species) and eliminated the alignment columns containing only gaps, as well as columns corresponding to gaps in the human sequence. Considering only chromosomes 1–22, X, Y, these alignments cover 2.36 Gb of the human genome in a total of 1.14 million alignment blocks. We also took advantage of MULTIZ alignments computed specifically for these three species [43] and repeated our analyses with these alignments available from the Galaxy web site (http://galaxy.psu.edu). Compared to sequence alignments where more species are considered, these offer the advantage of being less fragmented while maintaining similar coverage of the human genome (0.73 million alignment blocks cover 2.33 Gb). For the analysis of regions included in the phastBias gBGC tracts [32], we used the same alignments as Capra et al. [32], specifically, human – chimpanzee – orangutan – macaque (hg18 – panTro2 – ponAbe2 – rheMac2) alignments extracted from 44-way vertebrate alignments (http://hgdownload.soe.ucsc.edu/goldenPath/hg18/multiz44way/). In this case we retained alignment blocks that contained sequences from human, chimp and at least one outgroup species, either orangutan or macaque sequences, and which were further processed as described above. They cover 2.61 Gb of the human genome, in a total of 1.89 million alignment blocks.

The consensus positions in the underlying sequence were determined as the positions where the chimpanzee sequence was identical to macaque in the case of three-way alignments, and to either outgroup species in the case of four-way alignments. Discordant positions (“N” in Figure 3A) are positions where the chimpanzee sequence is different from either outgroup species, while gaps are assigned to positions where either the chimpanzee or both outgroup species contain gaps. Human-specific mutations were determined at positions where the human sequence is different from chimpanzee at consensus positions.

3. Results

While the detection of a significant W→S hotspot at the ADCYAP1 locus is consistent with a region under the influence of gBGC, we wanted to assess the suitability of the modified TLW for detecting gBGC at regions previously evaluated through other methods. For this purpose we applied this test to the previously described set of 202 human accelerated regions (HARs), which were identified as having significantly elevated rates of human-specific substitution [22]. Subsequent studies have tried to evaluate the impact of gBGC on the observed human-specific substitution rates, in line with ongoing concerns for the false identification of positively selected regions [29, 40]. Katzman and colleagues used population specific polymorphism data in 40 kb regions surrounding HARs, although such data can only be used to detect ongoing gBGC at the population level, but not species-specific gBGC that occurred after the split from chimpanzee [44]. More recently, Kostka et al. [28] have implemented a series of likelihood ratio tests (LRT) to determine the combined contribution of gBGC and positive selection. They assigned HARs to different classes to account for different intensities of positive selection and gBGC. One class, denoted C_b+, contained 32 HARs found to evolve under the strong influence of gBGC (four of these were assigned to the C_b+ class only after masking human- and chimp- ancestral CpG sites). Furthermore, Capra et al. [32] performed a genome-wide scan with a probabilistic model for the occurrence of gBGC, and defined a set of 9,370 such regions. Therefore, we used these datasets as reference for detecting the influence of gBGC using the modified TLW test.

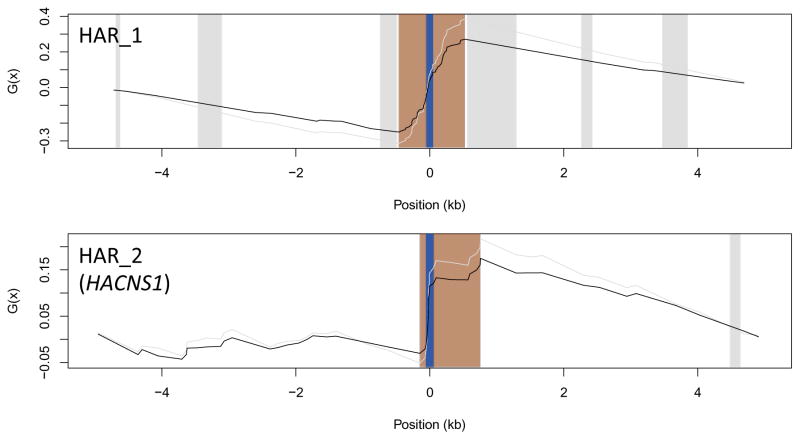
As a first step in applying the modified TLW test, we determined the chimp-macaque consensus sequences and the positions of human-specific mutations (W→S and all the other types) in regions around every HAR using human – chimpanzee – macaque alignments extracted from 28-way vertebrate alignments (see Methods). We first considered 5 kb centered on the midpoint of every HAR, and subsequently extended to regions of 10, 20, 30, and 40 kb to evaluate the influence of surrounding regions of different sizes. We detected the presence of W→S hotspots using the G^a function computed for each HAR and surrounding region combination. The influence of gBGC on a given HAR was dismissed if no hotspot was found to overlap the HAR. However, if a hotspot was detected, we determined its significance using the null distribution of the T statistic computed with 10,000 rounds of replicates specifically for that genomic region and number of substitutions. We randomly assigned human-specific W→S mutations to chimp-macaque consensus weak (A, T) positions, and other types of human-specific mutations to any chimp-macaque consensus position. Mutations were not assigned to discordant or gap positions. If the observed statistic was found to be significant at α=0.05, the HAR was considered to evolve under the strong influence of gBGC. For example, HAR1 and HAR2 (also known as HACNS1) have clear signals denoted by large regions of monotonically increasing G^a (Fig. 5), in agreement with previous reports of strong influence of gBGC at these loci [28, 40]. Overall, we found 25 HARs that overlap significant hotspots of W→S mutations in at least one of the five genomic environments considered, a number that reduces to 9 if correction for multiple testing (false discovery rate of 5%) is applied (Tables 1, S1). Since both our modified TLW test and the LRTs implemented by Kostka et al. [28] were designed to detect the impact of gBGC, we expect to observe a significant overlap between the findings of these two approaches. Indeed, we find that 13 out of 25 HARs (P=5.4×10⁻⁶, one-sided Fisher’s exact test) in our set were also included among the 32 HARs assigned to the C_b+ class, strongly supporting the convergence of both methods to detect the influence of gBGC (the overlap remains significant after correction for multiple testing, with five out of nine HARs, P=5.9×10⁻³). However, our results indicate that the number of HARs under the influence of gBGC is lower than reported by Kostka et al. [28], even if we consider the masking effect of stronger hotspots (Tables 1, S1). In contrast, our results are more similar both in size and significance of overlap (10 out of 25 HARs, P=3×10⁻⁸; if correction for multiple testing is considered, six out of nine HARs, P=1.5×10⁻⁶) with the more recent findings of Capra et al. [32], who found 13 HARs overlapping phastBias gBGC human tracts. Our estimates remain almost identical when the impact of gBGC is evaluated using human – chimpanzee – macaque alignments computed specifically for these species (see Methods, Table S2), indicating that our findings are robust relative to the alignments considered.

Figure 5.

The adjusted G^a function (black line) exemplified for the cases of HAR1 and HAR2, which are denoted by blue bars. Regions in orange correspond to significant hotspots of W→S mutations, and gray bars correspond to alignment gaps longer than 50 bps. The original G function is represented by a grey line.

Table 1.

Number of regions of interest that overlap significant hotspots of W→S mutations. Hotspots were evaluated in the context of genomic regions of different sizes, as indicated (e.g. 5 kb corresponds to a genomic region encompassing 2.5 kb upstream and 2.5 kb downstream of the HAR midpoint). FDR5 indicates the number of hotspots that pass the significance threshold of 5% false discovery rate; “Overall” indicate the total number of significant hotspots regardless of the size of the genomic region considered around HARs (i.e. union of those subsets); numbers in parentheses include HARs that overlap significant hotspots of W→S mutations if the masking effect of stronger hotspots was considered for second and third ranking hotspots.

Type of correction for multiple testing	Size of HAR genomic surroundings					Overall
	5 kb	10 kb	20 kb	30 kb	40 kb
HARs (out of 202)
No correction	18 (21)	12 (20)	10 (17)	12 (13)	10 (12)	25 (36)
FDR5	7 (7)	4 (5)	3 (3)	2 (4)	3 (4)	9 (11)
phastBias gBGC tracts (out of 9370)
No correction	5156 (5355)	4818 (5272)	4024 (4895)	3552 (4680)	3213 (4447)	6343 (7211)
FDR5	4087 (4269)	3659 (4152)	2580 (3488)	2017 (3188)	1699 (2946)	5131 (6068)

We then applied the modified TLW test to the entire set of 9,370 phastBias gBGC tracts by considering surrounding genomic regions of 5, 10, 20, 30, and 40 kb. We found that 6,343 (67.7%) tracts overlap a significant hotspot (before correction for multiple testing) in at least one of the five settings of genomic environment considered (Tables 1, S3). This number indicates that the majority of phastBias gBGC tracts (especially if masking effect for second or third ranking hotspots are considered; Tables 1, S3) do indeed detect regions that contrast strongly with the surrounding regions regarding the density of human-specific W→S mutations, consistent with a strong effect of gBGC. However, if any correction for multiple testing is considered, the number of tracts overlapping significant W→S hotspots decreases considerably (Tables 1, S3), indicating that the model-based approach implemented by Capra et al. [32] also detects a high number of regions (even if no correction for multiple testing is considered, this estimate approaches a quarter of all regions) where the presumed influence of gBGC does not produce W→S mutation hotspots that contrast significantly with the surrounding regions, and therefore are inconsistent with a strong impact of gBGC. An additional aspect that also contributes toward a higher rate of false positives is the influence of simple repeats. Unlike the case of HARs, which are regions detected in highly conserved regions, phastBias gBGC tracts are evaluated genome-wide irrespective of the underlying sequence. Of particular concern are simple repetitive regions, where the apparent effect of gBGC (e.g. hotspots of W→S mutations) could be due to alignment artifacts, or where apparent human-specific mutations could result from lineage-specific microsatellite amplification. For example, the phastBias gBGC tract defined between chrX:27164797–27165013 contains a significant hotspot of nine W→S mutations determined between a repeated TA dinucleotide in chimpanzee and orangutan and a CA dinucleotide in human (Fig. 7), which is unlikely to have been caused by gBGC. We found a total of 148 phastBias gBGC tracts with significant hotspots of W→S mutations that are annotated over at least 50% of their span as simple repeats (Table S4). In all these regions the effect of gBGC is therefore questionable. Overall, our results indicate that a strong influence of gBGC can be detected in fewer regions than estimated previously.

Figure 7.

Example of human-specific W→S mutational hotspot located in simple repeat region. The hotspot is located at chrX:27164869–27164885, and shown here along with four flanking nucleotides in the four species alignment. Species are indicated by the names assigned to their genome assemblies. Vertical bars indicate positions of identified human-specific mutations (in this case all mutations are T→C).

4. Discussion

Protein-coding genes or non-coding regions with lineage-specific accelerated rates of evolution are highly sought-after for their potential relevance to adaptive evolution, wherein mutations represent characters of great importance for species evolution. However, an alternative explanation to positive selection is provided by phenomena not linked to adaptive forces, such as gBGC, which could also lead to higher fixation rates in limited regions and thus could confound the detection of positive selection. While methods for the detection of gBGC have been proposed previously [28, 29], such methods depend on complicated models and make several assumptions that cannot be always verified. We postulate that an independent and radically different method might help refine the evaluation of gBGC. Here we take advantage of the gBGC property to affect both functional and neutral sites to propose an alternative method to detect gBGC. Since gBGC leads to the emergence of W→S mutations, we proposed and assessed a modified TLW test to detect hotspots of W→S mutations, as a distinguishing feature of gBGC.

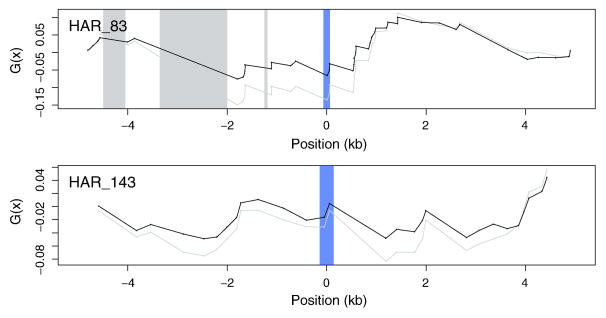
We show that a significant fraction of the regions found previously to evolve under the influence of gBGC also overlap significant hotspots of W→S mutations. However, our conservative estimate (i.e. after correction for multiple testing) includes less than one third of the previously reported number of HARs (9 out of 32), raising questions about the remaining HARs assigned to class C_b+, such as HAR_83 and HAR_143 (Fig. 6). One possibility is that such HARs could have evolved under the strong influence of gBGC only for short evolutionary periods. Such cases would fail to reach significance in the modified TLW test, but they could be considered better candidates for other evolutionary classes with a diminished impact of gBGC. Alternatively, these represent LRT false positive cases, supported by the fact that they are also not overlapping phastBias gBGC tracts. The problem of overestimating the influence of gBGC is apparent also in the set of phastBias gBGC tracts, since nearly one third of those do not have a significant W→S mutational hotspot that contrasts with the surrounding genomic regions. It is nonetheless possible that gBGC could have influenced these regions to a lesser extent (i.e. for a shorter period or with reduced intensity) and caution is advised in interpreting any mutational signals detected in such regions. It is also possible that the rate of false positives in phastBias tracts relative to significant W→S hotspots could be further reduced if the masking effect of neighboring hotspots is pursued more aggressively. In this study we only considered the masking effect in the case of hotspots that are ranked second or third in the considered genomic environment, which increased the number of phastBias regions with significant hotspots (before applying correction for multiple testing) from 67% to slightly above 75% (Tables 1, S3).

Figure 6.

The G^a function (black line) for genomic regions surrounding HAR83 and HAR143, which are both assigned to the C_b+ class, but do not overlap significant hotspots of W→S mutations. Blue bars correspond to HARs, while grey regions correspond to alignment gaps longer than 50 bps. The original G function is represented by a grey line.

Additionally, there are also HARs that are located within W→S hotspots that reach significance under the modified TLW test, but were not previously assigned to the class evolving under the strong influence of gBGC. Among the conservative set of nine HARs with significant W→S hotspots (Table 1), four (HAR_15, HAR_80, HAR_88, and HAR_98) were not assigned to the C_b+ class. Their non-inclusion in class C_b+ cannot be explained by a high number of non-W→S mutations because all of them have only one non-W→S mutation in addition to 2 to 4 W→S mutations. They most likely represent LRT false negative cases, since three of them also overlap phastBias gBGC tracts. The exception is HAR_98, which overlaps a hotspot with 12 W→S mutations that remains significant after correction for multiple testing only in the context of 5 kb surrounding sequences. This could be thought of as a false positive of the modified TLW test, as it does not pass the threshold of a more stringent correction for multiple testing (e.g. Bonferroni). Alternatively, it could be also thought of as a false negative of the phastBias approach, as its model is based on genome-wide data that might miss weaker signals. Ideally, such discordant findings could be resolved with additional independent methods. Other methods of investigating gBGC have been proposed, such as using the derived allele frequency spectrum of W→S substitutions in a population-based study. In one particular study [44], polymorphism data were collected by sequencing 40 kb flanking 49 HARs of interest (along with 13 control regions), but the authors acknowledged they could not resolve the above controversy for at least two reasons: i) forces generating the bias toward W→S substitutions are not constant over time, so regions detected through human-chimp-macaque comparisons might not be detected in current population studies; ii) potential signals detected in this manner might not come from the hotspot around the HAR of interest, since multiple W→S hotspots could exist in a 40 kb region.

The robustness of the modified TLW test is underscored by the significant agreement with previous methods in identifying the influence of gBGC on the mutational profiles of HARs. Notable, the overlaps with the results of Kostka et al. [28] and Capra et al. [32] are independently more significant (see Results) than the overlap between the results of these two methods (out of 32 and 13 HARs, respectively, six are common between them, P=7.6×10⁻³, one-sided Fisher’s exact test). This argues for the utility of the modified TLW test on a genome wide scale. For example, it can be used to prioritize regions of interest based on the strength of the W→S mutational hotspots found to overlap phastBias gBGC tracts, or even refine the boundaries of such regions. If we only consider the conservative set of 5,131 phastBias tracts that overlap a significant W→S hotspot in at least one of the five situations considered, nearly 80% of them (4,078) overlap a hotspot that extends beyond their boundaries, and thus they do not capture the entire set of W→S mutations that are the hallmark of gBGC.

Overall, the modified TLW test indicates that the influence of gBGC might not strongly influence as many HAR and phastBias gBGC tracts as reported previously. The discrepancy between the modified TLW test and previous methods varies based on the strength of correction imposed for multiple testing. For example, if we apply the Bonferroni correction instead of using a false discovery rate threshold of 5% in analyzing the HARs, we only find six HARs that overlap significant W→S hotspots: HAR_1, HAR_2, HAR_42, HAR_80, HAR_88, and HAR_105. Thus our findings indicate that most HARs and a non-negligible fraction of phastBias gBGC tracts are not strongly influenced by gBGC, which warrants further investigation of adaptive forces contributing to the fixation of mutations in these regions and refining of methods for detecting the effect of gBGC.

Highlights.

• We propose a new method for detecting regions with strong GC-biased gene conversion

• The method relies on detecting hotspots of weak-to-strong (A,T>C,G) mutations

• A hotspot detection method was adapted for lineage-specific weak-to-strong mutations

• We found significant overlap with results based on molecular evolutionary models

• Our results suggest lower impact of gBGC on HARs than previously estimated