Shape Classification Using Wasserstein Distance for Brain Morphometry Analysis

Abstract

Brain morphometry study plays a fundamental role in medical imaging analysis and diagnosis. This work proposes a novel framework for brain cortical surface classification using Wasserstein distance, based on uniformization theory and Riemannian optimal mass transport theory.

By Poincare uniformization theorem, all shapes can be conformally deformed to one of the three canonical spaces: the unit sphere, the Euclidean plane or the hyperbolic plane. The uniformization map will distort the surface area elements. The area-distortion factor gives a probability measure on the canonical uniformization space. All the probability measures on a Riemannian manifold form the Wasserstein space. Given any 2 probability measures, there is a unique optimal mass transport map between them, the transportation cost defines the Wasserstein distance between them. Wasserstein distance gives a Riemannian metric for the Wasserstein space. It intrinsically measures the dissimilarities between shapes and thus has the potential for shape classification.

To the best of our knowledge, this is the first work to introduce the optimal mass transport map to general Riemannian manifolds. The method is based on geodesic power Voronoi diagram. Comparing to the conventional methods, our approach solely depends on Riemannian metrics and is invariant under rigid motions and scalings, thus it intrinsically measures shape distance. Experimental results on classifying brain cortical surfaces with different intelligence quotients demonstrated the efficiency and efficacy of our method.

1 Introduction

Wasserstein distance has been widely studied and applied for shape analysis, due to its significant power to intrinsically compare similarities between shapes. Wang et al. [29] proposed a linear optimal transportation framework for comparing images. Schmitzer et al. [23] proposed Wasserstein based method for joint variational object segmentation and shape matching. Hong et al. [11] introduced a shape feature that characterizes local shape geometry for shape matching based on Wasserstein distance. However, these methods for shape analysis only work for 2D images. With the fast development of 3D scanning technologies, 3D shapes become more and more popular and analyzing 3D surfaces becomes important in medical imaging field.

3D surface based brain morphometry analysis usually takes brain thickness morphometry features [25]. Recent work [31, 32] showed that surface area feature may be independent of cortical thickness and itself provides a unique and important morphometry feature to study brain structural MRI images. With the clinical questions of interest moving towards identifying very early signs of brain functional and diseases, the corresponding statistical differences at the group level become weaker and harder to identify. An efficient and effective framework with a rigorous theoretical guarantee to classify brain cortical surfaces into different categories would be highly desired for preclinical imaging study.

Due to the difficult boundary parameterization and high dimension, conventional 2D shape classification methods can not be easily extended to 3D shape classification problems. Many methods have been proposed in order to describe shapes. Statistical based method [4] [22] represent objects with feature vectors in a multidimensional space, but they are not discriminating enough to make subtle distinctions between shapes. Topology based method [10] computes 3D shape similarity by comparing Multiresolutional Reeb Graphs, yet they can not describe the geometric differences. Geometry based method [17] [20] compare 3D shapes by embedding them to into canonical space, but the classifications are too restrictive. Shape space models have been proposed to provide suitable mathematical and computational descriptions for both shape representation and comparisons [16] [24] [33].

Therefore, in this work we first generalized the optimal mass transport map from Euclidean metrics to Riemannian metrics, such that our proposed framework is applicable to any general Riemannian manifolds. The computation is based on geodesic power Voronoi diagram which is an extension of the work [30].

According to Poincare uniformization theorem [21], all shapes can be conformally mapped to one of three canonical spaces: the unit sphere, the Euclidean plane or the hyperbolic plane. The area-distortion factor by the uniformization map gives a probability measure on the canonical uniformization space. All the probability measures on a Riemannian manifold form the Wasserstein space. Given 2 probability measures, there exists a unique optimal mass transport map between them. The transportation cost induced by the optimal mass transport map defines the Wasserstein distance between the two probability measures. Wassertein distance gives a Riemannian metric for the Wasssertein space. Figure 1 shows the computation of the proposed Riemannian optimal mass transport map between two brain cortical surfaces.

Fig. 1.

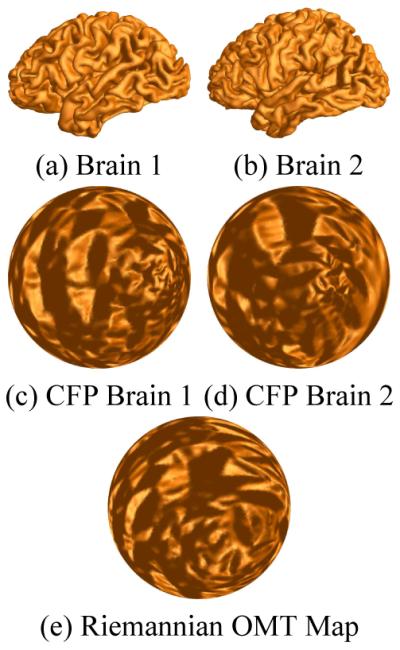
The computation of Wasserstein distance between the left hemisphere brain cortical surfaces. (a) shows an example of a 20-year-old female, with IQ score 88.89; (b) shows an example of a 21-year-old male, with IQ score 33.33. (c) and (d) are the spherical conformal parameterization (CFP) of (a) and (b), respectively. (e) shows the Riemannian optimal mass transport (OMT) map result from (c) to (d), which induces the Wasserstein distance between (a) and (b).

With the tools of uniformization mapping and our Riemannian optimal mass transport map, we proposed a novel framework for shape classification by Wasserstein distance. We applied our method for brain morphology study to classify human brain cortical surfaces with different intelligence quotient. The experimental results and comparisons with previous methods demonstrated the efficiency and efficacy of our method.

In summary, the main contributions of this work are as follows:

1. Introduced the optimal mass transport map to general Riemannian manifolds, which greatly improves the applicability of optimal mass transport map for shape analysis.

2. Presented a novel 3D shape classification framework for brain morphometry analysis using Wasserstein distance, based on uniformization theory and our Riemannian optimal mass transport map.

2 Previous Work

Brain morphometry study plays a fundamental role in medical imaging[14] [18] [19]. Chaplota et al [7] introduced a method using wavelets as input to neural network self-organizing maps and support vector machine for brain MR images classification. Singh et al. [27] presented an approach to classify an autistic group from controls using structural image. Zacharaki et al. [34] proposed brain tumor classification method combining conventional MRI and perfusion MRI. Im et al. [12] studied the brain complexity by interpreting the variation of Fractal dimension in the cortical surface of normal controls through multiple regression analysis with cortical thickness, sulcal depth, and folding area.

Various surface based shape analysis and classification methods were also proposed to solve real 3D shape problems. Unnikrishnan et al. [26] presented a multi-scale operators on point clouds that captures variation in shapes. Mahmoudi et al. [20] represented shapes by computing the histogram of pairwise diffusion distances between all points. Kurtek et al. [16] provided a Riemannian framework for computing geodesic paths which are important for comparing and matching 3D shapes. Jermyn et al. [13] defined a general elastic metric on the space of parameter domains for shape comparisons and analysis.

Compared with the elastic shape metric methods [13] [16], our metric is intrinsic yet theirs is extrinsic. The elastic shape (extrinsic) metric methods need to embed the surfaces into ${\mathbb{R}}^3$, which is not necessary in our method. The elastic shape metric assumes two shapes are isotopic. However, the proposed intrinsic method is applicable for general Riemannian manifolds. Our approach solely depends on Riemannian metrics and is invariant under rigid motions and scalings such that it intrinsically measures shape distance, and thus more effective and efficient for shape classification and brain morphology analysis.

3 Theory

This section briefly introduces the theoretic foundation, for thorough treatments, we refer readers to [9] for conformal geometry, and [15], [6] for optimal mass transport theory.

3.1 Conformal Mapping

Suppose S is a topological surface, a Riemannian metric g on S is a family of inner products on the tangent planes. Locally, a metric tensor is represented as a positive definite matrix (ɡ_ij). Let φ : (S₁, g₁) → (S₂, g₂) be a diffeomorphic map between two Riemannian surfaces, the pull back metric on the source induced by φ is φ*g₂ = J^T g₂J, where J is the Jacobian matrix of φ. The mapping is conformal or angle-preserving, if the pull back metric and the original metric differ by a scalar function, φ*g₂ = e^2λg₁, where $\lambda :S_1\to \mathbb{R}$ is called the conformal factor.

Hamilton’s surface Ricci flow conformably deforms the Riemannian metric proprotional to the curvature, such that the curvature evolves according to a non-linear heat diffusion process, and becomes constant everywhere.

Definition 1 (Surface Ricci Flow)

The normalized surface Ricci flow is defined as

$$\frac{{\mathit{dg}}_{\mathit{ij}}(p,t)}{\mathit{dt}}=\left(\frac{4\pi \chi \left(S\right)}{A\left(0\right)}-2K(p,t)\right)g_{\mathit{ij}}(p,t),$$

where χ(S) is the Euler characteristic number of the surface, A(0) is the total area at the initial time.

Theorem 1 (Uniformization)

Suppose (S, g) is a closed compact Riemannian surface with genus ɡ, then there is a conformal factor function $\lambda :S\to \mathbb{R}$, such that the conformal metric e^2λg induces constant Gaussian curvature. Depending on the χ(S) is positive, zero or negative, the const is +1, 0 or −1.

In the current work, we apply surface Ricci flow to deform the human cortical surface to the unit sphere.

3.2 Optimal Mass Transport

The Optimal mass transportation problem was first raised by Monge[5] in the 18th century. Suppose (S, g) is a Riemannian manifold with a metric g. Let μ and ν be two probability measures on S with the same total mass ∫_S dμ = ∫_S dν, φ : S → S be a diffeomorphism, the pull back measure induced by ν is φ*ν = det(J)ν ○ φ. The mapping is called measure preserving, if the pull back measure equals to the initial measure, φ*ν = μ. The transportation cost of φ is defined as

$$\mathcal{C}\left(\phi \right)≔{\int }_S{d}_{\mathbf{g}}^2(p,\phi (p\left)\right)d\mu \left(p\right).$$ (1)

The optimal mass transportation problem is to find the measure preserving mapping, which minimizes the transportation cost,

$$\begin{array}{c}\hfill {\min }_{\phi }\mathcal{C}\left(\phi \right)\hfill \\ \hfill s.t.\phi :S\to S,{\phi }^{\ast }\nu =\mu \hfill \end{array}$$

In the 1940s, Kantorovich introduced the relaxation of Monge’s problem and solved it using linear programming method [15].

Theorem 2 (Kantorovich)

Suppose (M, g) is a Riemannian manifold, probability measures μ and ν have the same total mass, μ is absolutely continuous, ν has finite second moment, the cost function is the squared geodesic distance, then the optimal mass transportation map exists and is unique.

If $S\subset {\mathbb{R}}^n$ is a convex domain in the Euclidean space, then Brenier proved the following theorem.

Theorem 3 (Brenier)

There is a convex function $u:S\to \mathbb{R}$, the optimal map is given by the gradient map p → ▽u(p).

Solving the optimal transportation problem is equivalent to solve the following Monge-Amperé equation,

$$\mathit{det}\left(\frac{{\partial }^{2}u}{\partial x_i\partial x_j}\right)\nu \circ \nabla u\left(\mathrm{x}\right)=\mu \left(\mathrm{x}\right).$$

3.3 Wasserstein Metric Space

Suppose (S, g) is a Riemannian manifold with a Riemannian metric g.

Definition 2 (Wasserstein Space)

For p ≥ 1, let ${\mathcal{P}}_p\left(S\right)$ denote the space of all probability measures μ on M with finite p^th moment, for some x₀ ∈ S, ∫_S d(x, x₀)^pdμ(x) < +∞, where d is the geodesic distance induced by g.

Given two probability μ and ν in ${\mathcal{P}}_p$, the Wasserstein distance between them is defined as the transportation cost induced by the optimal transportation map φ : S → S,

$$W_p(\mu ,\nu )≔\underset{{\phi }^{\ast }\nu =\mu }{\inf }{\left({\int }_M{d}_{\mathbf{g}}^p(x,\phi (x\left)\right)d\mu \left(x\right)\right)}^{\frac{1}{p}}.$$

The following theorem plays a fundamental role for the current work

Theorem 4

The Wasserstein distance W_p is a Riemannian metric of the Wasserstein space ${\mathcal{P}}_p\left(S\right)$.

Detailed proof can be found in [28].

3.4 Discrete Optimal Mass Transport

Let P = {p₁, p₂, … , p_k} be a discrete point set on S, h = {h₁, h₂, … , h_k} be the weight vector.

Definition 3 (Geodesic Power Voronoi Diagram)

Given the point set P and the weight h, the geodesic power voronoi diagram induced by (P, h) is a cell decomposition of the manifold (S, g), such that the cell associated with p_i is given by

$$W_i≔\{q\in S\mid d_{\mathbf{g}}^2(p_i,q)-h_i\le d_{\mathbf{g}}^2(p_j,q)-h_j\}.$$

Theorem 5 (Discrete Optimal Mass Transportation Map)

Given a Riemannian manifold (S, g), two probability measures μ and ν are of the same total mass. ν is a Dirac measure, with discrete point set support P = {p₁, p₂, ⋯ , p_k}, ν(p_i) = ν_i. There exists a weight h = {h₁, h₂, ⋯ , h_k}, unique up to a constant, the geodesic power Voronoi diagram induced by (P, h) gives the optimal mass transportation map,

$$\phi :W_i\to p_i,i=1,2,\cdots ,k,$$

furthermore

$${\int }_{W_i}d\mu ={\nu }_i,{\forall }_i.$$

Proof

Suppose $S={\cup }_{i=1}^k{\tilde{W}}_i$ is another partition of the manifold, such that ${\int }_{{\tilde{W}}_i}d\mu ={\nu }_i$. The mapping $\tilde{\phi }:{\tilde{W}}_i\to p_i$ is another measure-preserving mapping. By the definition of geodesic Voronoi diagram, given any point p ∈ W_i, suppose it belongs to ${\tilde{W}}_j$, then

$$d_{\mathbf{g}}^2(p,p_i)-h_i\le d_{\mathbf{g}}^2(p,p_j)-h_j,$$

this induces

$$\sum _{i=1}^k{\int }_{W_i}\left(d_{\mathbf{g}}^2\right(p,p_i)-h_i)d\mu \left(p\right)\le \sum _{j=1}^k{\int }_{{\tilde{W}}_j}\left(d_{\mathbf{g}}^2\right(q,p_i)-h_j)d\mu \left(q\right)$$

Then

$$\mathcal{C}\left(\phi \right)-\sum {\nu }_i{h}_i\le \mathcal{C}\left(\tilde{\phi }\right)-\sum {\nu }_j{h}_j$$

This shows for any measure preserving mapping, $\mathcal{C}\left(\tilde{\phi }\right)\ge \mathcal{C}\left(\phi \right)$.

The optimal weight for the geodesic power Voronoi diagram that induces the optimal transportation map can be found by

$$\frac{{\mathit{dh}}_i}{\mathit{dt}}={\nu }_i-{\int }_{W_i\left(\mathbf{h}\right)}d\mu .$$ (2)

4 Algorithm

4.1 Riemannian optimal mass transport map

This section gives the algorithmic implementation details for Riemannian optimal mass transport map (OMT-Map) generation using geodesic power Voronoi diagram.

Smooth metric surfaces can be approximated by piecewise linear triangle mesh. There are many ways to discretize a smooth surface, such that the piecewise linear metrics converge to the smooth metric, eg, the sampling is uniformand the triangulation is geodesic Delaunay. The geodesics on the triangle meshes can be efficiently computed using the algorithms in [30].

First, we repeat subdividing the triangle mesh until the size of each triangle is small enough to ensure the accuracy. Then from each point p_i in the point set P, we compute the geodesics to reach every other vertex on the subdivided mesh, this gives the geodesic distance from every vertex to p_i. Repeat this for all vertices in P.

Third, we find the optimal weight. We initialize all the weights to be zeros, then update the weight using the formula

$$\frac{{\mathit{dh}}_i}{\mathit{dt}}={\nu }_i-{\int }_{W_i\left(\mathbf{h}\right)}\mu \left(p\right)\mathit{dp}.$$

Details of the algorithm can be found in Alg. 1.

Algorithm 1.

Riemannian Optimal Mass Transport Map

Input: A triangle mesh M, measure μ and Dirac measure {(p1, ν1), (p2, ν2), ⋯ , (pk, νk)},  ${\int }_{M}u\left(p\right)\mathit{dp}={\sum }_{i=1}^k{\nu }_i$; a threshold ϵ.

Output: The unique discrete Optimal Mass Transport Map φ : (M, μ) → (P, ν).

Subdivide M for several levels, until each triangle size is small enough.

for all pi ∈ P do

Compute the geodesic from pi to every other vertex on M,

end for

h ← (0, 0, ⋯ , 0).

repeat

for all vertex vj on M do

Find the minimum weighted squared geodesic distance, decide which Voronoi cell vi    belongs to, vi ∈ Wt(h)

$t={\mathit{argmin}}_k{d}_{\mathrm{g}}^2(v_j,p_k)+h_k$

end for

for all pi ∈ P do

Compute the current cell area wi = ∫Wi(h) dμ,

end for

for all hi ∈ h do

Update hi, hi = hi + δ(νi − wi)

end for

until ∣νi − wi∣ < ϵ, ∀i.

return Power geodesic Voronoi diagram.

4.2 Wasserstein Distance

The OMT-Map algorithm can also be generalized to compute the Wasserstein distance between surfaces. Given two topological spherical surfaces (S₁, g₁), (S₂, g₂) with total area 4π. We first compute the conformal maps by [21] ${\varphi }_1:S_1\to {\mathbb{S}}^2$ and ${\varphi }_2:S_2\to {\mathbb{S}}^2$, where ${\mathbb{S}}^2$ is the unit sphere. The conformal factors e^2λ₁ and e^2λ₂ define two probability measures on the sphere, which can be computed by [21].

Then we discretize ${\mathbb{S}}^2$ into a discrete point set with measure (P, ν), where ν is computed as follows: first we compute geodesic voronoi diagram induced by P, suppose the Voronoi cell associated with p_i is W_i, then

$${\nu }_i≔{\int }_{W_i}{e}^{2\lambda \left(p\right)}\mathit{dA}\left(p\right),.$$ (3)

where dA is the spherical area element. Denote the measure e^2λ₁ dA as μ, use $({\mathbb{S}}^2,\mu )$ and (P, ν) as inputs of Algorithm 1, we compute the Optimal Mass Transport map $T:{\mathbb{S}}^2\to P$, W_i(h) → p_i, where p_i ∈ P, i = 1, 2, ⋯ , k. Therefore, the Wasserstein distance between S₁ and S₂ can be computed by

$$\mathit{Wasserstein}(\mu ,\nu )=\sum _{i=1}^k{\int }_{W_i}{d}_{\mathbf{g}}^2{(x,T(x\left)\right)}^2\mu \left(x\right)\mathit{dx}$$ (4)

Algorithm 2 gives the implementation details.

Algorithm 2.

Computing Wasserstein Distance

Input: Two topological spherical surfaces (S1, g1), (S2, g2).

Output: The Wasserstein distance between S1 and S2.

1. Scale and normalize S1 and S2 such that the total area of each surface is 4π.

2. Compute the conformal maps by [21] ${\varphi }_1:S_1\to {\mathbb{S}}^2$ and ${\varphi }_2:S_2\to {\mathbb{S}}^2$, where ${\mathbb{S}}^2$ is the unit  sphere, and ϕ1 and ϕ2 are with normalization conditions: the mass center of the image points  are at the sphere center.

3. Compute the conformal factors λ1 and λ2 by [8]. Construct the measure μ ← e2λ1dA.

4. Discretize ${\mathbb{S}}^2$ into a discrete point set with measure (P, ν), where ν is computed by Eqn. 3.

5. With $({\mathbb{S}}^2,\mu )$ and (P, ν) as inputs of Algorithm 1, we compute the Riemannian Optimal  Mass Transport map.

6. Wasserstein distance between S1 and S2 can be computed by Eqn. 4.

5 Brain Cortical Surface Classification

There have been much research into the relation between human intelligence and human brain. Earlier works have studied some significant factors such as cortical surface area, cortical thickness and cortical convolution [12] [18] [19]. To validate the correctness of our framework in real applications, we applied our method for the classification problem of brain cortical surfaces with different intelligence quotient (IQ), and compared with some existing works.

The biological properties of interest by our method are as follows: The brain cortical surface is conformally mapped to the unit sphere, the conformal factor represents the area distortion. In fact, the area distortion factor encodes the complete information of the original Riemannian metric of the brain: due to the conformality of the mapping, the metric on brain equals to the product of the conformal factor and spherical metric. Therefore, Wasserstein distance between the conformal factors gives the distance between the Riemannian metrics of the cortical surfaces. The Gaussian curvatures on the brains are induced by their metrics. This method is stronger than solely comparing curvatures.

Data preparation

The brain data is from the Center for Cognitive and Behavioral Brain Imaging at the Ohio State University. MRI recording was performed using a standard 12-channel head coil on a Siemens 3T Trio Magnetic Resonance Imaging System with TIM. The brain cortical surfaces are reconstructed from MRI images by FreeSurfer [2]. Our experimental dataset includes 50 males and 50 females, with ages ranging from 18 to 30 years uniformly distributed. Among all the brain data, we used the left hemisphere of the brain surface for experiments.

The intelligence quotient (IQ) was evaluated by an online version of Ravens Advanced Progressive Matrices (APM) [3]. The test consists of 36 questions and the IQ score is calculated by N_{correctAnswers}/N_total * 100. The IQ among the data ranges from 0 to 100, which are uniformly distributed. Figure 1 shows the computation of Wasserstein distance between two brain cortical surfaces. (a) shows an example of a 20-year-old female, with IQ score 88.89; (b) shows an example of a 21-year-old male, with IQ score 33.33.

Instead of claiming whether one human brain is intelligent or not, in our experimental settings we divided the IQ into three classes: A, B, and C, ranging from A : [0, 33), B : [33, 67) and C : [67, 100]. The data uniformly distributed in the three classes. For each gender, we randomly chose 12 examples from each class. Therefore, we created a training set of 72 examples, which is uniformly distributed with respect to gender and IQ. And the remaining examples are used as testing data.

For the classification experiments, we first computed the full pair-wise Wasserstein distance matrix based on our method. We indexed all the data of class A into i = 1, 2, …, 33, data of class B into i = 34, 35, …, 66 and data of class C into i = 67, 68, …100. Figure 2 (a) shows the visualization of the Wasserstein distance matrix encoded in a gray image. The distance is normalized from 0 to 1, where 0 indicates black and 1 indicates white. The entry of the matrix M_i,j is the Wasserstein distance between brain data i and brain data j. Then we can clearly see that, mostly, two surfaces in the same class induce smaller Wasserstein distance, yet two surfaces in different classes induce larger Wasserstein distance. The results further demonstrated the power of Wasserstein distance for measuring shape similarities.

Fig. 2.

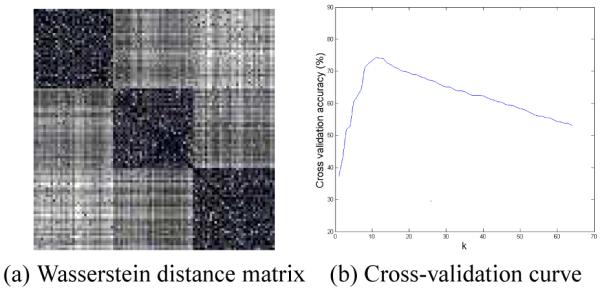
(a) Wasserstein distance matrix encoded in a gray image. The distance is normalized from 0 to 1, where 0 indicates black and 1 indicates white. The results show that, mostly, two surfaces in the same class induce smaller Wasserstein distance, yet two surfaces in different classes induce larger Wasserstein distance. (b) Cross-validation curve.

With the distance matrix, we classified the testing set by k-Nearest Neighbors (k-NN) classifier, where k is chosen to be 11 by running 9-fold cross-validation. The cross-validation curve is shown in Figure 2 (b). Table 1 shows the classification rate of our method is 78.57%.

Table 1.

Classification rate (CR) of our method and previous methods based on cortical surface area, cortical surface mean curvature and combination of previous two cortical measurements. The results demonstrated the accuracy of our method.

Method	CR
Our method	78.57%
Surface Area	53.57%
Surface Mean Curvature	57.14%
Combination of Area and Curvature	67.85%

To demonstrate the efficiency and advantages of our method, we compared our method with existing popular method. Previous work [14] shows that cortical surface area and cortical surface mean curvature have significant correlations to human intelligence, since they quantify the complexity of cortical foldings. Thus we computed the two cortical measurements and used surface area, mean curvature, and the combination of the two measurements as three types of features for classification, respectively. We used LIBSVM [1] as the classifier. Linear kernel and regularization parameter C = 4.5 were chosen by cross validation. Table 1 reports the classification rate of all the three comparison methods. The results indicated that our method outperforms previous methods.

6 Conclusion and Future Work

This work introduces a novel 3D shape classification framework for brain morphology study using Wasserstein distance, based on uniformization theory and Riemannian optimal mass transport theory. We generalized the the existing optimal mass transport map from Euclidean metrics to Riemannian metrics. The theoretical foundation is rigorous, and the computation is based on geodesic power Voronoi diagram.

Comparing to the existing methods, our algorithm solely depends on Riemannian metrics and is invariant under rigid motions and scalings, thus it intrinsically measures distance between shapes. We applied the proposed framework for classification of brain cortical surfaces with different intelligent quotient. The experimental results show that our method outperforms previous methods based on surface area and surface mean curvature. In the future, we will explore and validate broader applications in other medical imaging field by our framework.