A LASSO FOR HIERARCHICAL INTERACTIONS

Abstract

We add a set of convex constraints to the lasso to produce sparse interaction models that honor the hierarchy restriction that an interaction only be included in a model if one or both variables are marginally important. We give a precise characterization of the effect of this hierarchy constraint, prove that hierarchy holds with probability one and derive an unbiased estimate for the degrees of freedom of our estimator. A bound on this estimate reveals the amount of fitting “saved” by the hierarchy constraint.

We distinguish between parameter sparsity—the number of nonzero coefficients—and practical sparsity—the number of raw variables one must measure to make a new prediction. Hierarchy focuses on the latter, which is more closely tied to important data collection concerns such as cost, time and effort. We develop an algorithm, available in the R package hierNet, and perform an empirical study of our method.

1. Introduction

There are numerous situations in which additive (main effects) models are insufficient for predicting an outcome of interest. In medical diagnosis, the co-occurrence of two symptoms may lead a doctor to be confident that a patient has a certain disease whereas the presence of either symptom without the other would provide only a moderate indication of that disease. This situation corresponds to a positive (i.e., synergistic) interaction between symptom variables. On the other hand, suppose both symptoms convey redundant information to the doctor about the patient so that knowing both provides no more information about the disease status than either one on its own. This situation is again not additive, but this time there is a negative interaction between symptoms. Fitting regression models with interactions is challenging when one has even a moderate number, p, of measured variables, since there are $\left(\begin{array}{c}p\\ k\end{array}\right)$ interactions of order k. For this paper, we focus on the case of pairwise (k = 2) interaction models, although the ideas we develop generalize naturally to higher-order interaction models.

1.1. Two-way interaction model

We consider a regression model for an outcome variable Y and predictors X₁, …, X_p, with pairwise interactions between these predictors. In particular our model has the form

$$Y={\beta }_0+\sum _j{\beta }_j{X}_j+\frac{1}{2}\sum _{j\ne k}{\mathrm{\Theta }}_{jk}{X}_j{X}_k+\epsilon ,$$ (1)

where ε ~ N(0, σ⁶). Regardless of whether the predictors are continuous or discrete, we will refer to the additive part as the “main effect” terms and the quadratic part as the “interaction” terms. Our goal is to estimate β ∈ ℝ^p and Θ ∈ ℝ^p×p, where Θ = Θ^T and Θ_jj = 0. The factor of one half before the interaction summation is a consequence of our notational decision to deal with a symmetric matrix Θ of interactions rather than a vector of length p(p − 1)/2. We take Θ_jj = 0 throughout this paper because it simplifies notation, but everything carries over if we remove this restriction. Indeed, we provide this as an option in the hierNet (pronounced “hair net”) package.

We observe a training sample, (x₁, y₁), …, (x_n, y_n), and our goal is to select a subset of the p + p(p − 1)/2 main effect and interaction variables that is predictive of the response, and to estimate the values for the nonzero parameters of the model.

1.2. Strong and weak hierarchy

It is a well-established practice among statisticians fitting (1) to only allow an interaction into the model if the corresponding main effects are also in the model. Such restrictions are known under various names, including “heredity,” “marginality,” and being “hierarchically well-formulated” [Hamada and Wu (1992), Chipman (1996), Nelder (1977), Peixoto (1987)]. There are two types of restrictions, which we will call strong and weak hierarchy:

$$\begin{array}{llllll}\hfill \text{Strong}\text{hierarchy}:& {\widehat{\mathrm{\Theta }}}_{jk}\ne 0\hfill & \Rightarrow \hfill & {\widehat{\beta }}_j\ne 0\hfill & \text{and}\hfill & {\widehat{\beta }}_k\ne 0;\hfill \\ \hfill \text{Weak}\text{hierarchy}:& {\widehat{\mathrm{\Theta }}}_{jk}\ne 0\hfill & \Rightarrow \hfill & {\widehat{\beta }}_j\ne 0\hfill & \text{or}\hfill & {\widehat{\beta }}_k\ne 0.\hfill \end{array}$$

Some statisticians argue that models violating strong hierarchy are not sensible. For example, according to McCullagh and Nelder (1983),

“[T]here is usually no reason to postulate a special position for the origin, so that the linear terms must be included with the cross-term.”

To see that violating strong hierarchy amounts to “postulating a special position for the origin,” consider writing an interaction model as Y = β₀ + (β₁ + Θ₁₂X₂)X₁ + ···. First of all, we would only take β₀ = 0 if we have special reason to believe that the regression surface must go through the origin. Likewise, taking β₁ = 0 but Θ₁₂ ≠ 0 would only be appropriate if we actually believe that X₁’s effect on Y should only be present specifically when X₂ is nonzero. In most situations, we do not think that the variable X₂ that we measured is any more special than aX₂ + b. Yet if our model with X₂ violates strong hierarchy, then our model with aX₂ + b (for any b ≠ 0) is strongly hierarchical. This argument suggests that violations to hierarchy occur in special situations whereas hierarchy is the default.

Another argument in favor of hierarchy has to do with statistical power. In the words of Cox (1984):

“[L]arge component main effects are more likely to lead to appreciable interactions than small components. Also, the interactions corresponding to larger main effects may be in some sense of more practical importance.”

In other words, rather than looking at all possible interactions, it may be useful to focus our search on those interactions that have large main effects. Indeed, the method we propose in this paper makes direct use of this principle.

As a final argument for hierarchy, it is useful to distinguish between two notions of sparsity, which we will call parameter sparsity and practical sparsity. Parameter sparsity is what most statisticians mean by “sparsity”: the number of nonzero coefficients in the model. Practical sparsity is what someone actually collecting data cares about: the number of variables one needs to measure to make predictions at a future time. The hierarchy restriction favors models that “reuse” measured variables whereas a nonhierarchical model does not. The top left panel of Figure 1 gives a small example where this difference is manifest. In fact, a simple calculation shows that this difference can be quite substantial: we can have a hierarchical and a nonhierarchical interaction model with the same parameter sparsity but with the nonhierarchical method having a practical sparsity of k(k + 1) whereas the hierarchical method’s practical sparsity is just k.

Fig. 1.

Olive oil data: (Top left) Parameter sparsity is the number of nonzero coefficients while practical sparsity is the number of measured variables in the model. Results from all 100 random train-test splits are shown as points; lines show the average performance over all 100 runs. (Top right) Misclassification error on test set versus practical sparsity. (Bottom) Wheel plots showing the sparsity pattern at 6 values of λ for the strong hierarchical lasso. Filled nodes correspond to nonzero main effects, and edges correspond to nonzero interactions.

While taking these arguments to the extreme leads to the use of strong hierarchy exclusively, we develop the case of weak hierarchy in parallel throughout this paper. Weak hierarchy, as the name suggests, can be thought of as a compromise between strong hierarchy and imposing no such structure and appears as a principle in certain statistical methods such as classification and regression trees [Breiman et al. (1984)] and multivariate additive regression splines [Friedman (1991)].

1.3. Sparsity, the lasso and structured sparsity

The lasso [Tibshirani (1996)] is a method that performs both model selection and estimation. It penalizes the squared loss of the data with an ℓ₁-norm penalty on the parameter vector. This penalty has the property of producing estimates of the parameter vector that are sparse (corresponding to model selection). Given a design matrix X̃ ∈ ℝ^n×d and response vector y ∈ ℝⁿ, the lasso is the solution to the convex optimization problem,

$$\underset{{\beta }_0,\varphi }{\text{Minimize}}\frac{1}{2}{\Vert y-{\beta }_{0}1-\stackrel{\sim }{X}\varphi \Vert }^2+\lambda {\Vert \varphi \Vert }_1,$$

where 1 ∈ ℝⁿ is the vector of ones. The penalty parameter, λ ≥ 0, controls the relative importance of fitting to the training data (sum-of-squares term) and of sparsity (ℓ₁ penalty term). A natural extension of the lasso to our interaction model (1) would be to take ϕ^T = [β^T, vec(Θ)^T] and X̃ = (X:Z/2), where the columns of Z ∈ ℝ^n×p(p−1) correspond to elementwise products of the columns of X. We will refer to this method as the all-pairs lasso since it is simply the lasso applied to a data matrix which includes all pairs of interactions (as well as all main effects). It is common with the lasso to standardize the predictors so that they are on the same scale. In this paper, we standardize X so that its columns have mean 0 and standard deviation 1; we then form Z from these standardized predictors and, finally, center the resulting columns of Z. By centering y and X̃, we may take β̂₀ = 0.

The lasso’s ℓ₁ penalty is neutral to the pattern of sparsity, allowing any sparsity pattern to emerge. The notions of strong and weak hierarchy introduced in Section 1.2 represent situations in which we want to exclude certain sparsity patterns. There has been a growing literature focusing on methods that produce structured sparsity [Yuan and Lin (2006), Zhao, Rocha and Yu (2009), Jenatton et al. (2010), Jenatton, Audibert and Bach (2011), Bach (2011), Bach et al. (2012)]. These methods make use of the group lasso penalty (and generalizations thereof) which, given a predetermined grouping of the parameters, induces entire groups of parameters to be set to zero [Yuan and Lin (2006)]. Given a set of groups of variables, 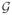, these methods generalize the ℓ₁ penalty by

$$\sum _{G\in \mathcal{G}}{d}_G{\Vert {\varphi }_G\Vert }_{{\gamma }_G},$$

where γ_G > 1, ϕ_G is ϕ projected onto the coordinates in G, and d_G is a nonnegative weight. Hierarchical structured sparsity is obtained by choosing 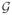to have nested groups. For example, Zhao, Rocha and Yu (2009) consider the penalty

$$\sum _{j\ne k}\{\mid {\mathrm{\Theta }}_{jk}\mid +{\Vert ({\beta }_j,{\beta }_k,{\mathrm{\Theta }}_{jk})\Vert }_{{\gamma }_{jk}}\}.$$

Likewise, the framework of Bach et al. (2012) if specialized to this paper’s focus would lead to a penalty of the form

$${\Vert \mathrm{\Theta }\Vert }_1+\sum _j{d}_j{\Vert ({\mathrm{\Theta }}_j,{\beta }_j)\Vert }_q$$ (2)

for some q > 1 and d_j > 0. In fact, Radchenko and James (2010) suggest a penalty for generalized additive models with interactions that reduces to (2) in the linear model case, with q = 2 and d_j independent of j.

1.4. This paper

Here, we propose a lasso-like procedure that produces sparse estimates of β and Θ while satisfying the strong or weak hierarchy constraint. In contrast to much of the structured sparsity literature which is based on group lasso penalties, our approach, presented in Section 2, involves adding a set of convex constraints to the lasso. Although we find this form of constraint more naturally interpretable, we show (Remark 3) that this problem can be equivalently expressed in a form that relates it to penalties from the structured sparsity literature such as (2).

A key advantage of our specific choice of penalty structure is that it admits a simple interpretation of the effect of the hierarchy demand. Unlike other hierarchical sparsity methods, which do not pay much attention to the particular choice of norms (as long as γ_G > 1), our formulation is carefully tailored to allow it to be related directly back to the lasso, permitting one to understand specifically how hierarchy alters the solution (Section 3.1). This feature of our estimator gives it a transparency that exposes the effects (both positive and negative!) of the hierarchy constraint. Furthermore, our characterization suggests that the demand for hierarchy is—analogous to the demand for sparsity—a form of “regularization.” We develop an unbiased estimator of the degrees of freedom of our method (Section 3.3) and an interpretable upper bound on this quantity, which also points to hierarchy as regularization. In particular, we show that we do not “spend” in degrees of freedom for main effects that are forced into the model by the hierarchy constraint.

Another difference from much of the structured sparsity literature, which aims to develop a broad treatment of structured and hierarchical sparsity methods, is that our focus is narrowed to the problem of interaction models. Our restricted scope allows us to address specifically the performance of such a tool to this important problem. In Section 4, we review previous work on the problem of hierarchical interaction model fitting and selection. These methods fall into three categories: Multi-step procedures, which are defined by an algorithm [Peixoto (1987), Friedman (1991), Turlach (2004), Nardi and Rinaldo (2012), Bickel, Ritov and Tsybakov (2010), Park and Hastie (2008), Wu et al. (2010)]; Bayesian approaches, which specify the hierarchy requirement through a prior [Chipman (1996)]; and, most related to this paper’s proposal, regularized regression methods, which are defined by an optimization problem [Yuan, Joseph and Zou (2009), Zhao, Rocha and Yu (2009), Choi, Li and Zhu (2010), Jenatton et al. (2010), Radchenko and James (2010)]. In Section 5, we study via simulation the statistical implications of imposing hierarchy on an interactions-based estimator under various scenarios (in both the lasso and stepwise frameworks). In Section 6 we present an efficient algorithm for computing our estimator. Real data examples are used to illustrate a distinction we draw between “parameter sparsity” and “practical sparsity” and to discuss hierarchy’s role in promoting the latter.

2. Our proposed method

In Section 1.3, we introduced the all-pairs lasso, which can be written as

$$\underset{{\beta }_0\in ℝ,\beta \in {ℝ}^p,\mathrm{\Theta }\in {ℝ}^{p\times p}}{\text{Minimize}}q({\beta }_0,\beta ,\mathrm{\Theta })+\lambda {\Vert \beta \Vert }_1+\frac{\lambda }{2}{\Vert \mathrm{\Theta }\Vert }_1\mathrm{s}.\mathrm{t}.\mathrm{\Theta }={\mathrm{\Theta }}^T,$$ (3)

where ||Θ||₁ = Σ_j≠k |Θ_jk| and q(β₀, β, Θ) is the loss function, typically $\frac{1}{2}{\sum }_{i=1}^n{(y_i-{\beta }_0-x_i^T\beta -\frac{1}{2}{x}_i^T\mathrm{\Theta }{x}_i)}^2=\frac{1}{2}{\Vert y-{\beta }_{0}1-X\beta -Z\text{vec}(\mathrm{\Theta })/2\Vert }^2$, but may also include a ridge penalty on the coefficients as discussed later or may be substituted for the binomial negative log-likelihood. The one-half factors in front of terms involving Θ are merely a consequence of the notational choice to represent Θ as a symmetric matrix (with Θ_jj = 0 for j = 1, …, p). In this paper, we propose a modification of the all-pairs lasso that produces models that are guaranteed to be hierarchical.

As motivation for our proposal, consider building hierarchy into the optimization problem as a constraint,

$$\begin{array}{l}\underset{{\beta }_0\in ℝ,\beta \in {ℝ}^p,\mathrm{\Theta }\in {ℝ}^{p\times p}}{\text{Minimize}}q({\beta }_0,\beta ,\mathrm{\Theta })+\lambda {\Vert \beta \Vert }_1+\frac{\lambda }{2}{\Vert \mathrm{\Theta }\Vert }_1\\ \mathrm{s}.\mathrm{t}.\mathrm{\Theta }={\mathrm{\Theta }}^T,{\Vert {\mathrm{\Theta }}_j\Vert }_1\le \mid {\beta }_j\mid \text{for}j=1,\dots ,p,\end{array}$$ (4)

where Θ_j denotes the jth row (and column, by symmetry) of Θ. Notice that if Θ̂_jk ≠ 0, then ||Θ̂_j||₁ > 0 and ||Θ̂_k||₁ > 0 and thus β̂_j ≠ 0 and β̂_k ≠ 0. While the added constraints enforce strong hierarchy, they are not convex, which makes (4) undesirable as a method. In this paper, we propose a straightforward convex relaxation of (4), which we call the strong hierarchical lasso,

$$\begin{array}{l}\underset{\begin{array}{c}{\beta }_0\in ℝ,{\beta }^{\pm }\in {ℝ}^p,\\ \mathrm{\Theta }\in {ℝ}^{p\times p}\end{array}}{\text{Minimize}}q({\beta }_0,{\beta }^{+}-{\beta }^{-},\mathrm{\Theta })+\lambda 1^T({\beta }^{+}+{\beta }^{-})+\frac{\lambda }{2}{\Vert \mathrm{\Theta }\Vert }_1\\ \mathrm{s}.\mathrm{t}.\mathrm{\Theta }={\mathrm{\Theta }}^T,\begin{array}{r}\hfill {\Vert {\mathrm{\Theta }}_j\Vert }_1\le {\beta }_j^{+}+{\beta }_j^{-}\\ \hfill {\beta }_j^{+}\ge 0,{\beta }_j^{-}\ge 0\end{array}\}\text{for}j=1,\dots ,p,\end{array}$$ (5)

where we have replaced the optimization variable β ∈ ℝ^p by two vectors β⁺, β⁻ ∈ ℝ^p. After solving the above problem, our fitted model is of the form f̂(x) = β̂₀ + x^T (β̂⁺ − β̂⁻) + x^T Θ̂x/2. While we might informally think of β⁺ and β⁻ as positive and negative parts of a vector β = β⁺ − β⁻, that is, that β^± = max{±β, 0}, this is not actually the case since at a solution we can have both ${\widehat{\beta }}_j^{+}>0$ and ${\widehat{\beta }}_j^{-}>0$. Indeed, if we were to add the constraints ${\beta }_j^{+}{\beta }_j^{-}=0$ for j = 1, …, p to (5), then these would be positive and negative parts and so ${\beta }_j^{+}+{\beta }_j^{-}=\mid {\beta }_j\mid$, giving us precisely problem (4). This observation establishes that (5) is a convex relaxation of (4).

The hierarchy constraints can be seen as an embedding into our method of David Cox’s “principle” that “large component main effects are more likely to lead to appreciable interactions than small components.” The constraint

$${\Vert {\mathrm{\Theta }}_j\Vert }_1\le {\beta }_j^{+}+{\beta }_j^{-}$$

budgets the total amount of interactions involving variable X_j according to the relative importance of X_j as a main effect. One additional advantage of the convex relaxation is that the constraint is less restrictive. If the best fitting model would have ||Θ_j||₁ large but |β_j| only moderate, this can be accommodated by making ${\beta }_j^{+}$ and ${\beta }_j^{-}$ both large.

Remark 1

Another possibility for the hierarchy constraint that we have considered is $\mid {\mathrm{\Theta }}_{jk}\mid \le {\beta }_j^{+}+{\beta }_j^{-}$; however, we have found that this can lead to an overabundance of interactions relative to main effects.

Remark 2

It is desirable to include in the loss function q an elastic net term, $(\epsilon /2)({\Vert \mathrm{\Theta }\Vert }_F^2+{\Vert {\beta }^{+}\Vert }^2+{\Vert {\beta }^{-}\Vert }^2)$, to ensure uniqueness of the solution [Zou and Hastie (2005)]. We think of ε > 0 as a fixed tiny fraction of λ, such as ε = 10⁻⁸λ, rather than as an additional tuning parameter. Such a modification does not complicate the algorithm, but simplifies the study of the estimator. In all numerical examples and in the hierNet package, we use this elastic net modification.

Remark 3

We prove in Section 2 of the supplementary materials [Bien, Taylor and Tibshirani (2013)] that (5) may equivalently be written as

$$\underset{\begin{array}{c}{\beta }_0\in ℝ,\beta \in {ℝ}^p,\\ \mathrm{\Theta }\in {ℝ}^{p\times p},\mathrm{\Theta }={\mathrm{\Theta }}^T\end{array}}{\text{Minimize}}q({\beta }_0,\beta ,\mathrm{\Theta })+\lambda \sum _{j}max\{\mid {\beta }_j\mid ,{\Vert {\mathrm{\Theta }}_j\Vert }_1\}+\frac{\lambda }{2}{\Vert \mathrm{\Theta }\Vert }_1.$$ (6)

This reparameterization of the problem shows its similarities to the group lasso based methods. In place of the more standard penalty ||(Θ_j, β_j)||_q of (2), we use max{||Θ_j||₁, |β_j|}. In Section 3.1, we show that this unusual choice of penalty admits a particularly simple interpretation for the effect of imposing hierarchy.

In Section 1.2, we also introduced the notion of weak hierarchy. By simply removing the symmetry constraint on Θ, we get what we call the weak hierarchical lasso,

$$\begin{array}{l}\underset{{\beta }_0\in ℝ,\beta \pm \in {ℝ}^p,\mathrm{\Theta }\in {ℝ}^{p\times p}}{\text{Minimize}}q({\beta }_0,{\beta }^{+}-{\beta }^{-},\mathrm{\Theta })+\lambda 1^T({\beta }^{+}+{\beta }^{-})+\frac{\lambda }{2}{\Vert \mathrm{\Theta }\Vert }_1\\ \mathrm{s}.\mathrm{t}.\begin{array}{r}\hfill {\Vert {\mathrm{\Theta }}_j\Vert }_1\le {\beta }_j^{+}+{\beta }_j^{-}\\ \hfill {\beta }_j^{+}\ge 0,{\beta }_j^{-}\ge 0\end{array}\}\text{for}j=1,\dots ,p.\end{array}$$ (7)

Even though at a solution to this problem, Θ̂ is not symmetric, we should ^b think of the interaction coefficient as (Θ̂_jk + Θ̂_kj)/2 since this is what multiplies the interaction term x_ijx_ik when computing f̂(x_i).

Remark 4

We can build further on the connection between (2) and (5) discussed in Remark 3. Our removal of the symmetry constraint in (7) is analogous to the technique of duplicating columns of the design matrix used in the overlap group lasso [Obozinski, Jacob and Vert (2011)].

A favorable property that distinguishes our method from previous approaches discussed in Section 4 is the relative transparency of the role that the hierarchy constraint plays in our estimator. This aspect is developed in Section 3.1.

Although our primary focus in this paper is on the Gaussian setting of (1), our proposal extends straightforwardly to other situations, such as the logistic regression setting in which the response is binary. In this case, we simply have q(β₀, β, Θ) be the appropriate negative log-likelihood, $-{\sum }_{i=1}^n{y}_{i}log{p}_i+(1-y_i)log(1-p_i)$, where $p_i={[1+exp(-{\beta }_0-x_i^T\beta -\frac{1}{2}{x}_i^T\mathrm{\Theta }{x}_i)]}^{-1}$. In Section 3 of the supplementary materials [Bien, Taylor and Tibshirani (2013)], we show that solving this problem requires only a minor modification to our primary algorithm. It should also be noted that our estimator (and the algorithms developed to compute it) is designed for both the p < n and p ≥ n setting.

As a preliminary example, consider predicting whether a sample of olive oil comes from Southern Apulia based on measurements of the concentration of p = 8 fatty acids [Forina et al. (1983)]. The dataset consists of n = 572 samples, and we average our results over 100 random equal-sized train-test splits. We compare three methods: (a) a standard lasso with main effects only (MEL), (b) the all-pairs lasso (APL), and (c) the strong hierarchical lasso (HL).

The top left panel of Figure 1 shows an interesting difference between HL and APL. We see that, on average, at a parameter sparsity level of five, the HL model uses four of the measured variables whereas APL uses six. Using the hierarchical model to classify a future olive oil, we only need to measure four rather than six of the fatty acids.

The top right panel of Figure 1 shows the predictive performance (versus the practical sparsity) of the three methods. It appears that HL enjoys the “best of both worlds,” matching the good performance of MEL for low practical sparsity levels (since it tends to pick out the main effects first) and the good performance of APL at high practical sparsity levels (since it can incorporate predictive interactions). Finally, the bottom panel of the figure provides a visual display of a sequence of HL’s solutions (by varying λ). Nonzero main effects are shown as filled nodes, and edges indicate nonzero interactions. Since all edges are incident to filled nodes, we see that strong hierarchy holds.

In the next section, we present several properties of our estimator that shed light on the effect of adding the convex hierarchy constraint to the lasso. Among these properties is an unbiased estimate of the degrees of freedom of our estimator. We view this degrees-of-freedom result as valuable primarily for the sake of understanding the effect of hierarchy. While such an estimate could be used for parameter selection, we prefer cross validation to select λ since this is more directly tied to the goal of prediction.

3. Properties

3.1. Effect of the constraint

A key advantage of formulating an estimator as a solution to a convex problem is that it can be completely characterized by a set of optimality conditions, known as the Karush–Kuhn–Tucker (KKT) conditions. These conditions are useful for understanding the effect that the hierarchy constraint in (5) and (7) has on our solutions. In this section, we will study the simplest case, taking q(β₀, β, Θ) to be the quadratic loss function with no elastic net penalty. We let

$$\begin{array}{l}{r}^{(-j)}=y-\widehat{y}+x_j{\widehat{\beta }}_j,\\ r^{(-jk)}=y-\widehat{y}+(x_j\ast x_k)({\widehat{\mathrm{\Theta }}}_{jk}+{\widehat{\mathrm{\Theta }}}_{kj})/2\end{array}$$

denote partial residuals (where * denotes elementwise multiplication, ŷ the vector of fitted values and x_j the jth predictor), and we assume that ||x_j||₂ = 1. For linear regression, the KKT conditions are known as the normal equations and can be written as

$${\widehat{\beta }}_j=x_j^T{r}^{(-j)},{\widehat{\mathrm{\Theta }}}_{jk}=\frac{{(x_j\ast x_k)}^T{r}^{(-jk)}}{{\Vert x_j\ast x_k\Vert }^2}.$$

The all-pairs lasso solution satisfies

$${\widehat{\beta }}_j=\mathcal{S}(x_j^T{r}^{(-j)},\lambda ),{\widehat{\mathrm{\Theta }}}_{jk}=\frac{\mathcal{S}[{(x_j\ast x_k)}^T{r}^{(-jk)},\lambda ]}{{\Vert x_j\ast x_k\Vert }^2},$$ (8)

where 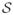denotes the soft-thresholding operator defined by 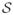(c, λ) = sign(c)(|c| − λ)₊. Written this way, we see that the lasso is similar to linear regression, but all coefficients are shrunken toward 0, with some coefficients (those for which $\mid x_j^T{r}^{(-j)}\mid \le \lambda$) set to zero. It is instructive to examine the corresponding statements for the strong and weak hierarchical lasso methods.

Property 1

The coefficients of the strong and weak hierarchical lassos with λ > 0 and taking q(β₀, β, Θ) to be the quadratic loss (with no elastic net penalty) satisfy:

• Strong:

  $$\begin{array}{l}{\widehat{\beta }}_j^{+}-{\widehat{\beta }}_j^{-}=\mathcal{S}(x_j^T{r}^{(-j)},\lambda -{\widehat{\alpha }}_j),\\ {\widehat{\mathrm{\Theta }}}_{jk}=\frac{\mathcal{S}[{(x_j\ast x_k)}^T{r}^{(-jk)},\lambda +{\widehat{\alpha }}_j+{\widehat{\alpha }}_k]}{{\Vert x_j\ast x_k\Vert }^2};\end{array}$$
• Weak:

  $$\begin{array}{l}{\widehat{\beta }}_j^{+}-{\widehat{\beta }}_j^{-}=\mathcal{S}(x_j^T{r}^{(-j)},\lambda -{\stackrel{\sim }{\alpha }}_j),\\ \frac{{\widehat{\mathrm{\Theta }}}_{jk}+{\widehat{\mathrm{\Theta }}}_{kj}}{2}=\frac{\mathcal{S}[{(x_j\ast x_k)}^T{r}^{(-jk)},\lambda +2min\{{\stackrel{\sim }{\alpha }}_j,{\stackrel{\sim }{\alpha }}_k\}]}{{\Vert x_j\ast x_k\Vert }^2}\end{array}$$

  for some α̂ ≥ 0, j = 1, …, p with α̂_j = 0 when ${\Vert {\widehat{\mathrm{\Theta }}}_j\Vert }_1<{\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}$ (and likewise for α̃_j).

Proof

See Section 1 of the supplementary materials [Bien, Taylor and Tibshirani (2013)].

The α̂_j, α̃_j appearing in the above two properties are optimal dual variables corresponding to the jth hierarchy constraint for the strong and weak hierarchical lasso problems, respectively. When ${\Vert {\widehat{\mathrm{\Theta }}}_j\Vert }_1<{\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}$, we have α̂_j = 0 (or α̃_j = 0) by complementary slackness. Comparing these expressions to those of the all-pairs lasso gives insight into the effect of the constraint. Property 1 reveals that the overall form of the all-pairs lasso and hierarchical lasso methods is identical. The difference is that the hierarchy constraint leads to a reduction in the shrinkage of certain main effects and an increase in the shrinkage of certain interactions. In particular, we see that when the hierarchy constraints are loose at the solution, that is, ${\Vert {\widehat{\mathrm{\Theta }}}_j\Vert }_1<{\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}$, the weak hierarchical lasso’s optimality conditions become identical to the all-pairs lasso (since α̃_j = 0) for all coefficients involving x_j. For the strong hierarchical lasso, when both the jth and kth constraints are loose, the optimality conditions match those of the all-pairs lasso for the coefficients of x_j, x_k and x_j * x_k. The methods differ when constraints are active, that is, when ${\Vert {\widehat{\mathrm{\Theta }}}_j\Vert }_1={\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}$, which allows α̂_j (or α̃_j) to be nonzero. Intuitively, this case corresponds to the situation in which hierarchy would not have held “naturally” (i.e., without the constraint), and the corresponding dual variable plays the role of reducing Θ̂_j in ℓ₁-norm and increasing ${\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}$ until the constraint is satisfied. The way in which the weak and strong hierarchical lasso methods perform this shrinkage is different, but both are identical to the all-pairs lasso when all constraints are loose.

3.2. Hierarchy guarantee

In Section 2, we showed that adding the constraint ||Θ_j||₁ ≤ |β_j| would guarantee that hierarchy holds. However, we have not yet shown that the same is true of the convex relaxation’s constraint, ${\Vert {\mathrm{\Theta }}_j\Vert }_1\le {\beta }_j^{+}+{\beta }_j^{-}$. In particular, while ${\widehat{\mathrm{\Theta }}}_{jk}\ne 0\Rightarrow {\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}\ne 0$, we could still have ${\beta }_j^{+}-{\beta }_j^{-}=0$. This would correspond to a model in which X_jX_k is used in the model, but X_j is not. Intuitively, we would expect that if ${\widehat{\beta }}_j^{+}>0$, then ${\widehat{\beta }}_j^{+}={\widehat{\beta }}_j^{-}$ is analogous to getting an exact zero in linear regression (i.e., a zero probability event). In this section, we establish that this is in fact the case.

In particular, we study (5) and (7) where q(β₀, β, Θ) includes an elastic net term. The importance of this modification is that it ensures uniqueness, simplifying the analysis. As noted in Remark 2, we think of ε as a small, fixed proportion of λ rather than as a separate tuning parameter.

Property 2

Suppose y is absolutely continuous with respect to the Lebesgue measure on ℝⁿ. If (β̂⁺, β̂⁻, Θ̂) solves (5), where q(β₀, β, Θ) is the quadratic loss with an ε > 0 ridge penalty, then strong hierarchy holds with probability 1, that is,

$${\widehat{\mathrm{\Theta }}}_{jk}\ne 0\Rightarrow {\widehat{\beta }}_j^{+}-{\widehat{\beta }}_j^{-}\ne 0\mathit{and}{\widehat{\beta }}_k^{+}-{\widehat{\beta }}_k^{-}\ne 0.$$

Proof

See Appendix A.

To understand how dropping the symmetry constraint leads to the “or” statement required of weak hierarchy, note that X_jX_k is in the weak hierarchical lasso model if and only if Θ̂_jk + Θ̂_kj ≠ 0. This holds only if Θ̂_jk ≠ 0 or Θ̂_kj ≠ 0.

Property 3

Suppose y is absolutely continuous with respect to the Lebesgue measure on ℝⁿ. If (β̂⁺, β̂⁻, Θ̂) solves (7), where q(β₀, β, Θ) is the quadratic loss with an ε > 0 ridge penalty, then weak hierarchy holds with probability 1, that is,

$$\frac{{\widehat{\mathrm{\Theta }}}_{jk}+{\widehat{\mathrm{\Theta }}}_{kj}}{2}\ne 0\Rightarrow {\widehat{\beta }}_j^{+}-{\widehat{\beta }}_j^{-}\ne 0or{\widehat{\beta }}_k^{+}-{\widehat{\beta }}_k^{-}\ne 0.$$

Proof

See Appendix A.

3.3. Degrees of freedom

In classical statistics, the degrees of freedom of a procedure refer to the dimension of the space over which its fitted values can vary. It is useful in that it provides a measure of how much “fitting” the procedure is doing. This notion can be generalized to adaptive procedures such as the lasso [Stein (1981), Efron (1986), Efron et al. (2004), Zou, Hastie and Tibshirani (2007)]. See (Ryan) Tibshirani and Taylor (2012) for a thorough discussion. If given data y ∈ ℝⁿ, a procedure h produces fitted values ŷ = h(y) ∈ ℝⁿ, the degrees of freedom of the procedure h is defined to be

$$df(h)=\frac{1}{{\sigma }^2}\sum _{i=1}^{n}cov(y_i,{\widehat{y}}_i).$$ (9)

Property 4

Suppose y ~ N(μ, σ⁶I_n). An unbiased estimate of the degrees of freedom of the strong hierarchical lasso, with quadratic loss and no ridge penalty, is given by

$${\widehat{df}}_{\lambda }=\text{rank}(\stackrel{\sim }{X}P),$$

where X̃ = (X:−X:Z/2: −Z/2) with Z containing the interactions, and P is a projection matrix which depends on the sign pattern of (β̂⁺, β̂⁻, Θ̂) and on the set of hierarchy constraints that are tight.

Proof

See Appendix B.

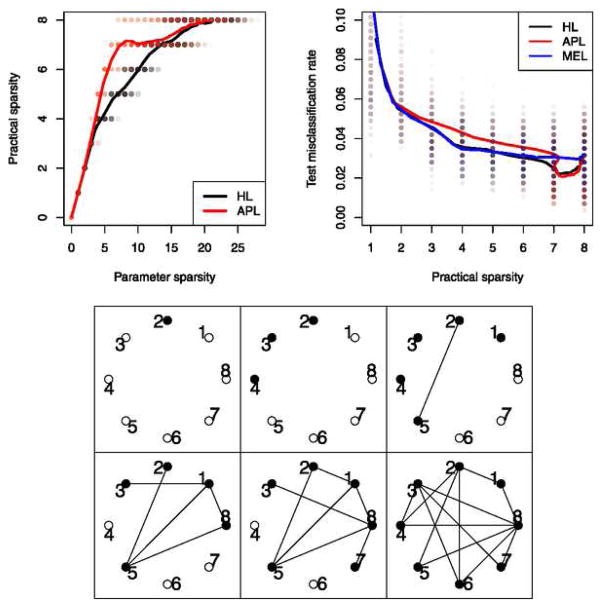
Figure 2 provides a numerical evaluation of how well ${\widehat{df}}_{\lambda }$ estimates df_λ. We fix X ∈ ℝ^n×p, β ∈ ℝ^p and Θ ∈ ℝ^p×p, and we generate B = 10,000 Monte Carlo replicates y⁽¹⁾, …, y^(B) ∈ ℝⁿ. For each replicate, we fit the strong hierarchical lasso along a grid of λ values to get ( ${\widehat{\beta }}_{\lambda }^{+(b)},{\widehat{\beta }}_{\lambda }^{-(b)},{\widehat{\mathrm{\Theta }}}_{\lambda }^{(b)}$) and ${\widehat{y}}_{\lambda }^{(b)}\in {ℝ}^n$. From these values, we compute Monte Carlo estimates of df_λ from the definition in (9) and of $E[{\widehat{df}}_{\lambda }]$.

Fig. 2.

Numerical evaluation of how well ${\widehat{df}}_{\lambda }$ estimates df_λ. Monte Carlo estimates of $E[{\widehat{df}}_{\lambda }]$ (y-axis) versus Monte Carlo estimates of df_λ (x-axis) for a sequence of λ values (circular) are shown. One-standard-error bars are drawn and are hardly visible. Our bound on the unbiased estimate is plotted with diamonds.

While ${\widehat{df}}_{\lambda }$ can be calculated from the data and is therefore useful as an unbiased way of calibrating the amount of fitting the strong hierarchical lasso is doing, this expression is difficult to interpret. However, it turns out that we can bound ${\widehat{df}}_{\lambda }$ by a quantity that does make more sense:

Property 5

Let $\mathcal{T}=\{j:{\Vert {\widehat{\mathrm{\Theta }}}_j\Vert }_1={\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}\},{\mathcal{A}}_{\beta }=\{j:{\widehat{\beta }}_j^{+}-{\widehat{\beta }}_j^{-}\ne 0\},{\mathcal{A}}_{\pm }=\{j:{\widehat{\beta }}_j^{\pm }>0\}$ and 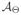= {jk: Θ̂_jk ≠ 0, j < k}. Then,

$${\widehat{df}}_{\lambda }\le \mid {\mathcal{A}}_{\beta }\mid +\mid {\mathcal{A}}_{\mathrm{\Theta }}\mid -\mid \mathcal{T}\cap ({\mathcal{A}}_{+}\mathrm{\Delta }{\mathcal{A}}_{-})\mid$$

holds almost surely, where 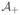Δ = ( \ ) ∪ ( \ ).

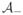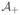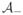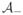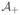Proof

See Appendix B.

By contrast, for the all-pairs lasso in the case that $p+\left(\begin{array}{r}\hfill p\\ \hfill 2\end{array}\right)<n$ and the design matrix is full rank, we have df_λ(APL) = E[| 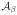| + | |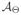] [Zou, Hastie and Tibshirani (2007)]. In other words, the strong hierarchical lasso does not “pay” (in terms of fitting) for those main effects, ${\widehat{\beta }}_j^{+}-{\widehat{\beta }}_j^{-}$, that are forced into the model by the hierarchy constraint to accommodate a strong interaction. Notice that we do pay for a nonzero main effect if both ${\widehat{\beta }}_j^{+}$ and ${\widehat{\beta }}_j^{-}$ are nonzero. This makes sense since the constraint could be satisfied with just one of these variables nonzero, but in this case it is advantageous to the fit to make both nonzero. In Figure 2, we find that this bound is in expectation visually indistinguishable from $E[{\widehat{df}}_{\lambda }]$.

4. Related work

There has been considerable interest in fitting interaction models in statistics and related fields. We focus here on an overview of methods that aim at forming predictive models that satisfy the hierarchical interactions restriction.

4.1. Multi-step procedures

Many statistics textbooks discuss a simple stepwise procedure in which one iteratively considers adding or removing the “best” variable (whether it be main effect or interaction); they add that one should only consider including an interaction if its main effects are in the model [e.g., see backward elimination in Agresti (2002), Section 6.1.3]. In doing so, they are enforcing the strong hierarchy restriction. Such procedures are ubiquitous [Nelder (1997), Peixoto (1987)] as are more recent versions [Friedman (1991), Bickel, Ritov and Tsybakov (2010), Park and Hastie (2008), Wu et al. (2010)]. Another approach is to perform model selection first without considering hierarchy and then to include any lower-order terms necessary to satisfy hierarchy as a post-processing step [Nardi and Rinaldo (2012)]. Finally, Turlach (2004) and Yuan, Joseph and Lin (2007) consider modifying the LARS algorithm [Efron et al. (2004)] so that hierarchy is enforced.

4.2. Bayesian approaches

Another set of procedures for building hierarchical interaction models comes from a Bayesian viewpoint. Chipman (1996) adapts the stochastic search variable selection (SSVS) approach of George and McCulloch (1993) to produce strong or weak hierarchical interaction models. SSVS makes use of a hierarchical normal mixture model to perform variable selection in regression. Every variable has a latent binary variable indicating whether it is “active.” Conditional on this latent variable, each coefficient is a 0-mean normal with variance determined by the latent importance of the coefficient. The original SSVS paper chooses a prior in which the importance of each variable is an independent Bernoulli. Chipman (1996) introduces dependence into the prior so that Θ_jk is important only if β_j and/or β_k is important as well.

4.3. Optimization-based approaches

Choi, Li and Zhu (2010) formulate a nonconvex optimization problem to get sparse hierarchical interaction models. They write Θ_jk = Γ_jkβ_jβ_k, where β are the main effect coefficients and then apply ℓ₁ penalties on β and Γ. Notice that Θ_jk ≠ 0 implies β_j ≠ 0 and β_k ≠ 0. The nonconvexity arises in writing Θ_jk as the product of optimization variables.

Most similar to this paper’s proposal is a series of methods which formulate convex optimization problems to give sparse hierarchical interaction models. Yuan, Joseph and Zou (2009) modify the nonnegative garrote [Breiman (1995)] by adding linear inequality constraints to enforce hierarchy. In this sense, our method can be seen as the adaption of their approach to the lasso.

Finally, as discussed in Section 1.3, another set of convex methods makes use of the group lasso penalty [Yuan and Lin (2006)]. Zhao, Rocha and Yu (2009) [and, relatedly, Jenatton, Audibert and Bach (2011)] describe composite absolute penalties (CAP), a very broad class of penalties that can achieve group and hierarchical sparsity. To achieve “hierarchical selection,” they put forward the principle that a penalty of the form ||(ϕ₁, ϕ₂)||_γ + |ϕ₁|, with γ > 1, induces ϕ₂ to be zero only when ϕ₁ is zero as well. For hierarchical interaction models, they suggest a penalty of the form λ Σ_j<k[|Θ_jk| + ||(β_j, β_k, Θ_jk)||_γj,k]. This framework has been developed in the structured sparsity literature [e.g., Bach et al. (2012)]. Radchenko and James (2010) introduce VANISH, which uses this nested-group principle to achieve hierarchical sparsity in the context of nonlinear interactions. Their penalty in the setting of (1) is Σ_j[λ₁||(β_j, Θ_j)||₂ + λ₂||Θ_j||₁]. As noted in Remark 3, our proposal is closer to CAP and VANISH than it may first appear. Our problem can be rewritten to have a penalty of the form λ Σ_j[max{|β_j|, ||Θ_j||₁} + (1/2)||Θ_j||₁]. In this sense, the penalty is in the spirit of CAP and related methods although it does not quite fall into the class of CAP (since ours involves a sum of norms of norms). It is most similar to VANISH in that it combines all of Θ_j into the term involving β_j.

5. Empirical study

5.1. Simulations

Our main interest in this section is to study the advantages and disadvantages of restricting one’s interaction models to those that honor hierarchy. Clearly, the effectiveness of such a strategy depends on the true model generating the data. We take n = 100 and p = 30 (435 two-way interactions) and consider four scenarios:

1. Truth is hierarchical: Θ_jk ≠ 0 ⇒ β_j ≠ 0, β_k ≠ 0;

2. Truth is anti-hierarchical: Θ_jk ≠ 0 ⇒ β_j = 0, β_k = 0;

3. Truth only has interactions: β_j = 0 for all j;

4. Truth only has main effects: Θ_jk = 0 for all jk.

In cases (I), (II), (IV), we set 10 elements of β to be nonzero (with random sign), and, in cases (I), (II), (III), we set 20 elements of the submatrix of Θ = Θ^T to be nonzero. The signal-to-noise ratio (SNR) for the main effects part of the signal is about 1.5 whereas the SNR for the interactions part is about 1.

We study the effectiveness of the hierarchy constraint in the context of both the lasso and forward stepwise regression. Forward stepwise regression refers to a greedy strategy for generating a sequence of linear regression models in which we start with an intercept-only model and then at each step add the variable that leads to the greatest decrease in the residual sum of squares. We choose forward stepwise as a basis of comparison since it has a simple modification that we think may be the hierarchical interactions approach most commonly used by statisticians. The modification is to restrict the set of interactions that could be added at a given step to only those between main effect variables currently in the model. A backward stepwise version of this approach is suggested in Peixoto (1987).

We compare six methods, corresponding to each cell of the following table:

	Hierarchical	All-pairs	Main effects only
Lasso	HL (our method)	APL	MEL
Fwd stepwise	HF	APF	MEF

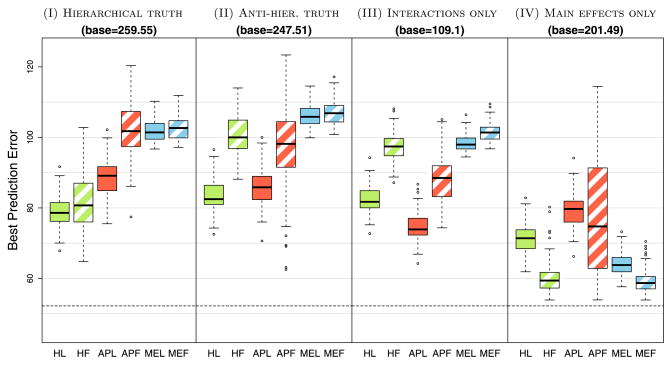
Each method has a single tuning parameter: for the lasso methods, the penalty parameter, λ, and for the forward stepwise methods, the number of variables, k. We fit each method along a grid of tuning parameter values and select the model with the smallest mean squared error, E||ŷ − μ||⁶. Note that such an operation is only possible in simulation since it requires knowing μ; however, doing so avoids the added variance of cross validation without being biased in favor of any particular method. The results presented are based on 100 simulations from the underlying model. Figure 3 shows the expected prediction error, σ⁶ + E[(ŷ − μ)⁶]. Panel (I) shows that when the truth is hierarchical, methods that assume hierarchy (HL, HF) do better than the rest. These methods have “concentrated” their power on the correct set of models and therefore receive the biggest payoff for being correct. APL does better than MEL and MEF since it succeeds in incorporating some of the correct interactions (recall that interactions make up one quarter of the signal). In panel (II), we notice our first surprise—that HL predicts well relative to the others even when the truth is not hierarchical! We would have expected APL (or APF) to be the clear winner in this situation since surely the hierarchy assumption can only be detrimental in this “anti-hierarchical” scenario. The reason APL does not outperform HL in this scenario is because APL has trouble identifying the main effects (it gets swamped by the 435 interaction variables). In light of Section 3.1, this is where the hierarchy constraint helps—main effects are penalized by less and interactions by more. Even though APL is better able to find the correct interactions than HL, as seen in panel (II) of Figure 4, APL does not predict as well as HL because it fails to find the main effects, which constitute three quarters of the signal. Relatedly, in a “hierarchical truth” scenario similar to (I) but with p > n (not presented here), we have in fact observed MEL doing better than APL (though not as well as HL) since APL is not able to detect interactions accurately enough to make up for its inferior ability to detect main effects. By contrast, HL does best in that scenario, aided by hierarchy to capture both the main effect and interaction components of the signal.

Fig. 3.

Prediction error: Dashed line shows Bayes error (i.e., σ²), and the base rate refers to the prediction error of ȳ_train. Green, red and blue colors indicate hierarchy, all-pairs, and main effect only, respectively; solid and striped indicate lasso and forward stepwise, respectively.

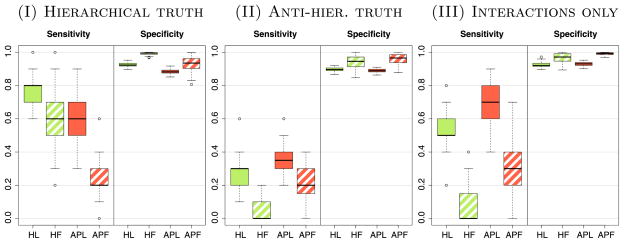
Fig. 4.

Plots show the ability of various methods to correctly recover the nonzero interactions. This is the sensitivity (i.e., proportion of Θ_jk ≠ 0 for which Θ●_jk ≠ 0) and specificity (i.e., proportion of Θ_jk ≠ 0 for which Θ●_jk ≠ 0) corresponding to the lowest prediction error model of each method.

In panel (III), we see a situation where APL does dominate HL. Since there are no main effects in the signal, all that is relevant is a method’s ability to find the interactions. HL identifies fewer correct interactions than APL since any main effect “information” that HL is using is spurious. Finally in panel (IV), we see a situation where MEF, HF, MEL do better than the rest. Here again we find that the hierarchy methods beat the all-pairs methods since they favor main effects.

It is particularly illuminating to note the difference in performance between HL and HF. HF in scenarios (II), (III) and (IV) performs very similarly to the main effect only models. In (II) and (III), HL does much better than HF both in terms of prediction error and in ability to correctly identify interactions. HL appears to be far less sensitive to violations of hierarchy than HF. This difference is attributable to the joint nature in which HL acts: the decision to include a main effect is made at the same time as decisions about interactions. This allows a strong interaction to “pull” itself into the model. By contrast, HF selects main effects with no regard to the information contained in the interactions.

5.2. Data examples

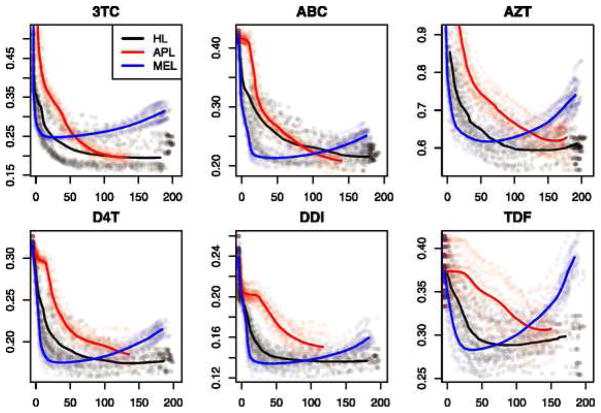
Rhee et al. (2006) study six nucleoside reverse tran-scriptase inhibitors (NRTIs) that are used to treat HIV-1. The target of these drugs can become resistant through mutation, and Rhee et al. (2006) compare a collection of models for predicting these drug’s (log) susceptibility—a measure of drug resistance—based on the location of mutations. In the six cases, there are between p = 211 and p = 218 sites with mutations occurring in the n = 784 to n = 1073 samples. While they focus on main effect only models, we consider here the all-pairs lasso (APL) and weak hierarchical lasso (HL) in addition to the standard main effects lasso (MEL). We train on half of the samples and test on the remaining samples. To reduce the dependence of the results on the particular random training-test split, we repeat this process twenty times and average the results. Figure 5 shows the average test RMSE versus the average practical sparsity for each of the six drugs. In all cases but ABC, we find that HL achieves a better test error at most levels of practical sparsity than APL. That said, if the number of mutations one has to measure is not of concern (so that we can choose for each method the minimum RMSE model), then no method dominates in all the situations. It is worth conceding—since this is a paper on interactions—that in several of the cases a pure main effects model appears to be the best option.

Fig. 5.

HIV drug data: Test-set RMSE versus practical sparsity (i.e., number of measured variables required for prediction) for six different drugs. For each method, the data from all 20 runs are displayed in faint colors; the thick lines are averages over these runs.

6. Algorithmics

Some of the fastest lasso solvers rely on coordinate descent, which amounts to iteratively applying (8) until convergence [Friedman, Hastie and Tibshirani (2010)]. Tseng (2001) proves that blockwise coordinate descent converges to the global minimum for a convex problem specifically when the nondifferentiable part of the problem is blockwise separable. In the case of the strong hierarchical lasso, the hierarchy constraints combined with the symmetry constraint couple all the parameters together, meaning that coordinate descent is prone to getting stuck at sub-optimal points. To see this, note that Θ_jk = Θ_kj appears in two constraints ${\Vert {\mathrm{\Theta }}_j\Vert }_1\le {\beta }_j^{+}+{\beta }_j^{-}$ and ${\Vert {\mathrm{\Theta }}_k\Vert }_1\le {\beta }_k^{+}+{\beta }_k^{-}$. By contrast, the constraints in the weak hierarchical lasso problem are blockwise separable so that blockwise coordinate descent on blocks of the form (Θ_j, ${\beta }_j^{+},{\beta }_j^{-}$) for j = 1, …, p does work. We begin by discussing our approach to solving the weak hierarchical lasso problem. In Section 6.2 we discuss how we can solve a sequence of weak hierarchical lasso problems that converges to a solution of the strong hierarchical lasso.

6.1. Solving the weak hierarchical lasso

While blockwise coordinate descent would work for solving the weak hierarchical lasso problem, we instead describe a generalized gradient descent approach. Given a problem of the form

$$\underset{\varphi }{\text{Minimize}}g(\varphi )+h(\varphi ),$$ (10)

in which g is convex and differentiable with a Lipschitz gradient and h is convex, generalized gradient descent works by solving a sequence of problems of the form 1

$${\widehat{\varphi }}_k\leftarrow \underset{\varphi }{argmin}\frac{1}{2t}{\Vert \varphi -[{\widehat{\varphi }}_{k-1}-t\nabla g({\widehat{\varphi }}_{k-1})]\Vert }^2+h(\varphi ),$$

where t is a suitably chosen step size [Beck and Teboulle (2009)]. These subproblems are easier to solve than (10) since they replace g by a spherical quadratic. Under the previously stated conditions, generalized gradient descent is guaranteed to get within O(1/k) of the optimal value after k steps; in fact, with a simple modification to the algorithm, this rate improves to O(1/k⁶) [Beck and Teboulle (2009)]. Looking back at (7), we take g to be the differentiable part, q(β₀, β⁺ − β⁻, Θ) + λ1^T (β⁺ + β⁻) and h to be the ℓ₁ penalty on Θ and the set of constraints. The subproblem is of the form

$$\begin{array}{l}\underset{{\beta }^{\pm }\in {ℝ}^p,\mathrm{\Theta }\in {ℝ}^{p\times p}}{\text{Minimize}}\frac{1}{2t}{\Vert {\beta }^{+}-{\stackrel{\sim }{\beta }}^{+}\Vert }^2+\frac{1}{2t}{\Vert {\beta }^{-}-{\stackrel{\sim }{\beta }}^{-}\Vert }^2+\frac{1}{2t}{\Vert \mathrm{\Theta }-\stackrel{\sim }{\mathrm{\Theta }}\Vert }_F^2+\frac{\lambda }{2}{\Vert \mathrm{\Theta }\Vert }_1\\ \mathrm{s}.\mathrm{t}.\begin{array}{r}\hfill {\Vert {\mathrm{\Theta }}_j\Vert }_1\le {\beta }_j^{+}+{\beta }_j^{-}\\ \hfill {\beta }_j^{+}\ge 0,{\beta }_j^{-}\ge 0\end{array}\}\text{for}j=1,\dots ,p,\end{array}$$

where (β̃⁺, β̃⁻, Θ̃) depends on the previous iteration’s solution and the data, X, Z and y. The exact form of (β̃⁺, β̃⁻, Θ̃) is given in Algorithm for solving (7), where q(β₀, β, Θ) includes an elastic net penalty as described in Remark 2 of Section 2. The above problem decouples into p separate pieces involving (Θ_j, ${\beta }_j^{+},{\beta }_j^{-}$) that could be solved in parallel:

$$\begin{array}{l}\underset{{\beta }_j^{\pm }\in ℝ,{\mathrm{\Theta }}_j\in {ℝ}^{p-1}}{\text{Minimize}}\frac{1}{2t}{({\beta }_j^{+}-{\stackrel{\sim }{\beta }}_j^{+})}^2+\frac{1}{2t}{({\beta }_j^{-}-{\stackrel{\sim }{\beta }}_j^{-})}^2+\frac{1}{2t}{\Vert {\mathrm{\Theta }}_j-{\stackrel{\sim }{\mathrm{\Theta }}}_j\Vert }^2+\frac{\lambda }{2}{\Vert {\mathrm{\Theta }}_j\Vert }_1\\ \mathrm{s}.\mathrm{t}.{\Vert {\mathrm{\Theta }}_j\Vert }_1\le {\beta }_j^{+}+{\beta }_j^{-},{\beta }_j^{+}\ge 0,{\beta }_j^{-}\ge 0.\end{array}$$ (11)

Algorithm 1.

WEAK–HIERNET: Generalized gradient descent to solve weak hierarchical lasso, (7), with elastic net penalty ε.

Inputs: X ∈ ℝn×p, Z ∈ ℝn×p(p−1), λ > 0. Initialize (β̂+(0), β̂−(0), Θ̂(0)).

For k = 1, 2, … until convergence:

Compute residual: r̂(k−1) ← y − X(β̂+(k−1) − β̂− (k−1)) − ZΘ̂(k−1)/2.

For j = 1, …, p: $$\begin{array}{r}({\widehat{\beta }}_j^{+(k)},{\widehat{\beta }}_j^{-(k)},{\widehat{\mathrm{\Theta }}}_j^{(k)})\leftarrow \text{ONEROW}(\delta {\widehat{\beta }}_j^{+(k-1)}-{tX}_j^T{\widehat{r}}^{(k-1)}),\\ \delta {\widehat{\beta }}^{-(k-1)}+{tX}_j^T{\widehat{r}}^{(k-1)}),\\ \delta {\widehat{\mathrm{\Theta }}}_j^{(k-1)}-{tZ}_{(j,·)}^T{\widehat{r}}^{(k-1)}),\end{array}$$

where ONEROW is given in Algorithm 3, δ = 1 − tε, and Z(j, ·) ∈ ℝn×(p−1) denotes the columns of Z involving Xj.

In Appendix C, we derive an algorithm, ONEROW, that solves (11) based on the observation that, in terms of an optimal dual variable α̂, a solution is simply Θ̂_j = 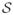[Θ̃_j, t(λ/2 + α̂)] and ${\widehat{\beta }}_j^{\pm }={[{\stackrel{\sim }{\beta }}_j^{\pm }+t\widehat{\alpha }]}_{+}$.

We solve (7) along a sequence of λ values, from large to small, using the solution from the previous λ as a warm start for the next. The WEAK-HIERNET algorithm gets within ε of the optimal value of (7) in O(p⁶ max{n, p}/ε) time.

6.2. Solving the strong hierarchical lasso

In Section 6.1, we noted that each step of generalized gradient descent conveniently decouples into p single-variable optimization problems. However, for the strong hierarchical lasso, (5), the symmetry constraint ties all variables together. We therefore make use of Alternating Direction Method of Multipliers (ADMM), which is a very widely applicable framework that allows convex problems to be split apart into separate easier subproblems [Boyd et al. (2011)].

Given a convex problem of the form Minimize_ϕf(ϕ) + g(ϕ), we rewrite it equivalently as Minimize_{ϕ, φ}f(ϕ) + g(φ) s.t. ϕ = φ, and then the ADMM algorithm repeats the following three steps until convergence:

1. ϕ̂ = argmin_ϕ[f(ϕ) + (ρ/2)||ϕ − φ̂ + û/ρ||⁶].

2. φ̂ = argmin_φ[g(φ) + (ρ/2)||φ − ϕ̂ − û/ρ||⁶].

3. û ← û + ρ(ϕ̂ − φ̂).

Thus the ADMM algorithm separates the two difficult parts of the problem, f and g, into separate optimization problems. The dual variable û serves to pull these two problems together, resulting in an algorithm that is guaranteed to converge to a solution as long as ρ > 0. In practice, the value of ρ affects the speed of convergence.

In our case, we use ADMM to separate the hierarchy constraints, involving (β⁺, β⁻, Θ) from the symmetry constraint, which will involve a symmetric version of Θ, which we call Ω:

$$\begin{array}{l}\underset{\begin{array}{c}{\beta }_0\in ℝ,{\beta }^{\pm }\in {ℝ}^p,\\ \mathrm{\Theta },\mathrm{\Omega }\in {ℝ}^{p\times p}\end{array}}{\text{Minimize}}q({\beta }_0,{\beta }^{+}-{\beta }^{-},\mathrm{\Theta })+\lambda 1^T({\beta }^{+}+{\beta }^{-})+\frac{\lambda }{2}{\Vert \mathrm{\Theta }\Vert }_1\\ \mathrm{s}.\mathrm{t}.\mathrm{\Omega }={\mathrm{\Omega }}^T,\mathrm{\Theta }=\mathrm{\Omega }\begin{array}{r}\hfill {\Vert {\mathrm{\Theta }}_j\Vert }_1\le {\beta }_j^{+}+{\beta }_j^{-}\\ \hfill {\beta }_j^{+}\ge 0,{\beta }_j^{-}\ge 0\end{array}\}\text{for}j=1,\dots ,p.\end{array}$$ (12)

The resulting ADMM algorithm is given in Algorithm 2, which is explained in greater detail in Section 4 of the supplementary materials [Bien, Taylor and Tibshirani (2013)]. Conceptually, the algorithm alternately updates two matrices, Θ and Ω. Throughout the algorithm, we update Θ by solving a version of problem (7), and we update Ω by symmetrizing a version of Θ. At convergence, Θ̂ = Ω̂, and thus Θ̂ is both symmetric and satisfies the hierarchy constraints.

Algorithm 2.

STRONG-HIERNET: Solve (5) via ADMM.

Inputs: X ∈ ℝn×p, Z ∈ ℝn×p(p−1), λ > 0, ρ > 0.

Initialize (β̂+, β̂−, Θ̂), Ω̂, Û.

Repeat until convergence: WEAK-HIERNET(X, Z, λ), but in the call to ONEROW replace the argument $\delta {\widehat{\mathrm{\Theta }}}_j^{(k-1)}-{tZ}_{(j,·)}^T{\widehat{r}}^{(k-1)}$ with $\delta {\widehat{\mathrm{\Theta }}}_j^{(k-1)}-{tZ}_{(j,·)}^T{\widehat{r}}^{(k-1)}+\rho [{\widehat{\mathrm{\Theta }}}_j^{(k-1)}-{\widehat{\mathrm{\Omega }}}_j]+{\widehat{U}}_j$. Also, initialize with (β̂+, β̂−, Θ̂). $\widehat{\mathrm{\Omega }}\leftarrow \frac{1}{2}(\widehat{\mathrm{\Theta }}+{\widehat{\mathrm{\Theta }}}^T)+\frac{1}{2\rho }(\widehat{U}+{\widehat{U}}^T)$. Û ← Û + ρ(Θ̂ − Ω̂)

7. Discussion

In this paper, we have proposed a modification to the lasso for fitting strong and weak hierarchical interaction models. These two approaches are closely tied, and our algorithms to solve the two exploit their similar structure. A key advantage of our framework is that it admits a simple characterization of the effect of imposing hierarchy. We compare our hierarchical methods to the lasso and to stepwise procedures to understand the implications of demanding hierarchy. We introduce a distinction between models that have a small number of parameters and those that require measuring only a small number of variables. The hierarchical interaction requirement favors models with the latter type of sparsity, a feature that is desirable when performing measurements is costly, time consuming, or otherwise inconvenient. The R package hierNet provides implementations of our strong and weak methods, both for Gaussian and logistic losses. This work has potential applications to genomewide association studies. In future work, we intend to extend this framework to contexts in which only certain interactions should be considered such as in gene-environment interaction models.

APPENDIX A: PROOFS OF STRONG AND WEAK HIERARCHY

We begin by proving Lemma 1, which characterizes all solutions to (5) as a relatively simple function of y. The structure of our proof is based on (Ryan) Tibshirani and Taylor (2011, 2012).

A.1. Characterizing the solution

For ease of analysis, we write (5) equivalently in terms of Θ⁺ and Θ⁻. Also, for notational simplicity, we write ϕ = (β⁺, β⁻, Θ⁺, Θ⁻) and X̃ = (X; −X;Z/2; −Z/2). The strong hierarchical lasso problem is the following:

$$\begin{array}{l}\underset{{\beta }^{+},{\beta }^{-},{\mathrm{\Theta }}^{+},{\mathrm{\Theta }}^{-}}{\text{Minimize}}\frac{1}{2}{\Vert y-\stackrel{\sim }{X}\varphi \Vert }^2+{\lambda }_1{1}^T({\beta }^{+}+{\beta }^{-})+{\lambda }_2\langle {11}^T,{\mathrm{\Theta }}^{+}+{\mathrm{\Theta }}^{-}\rangle \\ \mathrm{s}.\mathrm{t}.1^T({\mathrm{\Theta }}_j^{+}+{\mathrm{\Theta }}_j^{-})\le {\beta }_j^{+}+{\beta }_j^{-}\text{and}{\beta }_j^{+}\ge 0,{\beta }_j^{-}\ge 0\text{for}\text{each}j,{\mathrm{\Theta }}^{+}-{\mathrm{\Theta }}^{-}={\mathrm{\Theta }}^{+T}-{\mathrm{\Theta }}^{-T},{\mathrm{\Theta }}_{jk}^{\pm }\ge 0,{\mathrm{\Theta }}_{jj}^{\pm }=0.\end{array}$$

In introducing Θ^±, we are not in fact changing the problem since at a solution Θ̂^± = max{±Θ̂, 0} (for λ₂ > 0). To see this, note that given any feasible point with ${\mathrm{\Theta }}_{jk}^{+}>0$ and ${\mathrm{\Theta }}_{jk}^{-}>0$, we can produce a feasible point with strictly lower objective by reducing ${\mathrm{\Theta }}_{jk}^{+},{\mathrm{\Theta }}_{jk}^{-},{\mathrm{\Theta }}_{kj}^{+},{\mathrm{\Theta }}_{kj}^{-}$ all by equal amounts.

We will try to make this as close as possible in form and notation to (Ryan) Tibshirani and Taylor’s (2012) treatment of the generalized lasso problem. Our optimization problem is of the form

$$\underset{\varphi }{\text{Minimize}}\frac{1}{2}{\Vert y-\stackrel{\sim }{X}\varphi \Vert }^2+w^T\varphi \mathrm{s}.\mathrm{t}.D\varphi \ge 0,L\varphi =0.$$ (13)

The Lagrangian of this problem is

$$L(\varphi ;\mu ,\nu )=\frac{1}{2}{\Vert y-\stackrel{\sim }{X}\varphi \Vert }^2+w^T\varphi -{\mu }^{T}D\varphi +{\nu }^{T}L\varphi ,$$

where μ ≥ 0 and ν are dual variables. The KKT conditions for (ϕ̂(y), (μ̂(y), ν̂(y))) to be an optimal primal-dual pair are the following:

$$\begin{array}{l}{\stackrel{\sim }{X}}^T(y-\stackrel{\sim }{X}\widehat{\varphi })=w-D^T\widehat{\mu }+L^T\widehat{\nu },\\ {\widehat{\mu }}_i{(D\widehat{\varphi })}_i=0,\\ \widehat{\mu }\ge 0,\\ D\widehat{\varphi }\ge 0,L\widehat{\varphi }=0.\end{array}$$

Now, define the “boundary” and “active” sets as

$$\begin{array}{l}\mathcal{B}(\widehat{\mu })=\{i:{\widehat{\mu }}_i=0\},\\ \mathcal{A}(\widehat{\varphi })=\{i:{[D\widehat{\varphi }]}_i>0\}.\end{array}$$

These are not necessarily unique since (ϕ̂, (μ̂, ν̂)) may not be unique. In terms of the active set (ϕ̂), the KKT conditions become

$$\begin{array}{l}{\stackrel{\sim }{X}}^T(y-\stackrel{\sim }{X}\varphi )=w-D_{-\mathcal{A}(\widehat{\varphi })}^T{\widehat{u}}_{-\mathcal{A}(\widehat{\varphi })}+L^T\widehat{\nu },\\ {\widehat{\mu }}_{\mathcal{A}(\widehat{\varphi })}=0,\widehat{\mu }\ge 0,\\ L\widehat{\varphi }=0,D_{-\mathcal{A}(\widehat{\varphi })}\widehat{\varphi }=0.\end{array}$$

Solving for ϕ̂, we get the following characterization of a strong hierarchical lasso solution:

Lemma 1

Suppose ϕ̂ is a solution to the strong hierarchical lasso problem (5) [taking q(β₀, β, Θ) to be the quadratic loss] with (ϕ̂) = {i : [Dϕ̂]_i > 0}. Then, ϕ̂ can be written in terms of 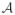(ϕ̂) and y as

$$\widehat{\varphi }={(\stackrel{\sim }{X}{P}_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})})}^{+}(y-{(P_{\text{null}(L)\cap \text{null(}{D}_{-\mathcal{A}(\widehat{\varphi })}\text{)}}{\stackrel{\sim }{X}}^T)}^{+}w)+b,$$

where b ∈ null(X̃) ∩ null(L) ∩ null( 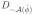) satisfies

$$D_i[{(\stackrel{\sim }{X}{P}_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})})}^{+}(y-{(P_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})}{\stackrel{\sim }{X}}^T)}^{+}w)+b]>0$$

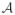for all i ∈ (ϕ̂).

Proof

Defining $\stackrel{\sim }{D}=\left(\begin{array}{c}{D}_{-\mathcal{A}(\widehat{\varphi })}\\ L\end{array}\right)$ and P = P_null(D̃) = , we solve for ϕ̂ in the same manner as is done in (Ryan) Tibshirani and Taylor (2012). Since D̃ϕ̂ = 0 is equivalent to Pϕ̂ = ϕ̂, we have PX̃^T (y − X̃Pϕ̂) = Pw. We see that Pw ∈ col(PX̃^T) and thus Pw = (PX̃^T)(PX̃^T)⁺Pw. Thus, PX̃^TX̃Pϕ̂ = PX̃^T(y − (PX̃^T)⁺Pw) from which we get

$$\widehat{\varphi }={(\stackrel{\sim }{X}P)}^{+}(y-{(P{\stackrel{\sim }{X}}^T)}^{+}Pw)+b$$

for b ∈ null(X̃P) and such that D̃b = 0 and D_iϕ̂ > 0 for i ∈ 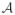(ϕ̂). To complete the result, we observe that the first two conditions reduce to b ∈ null(X̃) ∩ null(L) ∩ null( ).

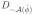We will use this characterization of a solution both to prove that the hierarchy property holds with probability one under weak assumptions and to derive an unbiased estimate of the degrees of freedom.

Before we do so, we write out $\stackrel{\sim }{D}=\left(\begin{array}{c}{D}_{-\mathcal{A}(\widehat{\varphi })}\\ L\end{array}\right)$ more explicitly and introduce a little notation that will be useful later. Every row of D corresponds to an inequality constraint, and we can describe these rows in terms of ten subsets,

$$\begin{array}{l}\mathcal{L}=\{j:1^T({\widehat{\mathrm{\Theta }}}_j^{+}+{\widehat{\mathrm{\Theta }}}_j^{-})<{\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}\},\mathcal{T}={\mathcal{L}}^c,\\ \mathcal{P}({\widehat{\beta }}^{\pm })=\{j:{\widehat{\beta }}_j^{\pm }>0\},\mathcal{Z}({\widehat{\beta }}^{\pm })=\mathcal{P}{({\widehat{\beta }}^{\pm })}^c,\\ \mathcal{P}({\widehat{\mathrm{\Theta }}}^{\pm })=\{j\ne k:{\widehat{\mathrm{\Theta }}}_{jk}^{\pm }>0\},\mathcal{Z}({\widehat{\mathrm{\Theta }}}^{\pm })=\mathcal{P}{({\widehat{\mathrm{\Theta }}}^{\pm })}^c.\end{array}$$ (14)

The set 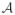(ϕ̂)^c is made up of 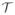, (β̂⁺), (β̂⁻), (Θ̂⁺) and (Θ̂⁻). The matrix D̃ has 2p+2p⁶ columns that can be partitioned as (D̃^β+ : D̃^β− : D̃^{Θ +}: D̃^Θ−) and a row for every constraint. The rows of this matrix are the following (where e_j and 1_p are row vectors):

$$\begin{array}{cccccc}\mathrm{R}1.\text{For}\text{each}j\in \mathcal{T},\hfill & (e_j\hfill & e_j& -e_j\otimes 1_p& -e_j\otimes 1_p& )\\ \mathrm{R}2.\text{For}\text{each}j\in \mathcal{Z}({\beta }^{+}),\hfill & (e_j\hfill & 0& 0& 0& )\\ \mathrm{R}3.\text{For}\text{each}j\in \mathcal{Z}({\beta }^{-}),\hfill & (0\hfill & e_j& 0& 0& )\\ \mathrm{R}4.\text{For}\text{each}jk\in \mathcal{Z}({\mathrm{\Theta }}^{+}),\hfill & (0\hfill & 0& e_j\otimes e_k& 0& )\\ \mathrm{R}5.\text{For}\text{each}jk\in \mathcal{Z}({\mathrm{\Theta }}^{-}),\hfill & (0\hfill & 0& 0& e_j\otimes e_k& )\\ \mathrm{R}6.\text{For}\text{each}j,\hfill & (0\hfill & 0& e_j\otimes e_j& 0& )\\ \mathrm{R}7.\text{For}\text{each}j,\hfill & (0\hfill & 0& 0& e_j\otimes e_j& )\\ \mathrm{R}8.\text{For}\text{each}j<k,\hfill & (0\hfill & 0& e_j\otimes e_k+e_k\otimes e_j& -e_j\otimes e_k-e_k\otimes e_j& ).\end{array}$$

We will refer to this in the proofs that follow.

A.2. Proof of strong hierarchy (Property 2)

Including the elastic net penalty, $(\epsilon /2){\Vert {\beta }^{+}\Vert }^2+(\epsilon /2){\Vert {\beta }^{-}\Vert }^2+(\epsilon /2){\Vert \mathrm{\Theta }\Vert }_F^2$, is equivalent to replacing X̃ and y in (13) by

$${\stackrel{\sim }{X}}_{\epsilon }=\left(\begin{array}{cccc}X& -X& Z/2& -Z/2\\ \sqrt{\epsilon }{I}_p& 0& 0& 0\\ 0& \sqrt{\epsilon }{I}_p& 0& 0\\ 0& 0& \sqrt{\epsilon }{I}_{p^2}& -\sqrt{\epsilon }{I}_{p^2}\end{array}\right)\text{and}{y}_{\epsilon }=\left(\begin{array}{c}y\\ 0_{(2p+p^2)\times 1}\end{array}\right).$$

Suppose we solve (13) with the above design matrix. By Lemma 1,

$$\widehat{\varphi }={({\stackrel{\sim }{X}}_{\epsilon }{P}_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})})}^{+}(y_{\epsilon }-{(P_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})}{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+}w)+b$$

for some b ∈ null(X̃_ε) ∩ null(L) ∩ null( 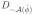) satisfying

$$D_i[{(\stackrel{\sim }{X}{P}_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})})}^{+}(y_{\epsilon }-{(P_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})}{\stackrel{\sim }{X}}^T)}^{+}w)+b]>0$$

for all i ∈ 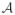(ϕ̂). Let S_v :ℝ^2p+2p2 → ℝ^|v| be the linear operator that selects the part of a vector corresponding to the variable v. Now, b ∈ null(X̃_ε) implies that S_β⁺ (b) = S_β⁻ (b) = 0 and S_Θ⁺ (b) = − S_Θ⁻ (b). We showed earlier that we cannot have ${\widehat{\mathrm{\Theta }}}_{jk}^{+}>0$ and ${\widehat{\mathrm{\Theta }}}_{jk}^{-}>0$. This means that for any jk, there must be an i ∉ 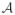(ϕ̂) for which D_iϕ̂ = 0 corresponds to $S_{{\mathrm{\Theta }}_{jk}^{+}}(\widehat{\varphi })=0$ or $S_{{\mathrm{\Theta }}_{jk}^{-}}(\widehat{\varphi })=0$. Thus, 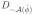b = 0 means that $S_{{\mathrm{\Theta }}_{jk}^{+}}(b)=0$ or $S_{{\mathrm{\Theta }}_{jk}^{-}}(b)=0$ for each jk. This implies that null(X̃_ε) ∩ null( 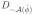) = {0} and thus b = 0.

We show now that $P({\cup }_j\{{\widehat{\beta }}_j^{+}={\widehat{\beta }}_j^{-}>0\})=0$. In terms of our above notation, this is

$$P\left(\underset{j}{\cup }\{{\widehat{\varphi }}^T(e_j^{+}-e_j^{-})=0,{\widehat{\varphi }}^T{e}_j^{+}>0,{\widehat{\varphi }}^T{e}_j^{-}>0\}\right)=0,$$ (15)

where $e_j^{\pm }\in {ℝ}^{2p+2p^2}$ is the vector with all zeros except for $S_{{\beta }^{\pm }}(e_j^{\pm })=1$. Let P = , and consider the set

$$\begin{array}{l}\mathcal{N}=\underset{\mathcal{A}}{\cup }\underset{j=1}{\overset{p}{\cup }}\{z:{[{({\stackrel{\sim }{X}}_{\epsilon }P)}^{+}(z-{(P{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+}w)]}^T(e_j^{+}-e_j^{-})=0,\\ {[{({\stackrel{\sim }{X}}_{\epsilon }P)}^{+}(z-{(P{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+}w)]}^T{e}_j^{+}>0,{[{({\stackrel{\sim }{X}}_{\epsilon }P)}^{+}(z-{(P{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+}w)]}^T{e}_j^{-}>0\}.\end{array}$$

In light of (14), fixing 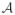automatically specifies 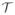, 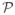(β̂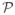^±), (Θ̂^±). The outer union is restricted to those subsets of 2p +2p⁶ elements that would have (Θ̂⁺) ∩ (Θ̂⁻) = Ø and (β̂⁺) ∩ (β̂⁻) ⊆ . The event in (15) is contained in {y_ε ∈ } since it corresponds to the case in which is (ϕ̂). We begin by showing that (ϕ̂) is in this restricted union with probability one. We have already argued that at a solution we must have ${\widehat{\mathrm{\Theta }}}_{jk}^{+}{\widehat{\mathrm{\Theta }}}_{jk}^{-}=0$ for all jk. Now, ${\widehat{\beta }}_j^{+}>0$ and ${\widehat{\beta }}_j^{-}>0$ together imply that $1^T({\widehat{\mathrm{\Theta }}}_j^{+}+{\widehat{\mathrm{\Theta }}}_j^{-})={\widehat{\beta }}_j^{+}+{\widehat{\beta }}_j^{-}$ since otherwise we could lower the objective by reducing ${\widehat{\beta }}_j^{+}$ and ${\widehat{\beta }}_j^{-}$ without leaving the feasible set. Therefore, it would be sufficient to show that P(y_ε ∈ ) = 0. We do so by observing that {y_ε ∈ } is a finite union of zero probability sets.

We begin by establishing that $\text{null}(I_{1:n}{(P{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+})=\text{null}(\stackrel{\sim }{X}P)$. To do so, we write P = UU^T for some U^TU = I. Now, row(X̃P) ⊆ row(P) = col(U), so we can write U = (U₁ : U₂), where row(X̃P) = col(U₁) and thus X̃PU₂ = 0. Since PU₂ = U₂, it follows that X̃U₂ = 0. Write $U_i^T=(U_i^{\beta +T}:U_i^{\beta -T}:U_i^{\mathrm{\Theta }+T}:U_i^{\mathrm{\Theta }-T})$ for i = 1, 2, and observe that $U_i^T{\stackrel{\sim }{X}}_{\epsilon }^T=[U_i^T{\stackrel{\sim }{X}}^T:\sqrt{\epsilon }{U}_i^{\beta +T}:\sqrt{\epsilon }{U}_i^{\beta -T}:\sqrt{\epsilon }(U_i^{\mathrm{\Theta }+T}-U_i^{\mathrm{\Theta }-T})]$ so that

$$\begin{array}{l}{U}_1^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_2=0+\epsilon [U_1^{{\beta }^{+}T}{U}_2^{{\beta }^{+}}+U_1^{{\beta }^{-}T}{U}_2^{{\beta }^{-}}+(U_1^{{\mathrm{\Theta }}^{+}}-U_1^{{\mathrm{\Theta }}^{-}})(U_2^{{\mathrm{\Theta }}^{+}}-U_2^{{\mathrm{\Theta }}^{-}})]\\ =\epsilon [U_1^T{U}_2-U_1^{{\mathrm{\Theta }}^{+}T}{U}_2^{{\mathrm{\Theta }}^{-}}-U_1^{{\mathrm{\Theta }}^{-}T}{U}_2^{{\mathrm{\Theta }}^{+}}]\\ =-\epsilon \left[0+\sum _{jk}{[U_1^{{\mathrm{\Theta }}^{+}}]}_{jk}{[U_2^{{\mathrm{\Theta }}^{-}}]}_{jk}+{[U_1^{{\mathrm{\Theta }}^{-}}]}_{jk}{[U_2^{{\mathrm{\Theta }}^{+}}]}_{jk}\right].\end{array}$$

Now, for each jk we must have jk ∈ (Θ⁺) ∪ (Θ⁻) since 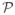(Θ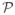⁺) ∩ (Θ⁻) = Ø. Thus, for each jk, there is a R4 or R5 row in 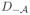and thus 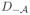(U₁ : U₂) = 0 implies that ${[U_1^{{\mathrm{\Theta }}^{+}}]}_{jk}=0$ or ${[U_2^{{\mathrm{\Theta }}^{-}}]}_{jk}=0$ for each jk and likewise ${[U_2^{{\mathrm{\Theta }}^{+}}]}_{jk}=0$ or ${[U_1^{{\mathrm{\Theta }}^{-}}]}_{jk}=0$. Therefore, $U_1^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_2=0$. Now,

$$\begin{array}{l}{I}_{1:n}{(P{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+}=\stackrel{\sim }{X}P{(P{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }P)}^{+}=\stackrel{\sim }{X}U{U}^T{(U{U}^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }U{U}^T)}^{+}\\ =\stackrel{\sim }{X}U{U}^{T}U{(U^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }U)}^{+}{U}^T=\stackrel{\sim }{X}U{(U^T{\stackrel{\sim }{X}}_{\mathcal{A}}^T{\stackrel{\sim }{X}}_{\epsilon }U)}^{+}{U}^T\\ =\stackrel{\sim }{X}(U_1{U}_2){\left(\begin{array}{cc}{U}_1^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_1& U_1^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_2\\ U_2^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_1& U_2^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_2\end{array}\right)}^{+}{U}^T\\ =\stackrel{\sim }{X}(U_{1}0){\left(\begin{array}{cc}{U}_1^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_1& 0\\ 0& U_2^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_2\end{array}\right)}^{+}{U}^T\\ =\stackrel{\sim }{X}{U}_1{(U_1^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_1)}^{+}{U}_1^T.\end{array}$$

Now, $U_1^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_1\succ 0$ since $U_1^T{\stackrel{\sim }{X}}_{\epsilon }^T{\stackrel{\sim }{X}}_{\epsilon }{U}_1=U_1^T{\stackrel{\sim }{X}}^T\stackrel{\sim }{X}{U}_1+J$ and ⪰ 0 and X̃U₁ has full column rank. Thus, $\text{null}(I_{1:n}{(P{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+})=\text{null}(U_1^T)=\text{null}(\stackrel{\sim }{X}P)$. This completes the first part of the proof.

Next, we show that $\stackrel{\sim }{X}P(e_j^{+}-e_j^{-})\ne 0$ as long as $[{({\stackrel{\sim }{X}}_{\epsilon }P)}^{+}{(y_{\epsilon }-{(P{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+}w)}^T]\times e_j^{\pm }>0$. Now, since j ∈ ∩ 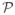(β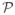⁺) ∩ (β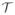⁻) ⊆ , the only row of D̃ that has ${\stackrel{\sim }{D}}_i(e_j^{\pm })\ne 0$ is the R1 row; but clearly ${\stackrel{\sim }{D}}_i(e_j^{+}-e_j^{-})=1-1=0$. Thus, $e_j^{+}-e_j^{-}\in \text{null}(\stackrel{\sim }{D})$ and $P(e_j^{+}-e_j^{-})=e_j^{+}-e_j^{-}$. It follows that

$$\stackrel{\sim }{X}P(e_j^{+}-e_j^{-})=\left(\begin{array}{c}2x_j\\ \sqrt{\epsilon }{e}_j\\ -\sqrt{\epsilon }{e}_j\\ 0\end{array}\right)\ne 0\text{assuming}\epsilon >0.$$

Putting these two parts of the proof together establishes that $I_{1:n}{(P{\stackrel{\sim }{X}}_{\epsilon }^T)}^{+}(e_j^{+}-e_j^{-})\ne 0$. Thus, {y_ε ∈ 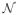} is a finite union of Lebesgue measure 0 sets. This shows that P(y_ε ∈ 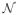) = 0 as long as y is absolutely continuous with respect to the Lebesgue measure on ℝⁿ.

A.3. Proof of weak hierarchy (Property 3)

An argument nearly identical to that of the previous section establishes that ${\widehat{\mathrm{\Theta }}}_{jk}\ne 0\Rightarrow {\widehat{\beta }}_j^{+}-{\widehat{\beta }}_j^{-}\ne 0$ with probability one. Thus, if ${\widehat{\beta }}_j^{+}-{\widehat{\beta }}_j^{-}=0$ and ${\widehat{\beta }}_k^{+}-{\widehat{\beta }}_j^{-}=0$, then both Θ̂_jk = 0 and Θ̂_kj = 0. It follows then that (Θ̂_jk + Θ̂_kj)/2 = 0. This establishes weak hierarchy.

APPENDIX B: DEGREES OF FREEDOM

B.1. Proof of unbiased estimate (Property 4)

The fit in terms of the active set is given by

$$\stackrel{\sim }{X}\widehat{\varphi }=(\stackrel{\sim }{X}P){(\stackrel{\sim }{X}P)}^{+}(y-{(P{\stackrel{\sim }{X}}^T)}^{+}w),$$

where P = . Of course, 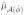= 0, and we can solve the KKT conditions to get the rest of the optimal dual variables in terms of the active set

$$\left(\begin{array}{c}{\widehat{\mu }}_{-\mathcal{A}(\widehat{\varphi })}\\ \widehat{\nu }\end{array}\right)={\stackrel{\sim }{D}}^{T+}[w-{\stackrel{\sim }{X}}^T(y-\stackrel{\sim }{X}\widehat{\varphi })]+c,$$

where c ∈ null(D̃) satisfies D̃^T+[w − X̃^T (y − X̃ ϕ̂)] + c ≥ 0.

Note that ϕ̂ = ϕ̂(y) and thus 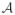(ϕ̂) and b depend on y even though we do not write this explicitly. We will continue writing ϕ̂ to mean specifically ϕ̂(y). For y′ in a neighborhood of y, we might guess that ϕ̂(y′) = f(y′) and (μ̂(y′), ν̂(y′)) = (g(y′),h(y′)), where

$$\begin{array}{l}f(y^{\prime })={(\stackrel{\sim }{X}{P}_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})})}^{+}(y^{\prime }-{(P_{\text{null}(L)\cap \text{null}(D_{-\mathcal{A}(\widehat{\varphi })})}{\stackrel{\sim }{X}}^T)}^{+}w)+b,\\ \left(\begin{array}{c}g{(y^{\prime })}_{-\mathcal{A}(\widehat{\varphi })}\\ h(y^{\prime })\end{array}\right)={\left(\begin{array}{c}{D}_{-\mathcal{A}(\widehat{\varphi })}\\ L\end{array}\right)}^{T+}[w-{\stackrel{\sim }{X}}^T(y^{\prime }-\stackrel{\sim }{X}f(y^{\prime }))]+c,\\ g{(y^{\prime })}_{\mathcal{A}(\widehat{\varphi })}=0.\end{array}$$

To verify this guess, we need to check that the pair (f(y′), (g(y′),h(y′))) satisfies the optimality conditions at y′,

$$\begin{array}{l}{\stackrel{\sim }{X}}^T(y^{\prime }-\stackrel{\sim }{X}f(y^{\prime }))=w-D^{T}g(y^{\prime })+L^{T}h(y^{\prime }),\\ g_i(y^{\prime }){(Df(y^{\prime }))}_i=0,\\ g(y^{\prime })\ge 0,Df(y^{\prime })\ge 0,Lf(y^{\prime })=0.\end{array}$$

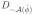First of all, Lf(y′) = 0 holds since L(X̃ )⁺ = 0 and Lb = 0. Likewise, f(y′) = 0. Now 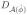f(y) > 0, so by continuity of f, we have 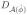f(y′) > 0 for all y′ in a small enough neighborhood, U₁, of y. This establishes that 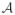(f(y′)) = 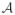(ϕ̂). Now 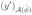= 0, so complementary slackness holds. To see that the first optimality condition holds, we can simply plug (g(y′),h(y′)) into the left-hand side. All that remains is to show that 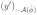≥ 0. If we knew that 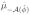> 0, then by continuity of g we could argue that over a small enough neighborhood, U₂, 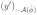> 0. However, it could be the case that μ̂_i = 0 for some i ∉ (ϕ̂), that is, i ∈ (ϕ̂) \ (ϕ̂). Nonetheless, one can show that there is a set of measure 0 for which y ∉ implies that (ϕ̂(y)) = (ϕ̂(y′)) and (ϕ̂(y)) = (ϕ̂(y′)) for all y′ in a neighborhood of y. Lemma 9 of (Ryan) Tibshirani and Taylor (2012) proves this result for a nearly identical situation.

The fit X̃ϕ̂(y) is a piecewise affine function of y. Using Stein’s formula for the degrees of freedom [as described in Ryan, Tibshirani and Taylor (2012)], we get that

$$df(\stackrel{\sim }{X}\widehat{\varphi })=E[\nabla ·\stackrel{\sim }{X}\widehat{\varphi }(y)]=E[\text{tr}\{(\stackrel{\sim }{X}P){(\stackrel{\sim }{X}P)}^{+}\}]=E[\text{rank}(\stackrel{\sim }{X}P)],$$

where P = .

B.2. Proof of bound on estimate (Property 5)

We bound this by an estimate that is more interpretable: $\text{rank}(\stackrel{\sim }{X}P)\le \text{rank}(P)=\text{nullity}\left(\begin{array}{c}L\\ D_{-\mathcal{A}(\widehat{\varphi })}\end{array}\right)$.

Clearly, R2–R7 are linearly independent rows. Thus, the rank of D̃ is at least | (β⁺)| + | (β⁻)| + | (Θ⁺)| + | (Θ⁻)| + 2p. Now, an R1 row is linearly independent of R2–R8 precisely when j ∈ has j ∈ (β⁺)Δ (β⁻). To see this, note that if j ∈ (β⁺) \ (β⁻), then R1 is certainly linearly independent of R2–R8 and likewise for j ∈ (β⁻) \ (β⁺); however if j ∈ (β⁺) ∩ (β⁻), then jk ∈ (Θ⁺) ∩ (Θ⁻) for all k ∈ {1, …, p} \ {j}, and therefore this row of R1 lies in the span of R3–R7. Thus, this means there are | \ ( (β⁺)Δ (β⁻))| additional linearly independent rows. Finally, we consider R8. Clearly, R8 lies in the span of R4–R5 for jk ∈ (Θ⁺) ∩ (Θ⁻) since jk ∈ (Θ⁺) =⇒ kj ∈ (Θ⁺) at a solution. But if jk ∈ (Θ⁺) ∪ (Θ⁻), then it is linearly independent of R1–R8. Therefore, R8 adds | (Θ⁺)|/2 + | (Θ⁻)|/2 to the rank where we have used that (Θ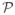⁺) ∩ (Θ⁻) = Ø at a solution (since λ⁶ > 0) and recalling that j < k for the rows of R8. In summary, we have shown that the row-rank is

$$\mid \mathcal{Z}({\beta }^{+})\mid +\mid \mathcal{Z}({\beta }^{-})\mid +\mid \mathcal{Z}({\mathrm{\Theta }}^{+})\mid +\mid \mathcal{Z}({\mathrm{\Theta }}^{-})\mid +2p+\mid \mathcal{T}\backslash (\mathcal{Z}({\beta }^{+})\mathrm{\Delta }\mathcal{Z}({\beta }^{-}))\mid +\mid \mathcal{P}({\mathrm{\Theta }}^{+})\mid /2+\mid \mathcal{P}({\mathrm{\Theta }}^{-})\mid /2.$$

Recalling that there are 2p +2p⁶ columns, we get that

$$\begin{array}{l}\text{nullity}\left(\begin{array}{c}L\\ D_{-\mathcal{A}(\widehat{\varphi })}\end{array}\right)=(2p+2p^2)-\text{rank}\left(\begin{array}{c}L\\ D_{-\mathcal{A}(\widehat{\varphi })}\end{array}\right)\\ =(p-\mid \mathcal{Z}({\beta }^{+})\mid )+(p-\mid \mathcal{Z}({\beta }^{-})\mid )+(p(p-1)-\mid \mathcal{Z}({\mathrm{\Theta }}^{+})\mid )+(p(p-1)-\mid \mathcal{Z}({\mathrm{\Theta }}^{-})\mid )-\mid \mathcal{T}\backslash (\mathcal{Z}({\beta }^{+})\mathrm{\Delta }\mathcal{Z}({\beta }^{-}))\mid -\mid \mathcal{P}({\mathrm{\Theta }}^{+})\mid /2-\mid \mathcal{P}({\mathrm{\Theta }}^{-})\mid /2\\ =\mid \mathcal{P}({\beta }^{+})\mid +\mid \mathcal{P}({\beta }^{-})\mid +\mid \mathcal{P}({\mathrm{\Theta }}^{+})\mid /2+\mid \mathcal{P}({\mathrm{\Theta }}^{-})\mid /2-\mid \mathcal{T}\backslash (\mathcal{P}({\beta }^{+})\mathrm{\Delta }\mathcal{P}({\beta }^{-}))\mid .\end{array}$$

APPENDIX C: SOLVING THE PROX FUNCTION

The Lagrangian of (11) is given by

$$L({\beta }^{\pm },\theta ;\alpha ,{\gamma }^{\pm })=\frac{1}{2t}{({\beta }^{+}-{\stackrel{\sim }{\beta }}^{+})}^2+\frac{1}{2t}{({\beta }^{-}-{\stackrel{\sim }{\beta }}^{-})}^2+\frac{1}{2t}{\Vert \theta -\stackrel{\sim }{\theta }\Vert }^2+\left(\frac{\lambda }{2}+\alpha \right){\Vert \theta \Vert }_1-({\gamma }^{+}+\alpha ){\beta }^{+}-({\gamma }^{-}+\alpha ){\beta }^{-},$$

where α is the dual variable corresponding to the hierarchy constraints and γ^± are the dual variables corresponding to the nonnegativity constraints. For notational convenience, we have written θ for Θ_j, and we have dropped the subscripts on β^±. The KKT conditions are

$$\begin{array}{l}({\widehat{\beta }}^{\pm }-{\stackrel{\sim }{\beta }}^{\pm })/t-{\widehat{\gamma }}^{\pm }-\widehat{\alpha }=0,(\widehat{\theta }-\stackrel{\sim }{\theta })/t+(\lambda /2+\widehat{\alpha })u=0,\\ {\widehat{\beta }}^{\pm }{\widehat{\gamma }}^{\pm }=0,\widehat{\alpha }({\Vert \widehat{\theta }\Vert }_1-{\widehat{\beta }}^{+}-{\widehat{\beta }}^{-})=0,\\ {\widehat{\beta }}^{\pm }\ge 0,{\Vert \widehat{\theta }\Vert }_1\le {\widehat{\beta }}^{+}+{\widehat{\beta }}^{-},\widehat{\alpha }\ge 0,{\widehat{\gamma }}^{\pm }\ge 0,\end{array}$$

where u_j is a subgradient of the absolute value function evaluated at θ̂_j. The three conditions involving γ^± implies that β̂^± = [β̃^± + tα̂]₊. The stationarity condition involving θ̂ implies that θ̂ = S(θ̃, t(λ/2+ α̂)). Now, define f(α) = ||S(θ̃, t(λ/2 + α))||₁ − [β̃⁺ + tα]₊ − [β̃⁻ + tα]₊. The remaining KKT conditions involve α̂ alone: α̂f(α̂) = 0, f(α̂) ≤ 0, α̂ ≥ 0. Observing that f is nonincreasing in α and piecewise linear suggests finding α̂ as done in Algorithm 3.

Algorithm 3.

ONEROW: Solve (11) via dual.

Inputs: ${\stackrel{\sim }{\beta }}_j^{+},{\stackrel{\sim }{\beta }}_j^{-}\in ℝ$, Θ̃j ∈ ℝp−1, λ ≥ 0. Find α̂. Define $f(\alpha )={\Vert S({\stackrel{\sim }{\mathrm{\Theta }}}_j,t(\lambda /2+\alpha ))\Vert }_1-{[{\stackrel{\sim }{\beta }}_j^{+}+t\alpha ]}_{+}-{[{\stackrel{\sim }{\beta }}_j^{-}+t\alpha ]}_{+}$. If f(0) ≤ 0, take α̂ = 0 and go to step 2. Form knot the set $\mathcal{P}={\{\mid {\stackrel{\sim }{\mathrm{\Theta }}}_{jk}\mid /t-\lambda /2\}}_{k=1}^p\cup \{-{\stackrel{\sim }{\beta }}^{\pm }/t\}$, and let = ∩ [0, ∞). Evaluate f(p) for p ∈ . If f(p) = 0 for some p ∈ , take α̂ = p and go to step 2. Find adjacent knots, p1, p2 ∈ , such that f(p1) > 0 > f(p2). Take $$\widehat{\alpha }=-f(p_1)[f(p_2)-f(p_1)]/(p_2-p_1).$$ Return Θ̂j = [Θ̃j, t(λ/2+ α̂)] and ${\widehat{\beta }}_j^{\pm }={[{\stackrel{\sim }{\beta }}_j^{\pm }+t\widehat{\alpha }]}_{+}$.