IMRT Treatment Planning on 4D Geometries for the Era of Dynamic MLC Tracking

Abstract

The problem addressed here was to obtain optimal and deliverable dynamic multileaf collimator (MLC) leaf sequences from four-dimensional (4D) geometries for dynamic MLC tracking delivery. The envisaged scenario was where respiratory phase and position information of the target was available during treatment, from which the optimal treatment plan could be further adapted in real time. A tool for 4D treatment plan optimization was developed that integrates a commercially available treatment planning system and a general-purpose optimization system. The 4D planning method was applied to the 4D computed tomography planning scans of three lung cancer patients. The optimization variables were MLC leaf positions as a function of monitor units and respiratory phase. The objective function was the deformable dose-summed 4D treatment plan score. MLC leaf motion was constrained by the maximum leaf velocity between control points in terms of monitor units for tumor motion parallel to the leaf travel direction and between phases for tumor motion parallel to the leaf travel direction. For comparison and a starting point for the 4D optimization, three-dimensional (3D) optimization was performed on each of the phases. The output of the 4D IMRT planning process is a leaf sequence which is a function of both monitor unit and phase, which can be delivered to a patient whose breathing may vary between the imaging and treatment sessions. The 4D treatment plan score improved during 4D optimization by 34%, 4%, and 50% for Patients A, B, and C, respectively, indicating 4D optimization generated a better 4D treatment plan than the deformable sum of individually optimized phase plans. The dose-volume histograms for each phase remained similar, indicating robustness of the 4D treatment plan to respiratory variations expected during treatment delivery. In summary, 4D optimization for respiratory phase-dependent treatment planning with dynamic MLC motion tracking improved the 4D treatment plan score by 4–50% compared with 3D optimization. The 4D treatment plans had leaf sequences that varied from phase to phase to account for anatomic motion, but showed similar target dose distributions in each phase. The current method could in principle be generalized for use in offline replanning between fractions or for online 4D treatment planning based on 4D cone-beam CT images. Computation time remains a challenge.

Introduction

The three main areas of technology-patient interactions in radiation oncology are imaging, treatment planning, and treatment delivery. To account for respiratory motion during imaging, four-dimensional (4D) computed tomography (CT) has been developed and its implementation is widespread: 4D CT was used in 44% of institutions in 2009, growing at a rate of 7% per year (1). To account for respiratory motion during treatment delivery, the era of dynamic multileaf collimator (MLC) tracking is nearly upon us: multiple groups using multiple vendor solutions have experimentally investigated dynamic MLC tracking (2, 3), with the first animal treatment being reported on (4). A relatively unexplored space is to use the degrees of freedom offered by dynamic MLC tracking for 4D treatment planning, in which the leaf shape can change during each phase of respiration to improve plan optimality. However, the mechanical constraints of the dynamic MLC need to be respected.

4D treatment planning with dynamic MLC motion tracking includes a constraint that an MLC imposes on leaf sequencing, which is not found in three-dimensional (3D) cases. MLC leaf sequences need to be specifically designed such that the maximum leaf dynamics (velocity and acceleration/ deceleration) are not exceeded when tracking tumor motion using an MLC. Therefore, compared with 3D treatment planning optimization, additional complexities for 4D optimization are: (1) optimization is performed over a number of CT images and (2) MLC leaf motion during phase-to-phase transitions is constrained by the maximum leaf dynamics.

3D intensity-modulated radiation therapy (IMRT) treatment planning optimization results in an MLC leaf sequence as a function of monitor units, MU, i.e., L(MU). The general goal of 4D optimization for IMRT treatment planning is to find a deliverable leaf sequence as a function of respiratory phase, θ, as well as MU, i.e., L(MU, θ), and radiation beam on/off, H, to minimize an objective function,

$$f\left[D\left(\text{L}\left(\text{MU},\theta \right),H\right)\right],$$ [1]

which represents a clinical objective of treatment planning. A 4D dose distribution to be delivered, D, is obtained from a deformable dose-summed 4D treatment plan, which is generated by accumulating the resultant doses of individual phase treatment plans, D_i , on the reference phase CT image, I_ref , using deformable dose summation (5-9):

$$D={\displaystyle \sum _{i=0}^{p-1}{H}_i{\lambda }_i{D}_i\left(I_i,I_{\text{ref}},{\mu }_i,\text{L}\left(\text{MU},{\theta }_i\right)\right),}$$ [2]

where i is a respiratory phase index from 0 to the maximum phase number, P−1, H is a Heaviside function indicating radiation beam on/off status for the given phase, and λ is fractional time spent per phase. A dose distribution of a given phase treatment plan, D_i, is computed on the given phase CT image, I_i, on the basis of L(MU, θ_i), and then deformed onto I_ref by a displacement vector field, μ , using a tri-linear dose interpolation algorithm (6, 7, 10). The variables of 4D optimization to be solved are L(MU, θ_i) and H_i. Note that the beam pause, H, for planning to account for the situation where higher than maximum leaf velocities are required or that the anatomy for a particular phase is dosimetrically undesirable, is distinct from the beam pause during delivery. The beam pause during delivery is to account for larger/faster than expected anatomic motion that causes the requested leaf positions to exceed their limits, e.g. due to a cough. 4D optimization for IMRT treatment planning and/or its delivery using a dynamic MLC technique has been investigated by several groups, although no proposed solutions are ideal. Keall et al. (11) proposed a method to explicitly include the temporal changes in anatomy during imaging, planning, and delivery of radiotherapy by adjusting the radiation beam on the basis of a temporally changing tumor position, such that motion of the radiation beam was synchronized with motion of the tumor. This study showed that 4D radiotherapy to explicitly account for anatomic motion allowed margin reduction from the clinical target volume (CTV) to the planning target volume (PTV) to achieve the goals of raised tumor dose and decreased normal tissue dose. Keall et al. (12) then provided a proof-of-principle example of the 4D radiotherapy treatment planning methodology to account for respiratory motion using dynamic MLC motion tracking. Treatment planning was simultaneously performed on each of a 4D CT image set in which an MLC-defined radiation beam aperture conformed to the PTV plus a penumbral margin at each respiratory phase. This study showed that 4D treatment planning with dynamic MLC motion tracking was feasible and offered an escalation in tumor doses and/or a reduction in treatment related complications.

Suh et al. (13, 14) and Gui et al. (15) introduced MLC leaf sequencing for 4D IMRT treatment planning optimization. Suh et al. (13) showed a deliverable 4D IMRT treatment planning method, where an IMRT treatment plan for a given respiratory phase was created by translating MLC leaf positions from the reference phase to the given phase by the difference in the tumor centroid position between the two phases of the 4D CT planning scan. This approach yielded a treatment planning scheme that is not optimal but, importantly, is deliverable with currently available technology. This study showed that accounting for one-dimensional tumor translation was practical and provided a reasonable plan. Suh et al. (14) then introduced a 4D IMRT treatment planning method using an algorithm developed for realtime dynamic MLC motion tracking in an offline manner. 4D IMRT treatment plans generated account for 3D tumor motion and thus motion hysteresis and non-linear motion of the tumor, and are deliverable on a treatment machine. This method integrated deliverable 4D IMRT treatment planning with dynamic MLC motion-tracking delivery by using the same algorithm between treatment planning and delivery for determining MLC leaf sequences, and thus has a clear path to clinical implementation. Gui et al. (15) introduced a simple and practical method of 4D IMRT treatment planning with dynamic tracking using a direct aperture deformation, which morphed the shape and position of radiation beam apertures optimized on the reference phase CT image to the other phase images. This study showed that the treatment plan generated on a phase-by-phase basis was similar to the “gold-standard” treatment plan that was optimized independently on each phase image, and better than that created by accounting for translation only. The limitation of these studies were that the 4D IMRT process was treated as a series of 3D problems for each phase, rather than solving the 4D problem, including the dose for each respiratory phase into the optimization process. These previous studies found, for a given phase θ_t , a deliverable leaf sequence for that phase, L(MU)_θi. In our current work we solve the 4D problem to simultaneously optimize L(MU, θ_i) over all phases.

Trofimov et al. (16) compared different 4D IMRT optimization schemes against full optimization, and showed that tumor tracking was better than the other techniques. This study provided a good framework of formulating 4D IMRT treatment planning optimization problems. However, they did not investigate a robustness of optimization methods with respect to delivery methods, thus they did not create leaf sequences nor include mechanical limitations of a treatment machine, such as MLC leaf motion constraints. Zhang et al. (9) incorporated respiratory tumor motion and deformation into treatment planning optimization for helical tomotherapy delivery. Time-dependent dose calculation was performed for each beamlet, a set of deformed beamlets was obtained by mapping the calculated dose back to the primary phase, and motion-incorporated optimization was performed. This method provided breathing-correlated delivery as the correlation between treatment delivery and a respiratory cycle was set in treatment planning with the help of guided breathing. However, they did not create MLC leaf sequences.

The significance of the robustness of 4D treatment plans was discussed in Nohadani et al. (17). A spatiotemporal treatment planning optimization method, which takes into account all respiratory phases through the 4D CT scan and provides a 4D optimal treatment plan that can be delivered throughout all respiratory phases, was developed. By taking all available information into account and providing a solution that is adaptive to the changes during treatment delivery, their phase-adapted 4D treatment plans are robust against motion, irregular breathing, MLC leaf sequencing, and delivery uncertainty. The 4D plans show significant improvement in target coverage and normal tissue sparing with higher delivery efficiency. An advantage of the Nohadani method over our current work is the explicit inclusion of robustness into the optimization process. A limitation is that leaf sequencing was not directly incorporated into the optimization process.

The aim of this study was to develop 4D optimization for respiratory phase-dependent IMRT treatment planning with dynamic MLC motion tracking, including MLC leaf motion constraints, which takes respiration-induced anatomic motion (including deformation, volume and density changes) into account and is robust to the variations of fractional time spent in respiratory phases within a given 4D CT planning scan.

Methods and Materials

4D Optimization for Respiratory Phase-dependent IMRT Treatment Planning

Without loss of generality, due to the computational burden, there were three simplifications in this study:

1. 4D optimization was performed only with two respiratory phases (end inhale and end exhale phases) out of all the phases of the 4D CT planning scan, i.e., Hi = 1 for end inhale (i = 0) and end exhale (i = 5). Therefore, only L(MU, θi) was the optimization variable. Note that the reference phase was the end inhale phase, i.e., I_ref = I₀.

2. An IMRT treatment plan consisted of two segments per treatment beam.

3. λ was assumed to be equal for all the respiratory phases.

Including the above simplifications reduced the general formalism of 4D optimization for IMRT treatment planning in equations [1] and [2] to find the function L(MU, θ_i) that minimizes

$$f\left[D\left(\text{L}\left(\text{MU},\theta \right),H\right)\right],$$ [3]

where

$$D=D_0\left({\text{I}}_0,\text{L}\left(\text{MU},{\theta }_0\right)\right)+D_5\left({\text{I}}_5,{\text{I}}_0,{\mu }_5,\text{L}\left(\text{MU},{\theta }_5\right)\right).$$ [4]

MLC Leaf Velocity Constraints

Since MLC leaf acceleration (measured to be about 50 cm s—²) is assumed to be sufficient for currently used dynamic MLC leaf-sequencing algorithms, only the maximum leaf velocity (measured to be about 3.3 cm s⁻¹) was used as a constraint for leaf sequencing (18-20). For leaf-sequencing algorithms for 3D treatment planning where MLC leaf positions vary with MU, the leaf velocity is constrained to the maximum leaf velocity, v_max, i.e., dL(MU)/dt ≤ v_max , where t is time in seconds and dL(MU)/dt is the pre-planned dose rate. For 4D optimization, dL(MU, θ_i)/dt ≤ v_max is an additional complexity for the respiratory phases where the radiation beam is on (H_t = 1).

For phase i, leafj, and control point k, the leaf velocity constraints are: (1) in terms of MU, L_i,j,k − L_i,j,k−l < v_max ΔMU •(t/MU), where ΔMU is MU difference between control points of k and k—1 and (2) in terms of θ, L_i,j − L_i,j−1j < v_max · λ_i, and L_i,j − L_i,j−1 < v_max · λ_i for tumor motion parallel (between phases of i and i—1) and perpendicular (between leaves of j and j—1) to the MLC leaf travel direction, respectively.

In this study, the maximum MLC leaf velocity was assumed to be 3.3 cm s⁻¹, which is a reasonable measurement based estimate (20). Given that the mean patient respiratory period is about 4 s (ranging 1 to 8 s) (21, 22), the time interval between the adjacent respiratory phases was assumed to be 4 /P s. Accordingly, the maximum allowed leaf displacement between the adjacent phases was 13.2 /P cm.

Optimization System

The Sparse Nonlinear Optimizer (SNOPT, Stanford Systems Optimization Lab, Stanford, CA) (23, 24) was employed as an optimization system in this study. SNOPT is a generalpurpose system to solve optimization problems involving many variables and constraints. It is suitable for large-scale linear and nonlinear programming and for linearly constrained optimization; and especially effective for nonlinear problems whose objective and/or constraint functions and their gradients are expensive to evaluate. The reason why SNOPT was chosen was because 4D treatment planning optimization deals with constrained MLC leaf sequences due to the leaf velocity constraint and is a large scale involving many variables to handle the 4D problem.

The snOptA interface in SNOPT minimizes a linear or nonlinear objective function, f [ D (L)], subject to constant lower and upper bounds, l and u, respectively, on both variables, L, and a number of sparse linear and/or nonlinear constraint functions, F (L):

$$\text{minimize\hspace{0.17em}}f\left[D\left(\text{L}\right)\right]\hspace{0.17em}\text{subject\hspace{0.17em}to}\hspace{0.17em}{l}_{\text{L}}\le \text{L}\le u_{\text{L}}\hspace{0.17em}\text{and}\hspace{0.17em}{l}_{\text{F}}\le \text{F}\left(\text{L}\right)\le u_{\text{F}}.$$

If gradients of any of the problem functions, F_m(L), that include both the objective and constraint functions in a set of {F_m(L)} are unknown, snOptA estimates the missing ones by finite differences.

To solve the nonlinear problems, a sparse sequential quadratic programming method is applied to SNOPT (23, 25). The sequential quadratic programming algorithm basically involves major and minor iterations. The major iterations generate a sequence of iterations that satisfies the linear constraints and converges to a point satisfying the nonlinear constraints and the first-order conditions for optimality. At each step of this iteration, the sequential quadratic programming algorithm obtains search directions towards the next iteration from a sequence of minor iterations, i.e., quadratic programming sub-problems. Each quadratic programming sub-problem minimizes a quadratic model of a certain Lagrangian function subject to a linearization of the constraints. An augmented Lagrangian merit function is reduced along each search direction to ensure convergence from any starting point. After the quadratic programming sub-problem is solved, new estimates of the nonlinear problem solution are computed using a line-search on the augmented Lagrangian merit function.

A Tool for 4D Optimization

An MLC-based IMRT treatment plan is basically a series of MLC leaf positions, i.e., an MLC leaf sequence as a function of MU. The MLC leaf sequence recorded in a computer file is used to control MLC leaf motion to deliver the treatment plan. In a research version of a commercial radiotherapy treatment planning system (Pinnacle 8.1, Philips Healthcare, Milpitas, CA), MLC leaf sequence files can be imported into a certain treatment plan; with all other requirements for dose computation set, a dose of the treatment plan with imported leaf sequences can be computed on the specified CT image.

Commercially available treatment planning systems provide IMRT optimization on a single CT image, i.e., 3D geometry, but do not provide IMRT optimization over multiple images of the 4D CT scan for dynamic MLC tumor tracking. Therefore, the 4D treatment planning optimization method was implemented by linking a separate optimization system (SNOPT) with Pinnacle.

A tool for 4D optimization for respiratory phase-dependent IMRT treatment planning that integrates the Pinnacle system and the SNOPT system was implemented in the C programming language (Figure 1). SNOPT performed optimization to find L(MU, θ_t) with the sensitivity of the changes of each MLC leaf position for each respiratory phase to the objective score of a deformable dose-summed 4D treatment plan, and passed it to Pinnacle after each iteration. With L(MU, θ_t) imported, Pinnacle computed D_i and D on the corresponding phase image of the 4D CT planning scan. Then, Pinnacle passed the objective score of a deformable dose-summed 4D plan to SNOPT. This iterative loop continued until the solution converged, yielding L(MU, θ), a 4D plan with the same number of segments in each beam as for the 3D input plans.

Figure 1:

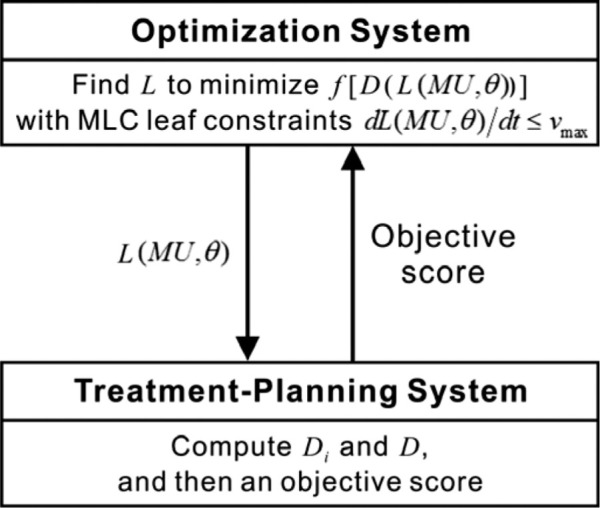
Integration of a commercially available treatment planning system and a general-purpose optimization system for 4D optimization for respiratory phase-dependent IMRT treatment planning. D_i = a 3D dose distribution of the phase i treatment plan; D = a 4D dose distribution to be delivered obtained from a deformable dose-summed 4D treatment plan; L = an MLC leaf sequence as a function of monitor units and respiratory phase; f = an objective function of optimization; MU = monitor units; θ = a respiratory phase; v_max = the maximum MLC leaf velocity.

For initialization of 4D optimization, individual phase plans were generated by optimizing an IMRT treatment plan individually on the end inhale and end exhale phase CT image for each patient in Pinnacle, where the input L(MU, θ_t) was obtained. The treatment plans with the input L(MU, θ_t) are termed “3D optimal” plans throughout. The jaw positions were adjusted such that the radiation field covered the PTVs on the end inhale and end exhale phase of the 4D CT planning scan with a 1-cm margin.

4D Optimization for Patients’ 4D CT Planning Scans

In order to show the principle of 4D treatment planning optimization, the 4D optimization tool described above was applied to the 4D CT planning scans of three lung cancer patients, whose tumor motion extent was more than or equal to 0.5 cm (Table I) (26). The 4D CT acquisition was performed as a part of an IRB-approved study (protocol 00-202) at The University of Texas M.D. Anderson Cancer Center. Patient A showing the largest tumor motion, Patient B showing the largest tumor volume, and Patient C showing the largest tumor motion hysteresis were selected from a previously reported data set (Table I) (13, 14, 27, 28).

Table I.

Centroid motion extent, volume, and location in the lungs, and local tumor stage of the GTV quantified from 4D CT planning scans of the three lung cancer patients chosen for this study selected from a larger dataset (13, 14).

Patients	Centroid motion (cm)	Volume (cm3)	Location in lungs	Local tumor stage	Characteristics
A	2.1	3	Lower/left/peripheral	T1N0	Largest motion
B	1.3	119	Lower/left/center	T4N0	Largest volume
C	0.6	1	Upper/left/center	TXN2	Largest hysteresis

Anatomy segmentation, treatment planning preparation, and plan evaluation were performed using Pinnacle. On the basis of the manually segmented contours on the end inhale phase CT image, contours on the other phases of the 4D CT scan were automatically generated using the large deformation diffeomorphic image registration algorithm developed at The University of North Carolina (6, 7, 10). The CTV enclosed the gross tumor volume (GTV) with an isotropic 0.8-cm margin (29), and then a 0.5-cm margin was added to create the PTV. Further details, reviews and analyses of the manual and automatically-generated contours are described elsewhere (28, 30, 31).

For IMRT treatment plans of lung tumors, the prescribed dose was 74 Gy (2 Gy per fraction, 5 times per week) to cover at least 95% of the PTV, within a dose range of 90 to 120% of the prescribed dose. For the organs at risk (OARs), the plan objective was designed to limit the maximum or minimum dose or dose-volume histogram (DVH) with the corresponding weighting factor for each OAR or planning OAR volume (PRV; OAR with margins for setup and/or organ motion): (1) no more than 45 Gy to the spinal cord PRV; (2) no more than 20 Gy (V_{20 Gy}) to 30% of the normal lung volume (both lungs without the GTV); (3) no more than 55 Gy (V_{55 Gy}) to 30% of the esophagus PRV; (4) no more than 40 Gy (V_{40 Gy}) to 50% of the heart volume; and (5) no more than 80 Gy to the entire normal thorax (entire thorax without the PTV). Beam arrangements were six coplanar, non-opposed, predominantly anterior-posterior, with beam angles adjusted depending on the tumor locations. Objectives and details about IMRT treatment plans have been reviewed by one radiation oncologist and described elsewhere (27).

On the basis of the GTV centroid position for each respiratory phase quantified from the 4D CT planning scan, a major axis of tumor motion was automatically determined for each beam angle using a least-squares fit (13, 14). Thus, for each beam, the collimator was rotated to align the MLC leaf travel direction parallel to the major axis of tumor motion. This step was performed because of the known decrease in delivery efficiency for the motion perpendicular to the MLC leaf travel direction (32).

Individual phase plans and deformable dose-summed 4D plans were evaluated and compared using objective scores and dose-volume evaluation metrics. The objective score, a single number calculated on the basis of the plan objectives described above, is an indicator of plan quality that takes into account the actually achieved dose distribution for the PTV and OARs/PRVs after plan optimization, relative to the initial constraints (27). The objective score is the only single quantitative metric that is considered during IMRT treatment planning optimization. The smaller the objective score, the better the treatment plan.

Results

4D optimization shows improvement in 4D plan quality (i.e., decrease in the objective scores) as shown in Figure 2. The treatment plans on the end inhale and end exhale phase were used to create the deformable dose-summed 4D treatment plan. The treatment plans for iteration 0 (input) are the 3D optimal plans. 4D treatment planning optimization with dynamic MLC tracking including MLC leaf motion constraints further improved the treatment plans from the ones already optimized in 3D geometry, and thus generated a better 4D treatment plan than the sum of individually optimized phase plans. In other words, 4D optimal plans are better than 3D optimal plans.

Figure 2:

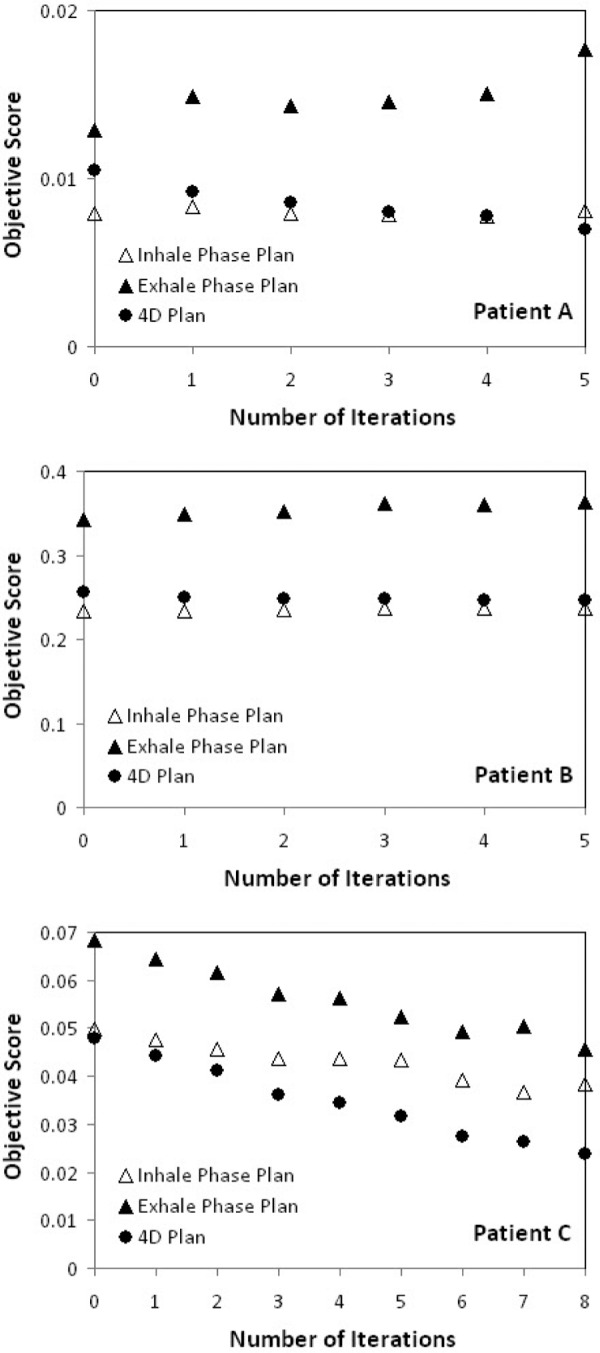
Objective score vs. number of iterations for the end inhale phase, end exhale phase and 4D treatment plan for Patients A, B, and C. Lower objective scores indicate the better plan quality.

In all three cases (as expected) the 4D objective score improved at each iteration. As shown in Figure 2, for Patient A the 4D objective score improved while the objective score for one of the phases (exhale) worsened; for Patient B the 4D objective score improved while the objective score for individual phases worsened; and for Patient C the 4D objective score improved while the objective score for individual phases improved. This variability may be due to patient to patient variations or the convergence of the individual phase plans with the Pinnacle system used as input to the 4D optimization.

The improvement in the individual phase plans was unexpected and shows the advantage of the SNOPT algorithm over that of the treatment planning system. The disadvantage was the long computation time – on the order of days per iteration. The implications of the computation time are expanded upon in the discussion.

The 4D objective score was between the objective score for the inhale phase and the exhale phase, yet closer to the inhale phase plan for Patients A and B. For Patient C, 4D the objective score is better than the objective score for individual phases.

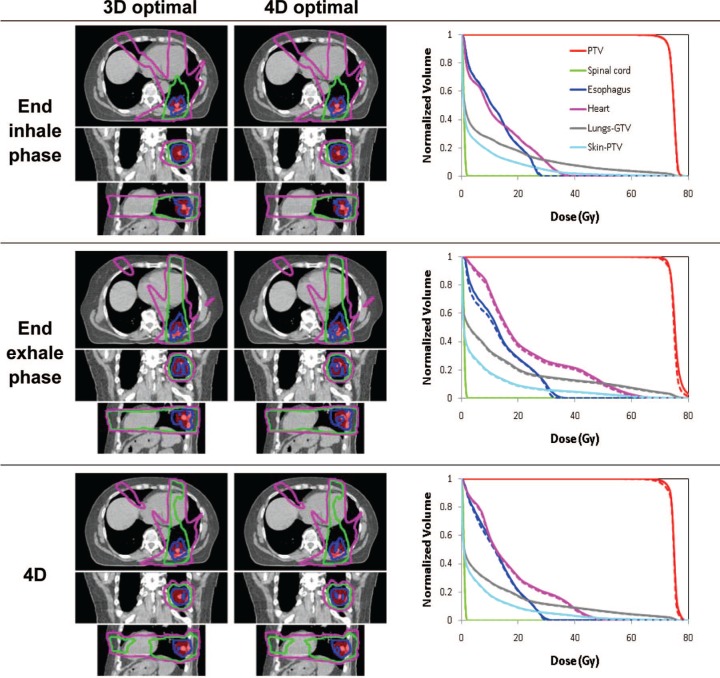
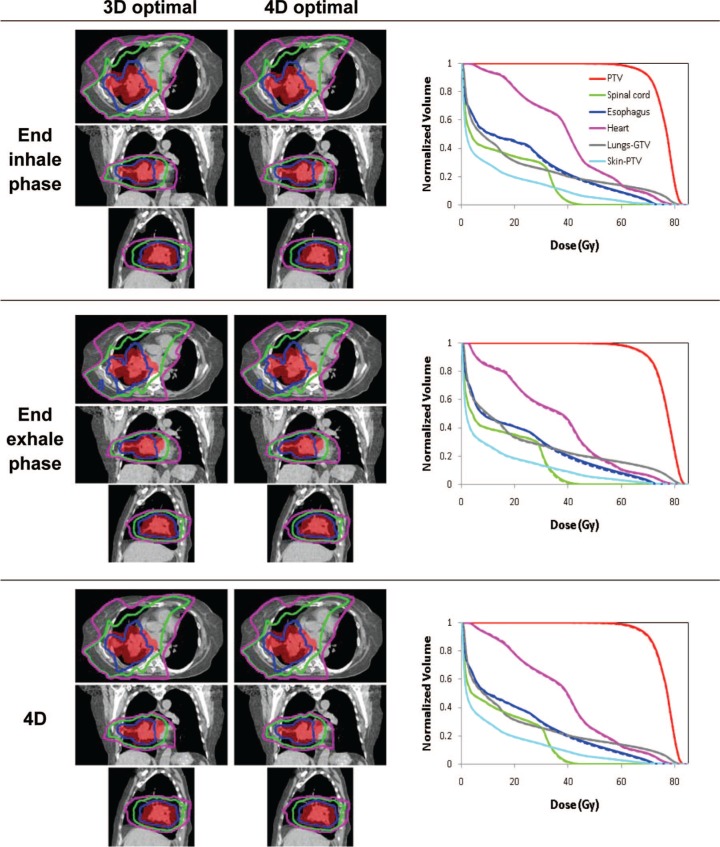
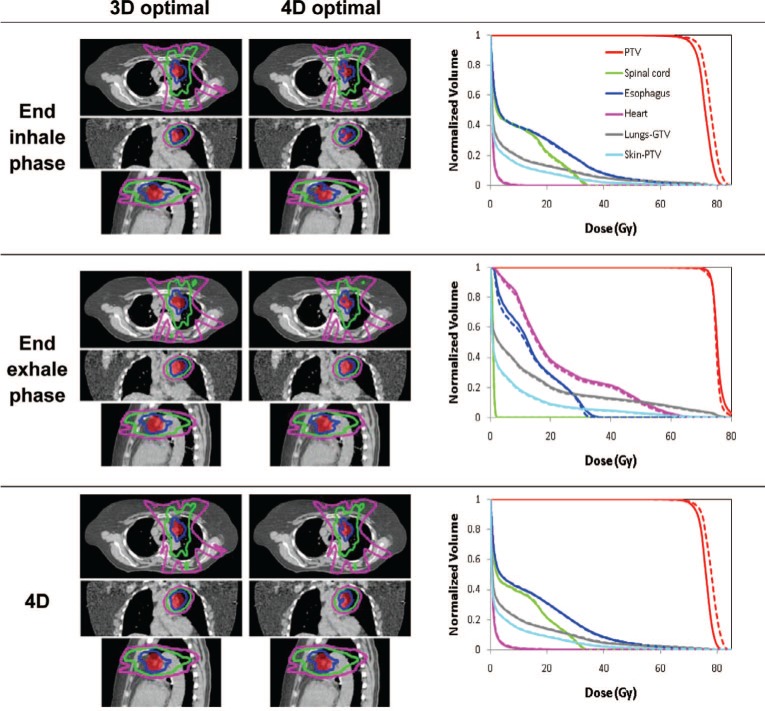
Figures 3-5 show the isodose distributions and DVHs for 3D optimal and 4D optimal plans (input and output of 4D optimization) for the three patients. The dose-volume metrics for 3D and 4D optimization are shown in Table II. The differences appear relatively minor except for Patient C (Figure 5) where the PTV dose curves are lower, though more uniform, for the 4D optimal plan.

Figure 3:

Isodose distributions for transverse, coronal and sagittal plane before (left) and after (right) optimization and dose-volume histograms for 3D optimal (dashed) and for 4D optimal (solid) for the end inhale and exhale phase plans and the 4D plan for Patient A.

Figure 4:

Isodose distributions for transverse, coronal and sagittal plane before (left) and after (right) optimization and dose-volume histograms for 3D optimal (dashed) and for 4D optimal (solid) for the end inhale and exhale phase plans and the 4D plan for Patient B.

Figure 5:

Isodose distributions for transverse, coronal and sagittal plane before (left) and after (right) optimization and dose-volume histograms for 3D optimal (dashed) and for 4D optimal (solid) for the end inhale and exhale phase plans and the 4D plan for Patient A.

Table II.

Comparison of target coverage and normal tissue sparing: dose-volume metrics of 4D treatment plans after 3D optimization and after 4D optimization for each patient. The prescribed dose is 74 Gy.

Patient	Optimization	$D_{95\%}^{\text{PTV}}$	$D_{\max }^{\text{PTV}}$	$D_{\text{mean}}^{\text{PTV}}$	MLD	$V_{20\hspace{0.17em}\text{Gy}}^{\text{Lungs}}$	$V_{30\hspace{0.17em}\text{Gy}}^{\text{Lungs}}$	$D_{\max }^{\text{Esophagus}}$	$D_{\text{mean}}^{\text{Esophagus}}$	$V_{55\hspace{0.17em}\text{Gy}}^{\text{Esophagus}}$	$D_{\max }^{\text{Cord}}$	$D_{0.1\%}^{\text{Cord}}$	$D_{\max }^{\text{Heart}}$	$D_{\text{mean}}^{\text{Heart}}$	$V_{40\hspace{0.17em}\text{Gy}}^{\text{Heart}}$	$D_{\text{mean}}^{\text{Skin}-\text{PTV}}$
A	3D	71.6	78.3	74.5	10.1	16.9	11.3	31.6	12.3	0	2.7	2.1	54.6	16.3	7.5	5.8
	4D	72.7	80.0	74.8	10.3	17.3	11.5	32.0	12.6	0	2.7	2.2	55.8	16.7	8.3	6.0
B	3D	63.6	85.7	75.6	19.9	30.1	24.8	72.1	18.7	8.8	46.0	44.6	78.5	37.8	50.7	10.5
	4D	65.3	86.5	75.8	20.8	31.2	25.8	73.3	19.4	9.5	46.7	45.2	78.7	38.2	52.1	10.5
C	3D	73.1	84.6	77.7	7.7	14.3	9.4	76.9	13.6	3.1	34.6	33.8	27.2	1.2	0	5.0
	4D	71.6	81.6	75.8	7.5	14.9	9.0	76.2	13.6	2.8	35.0	33.9	24.5	1.1	0	4.8

D_mean and D_max represent the dose received by mean and maximum volume of the PTV or OARs, respectively; MLD the mean lung dose; D_A% the dose received by A% of volume of the PTV or OARs (Gy); and V_BGy the fractional volume of OARs receiving at least B Gy (%).

Discussion

3D treatment planning with dynamic MLC tracking is an available technology, resulting in an MLC leaf sequence as a function of MU. 4D treatment planning with dynamic MLC tracking, on the other hand, develops MLC leaf sequence as a function of respiratory phase, in addition to MU, which represents a fundamentally new paradigm in radiotherapy treatment planning. How to perform 4D treatment planning is being investigated, but has yet to be fully resolved. A clinical scenario of 4D radiotherapy for lung or liver patients with implanted markers involves the following work flow: (1) a 4D CT planning scan is acquired pre-treatment; (2) on the basis of the 4D CT planning scan, 4D treatment planning with dynamic MLC motion tracking, in which spatial and morphological changes of tumors and normal tissues are included, is performed; (3) on the basis of the 4D treatment plan, treatment delivery that accounts for the tumor motion different from the motion in the treatment plan is performed, using real-time target localization, such as kV, MV, and/or optical imaging integrated with dynamic MLC motion tracking. In this study, respiratory phase-dependent IMRT treatment planning with dynamic MLC motion tracking was investigated. A tool for 4D treatment planning optimization was developed and applied to the 4D CT planning scans of three lung cancer patients. Respiratory phase-dependent IMRT treatment planning optimization includes MLC leaf motion constraints. The resultant 4D treatment plans take respiration-induced anatomic motion into account and are robust to the variations of fractional time spent in respiratory phases within a given 4D CT planning scan.

Keall et al. (11) and Reitzel et al. (33) stated that deliverable 4D treatment plans were created, but did not explicitly state how such treatment plans could be created. In this study, the MLC leaf motion constraints were explicitly defined and included in treatment planning optimization, and thus the resultant 4D treatment plans were deliverable. The delivery of 4D treatment plans to account for morphological changes observed on the 4D CT planning scan and motion variations occurring during the time of delivery is a parallel project.

Among different schemes of 4D treatment planning, respiratory phase-dependent IMRT treatment plans generated as a function of respiratory phase were employed in this study. This indicates that a treatment plan for a single patient changes from phase to phase, to account for anatomic motion due to respiration within a given 4D CT planning scan. As there is no further information about the patient respiration beyond the one 4D CT planning scan as it is often the case in clinic, variables such as day-to-day changes in tumor positions with respect to the skeletal anatomy are outside the scope of this study. As mentioned above, these kinds of variable motion would be taken care of during treatment delivery. Additionally, replanning on a new 4DCT geometry could be performed to have a plan based on a more recent estimate of the patient anatomy.

The optimal 4D IMRT treatment planning method is the one that develops treatment plans dosimetrically robust to variable motion expected during treatment delivery.

4D optimization generated a treatment plan that changes from phase to phase, but has similar dose distributions from phase to phase. Treatment planning robust to respiratory motion variations of fractional time spent in respiratory phases is to reduce phase-to-phase variations in dose distributions of the treatment plans. This robustness can be an advantage during treatment delivery, because it would result in dose distributions close to the planned dose distributions, even when a patient spends a different fraction of time in each respiratory phase during actual treatment delivery from the planned (i.e., as in a 4D CT planning scan). Therefore, a 4D treatment plan with a similar dose distribution in each phase is preferable to an equivalent 4D plan with large phase-to-phase variations in a dose distribution as patient respiratory patterns change between imaging (planning scan) and treatment planning, between treatment planning and delivery, and between treatment deliveries. The worst case would be that a patient spends time only in one respiratory phase during treatment delivery. For example, Figure 5 shows how different the treatment results would be if a patient breathes only in the end inhale phase or in the end exhale phase during the time of treatment delivery.

As shown in Figure 2, 4D optimization generated a better 4D treatment plan than the sum of individually optimized phase plans. This shows that including anatomic motion as an additional degree of freedom in radiotherapy treatment planning yields at least as good solutions with motion tracking as those with no motion. Therefore, motion can be seen as an opportunity to benefit radiotherapy treatment planning, rather than an obstacle. Additional explorations of using degrees of freedom of motion in addition to the MLC that would alleviate some of the leaf motion limitations could be performed by including optimization of the MLC carriage motion, couch motion or the linac itself if using e.g. a robotic (Cyberknife) or gimbaled (Vero) linac.

The current study was developed for MLC delivery using a conventional linear accelerator. An interesting question is whether this method could be transferred to other delivery modalities.

The computation time of the order of days per iteration, even with the planning simplifications, mean that the method needs substantial speed improvement prior to clinical implementation. The reason for the long calculation time is that there is limited information- only the objective score- being communicated between the treatment planning system and optimization system. Therefore, the optimization reverted to a finite difference method, in which the sensitivity of the objective function to each leaf position change was calculated at each iteration. Given the dose calculation time and communication in this research system, the process is very inefficient. Should such a system move towards clinical implementation, these issues would need to be addressed.

A further limitat ion of this study, and indeed any method that uses 4D CT and deformable registration, is to understand the shortcomings of these tools. 4D CT represents anatomic motion for only the brief time when the patient anatomy is being imaged and is prone to artifacts. Deformable registration also introduces small and sometimes large uncertainties for contour propagation and dose summation.

Conclusion

4D optimization for respiratory phase-dependent treatment planning with dynamic MLC motion tracking improved the 4D plan score by 26% on average compared with 3D optimization. 4D treatment plans generated changed from phase to phase to account for anatomic motion, but showed similar dose distributions in each phase. The current method could in principle be generalized for use in offline replanning between fractions or online 4D treatment planning based on 4D cone-beam CT images. Computation time remains a challenge.