EVALUATING SUBJECT-LEVEL INCREMENTAL VALUES OF NEW MARKERS FOR RISK CLASSIFICATION RULE

Abstract

Suppose that we need to classify a population of subjects into several well-defined ordered risk categories for disease prevention or management with their “baseline” risk factors/markers. In this article, we present a systematic approach to identify subjects using their conventional risk factors/markers who would benefit from a new set of risk markers for more accurate classification. Specifically for each subgroup of individuals with the same conventional risk estimate, we present inference procedures for the reclassification and the corresponding correct re-categorization rates with the new markers. We then apply these new tools to analyze the data from the Cardiovascular Health Study sponsored by the US National Heart, Lung, and Blood Institute (NHLBI). We used Framingham risk factors plus the information of baseline anti-hypertensive drug usage to identify adult American women who may benefit from the measurement of a new blood biomarker, CRP, for better risk classification in order to intensify prevention of coronary heart disease for the subsequent ten years.

1 Introduction

An integral part of evidence-based guidelines for disease prevention or management is a well-defined risk classification rule, which assigns each subject from a population of interest to one of several ordered risk groups. The assignment is based on the individual risk: the chance that the subject will experience a specific type of event during a given time period. Appropriate interventions will then be offered to subjects in each risk category. The risk is estimated using a scoring system with the subject’s “conventional” baseline risk factors/markers. For example, in the United States more than a half million women die of cardiovascular diseases (CVD) each year and the majority of such deaths are due to coronary heart disease (CHD). Recently, the American Heart Association (AHA) issued guidelines for the prevention of CHD in adult women (Mosca et al., 2004, 2007). Specifically, risk categories are defined by the individual’s predicted risk of having a CHD event in the next ten years. Adult American women are classified as being low risk (< 10%), intermediate risk (between 10% and 20%), or high risk (≥ 20%). Such risk threshold values have also been employed by the Adult Treatment Panel III (ATP III) of the National Cholesterol Education Program to develop an evidence-based set of guidelines on cholesterol management (Grundy et al., 2004). For subjects with intermediate or high risk, certain life style and pharmacologic interventions are recommended. The risk is estimated using a modified version of the Framingham Risk Score (FRS), which is a multivariate risk equation based on traditional risk factors such as age, blood cholesterol, HDL cholesterol, blood pressure, smoking status and diabetes mellitus (Wilson et al., 1998).

Now, suppose that new risk markers for such future events are available, and they may potentially improve the conventional risk estimation. Measuring these markers, however, may be invasive or costly. Under various settings, novel procedures have been proposed to quantify the overall incremental benefit from the new markers for the entire population of interest (Pepe et al., 2004; Cook, 2007; Tian et al., 2007; Uno et al., 2007; Pepe et al., 2008; Pencina et al., 2008; Chi and Zhou, 2008; Cook, 2008; Greenland, 2008). In a recent paper, Wang et al. (2006) concluded that almost all new contemporary biomarkers for prevention of CHD added rather moderate overall predictive value to FRS.

In general, for subjects whose conventional risk estimates are either extremely low or high, clinical practitioners are less likely to request additional marker measurements for their decision making. Unfortunately, rather little research has been done for developing a systematic procedure to identify a subset of individuals who would benefit significantly from new risk markers (D’Agostino, 2006). With respect to the aforementioned risk classification rule recommended by the AHA and ATP III, recently Cook et al. (2006) and Ridker et al. (2007) examined the incremental value of a new blood biomarker – the C-Reactive protein (CRP) measured by a highly sensitive assay – with a cohort of subjects from the Women’s Health Study (Buring and Hennekens, 1992). They concluded that subjects whose traditional risk scores are between 5% and 20% would benefit from this marker. Their claims were based on the reclassification rates with CRP among four discretized subgroups of the entire cohort determined by conventional risk estimates. However, large observed reclassification rates, which include both “good” and “bad” reclassification rates, does not equal to the benefit of a new marker. More recently, Prentice and his colleagues performed a comprehensive analysis on five pooled cohorts to examine the additive value of genetic variants to breast cancer risk models and conclude that “Inclusion of newly discovered genetic factors modestly improved the performance of risk models for breast cancer. The level of predicted breast-cancer risk among most women changed little after the addition of currently available genetic information.”(Waholder et al., 2010). One of their main analytic strategies employed to quantify the improvement of genetic markers is to examine how the addition of genetic data actually affected the risk stratification, i.e., the reclassification rate, for the case subjects with breast cancer and control subjects without breast cancer, separately. This can be viewed as a great improvement of the crude re-classification rate in the direction of detailed quantification of the “good” and “bad” reclassification. On the other hand, the incremental benefit of the “genetic markers” for risk stratification is evaluated for the entire population. It is useful to generalize the approach for identifying subgroup of patients, whose risk stratification may still be substantially improved by using new genetic markers in the risk prediction model (Mealiffe et al., 2010). Moreover, all the existing summary measures related to reclassification rate are simply point estimators lacking rigorous statistical inference procedure to provide appropriate precision measures.

In this article, we propose a systematic approach for evaluating the incremental value of a novel marker in risk stratification across subgroups of subjects and identify subjects who may benefit the most from the information of the new marker. To this end, for each subject in the study we construct two individual risk estimates, one based on the conventional risk markers and the other based on both the conventional and new markers. A subject may be reclassified into a different risk category with the new risk estimate. For the subset D of subjects with the same conventional risk estimate, we obtain consistent nonparametric functional estimates for the reclassification rates and their corresponding standard error estimates. Note the limitation that the large observed reclassification rates do not automatically imply that the new markers are important for given subsets of subjects. Consistent estimates for the proportions of subjects who are reclassified correctly are also needed for cost-benefit decision making. In this paper, we develop point and interval estimation procedures for making inference about such proportions.

As an illustration, consider the set D consisting of individuals who have the same conventional FRS estimate of 9% for experiencing CHD events within ten years. Based on the aforementioned prevention guidelines, individuals with this predicted risk would not be recommended for lipid-lowering drug therapy at present. Now, suppose that with the new markers, the estimate for the proportion of subjects in D reclassified to the next higher risk category is 25%. Furthermore, suppose that among those who are reclassified to the next higher risk category, the CHD events rate is 12%. The potential benefit with the new markers would be preventing 12% × 25% = 3% of subjects in D from having future CHD events. However, the costs consist of measuring new marker values for every subject in this subset, and giving possibly long-term, potentially toxic interventions to 25% of the individuals. Even if we decide that for this scenario the benefit outweighs the cost, we still need to know whether this reclassification scheme is better than a “random allocation” process. If we randomly move 25% of subjects in D to the next higher risk class, on average, 9% of these subjects would have CHD events. The question is whether the difference between the observed 12% and the null value of 9% represents a real gain or is simply due to sampling variation.

The new proposal is illustrated with a data set from the Cardiovascular Health Study (CHS) sponsored by the US National Heart, Lung and Blood Institute (Fried et al., 1991). This study is a prospective, population-based, long term follow-up cohort study to determine risk factors for predicting future coronary heart disease and stroke in adults 65 years or older. There were 5888 study subjects recruited between 1988 and 1993. For our analysis, we only considered data from the 3393 female participants. For each subject, we utilized the risk factors/markers values at her entry time to the study and her CHD event time by year 2003. The binary response variable is whether the subject experienced a CHD event (non-fatal MI, angina or CHD-related death) during ten year follow-up. For this data set, the median age at the baseline is 72.5 and there is no loss of follow-up for these endpoints. During the first 10 year follow-up, 19.5% of female participants experienced non-fatal MI, angina or CHD-related death. On the other hand, 37% of them died from non-CHD-related diseases. Among 3393 subjects, 52% of them were surviving in year 2003. In our analysis, the conventional risk factors consist of the Framingham risk factors and the anti-hypertensive drug usage. The new marker considered here is CRP. For the risk classification rule recommended by the ATP III, the CRP provides pointwise significant incremental values for subjects whose conventional risk estimates are around 10% and 20%. On the other hand, we cannot find any subgroup of individuals who would benefit from the new marker under the simultaneous inference setting when controlling the overall family-wise type I error rate of 0.05.

In the next section, we describe our proposed procedures for quantifying the incremental value of new markers. Procedures for making inference about the incremental values were proposed in Section 3. In section 4, we provide details of the analysis of the CHS data and of a simulation study for examining the performance of our procedures. Concluding remarks are given in Section 5.

2 Quantifying Incremental Values from New Markers

Consider a subject randomly drawn from the study population. Let Y be its binary response variable with Y = 1 denoting “cases” and Y = 0 denoting “controls”, U be the set of conventional markers and V be the set of new markers. Let p(U) = pr(Y = 1| U) and p(U, V) = pr(Y = 1| U, V), the risks of this subject conditional on U and {U, V}, respectively. Assume that the classification rule assigns each subject to one of L ordered risk categories {C₁, · · · , C_L}. A subject is classified to C₁ if its risk for Y = 1 is in the interval [ν_l−1, ν_l), where l = 1, · · · , L, and 0 = ν₀ < · · · < ν_L = 1. Based on p(U, V), the subject may be reclassified into a higher or lower risk category.

Now, suppose that the data {(Y_i, U_i, V_i), i = 1, · · ·, n} consist of n independent copies of (Y, U, V). For any given (u, v), the probabilities p(u) and p(u, v) cannot be consistently estimated well with fully non-parametric procedures unless the dimension of U or V is very low. A practical alternative is to consider a working model for approximating p(U) by a parametric model

$$g_1\left({\beta }^{\prime }X\right),$$ (2.1)

where X, a p×1 vector, is a function of U, β is an unknown vector of parameters and g₁(·) is a known, smooth, increasing function. Now, suppose that β is estimated by $\widehat{\beta }$ via an estimating function S₁(β). The risk for a subject with U = u, whose X = x, is estimated by ${\widehat{p}}_u=g_1\left({\widehat{\beta }}^{\prime }x\right)$.

With the additional marker set V, consider the working model for approximating p(U, V ) by

$$g_2\left({\gamma }^{\prime }W\right),$$ (2.2)

where W, a r × 1 vector, is a function of U and V, g₂(·) is a known, smooth, increasing function, and γ is a vector of unknown parameters. Let γ be estimated by $\widehat{\gamma }$ via an estimating function S₂(γ). For a subject with (U, V ) = (u, v) whose W = w; the estimated risk is $\widehat{p}\{u,v\}=g_2\left({\widehat{\gamma }}^{\prime }w\right)$. Note that when Models (2.1) and (2.2) are correctly specified, with reasonable estimating functions S₁(·) and S₂(·), ${\widehat{p}}_u$ and $\widehat{p}\{u,v\}$ are consistent estimators for p(u) and p(u, v), respectively.

Now, consider a random future subject with (Y, U, V ) = (Y ⁰, U ⁰, V ⁰). For a given 0 < s < 1, let D_s be the group of future subjects whose ${{\widehat{p}}_U}^0=s$ and $l_s={\sum }_{l^{\prime }=1}^{L}I(v_{l^{\prime }}\le s)$ be the corresponding risk category. For subjects in D_s with additional new marker information, the probability of a subject’s being classified to C_l with Y ⁰ = q, is

$${\eta }_l^{\left(q\right)}\left(s\right)=\mathrm{pr}\{\widehat{p}\{U^0,V^0\}\in (v_{l-1},v_l),Y^0=q\mid {\widehat{p}}_{U^0}=s\},\mathrm{for}q=0,1;l=1,\cdots L.$$ (2.3)

Here, the conditional probabilities are with respect to the data {(Y_i, U_i, V_i)}, Y ⁰, U ⁰ and V ⁰. The probability of a subject being classified to C_l is ${\eta }_l\left(s\right)={\eta }_l^{\left(0\right)}\left(s\right)+{\eta }_l^{\left(1\right)}\left(s\right)$. For the subgroup with ${\widehat{p}}_{U^0}=s$, the probability of crossing risk boundaries or being reclassified into other risk categories is $\mathcal{P}\left(s\right)={\sum }_{l\ne l_s}{\eta }_l\left(s\right)$. However, it is important to note that a large value of the reclassification rate P(s) does not automatically imply that the new markers are valuable for D_s. The quantity in (2.3) also plays an important role in cost-benefit decision making. For subjects who are re-assigned to a higher risk category, $\{{\eta }_l^{\left(1\right)}\left(s\right),l>l_s\}$ provides us with the proportion of subjects in D_s who would benefit from the new markers. On the other hand, for subjects who are moved down to a lower risk group, {η⁽⁰⁾(s), l < l_s} would reflect the incremental gain. They are the generalizations of the net reclassification improvement (NRI) of the subpopulation D_s :

$$\sum _{l=1}^L{\eta }_l^{\left(1\right)}\left(s\right)∕\xi \left(s\right)\mathrm{sign}(l-l_s)-\sum _{l=1}^L{\eta }_l^{\left(0\right)}\left(s\right)∕\{1-\xi \left(s\right)\}\mathrm{sign}(l-l_s)$$

and provide detailed information on the improvements by including the new biomarker, where $\xi \left(s\right)=\mathrm{pr}(Y^0=1\mid {\widehat{p}}_{U^0}=s)={\sum }_{l=1}^L{\eta }_l^{\left(1\right)}\left(s\right)$.

Moreover, it is important to know whether the above reclassification is more than a purely random allocation process. Specifically, if the new markers contribute nothing to the classification rule, one would expect that conditional on ${\widehat{p}}_{U^0}=s,{\widehat{p}}_{\{U^0,V^0\}}$ 0 is independent of Y ⁰. That is,

$${\eta }_l^{\left(1\right)}\left(s\right)={\eta }_l\left(s\right)\times \xi \left(s\right),l=1\cdots ,L.$$ (2.4)

The differences

$$\{D_l\left(s\right)={\eta }_l^{\left(1\right)}\left(s\right)-{\eta }_l\left(s\right)\xi \left(s\right),l=1,\cdots ,L\}$$ (2.5)

also play important roles for quantifying the incremental value of the new markers for future subjects in D_s. If V ⁰ improves the risk stratification for subjects in D_s, we expect D_l(s) > 0 for l > l_s and D_l(s) < 0 for l < l_s. To summarize the overall gain of V ⁰ in reclassification for D_s, a simple measure would be

$$D_{+}\left(s\right)=\sum _{l=1}^L\mathrm{sign}(l-l_s)D_l\left(s\right),$$

which represents the extent to which V⁰ results in correct reclassifications over and above random reallocations.

3 Estimating ${\eta }_l^{\left(q\right)}\left(s\right)$ with Possibly Censored Event Time Observations

Oftentimes the binary response Y indicates that either the event time of interest is greater or less than a specific time point via a long term follow-up study. To this end, let T₀ be the random event time and t₀ be a prespecified time point. Here, the binary variable Y = 1, if T₀ < t₀, 0, otherwise. The “response” Y may not be observed directly due to censoring. That is, T₀ may be censored by a random variable C. Let G(·) be the survival function of C. In this article, we assume that G(·) is independent of T₀, U and V. For T₀, one can only observe T = min(T₀, C) and Δ = I(T₀ ≤ C), where I(·) is the indicator function. Our data {(T_i, Δ_i, U_i, V_i), i = 1, · · · , n} consist of n independent copies of (T, Δ, U, V ). Note that if there is no censoring involved, G(·) = 1 and {Y_i, i = 1, · · · , n} can be observed completely.

To obtain the estimates ${\widehat{p}}_u$ and $\widehat{p}\{u,v\}$, one may assume proportional hazards working models for T₀ with U, and then for T₀ with U and V. With the maximum partial likelihood estimates for the regression coefficients and the estimates for the underlying cumulative hazard functions, we can estimate p(u) and p(u, v). However, if a working proportional model is not correctly specified, the regression coefficient estimator converges to a constant vector, as n → ∞, which may depend on the censoring distribution. Moreover, a good prediction model for short term survivors may not work well for predicting long term survivors. In this article, instead of modeling the entire hazard function of T₀, we use the approach taken by Uno et al. (2007) to model the conditional risks of experiencing an event by t₀ directly via (2.1) and (2.2).

To estimate β in (2.1), we let the estimating function S₁(β) be

$$\sum _{i=1}^n{\widehat{\omega }}_i{X}_i\{I\left(T_i<t_0\right)-g_1\left({\beta }^{\prime }{X}_i\right)\}=\sum _{i=1}^n{\widehat{\omega }}_i{X}_i\left(\right\{Y_i-g_1\left({\beta }^{\prime }{X}_i\right)\left\}\right),$$ (3.1)

where the weighting ${\widehat{\omega }}_i={\Delta }_{i}I\left(T_i<t_0\right)∕\widehat{G}\left(T_i\right)+I(T_i\ge t_0)∕\widehat{G}\left(t_0\right)$, and $\widehat{G}(\cdot )$ is the Kaplan-Meier estimator of G(·). Here, the weighting takes care of the problem due to censoring and I(T_i < t₀) = Y_i when ${\widehat{\omega }}_i\ne 0$. It is shown in Uno et al. (2007) that as n → ∞, the resulting estimator $\widehat{\beta }$ converges to a constant which is free of G(·) even when the model (2.1) is misspecified. Similarly, with additional V and Model (2.2), one can use the estimating function

$$S_2\left(\gamma \right)=\sum _{i=1}^n{\widehat{\omega }}_i{W}_i\{Y_i-g_2\left({\gamma }^{\prime }{W}_i\right)\}$$ (3.2)

to estimate γ.

Now, since ${\eta }_l^{\left(q\right)}\left(s\right)$ is between 0 and 1, we use a non-parametric local logistic likelihood estimation procedure to obtain consistent estimator η^(q)(s). Specifically, first consider a kernel-type nonparametric functional estimator based on the local likelihood “score” function for the standard logistic regression which relates the binary response $I\{\widehat{p}\{U_i,V_i\}\in (v_{l-1},v_l),Y_i=q\}$ to the regressor ${\widehat{\epsilon }}_i\left(s\right)=\psi \left({{\widehat{p}}_U}_i\right)-\psi \left(s\right)$. Here, we choose a proper transformation $\psi \left({\widehat{p}}_U\right)$ of ${\widehat{p}}_U$ to implement the smoothing, where ψ(·) is a known, non-decreasing function (Wand et al., 1991; Park et al., 1997). For any given s, l and q, this results in a score function of the intercept parameter a and slope parameter b:

$$\sum _{i=1}^n\left[h^{-1}\stackrel{1}{\widehat{\epsilon }}\left(s\right)\right]K_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}{\widehat{\omega }}_i\left[I\{{\widehat{p}}_{\{U_i,V_i\}}\in \left(v_{l-1,v_l}\right),Y_i=q\}-g_0\{a+b{\widehat{\epsilon }}_i\left(s\right)\}\right]$$ (3.3)

where g₀(x) = exp(x)/{1 + exp(x)}, K_h(x) = K(x/h)/h, K(·) is a known smooth symmetric kernel density function with a bounded support, and the bandwidth h > 0 is assumed to be $O\left(n^{-v}\right),\mathrm{for}1∕5<v<1∕2$. Let ${\widehat{\eta }}_l^{\left(q\right)}=g_0\left(\widehat{a}\right)$ where $\widehat{a}$ is the resulting estimator of the intercept by solving the equations: (3.3)=0, for q = 0, 1 and l = 1, · · · , L. Then η_l(s) and ξ(s) can be estimated by ${\widehat{\eta }}_l\left(s\right)={\widehat{\eta }}_l^{\left(1\right)}\left(s\right)+{\widehat{\eta }}_l^{\left(0\right)}\left(s\right)\mathrm{and}\widehat{\xi }\left(s\right)={\sum }_{l=1}^L{\widehat{\eta }}_l^{\left(1\right)}$ respectively.

In Appendix A, we show that ${\widehat{\eta }}_l^{\left(s\right)}\left(s\right)-{\eta }_l^{\left(q\right)}\left(s\right)\to 0$ in probability, uniformly in $s\in {\Omega }_h\equiv \left[\psi ({\rho }_l-h)\right]$, where [ρ_l, ρ_r] is a subset of the support of $\psi \left\{g_1\left({\beta }_0^{\prime }X\right)\right\}$ and β₀ is the limit of $\widehat{\beta }$. Furthermore, we show in Appendix B that for large n, the joint distribution of $\{{\left(nh\right)}^{1∕2}\{{\widehat{\eta }}_l^{\left(q\right)}\left(s\right)-{\eta }_l^{\left(q\right)}\left(s\right)\},q=0,1;l=1,\cdots ,L\}$ can be approximated by the distribution of

$$\left\{n^{-\frac{1}{2}}{h}^{\frac{1}{2}}\sum _{i=1}^n{\widehat{V}}_{li}^{\left(q\right)}\left(s\right)(V_i-1)+{\left(nh\right)}^{\frac{1}{2}}\{{\tilde{\eta }}_l^{\left(q\right)}(s,{\widehat{ϴ}}^{\ast })-{\tilde{\eta }}_l^{\left(q\right)}(s,\widehat{ϴ})\},q=0,1;l=1,\cdots ,L\right\}$$ (3.4)

given the data, where V = {V_i, i = 1, · · · , n} is a random sample from a given distribution with unit mean and unit variance and is independent of the data, $\widehat{ϴ}=(\widehat{\beta },\widehat{\gamma },\widehat{G}),{\widehat{ϴ}}^{\ast }=(\widehat{\beta },{\widehat{\gamma }}^{\ast },{\widehat{G}}^{\ast })$ is the perturbed version of $\widehat{ϴ},{\widehat{\mathcal{V}}}_{li}^{\left(q\right)}\left(s\right),{\tilde{\eta }}_l^{\left(q\right)}$ and ${\widehat{ϴ}}^{\ast }$ are given in (A·1), (A·2) and (A·3) of Appendix B, respectively. It is important to note that although asymptotically one only needs the first term of (3.4) since $\widehat{ϴ}$ is of order root-n, the inclusion of the second term improves the approximation to the distribution of ${\widehat{\eta }}_l^{\left(q\right)}\left(s\right)$ in finite sample. The independent realizations of (3.4) can easily be obtained by generating realizations from independent random samples of V. With a large number of realizations from (3.4), confidence interval estimates for $\left\{{\eta }_l^{\left(q\right)}\left(s\right)\right\}\mathrm{and}\left\{{\eta }_l\left(s\right)\right\}$ can be constructed via this large sample approximation. This perturbation-resampling method, which is conceptually similar to a wild bootstrapping (Davison and Hinkley, 1997), has been utilized successfully in solving many complicated problems in survival analysis.

As for any nonparametric functional estimation problem, the choice of the smooth parameter h is crucial for making inferences about η^(q)(s), η_l(s) and D_l(s). Here, we propose to use the standard K-fold cross validation procedure to obtain an “optimal” h. Specifically, we randomly split the data into K disjoint subsets of about equal sizes denoted by {J_k , k = 1, · · ·, K}. For each k, we use all observations which are not in J_k to estimate p(u) and p(u, v) by fitting the working models (2.1) and (2.2) and then with a given h, to estimate ${\eta }_l^{\left(q\right)}\left(s\right)$. Let the resulting estimators be denoted by ${\widehat{p}}_u^{(-k)}$, ${\widehat{p}}_{\{u,v\}}^{(-k)}$ and ${{\widehat{\eta }}_l^{\left(q\right)}}^{(-k)}\left(s\right)$. We then use the observations from J_k to calculate the prediction error

$$\mathrm{PE}\left(q\right)(k,l)=\sum _{j∊J_k}{\widehat{\omega }}_j{\left[I\{{\widehat{p}}_{\{U_j,V_j\}(-k)}^{}\in [v_{l-1},v_l],Y_j=q\}-{{\widehat{\eta }}_l^{\left(q\right)}}^{-k}\left\{{\widehat{p}}_{U_j}^{(-k)}\right\}\right]}^2.$$ (3.7)

Lastly we sum (3.7) over k = 1, · · ·, K, and then choose h by minimizing this sum of K prediction errors. Note that the optimal smooth parameter value may only work for this specific (l, q) of ${\widehat{\eta }}_l^{\left(q\right)}\left(s\right)$. Alternatively, one may obtain a uniform bandwidth, which minimizes the sum of (3.7) over k, q and l. The order of such a bandwidth estimator is expected to be n^−1/5 (Wand and Jones, 1995; Fan and Gijbels, 1996) and thus the final bandwidth for estimation can be obtained by multiplying the estimated bandwidth by n^−d0, for some d₀ ∈ (0, 3/10).

To correct for the potential over-fitting bias in estimating the reclassification rates, one may also use the K-fold cross-validation. For k = 1, …, K, we use all observations not in J_k to fit the regression models with and without the new markers and obtain ${\widehat{p}}_U^{(-k)}$ and ${\widehat{p}}_{\{U,V\}}^{(-k)}$. Then using observations in J_k, ${\widehat{p}}_U^{(-k)}$ and ${\widehat{p}}_{\{U,V\}}^{(-k)}$, we obtain an estimate for ${\eta }_l^{\left(q\right)}\left(s\right)$ based on equation (3.3), denoted by ${{\widehat{\eta }}_l^{\left(q\right)}}^k\left(s\right)$. Then the final cross-validated estimator of ${\eta }_l^{\left(q\right)}\left(s\right)$ is ${{\widehat{\eta }}_l^{\left(q\right)}}^{\mathrm{CV}}\left(s\right)=K^{-1}{\sum }_{k=1}^K{\widehat{\eta }}_l^{\left(q\right)}\left(s\right)$.

The proposed operational procedure can be briefly summarized as:

1. Construct a scoring system based on the conventional biomarkers predicting the binary outcome $Y=I\left(T<t_0\right):\{{\widehat{p}}_{\left\{U_i\right\}},i=1,\cdots ,n\}$.

2. Construct a scoring system based on the conventional as well as novel biomarkers predicting the binary outcome $Y=I\left(T<t_0\right):\{{\widehat{p}}_{\{U_i,V_i\}},i=1,\cdots ,n\}$.

3. Nonparametrically estimate

   $${\eta }_l^{\left(q\right)}\left(s\right)=\mathrm{pr}\{{\widehat{p}}_{U,V}\in \left(v_{l-1,v_l}\right),Y=q\mid {\widehat{p}}_U=s\},\mathrm{for}q=0,1$$

   based on $\{Y_i,{\widehat{p}}_{\{U_i,V_i\}},{\widehat{p}}_{\left\{U_i\right\}},i=1,\cdots ,n\}$.

4. Correct the estimation bias by applying cross-validation for steps 1-3.

5. Make inference on ${\eta }_l^{\left(q\right)}\left(s\right)$, P(s), D_l(s) and D₊(s) with the proposed re-sampling method.

4 Numerical Studies

We apply the proposed procedures to analyze the data from female participants in the Cardiovascular Health Study (CHS) with respect to the risk classification rule recommended by AHS for the 10-year risk of CHD events. There are two different ways to define the binary response variable Y. First, if a study subject died before her ten-year follow-up from a non-CHD cause, we let Y = 0 (no CHD event). If the subject experienced a CHD event (non-fatal MI, angina or CHD-related death), we let Y = 1. There are no loss-to-follow-ups for these endpoints, therefore, we observe all Y ’s in this analysis. For the second analysis, we let the time to death of other causes be an independent censoring variable C for the time to the CHD event. As we discussed in the introduction, we consider three risk categories (0, 10%], (10%, 20%] and (20%, 100%] in the analysis.

For both analyses, we consider an additive model (2.1) with g₁(·) being the anti-logit function. The vector X consists of the usage of hypertensive medication and all variables used in the model for deriving the FRS given in Wilson et al (1998). Specifically, the FRS model includes various dummy variables indicating levels of blood pressure, total cholesterol, and HDL, as well as age, age², present smoking status and diabetic status. Next, we fit the data using an additive model (2.2) with g₂(·) being the anti-logit function and W being the above risk factors/markers X and the log-transformed CRP variable. For estimating functions (3.1) and (3.2), the estimator $\widehat{G}(\cdot )$ is the standard K-M estimator with all death and CHD event times as censored observation for censoring variable C. For the nonparametric function estimation, we let K(·) be the Epanechnikov kernel, and $\psi (\cdot )=g_1^{-1}(\cdot )$. The smoothing parameter h = 0.11 was obtained through the 10-fold cross validation scheme. Specifically, we let h be the minimizer of ${\sum }_{l=1}^3{\sum }_{k=1}^{10}{\sum }_{q=0}^1{\mathrm{PE}}^{\left(q\right)}(k,l)$ in (3.7) for both ${\widehat{\eta }}_l^{\left(0\right)}$ and ${\widehat{\eta }}_l^{\left(1\right)}\left(s\right)$ multiplied by a normalizing constant n^−1/10. To approximate the distributions of these estimators, we used the resampling method (3.4) with 500 independent realized samples of {V_i, i = 1, · · ·, n}. In addition, to correct for the potential overfitting bias, we also obtained cross-validated estimates of η^(l) with h = 0.11. The results shown below are based on the cross-validated estimates although there appears to be a minimal bias for the present case.

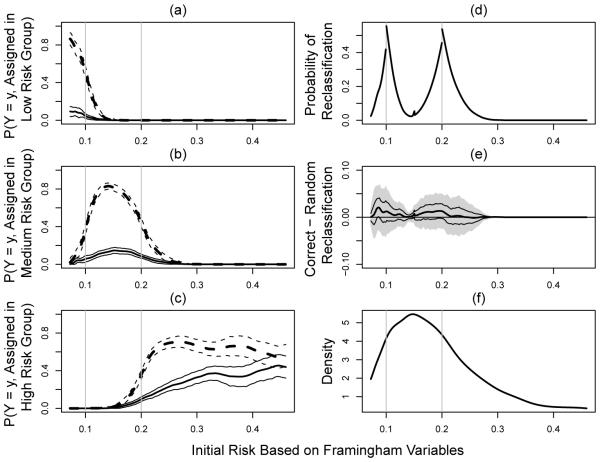
For the case where there is no censoring involved, we present the results of our analysis in Figure 1. Here, we choose the 2nd and 98th percentiles of the empirical distribution of $\{{\widehat{\beta }}^{\prime }{X}_i,i=1,\cdots ,n\}$ as the boundary points ρ_l and ρ_r, respectively. Therefore, the results presented here are for ${\widehat{p}}_U=s\in [0.07,0.46]$. Part (a)-(c) of the Figure are the estimated ${\eta }_l^{\left(y\right)}\left(s\right)$ along with their 95% point-wise confidence intervals, for l = 1, 2, 3 and y = 0, 1. Part (d) of the Figure gives the estimated re-classification rates over ${\widehat{p}}_U$. As expected, there are substantial re-allocations with the CRP around the boundary points for the risk classification rule. Part (e) shows estimates for the overall gain, D₊(s). The results suggest that although substantial reclassifications occurred, most of the reclassifications are not substantially better than random reallocations with estimated D₊ ranging from 0% to 2.1%. Only subjects with conventional risk estimates ${\widehat{P}}_U\in [0.085,0.088]\cup [0.29,0.33]$ have lower bounds of the 95% confidence interval slightly above zero. However, no subgroup of individuals would benefit from the additional CRP information based on simultaneous confidence intervals which controls for the overall type I error. That is, we cannot claim that the reclassification to risk categories by the new marker is better than a random allocation process. Part (f) of the Figure is a smoothed density estimate for ${\widehat{p}}_U$, which provides useful information regarding the relative size of the subgroup D_s of subjects such that ${\widehat{p}}_{U^0}=s$.

Fig. 1.

Evaluating CRP incremental values for female participants from Cardiovascular Heath Study by treating non-CHD death as non-event; (a)-(c): ${\eta }_l^{\left(y\right)}(\cdot )$, l = 1, 2, 3, (solid lines for y = 1 and dashed lines for y = 0; thick lines for point estimators and thinner lines for 95% confidence intervals); (d) proportion of reclassification to other risk categories; (e) net gain in reclassification as measured by D₊(s) (point estimator: thick solid line, 95% point wise confidence intervals: dashed lines, and simultaneous confidence intervals: shaded region); (f) density function of the initial risks.

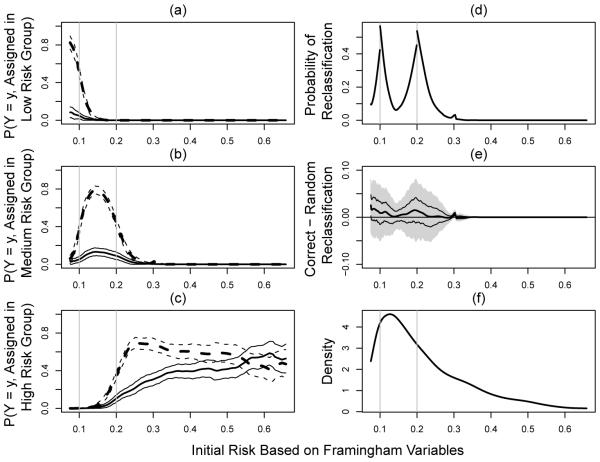
For the second set of analysis by treating non-CHD death as censoring, 18.8% of subjects are censored with respect to the CHD events of interest. For this case, the smoothing parameter is 0.14 via the 10-fold cross validation by minimizing ${\sum }_{l=1}^3{\sum }_{k=1}^{10}{\sum }_{q=0}^1{\mathrm{PE}}^{\left(q\right)}(k,l)$ in (3.7) with normalizing constant n^−1/10. We present the results in Figure 2 for ${\widehat{p}}_U=s\in [0.075,0.66]$ under the same settings as in Figure 1. The regions for which the CRP may be helpful are ${\widehat{p}}_U=s\in [0.075,0.076]\cup [0.29,0.30]\cup [0.35,0.38]$. However, the magnitude of gain is also very minimal with estimated D₊ ranging from 0% to 2.5% and no region appears to have a significant gain after controlling for the overall family-wise type I error.

Fig. 2.

Evaluating CRP incremental values for female participants from Cardiovascular Heath Study by treating non-CHD death as censoring; (a)-(c): ${\eta }_l^{\left(y\right)}(\cdot )$, l = 1, 2, 3, (solid lines for y = 1 and dashed lines for y = 0; thick lines for point estimators and thinner lines for 95% confidence intervals); (d) proportion of reclassification to other risk categories; (e) net gain in reclassification as measured by D₊(s) (point estimator: thick solid line, 95% point wise confidence intervals: dashed lines, and simultaneous confidence intervals: shaded region); (f) density function of the initial risks.

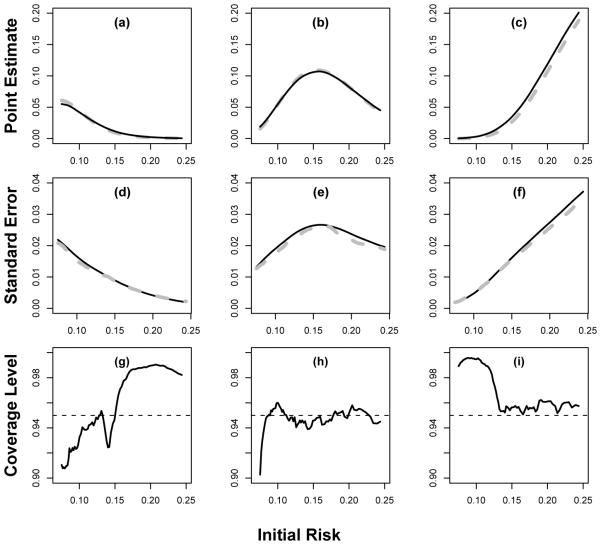
To assess the performance of the proposed procedure under practical settings, we conducted an extensive numerical study to examine the bias of our point estimator and the empirical coverage levels of its corresponding interval estimators for $\left\{{\eta }_l^{\left(q\right)}\right\}\left(s\right)$. Based on the results of the study, we find that the new proposed estimation procedure has negligible bias and the coverage levels are very close to the nominal counterparts. For example, in one of our simulation studies, we simulated data from a study similar to the CHS setting.

Specifically, we generated the event time with a lognormal model with the vector of covariates that is identical to that of the CHS study. First, for each subject, we generated its discrete covariates X_D, which include levels of blood pressure, total cholesterol, HDL, present smoking status and diabetic status, based on the empirical distribution of the CHS data. Then, for each given value of X_D, we generated the corresponding value of continuous covariates X_C = (Age, logCRP), from N (µ^XD, Σ), where µ^XD is the empirical mean of X_C given X_D and Σ is the empirical covariance matrix of X_C in the CHS dataset. Then, we generated the survival time T from log T = α₀ + α′ w + ε, where ε ~ N (0, σ²), w = (X_D, X_C, Age²), and (α₀, α₁, σ)′ was obtained from fitting this log-normal model to the CHS data but the coefficient of CRP was multiplied by a factor of two to represent the setting where CRP is indeed helpful in risk reclassification. The censoring was generated from a Weibull with shape and scale parameters obtained by fitting the two-parameter Weibull model to the CHS data. This results in about 78% of censoring and an overall 10-year event rate of 17%. As in the CHS example, we assess the accuracy of CRP for predicting the 10-year risk and reclassifying subjects into three risk categories with ν₁ = 0.1 and ν₂ = 0.2.

We considered a moderate sample size of 3000 and a relatively large sample size of 6000. For computational ease, the bandwidth for constructing the non-parametric estimate was fixed at h = 0.09 for n = 3000 and 0.07 for n = 6000. Here, these h’s were chosen as the averages of the bandwidths selected based on (3.7) with d₀ = 0.1 from 10 simulated datasets. For both settings, the non-parametric estimator has negligible bias, the estimated standard errors are close to their empirical counterparts, and the empirical coverage levels of the 95% confidence intervals are close to the nominal level. In Figure 3, we summarize the results of our findings performance for the point and interval estimation procedures for ${\widehat{\eta }}_l^{\left(1\right)}\left(s\right)(l=1,2,3)$ when n = 3000. The coverage levels are slightly lower or higher than the nominal level when s is near the boundaries of the support and the true reclassification rates ${\eta }_l^{\left(1\right)}\left(s\right)$ are close to 0. However, the coverage level improves when we increase the sample sizes. Similar performances were observed for ${\widehat{\eta }}_l^{\left(0\right)}\left(s\right)$. For example, when s = 0.2, the coverage levels for $\{{\widehat{\eta }}_1^{\left(0\right)}\left(s\right),l=1,2,3\}$ are (0.96, 0.93, 0.96) when n = 3000 and (0.96, 0.93, 0.95) = 6000. Other choice of the coefficient of CRP reflecting strong/weak association with the biomarker of interest was also used in the simulation and the corresponding results are fairly close to that reported above.

Fig. 3.

Performance of the proposed procedure under a mis-specified model with sample size 3000 where the underlying effect of CRP is twice as big as that estimated from CHS data: (a,b,c) the sample average of ${\widehat{\eta }}_l^{\left(1\right)}\left(s\right)(\mathrm{l}=1,2,3)$ (solid curve) compared to the truth (gray dashed curve); (d,e,f) the average of the estimated standard errors (solid curve) for ${\widehat{\eta }}_l^{\left(1\right)}\left(s\right)$ compared to the empirical standard error estimates (gray dashed curves); and (g,h,i) the empirical coverage of the 95% confidence intervals based on the proposed resampling procedures. The three columns represents l = 1, 2 and 3, respectively.

5 Remarks

In this article, we present a systematic approach to quantify the added value from new risk markers for classifying subjects into pre-specified risk categories. At each estimated conventional risk level, we provide point and interval estimates for the reclassification rates along with the corresponding proportions of accurate re-assignment for this subgroup of individuals. The proposed procedure is nonparametric and does not depend on any parametric assumptions on the underlying model generating the data. On the other hand, as a limitation, when the reclassification rate (when the new biomarker is uninformative) or pr(Y = 1) is low, a large sample size is often required to make reliable inferences. Furthermore, appropriate weighting scheme reflecting the relative importance of cases and controls can be conveniently accommodated. These quantities play vital roles for cost-benefit analysis even when the cost of measuring the new markers is not an issue or the re-categorization via the new markers is not generated from a random allocation process. In general, if the new markers improve the risk prediction and change the risk estimates drastically, one may expect the new marker to be helpful in risk reclassification for the entire population. However, in most practical settings, we expect that subjects whose conventional risk estimates are not around the risk threshold values would not benefit much from the new markers with respect to a better assignment of risk category. This is indeed confirmed with the results from extensive analysis of the data from the Cardiovascular Health Study. Thus, to optimize the usage of the new markers for risk classification, one may consider ascertaining the new markers only for subjects with conventional risk estimates in a certain range. The proposed procedures can be easily be extended to quantify the average gain for a range of subgroups by integrating D₊(s) over the range of interest.

Although the risk score is generally on a continuous scale, clinical practitioners almost always discretize the score for decision making. Furthermore, when there are multiple underlying disease subtypes or subpopulations, such a risk discretization may serve as a proxy for these subgroups. For example, a composite score consisting of several biomarkers, including cyclin E and Ki-67, stratified non-small cell lung cancer (NSCLC) patients into markedly different survival subgroups. Cyclin E expression is involved in the cell growth, highly predictive of early disease recurrence after surgery, and considered a good candidate as a molecular target for treatment. Risk groups determined by these biomarkers may represent underlying disease subtypes associated with different treatment responses. To illustrate how an underlying biological process may be approximated by such risk discretization, we conducted a simulation study where we generated the log survival time from N (4, 1) if D = 1 and N (0, 1) if D = 0; the “latent” binary group membership D is generated based on a probit model P (D = 1)X, Z) = (−2 + 2Z) and (X, Z) were generated from a multivariate normal. Suppose that we only observe (T, X, Z), the risk classification rule P (T ≤ 10)X, Z) ≥ 0.20 is a highly accurate approximation to the unobserved D with concordance rate as high as 90%. Here T is the survival time. Thus, if D represents unknown disease subtypes, appropriate binary risk classification rule is essentially separating disease subtypes and may guide more effective treatment.

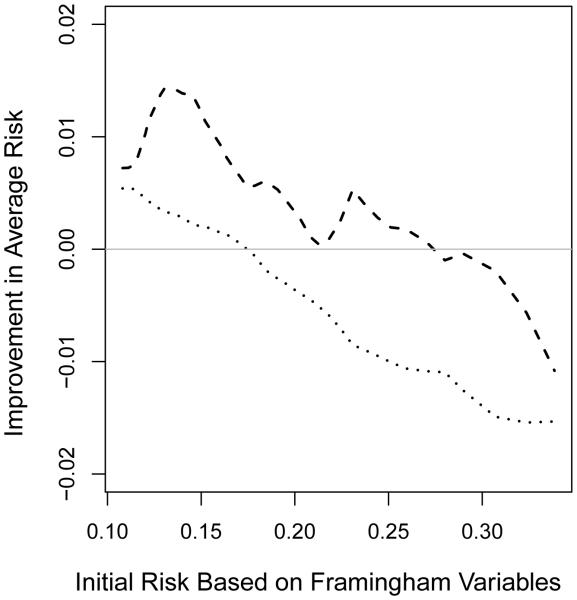
The determination of an appropriate set of risk thresholds is an important yet difficult problem. Appropriate cut-off values could potentially be chosen by evaluating the threshold effect of risk factors or performing cost-risk-benefit analysis. Most likely the new markers have non-trivial incremental values for patients whose conventional risk scores are in the neighborhood of the threshold values. The new proposal provides some guidance about how large this neighborhood would be. When there are no specific risk categories in classification, we may compare certain characteristics of the risk scores for “cases” and “controls” to evaluate the added value of new markers. For example, given an initial risk estimate of ${\widehat{p}}_U=s$, one may consider estimating the mean value of ${\widehat{p}}_{U,V}-{\widehat{p}}_U$ among these with Y = 1 and among those with Y = 0. If the new marker is indeed helpful for the group with ${\widehat{p}}_U=s$, one would expect that $E\{{\widehat{p}}_{U,V}-{\widehat{p}}_U\mid {\widehat{p}}_U=s,Y=1\}$ is positive and $E\{{\widehat{p}}_{U,V}-{\widehat{p}}_U\mid {\widehat{p}}_U=s,Y=0\}$ is negative. For the CHS example, as shown in Figure 4, the gain from CRP over the FRS score seems rather small. Further research is needed to justify this nonparametric estimation procedure.

Fig. 4.

Evaluating CRP incremental values with respect to improvement in mean risk among cases with Y = 1 (dashed curve) and among controls with Y = 0 (dotted curve) for female participants from Cardiovascular Heath Study by treating non-CHD death as non-event.

Appendix

Throughout, unless otherwise noted, we use the notation $\simeq$ to denote equivalence up to o_p(1) uniformly in s, $\lesssim$ to denote bounded above up to a universal constant, and $\mathcal{F}\left(x\right)$ to denote dF (x)/dx for any function F. We use ℙ_n and ℙ to denote expectation with respect to the empirical probability measure of {(T_i, Δ_i, X_i, W_i), i = 1, · · · , n} and the probability measure of (T , Δ, X, W ), respectively. Similarly ${\mathbb{G}}_n=n^{\frac{1}{2}}({\mathbb{P}}_n-\mathbb{P})$. Let β₀ and γ₀ denote the solution to the equations $E\left[X_i\{I\left(T_{0i}<t_0\right)-g_1\left({\beta }^{\prime }{X}_i\right)\}\right]=0$ and $E\left[W_i\{I\left(T_{0i}<t_0\right)-g_2\left({\gamma }^{\prime }{W}_i\right)\}\right]=0$, respectively. Let ${\stackrel{‒}{p}}_U=g_1\left({\beta }_0^{\prime }X\right)$. We assume that τ (·), the density function of $\psi \left({\stackrel{‒}{p}}_U\right)$, is continuously differentiable with bounded derivatives and bounded away from zero on the interval [ψ⁻¹(ρ_l), ψ⁻¹(ρ_u)] ⊂ (0, 1). We also assume that the marker values are bounded, ${({\beta }_0^{\prime },{\gamma }_0^{\prime })}^{\prime }$ belongs to a compact set Ω. For the bandwidth h, we assume that h = O(n^−v ), 1/5 < v < 1/2.

We first note that from Uno et al. (2007), we have

$$\mid \widehat{\beta }-{\beta }_0\mid +\mid \widehat{\gamma }-{\gamma }_0\mid +\underset{t\le t_0}{\sup }\mid \widehat{G}\left(t\right)-G\left(t\right)\mid =O_p\left(n^{-\frac{1}{2}}\right).$$ (A.0)

It follows that $\mid {\eta }_l^{\left(q\right)}\left(s\right)-{\stackrel{‒}{\eta }}_l^{\left(q\right)}\left(s\right)\mid =O_p\left(1\right)$, where ${\eta }_l^{\left(q\right)}\left(s\right)=E({\widehat{M}}_{li}^{\left(q\right)}\mid {\widehat{p}}_U=s),{\widehat{M}}_{li}^{\left(q\right)}=I\{{\widehat{p}}_{\{U_i,V_i\}}\in (v_0,v_1),Y_i=q\},{\stackrel{‒}{\eta }}_l^{\left(q\right)}\left(s\right)=E(M_{li}^{\left(q\right)}\mid {\stackrel{‒}{p}}_U=s),M_{li}^{\left(q\right)}=I\{{\stackrel{‒}{p}}_{\{U_i,V_i\}}\in (v_0,v_1),Y_i=q\}$, and $\stackrel{‒}{p}\{U,V\}=g_2\left({\gamma }_0^{\prime }W\right)$. It is also important to note that $E\left\{\omega s(T_0,X,W)\right\}=E\left\{s(T_0,X,W)\right\}$ for any function s(·, ·, ·), where ${\widehat{\eta }}_1^{\left(1\right)}(\cdot )$. We next derive the asymptotic theory for ${\widehat{\eta }}_1^{\left(1\right)}(\cdot )$, but note that the same arguments can be used to justify the asymptotic properties of other quantities. For the ease of notation, in Appendix A and B, we suppress the subscript l and supscript (q) from ${\widehat{M}}_{li}^{\left(q\right)}$ and $M_{li}^{\left(q\right)}$.

A. Uniform Consistency of ${\widehat{\eta }}_1^{\left(1\right)}(\cdot )$

At any given s, let ${\{\widehat{a}\left(s\right),\widehat{b}\left(s\right)\}}^{\prime }$ be the root of the estimating equation

$$\sum _{i=1}^n\left[h^{-1}\stackrel{1}{{\widehat{∊}}_i}\left(s\right)\right]K_h\left\{{\widehat{∊}}_i\left(s\right)\right\}{\widehat{\omega }}_i[{\widehat{M}}_i-g_0\{a+b{\widehat{∊}}_i\left(s\right)\}]=0,$$

$a\left(s\right)=g_0^{-1}\left\{{\eta }_1^{\left(1\right)}\left(s\right)\right\},b\left(s\right)=d\left[g_0^{-1}\left\{{\eta }_1^{\left(1\right)}\left(s\right)\right\}\right]∕ds={\stackrel{.}{\eta }}_1^{\left(1\right)}\left(s\right)∕{\stackrel{.}{g}}_0\left\{a\left(s\right)\right\}$ and

$$\widehat{\mathrm{d}}\left(s\right)=\left[\begin{array}{c}\hfill {\widehat{d}}_a\left(s\right)\hfill \\ \hfill {\widehat{d}}_b\left(s\right)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \widehat{a}\left(s\right)-a\left(s\right)\hfill \\ \hfill h^{-1}\{\widehat{b}\left(s\right)-b\left(s\right)\}\hfill \end{array}\right]$$

Our objective is to show that $\widehat{\mathrm{d}}\left(s\right)\to 0$ in probability as n → ∞. To this end, we note that for any given s, $\widehat{\mathrm{d}}\left(s\right)$ is the solution to the estimating equation $\widehat{\mathbb{S}}(\mathrm{d},s)=0$, where d = (d_a, d_b)′,

$${\widehat{\mathbb{S}}}_{(\mathrm{d},s)}=\left[\begin{array}{c}\hfill {\widehat{\mathbb{S}}}_1(\mathrm{d};s)\hfill \\ \hfill {\widehat{\mathbb{S}}}_2(\mathrm{d};s)\hfill \end{array}\right]=n^{-1}\sum _{i=1}^n\left[h^{-1}\stackrel{1}{\widehat{\epsilon }}\left(s\right)\right]K_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}{\omega }_i[{\widehat{M}}_i-\mathcal{G}\{\mathrm{d},s;\psi \left(\widehat{p}{U}_i\right),h\}]$$

and $\mathcal{G}(\mathrm{d},s;y,h)=g_0[a\left(s\right)+b\left(s\right)\{y-\psi \left(s\right)\}+d_a+d_b{h}^{-1}\{y-\psi \left(s\right)\}]$.

The first step is to show that $\widehat{\mathbb{S}}(\mathrm{d};s)$ is uniformly consistent for

$$\mathbb{S}(\mathrm{d};s)=\left[\begin{array}{c}\hfill {\mathbb{S}}_1(\mathrm{d};s)\hfill \\ \hfill {\mathbb{S}}_2(\mathrm{d};s)\hfill \end{array}\right]=\tau \left\{\psi \left(s\right)\right\}\left[{\eta }_1^{\left(1\right)\left(s\right)}-\int K\left(t\right)g_0\{a\left(s\right)+d_a+d_{b}t\}dt-\int tK\left(t\right)g_0\{a\left(s\right)+d_a+d_t\}dt\right]$$

We first show that

$$\stackrel{s}{\sup }\mid n^{-1}\sum _{i=1}^n{K}_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}{\widehat{\omega }}_i{\widehat{M}}_i-\tau \left\{\psi \left(s\right)\right\}{\eta }_1^{\left(1\right)}\left(s\right)\mid$$

and $\underset{\mathrm{d},s}{\sup }\mid n^{-1}{\sum }_{i=1}^n{K}_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}{\omega }_i\mathcal{G}\{\mathrm{d},s;\psi \left({\widehat{p}}_{U_i}\right),h\}-\tau \left\{\psi \left(s\right)\right\}\int K\left(t\right)g_0\{a\left(s\right)+d_a+d_{b}t\}dt\mid$ are both $O_p\left\{{\left(nh\right)}^{-\frac{1}{2}}\log \left(n\right)\right\}$. To this end, we note that from (A.0),

$$\mid n^{-1}\sum _{i=1}^n({\widehat{\omega }}_i-{\omega }_i)K_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}\mathcal{G}\{\mathrm{d},s;\psi ({\widehat{p}}_{U_i},h)\}\mid \le n^{-1}\sum _{i=1}^n\mid {\widehat{\omega }}_i-{\omega }_i\mid K_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}=O_p\left(n^{-\frac{1}{2}}\right)$$

This, together with the convergence of $n^{\frac{1}{2}}(\widehat{\beta }-{\beta }_0)$, implies that

$$\mid n^{-1}\sum _{i=1}^n{K}_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}{\widehat{\omega }}_i\mathcal{G}\{\mathrm{d},s;\psi ({\widehat{p}}_{U_i},h)\}-\tau \left\{\psi \left(s\right)\right\}\int K\left(t\right)g_0\{a\left(s\right)+d_a+d_{b}t\}dt\mid$$

$$\lesssim n^{-\frac{1}{2}}{h}^{-1}\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{H}}_{\delta }}+\left[n^{-\frac{1}{2}}\int K_h\{y-\psi \left(s\right)\}d{\mathbb{G}}_n\left[\omega \mathcal{G}\{\mathrm{d},s;\psi \left({\stackrel{‒}{p}}_U\right),h\}I\{\psi \left({\stackrel{‒}{p}}_U\right)\le y\}\right]\right]+O_p\left(n^{-\frac{1}{2}}\right)+h^2$$

where ${\mathcal{H}}_{\delta }=\{\omega I[\psi \left\{g_1\left({\beta }^{\prime }x\right)\right\}\le c]\omega I[\psi \left\{g_1\left({\beta }_0^{\prime }x\right)\right\}\le c]:\mid \mid \beta -{\beta }_0\mid \mid \le \delta ,y\}$ is a class of functions indexed by β and c. Furthermore, _δ is uniformly bounded by an envelop function in the order of ${\delta }^{\frac{1}{2}}$ with respect to L₂ norm. By the maximum inequality of van der Vaart and Wellner (1996), we have $E\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{H}}_{\delta }}\lesssim {\delta }^{\frac{1}{2}}(\mid \log \left(\delta \right)\mid +\mid \log \left(h\right)\mid )(1+{\delta }^{-\frac{1}{2}}{n}^{-\frac{1}{2}}(\mid \log \left(\delta \right)\mid +\mid \log \left(h\right)\mid ))$. This, coupled with $\mid \widehat{\beta }-{\beta }_0\mid =O_p\left(n^{-\frac{1}{2}}\right)$ implies that $n^{-\frac{1}{2}}{h}^{-1}\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{H}}_{\delta }}\lesssim O_p\left\{{\left(nh\right)}^{-\frac{1}{2}}{\left(n{h}^2\right)}^{-\frac{1}{4}}\log \left(n\right)\right\}$.

Secondly, with the standard arguments used in Bickel and Rosenblatt (1973), we have

$$\left[n^{-\frac{1}{2}}\int K_h\{x-\psi \left(s\right)\}d{\mathbb{G}}_n\left[\omega \mathcal{G}\{\mathrm{d},s;\psi \left({\stackrel{‒}{p}}_U\right),h\}I\{\psi \left({\stackrel{‒}{p}}_U\right)\le y\}\right]\right]+O_p\left\{{\left(nh\right)}^{-\frac{1}{2}}\log \left(n\right)\right\}$$

Therefore, for $h=n^{-v},1∕5<v<1∕2$,

$$\underset{\mathrm{d},s}{\sup }\mid n^{-1}\sum _{i=1}^n{K}_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}{\widehat{\omega }}_i\mathcal{G}\{\mathrm{d},s;\psi ({\widehat{p}}_{U_i},h)\}\tau \left\{\psi \left(s\right)\right\}\int K\left(t\right)g_0\{a\left(s\right)+d_a+d_{b}t\}dt\mid$$

is $O_p\left\{{\left(nh\right)}^{-\frac{1}{2}}\log \left(n\right)\right\}$. From (A.0), $\mid \widehat{\gamma }-{\gamma }_0\mid =O_p\left(n^{-\frac{1}{2}}\right)$, and similar arguments as given above,

$$\underset{s}{\sup }\mid n^{-1}\sum _{i=1}^n{K}_h\left\{{\widehat{∊}}_i\left(s\right)\right\}{\widehat{\omega }}_i{\widehat{M}}_i-\tau \left\{\psi \left(s\right)\right\}{\eta }_1^{\left(1\right)}\left(s\right)\mid =O_p\left\{{\left(nh\right)}^{-\frac{1}{2}}\log \left(n\right)\right\},$$

and hence ${\sup }_{\mathrm{d},s}\mid {\widehat{\mathbb{S}}}_1(\mathrm{d},s)-{\mathbb{S}}_1(\mathrm{d},s)\mid =O_p\left\{{\left(nh\right)}^{-\frac{1}{2}}\log \left(n\right)\right\}=o_p\left(1\right)$. From the same arguments as above, ${\sup }_{\mathrm{d},s}\mid {\widehat{\mathbb{S}}}_2(\mathrm{d},s)-{\mathbb{S}}_2(\mathrm{d},s)\mid =O_p\left\{{\left(nh\right)}^{-\frac{1}{2}}\log \left(n\right)\right\}=o_p\left(1\right)$. Therefore ${\sup }_{\mathrm{d},s}\mid \widehat{\mathbb{S}}(\mathrm{d},s)-\mathbb{S}(\mathrm{d},s)\mid =o_p\left(1\right)$. This uniform convergence, coupled with the fact that 0 is the unique solution to the equation S(d, s) = 0 with respect to d and all the eigenvalues of $\mathbb{A}\left(s\right)=-\partial \mathbb{A}(\mathrm{d};s)∕\partial {\mathrm{d}}^{\prime }{\mid }_{d=0}=\tau \left\{\psi \left(s\right)\right\}\mathrm{diag}\{1,\int v^{2}K\left(v\right)dv\}$ are uniformly bounded above zero, suggests that ${\sup }_{\mathrm{d},s}\mid \widehat{d}\left(s\right)\mid =O_p\{{\left(nh\right)}^{-\frac{1}{2}}\log \left(n\right)+h\}=o_p\left(1\right)$, which implies the consistency of ${\widehat{\eta }}_1^{\left(1\right)}\left(s\right)=g_0\left\{\widehat{a}\left(s\right)\right\}$.

B. Asymptotic distribution of ${\widehat{\eta }}_1^{\left(1\right)}(\cdot )$

It follows from a Taylor series expansion that

$${\left(nh\right)}^{\frac{1}{2}}{\widehat{d}}_a\left(s\right)={\left(nh\right)}^{\frac{1}{2}}\{\widehat{a}\left(s\right)-a\left(s\right)\}={\widehat{\mathbb{A}}}_1{\left(s\right)}^{\prime }{\left(nh\right)}^{\frac{1}{2}}\widehat{\mathbb{S}}(0;s)+O_p\left\{{\left(nh\right)}^{\frac{1}{2}}({\mid {\widehat{d}}_a\left(s\right)\mid }^2+{\mid {\widehat{d}}_b\left(s\right)\mid }^2)\right\}.$$

where ${\widehat{\mathbb{A}}}_1\left(s\right)$ is the first row of $\widehat{\mathbb{A}}\left(s\right)=-{\{\partial \widehat{\mathbb{S}}(\mathrm{d};s)∕\partial {\mathrm{d}}^{\prime }\}}^{-1}{\mid }_{\mathrm{d}=0}$. Using arguments similar to those in the previous section, one can show that ${\widehat{\mathbb{A}}}_1\left(s\right)$ converges to ${\mathbb{A}}_1\left(s\right)$, the first row of $\mathbb{A}\left(s\right)$, uniformly in s. Furthermore, with the convergence rate of ${\widehat{\mathbb{S}}}_1\left(\mathrm{d}s\right)$, it is not difficult to show that the remainder term is bounded by $O_p\{{\left(nh\right)}^{-\frac{1}{2}}\log {\left(n\right)}^2+{\left(nh\right)}^{\frac{1}{2}}{h}^2\}$ uniformly in s. It follows that

$${\left(nh\right)}^{\frac{1}{2}}{\widehat{d}}_a\left(s\right)=\frac{{\left(nh\right)}^{\frac{1}{2}}{\widehat{\mathbb{P}}}_{1}0;\left(s\right)}{\tau \left\{\psi \left(s\right)\right\}{\stackrel{.}{g}}_0}\left\{a\left(s\right)\right\}+O_p\{{\left(nh\right)}^{\frac{1}{2}}\log {\left(n\right)}^2+{\left(nh\right)}^{\frac{1}{2}}{h}^2\}.$$

This, together with the convergence rate of $\widehat{\mathbb{S}}(0;s)$, implies $\sup \mid {\widehat{d}}_a\left(s\right)\mid =O_p\left\{{\left(nh\right)}^{\frac{1}{2}}\log \left(n\right)\right\}$. It follows that ${\left(nh\right)}^{\frac{1}{2}}{\widehat{d}}_a\left(s\right)$ is asymptotically equivalent to

$$\frac{{\left(nh\right)}^{\frac{1}{2}}{\mathbb{P}}_n(K_h\left\{\widehat{∊}\left(s\right)\right\}\omega [\widehat{M}-{\mathcal{G}}_0\{s,\psi \left(\widehat{p}U\right)\}]}{\tau \left\{\psi \left(s\right)\right\}{\stackrel{.}{g}}_0\left\{a\left(s\right)\right\}}$$

where G₀(s, y) = g₀[a(s) + b(s){y − ψ(s)}]. We next show that ${\left(nh\right)}^{\frac{1}{2}}{\widehat{d}}_a\left(s\right)$ is asymptotically equivalent to

$${\left(nh\right)}^{\frac{1}{2}}{\tilde{d}}_2\left(s\right)=\frac{{\left(nh\right)}^{\frac{1}{2}}{\mathbb{P}}_n\left(K_h\left\{\epsilon \left(s\right)\right\}w\right)[M-{\mathcal{G}}_0\{s,\psi \left({\widehat{p}}_U\right)\}]}{\tau \left\{\psi \left(s\right)\right\}{\stackrel{.}{g}}_0\left\{a\left(s\right)\right\}}$$

i.e., ${\widehat{p}}_U$ and ${\widehat{p}}_{\{U,V\}}$ can be replaced by their respective ${\stackrel{‒}{p}}_U$ and ${\stackrel{‒}{p}}_{\{U,V\}}$ in ${\widehat{d}}_a\left(s\right)$, where $\epsilon \left(s\right)=\psi \left({\stackrel{‒}{p}}_U\right)-\psi \left(s\right)$. To this end, noticing the fact that $\tau \left\{\psi \left(s\right)\right\}{\stackrel{.}{g}}_0\left\{a\left(s\right)\right\}$ is bounded away from zero uniformly in s, we have

$${\left(nh\right)}^{\frac{1}{2}}\mid {\widehat{d}}_a\left(s\right)-{\tilde{d}}_a\left(s\right)\mid \gtrsim h^{-\frac{1}{2}}\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{F}}_{\delta }}+h^{-\frac{1}{2}}\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{H}}_{\delta }}+O_p\{{\left(nh\right)}^{\frac{1}{2}}\mid \widehat{\beta }-{\beta }_0\mid +\mid \widehat{\gamma }-{\gamma }_0\mid +h^2\}$$

where ${\mathcal{F}}_{\delta }=\{\omega yI\{g_2\left({\gamma }^{\prime }w\right)\in (v_0,v_1)\}I[\psi \left\{g_1\left({\beta }^{\prime }x\right)\right\}\le c]-\omega yI\{g_2\left({\gamma }_0^{\prime }w\right)\in (v_0,v_1)\}I(\psi \left\{g_1\left({\beta }_0^{\prime }x\right)\right\}\le c):\mid \gamma -{\gamma }_0\mid +\mid \beta -{\beta }_0\mid \le \delta ,c\}$ is the class of functions indexed by (γ, β, c). By the maximum inequality and $\mid \widehat{\beta }-{\beta }_0\mid +\mid \widehat{\gamma }-{\gamma }_0\mid =O_p\left(n^{-\frac{1}{2}}\right)$, we have $h^{-\frac{1}{2}}\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{F}}_{\delta }}=O_p\left\{h^{-\frac{1}{2}}{n}^{-\frac{1}{4}}\log \left(n\right)\right\}$. It follows that ${\left(nh\right)}^{\frac{1}{2}}{\widehat{d}}_a\left(s\right)-{\left(nh\right)}^{\frac{1}{2}}{\tilde{d}}_a\left(sq\right)$ is asymptotic o_p(1) uniformly in s. This, together with the standard arguments for local linear regression fitting, implies that ${\left(nh\right)}^{\frac{1}{2}}\left\{\widehat{a}\left(s\right)\right\}-a\left(s\right)$ converges to a normal with mean 0 and variance ${\sigma }^2={\stackrel{.}{g}}_0{\left\{a\left(s\right)\right\}}^{-2}$, where $m_2=\int K{\left(s\right)}^{2}ds$ and ${\sigma }^2\left(s\right)=m_2\tau {\left\{\psi \left(s\right)\right\}}^{-2}E[{\{M-{\eta }_1^{\left(1\right)}\left(s\right)\}}^2∕G\left(T_0\Omega t_0\right)\mid {\stackrel{‒}{p}}_U=s\mid ]$. Then, from a delta method, ${\left(nh\right)}^{\frac{1}{2}}\{{\widehat{\eta }}_1^{\left(s\right)}\left(s\right)-{\eta }_1^{\left(1\right)}\left(s\right)\}$ is asymptotically normal with mean 0 and variance σ²(s).

To justify the resampling method, we note that from (A.0),

$$n^{-\frac{1}{2}}{h}^{\frac{1}{2}}\sum _{i=1}^n{\widehat{\mathcal{V}}}_{li}^{\left(q\right)}\left(s\right)(V_i-1)+{\left(nh\right)}^{\frac{1}{2}}\{{\tilde{\eta }}_l^{\left(q\right)}(s,{\widehat{ϴ}}^{\ast })-{\tilde{\eta }}_1^{\left(q\right)}(s,\widehat{ϴ})\}=n^{-\frac{1}{2}}{h}^{\frac{1}{2}}\sum _{i=1}^n{\widehat{\mathcal{V}}}_{li}^{\left(q\right)}\left(s\right)(V_i-1)+o_{p^{\ast }}\left(1\right)$$

where $o_{p_{\ast }}\left(1\right)$ (1) is with respect to the product probability measure generated by the observed data and V,

$${\widehat{\mathcal{V}}}_{li}^{\left(q\right)}\left(s\right)=\widehat{\tau }{\left\{\psi \left(\widehat{p}{U}_i\right)\right\}}^{-1}{K}_h\left\{{\widehat{∊}}_i\left(s\right)\right\}{\widehat{\omega }}_i\{{\widehat{M}}_{li}^{\left(q\right)}-{\widehat{\eta }}_l^{\left(q\right)}\left(s\right)\},$$ (A.1)

$${\tilde{\eta }}_l^{\left(q\right)}(s,ϴ)=\frac{\sum _{i=1}^n\frac{O_i}{G\left(T_i\Lambda t_0\right)}{K}_{\tilde{h}}\{\psi \left(g_1\left({\beta }^{\prime }{X}_i\right)\right)-\psi \left(s\right)\}I\{g_2\left({\gamma }^{\prime }{W}_i\right)\in (v_{l-1},v_l),Y_i=q\}}{\sum _{i=1}^n\frac{O_i}{G\left(T_i\Lambda t_0\right)K_{\tilde{h}}\{\psi \left(g_1\left({\beta }^{\prime }{X}_i\right)\right)-\psi \left(s\right)\}}}$$ (A.2)

$\widehat{\tau }\left(s\right)={\sum }_{i=1}^n{K}_h\left\{{\widehat{\epsilon }}_i\left(s\right)\right\}∕n$ is the estimated density function of $\psi \left({\widehat{p}}_U\right),O_i={\Delta }_{i}I\left(T_i<t_0\right)+I(T_i\ge t_0)$ ${\widehat{\beta }}^{\ast }$ and ${\widehat{\gamma }}^{\ast }$ are the respective solutions to

$$\sum _{i=1}^n\frac{O_i}{{\widehat{G}}^{\ast }\left(T_i\Lambda t_0\right)}{X}_i\{Y_i-g_1\left({\beta }^{\prime }{X}_i\right)\}{V}_i=0,\sum _{i=1}^n=\frac{O_i}{{\widehat{G}}^{\ast }\left(T_i\Lambda t_0\right)}{W}_i\{Y_i-g_2\left({\gamma }^{\prime }{W}_i\right)\}{V}_i=0$$ (A.3)

${\widehat{G}}^{\ast }(\cdot )$ is the weighted Kaplan-Meier estimates with weights V and $\tilde{h}=h\times n^{d_0+1∕5-1∕7}$. Thus, conditional on the data the random variable given in (3.4) is asymptotically equivalent to $\widehat{\tau }{\left\{\psi \left(s\right)\right\}}^{-1}{\left(nh\right)}^{\frac{1}{2}}{\mathbb{P}}_n\left[K_h\left\{\widehat{\epsilon }\left(s\right)\right\}\widehat{\omega }\{\widehat{M}-{\widehat{\eta }}_1^{\left(1\right)}\left(s\right)\}(v-1)\right]$, which is asymptotical normally with mean zero and variance ${\widehat{\sigma }}^2\left(s\right)=h\widehat{\tau }{\left\{\psi \left(s\right)\right\}}^{-2}{\mathbb{P}}_n\left[K_h{\left\{\widehat{\epsilon }{\left(s\right)}^2\widehat{\omega }\right\}}^2{\widehat{\omega }}^2{\{\widehat{M}-{\widehat{\eta }}_1^{\left(1\right)}\left(s\right)\}}^2\right]$. From the same arguments given in Appendix A, ${\widehat{\sigma }}^2\left(s\right)\to {\sigma }^2\left(s\right)$ in probability, as n → ∞. Note that the second term, which accounts for the variability in $\widehat{ϴ}$, involves estimating the partial derivative of $P\{g_2\left({\gamma }^{\prime }{W}_i\right)\in [v_{l-1},v_l],Y_i=q\mid g_1\left({\beta }^{\prime }X\right)=s\}$ with respect to β and γ. Since the optimal bandwidth for such derivative functions is of order n^−1/7 which could be substantially larger than h used for the estimation of ${\widehat{\eta }}_l^{\left(q\right)}$, we find that the second term in (3.4) approximates the additional variability in $\widehat{ϴ}$ better when a larger bandwidth is used to obtain ${\tilde{\eta }}_l^{\left(q\right)}$. As a result, the standard bootstrap method, which essentially uses the same h for b ^-l performs poorly in finite sample.