Generative Method to Discover Genetically Driven Image Biomarkers

Abstract

We present a generative probabilistic approach to discovery of disease subtypes determined by the genetic variants. In many diseases, multiple types of pathology may present simultaneously in a patient, making quantification of the disease challenging. Our method seeks common co-occurring image and genetic patterns in a population as a way to model these two different data types jointly. We assume that each patient is a mixture of multiple disease subtypes and use the joint generative model of image and genetic markers to identify disease subtypes guided by known genetic influences. Our model is based on a variant of the so-called topic models that uncover the latent structure in a collection of data. We derive an efficient variational inference algorithm to extract patterns of co-occurrence and to quantify the presence of heterogeneous disease processes in each patient. We evaluate the method on simulated data and illustrate its use in the context of Chronic Obstructive Pulmonary Disease (COPD) to characterize the relationship between image and genetic signatures of COPD subtypes in a large patient cohort.

1 Introduction

We propose and demonstrate a joint model of image and genetic variation associated with a disease. Our goal is to identify disease-specific image biomarkers that are also correlated with side information, such as the genetic code or other biologically relevant indicators. Our approach targets diseases that can be thought of as a superposition of different processes, or subtypes, that are subject to genetic influences and are often present simultaneously in the same patient. Our motivation comes from a study of the Chronic Obstructive Pulmonary Disease (COPD), but the resulting model is applicable to a wide range of heterogeneous disorders.

COPD is a lung disease characterized by chronic and progressive difficulty in breathing; it is one of the leading causes of death in the United States [11]. COPD is often associated with emphysema, i.e., the destruction of lung air sacs, and an airway disease, which is caused by inflammation of the airways. In this paper, we focus on modeling emphysema based on lung CT images. Emphysema exhibits many subtypes. It is common for several subtypes to co-occur in the same lung [13]. Genetic factors play an important role in COPD [11], and it is believed that variability of COPD is driven by genetics [5]. We therefore aim to quantify the lung tissue heterogeneity that is associated with the genetic variations in the patient cohort.

CT imaging is used to measure the extent of COPD, and particularly of emphysema. The standard approach to quantifying emphysema is to use the volume of sub-threshold intensities in the lung as a surrogate measure for the volume of emphysema [6]. More recently, histograms [10], texture descriptors [15], and combination of both [16] have been proposed to classify subtypes of emphysema based on training sets of CT patches labeled by clinical experts. While histograms and intensity features have been shown to be important for emphysema characterization, the clinical definitions of disease subtypes are based on visual assessment of CT images by clinicians and are not necessarily genetically driven. In prior studies, association between image and genetic variants was established as a separate stage of analysis and was not taken into account when extracting relevant biomarkers from images.

Most methodological innovations in joint analysis of imaging and genetics have used image data as an intermediate phenotype to enhance the discovery of relevant genetic markers in the context of neuro-degenerative diseases [3]. In the context of COPD, Castaldi et al. [5] used local histograms to measure distinct emphysema patters and performed genome-wide association study (GWAS) to validate their results. In contrast to prior research in imaging genetics, we use the results of genetic analysis to help us characterize image patterns associated with the disease, in effect reversing the direction of analysis for disorders with high anatomical heterogeneity and available information on genetic influences. We model image and genetic variations jointly, and demonstrate efficient inference of co-occurrence pattern, as indicated by our results.

In this paper, we assume that a few important genetic markers associated with the disease are available. We build a generative model that captures the commonly occurring image and genetic patterns in a population. Each subject is modeled as a sample from the population-wide collection of joint image and genetic patterns. This abstraction at the population level reveals the associations between image-based and genetic subtypes and uses genetic information to guide the definition of image biomarkers for distinct disease subtypes. Our method is based on a non-parametric topic modeling [17], originally developed in machine learning for characterizing structure of documents. We build an analogy between topics contributing words to a document and disease subtypes contributing local image patterns and minor alleles to a patient. The closest work to our approach is by Batmanghelich et al. [2] who developed a topic model for global histograms of the lung intensity values. The model did not include local image patterns; genotype data was not considered as part of the model. In contrast, our topic model builds on rich local descriptors and integrates image and genetic information into a single framework. Our approach can be readily extended to include other clinical or demographic data.

We evaluate the method on a synthetic data set that matches our clinical assumptions, demonstrating substantial benefits of using a hierarchical population model to capture common patterns of heterogeneity in the image phenotype and in the genetic code. We also show that the genetic data as side information boosts the performance of the method compared to the baselines and a variant of our model without the genetic data. Finally, we illustrate an application of our method to a study of COPD and identify common emphysema subtypes associated with genetic factors implicated in COPD.

2 Model

In this section, we describe the generative model for image and genetic data based on a population-wide common patterns that are instantiated in each subject. Our notation is summarized in Table 1 and the generative process is illustrated in Fig. 1.

Table 1.

Model variables and Variational Bayes (VB) estimates used throughout the paper.

Model Variables
Isn	image descriptor of supervoxel n in subject s
Gsm	genetic location of minor allele m in subject s
$z_{\mathit{sn}}^I$	subject-specific topic that generates super-voxel n in subject s, $1\le z_{s,n}^I\le T$
$z_{\mathit{sm}}^G$	subject-specific topic that generates minor allele m in subject s, $1\le z_{s,m}^G\le T$
cst	population-level topic that serves as subject-specific topic t in subject s, 1 ≤ cst ≤ K
υ	parameter vector that determines the stick-breaking proportions of topics in a population template
πs	parameter vector that determines the stick-breaking proportions of topics in subject s
(μk, Σk)	mean and covariance matrix of image descriptors for population-level topic k
βk	frequency of different locations in genetic signatures for population-level topic k
ω	hyper-parameters of the Beta prior for υ
α	hyper-parameters for the Beta prior for πs
ηI	hyper-parameters of the Normal-Inverse-Wishart prior for (μk, Σk)
ηG	hyper-parameters of the Dirichlet prior for βk
VB Estimates
(μ̂k, Σ̂k)	mean and covariance of image descriptors for population-level topic k
β̂k	frequency of different locations in genetic signatures for population-level topic k

Fig. 1.

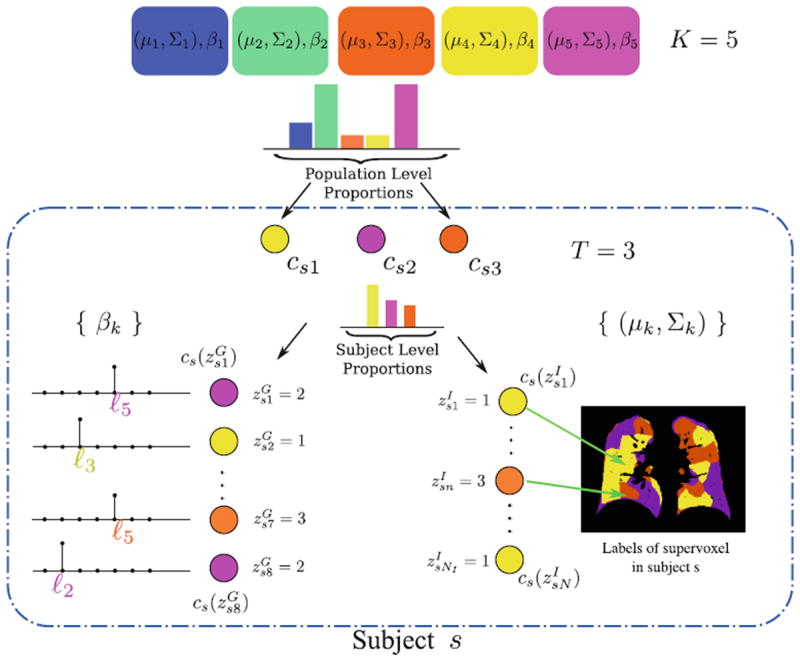
Subject s draws a subset of T topics from K population-level topics. Indices of the subject-level topics are stored in c_s1,.., c_sT drawn from a categorical distribution. At the subject level, indices of the supervoxels { $z_{\mathit{sn}}^I$} and locations of minor alleles { $z_{s,m}^G$} are drawn from the subject-specific categorical distribution. Vector c_s acts as a map from subject-specific topics to the population-level topics (i.e., $c_s(z_{\mathit{sm}}^G)$ or $c_s(z_{\mathit{sn}}^I)$).

Image and Genetic Data

We assume each subject in a study is characterized by an image and a genetic signature for the loci in the genome previously implicated in the disease. Based on the analogy to the “bag-of-words” representation [14], we assume that an image domain is divided for each subject into relatively homogeneous spatially contiguous regions (i.e., “supervoxels”). We let I_sn ∈ ℝ^D denote the D-dimensional descriptor of supervoxel n in subject s that summarizes the intensity and texture properties of the supervoxel. The genetic data in our problem comes in a form of minor allele counts (0, 1 or 2) for a set of L loci. Our representation for genetic data is inspired by the commonly used additive model in GWAS analysis [4]. In particular, we assume that the risk of the disease increases monotonically by the minor allele count. We let G_sm ∈ {1, ⋯, L} denote minor allele m in genetic signature of subject s. For example, suppose L = 2, and subject s has one and two minor alleles in locations ℓ₁ and ℓ₂ respectively. This subject is represented by a list of 3 elements G_s = {ℓ₁, ℓ₂, ℓ₂}.

Population Model

Our population model is based on the Hierarchical Dirichlet Process (HDP) [17]. The model assumes a collection of K “topics” that are shared across subjects in the population. We let $p_k^I$ and $p_k^G$ denote the distributions for the image and genetic signatures, respectively, associated with topic k. Each $p_k^I=N({\mu }_k,{\sum }_k)$ is a Gaussian distribution that generates super-voxel descriptors I_sn; it is parameterized by its mean vector μ_k ∈ ℝ^D and covariance matrix Σ_k ∈ ℝ^D × ℝ^D. Each $p_k^G=\mathrm{Cat}({\beta }_k)$ is a categorical distribution that generates minor allele locations G_sm; it is parameterized by its weight vector β_k ∈ (0, 1)^L.

When sampling a new subject s, at most T < K topics are drawn from the population-wide pool to determine the image and genetic signature of this subject. We let c_st denote the population topic selected to serve as subject-specific topic t (1 ≤ t ≤ T) in subject s. We also use c_s = [c_s1,…, c_sT] to refer to the entire vector of topics selected for subject s. c_s[t] = k indicates that population-level topic k was selected to serve as subject-specific topic t. The subject-specific topics inherit their signature distributions from the population prototypes, but each subject is characterized by a different subset and proportions of the population-level topics represented in the subject-specific data.

As T, K → ∞, this model converges to a non-parametric Hierarchical Dirichlet Process (HDP) [17]. Rather than choose specific values for T and K, HDP enables us to estimate them from the data. As part of this model, we employ the “stick-breaking” construction [17] to parameterize the categorical distribution for c_st:

$$c_{\mathit{st}}~\mathrm{Cat}­\mathrm{SB}(\upsilon ),$$ (1)

where Cat-SB(υ) is a categorical distribution whose weights are generated through the stick-breaking process from the (potentially infinite) parameter vector υ whose components are in the interval (0, 1). Formally, if we define a random variable x ~ Cat-SB(υ), then

$$p(x)\triangleq {\upsilon }_x\prod _{i=1}^{x-1}(1-{\upsilon }_i)\mathrm{for}x=1,\dots .$$ (2)

This parameterization accepts infinite alphabets. The stick-breaking construction penalizes high number of topics hence encouraging parsimonious representation of data. A similar construction enables an automatic selection of the number of topics at the population level and at the subject level. We employ a truncated HDP variant that uses finite values for T and K [9]. In this setup, υ ∈ (0, 1)^K−1. In contrast to finite (fixed) models, we set K to high enough value, and the estimation procedure uses as many topics as needed but not necessarily all K topics to explain the observations.

Subject-Specific Data

To generate an image descriptor for supervoxel n in subject s, we sample random variable $z_{\mathit{sn}}^I~\mathrm{Cat}­\mathrm{SB}({\pi }_s)$ from a categorical distribution parameterized by the vector of stick-breaking proportions π_s ∈ (0,1)^T−1. $z_{\mathit{sn}}^I=t$ indicates that the subject-specific topic t generates image descriptor I_sn:

$$I_{\mathit{sn}}\mid z_{\mathit{sn}}^I,c_s~N({\mu }_{c_s[z_{\mathit{sn}}^I]},{\sum }_{c_s[z_{\mathit{sn}}^I]}).$$ (3)

Similarly, to generate minor allele location m in subject s, we sample random variable $z_{\mathit{sm}}^G~\mathrm{Cat}­\mathrm{SB}({\pi }_s)$ and draw G_sm from the corresponding genetic signature of subject-specific topic $z_{\mathit{sm}}^G$:

$$G_{\mathit{sm}}\mid z_{\mathit{sm}}^G,c_s~\mathrm{Cat}({\beta }_{c_s[z_{\mathit{sm}}^G]}).$$ (4)

Priors

Following the Bayesian approach, we define priors for the remaining latent variables {υ_k, π_st} and the parameters of the likelihood distributions {μ_k, Σ_k, β_k}. For the computational reasons, we choose the priors from the exponential family. Specifically, we use the Beta distribution as the prior of the parameter vectors υ and π_s that determine the stick-breaking proportions at the population-wide and subject-specific levels, respectively:

$${\upsilon }_k~\mathrm{Beta}(1,\omega ),k=1,\dots ,K-1,$$ (5)

$${\pi }_{\mathit{st}}~\mathrm{Beta}(1,\alpha ),t=1,\dots ,T-1,$$ (6)

where ω > 0 and α > 0 are the corresponding shape parameters of the Beta distribution. For computational reasons, we also assume priors for image and genetic signature parameters that are conjugate for the corresponding likelihood distributions (3) and (4):

$${\mu }_k,{\sum }_k~\mathrm{NIW}({\eta }^I)\mathrm{and}{\beta }_k~\mathrm{Dir}({\eta }^G),$$

where NIW(η) is the Normal-Inverse-Wishart distribution with parameters η and Dir(η) is the Dirichlet distributions with parameters η.

3 Inference

Given a study of S subjects with their respective image descriptors {I_sn} and genetic signatures {G_sm}, we seek posterior distributions of the model parameters. Since exact computation of the posterior quantities is computationally intractable, we resort to an approximation. Due to the size of data and its dimensionality, sampling is computationally impractical. We therefore derive a Variational Bayes (VB) approximation [9]. For notational convenience, we define $D={\{I_{\mathit{sn}},G_{\mathit{sm}}\}}_{s=1}^S$ to be all image and genetic data, $S={\{z_{\mathit{sn}}^I,z_{s,m}^G,c_s,{\pi }_s\}}_{s=1}^S$ to be all subject-specific latent variables, and $P={\{{\mu }_k,{\sum }_{k,}{\beta }_k,{\upsilon }_k\}}_{k=1}^K$ to be all population-based latent variables. We omit fixed hyper-parameters to simplify the notation. Variational Bayes inference selects an approximating distribution q(S, P) for the true posterior distribution p(S, P∣D) by minimizing the cost functional

$$F(q)={\mathrm{E}}_q[\ln p(D,S,P)]-{\mathrm{E}}_q[\ln q(S,P)],$$ (7)

where E_q is the expectation with respect to the probability measure q and Eq. (7) can be thought of as the KL divergence between the approximating distribution and the true posterior distribution. Additional details and the update rules of the iterative inference algorithm can be found in the Appendix.

We use the parameters of the approximating distribution q(S, P) to construct estimates of the relevant model parameters. Specifically, we seek the estimates (μ̂_k, Σ̂_k) of the image descriptors and the estimates β̂_k of the associated genetic signatures for each population-level topic k. Moreover, for each subject s we estimate a distribution over the population topics for each supervoxel to visualize the spatial distributions of disease subtypes for clinical assessment.

4 Experiments

In this section, we demonstrate and evaluate the algorithm on simulated and real data. We use simulated data to study the advantages offered by the hierarchical model and investigate the effects of the side information (genetic data in our case) on the accuracy of recovering the latent topics. We also investigate the behavior of the model with respect to the hyper-parameters. We illustrate the method on a subset of a large-scale study of lung based on CT images of COPD patients. In this experiment, we characterize co-occurring image and genetic patterns in the data.

4.1 Simulation

To evaluate the performance of the method, we sampled the data from the proposed hierarchical model. In particular, we generated image and genetic signatures for S = 100 subjects from 20 population-level topics while limiting the number of subject-specific topics to 5. We used Beta(1, 8) and Beta(1, 1) for population-level and subject-specific stick-breaking proportions that govern the relative frequencies of the topics. Such choice generates higher variability of weights at the population level than those at the subject level. We drew the image signature parameters for population topics from a 2-dimensional NIW distribution with a zero mean vector, identity covariance matrix, and the shape and scale parameters set to 5 and 0.5. The subject-specific image signatures (N = 75 for all s) are drawn from Gaussian distributions whose parameters are determined by the corresponding image parameters of the population topic. The weights of the genetic signatures for each population-level topic are drawn from a Dirichlet distribution with all parameters set to one. The subject-specific genetic signatures (M = 65 for all s) are drawn from a categorical distributions determined by the weights of the corresponding genetic signature of the topic model.

Hyper-parameters ω and α control the model size, i.e., the number of topics at the population level and the subject level respectively. Of the two, the population-level parameter ω has a stronger influence on how well the model explains subject-specific data. We sweep a range (0.5, 5.0) for both parameters. Figure 2(Left) reports the value of the lower bound F (q*) for each pair of the parameter settings which we use for model selection. We observe that the algorithm’s performance depends smoothly on the parameter values. In subsequent experiments, we set α to the optimal values based on F (q*) and study the behavior of the model for a range of values of ω. Figure 2(Middle) reports the number of population topics estimated by the model as a function of ω. Not surprisingly, the model size grows with ω, but is quite stable for a wide range of values of ω.

Fig. 2.

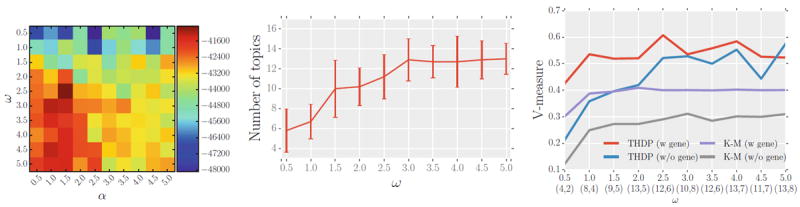
Simulated data results. Left: variational lower bound F (q*) for different values of (α, ω). Middle: the number of topics discovered by the model as a function of ω averaged over α. Right: normalized mutual information between the true and the discovered topics for our method and for k-means clustering (K–M) applied to pooled data. The number of discovered topics is reported in brackets under the corresponding value of ω (w gene, w/o gene). Two variants of our method are denoted by THDP.

To evaluate the effects of the hierarchical model and of joint modeling of image and genetic information, we compare our approach (with and without genetic data) to a k-means algorithm applied to the pooled data from all subjects. We apply the baseline k-means clustering to image data only, and also to the data set of image signatures of all supervoxels concatenated with the entire genetic signature of the same subject. Figure 2(Right) compares our method with the two k-means variants using a standard measure of normalized mutual information (v-measure) [12] between the true and discovered topics. The measure varies between 0 and 1; 1 corresponds to the perfect match. While adding genetic information to image features boosts the performance of our method and clustering on pooled data, our hierarchical model outperforms both baseline methods substantially for a wide range of values of ω. The difference between two variants of our method illustrates the value of the side information to improve the performance. Figure 3 illustrates this point on an example from our simulations for one setting of the parameters.

Fig. 3.

Example simulated image data using 2D features. (a) Features from all subjects pooled into one set. Colors correspond to true topics, unavailable to the algorithm. (b) Image features for a single subject in a set. (c) Topics recovered by our algorithm (with genetic data) for the same subject based on the whole data set. (d) Topics recovered by k-means clustering applied to the pooled data in (a) (Colour figure online).

4.2 COPD Study

We apply the method to CT images of lung in 2399 subjects from a the COPDGene study [11]. After automatic segmentation of the lung, we employ a modified version of super-voxelization method [1] to subdivide the lungs into coherent, spatially contiguous regions. From each supervoxel, we extract local histogram of the intensity (CT number) as a local descriptor. We choose to work with this particular descriptor because it has been shown to be highly informative for emphysema sub-typing [5]. Furthermore, working with such a straightforward image descriptor removes the confounding parameters introduced by more complex image descriptors and helps us to quantify the contribution of the model. For each supervoxel, we use PCA to map the local intensity histogram to a 30-dimensional vector, i.e., I_sn ∈ ℝ³⁰. The 30 principal components explain more than 99 % of variance in the entire data. Moreover, we complied a list of SNPs previously identified in genome-wide association studies for COPD or lung function measurements that define COPD (FEV1 and FEV1/FVC) [7]. Based on our experience with the simulated data and the expected number of disease subtypes, we set K = 30 and T = 10. Furthermore, we set α = 1, ω = 5 and set uninformative priors for the image and genetic signature parameters.

The method summarizes the population into 23 population-level topics. The number of topics per patient varies from one to four. Figure 4 visualizes the top four topics where each topic is an intensity distribution. The tables on the right are the top six minor alleles in the genetic signature of each topic. We observe that the genetic signatures (relative weights or rankings) vary across topics, suggesting variable genetic patterns that give rise to different image properties. To visualize the spatial distribution of the topics, we computed the membership value of the supervoxel in the population-level topics (i.e., ${\sum }_t{\varphi }_{\mathit{sn}}^I(t){\xi }_{\mathit{st}}$), which yields one image per topic for each subject. Then, we warped the resulting probability maps to a common coordinate frame (i.e., lung atlas). Figure 5 demonstrates average distributions of the three topics that tend to localize around the boundary of the lung.

Fig. 4.

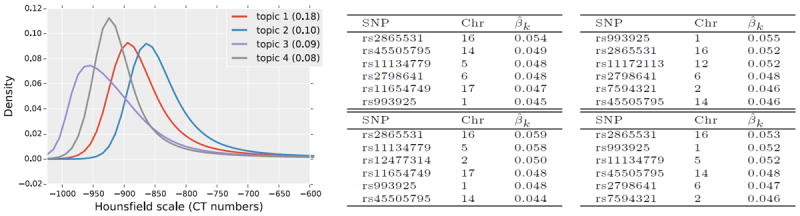
Four first topics, ranked according to their proportions. Each histogram density is one topic. The values inside of the brackets are the overall proportion computed from the posterior. The tables on the right report the top six SNPs for each topic with their estimated relative weights. We observe that the genetic signatures vary across topics.

Fig. 5.

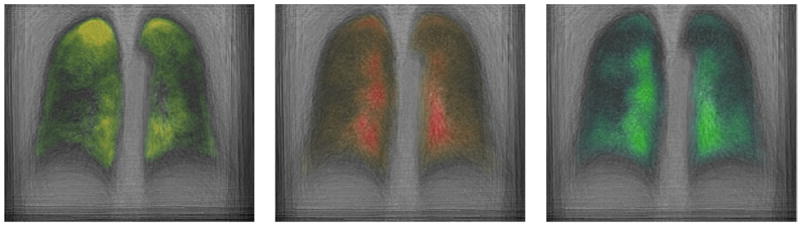
Spatial average distribution of three topics. The color indicates the posterior probability. The higher the intensity of the color, the higher the probability (Colour figure online).

5 Conclusions

We proposed and demonstrated a generative model based on the truncated Hierarchical Dirichlet Process to identify common image and genetic patterns in a population. The underlying assumption of our model is that every subject is a superposition of few topics. Our main contribution is to model side information-in this case, genetic variants - jointly with imaging data. We demonstrated the method on synthesized data and reported preliminary results for the COPD study (Fig. 5).

Once population-wide template of image and genetic variability has been constructed, it enables us to answer many interesting questions about the heterogeneity of the disease in the population and in individual subjects. In particular, investigating the variability of topic representation in different subjects and using subject-specific topic proportions promise to provide a handle on how the disease varies in a population and suggest numerous interesting directions for future work.

Appendix: Variational Bayes Inference Procedure

Combining all components of the model defined in Sect. 2, we construct the joint distribution of all variables in the model (Fig. 6):

$$\begin{array}{l}p(D,S,P)=\underset{\mathrm{population}­\mathrm{level\; topics}}{\underbrace{\prod _{k=1}^{K}p({\mu }_k,{\sum }_k;{\eta }^I)p({\beta }_k;{\eta }^G)p({\upsilon }_k;\omega )}}\times \\ \prod _{s=1}^S\prod _{t=1}^T\underset{\mathrm{topics\; for\; subject}s}{\underbrace{p(c_{\mathit{st}}\mid {\upsilon }_k)p({\pi }_{\mathit{st}};\alpha )}}\prod _{n=1}^N\underset{\mathrm{image\; topic}}{\underbrace{p(z_{\mathit{sn}}^I\mid {\pi }_{\mathit{st}})}}\underset{\mathrm{image\; likelihood}}{\underbrace{p(I_{\mathit{sn}}\mid z_{\mathit{sn}}^I,c_{\mathit{st}},\{{\mu }_k,{\sum }_k\})}}\\ \prod _{m=1}^M\underset{\mathrm{genetic\; topic}}{\underbrace{p(z_{\mathit{sm}}^G\mid {\pi }_{\mathit{st}})}}\underset{\mathrm{genetic\; likelihood}}{\underbrace{p(G_{\mathit{sm}}\mid z_{\mathit{sm}}^G,c_{\mathit{st}},{\beta }_k)}},\end{array}$$

where N and M are the number of supervoxels and minor alleles, respectively, identified for subject s.

Fig. 6.

Left: Graphical model that represents the joint distribution. The open gray and white circles correspond to the observed and the latent random variables, respectively. The full circles represent fixed hyper-parameters. Superscript I and G denote image and genetic parts of the model respectively. Right: Update rules for the variational parameters.

We choose a factorization for the distribution q that captures most model assumptions and yet is computationally tractable:

$$\begin{array}{ll}q(S,P)& =\underset{\mathrm{population}­\mathrm{level\; topics}}{\underbrace{\prod _{k=1}^K\mathrm{NIW}({\mu }_k,{\sum }_k;{\stackrel{\sim }{\eta }}_k^I)\mathrm{Dir}({\beta }_k;{\stackrel{\sim }{\eta }}_k^G)\mathrm{Beta}({\upsilon }_k;{\stackrel{\sim }{\omega }}_k)}}\times \\ & \prod _{s=1}^S\prod _{t=1}^T\underset{\mathrm{topics\; for\; subject}s}{\underbrace{\mathrm{Cat}(c_{\mathit{st}};{\xi }_{\mathit{st}})\mathrm{Beta}({\pi }_{\mathit{st}};{\stackrel{\sim }{\alpha }}_{\mathit{st}})}}\prod _{n=1}^N\underset{\mathrm{image\; topic}}{\underbrace{\mathrm{Cat}(z_{\mathit{sn}}^I;{\varphi }_{\mathit{sn}}^I)}}\prod _{m=1}^M\underset{\mathrm{genetic\; topic}}{\underbrace{\mathrm{Cat}(z_{\mathit{sm}}^G;{\varphi }_{\mathit{sm}}^G)}},\end{array}$$

where we choose an appropriate approximating distribution for each latent variable and use ~ to denote parameters of the approximating distributions. The optimization is defined in the space of the variational parameters {η̃^I, η̃^G, ω̃, ξ, α̃, ϕ^I, ϕ^G}. We omit the derivation of the updates due to space constraints; Algorithm 1 provides pseudocode for the resulting updates. We run the algorithm five times starting from different random initializations and report the result with the highest lower bound F (q).

Once the algorithm converges, we estimate the population-level quantities of interest as means of the corresponding approximating distributions:

$$\begin{array}{l}{\widehat{\mu }}_k=\mathrm{E}[{\mu }_k\mid D]\approx {\mathrm{E}}_q[{\mu }_k;{\stackrel{\sim }{\eta }}_k^I],{\widehat{\sum }}_k=\mathrm{E}[{\sum }_k\mid D]\approx {\mathrm{E}}_q[{\sum }_k^I;{\stackrel{\sim }{\eta }}_k^I],\\ {\widehat{\beta }}_k=\mathrm{E}[{\beta }_k\mid D]\approx {\mathrm{E}}_q[{\beta }_k^G;{\stackrel{\sim }{\eta }}_k^G].\end{array}$$

Each expectation above can be easily evaluated from the parameters of the corresponding distribution. In addition, we construct spatial maps that display the posterior probability of each population topic for each supervoxel in a particular subject s to visually evaluate the disease structure in that subject.