Leveraging anatomical information to improve transfer learning in brain-computer interfaces

Abstract

Objective

Brain-computer interfaces (BCIs) represent a technology with the potential to rehabilitate a range of traumatic and degenerative nervous system conditions but require a time-consuming training process to calibrate. An area of BCI research known as transfer learning is aimed at accelerating training by recycling previously recorded training data across sessions or subjects. Training data, however, is typically transferred from one electrode configuration to another without taking individual head anatomy or electrode positioning into account, which may underutilize the recycled data.

Approach

We explore transfer learning with the use of source imaging, which estimates neural activity in the cortex. Transferring estimates of cortical activity, in contrast to scalp recordings, provides a way to compensate for variability in electrode positioning and head morphologies across subjects and sessions.

Main Results

Based on simulated and measured EEG activity, we trained a classifier using data transferred exclusively from other subjects and achieved accuracies that were comparable to or surpassed a benchmark classifier (representative of a real-world BCI). Our results indicate that classification improvements depend on the number of trials transferred and the cortical region of interest.

Significance

These findings suggest that cortical source-based transfer learning is a principled method to transfer data that improves BCI classification performance and provides a path to reduce BCI calibration time.

1. Introduction

Brain-computer interfaces (BCIs) are designed to provide alternate communication pathways for the brain and hold potential to rehabilitate people with traumatic or degenerative brain damage. Yet, this technology still faces some obstacles including the time required to calibrate these systems (Blankertz, et al., 2008; Wolpaw, et al., 2002). A typical non-invasive BCI session can be divided into three phases: electroencephalography (EEG) cap setup, a calibration period to train a machine-learning algorithm, and a feedback phase in which the user controls some output, such as a computer, robotic prosthetic, or spelling system. The first two phases are simply means to an end – setup and training prepare the BCI system to infer a user’s intended action from recorded brain signals (Krauledat, et al., 2008). Given a fixed length BCI session, time spent in these two phases reduces time spent in the feedback phase, so techniques that shorten setup or training make BCIs more appealing for clinical and commercial applications by allocating additional time to the feedback phase. Recent improvements in recording hardware (e.g., rapidly deployable caps and dry electrodes) have reduced the setup time (Chi, et al., 2010), but less progress has been made in reducing the 20–30 minute training phase (Krauledat, et al., 2007; Lotte & Guan, 2010).

The purpose of the BCI training phase is to accumulate data to build a statistical model that can recognize spatial and temporal patterns in an individual’s neural activity. These patterns typically vary across subjects (and even across sessions within individual subjects) due to a number of factors, so training is required to tune the classifier to the available features. A branch of BCI research known as transfer learning is focused on reducing training time by reusing previously recorded data to calibrate a new system (Lotte & Guan, 2010; Krauledat, et al., 2008; Kindermans, et al., 2014). Recycled training data can originate from the same subject’s previous session(s) (i.e., subject-specific) or be transferred from other BCI users (i.e., subject-independent). Transfer learning thus provides a way to reduce or eliminate the need to collect training data for an ongoing BCI session by recycling preexisting training trials.

Past transfer learning strategies have employed a number of techniques to recycle BCI data. Many groups have developed methods to generate spatial filters and/or classifiers with the aim of creating BCI systems that are session- or subject-independent (Devlaminck, et al., 2011; Fazli, et al., 2009; Kang, et al., 2009; Kindermans, et al., 2014; Krauledat, et al., 2007; Krauledat, et al., 2008; Lotte & Guan, 2010; Tu & Sun, 2012; Wang, et al., 2012; Yang, et al., 2014, but see Samek, et. al., 2013 for an alternate approach). While the specific implementations vary, all of these methods transfer information based on EEG spatial patterns on the scalp, which neglect variation in individual cortical anatomy, head anatomy, and electrode locations.

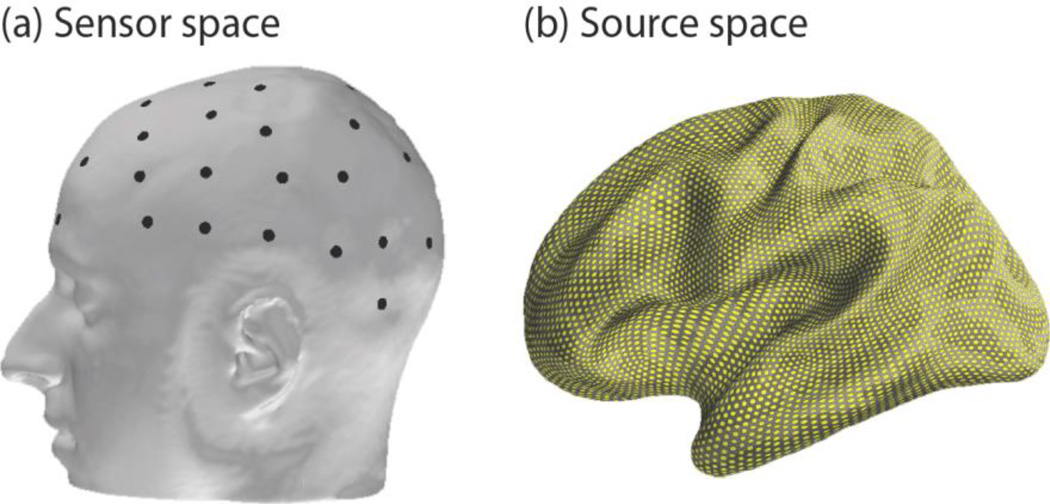
It is preferable to classify across-subject data after explicitly accounting for deviations in head morphology and electrode positioning. Source imaging achieves these goals by mapping EEG sensor measurements recorded from the scalp (or sensor space; figure 1, left) onto the underlying neural sources of the activity in the cortex (or source space; figure 1, right). Variation in individual anatomy and electrode placement is controlled as both are incorporated in the activity estimation process using structural MRI and electrode coregistration. Once brain activity is estimated in the source space, established neuroimaging tools allow for the morphing of brain activity between different subjects’ brain spaces – a technique known as spatial normalization (Friston, et al., 1995). In this way, we can estimate how brain activity from one subject would manifest in any other subject’s brain space. Therefore, the source space approach serves as a more robust reference frame for recycling non-invasive brain data across sessions and subjects.

Figure 1.

Visualization of the dichotomy between sensor and source space. (a) Sensor space where EEG (black dots) data are recorded. Past transfer learning research has focused primarily on data recorded and manipulated in this space. (b) Source space where cortical activity is estimated at approximately 7000 dipoles (yellow points) from EEG data.

This work explores the feasibility of transferring training trials through the source space to conduct subject-independent transfer learning in a single-trial BCI classification task. Compared to a subject-specific BCI classifier, we hypothesized that a system trained solely with data transferred from other subjects through the source space would yield equivalent or improved performance. To test this, we first simulated EEG data to examine classification gains when exploiting 3-dimensional anatomical information conferred by the source space. We then validated the simulation results by classifying the switching of attention in previously recorded EEG data. In the real EEG and most of the simulated EEG experiments, we found that the transfer learning method surpassed the subject-specific classifier with a moderately sized pool of transferred data. This work illustrates the potential of source space to achieve anatomically normalized transfer learning as well as provide a formal avenue to include neuroscience priors in BCI work.

2. Methods

2.1 Anatomical information

Structural information was obtained for 21 subjects using three T1-weighted MRI scans consisting of one structural multi-echo magnetization prepared rapid gradient echo scan and two multi-echo multi-flip angle (5° and 30°) fast low-angle shot scans. From this structural data, a 3-layer boundary element model (BEM) was constructed for each subject using FreeSurfer (http://surfer.nmr.mgh.harvard.edu/; Dale, et al., 1999) to characterize the propagation of neural electromagnetic fields through the different layers of the head to the EEG sensors (Baillet, 2010). Positions of EEG electrodes, cardinal landmarks (nasion, left/right preauriculars), and other points on the scalp were recorded using a 3Space Fastrak (Polhemus) to coregister the electrodes with the BEM’s coordinate frame.

2.2 Source vs. sensor space

The source space was modeled with a discretized spatial sampling of the cortex consisting of approximately 7000 current dipoles distributed across the entire cortical manifold, where each dipole modeled a localized primary neural current (Hämäläinen, et al., 1993). Using the BEM, the forward solution was obtained by calculating the influence of each dipole on every EEG electrode and stored in the gain matrix. In the real EEG data, sensor noise covariance matrices were calculated from 200 ms baseline periods before each trial for every subject. From each subject’s gain and noise covariance matrices, we computed an inverse solution, which uses sensor measurements to estimate cortical activity at each dipole in the source space. This calculation is ill-posed as about 7000 variable currents must be estimated from tens of EEG electrodes (60 here). Solving the inverse problem is a well-studied area that requires constraints to generate a solution (for a review, see Hämäläinen, et al., 1993; Baillet, et al., 2001). We calculated the inverse operator using the Minimum-Norm Estimate library (MNE; http://martinos.org/mne/), which determines a source activity profile that minimizes the difference between the expected and real EEG measurement profile while also minimizing a penalty for the size of the current solution vector’s ℓ₂-norm (Hämäläinen, et al., 2010; Gramfort, et al., 2014). This results in a unique, stable, and linear estimate of source activity (Gramfort, et al., 2014; Dale & Sereno, 1993; Hämäläinen & Ilmoniemi, 1984).

2.3 Simulated EEG data

The cortical dipoles in each of the N=21 subject’s cortical models were partitioned into anatomically defined cortical patches, or regions of interest (ROIs), using FreeSurfer’s automatic parcellation algorithm (Destrieux, et al., 2010). This technique uses cortical curvature to define a boundary between all gyri and sulci and then splits the cortical surface into distinct ROIs according to an anatomical atlas. We investigated 69 automatically defined non-overlapping sulcal and gyral ROIs, as well as 3 additional custom hand motor cortex ROIs to further study the effects of ROI size. The center of these hand motor ROIs was defined from a hand motor functional localization meta-study (Witt, et al., 2008). Three increasingly larger hand motor ROIs were then constructed by finding the modeled dipoles that satisfied two conditions: 1) they were part of FreeSurfer’s precentral gyrus ROI, and 2) were within 5, 10, and 15 mm of this center. To limit computational complexity, only ROIs located in the left hemisphere were used.

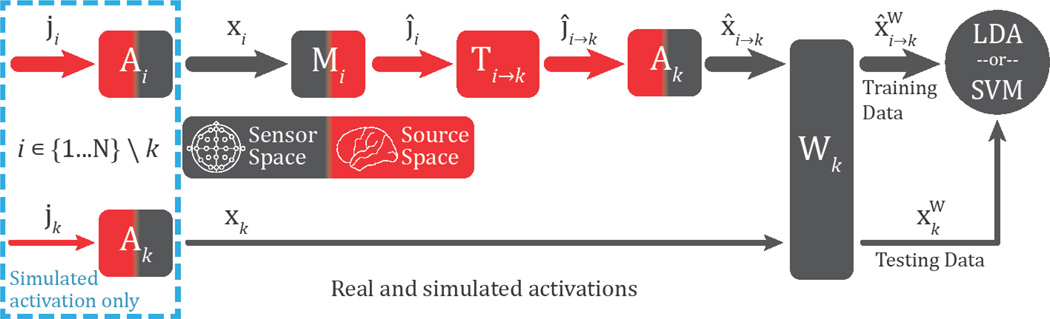
We conducted an EEG-based classification task using these 72 cortical ROIs to classify whether each had elevated or baseline levels of activity. To accomplish this, cortical activity j_i was simulated for the ith subject, where i ∈ {1 … N} at each ROI and normalized by the cortical area (as approximated by the number of included dipoles) to yield a constant current density. The simulated EEG profile x_i was then calculated by multiplying the activity j_i by the gain matrix A_i and adding Gaussian noise n_i (see figure 2, dashed blue box):

$${\mathbf{x}}_i={\mathbf{A}}_i{\mathbf{j}}_i+{\mathbf{n}}_i$$ (1)

Simulated EEG profiles consisted of a single time point of activity and each served as a trial. Sets of 10, 20, and 40 trials were simulated for each condition (elevated or baseline activity) for each subject. As there exists no ground truth as to which brain signals constitute “signal” and “noise” in real EEG recordings, it is difficult to estimate the SNR of experimentally recorded data; however, in simulations we had explicit control over the SNR. Thus, we repeated the simulation at SNRs of −15, −10, and −5 dB, as the resulting classification performances best spanned accuracies of actual BCI systems previously reported in the literature. As in the MNE toolbox (Gramfort, et al., 2013), SNR was defined as $10{\text{log}}_{10}({\sigma }_{\text{signal}}^2/{\sigma }_{\text{noise}}^2)$.

Figure 2.

Schematic of source-based transfer learning method. Blue, dashed box: In the simulation experiments only, cortical activity was generated for all subjects and multiplied by the appropriate gain matrix to simulate EEG activity. Top row: In both the simulated and real experiments, EEG data for subjects 1 to N (excluding subject k) were multiplied by the pseudoinverse matrix to obtain source activity estimates. Source estimates were subsequently morphed to subject k’s brain using the appropriate transformation matrix (see text for details and citations), multiplied by subject k’s gain matrix, and (optionally) weighted yielding N−1 sets of classifier training data in subject k’s sensor space. Bottom row: In both the simulated and real experiments, EEG data from the subject of interest (subject k) were (optionally) weighted yielding data to test the classifier. Note that no data from the subject of interest were used to train the BCI classifier.

2.4 Real EEG data

We also used EEG data from a previously recorded attentional modulation task (Larson & Lee, 2014) to complement our simulation study. For details on the experimental paradigm, see the previous manuscript. Briefly, N=10 subjects (all also a part of the previously mentioned 21 subject pool) listened to a target and masker auditory stream with each stream comprised of spoken letters. In the experimental condition analyzed here, each stream was delayed by 300 μs either in the right or left channel to elicit a leftward or rightward spatial percept. Before each trial, listeners were cued to either maintain attention to the same auditory stream (left or right) throughout the trial or switch streams halfway through during a gap period. Using EEG data from this gap period, we classified whether or not the subject switched auditory spatial attention. The subject was required to report a behavioral metric for each trial, and only correct trials were included in our analysis. For this reason, the number of trials varied for each subject (mean=38). For simplicity, EEG data was temporally averaged over the 600 ms gap period to create a single spatial profile (i.e., one time point) of activity just as in the simulated data.

2.5. Traditional vs. transfer learning training data

Two different training formulations were tested in this BCI classification task for both the simulated and real experiments: a traditional approach and the transfer learning approach. We emulated a traditional BCI classifier (detailed below) by training and testing on simulated (and real) EEG data from each of the 21 (10) subjects individually. The majority of current BCI applications use this subject-specific strategy, so the classification accuracy here served as a benchmark for our transfer learning technique. The transfer learning approach recycled EEG trials based on a leave-one-subject-out method—when training a classifier for subject k, we used trials from all other subjects and transferred them through the source space to subject k’s brain space for classifier training. In other words, the transfer learning approach was subject-independent, as no data from the subject of interest was used to train that individual’s BCI system.

For both the simulated and real EEG experiments, data transfer was achieved by first multiplying the training EEG activity for each subject i by the pseudoinverse of the gain matrix ${\mathbf{M}}_i={\mathbf{A}}_i^{†}$ to estimate the cortical currents ĵ_i (see figure 2):

$${\mathbf{ĵ}}_i={\mathbf{M}}_i{\mathbf{x}}_i$$ (2)

Next, brain activity was transferred by morphing these current activity profiles to subject k’s brain space in a manner analogous to the spatial normalization of brain activity across subjects in neuroimaging. This transfer step used an isotropic diffusion process described in Gramfort et al. (2014) and FreeSurfer’s spherical brain morphing procedure (Fischl, et al., 1999). Source estimates were first spatially smoothed onto a high-resolution version of the cortical mesh with the aforementioned diffusion process. Next, the mesh was inflated into a unit sphere where the entire set of sulcal/gyral boundaries, which delineate many functional areas, were optimally aligned with the target brain. A linear transformation from the original to the target sphere was then calculated and applied in FreeSurfer (using the morph maps function), and the spatially normalized data was subsampled to the target spatial resolution (of ~7000 dipoles). This entire set of linear algebra operations comprises the transformation matrix T_i→k. Therefore, the transformation of cortical activity from subject i to k was accomplished by multiplying each subject’s source estimates by the appropriate transfer matrix (see figure 2):

$${\mathbf{ĵ}}_{i\to k}={\mathbf{T}}_{i\to k}{\mathbf{ĵ}}_i$$ (3)

After the training trials from each of the N−1 subjects were transferred to subject k’s source space, the data were multiplied by subject k’s gain matrix and optionally weighted to generate N−1 sets of EEG training data for subject k’s classifier (see figure 2):

$${\hat{\mathbf{x}}}_{i\to k}^W={\mathbf{W}}_k{\mathbf{A}}_k{\mathbf{ĵ}}_{i\to k}$$ (4)

The weighting procedure will be discussed subsequently in section 2.7.

Using this leave-one-subject-out scheme, similar to previous transfer learning work (Fazli, et al., 2009), data from all i subjects trained the classifier while data from subject k was used to test the classifier. The simulations for both the traditional (subject-specific) and transfer learning (subject-independent) versions of the classification task were repeated 25 times per subject to ensure stability before comparison. All of the code for this analysis is online (http://github.com/LABSN/LABSN_pubs/tree/master/Wronkiewicz_JNE_2014/).

We repeated this classification task with different numbers of subjects in the training set to see how classification performance was affected by training pool size. In the simulation task, training sets ranged from 2 to 20 randomly selected subjects with 40 trials per condition and an SNR of −10 dB. As before, the classification was repeated 25 times with random subsets of i ∈ {1 … N} \ k subjects for each test subject k for stability. Here, classification accuracy was investigated in a set of ROIs relevant to common BCI paradigms, which included six cortical areas potentially associated with the P300 response, four areas associated with motor-imagery, three steady state visually evoked potential (SSVEP) areas, and one ROI in primary auditory cortex. In the real EEG data, training sets ranged from 2 to 9 randomly selected subjects with an average of 38 trials per condition, and the classification was also repeated 25 times. The transfer of real attentional data used the same process as in the simulation experiment.

2.6. Classification methods

In the simulation experiment, we used regularized Linear Discriminant Analysis (LDA) (Friedman, 1989) to classify whether each ROI had elevated or baseline levels of activity. A conventional regularization parameter of 0.05 was used as it optimized the subject-specific (benchmark) classifier’s performance. In the real EEG data, we used support vector machines (SVM) with a radial basis function kernel and an optimization strategy that was the same for both the benchmark and transfer-learning data. Leave-one-trial-out cross-validation was used in the simulated data, while 10-fold cross-validation was used in the real EEG data because of computational demands. LDA and SVMs were chosen for classification because of their efficiency and widespread use in the BCI field (for review, see Lotte, et al., 2007).

2.7. Simulation: weighting electrode importance

In the simulated experiment of this transfer learning approach, we also investigated the impact of weighting the EEG data according to the presumed location of active cortical sources. We hypothesized that the classifier training efficiency and accuracy could be improved by exploiting this spatial information. Weighting the EEG data warped the feature space by compressing the variance of signal dimensions that were deemed unimportant. As LDA attempts to simultaneously maximize the mean separation between classes and minimize within-class variance, this feature weighting made the discrimination boundary more sensitive to highly weighted EEG electrodes.

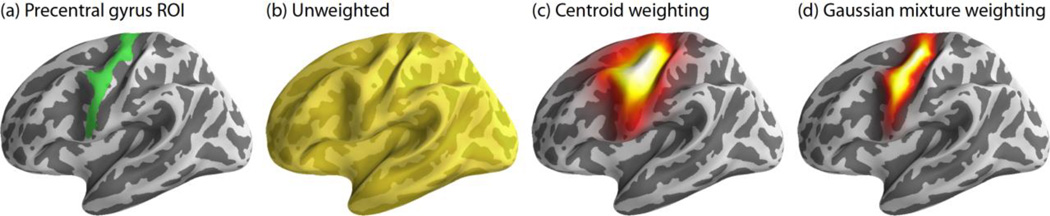
To achieve this weighting, we combined the gain matrix with each subject’s presumed ROI location to define cortical areas important for classification. The weighting was tested using three different formulations. Consider a region like the precentral gyrus, for example (figure 3a). The first and simplest method did not take location information into account and treated each dipole with equal importance (figure 3b). The second, called centroid weighting, found the spatial center-of-mass of the anatomical region and weighted importance of dipoles according to a cortical distance-based Gaussian decay (figure 3c). The last weighting strategy, Gaussian mixture weighting, used a Gaussian kernel spatially convolved with each dipole to accumulate each dipole’s contribution into a non-uniform weighting map (figure 3d) inspired by previous fuzzy ROI work (Lotte, et al., 2009b). Here, dipole importance was determined according to the number of times that a particular dipole belonged to the ROI under evaluation across the entire subject set. The centroid and Gaussian mixture methods both made use of a priori knowledge about the presumed origin of certain cortical activity to weight those areas more highly during classification. In all weighting schemes, cortical dipole weights were multiplied by the gain matrix A and normalized by the maximum weight to obtain a weighting profile in the sensor space. EEG data was weighted according to each method and classified to explore any potential increases in classifier accuracy when including information about the ROI’s spatial location.

Figure 3.

Three different weighting strategies for an exemplar ROI. (a) Precentral gyrus ROI (green). (b) Unweighted: dipoles are given equal weight when classifying. (c) Centroid weighting: dipoles are weighted by the cortical surface distance to the ROI’s center. (d) Gaussian mixture: dipoles are weighted according to a spatial convolution of a Gaussian kernel with their importance to generate a non-uniform weighting profile (see text for details).

3. Results

3.1 Simulation: transfer learning vs. traditional classification performance

We compared classification accuracies between a traditional BCI approach and our source space transfer learning method using simulated data. The traditional (subject-specific) classifier was trained and tested on data from each subject individually, and served as our benchmark. The (subject-independent) transfer learning method trained the classifier for the subject of interest using only transferred data from the other subjects.

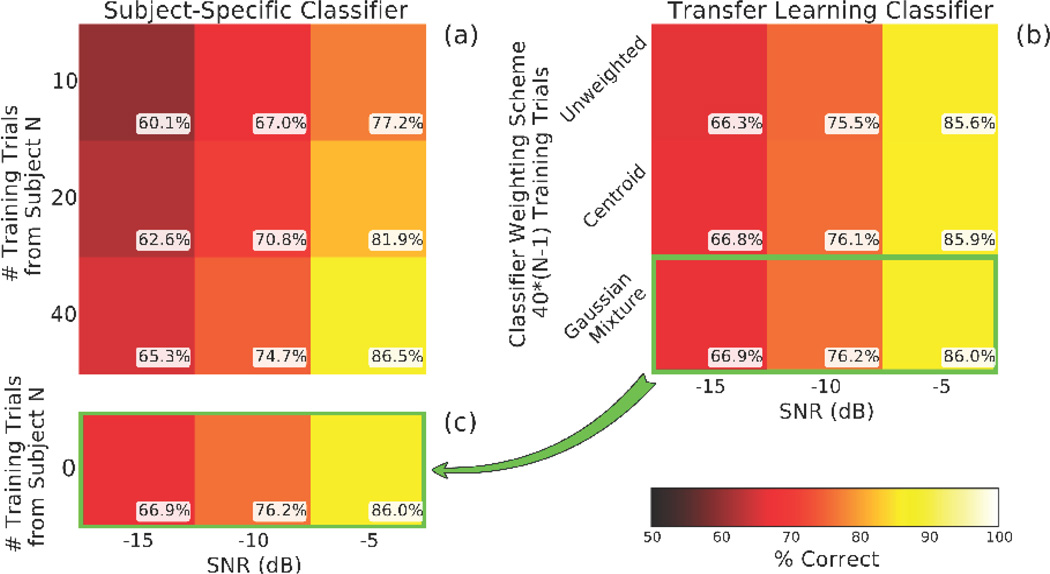
In the traditional classifier, average accuracy across all 72 ROIs increased with both SNR and trial count and spanned a range of accuracies typical for real-world BCIs (figure 4a). The transfer learning classifier, set at 40*(N−1) trials per subject, also showed accuracy increases with SNR and incremental gains with increasingly specific spatial weighting profiles (figure 4b). The most accurate transfer learning classifier (figure 4c; copy of bottom row of figure 4b) performed comparably to the subject-specific classifier and achieved a small improvement in the two conditions with the lowest SNR. Again, zero training trials originated from the subject of interest (whose data was being classified) in the transfer learning classifier.

Figure 4.

An LDA classifier trained with source-based transfer learning performed comparably to the traditional subject-specific classifier. Each score represents the average accuracy of 72 ROIs for 21 subjects repeated 25 times. (a) The traditional classifier was evaluated using 10, 20, and 40 training trials at SNRs of −15, −10, and −5 dB, and the classifier was trained and tested on each subject individually. (b) The transfer learning classifier was trained with three different weighting schemes. Each condition represents the average as in (a), but the classifier was trained exclusively on data from all other (N−1) subjects in the pool and then tested using data from the excluded subject. (c) The Gaussian mixture accuracy is copied for comparison with the bottom row of (a), where the traditional classifier showed performance levels in the same range as many actual BCI systems. The transfer learning method surpassed the subject specific classifier in the two lowest SNR conditions. Chance accuracy is 50%.

The percent accuracy difference between the (Gaussian mixture weighted) transfer learning and the traditional classifier for each ROI is shown in figure 5. Here, the SNR was set at −10 dB as the traditional classifier performance best represented real-world BCI systems when using a realistic training set size of 40 trials per class. Performance gains were not uniform across the cortical surface: the transfer learning approach better classified ROIs in many of the frontal and parietal dorsal areas, while the traditional classifier better classified ROIs in the occipital lobe and near the lateral sulcus (or Sylvian fissure).

Figure 5.

Difference in accuracy between the (Gaussian mixture weighted) transfer learning approach and the traditional BCI classifier at 72 ROIs distributed across the cortical surface. Lateral (left) and medial (right) views of cortical ROIs used in the classification task. Each ROI represents the average accuracy of 25 repetitions over 21 subjects. Here, the SNR was set at −10 dB as this gave a classification accuracy representative of real-world BCI systems in the traditional classifier.

3.2 Simulation: effect of training set size

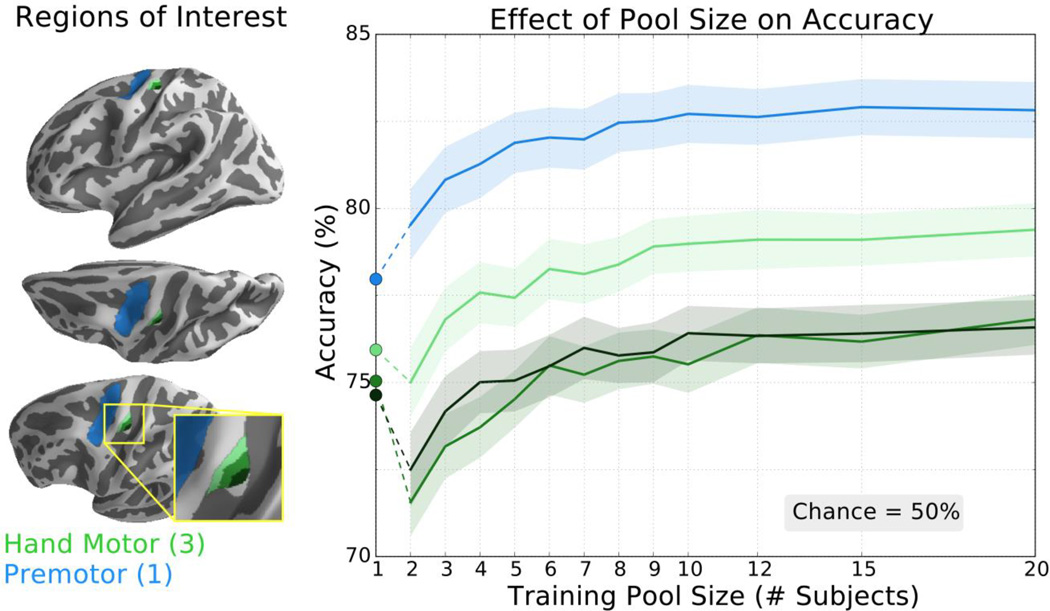
We further explored how training set size affected transfer learning performance in ROIs related to common BCIs. To assess classification improvements in motor imagery BCIs, we tested three increasingly larger ROIs in the hand motor knob (figure 6, increasingly lighter green shades) as well as the precentral sulcus (figure 6, blue). In all ROIs, the transfer learning approach eventually achieved a classification accuracy greater than the traditionally trained classifier (figure 6, circular markers). The pool size required to surpass the traditional classifier ranged from 2 to 6 subjects, and all ROIs reached an accuracy plateau after 10–12 subjects when using 40 trials per condition per subject.

Figure 6.

The classifier trained with transfer learning achieved higher classification accuracy than the traditional classifier for all tested ROIs related to motor imagery. Left: ROIs included small, medium, and large hand motor ROIs (increasingly lighter green shades; hand motor knob) and the premotor area (blue; pre-central sulcus). In the hand motor region, the three ROIs overlap so that each individual region contains the smaller ROI(s). Right: Accuracy of the transfer learning classifier ± SEM as a function of pool size for these motor imagery ROIs averaged over 21 subjects repeated 25 times. Accuracy of the subject-specific classifier is indicated by the circular markers, left. Chance accuracy is 50%.

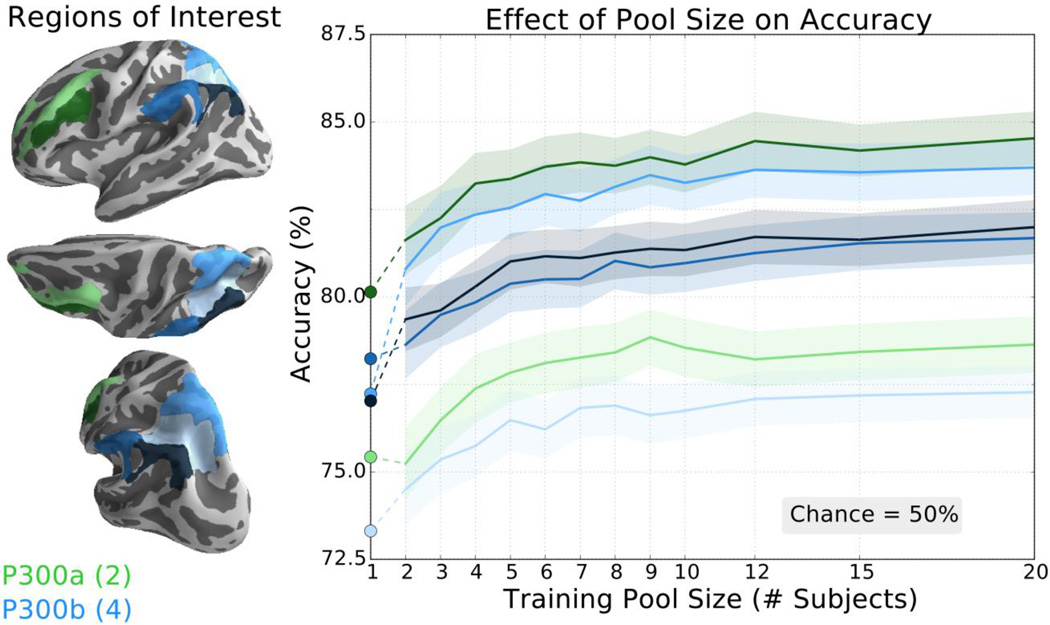
We repeated this analysis in six brain regions that are implicated in the P300 “oddball” event-related potential (ERP) in both early (figure 7; P300a, green) and late (figure 7; P300b, blue) components of this response. A large number of ROIs were tested here as the precise origin of the P300 ERP has remained elusive (Polich, 2007). For all ROIs, the transfer learning method surpassed the traditional classifier (figure 7, circular markers) when the pool was comprised of 3 or more subjects and showed diminished accuracy improvements after 8–10 subjects.

Figure 7.

The transfer learning classifier achieved higher classification accuracy than the traditional classifier for all tested ROIs thought to be related to the P300 ERP. Left: P300a ROIs included middle frontal gyrus and inferior frontal sulcus (light and dark green, respectively). P300b ROIs include intraparietal sulcus and transverse parietal sulci, superior parietal lobule, supramarginal gyrus, and angular gyrus (increasingly darker shades of blue, respectively). Right: Accuracy of the transfer learning classifier ± SEM as a function of pool size for these P300 ROIs averaged over 21 subjects repeated 25 times. Accuracy of the subject-specific classifier is indicated by the circular markers, left. Chance accuracy is 50%. Note scale difference from other BCI ROI figures.

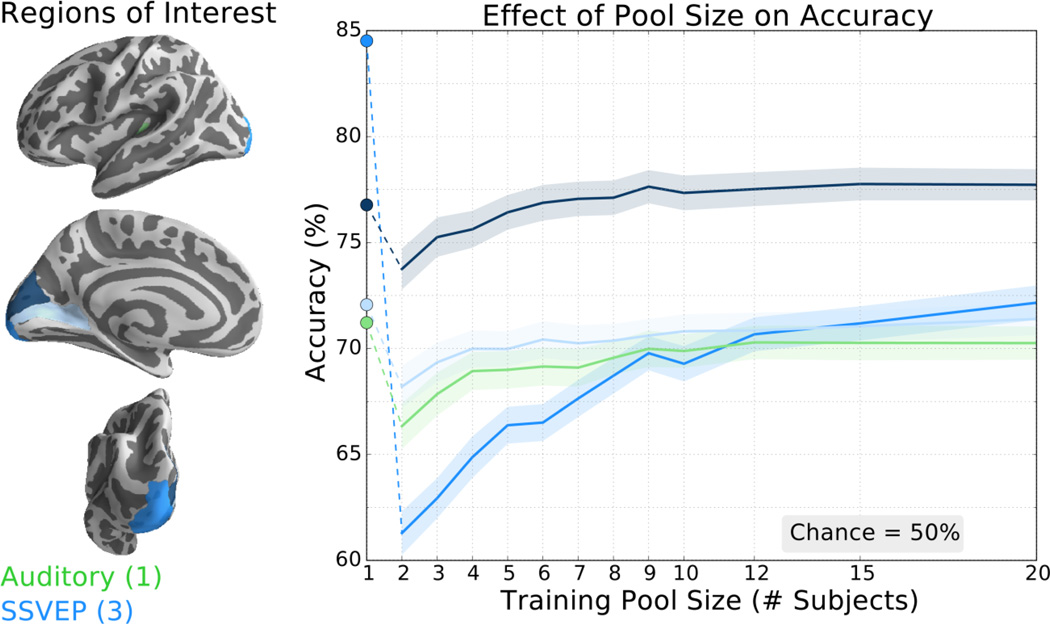
Finally, we evaluated three SSVEP regions in primary visual (figure 8, blue) and auditory regions (Heschel’s gyrus; figure 8, green). Here, only one of the three visual ROIs eventually reached accuracy levels matching that of the subject-specific accuracy (figure 8, circular markers). The transfer learning method also failed to reach the subject-specific training accuracy in the primary auditory ROI. Even so, only the occipital pole region of primary visual cortex showed an accuracy decrease of more than 1.5% for the largest pool size.

Figure 8.

The classifier trained with transfer learning achieved higher classification accuracy than the traditional classifier in one of the primary auditory and visual ROIs tested. Left: ROIs include components of primary auditory cortex (anterior transverse temporal gyrus; green) and primary visual cortex including calcarine sulcus, occipital pole, and cuneus (increasingly darker shades of blue, respectively). Right: Accuracy of the transfer learning classifier ± SEM as a function of pool size for the auditory and visual ROIs averaged over 21 subjects repeated 25 times. Accuracy of the subject-specific classifier is indicated by the circular markers, left. Chance accuracy is 50%. Note scale difference from other BCI ROI figures.

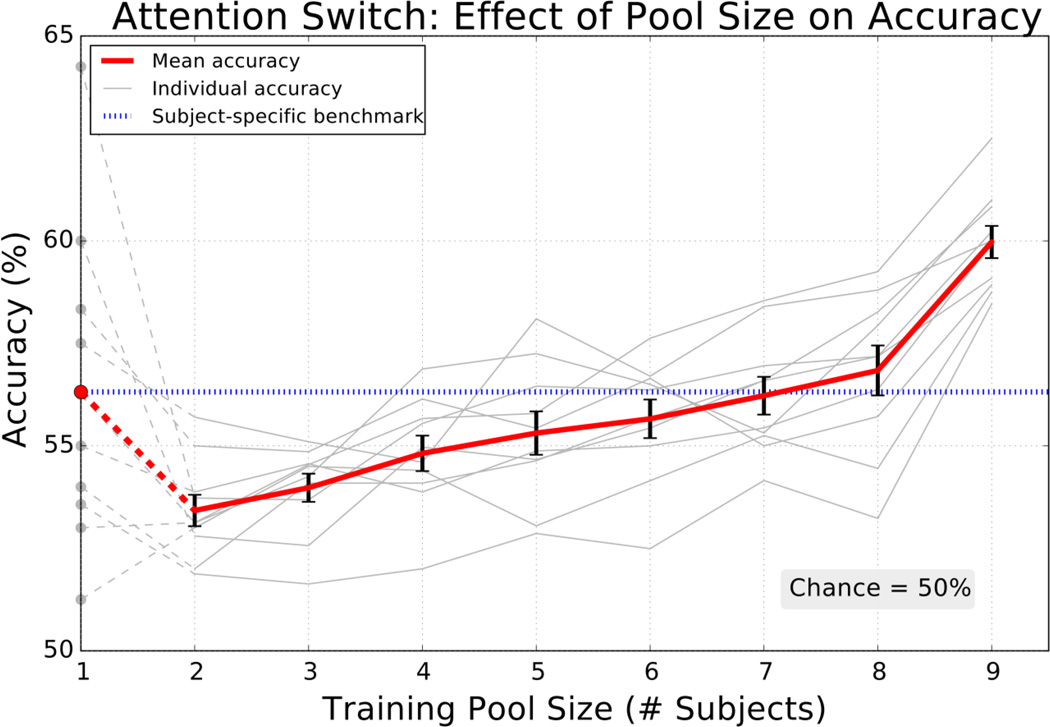
3.3 Real data: classification performance and effect of training set size

We tested the source-based transfer learning strategy on real EEG data from an attentional switching task. Subjects were instructed to maintain or switch attention between two auditory streams and data from the potential switching period was used to classify if spatial attention was reoriented (Methods). The transfer learning classifier increased with training pool size eventually surpassing the mean subject-specific accuracy (figure 9) consistent with P300 and motor imagery simulation results. When using the maximum of nine subjects, the transfer learning method performed 3.7 percent better than the subject-specific approach with an average accuracy of 60.0 percent. The accuracy continued to increase with the number of subjects in the training pool, but, unlike in simulation, improvements did not appear to reach a plateau by the 9^th subject.

Figure 9.

The transfer learning classifier achieved incremental performance gains in classifying real data from an attentional switching task and eventually surpassed the subject-specific benchmark. Mean ± SEM (red, black error bars) for 10 individual (gray) accuracies repeated 25 times when classifying attentional switching. Subject-specific classifier accuracy is indicated by the circular markers (left) and the mean is traced across all pool sizes for comparison (blue dotted line). Chance accuracy is 50% and the data consisted of 38 trials per condition per subject on average.

4. Discussion

This work demonstrates the feasibility of training a subject-independent BCI classifier (i.e., using data exclusively from other subjects) by transferring brain recordings from other subjects through the source space. The source space allows for the normalization of individual head anatomy and electrode locations, in contrast to a sensor space approach. We evaluated this approach using simulated cortical activations, which to provide ground truth regarding the spatial location and SNR of neural activity, as well as real EEG data from an attentional modulation task. A traditional subject-specific BCI training method, which was trained and tested on each individual’s data, served as our benchmark.

Both the simulated and real experiments suggest that a classifier trained with data transferred from fewer than 10 subjects through the source space tends to match or outperform a subject-specific classifier. In simulation, we found that the average classification accuracy was comparable to the benchmark for all realistic SNRs and training set sizes (figure 4) with up to 6.5% improvement (figure 5) and surpassed this subject-specific classifier in some BCI specific regions (figures 6–8). By more heavily weighting relevant cortical regions (essentially including functional localization priors), further incremental accuracy improvements were obtained (figure 4b). In real data, the transfer learning method classified attentional reorientation 3.7% better than the subject-specific classifier (figure 9).

This is encouraging for source-based transfer learning as we were unable to find a subject-independent transfer-learning study that reported an accuracy improvement. The majority of studies use session-independent data or a combination of subject-specific and subject-independent motor-imagery data and report small accuracy changes from their benchmark (almost all are within ±5%). The only exception that uses a true subject-independent approach (Fazli, et al., 2009) reported small decrease in accuracy, which was subsequently observed elsewhere (Samek, et al., 2013). This suggests that leveraging the tools and priors afforded by the source space can bring advantages to transfer learning (including classification of cortical activity not conventionally used in BCIs).

4.1 Source space transfer learning

The primary goal of transfer learning is to shorten or eliminate the time spent calibrating a BCI system by reusing training data. Theoretically, the most informative training data will always come from the subject in the ongoing BCI session, but compiling these training trials consumes a portion of that session’s time. Therefore, transfer learning techniques can be advantageous when they merely match the classification accuracy of subject-specific BCIs, or even sustain minor accuracy decreases, because of the time saved. This is especially relevant in clinical settings where the BCI user may have other health-related time obligations. Past transfer learning research, to the best of our knowledge, has been conducted exclusively in the sensor space, which makes assumptions about the data consistency across subjects and sessions.

A source space approach to transfer learning circumvents many of the assumptions associated with the sensor space. First, transferring spatial filters between subjects in sensor space does not explicitly account for individual variations in anatomical brain and head morphology. In source imaging, the use of individual head models obtained through MRI helps spatially normalize variation in cortical and head morphology and therefore, normalize effects of volume conduction as electromagnetic signals propagate from the cortex to the EEG sensors. Second, sensor space transfer learning assumes that differences in EEG electrode locations will be negligible between sessions. In practice, small shifts between the EEG and brain coordinate frames will result in a different composition of recorded brain activity, which may undermine algorithms based on spatial filtering (Ramoser, et al., 2000; Bashashati, et al., 2007). Coregistering electrodes to each individual’s head model normalizes this spatial jitter in the electrode positioning relative to the brain. Third, the electrode montage must be conserved to transfer training data as different electrode arrangements will alter the sensitivity to particular brain areas, especially when the number of electrodes is low. However, conforming to a specific montage is undesirable as it limits the ability to choose other arrangements that are more practical or target pre-determined brain regions. Source imaging allows the computation of source estimates regardless of the montage choice or number of electrodes (within a reasonable limit). Additionally, the work here focuses on transferring the cortical activations themselves (when data are at an earlier step in the BCI processing chain). Therefore, predetermining the feature generation method or classifier is not necessary like in many sensor-based strategies.

4.2 Leveraging neuroscience priors in the source space

The source space provides a generalized pathway for connecting BCIs to other neuroscience research. For example, neuroimaging information can help define a hand motor ROI for BCI control as demonstrated here. This is similar to preselecting the C3/C4 electrodes as control signals for an imagined hand motor task, but the source space allows the controlled targeting of specific ROIs independent of electrode positioning or montage choice. We showed that this targeting of a cortical region through electrode weighting gives incremental gains in transfer learning even with no training trials from the subject of interest. This targeting may aid in the development of BCIs driven by cortical regions beyond the small handful of paradigms that dominate the field (Vansteensel, et al., 2010). As an example, recent research has implicated the right temporal-parietal junction (RTPJ) in switching auditory attention between sound sources at different spatial locations (Larson & Lee, 2014; Larson & Lee, 2013). While we used data from this attentional paradigm, a system that is further optimized by using the precise RTPJ location might be used in a hearing aid BCI with spatially selective sound amplification that mirrors a user’s attention (Lee, et al., 2013). Even if a neuroscience prior is not available, past work has shown that non-standard target ROIs can be determined statistically (Lotte, et al., 2009a).

Operating in source space also opens the possibility to link findings from BCI research with other areas of neuroscience because of the shared spatial reference frame. Examples of these areas include functional and structural neuroimaging as well as invasive electrophysiological methods (acquiring signals via electrocorticography or microelectrode arrays, for example). Linking sensor-based BCI findings to the cortex is difficult with EEG scalp maps because they are only a proxy to the underlying brain activity. Thus, estimating cortical activity from non-invasive EEG data provides a standardized frame to both exploit knowledge from other areas of neuroscience as BCI priors and relate results with other existing bodies of literature.

4.3 The ideal training pool

To investigate the effects of training pool size in transfer learning, we explored a range of transferred training pool sizes. All simulated tests attained the highest proportion of total accuracy gain during first 8 to 10 subjects and diminishing improvements thereafter (with 40 training trials per class per subject). In the real EEG experiment, accuracy consistently increased as the training pool grew and but did not appear reach a plateau by the 9^th subject suggesting that more improvement might be possible with additional subjects. Additionally, we found that the maximum performance varied depending on the ROI, which may be a consequence of morphological inconsistencies across subjects leading to different compositions of recorded cortical activity. Another possibility is that electrode coverage over certain ROIs – traditionally, the occipital lobe is a relatively difficult place to obtain reliable electrode contact. Future work focused on subselecting training data for personalized training data pools may yield further accuracy improvements.

4.4 Caveats

This work has demonstrated the potential of source-based BCIs, but some practical concerns must be addressed. Source imaging requires that each subject undergo a structural MRI scan to build a source space model. This adds a separate scan session of approximately 20 minutes and scanner costs prior to the first BCI use, but only one MRI scan will typically ever be needed for an adult BCI user as the source space model can be reused. An electrode coregistration procedure is also necessary to create a coordinate transform between the EEG electrodes and the subject’s head model. Currently, the 3-dimensional mapping of each electrode adds several minutes to the cap setup, but there are groups actively developing accelerated coregistration techniques. This coregistration process is also likely to have some spatial error, but previous work has suggested that this has a minor impact on source localization (Larson, et al., 2014). Finally, an understanding of source imaging and associated software tools is necessary to generate the forward and inverse solutions. There already exists an active online community, however, where the tools (including all of those used in this work) are openly developed and shared with tutorials.

There are some limitations of the specific approach used here. This work focused on determining the feasibility of a source-based transfer learning for BCIs that spatially normalized head morphology across subjects. To have ground truth concerning the location and SNR of activity, the simulated data were comprised of single time point “snapshots” of cortical activity (in conjunction with actual head and brain models). This simplification allowed us to manipulate and evaluate spatial information in isolation but it did not explore temporal dynamics or functional variation across subjects. Past work has also detailed EEG nonstationarities arising from differences in mental strategy, fatigue, or attention (Krauledat, et al., 2007; Baillet, et al., 2001; Samek, et al., 2013; Lotte, et al., 2007) that were not considered in our simulation, but stationarity issues remain open questions throughout many areas of BCIs and neuroimaging (see Tsai, et al., 2014 for some early work on addressing this issue). Even so, these time averaging and non-stationary issues were present in the real (attentional) EEG data analyzed, and we still achieved classification results consistent with our simulation experiment despite these concerns. We also took transferred data to the sensor space before classification for computational simplicity, but previous research has demonstrated that classification directly in source space is possible (Besserve, et al., 2011; Qin, et al., 2004; Cincotti, et al., 2008).

5. Conclusions

In this work, we developed and evaluated a method to train a BCI classifier exclusively with data transferred from other subjects through the source space. Within transfer learning, utilizing the source space obviates many assumptions made in sensor space regarding both head morphology and electrode positioning and provides the opportunity to more easily incorporate neuroscience priors. Using this approach, we obtained higher average (single-trial) classification accuracy than a traditional approach for both simulated and real EEG data even in cortical regions not classically used in BCIs. Future work will focus on applying this source-based transfer learning methodology in a real-time paradigm and further exploring the benefits conferred by source imaging in BCIs.