Regulation of Blood Glucose Concentration in Type 1 Diabetics Using Single Order Sliding Mode Control Combined with Fuzzy On-line Tunable Gain, a Simulation Study

Abstract

Diabetes is considered as a global affecting disease with an increasing contribution to both mortality rate and cost damage in the society. Therefore, tight control of blood glucose levels has gained significant attention over the decades. This paper proposes a method for blood glucose level regulation in type 1 diabetics. The control strategy is based on combining the fuzzy logic theory and single order sliding mode control (SOSMC) to improve the properties of sliding mode control method and to alleviate its drawbacks. The aim of the proposed controller that is called SOSMC combined with fuzzy on-line tunable gain is to tune the gain of the controller adaptively. This merit causes a less amount of control effort, which is the rate of insulin delivered to the patient body. As a result, this method can decline the risk of hypoglycemia, a lethal phenomenon in regulating blood glucose level in diabetics caused by a low blood glucose level. Moreover, it attenuates the chattering observed in SOSMC significantly. It is worth noting that in this approach, a mathematical model called minimal model is applied instead of the intravenously infused insulin–blood glucose dynamics. The simulation results demonstrate a good performance of the proposed controller in meal disturbance rejection and robustness against parameter changes. In addition, this method is compared to fuzzy high-order sliding mode control (FHOSMC) and the superiority of the new method compared to FHOSMC is shown in the results.

INTRODUCTION

Diabetes is known to be an incurable and a lifetime disease. Moreover, it is responsible for significant mortality and charge in society. Furthermore, the number of diabetics is expected to highly increase in future. For this reason, tight glucose control in the diabetic patients is of great importance and has been the subject of extensive research over the years.[1]

Diabetes is a metabolic disorder classified into two main groups: type 1 and type 2 diabetes. Type 1 diabetes results from an autoimmune reaction that destroys the β-cells in the pancreas, preventing it to secrete enough insulin. However, in type 2 diabetes, the person develops a resistance to insulin. Both cases result in high blood glucose concentration levels. In a specific case, postprandial or after-meal hyperglycemia is a blood glucose level higher than 180 mg/dl 2 h after meal.[2] Chronically high blood glucose leads into some chronic complications, including cardiovascular diseases, kidney failure, blindness, stroke, and nontraumatic limb amputation.[3,4] On the contrary, hypoglycemia, blood glucose levels lower than 60 mg/dl, can cause loss of consciousness and coma. This phenomenon can be lethal.[4,5]

Due to the aforementioned complications, the maintenance of blood glucose levels at normal glucose concentrations or euglycemia (70–120 mg/dl) before meals and less than 180 mg/dl after meals is of crucial importance for diabetic individuals.[6] Over the last four decades, various controllers have been designed for insulin delivery in order to regulate the blood glucose level. Some of these controllers are simple like proportional-integral-derivatives controller[7,8,9,10] and fuzzy logic based controller.[11,12] However, others are more complicated such as feedforward-feedback controller,[4] H_∞ controller,[13,14,15] discrete linear model predictive controller,[16] nonlinear robust model predictive control (MPC),[17] generalized predictive controller,[18] gain-scheduling MPC,[19] multi-parametric MPC,[20] fuzzy high-order sliding mode control (FHOSMC),[21] and fuzzy scheduled robustness, tracking, disturbance rejection, and overall aggressiveness controller.[22] Some of these controllers are open-loop such as fuzzy logic controller. Open-loop programs deliver a predetermined amount of insulin to the patient. In fact, the amount of insulin is based on the insulin curve of pancreas secretion of a normal individual. Schematic of an open-loop control is shown in Figure 1a. The other controllers are closed-loop. In other words, they are designed based on a criterion which is in proportional to the error signal, the difference between the desired glucose level and actual one. A schematic of the closed-loop structure for controlling the blood glucose level in diabetic individuals is demonstrated in Figure 1b.[23]

Figure 1.

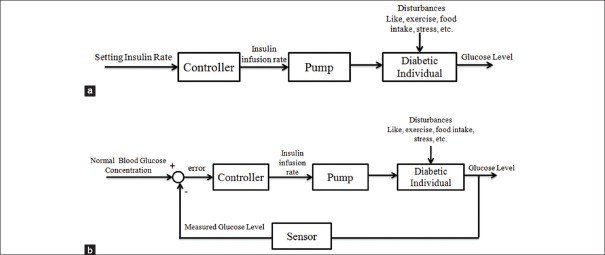
(a) Open-loop controller for a diabetic individual, (b) closed-loop controller for a diabetic individual[23]

However, each of these approaches has been able to partially tackle some challenges of regulating the blood glucose levels. These challenges include the existence of nonlinearities, noise, and inaccurate measurements, the existence of various sources of disturbance, and uncertainty affecting glucose regulation (e.g., stress, meal, and exercise).[24] Nonetheless, these obstacles are not completely solved and moreover, there are some other limitations, too. For example, although the exact parameter values of patients are required in model-based controllers, the glucose–insulin regulation system is nonlinear and time variable. Meanwhile, identification of the parameters of patients is expensive and invasive and most parameters are time variable, leading to uncertainty presence.[25] However, Hernaxndez et al.,[25] and Kaveh and Shtessel,[26] have utilized the properties of single order sliding mode control (SOSMC) and High order sliding mode control such as their nonlinearity and their independence on the parameters of model, to overcome the limitations of model-based controllers. Moreover, these approaches have significantly reduced the chattering phenomenon, which is the inherent part of the sliding mode controller. Nevertheless, not only these new approaches have not still solved the drawbacks of previous ones completely, but also have still suffered from hypoglycemia and hyperglycemia. Therefore, being more acute, hypoglycemia must be prevented by aggressive management of insulin delivery.

As it was mentioned, some controllers are based on a model of the diabetic patient. In other words, these kinds of controllers are model-based and for their designing, a model of insulin regulatory system for diabetic patient is required. A wide variety of mathematical models are developed for this goal such as minimal model,[27] Cobelli and Mari model,[28] Sorensen model,[29] Hovorka et al. model,[17] and Dalla Man et al. model.[30] A review of some of these models can be found in.[31,32] The three latter ones are more comprehensive than minimal model and even they have been used as virtual patients for testing the controller performance in some literatures. However, they are so complicated in terms of designing a controller. Therefore, there is a trade-off between the simplicity of the model for designing a controller and the accuracy of that. Nevertheless, as it can be noticed in[25] although the minimal model is far simple than the comprehensive ones, the amount of accordance of this model to other models are acceptable to a large extent. Moreover, it satisfies certain validation criteria while having the smallest number of parameters.[25] As a result, in this paper, the controller design is based on the minimal model.

In this paper, by employing the merits of fuzzy logic concept combined with SOSMC, a novel approach is proposed, called SOSMC combined with fuzzy on-line tunable gain (SOSMC-FOLTG). By applying this controller the insulin delivery rate and consequently, the amount of insulin delivered to type 1 diabetic individual is managed more aggressively. In other words, due to the decrease in the amount of insulin delivered at the time of entering the meal disturbance, this method leads to less possibility for hypoglycemia. Therefore, as it will be shown in the result section, it needs a much less control effort and as a result, prevents hypoglycemia much better than the previous methods. Besides, it also uses the distinguished properties of SOSMC such as its robustness versus model mismatches and disturbances and uncertainties in order to overcome inaccurate model parameters of patients and undefined dynamics. Moreover, this method will decrease the chattering observed in SOSMC significantly.

The remains of this paper are organized as follows. In background section, a background about designing the proposed controllers is given. It includes the minimal model for nondiabetics and diabetics and SOSM control concept. The procedure of SOSMC-FOLTG design is developed in desing procedure of the proposed controller section. Simulation results of an in silico trial with minimal model for three subjects are given in results and discussion section, followed by a conclusion.

BACKGROUND

In this part, some backgrounds needed for designing the proposed controller are presented. These requirements include the minimal model for nondiabetics and diabetics and SOSMC concept, which are discussed in the following subsections.

Bergman model

As mentioned before, in this paper, the controller design is based on the minimal model. This model is described as follows:[25]

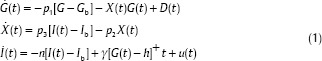
Where G(t), X(t) and I(t) are the glucose concentration in the blood plasma, insulin effect on glucose concentration disappearance, and insulin concentration in plasma, respectively. G_b indicates the nominal amount of glucose level and I_b is the basal preinjection level of insulin. u(t) is The control input, which shows the insulin infusion rate, p₁ is the insulin-independent glucose uptake rate, p₂ is the rate of reduction of the tissue glucose uptake ability, p₃ is the insulin dependent increase of the glucose uptake ability and n is the first order decay rate for insulin in blood. h is the threshold value of glucose above which the pancreatic cells release insulin. γ is the rate of insulin release of the pancreatic β-cells when glucose concentration is above the threshold. The “+” sign demonstrates the positive reflection to glucose intake and consequently the term γ[G(t)−h] t represents the pancreatic insulin secretion after a meal intake at t = 0 in a normal individual, but a diabetic patient who already is on insulin shots therapy does not have this natural control. Therefore, γ is considered zero for diabetics. Due to the fact that this paper is devoted to insulin therapy for type 1 diabetes mellitus patients, the parameters p₁ and γ are assumed to be zero in order to demonstrate the dynamic of this type of diabetes.[25,26]

Here D(t) represents the food intake as a disturbance. It has a decaying exponential form.[33] As it is said in,[34] G is in proportional to A×exp(−Bt), so the rate of G is in proportional to the derivative of this term. As a matter of fact, D(t) in Eq. 1 is the absolute amount of time derivative of A×exp(−Bt) according to the following form:

Where A, B > 0 and t is in (min) and D(t) is in (mg/dl/min).

Hence, with considering these points in mind and indicating G, X, and I as x₁, x₂, and x₃, Eq. 3 demonstrates minimal model for a type 1 diabetic person.

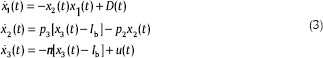
Single order sliding mode control concept

The SOSMC algorithm, as it is introduced in,[26] is used for systems with a relative degree of one. Inasmuch as the relative degree of minimal model is three, the sliding variable must be defined as following equation in order to obtain relative degree of one.

M = ë + c₁ė + c₀e      (4)

Where e = G_b − G(t) = G_b − x_1. Then, the SOSMC function can be designed as:[26]

u = –k|M|^0.5 sign(M)–β∫sign(M)dτ      (5)

DESING PROCEDURE OF THE PROPOSED CONTROLLER

Single order sliding mode control combined with fuzzy on-line tunable gain design

In recent years, fuzzy logic has been considerably used as a successful practical method in control systems with uncertainties. One fundamental feature of fuzzy logic is its ability to express human thinking.[35] On the other hand, because of the significant advantages of sliding mode control (SMC), this controller has gained more attention in recent years. Some of its merits are: Good robustness to parameter uncertainty, good transient performance, insensitivity to bounded disturbances, fast convergence rate, high control accuracy, a remarkable computational simplicity with respect to other robust control approaches, and easy implementation of the controller.[36,37,38] Therefore, due to the remarkable benefits of SMC and fuzzy control, many approaches have been developed to combine them, in some of which fuzzy logic theory is applied to adaptively tune the sliding mode gain of classical SMC. In this case, not only the robustness property of the sliding mode is maintained, but also the chattering is attenuated.[35]

In light of the advantages of combining the two methods of fuzzy logic and SMC, the proposed controller is designed from merging the SOSMC and fuzzy logic, in this paper. In other word, although SOSM controller reduces the amount of chattering significantly, in this method some chattering is still observed. Moreover, one drawback of SOSMC is its fixed coefficient, k, which causes a high insulin infusion rate even when it is not necessary, leading to a high risk of hypoglycemia. As a result, it is beneficial to reduce the amount of it by using fuzzy concept. In other words, fuzzy control is used to adaptively change the gain of SOSMC algorithm, which is denoted as k in Eq. 5. It can change in the range from 5 to 50 adaptively. By doing so, the control effort, and therefore the risk of hypoglycemia, will decrease. Moreover, the chattering observed in the control effort of SOSMC will significantly decrease. The scheme of SOSMC-FOLTG is shown in Figure 2a.

Figure 2.

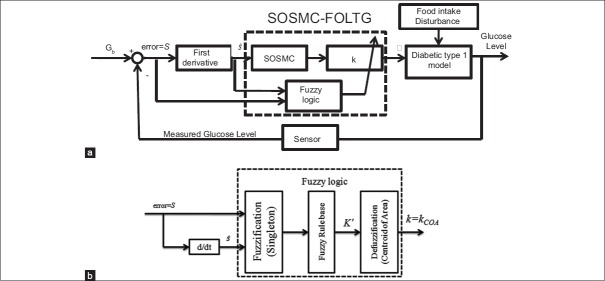
(a) Scheme of single order sliding mode control combined with fuzzy on-line tunable gain. (b) The structure of the fuzzy logic part used in (a)

To design the SOSMC-FOLTG, a fuzzy system consisting of two input linguistic variables, the error signal (S = e = G_b − G(t)) and its rate of change Ṡ=ė and one output, k (i.e., the gain of SOSMC), has been proposed in this paper. The structure of the fuzzy logic part in Figure 2a is shown in Figure 2b. As shown in Figure 2b, Singleton is used as the method of fuzzifier and centroid of area is used for defuzzifier. The fuzzy subset of k is denoted by K_S. Therefore, the fuzzy subsets of inputs and output are as follows:

S = {VVN, VN, N, M, SP}      (6)

Ṡ = {VN, N, Z, P}      (7)

K_s = {VS, S, M, B, VB}      (8)

Where the linguistic abbreviations are defined as VVN: Very very negative, VN: Very negative, N: Negative, M: Medium, SP: Small positive, Z: Zero, P: Positive, VS: Very small, B: Big, VB: Very big. By using these fuzzy sets, 20 fuzzy rules are defined. The rule base of the system with respect to Mamdani fuzzy model has been determined in Table 1. Figure 3 demonstrates the membership functions of the inputs and the output and the fuzzy surface.

Table 1.

Fuzzy rule bases (the output is the MF for the gain of SOSMC (K_S))

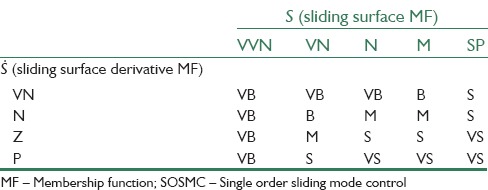
Figure 3.

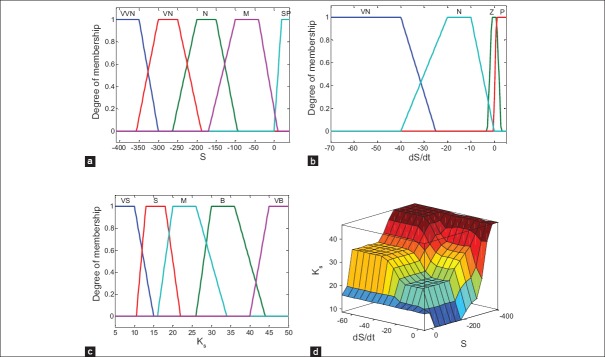
(a and b) The membership functions of the inputs (i.e., S,Ṡ), (c) the membership function of the output (i.e., K_S), (d) fuzzy surface

In order to elaborate on the procedure of selecting the kinds of fuzzy membership functions, and shapes of input and output subsets, the basic principle of that is presented as follows. First, through some simulations obtained from different kinds of membership functions such as sigmoid, triangle, and trapezoid, trapezoid was concluded to be more favorable. Therefore, trapezoid was utilized as the shapes of membership functions. Furthermore, input and output subset shapes were chosen in such a way that the amount of insulin delivered to the patient could reduce the error (S) effectively. For example, if the glucose level is above G_b level, which means a negative S, and if the procedure of the change in glucose level has a negative slope, which means a positive Ṡ a large amount of insulin should be delivered. However, in such a case, the amount of insulin delivered is less than that when S is negative and Ṡ is negative. In fact, in the second case, the error is increasing during time and thus, more insulin is needed to return the blood glucose level at the desired level. Moreover, if the error is very negative, it means that blood glucose level is much further from the desired level, and subsequently a much larger dose of insulin should be delivered to the patient compared to the case when the error is negative. Nonetheless, when the S is positive, it means that the level of blood glucose is lower than the desired level. Therefore, for avoiding the blood glucose levels to enter in the hypoglycemia region, a very small dose of insulin should be delivered.

The fuzzy output of the adaptive fuzzy system can be calculated by beneath equation:

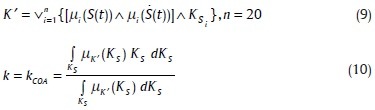
Where µ_i(S(t)), µ_i(Ṡ(t)) are the membership functions of the fuzzy input subsets. The number of each rule is i and the operators ∧,∨ denote the minimum and maximum, respectively. The K_Si denotes the fuzzy subset of output in rule number i. n denotes the number of rules.

RESULTS AND DISCUSSION

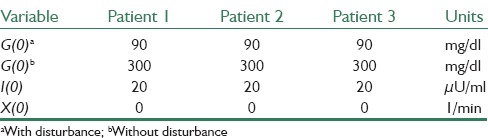
In this section, simulations are presented and discussed. For simulation goals, the minimal model is adopted with the three sets of numerical values, which presented in.[1] These parameter values are used as in silico patients to prove the robustness of new controllers. These parameters are presented in Table 2. In SOSMC, the parameter values are c₀ = 0.0001, c₁ = 0.02, k = 50 and β = 0.025 in Eq. 5 and finally k is adaptive for SOSMC-FOLTG and β is the same as that in SOSMC. The first initial values for parameters in Eq. 1 are presented in Table 3.

Table 2.

The parameter values of Bergman model for three patients

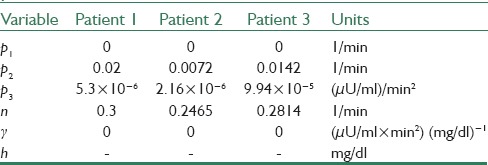
Table 3.

The initial state values used in simulations

The simulations are applied for analyzing two different situations: Analyzing the performance of the controller,

• When hyperglycemia occurs and a severe initial condition of glucose concentration average of G (t = 0) = 300 mg/dl is assumed

• When initial glucose is 90 mg/dl along with several meal ingestion events as disturbances.

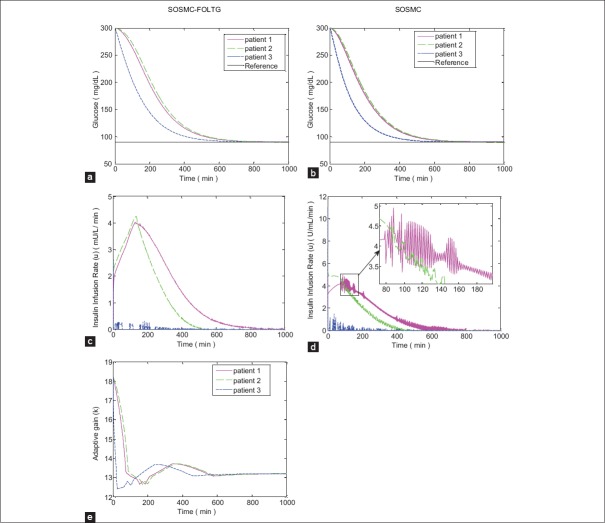
For the second situation three meal intakes, including A = 50, A = 70, and A = 80 for breakfast, lunch, and dinner, respectively, are considered. These disturbances enter the system at the time of 100, 460, and 880 min, respectively. Matlab/simulink is used for the simulation. The proposed controller is applied to the nonlinear model of minimal model. The simulation results from this part are illustrated in Figures 4 and 5. It is a critical point to notice that the scales of some figures of the same type, especially the figures for insulin infusion rate are not the same in order to show a better resolution of them.

Figure 4.

Simulation results with no external disturbances when hyperglycemia exists; (a and b) Blood glucose concentration; (c and d) insulin infusion rate, (e) changing procedure of adaptive gain of single order sliding mode control combined with fuzzy on-line tunable gain, that is, k

Figure 5.

Simulation results with three meal intake disturbances; (a and b) Blood glucose concentration; (c and d) Insulin infusion rate; (e) Changing procedure of adaptive gain of single order sliding mode control combined with fuzzy on-line tunable gain, that is, k

As can be seen in Figures 4 and 5 the new controller, SOSMC-FOLTG is compared with the conventional SOSMC. The glucose profiles in these two methods [Figures 4a and b, 5a, and b] are partly like each other. However, in SOSMC-FOLTG the chattering of the control effort observed in SOSMC is significantly reduced [Figures 4c and 5c]. The maximum amount of control effort has decreased considerably, as well.

It is worth mentioning that in (fuzzy) SOSMC the relative degree of sliding surface is one as the modified sliding surface in[26] has been used here. Therefore, in this case, just S and Ṡ are needed to converge to zero over time. These features have been tested and obtained through simulation, as well.

The changing procedure of adaptive gain in SOSMC-FOLTG, that is, k, versus time for two different cases without any disturbances and with tree meal disturbances, are shown in Figures 4e and 5e.

As what has been said in,[26] the SOSMC Eq. 5 guarantees finite time convergence of the sliding variable Eq. 4. Since sliding surface is a Herwitz polynomial in terms of the error signal, it provides the asymptotic convergence of the tracking error. Therefore, because fuzzy part only adjust the adaptive gain in Eq. 5 and has no other influences on SOSMC method, the blood glucose will be stabilized at its basal level asymptotically.

Moreover, for the evaluation of the new method, it is compared to FHOSMC, which can be found in.[21] For comparison between these two methods, some criteria are considered for three patients including, the reaching time of blood glucose level to 180 mg/dl (min), the steady state error for blood glucose concentration (mg/dl), the maximum of insulin infusion rate (μU/ml/min). Then, in two different cases (with hyperglycemia and with three meal intake disturbances) the averages of these criteria for three patients are calculated and the results are reported in Tables 4 and 5 as mean ± standard deviation.

Table 4.

The comparison of two controllers of SOSMC-FOLTG and FHOSMC based on several criteria when hyperglycemia exists

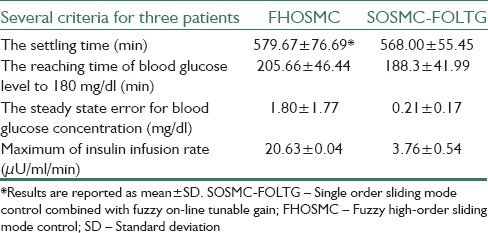
Table 5.

The comparison of two controllers of SOSMC-FOLTG and FHOSMC based on several criteria with three meal intake disturbances

In Figures 6 and 7 the simulations for FHOSMC are presented. By comparing the glucose profiles of FHOSMC and SOSMC-FOLTG, it is obvious that SOSMC-FOLTG can regulate the blood Glucose level faster. In fact, the settling time of SOSMC-FOLTG, when hyperglycemia exists, is 568.00 ± 55.45, but that of FHOSMC is 579.67 ± 76.69. The reaching time of blood glucose level to 180 mg/dl for SOSMC-FOLTG is 188.3 ± 41.99. However, this value for FHOSMC is 205.66 ± 46.44. In addition, the maximum amount of control effort in SOSMC-FOLTG, when hyperglycemia exists, is 3.76 ± 0.54, which is much less than that in fuzzy HOSMC (20.63 ± 0.04) leading to less risk of hypoglycemia. It is a very important factor because when the amount of insulin decreases, the risk of hypoglycemia will decrease. Actually, there is an inherent delay between the time of injecting insulin to the individuals and the time of affecting insulin on the blood glucose concentration. Furthermore, controlling of hypoglycemia is more important than that of hyperglycemia because hypoglycemia has acute and lethal dangers. Moreover, the steady state error in SOSMC-FOLTG is almost zero (0.21 ± 0.17 when hyperglycemia exists and 0.13 ± 0.12 in the presence of three meal intakes) whereas, it has a small quantity in FHOSMC (1.80 ± 1.77 when hyperglycemia exists and 1.96 ± 2.15 in the presence of three meal intakes). As it is shown the average of the reaching time of blood glucose level to 180 mg/dl (min), the steady state error for blood glucose concentration (mg/dl), and the maximum of insulin infusion rate (μU/ml/min) for SOSMC-FOLTG is more favorable than those for FHOSMC. This fact makes the new method superior to FHOSMC.

Figure 6.

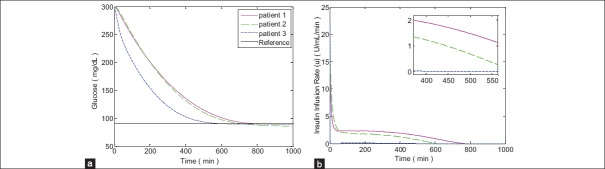
Simulation results with no external disturbances when hyperglycemia exists for fuzzy high-order sliding mode control (a) Blood glucose concentration, (b) Insulin infusion rate

Figure 7.

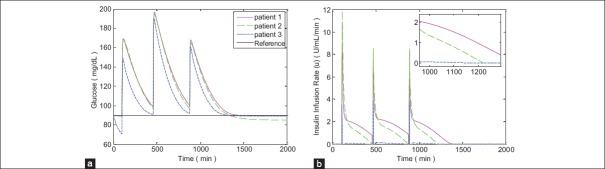
Simulation results with three meal intake disturbances for fuzzy high-order sliding-mode control; (a) Blood glucose concentration, (b) Insulin infusion rate

CONCLUSION

In this paper, a new algorithm, SOSMC-FOLTG, for a more effective regulating of the blood glucose level in type 1 diabetes has been presented. A SOSMC-FOLTG is proposed in order to control the insulin delivery rate more aggressively in a feedback controller. This method can stabilize the blood glucose concentration of a type 1 diabetic individual at the desired level. This stabilization has been done in the presence of three food intakes as external disturbances. The robustness of the algorithm has been confirmed through the parameters of three patients. This method is compared to SOSM and FHOSM controllers and the superiority of this approach has been shown in terms of alleviating the chattering phenomenon and reducing the control effort. Beside the advantages of SOSMC, which were mentioned before, the proposed SOSMC-FOLTG has some other merits, too. These merits are obtained through the fuzzy logic theory part in these proposed controller. For instance, this method has robustness versus uncertainties. It has been adaptively tuned the gain of control effort, as well as, it has alleviated the chattering phenomenon. Moreover, it has significantly decreased the amount of control effort and the risk of hypoglycemia as a result. It is worth noting that the proposed controller has preserved the robustness property of the SOSMC, as well.

BIOGRAPHIES

Soudabeh Taghian Dinani received both her B.Sc. and M.Sc. degrees in Electrical Engineering - Control from Isfahan University of Technology, Iran, in 2011 and 2014, respectively. Her research interests include adaptive control, nonlinear control, intelligent control, Neural Network, and biomedical engineering.

E-mail: s.taghian@ec.iut.ac.ir

Maryam Zekri (M’11) received the PhD degree in Electrical Engineering (Control) from Isfahan University of Technology, Iran, in 2008. She is currently is an associate professor in the Department of Electrical and Computer Engineering at Isfahan University of Technology. Her PHD thesis focused on Adaptive Fuzzy Wavelet Network Control Design for Nonlinear System. Her research interests are in the area of soft computing (Wavelet Network, Neural Network, Fuzzy Logic), Intelligent Control and Automatic Diagnosis of Disease.

E-mail: mzekri@cc.iut.ac.ir

Marzieh Kamali received a B.S. degree in Biomedical Engineering from Amirkabir University of Technology, Tehran, Iran in 2004. She received M.S. and Ph.D. degrees in Control Engineering from Isfahan University of Technology, Isfahan, Iran, in 2007 and 2012, respectively. She is currently an Assistant Professor at the department of electrical and computer engineering, Isfahan university of technology, Isfahan, Iran. Her research interests include: Adaptive control, Time Delay Systems and Fault tolerant control.

E-mail: m.kamali@cc.iut.ac.ir