Mechanics regulates ATP-stimulated collective calcium response in fibroblast cells

Abstract

Cells constantly sense their chemical and mechanical environments. We study the effect of mechanics on the ATP-induced collective calcium response of fibroblast cells in experiments that mimic various tissue environments. We find that closely packed two-dimensional cell cultures on a soft polyacrylamide gel (Young's modulus E = 690 Pa) contain more cells exhibiting calcium oscillations than cultures on a rigid substrate (E = 36 000 Pa). Calcium responses of cells on soft substrates show a slower decay of calcium level relative to those on rigid substrates. Actin enhancement and disruption experiments for the cell cultures allow us to conclude that actin filaments determine the collective Ca²⁺ oscillatory behaviour in the culture. Inhibition of gap junctions results in a decrease of the oscillation period and reduced correlation of calcium responses, which suggests additional complexity of signalling upon cell–cell contact. Moreover, the frequency of calcium oscillations is independent of the rigidity of the substrate but depends on ATP concentration. We compare our results with those from similar experiments on individual cells. Overall, our observations show that collective chemical signalling in cell cultures via calcium depends critically on the mechanical environment.

1. Introduction

Extracellular ATP plays important roles in cell proliferation, migration, differentiation, contraction and relaxation, wound healing, inflammation and cancer [1]. The process of chemosensing of ATP by fibroblast cells involves a multi-step cascade: ATP is detected by P2Y purinergic receptors on a cell membrane, followed by the release of second messenger molecules IP3 (inositol 1,4,5-triphosphate) from the membrane into the cytoplasm; IP3 is then involved in triggering the release of Ca²⁺ from the endoplasmic reticulum to the cytoplasm [2–4]. Following this initial excitation, cells are capable of exchanging information through gap junctions formed between physically contacting cells or through diffusing signalling molecules [5]. By enabling the exchange of information, gap junctions, which we found previously to be crucial in the early stages of collective chemosensing [6], regulate the cytoplasmic Ca²⁺ level [7].

Simultaneously, cells constantly respond to mechanical stresses imposed by their surroundings and sense the stiffness of the substrate on which they adhere. This property, called mechanosensitivity, has been observed experimentally for various cell types. Matrix rigidity influences cell spreading areas, the stability of adhesion complexes and stress fibres [8–11], motility [9,12,13] and proliferation rates [14,15]. More fundamental biological processes, such as the lineage specification of stem cells, control of cell growth and apoptosis, are also governed by the mechanical and geometrical properties of the cells and their environments [16–18]. To actively sense and respond to the mechanical signals from the environment, cells pull on their surrounding matrix [19]. This stress is generated by the actin–myosin cytoskeleton [20]; consequently, when myosin is inhibited by drugs such as blebbistatin, cell contraction is disrupted [21]. In addition, cell–substrate interaction is mediated by integrins, which mechanically link the interior of the cell to the binding sites in the extracellular matrix. Integrins can also activate chemical signalling pathways [7] that can lead to the Ca²⁺ release. However, high concentrations of calcium are also known to reduce the affinity of integrin–ligand binding, thus hindering cell–matrix adhesion [22,23].

Calcium oscillations have been observed in fibroblasts in response to various stimuli [24–26]. Additionally, a relationship between substrate mechanical sensing and Ca²⁺ oscillations has been studied, as presented non-comprehensively in table 1. In addition to its dependence on substrate stiffness, periodic Ca²⁺ oscillations have been seen to correlate with contractile events in fibroblasts and myofibroblasts [31]. The stresses generated by these contractile events are correlated directly to both cell spreading area and focal adhesion lengths [32,33]. These observations, along with the fact that Ca²⁺ is an important second messenger in transducing mechanical signals [34], suggest that the processes of chemosensing and mechanosensing in cells are coupled. While the studies indicated in table 1 provide quantitative dependence of Ca²⁺ oscillatory behaviour on the substrate stiffness for various cell types, they were performed mostly on single-cell systems with focus on spontaneous oscillations. Thus, quantification for agonist-induced Ca²⁺ oscillations in cell cultures, where emergent behaviour exists, remains unstudied and is the focus of this paper. We investigate this phenomenon for fibroblast cell cultures to understand how this coupling of chemo- and mechanosensing may play a role in a tissue where collective responses are crucial.

Table 1.

Summary of studies (non-comprehensive) of single-cell systems relating Ca²⁺ oscillations and substrate stiffness for various cell types. E denotes Young's modulus of the substrates.

study	experimental system	main findings
Godbout et al. [27]	rat subcutaneous myofibroblasts (SCMFs) on silicon substrates (E = 5–50 kPa)	spontaneous Ca2+ oscillation period increases with decreasing substrate stiffness, decreasing spreading area and decreasing adhesion size
Kim et al. [28]	human mesenchymal stem cells on polyacrylamide gel (E = 1–8.5 kPa)	spontaneous Ca2+ oscillation magnitudes, frequencies and RhoA activities decrease with decreasing substrate stiffness
Zhang et al. [29]	mouse hippocampal neurons on PDMS substrates (E = 46–457 kPa)	spontaneous Ca2+ oscillation amplitude, frequency and synaptic connectivity increase with increasing substrate stiffness
Franz et al. [30]	human mesenchymal stem cells on collagen gel (E = 0.3–1.1 kPa)	spontaneous Ca2+ oscillation frequency and level of osteogenic gene markers increases with increasing substrate stiffness, suggesting the importance of intercellular calcium in the mechanical signal transduction of the extracellular matrix to the human mesenchymal stem cell differentiation

In particular, we study the collective response of mouse fibroblast cells to ATP in various mechanical environments which mimic model tissues. In fibroblast cells, ATP has been found to stimulate cell growth [35]. ATP is present in concentrations of approximately 1 mM inside the cell and approximately 1 nM–1 μM outside the cell [36,37]. These intracellular and extracellular ATP levels are however dynamically regulated through releases and metabolism of ATP [38]. During signalling, nucleotides are released by a cell, leading to an increase in extracellular ATP concentrations. Therefore, we choose a range of extracellular ATP levels, which can disturb this equilibrium and thus induce signalling, of approximately 10 μM concentration.

We employ two different geometries for the cell cultures: a monolayer of cells cultured on top of a thin polyacrylamide (PA) gel, which we refer to as the two-dimensional configuration, and cells encapsulated in a gelatin-based hydrogel, which is a three-dimensional configuration. Our experimental system allows us to flow chemicals on top of the hydrogel or the cell monolayer with a flow rate that is controlled by a syringe pump. The elasticity of the PA gel and the hydrogel can be modified by changing the composition of each of its components. For our experiments, we pick a range of Young's moduli (E) between 85 and 36 000 Pa to mimic the elasticity of various soft tissue environments. The two-dimensional experiments are models of various epithelial and fibroblast cells in tissues [39], while the three-dimensional experiments are models of mucus that cover neuronal tissues, e.g. in the olfactory system [40,41]. These two systems have very different ranges of stiffness: Young's moduli of epithelial and fibroblast cells lie in the 100 Pa–100 kPa range [39,42], while moduli for mucus are in the 1–100 Pa range [43–45]. Inside the flow device, the collective response of fibroblast cells is monitored by measuring the level of cytosolic calcium in individual cells (as reflected by the level of fluorescence) during the exposure to ATP. The calcium dynamics of the cell cultures give us insight to how cells respond collectively to an external chemical when surrounded by substrates of different stiffness.

2. Material and methods

2.1. Cell culture and substrate preparation

NIH 3T3 mouse fibroblast cells (ATCC, Rockville, MD, USA) were cultured in Dulbecco's modified Eagle's medium (DMEM; ATCC) containing 1% penicillin (GIBCO, Grand Island, NY, USA) and 10% calf bovine serum (ATCC) and kept in an incubator at 37°C with 5% CO₂. The encapsulation of cells for our three-dimensional experiments was performed by suspending fibroblast cells in a biocompatible hydrogel (HyStem-C Hydrogel Kit; Advanced Biomatrix, San Diego, CA, USA), which comprised glycosil (thiol-modified hyaluronan), gelin (thiol-modified gelatin) and a thiol-reactive cross-linker, polyethylene glycol diacrylate (PEGDA). Cells were mixed with growth medium and the three hydrogel components in ratios specified in the electronic supplementary material, table S1. A small volume (approx. 45 μl) of this cell–hydrogel suspension was placed on a glass slide between two spacers, resulting in a hydrogel of thickness of approximately 450 µm, with the cells sedimented on the bottom due to being denser than the suspending liquid. In the final configuration, after the hydrogel cross-linked, the cells were located in a region that is approximately 20 µm away from the glass substrate. A poly(dimethylsiloxane) (PDMS; Sylgard 184, Dow Corning, Midland, MI, USA) cover was then placed on top of the gel solution, creating a channel between the gel and the PDMS for solvent flows, as shown in figure 1. Within 20 min, the hydrogel polymerized and fresh medium was delivered to the channel to keep the hydrogel from drying.

Figure 1.

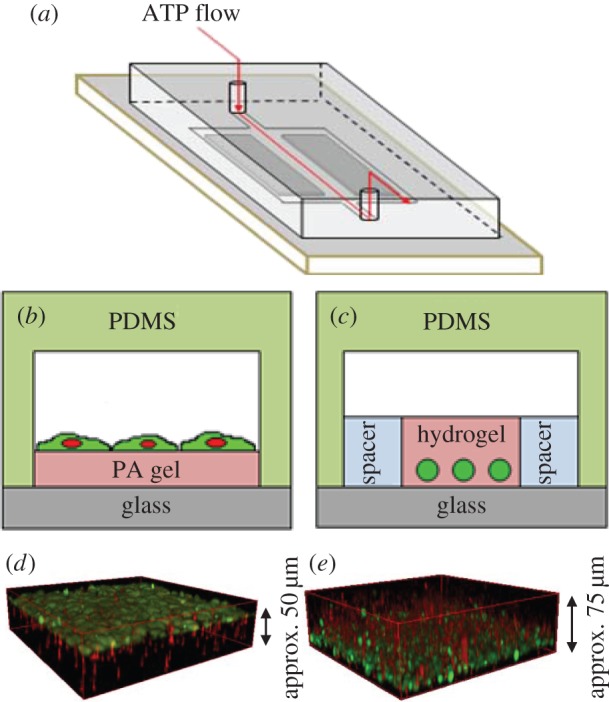
Experimental set-up used in chemosensing experiments with fibroblast cells. (a) Schematic of the flow device. (b,c) Cross-sectional view of two-dimensional and three-dimensional chemosensing experiments, respectively. In the two-dimensional set-up, cells (green) are cultured on top of polyacryamide (PA) gels with various values of Young's modulus and are directly in contact with ATP solution. In the three-dimensional set-up, cells are encapsulated in hydrogel with various values of Young's modulus. ATP flows on top and diffuses through the gel, exciting the cells located on the bottom. (d,e) Confocal z-stack three-dimensional reconstruction of fibroblast cells on top of PA gel (d) and inside the hydrogel (e). Red fluorescence represents the polystyrene beads embedded in the polyacrylamide gel or hydrogel, and green fluorescence represents the fibroblast cells. (Online version in colour.)

For the two-dimensional set-up, fibroblast cells were grown on a polyacrylamide (PA) gel (Bio-Rad, Hercules, CA, USA). Activated glass slides were prepared by soaking glass slides in 1% 3-aminopropyltrimethyoxysilane in deionized (DI) water for 10 min, followed by 10 min in DI water, 10 min in 0.5% glutaraldehyde in phosphate-buffered saline (PBS; ATCC) and finally 30 min in DI water. This treatment was performed to ensure binding of the PA gel to the glass surface. A small volume (approx. 5 µl) of PA solution mixtures of different ratios (electronic supplementary material, tables S2–S3) was placed on the activated glass slides, then covered with hydrophobic coverslips. This volume resulted in approximately 50 µm thick PA gels. After the PA gel polymerized (approx. 20 min at room temperature), the hydrophobic glass slide was peeled carefully. The cured PA gel was treated with fibronectin (Sigma-Aldrich, St Louis, MO, USA) overnight. A PDMS cover was then placed on top of the cured PA gel to create a channel. Cells were suspended in fresh growth medium in a desired concentration, flowed into the channel and then left to adhere on the PA substrate for 24 h. Prior to imaging, Fluo-4 calcium dye (Invitrogen, Carlsbad, CA, USA) was administered in growth medium and flowed into the device and left to incubate for 1 h.

2.2. Cell treatments for actin modification, gap junction inhibition and myosin inhibition

The actin fibres in fibroblast cells were modified using 1 µM jasplakinolide (Santa Cruz Biotechnology, Dallas, TX, USA), or 15 µM cyctochalasin-D (Sigma-Aldrich). Cells were incubated at 37°C with either treatment for 15 min prior to imaging.

Gap junction and myosin inhibitions were performed by treating cells with 50 µM palmitoleic acid (Sigma-Aldrich) and 50 µM blebbistatin (Sigma-Aldrich), respectively, in the incubator for 30 min prior to imaging.

2.3. Fabrication of the flow device

PDMS covers were made by pouring prepolymer of PDMS over a stainless steel template (Wet Jet Precision, Hildale, UT, USA). This set-up was then cured at 65°C for approximately 5 h following removal of air bubbles by vacuum. Once cured, covers were peeled off the template. The patterned side of the PDMS cover and the glass slide were plasma treated for 30 s, then brought into contact to form the flow chamber. This set-up created a flow chamber, dimensions 3 mm high × 5 mm wide × 50 mm long, in which ATP (Sigma-Aldrich) solution flowed. ATP flow was visualized by using a dye, sulforhodamine-B (MW = 558.66; Invitrogen), as a tracer.

2.4. Substrate elasticity measurements

Young's modulus of the hydrogel was determined by placing a steel bead (Bal-tec, Los Angeles, CA, USA) of a known weight on the gel and measuring the resulting substrate deformation [46]. Fluorescent beads were immersed in the substrate, and an xyz scan was performed using a confocal microscope to obtain the shape of the hydrogel displacement (electronic supplementary material, figure S1). From this displacement, the hydrogel's Young's modulus was calculated from

2.1

where R is the bead radius, a is the radius of the contact zone between the steel bead and the substrate, h is the thickness of the substrate, ρ is the bead density (7667 kg m⁻³), ρ_L is the gel density (1000 kg m⁻³), ν is the Poisson ratio, which equals 0.5 for gelatin [47], and E is the substrate's Young's modulus. Values of R, a and h were determined by fitting the deformed gel shape from the z-scan to a circle, as shown in the electronic supplementary material, figure S2. We measured the deformation and elasticity of hydrogels for the various compositions listed in the electronic supplementary material, table S1.

For PA gel, we used the recipes and the shear moduli values (G) given in Plotnikov et al. [48] and Yeung et al. [49], as summarized in the electronic supplementary material, tables S2–S3. Young's moduli values were then calculated as E = 2G (1 + ν), with ν = 0.487 for PA gel [50].

2.5. Fluorescence microscopy

Fluorescence was detected using a confocal microscope (Leica SP5; Leica Microsystems, Wetzlar, Germany). An argon laser at 488 nm was used to detect fluorescence from the calcium and a HeNe laser at 543 nm was used to detect sulforhodamine as an ATP tracer. A 20× oil immersion objective was used to visualize the samples. For each sample, a movie was taken at a single focal plane for 20 min at a rate of 1 frame s⁻¹. Image analysis and data processing were performed in Matlab (The MathWorks, Inc., Natick, MA, USA).

2.6. Immunofluorescence

Fibroblast cells were fixed in 4% paraformaldehyde (Electron Microscopy Sciences, Hatfield, PA, USA) in PBS for 20 min. Cells were then permeabilized in 1% Triton-X100 (Sigma-Aldrich) for 3 min and blocked in 5% normal goat serum, 1% Triton X-100 in PBS for 90 min at room temperature. For gap junction staining, immunofluorescense was performed using anti-connexin-43 antibody (Sigma-Aldrich) as the primary antibody and goat anti-rabbit IgG (H + L), Alexa Fluor^® 568 (Life Technologies, Grand Island, NY, USA) as the secondary antibody. F-actin was stained using rhodamine phalloidin (Life Technologies) and DNA was stained with DAPI (Life Technologies).

2.7. Quantifying single-cell response and oscillations

Each cell's fluorescent intensity I(t) was obtained by averaging the pixel colour values of 25 pixels around each cell's centre of mass as the cell fluoresced in response to ATP. The response curve R(t) was obtained by normalizing I(t) with a baseline intensity I_r that was obtained by averaging each cell's raw intensity over the first 60 s during flow of DMEM before the ATP solution arrived. Therefore, the response curve R(t) was calculated as R(t) = (I(t) − I_r)/I_r. A cell was referred to as responsive if, at any time, R(t) ≥ 0.5. To quantify the calcium oscillations, the response curve R(t) was first smoothed in Matlab (function: smooth( ), method: rloess) to remove high-frequency fluctuations. The oscillations were next detected in Matlab using the function peakfinder.m (available through Matlab File Exchange). This function found local peaks in the R(t) vector. Peaks were defined as local maxima with values greater than zero and above the surrounding data by 0.5. If a cell's response had two or more peaks, we referred to the cell as a responsive, oscillating cell (electronic supplementary material, figure S3).

3. Results

3.1. Polyacrylamide gel elasticity affects collective calcium response behaviour and oscillations in two-dimensional fibroblast cultures

We first examine the two-dimensional culture's calcium response after stimulation by ATP (electronic supplementary material, movies S1–S3). Figure 2a shows an example of a two-dimensional culture with various types of calcium responses. When a culture (i) is excited by ATP, a fraction of the cells exhibit calcium response (ii). Furthermore, a percentage of the initially responsive cells show further Ca²⁺ oscillations (iii). ATP is delivered inside the channel at a constant speed of 0.4 mm s⁻¹ (shear stress of approx. 0.15 mPa), which is controlled by a syringe pump. This low flow speed ensures no shear-induced calcium response, which typically occurs at approximately 2.5 Pa for fibroblasts [51].

Figure 2.

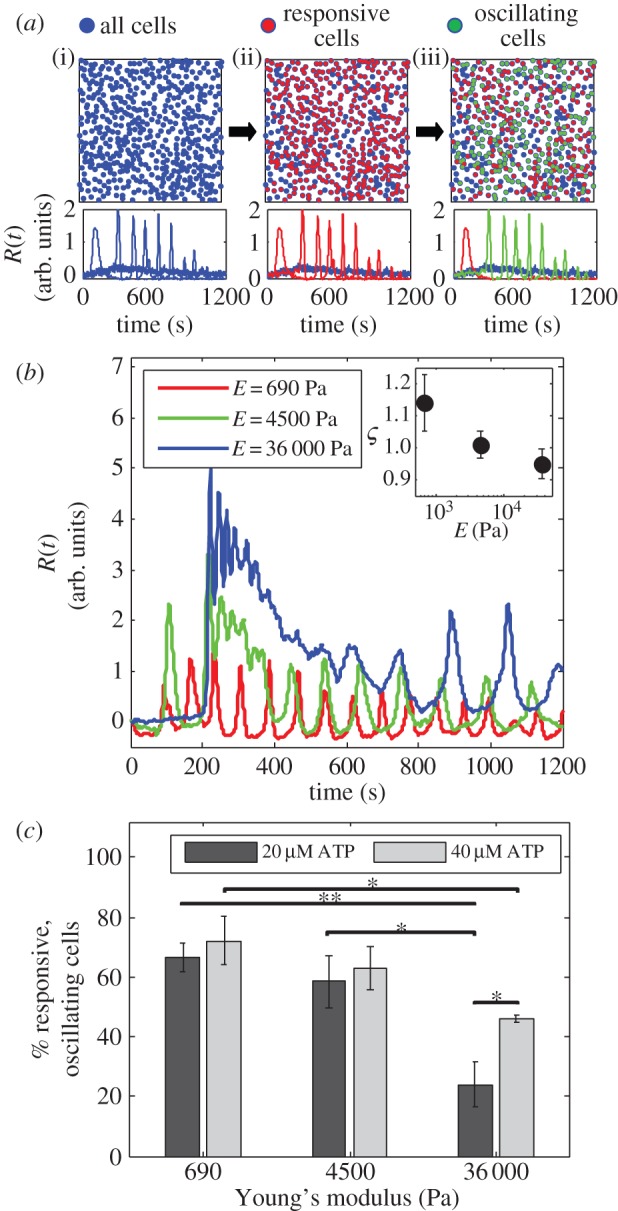
Response to ATP of fibroblast cells in a two-dimensional culture on PA gels. (a) When a fibroblast cell culture (i) is excited by ATP, only a fraction of cells respond (ii). Out of those that respond, a sub-fraction of cells oscillate (iii). (b) Typical calcium response curves for single cells on various PA substrates. Cells on a stiff substrate exhibit a strong initial response to ATP followed by decay in calcium intensity, while cells on a soft substrate show more persistent oscillations. Inset: average damping coefficient ς varies with substrate Young's modulus. A stiffer substrate produces a faster Ca²⁺ decay following ATP excitation. (c) The percentage of responsive, oscillating cells in a culture depends on the ATP concentration and the elasticity of the gel to which the cells adhere. Values are the average of three experiments and error bars are standard errors of the mean (*p ≤ 0.05, **p ≤ 0.01). (Online version in colour.)

In the range of PA gel elasticity that we investigate, 690 Pa ≤ E ≤ 36 000 Pa, various behaviours of chemical responses of individual cells are observed, as shown in figure 2b. We observe that a typical calcium response of cells adhering to a stiff PA gel (E = 36 000 Pa) consists of a high initial peak followed by decaying oscillations. Cells on softer gel (E = 690 Pa), on the other hand, show more persistent oscillations with slower decay over time. To quantify the decay of the signal, we define a damping coefficient ς for a response that has two or more peaks, by the ratio of one peak's magnitude to a preceding peak's magnitude. Note that ς > 1 is possible. We take an average of all ς values within a culture, compare this value for responses with three different substrates, and observe that this value decreases as gel stiffness increases (figure 2b, inset). This observation is consistent with our previous observations on a glass substrate (E = 10–100 GPa), where very few oscillations follow the initial calcium response [6].

When a dense cell culture (more than 1000 cells mm⁻²) responds to low concentrations of ATP (20–40 µM), we observe that the percentage of responsive, oscillating cells depends on both the concentration of ATP and the gel's Young's modulus. Cells cultured on softer substrates show higher percentages of oscillating cells than cells cultured on a stiff substrate (figure 2c). Despite these differences in behaviour, in our experiments with cultures of cells we find no dependence of the oscillation period on Young's modulus (electronic supplementary material, figure S4A), in contrast to what is reported by Godbout et al. [27] for spontaneous calcium oscillations in individual myofibroblasts. We interpret this difference in observations as an effect associated with the collective behaviour in our system, and the muscle-like contractile activity possessed by myofibroblasts that is not present in fibroblasts [52].

3.2. Collectivity alters the sensitivity of calcium oscillation behaviour to two-dimensional substrate stiffness

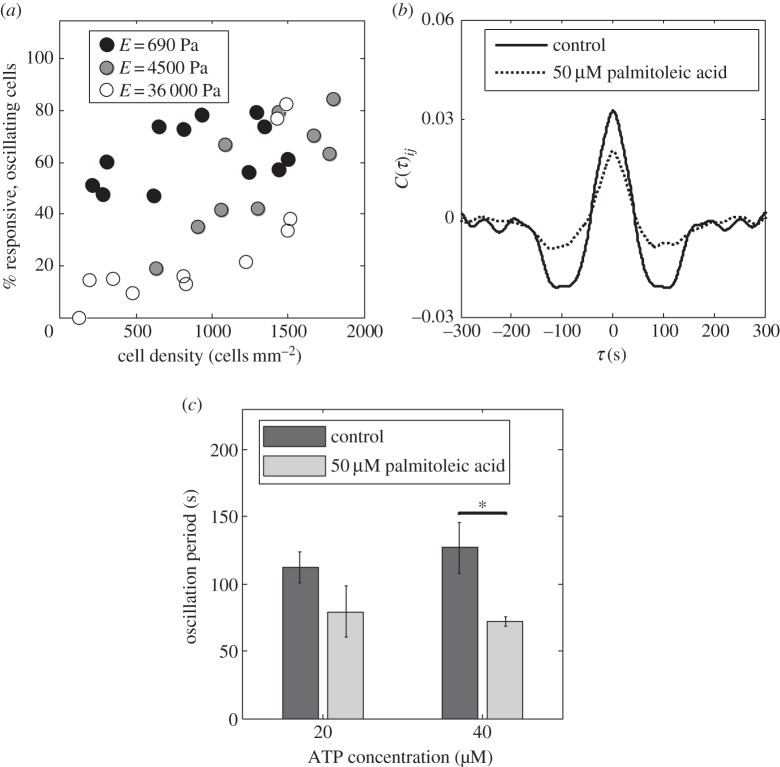
To further understand the mechanism of calcium oscillations, we consider the effect of gap junctions in cellular communication. Gap junctions were identified as crucial in preserving the spatial pattern of communication during the initial stages of collective chemosensing of fibroblast cells [6]. Here, we create cultures of varying density (100–2000 cells mm⁻²) on PA gel, and quantify the fraction of cells that exhibit oscillations. We observe that the fraction of responsive, oscillating cells in a culture is higher when the cells are located closer to each other for all values of Young's modulus (figure 3a). The effect of collectivity is however most pronounced at high elasticity (E = 36 000 Pa), where zero to 80% of the responsive cells can oscillate depending on the cell–cell distance. These responses are consistent with the role of gap junctions at cell–cell contacts.

Figure 3.

Effect of gap junctions on Ca²⁺ oscillations in cells on a two-dimensional PA gel. (a) Densely packed cultures have more cells showing Ca²⁺ oscillations, [ATP] = 20 µM. (b) Cross-correlation analysis for calcium response of fibroblast cells on PA gel (E = 4500 Pa) to 40 µM ATP; gap junction communication is correlated with a time scale of approximately 100 s, while this correlation is reduced when gap junctions are inhibited. (c) Gap junction inhibition by 50 µM palmitoleic acid results in Ca²⁺ oscillations with smaller period than those in communicating cells (E = 4500 Pa). Values are the average of three experiments and error bars are standard errors of the mean (*p ≤ 0.05).

Furthermore, to understand the interactions between cells when responding to ATP, we first calculate the rate of change of calcium intensity Ṙ(t) and then define the pair cross-correlation function C(τ)_ij for all pairs of nearest neighbours (i,j) in a cell culture:

3.1a

and

3.1b

where 〈dR_i(t)/dt〉 represents the time-averaged value, and σ_i is the variance of Ṙ_i(t). On intermediate stiffness gel (E = 4500 Pa), responses of high-density cell cultures (approx. 1500 cells mm⁻²) reveal synchronization events as indicated by the positive correlation peak at τ = 0, and the presence of a negative correlation peak at approximately 100 s, which corresponds to a communication time scale in the culture (figure 3b). Using this analysis, we investigate the role of gap junctions by treating the high-density cultures (approx. 1500 cells mm⁻²) with palmitoleic acid, a known gap junction inhibitor [53]. Addition of palmitoleic acid is expected to reduce the number of gap junctions (electronic supplementary material, figure S5). The response to ATP of a fibroblast culture with inhibited gap junctions is shown in the electronic supplementary material, movie S4. As shown in figure 3b, we find that cell cultures with fewer gap junctions still exhibit calcium oscillations and maintain similar correlations, however the peaks are less pronounced. These results demonstrate that gap junctions are crucial in maintaining regulated collective calcium dynamics in cell cultures.

The percentage of the responsive, oscillating cells in high-density cultures is unaffected by this treatment. However, cells that do not form gap junctions oscillate with a significantly smaller period (approx. 70 s) than those of gap-junctional communicating cells (more than 100 s; figure 3c).

3.3. Actin fibres affect calcium oscillation behaviour in two-dimensional substrates

It is known that a cell's cytoskeleton is affected by the substrate rigidity; in a softer environment, fewer, less organized actin stress fibres are formed [8,10,11,49]. This effect is a result of cell–substrate interactions, where cells use their actin–myosin cytoskeleton to generate stress on the matrix to actively sense and respond to the mechanical signals from the environment [19,20].

To test the effect of actin fibres on the cells' calcium response, we monitor the collective intercellular calcium dynamics in cell cultures, where the actin fibres are perturbed. First we use jasplakinolide, an actin polymerization inducer and stabilizer, the addition of which leads to more actin fibre formation in a cell [54,55]. Note that the times of treatment in our experiments are significantly shorter than the time scale on which formation of large actin aggregates caused by jasplakinolide treatment occurs [55], as shown by F-actin staining of our treated cell cultures (electronic supplementary material, figure S6). Second, we use cytochalasin-D, which depolymerizes actin filaments, resulting in a decrease in actin fibres [56]. In our experimental system, we observe that treatment with jasplakinolide results in a decrease in the percentage of responsive, oscillating cells in a culture (figure 4), while cytochalasin-D treatment results in an increase in the percentage of responsive, oscillating cells in a culture (figure 4b).

Figure 4.

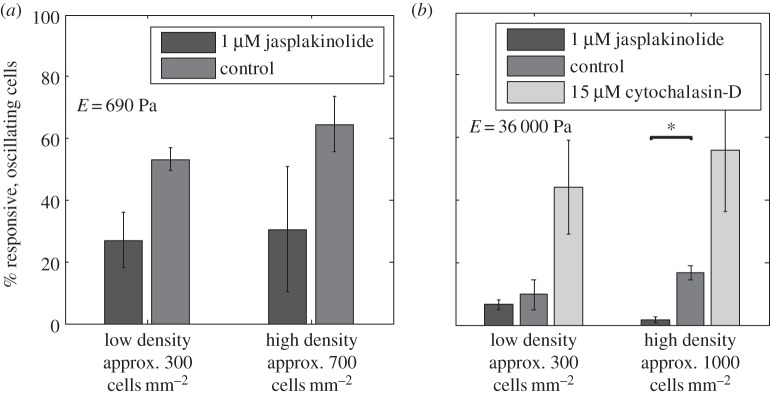
Effect of actin fibres on calcium responses in dilute and concentrated cell cultures, [ATP] = 20 µM. (a) Effect of 1 µM jasplakinolide (actin stabilizer) on cells' responses on soft gel (E = 690 Pa). (b) Effect of 15 µM cytochalasin-D (actin inhibitor) and 1 µM jasplakinolide on cells' responses on stiff gel (E = 36 000 Pa). Values are the average of three experiments and error bars are standard errors of the mean (*p ≤ 0.05).

An increase in the number of stable actin stress fibres caused by jasplakinolide can increase the pulling on the substrate, as if the cells are lying on a stiffer substrate. The opposite applies when cytochalasin-D is added; fewer actin fibres result in smaller stress generation, as if the cells are cultured on a softer substrate. The resulting decrease in the number of responsive, oscillating cells upon addition of jasplakinolide is consistent with our previous observation (figure 3a), where cells cultured on a stiffer substrate (E = 36 000 Pa) show less responsive, oscillating cells than those on a softer substrate (E = 690 Pa). Cytochalasin-D is known to reduce the Ca²⁺ response of individual fibroblast cells to ATP by changing the spatial relationship between phospholipase-C and IP3 receptors, thus impairing phospholipase-C-dependent calcium signalling [56]. In a culture with cellular communication, however, this effect is not necessarily seen (electronic supplementary material, figure S7). The differences in observations can be attributed to the collective effect in our system. The cells are excited by Ca²⁺ and other signalling molecules released by neighbouring cells, in addition to ATP; therefore, reduction of the initial Ca²⁺ response to ATP by cytochalasin-D does not imply a reduced collective response of the cell culture.

3.4. Hydrogel elasticity and cell contractility affect calcium response and oscillations in three-dimensional fibroblast cultures

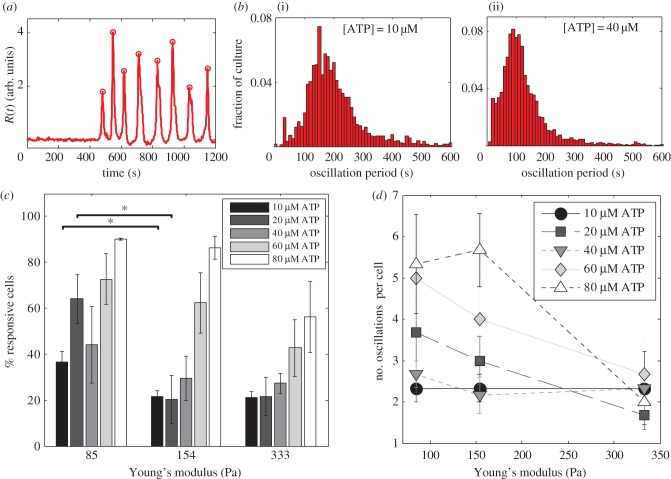
In a three-dimensional configuration, where the cells are embedded within a gel, ATP is delivered on top of the gel. The ATP then diffuses through the pore spaces to reach the cells located near the bottom due to density difference. The ATP profile at the plane of the cells is shown in the electronic supplementary material, figure S8. The total time scale of gelation and the experiment (less than 1 h) is less than the reported time for gap junction formation in fibroblasts, which is approximately 3 h [57]. Hence, we expect that signalling between cells is mainly diffusive. A typical response of fibroblast cells in the three-dimensional set-up is shown in the electronic supplementary material, movie S5, and figure 5a. We then calculate the percentage of responsive cells when encapsulated in hydrogel with different values of Young's modulus (figure 5c). More cells show calcium response when exposed to a higher concentration of ATP, which is expected as more ATP molecules can bind to available receptors on the cell membrane. In addition, for a given ATP concentration, we observe a higher fraction of cells showing calcium response when encapsulated in substrates with lower Young's modulus. Cell responses in soft three-dimensional configurations also show persistent calcium oscillations, which is consistent with our previous observations in the two-dimensional case with E = 690 Pa.

Figure 5.

Response to ATP of fibroblast cells encapsulated in a three-dimensional hydrogel matrix. (a) An example of a single-cell response to 40 µM ATP inside a hydrogel with E = 85 Pa. This response has seven oscillations (eight peaks) with a dominant period of approximately 120 s. (b) Distribution of oscillation periods for the response of fibroblast cells to 10 µM (i) and 40 µM (ii) ATP inside a hydrogel with E = 85 Pa. (c) Percentage of cells in a hydrogel-encapsulated culture that exhibit calcium response. (d) The number of oscillations for cells in a dense culture (more than 1500 cells mm⁻²) varies with the hydrogel's Young's modulus. Values are the average of three experiments and error bars are standard errors of the mean (*p ≤ 0.05). (Online version in colour.)

We further investigate calcium oscillations in our three-dimensional system by quantifying the number of response peaks during the oscillations and the oscillation period. In each culture, there is a distribution of oscillation periods, which varies with ATP concentration (figure 5b). We take the median of these distributions as the dominant oscillation period for a culture, and we observe that the oscillation period for fibroblast cells in a dense culture is independent of the substrate stiffness (electronic supplementary material, figure S4B). This oscillation period is however a function of the external ATP concentration.

When compared with our two-dimensional experiments, the oscillation periods in our three-dimensional case are up to approximately 40 s longer. We speculate that the slower oscillations are caused by the slow diffusion-limited signalling through the three-dimensional gel matrix, which is absent in the two-dimensional case.

Diffusion of both ATP and Ca²⁺ can happen in our three-dimensional cultures. During the delivery of ATP, ATP diffuses through the gel to reach the cells at the bottom of the gel layer. Following the initial release of Ca²⁺ to the cytoplasm in response to ATP, Ca²⁺ channels in cell membranes can open and close to allow transport of Ca²⁺ in and out of the cell, and this process can be triggered by various agonists [2,3]. Fibroblasts are also known to release ATP to the extracellular compartment upon physical perturbation, and this release is dependent on the level of external Ca²⁺ [58], which varies depending on the Ca²⁺ transport across the cell membrane. With ATP and Ca²⁺ present in the external medium and because the flow only occurs above the gel, diffusion of Ca²⁺ and ATP is a reasonable form of signalling among cells inside the three-dimensional gel. Using an approximate cell–cell distance (approx. 30–100 µm) obtained from our images and a typical diffusion coefficient of a small molecule in water (approx. 10⁻¹⁰ m² s⁻¹), we estimate the diffusion time scale to be approximately 10–100 s, which is consistent with the range of the time scales of oscillation periods that we see in our experiments (figure 5b). Therefore, we conclude that diffusion-limited signalling is a feasible mechanism of communication in three-dimensional cultures.

Although the oscillation period is unaffected, the number of oscillations in one cell's response varies with hydrogel elasticity. We observe that in stiffer gels (E = 333 Pa), out of the population of cells that oscillate, most cells only show one period of oscillations, while softer gels give rise to responses with larger numbers of oscillations, as shown in figure 5d. This trend is consistent for calcium responses throughout the range of ATP concentrations we study.

We also study the effect of cell–substrate interactions in our three-dimensional systems. Cell incubation with 50 µM blebbistatin, a myosin inhibitor, for 30 min reduces the percentage of responsive and responsive, oscillating cells in a culture (electronic supplementary material, figure S9). As cell viability is maintained upon addition of blebbistatin (electronic supplementary material, figures S10–S11 and tables S4–S5), this suggests that myosin-based contractility influences the cell's calcium dynamics.

4. Discussion

Mechanical and chemical sensing have been studied in various cell types; however, the link between the two remains unclear for cell cultures, where collective response exists. Chemically, ATP-induced calcium release in fibroblasts has been reported [35,59,60]. Mechanically, cells apply stress through stress fibres to sense the physical properties of their microenvironment. Such cell contractility is crucial due its involvement in many fundamental processes such as wound healing [61,62]. For fibroblasts in particular, exposure to high concentrations of ATP (more than or equal to 1 mM) is known to increase this contractile stress [63,64]. Motivated by these observations, we explore the phenomenology of the coupling between chemical and mechanical sensing by studying the calcium response of fibroblast cell cultures in various microenvironments, in particular how the cell–substrate interaction can affect the calcium dynamics.

As a cell's substrate is changed from soft to stiff, we observe that the calcium response approaches that of a cell on a glass, where a high initial reaction is followed by a decay with few oscillations [6]. In the case of a cell on stiff PA gel (E = 36 000 Pa), where the first response peak is high as shown in figure 2b, the cells need a longer time to adjust back to the baseline calcium level at which they can be excited again. On the contrary, cells on soft substrates, where initial responses are smaller, are able to reach the baseline intensity faster, allowing them to be re-excited more quickly. The difference in adjustment time results in fewer oscillations for cells on stiff substrates than on soft substrates. Our three-dimensional cell microenvironment behaves similarly; cells embedded on softer substrates (E = 85 Pa) show more calcium oscillations following the initial response peak.

Note that spontaneous hydrolysis of ATP can occur in the time scale of our experiment; the half-life of ATP is within minutes [38]. Calcium responses in individual fibroblasts due to other nucleotides have been reported, though some nucleotides are much more effective than others. For example, Homolya et al. [65] reported that, in wild-type fibroblasts, the rank order of potencies for nucleotide-induced intracellular Ca²⁺ increase was as follows: UTP ≥ ATP ≫ ADP > UDP. This hierarchy is confirmed in experiments with Swiss 3T6 cells, where extracellular ATP and UTP induce the release of calcium from intracellular stores in Swiss 3T6 cells; however, other nucleotides such as GTP, CTP, ADP and AMP do not produce the same effect [35]. Ferris et al. [4] also reported that the action of ATP is selective depending on its concentration: at 1–10 µM, ATP increases maximal IP3-induced Ca²⁺ flux by 50%, and this effect diminishes when the concentration of ATP is between 0.1 and 1 mM. On the other hand, ADP and AMP are less potent and GTP is incapable of producing this effect.

We performed new experiments where we excite our two-dimensional cell cultures on PA gel with ADP. At high density (approx. 1000 cells mm⁻²), we observe that the fractions of cell cultures that show Ca²⁺ response are similar for both nucleotides, i.e. ADP and ATP (electronic supplementary material, figure S12A). However at intermediate density (approx. 700 cells mm⁻²), we see a significant difference in the number of responses between the two nucleotides (electronic supplementary material, figure S12B). Our observation confirms previous findings regarding the smaller potency of ADP compared with ATP. In high-density cultures, we attribute the lack of difference between responses to the two nucleotides as the effect of collectivity; while not all cells are excited by ADP due to its smaller potency [35,65], the resulting Ca²⁺ response of a cell can cause Ca²⁺ response in other cells, thus resulting in a similar collective response of a cell culture to ATP. In conclusion, although both nucleotides do induce some response, our observations confirm that the responses that we report in our manuscript are indeed mostly due to ATP.

When a cell's environment is soft, a small number of actin stress fibres is formed [49], and adhesion sites are less pronounced. We interpret results from our two-dimensional cultures as cells cultured on a soft PA substrate form fewer actin fibres and therefore are not anchored as strongly to the substrate. A related observation in the literature is made in neutrophils, where actin dynamics are necessary to reset the sensitivity of receptors, thus enabling the neutrophils to respond repetitively to chemoattractants [66]. Similarly, we hypothesize that a softer PA gel or hydrogel influences the actin filaments' structure and dynamics, giving fibroblasts higher sensitivity to ATP, thus more oscillation peaks during a calcium response. This hypothesis is justified by our experiments with actin stabilizers and inhibitors. Upon cytochalasin-D treatment, cell cultures with reduced actin fibres generate smaller stresses like they do in soft substrates; therefore, we observed a higher fraction of responsive, oscillating cells in the culture. By contrast, jasplakinolide-treated cells with more stable actin fibres generate higher stresses, resulting in fewer oscillations.

Cell–cell interactions through gap junctions also influence a cell culture's oscillatory behaviour. The observed dependence of the number of responsive, oscillating cells on the cell density (figure 3a) suggests that oscillations are also a collective effect. The cell–cell distance dictates the fraction of a cell culture that exhibits calcium oscillations, where the dynamics is determined by gap-junctional communication between cells. Cells in three-dimensional cultures, where gap junctions do not form (electronic supplementary material, movie S5), also still exhibit calcium oscillations during response to ATP. This confirms that calcium oscillations can occur with and without this short-ranged type of interactions, resulting in calcium oscillations with different time scales. One generally accepted mechanism for Ca²⁺ oscillations in single cells is calcium-induced calcium release (CICR), which is probably responsible for the shorter oscillation period as shown in figure 3c. When cells are connected through gap junctions, IP3 and Ca²⁺ are transported from one cell to an adjacent cell, releasing Ca²⁺ from its storage to the cytoplasm. It is known that gap junctions can close upon elevated intracellular Ca²⁺ level [7]; however, we hypothesize that gap junction communication is not the only determining factor of the behaviour of the calcium oscillations. The coupling between gap junction dynamics, ATP-induced Ca²⁺ release and Ca²⁺-induced Ca²⁺ release can allow the oscillations to synchronize, thus giving rise to a larger time scale shown in the correlated response in figure 3b. Similar experiments were performed on rat hepatocytes where the cells were stimulated with noradrenaline and the calcium responses were measured. It was observed that gap junctions between the cells are required for coordination of the Ca²⁺ responses. However, in addition to gap junctions, Ca²⁺ signal propagation is also organized through the presence of the agonist and pacemaker-like cells [67]. The inhibition of gap junctions therefore does not eliminate Ca²⁺ responses and oscillations but reduces the correlation. The concurrent signalling events can result in two different oscillation frequencies during a single response: the higher frequency oscillations following the initial peak and the lower frequency oscillations later on in the response, as depicted in figure 2b. While most observations show that cells on a stiff substrate oscillate with higher frequency than on a soft substrate [27–30], we do not see such dependence in our cell cultures. We attribute this difference of observations to the effect of collectivity in our system where cell–cell interaction is present in addition to cell–substrate interaction.

For our three-dimensional system, we also report results on calcium responses of cells that are treated with blebbistatin, which is known to inhibit non-muscle myosin II in fibroblast cells but does not prevent cell spreading [68]. Our results indicate more than a 40% reduction in the number of responsive and oscillating cells (electronic supplementary material, figure S9) when fibroblasts are treated with 50 µM blebbistatin. Blebbistatin is known to prevent the formation of circumferential actin bundles, therefore disrupting the actin network coherence and causing cells to lose their ability to generate forces [68]. The mechanism behind this involves blebbistatin interfering with phosphate release by binding to the myosin–ADP–P_i complex [69]. As blebbistatin blocks myosin in an actin-detached state [68], we hypothesize that the mechanism of inhibition does not simply affect cell response the way soft substrates do, i.e. influencing the actin structure and dynamics to allow higher sensitivity to ATP. The inhibition probably has a more complex mechanism involving structural changes in the myosin, which affects cytoskeleton arrangement and cell contractility that is not completely understood yet. Disruption to the cytoskeleton can affect the chemical signalling pathways within the cells [20], one of which could be responsible for calcium responses and oscillations. Since all myosin IIs characterized follow a common basic enzymatic mechanism [70], the inhibition mechanisms of non-muscle myosin II such as those in fibroblast cells are expected to be similar.

In conclusion, we have demonstrated that collective chemical and mechanical sensing processes in fibroblast cells are coupled. Our observations lead us to conclude that the dynamics and arrangement of cytoskeleton and adhesion sites when adhering to environments of different stiffness is crucial in maintaining cell responsiveness, collective calcium response and oscillatory behaviour. The results presented highlight the importance of regulated agonist-induced calcium dynamics in cell cultures in diverse microenvironments that may be important in complex biological processes.

Authors' contributions

J.L., B. Sabass, B. Sun, M.E.R. and H.A.S. designed the research; J.L., B. Sabass, B. Sun performed the experiments; J.L., B. Sabass, B. Sun and H.A.S. analysed the data; and J.L., B. Sabass, B. Sun and H.A.S. wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

This work was partially supported by Firmenich SA, Corporate R&D, Geneva, Switzerland, through a research grant.