Abstract
Cancer dynamics are an evolutionary game between cellular phenotypes. A typical assumption in this modelling paradigm is that the probability of a given phenotypic strategy interacting with another depends exclusively on the abundance of those strategies without regard for local neighbourhood structure. We address this limitation by using the Ohtsuki–Nowak transform to introduce spatial structure to the go versus grow game. We show that spatial structure can promote the invasive (go) strategy. By considering the change in neighbourhood size at a static boundary—such as a blood vessel, organ capsule or basement membrane—we show an edge effect that allows a tumour without invasive phenotypes in the bulk to have a polyclonal boundary with invasive cells. We present an example of this promotion of invasive (epithelial–mesenchymal transition-positive) cells in a metastatic colony of prostate adenocarcinoma in bone marrow. Our results caution that pathologic analyses that do not distinguish between cells in the bulk and cells at a static edge of a tumour can underestimate the number of invasive cells. Although we concentrate on applications in mathematical oncology, we expect our approach to extend to other evolutionary game models where interaction neighbourhoods change at fixed system boundaries.
Keywords: evolutionary game theory, go-versus-grow game, spatial structure, heterogeneity, edge effect
1. Introduction
The importance of heterogeneity within tumours is gaining ground as one of the most important factors in the laboratory and clinic alike [1]. This heterogeneity exists at multiple scales, each of which presents its own unique set of challenges. One form of phenotypic heterogeneity that has been widely studied was first described by Giese et al. [2], when they showed that in gliomas migration and proliferation were mutually exclusive processes; motile cells are unable to proliferate while they are moving and proliferating cells are unable to move while they divide. This has been termed the go or grow dichotomy [3]. A proliferative or autonomous growth (grow) cell might switch to a motile or invasive (go) cell either through mutation, metabolic stress [4], undergoing the epithelial–mesenchymal transition (EMT) [5], or some other mechanism. EMT is generally characterized by the loss of cell–cell adhesion and a gain in motility and invasiveness in tumour cells and is often the first step in the metastatic cascade. The opposite, or mesenchymal–epithelial transition, occurs when the cells arrive at a distant site and shift their invasive phenotype to one of more aggressive clonal growth [6]. This combination of transitions is one of the hallmarks of several carcinomas such as prostate [7,8], breast [9] and other ductal cancers, where pre-invasive neoplasms are constrained by architectural boundaries (edges) such as the duct wall or basement membrane. Our goal in this work is to highlight the important and overlooked role of such edges in the evolutionary dynamics of the competition between go and grow cells.
Evolutionary game theory (EGT) is a mathematical approach to modelling frequency-dependent selection, where players interact strategically not by choosing from a set of strategies but instead by using a fixed strategy determined by their phenotype. Given the evolutionary nature of cancer [10,11], EGT has been applied to study how the interactions between different types of cells in a polyclonal tumour could drive the dynamics of a given cancer [12]. In its first application to oncology [13,14], EGT was used to analyse the circumstances that lead to coexistence of two phenotypes. Subsequent research [15] extended this idea to interactions between three players in the angiogenesis problem. Gatenby and Vincent adopted a game theory model heavily influenced by population dynamics to investigate the influence of the tumour–host interface in colorectal carcinogenesis [16,17] and suggested therapeutic strategies [18]. Our own work, as well as that of others, has shown that EGT can be used to study the conditions that select for more aggressive tumour phenotypes in gliomas [19,20], colorectal cancer [16,17], multiple myeloma [21] and prostate cancer [22]. Furthermore, EGT has been used to investigate the impact of treatment on cancer progression [23–25]. For an in depth overview of the game-theoretical approach to cancer, see Basanta & Deutsch [12].
In this study, we introduce spatial structure into the canonical ‘go versus grow’ game [26,27] in which proliferation and motility compete within a tumour. We use our direct spatial approximation to consider a familiar scenario for conservation biology: the edge effect of an ecological system (for example, a forest in landscape ecology) at a static boundary [28–30]. In tumour progression, this is analogous to a cancer cell surrounded entirely by other cancer cells as opposed to constrained by a physical boundary, such as a basement membrane, organ capsule, fibrous capsule, or blood vessel (figure 1). Note that we do not consider the unconstrained, dynamically growing edge of the tumour.
Figure 1.
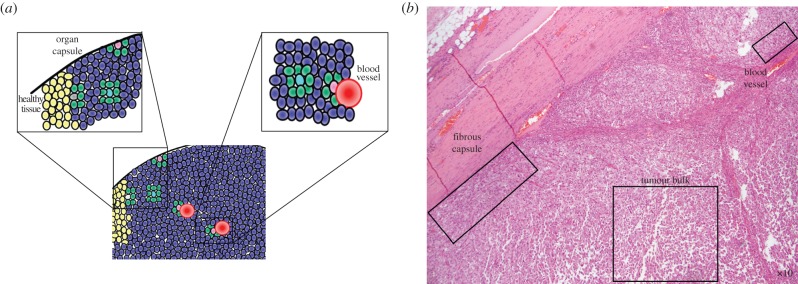
An idealized image of a hypothetical tumour (a), and a clinically produced micrograph of a sarcoma under low power stained with haematoxylin and eosin (b). A tumour cell (a: blue cells) has several different scenarios that affect the architecture of its neighbourhood geometry which we illustrate here. On short time scales, cells in a solid tumour experience largely static neighbourhood architectures; however, cells in the bulk of the tumour (a: turquoise; b: lower right box) have many more neighbours than cells against static boundaries (pink) like an organ capsule (a: left close-up), fibrous capsule (b: left box) or blood vessel (a: right close-up; b: upper right box). This change in relative number of neighbours affects evolutionary game dynamics. The boundary between the tumour and healthy cells (yellow), while of interest, is a dynamic edge and is not considered in this article. (Online version in colour.)
The static boundaries studied in this article are exciting in and of themselves, as the evolutionary dynamics that occur at static boundaries govern progression past key cancer stages: the change from in situ to invasive; locally contained to regional advanced growth; and the dramatic shift from local to metastatic disease. The former situation occurs early in the progression of most epithelial tumours, and it is commonly believed that it is at this point when the Warburg effect occurs, pushing cells towards the glycolytic (acid producing) phenotype which promotes invasion and motility—the so-called ‘acid-mediated invasion’ hypothesis [19,31–34]. The latter situation occurs when tumours are up against blood vessels and is likely the first opportunity for haematogenous dissemination, the first step in the metastatic process [35]. Here, we show a striking change in the evolutionary game dynamics from the tumour bulk to the tumour's physical boundary (figure 1). This study represents, to our knowledge, the first attempt to understand the effects of changing neighbourhood structure on evolutionary game dynamics of tumours.
2. Material and methods
2.1. Inviscid game for motility
To mathematically model the go or grow dichotomy [3], we considered the situation in which the tumour is made of a population of rapidly proliferating cells capable of autonomous growth (AG), along with a subpopulation which arises by a mutation or phenotypic change which confers motility/invasiveness (INV) to tumour cells. The game has two parameters: c represents the direct and indirect costs of motility incurred by cells with the INV phenotype resulting from the reduced proliferation rate of motile/invasive cells [3] and b is the maximum fitness a tumour cell will have under ideal circumstances when it does not have to share space or nutrients with other cells. As the units of measure are arbitrary, the ratio c/b can be considered alone to determine game-theoretic dynamics of the proportion of cell types. With INV as strategy 1 and AG as strategy 2, the game's payoff matrix is
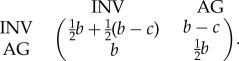 |
2.1 |
To understand the inviscid model [26], imagine two cells meeting at random in a resource spot; for an inviscid population this probability depends only on the cells' relative abundance but for the structured populations considered later, the probability of meeting again will be higher. If both cells are INV (motile), then one cell stays in the resource spot (i.e. a location that contains oxygen, glucose or other growth factors) and consumes the resources b, and the other pays a cost, c, to move and find a new empty site where it can then find resources, for a payoff b. If after a move a motile cell only finds a new empty spot with probability r, then the expected move payoff is rb − c. This can be captured as an indirect cost by adjusting the cost to be c′ = c + (1 − r)b without introducing an extra parameter. As the cell that has to move is chosen randomly from the two, the expected payoff for each cell is the average of the no-move (b) and move (b − c) payoffs. On the other hand, if an INV cell meets an AG cell then the INV cell will move, incurring the cost, c, before receiving the benefit, b, for a total fitness (b − c). The AG cell, however, will stay and consume all the resources (b). Finally, if two non-motile cells (AG) are in the same resource spot, then they simply share the resources, for a payoff of b/2.
Note that we are not explicitly modelling the mechanics of motility, but just their effects on cell fitness. Thus, our approach applies equally well to any other interaction with the same payoff structure. A more explicit account of the biomechanics of motility could inform the specific values of b and c, but the exact values of these parameters are not essential for our analysis and are beyond the scope of this study. We also expect the specific values of the payoffs to vary between tissues within a patient and across patients.
2.2. Direct approximation of spatial structure
A standard assumption in EGT is a perfectly mixed (inviscid) population, in which every cell in the population is equally likely to interact with every other cell [36]. This may be a reasonable assumption in some cases, but in most solid tumours (or any other situation being modelled) in which spatial structure is important, the validity of this assumption should be questioned [37]. The current solution to this is to map analytic EGT cancer models onto a lattice and run in silico experiments to simulate the resulting cellular automaton [26,38,39]. In such cases, the choices of the specific microdynamics to simulate are arbitrary and often left up to convention and the modeller's imagination, since direct empirical mechanisms at such a precise level are often unknown. Further, explicitly solving complex spatial structures is currently outside of existing mathematical tools, so computational approaches have to sacrifice the analytical power and full theoretical understanding of pure EGT approaches.
On occasion, computational modellers restore some analytical power by making mathematical approximations of the simulation that are already approximations of, or guesses at, the tumour's real spatial structure. To avoid this double approximation and to analytically model how spatial structure affects evolutionary games in the limit of large populations and weak selection, Ohtsuki & Nowak [40] derived a simple rule for taking a more direct first-order approximation of any spatial structure. This approach is based on the technique of pair-approximation [41–43] and is exact only for Bethe lattices (infinite trees of constant degree), but is highly accurate for any static structure where higher order terms, like the correlations between neighbours of neighbours, are negligible. For example, Ohtsuki and Nowak concentrated on the application of their tool to k-regular random graphs, which are locally tree-like and have negligible second-order and higher terms, but the transform can be used more broadly. While real spatially structured biological populations, such as solid tumours, can have non-negligible higher order interactions, Ohtsuki and Nowak's first-order approximation is an improvement over the common inviscid assumption that still allows us to explore a completely analytic model.
Given a game matrix A, one can compute the Ohtsuki–Nowak (ON) transform A′ = ONk(A) and then recover the dynamics of the spatially structured game A by simply looking at the inviscid replicator equation of A′. Here, we present the transform in a form that stresses its important qualitative aspects:
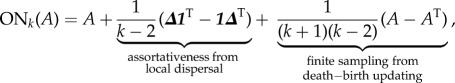 |
2.2 |
where 1 is the all ones vector and Δ is the diagonal of the game matrix A = [aij], i.e. Δi = aii; thus, Δ1T (1ΔT) is a matrix with diagonal elements repeated to fill each row (column). The first summand is the original payoff matrix. The second summand accounts for the more common same-strain interactions that are a consequence of local dispersal. The type of perturbation in the third summand was shown by Hilbe [44] to result from finite sampling of interaction partners. The summands are not arbitrary, and emerge as a whole from the pair-approximation technique. Our rationale for grouping the summands in this particular form is to help build intuition for equation (2.2). Effects of indirect interaction from more distant cells could be introduced as further corrections to equation (2.2), but would require more assumptions about the tumour microstructure [43]. Because local interactions between neighbouring cells are empirically well studied [45], the focus of the current study is incorporating only this first-order structure into an EGT model of cancer dynamics.
3. Results
Whenever b > c, the game in equation (2.1) is a social dilemma (like Prisoner's Dilemma or Hawk–Dove game; for a classification, see [46]) with invasive cells as the cooperators, and AG cells as defectors. Rules of thumb from EGT [47] suggest that cooperators benefit from the structure of small interaction neighbourhoods, in agreement with our biological intuition that, in this game, having the ability for conditional motion is of more use in a more constrained and viscous environment than in one where all cells are already stochastically moving around and interacting at random. We look at this formally by explicitly considering spatial effects on the previously inviscid model. Applying the transform from equation (2.2) to the game in equation (2.1) yields
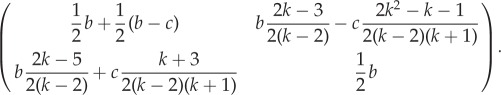 |
3.1 |
This game has three qualitatively different regimes that depend on the value of c/b and k:
(1) If (k + 1)/(k2 + 1) ≥ c/b, then there is a single stable fixed point with all cells invasive. All polyclonal tumours evolve towards this fixed point. For inviscid populations (k → ∞), this condition is satisfied only if motility is cost-free (c = 0) and hence the possibility of an all invasive tumour was not noted in previous non-spatial analysis [26].
- (2) If (k + 1)/(k2 + 1) < c/b < (k + 1)/(2k + 1), then the game has Hawk–Dove dynamics, and there is a stable polyclonal equilibrium with a proportion p of INV cells:
All polyclonal populations will converge towards this proportion of INV cells. In the unstructured limit as k → ∞, we have perfect agreement with our previous results [26] and recover the condition c/b ≤ 1/2 that was assumed for the inviscid equilibrium to exist and the exact numeric value of (b − 2c)/(b − c) for the equilibrium proportion of INV agents. For any finite k, however, the proportion of invasive cells is strictly higher.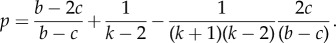
3.2 (3) If (k + 1)/(2k + 1) ≤ c/b, then the game has Prisoner's Dilemma dynamics and any polyclonal population converges towards all AG and the tumour remains non-invasive.
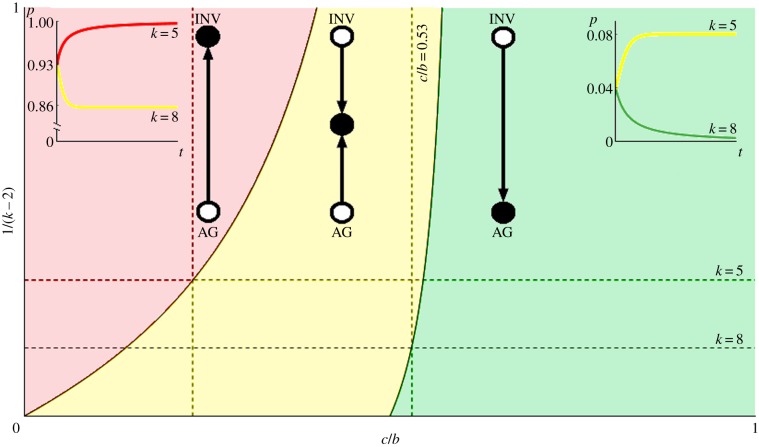
These three regimes are plotted in figure 2. When 1/(k − 2) = 0, we have the inviscid game and for 1/(k − 2) = 1 we have the most structured regime possible with small neighbourhoods (k = 3). The red region corresponds to a completely INV tumour, the yellow to a polyclonal tumour and the green to all AG. As we make the tumour more structured and reduce the number of neighbours, it becomes easier for the INV cells to be expressed in the tumour.
Figure 2.
Evolutionary game dynamics as a function of changing neighbourhood size and relative cost of motility. Here, we plot level of viscosity 1/(k − 2) versus relative cost of motility c/b. The parameter space is divided into three regions that correspond to qualitatively different dynamics. In the red, the population evolves towards all INV; in the yellow—towards a polyclonal tumour of INV and AG cells; and in the green the tumour remains all AG. When 1/(k − 2) = 0 (i.e. k → ∞) we recover the standard inviscid replicator dynamics of our previous work [26]. For 1/(k − 2) = 1 (k = 3, the top edge of the plot), we have the environment with the smallest local neighbourhood to which the ON transform applies. The first horizontal dotted line marks k = 5 (pink cell in figure 1) and the bottom line is k = 8 (teal cell in figure 1). The left vertical dotted line is at c/b = 0.23 and shows that it is possible to go from a polyclonal tumour in the bulk to a completely invasive population at a static edge. The right vertical dotted lines shows that is possible to see a qualitative shift from all AG to a polyclonal tumour in dynamics with the game fixed at c/b = 0.53 by decreasing k from 8 and 5 (increasing 1/(k − 2) from 1/6 to 1/3) at the tumour boundary. Example dynamics from a numerical solution of the replicator equation of the transformed game are shown in the insets, where proportion of INV (p) is plotted versus time (t). The equation specifying the dynamics is 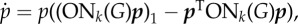 where pT = (p, 1 − p), G is the game in equation (2.1), and ONk is the transform from equation (2.2). The left inset corresponds to c/b = 0.23, an initial proportion of invasive agents of p0 = 0.93, k = 5 (tumour edge) for the red line and k = 8 (tumour bulk) for the yellow. The right inset corresponds to c/b = 0.53, an initial proportion of invasive agents of p0 = 0.04, k = 5 (tumour edge) for the yellow line, and k = 8 (tumour bulk) for the green. (Online version in colour.)
where pT = (p, 1 − p), G is the game in equation (2.1), and ONk is the transform from equation (2.2). The left inset corresponds to c/b = 0.23, an initial proportion of invasive agents of p0 = 0.93, k = 5 (tumour edge) for the red line and k = 8 (tumour bulk) for the yellow. The right inset corresponds to c/b = 0.53, an initial proportion of invasive agents of p0 = 0.04, k = 5 (tumour edge) for the yellow line, and k = 8 (tumour bulk) for the green. (Online version in colour.)
For example, consider the case where c/b = 0.53, and as in figure 1, in the tumour away from boundary (the turquoise cell) there are k = 8 neighbours and the dynamics favour all AG, so no INV cells will be present at equilibrium. For an example of replicator dynamics of this condition, see the green line of the right inset. If the solid tumour is pressed up against a static boundary then cells at the edge have fewer neighbours (e.g. k = 5, the pink cell) and the dynamics at the boundary favour a polyclonal population with about 8% of the cells INV. For an example of replicator dynamics for this condition, see the yellow line of the right inset. Note that the tumours represented by the green (k = 8) and yellow (k = 5) lines of the right inset have the same c/b = 0.53 and initial proportion of invasive cells p0 = 0.04 and yet the invasive phenotype is pushed to extinction in the tumour bulk (k = 8), but stabilizes near potentially dangerous level of invasive cells (p = 0.08) at the tumour edge (k = 5). Similar higher selection for invasiveness at the static edge is present for the more competitive environment of c/b = 0.23 in the left inset, but in this case we started the example replicator dynamics at p0 = 0.93. In this case, we have a polyclonal tumour bulk (k = 8) with p = 0.86 and convergence towards all invasive phenotypes at the static edge (k = 5). Of course, the specific parameter values above are for illustrative purposes. Actual change in k (just like c/b) will be experiment and geometry dependent—for example, we expect a more drastic decrease in k for a convex rather than a concave boundary.
The main message is that the edge effect can cause a polyclonal boundary in a tumour with a homogeneous all AG body. And while not yet shown to be universally applicable, this is in qualitative agreement with the experience of pathologists, such as the typical staining for motility (EMT) in figure 3, where we see the bone marrow space entirely invaded by carcinoma cells (pancytokeratin; figure 3a), but a stark difference in motile phenotype as illustrated by the nuclear staining by SLUG, which is only present in high concentration in cells against the static boundary of the bony trabecula. As with all interesting questions in biology, there can be many other causes involved in such specific experimental or clinical systems, and our result is focused on the idealized change in local architecture common to many of them. The effect to which we are drawing attention is different from and can occur in addition to other system-specific mechanisms or heterogeneity due to more traditional sources like gradients in metabolites and drugs.
Figure 3.
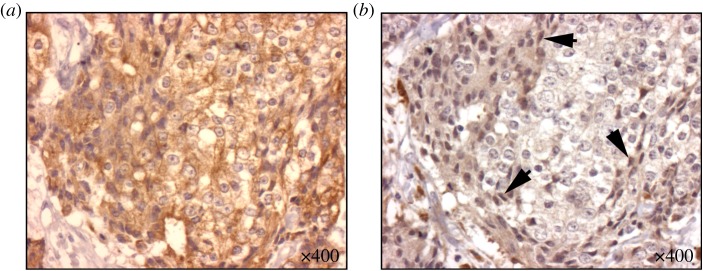
EMT is found to be upregulated near static boundaries within bone marrow in bony metastatic deposits of prostate cancer. In serial sections taken of bony metastatic deposits of prostatic adenocarcinoma at rapid autopsy, staining for SLUG is found to be increased near to the static boundaries created by the bony trabeculae. Nearly homogeneous pancytokeratin staining (a) reveals the ubiquity of metastatic carcinoma in this sample. In the next slice (b), stained for SLUG (a marker of EMT), we see increased uptake of the antibody in the carcinoma cells lining the static boundary, suggesting a more motile phenotype (highlighted by arrows) when compared with those in the neighbourhood representing the tumour bulk. (Online version in colour.)
4. Discussion
A standard assumption in EGT is that all players interact with all other players: the population is inviscid. There are a number of biological scenarios in which such an assumption could be misleading, and we consider such a scenario in the form of several key aspects of solid tumour progression. The role of spatial heterogeneity has been explored before in mathematical models studying evolutionary processes in cancer [48–50]. Those models show that different environments produce different selective pressures and that phenotypic heterogeneity results from, and drives, the spatial one. Our approach tackles a different question related to the nature of physical edges on cancer evolution for which we have applied the Ohtsuki–Nowak transform [40] to the standard go–grow game of mathematical oncology [26]. We have shown a quantitative effect: spatially structured tumours promote the invasive phenotype compared to inviscid tumours with the same ratio of cost of motility to benefit of resources c/b.
We also considered the decrease in neighbourhood size experienced by cells at the static boundary of a tumour, compared to cells within the tumour bulk. This could represent a number of feasible and very relevant scenarios, including a tumour against a blood vessel, organ capsule or fibrous capsule; or an in situ neoplasm at the basement membrane. We have shown that this change in neighbourhood for tumour cells can, independently from any other parameters, significantly affect the evolutionary stable strategies: in this case, a promotion of the INV phenotype. The edge effect allows a tumour that internally has no invasive phenotypes expressed to have a polyclonal boundary with both invasive and non-invasive cells, a scenario which is known to appear in several cancers, most notably prostate [51] in the form of peri-neural invasion, and the recently described perivascular invasion in melanoma [52] (previously called angiotropism). In each of these two scenarios, tumour cells express the motile phenotype, but only when against the physical structure in question. Another recent result suggesting the importance of effects of changes in local architecture is the work of Belmonte-Beitia et al. [53], in which the authors show that the dynamics of motility change drastically at the grey–white interface in glioblastoma in ways that cannot be predicted by simply comparing the behaviour in each zone individually.
The results of our mathematical model could have significant translational implications. Genetic heterogeneity has recently become recognized as the rule in cancer [54], but for as long as physicians have had microscopes, we have realized that spatial organizational heterogeneity was an equally defining factor. The Gleason score [55] is a classic example of greater heterogeneity predicting worse survival in prostate cancer. We have shown that a specific change in neighbourhood size at a static boundary can dramatically alter game dynamics, and select for novel phenotypes, and gives a rationale for working to understand within-tumour differences, not just at relatively long length scales [56], but also at architecturally different locations at short length scales, which can be done with the advent of single-cell technologies and laser capture microdissection [57].
We have shown that the local spatial structure of a tumour can strongly affect the evolutionary pressures on its constituent cells, even if all other factors are held constant. This can add yet another source of sampling bias to tissue biopsies and suggests that the architectural, not just the molecular, context is important. For instance, consider an idealized fine-needle aspiration biopsy [58], assuming the standard 0.7 mm needle samples a perfect column around 20 cells in diameter of tumour cells right next to a critical boundary such as a capillary. In our running example of c/b = 0.53 (figures 1 and 2), this would result in the sample containing only about 0.4% invasive cells since 19 out of every 20 cells are not at the boundary. This is below the detection levels of the state-of-the-art medical practice [59,60]. However, among the critical 1 out of every 20 cells at the boundary, a dangerous proportion of 8% would display the invasive phenotype. Thus, an oncologist performing a diagnostic fine-needle aspiration biopsy could be led to think that a tumour poses a low risk for invasion/metastasis, because the technique destroys the local structure of the tumour and mixes the cells at the critical tumour boundary with the (in this case) irrelevant tumour bulk.
Our model was motivated by the study of cancer, but the spatial edge effects in games of interacting players that we investigate could represent any number of other scenarios. While we have focused on the specifics of metastasis and cancer invasion, this method could yield insights into many other interesting problems ranging from ecology to medicine, and highlights the importance of neighbourhood geometry when studying the evolutionary dynamics of competing biological agents.
Acknowledgements
We would like to thank Colm Morrissey from the University of Washington and Marilyn Bui from the Moffitt Cancer Center for illustrative images used in this paper, and David Liao for extensive helpful feedback.
Authors' contributions
A.K., J.G.S. and D.B. designed the study, interpreted the results and wrote the manuscript. A.K. and J.G.S. carried out the mathematical modelling. All authors gave final approval for publication.
Competing interests
We declare we have no competing interests.
Funding
D.B. would like to acknowledge U01CA151924–01A1 for financial support. J.G.S. would like to thank the NIH for its generosity in providing a Loan Repayment Grant.
References
- 1.McGranahan N, Swanton C. 2015. Biological and therapeutic impact of intratumor heterogeneity in cancer evolution. Cancer Cell 27, 15–26. ( 10.1016/j.ccell.2014.12.001) [DOI] [PubMed] [Google Scholar]
- 2.Giese A, Bjerkvig R, Berens ME, Westphal M. 2003. Cost of migration: invasion of malignant gliomas and implications for treatment. J. Clin. Oncol. 21, 1624–1636. ( 10.1200/JCO.2003.05.063) [DOI] [PubMed] [Google Scholar]
- 3.Giese A, Loo MA, Tran N, Haskett D, Coons SW, Berens ME. 1996. Dichotomy of astrocytoma migration and proliferation. Int. J. Cancer 67, 275–282. () [DOI] [PubMed] [Google Scholar]
- 4.Godlewski J, et al. 2010. Microrna-451 regulates lkb1/ampk signaling and allows adaptation to metabolic stress in glioma cells. Mol. Cell 37, 620–632. ( 10.1016/j.molcel.2010.02.018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Polyak K, Weinberg RA. 2009. Transitions between epithelial and mesenchymal states: acquisition of malignant and stem cell traits. Nat. Rev. Cancer 9, 265–273. ( 10.1038/nrc2620) [DOI] [PubMed] [Google Scholar]
- 6.Chaffer CL, Weinberg RA. 2011. A perspective on cancer cell metastasis. Science 331, 1559–1564. ( 10.1126/science.1203543) [DOI] [PubMed] [Google Scholar]
- 7.Smith BN, Odero-Marah VA. 2012. The role of Snail in prostate cancer. Cell Adh. Migr. 6, 433–441. ( 10.4161/cam.21687) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Khan MI, Hamid A, Adhami VM, Lall RK, Mukhtar H. 2014. Role of epithelial mesenchymal transition in prostate tumorigenesis. Curr. Pharm. Des. 21, 1240–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Armstrong AJ, et al. 2011. Circulating tumor cells from patients with advanced prostate and breast cancer display both epithelial and mesenchymal markers. Mol. Cancer Res. 9, 997–1007. ( 10.1158/1541-7786.MCR-10-0490) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nowell PC. 1976. The clonal evolution of tumor cell populations. Science 194, 23–28. ( 10.1126/science.959840) [DOI] [PubMed] [Google Scholar]
- 11.Greaves M, Maley CC. 2012. Clonal evolution in cancer. Nature 481, 306–313. ( 10.1038/nature10762) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Basanta D, Deutsch A. 2008. A game theoretical perspective on the somatic evolution of cancer. In Selected topics on cancer modelling: genesis, evolution, inmune competition, therapy (eds Bellomo N, Chaplain M, De Angelis E.), pp. 1–16. Boston, MA: Birkhauser; ( 10.1007/978-0-8176-4713-1_5) [DOI] [Google Scholar]
- 13.Tomlinson IP. 1997. Game-theory models of interactions between tumour cells. Eur. J. Cancer 33, 1495–1500. ( 10.1016/S0959-8049(97)00170-6) [DOI] [PubMed] [Google Scholar]
- 14.Tomlinson IP, Bodmer WF. 1997. Modelling the consequences of interactions between tumour cells. Br. J. Cancer 75, 157–160. ( 10.1038/bjc.1997.26) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bach LA, Bentzen SM, Alsner J, Christiansen FB. 2001. An evolutionary-game model of tumour–cell interactions: possible relevance to gene therapy. Eur. J. Cancer 37, 2116–2120. ( 10.1016/S0959-8049(01)00246-5) [DOI] [PubMed] [Google Scholar]
- 16.Gatenby R, Vincent T. 2003. An evolutionary model of carcinogenesis. Cancer Res. 63, 6212–6220. [PubMed] [Google Scholar]
- 17.Gatenby R, Vincent T, Gillies R. 2005. Evolutionary dynamics in carcinogenesis. Math. Mod. Methods Appl. Sci. 15, 1619–1638. ( 10.1142/S0218202505000911) [DOI] [Google Scholar]
- 18.Gatenby R, Vincent T. 2007. Application of quantitative models from population biology and evolutionary game theory to tumor therapeutic strategies. Mol. Cancer Ther. 2, 919–927. [PubMed] [Google Scholar]
- 19.Basanta D, Simon M, Hatzikirou H, Deutsch A. 2008. Evolutionary game theory elucidates the role of glycolysis in glioma progression and invasion. Cell Prolif. 41, 980–987. ( 10.1111/j.1365-2184.2008.00563.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Basanta D, Scott JG, Rockne R, Swanson KR, Anderson ARA. 2011. The role of IDH1 mutated tumour cells in secondary glioblastomas: an evolutionary game theoretical view. Phys. Biol. 8, 015016 ( 10.1088/1478-3975/8/1/015016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dingli D, Chalub FACC, Santos FC, van Segbroeck S, Pacheco JM. 2009. Cancer phenotype as the outcome of an evolutionary game between normal and malignant cells. Br. J. Cancer 101, 1130–1136. ( 10.1038/sj.bjc.6605288) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Basanta D, Scott JG, Fishman MN, Ayala G, Hayward SW, Anderson ARA. 2012. Investigating prostate cancer tumour-stroma interactions: clinical and biological insights from an evolutionary game. Br. J. Cancer 106, 174–181. ( 10.1038/bjc.2011.517) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Basanta D, Gatenby RA, Anderson ARA. 2012. Exploiting evolution to treat drug resistance: combination therapy and the double bind. Mol. Pharm. 9, 914–921. ( 10.1021/mp200458e) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Orlando PA, Gatenby RA, Brown JS. 2012. Cancer treatment as a game: integrating evolutionary game theory into the optimal control of chemotherapy. Phys. Biol. 9, 065007 ( 10.1088/1478-3975/9/6/065007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Archetti M. 2013. Evolutionary game theory of growth factor production: implications for tumour heterogeneity and resistance to therapies. Br. J. Cancer 109, 1056–1062. ( 10.1038/bjc.2013.336) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Basanta D, Hatzikirou H, Deutsch A. 2008. Studying the emergence of invasiveness in tumours using game theory. Eur. Phys. J. B 63, 393–397. ( 10.1140/epjb/e2008-00249-y) [DOI] [Google Scholar]
- 27.Hatzikirou H, Basanta D, Simon M, Schaller K, Deutsch A. 2010. ‘Go or Grow’: the key to the emergence of invasion in tumour progression? Math. Med. Biol. 29, 49–65. ( 10.1093/imammb/dqq011) [DOI] [PubMed] [Google Scholar]
- 28.Saunders DA, Hobbs RJ, Margules CR. 1991. Biological consequences of ecosystem fragmentation: a review. Conserv. Biol. 5, 18–32. ( 10.1111/j.1523-1739.1991.tb00384.x) [DOI] [Google Scholar]
- 29.Murcia C. 1995. Edge effects in fragmented forests: implications for conservation. Trends Ecol. Evol. 10, 58–62. ( 10.1016/S0169-5347(00)88977-6) [DOI] [PubMed] [Google Scholar]
- 30.Pickett STA, Cadenasso ML. 1995. Landscape ecology: spatial heterogeneity in ecological systems. Science 269, 331–334. ( 10.1126/science.269.5222.331) [DOI] [PubMed] [Google Scholar]
- 31.Gatenby RA, Gillies RJ. 2004. Why do cancers have high aerobic glycolysis? Nat. Rev. Cancer 4, 891–899. ( 10.1038/nrc1478) [DOI] [PubMed] [Google Scholar]
- 32.Gatenby RA, Gawlinski ET, Gmitro AF, Kaylor B, Gillies RJ. 2006. Acid-mediated tumor invasion: a multidisciplinary study. Cancer Res. 66, 5216–5223. ( 10.1158/0008-5472.CAN-05-4193) [DOI] [PubMed] [Google Scholar]
- 33.Gillies RJ, Robey I, Gatenby RA. 2008. Causes and consequences of increased glucose metabolism of cancers. J. Nuclear Med. 49(Suppl. 2), 24S ( 10.2967/jnumed.107.047258) [DOI] [PubMed] [Google Scholar]
- 34.Epstein T, Xu L, Gillies RJ, Gatenby RA. 2014. Separation of metabolic supply and demand: aerobic glycolysis as a normal physiological response to fluctuating energetic demands in the membrane. Cancer Metab. 2, 7 ( 10.1186/2049-3002-2-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chambers AF, Groom AC, MacDonald IC. 2002. Metastasis: dissemination and growth of cancer cells in metastatic sites. Nat. Rev. Cancer 2, 563–572. ( 10.1038/nrc865) [DOI] [PubMed] [Google Scholar]
- 36.Hofbauer J, Sigmund K. 2003. Evolutionary game dynamics. Bull. Am. Math. Soc. 40, 479–519. ( 10.1090/S0273-0979-03-00988-1) [DOI] [Google Scholar]
- 37.Szabó G, Fáth G. 2007. Evolutionary games on graphs. Phys. Rep. 446, 97–216. ( 10.1016/j.physrep.2007.04.004) [DOI] [Google Scholar]
- 38.Bach LA, Sumpter DJT, Alsner J, Loeschke V. 2003. Spatial evolutionary games of interaction among generic cancer cells. J. Theor. Med. 5, 47–58. ( 10.1080/10273660310001630443) [DOI] [Google Scholar]
- 39.Mansury Y, Diggory M, Deisboeck TS. 2006. Evolutionary game theory in an agent based brain tumor model: exploring the genotype phenotype link. J. Theor. Biol. 238, 146–156. ( 10.1016/j.jtbi.2005.05.027) [DOI] [PubMed] [Google Scholar]
- 40.Ohtsuki H, Nowak MA. 2006. The replicator equation on graphs. J. Theor. Biol. 243, 86–97. ( 10.1016/j.jtbi.2006.06.004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Matsuda H, Tamachi N, Sasaki A, Ogita N. 1987. A lattice model for population biology. In Mathematical topics in population biology, morphogenesis and neurosciences (eds Teamoto E, Yumaguti M.). Lecture Notes in Biomathematics, vol. 71, pp. 154–161. Berlin, Germany: Springer; ( 10.1007/978-3-642-93360-8_15) [DOI] [Google Scholar]
- 42.Matsuda H, Ogita N, Sasaki A, Satō K. 1992. Statistical mechanics of population: the lattice Lotka–Volterra model. Progr. Theor. Phys. 88, 1035–1049. ( 10.1143/ptp/88.6.1035) [DOI] [Google Scholar]
- 43.Van Baalen M. 2000. Pair approximations for different spatial geometries. In The geometry of ecological interactions: simplifying spatial complexity (eds Dieckmann U, Law R, Metz JAJ.), pp. 359–387. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 44.Hilbe C. 2011. Local replicator dynamics: a simple link between deterministic and stochastic models of evolutionary game theory. Bull. Math. Biol. 73, 2068–2087. ( 10.1007/s11538-010-9608-2) [DOI] [PubMed] [Google Scholar]
- 45.Calvo F, Sahai E. 2011. Cell communication networks in cancer invasion. Curr. Opinion Cell Biol. 23, 621–629. ( 10.1016/j.ceb.2011.04.010) [DOI] [PubMed] [Google Scholar]
- 46.Stark H-U. 2010. Dilemmas of partial cooperation. Evolution 64, 2458–2465. ( 10.1111/j.1558-5646.2010.00986.x) [DOI] [PubMed] [Google Scholar]
- 47.Ohtsuki H, Hauert C, Lieberman E, Nowak MA. 2006. A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505. ( 10.1038/nature04605) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Anderson ARA, Weaver AM, Cummings PT, Quaranta V. 2006. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell 127, 905–915. ( 10.1016/j.cell.2006.09.042) [DOI] [PubMed] [Google Scholar]
- 49.Komarova NL. 2013. Spatial stochastic models of cancer: fitness, migration, invasion. Math. Biosci. Eng. 10, 761–775. ( 10.3934/mbe.2013.10.761) [DOI] [PubMed] [Google Scholar]
- 50.Thalhauser CJ, Lowengrub JS, Stupack D, Komarova NL. 2010. Selection in spatial stochastic models of cancer: migration as a key modulator of fitness. Biol. Direct. 5, 21 ( 10.1186/1745-6150-5-21) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Villers A, McNeal JE, Redwine EA, Freiha FS, Stamey TA. 1989. The role of perineural space invasion in the local spread of prostatic adenocarcinoma. J. Urol. 142, 763–768. [DOI] [PubMed] [Google Scholar]
- 52.Bald T, et al. 2014. Ultraviolet-radiation-induced inflammation promotes angiotropism and metastasis in melanoma. Nature 507, 109–113. ( 10.1038/nature13111) [DOI] [PubMed] [Google Scholar]
- 53.Belmonte-Beitia J, Woolley TE, Scott JG, Maini PK, Gaffney EA. 2013. Modelling biological invasions: individual to population scales at interfaces. J. Theor. Biol. 334, 1–12. ( 10.1016/j.jtbi.2013.05.033) [DOI] [PubMed] [Google Scholar]
- 54.Gerlinger M, et al. 2012. Intratumor heterogeneity and branched evolution revealed by multiregion sequencing. NEngl. J. Med. 366, 883–892. ( 10.1056/NEJMoa1113205) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gleason DF. 1992. Histologic grading of prostate cancer: a perspective. Hum. Pathol. 23, 273–279. ( 10.1016/0046-8177(92)90108-F) [DOI] [PubMed] [Google Scholar]
- 56.Sottoriva A, Spiteri I, Piccirillo SGM, Touloumis A, Collins VP, Marioni JC, Curtis C, Watts C, Tavaré S. 2013. Intratumor heterogeneity in human glioblastoma reflects cancer evolutionary dynamics. Proc. Natl Acad. Sci. USA 110, 4009–4014. ( 10.1073/pnas.1219747110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Angelo M, et al. 2014. Multiplexed ion beam imaging of human breast tumors. Nat. Med. 20, 436–442. ( 10.1038/nm.3488) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Soderstrom N. 1952. Puncture of goiters for aspiration biopsy. Acta Medica Scand. 144, 237–244. ( 10.1111/j.0954-6820.1952.tb15690.x) [DOI] [PubMed] [Google Scholar]
- 59.Lee H, Yoon T-J, Figueiredo J-L, Swirski FK, Weissleder R. 2009. Rapid detection and profiling of cancer cells in fine-needle aspirates. Proc. Natl Acad. Sci. USA 106, 12 459–12 464. ( 10.1073/pnas.0902365106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Glehr M, Leithner A, Gruber G, Wretschitsch P, Zacherl M, Kroneis T, Quehenberger F, Windhager R. 2010. A new fine-needle aspiration system. Surg. Innov. 17, 136–141. ( 10.1177/1553350610364991) [DOI] [PubMed] [Google Scholar]