GS-align for glycan structure alignment and similarity measurement

Abstract

Motivation: Glycans play critical roles in many biological processes, and their structural diversity is key for specific protein-glycan recognition. Comparative structural studies of biological molecules provide useful insight into their biological relationships. However, most computational tools are designed for protein structure, and despite their importance, there is no currently available tool for comparing glycan structures in a sequence order- and size-independent manner.

Results: A novel method, GS-align, is developed for glycan structure alignment and similarity measurement. GS-align generates possible alignments between two glycan structures through iterative maximum clique search and fragment superposition. The optimal alignment is then determined by the maximum structural similarity score, GS-score, which is size-independent. Benchmark tests against the Protein Data Bank (PDB) N-linked glycan library and PDB homologous/non-homologous N-glycoprotein sets indicate that GS-align is a robust computational tool to align glycan structures and quantify their structural similarity. GS-align is also applied to template-based glycan structure prediction and monosaccharide substitution matrix generation to illustrate its utility.

Availability and implementation: http://www.glycanstructure.org/gsalign.

Contact: wonpil@ku.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Glycans are one of the four fundamental components of cells (along with nucleic acids, proteins and lipids) and the most abundant and diverse biopolymers in nature (Ohtsubo and Marth, 2006). They are not only conjugated to proteins (glycoproteins) or lipids (glycolipids), but also exist as diffusible ligands (Cummings, 2009; Dwek, 1996; Varki et al., 2009). Protein glycosylation is one of the most important post-translational modifications, with more than half of all proteins expected to be glycosylated (Apweiler et al., 1999). Protein glycosylation falls into two general categories, N- and O-linked glycosylation. N-glycosylation links glycans to Asn residues in the sequon, Asn-X-Thr/Ser (where X can be any amino acid except Pro), of a nascent polypeptide (N-glycans) (Imperiali and Hendrickson, 1995), whereas O-linked glycosylation attaches glycans to Ser and Thr residues at sites which do not have a well-defined sequence motif (O-glycans) (Van den Steen et al., 1998). In particular, N-glycosylation is needed for proper folding of a protein as well as quality control in the endoplasmic reticulum (Rudd et al., 2001). Based on the lipid type, glycolipids can be classified into three main groups: glycoglycerolipids, glycosylphosphatidylinositols (GPI) and glycosphingolipids (Cummings, 2009). Hyaluronic acid is one of glycan (diffusible) ligands, which is not linked to either proteins or lipids and is secreted into extracellular compartments (Weigel et al., 1997).

Glycans play critical roles in many biological processes through covalent addition and/or specific protein-glycan recognition events. For example, they interact with diverse proteins and are involved in cell growth and development, tumor growth and metastasis, anticoagulation, inflammation, immune tolerance, intercellular adhesion, cell-cell communication and microbial attachment (Baenziger, 1985; Casu et al., 2004; Imberty and Varrot, 2008; Rabinovich and Toscano, 2009; Rudd et al., 2004). Glycans come in a diversity of sequences and structures by linking individual sugar units in a multitude of ways. They can be broadly classified as linear and branched sugars in terms of their sequence, and both forms are present in glycoconjugates (Lowe and Marth, 2003; Varki et al., 2009). The majority of the linear sugars are glycosaminoglycans and hyaluronic acid (Raman et al., 2005). Due to their flexible glycosidic linkages, glycans have an ensemble of diverse conformations (Petrescu et al., 1997; Woods et al., 1998), and such a structural diversity is essential for specific binding to their receptor proteins. For example, the pentasaccharide of ganglioside GM1 has different conformations upon binding to galectin-1 and cholera toxin (Siebert et al., 2003).

In contemporary structural biology, the comparison and alignment of protein structures are widely employed in studies such as hierarchical classification of the known structural space of protein domains (Andreeva et al., 2004; Greene et al., 2007), inference of protein function from structure (Godzik et al., 2007) and protein structure modeling (Moult et al., 2003). Protein structure comparison and alignment is a well-established area and there are currently many publicly available tools such as DALI (Holm and Sander, 1996), CE (Shindyalov and Bourne, 1998) and TM-align (Zhang and Skolnick, 2005).

The mammalian glycome encompasses a diverse and abundant repertoire of glycan structures, and could be larger than the proteome (Ohtsubo and Marth, 2006). Because of their significant roles in biology, understanding glycan structure and function in the context of their 3D structure is central to understanding biology. Despite the difficulties in crystallization, the rate of deposition of glycan-containing structures in the Protein Data Bank (PDB) (Berman et al., 2002) has been steadily increasing (Jo et al., 2011). As demonstrated in protein structural biology, fast and accurate computational tools for comparison and alignment of glycan structures are crucial to take an integrated approach to advance glycan structure-function relationships. However, developing a glycan structure alignment tool is challenging, given the unique structural features of glycans through different linkages and branching, resulting in a tree-like structure unlike proteins. To the best of our knowledge, there have been no such tools published to date.

To make a progress in the structural glycobiology field, we introduce a novel method, GS-align, for glycan structure alignment and similarity measurement. In particular, GS-align provides a size-independent structural similarity score, GS-score. Below, we first describe the alignment and scoring algorithms in details. Benchmark tests and representative examples are then presented to illustrate reliability and applicability of GS-align. Finally, we discuss both the advantages and limitations of our approach.

2 Materials and methods

2.1 Preparation of random glycan structures

To prepare a set of random glycan structures, biologically relevant glycan sequences that are largely different from each other were chosen from the KEGG GLYCAN database, a collection of experimentally determined glycan sequences (http://www.genome.jp/kegg/glycan) (Hashimoto et al., 2006). Using all the glycan sequence information in KCF (KEGG Chemical Function) format, carbohydrate (residue) names and linkage information between residues were extracted from the NODE and EDGE sections of each KCF file. Any glycan structures that contain ambiguous linkage information were discarded. The total number of the remaining glycan sequences was 10 983, and the glycan length (i.e. the total number of carbohydrate residues) ranged from 1 to 54 (as of May, 2014) (Supplementary Fig. S1A).

The CHARMM biomolecular simulation program (Brooks et al., 2009) was used to generate initial 3D glycan structures from the sequence obtained from the KEGG GLYCAN database. Glycans containing sugars whose topologies are not available in the CHARMM carbohydrate force field (Guvench et al., 2008) were discarded for this study. To account for only non-redundant (unique) glycan sequences, all files in KCF format were converted into string format data structures for easy comparison of different glycan sequences by each sugar position, glycosidic linkage carbon number and anomeric configuration. Redundant sequences were removed, and the final CHARMM-compatible unique KEGG glycan sequences (4907 entries) were obtained after excluding glycans containing furanose monosaccharides (58 out of 4965), as the current version of GS-align is not able to handle five-membered rings. Supplementary Figure S1B shows the numbers of final unique KEGG glycans in terms of glycan length.

To prepare non-homologous glycans for a given glycan length, called a ‘random glycan structure set’, a glycan sequence similarity score matrix was first obtained by an in-house glycan sequence alignment tool, which adopts tree-matching methods for glycan sequence similarity measurement (Aoki et al., 2003). Then, all the glycans were clustered using the average linkage clustering method with a sequence similarity score cutoff of 0, which is the median of all possible scores. Seventy clusters were identified for glycan lengths ranging from 4 to 12, which were determined based on the abundance and the structural diversity in the unique KEGG glycans, and their centroids were used as glycan sequences for the random glycan structure set. For each of the 70 glycans, 10 conformations were generated by randomly changing possible glycosidic dihedral angles (by 30° interval) using the IC EDIT and IC BUILD commands in CHARMM. If the newly generated random conformation had a CHARMM van der Waals energy <100 kcal/mol, the conformation was accepted. Supplementary Table S1 summarizes the number of glycan structures as a function of glycan length in the random glycan structure set.

2.2 Glycan structure alignment

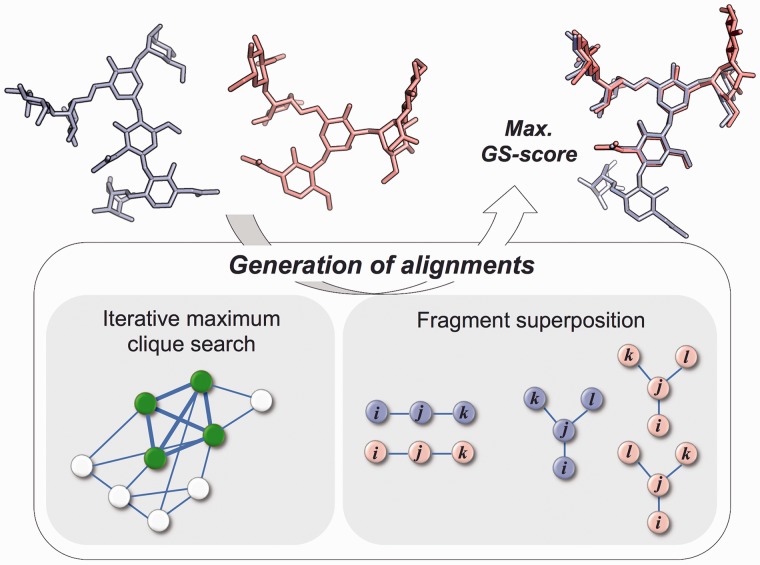
In GS-align, all possible alignments between two glycan structures are generated by iterative maximum clique search and fragment superposition, and the optimal alignment is determined by the maximum GS-score (see the next subsection for its definition). The overall algorithm is schematically illustrated in Figure 1. In the maximum clique search method, two given glycan structures (A and B) are represented by ring centroids and glycosidic oxygen atoms ($R^{(\text{A})}=\{r_1^{(\text{A})},r_2^{(\text{A})},\dots ,r_{\text{M}}^{(\text{A})}\}$ and $R^{(\text{B})}=\{r_1^{(\text{B})},r_2^{(\text{B})},\mathrm{\dots },r_{\text{N}}^{(\text{B})}\}$, where r is the coordinate of ring centroid or glycosidic oxygen). All combinations of inter-structural pairs ($P^{\text{AB}}=\{p_{11}(r_1^{(\text{A})},r_1^{(\text{B})}),p_{12}(r_1^{(\text{A})},r_2^{(\text{B})}),\dots ,p_{\text{MN}}(r_{\text{M}}^{(\text{A})},r_{\text{N}}^{(\text{B})})\}$) are generated using the representative points from the glycan structures.

Fig. 1.

Schematic illustration of the alignment algorithm in GS-align

Two pairs $p_{\text{ij}}(r_{\text{i}}^{(\text{A})},r_{\text{j}}^{(\text{B})})$ and $p_{\text{kl}}(r_{\text{k}}^{(\text{A})},r_{\text{l}}^{(\text{B})})$ are selected from $P^{\text{AB}}$ and then both distances $d(r_{\text{i}}^{(\text{A})},r_{\text{k}}^{(\text{A})})$ and $d(r_{\text{j}}^{(\text{B})},r_{\text{l}}^{(\text{B})})$ are calculated. If $|d(r_{\text{i}}^{(\text{A})},r_{\text{k}}^{(\text{A})})-d(r_{\text{j}}^{(\text{B})},r_{\text{l}}^{(\text{B})})|$ is less than a cutoff (d_cut), $p_{\text{ij}}$ and $p_{\text{kl}}$ are assigned to vertices of a product graph and connected by an edge. This procedure is applied to all pairs in $P^{\text{AB}}$. The generated product graph is searched for the maximum clique, the largest subset of vertices in which all vertices are connected to all other vertices. In our case, solving the maximum clique problem for the product graph is equivalent to identification of the largest subset of structurally aligned points. We used an improved branch and bound algorithm for fast maximum clique search (Konc and Janežič, 2007; Lee and Im, 2012). Two glycan structures are superposed using the rotation matrix obtained from the aligned point sets. GS-align repeats this procedure five times, increasing d_cut from 1 to 3.0 Å by an increment of 0.5 Å (so-called the iterative maximum clique search). Thus, five alignments are generated.

The second method to align two glycan structures is to use fragments from each glycan. A set of consecutively linked residues is extracted from each glycan. Both linear (three residues) and branched (four residues) fragments are considered and for branched fragments, additional fragments are generated by swapping l and k residues in Figure 1. For each fragment pair from two glycans, an initial alignment is obtained using equivalent residue pairs in the fragment pair. A set of optimal alignment residue pairs is identified based on the initial alignment. If the ring centroid distance between an aligned residue pair is  > 8 Å, the pair is discarded from the aligned residue pair set. GS-align then again superposes the glycan structures by the rotation matrix for the updated aligned residue pairs. This procedure generates additional alignments for all combinations of fragment pairs. Indeed, a strong complementary nature was found between the iterative maximum clique search and the fragment superposition; for example, when all random glycan structure pairs were aligned, 41% of the optimal alignments with the maximum GS-score were from the former and 59% from the later.

2.3 Glycan structure similarity measurement

GS-score is a scoring function to quantify structure similarity between two glycan structures:

$$\text{GS-score}=\text{Max}\left[\frac{1}{N_{\text{OG+Ring}}}\left({\displaystyle \begin{array}{l}\sum _i^{N_{\text{OG,ali}}}\frac{1}{1+{\left(d_{\text{OG,i}}/d_{\text{OG,0}}\right)}^2}\\ +{\displaystyle \sum _i^{N_{\text{Ring,ali}}}\frac{1}{1+{\left(d_{\text{Ring,i}}/d_{\text{Ring,0}}\right)}^2}}\end{array}}\right)\right]$$ (1)

where ‘Max’ denotes that the GS-score is the maximum of all possible alignments, N_{OG + Ring} = 2L_Target − 1 is the total number of oxygen atoms in the glycosidic linkages (OG) and sugar rings of a target glycan, L_Target is the length of the target glycan, and N_OG,ali and N_Ring,ali are the numbers of glycosidic oxygen atoms and sugar rings in the aligned residues, respectively. The aligned residue pairs (i.e. which residue of glycan A is structurally aligned onto which residue of glycan B in a given alignment generated from the iterative maximum clique search and fragment superposition) are identified using the shortest augmenting path algorithm to solve the linear sum assignment problem (LSAP) (Derigs, 1985; Gao and Skolnick, 2013). d_OG,i is the distance between the glycosidic oxygen atoms in the ith pair of aligned residues and d_Ring,i is the root-mean-square deviation (RMSD) between the sugar ring atoms (C1, C2, C3, C4, C5 and O5) in the ith pair of aligned residues (Supplementary Fig. S2). d_OG,0 and d_Ring,0 are the scaling factors to normalize the aligned distances. A final alignment is selected by the maximum GS-score alignment.

Figure 2 shows the average GS-scores calculated from all pairs of 700 random glycan structures (Supplementary Table S1) as a function of glycan length. The raw GS-score (rGS-score) is calculated using a constant value (3 Å) for d_OG,0 and d_Ring,0, based on the average distance between the centroids of adjacent sugar rings (3.26 Å). For the GS-score, glycan length-dependent scaling factors d_OG,0(L_Target) and d_Ring,0(L_Target) are used instead of the constant value, so that the average GS-score is not dependent on the glycan length for the random structure pairs. The scaling factors were empirically obtained from curve fitting to the plots of the average d_OG and d_Ring between an aligned residue pair as a function of L_Target (Supplementary Fig. S3), where L_Target is the length of the larger glycan in a glycan structure pair. The d_OG,0(L_Target) and d_Ring,0(L_Target) are

$$d_{\text{OG},0}(L_{\text{Target}})=1.36\sqrt{L_{\text{Target}}-2}-0.75$$ (2)

$$d_{\text{Ring},0}(L_{\text{Target}})=1.64\sqrt{L_{\text{Target}}-2}-0.30$$ (3)

Fig. 2.

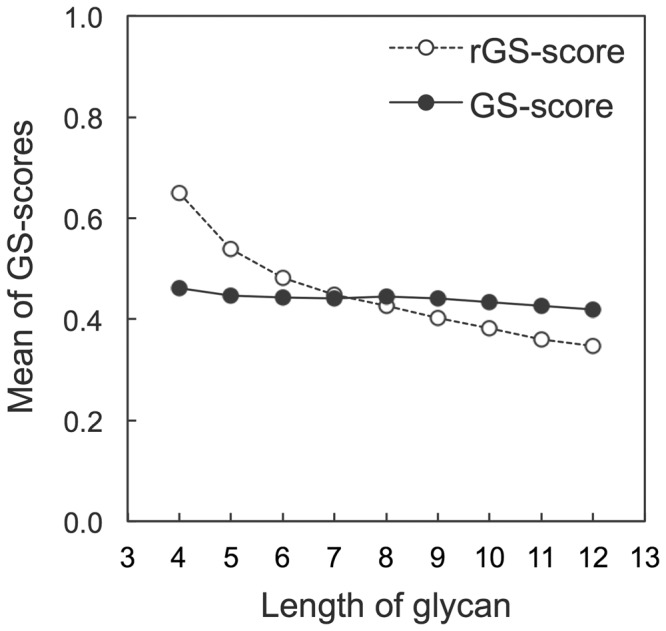
The average raw GS-score (rGS-score) and GS-score of random glycan pairs as a function of glycan length

As shown in Figure 2, the mean GS-scores, normalized by the glycan length-dependent d_OG,0 and d_Ring,0, are almost length-independent for the random glycan structures, but the rGS-score decreases from 0.65 to 0.35 as the glycan length increases. The average GS-score value for a random glycan structure pair is 0.44. Table 1 shows the statistical significance of the GS-score derived from the random glycan structures with diverse sequences and conformations. The GS-score distribution for all random glycans (of different sequences, lengths and conformations) was modeled by the normal distribution (Supplementary Fig. S4), and the P-values of representative GS-scores are given in Table 1. A GS-score of 0.69 is significant at P < 1 × 10⁻³.

Table 1.

Statistical significance of GS-score derived from the random structures of glycans with diverse sequences and conformations

GS-score	0.54	0.57	0.63	0.69	0.73	0.78	0.83
P-value	1 × 10 − 1	5 × 10 − 2	1 × 10 − 2	1 × 10 − 3	2 × 10 − 4	2 × 10 − 5	2 × 10 − 6

2.4 Preparation of N-glycan library

We downloaded the PDB files of X-ray crystallographic structures containing at least one protein chain whose resolution is <3 Å. Glycan Reader (Jo et al., 2011) was used for identification of protein chains that include covalently linked glycans. These protein chains were subsequently divided into N- and O-linked glycoproteins. The coordinates and residue names of the N-glycans were individually extracted from the glycan-containing PDB files (6320 PDB files, as of July, 2014) using Glycan Reader. The protein coordinates of the N-linked glycoproteins were also separately prepared from the PDB files. The total number of N-glycans in the library was 14  414 because multiple glycans can be attached to one protein chain.

3 Results

3.1 Glycan structure alignment by GS-align

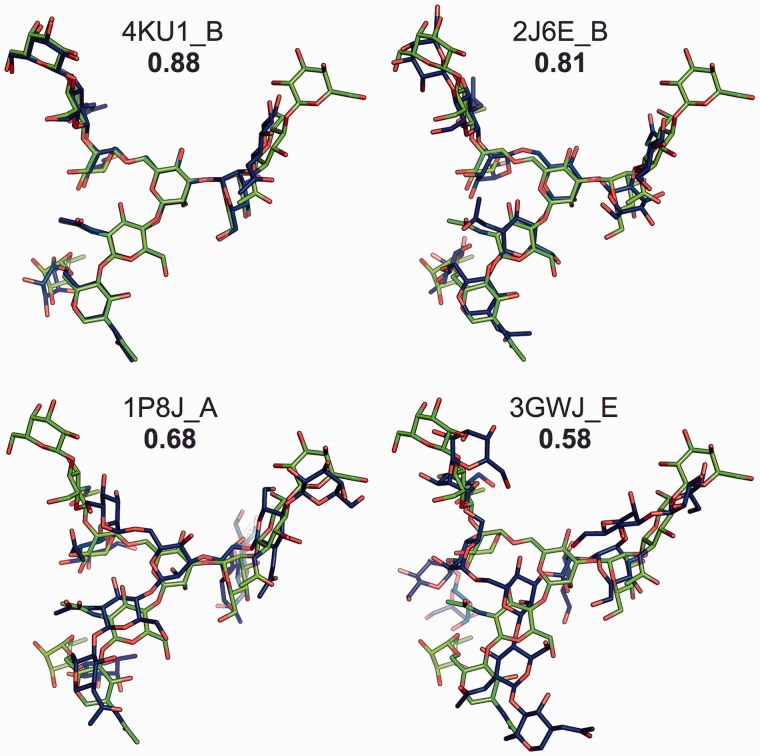
Figure 3 shows four representative examples to illustrate the alignment quality provided by GS-align. The representative alignments were obtained from PDB N-glycan library search by GS-align. For this search, a glycan structure consisting of 10 sugar residues in PDB:1L6X was used as the query (target) structure; the target and library glycans are colored in green and blue, respectively. The four representative alignment pairs were chosen to have the same coverage of 0.9 and various GS-scores. The coverage is defined as a ratio of aligned residues to the total number of residues in the target structure. If the distance between the centroids of sugar rings is within 5 Å, the library sugar residue is assigned as the aligned residue. Visual inspection of the four examples shows a clear correlation between GS-score and structural similarity. To measure the structural similarity quantitatively, we calculated the RMSD for the aligned residues. The calculated RMSDs are 0.46, 1.29, 2.05 and 2.67 Å for the corresponding GS-scores of 0.88, 0.81, 0.68 and 0.58, respectively.

Fig. 3.

Representative examples to illustrate the relationship between GS-score and structural similarity. Each glycan structure (blue) aligned to the target glycan (green) in PDB:1L6X_A is shown with its PDB id_chain id and GS-score

3.2 Benchmark: homologous and non-homologous N-glycoprotein sets

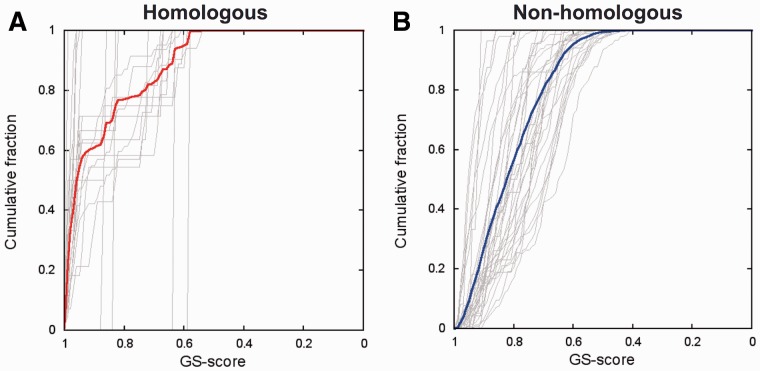
Recently, Jo et al. measured pairwise glycan structure similarity using the RMSD among N-glycan structures having the identical sequence (35 N-glycan sequences) (Jo et al., 2013). The N-glycan structures in homologous glycoproteins are found to be significantly conserved compared to those in non-homologous glycoproteins through a P-value analysis using a random glycan conformation background. An N-glycan structure pair is called ‘homologous’ or ‘non-homologous’ depending on the sequence similarity (with a 30% cutoff) and glycosylation sites between the parent proteins. An analysis of the cumulative fractions of homologous and non-homologous glycans structure pairs as a function of their P-value showed that ∼67% of the homologous N-glycan structure pairs have a statistically significant level (P < 0.05) of structural similarity, whereas ∼36% of non-homologous N-glycan structure pairs have the statistically equivalent level of structural similarity (Jo et al., 2013).

We performed the same analysis using GS-align against the same homologous and non-homologous sets. The only difference is that GS-align is used for structure alignment and similarity measurement, instead of the RMSD and P-value measurement (using the random glycan conformations). Figure 4 shows a cumulative fraction of glycan structure similarity as a function of GS-score for the homologous and non-homologous N-glycan structure pairs. The cumulative percentage of non-homologous glycans is 38% at the GS-score for which the cumulative percentage of homologous N-glycans is 67%, showing good agreement with the previous results, as well as a clear ability of GS-align to discriminate glycans of different conformations. The GS-score (0.87) that gives these cumulative percentages does not match the GS-score (0.57 in Table 1) at a P-value of 0.05 (used by Jo et al.) due to the different characteristics of the random structure sets and scoring functions used in both analyses. It should be noted that the cumulative percentages from the two sets at a GS-score of 0.69 (P < 1 × 10⁻³ in Table 1) are similar, indicating that the N-glycan structures in both sets are not very significantly different, although highly similar N-glycan pairs are observed more in the homologous set.

Fig. 4.

Cumulative fraction of glycan structure similarity using GS-score for the homologous and non-homologous protein sets. The gray lines in each plot represent individual 35 glycan sequences and thick solid lines the average over all glycan sequences

3.3 Benchmark: PDB N-glycoprotein search

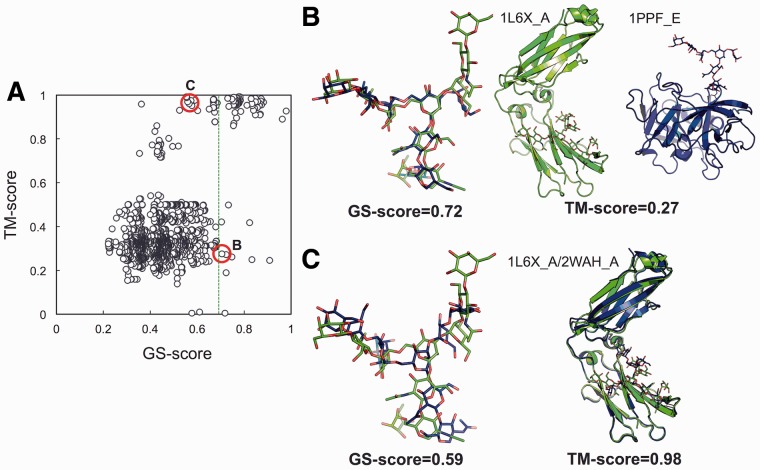
Figure 5 A shows a comparison between glycan similarity and glycoprotein similarity from a PDB N-glycan library search using a target glycan and its parent protein (PDB:1L6X_A). We used TM-align (Zhang and Skolnick, 2005) to measure the protein global structural similarity which is quantified by TM-score. Above a GS-score of 0.69 (P-value < 1 × 10 ^− 3, a green dotted line in the figure), most of the corresponding parent protein pairs show high structural similarity in their global fold (TM-score > 0.86). This indicates that glycans tend to have significant structural similarity when their parent proteins are structurally homologous, supporting the previous study of Jo et al. (2013). However, there are exceptional cases. Figure 5B shows an example in which proteins show low structural similarity (0.27 for entire proteins and 0.38 only for the glycan-bound domains), but their glycans have relatively high structural similarity with a GS-score of 0.72. This example demonstrates that a similar glycan structure can also be detected from a protein with different topology and function (1L6X_A: human immunoglobulin γ-1 chain C region and 1PPE_E: human leukocyte elastase). Figure 5C is an example in which proteins show a high TM-score (0.98), but their glycans have relatively low structural similarity with a GS-score of 0.59, demonstrating that glycan structures could be diverse, even though their parent protein structures are almost identical. In addition, it should be noted that most of the low GS-score cases with relatively high TM-scores of more than 0.7 in Figure 5 result from a mismatch in glycan lengths because the GS-scores in the plot were normalized by larger glycan structures among each pair. Supplementary Figure S5 shows the distribution plot of the GS-scores normalized by smaller glycan structures, indicating that smaller glycan fragments generally show high similarity to the fragments of the target glycan and thus a fragment assembly method would be promising in template-based glycan structure modeling.

Fig. 5.

Comparison of glycan similarity (GS-score) with glycoprotein similarity (TM-score) through PDB N-glycan library search. (A) TM-score versus GS-score plot. All PDB N-glycans and their parent proteins were structurally compared with the target glycan and its parent glycoprotein (PDB:1L6X_A), respectively. The green dotted line indicates a GS-score (0.69) whose P-value is 1 × 10⁻³. (B) An example where proteins show distinct folds, but the GS-score between their glycans is high. (C) An example where proteins show similar global folds, but the GS-score between their glycans is low. In these examples, the two pairs of glycans have the identical coverage (0.8)

3.4 Illustration for template-based glycan structure prediction

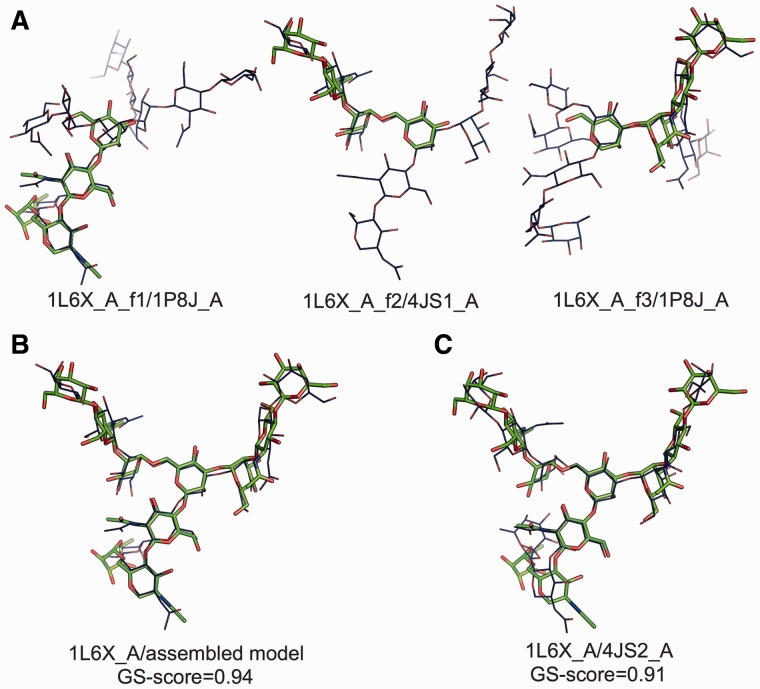
The procedure of comparative protein structure modeling usually consists of two main steps: (i) identifying templates (from the PDB) to the target sequence and (ii) building a full-length model using the templates. Like protein structure prediction, this approach could be a promising means of predicting glycan structures (Jo et al., 2013). Figure 6 shows a representative example to illustrate a potential application of GS-align to template-based glycan structure prediction. In this case, 1L6X_A glycan was fragmented into three partial structures, each of which has four residues (stick representation in green in Fig. 6A). Each glycan fragment was then used as the query structure to search for templates in the PDB N-glycan library. To put strict conditions on the library search, we excluded glycans whose parent proteins have a sequence identity >30% to 1L6X_A. In these searches, GS-score was normalized by the length of the fragment glycan, rather than those of larger template glycans, thereby aiming at detecting all template glycans containing similar structures to the query. Figure 6A shows the best template structures (line representation in blue) superposed onto the query fragment glycans. When a glycan structure was assembled from the three templates, the modeled structure is quite similar to the target glycan with a GS-score of 0.94 (Fig. 6B).

Fig. 6.

An example of template-based glycan structure prediction. (A) Three fragment structures from 1L6X_A glycan, each of which has four residues (stick representation in green), that were individually used as the query structure to search for templates in the PDB library. Three best template glycans (line representation in blue) were identified based on GS-score for each query structure. (B) Structure similarity between the target glycan and a structure assembled using the three-fragment templates in (A). (C) Structural similarity between the target glycan (entire 1L6X_A glycan) and its best template

Alternatively, one can use the entire 1L6X_A glycan to search for templates in the PDB N-glycan library. Structural similarity between the target glycan and its best template identified based on GS-score (normalized by larger glycan) shows a high GS-score of 0.91 (Fig. 6C). The TM-score between the parent proteins of the target glycan and the best template is 0.25. In this case, a PDB library glycan that maximally covers the target glycan can be a good template even when their parent proteins’ structures are different, as illustrated in Figure 5B.

In a practical situation in which one needs to predict a glycan structure from its sequence, a set of PDB template glycans could first be searched based on the sequence similarity to the target glycan and then adequate template structures could be identified after clustering all the templates. Although further intricate computational procedures would be needed to reliably generate a final glycan model, availability of good templates is a key factor to determine the quality of the predicted model. This example demonstrates that a set of substructures can be separately identified and assembled into full glycan structures for glycan structure modeling.

3.5 Illustration for developing monosaccharide substitution matrix

In protein bioinformatics, a substitution matrix such as PAM (Dayhoff et al., 1983) and BLOSUM (Henikoff and Henikoff, 1992) is used for sequence alignment. Proper usage of such a substitution matrix can significantly improve the quality of alignments, providing more biological insights into protein evolution, structure and function. Similarly, incorporation of information on monosaccharide substitution in conserved glycan structures into glycan sequence alignment could provide biologically more reliable alignment results.

Figure 7 illustrates a potential application of GS-align to deriving a monosaccharide substitution matrix. Figure 7A shows a representative example in which two different glycans (3SIO_E in green and 1CPO_A in blue) have very similar structure (GS-score = 0.90) but different monosaccharides (α-d-mannose versus α-d-lyxose) at two positions. As a separate example, Figure 7B shows the percentages of other monosaccharides that can substitute α-d-mannose as highly similar glycan structure pairs (GS-score ≥ 0.8); the percentage is calculated using all PDB N-glycans. For comparison, the percentage of α-d-mannose itself is also included in the table. A monosaccharide was assigned to the substituting monosaccharide if the RMSD between the sugar rings is ≤2 Å in the aligned structures.

Fig. 7.

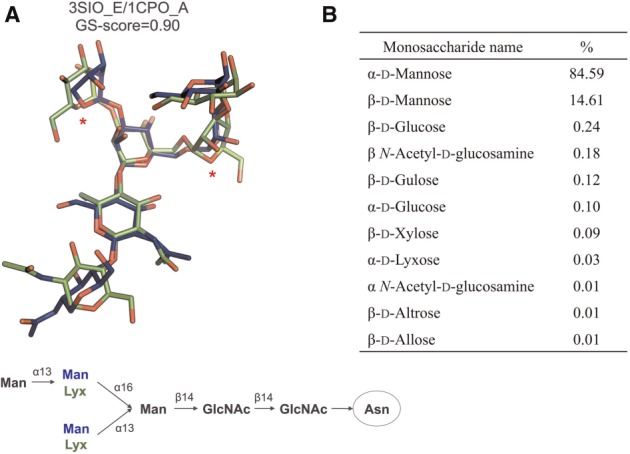
An example using GS-align for deriving a monosaccharide substitution matrix. (A) A representative example where two different glycans have similar structure (GS-score = 0.90) but different sequences. GlcNAc: N-acetyl-d-glucosamin, Man: d-mannose, Lyx: d-lyxose. Two unmatched residues (Man versus Lyx) are marked with red asterisks. (B) The percentages of other monosaccharides that can substitute α-d-Mannose in highly similar glycan structure pairs (GS-score ≥ 0.8). For comparison, the percentage of α-d-mannose itself is also included in the table

4 Discussion and conclusion

A comparative study of biological entities is a useful approach to get valuable insight into their biological relationships. Especially, when their 3D structures are available, this approach can provide more accurate information about possible distant evolutionary relationships that are difficult to detect based on sequence information alone. During the past two decades, many computational methods have been developed for this purpose. However, most methods are designed for protein structure comparison, and there is no currently available tool (to the best of our knowledge) for comparing glycan 3D structures in a sequence order- and size-independent manner. In particular, the branched nature of glycans makes it more difficult to work with their structures. Nonetheless, considering that glycans are one of the four fundamental classes of molecules that comprise living systems and play an essential role in a vast array of biological processes, there is an urgent need to develop a computational tool for structural comparison of glycans.

Here, we introduce GS-align for glycan structure alignment and similarity measurement. Our method works in a sequence order-independent manner and provides size-independent scores for the similarity of two glycan structures. We validate the reliability of our method through PDB N-glycan library search and glycan conformation comparison in the PDB homologous/non-homologous N-glycoprotein sets. The results indicate that GS-align is a robust computational tool to align glycan structures and quantify their structural similarity.

GS-align was used to illustrate its potential application to template-based glycan structure prediction. In the comparative structure modeling, the accurate assessment of the quality of the templates and the resulting model is essential to improve the structure prediction algorithms. GS-align can play a key role in this task during the development of glycan 3D structure prediction tools from glycan sequence information.

GS-align was also used to demonstrate its applicability to the development of a monosaccharide substitution matrix for accurate glycan sequence alignment. Aoki et al. developed a score matrix in a manner similar to BLOSUM (Aoki et al., 2005). They defined the appropriate classes of glycans and then produced glycan sequence alignments within each class using their tree-structure local exact matching algorithm. The alignment results were used to calculate the frequency of sequence alignment of ‘links’, which includes two monosaccharide names, an anomeric configuration (α or β), and connection information (e.g. 1-6, 1-4). On the other hand, we attempted to use the frequency of structural alignment of ‘residues’, which consists of a monosaccharide name, its anomeric configuration and the linkage information to any linked sugars. The current state of glycan data is not yet complete (Aoki et al., 2005), and it may make such a substitution matrix less reliable. To work around this problem, utilizing glycan fragments (Jo and Im, 2013) instead of whole structures could be an approach to increase the number of aligned monosaccharides for better statistics. Although our approach needs to be refined and statistically analyzed for validation, we expect that as in protein structure alignment, glycan structure alignment can eventually provide glycan sequence alignments with an accuracy that would not be achievable from sequence alignments alone, leading to better consideration of distant evolutionary relationships. The advanced measurement of glycan sequence similarity will also play a key role in accurate identification of better templates for comparative modeling-based glycan structure prediction.

The current GS-score is based on the coordinates of sugar ring centroids (sugar ring atoms) and glycosidic oxygen atoms for alignment (scoring). This approach can be efficiently used to search for an optimal alignment focusing on the topological similarity of glycans with significantly reduced computational costs. However, well-aligned monosaccharides could have different orientations of hydroxyl groups that can be modified with diverse chemical groups (e.g. amine, acetic acid, lactic acid, phosphate, sulfate, etc.). Therefore, it might be necessary to incorporate physicochemical features of the hydroxyl groups and chemical modifications into the current scoring function for more accurate measurement of the structural similarity. In addition, the current GS-align cannot handle furanoses forms (five-membered rings) of monosaccharides. Furanoses are often ignored by researchers because they are very minor compared to pyranose forms in overall glycan composition. In the PDB N-glycan library used in this study, there is only one glycan with a furanose ring. However, it is known that furanose monosaccharides are also a common constituent of O-glycans of plant glycoproteins and present in a number of glycoproteins of bacteria and protozoa (Lis and Sharon, 1993), suggesting a need of accounting for furanose rings in the GS-align scoring function. These will be done in future work.

Compared with the mature field of protein structure prediction and modeling, the current status of in silico structural glycobiology is rudimentary at best because of the paucity of computational tools. We hope that GS-align can be applied to diverse subjects involving structure comparison of glycans and eventually for addressing biological questions related to glycan functions.

Funding

NSF IIA-1359530, NIH U54GM087519, XSEDE MCB070009 (to WI), NIH GM-48835 (JS) and NRF of Korea 2008-0061987 (JL).

Conflict of Interest: none declared.