A Nonparametric, Multiple Imputation-Based Method for the Retrospective Integration of Data Sets

Abstract

Complex research questions often cannot be addressed adequately with a single data set. One sensible alternative to the high cost and effort associated with the creation of large new data sets is to combine existing data sets containing variables related to the constructs of interest. The goal of the present research was to develop a flexible, broadly applicable approach to the integration of disparate data sets that is based on nonparametric multiple imputation and the collection of data from a convenient, de novo calibration sample. We demonstrate proof of concept for the approach by integrating three existing data sets containing items related to the extent of problematic alcohol use and associations with deviant peers. We discuss both necessary conditions for the approach to work well and potential strengths and weaknesses of the method compared to other data set integration approaches.

Recent years have witnessed a growing interest in the development of statistical methods that allow for the combination of existing data sets, some of which may have been collected by different research teams over time. Data sets containing variables that store information obtained from identical measurement instruments can be combined using relatively straightforward procedures. However, when existing data sets contain variables that tap similar constructs but were obtained using differing measurement instruments, the problem of data set integration becomes considerably more complex.

The goal of the present research was to develop a flexible, broadly applicable approach to the integration of distinct data sets that is based on multiple imputation (Rubin, 1987) and the collection of new, conveniently sampled calibration data. Our approach complements existing data integration approaches by offering a solution when: (a) observed variables desired for analysis are not available in existing data sets but are related to other variables that are included in those data sets; or (b) variables desired for analysis are available in existing data sets, but the analyst is unwilling to rely on the strong assumptions about latent structure that may be required when alternative data integration approaches are employed. We also present diagnostic methods for evaluating the success of the data integration method in empirical applications, and identify when certain unverifiable assumptions must be made. We demonstrate proof of concept for the approach by integrating three existing data sets that include measures of problematic alcohol use and extent of association with deviant peers. Finally, we discuss potential strengths and limitations of the approach.

Background

Methods for the combination of existing data sets have been advanced within multiple disciplines. In the social and behavioral sciences, for example, data set integration has frequently been accomplished by using the methods of quantitative research synthesis—also known as aggregated data (AD) meta-analysis—in which an overall summary statistic (or effect size) is collected from or computed for each sampled data set (study), and statistical methods are used to estimate an effect size for the population of relevant data sets (studies). Cooper and Patall (2009) have detailed the many strengths of AD meta-analysis; however, meta-analytic methods are not optimal when the individual-level raw data are available (Glass, 2000), in part because the integration of individual-level data sets allows for the conduct of subgroup analyses not originally performed by the investigators and tests of within- and between-study moderators (Brown et al., 2011; Cooper & Patall).

In the fields of psychiatry and epidemiology, a straightforward “transform and recode” process is sometimes employed for data integration (e.g., Bath et al., 2010; Butler et al., 2010; Fortier et al., 2010), in which codes for response categories are merged and/or renamed for variable pairs that are judged to be sufficiently “comparable” (Bath et al.). Unfortunately, although both simple and potentially appropriate for variables deriving from constructs for which measurements are objective (e.g., descriptions of demographic characteristics like sex and annual income), the “transform and recode” approach is not optimal for creating commensurate measures across data sets because it makes the untested, strong assumption that transformed scores derived from different variables are identically related to an underlying target construct.

More recent developments in the psychological sciences have applied a measurement model integration (MMI; Curran & Hussong, 2009) approach, which presumes that an unobserved latent propensity gives rise to the observed (imperfect) measurements on any instrument or scale. In MMI, a latent structure measurement model is fit to the observed data, and the resulting parameter estimates are used to produce latent variable scale scores for all participants in a set of combined data sets. The estimated latent variable scores may then be used for subsequent interpretation and analysis. Many types of latent structure models can be used for MMI; for example, when data sets to be integrated include identical items from the same original measurement instrument, analysts can use a confirmatory factor-analytic model (cf. Meredith, 1993). In the more common situation that the data sets to be integrated include some non-overlapping items derived from different instruments, analysts can use traditional item response theory (IRT) model approaches to allow for equating, scaling, and linking of different measurement instrument items across samples. Bauer and Hussong (2009) have additionally developed an extension to the generalized linear factor analysis model that can accommodate items that vary across instruments and studies in terms of level of measurement (e.g., combinations of categorical and continuous items) and that allow for observed-variable moderators of measurement model parameters (for example, one could empirically evaluate whether measurement model parameters vary as a function of participant age, and then choose to include an age moderator in the model ultimately used to estimate latent variable scores). These and other MMI approaches are greatly facilitated by the presence of a set of “anchor” items that are observed in all of the data sets to be integrated (cf. Kolen & Brennan, 2004). In general, full-information maximum-likelihood (FIML) estimation is employed to estimate the models and to address the (partially) missing data generated by the non-anchor items.

The MMI approach possesses many strengths. Unlike the “transform and recode” approach, the MMI approach does not assume that all variables to be integrated are commensurate measures of the same construct; instead, the MMI method incorporates steps that allow for the explicit evaluation of measurement invariance (the extent to which identically sourced/worded observed items relate to an underlying construct in the same way across data samples) and measurement comparability (the extent to which items sourced from different measurement instruments/modalities measure the same underlying construct across data samples; Curran & Hussong, 2009). These are critical considerations in ensuring that resulting scores are valid measures of the intended construct for participants in all contributing samples. Curran and his colleagues (e.g., Curran et al., 2008), among others, have published empirical applications of MMI that have very carefully and thoughtfully addressed such considerations.

However, MMI analysts must posit and trust particular psychometric models for the variables to be integrated. The appropriateness of the assumptions underpinning these models can be difficult to evaluate, particularly when the number of anchor items is small or when the latent structures are multidimensional (Bauer & Hussong, 2009; Curran et al., 2007, 2008), and misspecification of these models can lead to estimated scale scores that are not valid or truly comparably-scaled measurements of the underlying latent construct (e.g., Yuan, Marshall, & Bentler, 2003). Moreover, the MMI approach is not intended for situations where key variables of interest are unavailable in the existing data sets. Accordingly, analysts may benefit from the availability of an alternative (or supplementary) approach.

A Nonparametric Multiple Imputation-Based Approach

Our proposed method views data integration is as an “incomplete data” problem (see, e.g., Cudeck, 2000, McArdle, 1994; see also Graham, Hofer, & MacKinnon, 1996, for a discussion of designs involving planned missing data). We conceive of a single concatenated data set comprised of the records from all data sets to be integrated; the data set contains blocks of missing values for variables present in one (or more) data sets but not in others. With this conceptualization, the integration problem becomes one of imputing the missing values—for example, by multiple imputation (Rubin, 1987)—enabling analysis of the larger sample.

Multiple imputation is not directly feasible in many data set integration settings, because the analyst often lacks information on the conditional relationships involving variables that are present in only one of the data sets to be integrated. One way to proceed is to make strong modeling assumptions about those conditional relationships (by imposing a latent structure model, for example). To reduce reliance on strong modeling assumptions, particularly in situations where there is little or no overlap of items across data sets, we propose obtaining data from a separate, conveniently-collected sample that includes variables from all data sets to be integrated. When needed, the calibration sample can additionally include key variables desired for analysis that are not measured in any of the existing data sets. The calibration data provide information about the missing conditional distributions among variables in the existing data sets, as well information about distributions for the (new) key variables given subsets of variables available in each of the existing data sets.

We concatenate the original data and calibration data sample, and perform multiple imputation on the resulting file. The completed, integrated data sets are then available for analysis based on standard multiple imputation inferences (Rubin, 1987). Alternatively, after constructing the completed concatenated files, the analyst can remove the calibration data and use only records resulting from the original data sets for analysis (Reiter, 2008).

In general, the imputation will need to handle many variables with large fractions of missingness, and so results will be sensitive to the quality of the imputation model, as well as to the quality of the calibration sample. To minimize parametric assumptions, our imputation approach employs chained imputation equations (Raghunathan et al., 2001) based on classification and regression trees (CART), as developed by Burgette and Reiter (2010). CART models approximate the conditional distribution of some dependent variable given multiple predictors. The algorithm sequentially partitions the predictor space so as to make the dependent variable increasingly homogeneous within the partitions. The partitions are found by recursive binary splits of the predictors; for continuous dependent variables, we find optimal split points using a minimum deviance criterion, and for categorical dependent variables we find optimal split points using the Gini impurity measure (Breiman et al., 1984). The series of splits can be effectively represented by a tree structure, with leaves corresponding to the subsets of units. We grow each branch of the trees until either (a) an additional split results in fewer than five observations in the successive leaf, or (b) we reduce the values of the decision criteria to less than .0001 times their values in the full data set. The values in each leaf represent the conditional distribution of the outcome for units in the data with predictors that satisfy the partitioning criteria that define the leaf.

The sequential CART models have several desirable features for the integration task. The CART models can handle categorical, continuous, and mixed variables simultaneously. Moreover, they can reflect distributions that are not easily captured with standard parametric models (see Hastie et al., 2009), and they include interactive and non-linear relationships—which often are of interest in data set integration settings—automatically in the model fitting. Finally, they can be applied with minimal tuning by the user. Thus, the approach has the advantage of being simple to implement but at the same time flexible enough to accommodate complex multivariate dependencies without overfitting. Indeed, simulation results obtained by Burgette and Reiter (2010) indicate that sequential CART models can outperform default parametric implementations of sequential regression imputation substantially in terms of mean squared error when estimating regression coefficients from the completed data sets. We note that when multiple imputation is directly feasible in data integration settings (as when there is sufficient overlap of items across contributing samples and all variables desired for analysis are available on existing data sets), the CART multiple imputation routines can be used without the collection of a calibration data sample.

We refer to our proposed data integration approach as calibration via nonparametric multiple imputation (CNMI). CNMI differs from MMI in a key way: CNMI separates the data set integration step from the substantive modeling step, whereas MMI performs both simultaneously. As noted in other missing data settings (e.g., Collins, Schafer, & Kam, 2001), separating the procedure for dealing with missing data from the analysis of the completed data can be advantageous. For example, because CNMI uses a nonparametric MI engine that preserves the multivariate associations observed in the data, the integration step is agnostic to assumptions about latent structure in the data, such as the dimensions of the latent variables, the form of the measurement models, the scoring methods to be employed, etc. Various models can be assessed and implemented on the completed data sets after the integration, without re-integrating the data for each new latent structure (or other type of) model under consideration (this is not to say that the CNMI approach is assumption free, as we will discuss later). Moreover, because it uses a de novo sample with all variables measured, the CNMI integration step does not need to rely on the existence of a sufficient number of anchor items, and in fact, can be implemented with no anchor items or to integrate previously unmeasured variables. Finally, the CNMI approach easily leverages any available variables in the data sets (e.g., other outcomes) that are predictive of missing values but not relevant for a substantive model.

Notwithstanding these potential advantages, we do not propose that the CNMI approach should supplant MMI procedures in cases where both are feasible, nor do we claim that CNMI will consistently outperform the MMI approach. In fact, when the analyst's hypothesized measurement model is correctly specified in MMI, there is no reason to collect additional data in a de novo sample, other than to provide an additional “bridge” for the integration, if resources permit. Moreover, as is well established in the multiple imputation literature (e.g., Collins, Schafer, & Kam, 2001), results from procedures that directly handle missing data in the substantive model (e.g., FIML-based approaches like MMI) will be more precise than those derived from separate estimation of the same model following multiple imputation, assuming the multiple imputation uses the same variables and assumptions as the one-step, substantive model-based approach. Rather, we offer the CNMI approach as an alternative (or supplementary) solution to the data set integration problem in circumstances under which FIML-based MMI procedures may not be feasible or appropriate, as when theory is insufficient to guard against the risk of missing data and/or measurement model misspecification, when there is very little or no overlap of items across contributing samples, or when variables unavailable on existing data sets are desired for analysis.

As noted by Curran and Hussong (2009) in their discussion of MMI, analysts must consider several key issues when evaluating the results of data integration procedures, including the potential impact of history and period effects, the representativeness of the integrated data, and measurement invariance. We turn now to a discussion of such issues in the CNMI context in particular.

Conditions and Assumptions Underpinning CNMI

Heterogeneity due to geography

Frequently, the data sets to be integrated are collected in different geographic regions (perhaps with non-probability samples). In such contexts, it can be difficult to describe the target population that corresponds to the concatenated data sets. At best, the conclusions from analyses of CNMI-integrated data are appropriate for the specific regions included in the contributing data samples. Extending conclusions to other regions requires extrapolations that cannot be checked with the observed data, regardless of the method of integration.

Ideally, de novo calibration data would be obtained from the same geographic regions as the data samples to be integrated. This ensures that the models can be tailored to particular geographies, for example, via the inclusion of a categorical predictor for geographic region in the CART models. This allows for the integration to incorporate variation in distributions by geographic region, because the calibration data include data from all regions. When collecting the de novo data from the target regions is not convenient or feasible, analysts seeking to use CNMI should include in the calibration data and imputation models any variables that are differentially distributed across the geographies and related to the substantive variables to be integrated (assuming that such variables are available in the individual data sets; otherwise there is no way to correct for such differences). For example, if one contributing sample (region) has more individuals of a certain demographic type than another contributing sample, and those demographics are relevant for predicting the substantive variables of interest, the analyst should collect the demographic variables in the calibration data and include them in the models. In such cases, the success of the CNMI relies on a conditional independence/exchangeability assumption: That is, we assume that given the demographic variables, the geographic location of the participant is not an important predictor of the missing items. If relevant demographic items are not available in the contributing samples, then analysts are forced to make strong assumptions that the distributions in the calibration data apply across all data sets, given the variables used in the imputation modeling.

Heterogeneity due to sampling design

When integrating data from several nationwide probability samples, which typically have complex sampling designs (e.g., clustering and oversampling of certain populations), it is possible to conceive of an underlying target population (assuming the data are collected contemporaneously). In this situation, the CNMI approach offers great flexibility for the analyst. The analyst could estimate models separately in each contributing study's completed (post-MI) data file, allowing one to use traditional design-based inference (Cochran, 1977) on each data set. Design-based point and variance estimates can be easily combined, since one needs only take a linear combination of the resulting estimates (possibly weighted by their precisions, as would be optimal for minimizing variance). Alternatively, the analyst could choose to re-weight individual observations in the concatenated completed data set, for example by calibrating to known population estimates, although this can be complicated with multi-stage sampling designs (Rubin, 1986). Either way, because the data integration step is separate from the substantive analysis, in CNMI one can deal with differential sampling designs in the model estimation process just as one would if provided a set of complete (non-missing) data.

As when dealing with geographic heterogeneity, CNMI analysts should include relevant design variables in the calibration survey and in the imputation models. This is similar in spirit to general advice on multiple imputation for missing data (Reiter, Raghunathan, & Kinney, 2006). The design variables allow one to assess and correct for differences in sampling designs at the imputation stage, again under the assumption that the distributions between responses and predictors are essentially identical across the different survey designs.

Finally, although not formally an issue of sampling design, CNMI assumes that any item and unit nonresponse within the samples has occurred at random. This assumption cannot be checked using the observed data; however, CNMI's separation of the integration from the substantive analysis does facilitate analyses of the sensitivity of final model conclusions to various assumptions about the nature of the missing data mechanism (e.g., missing at random or not missing at random; Rubin, 1976).

Heterogeneity due to history

Often the data samples to be integrated were originally collected at different time points. As Curran and Hussong (2009) note, the measurements associated with the various contributing samples can be affected by differences across time, for example, by changing attitudes or by the influence of significant events. CNMI can be particularly susceptible to such effects, because the collection of the calibration sample almost surely does not occur contemporaneously with the collection of the data samples to be integrated. We know of no way to correct for such issues without making strong assumptions about the nature of the time effects.

Recently, MMI approaches have been used to integrate longitudinal data (e.g., Curran et al., 2008). Conceptually, the CNMI approach can also apply to longitudinal data. The calibration data must include the same variables measured at the same time points. In practice, that may be challenging to accomplish, particularly when one uses a convenience sampling approach. It may be possible to collect fewer time points in the calibration sample, assuming that an ample number of time points from each individual data set have been collected to serve as a “bridge” for estimating the conditional distributions. Configuring such studies represents an intriguing area for future research.

Other design effects

The data collection methods used for the calibration sample will ideally be similar to those used for the data samples to be integrated. For example, if a variable is measured as part of an interview conducted exclusively by telephone, it would be preferable for that variable to be collected by telephone in the calibration survey. On the other hand, if the variable is collected sometimes by phone and other times by Internet, ideally we would include both modes of collection in the calibration survey and include an indicator for mode type in the imputation models. This would allow the integrated data set to reflect heterogeneity due to mode effects, which then can be dealt with at the analysis stage. For some models, especially in person sampling, available resources may make it infeasible to mimic a contributing study's design. In such cases, one can complete the calibration survey using a feasible mode of data collection, and compare the distributions of the resulting variables in the calibration and to-be-integrated data sets. Substantial differences could indicate a mode effect (or some other effect) that could raise doubt about the validity of the CNMI integration.

Heterogeneity due to measurement

Measurement invariance and measurement comparability play crucial roles in applications of CNMI, as they do in other data integration models. However, because CNMI separates the integration step from the analysis step, invariance and comparability for particular constructs are not a concern at the integration stage; these concerns arise at the analysis stage. At the integration stage for CNMI, the measurement assumption required is that the conditional distributions (conditional on demographic characteristics common across files) for variables to be integrated are the same (or at least similar) across the populations from which the data sets were sampled. This crucially implies that the relevant conditional distributions in the calibration data are the same as, or at least similar to, those in the other data sets. One can partially check this assumption empirically for variables measured in the calibration data and at least one of the to-be-integrated data sets; for example, one can compare the same conditional models across data sets estimated with the common variables, as we illustrate in our application below. However, for variables that are available only in the calibration data, one is forced to assume similar conditional distributions involving those variables. The CART imputation engine samples observed data values based on the predictors. Thus, if the calibration data do not span the predictor space in the other data sets, the method can generate draws from the wrong part of the conditional distribution for the outcomes. As an extreme example, if the calibration data include only older participants but one of the data sets includes many younger participants, and the outcome variables differ by age, the CART imputations will be based inaccurately on donors from nodes of older-age participants. Similar issues arise for imputing the distributions of the outcome variables. For example, suppose that the calibration data are collected from individuals at the upper tail of the Y distribution and the integrated data are from the lower tail: The CART imputations will use values from the upper tail and therefore impute poorly. Unfortunately, for non-overlapping measures, this type of assumption violation can be difficult to detect.

Below, we illustrate how calibration data and multiple imputation via sequential CART models can be used for data set integration. We do this from a methodological perspective, focusing on the details of the integration procedure and analyses that assess the quality of the multiple imputations.

Method

Data Sets to be Integrated

Our substantive research generally concerns the role of regulatory processes in the development and prevention of substance use disorders in adolescence and early adulthood. In the present study, we elected to focus on measured variables that tapped (a) the frequency and amount of alcohol use and (b) degree of association with deviant peers. We selected these variables because the latter construct is a known risk factor for the onset of alcohol use disorders, and because theoretical and empirical work (e.g., Dick & Kendler, 2012) has begun to explore the extent to which such risk factors might interact with genetic influences to predict the onset of problematic use. This research context, therefore, would appear ripe with needs (and opportunities) for the synthesis of existing data sets; we emphasize, however, that our method can be applied in any context in which the integration of data sets is desired.

The goal of our study was to develop general purpose methodology. Hence, our empirical work is aimed to demonstrate proof of concept rather than to provide a rigorous test of particular substantive hypotheses related to alcohol use. We therefore integrated three existing data sets, selected on the basis of (a) their ready availability to the study team and (b) their measurement of two primary constructs of interest. The included studies all produced large, multiple-wave data sets containing measurements of variables from multiple informants (e.g., target participant, parent, peer). We included and integrated data from original study records that corresponded to measurements taken when the participant was aged 19 or 20. Brief descriptions of the three data sets to be integrated are provided below.

Data set one—source: National Longitudinal Survey of Adolescent Health (Add Health)

Add Health is a large, longitudinal, school-based study of adolescent physical and mental health that began in 1994 with an in-school questionnaire administered to a sample of students in grades 7 through 12; the latest wave of data collection (Wave IV) occurred in 2007-2008. A sample of 80 high schools and 52 middle schools from the U.S. was selected with unequal probability of selection; incorporating systematic sampling methods and implicit stratification into the Add Health study design ensured the sample was representative of U.S. schools with respect to region of country, urbanicity, school size, school type, and ethnicity (Harris et al., 2009). The data included in the current study were from Wave III, collected through in-home interviews during 2001-2002 when respondents were between the ages of 18 and 26. Wave III was designed to assess young adult life events and was collected with the use of Audio CASI, an audio-enhanced, computer-assisted self-interview program.

Original study records included in data set to be integrated

From the larger Add Health data set, we retained records that met the following criteria: (a) the record was recorded in Wave III (the Wave during which the substantive variables of present interest were collected) and (b) the participant's age (computed by us, assuming a mid-month birthday, as the difference in years between the Wave III interview date and the participant's birthdate) was greater than or equal to 19 and less than 21. Of 15,197 observations stored on the Add Health Wave III data set, n = 3447 met age criteria for inclusion in our study data set.

Data set two—source: Child Development Project (CDP)

The CDP (Dodge et al., 1990) is a multiple-site, longitudinal study aimed at investigating the relationship between child and adolescent socio-emotional development and the development of antisocial behavior in early adulthood. In 1987 and 1988, during the year before entering kindergarten, N = 585 children from two cohorts were recruited for the study from Nashville, Tennessee, Knoxville, Tennessee, and Bloomington, Indiana. Study assessments have been conducted annually and include data from multiple informants, including the target children themselves as well as parents, teachers, peers, observers, and administrative (school and court) records.

Original study records included in data set to be integrated

The CDP variables used for the present study were taken from the Wave 15 Main Interview (Section 4: Drug and Alcohol Use) and Youth Self Report Form. Participant birthdates were collected from the Wave 13 demographics data set. From the larger CDP data set, we retained records that met the following criteria: (a) the record was recorded in Wave 15 (the Wave during which substantive variables of present interest were collected, and during which participants were expected to be of the target age); and (b) participant age (computed by us, assuming a mid-month birthday, as the difference in years between the Wave 15 interview date and the participant's Wave 13-recorded birthdate) was greater than or equal to 19 and less than 21. Two cohorts were reflected in the resulting sample. Of 467 CDP participants present on the Wave 15 interview dates data set, 457 were included on the separate data sets that contained measurement scale scores; of those, 399 had valid stored Wave 13 birth dates, and of those, n = 313 met age criteria for inclusion.

Data set three—source: Great Smoky Mountains Study (GSMS)

The GSMS is a longitudinal study of youth focused on the development of psychiatric disorder and the need for mental health services (Costello et al., 1996). Children from 11 counties in western North Carolina were selected for initial screening using a household equal probability sampling method; children with behavior problems were oversampled for enrollment in the study, as were Native American children. The GSMS reflects an accelerated, three-cohort design; the final study sample as of Wave 1 was comprised of N = 1338 children, aged 9, 11, and 13 at intake. Observed GSMS scores used in the present study were obtained using the GSMS's Young Adult Psychiatric Assessment (YAPA), a semi-structured interview assessment tool employed by the GSMS for data collection after study participants reached adulthood.

Original study records included in data set to be integrated

From the larger GSMS data set, we retained records meeting the criterion that participant age was greater than or equal to 19 and less than 21 as of the time of interview; n = 789 participant records met age criteria for inclusion in our study data set.

Items Selected from Data Sets to be Integrated

Items retained from the three existing data sets tapped participant alcohol use/abuse (including frequency of alcohol use and experiences with binge drinking) and degree of association with deviant peers. Available demographic variables including age, sex, education, ethnicity, marital status, and area of residence were also selected from each data set. Table 1 presents representative items retained from the existing data sets, including associated item stems, participant response choices, and coding of responses. In all, nine alcohol use and six peer deviance items were retained from Add Health, three alcohol use and one peer deviance item were retained from the CDP, and 12 alcohol use and four peer deviance items were retained from the GSMS data set. A full listing of retained items is available online.

Table 1.

Selected Items from Existing Data Sets to be Integrated

Items tapping alcohol use
Data set	Variable	Item stem	Response options
Add Health	H3TO41	During the past two weeks, how many times did you have five or more drinks on a single occasion, for example, in the same evening?	(number of times)
	H3TO43	During the past 12 months, on how many days have you been drunk or very high on alcohol?	0= none 1= 1 or 2 days in the past 12 months 2= once a month or less (3 to 12 times in the past 12 months) 3= 2 or 3 days a month 4= 1 or 2 days a week 5= 3 to 5 days a week 6= every day or almost every day
CDP	DAU15EDF	Have you ever had a drink first thing in the morning to steady your nerves or get rid of a hangover?	0= no 1= yes
	DAU15RDF	In the last 30 days, have you had a drink first thing in the morning to steady your nerves or get rid of a hangover?	0= no 1= yes
GSMS	CHA3I01	How many whole drinks per week have you consumed, on average, in the past 3 months?	(number of drinks)

Items tapping associations with deviant peers
Data set	Variable	Item stem	Response options
Add Health	H3TO52	My close friends would disapprove of my binge drinking.	1= strongly agree 2= agree 3= neither agree nor disagree 4= disagree 5= strongly disagree
	H3TO104	Of your three best friends, how many binge drink at least once a month?	0= none of my friends 1= one friend 2= two friends 3= three friends
CDP	Y15A39	I hang around with kids who get in trouble	0= not true 1= somewhat or sometimes true 2= very true or often true
GSMS	CAV8I02	How many of your friends use marijuana or other drugs?	0 = None 2= A few 3= Some 4= Most 5= All

Note. Add Health = National Longitudinal Study of Adolescent Health; CDP = Child Development Project; GSMS = Great Smoky Mountains Study of Youth.

Calibration Study

Our integration approach involves the collection of data from a de novo sample for use as calibration data. The calibration data set should include records for which all study variables are jointly observed, yielding information about associations that would otherwise be unavailable; as described further below, our calibration study also included an additional, “gold-standard” measure of problematic alcohol use, which was a variable unavailable on existing data sets that we wished to include in a substantive model to be estimated following data set integration. In general, collecting adequately powered, de novo calibration samples can be an expensive and time-consuming endeavor. However, with the rise of rapid-response survey outfits like CivicScience and Internet panels like Knowledge Networks, it is now feasible to obtain responses while leveraging others’ infrastructure for data collection. We used an Internet panel, as we now describe.

Participants

Participants in the calibration study were members of an existing research panel managed by Knowledge Networks (KN). The KN panel was developed and is continuously maintained through the use of a published sample frame of residential addresses that covers approximately 97% of U.S. households and consists of approximately 50,000 adult members. The KN website (www.knowledgenetworks.com) provides additional details about its panel and data collection practices. To promote maximum consistency with the data sets (samples) to be integrated, the KN sample was restricted in composition to 19- and 20-year-old participants.

Measures

Calibration sample participants produced scores for all items retained from the data sets to be integrated. Calibration sample participants additionally completed the Alcohol Use Disorders Identification Test (AUDIT; Babor & Grant, 1989), which we selected for inclusion in the study as a “gold standard” measure of alcohol use/abuse. The AUDIT (available online) is a brief 10-item instrument developed by the World Health Organization as a method of screening for problematic alcohol involvement. Multiple research studies over its two decades of use have demonstrated the validity and reliability of the AUDIT as a measure of alcohol use/abuse along a broad continuum of severity, and it has been shown to be a highly sensitive and specific measure of risk for harmful drinking and/or dependence across groups defined by gender, age, ethnicity, and culture (cf. Babor et al., 2001). The AUDIT may be administered via either oral interview or by questionnaire; we administered the AUDIT electronically. Responses to individual items were summed to produce an overall AUDIT scale score for each participant. Inclusion in the calibration sample of both the AUDIT scale items and items tapping alcohol use on the data sets to be integrated allowed us to ascertain the conditional distributions between the AUDIT items and variables measured on the existing data sets.

Procedure

Our goal for the calibration study was to obtain response data that were measured and collected in a fashion that was as similar as possible to that involved in the data collection procedures for the data sets to be integrated. Accordingly, the calibration study involved an online survey component, which collected responses to items from the Add Health and CDP data sets and the calibration sample-only AUDIT measure, and a telephone interview component, which collected the semi-structured interview responses associated with the GSMS's YAPA. KN panelists were contacted by e-mail and invited to complete the online survey. Those who provided informed consent and completed the online survey were asked to provide a telephone number that would be used to contact them for the telephone-based interview. Experienced KN phone interviewers, trained by GSMS personnel via teleconference, conducted the portions of the YAPA included in the calibration study.

In all, 764 KN panelists who fell within the target age range were invited to participate in the calibration survey. Panelists were initially offered a $20 incentive by KN to complete both the online and telephone portions of the study. Of these, 224 (29.3%) provided informed consent and completed both the online survey and phone interview, and 83 (10.9%) completed the online survey but did not complete the phone interview. Remaining panelists were contacted again and offered a larger incentive ($50) to participate in the study. Of these “re-ask” panelists, 18 completed both the online and phone interview components, and 83 completed the online survey but not the phone interview. Our final KN sample was therefore comprised of n = 242 panelists who completed both the online survey and phone interview. For the 408 KN panelists who completed the online survey, the panelists who did and did not complete the phone interview were not significantly different in terms of education, χ²(3,n = 408) = 5.46, p = .14, race, χ²(4,n = 408) = 2.29, p = .68, gender, χ²(1,n = 408) = 1.07, p = .30, or age, t(406) = 0.45, p = .66. Likewise, mean (non-missing) AUDIT sum scores did not significantly differ for panelists who did and did not complete the phone interview, t(290) = 0.07, p = .94.

AUDIT test development and validation studies have suggested that the recommended cut-off score of 8 (or higher) is sensitive and specific for the presence of alcohol use disorders (Babor et al., 2001). The final KN sample (n = 242) had a mean AUDIT score of 2.95 (SD = 4.45), with an observed range of 0 (40% of participants) to 26 (2 participants); 31 participants (13%) exceeded the recommended cutoff score of 8.

Recoding of Demographic Variables

We produced a set of demographic variables for the integrated data set using the “transform and recode” approach, under the assumption that this approach should be appropriate for variables (such as descriptions of demographic characteristics) for which measurements are relatively objective (factual). In general, response categories for the calibration sample were retained, and item responses present on the other data sets to be integrated were recoded to match the corresponding calibration sample score (e.g., the KN gender variable coding was 1 = “Male” and 2 = “Female”, whereas the CDP coding was 0 = “Male” and 1 = “Female”; the CDP outcomes were recoded to match those of the KN sample and were stored in a new variable named KN_gender). Note that some demographic variables were only available for a subset of the data sets to be integrated (e.g., the CDP data set does not contain information about educational attainment). For all other study variables, a multiple imputation procedure was employed for integration as described below.

Multiple Imputation Procedure

We began by combining the three data sets to be integrated (Add Health, CDP, and GSMS) and the de novo calibration sample data set (KN) into a single file, for which all items that were not observed in a particular data set were coded as missing. The layout of the resulting data set is depicted in Table 2. For each of the Add Health, CDP, and GSMS data sets we had a group of variables that was exclusive to it and the KN data, another group that was shared in common with all other data sets (i.e., the set of demographic variables), and a group of variables that contained missing values. Note that by design, records from the KN sample, except for the rare item-level missing data point, did not contain any of these “holes.” Our objective was to produce concatenated data for which all records had non-missing scores (that is, we wished to fill in the holes in Table 2). We made the critical assumption that conditional relationships in the available calibration data apply in the data sets to be integrated. This allowed us to use the KN data to build multivariate imputation models and thereby fill in plausible values of the missing data for each individual in the integrated samples. Note that consistent with recommendations made by Gottschall, West, and Enders (2012), our approach focused on imputation at the item, rather than scale-score, level.

Table 2.

Initial Layout of Combined Data Set

Data set	Add Health items	CDP items	GSMS items	“Gold standard” (AUDIT) items	Demographic variables (transformed/recoded)
Add Health	X	--	--	--	X
CDP	--	X	--	--	X
GSMS	--	--	X	--	X
KN	X	X	X	X	X

Note. Add Health = National Longitudinal Study of Adolescent Health; CDP = Child Development Project; GSMS = Great Smoky Mountains Study of Youth; KN = Knowledge Networks calibration study. Available data are marked with an ‘X’; missing data are denoted with ‘—’.

We used the software developed by Burgette and Reiter (2010) to implement the sequential CART procedure; code specific to our application is available from the second author. To begin the procedure, we created a completed matrix by generating initial imputations of the missing values. To do so, we paired each of the data sets to be integrated (Add Health, GSMS, and CDP) with a copy of the KN data set. We then applied Burgette and Reiter's method for generating starting values to each of the three paired data sets separately; for example, when we paired the Add Health and KN data sets, we generated initial imputed scores for the items observed on the CDP and GSMS data sets (and the missing-by-design AUDIT items). After obtaining initial values, we used CART to regress each variable with missing data, one at a time, on all other variables (columns) in the combined data set and replaced the values corresponding to the missing data with draws from the corresponding predictive distribution. In addition to substantive variables, each imputation model included the recoded demographic variables age, gender, level of educational attainment, ethnicity, household size, and geographic region (see Table 3) as predictors. We applied the software with default settings to create m = 100 imputed data sets, each of which contained all four samples. (As noted by van Ginkel and Kroonenberg, 2014, and Bodner, 2008, among others, it is beneficial to use large m when fractions of missing information are large; doing so stabilizes estimates of standard errors and degrees of freedom. We recommend making m as large as is computationally feasible.) Such data sets can be directly used by analysts using complete-data methods, and then combined using multiple imputation techniques in order to reflect the uncertainty associated with the imputation procedure (Schafer & Graham, 2002; Schafer & Olsen, 1998).

Table 3.

Descriptive Statistics, Integrated Demographic Variables

	Sample
	Add Health (n = 3447)	CDP (n = 313)	GSMS (n = 789)	Calibration (n = 242)
Age
M (SD)	20.12 (0.55)	19.44 (0.29)	19.40 (0.39)	19.96 (0.57)
Gender
% Female	43.40	49.84	53.11	38.84
% Male	56.60	50.16	46.89	61.16
Education
% Less than high school	0.52	.	28.13	7.44
% High school diploma	48.04	.	38.24	32.23
% Some college	51.15	.	33.38	59.92
% College degree	0.29	.	0.26	0.41
Ethnicity
% White	56.09	83.71	62.99	69.42
% Black	22.27	14.70	5.32	7.02
% Other	21.63	1.60	31.69	23.55
Marital Status
% Never married	92.94	.	78.20	89.26
U.S. Census Region of Residence
% Northeast	13.07	0.00	0.00	16.12
% Midwest	23.62	38.66	0.00	28.10
% South	41.08	61.34	100.00	28.10
% West	22.24	0.00	0.00	27.69

Note. Add Health = National Longitudinal Study of Adolescent Health; CDP = Child Development Project; GSMS = Great Smoky Mountains Study of Youth.

Results

The “transform and recode” alignment of demographic variables was straightforward. As mentioned previously, some demographic variables were only available for a subset of the data sets to be integrated. One of the demographic variables, race, was scored using very different response categories on the various data sets to be integrated; we produced a recoded variable that reflected the most common response categories of Black, White, and Other. Table 3 contains descriptive statistics for the recoded demographic variables for participants in the calibration sample and three existing data sets.

The CART imputation routine was executed as described above, producing m = 100 imputations for each contributing sample. Of primary importance for our purposes was to investigate the quality of the CNMI implementation for this integration. We did this in two steps. First, we evaluated the similarity of conditional distributions across data sets for variables present in multiple files. Second, we evaluated of the ability of the imputation model itself to capture the relationships in the data. We note that data were not available to evaluate the assumption of equivalent distributions for the AUDIT score (total or components) across data files, because the AUDIT variables were measured only in one data set. Accordingly, it was necessary to make untestable assumptions to perform the integration, for example, that the conditional distributions for the total AUDIT score, given both the score on the Add Health variable H3TO41 (which measured the number of times five or more drinks were consumed on a single occasion during the previous two weeks) and observed scores on demographic variables, were similar for individuals participating in the KN survey and those who participated in the Add Health survey.

To evaluate the similarity of the conditional distributions across data sets where possible, we compared partial correlations (which controlled for the transformed-and-recoded demographic variables) and Pearson correlations for selected alcohol use and peer deviance variables in the four data sets. Results for the partial correlations are displayed in Table 4; Pearson correlations showed similar patterns. Overall, the partial correlation point estimates for the KN data were close to those for the corresponding existing data set (sometimes remarkably so). As shown in Table 4, confidence intervals for the contributing and calibration samples overlapped substantially for all variable pairs.

Table 4.

Partial Correlations for Selected Variable Pairs within Contributing and Calibration Samples

	Sample
	Add Health		CDP		GSMS		Calibration
	pr	95% CL	pr	95% CL	pr	95% CL	pr	95% CL
	n = 687						n = 123
Add Health variables:
H3TO41-H3TO43	.53	(.48,.59)					.47	(.31,.60)
H3TO41-H3TO52	.25	(.18,.32)					.14	(−.05,.32)a
H3TO41-H3T104	.40	(.34,.46)					.27	(.09,.44)b
H3TO43-H3TO52	.35	(.28,.41)					.38	(.20,.52)
H3TO43-H3T104	.45	(.38,.50)					.46	(.30,.59)
H3TO52-H3T104	.47	(.41,.53)					.44	(.27,.57)
			n = 269				n = 131
CDP variables:
DAU15RDF-DAU15EDF			.51	(.41,.59)			.43	(.28,.56)
DAU15RDF-Y15A39			.13	(.01,.25)			.13	(-.04,.30)
DAU15EDF-Y15A39			.20	(.09,.32)			.38	(.21,.52)
					n = 756		n = 117
GSMS variables:
CHA3101-CAV8I02					.29	(.22,.35)	.18	(−.00,.36)

Note. Add Health = National Longitudinal Study of Adolescent Health; CDP = Child Development Project; GSMS = Great Smoky Mountains Study of Youth; pr = partial correlation estimate; 95% CL = 95% Confidence Limits. Confidence limits were obtained using Fisher's z transformation.

^aWhen two unusual observations are excluded, pr = .21.

^bWhen two unusual observations are excluded, pr = .32.

We next examined how well the imputation model captured the dependencies among the variables to be integrated. To do so, we used the replicated data approach of He et al. (2010), which we implemented as follows: In addition to the imputed data sets, we generated 100 replicated data sets in which the imputation models were used to generate entirely simulated copies of the data. That is, we replaced both the missing and observed data with imputations drawn from the models. (Routines for implementation are available in the software of Burgette and Reiter, 2010.) When such replicated data sets have noticeably different distributions than the complete data, it suggests that the imputation models fail to reflect the distributions of the data accurately, such that the imputed data sets may not be reliable for estimation. We note that this approach primarily assesses the quality of the imputation models and not the plausibility of the assumption of similar conditional distributions across data sets.

To motivate an example of this diagnostic, suppose that the main goal for data integration were to enable the use of information from all data sets to explore the relationship between alcohol use, as measured by the “gold standard” AUDIT measure, and peer deviance variables (as in the example analysis presented in Table 5). It would be essential to ensure that the imputation model captured the relationships between the AUDIT measures and the peer deviance predictors. Because only the KN calibration data include all variables, we could assess the effectiveness of the imputation model by evaluating whether the imputations preserved the relationships between the AUDIT measure and the peer deviance predictors in the KN sample.

Table 5.

Parameter Estimates for Substantive Model, Derived using Multiple Imputation Techniques (N = 4776)

Variable	B	SE B
Intercept	3.00	4.63
Gender (reference group is Male)
Female	−0.39	0.18	*
Race/ethnicity (reference group is White)
Black	−1.29	0 22	****
American Indian/Other	−0.73	0.21	***
Educational attainment (reference group is high school diploma not received)
Graduated from high school	−0.26	0.38
Some college	0.36	0.39
Bachelor's degree or higher	0.20	1.51
Age	0.08	0.23
Fixed effects for study membership (reference group is KN)
Add Health	−0.11	0.31
CDP	−0.65	0.45
GSMS	−0.73	0.39
Y15A39	0.92	0.26	***
H3TO104	1.22	0.13	****
CAV8I02	1.18	0.13	****
H3TO104 × Female	−0.02	0.16

Note. Add Health = National Longitudinal Study of Adolescent Health; CDP = Child Development Project; GSMS = Great Smoky Mountains Study of Youth.

^*p < .05.

**p < .01.

^***p < .001.

^****p < .0001.

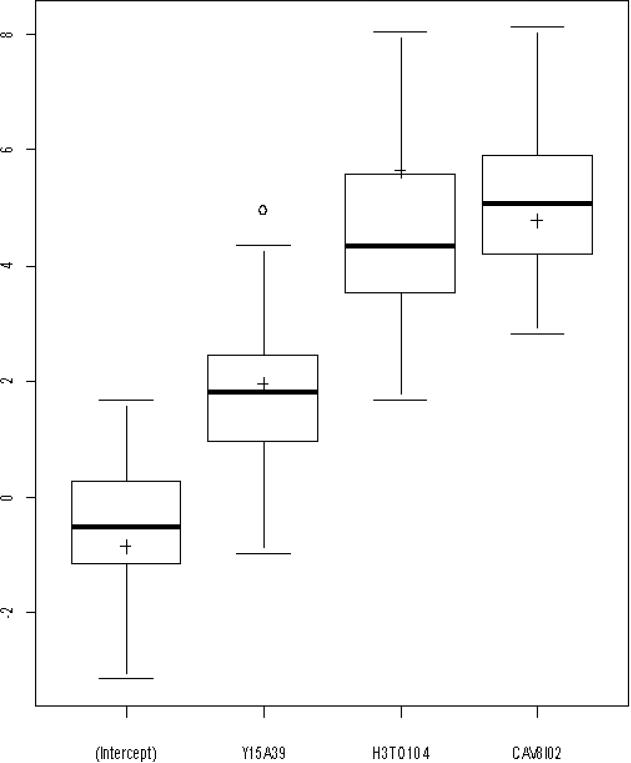
Figure 1 shows the standardized coefficients for the linear regression of the AUDIT measure on three peer deviance predictors, one from each of the three integrated data sets, as computed from the KN sample (crosses) and from the 100 predictive replications (box plots). As shown in Figure 1, the regression coefficients computed from the observed data lie within, or are very close to, the interquartile range of the empirical predictive distribution of regression coefficients, indicating that the model is in fact preserving not only the direction of the association between each predictor and the outcome, but also its magnitude. The finding that the replicated data sets generate substantive conclusions that do not meaningfully differ from those yielded by the KN sample suggests that there is no reason to doubt the reliability of the imputation model for this regression (again, given the unverifiable assumption that the conditional relationships for the AUDIT variable and the other alcohol use variables are similar across all data sets).

Figure 1.

Distribution of standardized coefficients for the regression of AUDIT score on peer deviance variables Y15A39, H3TO104, and CAV8I02 for both observed (crosses) and synthetic (box plots) data.

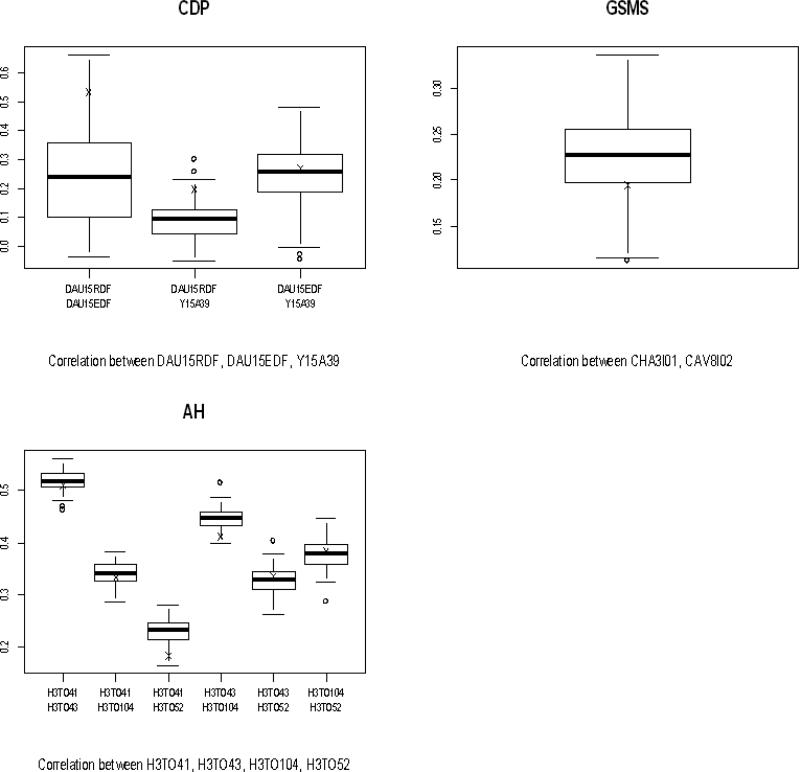
The replicated data sets can also be used to assess whether the imputation procedure adequately captured relationships among the integrated variables present in multiple data sets. To do this for our application, we computed correlations among pairs of fully observed variables within each original data set (Add Health, CDP, and GSMS) and compared them to the distribution of 100 replicated correlations for those same variables (using the same sets of original records for both the original data and the replicated data sets). Figure 2 displays box plots of the distribution of replicated correlations for several pairs of variables; the sample correlations from the original data sets are indicated with crosses. The magnitudes of sample correlations from the observed data tended to be either slightly over-estimated or under-estimated in the replicated data; however, in all cases, the signs of the correlations were preserved. If the correlations had been substantially different in the replicated and observed data (e.g., if most did not fall within the whiskers of the box plots), it would suggest that the model failed to capture associations among the variables effectively, such that we would be skeptical of the quality of the imputations for those variables. Because this was not the case, our assessment is that the imputation model appears to fit the combined data well. (This finding does not imply that the distributions are similar across data sets; the Add Health sample size, for example, is so relatively large that the imputations for the variables in Add Health primarily reflect the distribution from that data set.)

Figure 2.

Correlations among selected variables for both observed (crosses) and synthetic (box plots) data. AH = National Longitudinal Study of Adolescent Health; CDP = Child Development Project; GSMS = Great Smoky Mountains Study of Youth.

As previously discussed, the primary goal of our work was to develop methodology for data integration, as opposed to focusing on specific questions of substantive theoretical interest. However, having established the quality of the CNMI implementation for this integration, we were able to proceed to fit a simple substantive model to the integrated data sets for demonstration purposes. The model involved the linear regression of the new AUDIT measure on three peer deviance predictors, one from each of the three contributing samples, controlling for multiple demographic variables. Table 5 presents parameter estimates, derived using multiple imputation techniques, for this substantive model as computed for the integrated (all samples combined) data set. As shown in Table 5, the substantive model for the integrated data set included fixed effects for study membership, none of which was statistically significant. Results indicated that partial regression coefficients for all three peer deviance predictors (Y15A39, which corresponds to the CDP survey item “I hang around with kids who get in trouble”; H3TO104, which corresponds to the Add Health survey item “Of your three best friends, how many binge drink at least once a month?”; and the GSMS-originating CAV8I02, which corresponds to the item “How many of your friends use marijuana or other drugs?”) were significantly different from zero, with increasing scores on each peer deviance predictor associated with higher predicted AUDIT score, all else held constant. All else held constant, there was insufficient evidence to conclude that the magnitude of the relationship between H3TO104 and AUDIT score varied by gender. Results further indicated that being of female gender or of non-White race/ethnicity was associated with a significant reduction in predicted AUDIT score, and that partial regression coefficients for neither age (within the narrow range studied here) nor educational attainment were statistically significant, all else held constant.

Note that because the CNMI approach separates the data integration step from the substantive data analysis step, any substantive model could have been applied by us (or could be applied by future teams of researchers) to the CNMI-integrated data sets. Stated differently, when using the CNMI approach, the data integration step need not be repeated each time a new substantive model is tested.

Discussion

The present study demonstrates a proof of concept for a new method for the retrospective integration of data sets. Our procedure treated the data integration procedure as a missing data problem, and involved the application of nonparametric multiple imputation techniques. To reduce reliance on strong and possibly unverifiable modeling assumptions—such as hypothesized generative psychometric models—we collected data on all study variables from a de novo, independent sample, which yielded information about the missing conditional relationships among the variables to be integrated, and we separated the data integration step from the substantive data analysis. Overall, results indicated that the proposed procedure generated imputed data sets that preserved the relationships among study variables in the complete calibration data set.

We have already discussed the potential relative strengths and weaknesses of the CNMI approach. We should also note that in our study, all variables under consideration for analysis were included in the calibration sample and hence in the imputation models. This may not always be possible; for example, it may sometimes be infeasible to collect genotype or other cost-prohibitive data in calibration samples. Analyses of the completed data sets that involve variables not in the imputation models—we may call such variables omitted variables—are valid (non-trivially) when the missing values in the outcome and predictors of interest are conditionally independent of the omitted variables. For example, when the omitted variables include genotype data and the outcome variable is the AUDIT score, to use genotype information in modeling one would have to assume that any individual's AUDIT score is conditionally independent of genotype given their answers to the subset of questions about alcohol use (and demographics and peer relationships). This does not imply independence between the outcome variable and the omitted variables, because imputed outcomes are analyzed unconditional on the intermediate predictors. For example, once AUDIT scores were imputed, we would discard site-specific questions on alcohol use in models that regress AUDIT score on peer effects plus genetic effects.

The CNMI approach is one of several options for data integration. Clearly, practical concerns will play an important role when choosing a data integration technique. Our application of the nonparametric multiple imputation approach relied on the collection of a de novo calibration sample, an effort that does require additional investment of time and resources. We utilized an existing research panel for our calibration sample, as it was relatively inexpensive and the questions we asked were mostly amenable to online data collection; not all investigators will have access to such a panel, either because the service is cost-prohibitive, because in-person interviews are required, and/or because their population of interest (e.g., young children) cannot be accessed using existing sampling frames. Such factors could affect the overall expense and expected timeline of the data integration effort. However, when analysts are not willing to pre-specify the measurement model and latent structure, or when additional variables need be collected, the CNMI approach offers a reasonable alternative.

The integration of existing data sets is both a worthwhile pursuit and a problem of considerable methodological complexity. We hope that future research might carefully examine the extent to which our proposed approach, and other existing methods already in practice, are effective and valid under conditions commonly encountered in applied research. We anticipate that extensive simulation studies will be particularly informative, including, for example, studies that experimentally vary and evaluate the impact of factors such as the relative sizes of existing and calibration samples and the extent of violations of key assumptions.