Skip to main content
PMC home page
Acta Crystallographica Section D: Biological Crystallography logoLink to Acta Crystallographica Section D: Biological Crystallography
. 2015 Jul 31;71(Pt 8):1725–1735. doi: 10.1107/S1399004715010676

Three-dimensional structure of the human breast cancer resistance protein (BCRP/ABCG2) in an inward-facing conformation

Mark F Rosenberg a,b, Zsolt Bikadi c, Eszter Hazai a, Tobias Starborg a, Lawrence Kelley d, Naomi E Chayen b, Robert C Ford a, Qingcheng Mao e,*
PMCID: PMC4528803  PMID: 26249353

The first three-dimensional structure of human ABCG2 in the absence of nucleotides and transported substrates has been determined at 2.0 nm resolution. In this state, ABCG2 is in an inward-facing conformation.

Keywords: ABCG2, BCRP, ABC transporter, ATP-binding cassette transporter, cryo-electron microscopy, three-dimensional structure from two-dimensional crystals

Abstract

ABCG2 is an efflux drug transporter that plays an important role in drug resistance and drug disposition. In this study, the first three-dimensional structure of human full-length ABCG2 analysed by electron crystallography from two-dimensional crystals in the absence of nucleotides and transported substrates is reported at 2 nm resolution. In this state, ABCG2 forms a symmetric homodimer with a noncrystallographic twofold axis perpendicular to the two-dimensional crystal plane, as confirmed by subtomogram averaging. This configuration suggests an inward-facing configuration similar to murine ABCB1, with the nucleotide-binding domains (NBDs) widely separated from each other. In the three-dimensional map, densities representing the long cytoplasmic extensions from the transmembrane domains that connect the NBDs are clearly visible. The structural data have allowed the atomic model of ABCG2 to be refined, in which the two arms of the V-shaped ABCG2 homodimeric complex are in a more closed and narrower conformation. The structural data and the refined model of ABCG2 are compatible with the biochemical analysis of the previously published mutagenesis studies, providing novel insight into the structure and function of the transporter.

1. Introduction  

The overexpression of several members of the ATP-binding cassette (ABC) transporter superfamily is associated with multidrug resistance (MDR) in cancer cells. These transporters extrude chemotherapeutics from the cell, reducing intracellular drug concentrations (Deeley et al., 2006 ▸; Sarkadi et al., 2006 ▸). The human breast cancer resistance protein (BCRP or ABCG21) is one such ABC efflux drug transporter. ABCG2 is expressed in a wide range of solid, haematological and lymphoid malignancies, and has been associated with MDR and adverse disease outcomes in some of these tumours (Natarajan et al., 2012 ▸; Robey et al., 2007 ▸). ABCG2 may play a significant role in drug resistance in breast cancer. Multidrug-resistant MCF-7 breast cancer cells generate extracellular vesicles containing ABCG2, which can sequester anticancer drugs, preventing them from reaching their intracellular targets (Goler-Baron & Assaraf, 2011 ▸). Resistance to 5-fluorouracil (5-FU) in a breast cancer patient population was also found to be owing to ABCG2 overexpression (Yuan et al., 2009 ▸). A recent review also highlighted the importance of ABCG2 in acute myeloid leukaemia (AML), affecting response and survival rates (Xia & Smith, 2012 ▸).

ABCG2 is also highly expressed in organs important for the absorption (the small intestine), elimination (the liver and kidney) and distribution (for example, the blood–brain and blood–placental barriers) of drugs (Maliepaard et al., 2001 ▸), and has been recognized to be one of the key transporters important for drug disposition and tissue protection (Giacomini et al., 2010 ▸; Poguntke et al., 2010 ▸; Polgar et al., 2008 ▸). For example, human subjects carrying the common variant Q141K with reduced cell-surface expression and activity are at an increased risk for altered pharmacokinetics of drugs such as 9-aminocamptothecin (Zamboni et al., 2006 ▸), irinotecan (Zhou et al., 2005 ▸), rosuvastatin (Zhang et al., 2006 ▸) and sulfasalazine (Urquhart et al., 2008 ▸). ABCG2 also eliminates urate from the body, resulting in a higher risk of developing gout in male patients harbouring Q141K owing to elevated serum urate levels (Woodward et al., 2009 ▸).

Human ABCG2 is a glycosylated plasma-membrane protein with a molecular weight of approximately 75 kDa. Since its discovery in 1998, transport studies have shown that ABCG2 possesses broad substrate specificity, ranging from hydrophobic chemotherapeutics to hydrophilic organic anions conjugated to sulfate, glutathione and glucuronate (Ni, Bikadi, Rosenberg et al., 2010 ▸; Robey et al., 2009 ▸). It can also transport nucleoside drugs and their monophosphate derivatives (Fukuda & Schuetz, 2012 ▸). Most ABC transporters have a topology with two transmembrane domains (TMDs) and two nucleotide-binding domains (NBDs), in which each TMD is N-terminal to a cognate NBD (Hyde et al., 1990 ▸). Members of the G subfamily of ABC transporters such as ABCG2, however, show the reverse topology, with the NBD being N-terminal to the cognate TMD (Ni, Bikadi, Rosenberg et al., 2010 ▸; Polgar et al., 2008 ▸). ABCG2 is also unique in that it consists of only one NBD and one TMD fused together, and hence it must dimerize in order to form a functional transporter (Dezi et al., 2010 ▸; Xu et al., 2004 ▸). Previous mutagenesis studies have identified several residues in the TMD of ABCG2, including Arg482 and Pro485 in the third TM α-helix (TM3), that are important determinants of substrate specificity and/or overall transport activity (Honjo et al., 2001 ▸; Ni, Bikadi, Cai et al., 2010 ▸; Ni et al., 2011 ▸; Özvegy-Laczka et al., 2005 ▸). The mechanism by which ABCG2 transports drugs is still poorly understood at the molecular level. As proposed in the ATP-switch and constant-contact models (George & Jones, 2012 ▸; Linton & Higgins, 2007 ▸), an ABC transporter undergoes several major conformational changes that drive the transport of substances across the membrane. The open apo inward-facing and the outward-facing conformations have been demonstrated for the Escherichia coli ABC lipid transporter MsbA in a lipid environment using double electron-electron resonance spectroscopy (Zou et al., 2009 ▸), which supports the ATP-switch model. However, other studies seem to support the constant-contact model, in which the NBDs are proposed to maintain contact in the drug-transport cycle (Jones & George, 2009 ▸).

In eukaryotic ABC transporters and one class of prokaryotic ABC transporters, there is a growing body of evidence that coupling of ATP binding/hydrolysis at the NBDs to TMD movement is mediated via two intracellular loops (ICLs) formed by long extensions of the TM α-helices (Kerr et al., 2010 ▸). One of the ICLs crosses over from the opposing TMD so that a hinge-like movement of the two TMDs can be coupled to closure of the NBD–NBD interface and occlusion of ATP. In the G subfamily of ABC transporters, predictions based purely on hydrophobicity variation in the primary structure suggest that the ICLs are of differing lengths and are relatively short [for example, 28 and eight residues for the first (between TM2 and TM3) and the second (between TM4 and TM5) ICLs, respectively, in ABCG2 (Hazai & Bikádi, 2008 ▸; Li et al., 2007 ▸)] compared with the ICLs found in other ABC transporter families (for example, 49–60 residues for all four ICLs in ABCB1; Kos & Ford, 2009 ▸). These differences suggest that there is no cross-over of an ICL from one ABCG monomer to the opposing NBD, or at least that such a cross-over must be organized differently to the situation in other eukaryotic ABC transporter families. However, our recent mutagenesis and antibody labelling data on ABCG2 conflict with the computer-predicted model, revealing a long (40 residues) ICL2 connecting TM4 and TM5. This arrangement would be much more compatible with the classical model for ABC exporter structure and function (Rosenberg et al., 2010 ▸; Wang et al., 2008 ▸). Clearly, three-dimensional structural data for the ABCG subfamily are necessary to resolve these questions. In the present study, we have determined the three-dimensional structure of ABCG2 by cryo-electron microscopy (cryo-EM) of two-dimensional crystals grown in the absence of nucleotides and transported substrates. Here, we describe the structure of ABCG2 at 2.0 nm resolution. This study is based upon the two-dimensional crystallization studies of full-length ABCG2 that we have previously reported (Rosenberg et al., 2010 ▸). Although the structural data only relate to one conformational state, the resolution of the data is sufficient to identify the NBD and the TMD components of ABCG2 and their organization in the homodimeric complex. The NBDs of ABCG2 were separated and the TMDs showed a V-shaped conformation. This allowed the refinement of the homology-based structural model of ABCG2 that we previously developed, which should offer further insights into its mechanism of action.

2. Materials and methods  

2.1. Expression, purification and crystallization  

ABCG2 was expressed in the yeast Pichia pastoris and purified using a polyhistidine tag in the presence of N-dodecyl-β-d-maltoside. These procedures and the formation of two-dimensional crystals have been described previously (Rosenberg et al., 2010 ▸).

2.2. Image acquisition and processing  

Images were collected on FEI G2 Polara and Tecnai F20 field-emission microscopes operated at 300 and 200 kV, respectively. The specimen was maintained at <100 K throughout. Primary magnifications of 50 000–80 000× were used with a mean underfocus ranging from 200 to 1500 nm. Images were recorded in low-dose mode with total dose of 10–12 e Å−2. The crystals were imaged at tilt angles in the range 0–60° in order to obtain three-dimensional data. Images were recorded on a 4000 × 4000 pixel CCD camera and, for some data, on Kodak SO-163 film, which was developed for 12 min in full-strength Kodak D19 developer and then scanned as described previously (Rosenberg et al., 2010 ▸).

Images were processed using the 2dx software package (Gipson et al., 2007 ▸), which uses the MRC software (Crowther et al., 1996 ▸) to correct for lattice distortions and the effect of the contrast-transfer function before extracting structure factors from the crystal images. To prevent reference bias in the unbending routine, we used high signal-to-noise references (with IQ values of 2 and 3, where 1 is the highest signal to noise). Initial estimates of tilt angles were calculated from the lattice parameters using the EMTILT program (Amos et al., 1982 ▸), and crystal data were processed using the p121 plane-group symmetry as described previously (Rosenberg et al., 2010 ▸). The three-dimensional data set was merged using the same symmetry using the 2dx_merge component of the software package. The final three-dimensional map was calculated using CCP4 routines (Winn et al., 2011 ▸) with a negative B factor of −150 Å2. The maps were examined using the Chimera package (http://www.cgl.ucsf.edu/chimera; Pettersen et al., 2004 ▸) and real-space averaging of the two ABCG2 monomers in the homodimer.

2.3. Electron tomography  

Tomographic tilt series were recorded using an FEI G2 Polara transmission electron microscope operated at 300 kV. Tomography data were recorded using the FEI Tomography control software, with tilting between −65 and +65° with 2.5° increments up to +50° and then 1° increments up to 65°, as described previously (Rosenberg et al., 2011 ▸). The total electron dose was restricted to 40 e Å−2. Subsequent processing was carried out with the IMOD tomography package as described previously (Kremer et al., 1996 ▸). No fiducial gold markers were used. Therefore, tilted images were initially aligned using a patch-tracking algorithm similar to the approach used by Castaño-Díez et al. (2010 ▸), which tracks structural features through the tilt images. After editing, the mean residuals for the patches were <3 pixels using 2048 × 2048 images at 0.3 nm per pixel.

2.4. Subtomogram averaging  

To generate a three-dimensional map independent of electron crystallography, a subtomogram average was generated using the two-dimensional crystal unit cell as input by aligning subvolumes of ABCG2 using the Dynamo (Castaño-Díez et al., 2012 ▸) and EMAN2 (Tang et al., 2007 ▸) software with the preliminary average as a reference. Subtomogram averaging is not usually performed on two-dimensional crystals, but since the sample is crystalline the rotation of the particles is more limited, thus reducing the degrees of freedom of movement of the subvolumes, which may enhance the resolution of the final three-dimensional map. The resulting subtomogram average was generated from 100 subvolumes and the final volume was twofold-averaged using Chimera (Pettersen et al., 2004 ▸). Fourier shell correlation was used to ascertain the resolution from two independently determined subtomogram averages (Saxton & Baumeister, 1982 ▸). To determine whether our map is consistent with the results from high-resolution X-ray crystallography of ABC transporters, the X-ray structure of murine ABCB1 (PDB entry 4ksb; Ward et al., 2013 ▸) was placed into the subtomogram average by manual fitting and by automatic fitting using the Chimera command ‘fit in map’ (Pettersen et al., 2004 ▸).

2.5. Molecular modelling  

The original closed apo model of ABCG2 which we previously developed using the mouse ABCB1 structure as a template (PDB entry 3g60; Rosenberg et al., 2010 ▸) was used for model refinement based on the three-dimensional ABCG2 map of this study. The Situs software package (Wriggers, 2010 ▸) was used to align the original model with the ABCG2 map as follows. Visual inspection of the structural alignment implied significant differences between the ABCG2 map and the model, namely because of the spatial arrangement of the two monomers. Therefore, the new model was optimized by cutting the model into two symmetric halves, and the two halves were aligned individually. The resulting aligned halves were used as a template for modelling, resulting in a more closed form. Homology modelling of ABCG2 based on this artificial template was carried out using the MODELLER9.11 package (Šali & Blundell, 1993 ▸). A bundle of ten models from random generation of the starting structure were calculated using the very thorough molecular-dynamics model-optimization option in the MODELLER package. The best model was selected based on the DOPE score, a MODELLER score function reflecting model quality. Finally, the resulting homodimeric model of ABCG2 was structurally aligned using chains as rigid bodies by the Situs software package. The quality of the final model was evaluated using PROCHECK (Laskowski et al., 1993 ▸). The percentage of residues that were found in the allowed regions of the Ramachandran diagram was 99.1%. The value of the G-factor of the final open apo ABCG2 model was −0.2, which is an indication of good quality.

2.6. Accession codes  

The three-dimensional map of ABCG2 has been deposited in the EMDB with accession code EMD-2715.

3. Results  

3.1. Two-dimensional crystal formation  

For this study, ABCG2 was overexpressed in P. pastoris and purified with N-dodecyl-β-d-maltoside, and two-dimensional crystals were grown as described previously (Rosenberg et al., 2010 ▸). We did not reconstitute ABCG2 into a lipid bilayer, as commonly undertaken in electron crystallography. Instead, we followed an adaptation of a three-dimensional crystallization protocol without the addition of lipids, in which the two-dimensional crystals were grown on the surface of transmission electron microscope (TEM) grids. This methodology has been successfully used for crystallizing other membrane proteins such as H+-ATPase (Auer et al., 1999 ▸).

3.2. Plane group, crystal packing and resolution assessment  

TEM images showed large two-dimensional crystalline arrays of ABCG2 (Fig. 1 ▸). Electron tomography was used to measure the thickness and the basic organization such as the crystal packing of the two-dimensional crystals, which confirmed that they were single-layered (Fig. 2 ▸ a). The screw axis places two ABCG2 molecules in opposite orientations relative to the crystal plane (Rosenberg et al., 2010 ▸). The statistics for these crystals shown in Table 1 ▸ indicate that the resolution of the crystals extends to 2.0 nm. The unit-cell parameters for this batch of crystals were a = 6.98 nm, b = 12.25 nm, γ = 89.9°. These dimensions are larger than those we reported previously (Rosenberg et al., 2010 ▸), which were a = 5.73 nm, b = 8.8 nm, γ = 89.7°, although the two-dimensional plane group is the same. The projection maps also appeared to be different (Fig. 3 ▸). This could be because the ABCG2 in the crystals in this study is in a different conformation. Recently, the crystal structures of three inward-facing conformations of mouse ABCB1 derived from two different crystal forms have been described (Ward et al., 2013 ▸). These authors suggested that changes in the growth conditions could account for the differences in unit-cell parameters, which were considerable. Therefore, a conformational change accompanied by changes in crystal-growth conditions could account for the differences in unit-cell parameters observed in this study. Recently, various conformations of ABCB10 have also been shown in the absence of and in complex with different nucleotide analogues (Shintre et al., 2013 ▸). Moreover, for an unpublished ABCG2 crystal form in the presence of a drug, which had a smaller unit cell, we were able to fit the structures of Sav1866 (PDB entry 2hyd; Dawson & Locher, 2006 ▸) and MsbA (PDB entry 3b5y; Ward et al., 2007 ▸) into the three-dimensional map (data not shown).

Figure 1.

Figure 1

Open in a new tab

Electron-microscopic characterization of two-dimensional crystals of ABCG2. (a) Negative-stain electron-microscopic image of two-dimensional crystals of ABCG2 with 2%(w/v) uranyl acetate. The scale bar represents 35 nm. (b) A respective power spectrum. (c) An overview of the crystal at lower magnification, where the arrows show where the crystal originates. The scale bar represents 500 nm.

Figure 2.

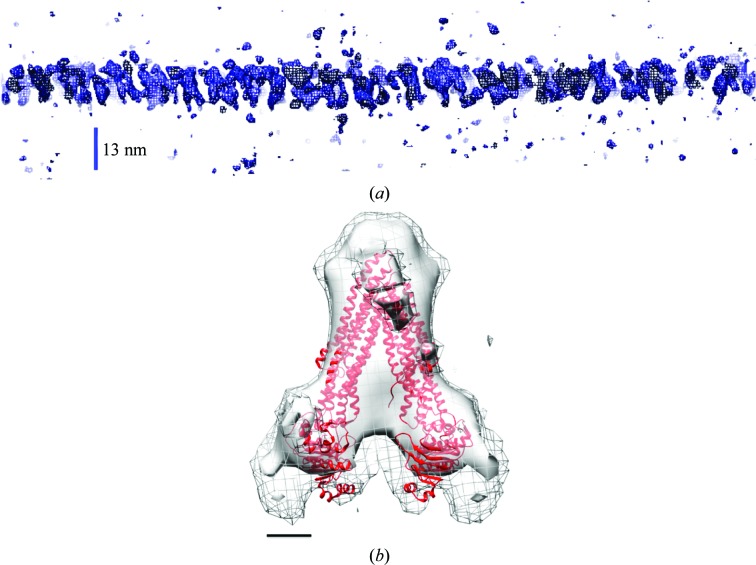
Figure 2

Open in a new tab

Tomographic characterization of two-dimensional crystals of ABCG2. (a) Three-dimensional tomographic volumes of ABCG2. A slice perpendicular to the crystal plane and along one crystal axis taken from an electron-tomographic reconstruction of the two-dimensional crystal zone is shown. This represents an unfiltered three-dimensional isosurface, which shows a single-layered, approximately 13 nm thick profile. (b) Subtomogram average side view of the ABCG2 homodimer. Two ABCG2 monomers form a V-shaped dimer with an angle of approximately 60° between their long axes. Threshold levels are 1.5σ (mesh) and 2σ (light grey). The map was fitted with an atomic model of murine ABCB1 (PDB entry 4ksb). The scale bar represents 2.0 nm.

Table 1. Data-analysis summary (projection and three-dimensional reconstruction).

Crystal plane-group symmetry p121
Crystal unit-cell parameters
a, b, c (nm) 6.98 1.3 (n = 5), 12.25 0.31 (n = 5), 20
() 89.9 0.4 (n = 5)
Open in a new tab

Projection data for resolution range 1002.0nm.

  IQ = 1 IQ = 2 IQ = 3 IQ = 4 IQ = 5 All IQs
Phase residual () 27.6 35.6 39.7 53.7 12.7 31.0
No. of comparisons 12 11 7 9 15  
Open in a new tab

Three-dimensional data.

No. of images 76
Range of defocus (m) 0.21.5
IQ range used 17
Tilt range used () 060
Total No. of measurements 3251
Total No. of fitted unique reflections 1752
Overall weighted phase residual () 27.4
Completeness to 1.6nm with 60 tilt (%) 76
Effective resolution cutoffs (nm) 2.0 (in-plane), 2.0 (vertical)
Open in a new tab

Figure 3.

Figure 3

Open in a new tab

The p121-symmetrized projection map of two-dimensional crystals of ABCG2 in the absence of nucleotides and transported substrates. The map was calculated from merged amplitudes and phases from five independent lattices of crystals embedded in vitreous ice. Densities above the mean and negative densities are shown by continuous and dotted lines, respectively. This represents a top view of the two-dimensional crystal along the z axis. The rectangular unit cell (6.98 × 12.25 nm) and the screw axes for plane group p121 have been drawn in. The approximate centre of the noncrystallographic twofold symmetry axis is indicated by an asterisk. The scale bar represents 2.0 nm.

Statistics of the processing and merging of the crystallo­graphic data from 76 images of two-dimensional crystals tilted up to 60° are given in Table 1 ▸. The good processing statistics (an overall weighted phase residual of 27.4° for a merged data set) suggests that we are dealing with well ordered two-dimensional crystals. No reference bias was used in the unbending routine since references with IQ 2 and IQ 3, which have high signal-to-noise ratios, were used (2dx Basel Workshop 2012, personal communication). Supplementary Fig. S1 shows examples of the computed Fourier transforms from images of exemplar crystals tilted to 0, 45 and 60° (from left to right). Lattice lines were fitted with smooth curves (see Supplementary Fig. S2) and sampled to generate a set of structure factors from which a reproducible three-dimensional map of ABCG2 was calculated. These low-resolution lattice lines display less deviation from the fitted curve for the phase component (upper panels) versus the amplitude component, which is typical for electron crystallography-derived data (Ford & Holzenburg, 2008 ▸). The absence of data owing to the so-called missing cone (tilting limit of 60°) and undersampling of data along the c direction means that the average resolution of the three-dimensional map will probably be close to the 2.0 nm resolution cutoff employed for the sampling of lattice lines along the c direction. The final three-dimensional map (Fig. 4 ▸) was generated with a negative temperature factor of −150 Å2, which is a suitable value for a map of 2.0 nm resolution along the a axis and 2.0 nm resolution along the c direction.

Figure 4.

Figure 4

Open in a new tab

Alignment of the murine ABCB1 structure (PDB entry 4ksb) with the ABCG2 map. The densities within the ABCG2 map (grey surface) and interpretation of the packing of the molecules using the mouse ABCB1 structure (red chain traces) as a guide are shown. The isocontour level is 1.7σ. This is from the side of the two-dimensional crystals along the a axis; the vertical height of the two-dimensional crystal is approximately 20 nm, with an individual molecule having a height of approximately 13 nm. The scale bar represents 2.4 nm.

3.3. Description of the three-dimensional map  

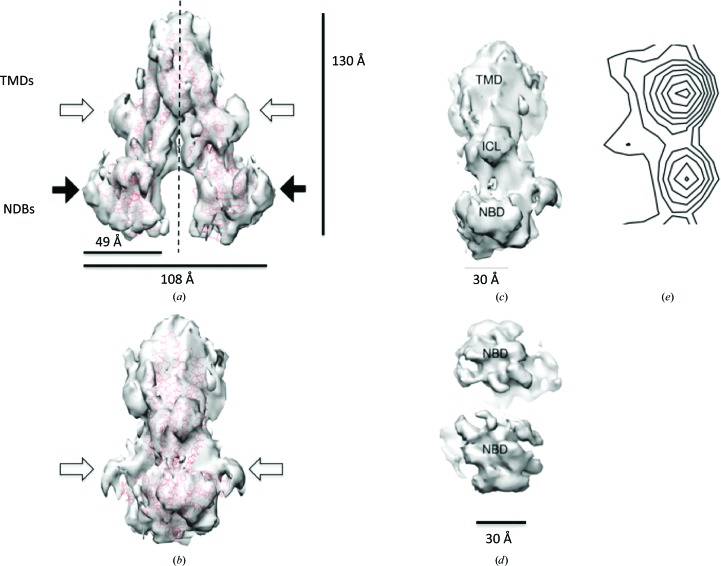
The analysis of two-dimensional crystals described above generated a clearly interpretable three-dimensional map, which allows the delineation of boundaries for the molecules (Fig. 4 ▸). The ABCG2 homodimer and the tomogram (see below) have a maximal total thickness of about 13 nm (Fig. 2 ▸ a). The tomogram also showed that the two-dimensional crystals were single-layered crystals and displayed p121 symmetry because of the ‘up/down’ configuration of the molecules (Fig. 2 ▸ a). In Fig. 4 ▸, which is viewed along the c axis, the high-density central regions of the map have a distinctive chevron or V shape subtending an angle of about 60° with each arm of the V, which is about 13 nm long and 11 nm across. These dimensions are similar to other homologous ABC transporters in the PDB. The V-shaped density is flanked at the upper and lower surfaces of the map by more globular densities of about 4.6 nm across and about 3.0 nm in depth. The V-shaped densities in the two crystallographic symmetries have a local noncrystallographic twofold (C2) symmetry axis (see also the dashed line in Fig. 5 ▸ a) and related halves of the unit cells are tightly packed next to each other in the map. Intercalation between V-shaped densities in adjacent unit cells along the c axis is significant, giving a tight packing of molecules in the crystal.

Figure 5.

Figure 5

Open in a new tab

Views of the ABCG2 dimer and an ABCG2 monomer after symmetry averaging from the electron-crystallographic data. The symmetrized map (semi-transparent grey surface) and the fitted mouse ABCB1 structure (PDB entry 4ksb; red chain trace) is shown in (a) as the front view, with the dotted lines showing the C2 symmetry axis. (b) Side view of the ABCG2 dimer. (c) View of an ABCG2 monomer from the twofold rotational symmetry axis looking outwards at a 2.0 nm thick slice. (d) View of the NBDs of an ABCG2 homodimer. The overall arrangement of the major domains between the ABCG2 map and the ABCB1 structure appears to be similar. The NBDs in (a) and (b) are indicated by black filled arrows. Additional densities in (a) and (b) (indicated by open arrows) are observed in the ‘beak’ regions between the TMD and the NBD as well as in the NBD regions close to the position of C-­terminus of ABCB1. The TMD, ICL and NBD regions in (c) and (d) are also depicted. The isocontour level is 1.7σ. (e) shows a projection map of the three-dimensional volume from above down onto the membrane plane by calculating a single slice through the volume using the map-generation program (FFT) in CCP4 in the z direction. Negative contour values were omitted for clarity. The scale bar in (e) is the same as that in (c).

The V-shaped molecules are standing up on their two open ends, with the next molecule hanging upside down with the open ends at the top. This is different from a previous interpretation that we calculated from a different batch of two-dimensional crystals, in which the V-shaped ABCG2 molecules were interpreted as lying horizontally in the two-dimensional crystal plane, so that the two open ends of the V-shaped molecules were at the top and bottom of the two-dimensional crystal layer (data not shown). This could be because in the study described in this manuscript we used a new batch of two-dimensional crystals. The earlier structure was much noisier, as supported by the statistics, which had an overall weighted phase residual of 47°, whereas in this study the overall weighted phase residual was 27.4° (a value of 90° corresponds to random data). The lattice dimensions in the earlier study were 5.8 × 8.8 nm, whereas in this manuscript they were 6.98 × 12.25 nm, also suggesting that the crystal packing might be different. This finding suggests that ABCG2 can exhibit alternate crystal packings, which may be related to ABCG2 exhibiting different conformational states (Rosenberg et al., 2010 ▸).

The most immediate interpretation of the density in the map is that the ABCG2 homodimer is in an inward-facing conformation with the V shape formed by the TMDs and the flanking globular domains being the NBDs. In this configuration, the crystal will have the more polar domains on each surface, whilst the more hydrophobic TMDs will be sandwiched in the centre of the crystal.

3.4. Interpretation of the three-dimensional map  

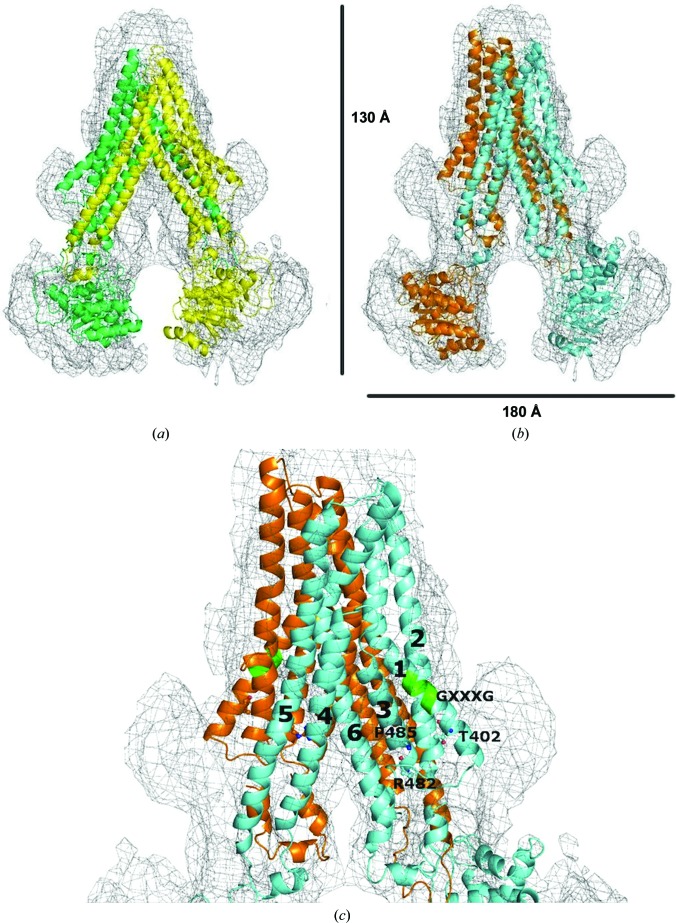
We used the murine ABCB1 coordinates (main-chain atoms) with an inward-facing conformation (PDB entry 4ksb; Ward et al., 2013 ▸) and fitted them to the homodimer density in the three-dimensional map of ABCG2 using the Chimera ‘fit to map’ function, as illustrated by the red tracings in Fig. 4 ▸. This ABCB1 structure was chosen because it was in an inward-facing state with the V shape constituting the angle, which appears to be more compatible with the three-dimensional map compared with other ABC transporter structures (see below). The fit was reasonable, with a correlation coefficient of 0.75 when a map for the fitted model (with a resolution cutoff of 2.0 nm) was compared with the experimental map. The average map value per atom for fitted main-chain ABCB1 was about 2.1σ above the mean density. Murine ABCB1 gave the best fit to this map, but the correlation coefficient suggests that there may be differences in the maps because the red chain traces do not entirely echo the EM-derived contours. This may reflect the fact that ABCG2 is radically different from existing ABC transporters because of the reverse topology present in this membrane protein, in which the nucleotide-binding domain (NBD) is N-terminal to the TMD, whereas the opposite is true for other ABC transporter subfamilies. Some densities that were not accounted for could be regions in ABCG2 that are not present in ABCB1 and seem to aid in crystalline packing. To confirm the orientation of the three-dimensional map, we used the Phyre2 server (Kelley & Sternberg, 2009 ▸) based on alignment with chain B of the murine ABCB1 structure (PDB entry 3g5u; Aller et al., 2009 ▸) to predict a protein structure for the NBD globular domain of ABCG2. This was successfully achieved with 100% confidence in the model. The predicted NBD structure was used to interrogate the three-dimensional map and docked with a correlation coefficient of 0.8 at the putative NBD site of the map, whereas the correlation coefficient was poorer when the predicted NBD structure was docked in other regions of the map. We also tried to fit the outward-facing Sav1866 structure (PDB entry 2hyd; Dawson & Locher, 2006 ▸) into the ABCG2 map. The fit was worse than that for the ABCB1 structure (PDB entry 4ksb), with a correlation coefficient of about 0.34 and an average map value per atom of 1.3σ and with more clashes between unit cells (Supplementary Fig. S3a). The MsbA structure (PDB entry 3b5w; Ward et al., 2007 ▸), a wide-open apo inward-facing conformation, was fitted into the ABCG2 map with a correlation coefficient of 0.42 and an average map value per atom of 0.90σ (Supplementary Fig. S3b). The murine ABCB1 structure (PDB entry 3g60; Aller et al., 2009 ▸), a closed apo inward-facing conformation, fitted better, with a correlation coefficient of 0.47 and an average map value per atom of 1.0σ (Supplementary Fig. S3c). We tried another inward-facing ABCB10 structure (PDB entry 3zdq; Shintre et al., 2013 ▸), which was also fitted with a reasonable correlation of 0.53 and an average map value per atom of 0.84σ above the mean density complemented by the additional symmetry of ABCB10 (Supplementary Fig. S3d).

3.5. Noncrystallographic symmetry averaging  

Noncrystallographic symmetry averaging was applied to the final density map using the fitted ABCB1 model (PDB entry 4ksb) as a guide to identify the local noncrystallographic twofold symmetry axis. Density within 2.0 nm of the fitted model was extracted and then averaged with a version of the map rotated by 180° around the local C2 symmetry axis (Figs. 5 ▸ a and 5 ▸ b). The correlation between the unrotated and rotated versions of the map was 0.7, which is likely to be a reflection of the lack of noise in the map and little deviation from twofold symmetry, and may confirm the presence of a noncrystallographic twofold axis perpendicular to the crystal plane. Although the ABCB1 structure (PDB entry 4ksb) is not symmetric, visual inspection with Chimera revealed that it was reasonably close to C2 symmetry, and the correlation coefficient was slightly higher for ABCB1 (PDB entry 4ksb) than for ABCB10 (PDB entry 3zdq) for the three-dimensional map fit.

3.6. ABCG2 structure  

The NBDs in the final symmetry-averaged map show a reasonably close correspondence in terms of shape to the expected NBD envelope and fold (Fig. 5 ▸). From sequence alignment of ABCG2 versus known NBD structures, the expected C-terminal end of the NBD lies at the bottom of the domain (Fig. 5 ▸ a, black filled arrows). As indicated, there are additional densities near the boundaries between the NBDs and TMDs (Fig. 5 ▸ a, open arrows) and in the NBDs close to the expected C-terminal region of the fitted NBD in the ABCG2 map (Fig. 5 ▸ b, open arrows). As well as helping to form crystalline contacts, they may be part of the sequence that is unique to ABCG2 (see below). Fig. 5 ▸(c) shows the three-dimensional map of one ABCG2 monomer after symmetry averaging, which indicates the approximate locations of the NBD, TMD or ICL regions in an ABCG2 monomer. Notably, densities representing the long cytoplasmic extensions from the TMDs that connect the NBDs are clearly visible (Fig. 5 ▸ a, the regions sandwiched between the open and black filled arrows), and these cytoplasmic extensions are likely to be the ICL regions. This appears to have a much rougher surface rendering, which suggests undersampling, giving the impression that these data do not correlate with the projection map characterized by smooth contours in Fig. 3 ▸. To allay this concern, we determined a projection of the three-dimensional volume from above down onto the membrane plane (Fig. 5 ▸ e). Fig. 5 ▸(e) shows a close correlation of one ABCG2 monomer with the projection map in Fig. 3 ▸, reinforcing the information obtained. Moreover, we used SPIDER (Frank et al., 1996 ▸) to project the volume shown in Fig. 5 ▸(c) in the Z direction over relevant slices. Reassuringly, this gave an equivalent map to Fig. 5 ▸(e) (data not shown). Fig. 5 ▸(d) shows the NBDs of an ABCG2 homodimer.

3.7. Subtomogram averaging  

To confirm the three-dimensional map, an independent method of subtomogram averaging was used to generate a subtomogram average with Dynamo (Castaño-Díez et al., 2012 ▸) and EMAN2 (Tang et al., 2007 ▸) (Fig. 2 ▸ b). Both methods produced similar maps and the findings presented here are from Dynamo. Fourier shell correlation indicated a resolution of 4.0 nm at 50% correlation (data not shown). The sub­tomogram average displayed a V-shaped three-dimensional map exhibiting twofold symmetry, with an angle of approximately 60° between the two monomers, similar to that described by electron crystallography. The X-ray structure of murine ABCB1 (PDB entry 4ksb; Ward et al., 2013 ▸) fitted the main globular density with a high correlation of 0.8 at 40 Å, suggesting that ABCB1 fitted into this 40 Å map, whilst the NBDs and TMDs are just resolved (Fig. 2 ▸ b). The dimer interface appears to be perpendicular to the crystal plane, which in this case corresponds to the expected membrane plane.

3.8. Molecular modelling  

We have previously developed homology models of ABCG2 based upon the membrane topology that we determined experimentally (Ni, Bikadi, Rosenberg et al., 2010 ▸; Rosenberg et al., 2010 ▸; Wang et al., 2008 ▸). To assist further structural and functional analysis and mechanistic understanding of ABCG2, we refined the closed apo model of ABCG2 based on the three-dimensional map determined in this study. We found that the model, particularly the TMDs, did not fit well to the map (Fig. 6 ▸ a). We therefore refined the model based on the experimental three-dimensional map. The quality of fitting for the final model was significantly improved, particularly in the TMD region (Fig. 6 ▸ b). The ICL2 between TM4 and TM5 is long enough to account for some densities between the TMD and the NBD and makes contact with the NBD. The identity and location of the TM α-helices of one ABCG2 monomer in a homodimeric complex are shown in Fig. 6 ▸(c). Several residues (Thr402 in TM1 and Arg482 and Pro485 in TM3) predicted to be in the TMD and previously shown to be functionally important are also indicated in the refined model (Fig. 6 ▸ c).

Figure 6.

Figure 6

Open in a new tab

Alignment of homology models to the ABCG2 map. (a) Fitting of the original closed apo inward-facing model to the map. (b) Fitting of the refined inward-facing model to the map. (c) A closer look at the TMDs. TM α-helices in the refined model are labelled 1, 2, 3, 4, 5 and 6 for TM1, TM2, TM3, TM4, TM5 and TM6 of one ABCG2 monomer (blue), respectively. Residues Thr402 (T402), Arg482 (R482) and Pro485 (P485) as well as the GXXXG motif are depicted near their locations in one ABCG2 monomer (blue). The three residues are indicated in ball-and stick representation and the GXXXG motif in TM1 is shown in green.

4. Discussion  

In the present study, we report the first three-dimensional structure of ABCG2 determined in the absence of nucleotides and transported substrates to a resolution of 2.0 nm in the vertical and in-plane directions. In this state, the homodimeric complex of ABCG2 displays an inward-facing conformation, with the NBDs widely separated from each other and the drug-transport pathway formed by the TMDs (Fig. 5 ▸ a). The ABCG2 map best matched the murine ABCB1 structure (PDB entry 4ksb), followed by the ABCB10 structure (closed apo; PDB entry 3zdq), the murine ABCB1 structure (closed apo; PDB entry 3g60) and the MsbA structure (open apo; PDB entry 3b5w), but did not match the Sav1866 structure (outward-facing; PDB entry 2hyd). It is worth noting that apart from the Sav1866 structure, the other four structures (PDB entries 4ksb, 3zdq, 3g60 and 3b5w) are all in an inward-facing conformations but with a varying degree of separation of the two NBDs. Structural studies to date suggest that when ABC transporters are not co-crystallized with nucleotides they generally tend to be in an inward-facing state. However, the degree of separation of the two NBDs may vary depending on the crystallization conditions or reflecting a range of flexibility that is critical for the binding and/or transport of diverse substrates, as demonstrated for ABCB1 (Aller et al., 2009 ▸; Jin et al., 2012 ▸; Ward et al., 2013 ▸). Likewise, three-dimensional structures of ABCB10 have also been determined in several inward-facing conformations in the absence and even the presence of nucleotide analogues (Shintre et al., 2013 ▸). The fitting of alternative models to the ABCG2 map suggests that the conformational state of ABCG2 observed in this study is likely to be an inward-facing closed apo state. Our results appear to support the ATP-switch model, in which an inward-facing state is proposed to be the conformational state prior to substrate binding and transport in the drug-transport cycle (Linton & Higgins, 2007 ▸). In contrast, in the constant-contact model, no matter whether a substrate is bound or transported or not, the NBDs never lose contact (George & Jones, 2012 ▸). However, this three-dimensional structure of ABCG2 may also represent a conformation specific to crystallization conditions. Therefore, to further understand the mechanism of ABCG2, it is important in the future to calculate its three-dimensional map in the presence of a transported substrate, which we have shown to possess a narrower and more symmetric conformation (Rosenberg et al., 2010 ▸).

The resolution of the three-dimensional structure of ABCG2 is sufficient to identify the NBD and the TMD as well as their organization in the homodimer based upon fitting to the ABCB1 structure (PDB entry 4ksb; Fig. 5 ▸). Two unique areas of the density in the ABCG2 map, namely the ‘beak’ regions, which are indicated by the open arrows pointing to the regions located between the TMD and the NBD (Fig. 5 ▸ a), cannot be accounted for by the fitted ABCB1 model (PDB entry 4ksb). Such areas may represent the ABCG2 domains that are not present in ABCB1 and seem to help in making crystalline contacts. ABCG2 has a linker region between the NBD and the TMD of almost 100 residues before the first predicted TM α-helix of the TMD, which is at around residue 390 (Wang et al., 2008 ▸). Therefore, another possibility is that the ‘beak’ regions may be accounted for by part of the relatively long linker region that extends from the N-terminus of the TMD to the C-terminus of the NBD, as illustrated in Supplementary Fig. S4. In addition, the putative NBDs in the ABCG2 map do not fully match the NBDs of the ABCG2 model (Fig. 6 ▸ b). This is likely to be because residues 285–390 that are part of the NBD and represent a relatively long linker region were not modelled owing to a lack of appropriate templates and were therefore missing in the NBDs of the model (Supplementary Fig. S4). Whether the ‘beak’ regions and the unmatched regions in the putative NBDs might be explained by the linker region or part of the NBD remains to be determined.

Although the resolution of the current map is not sufficient to trace the path of the polypeptide chain, nor to identify TM helices, the map can nevertheless be interpreted in terms of the experimental membrane topology of ABCG2 that we determined previously (Rosenberg et al., 2010 ▸; Wang et al., 2008 ▸). The experimental topology configuration would be close to the topology for the ABCB subfamily and the bacterial exporters Sav1866 and MsbA, but with a much shorter ICL (the first ICL1) connecting TM2 and TM3. The length (40 residues) of the second ICL2 connecting TM4 and TM5 of ABCG2 is only slightly shorter than those of ABCB1, Sav1866 and MsbA (49–60 residues). Based on this experimental topology and using the murine ABCB1 structure with PDB code 3g60 as a template, we developed an inward-facing closed apo model of ABCG2 (Rosenberg et al., 2010 ▸). The new experimental structural evidence has allowed the refinement of the closed apo model (Fig. 6 ▸ b). In the refined model, the TM4–ICL2–TM5 region crosses over to directly contact the NBD of an opposing monomer. Notably, ICL2 contains one cytoplasmic α-helix that is connected to the NBD of the opposing monomer and is likely to function as the coupling helix, analoguous to those in ABCB1, MsbA and Sav1866. As in ABCB1, MsbA and Sav1866, TM4 and TM5 in ABCG2 are closely packed parallel to each other. However, unlike in ABCB1, MsbA and Sav1866, which have two long ICLs each half transporter molecule (ABCB1 and MsbA) or each transporter molecule (Sav1866), there is only one such ICL (ICL2) in each ABCG2 molecule. The sequence alignment between ABCG2 and the two halves of ABCB1 illustrates this significant difference between the two ABC transporters (Supplementary Fig. S5). According to the refined model, the dimensions of the area of the TM4–ICL2–TM5 cross-over region of one monomer that directly contacts the NBD of the opposing monomer are approximately 1.5 × 4 nm. These unique features of the coupling helices might imply a different mechanism of coupling of ATP binding/hydrolysis to drug transport for ABCG2 versus other ABC transporters. The resolution of the current ABCG2 map is not sufficient to resolve molecular details of the NBD–TMD interface; thus, exactly how ICL2 interacts with the NBD is still not clear.

The refined model of ABCG2 provides novel insights into the biochemical data, which are otherwise difficult to interpret. Numerous studies have shown that mutations of Arg482 in TM3 significantly alter the substrate specificity of ABCG2 (Honjo et al., 2001 ▸; Miwa et al., 2003 ▸; Özvegy-Laczka et al., 2005 ▸). In addition, our recent mutagenesis studies indicate that Pro485 in TM3, which is just three residues apart from Arg482, is also an important determinant of the substrate specificity of ABCG2 (Ni et al., 2011 ▸). The reasons why Arg482 and Pro485 are crucial for the substrate specificity of ABCG2 are not known. We have proposed that Pro485 can introduce a structurally flexible hinge in TM3, and Arg482 in such a close position to Pro485 (Fig. 6 ▸ c) is actually part of the molecular hinge introduced by Pro485. According to the refined model, TM3 is a rather short TM α-helix connecting the TM4–ICL2–TM5 region, and TM3 also contacts the neighbouring TM1, TM2 and TM6 of the same ABCG2 monomer to form the drug-transport pathway (Fig. 6 ▸). Therefore, any significant conformational changes induced by the hinge in TM3 (through Pro485 and/or Arg482) would be expected to affect drug binding by directly changing the structure of the drug-binding cavity and/or the coupling between ATP binding/hydrolysis and drug transport by changing the configuration of TM4–ICL2–TM5 and hence the interaction with the NBDs. The degree of conformational change induced by the hinge may be dependent on the physical or chemical nature of the drug molecules, such as size or charge. Mutating Arg482 or Pro485 would affect or eliminate helical distortion of TM3 and helical packing with neighbouring TMs as well as the configuration of TM4–ICL2–TM5, therefore affecting drug binding and/or coupling with ATP hydrolysis for some substrates.

We and others have shown that mutations of Thr402 in TM1 cause a general reduction in the efflux activity of ABCG2 (Ni, Bikadi, Cai et al., 2010 ▸; Polgar et al., 2010 ▸). The refined model of ABCG2 shows that Thr402 is located in TM1 but outside the drug-transport pathway (Fig. 6 ▸ c), suggesting that Thr402 is not directly involved in interactions with drugs. On the other hand, Thr402 can make interactions with residues in TM2 and TM3 of the same ABCG2 monomer and thus play an important role in stabilizing helical packing in ABCG2. Therefore, mutations of Thr402 would destabilize the drug-transport pathway and hence reduce the transport activity of ABCG2. This finding is consistent with the location of Thr402 adjacent to the GXXXG helical dimerization motif in TM1 (see Fig. 6 ▸ c; Polgar et al., 2010 ▸).

In summary, the first three-dimensional structure of human ABCG2 determined in this study provides a molecular model that is consistent with the biochemical data on this transporter, with the results justifying the presence of a noncrystallographic twofold axis perpendicular to the two-dimensional crystal plane. The map is consistent with a model-building exercise in which ABCG2 in the absence of nucleotides and transported substrates might be in an inward-facing conformation. The structural data enhance our understanding of the structure, function and mechanism of ABCG2 and can be used to guide future structural and functional analysis of this transporter. Since we have shown that ABCG2 undergoes significant conformational changes upon drug binding (Rosenberg et al., 2010 ▸), the next step in our study is to calculate its three-dimensional map in the presence of a transported drug molecule.

Supplementary Material

Supporting Information.. DOI: 10.1107/S1399004715010676/mh5177sup1.pdf

d-71-01725-sup1.pdf (826.1KB, pdf)

Acknowledgments

QM acknowledges support from a National Institutes of Health grant (GM073715). MFR acknowledges funding by the Leukaemia and Lymphoma Research Charity (London) and by Wellcome Trust grants (081406/Z/06/Z and 097820/Z/11/Z). MFR and NC acknowledge funding by the Breast Cancer Now grant (2012NovPR059). LK acknowledges funding by a Biotechnology and Biological Sciences Research Council (BBSRC) grant (BB/J019240/1). We would like to thank Dr Peter Briggs of the University of Manchester for helping MFR write computer batch programs and Dr Doryen Bubeck of Imperial College London for making suggestions on the figures. We would also like to thank Dr Giulia Zanetti (Birkbeck College, London), Dr Daniel Castaño-Diez (Max-Plank Institute for Brain Research, Frankfurt Germany) and Vasileios Kargas (University of Manchester) for assistance with Dynamo and EMAN2, respectively. We would like to thank Dr Alan Roseman and Mr Alan Godwin (University of Manchester) for SPIDER scripts.

Footnotes

1

Abbreviations used: ABCG2, the second member of the G subfamily of the ABC transporter superfamily; ABCB1, the first member of the B subfamily of the ABC transporter superfamily or P-glycoprotein.

References

  1. Aller, S. G., Yu, J., Ward, A., Weng, Y., Chittaboina, S., Zhuo, R., Harrell, P. M., Trinh, Y. T., Zhang, Q., Urbatsch, I. L. & Chang, G. (2009). Science, 323, 1718–1722. [DOI] [PMC free article] [PubMed]
  2. Amos, L. A., Henderson, R. & Unwin, P. N. (1982). Prog. Biophys. Mol. Biol. 39, 183–231. [DOI] [PubMed]
  3. Auer, M., Scarborough, G. A. & Kühlbrandt, W. (1999). J. Mol. Biol. 287, 961–968. [DOI] [PubMed]
  4. Castaño-Díez, D., Kudryashev, M., Arheit, M. & Stahlberg, H. (2012). J. Struct. Biol. 178, 139–151. [DOI] [PubMed]
  5. Castaño-Díez, D., Scheffer, M., Al-Amoudi, A. & Frangakis, A. S. (2010). J. Struct. Biol. 170, 117–126. [DOI] [PubMed]
  6. Crowther, R. A., Henderson, R. & Smith, J. M. (1996). J. Struct. Biol. 116, 9–16. [DOI] [PubMed]
  7. Dawson, R. J. & Locher, K. P. (2006). Nature (London), 443, 180–185. [DOI] [PubMed]
  8. Deeley, R. G., Westlake, C. & Cole, S. P. (2006). Physiol. Rev. 86, 849–899. [DOI] [PubMed]
  9. Dezi, M., Fribourg, P. F., Di Cicco, A., Arnaud, O., Marco, S., Falson, P., Di Pietro, A. & Lévy, D. (2010). Biochim. Biophys. Acta, 1798, 2094–2101. [DOI] [PubMed]
  10. Ford, R. C. & Holzenburg, A. (2008). Trends Biochem. Sci. 33, 38–43. [DOI] [PubMed]
  11. Frank, J., Radermacher, M., Penczek, P., Zhu, J., Li, Y., Ladjadj, M. & Leith, A. (1996). J. Struct. Biol. 116, 190–199. [DOI] [PubMed]
  12. Fukuda, Y. & Schuetz, J. D. (2012). Biochem. Pharmacol. 83, 1073–1083. [DOI] [PMC free article] [PubMed]
  13. George, A. M. & Jones, P. M. (2012). Prog. Biophys. Mol. Biol. 109, 95–107. [DOI] [PubMed]
  14. Giacomini, K. M. et al. (2010). Nature Rev. Drug Discov. 9, 215–236. [DOI] [PMC free article] [PubMed]
  15. Gipson, B., Zeng, X. & Stahlberg, H. (2007). J. Struct. Biol. 160, 375–384. [DOI] [PMC free article] [PubMed]
  16. Goler-Baron, V. & Assaraf, Y. G. (2011). PLoS One, 6, e16007. [DOI] [PMC free article] [PubMed]
  17. Hazai, E. & Bikádi, Z. (2008). J. Struct. Biol. 162, 63–74. [DOI] [PubMed]
  18. Honjo, Y., Hrycyna, C. A., Yan, Q.-W., Medina-Pérez, W. Y., Robey, R. W., van de Laar, A., Litman, T., Dean, M. & Bates, S. E. (2001). Cancer Res. 61, 6635–6639. [PubMed]
  19. Hyde, S. C., Emsley, P., Hartshorn, M. J., Mimmack, M. M., Gileadi, U., Pearce, S. R., Gallagher, M. P., Gill, D. R., Hubbard, R. E. & Higgins, C. F. (1990). Nature (London), 346, 362–365. [DOI] [PubMed]
  20. Jin, M. S., Oldham, M. L., Zhang, Q. & Chen, J. (2012). Nature (London), 490, 566–569. [DOI] [PMC free article] [PubMed]
  21. Jones, P. M. & George, A. M. (2009). Proteins, 75, 387–396. [DOI] [PubMed]
  22. Kelley, L. A. & Sternberg, M. J. (2009). Nature Protoc. 4, 363–371. [DOI] [PubMed]
  23. Kerr, I. D., Jones, P. M. & George, A. M. (2010). FEBS J. 277, 550–563. [DOI] [PubMed]
  24. Kos, V. & Ford, R. C. (2009). Cell. Mol. Life Sci. 66, 3111–3126. [DOI] [PMC free article] [PubMed]
  25. Kremer, J. R., Mastronarde, D. N. & McIntosh, J. R. (1996). J. Struct. Biol. 116, 71–76. [DOI] [PubMed]
  26. Laskowski, R. A., MacArthur, M. W., Moss, D. S. & Thornton, J. M. (1993). J. Appl. Cryst. 26, 283–291.
  27. Li, Y.-F., Polgar, O., Okada, M., Esser, L., Bates, S. E. & Xia, D. (2007). J. Mol. Graph. Model. 25, 837–851. [DOI] [PubMed]
  28. Linton, K. J. & Higgins, C. F. (2007). Eur. J. Physiol. 453, 555–567. [DOI] [PubMed]
  29. Maliepaard, M., Scheffer, G. L., Faneyte, I. F., van Gastelen, M. A., Pijnenborg, A. C., Schinkel, A. H., van De Vijver, M. J., Scheper, R. J. & Schellens, J. H. (2001). Cancer Res. 61, 3458–3464. [PubMed]
  30. Miwa, M., Tsukahara, S., Ishikawa, E., Asada, S., Imai, Y. & Sugimoto, Y. (2003). Int. J. Cancer, 107, 757–763. [DOI] [PubMed]
  31. Natarajan, K., Xie, Y., Baer, M. R. & Ross, D. D. (2012). Biochem. Pharmacol. 83, 1084–1103. [DOI] [PMC free article] [PubMed]
  32. Ni, Z., Bikadi, Z., Cai, X., Rosenberg, M. F. & Mao, Q. (2010). Am. J. Physiol. Cell Physiol. 299, C1100–C1109. [DOI] [PMC free article] [PubMed]
  33. Ni, Z., Bikadi, Z., Rosenberg, M. F. & Mao, Q. (2010). Curr. Drug Metab. 11, 603–617. [DOI] [PMC free article] [PubMed]
  34. Ni, Z., Bikadi, Z., Shuster, D. L., Zhao, C., Rosenberg, M. F. & Mao, Q. (2011). Biochemistry, 50, 8057–8066. [DOI] [PMC free article] [PubMed]
  35. Özvegy-Laczka, C., Köblös, G., Sarkadi, B. & Váradi, A. (2005). Biochim. Biophys. Acta, 1668, 53–63. [DOI] [PubMed]
  36. Pettersen, E. F., Goddard, T. D., Huang, C. C., Couch, G. S., Greenblatt, D. M., Meng, E. C. & Ferrin, T. E. (2004). J. Comput. Chem. 25, 1605–1612. [DOI] [PubMed]
  37. Poguntke, M., Hazai, E., Fromm, M. F. & Zolk, O. (2010). Expert Opin. Drug Metab. Toxicol. 6, 1363–1384. [DOI] [PubMed]
  38. Polgar, O., Ierano, C., Tamaki, A., Stanley, B., Ward, Y., Xia, D., Tarasova, N., Robey, R. W. & Bates, S. E. (2010). Biochemistry, 49, 2235–2245. [DOI] [PMC free article] [PubMed]
  39. Polgar, O., Robey, R. W. & Bates, S. E. (2008). Expert Opin. Drug Metab. Toxicol. 4, 1–15. [DOI] [PubMed]
  40. Robey, R. W., Polgar, O., Deeken, J., To, K. W. & Bates, S. E. (2007). Cancer Metastasis Rev. 26, 39–57. [DOI] [PubMed]
  41. Robey, R. W., To, K. K. K., Polgar, O., Dohse, M., Fetsch, P., Dean, M. & Bates, S. E. (2009). Adv. Drug Deliv. Rev. 61, 3–13. [DOI] [PMC free article] [PubMed]
  42. Rosenberg, M. F., Bikadi, Z., Chan, J., Liu, X., Ni, Z., Cai, X., Ford, R. C. & Mao, Q. (2010). Structure, 18, 482–493. [DOI] [PMC free article] [PubMed]
  43. Rosenberg, M. F., O’Ryan, L. P., Hughes, G., Zhao, Z., Aleksandrov, L. A., Riordan, J. R. & Ford, R. C. (2011). J. Biol. Chem. 286, 42647–42654. [DOI] [PMC free article] [PubMed]
  44. Šali, A. & Blundell, T. L. (1993). J. Mol. Biol. 234, 779–815. [DOI] [PubMed]
  45. Sarkadi, B., Homolya, L., Szakács, G. & Váradi, A. (2006). Physiol. Rev. 86, 1179–1236. [DOI] [PubMed]
  46. Saxton, W. O. & Baumeister, W. (1982). J. Microsc. 127, 127–138. [DOI] [PubMed]
  47. Shintre, C. A. et al. (2013). Proc. Natl Acad. Sci. USA, 110, 9710–9715.
  48. Tang, G., Peng, L., Baldwin, P. R., Mann, D. S., Jiang, W., Rees, I. & Ludtke, S. J. (2007). J. Struct. Biol. 157, 38–46. [DOI] [PubMed]
  49. Urquhart, B. L., Ware, J. A., Tirona, R. G., Ho, R. H., Leake, B. F., Schwarz, U. I., Zaher, H., Palandra, J., Gregor, J. C., Dresser, G. K. & Kim, R. B. (2008). Pharmacogenet. Genomics, 18, 439–448. [DOI] [PMC free article] [PubMed]
  50. Wang, H., Lee, E.-W., Cai, X., Ni, Z., Zhou, L. & Mao, Q. (2008). Biochemistry, 47, 13778–13787. [DOI] [PMC free article] [PubMed]
  51. Ward, A., Reyes, C. L., Yu, J., Roth, C. B. & Chang, G. (2007). Proc. Natl Acad. Sci. USA, 104, 19005–19010. [DOI] [PMC free article] [PubMed]
  52. Ward, A. B. et al. (2013). Proc. Natl Acad. Sci. USA, 110, 13386–13391.
  53. Winn, M. D. et al. (2011). Acta Cryst. D67, 235–242.
  54. Woodward, O. M., Köttgen, A., Coresh, J., Boerwinkle, E., Guggino, W. B. & Köttgen, M. (2009). Proc. Natl Acad. Sci. USA, 106, 10338–10342. [DOI] [PMC free article] [PubMed]
  55. Wriggers, W. (2010). Biophys. Rev. 2, 21–27. [DOI] [PMC free article] [PubMed]
  56. Xia, C. Q. & Smith, P. G. (2012). Mol. Pharmacol. 82, 1008–1021. [DOI] [PubMed]
  57. Xu, J., Liu, Y., Yang, Y., Bates, S. & Zhang, J.-T. (2004). J. Biol. Chem. 279, 19781–19789. [DOI] [PubMed]
  58. Yuan, J., Lv, H., Peng, B., Wang, C., Yu, Y. & He, Z. (2009). Cancer Chemother. Pharmacol. 63, 1103–1110. [DOI] [PubMed]
  59. Zamboni, W. C., Ramanathan, R. K., McLeod, H. L., Mani, S., Potter, D. M., Strychor, S., Maruca, L. J., King, C. R., Jung, L. L., Parise, R. A., Egorin, M. J., Davis, T. A. & Marsh, S. (2006). Invest. New Drugs, 24, 393–401. [DOI] [PubMed]
  60. Zhang, W., Yu, B.-N., He, Y.-J., Fan, L., Li, Q., Liu, Z.-Q., Wang, A., Liu, Y.-L., Tan, Z.-R., Huang, Y.-F. & Zhou, H.-H. (2006). Clin. Chim. Acta, 373, 99–103. [DOI] [PubMed]
  61. Zhou, Q., Sparreboom, A., Tan, E.-H., Cheung, Y.-B., Lee, A., Poon, D., Lee, E. J. D. & Chowbay, B. (2005). Br. J. Clin. Pharmacol. 59, 415–424. [DOI] [PMC free article] [PubMed]
  62. Zou, P., Bortolus, M. & Mchaourab, H. S. (2009). J. Mol. Biol. 393, 586–597. [DOI] [PMC free article] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information.. DOI: 10.1107/S1399004715010676/mh5177sup1.pdf

d-71-01725-sup1.pdf (826.1KB, pdf)

Articles from Acta Crystallographica Section D: Biological Crystallography are provided here courtesy of International Union of Crystallography

RESOURCES