Differential effects of conductances on the phase resetting curve of a bursting neuronal oscillator

Abstract

The intrinsically oscillating neurons in the crustacean pyloric circuit have membrane conductances that influence their spontaneous activity patterns and responses to synaptic activity. The relationship between the magnitudes of these membrane conductances and the response of the oscillating neurons to synaptic input has not yet been fully or systematically explored. We examined this relationship using the phase resetting curve (PRC), which summarizes the change in the cycle period of a neuronal oscillator as a function of the input’s timing within the oscillation. We first utilized a large database of single-compartment model neurons to determine the effect of individual membrane conductances on PRC shape; we found that the effects vary across conductance space, but on average, the hyperpolarization-activated and leak conductances advance the PRC. We next investigated how membrane conductances affect PRCs of the isolated pacemaker kernel in the pyloric circuit of Cancer borealis by: (1) tabulating PRCs while using dynamic clamp to artificially add varying levels of specific conductances, and (2) tabulating PRCs before and after blocking the endogenous hyperpolarization-activated current. We additionally used a previously described four-compartment model to determine how the location of the hyperpolarization-activated conductance influences that current’s effect on the PRC. We report that while dynamic-clamp-injected leak current has much smaller effects on the PRC than suggested by the single-compartment model, an increase in the hyperpolarization-activated conductance both advances and reduces the noisiness of the PRC in the pacemaker kernel of the pyloric circuit in both modeling and experimental studies.

1 Introduction

For several decades, neuroscientists have been studying small neuronal networks with the aim of understanding how their biophysical parameters inform their overall output. In a single neuron, the voltage dependencies and maximal conductances of different types of membrane ion channels have profound, channel-specific effects on the neuron’s overall activity (Marder and Goaillard 2006; Hille 2001). Computational and experimental studies in both vertebrate and invertebrate neuronal networks have indicated that the conductances of these membrane ion channels in individual neurons can vary several-fold (Golowasch et al. 2002; Goldman et al. 2001; Golowasch et al. 1999; Marder and Goaillard 2006; Swensen and Bean 2005; Schulz et al. 2006; Goaillard et al. 2009). In addition, numerous studies have elucidated relationships between specific conductances and certain features of neuronal activity; for example, the A-type potassium current (I_A) influences firing rate (Connor et al. 1977), and the hyperpolarization-activated mixed ion current (I_H), or H current, affects burst duration and duty cycle in bursting neurons (Ouyang et al. 2007) and acts to generally stabilize oscillatory activity (Bose et al. 2014). One important matter to consider is how these membrane conductances influence network-level output. In other words, what are the functional consequences of modifying the intrinsic membrane conductances of one neuron type for the output of the neuronal network in which those neurons are found? In both vertebrate and invertebrate systems, a variety of rhythmic activity types can be generated by the same synaptic architecture (Koch et al. 2011). Prinz et al. (2004b) suggested in a large-scale modeling study that modifying intrinsic cellular properties alone, without altering synaptic properties, can result in a wide variety of network outputs. In experimental preparations, network-level output measures, including cycle period, are correlated with mRNA copy numbers associated with specific membrane conductances (Goaillard et al. 2009). Additionally, in the Pre-Bötzinger complex, isolated pacemaker neurons can spontaneously produce two distinct bursting patterns, which resemble the “sigh-like” and “eupneic-like” bursts that appear in intact network output. This suggests that the intrinsic membrane properties of the pacemaker neurons are critical determinants of the output of a network that is able to generate multiple behavioral rhythms (Tryba et al. 2008).

In studies involving intact networks, it can be difficult to tease apart the effects of a single neuron type’s conductances from the many other biophysical parameters of the network, including synaptic strengths and the membrane conductances of other neuron types. Avoiding the complications of intact networks, one can instead examine how an isolated (or partially isolated) neuron’s response to systematically delivered input is influenced by its ionic conductances. This topic has been studied in multiple contexts; various ion channel types have been shown to influence neuronal response to input in invertebrate neurons (Prinz et al. 2003a; Prinz et al. 2003b) as well as mammalian neurons (Day et al. 2005; Vervaeke et al. 2006). The H current, for example, has been implicated in inducing hyperexcitability in CA1 pyramidal cells after febrile seizures (Chen et al. 2001). We investigated the effect of specific conductances on neuronal response to input in a well-studied central pattern generator (CPG) known as the pyloric circuit, found in the stomatogastric ganglion (STG) of decapod crustaceans. This circuit produces a triphasic rhythm with a cycle period that reliably falls between 0.5 and 2 seconds, and the cellular and synaptic properties of the system have been well characterized (Marder and Bucher 2007; Stein 2009). The circuit consists of a pacemaker kernel that includes the anterior burster (AB) and two pyloric dilator (PD) neurons, in addition to two types of follower neurons, the lateral pyloric (LP) and pyloric constrictor (PY) neurons.

The response of a neuronal oscillator (such as the AB/PD complex) to synaptic input is dependent, in part, upon when that input was received relative to the oscillation (G. L. Brown and Eccles 1934). This effect can be conveniently summarized with the phase resetting curve, or PRC, which describes the change in oscillator period as a function of the phase at which an input perturbation was received (Pinsker 1977). While often used to predict phase-locking in neuronal networks with coupling between neurons, the PRC is also a highly succinct method of describing the functional consequences of synaptic input to an isolated neuronal oscillator’s output (Prinz et al. 2003b). It is thus a natural tool for us to use in our investigation of the effect of specific intrinsic membrane conductances upon the output of a neuronal oscillator. Here, we use a combination of computational and experimental approaches to systematically examine the effect of individual conductances on the PRC of the pacemaker kernel in the pyloric circuit. We first use a single-compartment model neuron database to catalogue the sensitivity of various PRC attributes to specific conductances. We then tabulate PRCs in the PD neuron of Cancer borealis while dynamic-clamp-injecting the neuron with ionic currents using maximal conductances of varying magnitudes, then determine how each of the currents affects PRC shape. We additionally report the effect of endogenous I_H on the neuronal response to synaptic input by tabulating the PRC of the PD neuron while pharmacologically blocking I_H. Finally, we use a four-compartment model of the pacemaker kernel to investigate: (1) the influence of the location of the H and leak conductances on the PRC and (2) how the H conductance affects noise in the PRC.

2 Methods

2.1 Model neuron database

To examine the effect of conductances on the PRCs of single-compartment model neurons, a previously described model neuron database was used (Prinz et al. 2003a). This database was constructed by independently varying the conductances of eight separate Hodgkin-Huxley-type currents. The currents modeled were: fast sodium (I_Na), fast and slow calcium (I_CaT and I_CaS), fast potassium (I_A), calcium-dependent potassium (I_KCa), delayed rectifier (I_Kd), hyperpolarization-activated (I_H), and leak (I_leak). The currents were modeled as by Liu et al. (1998) with the exception of I_H, which was modeled as by Huguenard and McCormick (1992). The currents from Liu et al. (1998) were based on experiments on stomatogastric neurons in lobster (Turrigiano et al. 1995), and the I_H current was based on guinea pig thalamic relay cells (Huguenard and McCormick 1992; McCormick and Pape 1990). The equations that describe the model currents, including the voltage dependences of the activating and inactivating time constants and the steady-state activation and inactivation variables, are described in full in Prinz et al. (2003a). Each of the eight conductances was assigned one of six equally spaced values within a conductance-specific range. For simplicity, here we use normalized conductance values rather than absolute values when referring to conductance levels. We call these normalized values M, where M can have a value of 0, 1, 2, 3, 4, or 5, with 5 indicating the conductance-specific maximum level. Voltage traces were then simulated for every conductance combination. The total number of model neurons in the database was thus 6⁸, or 1,679,616 model neurons. In the original model neuron database, 1,065,225 of these model neurons were classified as regular bursting neurons, and their corresponding PRCs were simulated using instantaneous inhibitory synaptic inputs with an amplitude of 1,000 nS and a duration of 25% of the model’s intrinsic burst period (Prinz et al. 2003a). While, in general, PRCs may be tabulated using either excitatory or inhibitory input, strong inhibitory stimuli were used for the present study in order to closely emulate the input that the pacemaker kernel receives within the intact pyloric network. Within the database, the majority (over 99%) of PRCs had advances at certain phases and delays at other phases (commonly known as type II); the remainder had only delays (type I). No PRC exhibited advances at all phases. These simulated PRCs were analyzed in the study presently described. PRCs of all types were used in the analysis.

2.2 Dissection

The STG and associated nerves were dissected from the animal as previously described (Mulloney and Selverston 1974; Dando and Selverston 1972). Live Jonah crabs (Cancer borealis) were purchased, shipped from The Fresh Lobster Company LLC (Gloucester, MA), and kept in artificial seawater (~12–13°C) until use. Animals were anesthetized in ice for 30–45 minutes before dissection. The stomach was removed from the animal and pinned flat in a large dish lined with Sylgard® (Dow Corning, Midland, MI). The stomatogastric nervous system (STNS) was dissected from the stomach and pinned in a Sylgard®-lined Petri dish. The STG was desheathed with a sharp pin and forceps, and the sheath was pinned to the Sylgard® on either side of the STG to expose the cell bodies and neuropil. During dissections, the preparation was immersed in saline (11 mM KCl, 440 mM NaCl, 13 mM CaCl₂•2H20, 26 mM MgCl₂•6H₂0, 11.2 mM Trizma® base, 5.1 mM maleic acid, pH 7.45±0.03). The saline was changed every 15–20 minutes while in the large dish, and every 10 minutes while in the Petri dish.

2.3 Electrophysiology

To obtain extracellular recordings of the PD, LP, and PY neurons, wells of petroleum jelly (Vaseline®) were built around one or both of the lateral ventricular nerves (lvns) and tested for impermeability. After the dissection, the preparation was moved to an electrophysiology rig. Fresh saline was chilled with a thermoelectric (Peltier) SC-20 Dual Inline Solution Heater/Cooler controlled by a CL-100 Bipolar Temperature Controller (Harvard Apparatus/Warner Instruments) and perfused onto the nervous system at a temperature of ~12–13°C. Temperature of the saline in the dish was continuously monitored using a BAT-12 Microprobe thermometer (Physitemp Instruments, Clifton, NJ). The extracellular activity was monitored from the lvn by placing a stainless steel wire electrode inside one of the wells and a second electrode outside the well. The signal from the wires was amplified using an A-M Systems Model 1700 Differential AC Amplifier. Before beginning intracellular injections, the extracellular trace was examined; any preparations that did not exhibit consistent, rhythmic bursting activity were excluded from analysis. To make sharp microelectrodes for intracellular recordings, borosilicate glass capillary tubes (OD 1 mm, ID 0.78 mm) were pulled with a P-97 Flaming/Brown Micropipette Puller (Sutter Instruments, Novato, CA). Electrodes were filled with 0.6 M K₂SO₄ and 20 mM KCl. Microelectrode resistances were between 10–25 MΩ. Intracellular electrodes were placed in a headstage and controlled with Leitz mechanical manipulators. An Axoclamp-2B amplifier (Axon Instruments, Foster City, CA) in discontinuous current clamp (DCC) mode was used to amplify the intracellular signal. The signal was digitized using a Digidata 1200A board (Axon Instruments) and recorded with Clampex 9.2 on a PC running Windows XP. Experimental files were analyzed with Spike2 (Cambridge Electronic Design, Cambridge, UK) and MATLAB (The Mathworks, Natick, MA) using a combination of in-built functions and custom-made scripts.

The PD neuron was identified by its intracellular voltage waveform and the timing of its bursts within the pyloric rhythm (visible in the lvn extracellular recording). After one of the PD neurons was found, the single chemical synapse (LP-to-PD) onto the pacemaker kernel was blocked by perfusing the bath with 10⁻⁵ M picrotoxin, resulting in pharmacological isolation of the pacemaker kernel from the rest of the circuit. During experiments in which I_H was pharmacologically blocked, we first obtained several PRCs while perfusing the preparation with crab saline that contained only picrotoxin, then switched to blocker saline containing picrotoxin and 5 mM CsCl (Sigma-Aldrich, St. Louis, Missouri) to block I_H. The preparation was perfused with blocker saline for approximately 25 minutes before rerunning PRC protocols.

2.4 Dynamic clamp

We used the Real Time Linux Dynamic Clamp Controller (RTLDC) (Dorval et al. 2001) to add artificial membrane currents and synaptic input to the PD neuron (Sharp et al. 1993a, 1993b; Prinz et al. 2004a). The voltage waveform was amplified via the amplifier headstage, sent to a DAQ board (National Instruments, Austin, Texas) through a rack-mounted BNC terminal block (BNC-2090, National Instruments), and digitized at 20 kHz. A program was written in C++ (adapted from code described in (Sieling et al. 2009)) to read the voltage waveform and calculate intrinsic membrane currents and synaptic currents. The intrinsic membrane currents were calculated using the general formula

$$I_x={\overline{g}}_x{m}_x^{p_x}{h}_x(V_m-E_x)$$

where ḡ_x indicates one of the maximal conductances for channel type x (Na, A, Kd, H, or leak), $m_x^{p_x}$ is the activation variable with exponent p_x, h_x is the inactivation variable, V_m is the membrane voltage, and E_x is the reversal potential. The values for each parameter are identical to those used to construct the model neuron database (Prinz et al. 2003a; Liu et al. 1998; Huguenard and McCormick 1992). The currents I_CaT, I_CaS, and I_KCa were not simulated due to the inability to measure calcium concentrations inside the PD neuron in real time. The synaptic input was modeled with an instantaneously activating synaptic conductance using the formula

$$I_{\mathit{syn}}={\overline{g}}_{\mathit{syn}}(V_m-E_{\mathit{syn}})$$

where ḡ_syn was 100 nS (when the synapse was active) and E_syn was −90 mV, as used in previous studies (Prinz et al. 2003b; Thirumalai 2002). Voltage traces were shifted and scaled to a standard slow-wave envelope at which the injected model currents were active. All injected currents were scaled relative to the measured input resistance of each neuron. For each of the five types of maximal conductances (hereafter referred to simply as “conductances”), a range of conductance values was chosen that produced visually detectable alterations of the membrane voltage waveform when injected into the PD neuron. During each experiment, an RTLDC program was run that dynamic-clamp-injected one of the five membrane currents into the PD neuron, using a specific conductance value within the chosen range. While injecting this intrinsic membrane current, the intrinsic burst period P_init was calculated by determining the average period over 20 bursts. Bursts were detected by isolating the slow-wave portion of the voltage waveform with a low-pass filter and detecting the rising phase of each oscillation with a simple voltage threshold (Sieling et al. 2009). After P_init was established, the program began to deliver periodic synaptic pulses (I_syn) to tabulate the PRC; this was done by setting ḡ_syn to 100 nS when the artificial synaptic stimulus was being injected and 0 nS at all other times. To obtain each PRC, 100 synaptic pulses were injected that began at specified stimulus times S_i after a burst was detected. The ith stimulus time S_i was defined as S_i = P_initk where k = {0, 0.01, 0.02 … 0.99}. The pulse phases were delivered in a random order. One injection was given every 3 to 4 cycles. For certain experiments, the stimulus duration was set at a constant 250 ms; for others, it was set at 25% of P_init.

For certain experiments, we injected membrane currents at 6 or 7 different conductance levels within the chosen range and tabulated one PRC at each conductance level. For other experiments, we injected currents at only 3 different conductance levels within the chosen ranges and tabulated 2 or 3 PRCs at each conductance level. The conductance levels were injected in random order (rather than in ascending or descending order) to ensure that any changes in the PRCs were indeed due to the injected membrane current and not to other, unknown changes in the system over time. Since the protocol was performed using DCC mode, the same electrode was used to inject current and record the membrane voltage.

In two cases, both PD neurons were clamped and had intrinsic membrane conductances added to them, and in one case, one PD was photoinactivated using Alexa 568 dye (Invitrogen, Carlsbad, CA) (Miller and Selverston 1982; Sieling et al. 2012).

2.5 Tabulating PRCs

All experimental PRCs were tabulated post hoc using MATLAB. The intrinsic bursting period that was used to calculate the PRC, P, was calculated as the average value of all unperturbed periods, including the initial 20 bursts recorded prior to beginning synaptic perturbations as well as the periods between those cycles that received artificial synaptic input. (Note that P may be slightly different from P_init due to the inclusion in the average of the burst periods between perturbed periods.) As in the model neuron database, the ith phase response was calculated with the formula (P_i′ − P)/P, where P_i′ is the length of the perturbed period. The ith input phase was calculated as the elapsed time between the time at which synaptic input was received and the beginning of the last burst, normalized by P. The PRC comprises a scatter plot of the phase response (on the y-axis) versus the input phase (on the x-axis). The time at which the first spike in a burst crossed a user-defined threshold (usually approximately −30 mV) was defined as phase zero.

In certain cases, the neuron would generally burst consistently but had transitory intervals of unusually slow or fast activity. Burst periods that were greater or less than 2.5 times the absolute deviation around the median (Leys et al. 2013) were considered outliers and were excluded from the analysis. Any phase responses that were measured during (or one period length before or after) these outlier intervals were similarly excluded. All PRCs and voltage traces were also visually examined for outliers; any outliers that occurred as a result of unusual PD activity (such as neuromodulatory events that caused a failure to spike), or because of a rare failure of the algorithm to properly detect the perturbed period, or as a result of artifacts in the voltage trace, were removed.

We statistically determined whether each membrane conductance significantly affected the PRC by finding the “extra sums of squares” (Sober and Sabes 2003; Draper and Smith 1981). This technique is used to measure the reduction of the residual sum of squares when a particular variable (or variables) is added to a regression model. The data are fit using a reduced model (R), which does not include the set of additional variables, and a full model (F), which includes all variables. An F-test is then used to determine whether the additional variable (or variables) is significantly predictive of the output. We fit each set of PRCs to these two polynomial regression models, defining the phase response as the output (Y_i) and the stimulus phase and membrane conductance levels as predictors X_i1 and X_i2, respectively. The reduced model only includes the stimulus phase X_i1 as a predictor and is defined with the following equation:

$$Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i1}^2+{\beta }_3{X}_{i1}^3+{\epsilon }_i$$

where β is a vector of parameters and ε is a vector of errors. The full model includes both the stimulus phase X_i1 and membrane conductance X_i2 levels as predictors and is defined with the following equation:

$$Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i1}^2+{\beta }_3{X}_{i1}^3+{\beta }_4{X}_{i2}+{\epsilon }_i$$

The relationship between the phase response and the stimulus phase is assumed to follow a cubic polynomial, and the relationship between the phase response and the membrane conductance level is assumed to be linear (approximating our observations of model PRCs with individually altered conductances, as well as biological PRCs with conductances altered via dynamic clamp). For the purposes of statistically determining effects of conductances on the PRC shape, any points on the PRC that occurred as a result of a “missed cycle” (Oprisan et al. 2004) were not included in the cubic fit. To determine significant differences between PRCs, a Bonferroni correction was applied; the critical value for each conductance was based upon the number of tests that were performed for that conductance. This analysis was performed in MATLAB by adapting code that was written and graciously provided by Dr. Samuel J. Sober (Emory University).

2.6 Four-compartment model

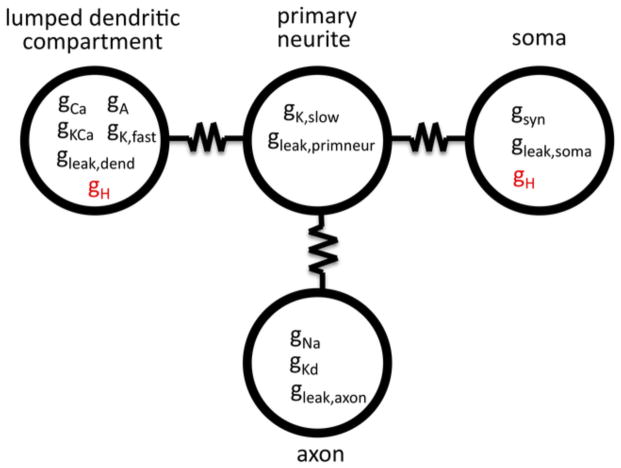
To determine how the locations of specific ion channels influence their effect on the PRC, we modified a multi-compartment model described in Maran et al. (2011). This model consists of four compartments that simulate: (1) the soma of one PD neuron, (2) a PD primary neurite, (3) a PD axon, and (4) the fine dendrites of both PDs and the AB neuron. To determine the effect of the leak current location within the four-compartment model on the PRC shape, ḡ_leak for either: (a) the soma compartment alone (ḡ_leak,soma), or (b) each of the four compartments (ḡ_leak,soma, ḡ_{leak,primneur}, ḡ_leak,axon, ḡ_leak,dend) was altered to take on a value of 0%, 33%, 67%, 100%, 133%, 167%, or 200% of its original value. The original, published version of the model does not include an H current. Thus, to determine the effect of the H current location within the four-compartment model on the PRC shape, we created two new versions of the model, one that had a model H current added to the soma compartment, and another that had a model H current added to the fine dendritic compartment (Fig. 1). The H current was identical to that used to construct the model neuron database (Prinz et al. 2003a) and was based on Huguenard and McCormick (1992).

Fig. 1. Four-compartment model of the pacemaker kernel.

To investigate the effect of leak current location on the PRC, the leak current was altered in either all four compartments or in the soma compartment alone of a model from Maran et al. (2011). To investigate the effect of H current location on the PRC, two versions of the model were constructed in which ḡ_H (shown in red) was either added to the lumped dendritic compartment or the soma compartment

All data analysis was performed using Spike2 and MATLAB; figures were generated with MATLAB, Inkscape, and Microsoft Office (Microsoft Corporation, Redmond, WA).

3 Results

3.1 The phase resetting curve of the STG pacemaker kernel

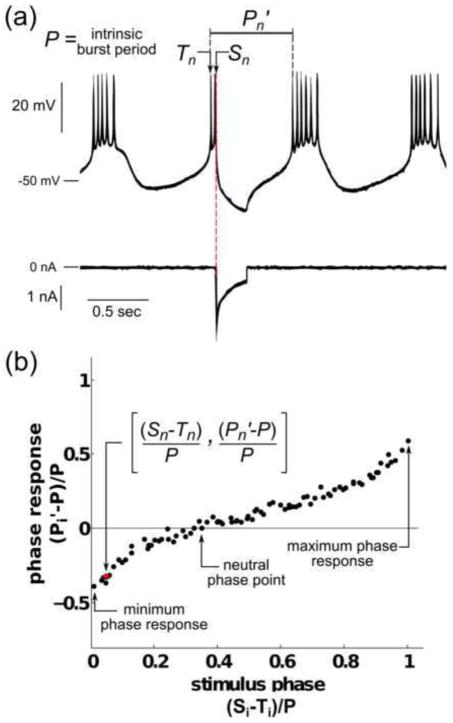
One method of summarizing the effect of synaptic input on a neuronal oscillator is by plotting the phase resetting curve (PRC) (Pinsker 1977; Pinsker and Kandel 1977), which is a plot of the change in the period of the oscillator, normalized by the intrinsic burst period, as a function of the phase of the oscillation at which the input perturbation was received (Fig. 2). If we indicate the intrinsic bursting period as P, and the ith period that was altered due to an input perturbation as P_i′, then the phase response (plotted on the y-axis) is defined as (P_i′−P)/P. If we indicate the time at which the ith perturbed period begins as T_i, and the time at which the ith input was received as S_i, then the stimulus phase (plotted on the x-axis) is defined as (S_i−T_i)/P. Reductions in the burst period (P_i′<P) are indicated as negative values, and increases in the burst period (P_i′>P) are indicated as positive values. Fig. 2 illustrates the response of a typical PD neuron to a stimulus S_n, where n is a particular instance of i. All PRCs tabulated in this study are immediate PRCs; they describe the change in the period that occurs due to the advance or delay of the burst immediately following the input perturbation. Three salient attributes of the PRC are indicated in Fig. 2b, including the minimum phase response, the maximum phase response, and the neutral phase point (defined as the stimulus phase at which the phase response curve crosses zero, with the rightmost zero crossing being used when multiple zero crossings exist). We note that the phrases “minimum phase response” and “maximum phase response” refer to real values rather than absolute values; thus, the largest negative value of a PRC, or the smallest positive value if no negative values exist, is considered the minimum phase response.

Fig. 2. The phase resetting curve in a regular bursting neuron.

(a) Voltage trace (top) of a biological PD neuron with intrinsic burst period P, and current trace (bottom) of injected artificial synaptic input. At time S_n, a pulse of artificial inhibitory synaptic input (100 nS) is given, resulting in the perturbed period P_n′. (b) PRC obtained from the PD neuron shown in (a). The ith stimulus phase, defined as the time from the beginning of the last burst, T_i, to the stimulus time, S_i, normalized by P, is plotted on the x-axis. The phase response, defined as the difference between the perturbed period P_i′ and P, normalized by P, is plotted on the y-axis. The phase response at i=n is highlighted in red. The minimum and maximum phase responses and the neutral phase point are labeled on the plot

3.2 Classifying model neurons

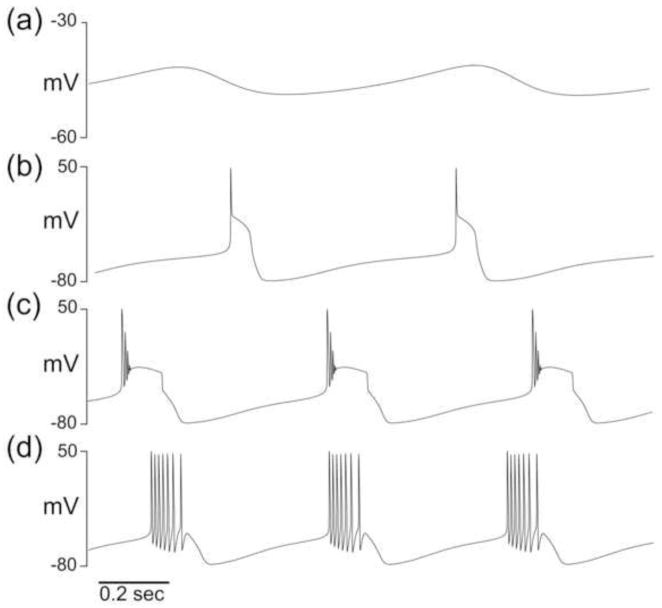
In the previously described single-compartment model neuron database, PRCs were simulated for each of the 1,065,225 models classified as regular bursters. Within this set of simulated PRCs, certain bursters had extreme delays. Those bursters with maximum PRC values not between 0 and 1 (0.3% of the population) were excluded from analysis, as were those with alternating burst attributes (Hudson and Prinz 2010). We restricted our analysis to multi-spike bursters alone, as classified in Hudson and Prinz (2010). Of the multi-spike bursters, we only included model bursters for which a majority of the spikes rose beyond 0 mV (in the case of two-spike bursters) or 20 mV (in the case of multi-spike bursters). This classification resulted in 292,313 model neurons that we term “PD-like” bursters (Fig. 3). Maximal conductances for all voltage traces of model neurons from the database shown in any of the figures in this paper are given in Appendix A.

Fig. 3. PD-like bursters were chosen from the model neuron database.

(a) Voltage trace of a model neuron with rhythmic, nonbursting activity. (b) Voltage trace of a model neuron classified as a one-spike burster. (c) Voltage trace of a model neuron that is classified as a multispike burster, but has a majority of spikes with peak amplitude below 20 mV. (d) Voltage trace of a model neuron that is classified as a multispike burster and has a majority of spikes with peak amplitude above 20 mV. Only model neurons that met the criteria of (d) were analyzed

3.3 Specific conductances have varying effects on PRC shape in PD-like burster populations

For all “PD-like” bursters, we determined the effect of each of the 8 conductances (ḡ_Na, ḡ_CaT, ḡ_CaS, ḡ_A, ḡ_KCa, ḡ_Kd, ḡ_H, ḡ_leak) on the distribution of three specific attributes of the PRC. These attributes were: 1) the maximum phase response (i.e. the greatest y-value of the PRC), 2) the neutral phase point (defined as the largest stimulus phase (x-value) at which the PRC has a phase response of zero), and 3) the minimum phase response (i.e. the lowest y-value of the PRC). The analysis was performed as follows: For each conductance ḡ_x, where x indicates Na, CaT, CaS, A, KCa, Kd, H, or leak, we separated the “PD-like” model neurons into 6 subpopulations, each of which had the conductance ḡ_x constrained to one of the six possible values and all other conductances unconstrained. We then generated a set of 6 histograms, one for each subpopulation, indicating the distribution of values of the maximum phase response. This was done for all 8 conductances, resulting in 8 sets of 6 histograms of maximum phase responses. These histograms, separated by conductance identity, are shown in Fig. 4. Similar sets of histograms showing the distributions of neutral phase points and minimum phase responses in each subpopulation are shown in Figs. 5 and 6, respectively.

Fig. 4. Conductances have varying effects on the maximum phase response by type.

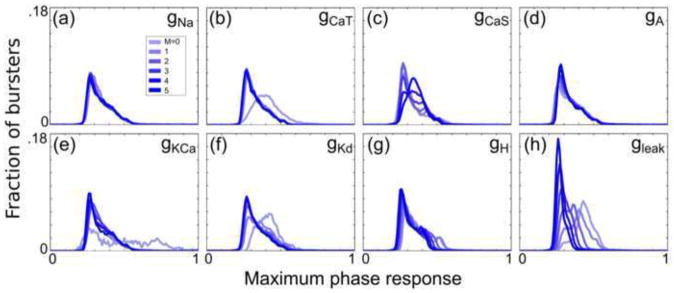
Histograms (bin width = 0.01) of the PRC maximum phase response were generated for 6 subpopulations of the 292,313 bursters that were analyzed. Subpopulations were created by constraining one of the 8 conductances to one of its 6 possible values. Histograms for each of the 8 sets of 6 subpopulations are plotted in (a–h) for the conductances ḡ_Na, ḡ_CaT, ḡ_CaS, ḡ_A, ḡ_KCa, ḡ_Kd, ḡ_H, and ḡ_leak, respectively

Fig. 5. Conductances have varying effects on the neutral phase point by type.

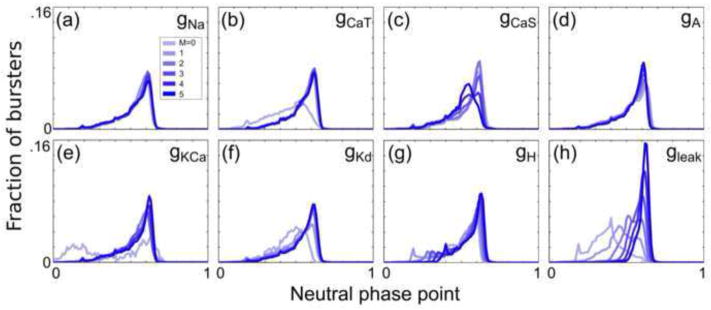
Histograms (bin width = 0.01) were generated for 6 subpopulations of all analyzed bursters in a similar manner to Fig. 4, but for the PRC neutral phase point

Fig. 6. Conductances have varying effects on the minimum phase response by type.

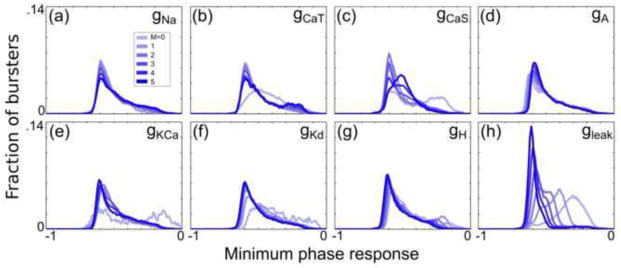
Histograms (bin width = 0.01) were generated for 6 subpopulations of all analyzed bursters in a similar manner to Fig. 4, but for the PRC minimum phase response

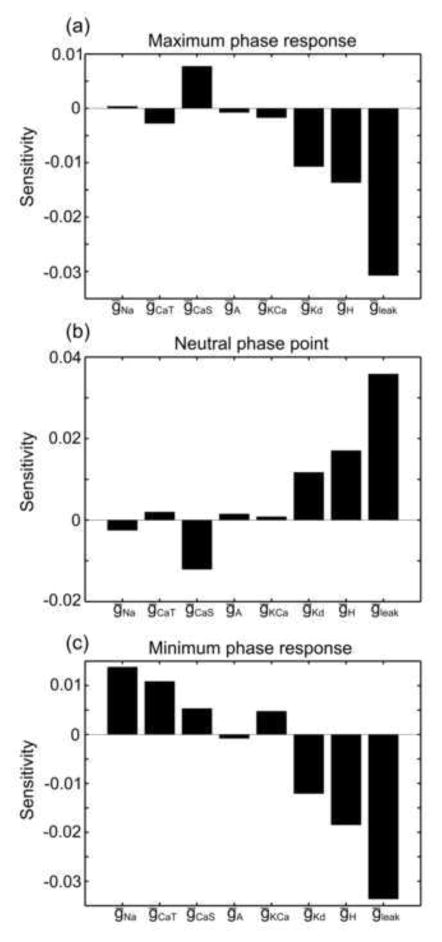
We then calculated the sensitivity of the maximum phase response to each conductance by finding the change in the mean value of each subpopulations’ maximum phase response relative to the change in each conductance value, normalized by the range of those conductance values in the database (Fig. 7a). The histograms for zero conductance values were not included in the calculation of sensitivity, since those histograms often had markedly different shapes from the other five histograms (see, for example, Fig. 4b) and were not considered representative of the overall relationship between maximum phase response and conductance level. Similar sensitivity analyses were performed for the neutral phase point and minimum phase response (Fig. 7b, c).

Fig. 7. PRCs appear most sensitive to the leak conductance.

Sensitivity plots show the sensitivity of the PRC attributes (a) maximum phase response, (b) neutral phase point, and (c) minimum phase response to the conductances ḡ_Na, ḡ_CaT, ḡ_CaS, ḡ_A, ḡ_KCa, ḡ_Kd, ḡ_H, and ḡ_leak

Figs. 4–6 demonstrate that the eight conductances of the single-compartment model have varying effects on the PRCs in the PD-like burster populations. The histograms indicate that the maximum phase response is generally reduced in PD-like burster populations with successively greater values of ḡ_leak. A similar effect is seen as ḡ_H is increased. The calcium conductances ḡ_CaT and ḡ_CaS, the calcium-dependent conductance ḡ_KCa, and the relatively fast-activating currents associated with ḡ_Na, ḡ_A, and ḡ_Kd have weaker effects on the distribution of the maximum phase response than do ḡ_H and ḡ_leak.

Histograms in Fig. 5 indicate that the neutral phase point generally increases in PD-like burster populations with successively greater values of ḡ_H and ḡ_leak. Similarly, Fig. 6 demonstrates that the PD-like burster populations exhibit decreasing minimum phase responses as ḡ_H and ḡ_leak increase.

The sensitivities of the PRC attributes to each of the eight conductances are summarized in Fig. 7. The PD-like bursters in the model neuron database were most sensitive to the ḡ_H and ḡ_leak conductances. The negative sensitivity of the maximum and minimum phase responses to ḡ_H and ḡ_leak, and the positive sensitivity of the neutral phase point to ḡ_H and ḡ_leak, indicate that the entire PRC advances as either of these conductances is increased. In terms of the oscillator’s activity, this means that the burst occurring immediately after the input perturbation is likely to occur sooner when greater amounts of ḡ_H and ḡ_leak are present in the model neuron.

3.4 Specific conductances have varying effects on PRC shape in families of PD-like bursters

To determine the effects of changing an individual conductance on a single neuron in the database, we also searched for “families” of PRCs within the set of PD-like bursters. Families were defined as sets of model neurons for which seven of the eight conductance values were identical and the eighth conductance was allowed to vary. Model neurons with a zero value for the eighth conductance were not analyzed, since the behavior of the model neuron with that zero conductance was often drastically different from the others in the family. Thus, each family could have a maximum of five members. Only families with at least three members that were classified as “PD-like” bursters were analyzed.

For each of the analyzed families, the value of the maximum phase response was plotted against the normalized value of the single, unconstrained conductance. The slope of this plot indicates the sensitivity of the maximum phase response to the conductance. The sensitivities of all analyzed families’ maximum phase responses were plotted in a box-and-whisker format for each of the eight conductances. The above procedure was repeated for the neutral phase point and minimum phase response. Fig. 8 shows two examples of distributions of minimum phase response sensitivities within burster families to the conductances ḡ_Na and ḡ_leak. While the median sensitivity of the minimum phase response to ḡ_Na is near zero (Fig. 8a), there exist both families in which increasing ḡ_Na reduces the minimum phase response (Fig. 8b) and families in which increasing ḡ_Na increases the minimum phase response (Fig. 8c).

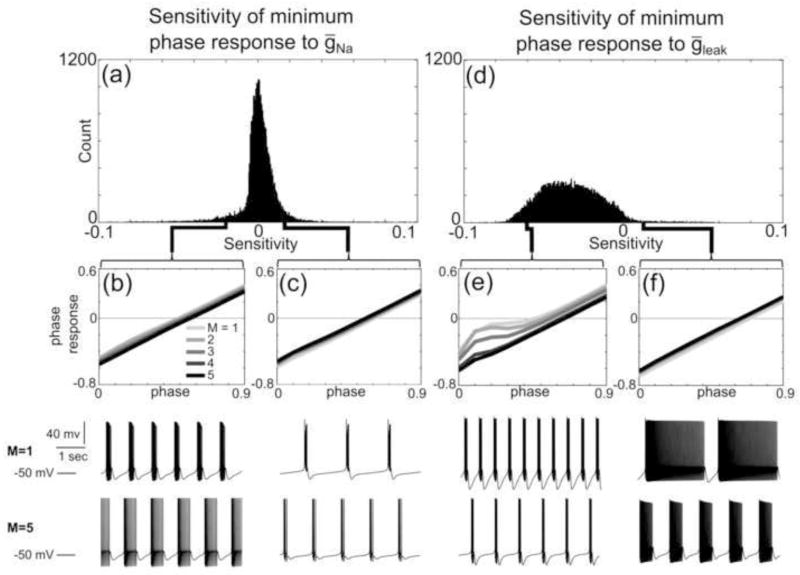
Fig. 8. Conductances can either increase or reduce the PRC minimum phase response.

(a) Histogram of sensitivities of minimum phase response of PRC families to ḡ_Na. (b) Example of a five-member PRC family with minimum phase responses that decrease with increasing ḡ_Na. All PRC family members are shaded from light to dark, with the lightest PRC having the lowest ḡ_Na value and the darkest PRC having the highest ḡ_Na value. ḡ_Na values of the model neurons corresponding to each PRC are given by multiplying the integer M by 100 mS/cm². The spontaneous activity patterns of the model neurons with the smallest (M=1, top) and largest (M=5, bottom) ḡ_Na values in the family are shown below the PRCs. (c) Example of a five-member PRC family with minimum phase responses that increase with increasing ḡ_Na. (d) Histogram of sensitivities of minimum phase responses of PRC families to ḡ_leak. (e) Example of a five-member PRC family with minimum phase responses that decrease with increasing ḡ_leak. ḡ_leak values of the model neurons corresponding to each PRC are given by multiplying the integer M by 0.01 mS/cm². The spontaneous activity patterns of the model neurons with the smallest (M=1, top) and largest (M=5, bottom) maximal ḡ_leak values in the family are shown below the PRCs. (f) Example of a five-member PRC family with minimum phase responses that increase with increasing ḡ_leak

The median sensitivity of the minimum phase response to ḡ_leak was the strongest of the eight conductances (Fig 8d); most PRC families’ minimum phase responses were reduced as ḡ_leak increased (Fig 8e). Notably, there still existed several examples of PRC families that had positive sensitivities to ḡ_leak (Fig. 8f).

Fig. 9 shows the sensitivities of PRC attributes to conductances for all families of PD-like bursters with at least three members. The sensitivities of the median families to each conductance are qualitatively similar to the sensitivities of the burster populations to each conductance (Fig. 7). Notably, the effect of any specific conductance on the PRC families is highly variable: Examples of PRC families with both negative and positive sensitivities existed for each of the eight conductances, as well as for all three PRC attributes.

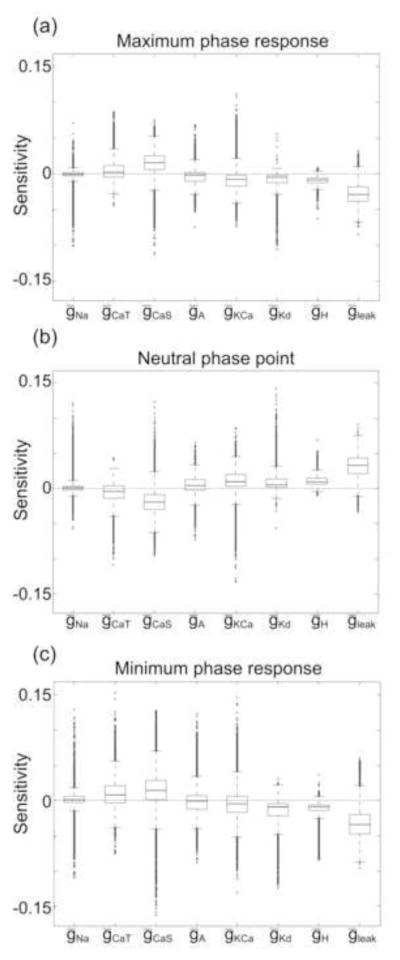
Fig. 9. The sensitivity of PRC families to specific conductances varies throughout conductance space.

Box plots indicating the spread of the sensitivities for all families of PRCs for “PD-like” model neurons. The bold, central lines in each box plot indicate the median sensitivity of the (a) maximum phase response, (b) neutral phase point, and (c) minimum phase response to each conductance. The lower and upper edges of each box indicate the 25^th and 75^th percentiles, respectively, and the whiskers (dashed black lines) extend to the furthest data points that are within 1.5 times the interquartile range (the difference between the 75^th percentile and the 25^th percentile). All data points beyond 1.5 times the interquartile range are indicated as open ovals. Both negative and positive sensitivities exist for all conductances

Examining the PRC families suggests that one cannot predict the magnitude, or even the direction, of the sensitivity of a particular PRC attribute to a specific conductance without considering the model neurons’ locations in conductance space.

3.5 Dynamic-clamp-injected H conductance regularizes and advances the PRC in the isolated pacemaker kernel

The single-compartment model database provides a broad description of specific conductance effects on PRCs. Our results indicate that, within the conductance ranges spanned by the database, the specific conductances ḡ_H and ḡ_leak produce, on average, the effects of strongest magnitude on the PRC. In the biological PD neuron, certain ion channels associated with specific currents are found in distinct spatial regimes. This segregation of specific conductances may influence conductance effects on the PRC in a way that is not captured by the single-compartment model. We thus investigated the effects of ḡ_Na, ḡ_A, ḡ_Kd, ḡ_H, and ḡ_leak on a biological PRC by continuously injecting varying levels of these conductances into the PD neuron using the dynamic clamp, tabulating the PRCs at each conductance level, and determining whether the PRCs differed significantly from each other.

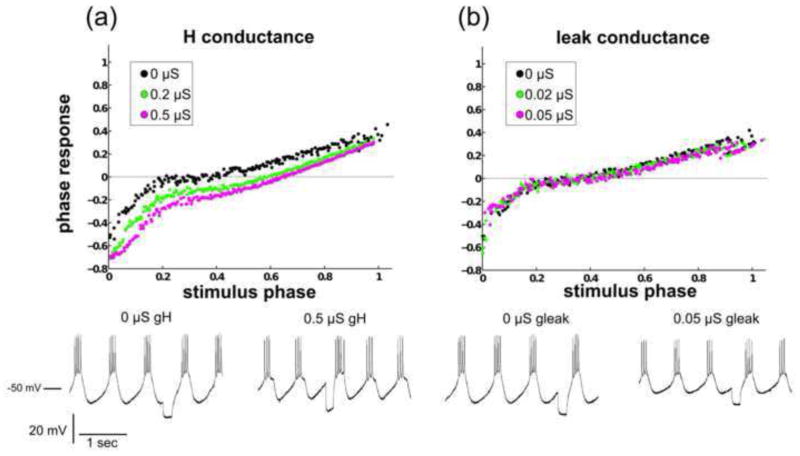
Adding increasing levels of ḡ_H to the PD neuron reliably caused the PRC to advance. In addition, the predictability of the phase response to consecutive stimulus phases was consistently increased. In other words, increasing ḡ_H reduced the error component in a low-order polynomial model of the PRC. Fig. 10a shows one sample set of PRCs with varying ḡ_H tabulated using a stimulus duration proportional to the period. The PRC taken while 0.5 μS ḡ_H was injected into the PD neuron (shown in pink) exhibits more advanced phases (p = 0) and greater predictability than the PRC with 0 μS ḡ_H injected (shown in black).

Fig. 10. Dynamic-clamp-injected H current advances and regularizes the PRC.

(a) As the H conductance is increased, the PRC is advanced and its variability is reduced. Voltage traces are shown for the lowest and highest levels of dynamic-clamp injected H current. In this example, ḡ_H was a significant factor in altering the PRC (p < 10⁻¹²). (b) Here, ḡ_leak was a significant factor in altering the PRC (p = 0.0003). However, the change in the phase response at any given stimulus phase as ḡ_leak is increased is relatively small. Voltage traces are shown for the lowest and highest levels of dynamic-clamp-injected leak current

The addition of ḡ_H produced a significant advancement of the PRC for all n under both types of stimuli tested, including a constant-duration 250 ms stimulus (n = 7) and a stimulus with a duration that was proportional to the intrinsic burst period (n = 4). All p-values were less than 10⁻¹². Qualitatively, these experimental results are in agreement with the results from the model neuron database, which show that as ḡ_H is increased in either a large population of PD-like bursters or in a set of PRC families, the PRC is most likely to advance.

The effect of increasing ḡ_leak levels on the PD’s PRC shape, in contrast, was inconsistent, lower in magnitude, and less significant than that of increasing ḡ_H. Fig. 10b shows one of the four sets of PRCs with varying ḡ_leak, tabulated with a stimulus duration proportional to the period (p = .0003). While the PRCs within this set, taken with different levels of ḡ_leak, are significantly different from one another, no strong advance or delay of the curve is present. PRCs were significantly different in 2 of 7 animals using a constant stimulus duration and in 3 of 4 animals using a stimulus with a duration proportional to the intrinsic bursting period. The relatively weak effect of ḡ_leak on the PRC, seen in multiple animals, is qualitatively different from the results from the single-compartment model neuron database, which had suggested that increasing ḡ_leak would, on average, advance the PRC (Fig. 7). The leak conductance had a significant effect on the PRC only in certain preparations, which may reflect the finding (as shown in Fig. 9) that the sensitivity of the PRC to a specific conductance is dependent upon the neuron’s location in conductance space.

As with ḡ_leak, ḡ_Na, ḡ_A, and ḡ_Kd exhibited relatively weak effects on the PRC. The effects of ḡ_A on the biological PRCs and the model PRCs were consistent with each other; in both cases, an effect was either weak or not present. However, the weak effects of ḡ_Na and ḡ_Kd in the biological neuron were again inconsistent with those from the single-compartment model neuron database, in which increasing ḡ_Na delayed the minimum phase response and ḡ_Kd advanced the entire PRC, though to a lesser degree than ḡ_H and ḡ_leak. Results for all conductances tested are summarized in Table 1.

Table 1.

Effects of dynamic-clamp-injecting conductances into PD neuron

	ḡNa		ḡA		ḡKd		ḡH		ḡleak
α	.005		.0055		.005		.0045		.0045
Stim. Dur. (ms)	250	0.25Pinit	250	0.25Pinit	250	0.25Pinit	250	0.25Pinit	250	0.25Pinit
Num. Sig.	1	0	0	1	3	0	7	4	2	3
n	5	5	5	4	5	5	7	4	7	4

The row “α” indicates the Bonferroni-corrected significance level used to determine whether each conductance type has a significant effect on PRC shape. For each n, the PRCs taken with varying levels of dynamic-clamp-injected conductances were considered statistically different from one another if the p-value was found to be less than α. The row “Stim. Dur. (ms)” indicates the duration of the stimulus pulse, which was either 250 ms or 25% the length of the intrinsic burst period P_init. The row “Num. Sig.” indicates the number of experiments that showed significant differences between the PRCs for a particular conductance and stimulus type. The row “n” indicates the total number of experiments for a particular conductance and stimulus type.

3.6 Effects of ḡ_H and ḡ_leak on the PRC are dependent upon their location in a multi-compartment model

We were interested in further exploring the effects of ḡ_leak and ḡ_H on the PRC, given that these currents had the strongest effects on the PRC in the single-compartment model and have been shown elsewhere to have significant effects on the biological PRC (Prinz et al. 2003b; Prinz et al. 2003a). We suspected that the discrepancy between the effect of ḡ_leak on PRCs in the model neuron database and its effect in the biological neuron partly arose from the fact that in the biological neuron, the locations of synaptic input, spike generation, and production of the voltage envelope are spatially separated. Injecting leak current solely into the soma may not adequately impact the mechanism that generates the slow-wave oscillation (Maran et al. 2011) and therefore may have little effect on the PRC. Conversely, in the single-compartment model neuron, all phenomena effectively occur at a single point in space. Thus, there is no attenuation of the leak current in the single-compartment model, and it may therefore have a stronger effect on the PRC than it does in the biological neurons.

Since the H channels are commonly found in the neuropil rather than the soma membrane of the PD biological neuron (Goeritz et al. 2011), similarly to other neuron types (Angelo and Margrie 2011), we also sought to determine whether increasing the H current in the neuropil would have a similar effect on the PRC as would increasing the H current in the soma (as was done with dynamic clamp injection).

We thus sought to resolve: (1) whether the discrepancy between ḡ_leak’s effects on the PRCs in the model and biological studies was indeed due to spatial segregation of the bursting mechanism and synaptic injection, and (2) whether the effect of ḡ_H on the PRCs that we saw in both the model and biological studies would still be present if the H current was altered in the neuropil rather than in the soma. To investigate these questions, we further examined PRCs in a more biologically realistic, multi-compartment model.

We sought to determine whether altering the leak current solely in the soma (as is done when artificially adding currents to the PD neuron with dynamic clamp) has different effects on the PRC from altering the leak current throughout the entire pacemaker kernel (which we analogize to altering the leak current parameter in a single-compartment model). To do this, we utilized a four-compartment model from Maran et al. (2011). Similar to previous neuron models (Soto-Trevino et al. 2005b), this model used multiple compartments to separate the location of synaptic input (soma), the location of spike generation (axon), and the location of the mechanisms underlying the production of the voltage slow wave (lumped dendritic compartment).

We examined PRCs while altering: (1) ḡ_leak in the soma compartment alone, and (2) ḡ_leak in all compartments, including the soma, axon, primary dendrite, and lumped dendritic compartment. Modifying ḡ_leak in the soma compartment alone had little effect on the PRC (Fig. 11a), with most phase responses changing by < 0.01 as ḡ_leak,soma was increased from 0% to 200% of its canonical value. Increasing ḡ_leak to 4000% of its canonical value, however, advanced the PRC, similarly to the model neuron database. Conversely, altering ḡ_leak in every compartment from 0% to 200% of their canonical values had relatively strong effects on PRC shape (Fig. 11b).

Fig. 11. The leak current’s effect on the PRC depends on its location in a 4-compartment model.

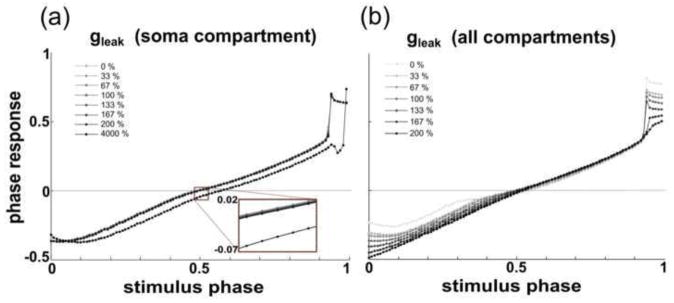
(a) Altering ḡ_leak in the soma compartment between 0% and 200% of its canonical value alters phase responses by less than 0.01. Increasing ḡ_leak,soma to 4000% of its canonical value results in an advance of the PRC, an effect that is qualitatively similar to that seen in the single-compartment model neuron database when ḡ_leak was increased by smaller increments. (b) Increasing ḡ_leak in each compartment from 0% to 200% of its canonical value noticeably alters the PRC shape, decreasing both the minimum and maximum phase response

We also sought to determine whether the location of the H current significantly affects its influence on the PRC. We added an H current (Huguenard and McCormick 1992) to either (1) the soma compartment or (2) the lumped dendritic compartment of the aforementioned four-compartment model. We then examined the effect of altering the newly added H current on the PRC in both versions of the model. In the version of the model with the H current in the soma (which is the location at which we dynamic-clamp-injected the H current into the PD neuron), the phase responses advanced by approximately 0.06 as the H current was increased from 0% to 200% of its canonical value (Fig. 12a). This result is qualitatively similar to that from the model neuron database and consistent with the results seen from the dynamic clamp studies. In the version of the model with the H current in the dendritic compartment, where the H channels exist in biological neurons, the phase responses generally advanced by less than 0.01 as ḡ_H was increased from 0 to 200% of its canonical value (Fig. 12b).

Fig. 12. The H current’s effect on the PRC depends on its location in a 4-compartment model.

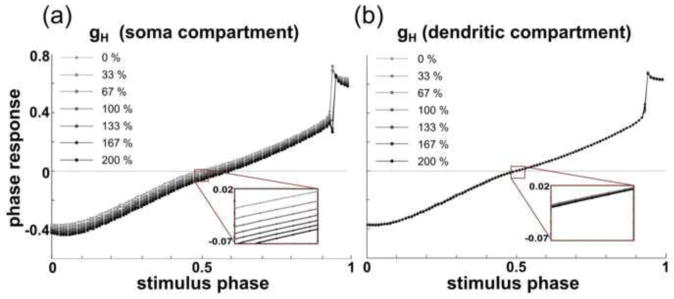
(a) Increasing ḡ_H in the soma compartment advances the entire PRC, similarly to the single-compartment model. As ḡ_H was increased from 0% to 200% of its canonical value, phases advanced by approximately 0.06. (b) Increasing ḡ_H in the lumped dendritic compartment from 0% to 200% of its canonical value caused phases to advance by approximately 0.01 or less

The above results suggest that the strong advancing effect of the H current seen in both the single-compartment model and the dynamic-clamp studies is a result of both methods’ simulating the H currents in a nonphysiological location. In both studies, the H currents are in the same compartment as that in which the synaptic current is received, and this lack of spatial separation between the locations of slow-wave generation, spike generation, and synaptic input may again be exaggerating the effect of the H current.

We thus wanted to resolve whether the endogenous H current in the biological PD neuron has similar effects on the PRC to the dynamic clamp-injected H current. We additionally asked whether the regularizing effect of the injected H current was also produced by the endogenous H current. To investigate these questions, we recorded and compared PRCs before and after blocking endogenous H current in the PD neuron.

3.7 Phase response is delayed, and its predictability decreases, when I_H is pharmacologically blocked

We investigated whether altering the endogenous H current in the biological PD neuron via pharmacological blockade would have a differing effect on the PRC than the injection of artificial H current via dynamic clamp. Typical values for the endogenous H conductance of the PD neuron are near 0.01 to 0.1 μS (Temporal et al. 2012), approximately an order of magnitude lower than the level of H conductance injected into the soma using the dynamic clamp. Upon blocking the H conductance, the PD burst period increased and exhibited greater variability. We saw two notable effects of blocking the H current on the PRC of the PD neuron. PRCs exhibited what appeared to be minor but significant delays in 1 of 2 animals when a 250 ms stimulus was applied and in 3 of 3 animals when a stimulus proportional to the intrinsic burst period was applied. In addition, the noisiness of the PRC consistently increased (in other words, the ability of a cubic polynomial to explain the variability in the cell’s phase response decreased) after the H current was blocked. As seen in previous studies, the effects of CsCl were rapidly reversible (Peck et al. 2006). The effect of blocking the H current on the PRC washed out in 2 of 3 cases, suggesting that the changes in the PRC were due to the addition of CsCl rather than other effects causing the PRC to change over time. Table 2 summarizes the results from all pharmacological experiments.

Table 2.

Effect of blocking H current on the PRC.

	IH Blocked
α	0.01
Stim. Dur. (ms)	250 ms	0.25Pinit
Num. Sig.	1	3
n	2	3

The row “α” indicates the Bonferroni-corrected significance level used to determine whether blocking the H current has a significant effect on PRC shape. For each n, the PRCs were considered statistically different from one another if the p-value was found to be less than α. The row “Stim. Dur. (ms)” indicates the duration of the stimulus pulse, and the row “Num. Sig.” indicates the number of experiments that showed significant differences between the PRCs for each stimulus type. The row “n” indicates the total number of experiments for a particular stimulus type.

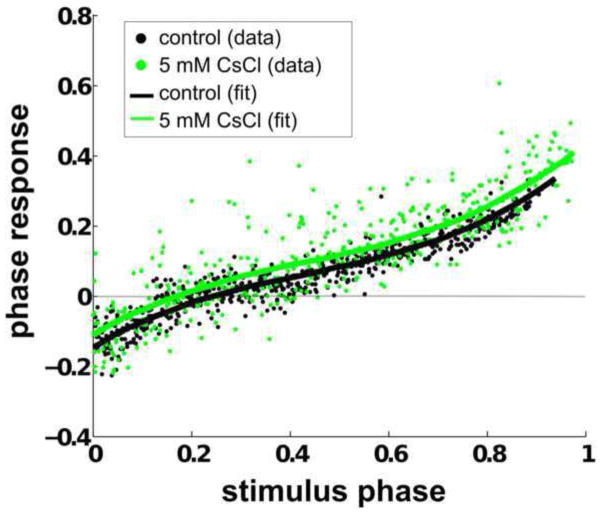
Fig. 13 shows an example set of PRCs taken before and after pharmacological blockade, each overlaid by their respective cubic polynomial fits. The polynomial fit for the PRC taken after pharmacological blockade is delayed, and the error that is not accounted for by the fit is increased. In this example, the mean squared error of the control PRC is 0.0013, and that of the PRC with 5 mM CsCl is 0.0065, suggesting that the noisiness of the PRC has increased.

Fig. 13. Pharmacological blockade of I_H delays the polynomial fit of the PRC.

Example set of PRCs tabulated before 5 mM CsCl was added to the PD neuron (shown as black circles) and afterward (shown as green circles). The polynomial fits for the control and treated PRCs are shown as black and green lines, respectively. The polynomial fits indicate that the PRC is slightly delayed when the H current is blocked. Pharmacological blockade increases the mean squared error by a factor of approximately 5. PRCs were tabulated with a stimulus of 250 ms duration

3.8 I_H increases predictability of the PRC in a four-compartment model with added noise

To ascertain that increasing gH is the cause of the reduction in the noisiness of the biological PRC, we added Gaussian noise to the current balance equation of each compartment in the four-compartment model of the AB-PD pacemaker complex, altered the level of gH in the soma, and examined the change in the noisiness of the PRC as gH was increased. All PRCs were fitted to fifth-order polynomials, since a third-order polynomial did not adequately fit the PRC data from the four-compartment model (as determined by inspecting a plot of the residuals that resulted from modeling the PRC data with a third-order polynomial). Fig. 14 shows two PRCs taken from a version of the four-compartment model with Gaussian noise added. The mean squared error is reduced when gH is increased from 0 μS to 0.48 μS in the soma. Since gH was the only parameter altered in the model, these results pinpoint gH as a significant factor in reducing noise in the PRC.

Fig. 14. Noise in the PRC is reduced when gH is increased in a four-compartment model of the AB-PD pacemaker complex.

PRCs with 0 μS gH (black) and 0.48 μS gH (magenta) added to the soma compartment. Gaussian noise was added to the current balance equation of each compartment in the model. When fitted to a fifth-order polynomial, the PRC of the model with 0 μS gH had a mean squared error of 4.5 × 10⁻⁴, and that of the model with 0.48 μS gH had a mean squared error of 7.3 × 10⁻⁵

4 Discussion

The phase resetting curve is a convenient method to describe the effect of an input stimulus on a neuronal oscillator. The intrinsic parameters of the oscillator, including the conductances of its membrane currents, have a profound influence on its activity type (Goldman et al. 2001; Hudson and Prinz 2010). We sought to determine whether these intrinsic membrane currents also produce specific effects upon the nature of the oscillator’s response to synaptic input by computationally and experimentally examining the PRC of a well-characterized neuronal oscillator. In this study, we found that: (1) Specific conductances have varying effects on the PRC in a single-compartment model, with ḡ_H and ḡ_leak generally causing the PRC to advance, (2) both endogenous and dynamic-clamp-injected H current cause the PRC to advance, though this effect is exaggerated when the H current is injected into the soma (as is done in dynamic clamp), (3) ḡ_H increases predictability of the biological PRC when modeling it as a low order polynomial, and (4) the effects of ḡ_H and ḡ_leak on the PRC depend on their location in the pacemaker kernel.

4.1 PRCs in the single-compartment model neuron database

The analysis of PD-like burster populations in the model neuron database provides a synoptic view of the relationship between specific conductances and PRC shape. In particular, ḡ_H and ḡ_leak have average effects of the greatest magnitude on the PRC, both generally causing the entire curve to advance. The delayed rectifier conductance, ḡ_Kd, has a similar effect, though to a lesser magnitude.

Previous studies exploring the effect of ḡ_H and ḡ_leak on the PRC have noted that their presence in a model neuron pacemaker does affect the nature of the response to synaptic input (Prinz et al. 2003b); the leak conductance is implicated in regulating pyloric pacemaker activity (Zhao et al. 2010) and has also been seen to substantially alter PRC shape in rat subthalamic nucleus neurons (Wilson et al. 2014). In the pyloric pacemaker, both currents cause the PRC to reach a “saturation point” at which it is no longer altered by further increasing the strength of the inhibitory synaptic input; without these currents, the model neuron’s PRC does not saturate until the synaptic input is strong enough to clamp V_m at the synaptic reversal potential. The leak current appears to affect PRC saturation more strongly than the H current (Prinz et al. 2003b). The fact that PRCs are more likely to saturate when the H currents and leak currents are present suggests that the PRCs of model neurons with large levels of leak and H currents may not be as sensitive to the other six conductances as would those PRCs of model neurons with low levels of leak and H currents. Our data suggest that this may be the case for the leak current: The minimum phase response histograms for varying levels of ḡ_leak (Fig. 6h) indicate a greater negative shift in the mean minimum phase response between populations of model neurons with ḡ_leak at levels M = 0 and M = 1 (the two lightest blue histograms) than between populations of model neurons with conductances at levels M = 4 and M = 5 (the two darkest blue histograms). A similar effect is seen in the maximum phase response (Fig. 4h) and neutral phase point (Fig. 5h). Within the ranges used to construct this database, ḡ_leak may exhibit an effect on the PRC that overrides those of other currents.

The results from our examination of individual PRC families also complement the findings from Prinz et al. (2003b) by indicating that when the synaptic strength is held constant and the conductance levels are varied (the converse of Prinz et al.’s protocol), the effects of increasing ḡ_leak may also cause the PRC to saturate after a point. Fig. 8e illustrates one family in which the differences between the PRCs at levels M = 4 and M = 5 are small compared to the PRCs in the same family with lower levels of leak current. This nonlinear relationship between the PRCs is not as evident in the families with altered gNa levels (Fig. 8b, 8c).

Examining the PRC families’ individual sensitivities to the conductances (Fig. 9) indicates that although certain conductances may cause most PRCs to be shifted either positively or negatively (i.e. the middle quartile range of the sensitivities is entirely above or below zero, respectively), for all eight conductances and all three PRC attributes, there are cases of PRC families in which the PRCs are shifted positively, and other cases in which the PRCs are shifted negatively, by increasing the value of one conductance. In other words, the effect of any specific conductance on the PRC cannot be determined without also examining the location of the respective model neuron in conductance space.

The effect of any single conductance on neuronal activity is dependent upon the values of other conductances in the membrane (Day et al. 2005; Marder and Goaillard 2006). It is possible that the magnitude of the effect of any given conductance on the PRC is itself related to the total current produced by the other conductances, with any specific current producing an outsized effect on PRCs when all other currents are relatively small. We explored this possibility by comparing the total value of the constrained conductances in each model neuron to the sensitivity of the model’s PRC’s minimum phase response to the final, unconstrained conductance; we saw that the influence of the total membrane conductance on individual conductance effects on the PRC is relatively minor (data not shown). Another interesting avenue of exploration is whether certain pairs of conductances result in the preservation of PRC shape. Several studies have demonstrated that parameters at the mRNA (Schulz et al. 2007; Tobin et al. 2009), cellular (Soofi et al. 2012; Ball et al. 2010; Hudson and Prinz 2010), and synaptic (Goaillard et al. 2009) levels exhibit pairwise correlations within solution spaces. Examining whether pairwise correlations also preserve PRC shape is a natural extension of these studies, since the PRC provides a functional view of the neuron’s role in determining network-level output.

4.2 Conductance location is a determinant of PRC shape

We used the dynamic clamp to examine the effects of specific conductances on PRC shape. We investigated five separate conductances but focused on ḡ_H and ḡ_leak. These two currents were of particular interest because: (1) They are generally active over the entire burst period and therefore likely to affect the general shape of the PRC, which covers all phases of the burst cycle, (2) The single-compartment model neuron database indicated that they generally had the effect of highest magnitude on the PRC out of all currents, and (3) These two currents influence the PRC’s sensitivity to synaptic strengths (after the strength is increased beyond a certain level) (Prinz et al. 2003b).

We saw two major effects of increasing ḡ_H in the soma of the PD neuron: The PRCs advanced, and the noisiness of the PRC was reduced. That the PRC advances is a sensible result; the H current is activated by hyperpolarization, so higher levels of ḡ_H will result in more inward current in response to a strong hyperpolarizing pulse, resulting in a neuron that is more likely to burst immediately following perturbation. Unexpectedly, we saw inconsistent and weak effects of increasing ḡ_leak on the PRC. We investigated whether the spatial separation of slow-wave generation, spike generation, and input location in the biological PD neuron played a role in producing the discrepancy between the database and dynamic clamp results by examining the four-compartment model. This model was developed with a goal of reproducing biological PRCs in the pacemaker kernel of the pyloric circuit and is thus suited to exploring the effects of conductance location and magnitude on inhibitory PRCs (Maran et al. 2011). This model was previously used to demonstrate that the spatial separation of the mechanisms generating different aspects of the burst waveform (i.e. the slow wave and the spikes) plays an important role in shaping the PRC of the AB/PD pacemaker kernel. The idea that the mechanisms underlying the slow waves and spiking portions of the waveform reside in different spatial regions of the neuron is not a new assumption, but has been extensively tested (Soto-Trevino et al. 2005a); we were therefore interested in determining how conductance location might play a role in affecting PRC shape in our system. Our findings indicate that conductance locations and magnitudes are crucial determinants of PRC shape, too. During our examination of the four-compartment model, we saw that doubling ḡ_leak in the soma alone had almost no effect on the PRC, but doubling ḡ_leak in every compartment had a substantial effect on PRC shape. This suggests that the lack of effect of the dynamic-clamp-injected leak current seen in the biological PRC may indeed be due to relatively weak electrical coupling between the dendritic compartment (where the slow wave is generated) and the soma (where synaptic inputs are applied). Thus, if we concentrate additional leak current in the soma compartment alone, we achieve a very different PRC shape than if we increase the general leakiness of the entire model neuron.

Previous studies have similarly demonstrated that the spatial distribution of specific ion channel types crucially determines certain aspects of neuronal output (Tucker et al. 2012). In addition to conductance distribution, the locus of synaptic input (perisomatic or distal dendritic) also significantly influences PRC shape (Schultheiss et al. 2010), as well as the behavior of networks of coupled cortical oscillators (Crook et al. 1998). We note that for technical reasons, all biological PRCs here were taken while delivering artificial synaptic input at the soma, while biological synaptic inputs are delivered to the dendritic branches of PD.

Much work has been done in the STNS to understand how the myriad factors in complex neuronal networks affect the activity of a single neuron or the neuronal network as a whole. The converse problem – predicting how specific details of neuronal activity will translate to effects on network function – is difficult, and results are often nonintuitive. Brute-force techniques for determining neuronal (Golowasch et al. 2002; Taylor et al. 2009; Prinz et al. 2003a) and network (Prinz et al. 2004b; Doloc-Mihu and Calabrese 2011) output have emerged, in part, as a result of the difficulty in predicting output from a set of inputs with nonlinear voltage dependence. In order to obtain an accurate picture of how a biological neuron’s activity will influence network-level function, the initial neuron model and its ion channel distributions should thus be judiciously chosen.

Previous work has suggested that the H current has similar effects on the phase resetting curve as the leak current (Prinz et al. 2003b); this was used as justification for not including the H current in the four-compartment model described in Maran et al. (2011). Our results show that this is not the case; the H current and leak current have distinguishable effects on the PRC, and these effects are partly dependent on conductance location. Thus, both currents should be included in future models that are used to predict neuronal responses to synaptic input, and their locations within the model should be biologically motivated.

4.3 Effect of the H current on neuronal output

Taken together, the experimental and modeling results involving manipulation of ḡ_H suggest that:

1. Blocking the ion channels associated with the endogenous H current (largely found in the neuropil) causes a slight delay in the PRC. Additionally, adding H current to the neuropil compartment of a pacemaker model results in a phase advance of less than 0.01.

2. Blocking the ion channels associated with the endogenous H current reduces the predictability of the PRC (see Fig. 13). The mean squared errors of the PRCs taken with CsCl were greater than those of the control PRCs when both were modeled with a cubic polynomial.

3. The dynamic-clamp-injected H current both advances and increases the predictability of the PRC (as does the endogenous current), but the effects are stronger than those of the endogenous current. The significance of the differences between the control PRCs and those that were dynamic-clamp-injected with H current was generally greater (i.e. the p-value was lower) than the significance of the differences between the control PRCs and those that had the intrinsic H current blocked with CsCl. These exaggerated effects of the dynamic clamp-injected ḡ_H may be due to two factors: (i) We injected greater levels of H current into the cell than is endogenously present, and (ii) We injected H current into the soma, where it is not usually found in biological neurons; our results from the four-compartment model suggest that the PRC is more strongly advanced when the H current is modeled in the soma than in the dendrites where the I_H channels are endogenously located.

A hyperpolarization-activated current is found in many neuron types (Dai et al. 2010; Aponte et al. 2006; Angelo et al. 2007; Chan et al. 2004), and its role has been examined at both the single-neuron (Ouyang et al. 2007) and network (Tohidi and Nadim 2009) levels. Angelo and Margrie (2011) reported that mitral cells under control conditions exhibited greater spiking regularity (i.e. ISIs exhibited a lower CV) than did cells treated with ZD7288, an I_H blocker. This effect is consistent with our findings in PD. The level of I_H in a pacemaker neuron may also influence network-level activity: Ermentrout et al. (2012) suggested that a higher level of I_H in a Golomb and Amitai conductance-based model of a two-cell network with reciprocal connections increases network synchrony (Golomb and Amitai 1997). In addition, the level of H current in the pacemaker kernel of the pyloric circuit is correlated with overall pacemaker activity (Tohidi and Nadim 2009).

An extensive body of literature supports the hypothesis that the H current serves to dampen fast fluctuations in vertebrate neurons. In rat hippocampal pyramidal cells, for instance, the H current plays a role, along with the M current and persistent Na⁺ currents, in promoting oscillatory activity in the theta frequency range (2–7 Hz) (Hu et al. 2004). Similar findings in guinea pig cortical neurons suggest that those currents that are active in the subthreshold regime produce a band-pass filter that reduces the ability of the neuron to respond to synaptic input outside that frequency range (Gutfreund et al. 1995). Our report that the H current exhibits a regularizing effect on the response to synaptic input aligns with reports from other studies that suggest the H current promotes stable or synchronous activity.

In addition to the STG, several studies in other systems have attempted to elucidate the mechanisms by which specific ionic conductances influence neuronal responses to synaptic activity. In cortical neurons, reducing the muscarine-sensitive current I_M (normally active at sub-threshold voltages) can convert excitatory PRC shapes from having regimes with both advances and delays (type II) to having only advances (type I) (K. M. Stiefel et al. 2008; Klaus M. Stiefel and Gutkin 2012). The application of carbachol (an agonist of acetylcholine that downregulates I_M) induces several cholinergic effects in cortical neurons, including changes in input resistance, resting potential, and spike-frequency adaptation (SFA) (Klaus M. Stiefel and Gutkin 2012). Downregulating I_M is known to reduce SFA (Yue and Yaari 2004; D. Brown 1988). Changes in input resistance and resting potential are not responsible for the change in PRC shape; rather, it is the reduction of SFA caused by downregulation of I_M that is associated with the conversion of type II to type I PRCs ( Klaus M. Stiefel and Gutkin 2012; K. M. Stiefel et al. 2008). It is possible that we see a similar mechanism at work in our studies; the H current in many ways has opposing effects to I_M (Hu et al. 2002), and increasing the H current as we did may have similar effects to cholinergic downregulation of I_M in PRCs of cortical pyramidal neurons.

4.4 Implications for overall network output

What might the changes to the shape of the PD neuron’s PRC tell us about the functioning of the pyloric circuit as a whole? In other words, how might the changes in the PD neuron’s response to synaptic input, effected by changes in its conductance values, translate to changes in overall network output?

One way that the conductance levels of the neurons in the pyloric circuit would be altered in the intact animal is through the actions of neuromodulators, such as red pigment concentrating hormone (RPCH) and dopamine (DA). The effects of these neuromodulators on overall network output have been well-characterized (Flamm and Harris-Warrick 1986a; 1986b; Dickinson and Marder 1989; Nusbaum and Marder 1988). By studying changes in PRC shape, we can examine the cellular-level actions of these neuromodulators and relate them to the neuromodulators’ effects on the overall circuit.

Our present studies have shown that increasing the H current in the PD neuron generally advances the PRC. At a stimulus phase of approximately 0.5, near the point at which the PD neurons in an intact network receives inhibitory input from LP, the phase response switches from a slight delay to a slight advance as the H current is increased (see Fig. 10a). DA is known to enhance the H current in AB. One might assume, given that an increase in H current leads to increased phase advances, that increasing DA might reduce the cycle period. However, DA enacts a complex set of changes to currents in the pyloric circuit, some of which have opposing effects on cell excitability (Flamm and Harris-Warrick 1986a; 1986b; Harris-Warrick et al. 1998); the addition of DA to the intact network actually slows down the rhythm rather than speeding it up. The increase in the pyloric cycle period results from DA inhibiting PD by enhancing its A current, as well as enhancing the activity of LP. How might the results from the present study inform what we already know about DA’s effects on the intact pyloric circuit?

If AB’s PRC is advanced by the addition of DA (due to the enhancement of AB’s H current), then the perturbation of the AB/PD complex at a particular phase by LP would result in a greater advance, leading to a shorter cycle period. In addition, DA is known to advance the phase of the onset of the LP burst within the cycle. Given the shape of the PRC seen in Fig. 10, this would lead to an even greater advance of the subsequent PD burst, leading to an even shorter cycle period. This suggests that the enhancement of the H current in AB causes the PRC to move in a direction that would encourage a reduction of the cycle period. However, due to the myriad other effects of DA on the pyloric circuit, this enhancement of the H current does not appear able to overcome the other, inhibitory effects of DA that ultimately lead to an increase in the cycle period (Harris Warrick et al. 1995).

Previous work has additionally shown that when the duration of input to an oscillator is increased, the PRC shifts to greater delays (Prinz et al. 2003b, Thirumulai 2006). Thirumulai et al. used PRC analysis to conclude that an increase in LP burst duration (caused by the presence of RPCH) is one factor that causes the pyloric cycle period to increase. However, the effect of RPCH on the overall cycle period is transient, while the effect of RPCH on the strength of the LP-to-PD synapse persists as long as RPCH is present. It is possible that an upregulation in the H current could aid in bringing the period back to its original value. RPCH is found as a cotransmitter with other neuromodulators (Thirumulai and Marder 2002). It may be that these other neuromodulators are partially responsible for diminishing RPCH’s effect on the cycle period through an alteration of the H current.

In summary, the effects of a neuromodulator on overall network output often result from a combination of individual cellular and/or synaptic effects that combine in often non-intuitive ways to produce alterations in network behavior. Characterizing the connections between changes in individual membrane conductances and the shape of the PRC, as we have done here, provides a framework in which to tease apart how effects of a neuromodulator on cellular excitability and response properties interact to produce physiologically meaningful network output alterations.

5 Conclusion

The premise of the work described here was that the PRC is a concise method of describing the functional significance of certain biophysical parameters of oscillatory neurons. The duration, amplitude, and direction of input from the presynaptic neuron are known to affect PRC shape (Oprisan et al. 2003; Prinz et al. 2003b). Here, we demonstrate that certain intrinsic membrane conductances of the postsynaptic neuron have significant effects on PRC shape as well. As seen in other systems, the H current promotes excitability and regularity of the pyloric pacemaker kernel’s response to synaptic input. We also determined that the effects of any given conductance are partially dependent upon the locations within the neuron of the ion channels associated with that conductance. Our findings have allowed us to make some general observations that may apply to other systems. When using a model to predict the response of a neuron to synaptic input, it is important that the model be appropriately designed to capture the effects of spatial differences between certain conductances (each with specific roles in shaping the voltage waveform) and the locus of current injection. The type of input response should be carefully considered as well; while the effects of inhibitory inhibition can be captured with a relatively simple model, a more complex model is required to capture the effects of excitatory input to the AB/PD complex (Maran et al. 2011). In addition, the interplay between short-term synaptic dynamics and cycle period (which is also influenced by membrane conductances) may influence the AB/PD response to synaptic input in a manner not captured here (Nadim et al. 2003; Mamiya and Nadim 2004). By gaining some insight into the functional consequences of synaptic input in an isolated system (as we have done here), we have improved our ability to understand the role of that system in the context of its intact neuronal network.

Appendix A

Table 3.

Conductance values (mS/cm²) used to generate traces in figures

Fig.	Na	CaT	CaS	A	KCa	Kd	H	Leak
3a	0	0	8	40	10	100	0.04	0.05
3b	100	12.5	2	0	15	25	0	0.01
3c	400	0	10	50	10	0	0.01	0.01
3d	500	2.5	6	10	20	50	0.05	0.01
8b (top)	100	2.5	2	10	125	5	0.03	0.01
8b (bottom)	500	2.5	2	10	125	5	0.03	0.01
8c (top)	100	2.5	2	40	5	25	0.02	0.02
8c (bottom)	500	2.5	2	40	5	25	0.02	0.02
8e (top)	500	2.5	6	10	20	50	0.05	0.01
8e (bottom)	500	2.5	6	10	20	50	0.05	0.05
8f (top)	200	2.5	10	40	10	100	0.01	0.01
8f (bottom)	200	2.5	10	40	10	100	0.01	0.05