Nonrenewal spike train statistics: causes and functional consequences on neural coding

Abstract

Many neurons display significant patterning in their spike trains (e.g. oscillations, bursting), and there is accumulating evidence that information is contained in these patterns. In many cases, this patterning is caused by intrinsic mechanisms rather than external signals. In this review, we focus on spiking activity that displays nonrenewal statistics (i.e. memory that persists from one firing to the next). Such statistics are seen in both peripheral and central neurons and appear to be ubiquitous in the CNS. We review the principal mechanisms that can give rise to nonrenewal spike train statistics. These are separated into intrinsic mechanisms such as relative refractoriness and network mechanisms such as coupling with delayed inhibitory feedback. Next, we focus on the functional roles for nonrenewal spike train statistics. These can either increase or decrease information transmission. We also focus on how such statistics can give rise to an optimal integration timescale at which spike train variability is minimal and how this might be exploited by sensory systems to maximize the detection of weak signals. We finish by pointing out some interesting future directions for research in this area. In particular, we explore the interesting possibility that synaptic dynamics might be matched with the nonrenewal spiking statistics of presynaptic spike trains in order to further improve information transmission.

Introduction

It is frequently assumed that neural activity can be described by the distribution of interspike intervals (ISIs: i.e. the times between consecutive action potentials) (Moore et al. 1966; Perkel et al. 1967a, b; Shadlen and Newsome 1998; Bastian and Nguyenkim 2001). This measure has been used to describe the firing patterns of both peripheral and central neurons (Maimon and Assad 2009). Such a description assumes that the spiking activity can be described by renewal process where all memory is erased after each action potential firing (Cox and Lewis 1966). The Poisson process is, perhaps, the best-known example of a renewal process: it is characterized by an exponential distribution of ISIs and has been frequently used to describe the firing of cortical neurons (Shadlen and Newsome 1998; Kara et al. 2000). There is, however, accumulating evidence that the spiking activities of many neurons are not well described by renewal processes as they display memory in their spiking activity that persists over multiple action potential firings (i.e. the probability of firing is influenced by the past spiking activity). Such memory can be quantified in terms of the ISI serial correlation coefficients ρ_j (Perkel et al. 1967a):

$$\begin{array}{c}{\rho }_j=\frac{\langle I_i{I}_{i^{+}j}\rangle -{\langle I_i\rangle }^2}{\langle I_i^2\rangle -{\langle I_i\rangle }^2}\\ \langle \dots \rangle =\frac{1}{N}\sum _{i=1}^N\dots \end{array}$$

where j is the lag. The ISI serial correlation coefficient, ρ_j, measures whether the value of ISI_i has any influence on the value of ISI_i+j (i.e. whether they are correlated). In particular, negative values of ρ_j imply that if the value of ISI_i is greater than average, then ISI_i+j will tend to have a value that is less than average and vice versa. Thus, if j = 1, then ρ₁ < 0 implies that long ISIs will tend to be followed by short ISIs and vice versa. For a renewal process, we have ρ_j = 0 for all j ≠ 0. As such, the value of a given ISI is independent of the values of the previous ISIs. A nonrenewal process is thus a process for which ρ_j ≠ 0 for at least one j ≠ 0.

Here, we focus on reviewing accounts of nonrenewal spike train statistics in experimental data, the mechanisms that generate such statistics, and their function in information processing.

Experimental observations of nonrenewal spike train statistics

We first begin with a comprehensive review of the known reports of nonrenewal spike train statistics in experimental data.

Overview

Neurons displaying nonrenewal spiking statistics have been found in many brain areas. The oldest report that is known to the authors is in the activity of motoneurons in humans (Hagiwara 1949). Subsequent studies have found nonrenewal spiking statistics in retinal cat retinal ganglion cells (Kuffler et al. 1957; Rodieck 1967; Levine 1980), cat superior olivary neurons (Goldberg et al. 1964; Tsuchitani and Johnson 1985), cat peripheral auditory fibers (Lowen and Teich 1992), cat cochlear nuclear neurons (Goldberg and Greenwood 1966), cat medullary sympathetic neurons (Lewis et al. 2001), cat sympathetic efferent fibers (Floyd et al. 1982), pigeon vestibular afferents (Correia and Landolt 1977), weakly electric fish electroreceptor neurons (Longtin and Racicot 1997; Chacron et al. 2000; Ratnam and Nelson 2000; Chacron et al. 2001b; Chacron et al. 2005b; Gussin et al. 2007), paddlefish electroreceptors (Bahar et al. 2001; Neiman and Russell 2001; Neiman and Russell 2004), catfish electroreceptors (Schäfer et al. 1995), weakly electric fish electrosensory pyramidal neurons (Doiron et al. 2003; Chacron et al. 2007), honeybee mushroom body neurons (Farkhooi et al. 2009), grasshopper auditory neurons (Schwalger et al. 2010), primate spinothalamic neurons (Surmeier et al. 1989), rat mesencephalic reticular neurons (Lansky and Radil 1987), primate somatosensory cortical neurons (Yamamoto and Nakahama 1983; Lebedev and Nelson 1996; Nawrot et al. 2007), as well as rat entorhinal cortical pyramidal and interneurons (Engel et al. 2008). We note that the last five studies challenge the notion that cortical neurons can be described by a renewal process such as the Poisson process and shall return to this point later.

Negative interspike interval correlations at lag 1

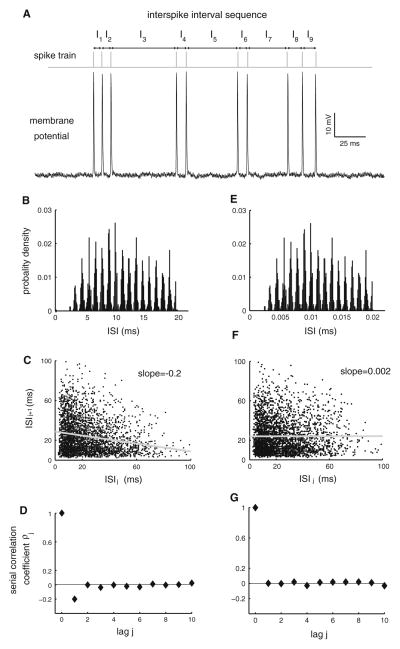
Several investigators have reported nonrenewal spike train statistics in the form of a negative ISI serial correlation coefficient at lag 1 that is significantly different from zero (Kuffler et al. 1957; Goldberg et al. 1964; Yamamoto and Nakahama 1983; Tsuchitani and Johnson 1985; Schäfer et al. 1995; Chacron et al. 2000; Chacron et al. 2007; Nawrot et al. 2007; Engel et al. 2008; Farkhooi et al. 2009). As mentioned above, this implies that ISIs that are shorter than average tend to be followed by ISIs that are longer than average and vice versa, thus giving rise to patterning in the spike train. Figure 1a shows an example recording from a pyramidal cell: it can be seen that this neuron tends to fire doublets as well as triplets of action potentials. Thus, short ISI tends to be followed by long ones and vice versa. The ISI distribution (Fig. 1b) does not capture this. However, a plot of the current ISI as a function of the preceding one, also known as the ISI return map (Doiron et al. 2003; Ellis et al. 2007; Toporikova and Chacron 2009) (Fig. 1c), can be used to illustrate this fact. The slope of a linear fit in this graph will then give us the ISI correlation coefficient ρ₁ (Wang 1998). It can be seen that, for this particular neuron, successive ISIs were negatively correlated, leading to negative serial ISI correlation coefficient at lag 1 (Fig. 1d).

Fig. 1.

Example of nonrenewal spike train statistics. a Voltage trace from a pyramidal cell of weakly electric fish. The spike times and ISIs (I₁,… I₉) are also shown. It is seen that short ISIs tend to be followed by long ones and vice versa. b ISI probability distribution obtained from the same cell. c ISI return map obtained from the same cell. The slope of the best-fit line (gray) is equal to the ISI serial correlation coefficient at lag one for the spike train. d ISI serial correlation coefficients ρ_j as a function of lag j. Note that we have ρ₁ < 0. e The ISI probability distribution obtained after randomly shuffling the ISI sequence. f The ISI return map is significantly altered by the shuffling procedure. g ISI serial correlation coefficients ρ_j as a function of lag j for the shuffled data. Note that ρ_j = 0 for j > 0

In order to better illustrate the effects of ISI correlations on the different measures that were just presented, we have randomly shuffled the ISI sequence. Such a procedure will preserve first-order ISI statistics such as the ISI distribution (compare Fig. 1b, e) but will eliminate any correlations between the ISIs by definition. The ISI return maps were similar in shape (compare Fig. 1c, f). However, computing the average slope of the return map (gray lines in Fig. 1c, f) reveals that the ISI shuffling procedure removes any correlations by calculating the average correlation coefficient. This is reflected in the ISI serial correlation coefficients (compare Fig. 1d, g).

Positive ISI correlations

In some spike trains, small positive serial correlations can decay over several successive lags without alternating in sign (Levine 1980; Lowen and Teich 1992; Lewis et al. 2001; Longtin et al. 2003; Gussin et al. 2007). Although these small positive serial correlations can be quite weak and in some cases might not be detectable using the ISI serial correlation coefficients themselves, they can be detected using other measures of variability such as the Fano factor (Lowen and Teich 1992; Chacron et al. 2001a; Lewis et al. 2001; Longtin et al. 2003). The Fano factor (Fano 1947) is defined as the variance to mean ratio of the spike count distribution (i.e. the number of spikes) during a time window T (Snippe and Koenderink 1992). Note that the spike-count distribution is also referred to as the pulse-number distribution. The Fano factor measures the spike variability at long timescales. It has been observed that the Fano factor increases as a power law (i.e. F(T) ∞ T^a with “a” being the power law exponent) for large T for a wide variety of spike trains (Lowen and Teich 1992, 1996; Lowen et al. 1997; Teich et al. 1997; Ratnam and Nelson 2000; Gussin et al. 2007). As power law dependencies are self-similar on multiple timescales, this phenomenon has been referred to a fractal firing pattern and has been reviewed extensively. It appears that this phenomenon is seen ubiquitously in experimental data (Teich 1992).

ISI correlations that alternate in sign over successive lags

Some neurons display ISI correlations that decay over several lags in an alternating fashion (i.e. a negative ISI correlation coefficient is followed by a positive one, which is then followed by a negative one that is weaker in magnitude, etc…). This is, perhaps, seen most prominently in the electroreceptors of the paddlefish in which these serial correlation coefficients decay over hundreds of lags (Bahar et al. 2001; Neiman and Russell 2001, 2004). Some bursting electroreceptors of weakly electric fish display alternating ISI correlations, but they tend to decay over at most a few lags (Chacron et al. 2001b, 2005a).

Summary

In summary, there are multiple reports of ISI correlations across different brain areas and organisms. These reports as well as the type of correlations reported are summarized in the table below (Table 1).

Table 1.

Summary of the types of ISI correlations seen experimentally

Reference	Organism and neuron type	ISI correlation structure
Bahar et al. (2001), Neiman and Russell (2001), Neiman and Russell (2004)	Paddlefish electroreceptors	Alternating ISI correlations that decay over several lags
Chacron et al. (2000), Chacron et al. (2005b), Gussin et al. (2007), Longtin and Racicot (1997), Ratnam and Nelson (2000)	Weakly electric fish electroreceptors	Negative ISI correlation at lag 1 and positive ISI correlations that decay over several lags
Chacron et al. (2001b)	Weakly electric fish electroreceptors	Alternating ISI correlations that decay over a few lags
Chacron et al. (2007), Doiron et al. (2003)	Weakly electric fish electrosensory pyramidal neurons	Negative ISI correlation at lag 1
Correia and Landholt (1977)	Pigeon vestibular afferents	Negative ISI correlation at lag 1
Engel et al. (2008)	Rat entorhinal cortical pyramidal and interneurons	Negative ISI correlation at lag 1
Farkhooi et al. (2009)	Honeybee mushroom body neurons	Negative ISI correlation at lag 1
Floyd et al. (1982)	Cat sympathetic efferent fibers	Negative ISI correlation at lag 1
Goldberg et al. (1964), Tsuchitami and Johnson (1985)	Cat superior olivary neurons	Negative ISI correlation at lag 1
Goldberg and Greenwood (1966)	Cat cochlear nuclear neurons	Negative ISI correlation at lag 1
Hagiwara (1949)	Human motoneurons	Negative ISI correlation at lag 1
Kuffler et al. (1957), Rodieck (1967), Levine (1980)	Cat retinal ganglion cells	Negative ISI correlation at lag 1
Lansky and Radil (1987)	Rat mesencephalic reticular neurons	Negative ISI correlation at lag 1
Lewis et al. (2001)	Cat medullary sympathetic neurons	Positive ISI correlations that decay over several lags
Lowen and Teich (1992)	Cat peripheral auditory fibers	Negative ISI correlation at lag 1 and positive ISI correlations that decay over several lags
Nawrot et al. (1997), Yamamoto and Nakahama (1983), Lebedev and Nelson (1996)	Primate somatosensory cortical neurons	Negative ISI correlation at lag 1
Schäfer et al. (1995)	Catfish electroreceptors	Negative ISI correlation at lag 1.
Schwalger et al. (2010)	Grasshopper auditory neurons	Positive ISI correlations that decay over several lags
Surmeier et al. (1989)	Primate spinothalamic neurons	Positive and negative ISI correlation at lag 1

Mechanisms that underlie the generation of nonrenewal spike train statistics

In this section, we review some of the mechanisms and mathematical models that give rise to nonrenewal spike train statistics.

Mechanisms that give rise to a single negative ISI correlation coefficient at lag 1

We will first concentrate on the mechanisms that give rise to a negative ISI correlation coefficient at lag 1. Intuitively, these mechanisms must have the following in common: when two or more action potentials occur during a short-time period (i.e. a short ISI), the mechanism must prevent or delay the onset of the next action potential firing thereby giving rise to a long ISI. There are both intrinsic and network mechanisms that can accomplish this.

Cumulative growth in the spike after hyperpolarization

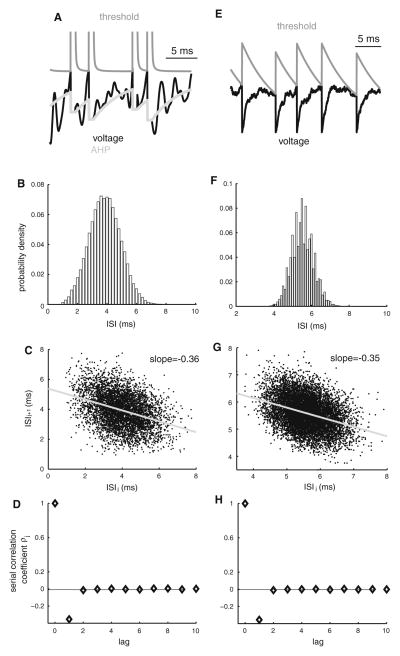
It was recognized early on that growth in the afterhyperpolarization (AHP) following each action potential during repetitive firing could give rise to negative interspike interval correlations (Eccles 1953; Goldberg et al. 1964). This has led to the formulation of a phenomenological model by Geisler and Goldberg (1966). This model is of the leaky integrate-and-fire type (Tuckwell 1988) in which the membrane potential is integrated in time until it reaches a given threshold value and is illustrated in Fig. 2a. Immediately after this, the threshold is set to infinity during the duration of the absolute refractory period and the voltage is decremented, thereby mimicking an increased AHP (Geisler and Goldberg 1966). It is important to note that repetitive firing will lead to an accumulation in the AHP (Fig. 2a, light gray), thereby increasing the distance between voltage and threshold and thereby delaying the next firing (Fig. 2a). As such, a sequence of short inters-pike intervals will give rise to large AHPs whereas longer interspike intervals will give rise to small AHPs. It is then easy to see that short/long interspike intervals will tend to be followed by long/short interspike intervals as larger AHPs will tend to delay the next action potential more than smaller AHPs (Geisler and Goldberg 1966). While the ISI probability distribution does not capture this (Fig. 2b), this is illustrated in the ISI return map (Fig. 2c) as well as the ISI serial correlation coefficients (Fig. 2d). Variants of this model have been later proposed and studied in detail (Smith and Goldberg 1986; Lansky et al. 1992; Keat et al. 2001; Liu and Wang 2001; Benda et al. 2010).

Fig. 2.

Mechanisms that give rise to nonrenewal spike train statistics. a Voltage (black) and threshold (dark gray) traces from the model proposed by Geisler and Goldberg (1966). An action potential is said to occur when the voltage is equal to the threshold. Immediately after, the threshold is set to infinity during the duration of the absolute refractory period and decreases back to its steady-state value. The voltage is the sum of noise and a variable (light gray) that is decremented immediately after an action potential. When two or more action potentials occur in rapid succession, there is a cumulative decrease in the voltage. c ISI probability distribution from this model. The ISI return map displays a negative slope (gray). d ISI serial correlation coefficients ρ_j as a function of lag j. Note that we have ρ₁ < 0. e Voltage (black) and threshold (gray) traces from the leaky integrate-and-fire model with dynamic threshold (LIFDT). Like in the Geisler–Goldberg model, an action potential is said to occur when the voltage is equal to the threshold. Immediately after, the voltage is reset to a constant (zero in this case) and the threshold is incremented by a constant amount after which it decays exponentially to a steady-state value. Repetitive firing can lead to accumulation in the threshold, causing it to be higher. We refer to this phenomenon as threshold fatigue. f ISI probability density for the LIFDT model. g The ISI return map for the LIFDT model also shows a negative slope. h ISI serial correlation coefficients ρ_j as a function of lag j for the LIFDT model. Note that we have ρ₁ < 0

Biophysical models of the accumulation in the AHP during repetitive firing based on the Hodgkin–Huxley formalism (Hodgkin and Huxley 1952) have also been proposed and studied with respect to accumulation in the AHP during repetitive firing. In particular, calcium-activated potassium channels have been shown to mediate the spike AHP (Sah 1996; Faber and Sah 2003). These channels are not sensitive to the transmembrane potential but are instead activated by increases in the internal calcium concentration (Sah and Faber 2002). A mathematical model that incorporates these channels has been shown to give rise to negative ISI correlations (Wang 1998). In this model, calcium accumulates inside the cell during repetitive firing, which causes an accumulation in the AHP, thereby delaying the onset of the next action potential, thereby giving rise to negative ISI correlations.

Threshold fatigue

While it was once thought that the action potential threshold was fixed, there is accumulating experimental evidence that this is not the case. Indeed, it is known that the threshold varies dynamically and is strongly dependent on the previous spiking history (Azouz and Gray 1999, 2000, 2003; Chacron et al. 2007). Variations in the action potential threshold have been frequently considered in mathematical models (Geisler and Goldberg 1966; Weiss 1966; MacGregor and Oliver 1974; Horn and Usher 1989; Eckhorn et al. 1990; Abeles 1991; Gabbiani 1996; Jolivet et al. 2006). In particular, a phenomenological model of the leaky integrate-and-fire type has also been studied. In this model, the threshold is incremented by a constant amount immediately after action potential firing and decreases exponentially to a baseline value during quiescence (Fig. 2e). Repetitive firing will lead to a cumulative increase in threshold that will delay the next firing due to an increased distance between voltage and threshold. We refer to this cumulative increase in threshold as threshold fatigue.

As such, although the biophysical mechanisms of cumulative growth of the AHP and of cumulative increases in the threshold are quite different in nature, the basic principle by which they give rise to negative ISI correlations is the same: an increased distance between voltage and threshold after repetitive firing. It is thus not surprising that both the leaky integrate-and-fire model with dynamic threshold and the previously mentioned model based on the accumulation of the AHP give rise to similar ISI distributions (compare Fig. 2b, f), ISI return maps (compare Fig. 2c, g), and ISI serial correlation coefficients (compare Fig. 2d, h). Moreover, both models have been shown to be qualitatively equivalent for the most part (Liu and Wang 2001), although a recent study has pointed out some differences in terms of spike frequency adaptation (Benda et al. 2010). The leaky integrate-and-fire model with dynamic threshold can furthermore successfully reproduce experimental data from the electroreceptors of weakly electric fish (Chacron et al. 2000, 2003, 2004a, c; Brandman and Nelson 2002; Chacron 2006; Savard et al. 2011) as well as vestibular afferents (Sadeghi et al. 2007). Recent experimental evidence shows that threshold fatigue is also present in electrosensory pyramidal neurons (Chacron et al. 2007). Such fatigue can be modeled by shifting the activation curve of the sodium current to larger voltages, which effectively raises the action potential threshold (Chacron et al. 2007). It is thus likely that threshold fatigue is due to cumulative sodium channel desensitization (Mickus et al. 1999). Multiple biophysical mechanisms can thus give rise to negative ISI correlations at lag 1.

Synaptic depression

The parallels between the leaky integrate-and-fire model with threshold fatigue and models of synaptic depression (i.e. a decrease in the postsynaptic potential amplitude during repetitive presynaptic stimulation) have been pointed out before (Chacron et al. 2003). Indeed, synaptic depression can give rise to relative refractoriness (Häusser and Roth 1997), and models of synaptic depression show similarities with the previously described leaky integrate-and-fire model with threshold fatigue (Fuhrmann et al. 2002; Goldman et al. 2002). In fact, it has been shown that such models can transform a Poisson presynaptic spike train (note that Poisson spike trains are renewal in nature) into a postsynaptic spike train that displays a negative serial correlation coefficient at lag 1 (Goldman et al. 2002). This can be understood intuitively as follows: it is clear that two or more presynaptic action potentials that occur in rapid succession will give rise to an amount of synaptic depression that is inversely proportional to the time between consecutive action potentials (i.e. the ISI). As such, the probability of an EPSP causing a postsynaptic action potential decreases with each subsequent presynaptic action potential as the EPSP amplitude decreases. Let us assume that only the first two EPSPs cause postsynaptic action potentials (i.e. a short ISI). A long period of silence in the presynaptic spike train is then necessary for the synapse to recover from depression so that a presynaptic action potential can again have sufficiently large amplitude to give rise to a postsynaptic action potential. As such, the short ISI in the postsynaptic neuron will tend to be followed by a long one. We therefore expect that, under these conditions, the postsynaptic spike train would display negative ISI correlations.

Delayed feedback

It is well known that neurons in cortical areas of the nervous system are the target of massive descending projections (Cajal 1909; Hollander 1970; Ostapoff et al. 1990; Maler et al. 1991; Sherman and Guillery 2002, 2006) and that such pathways can give rise to interesting dynamics such as bursting (Krahe and Gabbiani 2004; Chacron and Bastian 2008; Toporikova and Chacron 2009; Avila Akerberg et al. 2010). In particular, Doiron et al. (2003) showed that neurons with intrinsic renewal spike train statistics could display nonrenewal spike train statistics simply by introducing coupling between them through global delayed inhibitory feedback. This can be understood intuitively as follows. Because of temporal summation, short interspike intervals can give rise to delayed inhibition that can prevent subsequent firing in a manner similar to that of the AHP described above. As such, it is expected that the spike trains of individual neurons in a network coupled with inhibitory delayed feedback can display a negative ISI correlation at lag 1. We note that it is, however, possible that other network mechanisms might give rise to a negative ISI correlation at lag 1.

Mechanisms that give rise to positive ISI correlations

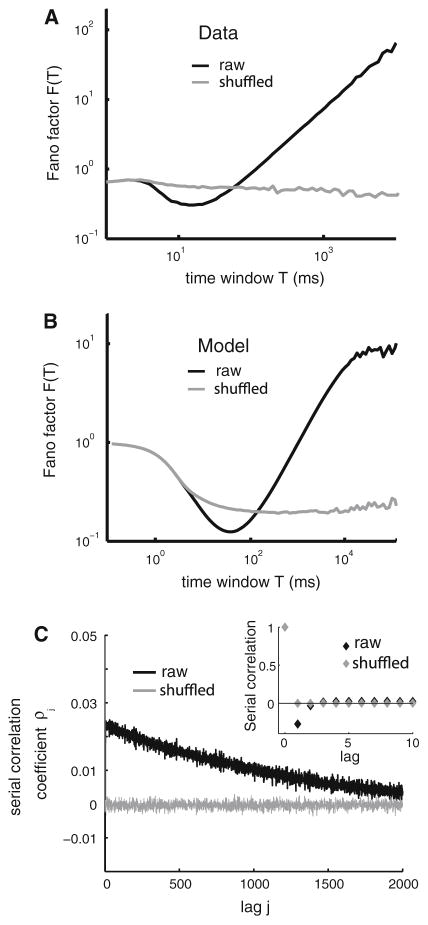
As mentioned above, weak and positive ISI correlations are often present in experimental data. One example spike train from an electrosensory afferent neuron shows a power law dependency at large time windows for the Fano factor (Fig. 3a, black). As randomly shuffling the ISI sequence eliminates this dependency (Fig. 3a, gray), it must be due to correlations between the ISIs (Lowen and Teich 1992). It has been shown experimentally (Lewis et al. 2001) that such behavior is caused by positive ISI correlations that decay over many lags.

Fig. 3.

Detecting positive ISI correlations in experimental data and models. a Fano factor F(T) (variance to mean ratio of the spike count distribution in a time window of length T) as a function of T for an electroreceptor afferent neuron of weakly electric fish. In particular, F(T) increases as a power law for large T as can be seen from the linear part of the graph (note the log–log scale). Also shown is the Fano factor computed from the data after randomly shuffling the ISI sequence (gray) which does not display this power law behavior. b The Fano factor F(T) as a function of T for an LIFDT model that is driven by a weak noise with a long correlation time (black) resembles that obtained from the experimental data. The Fano factor F(T) obtained after shuffling the ISIs is also shown (gray). c ISI serial correlation coefficients ρ_j as a function of lag j (black) and after random ISI shuffling (gray). It is seen that the model displays weak positive ISI correlations that decay slowly over thousands of lags. Random ISI shuffling eliminates these correlations (gray). The inset shows the ISI serial correlation coefficients ρ_j as a function of lag j but only for the first 10 lags, thus showing the negative serial correlation at lag 1 and that these positive ISI correlations can be easily missed because they are so weak in magnitude

Modeling and theoretical studies have shown that addition of a weak but colored zero-mean noise with a positive and slowly decaying autocorrelation function (i.e. a long correlation time) can give rise to positive ISI correlations that decay over many lags (Chacron et al. 2001a; Middleton et al. 2003a, 2003b). Intuitively, this can be understood as follows. Imagine that the noise is positive and thus promotes increased action potential firing (i.e. ISIs that are shorter than average). Since the noise has a long correlation time, it will tend to stay positive for a long time. As such, the ISIs will tend to stay shorter than average for this time, leading to positive ISI correlations (note that a similar argument can be made when the noise is negatively correlated). The Fano factor curve from such a model also shows power law scaling but only for a finite range of time windows before saturating (Fig. 3b, black). This is because the noise process has a finite correlation time and is unlike experimental data whose Fano factor seems to scale as a power law for as long as experimentally measurable (Lowen and Teich 1992). However, the range of time windows over which the Fano factor displays power law scaling can be extended to arbitrarily large values in the model by simply increasing the noise’s correlation time (Longtin et al. 2003; Middleton et al. 2003a, 2003b). Analysis of the serial correlation coefficients of the model reveals that coefficients at lags ≥2 are positive and decay over hundreds of lags (Fig. 3c). A recent study has uncovered a possible source for this noise in the stochastic opening and closing of voltage-gated potassium channels (Schwalger et al. 2010). Possible functional consequences for such correlations are discussed further in section IIIB.

Mechanisms that give rise to alternating ISI correlations

Alternating ISI correlations have been observed experimentally in paddlefish electroreceptors (Bahar et al. 2001; Neiman and Russell 2001, 2002, 2004, 2005). The sensory epithelial hair cells display ~25-Hz oscillations that can be recorded as voltage or current fluctuations in the canals leading from skin pores to the sensory epithelia. These cells then make excitatory synaptic contact unto the afferent terminals. These fire continuously (“spontaneously”) at a nearly fixed frequency in the range of 30–70 Hz. As such, paddlefish electroreceptors can be modeled as two unidirectionally coupled oscillators: the noisy 25-Hz oscillation from the epithelial hair cells drives the afferent fibers that show an intrinsic tendency to oscillate at 30–70 Hz. It was shown that both types of oscillators affect the firing of primary afferents, which results in an output that shows both fundamental frequencies (i.e. 25 Hz and 30–70 Hz). In particular, it was found that these ISI correlations were strongest in magnitude when the epithelial oscillation frequency is half that of the afferent fiber oscillator frequency (e.g. 25 and 50 Hz) (Neiman and Russell 2004). In this situation, one will get two action potentials per epithelial hair cell oscillation cycle. Therefore, an ISI shorter than average will be followed by an ISI longer than average, then an ISI shorter than average, etc… This alternating pattern of short and long ISIs is what causes the spike trains of paddlefish electroreceptors to display decaying ISI correlations that alternate in sign over successive lags (Neiman and Russell 2001, 2004, 2005).

Function of nonrenewal spike train statistics

In this section, we review the known functional consequences of nonrenewal spike train statistics. Before doing so, however, we review some concepts in signal detection, information theory, and noise shaping.

Neural coding

Neurons display trial-to-trial variability in their responses to repeated presentations of a given stimulus. While the function of this variability is still being debated (Stein et al. 2005), it is generally agreed that at least part of this variability arises from noise, which is due to the random opening of ion channels as well as the large synaptic bombardment that neurons are subjected to in vivo (Destexhe et al. 2003; London et al. 2010). It is possible to simply average away this variability in order to obtain an estimate of the mean response to a given stimulus, and this is frequently done when computing measures such as the peristimulus time histogram. However, it is at best unclear how the organism might perform this operation (Zohary et al. 1994). We will thus take the point of view here that neural variability must be taken into account.

Signal detection theory

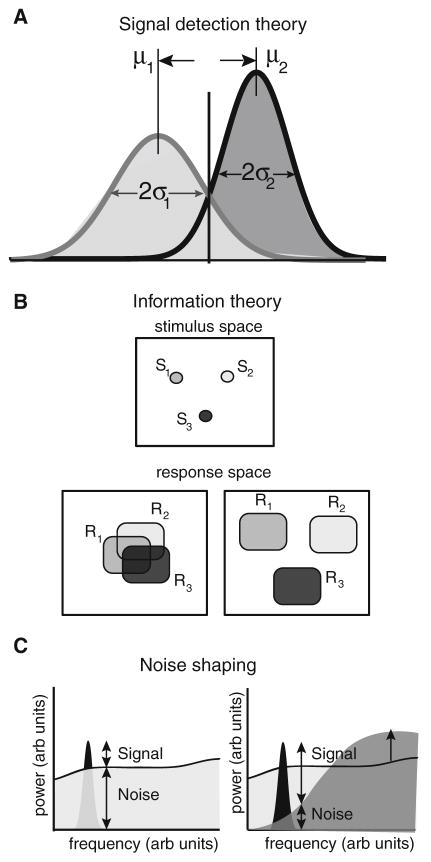
Signal detection theory (Green and Swets 1966) aims at quantifying the performance of an ideal observer in distinguishing between different alternatives. In most cases, signal detection theory is used to distinguish between two alternatives that give rise to different measured outputs. In most cases, the output is the number of action potentials (i.e. the pulse number) that occurs within a given time window (Snippe and Koenderink 1992). Since neurons display variability in their responses to repeated presentations of the same stimulus (Stein et al. 2005), the pulse number obeys a distribution with nonzero variance. The performance of the ideal observer is inversely related to the amount of overlap between the two distributions (Fig. 4a) and has been quantified using various measures such as the discriminability index d′ or the minimum probability of misclassification (Poor 1994). The discriminability index d′ is defined by (Green and Swets 1966):

$$d^{\prime }=\frac{\left|{\mu }_1-{\mu }_2\right|}{\sqrt{\frac{{\sigma }_1^2+{\sigma }_2^2}{2}}}.$$

Fig. 4.

Illustration of signal detection theory, information theory, and noise shaping. a Illustrating signal detection theory. The basic premise is that two different stimuli (1 and 2) will elicit two different response distributions with means μ₁, μ₂ and standard deviations σ₁, σ₂, respectively. The degree of separability between the two distributions can be assessed by computing d′. b Illustrating information theory. Information theory can be seen as a generalization of signal detection theory for more than 2 stimuli. It is assumed that different stimuli (S₁, S₂, S₃) will elicit different response distributions (R₁, R₂, R₃). If these have considerable overlap (bottom left panel), it is more difficult to know whether a given response was elicited by a given stimulus. In contrast, when these response distributions have no overlap, it then becomes easy to gain information as to which stimulus was presented when observing a given response. c Illustrating noise shaping. Shown are the power spectra of a signal (black) and the noise (gray). The signal-to-noise ratio (SNR) is then simply the ratio of signal and noise power and depends on frequency. If the noise power is high, then the signal-to-noise ratio is low (left). However, if noise power was to be transferred from frequencies contained in the signal to higher frequencies, then the SNR would be increased (right). Noise shaping is precisely the transfer of noise power from one frequency range to another, thereby conserving the total noise power (i.e. the power summed overall frequencies)

Within this framework, the optimal detector is the one that minimizes the degree of overlap between the pulse-number distributions obtained under different conditions and therefore maximizes d′. This can be done by increasing the difference between their means and/or decreasing their variances (Fig. 4a). We shall see below that negative ISI correlations reduce the spike count variance while positive ISI correlations increase the spike count variance and how this can increase or decrease signal detectability, respectively.

Information theory

Information theory was first developed in the context of communication channels (Shannon 1948) and has gained popularity in neuroscience (Borst and Theunissen 1999). Our goal here is not to provide an exhaustive review of the uses of information theory in neuroscience but merely to introduce some intuitive concepts. The interested reader is directed to the following references that provide a good summary of the uses of information theory in neuroscience (Rieke et al. 1996; Borst and Theunissen 1999; Dayan and Abbott 2001; Gabbiani and Cox 2010).

Let us assume that there is a stimulus set S = [S₁,…, S_N] and that each stimulus S_i gives rise to a set of neural responses R_i = [R_1i,…, R_Ni]. For example, the response could be the mean firing rate. When stimulus S₁ is presented, the response is R₁₁ on trial 1, R₁₂ on trial 2, etc… Because neurons display trial-to-trial variability in their responses to sensory input, a given sensory stimulus gives rise to a set of responses R_i (Fig. 4b). The number of possible responses increases with larger variability in general. In contrast, the distance between sets R_i and R_j is primarily determined by how different the responses to the different stimuli S_i and S_j are. Intuitively, if the sets R_i are disjoint (i.e. they do not overlap), then observing an individual response R_ik on trial k would allow us to tell which stimulus S_i was given on that trial (Fig. 4b). On the other hand, if there is large overlap between the sets R_i, then observing a given response R_ik will not allow us to tell which stimulus S_i was given on trial k. It is possible to make these intuitive concepts about information mathematically formal using the following definition for information (Shannon 1948; Cover and Thomas 1991):

$$I(R,S)=H(R)-H(R/S)$$

where I(R, S) is the information contained in the response R about the stimulus S. H(R) is the entropy of the response and H(R/S) is the entropy of the response given that we have observed the stimulus S. Intuitively, the entropy is related to the amount of uncertainty or randomness in a process. Thus, a process that has only one possible outcome (i.e. is completely predictable) would have zero entropy (the minimum), while a process that has uncertainty (e.g. a coin toss) would have higher entropy. We note that the entropy is always positive. As such, the mutual information I(R, S) is maximized when H(R) is maximized and H(R/S) is minimized. This corresponds to a case illustrated above where the set of responses obtained to different stimuli are as different as possible, but the response to a given stimulus is always the same. The mutual information is usually measured in bits, and X bits implies that the system can discriminate between 2^X stimuli in the noise-free situation (Thomson and Kristan 2005). As such, ISI correlations can alter information transmission by affecting the response entropy H(R) or the noise entropy H(R/S), or both. We will see below that ISI correlations can affect both.

Moreover, as sensory stimuli are frequently characterized by their temporal frequency content, it is more informative to look at the mutual information rate density (i.e. the mutual information rate per frequency) rather than the mutual information rate itself. This allows one to then quantify which frequency component contained in the stimulus is the neuron transmitting more information (Borst and Theunissen 1999). Te mutual information rate density at a given frequency f is related to the ratio of signal power to noise power in the response at that frequency (i.e. the signal-to-noise ratio or SNR). Greater SNR values give rise to greater MI density values. We will see below that ISI correlations can have differential effects on the MI density that are frequency dependent.

Noise shaping

We have mentioned earlier that neurons display variability in their responses to repeated presentations of the same stimulus. If one assumes that noise is detrimental to information transmission by neurons, then it makes sense to minimize this noise. However, as this might not be possible, one could then imagine the following scenario. If the signal that we want to encode contains temporal frequencies within a given range, then it may be possible to minimize the noise’s frequency content within that range by transferring power from that range to another. One would then have a greater SNR and thus increased information transmission in the former frequency range at the expense of a weaker SNR and thus reduced information in the latter frequency range. This concept is illustrated in Fig. 4c and is known as noise shaping. Note that, in the case of noise shaping, the total noise power (i.e. the power integrated over frequency) remains the same. Noise shaping is found in engineering devices such as Josephson junctions and sigma–delta modulators (Wiesenfeld and Satija 1987; Norsworthy et al. 1997; Yacomotti et al. 1999) and has been proposed to be used by the brain as a mechanism to deal with noise (Shin 1993; Shin 2001). Further, a modeling study has shown that a network of neurons coupled with inhibition could display noise shaping (Maar et al. 1999).

Effects of ISI correlations on neural coding

In this section, we review some of the important results on the function of ISI correlations in neural coding.

Effects of ISI correlations on signal detection

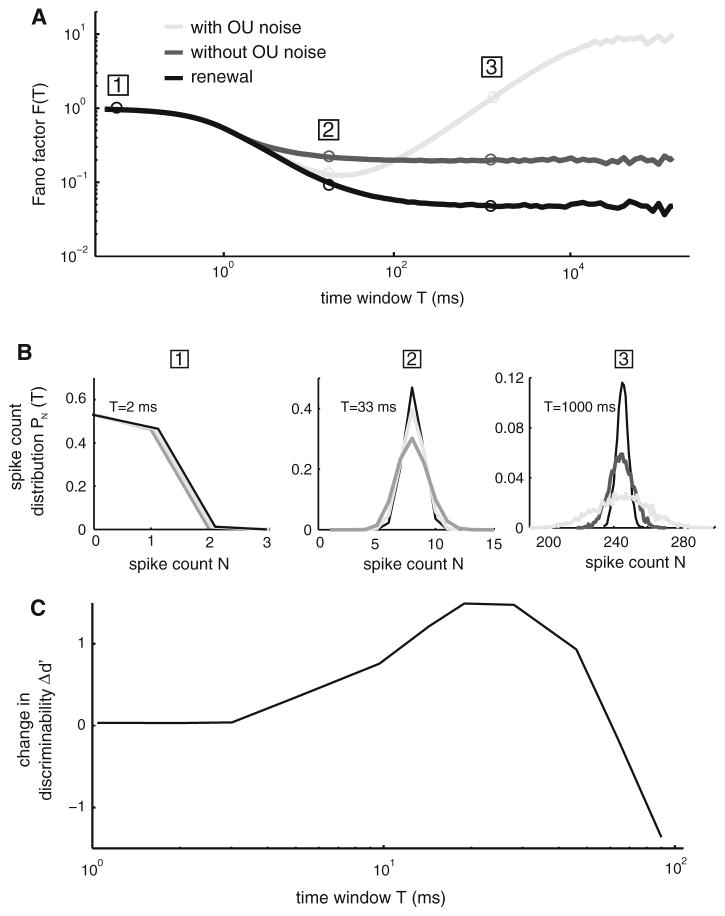
We first focus on the role of negative ISI correlations. Using a model of a spinal motoneuron and assuming a rate code, Birk (1972) showed that the decoded representation of a spike train with negative ISI correlations will display less variability than a spike train with the same firing rate but with independent ISIs (Birk 1972). Numerical simulations have since then shown that the pulse-number distribution of a spike train with negative ISI correlations displays less variance than that of a spike train with independent ISIs (Ratnam and Nelson 2000; Chacron et al. 2001a). This has important consequences for the detection of weak signals using signal detection theory as negative ISI correlations can then reduce the variance of the pulse-number distribution in a fixed time window (Fig. 5a), which can increase discriminability (Ratnam and Nelson 2000; Chacron et al. 2001a; Brandman and Nelson 2002; Goense and Ratnam 2003). However, the magnitude of the effect depends on the length of the time window (i.e. the integration time). The magnitude of the effect essentially depends on the difference between the Fano factors of the raw and shuffled ISI sequences (Fig. 5a, black and dark gray curves): for small time windows, these correlations will have little effect and maximum effect for larger time windows (Fig. 5b, black and dark gray curves).

Fig. 5.

Positive and negative ISI correlations act to create a minimum in spike train variability for a given time window T. a Fano factor F(T) from the LIFDT neuron model driven by a weak Ornstein–Uhlenbeck (OU) noise with a long correlation time (light gray). Also shown are the Fano factor F(T) computed from the same model without the OU noise (black) and after shuffling the ISI sequence (dark gray). b Spike count distributions P_N(T) obtained for all three conditions. For T = 2 ms (left), the distributions show almost complete overlap. However, for T = 33 ms (middle), the spike count distribution obtained from the LIFDT model without OU noise (black) shows the weakest variance, followed by the distribution obtained with the model with OU noise (light gray), followed by the distribution obtained after shuffling. However, for T = 1,000 ms (right), it is the distribution obtained from the model with OU noise (light gray) that has the highest variance. c Change in discriminability measure d′ (i.e. the difference between d′ computed from the model with OU noise and d′ computed after shuffling the ISI sequence) as a function of the time window length T. It is seen that the gain in discriminability is maximal for a value of T for which the Fano factor F(T) is minimum

In contrast to negative ISI correlations, the functional role of positive ISI correlations is less well understood. As mentioned previously, positive ISI correlations will tend to increase spike train variability, which is detrimental for signal detection. Their effect is to increase the spike count variance for large time windows (Fig. 5b, compare light and dark gray). It was shown that an interaction between short-term negative ISI and long-term positive ISI correlations could create a minimum in spike train variability as quantified by the Fano factor for a given time window (Ratnam and Nelson 2000; Chacron et al. 2001a; Longtin et al. 2003). This effect is illustrated in Fig. 5. One can then show that signal detection as quantified by d′ is minimum at that time window with respect to a renewal process (Fig. 5c). It is possible that such a coding strategy is used by weakly electric fish to detect prey as the pulse-number distributions in their peripheral electroreceptive neurons display minimal variability for integration timescales that correspond to the integration time window inferred from prey capture behavior (Nelson and MacIver 1999; Ratnam and Nelson 2000; Chacron et al. 2001a; Longtin et al. 2003). A recent study has shown similar effects in the Paddlefish electro-receptors (Engel et al. 2009). It is important to note that the value of the integration time for which the spike train variability as quantified by the Fano factor is minimum depends on many parameters such as the bias current and noise intensity. As such, it is possible to have neurons display minimum variability over a wide range of integration time window values (Middleton et al. 2003a, b).

Effects of ISI correlations on information transmission: noise shaping

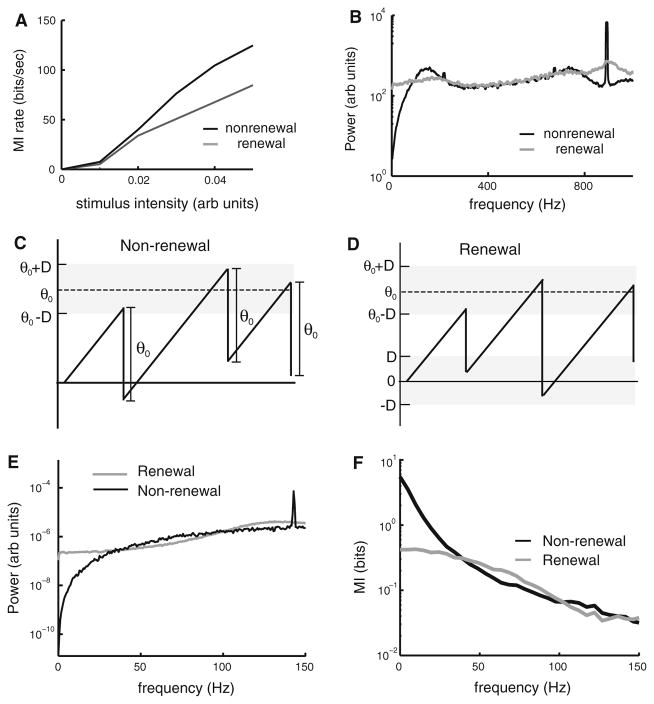
It was also found that negative ISI correlations can improve information transmission of time-varying stimuli (Chacron et al. 2001a) (Fig. 6a). This was done by comparing two mathematical models that had similar ISI distributions and responses to sensory input as quantified by linear systems identification (Chacron et al. 2001a). Chacron et al. (2001a) found that although negative ISI correlations reduced the signal entropy H(R), they reduced the noise entropy H(R/S) even more, thereby increasing the mutual information I(R, S) = H(R) − H(R/S).

Fig. 6.

Negative ISI correlations increase information transmission through noise shaping. a Mutual information rate as a function of stimulus intensity for nonrenewal (black) and renewal (gray) phenomenological models. These models were matched such as to have similar ISI probability densities and signal power in response to the stimulus. b Noise power spectra for nonrenewal (black) and renewal (gray) phenomenological models. It is seen that the nonrenewal model displays lower noise power at low frequencies. c Illustration of the voltage trace from a nonrenewal simplified model (black). Unlike the LIFDT or Geisler-Goldberg models, the voltage is a linear function of time and a threshold is randomly chosen from the interval [θ₀ − D; θ₀ + D]. When the voltage reaches the threshold, it is decremented by a constant amount θ₀. It can be shown that this model gives rise to a single negative ISI correlation coefficient at lag 1, similar to the LIFT model (D). Illustration of the voltage trace from a renewal simplified model (black). The voltage is still a linear function of time, and a threshold is randomly chosen from the interval [θ₀ − D; θ₀ + D]. However, when the voltage reaches the threshold, it is instead reset to a random value in the interval [− D; D]. It can be shown that this model gives rise to renewal spike train statistics. e Noise power spectra of the simplified nonrenewal (black) and renewal (gray) models. Note the similarity with b. f Mutual information rate densities computed from the nonrenewal (black) and renewal (gray) simplified models. Note that the mutual information rate density of nonrenewal model is larger than that of the renewal model for low frequencies. This demonstrates that noise shaping leads to information shaping

Any comprehensive understanding of coding in stimulus-evoked spike trains of neurons requires a characterization of neural discharge components that are directly associated with the stimulus (signal) and those that are not (noise) (Roddey et al. 2000; Stein et al. 2005; Faisal et al. 2008). In neurons that display high resting (i.e. in the absence of stimulation) discharge activity, the component that is associated with noise is given by the power spectrum of this resting discharge activity (Chacron et al. 2005a). This assumes that the stimulus intensity is small so that the perturbations brought about by the stimulus are small in magnitude and will thus scale linearly with the stimulus intensity. Experimental results have shown that this is the case in both electroreceptor (Chacron et al. 2005b) and vestibular afferents (Sadeghi et al. 2007), provided that the stimulus intensity is not too high (but see (Savard et al. 2011)). Investigators have therefore focused on understanding how ISI correlations can alter the power spectrum of the baseline activity. Comparing the baseline power spectra of renewal and nonrenewal models that have the same first-order ISI statistics reveals important differences (Fig. 6b). In particular, it is seen that the nonrenewal model displays lower power at low (<100 Hz) frequencies but higher power for higher (between 100 Hz and 200 Hz) frequencies (Fig. 6b).

This has prompted researchers to build two simple models for which it is possible to compute the resting discharge power spectrum analytically (Chacron et al. 2004b; Lindner et al. 2005). In the first model, once the voltage reaches a threshold, it is decremented by a constant amount following each action potential (Fig. 6c). This way it will keep the memory of the previous ISI onto the next one. In the second model, once the voltage reaches a threshold, it is reset to a random value (Fig. 6d). It is thus not surprising that the first model displays negative ISI correlations (as it will preserve memory) while the second does not. We shall henceforth refer to the first model as nonrenewal and the second model as renewal. Comparing the noise power spectra of both models revealed qualitatively similar differences with those seen with more realistic models (compare Fig. 6a, e). Further investigation revealed that both models have identical signal discharge components as quantified by their transfer functions (Chacron et al. 2004b) and that frequencies associated with a lower/higher resting discharge spectrum are associated with higher/lower information rates (Fig. 6f). This demonstrates how noise shaping by ISI correlations can lead to information shaping (i.e. increasing and reducing information in different frequency ranges).

Effects of nonrenewal spiking statistics on neural coding at the network level

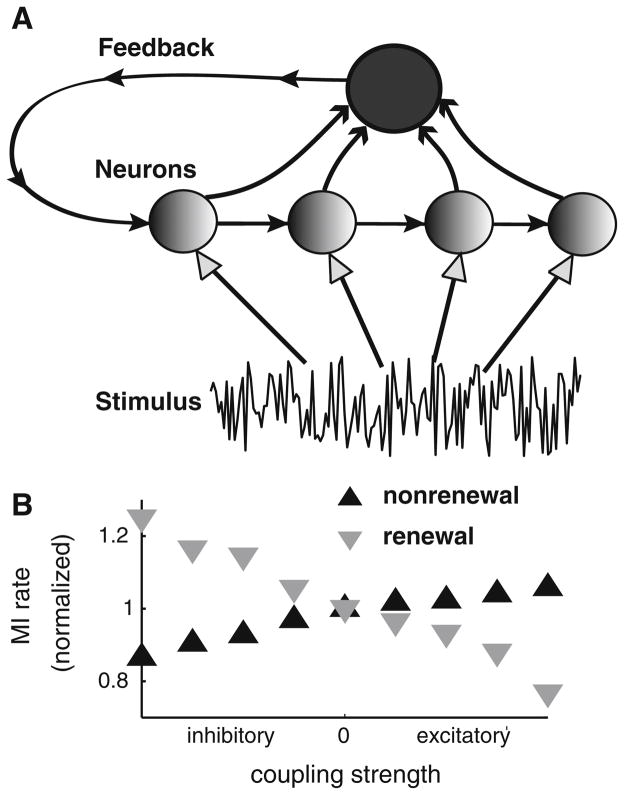
It is well known that the brain uses a distributed representation of information through neural populations. How well do networks of nonrenewal neurons transmit information in comparison with networks of renewal neurons? Two recent studies have explored this interesting question (Avila Akerberg and Chacron 2009; Avila Akerberg and Chacron 2010). These studies showed that renewal and nonrenewal neurons transmit information differentially when all-to-all coupling is introduced (Fig. 7a). Indeed, nonrenewal networks with excitatory/inhibitory coupling transmit more/less information than nonrenewal networks of the same size with no coupling. In contrast, renewal networks with excitatory/inhibitory coupling transmit less/ more information than renewal networks of the same size with no coupling (Fig. 7b). As such, excitatory and inhibitory couplings each have opposite effects on networks of renewal and nonrenewal model neurons. As anatomical studies have found that the majority of synaptic connections in the brain are excitatory, it is possible that such connections increase information transmission by neurons that display nonrenewal spike train statistics.

Fig. 7.

Effects of coupling on networks of nonrenewal and renewal model neurons. a Representation of the network connectivity. Each neuron in the network receives the same stimulus. The responses of all neurons in the network are then summed, and the resulting is then fed back to all neurons with a delay as either excitatory or inhibitory input. We note that this topology is mathematically equivalent to all-to-all coupling. b Mutual information rate normalized to its value for no coupling as a function of the coupling strength (negative values mean inhibitory coupling while positive ones mean positive coupling). It is seen that coupling affects the information transmitted by networks of renewal and nonrenewal neurons in opposite ways

Conclusions and future directions

In this section, we provide a brief summary of the reviewed results and outline some future directions for research pertaining to the effects of nonrenewal spike train statistics on neural coding.

Summary

We have reviewed the known mechanisms that give rise to ISI correlations and the known consequences of ISI correlations on information transmission and neural coding. Any of cumulative growth of the AHP, cumulative increase in threshold during repetitive firing, synaptic depression, or delayed inhibitory feedback can give rise to negative ISI correlations. In contrast, a weak noise with a long correlation time can give rise to positive ISI correlations that decay over many lags. In general, negative ISI correlations can significantly increase information transmission and signal detection by decreasing the noise entropy and spike count variance, respectively. However, their effects are dependent on the stimulus’ temporal frequency content as well as coupling between neurons. As such, it is clear that ISI correlations are found across senses and organisms and can have important effects on information transmission. However, the exact nature of these is likely to depend on multiple factors including the nature of the neural code used by a given brain area where neurons display nonrenewal spike train statistics and the decoding of the information transmitted by these neurons in higher-order areas. We thus conclude by highlighting some future directions addressing the following key issues: (1) developing an integrative approach to obtain a better understanding of the functional roles of nonrenewal spike train statistics; (2) understanding whether information carried in nonrenewal spike trains is actually decoded by higher-order neurons and, if so, how; and (3) are the effects of ISI correlations universal across systems?

Toward an integrative approach to understand how the mechanisms that give rise to nonrenewal spike train statistics affect information transmission

As mentioned previously, the mechanisms that give rise to nonrenewal spike train statistics can have other effects such as spike frequency adaptation. Moreover, recent studies have shown that these mechanisms not only alter the spike count variance but also can alter its mean and possibly higher moments (Chacron et al. 2007). Moreover, these mechanisms can also strongly alter temporal frequency tuning (Ellis et al. 2007; Mehaffey et al. 2008; Lindner et al. 2009; Peron and Gabbiani 2009). Yet, to date, all studies that have explored the role of nonrenewal spike train statistics on information transmission or signal detection have done so by comparing models that display identical first-order ISI statistics and frequency tuning. How these effects interact is largely unknown to this day. In order to better illustrate our point, we give a couple of examples below.

For example, in terms of signal detection theory, this implies that the mechanisms that give rise to ISI correlations can not only affect the spike count variance but also the mean spike count. As such, one could conceive a scenario where negative ISI correlations would lead to a lower spike count variance of each distribution as well as lead to a greater difference between their means. Both effects would then act synergistically to lead to better signal detection. Alternatively, one could conceive another scenario where the advantage of a reduced spike count variance is offset by a smaller separation between the means.

Alternatively, theoretical studies have shown that spike frequency adaptation reduces the response gain to low-frequency stimuli (Benda and Herz 2003), which might offset the decrease in noise power caused by negative ISI correlations and therefore the signal-to-noise ratio might remain the same. A recent study suggests that synaptic depression, which can cause negative ISI correlations as reviewed above, might actually not alter the signal-to-noise ratio (Lindner et al. 2009), although this is strongly dependent on the measure used.

We thus argue that future studies should take a more integrative approach (i.e. consider all the effects of the mechanisms that give rise to nonrenewal spike train statistics) in order to gain a better understanding of the effects of ISI correlations on information transmission.

Nonrenewal spike train statistics and population coding

Another shortcoming of previous studies interested in understanding the role of nonrenewal spike train statistics on information transmission is that they have mostly concentrated on single neurons. Although some recent theoretical studies have highlighted potentially interesting effects in networks of nonrenewal neurons (Avila Akerberg and Chacron 2009, 2010), the effects of nonrenewal spike trains statistics on population coding remain largely unexplored to this day. While peripheral sensory neurons such as auditory fibers or electroreceptors displaying non-renewal spike trains might not be coupled, this is certainly not the case for central neurons. Indeed, cortical neurons (Engel et al. 2008), cochlear nuclear neurons (Goldberg and Greenwood 1966) as well as electrosensory pyramidal cells (Chacron and Bastian 2008) all receive thousands of synaptic input and display nonrenewal spike train statistics. Such input most likely contributes to experimentally observed correlations between the activities of neighboring neurons across sensory systems (Meister et al. 1995; Averbeck et al. 2006; Averbeck and Lee 2006). While there is still an ongoing debate on whether these correlations are beneficial or detrimental for information transmission, it is widely agreed that their presence will significantly alter the way that information is transmitted by neural populations and its subsequent decoding by higher-order neurons (Nirenberg et al. 2001; Schneidman et al. 2003, 2006; Latham and Nirenberg 2005; Averbeck et al. 2006). How nonrenewal spike train statistics affect correlated activity among neurons is an interesting topic that has been largely overlooked so far. For example, it is known that electroreceptor afferents in weakly electric fish that display negative ISI correlations can synchronize in response to transient high-frequency stimuli (Benda et al. 2005, 2006; Chacron et al. 2005b), but do nonrenewal spike train statistics influence this synchronization and, if so, how? In general, further experimental and theoretical studies are needed to understand the effects of nonrenewal spike train statistics on population coding across systems.

Decoding information carried by nonrenewal spike trains

While it has been shown that ISI correlations can significantly alter information transmission, this information is only useful to the organism if it is being decoded by higher-order neurons. If such decoding does not occur, then one could argue ISI correlations are nothing more than an artifact caused by mechanisms with another function. We argue that this hypothesis has to be tested on a case-by-case basis and review some recent experimental results suggesting that such decoding actually does occur.

The decoding of information carried by nonrenewal spike trains is an important problem. We shall consider two cases here: decoding information carried by the spike count (rate coding) and decoding information carried in the timing of spikes (temporal coding).

For the spike count, it is clear that a temporal integrator neuron can simply integrate over the time window for which the spike train variability of its afferent nonrenewal neurons is minimum and therefore take advantage of the reduced variability provided by negative ISI correlations, and this has been argued previously (Ratnam and Nelson 2000; Chacron et al. 2001a; Engel et al. 2009). Such neurons have been observed in the anuran midbrain, and the mechanisms by which they achieve this function are well understood and have been described elsewhere (Edwards et al. 2008; Leary et al. 2008; Rose et al. 2010).

However, decoding information that might be contained in the timing of action potentials in nonrenewal spike trains is less well understood. A recent theoretical study has, however, proposed how synaptic plasticity could actually decorrelate a presynaptic spike train that displays ISI correlations (Nesse et al. 2010). Such decorrelation has obvious advantages for information transmission such as redundancy reduction and can be more easily decoded by downstream neurons (Barlow and Levick 1969). Nesse et al. (2010) provide a simple algorithm for decorrelation that can be tested experimentally.

Future experimental studies should focus on whether such algorithms are used by the central nervous system to decode information contained either in the spike count or in the spike timing of nonrenewal neurons.

Matching synaptic dynamics to nonrenewal spike train statistics in order to optimize weak signal detectability

While it has been shown that negative ISI correlations can reduce the spike count variance and thereby increase signal detectability, it is possible that other mechanisms might act in concert to further increase signal detectability. Recent experimental and theoretical evidences suggest that the dynamics of fast synaptic depression is matched to nonrenewal spike train statistics in order to maximize signal detection (Khanbabaie et al. 2010). It is important to note that the effects of synaptic depression are independent of those due to nonrenewal presynaptic spike train statistics. However, both act in concert in order to reduce variability and maximize signal detectability. This combination of these effects might be able to explain the remarkable behavioral acuity displayed by weakly electric fish when detecting prey (Khanbabaie et al. 2010). This study provides compelling evidence that the central nervous system uses multiple mechanisms in order to reduce spike train variability and support the hypothesis that information contained in nonrenewal spike trains is being decoded by higher-order neurons. However, further studies are needed to test for such cooperative mechanisms in other systems where sensory neurons display nonrenewal spike train statistics. In particular, the short-term synaptic depression described by Khanbabaie et al. (2010) is found in both the auditory and somatosensory systems.

Universality of nonrenewal spike train statistics

While it is frequently assumed that cortical neurons can be modeled by Poisson processes with a refractory period (Shadlen and Newsome 1998; Kara et al. 2000) due to their high variability (Softky and Koch 1993), this view is being challenged more and more (Engel et al. 2008; Farkhooi et al. 2009; Maimon and Assad 2009). In particular, recent studies have found that cortical neurons could display nonrenewal spike train statistics in vivo (Engel et al. 2008). A more recent paper has argued that it is possible that nonrenewal spike train statistics are far more prevalent in cortical neurons than was originally thought and might have been missed in extracellular recordings due to missed spikes (Farkhooi et al. 2009). Intracellular recordings from cortical neurons have shown that they can display significant patterning in their spiking activities (Engel et al. 2008), and further studies are needed to test this hypothesis.

Conclusion

In conclusion, we have reviewed the mechanisms that give rise to ISI correlations in neural spike trains, the known consequences of these correlations on information transmission, and have highlighted some key issues that future studies on this subject should focus on.