NEURAL HETEROGENEITIES AND STIMULUS PROPERTIES AFFECT BURST CODING IN VIVO

Abstract

Many neurons tend to fire clusters of action potentials called bursts followed by quiescence in response to sensory input. While the mechanisms that underlie burst firing are generally well understood in vitro, the functional role of these bursts in generating behavioral responses to sensory input in vivo are less clear. Pyramidal cells within the electrosensory lateral line lobe (ELL) of weakly electric fish offer an attractive model system for studying the coding properties of burst firing, because the anatomy and physiology of the electrosensory circuitry are well understood, and the burst mechanism of ELL pyramidal cells has been thoroughly characterized in vitro. We investigated the coding properties of bursts generated by these cells in vivo in response to mimics of behaviorally relevant sensory input. We found that heterogeneities within the pyramidal cell population had quantitative but not qualitative effects on burst coding for the low frequency components of broadband time varying input. Moreover, spatially localized stimuli mimicking, for example, prey tended to elicit more bursts than spatially global stimuli mimicking conspecific-related stimuli. We also found small but significant correlations between burst attributes such as the number of spikes per burst or the interspike interval during the burst and stimulus attributes such as stimulus amplitude or slope. These correlations were much weaker in magnitude than those observed in vitro. More surprisingly, our results show that correlations between burst and stimulus attributes actually decreased in magnitude when we used low frequency stimuli that are expected to promote burst firing. We propose that this discrepancy is attributable to differences between ELL pyramidal cell burst firing under in vivo and in vitro conditions.

Understanding the neural code remains a central problem in neuroscience. This understanding is in part complicated by the fact that neurons in the brain are highly heterogeneous (Bannister and Larkman, 1995a,b; Bastian and Nguyenkim, 2001; Häusser and Mel, 2003) and are not passive input-driven devices. Instead, they are capable of rich intrinsic dynamics such as oscillations (Gray and Singer, 1989; Stopfer et al., 1997; Doiron et al., 2003a) and bursting (i.e. the firing of packets of action potentials followed by quiescence) (Lemon and Turner, 2000; Sherman, 2001; Swensen and Bean, 2003; Krahe and Gabbiani, 2004; Sabourin and Pollack, 2009). Although much is known about the intrinsic mechanisms that lead to burst firing (Wang and Rinzel, 1995; Izhikevich, 2000; Krahe and Gabbiani, 2004), the functional role of burst firing is less well understood. Studies have shown that bursts of action potentials are critical for mediating cricket escape behavior in response to threatening stimuli (Marsat and Pollack, 2006). The function of burst firing is less well understood in vertebrates: a variety of functions have been proposed including feature detection (Gabbiani et al., 1996; Metzner et al., 1998; Sherman, 2001; Sherman and Guillery, 2002; Lesica and Stanley, 2004), coding for stimulus slope (Kepecs et al., 2002; Kepecs and Lisman, 2003; Doiron et al., 2007; Oswald et al., 2007) as well as amplitude (Doiron et al., 2007; Oswald et al., 2007), and improving the reliability of synaptic transmission (Izhikevich et al., 2003).

Studies conducted in simple systems with well-characterized anatomy and relatively simple behaviors are likely to yield significant insight into the mechanisms by which bursts of action potentials code for behaviorally relevant stimuli. Here we focused on understanding how heterogeneities in a particular neural population can influence the coding of stimulus attributes by burst firing in vivo in the well-characterized electrosensory system of the South American weakly electric fish Apteronotus leptorhynchus. These fish generate an electric field through electric organ discharge (EOD) and sense amplitude modulations of that field through an array of electroreceptor neurons located on the animal’s skin (Bullock et al., 2005). Natural stimuli comprise both spatially local and global stimuli: while prey objects or objects such as small rocks produce spatially localized electric images on the skin of the fish and are limited to low (<10 Hz) temporal frequencies (Nelson and MacIver, 1999), conspecific-related stimuli produce spatially diffuse electric images on the skin of the fish that contain temporal frequencies in the range 0–300 Hz (Zupanc and Maler, 1993; Zakon et al., 2002). Every primary electrosensory afferent fiber trifurcates and makes synaptic contact unto pyramidal cells within the three tuberous segments of the electrosensory lateral line lobe (ELL) of the hindbrain (Heiligenberg and Dye, 1982). These topographic maps of the body surface are known as the centromedial (CMS), centrolateral (CLS), and lateral (LS) segments. Pyramidal cells in these three maps differ in their responses to input both in vivo (Shumway, 1989; Krahe et al., 2008) and in vitro (Mehaffey et al., 2008b), which is partly due to the differential distribution of various ion channels (Maler, 2009a,b). Further, lesion studies have shown that the different maps mediate different electrosensory behaviors (Metzner and Juranek, 1997).

Recent anatomical studies have shown that pyramidal cells within each map can be subdivided into six classes (Maler, 2009a). Firstly, pyramidal cells can either be excited (E-type) or inhibited (I-type) by increases in EOD amplitude, and these functional differences are correlated with anatomical differences: namely the presence or absence of a basilar dendritic bush, respectively (Maler, 1979; Maler et al., 1981; Saunders and Bastian, 1984). These cell types correspond to ON and OFF cells found in other systems. Secondly, both E and I-type pyramidal cells can be subdivided into three subclasses: superficial, intermediate, and deep (Maler, 2009a). On one end, superficial pyramidal cells have large apical dendritic trees (Bastian and Nguyenkim, 2001), receive large amounts of plastic feedback (Bastian et al., 2004; Chacron et al., 2005c), have receptive fields with a large surround area (Bastian et al., 2002), display low rates of spontaneous firing in vivo (Bastian and Nguyenkim, 2001), and show the greatest selectivity in their responses to sensory input (Chacron et al., 2005c; Chacron, 2006). At the other end, deep pyramidal cells are characterized by small apical dendritic trees (Bastian and Courtright, 1991; Bastian and Nguyenkim, 2001), receive little feedback input that displays little plasticity (Bastian et al., 2004; Chacron et al., 2005c), have receptive fields with a small surround area (Bastian et al., 2002), display high rates of spontaneous firing in vivo (Bastian and Nguyenkim, 2001), and show little selectivity to sensory input (Chacron et al., 2005c; Chacron, 2006). Intermediate pyramidal cells have characteristics that lie in between those of superficial and deep pyramidal cells. Anatomical studies have furthermore shown large differences in the distributions of several ion channels and ligand-gated ionotropic receptors between deep and superficial pyramidal cells such as NMDA receptors (Harvey-Girard and Dunn, 2003; Harvey-Girard et al., 2007), small conductance (SK) calcium-activated potassium channels (Ellis et al., 2007b, 2008), and IP3 receptors (Berman et al., 1995).

ELL pyramidal cells also display an intrinsic burst mechanism that has been well characterized in vitro and relies on a somatodendritic interaction (Lemon and Turner, 2000; Doiron et al., 2001, 2002, 2003b; Noonan et al., 2003; Fernandez et al., 2005; Mehaffey et al., 2008a): somatic action potentials backpropagate into the apical dendritic tree where they cause a dendritic action potential that propagates back to the soma, leading to a depolarizing afterpotential (DAP) which can cause another somatic action potential. The strength of the DAP grows throughout the burst, leading to a shortening of the interspike interval. The burst terminates with a characteristic doublet when the interspike interval falls below the dendritic refractory period, causing dendritic failure and a large burst afterhypolarization (bAHP) in the soma (Noonan et al., 2003). Studies performed in vitro have shown a strong relationship between burst and stimulus attributes: stimuli of higher amplitude gave rise to bursts with shorter intraburst intervals (Doiron et al., 2007; Oswald et al., 2007). Additionally, it was shown that bursts and isolated spikes encode different features of sensory input: bursts were most responsive to the low frequency components while isolated spikes were most responsive to the high frequency components of time varying input (Oswald et al., 2004).

While much is known about pyramidal cell responses to behaviorally relevant input in vivo (Bastian et al., 2002; Chacron et al., 2005a; Chacron and Bastian, 2008; Krahe et al., 2008), comparatively little information is available about the coding properties of burst attributes with the exception that it has been shown that burst firing of pyramidal cells within the lateral segment could code for certain communication stimuli (Marsat et al., 2009). It is known that neurons within the torus semicircularis that receive input from ELL pyramidal cells respond specifically to bursts of action potentials (Fortune and Rose, 1997) thus suggesting that these bursts are important for neural coding. However, we do not know if neural coding by bursts is dependent on pyramidal cell heterogeneities and whether correlations exist in vivo between burst and stimulus similar to those observed in vitro (Oswald et al., 2004, 2007; Doiron et al., 2007). In ELL pyramidal cells, it was shown in vivo that synaptic bombardment causes calcium entry via NMDA receptors that activates dendritic SK channels. The resulting afterhyperpolarization (AHP) after each spike counteracts the DAP and leads to a premature termination of the burst before the characteristic doublet seen in vitro (Toporikova and Chacron, 2009). We therefore set out to investigate the coding properties of bursts and isolated spikes by different types of pyramidal cells in vivo using mimics of behaviorally relevant stimuli.

EXPERIMENTAL PROCEDURES

Animal housing

The weakly electric fish, Apteronotus leptorhynchus, was used exclusively in these studies. Animals were obtained from commercial suppliers and were housed in groups of four to eight in 50 gal. tanks with continuous aeration. Water temperature was maintained between 27 and 29 °C and water conductivity was between 200 and 1000 μS/cm as per published recommendations (Hitschfeld et al., 2009).

Experimental setup

The experimental procedures were described in detail previously (Bastian et al., 2002; Chacron et al., 2003a, 2005c; Chacron, 2006; Ellis et al., 2007a; Chacron and Bastian, 2008; Toporikova and Chacron, 2009). Briefly, the animal was immobilized by i.m. injection of D-tubocurarine chloride hydrate (Sigma, St-Louis, MO, USA) and respirated with aerated water from its home tank at a flow rate of ~10 ml/min. Note that, because the electric organ of Apteronotus is neurogenic, the EOD persists after immobilization. These experiments were thus performed with the animal’s natural EOD being present. Water temperature in the experimental tank was maintained between 27 and 29 °C. Lidocaine gel was applied topically on the skin surface covering the skull. After 2 min, an incision was made to expose the skull as done previously (Bastian et al., 2002; Krahe et al., 2008; Toporikova and Chacron, 2009). We then used cyanoacrylate to glue a metal post unto the skull for stability. Finally, a microdrill was used to expose the hindbrain. All procedures were approved by McGill University’s animal care committee.

Recording

Recording techniques were the same as used previously (Bastian et al., 2002). Extracellular single unit recordings from pyramidal cells in whole animals were made with metal-filled micropipettes (Frank and Becker, 1964). Recording sites as determined from surface landmarks, recording depths, the dorso–ventral location of the receptive field, and known physiological properties (Krahe et al., 2008) were limited to the centrolateral segment only. The extracellular signal was amplified and band-pass filtered (300–1000 Hz; Differential Amplifier Model 1700; A-M Systems, Carlsborg, WA, USA) and A-D converted at 10 kHz (Power 1401, Cambridge Electronic Design. Cambridge, UK). Spikes were detected offline using custom written routines in Matlab (The Mathworks, Nattick, MA, USA).

Stimulation

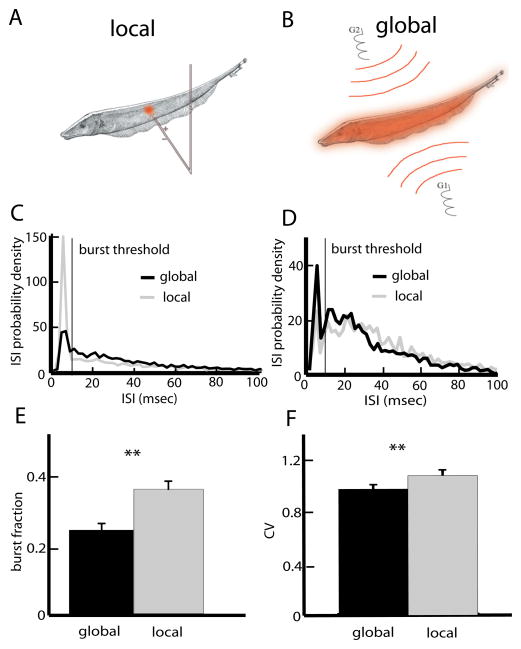
The stimulation protocol consisted of random amplitude modulations (RAM’s) of the animal’s own EOD. Typical contrasts (modulation amplitude to baseline EOD amplitude ratio) were similar to those used in previous studies (Bastian et al., 2002; Chacron et al., 2003a, 2005b,c; Chacron, 2006; Ellis et al., 2007a; Chacron and Bastian, 2008; Krahe et al., 2008). The RAMs were obtained by multiplying a computer-generated low-pass filtered white noise (8-th order butterworth, cutoff frequency 120 or 10 Hz) with a sinusoid that is phase-locked to the animal’s own EOD. This signal was then delivered via either local or global stimulation. With local stimulation (Fig. 1A), the stimulus was delivered using a small dipole positioned lateral to the animal. With global stimulation (Fig. 1B), the stimulus was delivered via two silver–silver-chloride electrodes positioned on each side ~25 cm away from the animal (Bastian et al., 2002).

Fig. 1.

ELL pyramidal cells display differential responses to stimuli with differing spatial extents. (A) Local stimulation geometry: a small dipole produces spatially localized AMs of the fish’s own EOD. (B) Global stimulation geometry: two electrodes (G1, G2) located lateral to the animal give rise to spatially diffuse AMs of the fish’s own EOD. (C) ISI probability densities from a representative superficial pyramidal cell under local and global noise stimulation. The noise’s temporal profile was identical in both situations. This cell had a greater tendency to display ISIs less than the burst threshold under local stimulation. (D) The ISI probability densities from an example deep pyramidal cell under local and global noise stimulation were quite similar. (E) Population-averaged burst fractions (i.e. the fraction of ISIs less than the burst threshold) under local and global stimulation. (F) Population averaged ISI coefficient of variation (CV) under local and global stimulation. Asterisks indicate statistical significance at the P=0.05 level using a Signrank test. For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.

Pyramidal cell classification

Previous studies (Bastian and Courtright, 1991; Bastian and Nguyenkim, 2001; Bastian et al., 2004) have established a strong negative correlation between the firing rate and dendritic morphology of ELL pyramidal cells and have determined approximate firing rate ranges for superficial, intermediate, and deep pyramidal cells: cells whose firing rate was less than 15 Hz were termed superficial, cells with firing rates greater than 30 Hz were termed deep, and cells with firing rates in between were termed intermediate (Chacron et al., 2005c; Chacron, 2006). We classified pyramidal cells as either E or I based on the average stimulus waveform preceding spikes in response to RAMs as previously described (Chacron et al., 2005c; Chacron, 2006; Chacron and Bastian, 2008).

Analysis

All analysis was performed in Matlab (The Mathworks, Nattick, MA, USA) using custom written routines. As a first step, the spike train was converted into a binary sequence with binwidth 0.5 ms and the RAM waveform was resampled at 2 kHz.

Burst analysis

We used an interspike interval threshold (Oswald et al., 2004; Ellis et al., 2007a; Chacron and Bastian, 2008) to separate the binary sequence obtained from all spikes into a binary sequence consisting of burst spikes and a binary sequence consisting of isolated spikes. Spikes separated by an interspike interval that is less than the threshold are considered part of a burst and spikes that are not part of a burst are termed isolated. The interspike interval threshold value, also termed the burst threshold, was computed as done previously (Bastian and Nguyenkim, 2001; Chacron and Bastian, 2008). The burst fraction was then computed as the fraction of interspike intervals that were less than or equal to the burst threshold (Oswald et al., 2004; Ellis et al., 2007a; Chacron and Bastian, 2008).

In order to quantify the correlations between burst and stimulus attributes, we characterized bursts using two measures. The burst length was simply defined as the number of spikes within each burst and the burst interval was determined as the time interval between the first two spikes of each burst. We note that redefining the burst interval as the time interval between the last two spikes of each burst or as the mean interspike interval during the burst did not qualitatively change our results (data not shown). We quantified the stimulus attributes using the stimulus amplitude and slope. The stimulus amplitude was defined as the maximum stimulus value within the burst while the stimulus slope was defined as the mean stimulus slope within the burst as used previously (Oswald et al., 2007). Note that the stimulus waveform was shifted by 8 ms to account for axonal transmission delays (Chacron et al., 2003a).

Mutual information analysis

Information theory was developed in the context of communication systems (Shannon, 1948) and relies on a numerical quantity termed mutual information. The mutual information quantifies the ability of a system to correctly discriminate between multiple stimuli and is typically expressed in bits: a value of X bits implies that the system can correctly discriminate between 2^X stimuli. The mutual information rate is defined as the mutual information per unit time. In the context of neural systems, investigators are typically interested in applying information theory in order to quantify the ability of neural populations to discriminate between different stimuli (Borst and Theunissen, 1999).

One important issue that one is faced with when computing mutual information is that it is in practice impossible to record neural responses to every possible stimulus and it is thus necessary to make approximations (Chacron et al., 2003b). A particularly attractive approximation is to use Gaussian noise stimuli since the mutual information rate can then be computed from only one presentation of the stimulus (Rieke et al., 1996). Moreover, as sensory stimuli are frequently characterized by their temporal frequency content, it is more informative to look at the mutual information rate density (i.e. the mutual information rate per frequency) rather than the mutual information rate. Previous studies have shown that a lower bound on the mutual information rate density I(f) is given by (Rieke et al., 1996):

$$I(f)=-{log}_2(1-C(f))$$

Where C(f) is the coherence function given by:

$$C(f)=\frac{{\mid SR(f)\mid }^2}{SS(f)RR(f)}$$

Where SR(f) is the cross-spectrum between the RAM waveform S and the binary sequence R, SS(f) is the power spectrum of the RAM waveform, and RR(f) is the power spectrum of the binary sequence. We estimated all spectral quantities using multi-taper estimation techniques (Jarvis and Mitra, 2001). We note that this approach has been used by previous studies (Borst and Theunissen, 1999; Chacron, 2006; Sadeghi et al., 2007; Krahe et al., 2008). Since the frequency components of Gaussian stimuli are independent, it is possible to obtain the mutual information rate by simply integrating the mutual information rate density (Rieke et al., 1996). Since the stimuli used in our study had frequency content between 0 and 120 Hz or between 0 and 10 Hz, we integrated I(f) between 0 and 120 Hz or between 0 and 10 Hz to obtain the mutual information rate.

We have previously shown that the coherence function C(f) can have a strong dependence on the stimulus’ spatial frequency content (i.e. the coherence C(f) to a given stimulus depends on whether it is presented with local vs. global stimulation geometry) (Chacron et al., 2003a, 2005c; Chacron, 2006). In this study, we want, in part, to test the hypothesis that this shift is due to changes in a neuron’s propensity to fire bursts of action potentials. We must therefore quantify both the change in frequency tuning and the change in burst firing that occurs when we transition from local to global stimulation geometry. While changes in burst firing can be quantified by the change in burst fraction, changes in frequency tuning can be quantified using a shift index that measures differences in the mutual information rate transmitted for the low (0–40 Hz) and high (40–80 Hz) frequency components of the stimulus. This shift index was calculated as ΔMI_low − ΔMI_high, where Δ represents the normalized difference between the values obtained with local and global geometries (Chacron et al., 2005c). To compute ΔMI_high, first MI_high was calculated for global stimulation by integrating the mutual information density between 40 and 80 Hz and then subtracted from MI_high computed for local stimulation. This difference was then normalized by the maximum mutual information value reached by that specific cell. For ΔMI_low, we first computed MI_low integrating the mutual information density between 0 and 40 Hz for local stimulation and then subtracting the value obtained for global stimulation. This difference was then normalized by the maximum mutual information value reached by that specific cell. A positive value of the shift index indicates that global stimulation led to higher information rate density at high RAM frequencies and/or lower densities at low RAM frequencies than local stimulation.

RESULTS

We investigated the burst coding properties of ELL pyramidal cells in response to broadband stimuli of differing spatial extents. Local stimuli impinge on only a fraction of the receptive field: their spatial extent mimics that of stimuli caused by small objects such as prey, plants, and rocks (Fig. 1A). On the other hand, global stimuli impinge on most of the animal’s skin surface: their spatial extent mimics that of stimuli encountered during social interactions with conspecifics (Bastian et al., 2002; Chacron et al., 2003a; Chacron, 2006) (Fig. 1B). Overall, we recorded from 48 pyramidal cells in 10 fish. 25 of these were classified as E-cells and the remaining 23 were classified as I-cells. It is important to note that the class of a given cell can be determined purely from physiological properties (Bastian and Courtright, 1991; Bastian and Nguyenkim, 2001; Bastian et al., 2002, 2004; Chacron et al., 2005c). Indeed, whether a given cell is E or I-type can be determined from its response to sensory input (Chacron et al., 2005c). Moreover, its subclass (i.e. superficial, intermediate, or deep) can be determined from the cell’s mean firing rate under baseline (i.e. no stimulation) conditions (Bastian and Nguyenkim, 2001; Bastian et al., 2004). We therefore used these measurements to determine as to which class and subclass a given cell belonged to.

Superficial and deep pyramidal cells display differential burst firing under local and global stimulation

We first quantified burst firing under local and global stimulation for superficial, intermediate, and deep pyramidal cells. Fig. 1C, D show interspike interval histograms (ISIH) from example superficial and deep pyramidal cells under local (gray) and global (black) stimulation. In both cases, burst firing was assessed by the proportion of interspike intervals below the burst threshold (vertical bar). For the superficial cell (Fig. 1C), burst firing was greater under local stimulation. In contrast, for the deep cell (Fig. 1D), the ISIHs under local and global stimulation were more similar with burst firing being only slightly greater under global stimulation. Overall, there were no significant differences between E and I-cells in terms of burst firing as quantified by the burst fraction for either local (P=0.644, Wilcoxon’s rank sum test, n=48) or global (P=0.961, Wilcoxon’s rank sum test, n=48) stimulation. Therefore, data from E and I-cells were pooled. At the population level, burst fractions were significantly greater under local stimulation than global stimulation (Fig. 1E) (P≪10⁻³, Signrank test, n=48), thereby confirming previous results (Chacron and Bastian, 2008). This change in burst firing is seen in measures of spike train variability such as the coefficient of variation (CV) which was significantly greater under local stimulation (P=0.0036, Wilcoxon’s rank sum test, n=48).

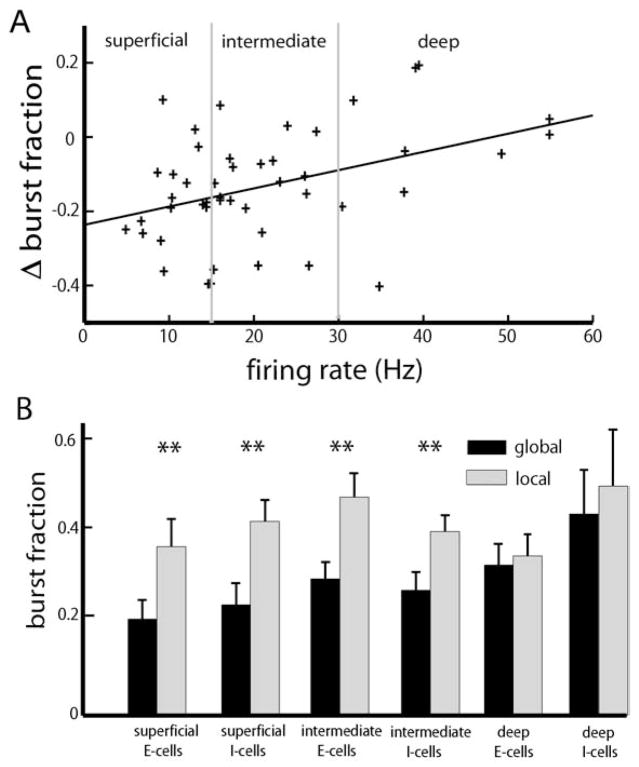
While it is clear that ELL pyramidal cells as a population display a greater propensity for burst firing under local stimulation (Chacron and Bastian, 2008), the examples shown in Fig. 1C, D strongly suggest that stimulus-induced changes in burst firing are dependent on pyramidal cell heterogeneities such as subclass (i.e. deep, intermediate, or superficial). To test this, we plotted the change in burst fraction when transitioning from global to local geometry as a function of the cell’s firing rate under baseline (i.e. no stimulation) conditions. There was a significant positive correlation (R=0.4042, P=0.0048, n=48) between the change in burst fraction and firing rate with a negative y-intercept (Fig. 2A) indicating that the change in burst fraction was greater for superficial as opposed to deep pyramidal cells. Finally, we partitioned the data according to E vs. I as well as superficial, intermediate, and deep cell subclasses. Our results show that there were significant changes in burst fraction contingent on stimulation geometry for superficial and intermediate but not for deep E and I-type pyramidal cells (Fig. 2B).

Fig. 2.

Effects of pyramidal cell heterogeneities on burst firing under local and global stimulation. (A) Change in burst fraction (global-local) as a function of the cell’s baseline firing rate. Superficial pyramidal cells (i.e. cells whose firing rates are less than 15 Hz) display reduced burst fraction under global stimulation but deep pyramidal cells (i.e. cells whose firing rates are greater than 30 Hz) showed little change. (B) Population-averaged burst fractions for E and I-type pyramidal cells of each class. “**” indicates statistical significance with P<0.01 (see text for details).

Information transmission by bursts and isolated spikes under local and global stimulation

We next segregated the spike train into burst spikes and isolated spikes using an interspike interval threshold as done previously (Chacron and Bastian, 2008) and computed the information rate densities for all spikes (solid black), bursts (solid gray), and isolated spikes (dashed black) for local and global stimulation for all six pyramidal cell classes as done previously (Oswald et al., 2004).

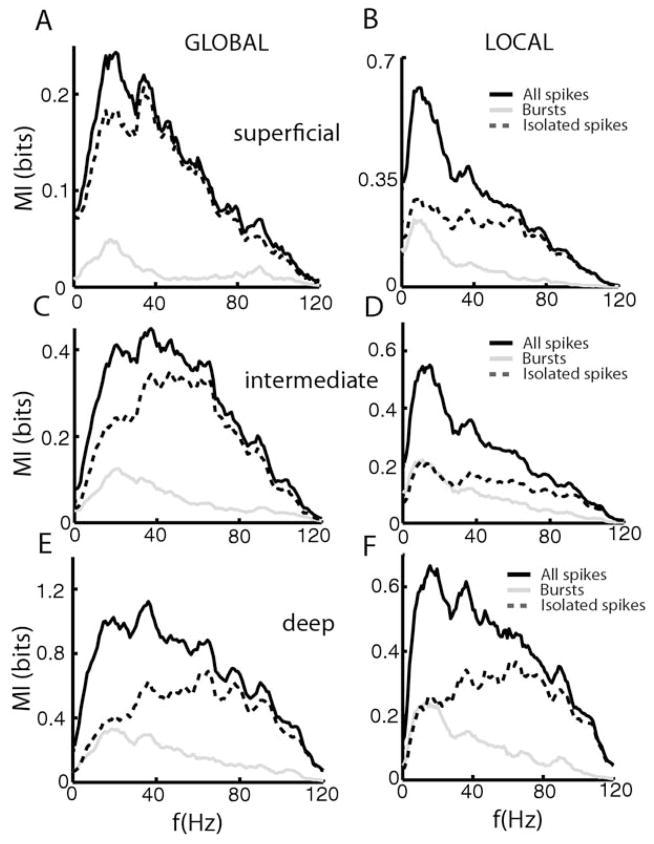
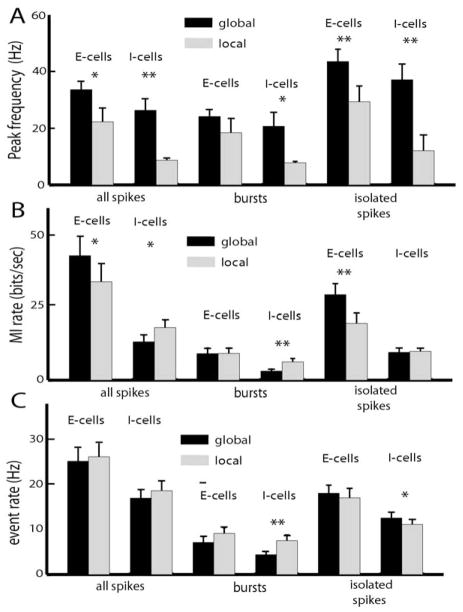
Superficial E-cells (Fig. 3A, B) showed large differences in the mutual information densities computed from all spikes (solid black line), burst spikes (solid gray line), and isolated spikes (dashed black line) contingent on stimulation geometry. The mutual information density computed from all spikes showed characteristic shifts in tuning from low to higher frequencies as we transitioned from local to global stimulation (Chacron et al., 2005c; Chacron, 2006). Even greater changes were observed for burst spikes that displayed almost no information content for global stimulation and greater mutual information density at low frequencies for local stimulation. The mutual information density of isolated spikes was very similar to that of all spikes for global stimulation (Fig. 3A, compare solid and dashed black lines) and displayed more broadband tuning for local stimulation (Fig. 3B, dashed black line). Overall, similar trends were observed for intermediate E-cells (Fig. 3C, D, dashed black line). In contrast, deep pyramidal cells showed almost no change in frequency tuning contingent on stimulation geometry (Chacron et al., 2005c; Chacron, 2006). In both cases, burst spikes were mostly tuned to low frequencies while isolated spikes were mostly tuned to high frequencies (Fig. 3E, F, solid dashed line).

Fig. 3.

Bursts and Isolated spikes code for different stimulus attributes under local and global stimulation for E-cells. Population-averaged mutual information rate densities for all spikes (black), bursts (gray), and isolated spikes (dashed) for superficial E-cells under global stimulation (A), for superficial E-cells under local stimulation (B), for intermediate E-cells under global stimulation (C), for intermediate E-cells under local stimulation (D), for deep E-cells under global stimulation (E), and for deep E-cells under local stimulation (F).

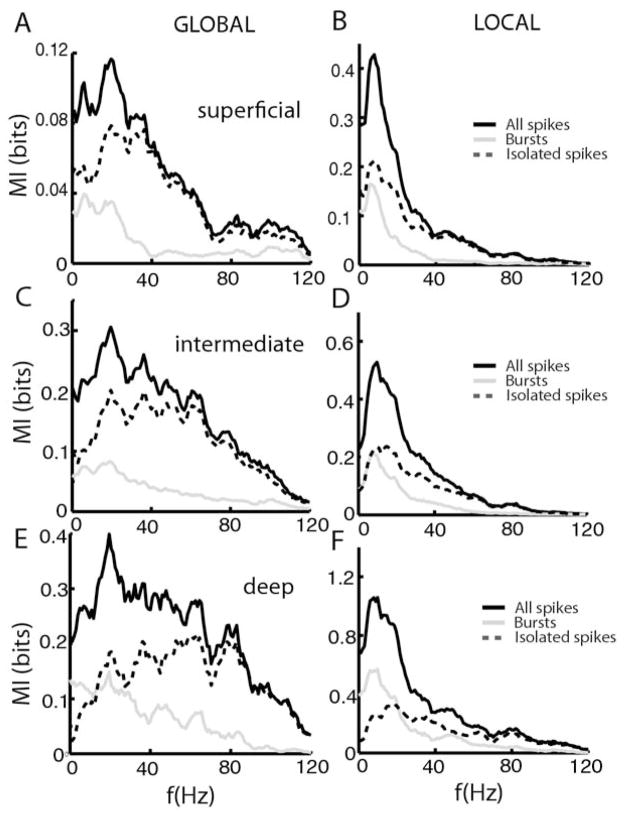
The situation for I-cells was overall similar for superficial, intermediate, and deep types. The mutual information densities computed from all spikes (solid black line) were mostly broadband under global stimulation for superficial (Fig. 4A), intermediate (Fig. 4C), and deep (Fig. 4E) cell types. For superficial and deep cells, the full spike trains contained the lowest and highest amounts of information, respectively. The mutual information densities computed from all spikes were greater at low frequencies under local stimulation for superficial (Fig. 4B), intermediate (Fig. 4D), and deep (Fig. 4F). In all cases, burst spikes were mostly tuned to low frequencies (compare solid gray lines) while isolated spikes were tuned to high frequencies (compare dashed black lines). It is interesting to note that isolated spikes showed a much greater change in tuning contingent on stimulation geometry than burst spikes did (Fig. 4). We note that, while both E and I cells showed strong changes in peak frequency tuning under global vs. local stimulation, the causes for this change are quite different. Indeed, while both E and I-cells tend to show decreased lower information rate density at low (<40 Hz) frequencies for global stimulation, only E cells show a concomitant increase in the information rate density for high (>40 Hz) frequencies (Figs. 3 and 4). As such, the increased frequency tuning of I-cells under global stimulation is really a reflection of their overall decreased response to such stimuli.

Fig. 4.

Bursts and Isolated spikes code for different stimulus attributes under local and global stimulation for I-cells. Population averaged mutual information rate densities for all spikes (black), bursts (gray), and isolated spikes (dashed) for superficial I-cells under global stimulation (A), for superficial I-cells under local stimulation (B), for intermediate I-cells under global stimulation (C), for intermediate I-cells under local stimulation (D), for deep I-cells under global stimulation (E), and for deep I-cells under local stimulation (F).

We next quantified these results by computing for each cell the frequency at which the information tuning curve was maximal, the peak frequency, for all spikes, burst spikes, and isolated spikes. We investigated the effects of pyramidal cell heterogeneities on these quantities by computing the correlation coefficient between the peak frequency and the mean firing rate under baseline conditions for each cell (E or I) under local and global stimulation. The results are shown in Table 1.

Table 1.

Summary of correlation coefficients between the peak frequency and the cell’s mean firing rate under baseline conditions. P-values are indicated in parentheses

	All spikes	Burst spikes	Isolated spikes
E-cells global	0.2215 (0.2874)	−0.0535 (0.7994)	0.7142 (<10−3)
E-cells local	0.6896 (<10−3)	0.5982 (0.0016)	0.8481 (≪10−3)
I-cells global	0.2661 (0.2313)	−0.2892 (0.1917)	0.4101 (0.058)
I-cells local	0.1443 (0.5218)	0.2096 (0.3492)	0.6299 (0.0017)

Overall, we found that deep E-cells had a higher peak frequency than superficial E-cells under local stimulation and this was reflected in the burst and isolated spike trains and can be seen in Fig. 3 as well. The isolated spikes of deep E-cells also displayed a larger peak frequency than those of superficial E-cells under global geometry. We also found that the isolated spikes of deep I-cells displayed a larger peak frequency than those of superficial I-cells under local geometry (Table 1).

We next looked at the putative dependence of the mutual information rate of all spikes, burst spikes, and isolated spikes on the cell’s mean firing rate under baseline activity by again computing cross-correlation coefficients. However, because it is known that the mutual information rate increases linearly with firing rate (Borst and Haag, 2001), we normalized the information rates by the respective firing rates (i.e. the mutual information rate obtained for burst spikes was normalized by the mean number of burst spikes per unit time during stimulation). After this normalization, we did not find any statistically significant correlation coefficients between the mutual information rate and the mean firing rate under any condition (data not shown). This indicated that the larger mutual information rates displayed by deep pyramidal cells were purely a consequence of their larger firing rates.

Because of the relative constancy of coding of bursts and isolated spikes for either E or I-cells under either local or global stimulation, we pooled our data over deep, intermediate, and superficial types. We found that the peak frequency from all spikes, bursts, and isolated spikes was always higher under global stimulation for both E and I-cells (Fig. 5A). Moreover, the peak frequency for bursts was significantly lower than that computed from isolated spikes (P<10⁻³, paired t-test, n=94), indicating that the two trains code for different frequency ranges under both local and global stimulation. We also computed the mutual information rates associated with bursts and isolated spikes. E-cells showed increased information rate under global stimulation. Segregation of the spike train into burst and isolated spikes revealed that it is increased information from the isolated spikes that is responsible (Fig. 5B). For I-cells, the information rate under global stimulation is significantly lower than under local stimulation (Fig. 5B), reflecting decreased tuning to low frequencies (Fig. 4). Segregation of the spike train into bursts and isolated spikes revealed that it was decreased information transmission by bursts that is responsible (Fig. 5B). Finally, we wanted to see whether changes in the burst or isolated spike rates would underlie changes in the information rate. We found that, for I-cells, the spike rate associated with bursts (i.e. the number of spikes per unit time belonging to bursts) was significantly lower under global stimulation (Fig. 5C). Therefore, the decreased information rate seen in I-cells under global stimulation is due to decreased information transmitted by bursts, which is in turn due to decreased burst spike rate. There was also a small but significant increase in the isolated spike rate for I-cells as we transitioned from local to global stimulation (Fig. 5C).

Fig. 5.

Summary of changes in pyramidal cell frequency tuning under local and global stimulation. (A) Population-averaged peak frequency tuning as measured by the mutual information rate density curves for E and I-type pyramidal cells of all three classes. (B) Population-averaged mutual information rates for all spikes, bursts, and isolated spikes obtained for E and I-type pyramidal cells of all three classes. (C) Population-averaged firing rate, burst rate, and isolated spike rate for E and I-type pyramidal cells of all classes. “*” indicates statistical significance with P<0.05 and “**” indicates statistical significance with P<0.01 (see text for details).

What can be concluded from these results? We show that bursts consistently code for lower frequencies than isolated spikes irrespective of stimulation geometry or pyramidal cell heterogeneities. While cells with higher firing rates tended to have larger burst and isolated spike rates, each spike coded for roughly the same amount of information irrespective of pyramidal cell heterogeneity for either E or I-cells under either local or global stimulation. Nevertheless, there are changes in burst firing contingent on stimulation geometry and these are mostly seen in superficial pyramidal cells that also show the greatest changes in frequency tuning (Figs. 3 and 4). This suggests that changes in burst firing are correlated with changes in frequency tuning.

Changes in bursting are correlated with changes in frequency tuning

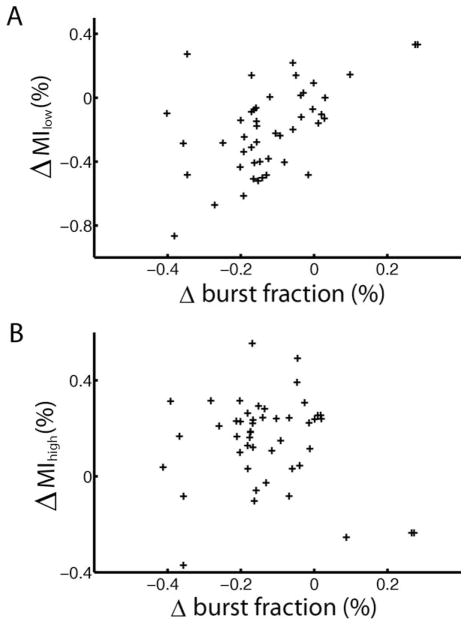
Our results demonstrate that bursts tended to code for the low frequency components of the stimulus irrespective of stimulus geometry or cell type. Next, we quantified the change in frequency tuning caused by the change in stimulation geometry by computing a shift index as before (Chacron et al., 2005c). This shift index is a measure of the cell’s change in tuning to both low and high frequencies (see methods). We found a strong correlation between the shift index computed from all spikes and the cell’s spontaneous firing rate (Table 2). Since the shift index is influenced by changes in the information at both low and high frequencies, we also quantified the relative changes in information density for the low and high frequency ranges. We found a significant correlation between the change in burst fraction and the change in low frequency (0–40 Hz) mutual information rate computed for all spikes (Fig. 6A, R=0.3035, P=0.01). However, the change in burst fraction was not correlated with the change in high frequency (40–80 Hz) mutual information rate (Fig. 6B, R=0.1012, P=0.4983). We also separately quantified the changes in the low frequency and high frequency information transmitted by bursts and isolated spikes. While there was a very strong correlation between the change in low frequency information transmitted by bursts and the change in burst fraction (R=0.6041, P≪10⁻³), all the other correlation coefficients were not statistically significant at the P=0.01 level and are summarized in Table 2.

Table 2.

Summary of obtained correlation coefficients and P-values (in parentheses) for the relationship between changes in frequency tuning as determined from all spikes, burst spikes, and isolated spikes and the cell’s spontaneous mean firing rate

	All spikes	Bursts	Isolated spikes
Shift index	0.3972 (0.0057)	0.2631 (0.074)	0.0858 (0.5662)
Information change low frequencies	0.3035 (0.01)	0.6041 (≪10−3)	−0.1126 (0.4513)
Information change high frequencies	0.1012 (0.4983)	−0.2832 (P=0.097)	0.1906 (0.1994)

N=47 in all cases.

Fig. 6.

Correlating changes in burst firing to changes in frequency tuning. (A) The change in low frequency (0–40 Hz) mutual information rate (local-global) plotted as a function of the cell’s change in burst fraction (local-global) showed a significant correlation (R=0.3035, P=0.01, n=47). (B) The change in high frequency (40–80 Hz) mutual information rate (local-global) as a function of the change in burst fraction (local-global) showed no significant correlation (R=0.1012, P=0.4983, n=47).

These results show that changes in burst firing are correlated with a decrease in the low frequency mutual information rate but not with the increase in high frequency information that is predominantly found in E-cells as we transition from local to global stimulation.

Correlations between burst and stimulus attributes

As mentioned previously, information theory aims to quantify a system’s ability to transmit information about a stimulus ensemble. However, information theory by itself does not provide us with the transformations that occur in the system in question. One approach to resolve this problem is to look for correlations between attributes of the stimulus and neural response (i.e. the neural spike train) as these correlations will imply that information is being transmitted. In this case, we are interested in characterizing putative correlations between burst and stimulus attributes.

Previous studies have shown that bursts signal particular features in the sensory environment (Gabbiani et al., 1996; Metzner et al., 1998; Sherman, 2001; Sherman and Guillery, 2002; Lesica and Stanley, 2004; Oswald et al., 2004; Marsat et al., 2009). We therefore turned our attention towards elucidating the features of the stimulus that are encoded by bursts. Moreover, we are interested in understanding how bursts code for these features: recent results obtained in vitro have shown that the interspike interval within a burst (the “burst interval”) was correlated with the maximum stimulus amplitude between the spikes (Doiron et al., 2007; Oswald et al., 2007). Alternatively, it has been shown that the number of spikes in a burst (the “burst length”) was correlated with stimulus attributes such as the stimulus’ slope (Kepecs et al., 2002; Kepecs and Lisman, 2003).

We therefore quantified putative correlations between burst and stimulus attributes in our dataset. The burst attributes analyzed were burst length and burst interval and the stimulus attributes were the maximum stimulus value during the burst (stimulus amplitude) and the average stimulus slope during the burst (stimulus slope). Thus, we computed four correlation coefficients: (1) burst length vs. amplitude, (2) burst length vs. slope, (3) burst interval vs. amplitude, (4) burst interval vs. slope.

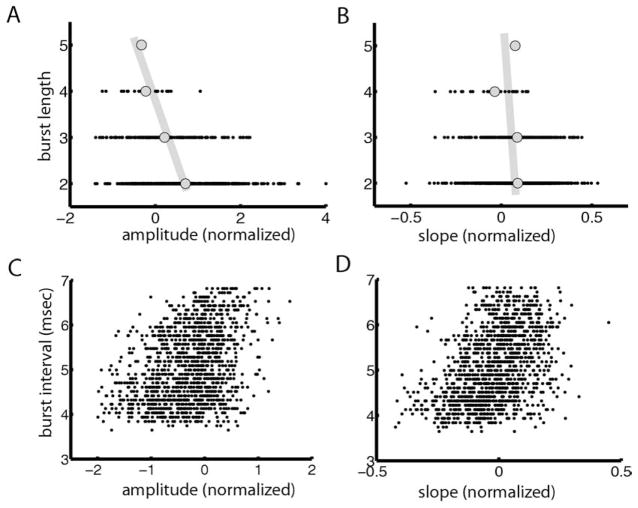
These quantities are shown for a representative I-cell under local stimulation in Fig. 7. We found a significant negative correlation between the burst length and stimulus amplitude (R=−0.3367, P≪10⁻³) (Fig. 7A). The correlation coefficient between burst length and stimulus slope was much weaker in magnitude but nevertheless significant (R=−0.0934, P=0.0054) (Fig. 7B). The correlation coefficients between the burst interval and stimulus amplitude and slope were significantly greater than zero (amplitude: R=0.3611, P≪10⁻³; slope: R=0.4239, P≪10⁻³; Fig. 7C, D). While this may appear surprising at first, we note that I-cells are actually inhibited by increases in the EOD amplitude. The signs of the correlation coefficients reflect this fact and are expected to be opposite to those that would be obtained if the cell were excited by increases in EOD amplitude.

Fig. 7.

Correlating burst attributes to stimulus attributes for a representative I-cell. (A) Number of spikes per burst (burst length) as a function of stimulus amplitude for an example cell showing a weak but significant negative correlation (R=−0.3367, P≪10⁻³). (B) Burst length as a function of stimulus slope showing a weak but significant correlation (R=−0.0934, P=0.0054). (C) Burst interval as a function of stimulus amplitude showing a significant correlation (R=0.3611, P≪10⁻³). (D) Average interspike interval during a burst as a function of stimulus slope showing a significant positive correlation (R=0.4239, P≪10⁻³).

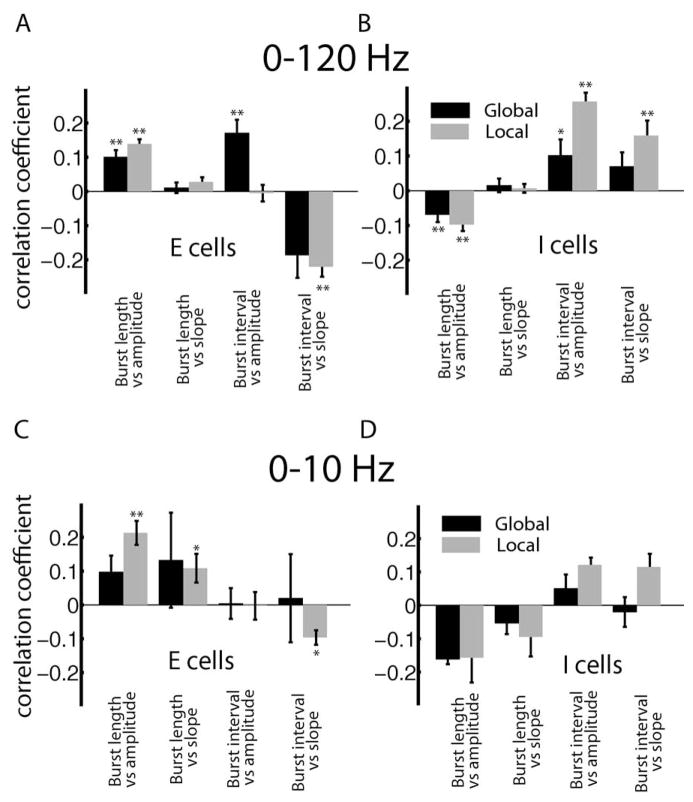
We next explored how these correlation coefficients varied with cell class and stimulation geometry. As we found no significant relationship between the correlation coefficient and the cell’s firing rate at the P=0.01 level (data not shown), the data were pooled across deep, intermediate, and superficial pyramidal cells. Overall, we found significant correlation coefficients that were weak (<0.2) in magnitude between burst length and stimulus amplitude for E (Fig. 8A) and I (Fig. 8B) cells. As expected from the above argument, E and I-cells had opposite correlations between burst length and stimulus amplitude. We found that the correlations between burst length and stimulus slope were not significant for either cell class. We also found significant correlations between burst interval and stimulus amplitudes as well as between burst interval and stimulus slope for E (Fig. 8A) and I (Fig. 8B) cells. In general, correlation coefficients were slightly larger in magnitude under local stimulation than under global stimulation, which probably reflects the fact that pyramidal cells typically respond more strongly to the low frequency components of time varying stimuli when these are presented with local geometry (Bastian et al., 2002). This is because stimuli presented with global geometry will activate feedback pathways that attenuate pyramidal cell responses (Bastian et al., 2004; Chacron et al., 2005c; Chacron, 2006).

Fig. 8.

Summary of population-averaged correlation coefficients obtained between burst and stimulus attributes for 0–120 Hz stimuli for E (A) and I (B) cells. The correlation coefficients obtained for 0–10 Hz stimuli for E (C) and I (D) cells are also shown. “**” and “*” indicate statistical significance at the P=0.01 and 0.05 levels using a signrank test, respectively.

Our results nevertheless show that correlations between burst and stimulus attributes were much weaker in magnitude than those predicted from modeling studies in the case of burst length vs. stimulus amplitude and slope (Kepecs et al., 2002) or observed experimentally in vitro in the case of burst interval vs. stimulus amplitude and slope (Oswald et al., 2007). How can this discrepancy be explained? It could be argued that the stimuli we used contained higher frequencies than those used previously as it was shown that the high frequency components of a time varying sensory stimulus can interfere with burst firing (Oswald et al., 2004). In order to address this issue, we used Gaussian noise stimuli that had a cutoff frequency of 10 Hz. Therefore, the stimulus’ temporal frequency content fell completely within the coding range of bursts and would elicit the most bursting in vitro (Oswald et al., 2004). We computed the correlation coefficients between burst length or interval and stimulus amplitude or slope for this low frequency stimulus.

While one might expect that using such stimuli would increase the magnitude of correlations between burst and stimulus attributes based on the above argument, our results show that this is not the case (Fig. 8C, D). Indeed, correlation coefficients between burst and stimulus attributes computed for 0–10 Hz noise stimuli were largely similar in magnitude to those computed for 0–120 Hz noise stimuli for both E (compare Fig. 8A, C) and I (compare Fig. 8B, D) cells.

The correlation coefficients between burst length and stimulus amplitude as well as between burst length and stimulus slope were significant for E-cells under local stimulation (Fig. 8C). There was furthermore a weak but significant negative correlation between burst interval and stimulus slope for E-cells under local stimulation. Surprisingly, all correlation coefficients obtained for I-cells were not significant. Even more surprisingly, the correlation coefficients between burst interval and stimulus amplitude and slope were actually weaker in magnitude for 0–10 Hz stimuli than those obtained for 0–120 Hz stimuli.

Finally, we note that the correlation coefficients were again larger in magnitude under local stimulation than global stimulation for the reasons mentioned above. Nevertheless, the correlation coefficients between burst interval and either of stimulus amplitude or slope remained much smaller than those observed in vitro for either of local or global stimulation. We also only found a significant correlation between burst interval and stimulus amplitude for local stimulation (R=−0.7344, P=0.0065, n=12).

DISCUSSION

Summary of results

We have investigated the coding properties of ELL pyramidal cell bursts and isolated spikes in vivo in response to mimics of prey and conspecific-related stimuli. We found that pyramidal cells of different classes responded differentially to the two stimulus categories. Specifically, superficial and intermediate pyramidal cells had greater tendencies to burst for local stimulation while deep pyramidal cells had similar tendencies to burst under both stimulation regimes. In order to understand which features of the stimulus elicited burst firing, we partitioned the spike train into bursts and isolated spikes. We found that, under both local and global stimulation, bursts tended to code for the low frequency components of the stimulus while isolated spikes tended to code for a much broader frequency range irrespective of pyramidal cell heterogeneities. We found a correlation between changes in pyramidal cell burst firing properties and their frequency tuning under local and global stimulation. Namely, the difference in low frequency mutual information rate between both stimulus categories was correlated with the difference in burst fraction. We also found that burst length (i.e. the number of spikes per burst) was correlated with stimulus amplitude but not slope. While the burst interval did display significant correlation with stimulus amplitude and slope, these correlations were much weaker in magnitude than those observed in vitro (Oswald et al., 2007).

Comparison between burst coding in vitro and in vivo

We have shown that the correlation coefficients between burst and stimulus attributes were weak in vivo. This is contrary to what has been observed in vitro where the burst interval codes for stimulus slope (Doiron et al., 2007; Oswald et al., 2007). The coding properties of burst length have been previously investigated in mathematical models of burst firing where it was found that burst length could code for input slope (Kepecs et al., 2002). Our experimental results show, however, that this is not the case in ELL pyramidal neurons. This difference is most likely due to the fact that Kepecs et al. (2002) considered burst dynamics that were slightly different than those found in ELL pyramidal neurons under in vivo conditions. Our results thus showed important differences between the coding properties of burst firing in ELL pyramidal cells in vitro and in vivo.

How does one explain such differences? One possible explanation is that the in vitro recordings by Oswald et al. (2007) were mostly from a different ELL map than our in vivo recordings. While this fact could a priori explain some of the differences, it is unlikely to explain all of them for two reasons: (1) Another study performed in vitro has shown that the bursting mechanism of ELL pyramidal cells was the same in all three maps (Mehaffey et al., 2008b); (2) A recent study performed in vivo has also shown similar burst firing as quantified by the burst fraction for ELL pyramidal cells across all three maps (Krahe et al., 2008). Further studies involving recordings from other ELL maps in vivo are however needed to fully test this hypothesis.

Another explanation would be that Oswald et al. (2007) used the last two spikes of each burst to define the burst interval whereas we used the first two. However, we saw no qualitative difference in our results when we used the last two spikes or the average interspike interval during the burst (data not shown), which strongly speaks against this possibility. We furthermore note that the weak correlation between burst interval and stimulus amplitude entails poor discriminability between different burst intervals caused by different stimulus amplitudes and it is thus expected that the signal detection analysis that Oswald et al. (2007) used would give poorer discriminability between interspike intervals if applied to our data.

Yet another possible explanation is that the burst dynamics of ELL pyramidal cells are quite different in vivo and in vitro as recently pointed out (Toporikova and Chacron, 2009). This seems to be most consistent with our results. For example, previous studies have shown that ELL pyramidal cell bursts are characterized in vitro by a decreasing interspike interval throughout the burst (Lemon and Turner, 2000) whereas no such patterning is seen in vivo (Bastian and Nguyenkim, 2001). Finally, in vitro studies predict that using stimuli with lower frequency content will promote burst firing that will code for these low frequencies (Oswald et al., 2004). However, our results showed that using 0–10 Hz stimuli led to correlation coefficients between burst and stimulus attributes that were weaker in magnitude than those obtained for 0–120 Hz stimuli, which further supports the hypothesis that the different burst dynamics seen in vivo may explain the discrepancies between our results and those obtained in vitro.

Nevertheless, we did see that bursts in ELL pyramidal cells tended to code for the low frequency components of the stimulus for both local and global stimulation, which is similar to what was seen previously in vitro (Oswald et al., 2004). Coding of low frequency stimuli by bursts has also been seen in thalamic relay neurons of the lateral geniculate nucleus (Lesica and Stanley, 2004; Lesica et al., 2006). This property of burst firing thus appears to be preserved in vivo as well as across sensory systems and thus appears to be a general property of excitable systems that is independent of particular burst dynamics (Oswald et al., 2004). This property is also consistent with bursts detecting particular features of sensory input (Gabbiani et al., 1996; Metzner et al., 1998; Chacron et al., 2001, 2004; Sherman, 2001; Krahe et al., 2002, 2008; Sherman and Guillery, 2002).

Our results also show that effects of pyramidal cell heterogeneities on the coding of information by bursts are quantitative rather than qualitative. This is a surprising result because heterogeneities in terms of dendritic tree morphology or distributions of ion channels can have profound consequences on burst firing (Mainen and Sejnowski, 1996; Häusser and Mel, 2003) and ELL pyramidal cells display large morphological and physiological heterogeneities (Bastian and Nguyenkim, 2001; Bastian et al., 2002, 2004; Harvey-Girard and Dunn, 2003; Chacron, 2006; Ellis et al., 2007b, 2008; Maler, 2009a,b). Further studies are needed to understand this surprising result.

Role of bursts in information coding by ELL pyramidal cells

We observed burst firing more prominently under local stimulation as compared with global stimulation and this change was correlated with the greater response to low frequencies seen under local stimulation. Previous studies have shown that indirect feedback unto pyramidal cells via parallel fibers from the caudal lobe of the cerebellum actively attenuates responses to the low frequency components of global stimuli (Bastian et al., 2004; Chacron et al., 2005c; Chacron, 2006; Chacron and Bastian, 2008) and is also likely responsible for the attenuated burst firing under global stimulation. As such, our results suggest that burst firing in pyramidal cells of the centrolateral segment of the ELL seen in vivo serves to signal the presence of a local stimulus (prey or rock) in the environment, in agreement with previous results showing that correlated bursts might encode this type of stimulus at the population level (Chacron and Bastian, 2008).

It was recently shown that pyramidal cell bursts can also reliably detect the occurrence of chirps (Marsat et al., 2009), which are a particular type of fast, high frequency, communication signal emitted by Apteronotus during aggressive and courtship encounters that occur on top of a low-frequency beat (Zakon et al., 2002). The ability to respond with bursts to these high frequency features of natural stimuli is, however, limited to E-type pyramidal cells in the lateral segment of the ELL. Pyramidal cells in the centrolateral segment, which were investigated here, fire bursts only in response to low-frequency events and have different physiological properties than lateral segment pyramidal cells (Krahe et al., 2008).

Control of burst firing in ELL pyramidal cells

Our present results confirm previous ones that have shown that pyramidal cell responses to sensory input are highly dynamic and are controlled by specialized neural circuitry that includes glutamatergic (Bastian, 1986; Chacron et al., 2005c; Chacron, 2006) as well as cholinergic and serotonergic feedback pathways (Johnston et al., 1990; Ellis et al., 2007a; Mehaffey et al., 2008a). At the cellular level, it has been demonstrated that pyramidal cell burst firing is tightly regulated by inhibition (Mehaffey et al., 2005, 2007) as well as voltage-gated conductances (Doiron et al., 2003b; Noonan et al., 2003; Fernandez et al., 2005; Ellis et al., 2007b). Small conductance calcium-activated potassium channels have been shown to regulate burst firing in vitro (Ellis et al., 2007b), which is particularly interesting since a recent study has shown that these channels also regulate burst dynamics in vivo (Toporikova and Chacron, 2009). Cholinergic and serotonergic neuromodulatory mechanisms regulate SK channels in other systems (Nicoll, 1988; Villalobos et al., 2005) and such neuromodulatory inputs are known to be present in the ELL (Phan and Maler, 1983; Johnston et al., 1990). Although the effects of the cholinergic pathway are beginning to be understood including a potential modulation of SK channels (Ellis et al., 2007a; Mehaffey et al., 2008a), the effects of the serotonergic pathway are still unknown. Further studies are needed to determine the roles played by these pathways in regulating burst firing and information processing by ELL pyramidal cells.

CONCLUSION

Our results have shown that neural heterogeneities generally had quantitative rather qualitative effects on the coding of sensory information by bursts of action potentials: bursts of action potentials tended to be elicited by the low frequency components of time varying stimuli irrespective of these heterogeneities. Similar coding of low frequencies is observed across sensory modalities and thus appears to be a general feature of coding by bursts of action potentials. However, we also observed weak correlations between burst and stimulus attributes: this is contrary to what is observed in vitro or predicted from modeling studies. Our results suggest that these differences are due to the fact that the burst dynamics of ELL pyramidal cells are different in vivo and in vitro. Thus, it will be critical to determine the influence of in vivo conditions on burst dynamics that have been characterized in vitro in order to understand the functional role of burst firing in the CNS.

Abbreviations

DAP

depolarizing afterpotential

ELL

electrosensory lateral line lobe

EOD

electric organ discharge