In vivo conditions influence the coding of stimulus features by bursts of action potentials

Abstract

The functional role of burst firing (i.e. the firing of packets of action potentials followed by quiescence) in sensory processing is still under debate. Should bursts be considered as unitary events that signal the presence of a particular feature in the sensory environment or is information about stimulus attributes contained within their temporal structure? We compared the coding of stimulus attributes by bursts in vivo and in vitro of electrosensory pyramidal neurons in weakly electric fish by computing correlations between burst and stimulus attributes. Our results show that, while these correlations were strong in magnitude and significant in vitro, they were actually much weaker in magnitude if at all significant in vivo. We used a mathematical model of pyramidal neuron activity in vivo and showed that such a model could reproduce the correlations seen in vitro, thereby suggesting that differences in burst coding were not due to differences in bursting seen in vivo and in vitro. We next tested whether variability in the baseline (i.e. without stimulation) activity of ELL pyramidal neurons could account for these differences. To do so, we injected noise into our model whose intensity was calibrated to mimic baseline activity variability as quantified by the coefficient of variation. We found that this noise caused significant decreases in the magnitude of correlations between burst and stimulus attributes and could account for differences between in vitro and in vivo conditions. We then tested this prediction experimentally by directly injecting noise in vitro through the recording electrode. Our results show that this caused a lowering in magnitude of the correlations between burst and stimulus attributes in vitro and gave rise to values that were quantitatively similar to those seen under in vivo conditions. While it is expected that noise in the form of baseline activity variability will lower correlations between burst and stimulus attributes, our results show that such variability can account for differences seen in vivo. Thus, the high variability seen under in vivo conditions has profound consequences on the coding of information by bursts in ELL pyramidal neurons. In particular, our results support the viewpoint that bursts serve as a detector of particular stimulus features but do not carry detailed information about such features in their structure.

1 Introduction

Understanding the neural code remains an important problem in neuroscience that is complicated by the fact that neurons often display complex intrinsic dynamics that influence their responses to sensory input. An example of such dynamics consists of those that give rise to burst firing (i.e. the firing of packets of action potentials followed by quiescence) which is seen ubiquitously in the CNS (Krahe and Gabbiani 2004). Although the intrinsic and network mechanisms that give rise to burst firing are generally well understood (Izhikevich 2000; Sherman and Guillery 2002; Krahe and Gabbiani 2004), the functional role of burst firing is less well understood. In particular, it has been proposed that bursts, when treated as a single event, can signal the presence of particular stimulus features (Gabbiani et al. 1996; Metzner et al. 1998; Sherman 2001; Sherman and Guillery 2002; Chacron et al. 2004a; Lesica and Stanley 2004; Oswald et al. 2004). Alternatively, other studies have shown strong correlations between various burst attributes (e.g. the temporal ordering of spikes within a burst or the number of spikes within a burst) and stimulus attributes (e.g. its amplitude of its rate of rise before burst onset), thereby suggesting that the detailed structure of a burst could provide information about the stimulus (DeBusk et al. 1997; Kepecs et al. 2002; Martinez-Conde et al. 2002; Oswald et al. 2007; Eyherabide et al. 2008; Gaudry and Reinagel 2008; Marsat and Pollack 2010; Samengo and Montemurro 2010). Studies conducted in simple systems with well-characterized anatomy and relatively simple behaviors are likely to yield significant insight into the functional role of burst firing.

Weakly electric fish benefit from well-characterized anatomy and physiology (Berman and Maler 1999) and detect amplitude modulations of their self-generated electric organ discharge (EOD) through an array of electroreceptor neurons located on the skin (Bullock et al. 2005). These make synaptic contact unto pyramidal cells within the hindbrain electrosensory lateral line lobe (ELL) which is composed of three parallel maps of the body surface (Shumway 1989; Krahe et al. 2008) that are essential for proper sensory processing of natural stimuli (Metzner and Juranek 1997). The physiological responses of pyramidal cells within the three maps show important differences and have been well characterized both in vivo (Bastian et al. 2002; Chacron et al. 2003; Bastian et al. 2004; Chacron et al. 2005a, c; Chacron 2006; Chacron et al. 2007; Chacron and Bastian 2008; Chacron et al. 2009; Toporikova and Chacron 2009; Avila Akerberg et al. 2010) and in vitro (Berman and Maler 1999; Oswald et al. 2004; Ellis et al. 2007a, b; Oswald et al. 2007; Mehaffey et al. 2008a, b).

Pyramidal cells display the tendency to fire bursts of action potentials both in vitro (Turner et al. 1994) and in vivo (Bastian and Nguyenkim 2001) through a well-characterized intrinsic burst mechanism that relies on a somatodendritic interaction (Lemon and Turner 2000; Doiron et al. 2002). Recent studies performed in vitro have suggested a burst interval code as the burst interval was found to be strongly negatively correlated with both the stimulus amplitude and slope (Oswald et al. 2007). However, a recent study performed in vivo found weak if at all significant correlations between the burst interval and either of stimulus amplitude or slope (Avila Akerberg et al. 2010). The causes for these differences are still not understood because the above-mentioned two studies were conducted in different ELL segments and furthermore used stimuli with differing temporal frequency content. Moreover, recent results have highlighted important differences between burst firing seen in vivo and in vitro: while bursting seen in vitro is characterized by a shortening of the ISI throughout the burst and terminates with a characteristic doublet, burst firing seen in vivo does not display any significant trend in the ISI within the burst (Bastian and Nguyenkim 2001) and is terminated early (i.e. before the doublet) through an accumulation in the spike afterhyperpolarization throughout the burst (Toporikova and Chacron 2009). We therefore set out to investigate the causes for the differences in burst coding seen in vitro and in vivo in ELL pyramidal cells using a combination of in vivo electrophysiology, in vitro electrophysiology, and mathematical modeling.

2 Methods

2.1 Experiments

All the experiments were performed on the weakly electric fish species Apteronotus leptorhynchus. Specimens were obtained from local importers and were acclimated to the laboratory as per published guidelines (Hitschfeld et al. 2009). All the experimental procedures for both in vivo and in vitro preparations were done according to experimental protocols approved by the McGill University Animal care committee.

2.2 In vivo electrophysiology

The experimental procedures were described in detail previously (Bastian et al. 2002; Chacron et al. 2003; Chacron et al. 2005a; Chacron 2006; Ellis et al. 2007a; Chacron and Bastian 2008; Toporikova and Chacron 2009). Briefly, D-tubocurarine chloride hydrate (Sigma, St-Louis, MO) was injected intramuscularly and the animal was then respirated with aerated water from its home tank at a flow rate of ~10 ml/min. The EOD persists after immobilization due to the fact that the electric organ of Apteronotus is neurogenic in nature. Therefore, the experiments were performed by perturbing the animal’s own EOD as described below. The temperature of the water in the experimental tank was kept between 27 and 29°C. Surgical techniques were the same as those described previously (Bastian et al. 2002; Krahe et al. 2008; Toporikova and Chacron 2009; Avila Akerberg et al. 2010).

2.3 In vivo recording

The recording techniques used in this study were the same as the ones used previously (Bastian et al. 2002; Avila Akerberg et al. 2010). Metal-filled micropipetes were used for obtaining extracellular single unit recordings from pyramidal cells in whole animals (Frank and Becker 1964). The recording sites were limited to the centrolateral and lateral segments and were determined by surface landmarks and recording depth and the dorso-ventral location of the receptive field (Krahe et al. 2008). The extracellular signal was amplified and band-passed filtered (300–1,000 Hz; Differential Amplifier Model 1700; A-M Systems, Carlsborg, WA) and A-D converted at 10 kHz (Power 1401, Cambridge Electronic Design. Cambridge, UK). Spikes were detected offline using custom written routines in Matlab (The Mathworks, Nattick, MA).

2.4 In vivo stimulation

The fish were stimulated with a protocol that consisted of random amplitude modulations (RAM’s) of the animal’s own EOD. Typical contrasts (the ratio of the modulation amplitude and the baseline EOD amplitude) were similar to those used in previous studies (Bastian et al. 2002; Chacron et al. 2003; Bastian et al. 2004; Chacron et al. 2005a, b, c; Chacron 2006; Chacron et al. 2007; Ellis et al. 2007a; Chacron and Bastian 2008; Krahe et al. 2008; Avila Akerberg et al. 2010). The RAM’s were obtained by multiplying a computer-generated low-pass filtered white noise (8-th order butterworth, cutoff frequency 10 Hz) with a sinusoid that is phase-locked to the animal’s own EOD. The signal was then isolated from ground and delivered using a small dipole positioned lateral to the animal.

2.5 In vitro electrophysiology

The animals were first deeply anaesthetized by immersing them in a solution of 3-aminobenzoic acid (MS-222) and then artificially respirated to perform surgery. ELL tissue slices of 300–400 μm were then prepared as described previously (Turner et al. 1994; Ellis et al. 2007b; Mehaffey et al. 2008b) and were maintained by constant perfusion (2–3 mL/min) of artificial cerebrospinal fluid (ACSF, composition in mM: 126 NaCl, 2.5 KCl, 1.2 NaH₂PO₄, 1.2 MgCl₂, 18 NaHCO₃, 2.4 CaCl₂, and 11 D-glucose) as well as superfusion with carbogen (5% CO₂/95% O₂).

2.6 In vitro recording

Intracellular recordings from ELL pyramidal cells were achieved using sharp glass micropipetes with typical resistances ranging from 80 MΩ to 120 MΩ and were limited to the lateral and centrolateral segments. An axoclamp 900A was used to amplify the recorded potential difference between the tip of the recording electrode and a ground wire placed in the bath as well as to deliver current injection through the recording electrode. Data was acquired at 10 kHz using a digidata 1440A and Clampex 9.0 software (Molecular Devices). The data was acquired with a sampling rate of 10 kHz using a digidata 1440A and Pclamp software (Molecular devices).

2.7 In vitro stimulation

We used DC current injection to maintain each cell just below its firing threshold and typical values used were −0.5 nA. We henceforth refer to this holding current as the baseline holding current. In order to mimic sensory stimulation, we injected through the glass electrodes a time varying current as done previously (Oswald et al. 2004; Ellis et al. 2007b; Mehaffey et al. 2008a) that consists of low-pass filtered (8th order Butterworth, 10 Hz cutoff) Gaussian white noise with mean 0.4 nA and standard deviation σ_stim. We shall henceforth refer to this waveform as the stimulus. In order to mimic synaptic input (Manwani and Koch 1999), we also injected a low-pass filtered Gaussian white noise (8th order butterworth, 10 Hz cutoff) with mean 0.4 nA and standard deviation σ_noise. We shall henceforth refer to this waveform as the noise. Note that the stimulus and noise waveforms were not correlated with one another.

2.8 Spike train analysis

All the analysis was done in Matlab (The Mathworks, Nattick, MA) using custom written routines. We obtained a binary sequence with binwidth dt=0.5 ms from the spike times by setting the content of bin i to 1 if there is one spike time such that i*dt≤t_i≤(i+1)*dt and to 0 otherwise. Note that since dt is set below the absolute refractory period of ELL pyramidal cells which is typically (1–2 ms), there can be at most one spike time within any given bin.

2.9 Burst classification

We used an interspike interval criterion (Oswald et al. 2004; Ellis et al. 2007a; Chacron and Bastian 2008; Avila Akerberg et al. 2010) to segregate the spikes that belong to a burst from those that don’t. The burst threshold was determined from the autocorrelation function of the interspike intervals and was computed individually for each cell as done previously (Bastian and Nguyenkim 2001; Chacron and Bastian 2008; Avila Akerberg et al. 2010). Specifically, we computed the autocorrelation function from each cell and determined the 99.9% confidence interval for a Poisson processes with the same firing rate as the cell in question. The burst threshold value was set to the lag at which the autocorrelation function first crosses the burst threshold from above (Bastian and Nguyenkim 2001; Chacron and Bastian 2008; Avila Akerberg et al. 2010). Note that the autocorrelation functions of ELL pyramidal cells display strong peaks in the autocorrelation function that are characteristic of burst firing (Bastian and Nguyenkim 2001).

2.10 Burst attributes

We quantified bursting by the burst ISI defined as the ISI of the first two spikes of a burst as well as the burst length defined by the number of action potentials in a burst. We note that defining the burst ISI instead as the ISI between the last two spikes of a burst, as done previously (Oswald et al. 2007), does not affect the qualitative nature of our results both in vivo (Avila Akerberg et al. 2010) and in vitro (data not shown).

2.11 Stimulus attributes

We tested whether the burst attributes defined above were correlated to the following stimulus attributes: the maximum amplitude and the slope. The first is computed as the maximum amplitude of the stimulus during the time between the first two spikes of the burst whereas the former is computed as the average slope during the burst ISI as done previously (Avila Akerberg et al. 2010). We note that qualitatively similar results could be obtained when the stimulus amplitude and slope were computed over the full burst duration (data not shown). We note that, for the in vivo data, the stimulus waveform was shifted by 8 ms to account for axonal transmission delays as done previously (Chacron et al. 2003; Avila Akerberg et al. 2010).

2.12 Mathematical modeling

Our pyramidal cell model contains two compartments and reproduces the main features of ELL pyramidal cell burst firing seen in vitro (Doiron et al. 2002; Oswald et al. 2004; Doiron et al. 2007). The model consists of somatic and dendritic compartments connected through an axial resistance of 1/g_c (g_c: coupling conductance). Both compartments contain the essential spiking currents: fast inward Na⁺ (I_Na,s, I_Na,d) and outward delayed rectifying (Dr) K⁺ (I_Dr,s, I_Dr,d), and passive leak currents (I_leak). The presence of spiking currents in the dendrite enables the active backpropagation of somatic action potentials required for bursting. We also included an NMDA conductance as well as an SK channel in the dendrite as done previously to mimic the burst firing in vivo: a full justification of the model equations and parameter values can be found elsewhere (Toporikova and Chacron 2009). The membrane potentials at the soma, V_s, and the dendrite, V_d, are given by:

$$\begin{array}{l}{C}_m\frac{d{V}_S}{dt}=I_{\mathit{app}}+I_{\mathit{NaS}}+I_{\mathit{DrS}}+\frac{g_c}{k}(V_D-V_S)+g_L(V_L-V_S)+I_{\mathit{stim}}(t)+D\xi (t)\\ C_m\frac{d{V}_D}{dt}=I_{\mathit{NaD}}+I_{\mathit{DrD}}+\frac{g_c}{1-k}(V_S-V_D)+g_L(V_L-V_D)+I_{Ca}+I_{SK}\end{array}$$

where ξ(t) is Gaussian white noise with zero mean and standard deviation unity, D is the noise intensity, I_stim is a low-pass filtered (8th order Butterworth, 10 Hz cutoff) Gaussian noise with zero mean and standard deviation D. I_app is a constant bias current, g_c is the coupling conductance, and k is the ratio between the soma area and the total area. The currents are given by:

$$\begin{array}{c}{I}_{\mathit{NaS}}=g_{\mathit{NaS}}{m}_{\infty ,S}^2(1-n_S)(V_{Na}-V_S)\\ I_{\mathit{DrS}}=g_{\mathit{DrS}}{n}_S^2(V_K-V_S)\\ I_{\mathit{NaD}}=g_{\mathit{NaD}}{m}_D^2{h}_D(V_{Na}-V_D)\\ I_{\mathit{DrD}}=g_{\mathit{DrD}}{n}_D^2(V_K-V_D)\\ I_{Ca}=g_{\mathit{NMDA}}(V_{Ca}-V_D)\\ I_{SK}=g_{SK}\frac{[Ca]}{[Ca]+k_{ca}}(V_K-V_D)\end{array}$$

The parameter g_X is the maximal conductance (in mS/cm²) of channel X, whereas m is an activation gating variable and h, n, and p are inactivation gating variables. Each is described by an equation of the form:

$$\frac{dx}{dt}=\frac{x_{\infty }(V)-x}{{\tau }_x}$$

where x_∞(V) is the infinite conductance curve and τ_x is the time constant of variable x (x = m,h,n, or p). Each infinite conductance curve is modeled as a sigmoid:

$$x_{\infty }(V)=\frac{1}{1+exp\left(\frac{V_x-V}{S_x}\right)}$$

The values of g_max, V_x, τ_x, s_x, used in the model for each of the currents are: g_c=1 mS/cm², g_L=0.18 mS/cm², g_NaS= 55 mS/cm², g_DrS=20 mS/cm², g_NaD=5 mS/cm², g_DrD=15, g_NMDA=20 mS/cm², g_SK=10 mS/cm², V_Na=40 mV, V_K= −88.5 mV,V_Ca=70, V_L=−70, V_mS=−40 mV, V_nS=−40 mV, V_mD=−40 mV, V_nD=−40 mV, V_hD=−52 mV, V_pD=−65 mV, τ_nS=0.39 ms, τ_nD=0.9 ms, τ_hD=1 ms, τ_pD=5 ms, τ_s=5 ms, s_mS=3, s_nS=3, s_mD=5, s_nD=5, s_hD=−5, s_pD=−6, s_s=6. Other parameters are: C_m=1 μF/cm², I_app=5 μA/cm². The equations were integrated using an Euler algorithm with a time step of 0.0025 ms.

The Ca²⁺ dynamics are modeled by:

$$\frac{d[Ca]}{dt}=f_{Ca}(\alpha I_{Ca}-k_{ex}[Ca])$$

Here [Ca] is the intracellular calcium concentration in μM, f_Ca=0.03 ms⁻¹ is a constant reflecting fraction of bounded to free Ca²⁺ (Wagner and Keizer 1994), α=0.0055 μM/(μA/cm²) is the Ca²⁺ conversion constant, and k_ex =1 μM⁻¹ is the Ca extrusion ratio (Nowak et al. 1984; Mayer and Westbrook 1987; Reynolds and Miller 1990). The model was simulated using an Euler-Maruyama integration algorithm (Kloeden and Platen 1999) with integration time step dt=0.0025 ms.

3 Results

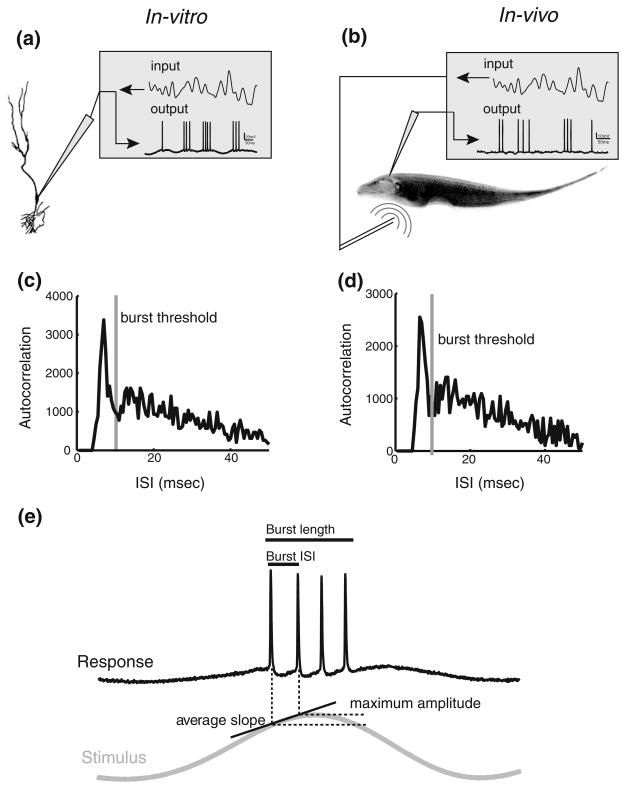
We investigated the coding of stimulus attributes by bursts both in vivo and in vitro. As such, we performed experiments in which burst coding was compared in vivo and in vitro within the same ELL segments using stimuli that had the same temporal frequency content. Previous studies have shown that ELL pyramidal cells display similar temporal frequency tuning to sensory stimulation in vivo and current injection in vitro (Krahe et al. 2008; Mehaffey et al. 2008b). Figure 1(a) and (b) show the experimental setups in vitro and in vivo, respectively.

Fig. 1.

Experimental methods. (a): In vitro experimental set up. Sharp intracellular recordings were taken from pyramidal cells in ELL slices. The input consisted of a low-pass filtered Gaussian white noise (0–10 Hz 8th order Butterworth) that was injected as a current through the recording electrode. (b): In vivo experimental set up. The fish is stimulated via a small dipole located close to the fish’s skin. Extracellular recordings were taken from ELL pyramidal cells. (c): Spike train autocorrelation function from in vitro data showing the burst threshold. (d): Spike train autocorrelation function from in vivo data showing the burst threshold. Note the similarity between the autocorrelation functions obtained from in vitro and in vivo data. (e): Burst and stimulus attributes. The burst attributes are the burst length and burst ISI while the stimulus attributes are the average slope and maximum amplitude reached during the first ISI of the burst

3.1 Burst coding observed in vitro is different from that observed in vivo

While we recorded from ELL pyramidal cells in vivo under sensory stimulation (Fig. 1(b)), we mimicked sensory stimulation in vitro by intracellular current injection (Fig. 1(a)). Note that previous studies have shown that the frequency tuning of pyramidal cells to current injection in vitro are similar to those seen to sensory stimuli in vivo across the ELL segments (Krahe et al. 2008; Mehaffey et al. 2008a). The mean firing rates obtained from our in vivo and in vitro datasets were not significantly different (in vivo: 19.9±11.3 Hz; in vitro: 18.5±6.0 Hz; t-test, p=0.53, df=32). We used an interspike interval threshold to identify bursts. Specifically, the value of the ISI threshold was chosen to be the lag at which the autocorrelation function crosses the 99.9% confidence interval from above as done previously (Bastian and Nguyenkim 2001; Chacron and Bastian 2008; Avila Akerberg et al. 2010). The ISI threshold and autocorrelation function from an example neuron are shown under in vitro (Fig. 1(c)) and in vivo conditions (Fig. 1(d)) and were similar in shape. Moreover, the burst thresholds obtained in vivo and in vitro were not significantly different (in vivo: 11.5±0.85 ms; in vitro: 11.7 ±1.83 ms; t-test, p=0.85, df=32)

We quantified burst attributes by computing the burst ISI (i.e. the ISI between the first two spikes of a burst) as well as the burst length (i.e. the number of spikes within the burst) (Fig. 1(e)). The stimulus was quantified by its amplitude (i.e. the maximum amplitude that occurs during the burst ISI) and slope (i.e. the maximum of the slope within the burst ISI) (Fig. 1(e)).

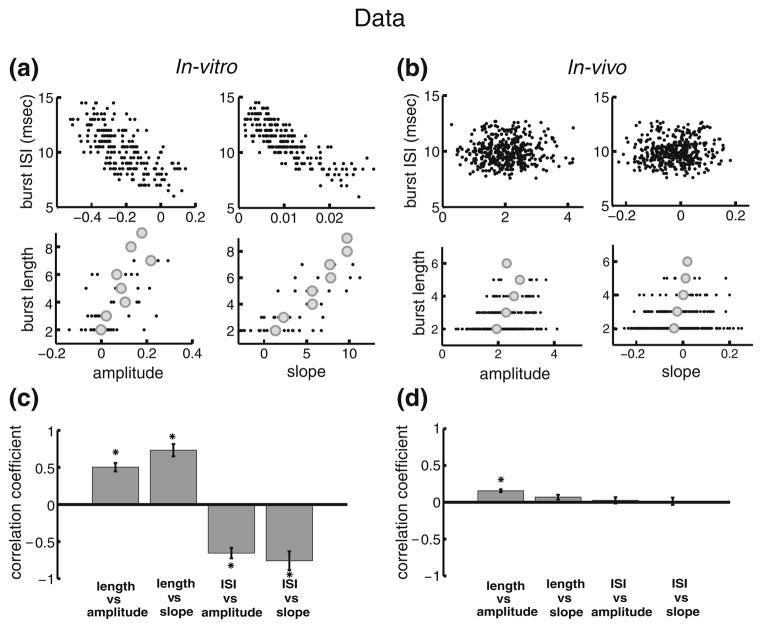
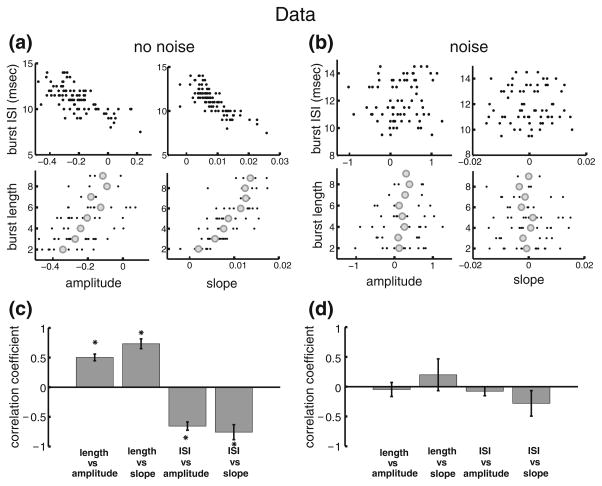
Figure 2(a,b) show the correlations between burst and stimulus attributes from two typical example pyramidal neurons in vitro and in vivo, respectively. It is seen that, in vitro, there is a significant negative correlation between the burst ISI and stimulus amplitude (Fig. 2(a), upper left) as well as slope (Fig. 2(a) upper right), which is similar to what was observed previously (Oswald et al. 2007). Moreover, there was a significant positive correlation between burst length (i.e. the number of spikes in a burst) and stimulus amplitude (Fig. 2(a) lower left) as well as slope (Fig. 2(a) lower right). In contrast, correlations between burst and stimulus attributes were far less evident in vivo (Fig. 2(b)). Indeed, the correlations between the burst ISI and either or stimulus amplitude (Fig. 2(b), upper left) or slope (Fig. 2(b), upper right) were significantly less pronounced (Fig. 2(b), upper two panels). Moreover, correlations between the burst length and either of stimulus amplitude (Fig. 2(b), lower left) or slope (Fig. 2(b), lower right) were also significantly less pronounced (Fig. 2(b), lower two panels).

Fig. 2.

Burst coding is different in vitro and in vivo. (a): Plots of burst attributes versus stimulus attributes in vitro. The panels show the: burst ISI vs. amplitude, upper left; burst ISI vs. slope, upper right; burst length vs. amplitude, lower left; burst length vs. slope, lower right. (b): plots bursts attributes versus stimulus attributes in vivo. The panels show the: burst ISI vs. amplitude, upper left; burst ISI vs. slope, upper right; burst length vs. amplitude, lower left; burst length vs. slope, lower right. (c): in vitro population averages (n=6) of the correlation coefficients for each of the plots in panel A. (d): in vivo population averages (n=13) of the correlation coefficients for each of the plots in panel B. “*” indicates statistical significance at the P=0.01 level using a signrank test

Similar results were seen across our datasets obtained in vivo and in vitro. Indeed, while correlation coefficients between burst and stimulus attributes were large in magnitude and significant in vitro (Fig. 2(c)), the correlation coefficients between these same burst and stimulus attributes were small in magnitude and not significantly different than zero in vivo with the exception of the correlation coefficient between burst length and stimulus amplitude (Fig. 2(d)).

These results show that differences between burst coding in vivo and in vitro do not result from comparing recordings that were performed in different ELL segments or from using stimuli with differing temporal frequency content.

Overall, there were no significant correlations between stimulus attributes (i.e. between the amplitude and slope) either for in vivo (R=0.08, p=0.29, n=14) or in vitro (R= 0.05, p=0.63, n=19) conditions. However, we observed a weak but significant correlation coefficient between the burst ISI and burst length for our in vitro data (R=−0.3506, p≪0.01, n=19). This correlation was not significant in vivo (R=−0.037, p=0.11, n=14).

Further, we note that defining the burst ISI as the ISI between the last two spikes of a burst, as done previously, gives rise to qualitatively similar results both in vivo (Avila Akerberg et al. 2010) and in vitro (data not shown). Further, previous studies have shown that using a 120 Hz cutoff frequency rather than a 10 Hz cutoff as done here gives rise to qualitatively similar results in vivo (Avila Akerberg et al. 2010). It is expected that increasing the cutoff frequency will decrease the magnitude of correlations between stimulus and burst attributes as high frequencies tend to inhibit burst firing (Oswald et al. 2004).

3.2 Modeling differences in burst coding seen in vitro and in vivo

We next tested the hypothesis that the differences in burst coding seen in vitro and in vivo are due to differences between burst dynamics as observed in vitro and in vivo. Indeed, bursting in ELL pyramidal neurons is intrinsic and relies on a somatodendritic interaction (Turner et al. 1994; Lemon and Turner 2000). Somatic action potentials back-propagate into the proximal apical dendrites where they trigger a dendritic spike that propagates back to the soma, leading to a depolarizing afterpotential (DAP) and promotes the firing of another somatic action potential. This DAP grows in size throughout the burst, which leads to a progressive depolarization and a shortening of the inter-spike interval (ISI) throughout the burst (Lemon and Turner 2000). The burst terminates with a characteristic doublet when the ISI becomes shorter than the dendritic refractory period (Noonan et al. 2003), which leads to dendritic failure characterized by the absence of a dendritic spike and terminates the burst. In contrast, studies performed in vivo have shown that there was no significant shortening of the ISI within burst firing (Bastian and Nguyenkim 2001). Moreover, a recent study found that ELL pyramidal cell bursts in vivo did not terminate with dendritic failure under control conditions (Toporikova and Chacron 2009). This is because dendritic small conductance calcium-activated potassium currents are activated in vivo and give rise to an afterhyperpolarization that counteracts the DAP. It turns out that this afterhyperpolarization grows at a faster rate than the DAP and can lead to an “early” termination of burst firing (i.e. before a dendritic failure) (Toporikova and Chacron 2009).

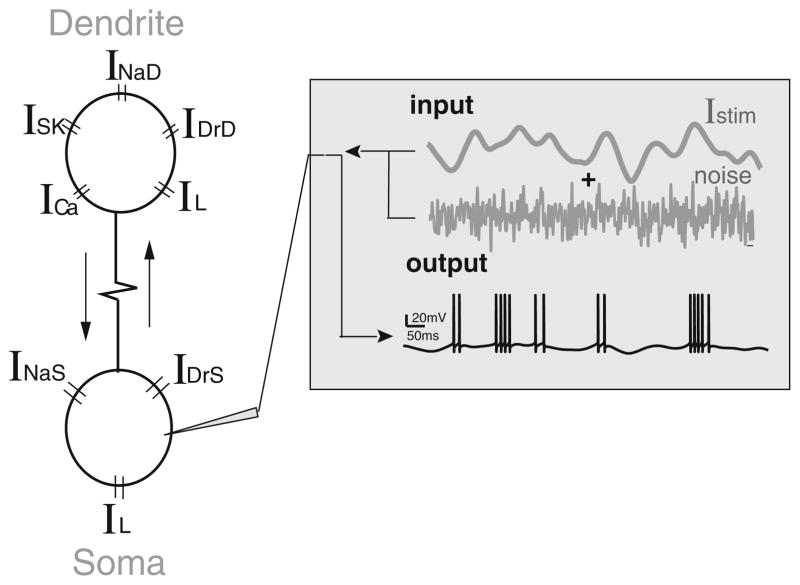
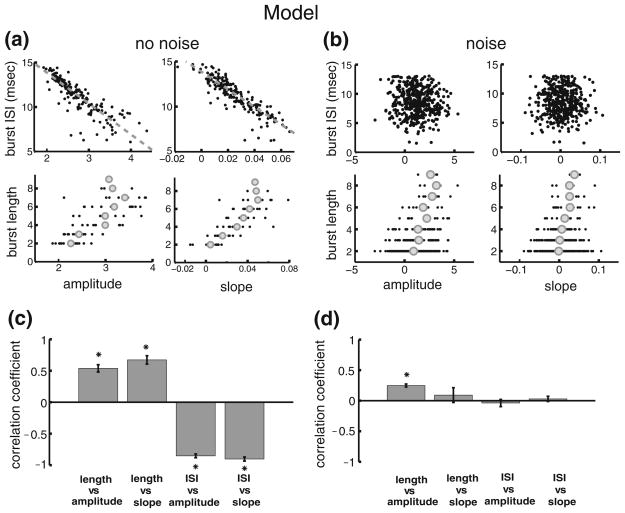
In order to test the hypothesis that differences between ELL pyramidal cell burst firing seen in vivo and in vitro could account for the differences in coding, we computed correlations between burst and stimulus attributes in a mathematical model of pyramidal cell burst activity in vivo based on the Hodgkin-Huxley formalism (Toporikova and Chacron 2009). The model consists of two compartments (one somatic and one dendritic) that each contains the necessary membrane conductances to elicit burst firing (Fig. 3(a)). Our results show that correlations between burst and stimulus attributes computed from the model when sensory stimulation is mimicked by somatic current injection are similar to those obtained in vitro (compare Figs. 2(a) and 4(a)). Indeed, a strong negative correlation was observed between the burst ISI and stimulus amplitude as well as slope (Fig. 4(a), upper two panels) whereas strong positive correlations were observed between the burst length and stimulus amplitude as well as slope (Fig. 4 (a), lower two panels). These results strongly speak against the hypothesis that differences between burst coding in vivo and in vitro are due to differences in burst firing. Moreover, we note that similar results could be obtained by injecting the stimulus current into the dendritic compartment (data not shown).

Fig. 3.

Schematic of the two-compartmental bursting model. Our model consists of two compartments that are coupled with a resistance. The somatic compartment contains leak (I_L), spiking sodium (I_NaS), and delayed rectifier potassium (I_DrS) currents. The dendritic compartment contains leak (I_L), spiking sodium (I_NaD), delayed rectifier potassium (I_DrD), NMDA (I_NMDA), and small conductance calcium-activated potassium (I_SK) currents. The model is fed with an input that consists of a stimulus current (low-pass, 0–10 Hz, filtered Gaussian white noise) and a noisy current

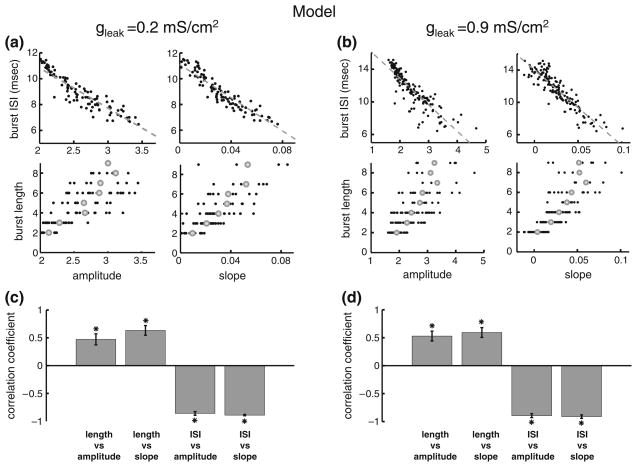
Fig. 4.

Effects of the membrane resistance on correlations between burst and stimulus attributes. (a): plots of burst attributes versus stimulus attributes for low leak conductance. The plots are: burst ISI vs. amplitude, upper left; burst ISI vs. slope, upper right; burst length vs. amplitude, lower left; burst length vs. slope, lower right. (b): plots of bursts attributes versus stimulus attributes for high leak conductance. The plots are: burst ISI vs. amplitude, upper left; burst ISI vs. slope, upper right; burst length vs. amplitude, lower left; burst length vs. slope, lower right. (c): ensemble averages over 10 stimulus presentations without noise of the correlation coefficients for each of the plots in panel A. (d): ensemble averages over 10 presentations of the stimulus presentations with a different realization of the noise of the correlation coefficients for each of the plots in panel B. “*” indicates statistical significance at the P=0.01 level using a signrank test

3.3 Increasing the input conductance preserves correlations between burst and stimulus attributes in the model

The differences between in vivo and in vitro conditions are well known. Indeed, the intense synaptic bombardment in vivo causes neurons to be in a “high-conductance” state (Destexhe et al. 2001, 2003). We thus first tested whether increasing the membrane conductance might explain the differences in correlations between burst and stimulus attributes observed in vitro and in vivo in ELL pyramidal cells. Comparing experimental measurements of the membrane time constant in ELL pyramidal cells in vitro (Berman and Maler 1998) and in vivo (Toporikova and Chacron 2009) reveals that the time constant in vivo is ~3 fold lower than in vitro. We increased the leak conductance g_leak 5-fold in our model. Our results show that this had negligible effect on correlations between burst and stimulus attributes (compare Fig. 4(a and b)) as quantified by the correlation coefficients (compare Fig. 4(c and d)). These results speak strongly against the hypothesis that increased conductance alone can account for the differences in correlations between burst and stimulus attributes observed in vitro and in vivo in ELL pyramidal cells.

3.4 Increasing variability decreases correlations between burst and stimulus attributes in the model

The intense synaptic bombardment in vivo also gives rise to large membrane potential fluctuations (Destexhe et al. 2001, 2003). These fluctuations cause increased variability in the spiking activity obtained in response to repeated presentations of the same stimulus (Stein et al. 2005). Of course, it is expected that such variability will lead to a lowering of correlations between stimulus and response attributes, so we specifically tested the following hypothesis: are the levels of variability seen in vivo under baseline activity sufficiently high to account for the lower correlation between burst and stimulus attributes? We tested this by mimicking the fluctuations in the membrane potential by directly injecting noise as well as the stimulus in the model’s somatic compartment. Moreover, the noise intensity was calibrated such that the variability as quantified by the coefficient of variation (i.e. the standard deviation to mean ratio of the ISI distribution) displayed by our model in the absence of stimulation was between 0.4 and 0.8, which is within the range observed in vivo for the baseline activity (i.e. the activity obtained in the absence of stimulation) of ELL pyramidal cells (Bastian and Nguyenkim 2001). Previous theoretical studies have investigated the consequences of variability in the baseline activity on information transmission (Chacron et al. 2004b; Chacron et al. 2005b, d; Lindner et al. 2005). In particular, the power spectrum of the baseline activity can be seen as a “noise spectrum” and determines the amount of noise at each frequency during stimulation (Sadeghi et al. 2007). As such, a more variable baseline activity will give rise to greater noise power and thus, a lower signal-to-noise ratio and information transmission. Previous experimental studies have shown that ELL pyramidal cells with higher baseline variability tended to transmit lower amounts of information than ELL pyramidal cells with lower baseline variability, and that this was due to increased trial-to-trial variability in the former (Chacron 2006). As such, we expect that the noise injected will provide an accurate mimic of the levels of uncorrelated noise present under in vivo conditions during stimulation.

Our results show that adding such noise leads to a lowering in magnitude of the correlation coefficients between burst and stimulus attributes (compare Fig. 5 (a and b)). Indeed, correlations between the burst ISI and the stimulus amplitude (compare Fig. 5(a and b), upper left) and slope (compare Fig. 5(a and b), upper right) were rendered non significant while those between the burst length and stimulus amplitude (compare Fig. 5(a and b), lower left) and slope (compare Fig. 5(a and b), lower right) were also weakened in magnitude.

Fig. 5.

Our model of in vivo burst dynamics reproduces experimental results obtained in vitro. (a): plots of burst attributes versus stimulus attributes without noise injection. The plots are: burst ISI vs. amplitude, upper left; burst ISI vs. slope, upper right; burst length vs. amplitude, lower left; burst length vs. slope, lower right. (b): plots of bursts attributes versus stimulus attributes with noise injection. The plots are: burst ISI vs. amplitude, upper left; burst ISI vs. slope, upper right; burst length vs. amplitude, lower left; burst length vs. slope, lower right. (c): ensemble averages over 10 stimulus presentations without noise of the correlation coefficients for each of the plots in panel A. (d): ensemble averages over 10 presentations of the stimulus presentations with a different realization of the noise of the correlation coefficients for each of the plots in panel B. “*” indicates statistical significance at the P=0.01 level using a signrank test

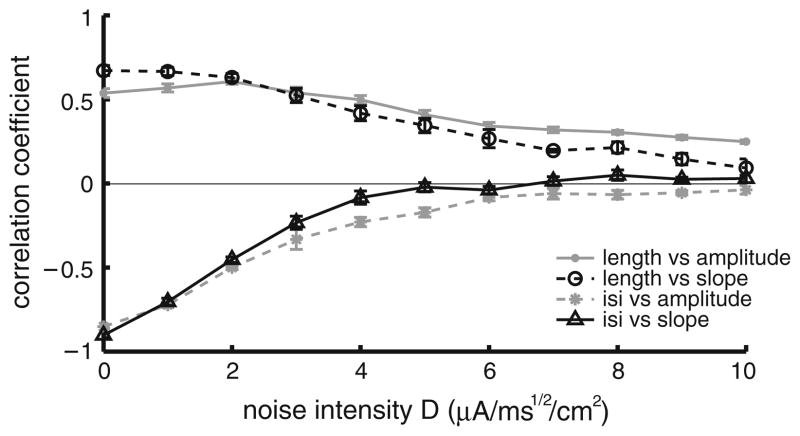
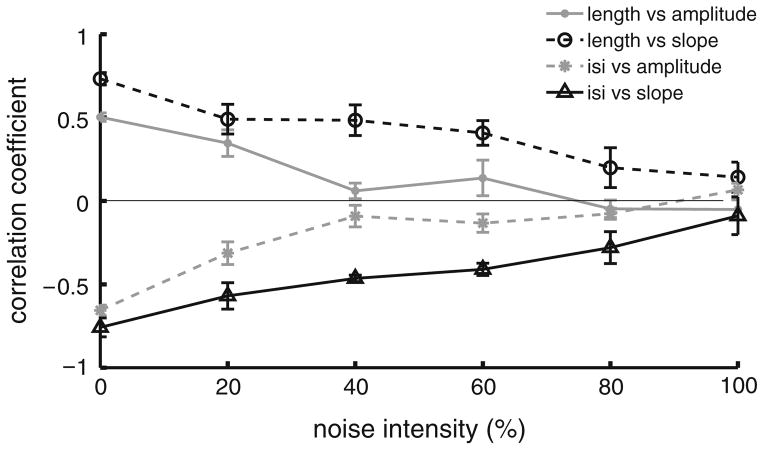
The effects of noise on correlations between burst and stimulus attributes are further seen in Fig. 6 where the correlation coefficients between burst and stimulus attributes are plotted as a function of noise intensity. Our model therefore predicts that the variability displayed by ELL pyramidal neurons in their baseline activities in vivo can account for the low magnitude of correlation coefficients between burst and stimulus attributes. We note that similar results were obtained when the noise was injected in the dendritic compartment as well as when we used white noise rather than colored noise (data not shown).

Fig. 6.

Injecting a noisy current to the model cells reduces the magnitude of the correlation coefficients between burst and stimulus attributes. Shown are the different correlation coefficients as a function of noise intensity: burst length vs. stimulus amplitude (gray solid dots), burst length vs. stimulus slope (black open circles), burst ISI vs. stimulus amplitude (gray stars) and burst ISI vs. stimulus slope (black open triangles). Each point represents an average over 10 realizations of the stimulus and noise waveforms

3.5 Verifying the model’s prediction: noise injection in vitro

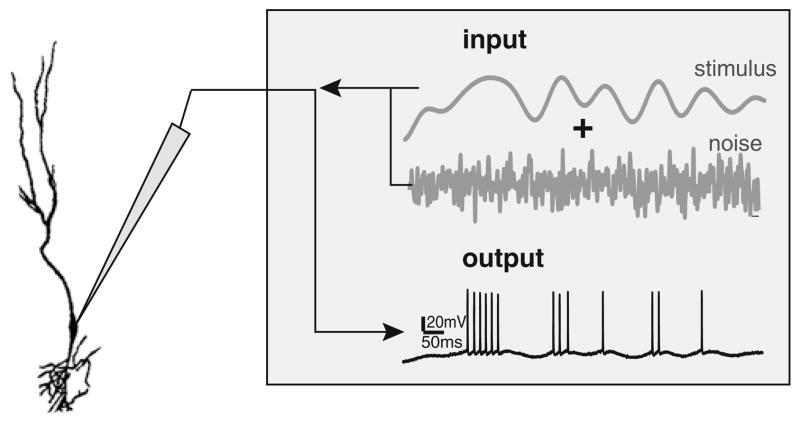
Our modeling results predict that increased variability under in vivo conditions can account for the differences in burst coding properties observed in vitro and in vivo in ELL pyramidal neurons. Since it is not possible to “remove” the variability seen in vivo, we instead injected a noisy current through the recording electrode in vitro (Fig. 7(a)). We then systematically varied the relative strength of the noise compared to that of the signal. Our results show that this injection leads to a lowering in magnitude of the correlations between burst and stimulus attributes in an example neuron (compare Fig. 8(a,b)). Indeed, when the noise intensity is null, the correlation coefficients between the burst ISI and the stimulus amplitude (Fig. 8(a), upper left) and slope (Fig. 8(a), upper right) were strong and negative. Moreover, the correlation coefficients between the burst length and the stimulus amplitude (Fig. 8(a), lower left) and slope (Fig. 8(a), lower right) were strong and positive. However, when the noise reaches a similar intensity as the stimulus current, which is needed in order to reproduce the variability seen in vivo in ELL pyramidal cells, the correlations between burst and stimulus attributes decrease in magnitude (Fig. 8(b)). Indeed, we observed weak if at all significant correlations between the burst ISI and either of stimulus amplitude (Fig. 8(b), upper left) or slope (Fig. 8(b), upper right). Moreover, correlation coefficients between the burst length and either of stimulus amplitude (Fig. 8(b), lower left) or slope (Fig. 8(b), lower right) were considerably weaker in magnitude. Similar trends were seen across our dataset. While the correlation coefficients between burst and stimulus attributes with no noise injected were all strong in magnitude and significant (Fig. 8(c)), these same correlation coefficients were weak and not significantly difference from zero when noise was injected (Fig. 8(d)). Our experimental results show that the magnitude of the correlation coefficients between burst and stimulus attributes decreases as a function of the noise intensity (Fig. 9), as predicted by our model (compare Fig. 9 with Fig. 6).

Fig. 7.

Experimental representation of adding a noise current to the stimulus in an in vitro setup. The cells were stimulated via an electrode and the input consisted of a time varying signal and a noisy current. The output spike train sequence was recorded through the same electrode

Fig. 8.

Injecting a noise current in vitro is detrimental to correlations between burst and stimulus attributes. (a): plots of burst vs. stimulus attributes for an example pyramidal cell without noise injection. The panels show: burst ISI vs. amplitude, upper left; burst ISI vs. slope, upper right; burst length vs. amplitude, lower left; burst length vs. slope, lower right. (b): plots of bursts attributes versus stimulus attributes for an example cell with noise injection. The panels show: burst ISI vs. amplitude, upper left; burst ISI vs. slope, upper right; burst length vs. amplitude, lower left; burst length vs. slope, lower right. (c): Population averages (n=6) of the correlation coefficients without noise injection for each of the plots in panel A. (d): population averages (n=6) of the correlation coefficients for each of the plots in panel B. “*” indicates statistical significance at the P= 0.01 level using a signrank test

Fig. 9.

Plot of the correlation coefficients between burst and stimulus attributes as a function of noise intensity obtained experimentally in vitro. Shown are the correlation coefficients between burst length vs stimulus amplitude (gray solid dots), burst length vs stimulus slope (black open circles), burst ISI vs stimulus amplitude (gray stars) and burst ISI vs stimulus slope (black open triangles)

4 Discussion

4.1 Summary of results

Previous studies performed in vitro in ELL pyramidal cells support the notion that bursts can carry information about the stimulus in their temporal structure as they have shown the presence of strong correlations between burst and stimulus attributes (Oswald et al. 2007). However, our previous study from the same cells in vivo did not find such correlations (Avila Akerberg et al. 2010). In order to better understand the causes for this difference, we investigated burst coding in ELL pyramidal cells using a combination of in vitro, in vivo electrophysiology, as well as mathematical modeling. We first showed that differences in correlations between burst and stimulus attributes were not attributable to the fact that previous in vivo and in vitro recordings were made from different ELL segments. Indeed, our experimental data gathered in vitro from the lateral and centro-lateral segments showed strong correlations that were similar to those reported previously for pyramidal cells within the centromedial segment (Oswald et al. 2007). We then tested whether this difference could be attributed to differences in burst firing seen in vitro and in vivo in ELL pyramidal cells (Bastian and Nguyenkim 2001; Toporikova and Chacron 2009). To do so, we simulated a previously developed biophysical model of ELL pyramidal cell bursting in vivo to somatic current injection mimicking the experiments done in vitro. Our results show that this model reproduced the correlations between burst and stimulus attributes seen in our in vitro data. Therefore, differences in correlations between burst and stimulus attributes seen in vivo and in vitro are most likely not due to differences between bursting seen in vitro and in vivo. We next hypothesized that these differences were due to the massive synaptic bombardment experienced by neurons in vivo (Destexhe et al. 2001, 2003), which contributes to both increased conductance and variability in spiking activity due to large membrane potential fluctuations (Stein et al. 2005). To test this hypothesis, we increased the leak conductance and introduced a noise source that was uncorrelated with the stimulus in our model. Our results showed that increasing the leak conductance had negligible effect on the correlations between burst and stimulus attributes. However, increasing the noise intensity in order to match the variability seen in vivo in ELL pyramidal cells under baseline activity strongly decreased the magnitude of correlations between burst and stimulus attributes to levels that matched those seen experimentally in vivo. As such, our model predicted that the variability in the baseline activity seen under in vivo conditions could account for the differences in correlation between burst and stimulus attributes as observed in vitro and in vivo in ELL pyramidal neurons. In order to test this prediction, we injected both noise and stimulus currents in vitro and found that this led to a decrease in the magnitude of correlations between burst and stimulus attributes, as predicted from our model. Furthermore, noise intensities that could reproduce the variability seen in vivo in ELL pyramidal cells gave rise to correlation coefficients between burst and stimulus attributes whose values were similar to those seen experimentally in vivo. Our results therefore show that the variability induced by synaptic bombardment in vivo is sufficient to eliminate correlations between burst and stimulus attributes in ELL pyramidal neurons.

4.2 Do bursts contain information about sensory stimuli in their structure?

Previous results obtained in vitro in ELL pyramidal cells have shown that the burst ISI was strongly negatively correlated with both the stimulus amplitude and the stimulus slope (Oswald et al. 2007). As a consequence, Oswald et al. (2007) showed that an ideal observer could distinguish different stimulus amplitudes using the amount of time between two consecutive spikes within a burst. As the value of the burst ISI was typically <10 ms and the time scales associated with the stimulus were in that study were greater than 16 ms, they showed that information about the stimulus is contained in the structure of the burst at time scales that are smaller than those contained in the stimulus, which constitutes a temporal code by definition (Theunissen and Miller 1995; Dayan and Abbott 2001; Jones et al. 2004; Sadeghi et al. 2007). Our previous results obtained in vivo did not find such strong correlations between burst and stimulus attributes (Avila Akerberg et al. 2010). In particular, the correlation coefficients between the burst ISI and either of the stimulus amplitude or slope were not significantly different than zero. It is therefore unlikely that the interval code in bursts proposed by Oswald et al. (2007) is present in ELL pyramidal neurons under in vivo conditions.

Our results instead support the notion that bursts in ELL pyramidal neurons are produced primarily to signal the presence of particular features in the sensory environment rather than carry information about their details (i.e. feature detection) (Gabbiani and Koch 1996; Metzner et al. 1998; Sherman 2001; Sherman and Guillery 2002). This is because the correlation coefficients between burst and stimulus attributes were weak and non-significant for the most part. In fact, only the number of spikes within the burst (i.e. the burst length) was weakly but significantly correlated with the stimulus amplitude in vivo. This suggests a code in which bursts of larger length are more likely to be elicited by stimuli with larger amplitudes. This is consistent with the proposed functional role of feature detection by bursts as bursts of larger length are more likely to overcome synaptic unreliability and thus to be transmitted to higher brain centers (Lisman 1997).

4.3 Burst dynamics and coding

Burst firing is seen ubiquitously in the central nervous system and can be caused by a multitude of intrinsic and network mechanisms (Rinzel 1987; Wang and Rinzel 1995; Izhikevich 2000; Doiron et al. 2002). As such, an important question pertains to whether differences in the mechanisms that give rise to burst firing can also give rise to differences in sensory coding. This question has been investigated in part. Indeed, a previous modeling study using a minimal model of a Hippocampal pyramidal neuron has shown burst duration coding in the form of a positive correlation between stimulus slope and burst length (Kepecs et al. 2002). This is consistent with experimental results showing correlations between the burst length and stimulus attributes such as orientation (DeBusk et al. 1997; Martinez-Conde et al. 2002), velocity (Arganda et al. 2007), luminance (Gaudry and Reinagel 2008), and sound (Eyherabide et al. 2008; Marsat and Pollack 2010). While our modeling results and in vitro data also show a positive correlation between stimulus slope and burst length for ELL pyramidal neurons, our results suggest that the weak correlation between burst length and stimulus amplitude can be accounted by the high variability displayed by ELL neurons in vivo. We note however that our results in no way rule out the possibility that such correlations might be present in other systems. Moreover, our results do not rule out the possibility that burst attributes in ELL pyramidal neurons code for stimulus attributes that are different than those considered here such as stimulus phase (Samengo and Montemurro 2010) or negative deflections preceding the burst (Gaudry and Reinagel 2008), or for nonlinear correlations between burst and stimulus attributes. Further studies are needed to address these important questions.

It is well known that the high conductance state of neurons in vivo can have a dramatic influence on their responses to input (Destexhe and Paré 1999; Destexhe et al. 2003). In particular, this synaptic bombardment increases the subthreshold membrane conductance as well as the variability in the spiking activity. Our results suggest that it is the latter that plays the largest role in determining burst coding as we were able to reproduce the correlations between burst and stimulus attributes seen in vivo by simply injecting current noise in vitro. We however note that our results provide only a potential explanation of the differences in correlations between burst and stimulus attributes in ELL pyramidal neurons under in vivo and in vitro conditions and that other mechanisms (e.g. involving changes) might account for these differences. Indeed, it is known that in vivo conditions can have a strong influence on the generation of bursts of action potentials in the electrosensory system (Toporikova and Chacron 2009) as well as in other systems (Wolfart et al. 2005). While our modeling and in vitro experimental results suggest that these differences do not qualitatively affect correlations between burst and stimulus attributes in the former, further experimental studies performed in vivo are needed to verify this prediction.

4.4 Role of variability in neural coding

While it is undeniable that neurons display trial-to-trial variability in their responses to repeated presentations of the same stimulus (Dean 1981; Tolhurst et al. 1983; Mainen and Sejnowski 1995) and that this variability originates largely from synaptic input from other neurons (Stein et al. 2005), the role of this variability in neural coding is still a matter of debate. Is it merely a source of noise that should be averaged away or does it permit neurons to transmit extra information? Our results are mostly consistent with the former hypothesis. However, we note that our results were obtained using single neuron recordings and that different conclusions could be drawn when looking at coding by populations of neurons. Indeed, multi-unit recordings from ELL pyramidal neurons in vivo have revealed that bursts tend to occur in synchrony in neighboring cells (Chacron and Bastian 2008). Further studies should focus on population coding in order to determine the functional role of bursts in the ELL in vivo and are beyond the scope of this study. We nevertheless note that bursts from ELL pyramidal cells appear to be a behaviorally relevant signal as midbrain neurons that receive direct synaptic input from ELL pyramidal cells respond selectively to these (Fortune and Rose 1997). This is supported by recent studies showing that ELL pyramidal neurons respond to communication stimuli with bursts of action potentials (Marsat et al. 2009; Marsat and Maler 2010). Further studies are needed to investigate potential correlations between burst and communication stimuli attributes and their role in mediating behavior. This is an important question as bursts have been shown to be relevant in mediating escape behavior (Marsat and Pollack 2006).

4.5 Conclusion

Our results show that the high variability of neurons in vivo can be highly detrimental to information coding by burst structure in single neurons. They suggest that information is solely contained in the occurrence of a burst in ELL pyramidal neurons and support the notion that bursts can be treated as a single unit of information (Izhikevich et al. 2003).