Scholte wave generation during single tracking location shear wave elasticity imaging of engineered tissues

Abstract

The physical environment of engineered tissues can influence cellular functions that are important for tissue regeneration. Thus, there is a critical need for noninvasive technologies capable of monitoring mechanical properties of engineered tissues during fabrication and development. This work investigates the feasibility of using single tracking location shear wave elasticity imaging (STL-SWEI) for quantifying the shear moduli of tissue-mimicking phantoms and engineered tissues in tissue engineering environments. Scholte surface waves were observed when STL-SWEI was performed through a fluid standoff, and confounded shear moduli estimates leading to an underestimation of moduli in regions near the fluid-tissue interface.

1. Introduction

Developing functional tissue constructs that mimic the physical environment of native tissues is a major challenge in tissue engineering.¹ Mechanical properties of engineered tissues can influence cell functions that are important for tissue regeneration, and affect the integration of tissue constructs post-implantation.² Monitoring the mechanical properties of engineered tissue constructs during the fabrication process is critical for identifying appropriate fabrication conditions necessary for developing viable and implantable constructs. Standard direct mechanical tests destroy tissue samples and, therefore, are not suitable for characterizing the development of engineered tissue samples over time.³ Furthermore, direct mechanical tests provide only bulk measurements of mechanical properties and do not enable measurements of localized regions within tissue samples. Ultrasound elastography describes a variety of techniques that can create quantitative images of the mechanical properties of native soft tissues, nondestructively.^4–7

The goal of the current work was to investigate the feasibility of employing single tracking location shear wave elasticity imaging (STL-SWEI) to quantify shear moduli of three-dimensional (3-D) engineered tissues within standard tissue engineering fabrication environments. In the STL-SWEI technique, an acoustic radiation force is applied remotely at a localized region within the tissue sample, and the speed of the resulting shear wave is used to quantify the shear modulus of the tissue, non-invasively.^8–10 STL-SWEI is a non-destructive technique that does not require direct contact with tissues, thus it is advantageous for use in the sterile environments required for tissue engineering. Fluid-solid interfaces are present in many tissues in vivo (e.g., blood vessels, heart) and similarly, exist during tissue fabrication in vitro due to the presence of culture media. However, the interface between the solid engineered tissue and the fluid culture medium may lead to the production of surface waves. Previous work investigated Scholte waves generated at interfaces between an inviscid fluid and an elastic solid after transient point loading.¹¹ In that work, the Scholte waves were slower than the shear waves generated within the elastic solid.¹¹ Experiments in this paper are designed to evaluate the use of STL-SWEI of phantoms and engineered tissue constructs within standard tissue engineering protocols, and to evaluate whether Scholte waves confound estimates of the shear modulus of engineered tissues near the fluid-solid interface.

2. Methods

2.1. Fabrication of uniform tissue-mimicking phantoms and cell-embedded, collagen-based engineered hydrogels

Uniform tissue-mimicking gelatin (62 g/L) phantoms containing cornstarch scatterers (186 g/L) were fabricated as described previously.^8,9 Three separate gelatin phantoms were fabricated in cylindrical Teflon molds (80 mm in diameter, 60 mm thick). Smaller cylindrical phantoms (26 mm in diameter, 6 mm thick) were sectioned from each of the larger phantoms.

Neutralized collagen solutions were prepared on ice by combining type I collagen (BD Biosciences, Bedford, MA) with 2X Dulbecco's Modified Eagle Medium (DMEM, Invitrogen, Carlsbad, CA) and 1X DMEM such that the final mixture contained 1X DMEM and collagen at a concentration of 2 mg/mL. The collagen mixture was then degassed in a vacuum chamber for 40 min. Mouse embryonic fibroblasts were cultured as described previously.¹² Cell-embedded collagen gels were fabricated by mixing fibroblasts with the degassed collagen mixture to obtain a final cell concentration of 4 × 10⁵ cells/mL (n = 3 samples). Aliquots of the collagen/cell mixture were added into 6-well Flex I^® tissue culture plates (Flexcell^® Int'l Corp., Hillsborough, NC). The collagen/cell mixtures were allowed to polymerize at 37  °C, 8% CO₂ for 1 h. Following this incubation, the wells were filled with 4.5 mL of 1X DMEM with 25 mM HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid). Each cell-embedded collagen hydrogel was 26 mm in diameter and 5 mm thick.

2.2. STL-SWEI technique

A Siemens VF7-3 linear array transducer with 192 elements was used for all STL-SWEI experiments. The linear array (center frequency of 4.21 MHz, F-number of 3.5) was operated using a Siemens Sonoline Antares scanner (Siemens Medical Solutions USA, Inc., Issaquah, WA). The scanner was equipped with an Ultrasound Research Interface package that allowed acquisition of beamformed RF echo data sampled at 40 MHz and digitized with 16-bit resolution.^8,9 The scanner was remotely controlled via a separate network connected to a computer that was used to implement the STL-SWEI sequence.

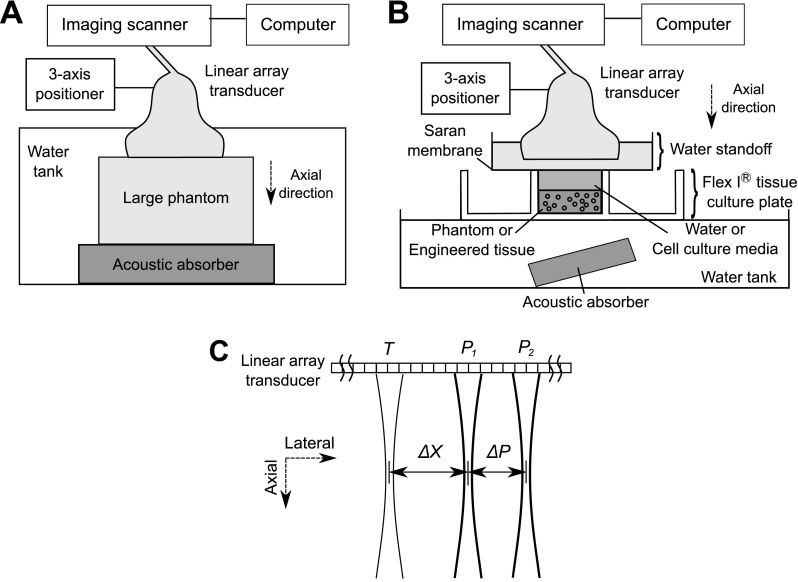
Schematics of the experimental set-ups for STL-SWEI of gelatin phantoms and cell-embedded collagen constructs are shown in Fig. 1. STL-SWEI was first performed to estimate the shear modulus of the large, uniform gelatin phantoms using the arrangement shown in Fig. 1(A). Each large gelatin phantom was placed on top of an acoustic absorber and submerged in a tank filled with degassed, deionized water [Fig. 1(A)]. For STL-SWEI, the linear array transducer was mounted on a three-axis positioner (Velmex, Inc., Bloomfield, NY) and positioned either in contact with the top surface of the phantom, or in the water tank, 1.7 cm above the top of the phantom. Three independent imaging planes within each large gelatin phantom were scanned at a focal depth of 2 cm. A region of interest (ROI) (0.6 cm axially, 2 cm laterally), centered at the focal depth within the phantom, was selected for each imaging plane.

Fig. 1.

Schematic of the experimental set-up for conducting STL-SWEI of (A) large uniform phantoms submerged in a water tank and (B) smaller phantoms and engineered tissues in tissue culture plates. (C) Schematic of locations of the tracking and pushing beams in one ensemble in the STL-SWEI sequence. ΔX is the lateral distance between the first pushing location at P₁ and the tracking location at T. ΔP is the lateral distance between the two pushing locations at P₁ and P₂.

The apparatus shown in Fig. 1(B) was used for STL-SWEI of small gelatin phantoms and cell-embedded collagen constructs contained within tissue culture plates. Small gelatin phantoms were placed within the wells of Flex I^® tissue culture plates (Flexcell Int'l Corp., Hillsborough, NC) for STL-SWEI [Fig. 1(B)]. Cell-embedded collagen gels were fabricated within wells of Flex I^® plates and STL-SWEI was performed 2 h after fabrication [Fig. 1(B)]. For imaging either the small gelatin phantoms or the cell-embedded hydrogels, the linear array transducer was positioned such that the transducer focus was centered at the middle of the gel at a focal depth of 3 mm. The Flex I^® plate was positioned within a water tank to reduce reflections from the bottom of the plate. A tilted acoustic absorber was placed below the Flex I^® plate to reduce acoustic reverberations within the imaging field of view. To provide a path for acoustic propagation, the wells containing the phantoms were filled with degassed, deionized water, and those containing cell-embedded collagen gels were filled with 1X DMEM with 25 mM HEPES. An acoustic standoff containing degassed, deionized water was then placed above each well.

The STL-SWEI sequence performed is briefly described as follows.^8–10 The linear array transducer was used to generate both pushing and tracking pulses each with a center frequency of 4.2 MHz. A pushing signal, consisting of two 70-μs sine-bursts separated by a pulse repetition period (PRP) of 134 μs, was applied at location P₁ [Fig. 1(C)]. The resulting shear wave was then tracked at location T, a lateral distance ΔX away from P₁ [Fig. 1(C)] using 192 tracking beams in pulse-echo mode (0.5 μs duration, 134 μs PRP).^8,9 A second pushing pulse was then applied at a different location P₂, a distance ΔP away from P₁ [Fig. 1(C)]. The resulting shear wave was tracked again at location T. This imaging sequence corresponded to one ensemble [Fig. 1(C)]. ΔP was 3.54 and 0.89 mm for gelatin phantoms and cell-embedded constructs, respectively. ΔX was 1.77 and 2.66 mm for gelatin phantoms and cell-embedded constructs, respectively. An imaging plane consisted of 40 ensembles with 0.5 mm between ensembles, thereby encompassing a lateral distance of 2 cm.

Axial tissue displacements were estimated by performing the normalized cross-correlation between pairs of consecutive tracked RF lines.^8–10 The finite difference method was used to compute the material velocity signals from the displacement estimates.^8–10 An average of ten velocity measurements was computed to improve the signal-to-noise ratio and reduce variance in shear modulus estimates. The average velocity signals associated with the two shear waves were cross-correlated to compute the difference in arrival times, ΔT, of the shear waves. Shear wave speed, c_s, was estimated as ΔP/ΔT, and the shear modulus, G, was computed as G = ρc_s², where ρ is the density of the material.^8–10 Images of shear modulus estimates were generated and overlaid onto corresponding B-scan images.

2.3. High-frequency B-scan and integrated backscatter coefficient measurements

To assess regional variations in cellular backscatter within cell-embedded collagen hydrogels, acoustic backscatter measurements were conducted immediately after STL-SWEI using a high-frequency (38-MHz, 13–47 MHz bandwidth, F-number of 3.3, −6 dB beamwidth of 170 μm) single-element, focused transducer (P150-2; Olympus, Waltham, MA).^12,13 The transducer was driven by a pulser-receiver (5073PR; Olympus), and backscattered signals were amplified and digitized using a digital oscilloscope. The transducer was translated laterally using a three-way positioner to scan an imaging plane. Neighboring RF lines in each plane were separated by 106 μm. A B-scan image was generated offline for each imaging plane by envelope detection and log compression to the backscattered signals.^12,13 Each B-scan image was used to select ROIs, and each ROI had dimensions of 8 RF lines laterally (0.85 mm) and 25 axial pulse lengths (1 mm). The integrated backscatter coefficient (IBC) of each ROI was then calculated using Eqs. (1)–(4) in Ref. 12. Parametric images of calculated IBC values, spanning the entire thickness of the gel, were generated for each imaging plane.^12,13

3. Results

To estimate shear moduli within the large, uniform gelatin phantom, imaging was performed at three independent imaging planes. B-scan and STL-SWEI of the large uniform gelatin phantom showed uniform echogenicity and shear modulus estimates, as shown within a representative ROI (1 cm axially, 2 cm laterally, 2-cm focal depth within phantom) [Fig. 2(A)]. Estimated shear modulus of the large, uniform gelatin phantom was 2.3 ± 0.13 kPa (mean ± SD).

Fig. 2.

(Color online) STL-SWEI of uniform tissue-mimicking phantoms. Shown are representative B-scan and overlaid color images of shear modulus estimates of phantoms under different configurations. (A) A large uniform, gelatin phantom imaged as in Fig. 1(A). (B) A smaller gelatin phantom (sectioned from the large phantom) placed in a tissue culture plate imaged as in Fig. 1(B). (C) The smaller gelatin phantom was removed from the tissue culture plate and submerged in a water tank and imaged. (D) The smaller phantom was placed at an angle and imaged. (E) STL-SWEI performed at the interface between the water and larger phantom. Images are representative of three separate samples. Scale bar, 4 mm.

To assess the feasibility of imaging phantoms in tissues culture plates, smaller phantoms were sectioned from the larger phantom and imaged within Flex I^® plates. B-scan imaging of small gelatin phantoms contained within wells of tissue culture plates indicated uniform echogenicity within the phantom [Fig. 2(B)]. However, parametric images of the shear modulus estimates indicated two regions of distinctly different shear moduli [Fig. 2(B)]. The mean shear modulus estimate of the deeper region was 2.2 kPa, which was comparable to the estimated shear modulus of the larger uniform phantom from which the small phantom was obtained. In contrast, the mean shear modulus estimate of the shallow region was 1.4 kPa, or ∼64% of the modulus of deeper regions.

A series of experiments were then performed to investigate the observed regional variation in shear modulus within the smaller phantom. First, the smaller phantom was removed from the Flex I^® plate, placed above an acoustic absorber in a water tank, and imaged. Shear modulus images of the small phantom either inside [Fig. 2(B)] or outside [Fig. 2(C)] the Flex I^® plate were comparable, indicating that the presence of the tissue culture plate did not affect STL-SWEI results. To determine whether there were inhomogeneities in the smaller phantom, the phantom was next inverted and imaged. The shear modulus image of the inverted phantom (data not shown) was the same as that shown in Fig. 2(C). Moreover, the shear modulus image of the small phantom placed at an angle indicated that the region with lower shear modulus estimate followed the orientation of the water-phantom interface [Fig. 2(D)]. In addition, the larger, uniform gelatin phantom was re-imaged with the transducer not directly coupled to the phantom; specifically, the transducer was in the water at a distance of 1.7 cm above the phantom. As shown in Fig. 2(E), a region of lower shear modulus now appeared in the shear modulus images at the interface between the water and the large, uniform phantom. In both small and large phantoms, the thickness of the region with lower shear moduli was comparable [Figs. 2(B) and 2(E)]. These results suggested the presence of Scholte surface waves^11,14 generated at the fluid-phantom interface after acoustic radiation force excitation, leading to an underestimation of the shear modulus near the interface.

To investigate how Scholte surface waves confounded shear modulus estimates at the solid/fluid interface, material velocity wave profiles were analyzed at different depths within small phantoms contained within tissue culture plate wells (Fig. 3). Each material velocity profile represents the axial component of the material velocity as a function of the time it took for the shear wave to propagate from the region of excitation to the tracking location. The material velocity profiles corresponding to the propagating shear wave generated by the first (P₁) and second (P₂) acoustic radiation force excitations are denoted by the blue and red curves, respectively [Fig. 3(B)–3(D)]. Material velocity wave profiles corresponding to a location within deeper regions of the phantom show that the time difference between the peaks of the waves is 1.2 ms [Fig. 3(B)]. Wave profiles corresponding to a location within shallower regions show that the time duration between wave peaks is longer (1.5 ms) [Fig. 3(C)], resulting in an estimated wave speed that is ∼80% of that at deeper regions [Fig. 3(B)]. Theoretically, the speed of Scholte waves is 84% that of shear waves (using theorems 2 and 7 in Ref. 14), which is in close agreement with our experimental results. This is consistent with the observed decrease in shear modulus estimate by 36% near the fluid/solid interface because of the squared relationship between the shear wave speed and shear modulus. Interestingly, the material velocity profiles corresponding to the transition point between the shallow (low modulus) and deeper (high modulus) regions show two peaks associated with each material velocity profile (Fig. 3D). The first peak in each profile occurs at the same time as those in the deeper region, i.e., 2.2 and 3.4 ms for the P₁ and P₂ excitations, respectively. The second peak in each profile occurs at the same time as those in the shallow region, i.e., 3.2 and 4.7 ms for the P₁ and P₂ excitations, respectively. These results suggest that Scholte waves are generated at the water-phantom interface after each acoustic radiation force excitation. The relative amplitude of the Scholte wave compared to the shear wave is dependent on the depth within the sample; the Scholte wave amplitude decreases exponentially with increasing depth.¹⁴ The Scholte wave is more prominent in the shallow region near the fluid/solid interface, whereas the true shear wave is more prominent at deeper regions within the sample. The sharp transition in the estimated shear modulus with increasing depth was observed because the arrival time of the wave at the tracking location was computed based on the global peak of the material velocity signal corresponding to each wave (Fig. 3). The transition with increasing depth occurred when the peaks of the shear wave exceeded those of the Scholte waves [Figs. 3(B)–3(D)].

Fig. 3.

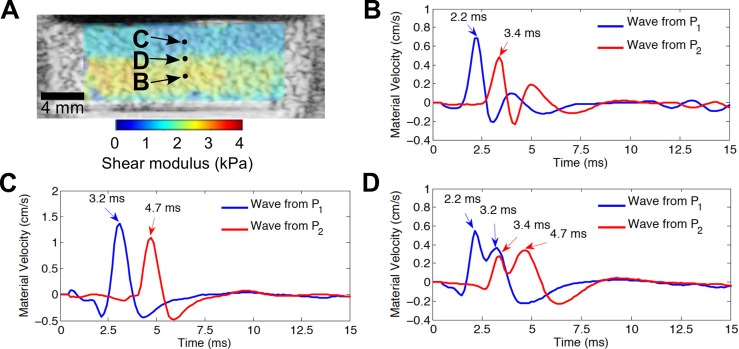
(Color online) Profiles of waves propagating within phantom. (A) B-scan and overlaid shear modulus images of a uniform gelatin phantom in a tissue culture plate. Wave profiles are presented as the axial component of the material velocity as a function of the time it took for the wave to propagate laterally from the region of excitation to the tracking location. Wave profiles corresponding to (B) a location within the deeper region with higher shear modulus estimates, (C) a location within the shallow region with lower shear modulus estimates, and (D) the transition point between the shallow region and the deeper region. Blue and red curves correspond to profiles of the propagating waves generated by the first acoustic radiation force excitation at location P₁ and the second acoustic radiation force excitation at location P₂, respectively. Results are representative of three separate samples.

STL-SWEI was then performed on cell-embedded collagen constructs contained within the wells of a Flex I^® plate. Shear modulus images of a representative cell-embedded collagen gel are shown in Fig. 4(A) for an imaging plane (8 mm from the gel center). Regions near the top 1.6 mm of the gel had shear modulus estimates of 0.10 ± 0.03 kPa (mean ± SD) averaged over four imaging planes, while the deeper regions (1.6 to 4.5-mm depths) had shear modulus estimates of 0.16 ± 0.02 kPa. Thus, shear modulus estimates of the region near the fluid/solid interface were ∼63% that of deeper regions, similar to those results obtained for gelatin phantoms in Flex I^® plates (Fig. 2). Material velocity profiles at various depths within the cell-embedded collagen gels (data not shown) exhibited the same trends as those of the gelatin phantoms (Fig. 3). Corresponding high-frequency B-scan images and parametric images of the IBC [Fig. 4(B)] of cell-embedded collagen hydrogels indicated a uniform distribution of cell scatterers in the imaging plane, indicating that observed differences in shear moduli were not attributable to a greater presence of cells in the deeper regions compared to the shallow regions.

Fig. 4.

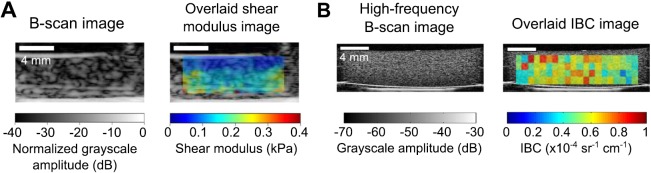
(Color online) STL-SWEI of cell-embedded collagen hydrogels. (A) Shown are representative B-scan and overlaid shear modulus images of a cell-embedded hydrogel obtained at an imaging plane at 8 mm from the gel center. (B) High-frequency (38 MHz) B-scan image and overlaid parametric image of the IBC at the same imaging plane shown in (A). Images are representative of three separate samples. Scale bar, 4 mm.

4. Discussion

Ultrasound elastography holds potential as a non-destructive, non-invasive tool to evaluate the mechanical properties of engineered tissues during their fabrication and development.¹⁵ This work investigated the feasibility of using STL-SWEI to quantify shear moduli of tissue mimicking phantoms and 3-D engineered tissues under standard tissue engineering environments. Results indicated that the generation of Scholte surface waves at the fluid/solid interface can confound the estimation of shear modulus near the interface. However, shear modulus estimates of regions away from the interface were within the expected range of shear moduli. Effects of Scholte waves may also have important implications for acoustic radiation force-based elasticity imaging of native tissues in vivo when fluid-tissue interfaces are present, such as in the heart or blood vessels.