Abstract
We present results of a pulsed dynamic nuclear polarization (DNP) study at 0.35 T (9.7 GHz/14.7 MHz for electron/1H Larmor frequency) using a lab frame-rotating frame cross polarization experiment that employs electron spin locking fields that match the 1H nuclear Larmor frequency, the so called NOVEL (nuclear orientation via electron spin locking) condition. We apply the method to a series of DNP samples including a single crystal of diphenyl nitroxide (DPNO) doped benzophenone (BzP), 1,3-bisdiphenylene-2-phenylallyl (BDPA) doped polystyrene (PS), and sulfonated-BDPA (SA-BDPA) doped glycerol/water glassy matrices. The optimal Hartman-Hahn matching condition is achieved when the nutation frequency of the electron matches the Larmor frequency of the proton, ω1S = ω0I, together with possible higher order matching conditions at lower efficiencies. The magnetization transfer from electron to protons occurs on the time scale of ∼100 ns, consistent with the electron-proton couplings on the order of 1-10 MHz in these samples. In a fully protonated single crystal DPNO/BzP, at 270 K, we obtained a maximum signal enhancement of ε = 165 and the corresponding gain in sensitivity of due to the reduction in the buildup time under DNP. In a sample of partially deuterated PS doped with BDPA, we obtained an enhancement of 323 which is a factor of ∼3.2 higher compared to the protonated version of the same sample and accounts for 49% of the theoretical limit. For the SA-BDPA doped glycerol/water glassy matrix at 80 K, the sample condition used in most applications of DNP in nuclear magnetic resonance, we also observed a significant enhancement. Our findings demonstrate that pulsed DNP via the NOVEL sequence is highly efficient and can potentially surpass continuous wave DNP mechanisms such as the solid effect and cross effect which scale unfavorably with increasing magnetic field. Furthermore, pulsed DNP is also a promising avenue for DNP at high temperature.
INTRODUCTION
Dynamic nuclear polarization (DNP) is a process whereby the large polarization present in an electron spin reservoir of a paramagnetic polarizing agent is transferred via microwave irradiation to nuclei, thereby enhancing the nuclear spin polarization. The initial mechanism supporting the DNP process, the Overhauser effect (OE), was proposed in 19531 and confirmed experimentally2,3 in samples with mobile electrons (i.e., metals, solutions, and 1D conductors). In contrast, in insulating solids, such as glycerol/water glasses and biological samples, the OE was thought to be forbidden, but we have recently observed Overhauser enhancements using polarizing agents with narrow EPR spectra that exhibit strong 1H − e− hyperfine couplings.4 Furthermore, in these sorts of samples, DNP processes can also be mediated by three other mechanisms – the solid effect (SE),5,6 the cross effect,7–11 and/or thermal mixing.12
Initially, the primary application of DNP was preparation of polarized targets for neutron scattering experiments;13 however, over the past decade, DNP has been used extensively to enhance the inherently low sensitivity of nuclear magnetic resonance (NMR) signals.14–19 Enhancements on the order of 102 − 103 were made possible via the solid effect using narrow-line radicals20–23 and cross effect using biradicals24–27 as polarizing agents and high frequency gyrotrons as microwave sources.28–30 The latter operate in the 140-560 GHz regime and enable DNP to be performed at magnet field strengths used in contemporary NMR experiments (5-20 T).
All of the DNP mechanisms mentioned above employ continuous wave (CW) microwave irradiation. In addition, all of them, except for the OE in insulating solids, scale unfavorably with the magnetic field, displaying a field dependence where n ∼ 1-2 or larger. Thus, for DNP to be successful at high magnetic fields and broadly applicable, a strategy to overcome this deficiency is required. An analogous situation existed in the early 1970s in solution NMR where 1H-13C nuclear Overhauser enhancements were shown to vanish above 60-100 MHz 1H frequencies, and therefore it was predicted that high fields would not be useful for 13C protein NMR.31 The development of J-mediated transfers, in particular, the insensitive nuclei enhanced by polarization transfer (INEPT) pulsed experiment, circumvented this problem because it is field-independent.32 Similarly, time domain DNP experiments are, in principle, field-independent, and, when the instrumentation becomes available, they can be performed efficiently at high Zeeman fields.
To date, there are a handful of sequences for pulsed DNP including nuclear orientation via electron spin locking (NOVEL),33 the integrated solid effect (ISE),34 DNP in the nuclear rotating frame (NRF) DNP,35 and dressed state solid effect (DSSE).36 Neither NRF DNP nor DSSE requires a strong microwave field. NRF DNP is essentially solid effect in the NRF instead of the nuclear lab frame. The mixing of state is inversely proportional to the radio frequency (RF) field instead of the B0 field. The sensitivity gain in NRF DNP is the result of the ability to recycle the NMR experiment at the rate of the nuclear T1ρ instead of the nuclear T1. DSSE utilizes an off-resonance RF field to drive the polarization transfer. The matching condition requires that the RF field is applied off-resonance and the resonance offset is governed by the isotropic hyperfine coupling as well as the microwave field strength.
Both NOVEL and ISE, on the other hand, rely on the Hartman-Hahn matching condition between the electron rotating frame and the nuclear lab frame and thus require strong microwave field strengths. Similar to cross polarization in NMR, the polarization transfer is driven by the dipolar coupling, which is typically on the order of MHz, resulting in a short sub-microsecond contact time. Both sequences were originally developed for neutron spin polarizer experiments using short-lived photoexcited triplet states. In these experiments, NOVEL showed very modest efficiency. An enhancement of ∼10 was obtained for 29Si in uniaxially stressed silicon doped with boron acceptors,33 and ε ∼ 200 was observed for 1H using a photoexcited triplet state of pentacene doped naphthalene.37 In both cases, the efficiency is less than 1%. NOVEL was soon replaced by ISE which gives a much higher efficiency due to the adiabatic sweep of the magnetic field.34,38–40 Note that both of these samples were especially chosen to demonstrate the NOVEL or ISE effect. Thus, one of our goals in the results reported here was to investigate the potential of the NOVEL sequence in samples used in current applications of DNP in NMR, i.e., samples doped with a few tens of mM of stable free radicals such as the narrow-line species 1,3-bisdiphenylene-2-phenylallyl (BDPA) or nitroxides, both of which are used in contemporary CW DNP experiments. We found that enhancements on the order of 102 can be obtained on these samples. For example, we obtained an enhancement of 323 corresponding to 49% efficiency in a sample of partially deuterated polystyrene (PS) doped with 2% BDPA. Our results suggest that pulsed DNP NOVEL is an excellent candidate for DNP at high field and high temperature.
BACKGROUND
In this section, we derive the matching condition that will be used in our discussion (vide infra). To this end, it is sufficient to consider a 2-spin system consisting of nuclear spin I and electron spin S. For an extensive theoretical discussion of the NOVEL sequence, readers are directed to the papers by Henstra and Wenckebach.41,42 In the lab frame, the Hamiltonian for the NOVEL experiment has the form
| (1) |
wherein the first two terms are the Zeeman interactions; the third is the electron-nuclear interaction; and the fourth is the microwave spin lock field. Upon transforming to the microwave rotating frame using the following operator
| (2) |
the Hamiltonian is truncated to
| (3) |
where ΩS is the microwave offset
| (4) |
Transformation to the tilted frame is achieved with the operator
| (5) |
where the angle θ is defined as
| (6) |
The Hamiltonian is transformed to
| (7) |
where
| (8) |
The sign of ωeff depends on the phase as well as the offset of the microwave.
Next, we redefine the transverse axes of the nuclear spin by the following transformation:
| (9) |
where the angle ϕ is defined as
| (10) |
Leading to the Hamiltonian
| (11) |
where A and B are secular and pseudo-secular hyperfine coupling constants, respectively,
| (12) |
| (13) |
Using perturbation theory, we can separate the Hamiltonian
| (14) |
wherein the unperturbed Hamiltonian H0 and the perturbation H1 are given as
| (15) |
| (16) |
Using the direct product basis set,
| (17) |
As usual we define the subspace spanned by and as the double quantum (DQ) subspace and that spanned by and as the zero quantum (ZQ) subspace. In the NOVEL experiment, the inter-subspace splitting is approximately ω0I, which is very large compared to the perturbation even at a magnetic field as low as 0.35 T. On the other hand, if the matching condition is fulfilled, states in the either DQ or ZQ subspace are degenerate, resulting in a complete intra-subspace state mixing as a result of the perturbation and, thus, the polarization transfer. The perturbation can be truncated to contain only DQ (flip-flip) and ZQ (flip-flop) terms as the following:
| (18) |
For the positive ωeff, the degeneracy in the DQ subspace leads to the matching condition
| (19) |
If the microwave offset is negligible, the matching condition is simplified to
| (20) |
and the nuclear Larmor frequency equals the Rabi frequency of the electron. In other words, the nutation of the nucleus in the laboratory frame matches that of the electron in the rotating frame. We note that Hartmann and Hahn also mentioned the possibility of this type of rotating frame-laboratory frame cross polarization.43
EXPERIMENTAL
Samples
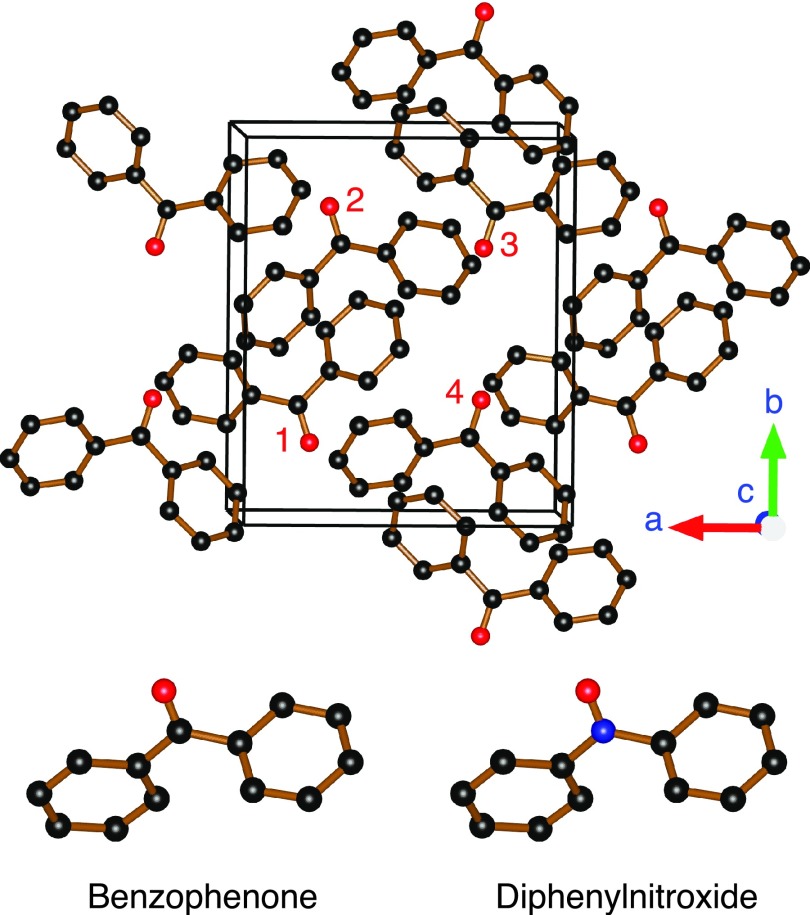
Preparation of samples containing 2% BDPA (weight ratio) doped in PS and 40 mM sulfonated-BDPA (SA-BDPA) doped in glycerol/water glassy matrices is described elsewhere.4 Single crystals of benzophenone (BzP) doped with diphenylnitroxide (DPNO) were grown from ethanol upon slow evaporation. 12 mg of 10% DPNO stock (courtesy of Dr. Tien-Sung Lin, Washington University, St. Louis) and 188 mg of BzP (Sigma Alrdrich) were dissolved in 1 g of ethanol. The final sample contained 0.6% or 40 mM of the DPNO radical which is similar to the concentrations normally used in DNP applications.14,17–19 Single crystals were harvested and polished to fit into a quartz capillary of 0.4 mm inner diameter for experiments at 5 T. For experiments at 0.35 T, a larger sample that fit into a 4 mm EPR sample tube was used. In order to suppress the 1H NMR signal from trapped solvent, we used perdeuterated ethanol (Cambridge Isotope). Figure 1 shows the crystal structure of BzP according to Fleischer et al.45 BzP has an orthorhombic structure with the P212121 space group and therefore four molecules per unit cell. The similarity in the molecular structures of BzP and DPNO (Figure 1) allows DPNO to substitute into the host crystal of BzP with negligible perturbation.46,47 Figure 1 was generated using VESTA software.44
FIG. 1.
(Top) Crystal structure of benzophenone. The crystal has space group symmetry P212121 with four molecules per unit cell. Molecules 1–4 are of the same unit cell represented by the rectangular parallelepiped. Molecules 2–4 are 180° rotated about the crystallographic a, b, and c axes, respectively, with respect to molecule 1. (Bottom) Molecular structures of benzophenone (left) and diphenylnitroxide (right) with oxygen atoms in red, nitrogen in blue, and carbon atoms in black. The figure was rendered in VESTA software.44
Experiments
Experiments at 5 T were carried out on a homebuilt pulsed DNP/EPR/NMR spectrometer operating at 5 T or 140 GHz/211 MHz of electron/1H Larmor frequency.22 Experiments at 0.35 T were performed on a Bruker ElexSys E580 X-band EPR spectrometer using an EN 4118X-MD4 pulsed ENDOR resonator. The RF coil of the probe also serves as the NMR sample coil upon the integration of a module of tuning and matching capacitors. The RF excitation and detection of NMR signals were done with an iSpin-NMR spectrometer purchased from Spincore Technologies, Inc. (Gainesville, FL, US). The 1H NMR signals were acquired via a solid echo sequence with 8-step phase cycling. The signals were processed using a custom-built MATLAB program.48
RESULTS
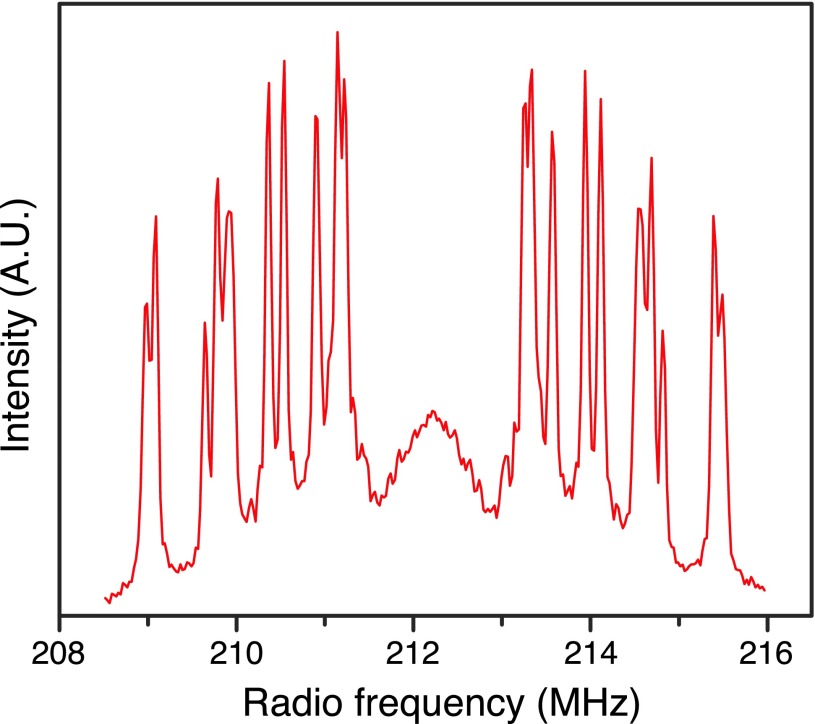
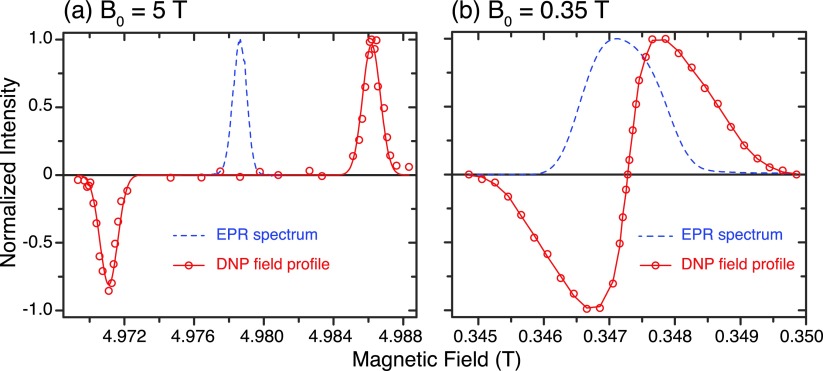
The quality of the single crystals is best assessed using high frequency EPR techniques as it allows observation of any inhomogeneity in the g value due to imperfections in the single crystal. Figure 2 shows the Davies ENDOR spectrum obtained from a single crystal grown from 90% BzP-d10/10% BzP-h10 doped with DPNO at 5 T. Even though the exact orientation of the crystal was not determined, it is certain that the magnetic field lies in the crystallographic ab-plane. The deuteration of the sample suppresses the contribution from matrix protons, which permits the observation of all ten pairs of sharp resonances from ten protons of each DPNO molecule. Figure 3(a) presents the EPR spectrum and the 1H DNP field profile from a sample with 94% 13C carbonyl labeled BzP-h10. In this case, the crystal was orientated such that B0 is aligned with the crystallographic b-axis. Thus, the EPR spectrum displays one sharp peak corresponding to gxx = 2.0091 with four-fold degeneracy, a result that is consistent with a previous study.46 The DNP field profile is indicative of a well-resolved solid effect.
FIG. 2.
Davies ENDOR spectrum of a single crystal of 90% deuterated BzP doped with 0.6% DPNO at 5 T and 80 K. The magnetic field lies in the ab crystallographic plane. Ten pairs of sharp peaks correspond to ten 1H’s on DPNO molecule.
FIG. 3.
EPR spectrum (dashed blue) and DNP field profile (red) of single crystal DPNO/BzP at 5 T (a) and 0.35 T (b). The magnetic field B0 is along the crystallographic b-axis of the crystal; thus, the EPR spectra contain only one peak with four-fold degeneracy. The DNP field profile at 5 T shows a well-resolved solid effect as opposed to an unresolved solid effect at 0.35 T. The maximum enhancement is 330 at 0.35 T and remains unknown at 5 T. Experiments at 5 T were performed at 80 K, whereas experiments at 0.35 T were performed at 270 K.
Figure 3(b) shows the echo detected EPR spectrum and the 1H DNP field profile of a single crystal DPNO/BzP at 0.35 T. Again, the crystallographic b-axis of the crystal was aligned with B0. The spectrum exhibits a linewidth of 8.6 G due to unresolved hyperfine couplings, consistent with previous studies on similar samples.46,47 The b-axis was chosen because of the narrow EPR linewidth, allowing more efficient microwave excitation.
The 1H DNP field profile in Figure 3(b) was obtained at the microwave field strength of ω1S = 2.4 MHz and microwave frequency of ω0S = 9.7224 GHz. The DNP enhanced 1H NMR signal was measured as a function of the B0 field. The enhancement is defined as . The DNP field profile resembles an unresolved solid effect in which the EPR linewidth (24 MHz) is greater than the Larmor frequency of 1H (14.7 MHz), but smaller than twice that frequency. Despite the overlap between the positive and negative solid effects, the maximum enhancement was as high as 330 due to the extensive state mixing present at low magnetic field. For subsequent pulsed DNP experiments, the magnetic field was carefully adjusted to the exact center of the field profile to avoid contribution of the SE in the DNP enhancement.
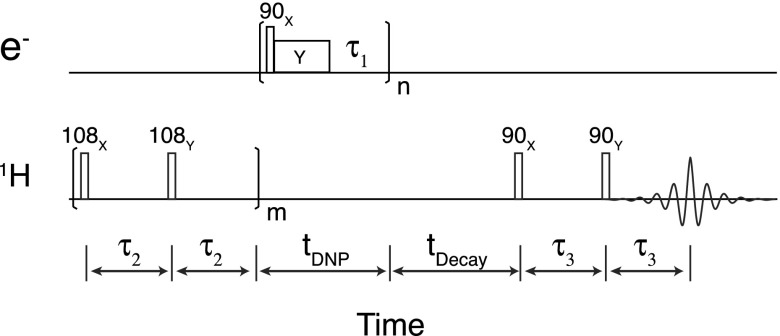
Figure 4 shows the pulse sequence for NOVEL experiment. After a period of 1H presaturation, the magnetization of 1H builds up with (on signal) or without (off signal) microwave pulses. For the solid effect DNP, the microwave pulses are simply a continuous wave irradiation. On the other hand, for NOVEL experiment, a sequence consisting of a 90° flip pulse, a spin lock pulse (mixing time), and a delay is applied repeatedly. The buildup time constant TB of the DNP enhanced NMR signal is measured by varying the length of the buildup period. The T1 relaxation of 1H is obtained by varying the decay period that follows buildup.
FIG. 4.
Timing scheme for NOVEL pulsed DNP. After a period of presaturation, the magnetization of 1H build ups for a period of tDNP. The decay period can be used to measure the T1 of protons. The DNP enhanced 1H signal is then read out by a solid echo sequence. The fixed parameters include τ2 = 5 ms, m = 8, and τ3 = 20 μs. Other parameters such as the mixing time (tmix or the length of the microwave Y pulse) and the repetition time (essentially τ1) were optimized as described in Figure 5.
For the pulsed DNP NOVEL sequence, the microwave field strength, the mixing time (the length of the microwave Y pulse in Figure 4), and the repetition time (essentially τ1 in Figure 4) require optimization. The microwave field strength was calibrated by measuring the nutation frequencies at different microwave power levels. Data illustrating the optimization of the mixing time and the repetition time are given in Figure 5 for a DPNO/BzP sample with the microwave field strength set to ∼14.7 MHz. In Figure 5(a), we varied the mixing time, which reveals a rapid increase in the signal intensity after ∼100 ns, followed by a slower progression. We then measured the signal as a function of the repetition time at different mixing times ranging from 50 ns to 2 μs at 270 K (Figure 5(b)). At this temperature, we were only able to observe the decay of the signal with respect to the repetition time. As we lowered the temperature to 150 K (Figure 5(c)), we could clearly see the maxima at ∼130 μs of repetition time. At 270 K, the optimum conditions were τmix ∼ 100 ns and τ1 = 40 μs of repetition time. Longer locking pulses required a longer repetition time subject to the 1% duty cycle available with the traveling-wave tube (TWT) amplifier, leading to lower DNP efficiency. Overall, we obtained a higher enhancement at 270 K. The same optimizations were performed on BDPA/PS sample at 300 K (data not shown), yielding a τmix ∼ 150 ns and τ1 = 36 μs.
FIG. 5.
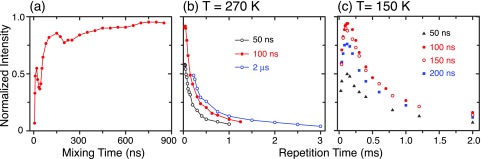
Optimization of the NOVEL pulse sequence in DPNO/BzP. (a) The signal intensity increases quickly after τmix ∼ 100 ns and exhibits a transient oscillation. Both features are consistent with the electron-1H dipolar coupling in the order of 1-10 MHz. Optimization in terms of the repetition time (essentially τ1) at 270 K (b) and 150 K (c) with different mixing times. At 270 K, we observed mostly the decay of the signal with respect to the repetition time. At 150 K, the signal intensity reached the maxima at ∼130 μs of repetition time.
Figure 6(a) reveals the enhancement obtained via the NOVEL sequence as a function of ω1S in a fully protonated BzP single crystal doped with 0.6% DPNO at 270 K. The matching condition clearly occurs at ω1S = ω0I ≈ 14.7 MHz and an enhancement of up to 165 is observed (Figure 6(b)). The TB and T1 time constants are given in Figure 6(c). Figures 7 and 8 show the enhancement obtained in BDPA/PS at 300 K and SA-BDPA in glycerol-d8/D2O/H2O at 80 K.
FIG. 6.
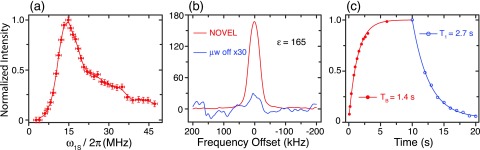
(a) Matching condition of the NOVEL pulse sequence in a DPNO/BzP sample at 270 K. The enhancement was measured as a function of the microwave field strength. The spin lock pulse is fixed to 100 ns, whereas the length of the flip pulse is adjusted to give a 90° tip angle. The matching occurs at ω1S = ω0I. (b) 1H spectra with (red) and without (blue) DNP. For the DNP enhanced spectrum, the sample was polarized for 10 s with a 16 ns flip pulse followed by a 100 ns spin lock pulse. The repetition time was 40 μs. The off spectrum was obtained with 10 s of recovery time. The enhancement in signal intensity was ε = 165. The intensities were normalized to the μw off signal. (c) DNP buildup time constant TB using NOVEL pulse sequence and the spin-lattice relaxation time constant T1. Reduction in the buildup time constant results in a sensitivity gain of .
FIG. 7.
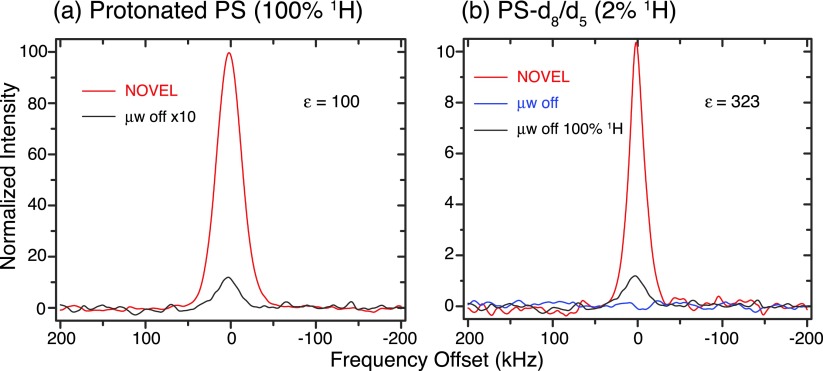
NOVEL experiments in BDPA/PS samples at 300 K using 150 ns mixing and 36 μs repetition time. (a) In a fully protonated sample, we obtained an enhancement of 100. (b) In a sample with mixed PS-d8/d5 (95:5), the 1H concentration is diluted by a factor of 50, making it impossible to acquire the off signal in a reasonable amount of time. We, therefore, estimate the enhancement in the sample using the off signal of the fully protonated sample as the reference. Taking into account the dilution factor and the amount of sample, we obtained an enhancement of 323. The intensities were normalized to the μw off signal from protonated PS sample.
FIG. 8.
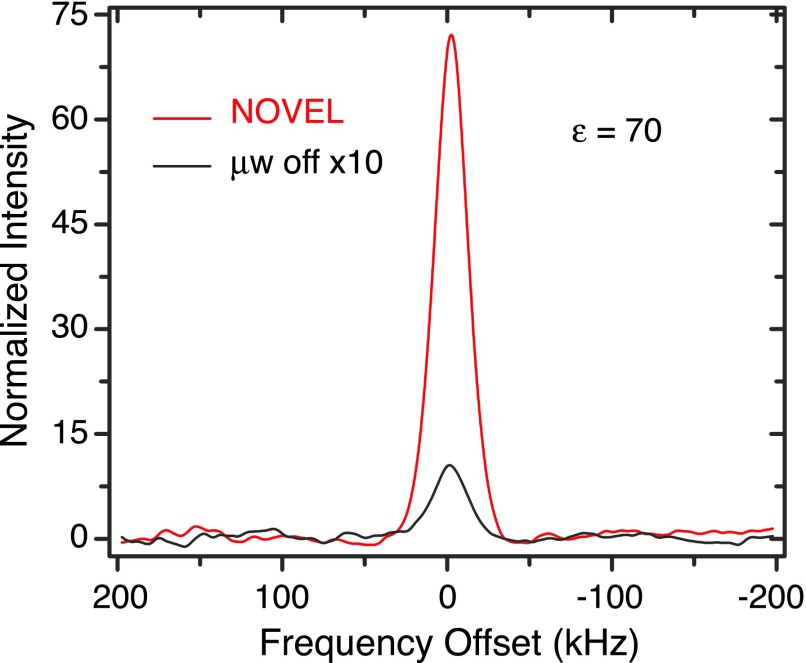
NOVEL experiments in glycerol-d8/D2O/H2O glassy matrix doped with 40 mM SA-BDPA at 80 K. The DNP enhanced signal was obtained using 150 ns mixing time, 8 ms of repetition time, and 24 s of DNP buildup time. The enhancement is 70.
DISCUSSION
In DNP experiments using a free radical dopant, the theoretical limit for the enhancement is given by the ratio γe/γn which is ∼658 for 1H. The enhancement of 165 (Figure 6(b)) that we obtained in a protonated sample of DPNO/BzP corresponds to 25% of the theoretical efficiency. We attribute the improvement in the efficiency over previous studies to the increase in the radical concentration as well as the narrow EPR linewidth. In the original study by Henstra33 on uniaxially stressed boron-doped silicon, the acceptor concentration was 1017 cm−3 or 0.16 mM which is about two orders of magnitude more dilute than that used in contemporary DNP experiments.14 Moreover, the EPR linewidth was 60 MHz compared to 24 MHz in our case, resulting in lower excitation efficiency. In another example of naphthalene doped with pentacene,37 excited triplet states are created by laser irradiation. In such a case, the concentration of electron is limited by both the dopant concentration (<5 mM) and the efficiency of the optical excitation (<5%).
The enhancement that we obtained is, to some degree, limited by the 1% duty cycle of the TWT microwave amplifier. Figure 5(c) shows the dependence of the enhancement on the repetition time in DPNO/BzP sample at 150 K. The enhancement increases quickly and then decays. We attribute this observation to two competing factors including the electron spin-lattice relaxation and the number of times that electrons transfer magnetization to protons. At 270 K (Figure 5(b)), we only observed the decay of the signal as a result of the short electron T1 and the limitation in the duty cycle of the TWT amplifier. Nevertheless, we obtained a higher enhancement at 270 K. The NOVEL sequence was originally developed for short-lived photo excited triplet states, which requires fast polarization transfer and allows fast repetition. It partially explains why the sequence works well at high temperature where the short T1e gives rise to a larger number of polarization transfer events per unit time or, in other words, a faster recycling of the electron polarization. Furthermore, a short T1e reduces the saturation of the electron polarization. A similar effect was reported20,21 for the solid effect even though the microwaves were off-resonance. For the NOVEL sequence, such an effect might be more detrimental because the microwaves are on-resonance with the EPR transitions.
Despite the limitation in the duty cycle of the TWT amplifier, we have obtained an unprecedented high DNP efficiency in fully protonated samples: 165 in DPNO/BzP at 270 K (Figure 6(b)) and 100 in BDPA/PS at 300 K (Figure 7(a)). Furthermore, partial deuteration of the BDPA/PS sample, leaving 2% protons, results in an enhancement of 323, which is a ∼3.2-fold improvement and corresponds to 49% efficiency (Figure 7(b)). It is worth noting that in quasi-equilibrium (infinite mixing time), the efficiency of a non-adiabatic cross polarization from 1H to other nuclei in a static sample is 50% and the maximum of the transient oscillation is less than 75%.49 We expect a similar upper bound for the efficiency of the NOVEL sequence. The efficiency of 49% is, therefore, very close to the optimum value and, to the best of our knowledge, is the highest efficiency reported for NOVEL sequence.
The mixing time dependence curve of both the DPNO/BzP (Figure 5(b)) and BDPA/PS (not shown) displays the characteristics of a dipolar driven cross polarization process. In DPNO/BzP, the intensity increases rapidly after ∼100 ns, in good agreement with the electron-1H couplings up to ∼10 MHz.46,47,50 Similarly, for BDPA/PS, the corresponding mixing time is ∼150 ns, consistent with a somewhat weaker coupling of ∼5.5 MHz in BDPA.51,52 After the quick rise, the curve exhibits a transient oscillation due to the dipolar coupling which is another characteristic of a cross polarization experiment, a result that has also been observed previously in NOVEL experiments.37
The matching conditions in both DPNO/BzP (Figure 6(a)) and BDPA/PS (not shown) show a maximum at ∼14.7 MHz and a long tail extending well beyond 3 ω0I. The feature at high microwave field strength was first observed in naphthalene doped with pentacene-h14,37 and recently in naphthalene doped with pentacene-d14.39 However, in both cases, the tail ended well below 2 ω0I. We think that our observation is likely the result of high order processes involving one electron and multiple protons as suggested by Eichhorn et al.39 Another possibility is that at ω1S > ω0I, not only the EPR transitions but also the double quantum and zero quantum transitions are excited by the microwaves. The details of the DNP process in this regime are then dependent on relaxation. In both scenarios, the feature at high microwave power is a first order perturbation effect which should vanish at higher magnetic fields.
We notice the reduction of the buildup time constant of the 1H polarization during DNP compared to the nuclear spin-lattice relaxation (Figure 6(c)). This behavior was observed for the SE at 5 T.20–22 The short TB enables a faster recycle of NMR experiment, resulting in a net gain in sensitivity of for the DPNO/BzP sample. We explain this by the fact that both SE and NOVEL are 2-spin processes; the same semi-classical rate equation treatment used for the SE can, therefore, be applied to the NOVEL experiment. In this treatment, the DNP effect is encoded in a DNP rate constant that acts to increase the buildup rate of the NMR signal, thus, shorten the buildup time constant. This effect has only been observed in the case of large enhancement corresponding to large differentiation between T1 and TB.
At 0.35 T, the solid effect outperforms NOVEL DNP by a factor of ∼2 (330 vs. 165 for DPNO/BzP and 200 vs. 100 for BDPA/PS). As the magnetic field increases, the efficiency of the SE decreases rapidly as predicted by theory and also observed in experiments.4,17,19,53 Pulsed DNP, in general, and the NOVEL experiment, in particular, do not depend on the B0. An analogy is that cross polarization is operating at all magnetic fields in solid state NMR. We predict that at magnetic fields of 0.5 T and above, NOVEL DNP would surpass the SE. With the recent advances in the gyroamplifier technology, 54–56 we anticipate that pulsed DNP will become available at high magnetic fields in the near future. Furthermore, current applications of CW DNP in NMR require operation at cryogenic temperatures, which imposes limitations in many cases. Our results suggest the issue can be circumvented using NOVEL pulse sequence.
Finally, we implemented the NOVEL pulse sequence on a sample containing 40 mM SA-BDPA in a glycerol-d8/D2O/H2O (60/30/10 volume ratio) glassy matrix at 80 K, the sample conditions frequently used in current applications of DNP in NMR. Figure 8 shows the NMR signal obtained with and without NOVEL. The mixing time was set to 150 ns, the same as what we used for BDPA/PS, because the sulfonation process retains all the protons that are strongly coupled to the electron in BDPA.57 The repetition time was optimized at 8 ms due to longer T1e at 80 K. We obtained an enhancement of 70. The long repetition time allows longer mixing time. However, as seen in Figure 5(a), the enhancement almost reaches maximum at 150 ns of mixing time. Using a mixing time of up to 8 μs results in a slight increase (∼10%) in the enhancement.
CONCLUSIONS
In summary, we demonstrate that pulsed DNP via the NOVEL sequence is highly efficient under sample conditions that are currently used for contemporary DNP/NMR applications despite the limitation in the duty cycle of the TWT microwave amplifier. Except for the repetition time that is subject to the duty cycle of the TWT, all other parameters including the matching condition, the mixing time, and the polarizing time are fully optimized. The mixing time and the transient oscillation in the mixing time dependence curve are consistent with a dipolar driven cross polarization process. In a fully protonated single crystal DPNO/BzP, at 270 K, we obtain an enhancement of 165 which is 25% of the theoretical limit. Reduction in the buildup time constant of the NMR signal under DNP gives rise to a net gain in sensitivity of 230. By partially deuterating the BDPA/PS sample, we obtained an enhancement of 323 at 300 K, corresponding to 49% efficiency. We also observed a significant enhancement in a sample containing 40 mM SA-BDPA in a glycerol/water glassy matrix at 80 K. We believe that the NOVEL pulse sequence is a strong candidate for pulsed DNP NMR at high fields. Since this method does not have field dependence, time domain DNP at high field could lead to larger enhancements than the CW counterparts such as the solid effect and cross effect. Finally, we note that NOVEL sequence can operate in a wide range of temperatures and, in some cases, favorably at room temperatures.
Acknowledgments
This research was supported by grants to R.G.G. from the National Institutes of Biomedical Imaging and Bioengineering, Grant Nos. EB-002804 and EB-002026 and to T.M.S. from the National Institutes of Health of General Medical Sciences, Grant No. GM095843. We thank Dr. Ralph Weber (Bruker BioSpin, Billerica, MA), Dr. Thomas Pratum (Western Washington University, Bellingham, WA), Ajay Tharkar, and Jeff Bryant for technical assistances. We are grateful to Dr. Albert A. Smith for helping with the ENDOR experiment at 5 T and Qing Zhe Ni for insightful discussions.
REFERENCES
- 1.Overhauser A. W., Phys. Rev. 92, 411 (1953). 10.1103/PhysRev.92.411 [DOI] [Google Scholar]
- 2.Carver T. R. and Slichter C. P., Phys. Rev. 92, 212 (1953). 10.1103/PhysRev.92.212.2 [DOI] [Google Scholar]
- 3.Carver T. R. and Slichter C. P., Phys. Rev. 102, 975 (1956). 10.1103/PhysRev.102.975 [DOI] [Google Scholar]
- 4.Can T. V., Caporini M. A., Mentink-Vigier F., Corzilius B., Walish J. J., Rosay M., Maas W. E., Baldus M., Vega S., Swager T. M., and Griffin R. G., J. Chem. Phys. 141, 064202 (2014). 10.1063/1.4891866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Abragam A. and Proctor W. G., C. R. Acad. Sci. 246, 2253 (1958). [Google Scholar]
- 6.Erb E., Motchane J. L., and Uebersfeld J., C. R. Acad. Sci. 246, 2121 (1958). [Google Scholar]
- 7.Kessenikh A. V., Lushchikov V. I., Manenkov A. A., and Taran Y. V., Sov. Phys. - Solid State 5, 321 (1963). [Google Scholar]
- 8.Kessenikh A. V., Manenkov A. A., and Pyatnitskii G. I., Sov. Phys. - Solid State 6, 641 (1964). [Google Scholar]
- 9.Hwang C. F. and Hill D. A., Phys. Rev. Lett. 18, 110 (1967). 10.1103/PhysRevLett.18.110 [DOI] [Google Scholar]
- 10.Hwang C. F. and Hill D. A., Phys. Rev. Lett. 19, 1011 (1967). 10.1103/PhysRevLett.19.1011 [DOI] [Google Scholar]
- 11.Wollan D. S., Phys. Rev. B: Condens. Matter Mater. Phys. 13, 3671 (1976). 10.1103/PhysRevB.13.3671 [DOI] [Google Scholar]
- 12.Wind R. A., Duijvestijn M. J., van der Lugt C., Manenschijn A., and Vriend J., Prog. Nucl. Magn. Reson. Spectrosc. 17, 33 (1985). 10.1016/0079-6565(85)80005-4 [DOI] [Google Scholar]
- 13.Abragam A. and Goldman M., Nuclear Magnetism: Order and Disorder (Clarendon Press, Oxford University Press, Oxford, New York, 1982). [Google Scholar]
- 14.Ni Q. Z., Daviso E., Can T. V., Markhasin E., Jawla S. K., Swager T. M., Temkin R. J., Herzfeld J., and Griffin R. G., Acc. Chem. Res. 46, 1933 (2013). 10.1021/ar300348n [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rossini A. J., Zagdoun A., Lelli M., Lesage A., Coperet C., and Emsley L., Acc. Chem. Res. 46, 1942 (2013). 10.1021/ar300322x [DOI] [PubMed] [Google Scholar]
- 16.Tycko R., Acc. Chem. Res. 46, 1923 (2013). 10.1021/ar300358z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Maly T., Debelouchina G. T., Bajaj V. S., Hu K. N., Joo C. G., Mak-Jurkaukas M. L., Sirigiri J. R., van der Wel P. C. A., Herzfeld J., Temkin R. J., and Griffin R. G., J. Chem. Phys. 128, 052211 (2008). 10.1063/1.2833582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Barnes A. B., De Paepe G., van der Wel P. C. A., Hu K. N., Joo C. G., Bajaj V. S., Mak-Jurkaukas M. L., Sirigiri J. R., Herzfeld J., Temkin R. J., and Griffin R. G., Appl. Magn. Reson. 34, 237 (2008). 10.1007/s00723-008-0129-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Can T. V., Ni Q. Z., and Griffin R. G., J. Magn. Reson. 253, 23 (2015). 10.1016/j.jmr.2015.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Corzilius B., Smith A. A., and Griffin R. G., J. Chem. Phys. 137, 054201 (2012). 10.1063/1.4738761 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Smith A. A., Corzilius B., Barnes A. B., Maly T., and Griffin R. G., J. Chem. Phys. 136, 015101 (2012). 10.1063/1.3670019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Smith A. A., Corzilius B., Bryant J. A., DeRocher R., Woskov P. P., Temkin R. J., and Griffin R. G., J. Magn. Reson. 223, 170 (2012). 10.1016/j.jmr.2012.07.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hovav Y., Feintuch A., and Vega S., J. Magn. Reson. 207, 176 (2010). 10.1016/j.jmr.2010.10.016 [DOI] [PubMed] [Google Scholar]
- 24.Hu K., Yu H., Swager T., and Griffin R., J. Am. Chem. Soc. 126, 10844 (2004). 10.1021/ja039749a [DOI] [PubMed] [Google Scholar]
- 25.Song C., Hu K.-N., Joo C.-G., Swager T. M., and Griffin R. G., J. Am. Chem. Soc. 128, 11385 (2006). 10.1021/ja061284b [DOI] [PubMed] [Google Scholar]
- 26.Sauvee C., Rosay M., Casano G., Aussenac F., Weber R. T., Ouari O., and Tordo P., Angew. Chem., Int. Ed. 52, 10858 (2013). 10.1002/anie.201304657 [DOI] [PubMed] [Google Scholar]
- 27.Zagdoun A., Casano G., Ouari O., Schwarzwalder M., Rossini A. J., Aussenac F., Yulikov M., Jeschke G., Coperet C., Lesage A., Tordo P., and Emsley L., J. Am. Chem. Soc. 135, 12790 (2013). 10.1021/ja405813t [DOI] [PubMed] [Google Scholar]
- 28.Becerra L., Gerfen G., Temkin R., Singel D., and Griffin R., Phys. Rev. Lett. 71, 3561 (1993). 10.1103/PhysRevLett.71.3561 [DOI] [PubMed] [Google Scholar]
- 29.Barnes A. B., Markhasin E., Daviso E., Michaelis V. K., Nanni E. A., Jawla S. K., Mena E. L., DeRocher R., Thakkar A., Woskov P. P., Herzfeld J., Temkin R. J., and Griffin R. G., J. Magn. Reson. 224, 1 (2012). 10.1016/j.jmr.2012.08.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Barnes A. B., Nanni E. A., Herzfeld J., Griffin R. G., and Temkin R. J., J. Magn. Reson. 221, 147 (2012). 10.1016/j.jmr.2012.03.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Oldfield E., Norton R. S., and Allerhand A., J. Biol. Chem. 250, 6368 (1975). [PubMed] [Google Scholar]
- 32.Morris G. A. and Freeman R., J. Am. Chem. Soc. 101, 760 (1979). 10.1021/ja00497a058 [DOI] [Google Scholar]
- 33.Henstra A., Dirksen P., Schmidt J., and Wenckebach W. T., J. Magn. Reson. 77, 389 (1988). 10.1016/0022-2364(88)90190-4 [DOI] [Google Scholar]
- 34.Henstra A., Dirksen P., and Wenckebach W. T., Phys. Lett. A 134, 134 (1988). 10.1016/0375-9601(88)90950-4 [DOI] [Google Scholar]
- 35.Farrar C. T., Hall D. A., Gerfen G. J., Rosay M., Ardenkjaer-Larsen J. H., and Griffin R. G., J. Magn. Reson. 144, 134 (2000). 10.1006/jmre.2000.2025 [DOI] [PubMed] [Google Scholar]
- 36.Weis V., Bennati M., Rosay M., and Griffin R. G., J. Chem. Phys. 113, 6795 (2000). 10.1063/1.1310599 [DOI] [Google Scholar]
- 37.van den Heuvel D. J., Henstra A., Lin T.-S., Schmidt J., and Wenckebach W. T., Chem. Phys. Lett. 188, 194 (1992). 10.1016/0009-2614(92)90008-B [DOI] [Google Scholar]
- 38.Kagawa A., Murokawa Y., Takeda K., and Kitagawa M., J. Magn. Reson. 197, 9 (2009). 10.1016/j.jmr.2008.11.009 [DOI] [PubMed] [Google Scholar]
- 39.Eichhorn T. R., van den Brandt B., Hautle P., Henstra A., and Wenckebach W. T., Mol. Phys. 112, 1773 (2014). 10.1080/00268976.2013.863405 [DOI] [Google Scholar]
- 40.Tateishi K., Negoro M., Nishida S., Kagawa A., Morita Y., and Kitagawa M., Proc. Natl. Acad. Sci. U. S. A. 111, 7527 (2014). 10.1073/pnas.1315778111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Henstra A. and Wenckebach W. T., Mol. Phys. 106, 859 (2008). 10.1080/00268970801998262 [DOI] [Google Scholar]
- 42.Henstra A. and Wenckebach W. T., Mol. Phys. 112, 1761 (2014). 10.1080/00268976.2013.861936 [DOI] [Google Scholar]
- 43.Hartmann S. R. and Hahn E. L., Phys. Rev. 128, 2042 (1962). 10.1103/PhysRev.128.2042 [DOI] [Google Scholar]
- 44.Momma K. and Izumi F., J. Appl. Crystallogr. 44, 1272 (2011). 10.1107/S0021889811038970 [DOI] [Google Scholar]
- 45.Fleischer E. B., Sung N., and Hawkinson S., J. Phys. Chem. 72, 4311 (1968). 10.1021/j100858a065 [DOI] [Google Scholar]
- 46.Lin T. S., J. Chem. Phys. 57, 2260 (1972). 10.1063/1.1678578 [DOI] [Google Scholar]
- 47.Cheng C., Lin T. S., and Sloop D. J., J. Magn. Reson. 33, 71 (1979). 10.1016/0022-2364(79)90191-4 [DOI] [Google Scholar]
- 48.MathWorks, MATLAB, MathWorks, Natick, MA, 2010.
- 49.Muller L., Kumar A., Baumann T., and Ernst R. R., Phys. Rev. Lett. 32, 1402 (1974). 10.1103/physrevlett.32.1402 [DOI] [Google Scholar]
- 50.Maniero A. L. and Brustolon M., J. Chem. Soc., Faraday Trans. 1 84, 2875 (1988). 10.1039/f19888402875 [DOI] [Google Scholar]
- 51.Dalal N. S., Kennedy D. E., and McDowell C. A., J. Chem. Phys. 61, 1689 (1974). 10.1063/1.1682163 [DOI] [Google Scholar]
- 52.Weis V., Bennati M., Rosay M., Bryant J. A., and Griffin R. G., J. Magn. Reson. 140, 293 (1999). 10.1006/jmre.1999.1841 [DOI] [PubMed] [Google Scholar]
- 53.Hu K.-N., Debelouchina G. T., Smith A. A., and Griffin R. G., J. Chem. Phys. 134, 125105 (2011). 10.1063/1.3564920 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Joye C. D., Shapiro M. A., Sirigiri J. R., and Temkin R. J., IEEE Trans. Electron Devices 56, 818 (2009). 10.1109/TED.2009.2015802 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kim H. J., Nanni E. A., Shapiro M. A., Sirigiri J. R., Woskov P. P., and Temkin R. J., Phys. Rev. Lett. 105, 135101 (2010). 10.1103/PhysRevLett.105.135101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Nanni E. A., Lewis S. M., Shapiro M. A., Griffin R. G., and Temkin R. J., Phys. Rev. Lett. 111, 235101 (2013). 10.1103/PhysRevLett.111.235101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Haze O., Corzilius B., Smith A. A., Griffin R. G., and Swager T. M., J. Am. Chem. Soc. 134, 14287 (2012). 10.1021/ja304918g [DOI] [PMC free article] [PubMed] [Google Scholar]