Core geometry in perspective

Abstract

Research on animals, infants, children, and adults provides evidence that distinct cognitive systems underlie navigation and object recognition. Here we examine whether and how these systems interact when children interpret 2D edge-based perspectival line drawings of scenes and objects. Such drawings serve as symbols early in development, and they preserve scene and object geometry from canonical points of view. Young children show limits when using geometry both in non-symbolic tasks and in symbolic map tasks that present 3D contexts from unusual, unfamiliar points of view. When presented with the familiar viewpoints in perspectival line drawings, however, do children engage more integrated geometric representations? In three experiments, children successfully interpreted line drawings with respect to their depicted scene or object. Nevertheless, children recruited distinct processes when navigating based on the information in these drawings, and these processes depended on the context in which the drawings were presented. These results suggest that children are flexible but limited in using geometric information to form integrated representations of scenes and objects, even when interpreting spatial symbols that are highly familiar and faithful renditions of the visual world.

1. Introduction

Line drawings — two-dimensional (2D) representations of three-dimensional (3D) scenes and objects — are universally perceptible across human cultures (Kennedy & Ross, 1975), appear early in human prehistory (Biederman & Kim, 2008; Clottes, 2008), and pervade the environments of young children in modern societies (DeLoache, 2004). Embedded in these drawings are the inherent geometries that capture the scenes and objects in our 3D world (Gombrich, 1977). Although much research has explored children's understanding of the symbolic function of line drawings and other pictures (DeLoache, 1987; 1991; 2004), little research has probed how children use the geometric properties of line drawings to interpret the scenes and objects that they represent. Such research is important because previous studies have linked children's use of the geometry in one kind of spatial symbol —overhead purely geometric maps —not only to the geometric representations humans share with other animals (Dillon, Huang & Spelke, 2013; Landau & Lakusta, 2009; Uttal, 2000; Vasilyeva & Bowers, 2006), but also to the abstract geometric understanding that is unique to humans (Dillon & Spelke, in review). Still, young children show limits in their use of geometry during map reading, which may result from the unusual viewpoints that they present. Questions thus remain regarding whether and in what way highly realistic perspectival pictures might engage these geometric systems. Answers to such questions may reveal how spatial symbols in general, and realistic drawings in particular, link our limited shared geometric capacities to the highly complex geometric intuitions that form the foundation of uniquely human science and mathematics.

Studies in developmental psychology, comparative psychology, cognitive neuroscience, and other fields provide evidence for two core systems of geometry that are phylogenetically ancient (Cheng, 1986; Chiandetti & Vallortigara, 2008; see Cheng & Newcombe, 2005, and Spelke & Lee, 2012, for reviews) and early emerging (Hermer & Spelke, 1996; Landau & Jackendoff, 1993; Schwartz & Day, 1979; Spelke, Lee & Izard, 2010). One system represents the layout of the environment by encoding the distances and directions of its extended surfaces (Dilks, Julian, Kubilius, Spelke & Kanwisher, 2011; Epstein & Kanwisher 1998; Lee, Sovrano & Spelke, 2012; O'Keefe & Burgess, 1996; Wills, Cacucci, Burgess & O'Keefe, 2010). The other system represents the shapes of objects by encoding the relative lengths and angles of their edges, as well as their major and minor axes (Biederman & Cooper 1991; Dehaene, Izard, Pica & Spelke, 2006; Schwartz & Day, 1979; Smith, 2009). These systems activate different brain regions (Dilks et al., 2011; Dilks, Julian, Paunov & Kanwisher, 2013; Epstein & Kanwisher 1998) and rely on different information (Schyns & Oliva, 1994).

Developmental research has revealed a contrast between children's limited use of geometry in tasks assessing non-symbolic abilities for navigating scenes and recognizing objects and their more flexible use of geometry in the symbolic realm. For example, when children are disoriented in a symmetrical room, they fail to use patterns of 2D forms on the walls or the floor to reorient themselves unless these forms give rise to perceptual asymmetries in the 3D layout (Huttenlocher & Lourenco, 2007; Lee & Spelke, 2011; Lee, Winkler-Rhoades & Spelke, 2012; Lourenco, Addy & Huttenlocher, 2009). When maps use 2D forms to symbolize a 3D layout, however, children are able to use that 2D information to find locations in the layout (Shusterman, Lee & Spelke, 2008; Vasilyeva & Bowers, 2006; Winkler-Rhoades, Carey & Spelke, 2013; Uttal & Wellman, 1989). These findings suggest that 2D geometric forms can activate the core system for navigation when the forms are presented as symbols, like overhead maps, but not when the forms are presented as surface markings in non-symbolic tasks. These studies do not reveal, however, what geometric information children rely on when using maps or pictures to find locations in the environment.

Other studies have begun to address this question, providing evidence that young children use relationships of distance or angle to interpret overhead maps (Huttenlocher & Vasilyeva, 2003; Shusterman, et al., 2008; Vasilyeva & Bowers, 2006; Uttal, 1996; Uttal, Gentner, Liu & Lewis, 2008; Uttal & Wellman, 1989). For example, Huang & Spelke (2013) presented 4-year-old children with an overhead map of a room in the shape of a 30-60-90 triangle and asked them to find locations in the room that were indicated on the map. Children performed best when targets were located at the room's most geometrically distinct side or corner (the 30° angle and the side across from it), indicating that they extract and use relative distance or angle information when interpreting a layout based on a map.

Both Huang & Spelke (2013) and Dillon, Huang & Spelke (2013) adopted an individual differences approach to probe the relationships between children's sensitivity to distance and angle when they navigate, recognize objects, and interpret spatial symbols. Dillon et al. (2013) presented 4-year-old children with overhead maps of fragmented triangular rooms: One room consisted only of the triangle's sides, which isolates the distance and directional information children use to specify locations in the navigable layout; and the other consisted only of the triangle's corner angles, which isolates the angle information children use to specify the shapes of landmark objects (Lee, et al., 2012). Children's success in the side-only room was predicted by their performance on a non-symbolic task assessing navigation by distance and direction. Moreover, children's success in the corner-only room was predicted by their performance on a non-symbolic task assessing shape analysis by angle and length. Nevertheless, children's ability to interpret the same maps in these two different contexts was uncorrelated. These findings suggest that children's interpretation of maps can depend on non-symbolic geometric information from either of their core systems of geometry, depending on the context in which the maps are presented (Dillon et al., 2013).

The findings from these studies probing young children's understanding of overhead maps may nevertheless underestimate children's geometric competence, as the ability to recognize 3D shape information in line drawings presenting familiar views appears very early in human development. Nine-month-old infants are able to recognize objects in line drawings that depict edge-based contour information without the addition of any color or texture cues (Jowkar-Baniani & Schmuckler, 2011; Shinskey & Jachens, 2014). Unlike maps, perspectival line drawings preserve scene and object information from canonical perspectives, depicting the junctions of surfaces at angles and the curvature and extent of object contours (Biederman, 1987; Landau, Hoffman & Kurz, 2006). Young children extract information relevant to object naming (Ganea, Pickard & Deloache, 2008) and action imitation (Simcock & Deloache, 2006) more readily from realistic drawings and photographs than from less iconic line drawings and cartoons. All these findings raise the possibility that children will integrate information from their two core systems of geometry more readily when they view perspectival drawings or photographs than when they view maps or other less iconic spatial symbols.

The present experiments therefore examine whether and how the geometry embedded in 2D perspectival pictures engages our early-emerging systems for navigating the environment and recognizing objects. We ask whether such representations facilitate more integrated geometric representations of scenes and objects than do overhead maps. Experiment 1 used a within-participants object placement task to evaluate what geometric information children rely on when interpreting pictures of scenes or pictures of objects. We investigated patterns in children's correct and erroneous responses to determine whether they relied on the distances and directions of extended surfaces and on the shape properties of landmarks in each context. Experiment 1 also sought to replicate, in children, findings with adults and infants (Biederman & Ju, 1988; DeLoache, Strauss & Maynard, 1979; Shinskey & Jachens, 2014; Walther, Chai, Caddigan, Beck & Fei-Fei, 2011) that the addition of color and texture information in full-color photographs offers no significant advantage over pictures that more simply capture the occluding edges essential to the hardware of our visual system (Sayim & Cavanagh, 2011; von der Heydt, Peterhans & Baumgartner, 1984). Experiments 2 and 3 used an individual differences approach (after Huang & Spelke, 2013; Dillon et al., 2013) to probe the relationships between children's sensitivity to geometry when they interpret symbolic line drawings and when they navigate or recognize objects without spatial symbols. Because of the greater familiarity of perspectival views of scenes and objects, children might engage geometric information in a more integrated fashion when interpreting line drawings than when interpreting overhead maps. Alternatively, because line drawings transform 3D geometry into two dimensions and serve as symbols early in development, just as maps do, children may treat them similarly and recruit each system of core geometry based on the context in which they are presented.

2. Experiment 1

In Experiment 1, we investigated whether 4-year-old children would use pictures — line drawings or photographs — of a novel room and a novel object to locate places either in the room or on the object. The room and object differed in some visual properties, but were geometrically similar and were comprised of surfaces of similar relative shapes and sizes. In addition, each context preserved essential scene or object properties: scenes are typically large, concave, and navigable whereas objects are typically small, convex, and manipulable. The room was a standard indoor environment emptied of furniture. We used Legos to construct the object because Legos and pictures of Legos are familiar to children. Moreover, Legos can capture the same geometric relationships as a room, and they have been found to elicit these geometric representations reliably in adults (Epstein & Kanwisher, 1998). Thus, the Lego object was likely to be interpreted by children as a manipulable object rather than as a small-scale navigable layout, and it captured much of the same geometric structure as the room.

During the experiment, children stood in the depicted room or sat at a table facing the depicted object. They then were shown a picture of the room or the object and asked to place a toy at a location in the room or on the object as indicated by a dot in the picture. Across trials, children viewed pictures of the room or object from different perspectives (all at eye-level and upright, but varying in facing direction) and specifying different placement locations. By analyzing children's successful and erroneous responses, we asked whether children used the same or different geometric information to locate the targets in the depicted scene and on the depicted object.

2.1. Methods

2.1.1. Participants

Forty-eight 4-year-old children (22 females; mean age 4;6, range 4;0-4;11) saw pictures of an indoor scene and a table-top object. They were tested on their ability to interpret line drawings (N=24) or photographs (N=24) in these two contexts.

2.1.2. Design

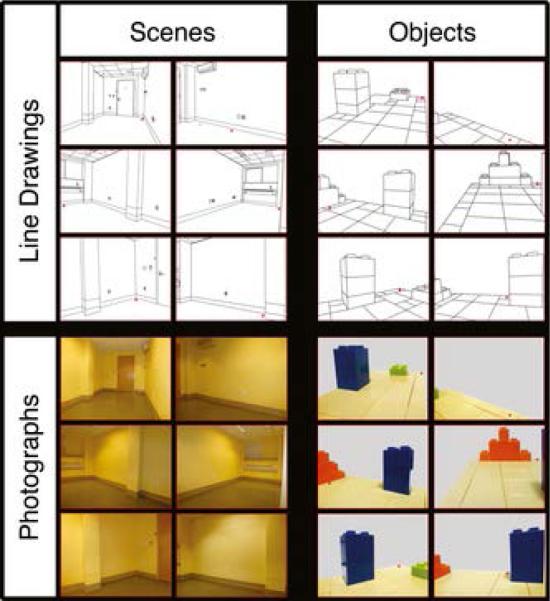
Children were randomly assigned to view pictures of either type. Picture type (line drawings versus photographs) was a between-participants variable, with identical task instructions used for both types. Context (scene or object) varied within participants, with the order of the two contexts counterbalanced across children. In each context, children received 6 test trials with pictures presenting different views of the scene or object while they faced one of 4 directions relative to the scene or object. Figure 1 shows the complete set of line drawings and photographs presented to children. The order of these trials and children's facing direction when viewing each picture were counterbalanced randomly across participants.

Figure 1.

Line drawings and photographs used in Experiment 1. Pictures of scenes and objects were designed to be as structurally similar as possible. In the line drawings, lines demarcated changes in contour, superposition, and perspective, but not changes in brightness.

2.1.3 Displays and procedure

In the scene context, the experimenter and participant entered a 5.44m × 2.51m lab testing room, which had been emptied of furniture but had a door on one short wall, a window on the opposite short wall, and large column against one long wall. Six color photographs were taken of the room from 6 perspectives 97cm off the ground (the height of a typical 4-year-old child). Six line drawings were created by tracing the edges of surfaces within each photograph. A single red dot was added to each picture to indicate the target location. There were 6 different test trials (and target locations) per condition and 10 possible response locations, indicated by red disks on the floor. Three of these 6 targets were located in the corners of the room, and the other three targets were located at or near landmarks in the room. Each target was defined by a unique combination of geometric and landmark relations, such that 100% correct responding was theoretically possible. Figure 2 shows an overhead schematic of the targets and response locations.

Figure 2.

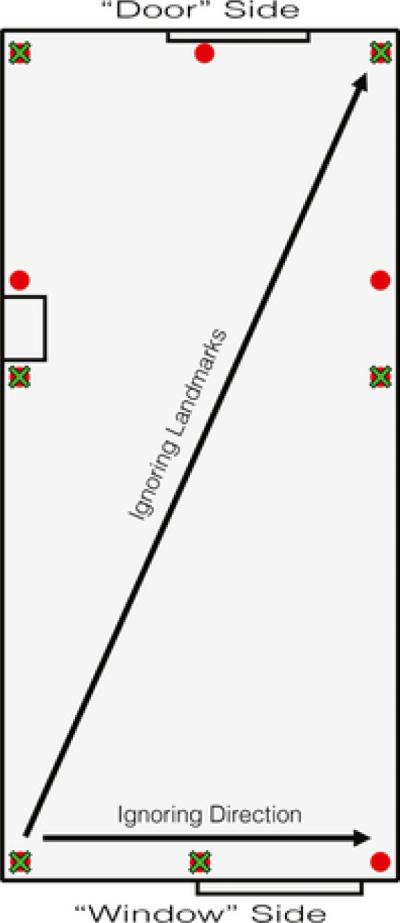
Overhead schematic of the target (x) and non-target locations used in both the scene and object contexts in Experiment 1. Six target locations and 10 possible response locations allowed for precise classification of successful and erroneous responses. If children ignored landmark information, then they might have confused the corner by the door with the geometrically equivalent corner by the window. Moreover, if children ignored directional information, then they might have confused the corners to the left and to the right of the window. Error classification in the object context resembled that of the scene context but occurred with reference to the corresponding sides and landmarks of the Lego object.

On each trial, the child and the experimenter stood in the center of the room where the experimenter (who looked only at the picture or the child until the child completed the object placement) showed the child one of the line drawings or photographs, pointed to the target location on that picture marked by the dot, and asked the child to place a toy at that location in the room. Before the test trials, the child was acclimated to the room by standing at its center and turning around to point to each wall. Then, two practice trials were presented that used color rather than geometry to specify a target location. The response location for each trial was recorded.

For the object context, a 5.5cm × 11cm × 2cm Lego object was built with three salient landmarks that were distinguished by shape, color, and location and placed at locations corresponding to the three walls at which the door, window, and column appeared in the room. Six color photographs of the object were taken to capture the same geometric and landmark information depicted in the scene context. Line drawings of the object were traced from these photographs. The object was affixed to a white rotating table (34.80cm in diameter), which was placed on top of a larger table in a lab testing room. Before the test trials, the child was acclimated to the object by turning the rotating table so that each side of the object faced them once. Children were encouraged to turn the table during the test trials to get different views of the object. Before the test trials, two practice trials were presented that used color rather than geometry to specify a target location. Test trials used the same procedure as the scene context as well as corresponding perspectives, target locations, and response locations (indicated by 10 red spots on the Lego object). Children's response for each trial was recorded.

2.1.4 Response classification

If young children engage core abilities to navigate the environment and recognize objects when interpreting pictures, then they should be just as successful when targets are located at the junctions of extended surfaces in the environment as when they are located near objects in both contexts. However, if children's responses depend on the context it which a picture is presented (i.e., whether the picture depicts a scene or an object), then they should rely more on the distances and directions of the extended surface layout when interpreting pictures of scenes and more on local landmarks features when interpreting pictures of objects. In this latter case, children would succeed more often in the scene context when targets are located at the junction of extended surfaces, and they would succeed more often in the object context when targets are located at or near objects. To test these possibilities, we compared the proportion of children's correct responses to the three corner targets and three landmarks targets in the room or on the object.

Additionally, if children rely equally on extended surface information and object shape information in both contexts, then their placement errors should not differ across the two contexts. Alternatively, if children rely more on extended surface information in the scene context and on object shape information in the object context, then they should make more placement errors by ignoring 2D shape information in the scene context and more errors by ignoring directional information in the object context. To test these possibilities, we classified and analyzed children's error responses. Landmark errors were consistent with the relative distance and directional relations between the two walls of the room but inconsistent with the local landmark or surface information in the room, which would distinguish, for example, the corner by the door from the diagonally opposite corner by the window. Direction errors, on the other hand, were consistent with landmark information but not with the distance or directional relations that would distinguish, for example, a target to the left of the window with one to its right (Fig. 2). Error classification in the object context resembled that of the scene context but occurred with reference to the corresponding sides and landmarks of the Lego object. Because of the geometric structure of the room and of the object, the number of possible landmark and direction errors was not equal: There were 5 ways to make landmark errors (i.e., going to the diagonally opposite corner), but 9 ways to make direction errors (i.e., going to the left or right of a target at a landmark). Children's error scores therefore were normalized by the total number of possible errors in each category.

2.2. Results

Initial analyses evaluated children's correct responding across all 6 trial locations. No performance differences emerged between male and female children (scene context: t(46) = 0.09, P = .93; object context: t(46) = 0.67, P = .51) or between children who viewed pictures in the scene and object contexts in different orders (scene context: t(46) = 0.22, P = .83; object context: t(46) = −0.83, P = .41). Children tended to perform better with photographs than with line drawings, but this difference was not significant in either the scene context (t(46) = 1.57, P = .12) or the object context (t(40.39) = 1.47, P = .15). Responses were collapsed across gender, order of contexts, and picture type for all further analyses.

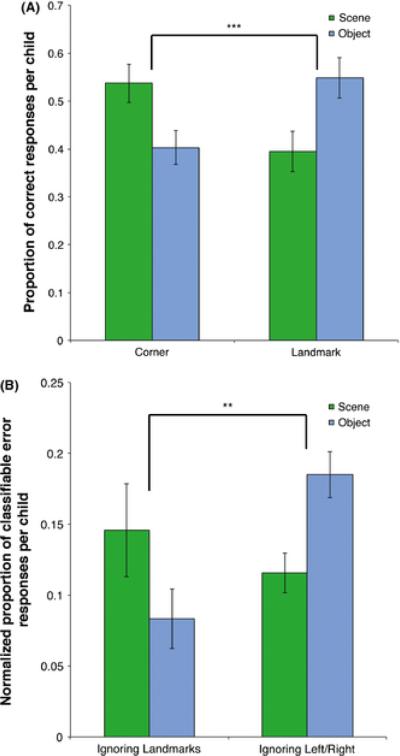
We used a within-participants ANOVA to evaluate whether children's success at the targets located at either the corners or the landmarks of the room or object differed based on the context in which the pictures were presented. We found no significant effect of Context (F(1, 47) = 0.06, P = .80) or Target Location (F(1, 47) = 0.01, P = .92), indicating that overall success did not differ in either context or at either type of target location. However, we did find a significant Context × Target Location interaction (F(1, 47) = 16.78, P < .001; Fig. 3A), indicating that children's success at different target locations depended on the context in which the picture was presented. Direct comparisons of children's successful responding across contexts revealed that children performed significantly better at corner target locations in the scene context (t(47) = 3.22, P < .01) and at landmark target locations in the object context (t(47) = −2.69, P =.01). These results are inconsistent with the hypothesis that pictures facilitate representations of scenes and objects that rely equally on extended surface and landmark shape information. Instead, they are consistent with past findings that young children rely selectively on different geometric information when using overhead maps to find targets located either at the midpoint of extended surfaces in the environment or at landmarks in that environment (Huang & Spelke, 2013).

Figure 3.

(A) Proportion of correct responses at targets located at the junction of extended surfaces (corners) or at landmarks. Children were more successful at corner targets in the scene context and landmark targets in the object context. (B) Children's error responses also varied across the two contexts, with relatively more errors where they ignored landmarks in the scene context and relatively more errors where they ignored direction in the object context.

Children succeeded on almost half of the trials in each context (.47 responses), performing well above chance (Ps < .001). However, children also made a large proportion of landmark and direction errors (.31). The remaining errors not classifiable by our criteria (.22 were distributed across the remaining response locations (M = .03, σ² < 8.6 × 10⁻⁴) with no apparent patterns.

Using a within-participants ANOVA, we tested the relative frequencies with which children ignored landmarks or ignored direction across the scene and object contexts. We found no significant effect of Context (F(1, 47) = 0.05, P = .83) or Error Type (F(1, 47) = 2.07, P = .16), indicating that overall error rates did not differ across contexts and that neither error type was more prominent. However, we did find a significant Context × Error Type interaction (F(1, 47) = 7.74, P = .01; Fig. 3B). Direct comparisons of children's error patterns across contexts revealed that children made significantly more direction errors in the object context (t(47) = −3.22, P < .01) and marginally more landmark errors in the scene context (t(47) = 1.84, P =.07). These results provide no evidence that children analyze pictures of scenes and objects in an integrated fashion. Instead, they are consistent with past findings that young children make errors by failing to integrate core geometric relations in tests of abstract geometric intuitions (Dillon & Spelke, in review; Izard, Pica, Spelke & Dehaene, 2011) and in understanding of overhead maps (Dillon et al., 2013). Children in the present study produced both successful and erroneous responses that appeared to differentially favor the distance and directional relations used for navigation when interpreting perspectival pictures of a 3D navigable layout but the shape relations used for form analysis when interpreting perspectival pictures of a 3D object.

One additional analysis of the findings from Experiment 1 aimed to elucidate whether children's ability to interpret pictures of scenes and objects relied on any common information across the two contexts. If children extracted shared geometric information from pictures of scenes and pictures of objects, then children who performed better with pictures of scenes should have also tended to perform better with pictures of objects. A bivariate correlation, however, revealed no significant association between children's ability to interpret pictures of scenes and objects (r(46) = .14, P = .35). These results thus suggest that children's interpretation of pictures not only is rooted in their sensitivity to geometric information rather than in some more general cognitive ability but also relies on different geometric information in different contexts.

2.3. Discussion

Although photographs offer color and texture cues missing from line drawings, children interpreted photographs and line drawings of scenes and objects at similar levels of performance, as in previous studies with adults and infants (Biederman & Ju, 1988; Shinskey & Jachens, 2014; DeLoache et el., 1979; Walther et al., 2011). Thus line drawings, which depict contour, superposition, and perspective, provided children with enough structural and geometric information about the 3D world to allow them to find targets without the addition of surface color or texture.

Children in the present study succeeded in relating different geometric information from two separate core systems to spatial symbols of high visual fidelity. Nevertheless, children's patterns of responding reflected limitations similar to what has been observed in children's interpretation of overhead maps: They relied on extended surface information when interpreting pictures of scenes and landmark shape information when interpreting pictures of objects. If children had used the shapes of landmarks to find locations in the scene context, then they would have had equal success at corner and landmark targets and would have consistently distinguished between geometrically congruent locations, avoiding landmark errors. Similarly, if children had used distance and directional relations to find locations in the object context, then they would have had equal success at corner and landmark targets and would have distinguished between locations to the left and right of a landmark, avoiding direction errors. This pattern of results is further surprising given that the room landmarks were both more permanent and potentially more salient than the Lego landmarks: Children have names for the room landmarks (e.g. door, window, etc.), and walked through one of the landmarks to get into the room, whereas they have no distinctive names for the Lego pieces that composed each landmark, and they were not required to act on any of these landmarks. Indeed, because Legos can be reconfigured, the pieces that served as landmarks in the object have no enduring existence or function.

Children's above-chance performance in the two contexts despite these errors presents two possibilities. First, children may have succeeded by sometimes relying on representations of landmarks in the scene context and representations of direction in the object context, indicating that they were partially but not completely integrating geometric information in both tasks. However, since the room and object were not perfectly symmetrical and included multiple features, children's success may have still depended only on one core system in each case. In particular, one long wall of the room contained a large protuberance like those children can use for navigation (Lee & Spelke, 2010). This feature would have allowed children to distinguish between targets at the two opposite corners of the room by encoding the contrasting distances and directions from that protuberance rather than from a landmark object. Similarly, the object contained multiple landmarks, allowing children to encode a target as located between two such landmarks rather than to the left or right of just one. The present analysis does not distinguish between these possibilities or reveal whether children have some capacity, albeit an imperfect one, for integrating geometric information across the two core systems. Experiment 2 begins to address this question by using an individual differences approach to test for interrelationships between children's core systems of geometry dedicated to navigation and object recognition and their interpretation of perspectival line drawings of scenes. This approach allows us to test the prediction that children's interpretation of line drawings can be significantly explained by one or both of their core geometric sensitivities.

3. Experiment 2

Experiment 2 was conducted on 4-year-old children who had also participated in a separate study of navigation, visual form analysis, and map interpretation (Dillon et al., 2013). In the present experiment, children were given a line drawing interpretation task depicting scenes, similar to that of the scene context in Experiment 1. Their performance on this task was then compared to their performance on the tests of reorientation and visual form analysis that were conducted for the other study (Dillon et al., 2013). Using hierarchical regression analyses, we evaluated whether children's performance on the reorientation and form analysis tasks predicted their interpretation of the line drawings of scenes, after controlling for age and verbal ability. If the response patterns in the scene context of Experiment 1 indeed depended on children's recruitment of the geometric information they use to navigate, then children who recruit this system more effectively in a non-symbolic reorientation task should be better able to interpret line drawings of scenes. In addition, if children recruit the geometric information they use to analyze visual forms (at least partially) to interpret drawings of scenes, then those children who perform better on a non-symbolic test of visual form analysis should also perform better on the line drawing task depicting scenes.

3.1. Methods

3.1.1 Participants

Forty-five 4-year-old children (23 females; mean age 4;6, range 4;0-4;11) visited the lab to participate in two testing sessions for a study of map interpretation (Dillon et al., 2013). All these children also completed the line drawing task in Experiment 2.

3.1.2 Design, procedure, and analyses

Children were asked to use perspectival line drawings to locate targets in a depicted lab testing room, which had been emptied of furniture (as in the scene context of Experiment 1). Because Experiment 2 aimed to test for relationships between non-symbolic and symbolic uses of geometry, but not to examine response patterns, the task was designed so that children could achieve higher levels of performance than in Experiment 1. Five trials with 5 possible response locations were included, counterbalancing the picture-presentation direction with the restriction that the target was never entirely out of view behind the child.

Children in the present experiment also participated in the experiment of Dillon et al. (2013), which consisted of 4 tasks conducted over two visits to the lab. Three of these tasks contributed data to the present analyses and are therefore described here (see Dillon et al., 2013, for a full description of these tasks). In one visit, children completed two non-symbolic tasks used to elicit core geometric representations in young children and animals. The first was a navigation task in which children were disoriented within two rectangular environments with different aspect ratios and then were allowed to reorient by the shape of each environment to locate a hidden object. The second was a visual form analysis task in which children were presented with a succession of 9 visual arrays displaying 5 similar shapes and one shape-deviant that differed in either proportional length, angle size, global shape, or relations of parallelism and alignment. Children were asked to pick out the form that did not belong with the rest. On a different visit, children completed the Peabody Picture Vocabulary Test (PPVT), a measure of verbal intelligence (Dunn & Dunn, 1997), which followed the line drawing interpretation task described above. Twenty-three children completed the set of non-symbolic tasks on their first visit followed by the line drawing and verbal task on their second visit, and 22 children completed these sets of tasks in the opposite order. To determine if and how the different geometric relations used in navigation and visual form analysis related to children's interpretation of line drawings of scenes, we conducted hierarchical regression analyses based on children's average scores across conditions that yielded above-chance performance.¹

3.2. Results

No performance differences were found between male and female children on the line drawing task (t(43) = 1.25, P = .22) or between children who completed the line drawing task on their first or second visit (t(43) = −0.27, P = .79). These findings accord with those of Dillon et al. (2013), who found no gender or order effects in the other geometric tasks. Finally, children performed above chance (0.2) on the line drawing task (t(44) = 12.03, P < .001).

3.2.1. Hierarchical regression analysis

Children exhibited appropriately distributed variability in their responses in the line drawing task (M = .69, σ² = 0.08) as well as in the other three tasks considered in the present analyses (see Dillon et al., 2013; Chapman & Chapman, 1978). As confirmation that parametric tests were appropriate for these data, the approximate normality of regression residuals was confirmed by comparison to the standard bell curve and examination of QQ-plots.

Age was a significant predictor of children's performance on the line drawing interpretation task β(Age) = 0.36; P = .02, but children's verbal abilities were not (β(PPVT) = 0.20; P = .17). After controlling for these effects, children's performance on the line drawing interpretation task was predicted by their use of distance and direction on the reorientation task (β(Reorientation) = 0.28; P = .05; Fig. 4) but not by their use of relative length, angle, and global shape on the visual form analysis task (β(VFA) = 0.05; P = .74). These results are inconsistent with the hypothesis that children's interpretation of line drawings might rely on an integrated representation of the geometry dedicated to navigation and object recognition: Children relied on the geometric information used for navigating 3D environments —the distances and directions of extended surfaces in an indoor scene — but not the geometric information used for recognizing object shapes to analyze the 3D information represented in the 2D line drawings of scenes. As a result, children's interpretations of line drawings of scenes appear to be consistent with previous findings testing young children's understanding of overhead maps, which find limited reliance on the geometric information used for navigation or object recognition based on context.

Figure 4.

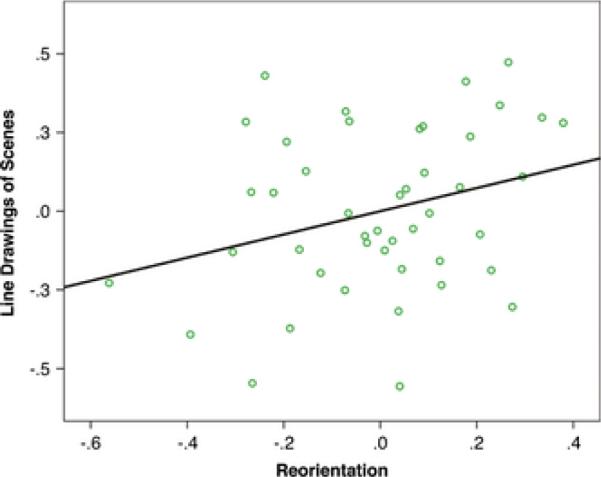
Experiment 2: Partial regression plot showing the relationship between children's scores on the reorientation task and the line drawing interpretation task depicting scenes, after controlling for age and verbal intelligence.

3.3. Discussion

The findings of Experiment 2 provide further evidence that children recruit representations guiding navigation but not object shape analysis to interpret line drawings of scenes. Even though the line drawings in Experiment 2 consisted of a collection of 2D shapes on a 2D surface and presented scenes from familiar viewpoints, children showed no evidence of recruiting representations supporting the analysis of visual forms. The reasons for these finding are unclear. First, it is possible that children selectively recruit the geometric representations used to recognize object shapes when analyzing drawings of objects but not scenes, as suggested by the findings from Experiment 1 and by previous work on overhead maps. Thus, children's performance on a form analysis task may not relate to their performance on the scene condition of the line drawing task because the two tasks depend on different geometric information. Alternatively, the visual form analysis task used in Experiment 2 simply may not capture meaningful variation in children's sensitivity to geometric shape properties when such properties are presented in perspectival pictures capturing objects from canonical points of view. Experiment 3 addressed these possibilities by testing whether children's performance on the same visual form analysis task was related to their interpretation of line drawings of objects, as suggested by the findings in Experiment 1 and predicted by the thesis explaining children's limited use of geometry in overhead maps.

4. Experiment 3

Experiment 3 used an individual differences method similar to that of Experiment 2, but abbreviated to a single session and with a smaller group of children. The test of verbal intelligence was eliminated since it did not capture any significant variation in children's line drawing interpretation in Experiment 2. Children in Experiment 3 performed the same line drawing interpretation task as in the object context of Experiment 1 and the same test of visual form analysis that entered into the analysis of Experiment 2. We asked whether performance on the form analysis task predicted performance on the line drawing task depicting objects, even though it did not predict performance on the line drawing task depicting scenes. If children rely only on the geometric information used for navigation to interpret all perspectival line drawings or if the visual form analysis task fails to capture children's sensitivity to object shape properties in perspectival drawings, then, as in Experiment 2, there should be no relationship between children's performance on the visual form analysis task and their performance on the line drawing task depicting objects. However, if children recruit different geometric representations for analyzing drawings of scenes versus objects, then those who excel at analyzing the shapes of visual forms might also excel at interpreting the 2D shapes in line drawings of objects.

4.1. Methods

Twenty-four 4-year-old children (11 females; mean age 4;6, range 4;0-4;11) participated in this experiment. One additional child was excluded from the analysis due to a failure to follow the task directions.

Children interpreted line drawings from the object context of Experiment 1 and were measured on their ability to analyze visual forms based on length, angle, global shape, and alignment relations. The visual form analysis task was the same task used in Experiment 2, which was based on that of Dillon et al. (2013) and consisted of the 9 items from that task on which children showed above-chance performance. Twelve children completed the line drawing interpretation task first followed by the visual form analysis task, and 12 children completed these tasks in the opposite order.

4.2. Results

We found no performance differences between male and female children on either of the tasks (line drawings: t(22) = 0.68, P = .50; visual form analysis: t(22) = 0.89, P = .38) and no performance differences between children who completed the line drawing task first and those who completed the visual form analysis task first (line drawings: t(22) = −0.36, P = .72; visual form analysis: t(22) = −0.68, P = .50).

Children performed above chance on the form analysis task (t(23) = 6.82, P < .001), consistent with past research using this task with children and adults (Dehaene et al., 2006; Dillon et al., 2013). Children also performed above chance on the line drawing interpretation task (t(23) = 6.24, P < .001). These data met the specifications for use in hierarchical regression analyses as described above (visual form analysis: M = .54, σ² = 0.07; line drawings: M = .45, σ² = 0.08). Age was not a significant predictor of children's performance on the line drawing task (β(Age) = 0.03; P = .87), but critically, performance on the line drawing and visual form analysis tasks was systematically related: After controlling for age, children's visual form analysis scores predicted their performance on the line drawing task depicting objects (β(VFA) = 0.54; P = .02; Fig. 5).

Figure 5.

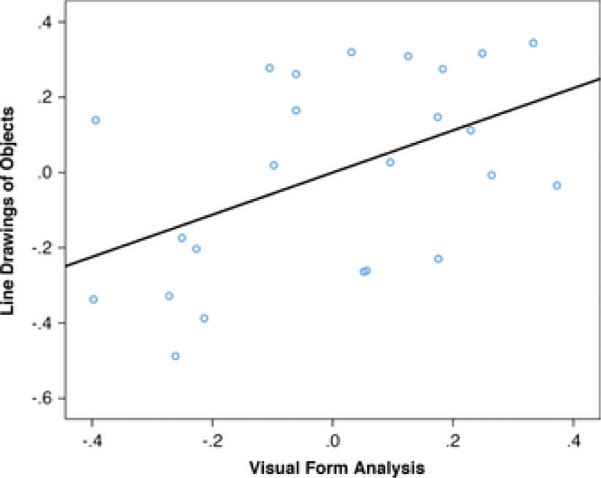
Experiment 3: Partial regression plot showing the relationship between children's scores on the visual form analysis task and their scores on the line drawing task depicting objects, after controlling for age.

4.3. Discussion

Although children's ability to analyze visual forms was not related to their ability to interpret line drawings of scenes in Experiment 2, it was related to their ability to interpret line drawings of objects in Experiment 3. Together with the findings of Experiment 2, the present findings thus suggest that children's failure to recruit the geometric information used for object shape analysis in Experiment 2 was not due to a failure in the non-symbolic shape analysis task to capture any meaningful variation in children's interpretation of perspectival pictures. Instead, these results reveal that children's interpretation of high fidelity spatial symbols is similar to their interpretation of overhead maps: children flexibly interpret perspectival line drawings by recruiting the non-symbolic geometric information used for navigation or object recognition based on context.

5. General Discussion

Together, the findings from these three experiments suggest that children are flexible in using distance and directional information as well as object shape information to interpret perspectival line drawings, but limited in their ability to combine this information to achieve integrated geometric representations of scenes and objects. Such flexibility and limitations are similar to those observed in children's interpretation of overhead maps. This conclusion depends on three main findings. First, 4-year-old children interpret pictures of scenes by relying on the same geometric relations of distance and direction that guide their navigation through extended surface layouts. Second, 4-year-old children interpret pictures of objects by relying on the same shape information that guides their recognition of objects and small-scale visual forms. Third, 4-year-old children show no evidence of integrating the geometric information from their two core systems. We discuss each conclusion in turn and describe how together they might begin to elucidate the developmental foundations of symbolic and abstract geometric understanding.

5.1 Core geometry for navigation guides children's interpretations of depicted scenes

When interpreting pictures of scenes, children in Experiment 1 exhibited key signatures of relying on the same geometric information they use to navigate the environment. Specifically, children relied on distance and directional information to find either the correct targets or targets at diagonally opposite locations in the room, and they erred by ignoring the shapes of surface markings and landmarks, as they do during other symbolic (Dillon et al., 2013; Huang & Spelke, 2013) as well as non-symbolic navigation tasks (see Cheng & Newcombe, 2005; Cheng, Huttenlocher & Newcombe, 2013; Spelke & Lee, 2012). In Experiment 2, children's ability to interpret line drawings of scenes was predicted by their performance on a non-symbolic navigation task but not by their performance on a non-symbolic form recognition task. Findings from both experiments thus provide evidence that children use common geometric information to navigate their environment without spatial symbols and with spatial symbols of varying levels of visual fidelity.

This finding is striking for two reasons. First, because line drawings of scenes depict 2D visual forms on a 2D surface, one might have expected children to interpret them by recruiting the geometric sensitivities used to analyze 2D visual forms. Contrary to this expectation, children interpreted the 2D small-scale pictures of scenes using the same geometry as they would to interpret the 3D navigable layouts themselves. Nevertheless, children succeeded in using the 2D forms to analyze the 3D layout, an achievement not found in purely non-symbolic navigation tasks (Huttenlocher & Lourenco, 2007; Lee & Spelke, 2011; Lee, et al., 2012; Lourenco, et al., 2009). Second, because line drawings depict their referent with high visual fidelity, one might have expected that children would more easily extract from them geometric information relevant to both navigation and object shape analysis. However, children appear just as limited in using integrated geometric information in these pictures as they do in pictures presenting unusual viewpoints such as overhead maps. As is the case with overhead maps, the referent of the line drawing, not the properties of the drawing itself, appear to guide children's interpretation of their geometry.

5.2 Core geometry for form analysis guides children's interpretation of depicted objects

When interpreting pictures of objects, children in Experiment 1 exhibited key signatures of relying on the same geometric information they use to recognize object shapes. Specifically, children relied on relative length and angle relations defining the shapes of landmarks to choose either the correct targets or the incorrect targets located near, but on the wrong side of, the object's landmarks. In making these errors, children ignored directional information as they do during non-symbolic form analysis tasks, in which children and adults often confuse objects and forms with their mirror images (Gregory & McCloskey, 2010; Dehaene et al., 2006). In Experiment 3, children's ability to interpret line drawings of objects was predicted by their performance on a non-symbolic form analysis task. These findings provide evidence that children use common geometric information to recognize the shapes of objects with or without spatial symbols.

Experiments 1 and 3 further suggest that children do not directly engage non-symbolic geometric information for navigation when interpreting perspectival line drawings of objects, even when such drawings capture the spatial structure of scenes. Neuroimaging studies targeting the parahippocampal place area (PPA) show that this brain region responds to global scene structure, including “Lego scenes” that look very much like those tested in the object conditions of Experiments 1 and 3 (Epstein, Harris, Stanley & Kanwisher, 1999). Though such Lego scenes activate cognitive systems dedicated to scene recognition, they may nevertheless engage geometric representations dedicated to object recognition when such Lego scenes indicate a Lego object, as they do in Experiments 1 and 3. The flexibility children displayed in interpreting the scene-like pictures of the Lego object, relative to Lego object itself, suggests that a drawing's symbolic meaning affects the geometric information recruited for its interpretation. Thus, one extension of the present work would be to analyze children's interpretation of the very same drawings of the same Lego structure both in the context of a large-scale Lego scene and also in the context of a small-scale object made of Legos.

These results are consistent with other findings that a highly realistic drawing or photograph may serve as a symbol for children, with the geometric elements of the picture remaining open to interpretation based on the context in which it is presented. Although young infants may attempt to perform actions on pictures that suggest confusion between the picture and its referent (DeLoache, Pierroutsakos & Uttal, 2003), these actions disappear in the second year of life and are replaced by acts of pointing and naming (DeLoache, Pierroutsakos, Uttal, Rosengren & Gottlieb, 1998). Moreover, when 18- and 24-month-old children were repeatedly presented with a novel word, “whisk,” applied to a line drawing of a whisk, they chose either the real object alone or the real object and the drawing when later asked for the “whisk” (Preissler & Carey, 2004). This finding holds not only for highly iconic symbols, but also for more abstract spatial symbols such as overhead maps. Still, other symbolic representations may be entirely devoid of any iconicity, and it is unknown how this level of abstraction would manifest in children's treatment of scenes and objects. For example, it is possible that children would interpret the relative heights on a bar graph identically regardless of whether they represented the relative distances between houses in a neighborhood or the relative positions of parts on an object (Friel, Curcio & Bright, 2001). To our knowledge, this possibility has not been tested.

5.3. Children show no evidence of integrating core geometric representations when interpreting perspectival pictures

Although children showed equal success in interpreting structurally similar 2D perspectival pictures of scenes and objects, we found no indication that they combined extended surface representations of distance and direction with small-scale shape representations of relative length and angle to find targets in the 3D layout. In Experiment 1 children extracted geometric information from pictures of both scenes and objects, but did not use this information in an integrated fashion. When interpreting pictures of scenes, children's successful and erroneous responses indicated that they relied on distance and directional information more than landmark shape information. When interpreting pictures of objects, in contrast, the same two measures indicated that children relied on landmark shape information more than directional information. This negative conclusion does not imply, however, that children are unable to effect such combinations when reading spatial symbols. The picture interpretation tasks used in the present studies invited, but did not require, such combinations. It is possible that children would show integration of these types of geometric information if they were given a task that requires these combinations.

Nevertheless, the present findings remain surprising, given that previous work has shown an advantage of highly realistic pictures encouraging children to extract relevant information from symbolic representations in domains other than geometry (Ganea, et al., 2008; Simcock & Deloache, 2006). Instead, the present findings are consistent with previous evidence that young children fail to use the geometric relations of distance and angle in an integrated fashion when they navigate by spatial symbols such as overhead maps (Dillon et al., 2013) or perform more abstract triangle completion tasks (Dillon & Spelke, in review; Izard et al., 2011). It is possible that children will begin to exhibit integrated geometric knowledge during picture interpretation when they also begin to show an integrated understanding of distance and angle in these other abstract geometry tasks. Alternatively, children may show more integrated knowledge when they confront pictures earlier than when they confront maps or verbal tests of abstract geometric intuitions, but this difference might not be apparent at age 4 years. For example, pictures may better foster the encoding of spatial expressions and object names in older children.

6. Conclusion: Core geometry in perspective

Understanding spatial symbols, such as maps and line drawings, is essential to functioning in our highly symbolic human culture. Such understanding requires the integration of information from two core systems of geometry, but this integration undergoes a protracted development that is not complete until adolescence (Dillon & Spelke, in review; Izard et al., 2011). At age 4 years, children's interpretation of spatial symbols does not appear to benefit from more familiar and realistic depictions of their referents. Future research with perspectival drawings could test the same children on all the measures used in the present experiments to elucidate how each core system might specifically contribute to children's interpretation of highly iconic spatial symbols.

The present findings already suggest that pictures of all kinds serve as media in which children deploy different core geometric representations flexibly, and they therefore may offer children the opportunity to relate these representations to one another: Spatial symbols represent both 3D scenes and objects, joining the distance and directional information used to navigate with the relative length and angle information used to recognize objects by their shapes. If these suggestions are correct, cognitive scientists may elucidate the processes by which geometric abstractions arise by charting the development of children's engagement with the abstract geometric relations presented in pictures, perspectival art, and other spatial symbols. Further, if abstract geometric understanding builds on core mechanisms that emerge in infancy and are used throughout our lives, then efforts to enhance those capacities through education may benefit from a pedagogy that links the formal systems children must master to their everyday acts of navigation, object recognition, and pictorial interpretation. For example, training studies could investigate whether intense experience with spatial symbols affects the emergence and growth of abstract geometric intuitions. Continued research probing the mechanisms of change in spatial cognitive development, combining studies of navigation and object recognition with studies of pictorial perception and interpretation, may ultimately shed light on the uniquely but universally human geometric understanding at the foundation of science and mathematics.