Model-Based Oscillometric Blood Pressure Measurement: Preliminary Validation in Humans

Abstract

We conceived new oscillometric blood pressure (BP) estimation methods based on physical modeling. The crux of these methods is to simultaneously estimate the arterial stiffness and BP of the patient from a standard oscillometric waveform. Hence, in contrast to previous methods, the BP estimation is specific to the patient at the time of measurement and is robust against arterial stiffening. We conducted initial testing of one of the methods against invasive reference brachial BP measurements in eight cardiac catheterization patients before and after nitroglycerin infusions. The method achieved systolic, diastolic and mean BP root-mean-squared-errors of 7.2, 7.6 and 6.7 mmHg. These errors were, on average, 40% lower than an existing high-end method.

I. Introduction

Oscillometry is perhaps the most popular, non-invasive and automatic blood pressure (BP) measurement method (Fig. 1a). This method employs an inflatable arm cuff with a pressure sensor inside it. The measured cuff pressure not only rises and falls with cuff inflation and deflation but also shows tiny oscillations indicating the pulsatile blood volume (BV) in the artery. The amplitude of these oscillations varies with the applied cuff pressure, as the arterial stiffness is nonlinear. BP values are then estimated from the oscillometric cuff pressure waveform using population-based methods such as fixed-ratios (Fig. 1a) [1]. As a result, oscillometry is notoriously inaccurate, especially during arterial stiffening (Fig. 1b) [2]–[6].

Fig. 1.

Current oscillometric BP measurement methods. (a) The popular fixed-ratios method estimates mean BP (MP) as the cuff pressure at which the amplitude of its oscillation (caused by arterial volume pulsation) is maximal, and then estimates systolic and diastolic BP (SP and DP) as the cuff pressures at which the oscillation amplitudes are some ratios of the maximum. (b) The current methods are error prone, as they are population based [2]–[6].

We conceived new oscillometric BP estimation methods based on physical modeling. The crux of these methods is to simultaneously estimate the arterial stiffness and BP of the patient from a standard oscillometric waveform. In this way, in contrast to previous methods, the BP estimation is specific to the patient at the time of measurement and is robust against arterial stiffening. We evaluated one of the methods against invasive brachial BP measurements in eight cardiac catheterization patients before and after nitroglycerin infusions. Our preliminary results show major reductions in BP estimation error compared to an existing high-end method.

II. Model-Based Oscilometric BP Estimation Method

A. Physical Model

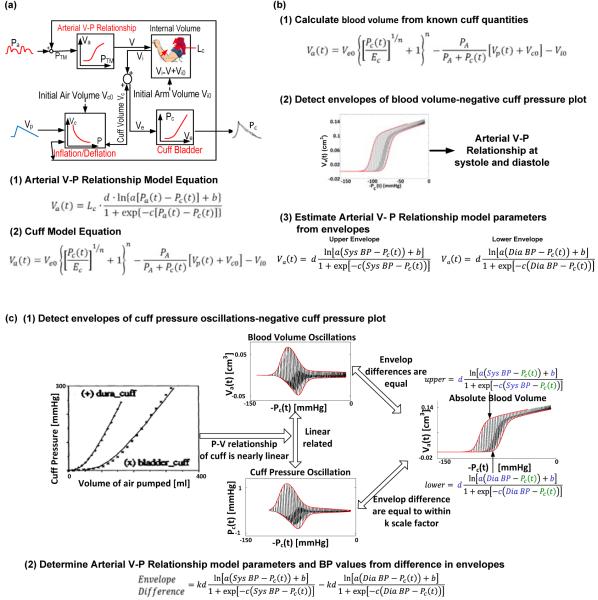
We used an established model of oscillometry (Fig. 2a) [7]. We describe the physical model below.

Fig. 2.

Physical model-based oscillometric BP estimation methods. BP is estimated via subject-specific physical modeling rather than population-based formulas. In this way, BP may be estimated more accurately than the fixed-ratios and other existing methods. (a) Physical model of oscillometry [7]. (b) Method 1 estimates BP values from the oscillometric cuff pressure waveform and a priori measurements on the employed cuff [8]. (c) Method 2 estimates BP values from only the oscillometric cuff pressure waveform without requiring detailed knowledge of the cuff properties.

The model transforms BP [P_a(t)] and the volume of air pumped into and leaving the cuff [V_p(t)] into cuff pressure [P_c(t)]. The transformation accounts for the (1) BP-dependent arterial compliance in the form of a nonlinear BV to trans-mural pressure relationship (Arterial V-P Relationship); (2) coupling of BV to the cuff (Artery-Cuff Link); (3) elasticity of the cuff bladder (Cuff Bladder); and (4) compressibility of air within the cuff (Inflation/Deflation).

1) Arterial V-P Relationship

The BV under the cuff [V_a(t)] is determined via its trans-mural pressure, which is the difference between BP and cuff pressure, according to the following nonlinear relationship:

$${\mathrm{V}}_{\mathrm{a}}\left(\mathrm{t}\right)=\mathrm{d}\frac{\text{ln}[\mathrm{a}({\mathrm{P}}_{\mathrm{a}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{c}}\left(\mathrm{t}\right))+\mathrm{b}]}{1+\text{exp}[-\mathrm{c}({\mathrm{P}}_{\mathrm{a}}\left(\mathrm{t}\right)-{\mathrm{P}}_{\mathrm{c}}\left(\mathrm{t}\right))]}$$ (1)

where a, b, c, and d are patient-specific parameters at the time of measurement.

2) Artery-Cuff Link

BV is linked to the cuff through the volume of the arm [V_i(t)] as follows:

$${\mathrm{V}}_{\mathrm{i}}\left(\mathrm{t}\right)={\mathrm{V}}_{\mathrm{a}}\left(\mathrm{t}\right)+{\mathrm{V}}_{\mathrm{io}}$$ (2)

where V_io is the arm volume corresponding to a collapsed artery.

3) Cuff Bladder

The cuff pressure is determined by the external cuff volume, which is the sum of the cuff volume [V_c(t)] and the arm volume, according to the following relationship:

$${\mathrm{P}}_{\mathrm{c}}\left(\mathrm{t}\right)={\mathrm{E}}_{\mathrm{c}}{\{{[({\mathrm{V}}_{\mathrm{c}}\left(\mathrm{t}\right)+{\mathrm{V}}_{\mathrm{i}}\left(\mathrm{t}\right))∕{\mathrm{V}}_{\mathrm{eo}}]}^{1∕\mathrm{n}}-1\}}^{\mathrm{n}}$$ (3)

where E_c is the maximum cuff elastance, V_eo is the zero stretch volume of the bladder, and n is a constant of nonlinearity.

4) Inflation/Deflation

The cuff volume is determined by the cuff pressure and the volume of air pumped into and leaving the cuff according to the Boyle’s law as follows:

$$[{\mathrm{P}}_{\mathrm{A}}+{\mathrm{P}}_{\mathrm{c}}\left(\mathrm{t}\right)]{\mathrm{V}}_{\mathrm{c}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{A}}[{\mathrm{V}}_{\mathrm{p}}\left(\mathrm{t}\right)+{\mathrm{V}}_{\mathrm{co}}]$$ (4)

where P_A is atmospheric pressure, and V_co is the initial air volume in the cuff and is equal to V_eo − V_io.

In sum, Eqn. (1) relates BV to arterial quantities, and the combination of Eqns. (2) to (4) yields a second equation relating BV to cuff quantities. These two equations govern the model (Fig. 2a).

B. BP Estimation Methods

Based on this physical model, we devised two oscillometric BP estimation methods (the first method was described previously [8]). The main idea is to estimate the arterial V-P relationship model parameters and the BP based on the analysis of an oscillometric waveform. In this way, BP estimation is specific to the patient at the time of measurement. Further, by determining the patient-specific arterial V-P relationship, these methods should be robust to arterial stiffening. The common steps of the methods are to: 1) determine V_a(t); 2) estimate the arterial V-P relationship model parameters along with systolic BP (SP) and diastolic BP (DP) from the envelopes of a plot relating V_a(t) to the measured P_c(t); and 3) compute P_a(t) from V_a(t), the measured P_c(t), and the arterial V-P relationship. The methods differ mainly in the way V_a(t) is determined.

1) Method 1

This method determines V_a(t) after a priori measurement of the cuff model parameters, which are constant per cuff (Fig. 2b) [8]. First, V_a(t) is computed from these cuff parameter values, the measured P_c(t), and the applied V_p(t) via the second model equation in Fig. 2a. Second, the upper and lower envelopes of the plot relating V_a(t) to -P_c(t) are detected to yield the arterial V-P relationships at systole and diastole. Third, these envelopes are represented with the first model equation wherein P_a(t) is set to SP and DP. Fourth, the parameters a, b, c, and d along with SP and DP are estimated by finding the model equations, which when applied to the envelope values for P_c(t), best predicts the envelope values for V_a(t) in the least squares sense. Lastly, P_a(t) is computed by applying V_a(t) and P_c(t) to the first model equation in Fig. 2a equipped with the parameter estimates, and mean BP (MP) is set to the mean value of P_a(t).

2) Method 2

This method does not require any knowledge of the cuff model parameters and is rooted in two recognitions (Fig. 2c). One recognition is that the difference between the upper and lower envelopes of the plot relating V_a(t) to -P_c(t) is equal to the difference in the envelopes of the plot relating V_a(t) oscillations (obtained by high-pass filtering V_a(t)) to -P_c(t). The other recognition is that the pressure-volume relationship of actual cuffs is nearly linear over a wide range [7]. Hence, the measured P_c(t) oscillations (obtained by high-pass filtering P_c(t)) and the undetermined V_a(t) oscillations are assumed to be linearly related. So, first, the difference in the upper and lower envelopes is detected from the plot relating P_c(t) oscillations to -P_c(t). Second, this difference is represented as the (scaled) first model equation with P_a(t) set to SP minus the same equation with P_a(t) set to DP. Third, all parameters are similarly estimated from the envelope values. Fourth, scaled V_a(t) is determined by adding the scaled first model equation equipped with the parameter estimates and P_a(t) set to DP to the P_c(t) oscillations Lastly, P_a(t) and MP are likewise computed.

III. Methods

A. Experimental Data

We studied data from eight patients obtained via a previous study [5]. In this IRB-approved study, the patients were referred for diagnostic cardiac catheterization and had arterial stiffening. BP [P_a(t)] via a high fidelity catheter (Millar) in the right brachial artery and oscillometric cuff pressure waveforms [P_c(t)] via a cuff (Microlife) placed on the left arm were simultaneously recorded at a sampling rate of >250 Hz from each patient before and after nitroglycerin infusion to reduce BP. Two oscillometric cuff pressure waveforms were obtained per measurement, and the oscillometric BP estimates of the Microlife device were also recorded. Since we did not have data on the cuff properties, we were only able to test Method 2 with these data.

B. Data Analysis

We applied Method 2 to the oscillometric cuff pressure waveforms and averaged the resulting BP estimates over each set of two consecutive waveforms. We then quantitatively evaluated the SP, MP and DP estimates of the method against the invasive reference measurements. For comparison, we likewise assessed the BP estimates from the Microlife device.

IV. Results

Table I shows the average BP levels of the patients before and after nitroglycerin infusions. Table II shows the bias, precision and root-mean-squared-error (RMSE, which is equal to the square root of the bias squared plus the precision squared) of the SP, MP and DP estimates of the model-based method and the Microlife device. The model-based method was significantly more accurate than the high-end device, with RMSE values that were, on average, 40% lower. Further, this method achieved errors that were within AAMI bias and precision limits of 5 and 8 mmHg.

Table I.

Average BP levels.

	SP [mmHg]	MP [mmHg]	DP [mmHg]
Before NTG	145±15	102±9	74±12
After NTG	138±14	95±11	72±13

NTG is nitroglycerin.

Table II.

Errors of the model-based oscillometric BP estimation method (Method 2) and a high-end method.

		Bias [mmHg]	Precision [mmHg]	RMSE [mmHg]
SP	Method 2 Microlife	−5.0 −7.0	5.2 9.2	7.2 11.3
MP	Method 2 Microlife	0.3 −11.2	7.8 8.0	7.6 13.7
DP	Method 2 Microlife	−2.5 4.8	6.4 9.6	6.7 10.5

RMSE is root-mean-squared-error.

V. Discussion

In summary, we conceived model-based oscillometric BP estimation methods and assessed the accuracy of one of the methods based on an initial set of in-human experimental data. Our results show that the methods have the potential to significantly improve the accuracy of oscillometry.

The model-based oscillometric BP estimation methods assume that compressibility of tissue and viscoelasticity of the arterial wall are negligible. Firstly, although tissue can certainly be condensed, its compressibility around the crucial zero trans-mural pressure regime (which typically amounts to an applied cuff pressure of ~100 mmHg) is not significant, if not negligible, since it is largely compressed already. Secondly, while arteries are not purely elastic, arterial compliance is maximal around the neighborhood of zero trans-mural pressure (i.e., about ten times larger than its value at normal trans-mural pressures of 100 mmHg) [7]. So, elastic wall behavior dominates viscous wall behavior during oscillometry. Hence, we contend that the major, simplifying assumptions of the methods are quite reasonable. Nevertheless, extensive validation of the model-based oscillometric BP estimation methods in a diverse patient population is certainly a must for clinical adoption.