Modern Perspectives on Numerical Modeling of Cardiac Pacemaker Cell

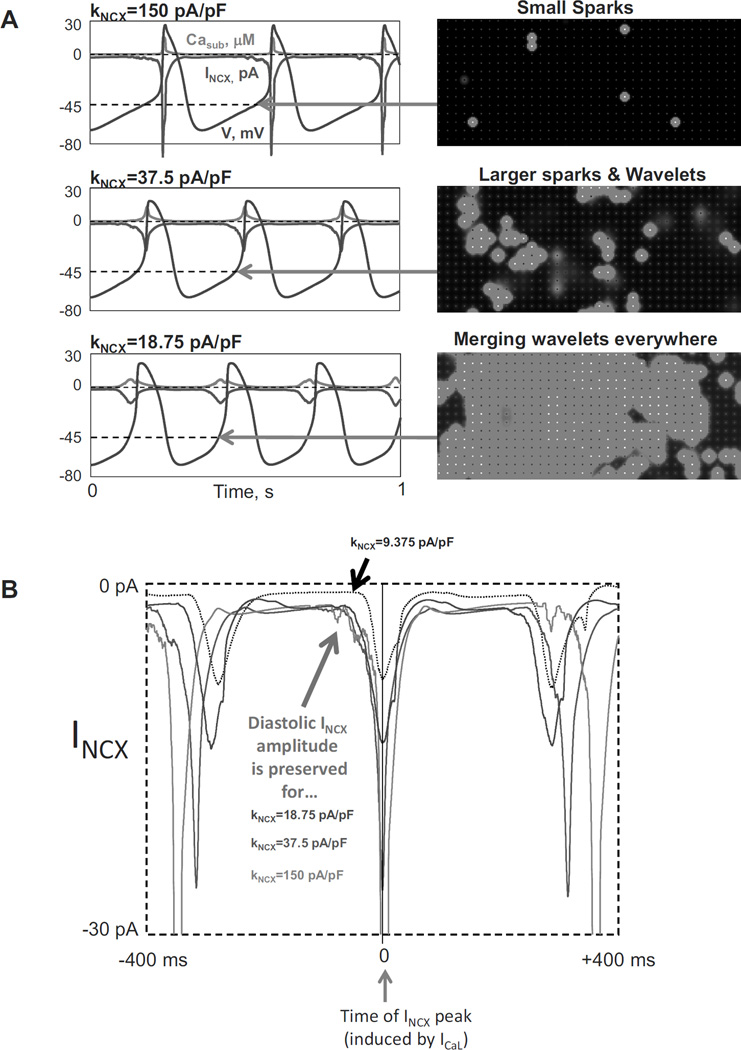
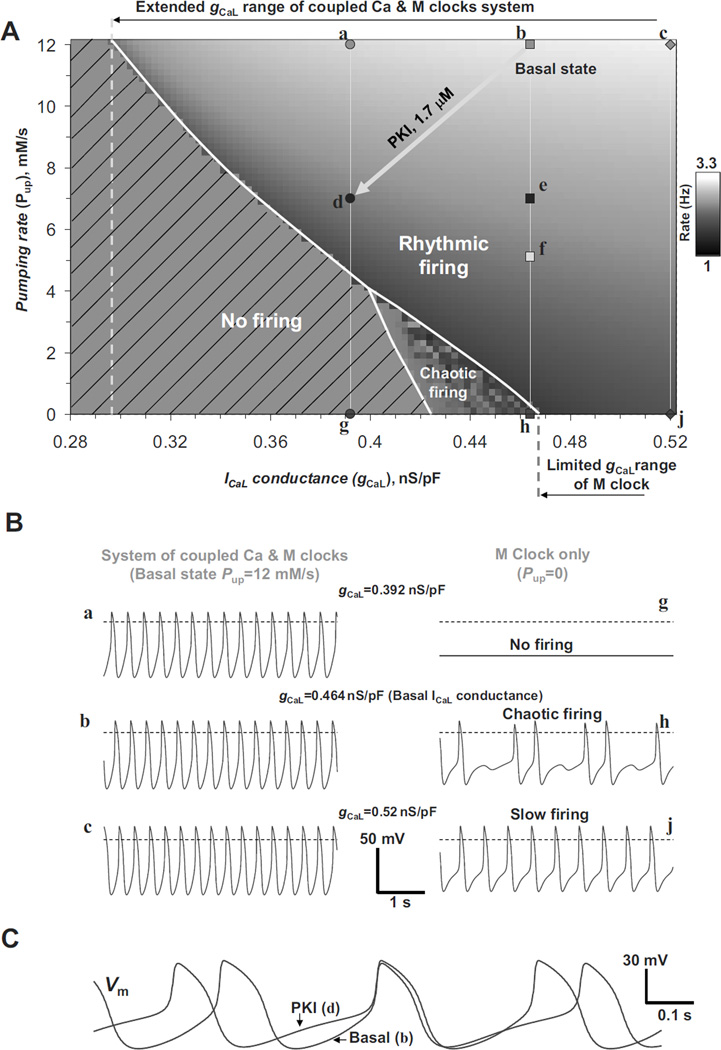
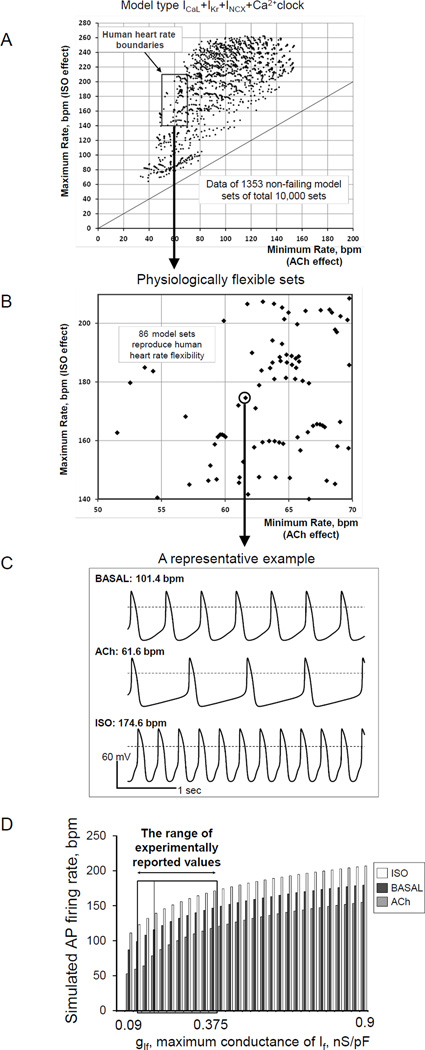
Abstract

Cardiac pacemaking is a complex phenomenon that is still not completely understood. Together with experimental studies, numerical modeling has been traditionally used to acquire mechanistic insights in this research area. This review summarizes the present state of numerical modeling of the cardiac pacemaker, including approaches to resolve present paradoxes and controversies. Specifically we discuss the requirement for realistic modeling to consider symmetrical importance of both intracellular and cell membrane processes (within a recent “coupled-clock” theory). Promising future developments of the complex pacemaker system models include the introduction of local calcium control, mitochondria function, and biochemical regulation of protein phosphorylation and cAMP production. Modern numerical and theoretical methods such as multi-parameter sensitivity analyses within extended populations of models and bifurcation analyses are also important for the definition of the most realistic parameters that describe a robust, yet simultaneously flexible operation of the coupled-clock pacemaker cell system. The systems approach to exploring cardiac pacemaker function will guide development of new therapies, such as biological pacemakers for treating insufficient cardiac pacemaker function that becomes especially prevalent with advancing age.

1. Introduction

Numerical modeling is an indispensable tool of the modern science. Intertwining experimentation and theoretical studies is an important driving force of our exploration of complex biological phenomena. In many cases, numerical modeling is the only feasible way to accurately interpret experimental data describing a complex biological system, whose behavior could be counterintuitive. Furthermore, numerical modeling extends our exploratory horizons beyond experimental data, provides novel mechanistic insights, and helps in assessing the actions of drugs (1, 2). Failure of a model to explain novel experimental data requires a shift in the existing paradigm, brought on by creative minds that put forward new theories and new hypotheses to be tested. A pioneer of cardiac cell modeling, Denis Noble noted “We often learn as much from the failures as from the successes of mathematical models.” (3).

Cardiac impulse initiation, the fundamental biological phenomenon indispensable for heart function and life, has been traditionally explored by both numerical modeling and experimental approaches. The present understanding of cardiac pacemaker function has evolved (and continues to evolve) through several paradigm shifts. In 2006 in this journal, we had systematically reviewed (4) the major milestones of the evolution from Galvani and Bernstein, Bozler and Weidman, Noble and DiFrancesco, to our Ca²⁺-clock hypothesis. The evolution of thought regarding cardiac pacemaker cell function switched back and forth between intracellular origin (e.g. a “metabolic” intracellular clock (5) or sarcoplasmic reticulum (SR)-based Ca²⁺-clock (4)) and cell membrane origin of heartbeat initiation (membrane clock or M-clock (6)). While the ability of the SR to generate oscillatory Ca²⁺ releases was discovered long time ago ((7), review (8)), the intracellular Ca²⁺ oscillator had been considered mainly as a pathological phenomenon in pacemaker cells; thus an important milestone of 1990s to early 2000s was the recognition of its contribution into NORMAL pacemaker function (9). A more recent paradigm shift was the realization that both intracellular and cell membrane initiation mechanisms are actually tightly dynamically coupled to each other and are indispensable for normal pacemaker function that led to the idea of a “coupled-clock” system (10) (Fig.1A, for more details see review (11)).

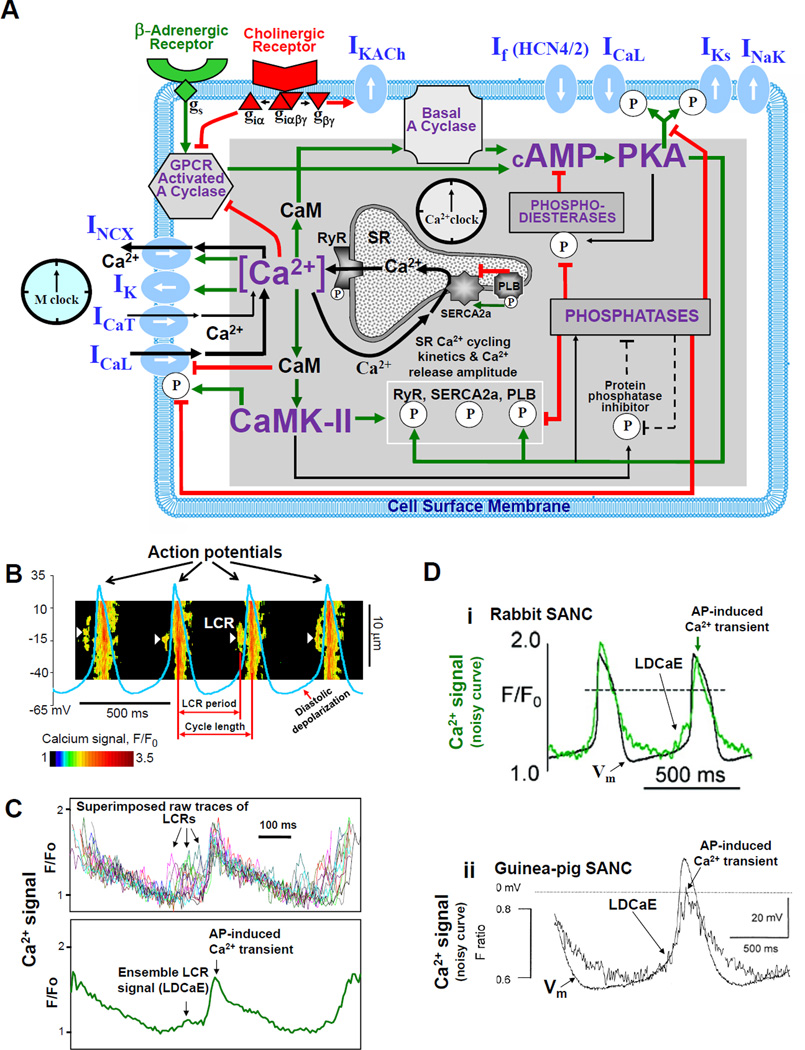
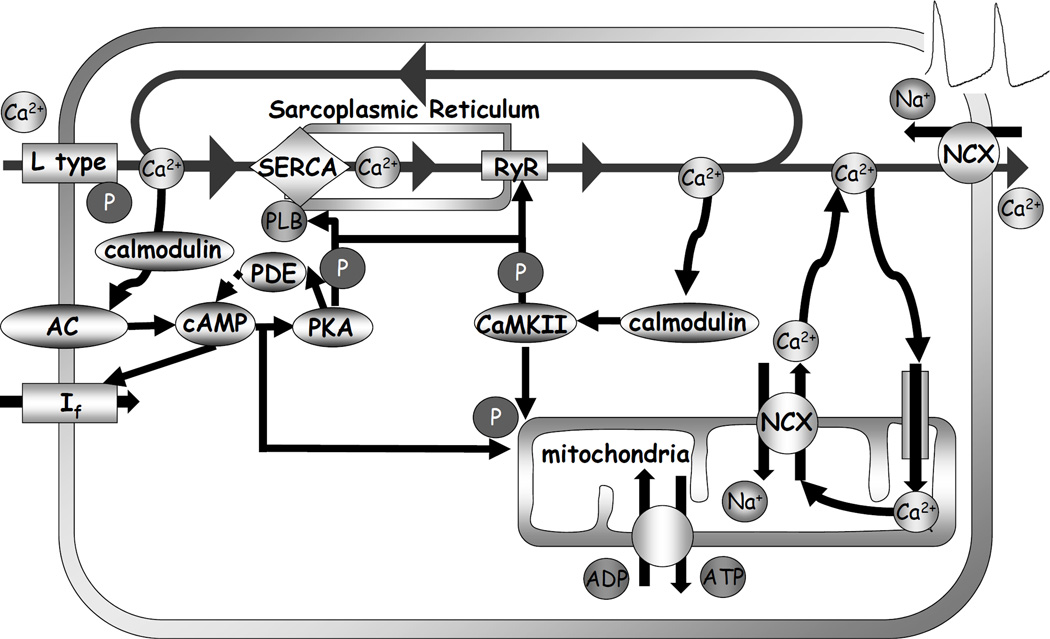
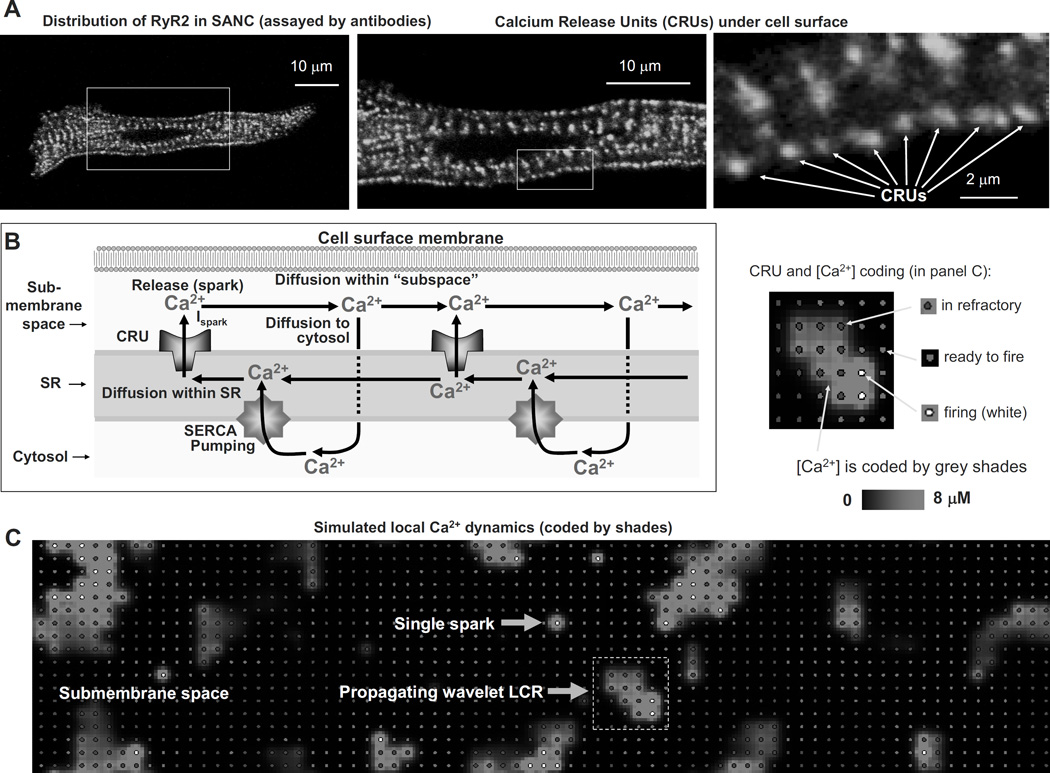
Figure 1.

SA node cell is a coupled-clock system of voltage membrane clock (M-clock) and an intracellular, sarcoplasmic reticulum (SR)-based Ca²⁺ clock. A: Schematic illustration of interactions of key molecules comprising the system (PLB = phospholamban). Note that common regulatory factors (purple large lettering) govern the function of both the Ca²⁺-clock (gray intracellular area) and the M-clock (light-blue cell membrane area with blue labels depicting electrogenic proteins). These common factors act as nodes within the system to couple the function of both clocks activities. The system is balanced as illustrated by traffic-light-like colors: green arrows designate signaling driving action potential (AP) firing but red lines show suppression, maintaining a given steady-state level of cAMP and protein phosphorylation. G protein-coupled receptors (green and red shapes within the membrane) modulate both the Ca²⁺-clock and M-clock function via those same crucial signaling nodes of the system. Modified from (11). B: Definition of diastolic depolarization, local Ca²⁺ releases (LCRs), LCR period, and cycle length. Line-scan image of LCRs (white arrows) is superimposed with spontaneous APs recorded in rabbit SANC. C: upper panel, LCRs imaged by confocal microscopy; lower panel, temporal average of the LCRs creates ensemble LCR signal or Late Diastolic Ca²⁺ Elevation (LDCaE) that precedes AP-induced Ca²⁺ transient. D: LDCaE in single SANC of rabbit (sub-panel I, modified from (53)) and guinea-pig (sub-panel ii, modified from (51), published with permission).

This article is the first systematic review dedicated to numerical modeling of pacemaker cell function based on the coupled-clock theory. It summarizes the present state of numerical modeling of the cardiac pacemaker cell as the coupled-clock system. In addition to the two coupled clocks, we also review new emerging numerical modeling approaches which include local Ca²⁺ control, mitochondrial function, biochemical regulation of cAMP production, and protein phosphorylation that drive the pacemaker coupled clock function. We also discuss existing controversies and suggest how these might be resolved in future studies. Because we have broadly and systematically reviewed the evolution of pacemaker mechanisms (4), this critical review discusses only those limited historical aspects that help in resolving existing controversies. Some sections are accompanied by “mini-summaries” that recap major ideas that we believe are important for realistic numerical modeling of cardiac pacemaker cells and may provide a new framework for future work.

2. Basic concepts: Cardiac pacemaker cells and the Diastolic Depolarization (DD)

Pacemaker cells within the heart that have “Clocks” with the briefest rhythmic periods “capture” or trigger other excitable cells. Sinoatrial node cells (SANC) are the dominant cardiac pacemaker cells, because they exhibit shorter periods between spontaneous action potential (APs) than do atrioventricular nodal cells or His-Purkinje cells. Thus, SANC normally initiate the cardiac impulse by generating spontaneous APs that are conducted to the ventricle and entrain the duty cycle of ventricular myocytes.

Different types of heart cells, i.e., pacemaker cells within the sinoatrial node and contractile ventricular myocytes within myocardium, determine the rate and strength, respectively, of the heart beat. During diastole the myocytes maintain their resting potential close to the K⁺ equilibrium potential of −90 to −80 mV. In contrast, the heart’s pacemaker cells generate spontaneous rhythmic changes of their membrane potential, known as the slow diastolic depolarization (DD) that starts from the maximum diastolic potential (MDP) of about −65 mV. When the membrane potential (V_m) reaches an excitation threshold of about −40 mV, the pacemaker cell spontaneously generates the next AP (blue curve in Fig.1B).

3. A modern view on the cardiac pacemaker mechanism: a coupled clock system

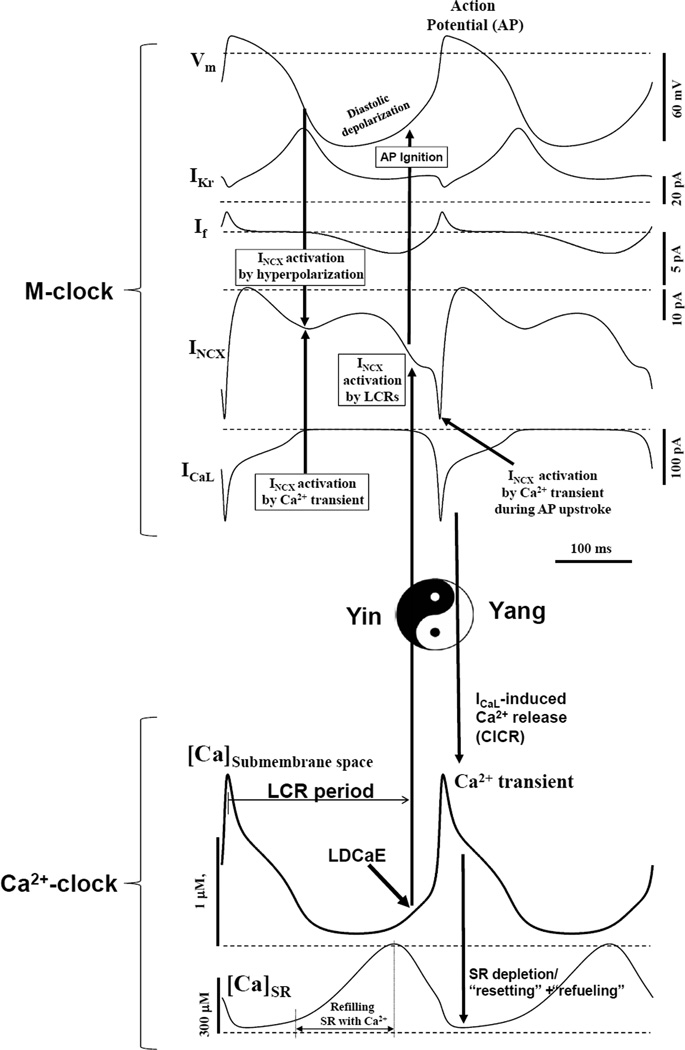
A modern perspective considers SANC, per se, as a system, comprised of several levels of complexity and integrated intracellular and cell membrane components (Fig.1A) resulting in coupled electrical and intracellular Ca²⁺ signals (Fig.1B–D) required for normal pacemaker function. Figure 2 shows the dynamic interplay of major ion currents and Ca²⁺ signal dynamics predicted by a contemporary numerical SANC model (discussed below) that embraces many of these interactions.

Figure 2.

Maltsev-Lakatta model (10) predicts the “yin-yang” type, synergistic interactions within the coupled-clock system of SANC (see text for details). Modified from (10).

3.1. Membrane clock

The ensemble of electrogenic molecules within the cell membrane (i.e. ion channels and ion transporters, Fig.1A in blue) imparts the ability of the pacemaker cell to generate DD and rhythmic APs (i.e. automaticity). When activation and inactivation kinetics of the cell membrane ion channels are described by Hodgkin-Huxley (H-H) gating mechanism and assembled together within a context of numerical models in different combinations and contributions, they are able to generate DD and pacemaker potentials observed experimentally. This subsystem of sarcolemmal molecules forming a voltage membrane oscillator was conceptualized as a membrane clock (4) (M-clock, for short). The first M-clock-based pacemaker cell model was developed in 1960 by Denis Noble (6), and it included only two voltage-gated currents (a fast inward Na⁺ current and a slow, delayed rectifier K⁺ current I_K) and a hypothetical time-independent, leak-like Na⁺ background current (I_b,Na). In this first simple model the DD was generated by the inward-going I_b,Na, as the conductance of outward-going I_K underwent a time-dependent decay (dubbed the “g_K” mechanism). Inspired by the H-H theory, a multitude of extensive voltage-clamp studies identified and characterized specific sarcolemmal ion currents. Table 1 summarizes the properties of major currents found in SANC. Interested readers are referred to excellent reviews (38, 39) to learn further details of specific properties of each current, including selectivity, conductance, complex gating schemes, and, when known, their molecular basis. Based on the gating schema of the currents, numerous numerical models have been developed and until recently have dominated the cardiac pacemaker field for several decades. For example, the pacemaker M-clock has been the predominant feature in at least 12 SANC numerical models (40). Major M-clock mechanisms include the aforementioned g_K decay mechanism, hyperpolarization-activated funny current (I_f) (41), T-type Ca²⁺ current (I_CaT) (14–16), L-type Ca²⁺ current (I_CaL) (14), and a sustained inward current (I_st) (26). (Please note that I_st is different from another current called sustained outward current I_sus, that is 4-amonpyridine-sensitive component of I_to). The most recent update on numerical modeling of I_f was published by Verkerk and Wilders (42).

Table 1.

Major ion currents reported in SA node and SANC of various species.

Group of currents	Ion current	References
Voltage-gated Na+ current	INa (absent in primary SANC)	(12, 13)
Voltage-gated Ca2+ currents (ICa= ICaL+ICaT)	ICaL, High voltage-activated, L-type Ca current	(14)
	ICaT, Low voltage-activated, T-type Ca current	(14–16)
Voltage-gated K+ currents (I4-AP=Ito+Isus and IK=IKr+IKs)	Ito, 4-AP sensitive transient K+ current	(17, 18)
	Isus, 4-AP sensitive sustained outward K+ current (the sustained part of initially discovered Ito or I4-AP)	(18, 19)
	IKr, the rapidly activating component of IK exhibiting strong inward rectification (mouse, rat, guinea pig, rabbit)	(20, 21)
	IKs, the slowly activating component of IK exhibiting only weak rectification (guinea pig, pig)	(21)
	IK1, inwardly rectifying K+ current (mouse, rat, and monkey)	(22)
Voltage-gated monovalent cation non-selective currents	Hyperpolarization-activated, “funny” current, If or Ih	(23–25)
	Sustained inward current Ist (non-selective)	(26)
ACh-activated K+ current	IKACh	(27)
Background and ion transporter currents	Store-operated Ca2+ current (mouse)	(28)
	Background Na+ current, Ib,Na	(29)
	Na+/K+ pump current, INaK or Ip	(30, 31)
	Na+/Ca2+ exchanger current, INaCa or INCX	(32–36)
	Cl− current, ICl Present in about one third of rabbit SANC	(37)

It has been later realized, however, that a direct application of the H-H approach to understanding the cardiac pacemaker function is problematic and insufficient (10, 43, 44). M-clock-based models fail to reproduce many experimental results, especially a substantial AP firing rate reduction or a cessation of automaticity of pacemaker cells produced by specific inhibition of Ca²⁺ cycling (9, 32, 33, 45, 46) or PKA-dependent phosphorylation (47). These experimental results, however, are reproduced by novel numerical modeling (described below), in which M-clock mechanisms do not operate in isolation, but dynamically interact with intracellular signaling, i.e. within the complex integrated system of intracellular and cell membrane proteins, as shown schematically in Figure 1A. We believe that realization and validation of these two-way symbiotic interactions (marked “Yin-Yang” in Fig.2) is the key to resolving many existing controversies within the cardiac pacemaker field (discussed below in Section 5).

Mini-summary

1. The ensemble of ion currents generated by electrogenic proteins of cell surface membrane is defined as the M-clock.

2. While the ion currents are the immediate cause of any membrane potential change, they are dynamically modulated by rhythmic intracellular signaling.

3. Despite the fact that the M-clock generates perfect pacemaker potentials in silico and has been considered as the dominant pacemaker mechanism for more than 50 years, numerical models based mainly on M-clock cannot explain recent experimental results and become obsolete.

4. Modern numerical modeling includes emerging powerful intracellular pacemaker mechanisms dynamically coupled to M-clock.

3.2. Calcium-clock

A powerful intracellular pacemaker mechanism is linked to the SR, a major Ca²⁺ store in cardiac cells. It has a molecular Ca²⁺ pump (SERCA) and Ca²⁺ release channels (ryanodine receptors, RyRs) and, when Ca²⁺ is available, is capable of generating almost periodic, rhythmic Ca²⁺ oscillations, independent of cell surface membrane function (7, 48). Thus, the SR has been conceptualized as a Ca²⁺ clock (in grey in Fig.1A) (4). The Ca²⁺ clock is active in the basal state in cardiac pacemaker cells and contributes to their DD via multiple Ca²⁺ dependent processes embodied within the cell surface membrane.

Specifically, Ca²⁺ clock generates localized diastolic Ca²⁺ releases (dubbed Local Ca²⁺ Releases or LCRs, Fig.1B) in pacemaker cells in the absence of Ca²⁺ overload as documented in confocal imaging of Ca²⁺ dynamics in mammalian SANC and atrial subsidiary pacemaker cells combined with non-invasive perforated patch-clamp electrophysiology (35, 49). These LCRs are initiated beneath the cell surface membrane during DD via spontaneous activation of RyR. In confocal line-scan recordings, LCRs appear as 4–10 µm Ca²⁺ wavelets during and following the dissipation of the global systolic transient effected by the prior AP, and crescendo during the DD, peaking during the late DD, as they merge into the global cytosolic Ca²⁺ transient triggered by the next AP. A high-speed camera detects from 8 to 27 (13 on average) LCRs per cycle during spontaneous AP firing by rabbit SANC, with the LCR size increasing as DD progresses from the MDP to the AP threshold (50). The individual diastolic LCRs form an ensemble Ca²⁺ signal (i.e. integral of all LCRs, Fig.1C,D) reported in single pacemaker cells of numerous species (35, 49, 51–55). Joung et al. (56) coined the term “Late Diastolic Ca²⁺ Elevations” (LDCaE) for this LCR-generated signal when it was found in SA node tissue (56, 57).

LCR occurrence does not require triggering by depolarization of the surface membrane: persistent rhythmic oscillatory membrane currents can be activated by rhythmic LCRs during voltage-clamp (at potentials that prevent cell Ca²⁺ depletion, e.g. −10 mV) (48). Both persistent LCRs and the net membrane current exhibit simultaneous fluctuations of the same frequency (47, 48), and both are abolished by ryanodine (58). Sustained LCR activity is also observed in chemically “skinned” SANC (i.e. having a detergent-permeabilized cell surface membrane) bathed in a physiological [Ca²⁺] of 100 nM (47, 48). LCRs are generated as rhythmic events at rates of 1 to 5 Hz, i.e. encompassing those of spontaneous AP firing in SANC. In the absence of β-Adrenergic Receptor (β-AR) stimulation (i.e. in the basal state) the Ca²⁺ clock is present and operative in the pacemaker cells, but not in contractile cardiac muscle cells under normal conditions. Rhythmic LCRs occur not because of an elevated intracellular [Ca²⁺] (minimal diastolic [Ca²⁺] is low, ~160 nM, in SANC (48)) but because phosphorylation of Ca²⁺ cycling proteins is enhanced in these pacemaker cells (47), whereas phosphorylation state of these proteins in the muscle cells is suppressed (59).

Mini-summary

1. An SR-based “Ca²⁺ clock” is a fundamental property of cardiac cells.

2. During spontaneous AP firing, SR of SANC generates two major Ca²⁺ releases: one is the AP-induced Ca²⁺ transient via classical Ca²⁺-induced Ca²⁺ release (CICR) mechanism and the other is the LCR mechanism during DD.

3. LCRs are driven by enhanced pumping and release due to an enhanced phosphorylation state of SR Ca²⁺ cycling proteins and free Ca²⁺ available for cycling (i.e. oscillatory substrate).

3.3. The coupled-clock system: its interactions and phosphorylation-driven mechanism

Interaction of the clocks occurs throughout the entire pacemaker cell duty cycle. During DD, the ensemble LCR signal (i.e. LDCaE) activates inward I_NCX that accelerates DD and “ignites” the next AP (Fig.2, “AP ignition”). Thus, the timing of this acceleration is crucial for the cycle length and therefore for the beating rate under given conditions. This crucial timing has been characterized in terms of the LCR period, determined as the delay between the AP-triggered global cytosolic Ca²⁺ transient and LCR emergence during DD (“LCR period” in Figs 1B, 2).

The most recent paradigm shift in our understanding of cardiac pacemaker function was the realization that while LCRs are generated by the SR (i.e. by the Ca²⁺ clock), the LCR period is not an exclusive property of the SR, but it reflects the functional state of the entire system that also includes ion currents of the M-clock. As a matter of fact, the LCR period is regulated not only by the kinetics of SR Ca²⁺ pumping and release, but also by the quantity of intracellular Ca²⁺ made available for pumping into the SR via sarcolemmal Ca²⁺ flux (Fig.2, “refueling”) which is regulated by membrane ion channels and transporters. The contributions of L-type Ca²⁺ channels (LCCh) and NCX to the Ca²⁺ balance and, hence, LCR period are obvious. But K⁺ channels, and even funny channels (I_f panel in Fig.2), are also indirectly implicated in the Ca²⁺ balance: K⁺ channels repolarize membrane potential to deactivate LCCh and to activate I_NCX, and funny channels limit hyperpolarization and, hence, Ca²⁺ efflux via NCX. Thus, the LCR period embraces complex interactions of cell membrane electrogenic molecules and intracellular Ca²⁺ cycling molecules (Fig.1A) and is a “readout” of the restitution kinetics that define the “ticking speed” of the coupled-clock system.

While individual wavelet-like LCRs exhibit a degree of stochasticity in their occurrence, they form LDCaE that appears fairly synchronously and rhythmically, i.e. approximately at the same time during DD, determined (on average) by the functional state of the complex protein phosphorylation regulatory network (Fig.1A) in a given steady-state condition. A major feature of this network is a relatively high level of basal cAMP (47) and PKA-dependent and CaMKII-dependent phosphorylation of proteins in SANC (both in SR and cell membrane) that is achieved due to a high constitutive level of activation of adenylyl cyclases (ACs) that drives spontaneous LCRs.

Although SANC, like ventricular myocytes, express high levels of Ca²⁺-inhibited AC types 5 and 6 (60), the discoveries of Ca²⁺-activated AC types, i.e. AC1 and AC8, in rabbit and guinea-pig SANC (61, 62) and localization of the basal Ca²⁺-activated AC activity within lipid raft microdomains (62) link Ca²⁺ to localized cAMP production (Fig.1A). Ca²⁺ binds to calmodulin to activate AC, leading to a high basal level of cAMP-mediated, PKA-dependent phosphorylation of surface membrane and intracellular proteins involved in cell Ca²⁺ balance and SR Ca²⁺ cycling (47, 62) (Fig.1A).

Steady levels of activation of the effector proteins are ensured, in turn, by mechanisms to damp this complex cAMP-phosphorylation-driven signaling (Fig.1A, red arrows). Basal phosphodiesterase activity is one such restraining mechanism to reduce the high constitutive AC activity in SANC (63). Basal activation of phosphoprotein phosphatases in SANC (64) is another mechanism that limits PKA and CaMKII-dependent phosphorylation. The net result of basal activation of phosphodiesterase and phospho-protein phosphatases is that the basal LCR period and AP cycle length are maintained near the midpoint of their functional ranges. Other restraining mechanisms of the system limit Ca²⁺ influx and hence cell Ca²⁺ load, for example, calmodulin-mediated LCCh inactivation, which limits Ca²⁺ influx via LCCh during each AP. Thus, the robustness of the coupled-clock system is imparted by its numerous functional redundancies and dual regulation of SR Ca²⁺ cycling and membrane ion current generators by a common set of factors (coupling factors or nodes, Fig.1A, purple labels). The system activity is kept in check by “brakes” (Fig.1A, red arrows) represented by phosphodiesterase and phosphatase activities, voltage-dependent negative feedback on ion fluxes and calmodulin-dependent modulation of LCCh.

Mini-summary

1. LCR ensemble signal (LDCaE) during DD activates I_NCX that accelerates DD and therefore the LCR timing regulates DD and thus the AP firing rate.

2. Ca²⁺ fluxes via surface membrane proteins regulate intracellular Ca²⁺, and therefore the LCR period is a property of the entire coupled-clock system, not just a sole function of SR cycling proteins.

3. cAMP, Ca²⁺, and PKA- and CaMKII- dependent protein phosphorylation, are major regulatory nodes of the coupled system (Fig.1A).

4. The system is restrained from “explosion” by molecular “brakes” (Fig.1A, red arrows) that keep the system regulation under basal condition close to its mid-range.

5. The complex interactions depicted in Figure 1A are the essence of the system’s ability to function as a clock, i.e. despite substantial transient cell Ca²⁺ changes during each AP cycle, the steady-state average cell Ca²⁺ balance and levels of phosphorylation of M and Ca²⁺-clock proteins remain stable, so that all events recur each cycle in same sequence, timing, and magnitude, thus ensuring a stable AP CL.

4. Novel numerical models based on the coupled-clock mechanism

4.1. New insights derived from first coupled-clock model of 2009

First attempts (54, 65) to numerically model LCRs and their ensemble signal (LDCaE in current terminology) used a smooth function, such as a sine function, with a given phase and amplitude, directly mimicking their experimentally measured values. These phenomenological Ca²⁺ release formulations were integrated into a SANC model (such as 2002 Kurata model (66)) that mimicked experimentally observed Ca²⁺ signals in SANC. While this kind of relatively simple modeling demonstrated a capability of Ca²⁺ releases to generate powerful NCX currents contributing to the DD, it remained essentially naive and did not embrace a numerical mechanism of Ca²⁺ “clocking”. Next theoretical model of cardiac pacemaker function known as Maltsev-Lakatta model (or ML model) predicted oscillatory LCR signals driven by SR Ca²⁺ pumping and release kinetics. Key predictions of the ML model are shown in Figure 2.

While the ML model originated prior 2002 Kurata et al. model (66), it has many features that have provided (and continue to provide) new insights into cardiac pacemaker cell function. The SR Ca²⁺ release approximation was adopted from formulations suggested earlier by Shannon et al. (67). This model was constructed and optimized based on the results of a wide-scale parametric sensitivity analysis of classic formulations of membrane clock and Ca²⁺ cycling (within 100s of thousands of specific models, see Section 6.1 for details). This approach allowed to find realistic numerical solutions that reproduced the new experimental results.

Specifically the ML model reproduces effects of basal phosphorylation of phospholamban and RyR (47) by enabling higher rates of SR Ca²⁺ pumping and release vs. prior SANC models and models of cardiac muscle cells. With these fundamental changes, SR indeed becomes a numerical Ca²⁺ oscillator based on a simple Release-Pumping-Delay mechanism. The oscillator operates within a broad range of parameters and generates Ca²⁺ releases over a wide range of frequencies (1.3 to 6.1 Hz) that encompass physiological heart rates of many mammalian species.

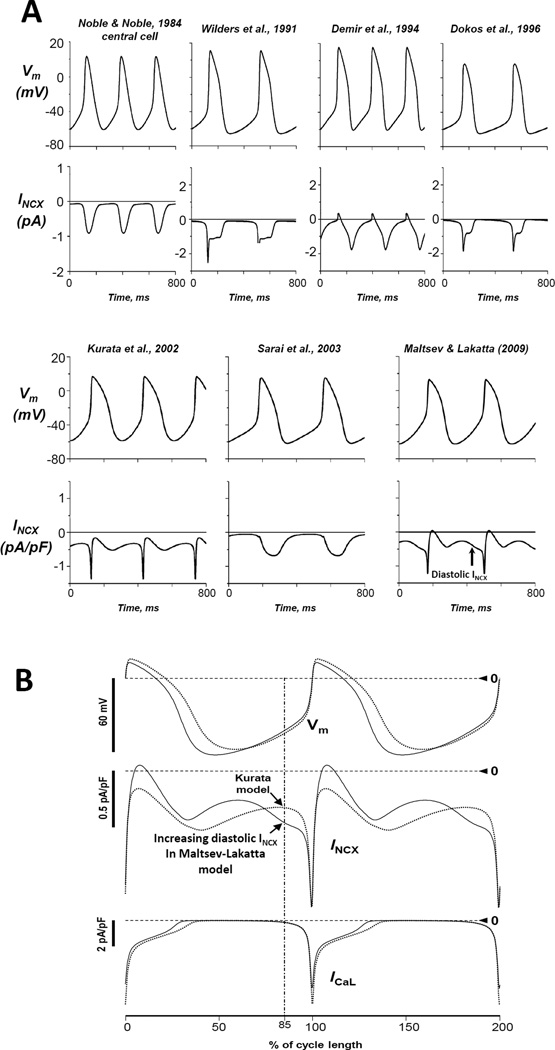
The integrated Ca²⁺ clock and M-clock within the ML model generates substantial diastolic Ca²⁺ release and I_NCX, found previously experimentally (35), but absent in prior models (Fig.3A). Figure 3B shows that diastolic I_NCX substantially increases before I_CaL activation in the model, but not in Kurata et al. model (66). The ML model faithfully reproduces new experimental results with perturbation of Ca²⁺ cycling (e.g. ryanodine effect) and phosphorylation (e.g. PKA inhibition). Importantly, SR Ca²⁺ clock not only modulates the M-clock, but that the M-clock, in turn, also affects Ca²⁺ clock (Fig.2). Functions of both clocks are simultaneously and dynamically coupled in the model via multiple coupling factors, such as Ca²⁺ cAMP, PKA, and CaMKII. Thus, the complex model behavior and regulation are characterized in new terms “coupling factors” and “the coupled clock system”: “the coupled clock system is very robust and, importantly and advantageously, also very flexible” (10). Indeed, surprisingly the coupled system exhibited a greater robustness and flexibility than M-clock operating alone (see section 6.1 for details).

Figure 3.

A: Comparison of I_NCX dynamics in different pacemaker cell models. A: Only Maltsev-Lakatta model (10), featuring Ca²⁺ clock, exhibits substantial increase in diastolic I_NCX. Modified from (44). B: In contrast to Kurata et al. model (66) (dotted curves), the ML model (solid curves) exhibits strong increase of inward I_NCX during DD clearly before activation of I_CaL. The cycle lengths were 307.5 ms and 333 ms for Kurata et al. model and the Maltsev-Lakatta model, respectively. The vertical dash-dot line of 75% of cycle length illustrates approximate timing for I_CaL activation. Modified from (10).

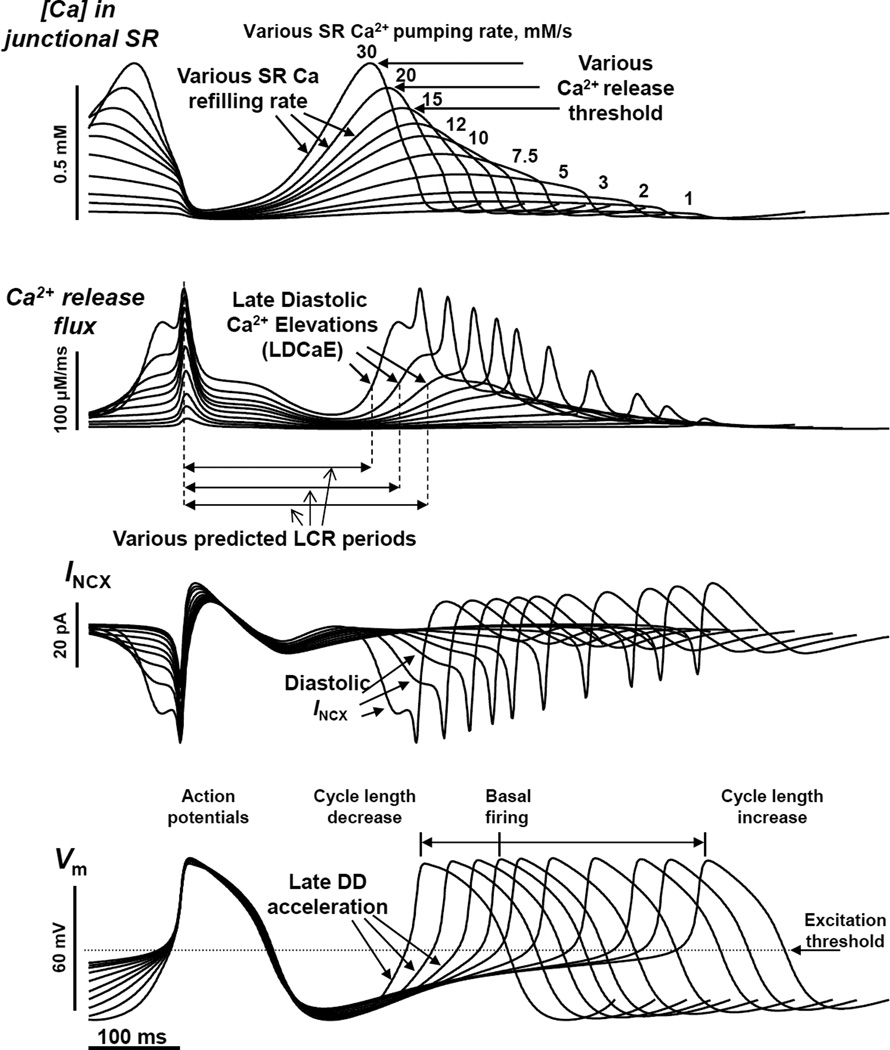
Additional numerical model simulations provide further mechanistic insights into the complex SR restitution process and its control of the AP cycle length (Fig.4). The simulations predict the wide range of pacemaker rate regulation via variations in the maximum SR Ca²⁺ pumping rate (P_up, reflecting the number of functional SERCA molecules and phospholamban phosphorylation by PKA, 1 to 30 mM/s). In particular, the more rapid the SR Ca²⁺ pumping kinetics, the sooner the SR gets refilled with Ca²⁺ to achieve the threshold required for spontaneous diastolic release (reflected in the ensemble LCR signal, i.e. LDCaE). The earlier Ca²⁺ release at higher P_up generates an earlier I_NCX which accelerates DD rate at an earlier time, leading to an increase of the AP firing rate. The ML model prediction of the crucial importance of SR Ca²⁺ refilling kinetics for SANC AP firing rate has been confirmed in other numerical modeling studies (43, 68) and also experimentally, specifically by measuring SR Ca²⁺ signals (via a Fluo-5N indicator) (69).

Figure 4.

The Maltsev-Lakatta model (10) predicts the wide range of pacemaker rate modulation via variations in SR Ca²⁺ pumping rate (1 to 30 mM/s), mimicking various degrees of PKA-dependent phospholamban phosphorylation. Modified from (10).

Another interesting prediction of the ML model is that at higher pumping rates the diastolic release occurs not only earlier, but also stronger. This highly synchronized release generates a stronger I_NCX that allows to reach the AP threshold in a shorter time (i.e. ensures robust AP ignition).

Mini-summary

1. Classical theoretical models portray SANC pacemaker mechanisms mainly as an M-clock (40). The coupled-clock ML model differs fundamentally from the mainly-M-clock-based models, and uniquely reproduces many experimentally documented features of pacemaker cells.

2. The ML model and its numerous specific “parametric-space” derivatives provide a new framework for further numerical investigation of the coupled-clock pacemaker system to discover the best match for existing and future experimental results.

4.2. Novel interpretation of ivabradine-induced bradycardia

Ivabradine at low concentrations (below 3 µM) specifically inhibits I_f, i.e. it does not directly suppress L-type current (70), SR Ca²⁺ cycling (71) and other surface membrane ion channels (72). A beneficial effect of ivabradine for heart rate reduction has been confirmed in clinical trials (review (73)) and interpreted solely on the basis of I_f inhibition. Within the coupled-clock theory discussed above, however, SANC normal automaticity is regulated by a crosstalk between M-clock and Ca²⁺ clock and, indirect suppression of the Ca²⁺ clock is therefore expected to further contribute to the steady-state ivabradine-induced bradycardia. This interesting hypothesis has been recently tested by Yaniv et al. (71) in rabbit SANC. Indeed, ivabradine-induced slowing of the AP firing rate is accompanied by indirect reduction of SR Ca²⁺ load, slower intracellular Ca²⁺ cycling kinetics, and prolongation of the LCR period.

Numerical model simulations, also performed by Yaniv et al. (71) using the modified coupled-clock ML model (74), provided further insights into the complex ivabradine effects (Fig.5). We predicted that a reduction in I_f indirectly inhibits Ca²⁺ clock: it initiates a reduction in number of APs per unit time that reduces the Ca²⁺ influx per unit time. This reduction in net Ca²⁺ influx results in a reduction in Ca²⁺ available for pumping (because of a reduction in cytosolic Ca²⁺), reducing the SR Ca²⁺ load and prolonging the period of local Ca²⁺ release. Prolongation of LCR period shifts the Ca²⁺ activation of I_NCX to a later time during DD, which further reduces the AP firing rate, leading to further reduction in Ca²⁺ influx per unit time. In other words, inhibition of the Ca²⁺ clock induces further indirect suppression of the M-clock, and so on, until the system reaches a new steady-state bradycardia. Importantly, this entrainment between the two clocks (documented within the context of a coupled-clock numerical model) is required to explain the experimentally verified AP firing rate reduction by ivabradine.

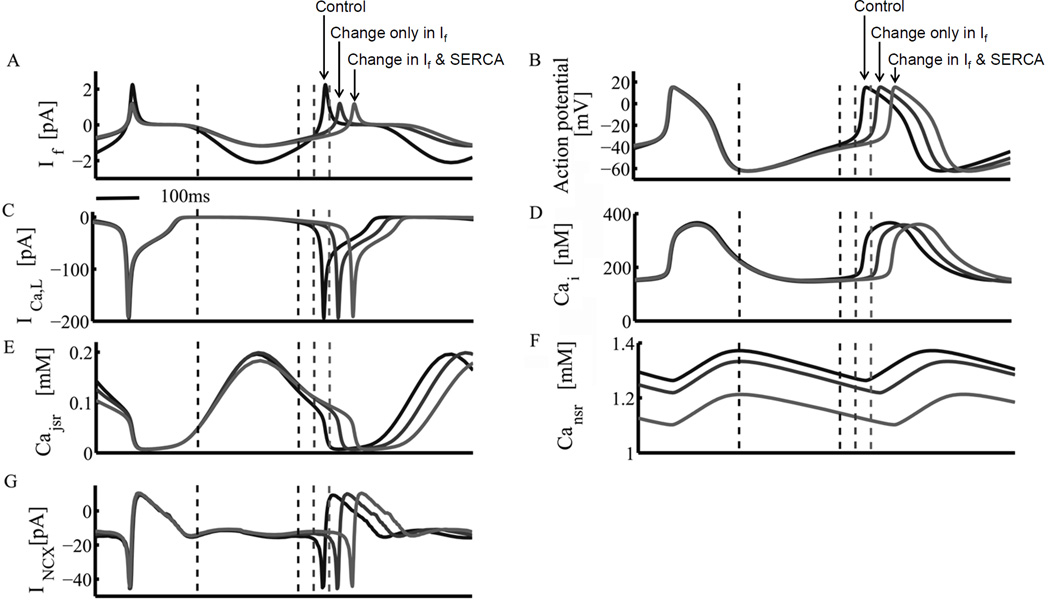
Figure 5.

Effect of a specific reduction of I_f on AP firing rate is mediated via perturbation of both M-clock and Ca²⁺ clock. Simulations using the Maltsev-Lakatta model (10) with integrated mitochondrial Ca²⁺ dynamics predict the effects of IVA on (A) I_f, (B) AP, (C) I_CaL, (D) cytosolic Ca²⁺, (E) junctional, (F) network SR [Ca²⁺], and (G) sarolemmal I_NCX. “Control”: model simulations prior to drug. “Change only in I_f”: model simulations when only I_f conductance is reduced. “Change in I_f and SERCA”: model simulations when both I_f and SR Ca²⁺ pumping (SERCA) parameters were changed. The dashed lines represent the respective diastolic DD phases. From (71).

The numerical model predicts that the complex effects of ivabradine do not end with this kind of “biophysical” entrainment, but also include a “biochemical” component. The initial decrease in Ca²⁺ influx decreases Ca²⁺-activated CaMKII and adenylyl cyclases-cAMP/PKA signaling. The resultant reductions in phosphorylation of Ca²⁺ cycling proteins and membrane proteins further reduce the net Ca²⁺ influx and the SR Ca²⁺ loading and both further reduce AP rate; and, in parallel, the resultant reduction in cAMP further shifts the I_f activation curve. Further numerical model simulations (71) in the absence of this additional “biochemical” crosstalk can account for only about 50% of the experimentally measured reduction in steady-state AP firing rate that occurs in response to ivabradine. The full ivabradine effect can be explained only on the basis of almost equal contributions by the “biophysical” and “biochemical” components.

The bradycardiac effect actually is fully symmetric with respect to the two coupling clocks, i.e. it does not matter of which clock was directly or indirectly perturbed first (71). The LCR period and AP cycle length shift toward longer times almost equally by either direct perturbations of the M-clock (by ivabradine) or of the Ca²⁺ clock (by cyclopiazonic acid, a specific inhibitor of the SR Ca²⁺ pump). During both perturbations the LCR period reports the crosstalk between the clocks. Based on this finding, the steady-state bradycardia associated with different HCN4 mutations is likely mediated, only in part by I_f inhibition, and in part, by change in Ca²⁺ clock due to the clocks’ cross-talk (75). The same is true for mutations of Ca²⁺ regulatory protein (71, 75): only part of the bradycardia effect is explained by a direct change of the Ca²⁺ clock, but the full effect is explained by the coupling of Ca²⁺ clock and M-clock (including e.g. aforementioned cAMP-dependent effect on I_f).

A recently updated ML model by Severi et al. (76), in which I_f amplitude was set substantially larger than in the ML model, can, even with limited crosstalk between the membrane and Ca²⁺ clocks, reproduce the steady-state changes in spontaneous AP firing rate in response to ivabradine (75). However, this model predicts only a modest decrease in SR Ca²⁺ load, which is not in accord with experimental results. Therefore, computational models that predict changes in steady-state spontaneous AP firing rate by ivabradine mainly via changes only in membrane clock (I_f), and not via crosstalk between the clocks are likely not realistic.

Mini-summary

Selective inhibition of either Ca²⁺ clock or M-clock produces …

1. the same effect, i.e. increase in both LCR period and AP firing cl.

2. a suppression of both clocks within this system.

3. a reduction in cAMP/PKA and CaMKII signaling.

4.3. A novel quantitative explanation of autonomic modulation by the coupled-clock theory

Classical numerical models attribute regulation of normal cardiac automaticity in SANC largely to G protein-coupled receptor (GPCR) modulation of sarcolemmal ion currents, specifically I_f, I_CaL, I_Kr, and I_Ks (77). More recent experimental evidence (summarized in (11)), however, indicates that GPCR modulates SANC automaticity over a wide physiologic range, e.g. from 60 to 240 bpm in humans, via variation in GPCR signaling (Fig.1A, green and red shapes) that links both β-AR and ChR to the very same nodes (or coupling factors) of the coupled-clock system (Fig.1A, purple labels, i.e. PKA, CaMKII, cAMP and Ca²⁺) that regulate basal state LCR period: Stimulation of sympathetic β-Adrenergic Receptor (β-AR) in SANC, via G_s activation, increases the spontaneous AP firing rate via effect on proteins of both clocks. As a result, the enhanced and coupled function of the clocks not only modulates ion channel function (as in classical mechanism), but also modulates diastolic LCRs occurrence (i.e. in earlier and more synchronized and abundant LCR occurrence in rabbit SANC (47)). In contrast, Cholinergic Receptor (ChR) stimulation results in later, rare and less synchronized LCR occurrence (78).

This new experimentally discovered LCR-dependent mechanism of autonomic modulation has been recently explored by using the ML model featuring coupled-clock pacemaker mechanism (43). Ca²⁺ release characteristics in the model were graded by variations in the SR Ca²⁺ pumping capability (P_up) by SERCA, but ion channels were simultaneously modulated as previously reported in voltage-clamp studies. SERCA activity is partially inhibited by phospholamban (Fig.1A). This inhibition wanes and SERCA activity increases when phospholamban becomes phosphorylated via cAMP-dependent PKA signaling. Thus, P_up variations in the model mimic, in part, various degrees of phosphorylation of phospholamban by PKA due to autonomic modulation via GPCR and GPCR-activated AC (Fig.1A).

The novel numerical model (43) of pacemaker rate modulation via GPCR is based on numerous complex synergistic interactions between sarcolemmal and intracellular processes via membrane voltage and Ca²⁺. Major interactions include changes of I_NCX that couple the respective changes in phase and amplitude of diastolic Ca²⁺ releases to the DD rate and ultimately to the AP potential firing rate (Fig.6A). Concomitantly, changes in amplitude and frequency of I_CaL activation shift cell Ca²⁺ balance to support the respective Ca²⁺ cycling changes.

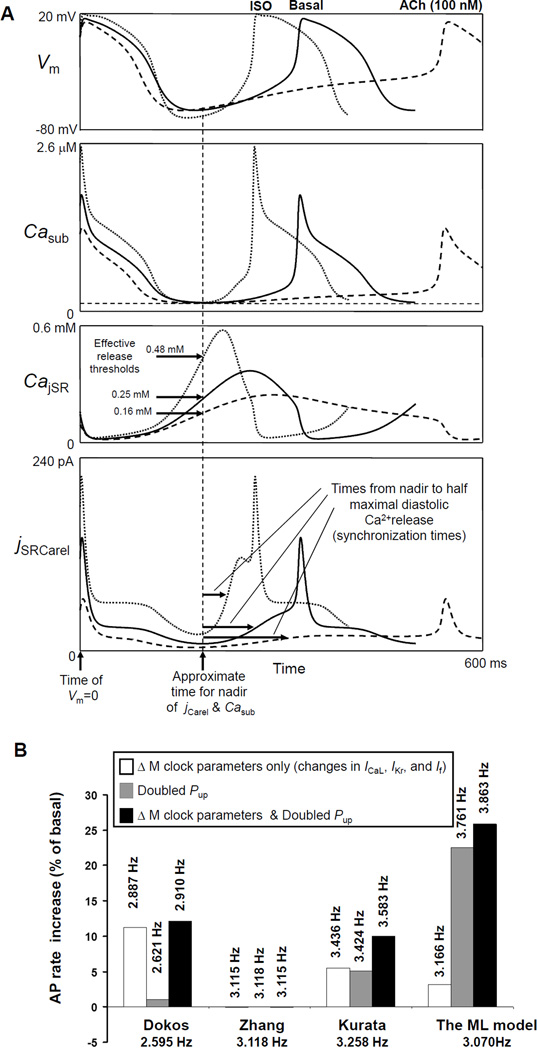
Figure 6.

Numerical modeling of GPCR modulation of AP firing rate in rabbit SANC. A: The coupled-clock ML model prediction for the mechanisms of spontaneous Ca²⁺ release in rabbit SANC and their modulation by β-AR (ISO) or ChR (ACh) stimulation. Panels show model simulations of simultaneous changes in membrane potentials (V_m), submembrane [Ca²⁺] (Ca_sub), [Ca²⁺] in junctional (i.e. Ca²⁺ releasing) SR (Ca_jSR), and Ca²⁺ release flux (j_SRCarel). The Ca²⁺ release becomes more synchronized and occurs earlier in case of ISO, but less synchronized and occurs later in case of ACh, as reflected by times to half maximum of the diastolic release (in j_SRCarel panel). Modified from (43). B: Only the ML model predicts the full scale of β-AR stimulation effect reported within the range of 25–30% increase in AP firing rate in rabbit SANC. SANC models, lacking diastolic Ca²⁺ release, substantially underestimate the effect of β-AR stimulation. Models are labeled as follows: “Dokos” (79), “Zhang” (80), “Kurata”(66). Respective bars show the model predictions for the effects of experimentally reported changes of M-clock parameters, doubling the capability of SR Ca²⁺ pumping, P_up, or both changes combined. Spontaneous rate change was negligible (within 0.1%) in Zhang et al. model (Note this model has no Ca²⁺ dynamics, i.e. [Ca²⁺]=const). Absolute AP firing rates predicted by the models are shown by labels at the respective bars. Modified from (43).

The model faithfully predicted the entire range of physiological chronotropic modulation of SANC by activation of β-AR or ChR only when experimentally documented changes of sarcolemmal ion channels are combined with a simultaneous increase/decrease in SR Ca²⁺ pumping capability. In contrast, prior models developed by Dokos et al. (79), Zhang et al. (80) and Kurata et al. (66) mainly based on M-clock function do not predict β-AR stimulation effect with experimentally documented changes in I_CaL, I_Kr, and I_f and doubled SR Ca²⁺ pumping capability (Fig.6B).

Mini-summary

1. Autonomic modulation of AP firing rate by SANC involves changes not only in ion channels but also in Ca²⁺ cycling proteins and both effects are predicted by the coupled-clock numerical model simulations.

2. Ca²⁺ clock is regulated by ion channels via their contribution to cell Ca²⁺ balance.

3. Varying degree of phosphorylation of proteins comprising the coupled-clock system is a key factor in the new mechanism of autonomic modulation of AP firing rate.

4. GPCR signaling translates autonomic modulation to effector proteins of both clocks via the same coupling factors (Ca²⁺ and PKA-dependent phosphorylation) that ensure robust pacemaker cell function in the basal state.

5. This universal (coupled-clock) mechanism confers robustness and simultaneously flexibility to cardiac pacemaker cell system that cannot be achieved by the M-clock alone.

4.4. Kinetics and magnitude of AC-cAMP/PKA signaling

It has been shown that basal, steady-state levels of cAMP and the phospholamban phosphorylation are relatively high vs. ventricular myocytes, and they increase further in response to β-AR stimulation (47) or decrease in response to ChR stimulation (78). However, a realistic numerical modeling of the complex networks of enzymatic cascades that regulate cardiac pacemaker function (Fig.1A) ought to include kinetic properties of the system components. These, however, remain mainly unknown and require dedicated studies. Specifically, it is important to quantify experimentally and numerically the kinetics of cAMP formation, PKA activation and protein phosphorylation, and their relationships to changes in spontaneous AP firing rate. The cAMP formation rate has been reported by measuring AC activity in suspension of lysates of pacemaker cells (62). The cAMP formation rate turned out to be Ca²⁺ dependent. A recent pilot study by Yaniv et al. (81) has made the first attempt to measure the live kinetics and magnitude of PKA activity in single pacemaker cells. Cultured rabbit SANC were infected with an adenovirous expressing the PKA activity FRET sensor, AKAR and changes in kinetics and magnitude of PKA activity were measured in response to graded β-AR stimulation (using isoproterenol). In parallel, the AP firing rate kinetics were measured in another subset of cells. PKA and AP firing rate kinetics change in parallel in response to different isoproterenol concentrations (Yaniv et al. unpublished observations).

A novel integrative numerical model has been developed based on the ML model to simulate the expected rate of cAMP production and the kinetics and magnitude of protein phosphorylation (81). The model includes previously measured steady-state AC-activity, cAMP and phospholamban phosphorylation levels in response to perturbation that influence cAMP/PKA signaling and the changes in the kinetics and magnitude of PKA activation. In response to maximal β-AR stimulation the model simulations predict that the rate of cAMP generation was slower than that of the experimentally measured PKA activation.

Mini-summary

1. Despite their crucial functional importance (discovered experimentally), the complex networks of enzymatic cascades in pacemaker cells remain basically unexplored numerically.

2. The first coupled-clock numerical model based on recent measurements of PKA kinetics via a FRET sensor, demonstrates that the signaling cascade “Ca²⁺→CaM→CaM-activated-AC→cAMP→PKA→ phosphorylation” (Fig.1A) regulates the spontaneous AP firing rate of SANC across its entire physiological range.

3. Further progress in numerical studies requires obtaining additional data on kinetics and magnitude of activity of the cAMP/PKA and CaMKII signaling in response to different perturbations.

4. Because both cAMP and phosphorylation signaling are highly compartmentalized, an important aspect of future realistic modeling is regulation of local interactions within the enzymatic pathways.

4.5. SANC energetics

Recent studies characterized major mechanisms that control ATP supply and demand in SANC (74, 82, 83). The mitochondrial density and respiration rate (which, in a physiologically coupled mitochondrial system, reflects the rate of mitochondrial ATP production) in SANC are similar to that in electrically stimulated ventricular myocytes at 3 Hz (82). However “the energy budget” is managed differently in the two cell types: the myofilament force production is the major ATP consumer in ventricular myocytes, while in SANC synthesis of cAMP and cell ionic homeostasis (especially Ca²⁺ cycling maintenance) are the major ATP consumers. Moreover, the control mechanisms that match ATP supply to demand in SANC are different from those in ventricular myocytes. In ventricular myocytes cytosolic Ca²⁺ enters mitochondria through the mitochondrial uniporter (84) and is extruded by the mitochondrial NCX (85). Changes in mitochondrial Ca²⁺ in these cells alter the activity of several mitochondrial enzymes that take part in ATP production (see review (86)). In contrast to ventricular myocytes, in which Ca²⁺ and ADP/Pi directly signal to the mitochondria to regulate basal state ATP supply (for review cf (87)), in SANC a reduction of Ca²⁺ influx into the mitochondria does not significantly alter the ATP level in the basal state. Instead, Ca²⁺-calmodulin activation of cAMP/PKA and CaMKII signaling in SANC has a major role to link basal ATP utilization and mitochondrial ATP production: a gradual reduction in cAMP/PKA (82) and/or CaMKII (74) signaling is accompanied by gradual reduction in ATP and a reduction in AP firing rate. At high ATP demand, however, both Ca²⁺ directly and indirectly, via calmodulin activation of cAMP/PKA and CaMKII signaling, control ATP supply to demand matching (83).

Mini-summary

1. Future modeling approach should include ATP production mechanisms and the limit of available ATP at low demand.

2. The Ca²⁺-activated-cAMP/PKA signaling cascade that drives spontaneous AP firing of SANC is a unique core feed-forward system, that not only drives the basal ATP consumption but also regulates the ATP production. Therefore, numerical models of cAMP/PKA signaling should also include this signaling to mitochondrial ATP production.

3. A decease in spontaneous AP firing rate is associated with decrease in the ATP level.

4. Although only a prototype model exists to correctly describe the ATP energetics balance in SANC (88), future models that attempt to describe the effect of reduction in cAMP/PKA and CaMKII signaling on spontaneous AP firing rate should take into account that ATP may not be available to ATP-dependent mechanisms (e.g., Na⁺/K⁺ATPase, SERCA pump) and that part of the reduction in spontaneous AP firing rate is due to lack of available ATP.

4.6 Mitochondria in SANC dynamically buffer cytosolic Ca²⁺

Similar to ventricular myocytes, mitochondrial Ca²⁺ flux in SANC plays a fundamental role in buffering cytosolic Ca²⁺ and modulates SR Ca²⁺ load under normal conditions (74). And therefore it must indirectly affect SR Ca²⁺ release (Fig.7). Recent experimental studies have shown that, indeed, an increase in mitochondrial Ca²⁺ by inhibition of mitochondrial NCX also decreases the SR Ca²⁺ load and as expected on the basis of coupled-clock theory, reduces the ensemble LCR Ca²⁺ signal (74). In contrast, a reduction in mitochondrial Ca²⁺ by inhibition of the mitochondrial uniporter increases the SR Ca²⁺ load and increases ensemble LCR Ca²⁺ signal. Therefore, changes in Ca²⁺ cycling into and out of mitochondria in SANC modulate basal coupled-clock system automaticity.

Figure 7.

Schematic illustrations of the coupled clock system that includes a mitochondrial Ca²⁺ flux. From (71).

To quantitatively simulate SR and mitochondrial dynamics, surface membrane currents and AP firing rate when mitochondrial Ca²⁺ is perturbed, the SANC coupled-clock numerical model (10) was extended to include mitochondrial Ca²⁺ fluxes (74). Simulations of the extended coupled-clock numerical model predicted both systolic and diastolic levels of mitochondrial [Ca²⁺], whereas experimental data do not permit quantification of these levels, rather only an average level of mitochondrial [Ca²⁺] can be measured (using Mn²⁺ quench technique (74)). Moreover, the model simulations predict that the major M-clock component that induces change in spontaneous AP firing rate when mitochondrial Ca²⁺ is perturbed is the sarcolemmal NCX, due to changes in its current kinetics altered indirectly by changes in LCR characteristics.

Mini-summary

1. Changes in Ca²⁺ cycling into and out of mitochondria in SANC modulate basal coupled-clock system automaticity via an impact on cell Ca²⁺, SR Ca²⁺ loading and on the SR Ca²⁺ release characteristics.

2. This mitochondrial Ca²⁺-SR Ca²⁺ crosstalk is important for SANC pacemaker function. A prototype numerical model has recently been devised (74).

5. Controversies, unsolved problems and their possible solutions

5.1. Asymmetric interactions of M-clock and Ca²⁺ cycling in earlier models

Historically, the first Noble model of 1960–1962 (6, 89) and MNT models (90) had fixed ion concentrations, and could not describe Ca²⁺ dynamics. In the early 1980s this problem was approached by including formulations for ion concentrations in their pacemaker models (Noble 1984 (91)). This move followed basically an approach undertaken earlier by Beeler and Reuter in 1977 (92) to introduce [Ca²⁺] into AP model of a ventricular myocyte. While the upgraded Purkinje cell model [DiFrancesco-Noble model of 1985 (93)] and its SANC modification [Noble-Noble model of 1984 (91)] included Ca²⁺ dynamics, precise studies on Ca²⁺ dynamics in pacemaker cells have not been performed until very recently, so that the model formulations were chosen mainly to simply reproduce AP-induced Ca²⁺ transient, similar to ventricular myocytes. Specifically, describing their model, DiFrancesco and Noble wrote “There are too many arbitrary factors and, in any case, the major issue of whether Ca²⁺ release is Ca²⁺-induced or voltage-induced (or, perhaps, both) is still controversial. Our purpose here is therefore largely limited to reproducing the known [Ca]i transient time course… Even a primitive model, here, is much better than no model at all. “

In their recent article “Competing oscillators in cardiac pacemaking: historical background” (94), Noble et al., while accepting the idea that mutual entrainment of the intracellular Ca²⁺ oscillator and surface membrane oscillator (Ca²⁺ clock and M-clock in our terminology) controls normal automaticity of the heart’s pacemaker cells, attempted to make the case that these oscillators are asymmetric. Specifically, the authors claim that the surface membrane voltage oscillator operates independently of the intracellular SR Ca²⁺ oscillator. Further they contended that the membrane oscillator can maintain its normal function in the absence of the intracellular Ca²⁺ oscillator. In our opinion, in silico simulations of sinoatrial node cell function in the context of older numerical models, like the 1984 model, that lead to the idea of asymmetry within the coupled membrane-Ca²⁺ oscillator system (with membrane oscillator dominance) are not realistic because a plethora of robust experimental data assembled by numerous investigators demonstrates that the membrane oscillator in pacemaker cells cannot function normally without the intracellular Ca²⁺ oscillator. When intracellular Ca²⁺ cycling is disrupted, the generation of spontaneous AP firing becomes substantially slow, dysrhythmic, or ceases altogether (see review (11)). In contrast, in silico, in the original 1984 model (publically available at CellML.com) complete inhibition of SR Ca²⁺ release (i_rel=0) has little effect on AP firing rate or rhythm (the in silico rate actually slightly increases, rather than decreases). A major reason that the membrane oscillators in such models continue to fire APs in the absence of intracellular Ca²⁺ cycling may be because these are artificially wired to beat spontaneously, by incorporation of parameters that guarantee sustained spontaneous activity into the model’s formulation. (Of note, a large collection of these parameters had been available to modelers from numerous experimental voltage clamp data obtained prior to the realization of the importance of intracellular Ca²⁺ cycling). Thus, these older pacemaker models have a built-in asymmetry by their design and thus cannot prove an asymmetry of the real pacemaker cells.

The reason for failure of the 1984 model and others like it to reproduce the robust experimental data regarding the crucial role of intracellular Ca²⁺ cycling in pacemaker cell function becomes apparent when one takes into account that these experimental data robustly demonstrate that SR Ca²⁺ release occurs at two specific times within each SANC AP cycle (see mini-summary for section 3.2 item b) 1) spontaneously, during DD, i.e. before AP upstroke; and 2) in response to the AP-induced activation of L-type channels that trigger SR Ca²⁺ release. The 1984 model portrays only the latter Ca²⁺ release, i.e. that in response to the AP, and thus lacks a formulation for Ca²⁺ release or its attendant activation of NCX current during DD. In essence, the 1984 model represents a classical model of excitation-induced Ca²⁺ release as it happens in ventricular muscle cells, and thus does not capture the essence of the hypothesis, based upon the experimental data, of coupled-clock pacemaker system (11).

Nonetheless, in their review (94) Noble et al. insist that NCX current in the 1984 model simulations is indeed activated during DD prior to activation of voltage-gated L-type Ca²⁺ current. A careful examination of their Figure 2 in that paper, however, reveals that, in contrast to the experimental result at −44 mV (left top panel) of Brown et al.(95), the model-simulated NCX current (right bottom panel) appears only at a much higher voltage (about −30 to −28 mV, dashed lines), i.e. during the AP upstroke, following the completion of the spontaneous DD (left bottom panel). Furthermore, application of the original 1984 model (publically available at CellML.com) for the simulations of experimental data at −44 mV (left top panel) fails to reproduce a notable NCX current peak (not shown). This is not surprising because in the original report of their data (95) Brown et al. explicitly state that “The results and computer reconstructions convince us that the i_si current is composed of two components: the slower of these, i_NaCa, may be inward (sodium) current associated with electrogenic sodium-calcium exchange. This is preceded and apparently triggered by a gated component, i_Ca,f (L-type Ca²⁺ current in current terminology) which has much faster kinetics”. In other words, the role for intracellular Ca²⁺ release as portrayed in asymmetric numerical models which dominated the pacemaker field in 1984, was that Ca²⁺ current triggers Ca²⁺ release (CICR), as it normally does in cardiac ventricular muscle.

As we discussed above, in contrast to the asymmetric nature of the pacemaker’s coupled oscillators based upon 1984 model simulations detailed by Noble et al. (94), recent numerical modeling (10) of experimental data points to the idea that the cardiac pacemaker cell is, in fact, a system of symmetrically entrained, inter-dependent oscillators. In other words, during spontaneous AP firing, on a cycle-to-cycle basis, the Ca²⁺ oscillator entrains the membrane oscillator by generating spontaneous rhythmic NCX current, prompting the generation of the next AP; but in doing so, loses Ca²⁺ (its “fuel”) via Ca²⁺ efflux by NCX. The resultant AP generated by the membrane oscillator, however, injects sufficient Ca²⁺ into the cell during each cycle to replace lost Ca²⁺ and maintains steady-state SR Ca²⁺ load and Ca²⁺ oscillator function. During voltage clamp near the maximum diastolic potential regularly occurring APs do not occur and the cell and SR lose Ca²⁺ via NCX. In this case, the SR becomes relatively Ca²⁺ depleted (48). Spontaneous Ca²⁺ oscillations become damped and die out, because the entrained Ca²⁺ oscillator, like an engine of a car, stops running when its fuel runs out. In order to examine the true oscillatory properties of the intracellular Ca²⁺ oscillator in the absence of APs, the Ca²⁺ available for SR to pump must be maintained, e.g. by voltage clamping near reversal potential of NCX (to minimize Ca²⁺ loss) or by surface membrane permeabilization, which permits clamping [Ca²⁺] at a given level (11). Data gleaned from such experiments in which Ca²⁺ is maintained constant clearly demonstrate that SR generates sustained, rhythmic local Ca²⁺ releases (10, 11).

Mini-summary

1. The asymmetry of the Ca²⁺ and voltage oscillators in the older models was built-in by the modelers due to large freedom in choosing model parameters in the absence of relevant experimental data at the time.

2. While older pacemaker cell models, like Noble 1984 model (91), include formulations for Ca²⁺ cycling and reproduce AP-induced Ca²⁺ transient, they fail to reproduce pacemaker-cell-unique diastolic Ca²⁺ release and its associated diastolic I_NCX that precede I_CaL activation and AP upstroke (Fig.3).

3. Recent models based on the coupled-clock mechanism and new data obtained by modern experimental and numerical techniques suggest that Ca²⁺ clock and M-clock are equally, i.e. symmetrically, important for normal cardiac pacemaker cell function due to their dynamic (beat-to-beat) interactions (see below).

5.2. The problem of “Ca²⁺ overload” traditionally associated with pathological conditions

The issue of Ca²⁺ overload in cardiac cells has been previously extensively discussed in our 2006 review in this journal (4). However, the Ca²⁺ overload still remains an issue in the literature as far as the coupled-clock pacemaker concept is concerned. Noble et al. (94), point out that a crucial feature of the coupled-clock M-L model (10), i.e. NCX activation by spontaneous diastolic Ca²⁺ release prior to the next AP upstroke, shows “similarities to delayed afterdepolarization” (or DAD). Yes, indeed. Originally, DADs had been interpreted as a pathological or abnormal phenomenon because these were provoked by poisoning Na/K pump of Purkinje fibers that resulted in marked Ca²⁺ overload. However, in SANC the occurrence of LCRs that contribute to DD during each diastole are physiologic (not associated with Ca²⁺ overload). As discussed above, the minimal diastolic Ca²⁺ levels in pacemaker cells are low, ~ 160 nM (48), i.e. similar to the diastolic Ca²⁺ levels in ventricular myocytes under normal conditions. The spontaneous LCRs are driven instead by a high basal state of phosphorylation of Ca²⁺ cycling and cell membrane proteins, rather than Ca²⁺ overload. These fundamental features of cardiac pacemaker cells are absent in older numerical models, like the 1984 model, and have been modeled only more recently (10, 43).

Mini-summary

1. Partially synchronized, spontaneous Ca²⁺ releases, which are abnormal for cardiac muscle cells, are required for normal function of cardiac pacemaker cells.

2. The spontaneous LCRs occur in pacemaker cells due to enhanced phosphorylation mechanism in the absence of Ca²⁺ overload.

5.3. Controversy regarding effects of cytosolic Ca²⁺ buffering

Chelation of intracellular Ca²⁺ in rabbit SANC by BAPTA (33, 46, 96), but not EGTA (46), applied intracellularly, markedly slowed or abolished spontaneous SANC beating. A strong negative chronotropic effect of EGTA, however, has been reported in guinea pig (SANC (97) and AV node cells (98)). That intracellular Ca²⁺ buffering blocks spontaneous AP generation is strong evidence that normal automaticity of these cells is tightly linked to intracellular Ca²⁺ dynamics. More recently Himeno et al. (99), however, reported patch clamp experiments and numerical modeling in guinea pig SANC which seem to refute the idea of a key role of Ca²⁺ dynamics in SANC function. The authors found that the spontaneous AP rate little changed when BAPTA, a Ca²⁺ chelator, was acutely infused via a patch pipette into SANC. The AP firing rate decreased, but only after several minutes of BAPTA infusion. They interpreted this result to indicate that while Ca²⁺ homeostasis is likely important (e.g. to support generation of cAMP by Ca²⁺-activated ACs. Fig.1A), the Ca²⁺ dynamics, per se, (i.e. Ca²⁺ clock) are not important for spontaneous AP firing.

There is an alternative interpretation of this result (100). In short, the unexpected BAPTA effect can be explained on the basis of a small, artifactual patch seal leak current, a well-recognized artifact in whole-cell patch-clamp experiments that occurs when the membrane patch is ruptured. The occurrence of such leak currents immediately after patch rupture in the Himeno et al. experiments is evidenced by a clearly notable acute depolarization of MDP and an acute cell contracture (incomplete relaxation). The artifactual leak currents pose a serious problem during measurements of spontaneous AP firing because the DD is driven by a net current of a few pico-Amperes (25). In other words, small leak currents associated with seal electrical conductance likely shift the current balance of tiny DD currents, artificially increase the DD rate, and offset the true BAPTA effect that would, in the absence of the artifact, suppress the DD and prolong the cl. When a small leak current (~8 pA during DD through a 6 GΩ seal resistance) is introduced into numerical model formulations (simulating experimental conditions of Himeno et al.), the coupled-clock ML-model does not fail, but continues to generate spontaneous APs when its Ca²⁺-clock is acutely disabled (SR Ca²⁺ pumping rate set to zero), i.e. exactly as reported experimentally by Himeno et al. (99). The apparent long-term effects of BAPTA in Himeno et al. (99) study can be explained, in turn, by that in transition from perforated patch clamp to whole cell configuration, the perforating agent (amphotericin-B) quickly diffuses from patch pipette into cytosol and perforates the whole-cell membrane resulting in large artifactual leak currents and excitability loss.

Mini-summary

1. Intracellular Ca²⁺ buffering interferes with Ca²⁺ clock function that slows AP firing rate or halts automaticity.

2. Taking into account a delicate balance of ion currents (and high electrical resistance of SANC membrane) during DD, the results of whole-cell patch recordings should be treated with caution.

5.4 Beat-to-beat regulation of the cycle length by Ca²⁺ dynamics

While we have suggested an alternative explanation to the patch clamp results reported by Himeno at al. (99) (see previous section), the issues addressed by the authors are crucial in the context of beat-to-beat regulation of a coupled-clock pacemaker system and have prompted a new series of experimental and numerical modeling studies.

The role of Ca²⁺ in beat-to-beat regulation of SANC AP firing has been addressed further in a recent study by Yaniv et al. (101). When single isolated SANC are loaded with a caged Ca²⁺ buffer, NP-EGTA, the buffer markedly suppresses spontaneous diastolic LCRs and uncouples them from AP generation, causing AP firing to become markedly slower and dysrhythmic. When Ca²⁺ is acutely released from the caged compound by flash photolysis, intracellular Ca²⁺ dynamics are acutely restored and rhythmic APs resume immediately (at the same AP firing beat) to a normal AP firing rate. After a few rhythmic cycles, however, these effects of the flash wane as interference with Ca²⁺ dynamics (NP-EGTA dynamically buffers intracellular Ca²⁺) by the caged buffer is reestablished. The acute, virtually instant, effect of the flash-induced Ca²⁺ release on the cycle length underscores importance of Ca²⁺ dynamics on the beat-to-beat basis.

Another recent study by Yaniv et al. (102) demonstrates that application of low concentrations of caffeine (2–4mM) to isolated single rabbit SA node cells under physiological conditions also acutely reduces their spontaneous AP cycle length.

Numerical simulations, using a modified ML “coupled-clock” model, faithfully reproduce the effects of cycle length prolongation and dys-rhythmic spontaneous beating produced by cytosolic Ca²⁺ buffering and also the acute cycle length reduction produced by both caffeine and flash-induced Ca²⁺ release (102). Three contemporary numerical models, Kurata et al. (66), Severi et al. (76) and the original ML model (10), fail to reproduce the experimental results (102). This most recent modification of ML model predicts that Ca²⁺ releases acutely change the cycle length via activation of the Na⁺/Ca²⁺ exchanger current. Time-dependent cycle length reductions after flash-induced Ca²⁺ releases (“memory” effect) are linked to changes in Ca²⁺ available for pumping into SR which, in turn, changes the SR Ca²⁺ load, diastolic Ca²⁺ releases and NCX current. These results support the idea that Ca²⁺ regulates cycle length in cardiac pacemaker cells on a beat-to-beat basis, and suggest a more realistic numerical mechanism of this regulation. Moreover, the model predicts that an increase in the sensitivity of RyR activation by lumenal SR Ca²⁺ (compared to submembrane) faithfully reproduces all changes in parameters of AP-induced Ca²⁺ transients measured experimentally in the low-caffeine experiments.

Finally, it was shown that while the entire LCR ensemble accelerates DD via activation of I_NCX, the intrinsic beat-to-beat variations in activation of individual stochastic LCRs generate the respective intrinsic noise in a non-linear DD component leading to cycle length variations; and this noise can be pharmacologically reduced or increased by respective perturbation of Ca²⁺ cycling in SANC (65). The beat-to-beat regulation of SANC AP cycle length by the fluctuating LCR ensemble has been recently directly demonstrated by measuring local Ca²⁺ signals by a high speed camera simultaneously with membrane potential recording (50). The study demonstrated that while the timing of each LCR occurrence during DD varies, the averaged period for all LCRs (i.e. the entire LCR ensemble) in a given cycle closely predicts the time of occurrence of the next AP, i.e. the AP cycle length. The crucial impact of the LCR ensemble on the fluctuations of AP cycle length had previously been demonstrated by numerical modeling (65). In this older, naive model, however, the LCRs, per se, were not predicted by the model, but rather described by an ensemble of sine functions directly mimicking characteristics of LCRs measured experimentally (as discussed in Section 4.1). Realistic numerical modeling of the intrinsic beat-to-beat variations of the AP cycle length requires inclusion of a theoretical mechanism of LCR generation in SANC based on local Ca²⁺ control mechanisms (Section 5.8).

Mini-summary

1. Ca²⁺ regulates AP cycle length in SANC on a beat-to-beat basis.

2. Intrinsic cycle length variability in single SANC is linked to beat-to-beat variations in the average period of individual LCRs each cycle.

3. A new modification of ML model has been recently developed to reproduce new experimental data on beat-to-beat regulation using flash-induced and caffeine-induced Ca²⁺ releases.

4. Future numerical modeling of beat-to-beat regulation ought to be based on local control mechanisms (for details see Section 5.8 below).

5.5. The problem of sodium regulation

Because the ML model considers dynamic variations of voltage and ion concentrations, it belongs to a so called “second-generation” of models (40). While models of this type describe complex and physiologically realistic interplay of electrophysiological and ionic mechanisms, some models have problems with 1) “degeneracy” i.e. the existence of a continuum of equilibrium points and 2) slow ion concentration drifts ((103–105), review (40)). For example, steady-state ion balance is achieved within hours of simulations in a model of atrial cell AP by Kneller et al. (104)). A slow drift in Luo–Rudy dynamic model for ventricular cells was found to be due to the external stimulation current (103). While pacemaker cell modeling does not include external stimulation currents, a suggested practical solution to the problems of drift and degeneracy is to set the intracellular [Na⁺] and [K⁺] to constant values and treat them as independent model parameters (40, 106). Thus, intracellular [Na⁺] and [K⁺] were fixed to 10 mM and 140 mM, respectively, in Kurata et al. (107) and the ML model (10).

Fixing [Na⁺], on the other hand, obviously imposes a substantial limitation to the exploration of the pacemaker cell system, because the level of intracellular [Na⁺] is an important variable that determines functions of key molecules, e.g. the NCX and the electrogenic Na⁺/K⁺ pump. Experimental data on Na⁺ regulation in SANC, however, is extremely limited (31, 108), preventing accurate modeling of [Na⁺] dynamics. For this reason a finding in a recent theoretical study of Kurata et al. (109) that I_f decreases the robustness of SANC pacemaking via I_f-dependent changes in intracellular [Na⁺], should be treated with caution. While a recent model by Severi et al. (76) describes Na⁺ dynamics, their model could not keep Na⁺ homeostasis upon intracellular Ca²⁺ buffering and, therefore, failed to reproduce negative chronotropic effect observed experimentally under these conditions (102).

Mini-summary

1. While Na⁺ regulation in SANC is an important part of cardiac pacemaker cell function, its present numerical modeling is likely unrealistic, due, in part, to a paucity of experimental measurements of Na⁺ in pacemaker cells.

2. Additional experimental and numerical model studies are required to clarify the role and the mechanisms of Na⁺ regulation in SANC.

5.6. Energy consumption principle: issue of I_NaK matching I_b,Na

The energy consumption principle is yet another important issue (also related to Na⁺ regulation discussed above) that had been raised by DiFrancesco in relation to considerations of the size of currents required for pacemaking (110). According to this principle “all possible systems compatible with activity, the one which is most likely to be selected is the least energy consuming.” In this regard, large background currents, such as I_b,Na, remaining within formulations of pacemaker cell models since 1960 (6), provide constant ion fluxes (i.e. Na⁺ influx via I_b,Na) during all phases of the AP and basically shortcut the membrane. If such currents were present in a real SA node cell, the cell energy budget to retain ion (Na⁺) homeostasis would be terribly high (44). Indeed, for example, in the Kurata et al. model (66), the magnitude of I_NaK (and therefore the magnitude of the related energy budget) was linked to the influx of Na⁺ through I_b,Na (and I_st) and efflux of K⁺ through K⁺ channels. Thus, presence of a large-scale I_b,Na (alone, or in combination with I_st) in a model automatically imposes the presence of a respective, large-scale I_NaK.

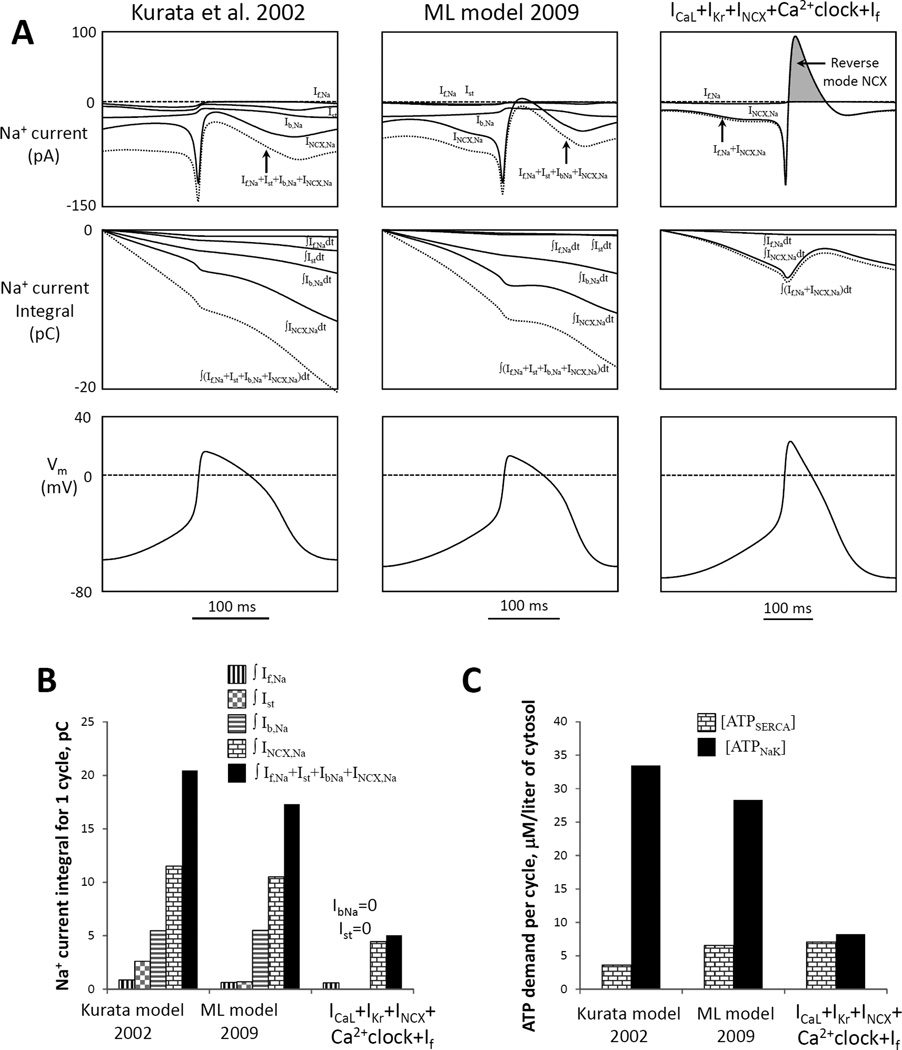
DiFrancesco further argues that “limiting, as with If, the inward current to the size and time-window strictly necessary to only generate the diastolic depolarization clearly helps reduce the energy consumption.” We believe that this is also true for the component of I_NCX that is activated by LCRs in the time window of DD. Furthermore, a broad parametric sensitivity analysis has recently demonstrated that in some SANC models, I_NCX can operate in the reverse mode during the AP (Fig.8A) and assist in extrusion of Na⁺, resulting in less Na⁺/K+ ATPase activity to keep cell Na⁺ balance (44). In this case the integral of Na⁺ influx is substantially reduced compared to prior models (black bars in Fig.8B), and the energy budget is greatly improved (Fig.8C). While this type of model seems to be more realistic based on the energy consumption principle, it requires further experimental validation.

Figure 8.

A flexible and robust pacemaker model with minimal set of components (44) features a small steady-state influx of Na⁺ and is expected to be more energy-efficient in terms of Na⁺ balance regulation (i.e. requires less ATP-dependent Na⁺ extrusion) vs. prior models Kurata et al. (66) and Maltsev and Lakatta (ML) (10). A: Top panels show simulations of trans-membrane Na⁺ currents via different mechanisms (I_f,Na, I_st, I_b,Na, I_NCX,Na) and their sum (dotted lines) in different models for one AP cycle (MDP-to-MDP, bottom panels). Middle panels: respective time-dependent integrals of Na⁺ currents of the top panels reflecting Na⁺ accumulation (during one AP cycle) in the absence of Na⁺ extrusion by ATPases. B: Respective integrals of Na⁺ currents in panel A calculated for one AP cycle. All three models have cell electric capacitance of 32 pF. C: Cell energy budget to maintain Na⁺ homeostasis [ATP_NaK] and to pump Ca²⁺ to the SR [ATP_SERCA] estimated by three models of SANC. From (44).

Mini-summary

1. The energy consumption principle is an important concept with respect to developing realistic pacemaker cell models.

2. Because background currents increase energy expenditure, their magnitude and existence should be carefully considered in numerical models in order to avoid unrealistically high energy budgets.

3. A large contribution of I_b,Na in contemporary models contradicts the energy consumption principle.

4. In contrast to background currents, voltage activation of I_f and voltage- and LCR- activation of I_NCX (generating Na⁺ influx) during DD occurs during a short time window at a relatively small energy cost.

5. Reverse mode NCX, extruding Na⁺ during AP, might be an additional resource to save cell energy (as predicted by some numerical models). This possibility, however, needs an experimental validation.

5.7. Ion currents lacking molecular identity and selective blockers: I_b,Na and I_st

As we discussed in section 3.1., H-H theory and its application to heart pacemaker cells by Noble in 1960 (6) inspired numerous voltage clamp studies which identified numerous ion currents in pacemaker cells (some of them listed in Table 1). All these currents were included in subsequent pacemaker cell numerical model updates (40). Therefore the present model formulations (reflecting the full history of ion current discoveries) become extremely complicated, featuring about a dozen of different ion currents. Some ion currents, however, still lack a molecular identity and selective blockers, despite the fact that they were identified in patch clamp recordings a long time ago. Thus, for future realistic modeling, it is critical to clarify if these currents are generated by unique, still unidentified molecules or by a combination of some known molecules (generating other currents). For example, both I_b,Na and I_st are Na⁺ currents. Given the lack of selective blockers, these currents (when experimentally recorded) could be generated, at least in part, by NCX. If so, then in the old detailed models this part of Na⁺ flux is counted twice or thrice, i.e. by in I_NCX, I_st, and I_b,Na, resulting in overestimation of total Na⁺ flux and, therefore, nonrealistic (worse than real) energy expenditure to keep Na⁺ homeostasis in these models.

Given the paucity of I_b,Na measurements reported in the literature, the magnitude or even the existence of I_b,Na is clearly challenged by the molecular identity consideration, and also by the energy budget consideration (c.f. previous section). It has been speculated that a Na⁺-H⁺ mechanism contributes to the background current because it is reduced by amiloride (29). Another interesting idea is that background current is generated by a non-transported Na⁺-Ca²⁺ leak of NCX (111). It can be also generated by a normal NCX operation in the forward mode: Indeed, a persistent component of inward I_NCX has been reported in guinea pig SANC (97) at the MDP and during the early DD. This I_NCX persistent component is also predicted by the ML model simulations (Fig.2, “I_NCX activation by hyperpolarization” and “I_NCX activation by Ca²⁺ transient”). A radical idea is that a background current does not exist in SANC, but is simply an artifact of the seal leak that always accompanies a whole-cell patch clamp recording (25).

A non-selective I_st (26) has many characteristics of I_CaL, e.g. it is sensitive to dihydropyridines and has a reversal potential close to 37 mV. However, I_st is activated at more negative potentials than I_CaL and achieves its peak at about −50 mV (112), i.e. exactly when LCRs begin to occur and activate I_NCX during DD. I_st exhibits other characteristics of I_NCX: it is mainly carried by Na⁺, increased at lower extracellular [Ca²⁺], but reduced at lower extracellular [Na⁺] (26). Thus, it is possible that I_st reflects combined (direct and indirect) effects of I_NCX and I_CaL. In this case I_st sensitivity to dihydropyridines can be explained within the coupled-clock theory: a selective reduction of I_CaL reduces Ca²⁺ influx, the cell Ca²⁺ and SR Ca²⁺ loads, and hence reduces LCRs and LCR-induced I_NCX.

However, the issue with I_b,Na and I_st representing phenomenological surrogates of other currents (I_CaL, I_NCX) cannot be resolved by numerical model simulations, per se, and probably requires a dedicated experimental study combined with numerical modeling. Indeed, any current representing a combination of fundamentally important currents would also seem to be extremely important in simulations (including autonomic modulation in case of I_st (113)); but this result would be obviously misleading and provide no guidance for emergent new technologies, such as genetically engineered biological pacemakers (discussed below) targeting specific molecules.

A recent pacemaker cell numerical model developed by Kharche et al. (114) was claimed to be “with molecular bases”. This model, however, still includes formulations and substantial contributions of I_b,Na and I_st having no molecular bases. Interpretations of numerical model simulations with contributions of these (and other) currents with no molecular identity can be misleading because their contributions will inevitably replace, in part, the contributions of other currents produced by known molecules. A recent large-scale parametric sensitivity analysis of numerical models of SANC based on a minimal set of sarcolemmal electrogenic proteins and an intracellular Ca²⁺ clock discovered a large cohort of models lacking I_b,Na and I_st that can generate robust, flexible, and energy-efficient cardiac pacemaking (44). This study indicates that inclusion of I_b,Na and I_st is not required for realistic (molecular based) modeling of pacemaker cell function.

Mini-summary

1. Some currents, such I_b,Na and I_st, in formulations of contemporary numerical pacemaker cell models have no molecular identity.

2. The continued inclusion of these ion currents into pacemaker cell numerical models becomes problematic because their presence “steals” importance from the true molecular mechanisms of cardiac pacemaking.

3. Numerical models generating robust, flexible, and energy-efficient cardiac pacemaking can be constructed without I_b,Na and I_st contributions (44).

5.8. Local Ca²⁺ control mechanisms

Within a traditional electrophysiological approach to cardiac cell pacemaker function (using the M-clock perspective), local activation of effector molecules, i.e. ion channels, do not matter, because a local electric charge change on the cell membrane associated with an opening of a channel (or a group of channels) becomes almost instantaneously spread over the entire cell membrane capacitor. The charge equilibrates for the whole cell length within ~20 microseconds estimated based on calculations of the propagation velocity of the electric charge disturbance using a cable equation (see Appendix in (54)). Thus from the “M-clock” perspective, approximation of the cell membrane as a single electric capacitor is well justified.

The situation with local signaling is fundamentally different with respect to Ca²⁺ dynamics. Ca²⁺ releases are generated locally and, in contrast to the membrane potential, the released Ca²⁺ does not propagate instantly across the length of the cell. Rather it diffuses relatively slowly and activates (recruit to fire) RyR via local CICR along the way, thus forming LCRs. The LCRs activate local NCX currents and local pumping (via SERCA). There is an entirely different and unexplored world of cardiac pacemaker mechanisms waiting to be discovered using a combination of powerful theoretical and experimental approaches that have been developed in classical studies of excitation-contraction coupling in cardiac muscle cells (review (115)), but previously thought to be hardly related to cardiac pacemaker mechanisms.

While the LCRs have been identified in pacemaker cells by confocal microscopy more than 10 years ago (35, 49), their theoretical formulations and numerical modeling lag behind. As the matter of fact, almost all numerical pacemaker cell models developed so far belong to so-called “common pool” models that simulate only total (“global”) Ca²⁺ signals, but contain no terms that explore local Ca²⁺ control and RyR recruitment in SANC (i.e. LCRs). In short, Ca²⁺ signals (if any) in each cell compartment, e.g. cytosol, submembrane space, free (or network) SR, junctional SR, are described in common pool models by only one variable (Ca_i, Ca_sub, Ca_nSR, Ca_jSR, respectively, in Kurata et al. and the ML model).

A fundamental insufficiency of common pool models and crucial importance of local Ca²⁺ signaling in cardiac cells was demonstrated in a seminal report of local Ca²⁺ control theory (116). This theory explained graded CICR phenomenon via statistics of success and failure of an initiating event (such as an opening of LCCh) to recruit stochastic Ca²⁺ release units (CRUs) to fire. With respect to pacemaker cells, persisting roughly periodic LCRs observed in depolarized rabbit SANC are reproduced by a model of a locally distributed SR linked to submembrane space consisting of a two dimensional array of stochastic, diffusively coupled CRUs with fixed refractory period (117) (Fig.9). Because previous experimental studies (118) showed that β-AR stimulation increases the rate of Ca²⁺ release through each CRU (dubbed I_spark), it is interesting to explore the link between LCRs and the I_spark. Numerical model simulations (117) show that increasing I_spark facilitates CICR and local recruitment of neighboring CRUs to fire more synchronously. These complex local interactions lead to a progression in simulated LCR size (from sparks to wavelets to global waves), LCR rhythmicity, and decrease of LCR period that parallels the changes observed experimentally with β-AR stimulation. The transition in LCR characteristics is steeply non-linear over a narrow range of I_spark, resembling a phase transition. Thus the (partial) periodicity and rate regulation of the “Ca²⁺ clock” in SANC are, at least in part, emergent properties of the diffusive coupling of an ensemble of interacting stochastic CRUs. The variation in LCR period and size with I_spark is sufficient to account for β-adrenergic regulation of SANC AP firing rate.

Figure 9.

Development of the numerical model of local Ca²⁺ dynamics in rabbit SANC: Ca²⁺ Release Units, (CRUs) and Ca²⁺ cycling. A: RyR clusters, i.e. CRUs, are observed in confocal images of immuno-fluorescence in rabbit SANC under cell surface membrane. B: Schematic illustration of local Ca²⁺ cycling through cell compartments (submembrane space, SR, and cytosol) in a new local Ca²⁺ control model of SANC (117, 119). Local Ca²⁺ fluxes in the model are shown by arrows. Ca²⁺ wave travels from left to right. C: Instantaneous distributions of local [Ca²⁺] in the submembrane space predicted by the model: a single Ca²⁺ spark and a wavelet LCRs (propagating from left to right). Inset: Illustration of shade-coding for CRU states and [Ca²⁺]. Modified from (117).

Although the aforementioned model simulations (117) provide new insights into LCR formation and β-AR stimulation of the local Ca²⁺ clock, they lack interactions with M-clock. A new, fully integrated model, featuring the local Ca²⁺ control approach with complete electrophysiological formulations (i.e. M-clock), has been recently developed (119) and applied to interpret results obtained in an incomplete knock-out (KO) NCX mouse model (120). SANC isolated from the incomplete KO mice exhibited no changes in AP firing rates, Ca²⁺ transient shapes, or ion current densities (other than I_NCX) measured under voltage clamp. However, the cells were insensitive to β-adrenergic receptor (β-AR) stimulation. Based on these and other results, Gao et al. (120) concluded that NCX expression is required for increasing sinus rates, but not for maintaining resting heart rate.

Numerical model simulations, however, demonstrate that local Ca²⁺ control mechanisms substantially contribute to I_NCX stabilization in SANC so that when the expression of NCX molecules is substantially reduced (to 20% of control, wild type), the diastolic I_NCX remains almost unchanged (Fig.10). Specifically, lower NCX expression facilitates local CICR and larger (diastolic) local Ca²⁺ releases (Fig.10A, right-hand panels) that stabilize diastolic I_NCX (Fig.10B). Further reduction of NCX expression results in arrhythmia and a cessation of automaticity (119), reproducing experimental findings in other (more complete) KO models (121, 122).

Figure 10.

The magnitude of diastolic I_NCX is stabilized by powerful local Ca²⁺ control mechanisms in SANC. A: Numerical simulations using a new local Ca²⁺ control model (119) predict dynamics of membrane potential, I_NCX and Ca_sub, with respective k_NCX values (reflecting NCX expression) indicated at the top of each panel. Images on the right illustrate the instantaneous local submembrane [Ca²⁺] at −40 mV by grey shades, from black (200 nM) to light gray (1000 nM). Ca²⁺ release units, i.e. clusters of RyRs, are shown by dots in mid-grey and white (when firing). B: Simulations of the local control model demonstrate that diastolic I_NCX is preserved within a broad range of k_NCX variations. The three I_NCX traces are the same as in panel A but shown with substantial zoom to clearly demonstrate the I_NCX magnitude and dynamics. The traces were synchronized at their peak induced by I_CaL via CICR mechanism at the beginning of an AP. I_NCX substantially decreased only when k_NCX decreased dramatically (dotted curve). From (119).

In addition to the important local NCX-RyR interactions, revealed by the new models, there are several further considerations as to why specific mechanisms are expected to be so different in the future local control models vs. present common pool models. Local [Ca²⁺] in the vicinity of a Ca²⁺ spark or an LCR could be two orders of magnitude higher than average diastolic Ca²⁺ levels attained in common pool models. This difference has important consequences for approximation of SR Ca²⁺ pumping and release and also RyR-LCCh crosstalk in the models:

1) The SR Ca²⁺ pumping is more efficient in local control models. Indeed, the SR Ca²⁺ pumping rate is determined by a function of cytosolic [Ca²⁺]. Because each LCR results in very high local Ca²⁺ concentrations, it fully activates Ca²⁺ pumping of the SR in its vicinity. On the other hand, in common pool models a diastolic Ca²⁺ release of a similar magnitude (e.g. an LCR) is spatially averaged over the entire compartment (i.e. pool, such as the cytosol), and [Ca²⁺] does not reach the high levels achieved in the local model. Therefore in a common pool model in response to a small total Ca²⁺ release of an LCR the SERCA operates in the region close to the foot of the sigmoid curve relating Ca²⁺ pumping rate to the [Ca²⁺]. As a result only a relatively slow pumping rate is achieved in this case.

Additional numerical model simulations (119) show that the local Ca²⁺ control mechanism can ensure low (physiological) levels of diastolic Ca²⁺, despite a substantial reduction in Ca²⁺ efflux capabilities (achieved mainly via NCX), e.g. in the incomplete NCX KO cells (120). In contrast, common pool models predict unrealistic high diastolic [Ca²⁺] levels (119) which contradict the experimental measurements in these cells (120).

2) The SR Ca²⁺ release is also fundamentally different in local control models. A Ca²⁺ spark can effectively recruit neighboring CRUs to fire more Ca²⁺ sparks. Thus, LCRs are generated via propagating CICR that is described by stochastic recruitment of the CRUs. Common pool models do not describe this local Ca²⁺ diffusion-reaction paradigm. Their Ca²⁺ release is often described by a simple sigmoid (or power) function, relating global Ca²⁺ release flux to a global [Ca²⁺] in the release pool (e.g. Ca_sub in Kurata et al. model (66)). Because any initiating Ca²⁺ release is instantaneously spread over the entire release pool in these models, it results in a relatively small change in the global [Ca²⁺]. In this case CICR is small because Ca²⁺ release flux remains almost unchanged at the foot of the sigmoid (or power) function in response to the small change in [Ca²⁺]. Whether or not the global release emerging from a multitude of wavelet-like LCRs can be reduced to a simple function of characteristics of interacting components (CRUs, buffers, diffusion coefficients, etc.) is not obvious and needs special theoretical considerations, similar to those in statistical physics.

3) RyR-LCCh crosstalk is another crucial interaction that can be realistically described only by local Ca²⁺ control mechanisms. One classical interaction happens during AP (similar to ventricular myocytes) when LCCh recruit RyR to generate Ca²⁺ transient. As we mentioned, these interactions are correctly described by local Ca²⁺ control theory developed by Stern (116). Also, a diastolic LCR (preceding an AP) can affect neighboring LCCh function via Ca²⁺ -dependent inactivation mechanism. Finally, threshold openings of LCCh can occur at membrane potentials (close to −45 mV) embracing the late DD phase and thereby facilitate local CICR, i.e. LCR generation, that, in turn, generate more local I_NCX and accelerate DD further, activating more LCCh openings, etc. This positive-feedback local process is analogous to an avalanche or a “rocket launch” and might have evolved in nature for a fail-safe generation of AP at the right time to ensure rhythmic pacemaker function.

There are several specific open problems that could be approached in the nearest future by the new local Ca²⁺ control models. The current model of LCR (117, 119) assumes a given restitution time for CRU during which it cannot fire a next release. Future studies ought to approach emergence of local Ca²⁺ clocking based on local SR Ca²⁺ pumping, refilling, and release mechanisms, predicting the restitution time, rather than taking it as an independent, phenomenological parameter of the model. A crucial importance of SR Ca²⁺ refilling kinetics for AP firing rate in SANC has been demonstrated in experimental studies utilizing direct measurements of local intra-SR Ca²⁺ signals (69). It is important to note that recent studies of Ca²⁺ spark mechanisms (123) demonstrated that Ca²⁺ sparks can operate (activate and terminate) without a time dependent inactivation (never observed in studies of cardiac RyR channel gating in planar lipid bilayers). Thus, Ca²⁺ release restitution is not an inherent property of RyR molecules, but rather an emergent property of the system that includes complex interactions among local Ca²⁺ SR depletion-refilling, cytosolic Ca²⁺ depletion (via Ca²⁺ diffusion and SERCA pumping), and Ca²⁺-dependent activation of RyR opening.

The first successful attempts to create such new models have been recently reported (124, 125). These new models have revealed a crucial importance of the spatial organization of the RyR and SERCA networks within SANC for pacemaker function. Specifically new simulations (124) demonstrated that the irregularity in RyR distribution in SANC is not a noise or imperfection, but rather a functional modality of the pacemaker cells that allows them to gradually engage CRUs to satisfy the chronotropic demand of the heart at a given condition.

The most recent SANC model simulates stochastic spontaneous diastolic Ca²⁺ release in 3 dimensions (125), based on explicit gating of individual Ca²⁺ channels (both RyR and LCCh), without assuming either a discrete sub-membrane compartment (used in many prior models (10, 66, 76, 117, 119)) or an inactivated state of the RyR. The model succeeded in reproducing propagating LCRs and realistic pacemaker rates only when RyR locations were assigned taking into account irregular, hierarchical distribution of RyR clusters observed in 3D confocal scan sections of immunofluorescence staining. The RyR spatial distribution was modelled as a variable network of RyR clusters, with small clusters intermediate between major ones, located immediately below the surface membrane. Interestingly, when the RyR sensitivity to Ca²⁺ is very high or NCX density is low, there is a paradoxical regime in which synchronization is lost, causing sympathetic stimulation to reduce rather than increase beating rate. This regime may be important for rhythm abnormalities caused by heart failure, RyR mutations, or pharmacological NCX blockade (126).

As mentioned above, LCR sizes undergo a phase-like transition with increasing of I_spark (i.e. Ca²⁺ release magnitude) in an agent-based model of stochastic recruitment of CRU to fire (117). How the interaction between the CRUs via CICR causes self-organization of Ca²⁺ spark clusters has recently been also studied in another agent-based model (of a mouse ventricular myocyte) (127). The statistics of the LCR sizes follow an exponential distribution when the coupling between CRUs is weak. As the interactions between CRUs strengthen, the LCR size distribution changes to a power-law distribution, which is indicative of criticality in complex nonlinear systems. The criticality underlies the formation and propagation of Ca²⁺ wavelets and waves resulting in whole-cell Ca²⁺ oscillations. While self-organized criticality describes (in statistical terms) numerous phenomena in nature from earthquakes and solar flares to fluctuations of stock market prices (128), the theory does not provide clean solutions as to how the macroscopic properties emerge from interactions of complex system components. Moreover, criticality was found in permeabilized ventricular myocytes with perpetuating Ca²⁺ releases of different sizes (127). During spontaneously AP firing by SANC, however, the Ca²⁺ release dynamics is further complicated by AP-induced Ca²⁺ release each cycle that would obviously prevent emergence of larger and longer lasting events, which are essentially required for criticality (Note, criticality is characterized by a power law distribution of events on a broad time or space scale, usually reported on a log-log plot).

Mini-summary

1. Existing common pool models of SANC are incomplete: the amplitudes of Ca²⁺ dynamics can differ from those attained locally by two orders of magnitude. These naive models lack specific terms to describe true biophysical mechanisms of Ca²⁺ dynamics in SANC, such as local diffusion-reaction for the release, local efficient pumping and local NCX activation.

2. A new generation of model featuring local Ca²⁺ control will provide novel insights into cardiac pacemaker cell function.

3. The local control models can approach the current open problems, such as the existence of submembrane space, specific local interactions of RyR, SERCA, NCX and LCCh, underlying emergence and maintenance of local and global Ca²⁺ clocking, and robust and yet flexible cardiac pacemaker function.

4. The concepts of the phase transition (117) and self-organized criticality (127) can serve as general theoretical frameworks to approach emergence of a multitude of Ca²⁺ oscillatory signals in SANC at different scales of space and time. However insights from these theoretical concepts are presently limited to reductionist studies of isolated Ca²⁺ clock (i.e. in permeabilized or depolarized cells) and numerical models.

6. Modern numerical and theoretical approaches to explore cardiac pacemaker function

6.1. Parametric sensitivity analysis

Numerical modeling is utilized to interpret experimental data in order to gain further insights into the complexity of pacemaker cell function and ultimately to establish general pacemaker mechanisms. Achieving this goal, however, is complicated by the fact that the SA node is a highly heterogeneous structure with substantial cell-to-cell variations of functional expression of many key molecules. For example, in rabbit SANC the density of I_CaL varies by an order of magnitude (129) and I_f density varies 3 fold (13), with the density being smaller in SANC of smaller size. The classical approach in the pacemaker field, however, has been to develop and to report a numerical model with a unique set of model parameters (40) that ideally would describe present experimental results (average data) and hopefully embrace a general pacemaker mechanism to serve as a prototype of a “unified” or “typical” pacemaker cell. Reporting just a unique set of parameters, however, obviously uncovers neither the robustness of the model (and hence of the suggested mechanisms), nor realistic behavior of the SA node comprised of cells with their intrinsic large-scale variations (e.g. I_CaL and I_f).

A modern computational approach to address such problems and to gain broader insights into physiological function is to explore not just a single model of the system, but a large population of models (recently reviewed by Cummins et al. (130)). This approach is based on ample computation power of modern computers and tests system behavior within all, or almost all, possible combinations of parameters measured experimentally, i.e. within thousands or even millions of individual models of different cell types. It has been used in particular by Marder et al. to generate large databases of model neurons (131, 132). A large variety of models of ventricular myocytes with different properties have been also successfully tested to identify the roles of particular model components on AP characteristics (133) and various cell behaviors, including responses to drugs (2).

The parameter-sensitivity approach in SANC modeling was initiated by Kurata et al. (66) and has been extended more recently for a coupled-clock SANC system (10, 44, 134). This approach holds promise for addressing cell-to-cell variability and for developing a more definitive understanding of the complex pacemaker cell functions. Figure 11 shows a simple example of such analysis of complex interplay of I_CaL and SR Ca²⁺ pumping in a population of 5,917 numerical models revealing parameter combinations yielding either rhythmic AP firing (color-coded areas) or pacemaker failure. This example actually shows the integrated operation of the M- and Ca²⁺ clocks: the border for rhythmic firing (the bifurcation yellow line) extends towards lower I_CaL conductance values when Ca²⁺ clock function enhances (as SR Ca²⁺ pumping enhances). And vice versa, without rhythmic ignition signals generated by Ca²⁺ clock, M-clock substantially slowed (vector c→j), became dysrhythmic (vector b→h), or ceased (vector a→g). This parametric analysis demonstrates the synergism of M- and Ca²⁺ clocks in generating robust and flexible pacemaking.

Figure 11.

A: A parametric system analysis (“population-based” modeling) using the ML model (10) with simultaneous variations in I_CaL conductance and SR Ca²⁺ pumping rate. The image shows the result of 97(x) × 61 (y) = 5917 simulations (each pixel = 0.0025 nS/pF × 0.2 mM/s). The resultant AP firing rate of the system is illustrated by various grey shades on the right; stripped areas indicate no firing; and mosaic areas indicate chaotic firing. B: Simulation traces for specific points of interest in panel A, illustrating more robust system operation when Ca²⁺ clock is functional. C: simulations of the effect of moderate PKA inhibition by 1.7 µM PKI (represented by vector bd in panel A). From (10).

The multi-parameter sensitivity analysis can also illustrate the system response to a complex perturbation (e.g. moderate PKA inhibition) that affects both clocks and therefore is represented by a vector (b→d) in the parametric space. Thus, in general, this new approach permits identification of physiologically important ranges of parameter combinations to simulate experimental data and to learn how the system robustness and flexibility emerge from the complex interplay of molecules within the coupled-clock system. This approach can be further extended in future studies to provide insights into pathological behaviors, such as sick sinus syndrome or sinus tachycardia (130).

Mini-summary

1. The sensitivity analysis within a large population of models is a modern trend in computational studies. It generates and explores model predictions for combinations of parameters by varying their specific values over a meaningful range, covering individual cell-to-cell variations, physiological (and pathophysiological) responses, and responses to drugs or genetic modifications.

2. Population-based modeling can be used to explore the complex interplay of intracellular and cell membrane molecular components in SANC

3. This approach has demonstrated that a synergism of coupled Ca²⁺ clocks and M-clocks confers robust and flexible pacemaker function (10)

6.2. The “Minimal Models” (or Occam’s razor) approach to establish general pacemaker mechanisms and to guide engineering of future biological pacemakers

Another approach to establish general mechanisms of cardiac pacemaker function follows Occam’s razor principle (the principle of parsimony) and tests whether essential, common properties of cardiac pacemaker cell function (i.e. robustness and flexibility) can be achieved with fewer (or with minimal number of) functional components, rather than with numerous components of the current detailed models. Such an approach, combined with a wide scale parametric sensitivity analysis described above, has been applied to delineate general pacemaker mechanisms in hundreds of thousands of numerical models, featuring combinations of only 4 or 5 key electrogenic molecules and a Ca²⁺ clock (44). The extended ranges of SR Ca²⁺ pumping (i.e. Ca²⁺ clock performance) and conductance of ion currents were sampled, yielding a large variety of parameter combination, i.e. specific model sets.

Each set’s ability to simulate autonomic modulation of human heart rate in response to stimulation of cholinergic and β-AR receptors was tested. Only those models that include a Ca²⁺ clock (including the minimal 4-parameter model “I_CaL+I_Kr+I_NCX+Ca²⁺ clock”) were able to reproduce the full range of autonomic modulation (44) (Fig.12A–C). Inclusion of I_f or I_CaT decreased the flexibility, but increased the robustness of the models (a relatively larger number of sets did not fail testing). The models comprised of components with clear molecular identity (i.e. lacking I_b,Na & I_st) portray more realistic pacemaking: A smaller Na⁺ influx is expected to demand less energy for Na⁺ extrusion (as discussed in Section 5.6, see also Fig.8). The new large database of the reduced coupled-clock numerical models provide a conceptual basis for a general theory of robust, flexible, and energy-efficient pacemaking based on realistic components. This numerical tool can also help in designing biological pacemakers with desired properties using a minimal set of specific electrogenic molecules.

Figure 12.

A: Results of sensitivity analysis (“population-based” modeling) of a 4-parameter model type I_CaL+I_Kr+I_NCX+Ca²⁺clock. The model type was tested in 10,000 parameter sets. Data points show predictions for maximum and minimum spontaneous AP firing rate achieved with β-AR (ISO) and ChR (ACh) stimulation (along Y and X axis, respectively). B: a more detailed representation of all data points within the boundaries of normal human heart operation, including different ages and level of fitness (shown by square in panel A). C: an example of APs in basal state and also in ACh test and ISO test. D: Results of sensitivity analysis over a wide range of I_f conductance (g_If on X-axis, all other parameters are fixed). When g_if is increased beyond the experimentally measured range, both the minimum rate (ACh, grey bars) and the maximum rate (ISO, white bars) increase concurrently, so that the relative rate flexibility is compromised. The double head arrow shows the range of I_f conductance (g_If) that simulates the respective range of I_f densities measured experimentally (13). From (44).

One specific insight, which has been validated experimentally, relates to I_f expression. A study in dogs (135) compared two types of bio-pacemakers with adenylyl cyclase (AC1 type) expression and combined expression of AC1 and I_f. This study showed that I_f is not required for bio-pacemaking, but the artificial increase in I_f results in a higher basal heart rate, i.e. very similar to results of the numerical model study (Fig.12D). A similar

Mini-summary

1. Employing Occam’s razor to explore the pacemaker system behaviors with minimal set of components can be helpful for establishing general pacemaker mechanisms.

2. The results of such analyses can also aid in designing biological pacemakers that require minimum manipulations of specific molecular targets to acquire desired performance in terms of stable rhythm and AP firing rate range.

6.3. Bifurcation analysis

Finally, another powerful approach to study complex pacemaker cell function is stability and bifurcation analyses which were pioneered and developed by Kurata et al. (66, 134). These analyses establish equilibrium points (EP), at which the system is stationary (i.e., the oscillatory system fails to function), the periodic orbits (limit cycles, “LC”), and their stability as functions of model parameters. The difference of this theoretical approach (i.e. strict bifurcation analysis based on the concepts of bifurcation theory) from simple numerical solutions (10, 44) (discussed above) is that it can be used for more systematic and complete evaluation of dynamical properties of nonlinear systems such as SANC. Bifurcation analyses can determine stable and unstable EPs (and LCs) and assess their stability more rapidly and accurately than simple numerical integration of differential equations, which can determine only stable EPs (and LCs) but not unstable EPs (or LCs) or how key parameters affect instability of EPs. Furthermore, strict bifurcation analyses can explore complex nonlinear systems with multi-stability (coexistence of multiple stable EPs and LCs), whereas simple numerical integrations often provide incomplete or inaccurate results (for a detailed comparisons see (136)). On the other hand, simple numerical integrations can evaluate temporal behaviors of SANC, such as transient and arrhythmic (chaotic) behaviors, which cannot be determined by the strict bifurcation analysis. Furthermore, future application of bifurcation theory to examine behaviors of local Ca²⁺ control models is not trivial and needs to be established.

The most recent study performed by Kurata et al. (134) using bifurcation analysis confirmed crucial importance of SR Ca²⁺ pumping, NCX function, and I_CaL activation for the coupled-clock system operation reported in previous studies using direct numerical integration (10). Their analysis also revealed that the ML model does not exhibit Ca²⁺ oscillations at any clamped voltage and requires further tuning to reproduce oscillatory local Ca²⁺ releases and total membrane current reported in experimental studies (47, 48).

Mini-summary

1. Strict bifurcation analyses are a powerful theoretical method to explore the mechanisms of different behaviors of dynamical systems, such as SANC.

2. This method does not substitute or exclude analyses using simple numerical integration. Both methods have pros and cons and complement each other.

3. Bifurcation analyses have confirmed a crucial importance of Ca²⁺ cycling for normal SANC function.

7. Summary and future directions

We have summarized the present state of numerical modeling approaches to cardiac pacemaking as a complex phenomenon that include integrated function of intracellular and cell membrane proteins. Mini-summaries after each section provide postulates and helpful statements to guide the future development of this research area. In short, we believe that the time of presenting insights from only a single set of parameters has passed. Rather, numerical modeling of pacemaker cells should explore the pacemaker cell system using sensitivity analyses in large- scale model populations and bifurcation analyses providing robust and ubiquitous insights. These new powerful approaches become possible due to easily available increased computing power. Studies, in which pacemaker cell function is reduced to only essential components (“Occam’s razor” approach), can also help establish general pacemaker mechanisms, because in this case, basically all possible individual models can be examined using the population-based approach. This approach can also aid in designing biological pacemakers that require minimum manipulations of specific molecular targets to acquire desired performance in terms of stable rhythm and AP firing rate range.

We believe that the time of describing cardiac pacemaker cell essentially as a membrane voltage oscillator (via an interplay of H-H kinetics) has also passed. Numerous experimental studies validated by extensive numerical modeling over the last decade have established that pacemaker cell function cannot be reduced to functions of only sarcolemmal ion channels; rather, it is generated by a complex system of dynamically interacting components residing in cell membrane and inside the cells. In this critical review we have tried to approach existing paradoxes and controversies based on this ground.

Important future advances of the pacemaker cell modeling will include (a) more quantitative localization data describing nanoscale relations between RyR clusters, LCChs, NCX, and SERCA; (b) measurements of local SR Ca²⁺ refilling ("blink" kinetics) and/or restitution of sparks and LCRs, analogous to experiments that have been performed in ventricular cells, (c) better measurements of mitochondrial Ca²⁺ uptake and extrusion specifically in the SA node, (d) integration of biochemical pathways (especially linked to local cAMP production and protein phosphorylation), (e) and molecule-based modeling (i.e. limited to components with clear molecular identity).

While our review is focused on the cellular mechanisms of cardiac impulse initiation, the pacemaker function of the heart is determined by further complex integration of the cell signals within SA node tissue that include both pacemaker and non-pacemaker cells (e.g. fibroblasts, neurons, etc. The interested reader is referred to the most recent achievements in the numerical modeling in this exciting area of research (137, 138), including pathological aspects of SA node function (139, 140).