Abstract
Plane wave imaging has greatly advanced the field of shear wave elastography thanks to its ultrafast imaging frame rate and the large field-of-view (FOV). However, plane wave imaging also has decreased penetration due to lack of transmit focusing, which makes it challenging to use plane waves for shear wave detection in deep tissues and in obese patients. This study investigated the feasibility of implementing coded excitation in plane wave imaging for shear wave detection, with the hypothesis that coded ultrasound signals can provide superior detection penetration and shear wave signal-to-noise-ratio (SNR) compared to conventional ultrasound signals. Both phase encoding (Barker code) and frequency encoding (chirp code) methods were studied. A first phantom experiment showed an approximate penetration gain of 2-4 cm for the coded pulses. Two subsequent phantom studies showed that all coded pulses outperformed the conventional short imaging pulse by providing superior sensitivity to small motion and robustness to weak ultrasound signals. Finally, an in vivo liver case study on an obese subject (Body Mass Index = 40) demonstrated the feasibility of using the proposed method for in vivo applications, and showed that all coded pulses could provide higher SNR shear wave signals than the conventional short pulse. These findings indicate that by using coded excitation shear wave detection, one can benefit from the ultrafast imaging frame rate and large FOV provided by plane wave imaging while preserving good penetration and shear wave signal quality, which is essential for obtaining robust shear elasticity measurements of tissue.
Keywords: coded excitation, shear wave, elastography, Barker, chirp, shear wave detection
INTRODUCTION
Coded excitation has been applied to medical ultrasound imaging for over two decades [1, 2]. Coded ultrasound signals possess superior penetration and signal-to-noise-ratio (SNR) compared to conventional ultrasound signals, and have found many important applications such as B-mode imaging [2-8], synthetic aperture imaging [9, 10], color flow imaging [11-13], strain imaging [14], and acoustic radiation force impulse (ARFI) imaging [15]. Coded excitation enhances ultrasound signal SNR by elongating the duration of the ultrasound pulse so that more energy can be deposited into the tissue. This takes advantage of the fact that the thermal index of the conventional short imaging pulses are typically well below the regulatory limit by Food and Drug Administration (FDA). The deteriorated range resolution caused by the long coded pulses can be recovered by the process of decoded filtering (or RF compression), which is typically done by correlating the received radiofrequency (RF) signal with the transmitted code [2, 16]. Recently, base-band compression has been introduced to improve compression efficiency [17, 18]. By careful design of the coding and decoding methods, one can achieve a robust imaging system with high SNR, good range resolution and excellent penetration [1, 4, 5, 7].
The improved penetration and imaging SNR provided by coded ultrasound signals can be beneficial to shear wave motion detection, because the quality of the shear wave signal is closely related to the quality of the ultrasound signal [19-22]. For the last decade, the concept of using plane wave imaging for shear wave detection has greatly advanced the field of shear wave elastography (SWE), thanks to the ultrafast imaging frame rate and the large field-of-view (FOV) provided by plane waves [23-26]. The high imaging frame rate is essential to capture the fast propagating shear waves in stiff lesions such as breast cancer [27], and the large FOV is essential to perform large-volume sampling of tissues for applications such as liver fibrosis staging [28, 29]. The drawback of plane wave imaging, however, is the decreased penetration and low RF signal SNR due to the lack of transmit focusing, which makes it challenging to use plane waves to detect small tissue motions caused by shear waves in deep tissues and in obese patients. Although coherent spatial compounding has been proposed to significantly improve the SNR of plane waves [23, 30], the penetration of plane waves is still problematic due to lack of transmit focusing. The goal of this study, therefore, was to implement coded excitation in plane wave imaging for shear wave detection, with the hypothesis that shear wave signal SNR and shear wave detection penetration can be significantly improved by using coded ultrasound signals.
Both phase encoding and frequency encoding methods [1] were investigated in this study. Two representative codes were selected for each method: the Barker code for phase encoding, and the linear frequency modulated (FM) chirp for frequency encoding. The Barker code is bi-phase and thus less demanding to the system transmitter than the chirp code. However the longest length Barker code has a length of 13 bits, which limits its improvement of SNR and suppression of range side lobes [1]. Linear FM chirp, on the other hand, is not limited by length, but may suffer from degradation in range side lobes and also has higher hardware demands on the transmitters and the bandwidth of the transducers. Fortunately, the range side lobes can be reduced by mismatched filtering and envelope-windowing of the transmitted chirp signal by the natural bandwidth of the ultrasound transducer [4], and one can also reduce the hardware demands by using the pseudo-chirp technique [2]. This paper, therefore, compares the performance of coded ultrasound signals for shear wave detection to conventional short ultrasound pulses, and also compares the performance of different coded signals.
This paper is structured as follows: In the Materials and Methods section, we introduce the relationship between ultrasound SNR and shear wave SNR, followed by experiment designs for evaluating the performance attributes of coded excitation for shear wave detection, including penetration, sensitivity to motion, and robustness to weak RF signal. In the Results section, we first show two phantom studies (with and without a pork belly layer) to systematically compare the performance of coded excitation and conventional detection methods, followed by an in vivo liver case study to demonstrate the feasibility of using the proposed method for in vivo applications. We close the paper with discussion and conclusions.
MATERIALS AND METHODS
A. Ultrasound signal SNR and shear wave signal SNR
Shear wave motion signals are derived from ultrasound RF signals by a variety of methods [31]. Regardless of the differences among these methods, the shear wave motion signal SNR is related to the RF signal SNR, given by the Cramér-Rao Lower Bound proposed in [32] and [19]. Here we follow Walker and Trahey [19]:
| (1) |
where σ(Δt – Δt̂) is the standard deviation of the jitter error of shear wave motion detection (which is inversely proportional to the shear wave signal SNR), f0 is the center frequency of the transmitted signal, T is the window size used for motion calculation, B is the fractional bandwidth, ρ is the correlation coefficient between the RF signals used for motion calculation, and SNRRF is the SNR of the ultrasound signal. If assuming identical ultrasound center frequency, window size, fractional bandwidth, and a correlation coefficient of 1 (since minimal RF decorrelation is expected for shear wave imaging) for different imaging pulses, then Eq. (1) can be approximately reduced to:
| (2) |
where SNRSW is the shear wave motion SNR and is inversely proportional to the standard deviation of the jitter error. Equation (2) can be used to approximately predict the outcome of shear wave signal SNR given different ultrasound signal SNRs under the same shear wave generation setting.
B. Prediction of shear wave signal SNR for the coded ultrasound signals
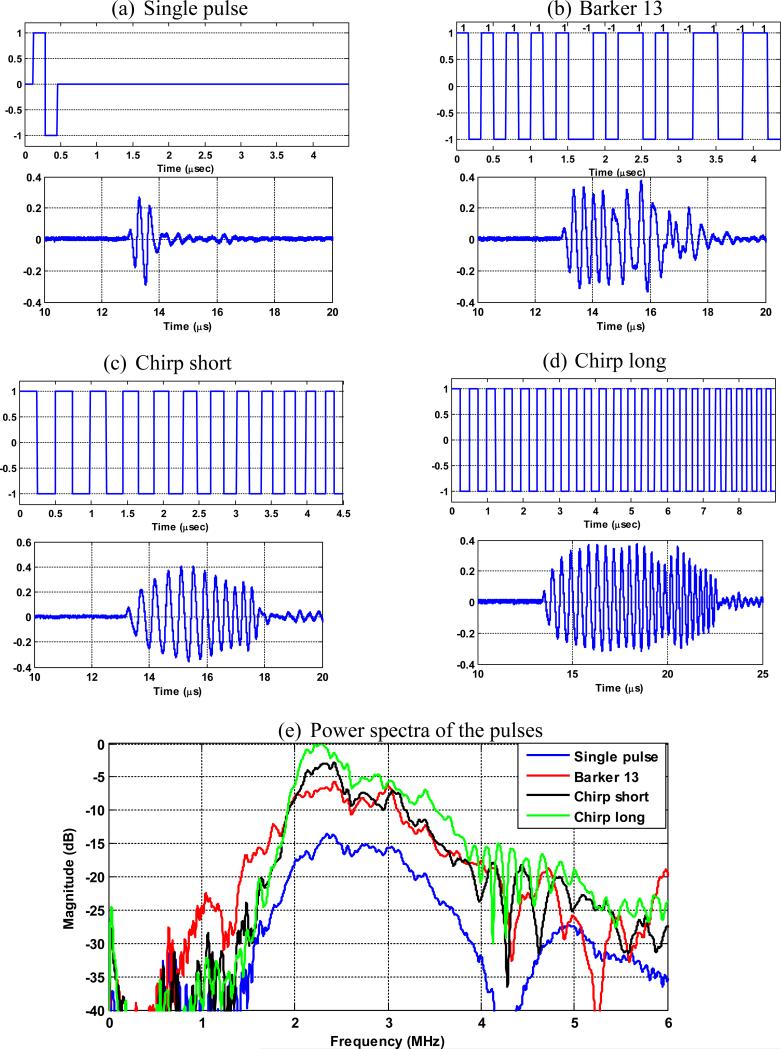
Four imaging pulses were studied in this paper to form plane waves: a conventional short imaging pulse (f0 = 3 MHz, pulse duration ≈ 0.33 μs), a Barker code with length of 13bits (f0 = 3 MHz, pulse duration ≈ 4.36 μs), a short linear FM pseudo-chirp pulse (f0 from 2 MHz to 4 MHz, pulse duration ≈ 4.49 μs), and a long linear FM pseudo-chirp pulse with twice the duration of the short chirp pulse (f0 from 2 MHz to 4 MHz, pulse duration ≈ 8.98 μs). The short chirp pulse was designed to have the same duration as the Barker pulse, and the long chirp pulse was designed to investigate the advantage of the chirp pulses over Barker code in terms of longer code length. The coded pulses were programmed on a tri-state pulser of the Vantage ultrasound research system (Verasonics Inc., Redmond, WA) [33]. A curved array transducer (C5-2v, Verasonics Inc., Redmond, WA) was used throughout this study. The bandwidth of the transducer is from 2 MHz to 5 MHz. The transmitted waveforms from the C5-2v were measured in a water tank by a hydrophone (HGL-0200, Onda Coorporation, Sunnyvale, CA) and the frequency spectra were obtained using Fourier transform. The programmed code, the transmitted waveforms, and the corresponding spectra of the 4 pulses are shown in Fig. 1.
Figure 1.
The programmed code (the first row in each panel) of the (a) single pulse, (b) the Barker 13 pulse, (c) the chirp short pulse, and (d) the chirp long pulse. (e) Power spectra of the 4 different pulses normalized to the maximal power amplitude of the 4 pulses (chirp long).
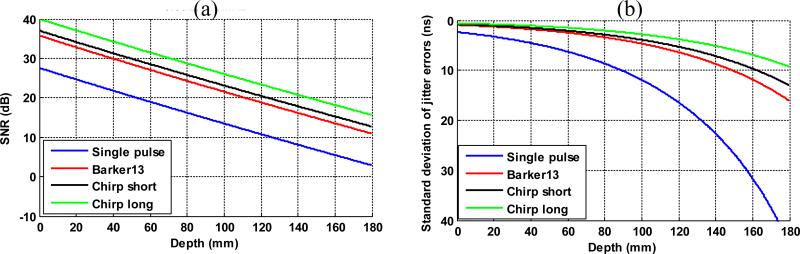
Figure 1(e) shows that the chirp long pulse has the highest energy magnitude across the bandwidth of the C5-2v (2 to 5 MHz). The center frequency f0(given by the centroid of the spectrum) and fractional bandwidth B (full-width at half-maximum divided by center frequency) are 2.73 MHz and 57.3% for the single pulse; 2.64 MHz and 65.5% for the Barker 13 pulse; 2.51 MHz and 57.9% for the chirp short pulse; and 2.53 MHz and 58.2% for the chirp long pulse. To predict the shear wave signal SNR of the 4 detection pulses, it is reasonable to assume that the 4 pulses have similar center frequency and bandwidth, and therefore Eq. (2) can be used. Because it is challenging to estimate the actual ultrasound noise level for the calculation of ultrasound SNR, it was assumed that the chirp long pulse has an SNR of 40 dB, so that the noise amplitude can be inversely estimated given the signal amplitude of the chirp long pulse. To estimate the signal amplitude of the chirp long pulse, the energy of the spectrum from 2 MHz to 5 MHz (as shown in Fig. 1(e)) was summed. Then the noise amplitude was calculated by dividing the signal amplitude by the assumed SNR of 40 dB. Note that 40 dB was an assumed SNR level for the purpose of convenient comparisons among different pulses and therefore can be replaced by any quantities or variables. This same noise amplitude was then used for all detection pulses to calculate ultrasound SNR. To study the behavior of shear wave SNR as a function of imaging depth, a 0.5 dB/cm/MHz attenuation coefficient was applied to the power spectrum of each detection pulse to estimate the ultrasound SNR and then the shear wave motion SNR at each depth. Figure 2 shows the prediction of the behavior of the ultrasound SNR and shear wave motion SNR (in the form of standard deviation of jitter error) as a function of depths. One can see that theoretically, all the coded pulses would provide higher shear wave SNR than the conventional single pulse; and the chirp long pulse would outperform the Barker 13 pulse and the chirp short pulse. In shallow regions where ultrasound SNR is high, all pulses provide similar performance and the jitter error plateaus, which indicates that the shear wave SNR would plateau above certain ultrasound SNR. This agrees with the results shown in Walker and Trahey's study [19].
Figure 2.
The predicted ultrasound SNR (a) and shear wave SNR (b) as a function of imaging depth (in form of standard deviation of jitter error) of the 4 different imaging pulses given 0.5 dB/cm/MHz ultrasound attenuation.
C. RF compression and shear wave motion calculation
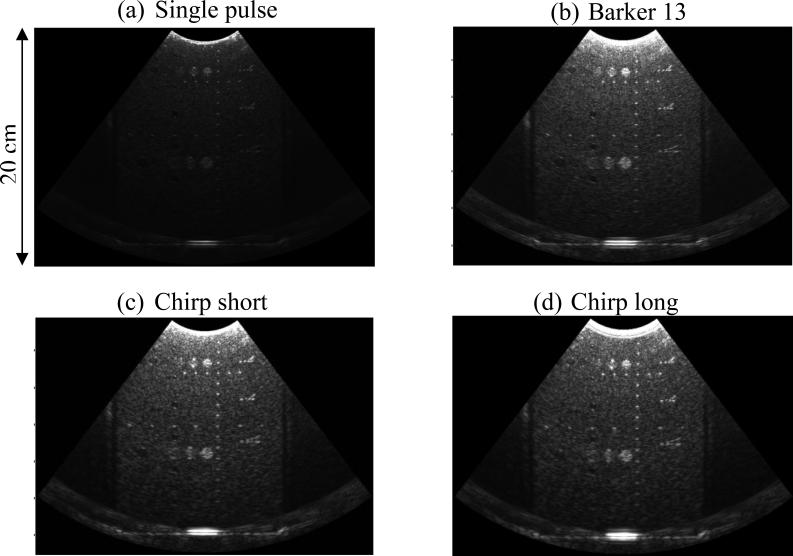
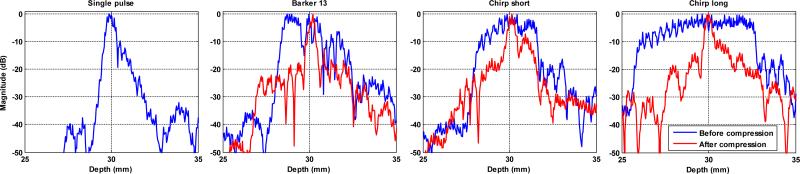
The Vantage Verasonics system uses pixel-oriented software beamforming to beamform the RF signals that are collected in the channel data [34]. Before beamforming, the RF signal was compressed with decoding filters to recover range resolution. For the Barker 13 code, the spectrum inversion-based decoding filter [5] was used for the RF compression. For the chirp codes, matched filtering [4] was used instead of mismatched filtering because the transmitted chirp signals are already envelope-windowed by the natural bandwidth of the transducer, as shown in Figs. 1(c) and (d). Figure 3 shows the B-mode images of a phantom (Model 040GSE, CIRS Inc., Norfolk, VA) obtained by using the 4 different detection pulses in the form of plane waves. One can see substantial improvement of B-mode imaging penetration from the coded pulses, as well as the preserved range resolution on the wires and cyst targets after RF compression. Figure 4 shows the RF signals (before and after compression) of a thin wire submerged about 30 mm deep in the water from the 4 detection pulses. One can see that after compression, the main lobe widths of the coded pulses are comparable to that of the single pulse. The nonlinear propagation in water may have compromised the RF compression and resulted in deteriorated axial resolution (i.e. strong range lobes for the coded pulses). Nevertheless, the axial resolution for coded pulses was significantly improved after RF compression. The RF compressed channel data are beamformed and down-mixed to generate in-phase/quadrature (IQ) data. The IQ data of consecutive frames were then used to estimate axial particle velocity (Vz) caused by shear wave propagation. The one-dimensional autocorrelation method [35] was used to calculate Vz.
Figure 3.
B-mode images obtained by (a) single pulse, (b) Barker 13 pulse, (c) chirp short pulse, and (d) chirp long pulse. All imaging parameters were controlled to be identical for the 4 pulses.
Figure 4.
Envelope signals (before and after compression) of a thin wire obtained from the 4 detection pulses.
D. Phantom experiment I
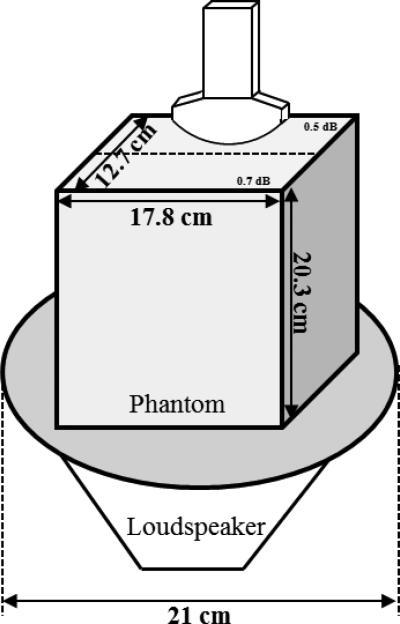
To systematically study the performance of the 4 pulses for shear wave detection throughout a large range of depth, a loudspeaker setup was used to produce stable and controllable shear waves into a large phantom (Model 040GSE, CIRS Inc., Norfolk, VA) with a dimension of 17.8 cm × 12.7 cm × 20.3 cm (length x width x height). The loudspeaker setup is similar to the one used in a previous external vibration study [29]. Figure 5 shows the schematic plot of the experiment setup. To obtain repeatable shear wave patterns, the loudspeaker was synchronized with the Vantage system by triggering, so that the Vantage system always started shear wave detection 200 ms after the vibration was started. The phantom was positioned on top of the loudspeaker. The positions of the phantom, loud speaker and ultrasound transducer did not change during these experiments. The total detection duration was 46 ms and the total vibration duration was 400 ms. A 50 Hz continuous vibration was used throughout the phantom study. For shear wave detection, the 4 detection pulses were transmitted in the form of plane waves at a pulse-repetition-frequency (PRF) of 2500 Hz. A 5-angle plane wave spatial compounding (−9°, −4.5°, 0°, 4.5°, 9°) was used to reduce speckle noise and improve ultrasound SNR [23, 30], which brings the effective PRF down to 500 Hz (2500 Hz / 5 angles = 500 Hz).
Figure 5.
Schematic plot of the experiment setup.
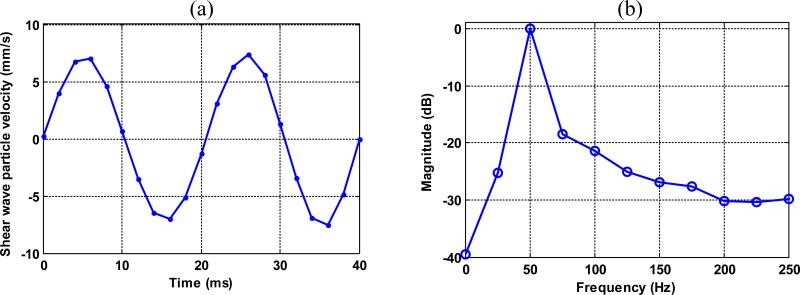
To analyze shear wave signal SNR, a Fourier transform was performed on the shear wave signal along the temporal direction for each imaging pixel. Figure 6(a) shows a typical shear wave motion signal from a single pixel, and Fig. 6(b) shows the Fourier transform of the signal. In each spectrum at each pixel, as shown in Fig. 6(b), the signal energy at 50Hz was considered as shear wave signal, and the rest of the spectrum was averaged and considered as shear wave detection noise. Shear wave motion SNR was then obtained by calculating the ratio of shear wave signal to the detection noise.
Figure 6.
(a) Shear wave motion signal from a single pixel. (b) The Fourier transform of the signal in (a).
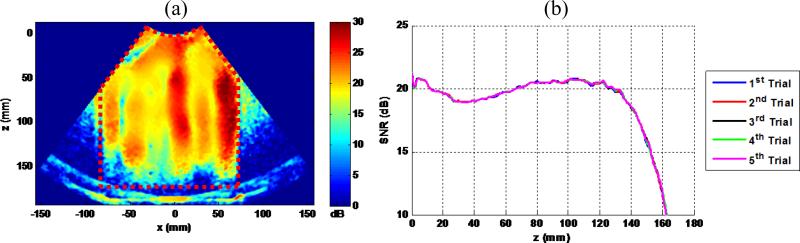
Figure 7(a) shows a typical shear wave motion SNR map obtained using this method with the single pulse transmission. Variations of shear wave motion SNR can be observed inside the phantom (indicated by the region inside the red dashed lines), which are caused by inhomogeneous distributions of shear wave energy at different spatial locations due to standing waves. To measure shear wave motion SNR as a function of depth, a mean shear wave motion SNR was calculated by averaging the SNR values of all imaging pixels at the same depth. Figure 7(b) shows the shear wave motion SNR-depth plot obtained using the map in Fig. 7(a) (1st trial), as well as 4 more SNR-depth plots obtained from 4 other independent data acquisitions (trials 2 to 5). It can be seen that the shear wave pattern and shear wave motion SNR are very repeatable. As mentioned above, because the positions of the transducer, the phantom and the loudspeaker were fixed, it is feasible to use this proposed method to systematically compare the shear wave detection performance of the 4 different detection pulses.
Figure 7.
(a) A typical shear wave motion SNR map obtained by the proposed experiment setup. The red dashed lines indicate the phantom region. (b) plots of shear wave motion SNR versus depth from the 5 independent trials. The plots are almost all overlapping, demonstrating good repeatability of shear wave motion SNR measurement.
In the first part of the phantom experiment, the 0.5 dB/cm/MHz attenuation section of the CIRS 040GSE phantom was directly imaged by the C5-2v transducer with the 4 detection pulses, as shown in Fig. 5. Three experiments were designed:
-
1)
To test penetration of shear wave detection, the same ultrasound transmit voltage (140 Vpp (peak-to-peak voltage)) and loudspeaker input voltage (800 mVpp) were used for all the detection pulses. One acquisition was taken for each detection pulse.
-
2)
To test sensitivity to shear wave motion, the ultrasound transmit voltage was fixed at 140 Vpp for all detection pulses, and the loudspeaker input voltage was gradually turned down from 800 mVpp to 100 mVpp with a step size of 100 mVpp. One acquisition was taken for each detection pulse at each loudspeaker input voltage (32 data acquisitions in total). This experiment was designed to simulate an in vivo situation where shear wave motion is weak (i.e. poor shear wave generation) but RF signal is strong.
-
3)
To test robustness to weak RF signal, the loudspeaker input voltage was fixed at 800 mVpp for all the detection pulses, and the ultrasound transmit voltage was gradually turned down from 140 Vpp to 10 Vpp, with a step size of 20 Vpp from 140 Vpp 20 Vpp, and a step size of 10 Vpp from 20 Vpp to 10 Vpp. One acquisition was taken for each detection pulse at each ultrasound transmit voltage (32 data acquisitions in total). This experiment was designed to simulate an in vivo situation where RF signal is weak (i.e. strong ultrasound attenuation) but shear wave motion is strong.
For each data acquisition, a 2D shear wave motion SNR map and a SNR-depth plot similar to Fig. 7 were reconstructed.
E. Phantom experiment II
To simulate in vivo imaging, a piece of excised pork belly (about 3 cm thick) was positioned between the transducer and phantom (Fig. 8), to introduce more attenuation and ultrasound reverberation clutter noise to shear wave detection. A thin layer of degassed water was poured between the pork belly and phantom surface to ensure good coupling. Steps 2) and 3) from the previous phantom study were repeated for this experiment setup. The 0.5 dB/cm/MHz attenuation section of the phantom was imaged. For each data acquisition, a 2D shear wave SNR map and a SNR-depth plot similar to Fig. 7 were reconstructed.
Figure 8.
Experiment setup with a piece of excised pork belly in between the transducer and the phantom.
F. In Vivo liver case study
This part of the study was designed to compare in vivo performance of the coded ultrasound signals for shear wave detection. In order to achieve fair comparisons of the 4 detection pulses with identical imaging situations (e.g. similar FOV of the liver and similar shear wave motion inside the liver), the 4 detection pulses were programmed into one shear wave acquisition sequence. Upon triggering, the loudspeaker vibrated at 50 Hz continuously for 200 ms to reach a steady state of shear wave generation inside the liver. Then the Vantage system started shear wave detection (with the loudspeaker kept on) with the single pulse for 40 ms, followed by 40 ms of Barker 13 detection, 40 ms of chirp short detection, and 40 ms of chirp long detection. The entire data acquisition was done within 200 ms, which is short enough to assume that the liver inside the FOV was stationary given that the subject was also asked to hold their breath. Each detection pulse detects 2 cycles of the 50 Hz shear wave within the 40 ms window, therefore, the shear wave signal can be assumed to be identical for the 4 pulses. A real-time B-mode imaging sequence was programmed with the shear wave detection sequence for live B-mode guidance.
In this case study, a healthy volunteer with Body Mass Index (BMI) of 40 was recruited. The study was approved by the Institutional Review Board (IRB) of the Mayo Clinic and written consent was obtained from the subject. The ultrasound safety parameters (Table I) of all the detection pulses are all below FDA regulatory limits [36]. The mechanical index (MI) and thermal index (TI) were measured following the NEMA (National Electrical Manufacturers Association) standards [37]. The soft tissue thermal index (TIS) for unscanned modes with aperture > 1cm2 was used to calculate TI for all the shear wave detection pulses. The acoustic power was determined using hydrophone planar scanning methods. The duration of each detection pulse is calculated using a PRF of 2500 Hz and total detection duration of 40 ms (i.e. 100 firings). An effective shear wave imaging PRF of 1 Hz (i.e. one shear wave detection event per second) was assumed for the thermal model. To measure probe surface temperature rise (TR), a 30 gauge type T thermocouple (Omega Engineering Inc., Stamford, CT) was sandwiched between the transducer and a piece of pork belly and five repeated measurements were taken for each detection pulse (five separate transmissions for the five measurements). The TR within the tissue was calculated using the following equation from Palmeri et al.[38]:
| (3) |
where α is the ultrasound attenuation and was assumed to be 0.7 dB/cm/MHz to be conservative; I is the ISPPA (spatial peak, pulse average intensity, nonderated to be conservative), t is the time of the ultrasound transmission (40 ms), and cv is the heat capacity per unit volume (4.2 mWs/cm3/°C).
Table I.
Summary of measured ultrasound safety parameters of the four detection pulses
| Single pulse | Barker 13 | Chirp short | Chirp long | FDA Regulatory Limit | ||
|---|---|---|---|---|---|---|
| MI | 0.44 | 0.47 | 0.54 | 0.61 | 1.90 | |
| TI | 0.01 | 0.04 | 0.08 | 0.16 | 6 | |
| ISPTA, 0.3 (mW/cm2) at 2500 Hz PRF | 34.4 | 137.3 | 153.7 | 321.6 | 720 | |
| TR (°C) | Probe surface Within tissue | < 0.1 | < 0.1 | < 0.1 | 0.2 | 6 |
| 0.008 | 0.032 | 0.036 | 0.075 | |||
The subject was laid supine on the examination bed with the back coupled to the loudspeaker with right arm abducted [29]. A relatively large liver region free of major vessels was located. A total of 5 data acquisitions were obtained with 5 separate breath-holds. Similar to the processing method introduced in the phantom studies, shear wave SNR was calculated by taking the ratio of shear wave energy at 50 Hz to the detection noise. The average shear wave SNR from the 5 data acquisitions was used to compare the performance of the 4 detection pulses.
RESULTS
A. Phantom experiment I
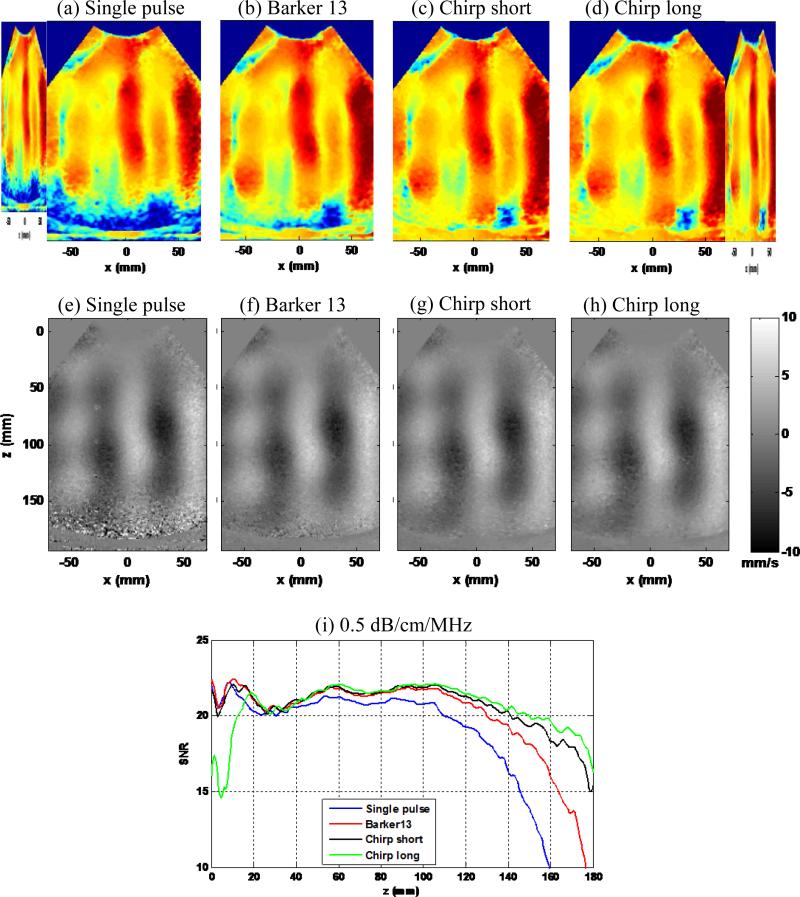
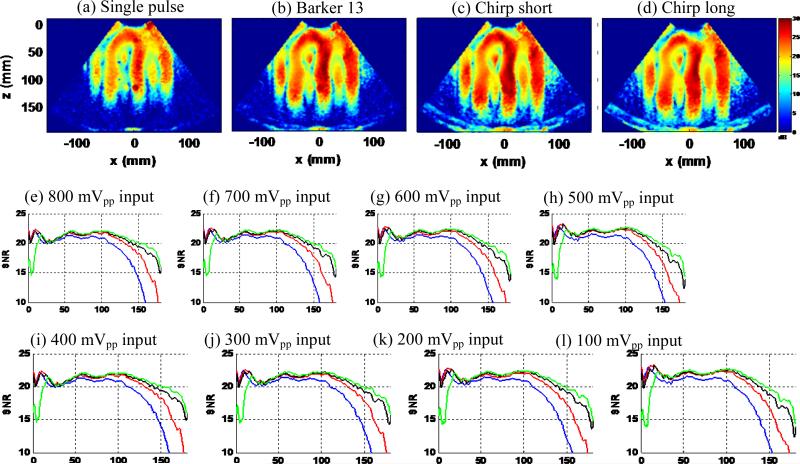
Figure 9 shows the shear wave SNR maps (Figs. 9(a)–(d)), snapshots of the shear wave motion at a time instant (Figs. 9(e)-(h)), and SNR-depth plots of the 4 detection pulses, with maximal ultrasound transmit voltage (140 Vpp) and loudspeaker input voltage (800 mVpp). One can clearly see the penetration gain of the coded pulses from the SNR maps and the shear wave motion plots: the coded pulses could all reach the bottom of the phantom while the single pulse could not. The SNR-depth plot in Fig. 9(i) shows the details of the SNR behavior as a function of depth for the 4 pulses. One can see that the shear wave motion SNR of all coded pulses is higher than the single pulse beyond 4 cm of depth. The chirp long pulse shows the highest shear wave motion SNR beyond 10 cm of depth, followed by the chirp short pulse and the Barker 13 pulse. The SNR curves for different pulses merge together for depths shallower than 4 cm, which indicate a plateau of shear wave motion SNR when ultrasound SNR is above a certain threshold. These shear wave SNR results are in good agreement to the predicted SNR behavior shown in Fig. 2(b) in terms of the relative positions of the curves. If using a shear wave SNR cutoff of 15 dB, the gain in penetration of shear wave detection is approximately 2 cm for Barker 13, 3 cm for chirp short, and 4 cm for chirp long.
Figure 9.
Experiment I part 1): penetration performance. (a)-(d): Shear wave SNR maps of the 4 detection pulses. (e)-(h): Snapshots of the shear wave motion at the same time instant for the 4 detection pulses. (i): Shear wave SNR-depth plot of the 4 detection pulses.
Figure 10 shows the results of the second experiment, which was designed to test the sensitivity to shear wave motion of the 4 detection pulses. Figures 10 (a)-(d) show the shear wave SNR maps obtained from the minimal loudspeaker input voltage (100 mVpp). One can see that all coded pulses showed higher sensitivity to motion than the single pulse, with the chirp long pulse having the highest sensitivity. It is interesting to see that given the same weak motion, the coded ultrasound signals could still detect the motion well while the single pulse could not. This implies that in some in vivo shear wave imaging situations, the shear wave generation might actually be robust – it might be the compromised shear wave detection pulses that sometimes could not pick up the motion signal. Figures 10 (e)-(l) show the detailed shear wave SNR-depth plots obtained from all loudspeaker input voltages. All coded pulses show higher shear wave SNR than the conventional single pulse for all configurations. The chirp long pulse shows the highest sensitivity to motion, and both of the chirp pulses show better sensitivity to motion than the Barker 13 code for all the experiments, which are consistent with the theoretical predictions above. At the 100 mVpp input voltage, the single pulse suffered from weak shear wave motion and strong ultrasound attenuation. The shear wave SNR fell below 15 dB beyond 10 cm of depth. However the chirp pulses could still detect robust shear wave signals with greater than 15 dB SNR until 15 cm depth, which is about a 5 cm gain of penetration as compared to the single pulse.
Figure 10.
(a) – (d): shear wave SNR maps of the 4 detection pulses at minimal loudspeaker input voltage of 100mVpp. (e) – (l): shear wave SNR-depth plots of the 4 detection pulses with gradually decreased input voltages (800 mVpp to 100 mVpp).
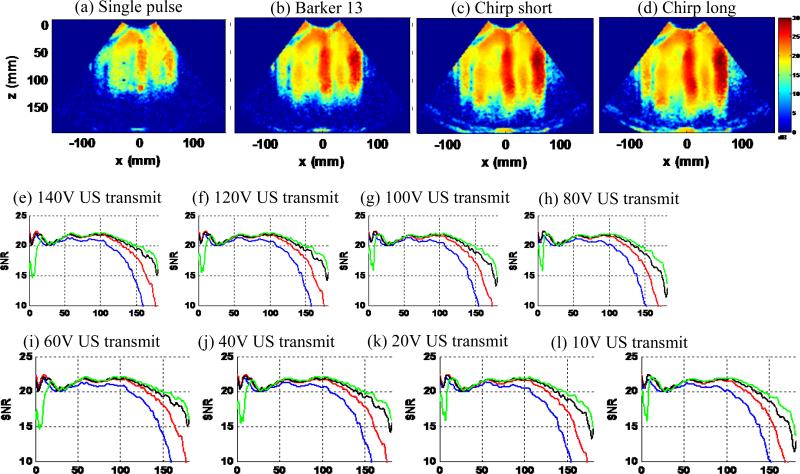
Figure 11 shows the results of the third experiment, which was designed to test the robustness to weak RF signals of the 4 detection pulses. Figures 11(a)-(d) show the shear wave SNR maps with minimal ultrasound transmit voltage (10 Vpp). Figures 11(e)-(l) show the detailed SNR-depth plots of the 4 detection pulses with decreased ultrasound transmit voltage (from 140 Vpp to 10 Vpp). The decreased ultrasound transmit voltage was used to simulate weakened ultrasound RF signal. Again, as shown in Fig. 11, all coded pulses show significantly higher shear wave detection SNR and penetration than the single pulse. At 10 Vpp transmit voltage, the chirp long signal could still reach about 15 cm penetration, while the single pulse fell apart at about 8 cm. The chirp pulses, especially the chirp long pulse, had better performance than the Barker 13 pulse. These results indicate that in in vivo imaging situations where shear wave motion is strong but ultrasound attenuation is high (i.e. in obese patients), the coded pulses can substantially improve shear wave motion detection thanks to their high robustness to weak RF signals. It takes more ultrasound attenuation to severely deteriorate the shear wave signals detected by coded pulses than by conventional short pulses. Note that the ultrasound attenuation introduced here was simulated by decreasing the ultrasound transmit voltage, which does not include the effect of frequency dependent attenuation. Frequency dependent attenuation can compromise the performance of the coded pulses. This will be discussed later in the paper.
Figure 11.
(a)-(d): shear wave SNR maps of the 4 detection pulses at minimal ultrasound transmit voltage of 10V. (e)-(l): shear wave SNR-depth plots of the 4 detection pulses with gradually decreased ultrasound transmit voltage (140 V to 10 V).
B. Phantom experiment II
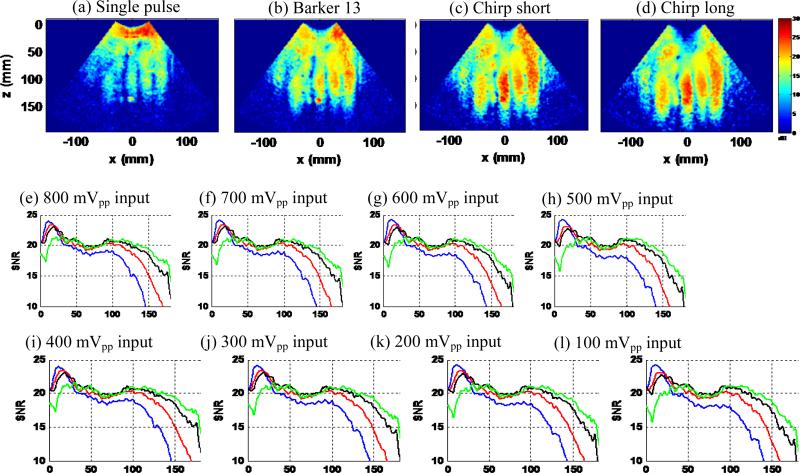
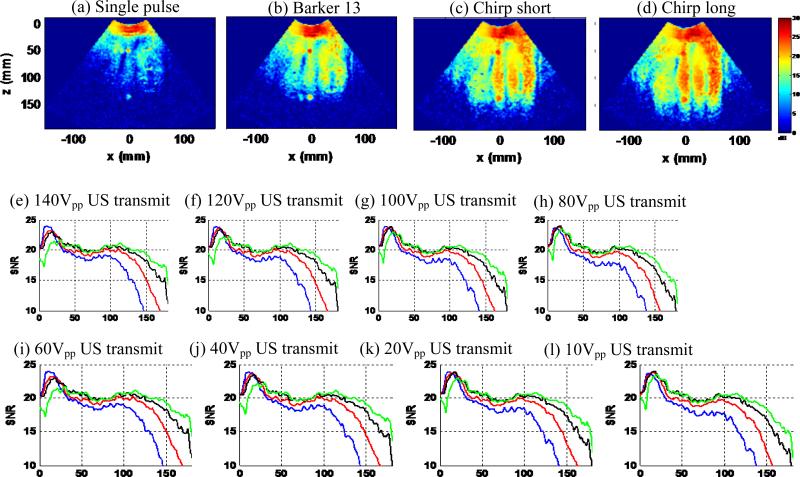
This part of the experiment added a piece of excised pork belly on top of the phantom to increase ultrasound attenuation and introduce reverberation clutter noise, and then repeated the tests shown in the previous section. The pork belly used in this study was mainly composed of fat and the experiment was conducted at room temperature. Based on Goss et al. [39], the pig fat at 20 °C has an ultrasound attenuation of 3.5 dB/cm/MHz, which should be a reasonable estimate of the attenuation of the pork belly used in this study. Figure 12 shows the shear wave motion SNR maps (at minimal loudspeaker input voltage) and SNR-depth plots of the 4 detection pulses with gradually decreased input voltage. Figure 13 shows the shear wave motion SNR maps (at minimal ultrasound transmit voltage) and SNR-depth plots with gradually decreased ultrasound transmit voltage. The first 3 cm corresponds to the position of the pork belly and one can ignore the shear wave SNR results within this region. Similarly to the results in Figs. 10 and 11, all coded pulses outperformed the single pulse under the same imaging configuration. One can clearly see the overall decrease of shear wave SNR caused by the pork belly. The single pulse struggled in all imaging setups while the chirp long pulse was able to image through the pork belly fairly well to 10 cm of depth. None of the coded pulses were affected by the reverberation clutter noise introduced by the pork belly, as indicated by the good shear wave SNR beyond 3 cm of depth. However inside the pork belly, the coded pulses give lower SNR at high ultrasound transmit voltage (Fig. 12), and the SNR gets much higher inside the pork belly at low ultrasound transmit voltage (Fig. 13). This may be caused by the strong reverberations of the long coded pulses inside the pork belly. Nevertheless, the shear wave detection did not seem to be affected by the reverberation beyond the pork belly region, and it is of less interest to obtain strong shear wave signals inside the subcutaneous fat and muscle tissue in vivo.
Figure 12.
Pork belly phantom study I. (a-(d): shear wave SNR maps of the 4 detection pulses at minimal loudspeaker input voltage of 100 mVpp. €-(l): shear wave SNR-depth plots of the 4 detection pulses with gradually decreased input voltages (800 mVMpp to 100 mVpp).
Figure 13.
Pork belly phantom study II. (a)-(d): shear wave SNR maps of the 4 detection pulses at minimal ultrasound transmit voltage of 10 Vpp. (e)-(l): shear wave SNR-depth plots of the 4 detection pulses with gradually decreased ultrasound transmit voltage (140 Vpp to 10 Vpp).
C. In vivo liver case study
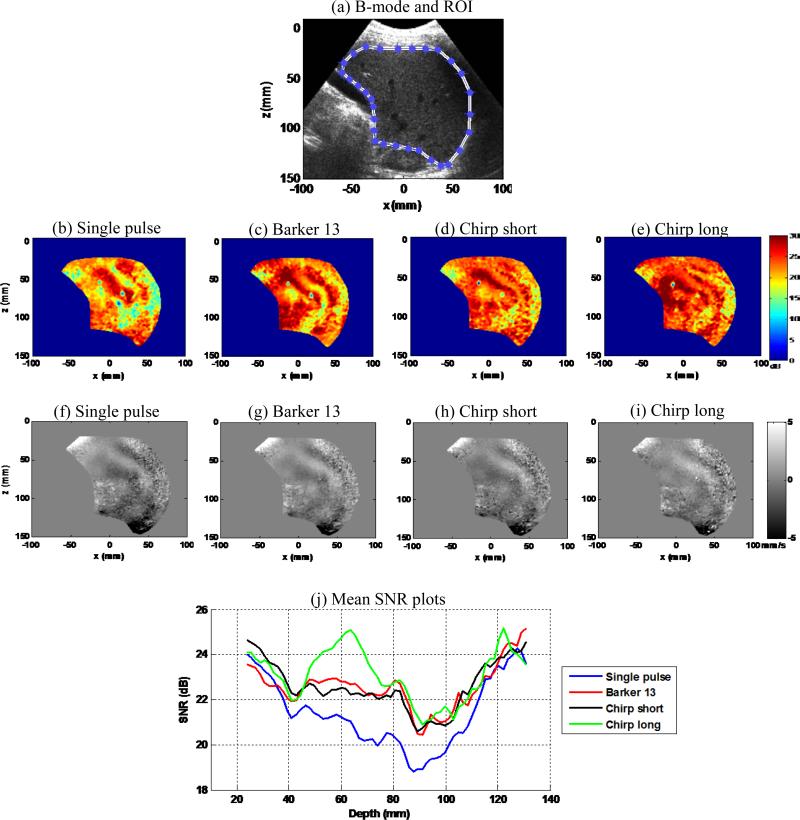
Figure 14(a) shows an example of the liver B-mode image from one of the five data acquisitions. A region-of-interest was manually selected to segment the liver for SNR analysis. Figures 14(b)-(e) show shear wave SNR maps of the 4 detection pulses from one of the five data acquisitions. Figures 14(f)-(i) show snapshots of the shear wave motion signal of the 4 detection pulses at the same time instant from one of the five data acquisitions. Figure 14(j) shows the averaged SNR-depth plots from the 5 data acquisitions for the 4 detection pulses. These results indicate that all the coded pulses provide higher shear wave SNR than the single pulse, and the chirp long pulse provided the highest SNR. The first 9 cm of the SNR-depth plots are in good agreement with the phantom study results and the theoretical predictions shown above. Beyond 9 cm, all the SNR plots merged to a similarly high value. This was caused by the lower liver capsules that provide strong ultrasound reflections and thus strong RF signals, which would increase the shear wave SNR. Overall, from this challenging subject with high BMI, the shear wave motion SNR provided by the coded pulses are in general substantially higher than by the single pulse. The coded excitation technique enables strong penetration of the plane waves so that both high frame rate and large FOV (both width and depth) shear wave detection can be realized. Note that the FOV size in Fig. 14 was large enough to contain the entire liver, which is comparable to 2D Magnetic Resonance Elastography (MRE) [40]. However, with the ultrafast frame rate provided by plane wave imaging, one can achieve much higher frame-rate shear wave imaging than MRE.
Figure 14.
(a) B-mode image of the liver and manually selected region-of-interest (ROI) for SNR calculation. (b)-(e) Shear wave SNR maps of the 4 detection pulses from one data acquisition. (f)-(i) Snapshots of the shear wave motion at the same time instant for the 4 detection pulses from one data acquisition. (j) SNR-depth plots of the 4 detection pulses. The SNR value for each pulse was averaged over the 5 independent data acquisitions.
DISCUSSION
This paper presents a systematic study of the feasibility of implementing coded excitation for shear wave detection with plane wave imaging, with the hypothesis that coded ultrasound signals can significantly improve shear wave detection penetration and shear wave signal SNR. The first phantom study demonstrated an approximate gain in penetration of 2 cm, 3cm, and 4 cm for the Barker 13 pulse, the chirp short pulse, and the chirp long pulse respectively, for shear wave motion detection. Both the phantom experiments with and without pork belly showed substantial gain in penetration and shear wave SNR for the coded pulses. All coded pulses demonstrated substantially higher sensitivity to motion as well as robustness to weak RF signal than the conventional short pulse. Due to the longer duration which offers higher ultrasound SNR, the chirp long pulse showed the best performance among the three coded pulses. The shear wave motion SNR could be well predicted by the ultrasound SNR using the theory proposed by Walker and Trahey [19], as indicated by the good agreement between the theoretical prediction results and the phantom study results. The in vivo case study on a challenging subject demonstrated the feasibility of using the proposed method for in vivo applications. All coded pulses could provide good shear wave SNR inside the whole FOV of liver, with the chirp long pulse providing the best performance.
The mismatch of the SNR curves between the theoretically-predicted ones (e.g. Fig. 2) and the experiment results (e.g. Fig. 9) is primarily caused by the heterogeneous shear wave field. As mentioned above, synchronized triggering sequences and fixed positions of the probes, phantoms, and loudspeakers were used to obtain repeatable pattern of shear wave motions. The theory assumes a homogeneous shear wave motion field, but in reality it is very challenging to produce such a homogeneous shear wave motion field with equal shear wave amplitude throughout the phantom. Therefore, it is very challenging to obtain a uniform shear wave SNR map, and consequently the behavior of the shear wave SNR curves from experiments is affected by the shear wave pattern. Nevertheless, since the same shear wave motion was being detected by the 4 imaging pulses, it is still feasible to compare the performance of the 4 pulses under the same conditions. One can also see that the chirp long pulse has a consistently low SNR in the near field. This is because the duration of the chirp long pulse was about 9 μs, which corresponds to about 7 mm of near field “dead zone” because the system could not receive echo until after pulse transmission was finished. This can also be seen on the B-mode images shown in Fig. 3. Therefore, the shear wave detection in the “dead zone” was unreliable and shear wave SNR was low.
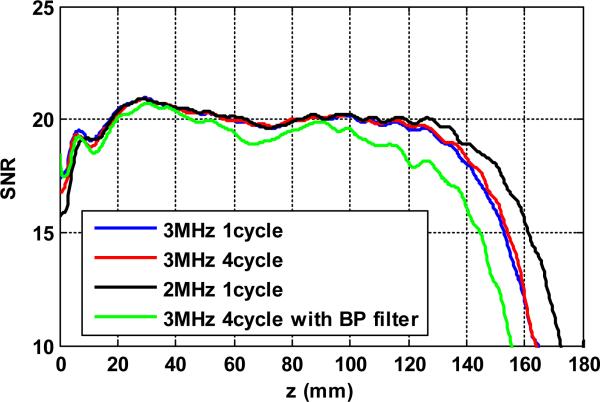
The conventional single pulse used in this study was chosen in a way such that the center frequency and the bandwidth of the single pulse are similar to those of the coded pulses, as shown in Fig. 1(e). The main reason for doing this is to achieve similar conditions among the different pulses in terms of center frequency, bandwidth, etc., as indicated by Eq. (1), so that a convenient comparison among the different pulses could be achieved. In practice, to improve the SNR and penetration of the conventional single pulses for shear wave detection, one can either increase the pulse length, lower the center frequency, or adding a bandpass filter to the RF signal to suppress out-of-band noise. Figure 15 shows an example of the shear wave detection SNR performance of 3 conventional single pulses: 3 MHz center frequency with 1-cycle pulse length (the same one used in this study), 3 MHz center frequency with 4-cycle pulse length, and 2 MHz center frequency with 1-cycle pulse length. Also shown in Fig. 15 is the shear wave SNR from the bandpass filtered 3 MHz 4-cycle conventional pulse (bandpass filter center frequency = 3 MHz, bandwidth = 45%). The same setup used in this study was used to compare the three pulses with 140 Vpp transmission voltage and 800 mVpp vibration amplitude. From Fig. 15 one can see that all three pulses have similar shear wave SNR for less than about 11 cm depth, and then the 4-cycle 3MHz pulse gained slightly better penetration than the 1 cycle pulse, while the 2MHz pulse gained significantly higher penetration than both of the 3 MHz pulses. Although the longer pulse length increases the total amount of energy deposited into the tissue, because the center frequency is still 3 MHz, this pulse still suffers from significant attenuation beyond a certain depth. From the shear wave SNR standpoint of view shown in Eq. (1), increased pulse length decreases the bandwidth of the pulse (i.e. the time bandwidth product remains constant), and therefore the shear wave SNR performance was not improved significantly (according to Eq. (1)). For the 2 MHz pulse, attenuation was significantly less and therefore the penetration performance was improved. As compared to Fig. 9, however, the 2 MHz single pulse did not improve the SNR in shallower depth as the coded pulse did. One possible reason is that the time-bandwidth product of the 2 MHz single pulse is smaller than that of the coded pulses, and therefore the coded pulses outperformed the single pulse thanks to a higher ultrasound SNR provided by a higher time-bandwidth product. The bandpass filtered signal did not show significant improvement for shear wave detection as expected. One possible reason is that the ultrasound SNR for these uncoded conventional pulses has plateaued in the near field. Increasing the pulse duration or bandpass filtering the signal does not further increase the ultrasound SNR and shear wave SNR due to fixed time-bandwidth product. Another possible reason is that the experiment was conducted in a tissue-mimicking phantom with high echogenicity. The implementation of bandpass filter may be significant for in vivo applications with low ultrasound echo amplitude. The bandpass filtered signal had worse penetration than the unfiltered signal for depth > 10 cm, possibly due to the removal of lower frequency component by the narrow bandpass filter.
Figure 15.
Shear wave SNR-depth plots of 3 conventional single pulses.
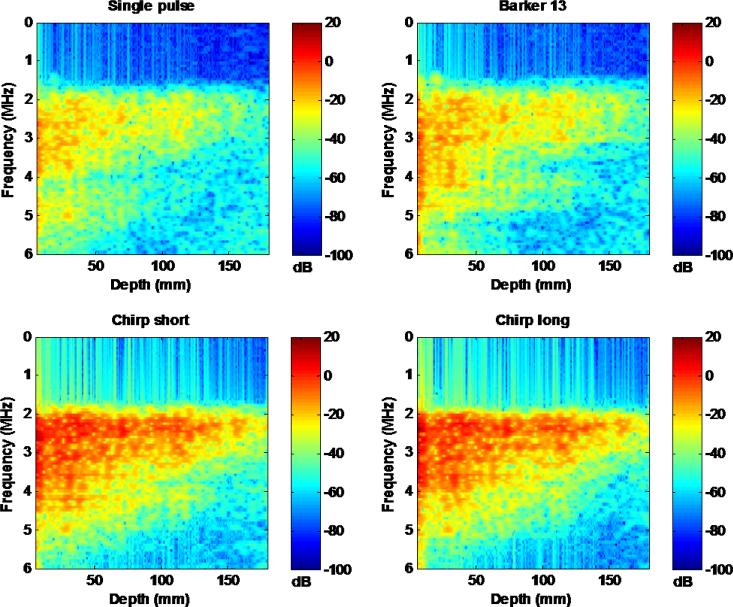
The performance of the coded pulses can be further improved by designing decoding filters that account for frequency dependent attenuation [7]. Figure 16 shows the spectrograms of the 4 detection pulses using a short-time Fourier transform on a single A-line. One can clearly see that the high frequency components of the pulses attenuate faster than the low frequency components. The decoding filters used in this study did not account for such frequency dependent attenuation. Therefore, the efficacy of RF compression could be compromised. In practice, it is challenging to adaptively design depth-dependent decoding filters because of unknown tissue attenuation. Future study is needed to investigate the impact of depth-dependent filtering on shear wave detection with coded excitation.
Figure 16.
Spectrograms of the 4 detection pulses using short-time Fourier transform. All spectrograms were normalized to the maximal power of the single pulse.
As briefly mentioned above, the proposed shear wave motion detection with coded excitation can be used for other shear wave sources as well such as acoustic radiation force and intrinsic physiological motion [41, 42]. As shown in Figs. 10 and 12, the coded pulses have higher sensitivity to shear wave motion than the short single pulse. The higher sensitivity is given by the higher ultrasound SNR of these coded pulses. In challenging tissues such as deep liver, kidney, and heart, the shear wave motion can be rather small. Using coded pulses can help better detect these motions. In less challenging tissues such as thyroid and breast where shear wave motion produced by acoustic radiation force is strong, one can potentially reduce the push beam intensity to reduce the shear wave amplitude, because the coded pulses may still be able to robustly detect these shear wave signals. The reduced push beam intensity can decrease the cooling period for the probe and tissue and potentially improve the shear wave imaging frame rate.
In this study, only plane wave imaging was investigated for shear wave detection with coded excitation. However, the same principle can be applied to other detection beams such as focused detection beams [43] and diverging beams [21, 44]. Also, this study only proposed the use of coded excitation for plane waves for shear wave detection. The same principles can be applied to other plane wave imaging applications such as ultrafast Doppler and functional ultrasound imaging [45]. Note that the same limitations and challenges of coded excitation in the context of medical ultrasound imaging, such as frequency-dependent attenuation in tissues, the time-bandwidth limitations imposed by medical ultrasound applications, and potential thermal issues, should also apply to these applications. One can optimize the coded excitation technique based on a specific application to best balance the tradeoffs.
The chirp long code showed better performance than the chirp short code and the Barker 13 code in this study, and both chirp codes showed better performance than the Barker 13 code. The codes were designed to achieve similar center frequency and bandwidth for the different pulses so that a simplified version of Eq. (1) could be used to predict the shear wave SNR. The chirp codes have stronger low-frequency content in the spectrum than the Barker 13 code, which may facilitate better penetration for the chirp codes. Meanwhile, the probe response to the Barker 13 code did not seem to be as good as the response to the chirp codes, as shown in Fig. 1. This may cause less efficient transmission of ultrasound energy for the Barker code and compromise its performance in shear wave detection. The chirp long code demonstrated the advantage of using chirp coded excitation in terms of no code length limitations. However one cannot use an extremely long chirp code due to the large near-field dead zone and possible waste of energy – it was shown that when ultrasound SNR is beyond a certain level, shear wave motion SNR plateaus. One can optimize the length of the chirp code based on different applications.
Plane wave imaging is usually not limited by MI due to the lack of transmit focusing. Increasing transmit voltage is an option for increasing plane wave imaging SNR, but the transmit voltage is limited by power supply and transducer elements breakdown voltage. With these limitations, the use of coded pulses becomes a viable solution to boost plane wave imaging SNR and shear wave signal SNR. Coded pulses may have thermal issues due to the long duration pulses, and therefore can be limited for real-time B-mode imaging. However, in the context of shear wave imaging where shear elasticity maps are refreshed once or twice per second, thermal issues are minimal and can be neglected, as shown in Table I.
The decoding processing time was about 12 seconds for all the coded pulses when using MATLAB scripts on an Intel Xeon 12-core 2.66 GHz computer. One can dramatically reduce the processing time by using GPU processing or other parallel processing tools. Fast decoding is necessary for real-time shear wave imaging.
There are some limitations of this study. First, the single pulse spectrum (i.e. the Fourier transform of Fig. 1(a) upper panel) extends from 0.7 MHz to 3.9 MHz, and some of the low frequency components are outside the bandwidth of the probe (66.5% of energy is within the 2-5 MHz bandwidth of the probe). A dual-cycle single pulse would have fit the bandwidth of the transducer better (with 78.2% energy within the 2-5 MHz bandwidth of the probe) than the single-cycle pulse. Nevertheless, as shown in Fig. 15, the single cycle 3 MHz pulse performed similarly to the elongated pulse. As discussed above, one possible reason is that the time-bandwidth product of uncoded pulses is constant and therefore ultrasound SNR does not improve with elongated pulses. Another possible reason is that the SNR of ultrasound echo is relatively high for shear wave imaging in tissues or phantoms as compared to echo from blood, thus limiting the benefit of longer pulse duration for single frequency pulses. Therefore, results obtained with the single cycle pulse in this study as a reference are still meaningful. Second, other phase encoding methods such as Golay codes were not studied. Golay codes do not have the length limitation of the Barker code and may achieve similar performance to the chirp codes. However, Golay codes require multiple transmit events, which may reduce motion detection PRF, and are also susceptible to physiological or gross motion. Third, Fig. 4 shows that the pulse compression performance was not optimal in this study. A few factors that may contribute to this are nonlinear propagation in water when creating the decoding filter, the use of a 3-level pulser, and suboptimal decoding filter design. Degraded pulse compression compromises the contrast of the coded pulses, which may be significant for certain shear wave elastography applications such as breast imaging where good contrast is critical for complex hypoechoic targets. Future studies are needed to optimize the decoding filters performance based on the 3-level pulser of the Vantage system and study the contrast performance of coded pulses both in vitro and in vivo. Finally, only a curved array was investigated in the study. Future study is needed to investigate linear array and phased array transducers for various shear wave applications.
CONCLUSIONS
This study investigated the feasibility of using coded excitation for shear wave detection, to increase the shear wave motion SNR and shear wave motion detection penetration for plane wave imaging. Both phantom results and the in vivo liver case study results demonstrated substantial improvement of shear wave motion SNR and detection penetration using the coded pulses as compared to the conventional short pulse. The coded pulses also showed significantly higher sensitivity to shear wave motion and robustness to weak RF signal than the conventional short pulse. The chirp pulses showed better performance than the Barker pulse, with the chirp long pulse demonstrating the best performance. These results are very promising for implementing coded excitation in shear wave detection for shear wave elastography, to facilitate robust shear elasticity measurements of tissue.
ACKNOWLEDGEMENTS
This work was supported by American Heart Association (AHA) postdoctoral fellowship 14POST20000009, and National Institutes of Health (NIH) grants R01EB002167, R01DK106957, and R01DK092255. The content is solely the responsibility of the authors and does not necessarily represent the official views of AHA or NIH. The authors thank Randall Kinnick and Thomas Kinter for their experiment assistance.
Footnotes
DISCLOSURES
Mayo and some of the authors have financial interest in the technology described here.
REFERENCES
- 1.Chiao RY, Hao X. Coded excitation for diagnostic ultrasound: a system developer's perspective. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2005 Feb;52(2):160–70. doi: 10.1109/tuffc.2005.1406543. [DOI] [PubMed] [Google Scholar]
- 2.O'Donnell M. Coded excitation system for improving the penetration of real-time phased-array imaging systems. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 1992;39(3):341–51. doi: 10.1109/58.143168. [DOI] [PubMed] [Google Scholar]
- 3.Haider B, Lewin PA, Thomenius KE. Pulse elongation and deconvolution filtering for medical ultrasonic imaging. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 1998;45(1):98–113. doi: 10.1109/58.646915. [DOI] [PubMed] [Google Scholar]
- 4.Misaridis T, Jensen JA. Use of modulated excitation signals in medical ultrasound. Part II: Design and performance for medical imaging applications. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2005 Feb;52(2):192–207. doi: 10.1109/tuffc.2005.1406546. [DOI] [PubMed] [Google Scholar]
- 5.Wang Y, Metzger K, Stephens DN, Williams G, Brownlie S, O'Donnell M. Coded excitation with spectrum inversion (CEXSI) for ultrasound array imaging. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2003 Jul;50(7):805–23. doi: 10.1109/tuffc.2003.1214501. [DOI] [PubMed] [Google Scholar]
- 6.Welch LR, Fox MD. Practical spread spectrum pulse compression for ultrasonic tissue imaging. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 1998;45(2):349–55. doi: 10.1109/58.660145. [DOI] [PubMed] [Google Scholar]
- 7.Eck K, Brenner AR, Wilhelm W, Noll TG. Improvement of site resolution and dynamics in ultrasound imaging by depth-dependent mismatched filter pulse compression. Biomedizinische Technik. Biomedical engineering. 1997;42(Suppl):99–100. doi: 10.1515/bmte.1997.42.s2.99. [DOI] [PubMed] [Google Scholar]
- 8.Chiao RY, Rhyne TL. Harmonic Golay-coded excitation with differential pulsing for diagnostic ultrasound imaging. 2002 6491631 B2, U. Patent.
- 9.Misaridis T, Jensen JA. Use of modulated excitation signals in medical ultrasound. Part III: High frame rate imaging. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2005 Feb;52(2):208–19. doi: 10.1109/tuffc.2005.1406547. [DOI] [PubMed] [Google Scholar]
- 10.Chiao RY, Thomas LJ. Synthetic Transmit Aperture Imaging Using Orthogonal Golay Coded Excitation. IEEE International Ultrasonics Symposium. 2000:1677–1680. [Google Scholar]
- 11.Zhao H, Mo LY, Gao S. Barker-coded ultrasound color flow imaging: theoretical and practical design considerations. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2007 Feb;54(2):319–31. doi: 10.1109/tuffc.2007.246. [DOI] [PubMed] [Google Scholar]
- 12.Muzilla DJ, Chiao RY, Hall AL. Method and apparatus for color flow imaging using coded excitation with single codes. 1999 5938611, U. S. Patent.
- 13.Chiao RY. Method and apparatus for flow imaging using Golay codes. 2001 6,312,384, U. S. Patent.
- 14.Liu J, Insana MF. Coded pulse excitation for ultrasonic strain imaging. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2005 Feb;52(2):231–40. doi: 10.1109/tuffc.2005.1406549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liu D, Ebbini ES. Viscoelastic property measurement in thin tissue constructs using ultrasound. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 2008;55(2):368–383. doi: 10.1109/TUFFC.2008.655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Misaridis T, Jensen JA. Use of modulated excitation signals in medical ultrasound. Part I: Basic concepts and expected benefits. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2005 Feb;52(2):177–91. doi: 10.1109/tuffc.2005.1406545. [DOI] [PubMed] [Google Scholar]
- 17.Yoon C, Lee W, Chang J, Song TK, Yoo Y. An efficient pulse compression method of chirp-coded excitation in medical ultrasound imaging. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2013 Oct;60(1):2225–9. doi: 10.1109/TUFFC.2013.2815. [DOI] [PubMed] [Google Scholar]
- 18.Ramalli A, Guidi F, Boni E, Tortoli P. Real-time base-band pulse compression imaging. IEEE International Ultrasonics Symposium. 2013:2002–2005. [Google Scholar]
- 19.Walker WF, Trahey GE. A fundamental limit on delay estimation using partially correlated speckle signals. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control. 1995 Mar;42(2):301–308. [Google Scholar]
- 20.Deffieux T, Gennisson JL, Larrat B, Fink M, Tanter M. The variance of quantitative estimates in shear wave imaging: Theory and experiments. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 2012;59(1):2390–2410. doi: 10.1109/TUFFC.2012.2472. [DOI] [PubMed] [Google Scholar]
- 21.Song P, Zhao H, Urban MW, Manduca A, Pislaru SV, Kinnick RR, Pislaru C, Greenleaf JF, Chen S. Improved shear wave motion detection using pulse-inversion harmonic imaging with a phased array transducer. IEEE Transactions on Medical Imaging. 2013;32(12):2299–2310. doi: 10.1109/TMI.2013.2280903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Urban MW, Chen S, Greenleaf JF. Error in estimates of tissue material properties from shear wave dispersion ultrasound vibrometry. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 2009 Apr;56(4):748–758. doi: 10.1109/TUFFC.2009.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tanter M, Bercoff J, Sandrin L, Fink M. Ultrafast compound imaging for 2-D motion vector estimation: application to transient elastography. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2002 Oct;49(10):1363–74. doi: 10.1109/tuffc.2002.1041078. [DOI] [PubMed] [Google Scholar]
- 24.Bercoff J, Tanter M, Fink M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2004 Apr;51(4):396–409. doi: 10.1109/tuffc.2004.1295425. [DOI] [PubMed] [Google Scholar]
- 25.Song P, Zhao H, Manduca A, Urban MW, Greenleaf JF, Chen S. Comb-push ultrasound shear elastography (CUSE): a novel method for two-dimensional shear elasticity imaging of soft tissues. IEEE Transactions on Medical Imaging. 2012;31(9):1821–1832. doi: 10.1109/TMI.2012.2205586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Song P, Urban MW, Manduca A, Zhao H, Greenleaf JF, Chen S. Comb-Push Ultrasound Shear Elastography (CUSE) With Various Ultrasound Push Beams. IEEE Transactions on Medical Imaging. 2013;32(8):1435–1447. doi: 10.1109/TMI.2013.2257831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tanter M, Bercoff J, Athanasiou A, Deffieux T, Gennisson JL, Montaldo G, Muller M, Tardivon A, Fink M. Quantitative assessment of breast lesion viscoelasticity: Initial clinical results using supersonic shear imaging. Ultrasound in Medicine and Biology. 2008 Sep;34(9):1373–1386. doi: 10.1016/j.ultrasmedbio.2008.02.002. [DOI] [PubMed] [Google Scholar]
- 28.Bavu É, Gennisson J-L, Couade M, Bercoff J, Mallet V, Fink M, Badel A, Vallet-Pichard A, Nalpas B, Tanter M, Pol S. Noninvasive in vivo liver fibrosis evaluation using Supersonic Shear Imaging: a clinical study on 113 hepatitis C virus patients. Ultrasound in Medicine & Biology. 2011;37(9):1361–1373. doi: 10.1016/j.ultrasmedbio.2011.05.016. [DOI] [PubMed] [Google Scholar]
- 29.Zhao H, Song P, Meixner DD, Kinnick RR, Callstrom MR, Sanchez W, Urban MW, Manduca A, Greenleaf JF, Chen S. External Vibration Multi-Directional Ultrasound Shearwave Elastography (EVMUSE): Application in Liver Fibrosis Staging. Ieee Transactions on Medical Imaging. 2014 Nov;33(1):2140–8. doi: 10.1109/TMI.2014.2332542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Montaldo G, Tanter M, Bercoff J, Benech N, Fink M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2009 Mar;56(3):489–506. doi: 10.1109/TUFFC.2009.1067. [DOI] [PubMed] [Google Scholar]
- 31.Pinton GF, Dahl JJ, Trahey GE. Rapid tracking of small displacements with ultrasound. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2006 Jun;53(6):1103–17. doi: 10.1109/tuffc.2006.1642509. [DOI] [PubMed] [Google Scholar]
- 32.Carter GC. Coherence and Time-Delay Estimation. Proceedings of the IEEE. 1987 Feb;75(2):236–255. [Google Scholar]
- 33.Flynn JA, Kaczkowski P, Linkhart K, Daigle RE. Arbitrary Waveforms Using a Tri-State Transmit Pulser. IEEE International Ultrasonics Symposium. 2013:41–44. [Google Scholar]
- 34.Daigle RE. Ultrasound imaging system with pixel oriented processing. 2009:US20090112095A1.
- 35.Kasai C, Namekawa K, Koyano A, Omoto R. Real-time two-dimensional blood flow imaging using an autocorrelation technique. IEEE Transactions on Sonics and Ultrasonics. 1985;SU-32(3):458–64. [Google Scholar]
- 36.Herman BA, Harris GR. Models and regulatory considerations for transient temperature rise during diagnostic ultrasound pulses. Ultrasound in Medicine & Biology. 2002 Sep;28(9):1217–24. doi: 10.1016/s0301-5629(02)00558-6. [DOI] [PubMed] [Google Scholar]
- 37.AIUM/NEMA . Standard for real-time display of thermal and mechanical acoustic output indices on diagnostic ultrasound equipment. Revision 2. AIUM; Laurel, MD: 2009. [Google Scholar]
- 38.Palmeri ML, Nightingale KR. On the thermal effects associated with radiation force imaging of soft tissue. IEEE Trans Ultrason Ferroelectr Freq Control. 2004 May;51(5):551–65. [PubMed] [Google Scholar]
- 39.Goss SA, Johnston RL, Dunn F. Compilation of empirical ultrasonic properties of mammalian tissues. II. The Journal of the Acoustical Society of America. 1980 Jul;68(1):93–108. doi: 10.1121/1.384509. [DOI] [PubMed] [Google Scholar]
- 40.Yin M, Talwalkar JA, Glaser KJ, Manduca A, Grimm RC, Rossman PJ, Fidler JL, Ehman RL. Assessment of hepatic fibrosis with magnetic resonance elastography. Clinical gastroenterology and hepatology : the official clinical practice journal of the American Gastroenterological Association. 2007 Oct;5(10):1207–1213. e2. doi: 10.1016/j.cgh.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kanai H. Propagation of spontaneously actuated pulsive vibration in human heart wall and in vivo viscoelasticity estimation. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2005 Nov;52(11):1931–42. doi: 10.1109/tuffc.2005.1561662. [DOI] [PubMed] [Google Scholar]
- 42.Provost J, Lee WN, Fujikura K, Konofagou EE. Electromechanical wave imaging of normal and ischemic hearts in vivo. IEEE Transactions on Medical Imaging. 2010 Mar;29(3):625–635. doi: 10.1109/TMI.2009.2030186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dahl JJ, Pinton GF, Palmeri ML, Agrawal V, Nightingale KR, Trahey GE. A parallel tracking method for acoustic radiation force impulse imaging. Ieee Transactions on Ultrasonics Ferroelectrics and Frequency Control. 2007 Feb;54(2):301–312. doi: 10.1109/tuffc.2007.244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hasegawa H, Kanai H. High-frame-rate echocardiography using diverging transmit beams and parallel receive beamforming. Journal of Medical Ultrasonics. 2011 Jul;38(3):129–140. doi: 10.1007/s10396-011-0304-0. [DOI] [PubMed] [Google Scholar]
- 45.Tanter M, Fink M. Ultrafast imaging in biomedical ultrasound. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 2014;61(1):102–119. doi: 10.1109/TUFFC.2014.6689779. [DOI] [PubMed] [Google Scholar]