The Infant Orienting With Attention task: Assessing the neural basis of spatial attention in infancy

Abstract

Infant visual attention develops rapidly over the first year of life, significantly altering the way infants respond to peripheral visual events. Here we present data from 5-, 7- and 10-month-old infants using the Infant Orienting With Attention (IOWA) task, designed to capture developmental changes in visual spatial attention and saccade planning. Results indicate rapid development of spatial attention and visual response competition between 5 and 10 months. We use a dynamic neural field (DNF) model to link behavioral findings to neural population activity, providing a possible mechanistic explanation for observed developmental changes. Together, the behavioral and model simulation results provide new insights into the specific mechanisms that underlie spatial cueing effects, visual competition, and visual interference in infancy.

From the first moments of life, infants undergo profound visual development. After only a few hours of visual experience, neonates demonstrate visual preferences for simple high-contrast objects and shapes (Johnson, 1992) and begin to recognize their mother’s face (Bushnell, 2001). These early visual behaviors are mediated by neural development, and change rapidly over the first several months of postnatal life. This close coupling of eye movements and underlying neural circuitry make orienting tasks an ideal means of assessing functional neural development. For example, young infants will reliably orient toward abruptly appearing visual events. These eye movements are likely automatic or reflexive, and are largely mediated by the superior colliculus and frontal eye fields (see for example: Atkinson, 1984; Johnson, 1990). Thus, infants who fail to demonstrate this basic orienting response may lack sufficient cortical and/or subcortical development in these areas.

Over the next several months of postnatal life, infants show rapid improvements in both endogenously generated volitional saccades (i.e., goal directed), and inhibitory control of reflexive saccades (i.e., resistance to distraction). For example, by 3–4 months, infants can learn to suppress reflexive saccades to an attentional pre-cue that appears contralaterally to an attractive stimulus (Johnson, 1995), and can learn to make anticipatory saccades to expected target locations (Canfield & Haith, 1991; Canfield & Kirkham, 2001; Haith, Hazan, & Goodman, 1988). Both anti-saccade and anticipatory looking tasks require a sufficiently developed prefrontal cortex, likely including the frontal eye fields (FEF) and dorsolateral prefrontal cortex (DLPFC: Johnson, 1995). Thus, infant orienting offers a unique peek into underlying neural development.

Several tasks use basic visual orienting responses to assess infant attention and neural development. For example, the “Gap Task” was designed to assess an infant’s ability to disengage attention from a salient central cue in favor of a new, peripheral input. By examining the relative influence of a peripheral spatial attention cue presented either simultaneously with a central fixation stimulus (overlap) or after the offset of the central fixation stimulus (gap) researchers have demonstrated significant increases in orienting latency to the peripheral targets when the fixation stimulus remains visible (i.e., overlap condition). This effect is thought to reflect the increased time it takes to disengage fixation from it’s current locus of attention (Csibra, Tucker, & Johnson, 1998; Hood & Atkinson, 1993; Matsuzawa & Shimojo, 1997). Others have used similar tasks to assess the cortical components involved in shifting attention under conditions of competition. For example, Atkinson and colleagues have developed a task based on the gap effect, which calculates the relative deficit in attention shifting under conditions of visual competition (e.g., overlap) and non-competition (e.g., gap or no gap). Unlike the Gap Task however, this “Fixation Shift” task was designed to provide a qualitative score of cortical attentional functioning, which appears to be a sensitive indicator of perinatal neural deficit and injury (Atkinson & Braddick, 2012).

Both the Gap Task and the Fixation Shift Task tap components of attention that are implicated in multiple aspects neural functioning. There are, however, several other components of visual orienting that have an important impact on visual cognition. For example, spatial cueing tasks tap a fundamentally different aspect of visual attention, and generally rely on the robust tendency of eye movements to be faster and more accurate to peripheral targets that were preceded by a brief spatial cue, than to targets that were not preceded by a cue (see for example Posner & Petersen, 1990). Evidence of a spatial cueing effect suggests the presence of covert attentional orienting mechanisms, likely mediated by parietal cortex (Woldorff et al., 2004). These covert attention mechanisms and saccadic eye movements are thought to be closely coupled under naturalistic viewing conditions for both voluntary (i.e., visual search) and reflexive (i.e., motion detection, abrupt onset) saccades (see for example: Yantis & Jonides, 1984; 1996). Critically, the covert shift of attention that precedes both endogenous and exogenous eye movements has been shown to be mediated by the same large-scale neural networks (Peelen, Heslenfeld, & Theeuwes, 2004).

Using a spatial cueing task, several researchers have demonstrated that like adults, infants show increased speed and accuracy for target locations that were preceded by a brief attention cue. This effect was most pronounced when the central fixation stimulus was terminated prior to the onset of the cue and target, eliminating the need for the infant to first disengage from the central fixation stimulus before engaging with the peripheral target (e.g., Hood & Atkinson, 1993). These spatial cueing effects have been demonstrated in infants as young as 3–6 months (for reviews see: Atkinson & Braddick, 2012; Colombo, 2001) and are typically taken as evidence that parietal cortex is at least partially functional around the third month, with particular improvements around 6 months and beyond.

Using a modified spatial cueing paradigm, Fan and colleagues developed a task that assesses functioning across three anatomically distinct attentional networks, the Attention Network Task, or ANT (Fan, Fossella, Sommer, Wu, & Posner, 2003; Fan, McCandliss, Fossella, Flombaum, & Posner, 2005; Fan, McCandliss, Sommer, Raz, & Posner, 2002). This work may have important implications for infant attentional work, as the neural components that make up these attention networks develop at different rates. The Alerting Network is responsible for increases in baseline arousal and readiness, allowing for rapid detection of new peripheral events such as the presentation of a spatial cue. This network consists primarily of right frontal and parietal cortex. The Orienting Network drives shifts of attention, bringing the focus of attention in line with perceptual inputs, and consists of the superior parietal lobe, superior colliculus, frontal eye fields and temporal parietal junction. The Executive Network is involved in resolving response competition, and primarily reflects activity in the prefrontal cortex (Fan et al., 2005; Posner & Rothbart, 2007). Though the ANT is not suitable for use in infants, we have attempted to capture the multi-component spirit of this task in the IOWA task presented here.

The IOWA task was designed to assess visual orienting proficiency (e.g., speed and accuracy) across varying degrees of visual competition, and relies on well-established spatial cueing effects to detect and measure each infant’s ability to covertly shift attention and to make fast and accurate eye movements to a peripherally appearing target. The task consists of several different spatial cue conditions, each measuring a unique aspect of visual orienting. Data from these conditions provide rich descriptive information regarding the development of covert attention, saccade planning, visual competition, and orienting speed. Trials are very quick, reducing fatigue and habituation effects, and making it possible to collect much more data per infant than has typically been possible. The measures can then be combined into composite scores, providing specific measures of attentional development for each infant that are directly comparable both within and across ages, and are free from the confounding effects of gross differences in orienting speed. Although this task was primarily designed to assess individual differences in visual attention, as a first step, it is necessary to establish sensitivity to well-established age-based norms of development. Thus, we present here the first data from the IOWA task collected from 5-, 7-, and 10-month-old infants.

In addition to presenting data from the IOWA task, we also present a neurocomputational model of the development of visual attention that both qualitatively and quantitatively captures data from this task. Neurocomputational models are useful tools in early development because they allow us to probe how changes in brain function—such as changes in excitatory and inhibitory neural interactions—are related to behavioral measures in infancy (Perone & Spencer, 2013b; 2013a; 2014; Perone, Simmering, & Spencer, 2011). Critically, we can manipulate different aspects of a model over development to ask whether specific changes in model parameters are strongly constrained by the pattern of behavioral data. This can be an important first step in generating hypotheses about changes in brain function that can be tested more directly using, for instance, task-based functional neuroimaging (Buss, Wifall, Hazeltine, & Spencer, 2014b; Spencer & Buss, 2013). Here we present a modified dynamic neural field (DNF) model of spatial attention and saccade planning, that has successfully been used to capture saccade planning in adults and non-human primates (Kopecz & Schöner, 1995; Schneegans, Spencer, Schöner, Hwang, & Hollingworth, 2014; Trappenberg, Dorris, Munoz, & Klein, 2001; Wilimzig, Schneider, & Schöner, 2006). The DNF model provides a neurally-grounded computational framework for probing the changes that underlie developmental shifts in infants’ performance in the IOWA task. We show how a cascade of changes in the strength of neural interactions (local excitation, surround inhibition) within and between early visual processing areas, spatial attention, and a saccade motor field effectively capture infants’ performance. The model, therefore, offers a novel platform to probe the development of several orienting mechanisms in infancy, and helps ground these mechanisms of attentional development in complex, real-time neural population dynamics.

To summarize, we hypothesize several key findings. First, we predict that overall RT will decrease with age. This will manifest as shorter look latencies across all conditions. Second, we predict that the relative strength of spatial cueing effects will vary as a function of condition and age. Specifically, we hypothesize that all infants will demonstrate simple facilitation effects for valid cues, but only older infants will demonstrate strong inhibition for the invalid and double cue conditions. Finally, we hypothesize that these age-related changes in spatial attention are driven primarily by changes in the strength and specificity of neural interactions within and between perception, attention, and motor planning areas of the brain. To test this hypothesis, we will attempt to capture the observed developmental effects using a DNF model of spatial attention. By explicitly testing candidate mechanisms of development in an established model of saccade planning, we hope to both provide critical insights into neurobiological theories of infant attention development, and generate new testable hypotheses.

Method

Participants

The final sample consisted of 72 infants, 24 5-month-olds (M = 23.59 weeks, SD = 1.95, 12 males and 12 females), 24 7-month-olds (M = 32.68 weeks, SD = 1.71, 8 males and 16 females) and 24 10-month-olds (M = 44.52 weeks, SD = 2.32, 12 males and 12 females; 24 at each age). An additional 16 subjects were tested but not included in the final analysis due to fussiness (N = 2 at 5 months, N = 2 at 7 months, N = 3 at 10 months), lack of interest (N = 3 at 5 months, N = 2 at 10 months), and equipment failure/experimenter error (N = 2 at 5 months, N = 2 at 10 months). All infants included in this investigation were healthy and full-term, with no history of birth complications or vision problems. All but one of the infant mothers had graduated high school, and 57.8% had completed at least a bachelor’s degree. Of the 72 infant participants, one was reported by their parents as Asian, one as Native Hawaiian, and 8 chose not to answer. The remaining 63 infants were reported as White, with 3 reported as Hispanic.

Infant names were obtained from county birth records, and all parents were contacted by letter and received a follow-up phone call to schedule their appointment. Families were not paid for their participation, but infants received a small toy and parents’ parking expenses were reimbursed.

Stimuli and Apparatus

A Macintosh G5 computer was used to present the stimuli on a single, 37″ LCD color monitor with a viewable surface of 44.6° (w) by 25.9° (h) at a distance of 100cm. Infants were tested in a dimly lit experimental room in which a black curtain hung from the ceiling to the floor to obscure the view of the observer and equipment. The curtain had two openings in it. One opening revealed the 37″ LCD monitor, and the other revealed a low-light TV camera lens used to view infants’ looking behavior in real time. Infants sat in front of the monitor, and their eye movements were recorded as they viewed the events of each trial. All events were presented on a gray background (RGB:136,136,136). The central fixation stimulus consisted of a brightly colored, dynamic smiley face, that appeared at the center of the monitor, and morphed in shape (i.e., bounced and squished from skinny to fat and back again) from 2.4° (w)×2.9° (h), to 4.1° (w)×1.8° (h) at a rate of approximately 1.5 Hz. All spatial pre-cues and targets were constrained to appear 11° either to the left or right of fixation, only the relative location of cue and target were varied across condition. The visual attentional pre-cue consisted of a small black circle (1° diameter) that lasted 100ms, and was generally paired with an auditory attention cue consisting of a 50 Hz pure tone. The spatial pre-cue allowed us to probe the influence of peripheral attention mechanisms, while the auditory attention cue provided an alerting mechanism to help prepare the infant for a behavioral response. The effects of these separate cueing mechanisms were critical for our baseline comparison conditions. Targets for each condition consisted of 52 colorful gifs of everyday objects (e.g., cheeseburger, mailbox, coffee mug, etc.) and appeared 100ms after the offset of the pre-cue interval. All targets subtended 4.8° (w) by 4.4° (h) of visual angle, and total area, contour, chromatic and luminance contrast varied randomly across targets. To rule out possible target-specific effects, we examined RT by target type and found the RTs for all target types to be normally distributed, and all were +− 2 SD from the mean (M =187.49, SD = 13.74ms).

Design and Procedure

This experiment incorporated a 3×5×2 mixed design with Age (5 months, 7months, 10 months) as the between subjects factor, and Condition (double cue, invalid cue, no cue, tone cue, and valid cue) and Side of Target (left or right) as within subjects variables. Each infant saw up to 7 blocks of 10 trials for a total of 70 trials. Each block contained two trials from each cue condition (one with target on left, and one with target on right) presented in random order. Infants who did not complete at least 4 blocks of trials were excluded from analysis. Targets were drawn randomly without replacement for each block from a pool of 52 images.

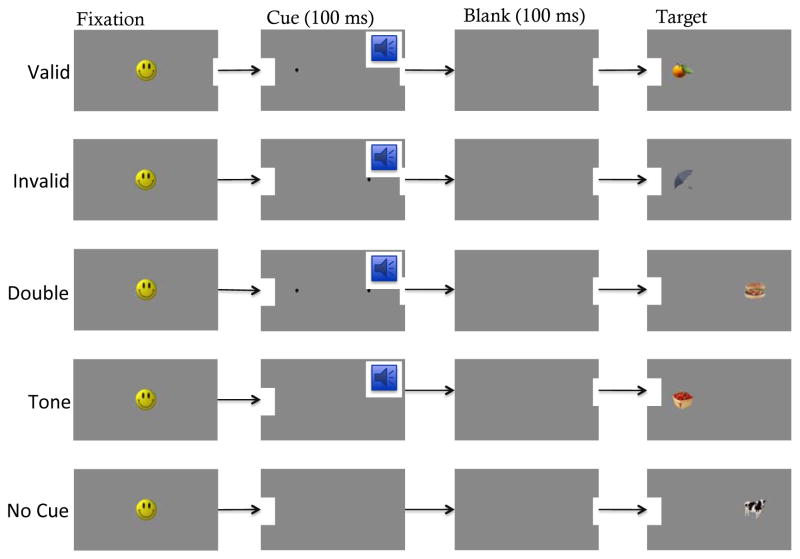
The IOWA tasks consists of three experimental conditions that vary in the degree of cue/target competition, and two control conditions that serve as baseline measures of gross orienting speed to the target in the absence of a spatial pre-cue (see Figure 1). Each of the three experimental conditions used in the current study contained a 100ms spatial pre-cue paired with a pure tone. These cues appeared to the left or right of fixation either in the same location as the target (valid cue), contralateral to the target (invalid cue), or on both sides (double cue). Neither of the two control conditions contained a spatial cue: The tone cue condition contained only the 100ms tone, and the no cue condition contained neither a spatial nor a tone cue.

FIGURE 1.

Experimental and control conditions for the Infant Orienting With Attention, or IOWA Task.

During the experimental session, infants sat on their parent’s lap 100cm in front of a large computer monitor. Parents wore opaque glasses to reduce bias. A trained observer sat out of sight and recorded infant eye movements (latency and direction) via live video feed. Before each trial, an attractive fixation stimulus (i.e., morphing smiley face) was presented in the center of the monitor. Once the observer determined the participant was looking at the fixation stimulus, a key on the computer keyboard was pressed that ended the fixation stimulus, and initiated a 100ms cue period, then a 100ms delay interval, then finally the presentation of the target. This target remained visible until the infant made an eye movement, and the observer made a speeded button press indicating a look to either the left or the right. This button press simultaneously ended the trial, and re-initiated the central fixation stimulus. If an infant did not make an eye movement to the target within 2000ms of the target presentation, the trial was ended and repeated, beginning again with the fixation stimulus.

Reaction times and directional responses were calculated for each trial by means of frame-by-frame coding. The original videos were captured at a rate of 30 fps or 33ms per frame. These 33ms time bins allowed for accurate coding of both directionality and latency of the infant’s first saccade. Although eyetracking offers a level of spatial precision not possible with frame-by-frame coding, the temporal precision of frame-by-frame coding (i.e., 30Hz) rivals most entry-level eye trackers. Moreover, frame-by-frame coding is externally verifiable, and tends to produce more data points per infant (no data loss due to inability to calibrate, poor, or drifting calibration, no loss of pupil visibility or corneal reflection, no loss of babies due to slow or repeated calibrations, etc.). Responses were coded as “correct” if the participant’s first saccade was to the side of the display that contained the target, and “incorrect” for any other response. The timing and accuracy of these responses served as the primary dependent measures. Twenty-five percent of the data were recoded by a second trained observer. Reliability was very high (r = .98, Mean Difference = 24.01ms, SD = 11ms).

Results

Primary dependent measures for the IOWA task consisted of reaction time (RT) and accuracy. Reaction time (ms) was calculated by counting the number of frames from the beginning of the target presentation to the first frame in which lateral motion ceased after an eye movement. This was determined by finding the first two consecutive frames in which the eyes remained stationary on the target and using the first of the two frames to calculate RT. Accuracy was determined by calculating percent correct (i.e., looks to the target) for each condition. Only correct trials were included in reaction time analyses. Before analyzing these data, we filtered any looks that were too fast to be considered reactive saccades (<100ms, 272 trials filtered for 6.8% trial loss), and too slow to reflect on-task behavior (>1000ms, 16 trials filtered for 0.4% trial loss). This ensured that the remaining looks occurred in response to the appearance of the target and not the appearance of the cue or any other distracting event.

Group Reaction Times

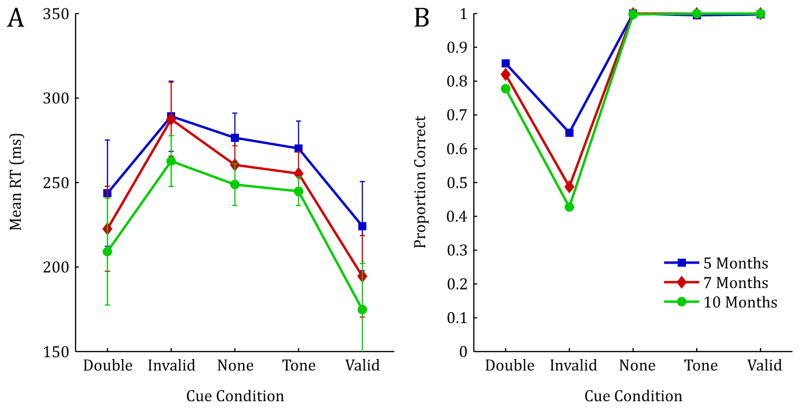
In general, RTs decreased with age, and all participants were fastest in the conditions that contained a valid spatial cue (valid and double cue conditions), and slowest for the invalid cue condition, with intermediate RTs for both baseline control conditions (see Figure 2A). These general observations were confirmed using a 5×3 mixed model ANOVA with Condition (valid cue, invalid cue, double cue, no cue, tone cue) as the within subjects factor, and Age (5mo, 7mo, 10mo) as the between subjects factor. Note that preliminary analyses revealed no effect of side of target presentation (left or right), thus, all analyses were collapsed across this variable. This analysis revealed a significant main effect of Condition, F(4, 276) = 77.005, p < .001, ηp² = .527, indicating a strong spatial cueing effect. There was also a significant main effect of Age, F(2, 69) = 3.877, p = .025, ηp² = .101, indicating a significant reduction in RT measures with increasing age. Finally, this analysis revealed a significant Condition by Age interaction, F(8, 276) = 2.008, p = .046, ηp² = .055. This interaction indicates that the effectiveness of the spatial pre-cue varied across age and condition, with particular differences in valid, invalid, and double cue conditions (see Figure 2A).

FIGURE 2.

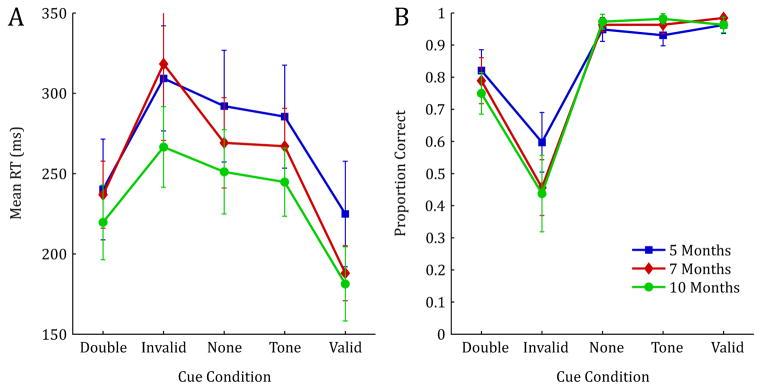
Reaction time measures (correct trials only) and proportion correct for 5, 7, and 10-month-old infants. Error bars represent 1 SD.

To probe this interaction further, we conducted simple effects tests across age for each condition. Results revealed significant between-age effects for three cue conditions: invalid cue, F(2,69) = 3.466, p = .037, ηp² = .091; tone cue, F(2,69) = 3.671, p = .031, ηp² = .096; and valid cue F(2,69) = 5.203, p = .008, ηp² = .131. Pairwise comparisons on these effects were conducted using a Dunn-Sidak correction to protect against Type I error. These comparisons revealed significant developmental differences between 7- and 10-month-olds for the invalid cue condition (p=.048), between the 5 and 10-month-olds (p=.026) for the tone cue condition, and between the 5- and 7-month-olds (p=.040) as well as the 5- and 10-month-olds (p=.011) for the valid cue conditions.

Group Accuracy Measures

Means from the accuracy data reveal that, as expected, overall percent correct was the highest for conditions that contained either a valid spatial cue, or no spatial cue (valid cue, tone cue and no cue) and lowest for the invalid condition, with intermediate accuracy for the double cue condition (see Figure 2B). These data were analyzed using a 5×3 mixed model ANOVA with Condition (valid cue, invalid cue, double cue, no cue, tone cue) as the within subjects factor and Age (5mo, 7mo, 10mo) as the between subjects factor. This analysis revealed a significant main effect of Condition, F(4,276) = 256.995, p < .001, ηp² = .788, indicating that the ability to make correct eye-movements to the target was significantly impaired for conditions that contained high levels of cue/target response competition; namely the invalid and double cue conditions. Though there was no main effect of age, there was a significant Condition by Age interaction, F(8,276) = 4.458, p < .001, ηp² = .114. Inspection of Figure 2B reveals that while performance is near ceiling for all ages in conditions that contain no cue/target competition (valid cue, tone cue, no cue), there are developmental differences in accuracy, particularly in the invalid condition.

To statistically probe these developmental effects, we conducted simple effect tests across age for each condition. Results revealed a significant between-age effect for both the invalid cue condition, F(2,69) = 4.528, p = .014, ηp² = .116, and the tone cue condition, F(2,69) = 5.767, p = .005, ηp² = .143. Pairwise comparisons revealed significant differences between 5- and 10-month-old infants (p=.023), and marginal differences between the 5- and 7-month-olds (p=.052) for the invalid cue condition, and significant differences between the 5- and 10-month-old infants (p=.004) for the tone cue condition.

Composite Attention Score Calculations

To facilitate global comparisons between ages, four composite scores were created from the infant reaction time data, and each score reflects a critical aspect of performance on this task. The four scores are: Mean Reaction Time, Cue Facilitation, Cue Interference, and Cue Competition. Due to the complexity of interpreting performance across multiple conditions using raw RT and accuracy, these scores were created and normalized by each infant’s own baseline RT to facilitate the examination of unique attentional signatures for each infant. Though simple difference scores are common in adult and child looking tasks, some form of normalizing is critical when comparing participants suspected of having large mean RT differences, such as infants of different ages. For example, imagine Infant A has a mean RT of 300ms in the tone cue condition, and 200ms in the valid condition, while Infant B has a mean RT of 400 in the tone cue condition, and 300ms in the valid condition. A simple difference score would equate the degree of valid cue facilitation across both infants (e.g., Infant A: 300–200=100ms change, Infant B: 400–300=100ms change). However, Infant A showed a much higher degree of facilitation than Infant B, as Infant A’s RT was 50% faster for the valid condition, whereas Infant B’s RT was only 25% faster. Although we explored raw RT as a function of condition in the section entitled Group Reaction Time, here we chose to focus on normalized difference scores to better assess the relative influence of the spatial and tone cue for a given individual. Whereas raw difference scores provide information about absolute orienting speed, normalized difference scores allows us to assess the strength of the spatial cueing effect separate from differences in raw orienting speed. Only correct trials were used in calculating these scores. Note, we used mean tone cue as the baseline measure for all subtraction scores, as it was structurally identical to the valid, invalid and double-cue conditions in every way except for its lack of a spatial cue. Thus, a positive difference score can only be attributed to the specific effects of the spatial cue.

Mean Reaction Time

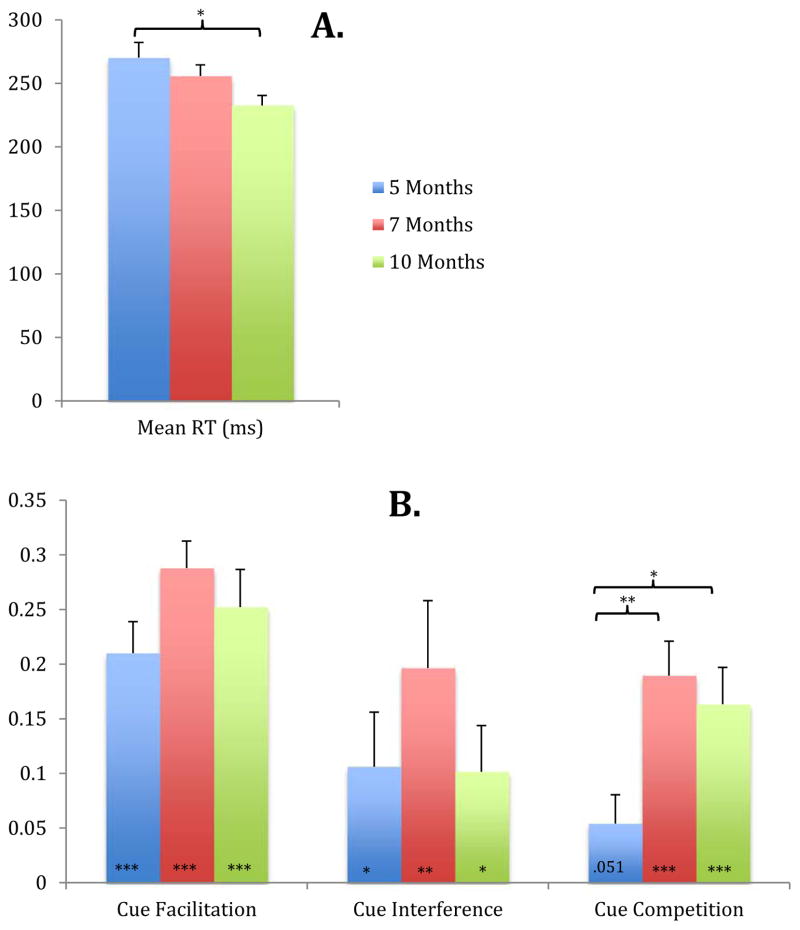
The Mean Reaction Time score was calculated by averaging together reaction times across all five cue conditions. Although we have presented a more detailed reaction time analysis above, this Mean Reaction Time score offers a global assessment of overall speed of orienting and allows for quick developmental comparisons. A one-way ANOVA conducted to examine changes in Mean Reaction Time across the three age groups revealed a significant Age effect, F(2,69)=3.877, p=.025. A follow-up Sidak test revealed that, as expected, 10-month-old infants were significantly faster than 5-month-old infants (p = .022). No other age comparisons were significant. Thus, overall reaction time decreases with age between 5 and 10 months (see Figure 3A).

FIGURE 3.

Mean RT (A) and Attention scores (B) for 5, 7, and 10-month-old infants. Cue Facilitation = (Tone RT - Valid RT)/Tone RT; Cue Interference = (Invalid RT – Tone RT)/Tone RT; Cue Competition = (Double RT – Valid RT)/Tone RT. Note: Asterisks at the base of the Cue Facilitation, Cue Interference, and Cue Competition bars indicate significance compared to zero, asterisks above the bars indicate significant between-age differences. For all comparisons, significance is indicated as follows: * p<=.05, **p<=.01, and ***p<=.001. Error bars represent 1 SEM.

Cue Facilitation

The Cue Facilitation score was calculated by determining the proportion decrease in reaction time (i.e., increase in speed) for the valid cue condition relative to the ‘baseline’ tone cue condition normalized to each infant’s baseline (toneRT-validRT)/toneRT. A higher score indicates that the infant’s reaction time was substantially reduced by the presence of an ipsilateral attentional pre-cue (i.e., a large facilitation effect). One-sample (2-tailed) t-tests comparing Cue Facilitation scores to zero for each age indicate that all age groups showed significant Cue Facilitation effects: t(23)= 7.300, p < .001 at 5 months, Cohen’s d = 3.044, t(23)= 11.694, p < .001 at 7 months, Cohen’s d = 4.877, and t(23)= 7.321, p < .001 at 10 months, Cohen’s d = 3.053 (see Figure 3B).

Cue Interference

Cue Interference was calculated by measuring the increase in reaction time for the invalid cue condition relative to the baseline tone cue condition, again normalized to each infant’s baseline (invalidRT-toneRT)/toneRT. A higher score indicates that the infant’s reaction time to the target was substantially slowed by the presence of a contralateral attentional pre-cue (i.e., a large interference effect). Though interference sores were generally lower than facilitation scores, a one-sample (2-tailed) t-test comparing Cue Interference scores to zero at each age revealed a significant cue interference effect at every age: 5 months, t(23)= 2.129 p = .044, 7 months, Cohen’s d = .888, t(23)= 11.694 p = .004, Cohen’s d = 1.329, and at 10 months, t(23)= 2.402 p = .025, Cohen’s d = 1.002 (see Figure 3B). Thus, all infants suffered a reaction time penalty for the invalid trials relative to baseline.

Cue Competition

The Cue Competition score was calculated as the proportion increase in reaction time for the double cue condition relative to the valid cue condition, normed by each infant’s baseline (doubleRT-validRT)/toneRT. This score provides a measure of orienting inhibition produced by the presence of two competing attention cues. A large score indicates a relatively high degree of response competition, or a slowing down of reaction time when there are two competing attention pre-cues relative to only a single cue (valid cue). A one-sample (2-tailed) t-test comparing scores for the three age groups to zero revealed only a marginal effect of Cue Competition effects at 5-months, t(23)= 2.58 p = .051, with significant effects at 7- and 10-months; t(23)= 6.006 p < .001, Cohen’s d = 2.505, and t(23)= 4.854 p < .001, Cohen’s d = 2.024, respectively (see Figure 3B).

Composite Attention Score by Age Comparisons

To probe for Age by Attention Score interactions, we next conducted a 3×3 mixed model ANOVA with Attention Score (cue facilitation, cue interference, cue competition) as the within subjects factor, and Age (5mo, 7mo, 10mo) as the between subjects factor. This analysis revealed both a significant main effect of Age, F(2, 69) = 3.950, p = .024, ηp² = .103, and a significant main effect of Attention Score, F(2, 69) = 10.309, p < .001, ηp² = .130. The interaction was not significant (see Figure 3B).

Simple effects tests were conducted to probe for developmental changes within each attention score. These analyses revealed only significant developmental effects for the cue competition score, F(2,69) = 5.490, p = .006, ηp² = .137. Pairwise comparisons on these effects were conducted using a Dunn-Sidak correction to protect against Type I error. These comparisons revealed significant developmental differences between 5- and 7-month-olds (p=.008), and between the 5 and 10-month-olds (p=.041) for the cue competition score (see Figure 3B).

Discussion

Taken together, results from the reaction time data, accuracy data, and individual attention measures reveal the presence of spatial cueing effects at all ages, with a particularly large increase in the strength of this effect between 7 and 10 months. Previous work examining attention in infants has suggested the presence of covert attention by 4 months (Johnson & Tucker, 1996; Posner, Johnson, & Rothbart, 1994; Richards, 2000). Our results are consistent with these findings, and extend this previous work by allowing us to look independently at several individual components of attention: cue facilitation, cue interference and cue competition, as well as the relative strength of each of these effects as they emerge over the first year of life. The IOWA task is the first attentional battery task for infants designed to provide independent attention scores across several functionally and neurally distinct aspects of attention. Moreover, unlike raw orienting speed measures, these attention scores allow for direct comparison of relative attentional functioning within or between individuals, free from the confounding effects of mean orienting speed differences. Finally, the ability to collect numerous data points per infant makes it possible to uncover even subtle differences in spatial cueing effects.

Results from our group reaction time data reveal significant within-age differences between cue conditions, with the fastest responding occurring in valid cue conditions, and slowest responding appearing in invalid cue conditions. Between-age findings reveal interesting non-linearities, with 7-month-olds showing relatively slow RTs in the invalid cue condition, and relatively fast RTs in the double cue condition. Results from the group accuracy data also reveal significant within-age condition effects, as well as several significant between-age differences in accuracy, particularly for the tone cue, and invalid cue conditions. Taken together, these reaction time and accuracy results reveal several key developmental trends. For example, although 10-month-old infants are significantly faster than 5-month-old infants in the invalid cue condition, they also have significantly higher errors. This may reflect developmental differences in the amount of time it takes to program and initiate a saccade, as 10-month-old infants reach the point of no return more quickly than the 5-month-old infants, erroneously looking to the invalid cue. This developmental accuracy effect may be driven by increased perceptual sensitivity to the small attention cue, increased sensitivity to peripheral targets, or increased neural transduction rates (see for example Canfield, Wilken, Schmerl, & Smith, 1995). In addition, the relatively fast RT of the 5-month-old infants for the double and invalid cue conditions suggests mechanisms responsible for increase RT of older infants under conditions of visual competition are not yet influencing 5-month-old performance.

To help unpack these raw reaction time and accuracy measures, we developed a series of attention scores, which allow us to assess the relative effects of facilitation, interference, and competition independent of developmental improvements in reaction time. In general, all infants showed high levels of Cue Facilitation, or the classic spatial cueing effect – faster reaction times to targets that were preceded by a valid spatial cue compared to baseline trials. There were no developmental differences in Cue Facilitation, indicating that despite the finding that 10-month-olds are significantly faster than 5-month-olds, all ages showed a significant speed benefit when targets were validly cued. All infants showed significant Cue Interference effects, or a slowing of RT relative to baseline for trials in which the cue appeared opposite the target. It is interesting to note that Cue Interference scores are lower in general than Cue Facilitation scores, suggesting that facilitation and interference may reflect different neural processes, each with its own developmental trajectory. The lack of developmental improvements for both facilitation and interference scores implies that mechanisms responsible for covert orienting are already well-established by 5 months, the youngest ages tested here. Future work will need to include younger infants to probe these early-appearing attentional mechanisms.

Our results also revealed strong Cue Competition effects for 7- and 10-month-old infants, with only marginal effects at 5 months. These effects indicate that older infants are able to perceive rapid, simultaneous inputs, and that this visual competition can influence the speed and accuracy of subsequent eye movements. Five-month-old infants either were unable to perceive the two competing spatial cues, or the multiple inputs did not effectively compete for attention, resulting in a relatively low cue competition score. Importantly, Cue Competition shows a significant increase from 5 to 10 months, suggesting that mechanisms necessary to quickly perceive and orient in the face of multi-item competition (e.g., bilateral parietal cortex, myelination of corpus callosum, etc.) are still undergoing development at 5 months. This is consistent with many behavioral findings demonstrating deficits in tasks that require attention to multiple objects (Oakes, Messenger, Ross-Sheehy, & Luck, 2009; Oakes, Ross-Sheehy, & Luck, 2006; Ross-Sheehy, 2005; Ross-Sheehy, Oakes, & Luck, 2003; 2011) and fits nicely with neuroimaging work demonstrating the progression of myelination from relatively early visual areas: optic radiations from 3–4 months, to medial attentional areas: occipital and parietal lobes from 4–6 months, and finally to more frontal attentional areas: genu of the corpus callosum, frontal and temporal lobes from 6–8 months (Deoni et al., 2011).

What can account for these nuanced patterns of development? Many factors likely play a role including increased speed of processing (perceptual, cognitive, motor), increased strength of input from retinal and early visual processing areas, decreased “noise” in the system, increased lateral competition, increased synaptic density, myelination, and so on. Given the complexity of the results and the myriad developmental possibilities, we explore our findings using a dynamic neural field (DNF) model. One advantage to using a neurally grounded model is that we can determine what developmental changes are necessary to capture the pattern of RTs and accuracy across conditions and ages. Moreover, we can examine how constraining the pattern of results is; by determining if multiple developmental approaches can effectively capture the data.

Capturing Development in the IOWA Task:A Dynamic Neural Field Model

To explore the possible neural mechanisms underlying the observed changes in infants’ looking behavior over development, we present a DNF model of infant saccade planning. This model builds on existing models of saccadic motor planning in adults (Schneegans et al., 2014). It combines these approaches with the Spatial Precision Hypothesis (SPH), a theoretical account of developmental changes in neural population dynamics that has been used to explain developmental changes in looking and learning dynamics in infancy (Perone & Spencer, 2013a; 2013b; 2014), changes in visual working memory capacity in infancy (Perone et al., 2011), and changes in spatial working memory performance during childhood (Schutte & Spencer, 2009).

The DNF model belongs to a family of neuro-dynamic models that describe the formation of a saccade motor plan through the evolution of activation patterns over retinocentric maps of possible saccade endpoints (Kopecz & Schöner, 1995; Trappenberg et al., 2001; Wilimzig et al., 2006). These maps reflect the functional organization of neural populations in the superior colliculus and FEF involved in saccade generation. Visual stimuli as well as cognitive inputs locally increase activation levels within the maps. Lateral interactions shape the temporal evolution of activation distributions through local self-excitation and long-range inhibition, creating competition between different active regions. If a single location within the map forms a peak of activation that overcomes competition from other regions, a saccade to that retinocentric location is initiated. Models of this type have successfully accounted for fundamental behavioral signatures in saccade generation in adults, including reaction times in the gap-step-overlap paradigm and metric properties of averaging saccades (Kopecz & Schöner, 1995; Trappenberg et al., 2001), and activation patterns in these models are consistent with neural activity in the superior colliculus {Marino:2012cl}.

Within the DNF model, the SPH is implemented to capture developmental changes in neural population dynamics that are reflected in behavior (Perone et al., 2011; Schutte & Spencer, 2009; Schutte, Spencer, & Schöner, 2003; Spencer, Simmering, Schutte, & Schöner, 2007). The SPH posits that excitatory and inhibitory neural interactions both within cortical fields and between cortical fields get stronger over development. This could arise from multiple sources. For instance, repeated exposure to spatial input patterns from the retina plays an important role in the formation of spatial maps in early visual cortex. Experience with such input patterns could also strengthen lateral connectivity. Similarly, as cortical populations are myelinated there will be an enhancement of neural efficiency (Deoni et al., 2011; Deoni, Dean, O’Muircheartaigh, Dirks, & Jerskey, 2012), effectively boosting the strength of excitatory and inhibitory interactions. Here, we specifically test whether such changes in neural interaction patterns can account for the observed developmental changes in saccade behavior in the IOWA task.

Model Architecture

The concrete model implementation that we use is derived from a previous DNF model that accounts for dynamic interactions between visual working memory and saccade target selection in adults (Schneegans et al., 2014) which has been simplified for the IOWA task. The model architecture is shown in Figure 4. It consists of two DNFs defined over a single dimension that corresponds to the horizontal axis of retinocentric visual space, with the fovea in the center. Activation distributions in these layers are shown as blue plots in Figure 4. The system receives visual input that reflects the horizontal locations of salient visual stimuli (top layer in Figure 4A). The visual input is preprocessed by a simple filtering operation (green plot in Figure 4A) and then fed into the first DNF, the spatial attention field. The spatial attention field features lateral interactions that come into effect when the activation level at any point approaches the output threshold at zero (see Appendix for details). Self-excitation then further increases the activation level in the direct vicinity of this point, while long-range inhibition suppresses activation levels everywhere else in the field. These interactions generate a competition effect that typically leads to the selection of a single area of strong activation (i.e., an activation ‘peak’).

FIGURE 4.

Evolution of activation patterns in the DNF model during a trial in the invalid condition. Each panel shows the situation during a certain period of the simulation. The simplified, one-dimensional visual stimulus is shown on top, the visual input derived from it and the activation distributions in the spatial attention field and saccade motor field are plotted below. In addition, the activation states of the modulatory fixation node (triangle pointing up) and gaze change node (triangle pointing down) are shown in the axis of the spatial attention field, the activation of the saccade reset node is shown in the axis of the saccade motor field. The general connection pattern between the fields is shown in the first panel. (A) Fixation period. (B) Presentation of the pre-cue and simultaneous activation of the gaze change to reflect the tone cue. (C) Presentation of the target stimulus. (D) Attentional selection of the target location and initiation of a saccade.

The supra-threshold regions of the spatial attention field provide input to the second DNF, the saccade motor field. This field features strong local excitatory and global inhibitory interactions (see Appendix). If input from the attention field drives activation over the output threshold to trigger these interactions, the saccade motor field quickly produces a strong activation peak at this location that suppresses activation at all other parts of the field. This peak drives a saccadic eye movement as long as it persists, with the instantaneous displacement being proportional to the eccentricity of the peak in the field. At the same time, above-threshold activation also drives a discrete saccade reset node which functions as a simple neural integrator. Once the activation of this node reaches a threshold, it strongly inhibits the saccade motor field, suppressing the activation peak and thus terminating the saccade signal. The visual input to the system is suppressed during the saccade, and is shifted to reflect the new retinal stimulus pattern after the gaze shift is completed.

The foveal region of the spatial attention field plays a special role: it does not project to the saccade motor field (since no saccade can be made to an already fixated location), but activation here still competes with extra-foveal regions by means of lateral interactions. It therefore serves as a fixation region that inhibits the initiation of saccades while it is activated by a foveal visual stimulus. This effect is used to modulate the system’s behavior by input from two discrete nodes. The fixation node increases activation in the foveal region and thereby suppresses any saccadic eye movements, while the gaze change node inhibits the foveal region and moderately excites all extra-foveal parts of the field. In the original model (Schneegans et al., 2014), these two nodes were employed to globally modulate saccade behavior depending on task instructions. In modeling of the IOWA task, the gaze change node is used to emulate the tone cue. It is activated while the tone cue is presented, and slightly facilitates saccade initiation. This was chosen as a straightforward way to reproduce the observed effects of the spatially unspecific tone cue in the experimental data.

Operation of the Model

The different panels in Figure 4 show changes in activation in the DNF model during the simulation of a single trial of the IOWA task (using the invalid condition). Note that activation in the DNF model evolves continuously; these figures show only snapshots of activation at key moments in time. Figure 4A shows the model’s neural activation profile when the fixation stimulus is presented. This stimulus induces a strong activation peak at the foveal location of the spatial attention field, but no activation in the saccade motor field. Next, the pre-cue is presented for 100ms to the left of fixation (Figure 4B). This creates a peak of activation in the left part of the visual field. The simultaneously presented tone cue activates the gaze change node, which contributes to the fast decline of the foveal activation seen in Figure 4B. The peak in the spatial attention field also drives activation at the same location in the saccade motor field, but in the trial shown here, this activation does not reach the output threshold to produce a peak, so no saccade is initiated at this time.

Figure 4C shows the activation patterns briefly after the presentation of the target stimulus. The pre-cue stimulus has been turned off and there was a 100ms gap, but there is still some persistent activation at the location of the pre-cue in the left part of the spatial attention field. At the same time, stronger activation rises at the location of the salient target stimulus. The two active regions briefly compete with each other by means of the inhibitory lateral interactions. The activation at the target location prevails, but the competition slows down the build-up of activation. In Figure 4D, the activation on the left side of the spatial attention field has been completely suppressed, and a single strong peak induced by the target stimulus remains on the right. This peak drives activation in the saccade motor field beyond the output threshold and thereby initiates a saccade towards the stimulus. In subsequent time steps, this saccade peak will be suppressed as the saccade reset neurons become active, and the system completes the saccade (not shown). Note that the details of the saccade metric were not a focus of the present study; thus we do not discuss this aspect of the model further. That said, the DNF model could, in principle, capture these details of infants’ saccade orienting responses if, for instance, infants’ eye movement were recorded with an eye tracker (for simulations of saccade metrics, see Schneegans et al., 2014).

Choice of Parameters and Developmental Changes

Parameter values for the DNF model were chosen by hand to produce the general model behavior described above—that is, the correct sequence of peaks across layers of the model that underlies saccade planning and generation on each trial—and to obtain a fit of the experimental RT and accuracy data. In practice, final values were achieved through an iterative process where we first obtained the right qualitative sequence of peak states across the layers for each trial type (see, e.g., Figure 4). Then, we began running batches of many simulations of each trial type, computing RT and accuracy values to compare the model’s performance to infants’ performance. Parameters were then fine-tuned iteratively in an effort to move closer to the quantitative values.

To obtain models for the different age groups, specific parameter values were varied in accordance with the SPH. The strengths of lateral excitation, local surround inhibition, and global inhibition in the spatial attention field were increased in a unique pattern to capture age differences in the strength of the spatial cueing effect. The resulting patterns of interaction strengths in the spatial attention field are shown in Figure 5. In addition, the strength of the feed-forward connection was increased over age groups, and the strength of interactions in the saccade system (lateral interactions in the saccade motor field and interactions between the field and the saccade reset node) were all linearly increased from 5-month-olds to 10-month-olds. Finally, the strength of random noise in the spatial attention field and the saccade motor field was linearly decreased over age groups.

FIGURE 5.

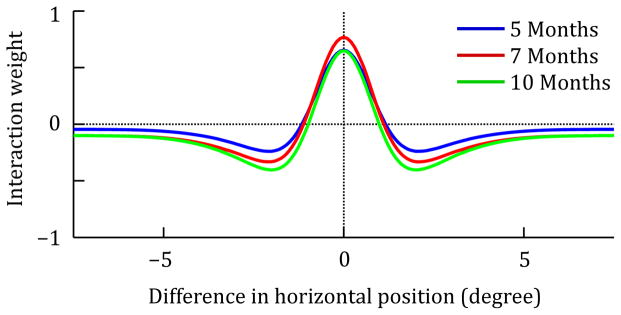
Change of lateral interaction patterns in the spatial attention field to capture development. The plots show the interaction weights used for simulating each age group as a function of distance in visual space. The interaction patterns combine local self-excitation (positive weights), local surround inhibition and global inhibition (negative weights).

None of these developmental changes affects only a single task condition. Instead, they interact in a non-linear fashion to determine saccade metrics in all experimental conditions. This makes the task of model fitting quite challenging, but it also means that the pattern of behavioral results can be constraining such that only a few parameter sets fit the data well. We explored this by fitting the empirical data and then asking whether other developmental changes are equally effective in capturing the empirical trends. Note that the simulation results presented below cannot prove that the specific parameter values and their variation for different age groups correctly reflect the true biological basis for developmental changes in saccade behavior, but they can show whether the SPH provides a viable explanation for these changes. Note also that although technically the model has a large number of free parameters, there are significant constraints on parameter values imposed by the fact that this is a neural process model. For instance, to achieve localized activation peaks within a field requires a specific balance among inputs to the field, the strength of local excitation, and the strength of lateral inhibition. Indeed, the vast majority of possible combinations of parameter values will not yield any saccade metrics at all because they fail to produce localized activation peaks in the saccade motor field in response to the simulated visual stimuli.

Simulation Method

The model describes the continuous evolution of neural activation patterns in the DNFs through a set of differential equations (see Appendix). For numerical simulations, the equations are solved with the Euler method, using a discrete sampling in space and time. The spatial dimension of each field is sampled at 301 equidistantly distributed points, covering a visual space from −15° to 15° of visual angle. The change of activation is computed in steps of one millisecond.

Visual stimuli are applied to the model in the form of one-dimensional intensity patterns that are fed into the spatial attention field, matched in size to the mean diameters of each stimulus type in the behavioral study. The spatially unspecific tone cue is captured via an input to the gaze change node. The timing of all stimuli is the same as in the behavioral study.

Two behavioral measures are derived from the activation time course of the saccade motor field: The time of saccade completion and the direction of the saccade. The time of saccade completion is determined as the time when a salient peak has formed in the saccade motor field and is suppressed again by the saccade reset node. A fixed delay of 75ms is added to this time to account for the transmission of visual signals to the saccade planning structures and for the execution of the generated motor signal. The reaction time in one simulation trial is determined as the time from target onset to saccade completion. The direction of the saccade is determined from the location of the peak (either left or right of the field center), and a trial counted as an error if this direction did not match the target direction.

For each age group and condition, 400 simulated trials were performed. Random noise was added to the field activations in each time step to reflect stochastic neural processes, and to sample the stochastic behavior of the model (not depicted in Figure 4). Reaction times and error rates were determined by averaging over trials, just as they were in the behavioral study.

Results and Discussion

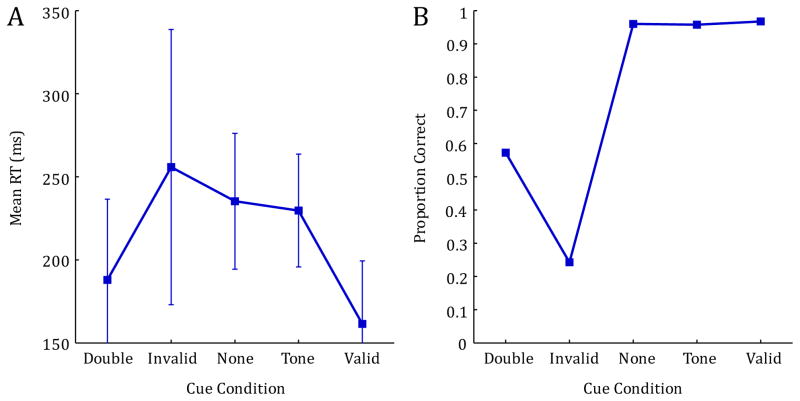
The simulation results are shown in Figure 6. As can be seen, the model does a good job of capturing the global patterns in both reaction time and accuracy data. The root mean square error of the model fit over all conditions and age groups is 12.8 ms for the RT data and 0.04 for the accuracy data. Overall, RTs in the simulation decrease over development, consistent with the empirical data. The basic effects of cue facilitation, cue interference, and cue competition can be seen in all three age groups, but the strength of these effects varies between age groups as in the experimental results. We will explain how the differences in RTs between conditions emerge from the field dynamics, and how they are affected by the changes of interaction parameters used to model the different age groups.

FIGURE 6.

Simulation results for reaction time measures (correct trials only) and proportion of correct trials, using different parameter settings to capture behavioral results of 5, 7, and 10-month-old infants. Error bars for reaction times represent 1 SD.

Cue facilitation arises in the model because a valid pre-cue increases the activation level in the attention field at the location of the target stimulus. When the target stimulus is then presented, it takes less time to form a strong activation peak in this field, and consequently a saccade can be initiated more quickly. In some trials, the pre-cue alone is sufficient to induce a saccade, leading to even faster RTs in this condition. This basic mechanism of cue facilitation does not depend on lateral interaction in the attention field, but only on the temporal dynamics of field activation. Consequently, the effect is quite pronounced in the simulations even for the 5-month-olds (cue facilitation score s_cf = 0.17). However, as local self-excitation increases over development, this effect increases because excitatory interactions reduce the decay of activation during the delay period between pre-cue and target presentation. Consequently, the facilitation effect is stronger in the simulations for the 7-month-olds (s_cf = 0.24) and 10-month-olds (s_cf = 0.29).

Cue interference in the case of an invalid pre-cue is a result of the inhibitory interactions within the fields (in particular global inhibition), as described above and illustrated in Figure 4. The invalid pre-cue raises the activation level at one location in a field, which suppresses activation everywhere else and therefore increases the time it takes for the target stimulus to form a peak. The strength of this effect depends directly on the strength of long-range (global) inhibition, and it is therefore weak in the 5-month-olds (cue interference score s_ci = 0.07) where global inhibition strength is low. At the same time, the strength of this effect also depends on the excitatory and local inhibitory interactions. The more stable the activation peak induced by the pre-cue is, the more effectively it can interfere with peak formation in response to the target stimulus. Due to these factors, the interference is overall strongest in the simulations for the 7-month-olds (s_ci = 0.12), and decreases again for the 10-month-olds (s_ci = 0.07). The probability with which the pre-cue can induce a peak in the saccade motor field and thereby initiate an erroneous saccade in the invalid condition likewise depends on peak stability in the attention field. It is also dependent, however, on the strength of the feed-forward connections from the attention field to the saccade motor field. These are strongest in the 10-month-olds, which therefore have the highest proportion of incorrect saccades in this condition.

Similar to cue interference, cue competition is also driven by global inhibition in the attention field, but modulated by local interactions. When two pre-cues are presented simultaneously in the double cue condition, the resulting activation peaks in the attention field inhibit each other and their activation levels remain relatively low. The facilitating effect for the target stimulus is therefore reduced compared to the valid cue condition, and RTs are consequently longer. The exact amount of facilitation that remains depends on the balance between inhibition that mediates competition between peaks and self-excitation that keeps individual peaks stable. The resulting cue competition scores obtained in the simulation are s_cc = 0.07 for 5-month-olds, s_cc = 0.11 for 7-month-olds, and s_cc = 0.14 for 10-month-olds. The cue competition effect is also visible in the proportion of correct saccades. Without any long-range interactions, the pre-cues on either side should have the same chance of inducing an early saccade as the single pre-cue has in the invalid condition. We would then expect the number of erroneous saccades in the double cue condition to be half that of the invalid cue condition (given that equal numbers of pre-cue induced saccades should be directed to the target side and the opposite side when two cues are present). In fact, however, the rate of erroneous saccades in the double cue condition is lower than that in all age groups. This directly shows the effect of long-range inhibition, which suppresses overall activation levels when two cues are presented simultaneously and thereby reduces the likelihood for either cue to induce a saccadic eye movement.

Finally, the decrease in mean RT over age groups (261ms for 5-month-olds, 244ms for 7-month-olds, and 228ms for 10-month-olds) is driven by two main factors. First, the increase in the strength of feed-forward connections between the attention field and saccade motor field allows for faster formation of a saccade peak in response to a visual stimulus. Second, the stronger interactions in the saccade system drive faster production of the saccade signal and faster termination of the saccade.

Given these findings, we may ask why the stronger feed-forward connections and faster saccade generation are not present earlier in development. Of course, it may simply be matter of neural and synaptic maturation that is necessary for fast transmission from the visual stimulus to the saccade motor signal. But we propose that weaker connection patterns for the saccade system may also be a functional necessity to ensure stable behavior. To illustrate this, we created a hybrid model from different developmental stages. We combined the strong feed-forward connections and strong interactions in the saccade field that are responsible for rapid saccade generation in the model for the 10-month-olds with the remaining settings from the 5-month-olds (in particular, weaker interactions in the attention field and higher noise levels).

The simulation results for this hybrid model are shown in Figure 7. The RTs are indeed comparable and even slightly faster than in the model for the 10-month-olds. Critically however, the model shows very high variability in RTs throughout all conditions, and high error rates. Thus, with these hybrid settings, the model reacts strongly even to weak visual stimulation and to activation noise, and is less consistent in its saccade generation. This indicates that the stronger lateral interactions in the attention field and decreased noise levels are a prerequisite for a rapid and yet robust saccade generation. This is consistent with the central idea of the spatial precision hypothesis: An increase of lateral interaction strengths (with balanced excitation and inhibition) endows neural representations with greater stability, allowing them, for instance, to hold on to selection decisions in the presence of fluctuating inputs. Here, the interactions in the attention field help to normalize activation strengths and thereby balance the stronger feedforward projections that are necessary for rapid saccade generation.

FIGURE 7.

Simulation results for a hybrid model combining parameter settings from the models for 5-month-olds and 10-month-olds. The plots show reaction time measures (correct trials only) and proportion of correct trials. Error bars for reaction times represent 1 SD.

The DNF model does not only allow us to explore the effects of alternative parameter choices, but it can also make specific predictions for new experimental settings. As a concrete example, we simulated an “overlap” variant of the IOWA task in which the central fixation stimulus remains active until a saccade is made. We used the same parameter values as in the fits of experimental results described above, and followed the same simulation procedure. The simulation results for saccade latencies and accuracy in this task variant are shown in Figure 8.

FIGURE 8.

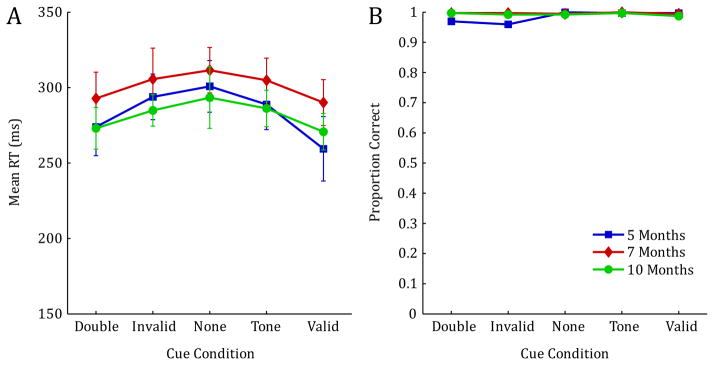
Model predictions for an overlap variant of the IOWA task in which the fixation stimulus remains active until a saccade is made. Parameter settings and simulation procedure are the same as in Figure 6.

The simulation results show marked differences from the original model fits presented in Figure 6; these differences constitute predictions of the model for the new task variant. First, mean RTs are significantly increased throughout all conditions and age groups. This is consistent with gap-overlap effects in saccade behavior, which have already been explained in earlier DNF models (Wilimzig, Schneider, Schöner, 2006). Second, RT differences across conditions are markedly reduced within each age group. Due to lateral inhibition in the model, the active peak for the central fixation cue suppresses activation that is induced by the pre-cues in the different conditions, thereby reducing their overall effect on RTs. This is also reflected in the accuracy results, which show that invalid pre-cues induce very few erroneous saccades in this experimental setting. On a more detailed level, the results also show that the presence of the fixation cue has a weaker overall effect in the simulations of the 5-month-olds than in the other age groups, due to the weaker lateral interactions used for this age group.

General Discussion

Presented here are data from a novel task designed to probe developmental changes in spatial attention and saccade orienting in infants. We found robust developmental differences across conditions in both reaction time and accuracy measures. To better understand the possible mechanisms that underlie the complex changes we observed, we modeled the data using a DNF model of spatial attention and saccade planning. Together, behavioral and simulation results from the current study provide a rich and detailed picture of how attention changes over development. In the sections that follow, we highlight key components of performance on the IOWA task and discuss implications of our work for understanding the mechanisms that underlie changes in spatial attention in the first year.

Developmental changes in reaction time

Ten-month-old infants had significantly faster mean reaction times than 5-month-old infants. These changes likely reflect increases in processing speed, due to improvements in the strength and efficiency of neuronal activity. This was directly examined in the DNF model by increasing the strengths of both feedforward connections and lateral interactions over development. The increase of lateral interactions implements the spatial precision hypothesis (SPH), and serves to balance the increased activation produced by stronger feedforward connections. Although we implemented these changes in the model “by hand”, they are consistent with other data suggesting increases in synaptic strength, specificity, and neural efficiency in the first year of life (Johnson, 1997) and with simulation results showing that such effects can arise from Hebbian processes in an autonomous visual exploratory system (Perone & Spencer, 2013a).

Developmental changes in error rate

For both the behavioral data and the model data, we saw an increase in overall error rates across 5-, 7- and 10-month-olds driven primarily by developmental differences in percent correct for the invalid and double cue conditions. Based on simulation results, it seems likely that increasing error rates for older infants are driven by stronger feedforward connections, allowing older infants to more rapidly detect and ultimately orient to the invalid cues.

Developmental changes in spatial cueing effects

All infants demonstrated faster reaction times for the valid cue trials relative to baseline, and slower reaction times for the invalid cue trials relative to baseline, though cue facilitation effects appeared much stronger than interference effects. Traditionally, facilitation effects for validly cued trials relative to baseline have been taken as evidence of the emergence of covert attention. Interestingly, results from the DNF model show that this spatial cueing effect can manifest with relatively weak neural interactions within attentional cortical fields as long as there is no visual competition. In this case, residual activation at the cue position in the attention field is sufficient to decrease reaction times in the valid condition. This finding leads to the prediction that facilitation effects develop earlier than interference effects, and may be spared in infants who would otherwise show deficits in spatial orienting, such as preterm infants. Indeed this appears to be the case (Ross-Sheehy, Perone, & Kellen, 2015).

In the DNF model, this can be explained by the fact that cue interference, unlike cue facilitation, directly depends on the presence of lateral interactions within neural representations. Specifically, long-range inhibition allows activation in one part of the field to interfere with the build-up of activation in another, distant part. Note, however, that the strength of interference is also modulated by more local interactions, both excitatory and inhibitory. These local interactions influence how long activation from the pre-cue can be sustained, and how long it can influence activation induced by the target stimulus.

Developmental changes in cue competition effects

Cue competition scores were significantly higher at 7 and 10 months than at 5 months, reflecting increases in reaction times for the double cue condition relative to the valid cue condition. In the DNF model, the cue competition effect is brought about in a similar fashion as the cue interference effect, being driven by long-range inhibition and modulated by the effects of local interactions on the stability of activation peaks. The increase of these interaction strengths over development leads to the higher cue competition scores at 7 and 10 months.

Comparison to other DNF models

The DNF model described here was derived from the model by Schneegans et al. (2014). This model shares similarities with DNF models by Perone and Spencer (Perone & Spencer, 2013a; 2013b) used to model patterns of looking and learning in infancy. These researchers included a set of discrete fixation nodes to capture aspects of spatial attention (for a related approach see Robertson, Guckenheimer, Masnick, & Bacher, 2004). Critically, their focus was on featural attention and how infants distribute their looks through time as they learn about a visual stimulus. In particular, Perone and Spencer (Perone & Spencer, 2013a; 2013b; 2014) showed that their DNF model captures canonical habituation behavior in infancy, as well as looking dynamics in preferential looking tasks. One goal of future work will be to integrate this account with the DNF model reported here. The model by Schneegans et al. (2014) provides a guide for that integration in that it addresses interactions between spatial and feature attention.

The other critical connection point between the present report and previous DNF models was our use of the SPH to capture developmental change. The SPH was initially proposed to explain developmental changes in spatial cognition (Schutte et al., 2003; Schutte & Spencer, 2009). More recently, several papers have demonstrated that these same changes also capture developmental changes in feature working memory, both in infancy (Perone et al., 2011) and in early childhood (Simmering-Best, 2015). Moreover, the SPH has played a key role in recent models of word learning (Samuelson, 2009) and executive function (Buss & Spencer, 2014). Thus, this developmental hypothesis has achieved extensive support across a range of ages and domains.

One critique of the SPH, however, is that all of these studies have relied on ‘by hand’ tuning of parameters. Thus, in a recent paper, Perone and Spencer (2014) explored whether the SPH might emerge autonomously over development. These researchers showed that an autonomous visual exploratory system endowed with a simple excitatory memory trace mechanism could change itself over time as it explored a virtual world. In particular, as excitatory memory traces accumulated across 300,000 simulated time steps (several months of simulated experience), peaks became more robust, with stronger local excitation and lateral inhibition. These results show that the same type of changes implemented here ‘by hand’ can emerge autonomously over development.

Thus, there is strong evidence that the SPH offers a robust account of developmental change at the neural level. Future work will be needed to explore whether the SPH can be directly tested at the neural level, for instance, relating this hypothesis to structural changes in local myelin content (Deoni et al., 2011; 2012) or to functional neuroimaging (Buss, Fox, Boas, & Spencer, 2014a).

Relationship between the DNF model and other theories

The developmental findings for both the behavioral and simulation data fit well with current theories of attention development. Development in the DNF model is driven by increases in the strength and specificity of neural interactions within and between fields. At the most general level, the changes implemented in the model are consistent with previous theories suggesting that developmental improvements in orienting after 3 months may be driven primarily by improvements in neural transduction (Atkinson, 1984; Canfield & Kirkham, 2001).

Several other computational models have been proposed to capture different aspects of visual looking and learning in infancy that extend beyond spatial attention. For instance, several neural network models have been used to capture patterns of habituation in infancy, including both autoencoder models and autoassociator models (French, Mareschal, Mermillod, & Quinn, 2004; Gureckis & Love, 2004; Shultz & Cohen, 2004; Sirois & Mareschal, 2004). Although these models have shed light on why infants habituate and how they form categories, these models are limited in the context of the present report because they do not simulate infants’ looking behavior. Given this, these models are not a good proxy for the type of data reported here.

Regarding other models of visual attention in the cognitive neuroscience literature, early conceptual models of spatial attention typically assumed a single, discrete spotlight of attention (Posner & Petersen, 1990; Treisman & Gelade, 1980), which has influenced infant models of attention, particularly those that posit functionally distinct attentional mechanisms such as switching and disengaging (Csibra et al., 1998; Hood, 1993; Hood & Atkinson, 1993; Hood, Atkinson, Wattam-Bell, & Braddick, 1992; Johnson, Posner, & Rothbart, 1991; Matsuzawa & Shimojo, 1997; Posner et al., 1994; Posner, Clohessy, Rothbart, & Vecera, 1991). Computationally, this was often realized as a winner-takes-all (WTA) mechanism in neural networks (Itti & Koch, 2000; Wolfe, 1994). However, the WTA approach is not satisfactory for explaining graded effects of visual attention as observed in the present experiment. The present model instead employs an extension of the WTA method in which the allocation of attention is described as a dynamic process, driven by visual input as well as top-down inputs and modulated by neural interactions. This follows comparable earlier work by Standage, Trappenberg, and Klein (2005) and Zirnsak, Beuth, and Hamker (2011). The approach allows graded levels of attention, and while the neural interactions promote the selection of a single location (consistent with a single spotlight of attention), they still allow spatial attention to be distributed over multiple locations under certain conditions. A more discrete selection of a single location in the present model is made in a separate representation that directly reflects a saccadic motor plan, consistent with earlier models of saccade planning (Trappenberg et al., 2001).

Novel insights for classic spatial attention paradigms

Our dynamic field model offers some novel insights regarding the source of spatial cueing effects. First, both our behavioral and modeling data suggest that changes in the presence of facilitation and inhibition effects are more graded than previously thought. Second, our results suggest that increases in facilitation for valid cues may be driven by improvements the strength and speed of neurons connecting perceptual and motor planning areas of cortex. Importantly, this effect can manifest even without an explicit attentional “shift”. Third, our results demonstrate that increases in the presence of interference for invalid cues may be driven by improvements in lateral inhibitory connections that extend across the extent of the spatial representation. For invalid cues, this competition manifested between the contralateral (invalid) cue representation and subsequent target, whereas for the double cues, this competition manifested directly between each cue. Finally, although our results are consistent with classic accounts of an attentional spotlight, and demonstrate the type of visual competition effects typically associated with separate orienting and disengaging mechanisms (i.e., faster to orient when there is no competition), it is important to note that these effects emerged dynamically as the result of changing neural interactions within and between neural areas. This insight may be particularly important for future infant studies, calling for a shift away from qualitative measures of attention, to more quantitative assessments of change over time

Conclusions

Behavioral results from the IOWA task offer a novel approach to the study of infant attention. Though the current paper focused on developmental changes in spatial attention across ages, the IOWA task was designed to provide a robust assessment of attention at the level of the individual, facilitating the study of individual differences in infant attention and later outcomes. Indeed, we are currently using the IOWA task to examine links between attention, scanning patterns, and visual short-term memory, as well as attentional deficits in preterm infants (Ross-Sheehy et al., 2015). Results presented here fit nicely within the growing framework of attention measures aimed at understanding complex relations between attention, looking, and learning in infants, children, and adults (Atkinson & Braddick, 2012; Elsabbagh et al., 2013; 2009; Fan et al., 2002; 2005; Posner, Fan, Wu, & Fossella, 2001). Future work will be aimed at using the IOWA task and the DNF model to explore additional developmental issues, such the origin of individual differences, the relation between early visual attention and later cognitive development, and the causes/effects of atypical development.

Appendix

Model description

The neurodynamic model consists of two DNFs, which we identify in the equations through unique indices a for attention field and m for saccade motor field. In addition, there are three dynamic nodes (modeling pools of neurons with homogenous properties), which modulate activation patterns in a global fashion: the fixation node, x, the gaze change node, g, and the saccade reset node, r. Parameters of projections have a two-letter index, with the first letter indicating the target, the second the source of the projection.

The fields all describe an activation distribution over a one-dimensional space in a retinocentric reference frame (with position zero corresponding to the fovea), corresponding to the horizontal dimension of visual space in the behavioral study. Each field produces an output, f(u), computed as a sigmoid function (with steepness parameter β) from the activation:

$$f(u)=\frac{1}{1-exp(\beta u(x))}$$

This output is convolved with different interaction kernels to describe its influence on other points in the field or on other fields. These kernels can all be described as differences of Gaussians with a global inhibitory term:

$$w(x)=\frac{c_{\mathit{exc}}}{\sqrt{2\pi }{\sigma }_{\mathit{exc}}}exp\left(-\frac{x^2}{2{\sigma }_{\mathit{exc}}^2}\right)-\frac{c_{\mathit{inh}}}{\sqrt{2\pi }{\sigma }_{\mathit{inh}}}exp\left(-\frac{x^2}{2{\sigma }_{\mathit{inh}}^2}\right)-c_{gi}$$

The parameter values for all interactions are given in Table A2 below. The convolution operation is given by

$$[w\ast f(u)](x)=\int w(x-x^{\prime })f\left(u(x^{\prime })\right)d{x}^{\prime }$$

The visual scene v is given as a one-dimensional, binary intensity pattern, with values of one at spatial locations occupied by a stimulus and zero otherwise. Stimulus sizes reflect mean stimulus diameters in the experiment. The visual input i for the attention field is derived from this pattern by convolution with a Gaussian kernel W_ν:

$$i(x)=[w_v\ast v](x)$$

The activation u_a of the attention field is governed by a differential equation (dependence on time is omitted in this and all following equations for conciseness):

$$\tau {\stackrel{.}{u}}_a(x)=-u_a(x)+h_a+i(x)+[w_{aa}\ast f(u_a)](x)+f(u_x)w_x(x)-f(u_g)w_{ag}(x)-c_{ar}f(u_r)+q_a\xi (x)$$

The time constant τ = 60 ms⁻¹ is shared by all fields and nodes of the model. The field has a resting level h_a (see Table A1 for values of field parameters) and features lateral interactions consisting of local excitation, local surround inhibition, and global inhibition, described by the kernel W_aa. Its activation is globally modulated by input from the fixation node and the gaze change node, described by weight patterns W_ax (a Gaussian pattern centered on the fovea) and the negative weight pattern W_ag (yielding effectively an inverted Gaussian with global excitation). The saccade reset node globally suppresses the attention field with strength C_ar. Random noise ξ with noise strength q_a is added to each field location in every computation step. The noise is drawn from a normal distribution and spatially smoothed with a Gaussian kernel:

$$\xi (x)=[w_q\ast \zeta ](x),\zeta (x)~\mathcal{N}(0,1)$$

The fixation node and gaze change node follow the same general dynamic equation as the field, but are purely driven by external input, i_x and i_g, respectively, without any lateral interactions:

$$\begin{array}{l}\tau {\stackrel{.}{u}}_x=-u_x+h_x+i_x-c_{xr}f(u_r)+q_x\xi \\ \tau {\stackrel{.}{u}}_g=-u_g+h_g+i_g-c_{gr}f(u_r)+q_g\xi \end{array}$$

The external input for the gaze change node is set to a base level of four (reflecting the behavioral context of free exploration) and increased to 8 during the time the tone cue is active. The fixation node does not receive any input in the current simulation setting. Both nodes are suppressed when a saccade is executed due to strong inhibitory input from the saccade reset node.

The dynamics of the saccade motor field is described by the differential equation:

$${\tau }_m{\stackrel{.}{u}}_m(x)=-u_m(x)+h_m(x)+[w_{ma}\ast \check{f}(u_a)](x)+[w_{mm}\ast f(u_m)](x)-c_{mr}f(u_r)+q_m\xi$$

It receives driving input from the spatial attention field. In computing this input, the attention field output is suppressed in the foveal region:

$$\check{f}\left(u_a(x)\right)=\left(1-exp\left(-\frac{x^2}{2{\sigma }_{ma}^2}\right)\right)f\left(u_a(x)\right)$$

The result is then convolved with a Gaussian kernel W_ma. Lateral interactions within the saccade motor field are described by the kernel W_mm, consisting of local self-excitation and global inhibition. As in the attention field, the activation in the saccade motor field is globally suppressed by the saccade reset node, with inhibitory strength C_mr.

The dynamic equation for the saccade reset node is:

$${\tau }_m{\stackrel{.}{u}}_r=-u_r+h_r+c_{rm}\int f\left(u_m(x)\right)dx+c_{rr}f(u_r)+q_r\xi$$

The node receives input from the saccade motor field, integrated over the whole spatial dimension, and its activation level is stabilized by self-excitation with strength C_rr.

The amplitude α of a saccade is determined by integrating the output of the saccade motor field both spatially and temporally over the whole time that a supra-threshold activation peak persists in the field. In this integration, the output from each field location is scaled by its eccentricity, such that more eccentric peaks produce larger saccade amplitudes. The result is then scaled with global factor C_sacc =0.015:

$$\alpha =c_{\mathit{sacc}}\iint f\left(u_m(x,t)\right)·xdxdt$$

In the current study, only the direction of the saccade is used in the analysis (α>0 or α<0). The time of saccade completion is determined as the time when the saccade reset node output falls below a threshold θ_end =0.05 (after it had previously exceeded a threshold θ_start =0.95 to indicate saccade initiation), plus a fixed delay of 75ms.

The parameter values below and in Tables A1 and A2 are given as triplets reflecting the three age groups (5, 7, and 10-month-olds) if the parameter is changed over development. The parameter values for the node interactions are C_ar = C_mr = [18,24,30], C_xr = C_gr =5, C_rr = 2.5, C_rm = [0.9, 1.2, 1.5].

Table 1.

Field parameters

field	resting level h	sigmoid steepness β	noise level q
a	−5	1	[0.55, 0.5, 0.45]
m	−5	4	[0.6, 0.55, 0.5]
r	−5	4	0.05
x, g	−5	1	0.05

Table 2.

Field interaction parameters. Parameter values are given for the adult age group. Values for infant age groups are derived by scaling these parameters with the appropriate factors.

interaction kernel	Cexc	σexc	Cexc	σinh	Cgi
Wν	8	2.5	0	-	0
Waa	[22, 27, 27]	8	[20, 24, 30]	20	[0.045, 0.1, 0.1]
Wax	5	8	0	-	0
Wag	10	8	0	-	2
Wmm	[30, 40, 50]	8	0	-	[0.75, 1.0, 1.25]
Wma	[6.75, 7.4, 9.75]	10	0	-	0