First Passage Times, Lifetimes, and Relaxation Times of Unfolded Proteins

Abstract

The dynamics of proteins in the unfolded state can be quantified in computer simulations by calculating a spectrum of relaxation times which describes the time scales over which the population fluctuations decay to equilibrium. If the unfolded state space is discretized we can evaluate the relaxation time of each state. We derive a simple relation that shows the mean first passage time to any state is equal to the relaxation time of that state divided by the equilibrium population. This explains why mean first passage times from state to state within the unfolded ensemble can be very long but the energy landscape can still be smooth (minimally frustrated). In fact, when the folding kinetics is two-state, all of the unfolded state relaxation times within the unfolded free energy basin are faster than the folding time. This result supports the well-established funnel energy landscape picture and resolves an apparent contradiction between this model and the recently proposed kinetic hub model of protein folding. We validate these concepts by analyzing a Markov State Model of the kinetics in the unfolded state and folding of the mini-protein NTL9 constructed from a 2.9 millisecond simulation provided by D. E. Shaw Research.

It has been more than fifty years since the protein-folding problem was first posed [1]. That proteins can fold into their native conformations so fast despite their vast number of possible conformations, is a puzzle that came to be known as the Levinthal paradox. The “funnel energy landscape” provided a way to visualize the solution to the puzzle, but it has deeper meaning beyond the pictures [2, 3]. The recently introduced kinetic hub model [4] of folding calls into question one aspect of the protein folding funnel namely the smoothness of the funnel; yet it is an important characteristic which is associated with the principle of minimal frustration [5, 6]. Also, in contrast to the smooth funnel model, the kinetic hub model assigns a significant role to non-native interactions in the folding process. The hub model refers to kinetic features of protein folding, i.e. the properties of first passage times within the unfolded free energy basin and between unfolded and folded states; and also to topological features of protein folding, i.e. the connectivity of unfolded states with each other. In this manuscript we resolve an apparent contradiction between kinetic features of the hub model and the smooth funnel model of protein folding; we also comment on the meaning of the hub-like network topology in light of our kinetic analysis.

In a recent paper [7] we addressed the question “how long does it take to equilibrate the unfolded state of a protein.” We found that when a protein equilibrates within the unfolded state free energy basin on a faster time scale than the time it takes to fold, the folding will follow two-state kinetics [8–10], regardless of the number of folding pathways and barriers. So if there are multiple pathways with different barriers, these features of the energy landscape will be hidden from direct observation when the population fluctuations within the unfolded ensemble equilibrate more rapidly than the time course of the folding [11]. The mean first passage times (MFPTs) from state to state within the unfolded ensemble can be expressed in terms of the eigenvalues and eigenvectors of the transition matrix with an absorbing boundary condition at the target state. We showed that for mini-proteins, the MFPTs within the unfolded basin are typically much longer than the time required for the population fluctuations to relax. In this manuscript we derive a simple expression that relates the relaxation times of the individual coarse grained states to the MFPTs to those states; this is a very general relation that is valid whether the relaxation is fast or slow compared to the folding process.

The relaxation time, introduced in our previous study quantifies the process of the population fluctuations decaying to their equilibrium values. The definitions of the relaxation time of state i and the total relaxation time are

$${\tau }_i^{\mathit{relax}}=\underset{0}{\overset{\infty }{\int }}\frac{{\mathrm{T}}_{\text{ii}}(t)-{\mathrm{P}}_{\text{eq}}(\mathrm{i})}{1-{\mathrm{P}}_{\text{eq}}(\mathrm{i})}dt$$ (1)

$${\tau }_{\mathit{tot}}^{\mathit{relax}}=\sum _i{\mathrm{P}}_{\text{eq}}(\mathrm{i}){\tau }_{\mathrm{i}}^{\text{relax}}$$ (2)

where T_ii(t) is the i^th diagonal element of the transition matrix and P_eq(i) is the equilibrium population of state i. ${\tau }_{\mathit{tot}}^{\mathit{relax}}$ is simply the weighted average of the relaxation times of all the states within a particular ensemble.

Another important time scale is the MFPT to a state i. The MFPT to state i is the average time that a trajectory takes to reach state i for the first time, with the initial conditions chosen according to the thermodynamic equilibrium populations excluding state i, which can be expressed as

$${\text{MFPT}}_{\mathrm{i}}=\sum _{j\ne i}\frac{{\mathrm{P}}_{\text{eq}}(\mathrm{j})}{(1-{\mathrm{P}}_{\text{eq}}(\mathrm{i}))}·\underset{0}{\overset{\infty }{\int }}t·\frac{d{\mathrm{T}}_{\text{ji}}^{\text{abs}\to \mathrm{i}}(t)}{dt}dt$$ (3)

where ${\mathrm{T}}_{\text{ji}}^{\text{abs}\to \mathrm{i}}(t)$ is the element from the transition matrix with an absorbing boundary condition at state i, T^abs→i.

Another time scale of the system which can be used to characterize the dynamics is the lifetime of a state. The lifetime of state i is defined as the average time that a trajectory stays at state i during each visit. Note that the probability density P_i(t) for the lifetime distribution of a state i in a Markov State Model (MSM) is an exponential distribution,

$$P_i(t)={\lambda }_i{e}^{-{\lambda }_{i}t}$$ (4)

where λ_i is the sum of all the outgoing rate constants from state i.

We consider the following scheme to characterize the dynamics of the unfolded free energy basin of a protein. We choose any state i and follow the motions between state i and all the other states within the unfolded basin which we label U-i. In general, the distribuition of U-i lifetimes is not single exponential. However, we can relate the average lifetimes of the states i and U-i to their corresponding populations:

$${\tau }_{U-i}^{\mathit{life}}={\tau }_i^{\mathit{life}}(\frac{1}{{\mathrm{P}}_{\text{eq}}(\mathrm{i})}-1).$$ (5)

In reference [7], we showed that the following relation holds when the equilibration within the unfolded basin is much faster than the folding time; in that case:

$${\text{MFPT}}_{\mathrm{i}}\approx {\tau }_{U-i}^{\mathit{life}}.$$ (6)

In other words, when the unfolded free energy basin equilibrates rapidly, the MFPT to any state i within the unfolded state ensemble (U) is approximately equal to the lifetime of the collective state formed from all the other states within the unfolded basin excluding state i.

The lifetimes and relaxation times of the states within the unfolded basin are fundamental time scales which characterize the kinetics within the unfolded basin, many kinetic and thermodynamic quantities can be written in terms of them. For example, the equilibrium conditions can be expressed as:

$${\mathrm{P}}_{\text{eq}}(\mathrm{i})=\frac{{\lambda }_i^{-1}}{{\lambda }_i^{-1}+\overline{t_l}}=\frac{1}{1+{\lambda }_i\overline{t_l}}$$ (7)

$${\mathrm{P}}_{\text{eq}}(\mathrm{U}-\mathrm{i})=\frac{{\displaystyle \sum _l}{t}_l}{T}=1-{\mathrm{P}}_{\text{eq}}(\mathrm{i})$$ (8)

where t_l denotes the time that a trajectory stays at state U-i in the l^th visit, as schematically illustrated in Fig. 1, and T is the total length of the trajectory.

Figure 1.

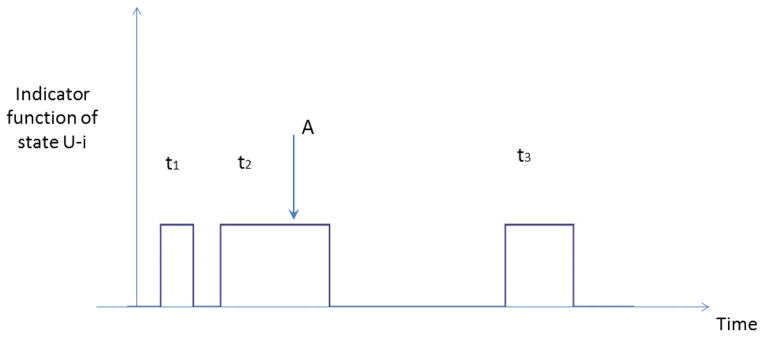
The indicator function of the collective state U-i is one when the trajectory is in state U-i and zero otherwise. t₁, t₂ and t₃ are three realizations of the lifetimes of state U-i. Point A is a typical starting point of the first passage time to state i.

We now show that the MFPT to state i can be expressed as a ratio of the second and first moments of the lifetime distribution of the collective state U-i. We consider a very long trajectory of total length T which moves between state i and state U-i many times as shown schematically in Fig. 1. The MFPT to state i can be calculated by picking a point at random while the trajectory is in state U-i, for example point A in Fig. 1, and clocking the time it takes to get to state i from point A in state U-i. This is repeated many times to build up the passage time distribution. Suppose point A is chosen as the starting point, which as shown in the figure is located during the second visit to U-i with lifetime t₂. The probability of starting from point A is equal to the product of the probability of choosing a starting point within the second visit of the trajectory to U-i, which is given by $\frac{t_2}{{\displaystyle \sum _n}{t}_n}$, times the averaged first passage time from point A to state i, which is given by $\frac{t_2}{2}$, since the point A can be located at any point in time along the second visit of the trajectory to state U-i with equal probability. The weighted sum of all possible first passage times to state i from any place along the trajectory while it is in state U-i can then be written:

$${\text{MFPT}}_{\mathrm{i}}=\sum _l\frac{t_l}{{\displaystyle \sum _n}{t}_n}\times \frac{t_l}{2}$$ (9)

where t_l and t_n are the lifetimes of state U-i during the l^th and n^th visit of the trajectory to state U-i.

Dividing both the numerator and the denominator of the right hand side of eq. 9 by N, which is the total number of visits to state U-i, gives

$${\text{MFPT}}_{\mathrm{i}}=\frac{1}{2}·\frac{\overline{t_l^2}}{\overline{t_l}}.$$ (10)

Eq. 10 shows the fact that the MFPT to state i can be expressed as one half of the second moment divided by the first moment of the lifetime distribution of state U-i.

To write the relaxation times in terms of lifetimes is more complicated. The diagonal transition matrix elements in eq. 1 need to be decomposed into the sum of the contributions from various classes of trajectories, which are associated with different numbers of departures from the starting state, shown as follows,

$$\begin{array}{l}{\mathrm{T}}_{\text{ii}}(t)=e^{-{\lambda }_{i}t}+\underset{0}{\overset{t}{\int }}{\lambda }_i{e}^{-{\lambda }_i{t}_1^{\prime }}d{t}_1^{\prime }·\underset{t_1^{\prime }}{\overset{t}{\int }}d{t}_2^{\prime }{P}_{U-i}(t_2^{\prime }-t_1^{\prime })·e^{-{\lambda }_i(t-t_2^{\prime })}\\ +\underset{0}{\overset{t}{\int }}{\lambda }_i{e}^{-{\lambda }_i{t}_1^{\prime }}d{t}_1^{\prime }·\underset{t_1^{\prime }}{\overset{t}{\int }}{P}_{U-i}(t_2^{\prime }-t_1^{\prime })d{t}_2^{\prime }·\underset{t_2^{\prime }}{\overset{t}{\int }}{\lambda }_i{e}^{-{\lambda }_i(t_3^{\prime }-t_2^{\prime })}d{t}_3^{\prime }·\underset{t_3^{\prime }}{\overset{t}{\int }}d{t}_4^{\prime }{P}_{U-i}(t_4^{\prime }-t_3^{\prime })·e^{-{\lambda }_i(t-t_4^{\prime })}+\cdots \end{array}$$ (11)

where $P_{U-i}(t_2^{\prime }-t_1^{\prime })$ represents the probability density that the trajectory leaves state U-i at $t_2^{\prime }-t_1^{\prime }(t_2^{\prime }>t_1^{\prime })$. The first term in the equation above is the probability that the trajectory never leaves state i within the time t. While the second term corresponds to the probability that the trajectory leaves state i at time $t_1^{\prime }$ and comes back to state i at time $t_2^{\prime }$, then stays in state i through the end of the time t. The third term corresponds to the case that the trajectory leaves state i twice at time $t_1^{\prime }$ and $t_3^{\prime }$ respectively and then returns to state i at time $t_2^{\prime }$ and $t_4^{\prime }(t_4^{\prime }>t_3^{\prime }>t_2^{\prime }>t_1^{\prime })$. The remaining terms can be similarly expressed.

Laplace transforming eq. 11 and using the convolution theorem [12], we have

$$\begin{array}{l}{\stackrel{\sim }{T}}_{ii}(s)=\frac{1}{s+{\lambda }_i}+\frac{{\lambda }_i}{s+{\lambda }_i}·{\stackrel{\sim }{P}}_{U-i}(s)·\frac{1}{s+{\lambda }_i}+\frac{{\lambda }_i}{s+{\lambda }_i}·{\stackrel{\sim }{P}}_{U-i}(s)·\frac{{\lambda }_i}{s+{\lambda }_i}·{\stackrel{\sim }{P}}_{U-i}(s)·\frac{1}{s+{\lambda }_i}+\cdots \\ =\frac{1}{s+{\lambda }_i}[1+\frac{{\lambda }_i}{s+{\lambda }_i}·{\stackrel{\sim }{P}}_{U-i}(s)+(\frac{{\lambda }_i}{s+{\lambda }_i}·{\stackrel{\sim }{P}}_{U-i}(s))·(\frac{{\lambda }_i}{s+{\lambda }_i}·{\stackrel{\sim }{P}}_{U-i}(s))+\cdots ]\end{array}$$ (12)

where s is the complex argument of the Laplace transform. Eq. 12 is a geometric series which can be summed,

$${\stackrel{\sim }{T}}_{ii}(s)=\frac{1/(s+{\lambda }_i)}{1-{\lambda }_i{\stackrel{\sim }{P}}_{U-i}(s)/(s+{\lambda }_i)}.$$ (13)

To express P̃_U−i(s) in terms of the complex argument s, we use the Taylor expansion,

$$\begin{array}{l}{\stackrel{\sim }{P}}_{U-i}(s)=\underset{0}{\overset{\infty }{\int }}{e}^{-st}{P}_{U-i}(t)dt\\ =1-s\overline{t_l}+\frac{1}{2}{s}^2\overline{t_l^2}-\cdots .\end{array}$$ (14)

To express the relaxation time of state i in eq. 1 in terms of the lifetimes of state U-i, estimate the integral by taking the s → 0 limit,

$$\underset{0}{\overset{\infty }{\int }}({\mathrm{T}}_{\text{ii}}(t)-{\mathrm{P}}_{\text{eq}}(\mathrm{i}))dt=\underset{s\to 0}{lim}({\stackrel{\sim }{T}}_{ii}(s)-\frac{{\mathrm{P}}_{\text{eq}}(\mathrm{i})}{s}).$$ (15)

Substituting T̃_ii(s) and P_eq(i) using eq. 13 and 7 and ignoring the terms of O(s³) or higher, leads to the following relation:

$$\underset{0}{\overset{\infty }{\int }}({\mathrm{T}}_{\text{ii}}(t)-{\mathrm{P}}_{\text{eq}}(\mathrm{i}))dt=\underset{s\to 0}{lim}(\frac{1}{s(1+{\lambda }_i\overline{t_l})-\frac{{\lambda }_i}{2}{s}^2\overline{t_l^2}+O(s^3)}-\frac{1}{s(1+{\lambda }_i\overline{t_l})})$$ (16)

$$=\frac{1}{2}\frac{\overline{t_l^2}}{\overline{t_l}}·\frac{1}{1+{\lambda }_i\overline{t_l}}·\frac{{\lambda }_i\overline{t_l}}{1+{\lambda }_i\overline{t_l}}.$$ (17)

On the right hand side of eq. 17, the first term is MFPT to state i (eq. 10), the second term is P_eq(i) (eq. 7), and the third term is 1 − P_eq(i) (eq. 8). Therefore, the general relationship between the MFPT and the relaxation time can be written as,

$${\text{MFPT}}_{\mathrm{i}}=\frac{{\tau }_i^{\mathit{relax}}}{{\mathrm{P}}_{\text{eq}}(\mathrm{i})}·$$ (18)

A similar result was derived by Szabo et al [13, 14] in a different context using a Green’s function approach. The analysis above is exact and general for the relationship between the MFPTs and relaxation times no matter what the shape of the energy landscape is.

We constructed an MSM for the dynamics of NTL9 from a 2.9 millisecond MD trajectory provided by D. E. Shaw Research [15–17].

In Fig. 2B, the spectrum of the implied timescales for NTL9 is shown. With the unmodified equilibrium boundary conditions, there is a major gap between the slowest implied timescale and other implied timescales, which means that the folding is two-state. After applying a reflecting boundary at the folded state (F) [7], the dynamics is restricted to be within U. In table I, when a reflecting boundary at F is imposed, the relaxation times within U (~ 0.4μs) are much faster compared to the slowest implied timescale (~ 7μs) with unmodified equilibrium boundary conditions. Together these results show that two-state folding follows a paradigm: all the unfolded states pre-equilibrate before the U ensemble folds with single exponential kinetics at the slowest implied timescale as the equilibration within U is an order of magnitude faster than the folding process.

Figure 2.

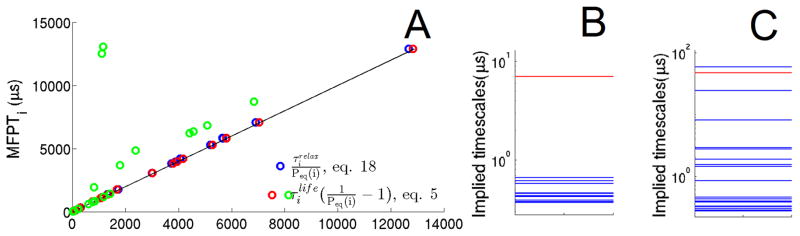
20-node MSM of NTL9 (the original and the rugged networks). (A) The y coordinates of all the circles are the MFPTs calculated from eq. 3. The x coordinates of all the circles are calculated as shown in the legend. Both of the red and blue circles come from the original NTL9 network. While the green circles are the results from the rugged NTL9 network, which are scaled down by fivefold to fit in the figure. The solid line is y=x. (B) It shows the implied timescales of the original network at lag time of 20ns. (C) The implied timescale spectrum of the rugged network. The red lines in both B and C highlight the implied timescale corresponding to the dynamics between the F and U ensemble.

Table I.

Important timescales including folding time, slowest implied timescale (unmodified equilibrium BC), total relaxation times with different BCs for NTL9 and the rugged NTL9 networks. To study the intra U-state relaxation, reflecting BC at F state is applied. All the total relaxation times in reflecting at F state BCs are much shorter (an order of magnitude) than the slowest implied timescale except the rugged NTL9 network.

Protein	Granularity	Tfold (μs)	Slowest $t_n^{\mathit{implied}}$ (μs)	${\tau }_{\mathit{tot}}^{\mathit{relax}}$ in unmodified equilibrium BC (μs)	${\tau }_{\mathit{tot}}^{\mathit{relax}}$ in reflecting BC (μs)
NTL9	20	8.38	6.97	6.79	0.36
	100	9.96	8.27	7.52	0.76
Rugged NTL9	20	12.52	59.02	10.26	79.04

Extremely long MFPTs (~ 1ms) between different regions within the unfolded state ensemble are observed in NTL9 [4], which are orders of magnitude longer than the interconversion between unfolded and folded states. This observation was attributed to non-native interactions and the enormity of conformational space. Using equation 18 we can reconcile the apparent contradiction between the long MFPTs between different regions of the NTL9 unfolded state ensemble, and the rapid equilibration within the unfolded state ensemble [2, 5, 18–20]. There are two contributions to the MFPT to state i. The first comes from the relaxation time of state i, which depends on the structure of the entire free energy landscape of the unfolded basin. Secondly, the MFPT to state i is inversely proportional to the equilibrium population of state i. The fact that many mini-proteins including NTL9 exhibit fast equilibration within the unfolded free energy basin, is hidden by the extremely long MFPTs between regions of the unfolded state ensemble with small populations. For NTL9, long MFPTs to the unfolded states are mainly due to their small unfolded populations even though all of the relaxation times within U are very short (~ 400ns) under reflecting boundary conditions. The kinetic hub model of folding also emphasizes topological features of the folding problem, namely that the native state has high network connectivity, hence use of the term “hub” [21–23]. While the theory we present focuses on kinetic aspects of protein folding, the kinetic and topological features are not completely separate. That the total relaxation times ${\tau }_{\mathit{tot}}^{\mathit{relax}}$ within the unfolded basin of NTL9 and other mini-proteins are much faster than the folding time suggests that on these short time scales, the first passage paths between any two unfolded states are direct. This is indeed what we found. Therefore, whether or not the connectivity appears to be hub like depends on the time window you are looking at. At short times, of the order of the relaxation time of the unfolded state ensemble, the connections between any two unfolded states are direct, while at longer times the folded state acts as a hub.

We now clarify the relationship between the relaxation times and lifetimes in the case of rapid equilibration. Combining eq. 17 and 18 and considering that the resolution of the MSM is fine grained so that the populations of individual unfolded states are relatively small, an approximate expression can be written,

$${\tau }_i^{\mathit{relax}}\approx \frac{\overline{t_l^2}}{2\overline{t_l}}{\tau }_i^{\mathit{life}}$$ (19)

where as above, $\overline{t_l}$ and $\overline{t_l^2}$ are the first and second moments of the lifetime distribution of state U-i and ${\tau }_i^{\mathit{life}}$ is the average lifetime of state i. In the case of rapid equilibration, the lifetime distribution of state U-i t_l obeys an exponential distribution, and therefore the coefficient of the lifetime ( $\frac{\overline{t_l^2}}{2\overline{t_l}}$) is 1. So in the limit of rapid equilibration within the unfolded free energy basin, the relaxation time of a state is approximately equal to its lifetime. When the condition of rapid equilibration doesn’t hold, the coefficient of the lifetime gets much larger than 1 so that the relaxation time becomes much longer than the lifetime.

In Fig. 2A we compare MFPTs to the NTL9 unfolded states using the exact formula for the MFPTs expressed in terms of relaxation times (eq. 18) with the corresponding results using the approximate expression involving lifetimes (eq. 5 and 6). We see that the exact and approximate results agree very well with each other, because NTL9 is a two state folder. What happens when fast equilibration within U no longer holds? To examine this case, we introduced an internal barrier in the unfolded state ensemble. As expected (eq. 19), the relaxation times can become much larger than the lifetimes in the case of slow equilibration within U. The green circles in Fig. 2A deviate from the reference MFPTs. Furthermore, Fig. 2C and the last row of table I show that the total relaxation time within U is even slower than the folding time for the rugged NTL9. These results confirm that the relaxation times within the unfolded free energy basin reflect the ruggedness of the free energy landscape.

In this Letter we have derived a general expression which relates the MFPT to any state to the corresponding relaxation time of that state. The MFPT is proportional to the relaxation time ( ${\tau }_i^{\mathit{relax}}$) of that state, which reflects the degree of ruggedness of the unfolded basin. Secondly, the MFPT to any state i is inversely proportional to the equilibrium population of that state. For mini-proteins which follow two-state folding, the generally long MFPTs to unfolded states reflects the small equilibrium populations of the target states and this depends on the resolution of the model; while the relaxation times of these unfolded states are short due to the smooth landscape of the unfolded basin. Finally, we note that our results are also consistent with a recent study [24] which showed that nonnative interactions play no role in determining the folding mechanism of a two state folder.