Abstract
When the transmembrane voltage is periodically varied with time, the conductance of voltage-sensitive ion channels shows hysteretic behavior. Although this phenomenon has been used in studies of gating of the voltage-dependent anion channel, VDAC, from the outer mitochondrial membrane for nearly four decades, full hysteresis curves have never been reported, since the focus was only on the channel opening branches of the hysteresis loops. Here we study hysteretic response of a multichannel VDAC system to a triangular voltage ramp whose frequency varies within three orders of magnitude, ranging from 0.5 mHz to 0.2 Hz. We find that in this wide frequency range the area encircled by the hysteresis curves changes by less than a factor of three, thus suggesting a broad distribution of the characteristic times and strongly non-equilibrium behavior. At the same time, hysteresis branches corresponding to VDAC opening show quasi-equilibrium two-state behavior. This allows calculating usual equilibrium gating parameters, the gating charge and voltage of equipartitioning, which turn out to be virtually insensitive to the ramp frequency. To rationalize this peculiarity, we hypothesize that during voltage-induced closure and opening the system explores different regions of the complex free energy landscape, where, in the opening branch, it follows quasi-equilibrium paths.
Keywords: Channel reconstitution, Lipid bilayers, Beta-barrel pores, Voltage gating
Introduction
The voltage-dependent anion channel, VDAC, is the major protein of the mitochondrial outer membrane and is known to be responsible for most of the metabolite exchange across the membrane. When reconstituted into lipid bilayers, this 32 kDa membrane protein forms a monomeric beta-barrel channel of 4±0.1 nS conductance in 1 M KCl. The characteristic and conserved property of the channel is voltage gating. Under the applied voltages of ∣V∣ > 30 mV the channel reconstituted into a planar lipid bilayer undergoes transitions between a high-conducting open state and the so-called “closed” states characterized by a variety of lower-conducting conformations (Colombini 1989, 2012, Schein et al. 1976). Though voltage gating of beta-barrel channels, such as bacterial porins and a number of toxins (Arbing et al. 2001, Bainbridge et al. 1998b, Bowen et al. 1985, Bredin et al. 2002, Brunen and Engelhardt 1993, Delcour et al. 1989, Nestorovich et al. 2003, Schindler and Rosenbusch 1978, VanGelder et al. 1997), has been long recognized as their common intrinsic property (Bainbridge et al. 1998a, Robertson and Tieleman 2002, Zachariae et al. 2012), the underlying molecular mechanisms of this intriguing phenomenon are still debated. Moreover, it is not even clear how much they have in common.
Due to the special role of VDAC in mitochondrial homeostasis, its gating is among the most studied. The diverse current ideas on the mechanism of beta-barrel channel gating include the motion of the external loops that connect beta-strands of the barrels (Arbing et al. 2001, Brunen and Engelhardt 1993, Soares et al. 1995, Watanabe et al. 1997), some crucial perturbation of the electrostatic field distribution inside the channel lumen (Bainbridge et al. 1998a, Robertson and Tieleman 2002), and large voltage-induced conformational changes of the protein structure (Colombini 1989, Zachariae et al. 2012). In what concerns VDAC, the most developed so far model (Colombini 2012, Peng et al. 1992, Song et al. 1998, Thomas et al. 1993) proposes the voltage-induced significant structural rearrangements of the channel. This model is supported by the high sensitivity of the channel to osmotic stress (Zimmerberg and Parsegian 1986).
The functional role of the gating is backed by the finding that ATP translocates through VDAC’s open state but not through its closed states (Rostovtseva and Colombini 1996, 1997). Therefore, by gating, VDAC is able to increase or decrease both ATP delivery to the cytosol and ADP access to the electron transport chain complexes in the mitochondrial inner membrane, thus directly affecting mitochondrial energy conversion. According to this model, VDAC closure limits mitochondrial oxidative phosphorylation, while VDAC opening favors it. Any restriction to the metabolite exchange through VDAC could lead to an essential disturbance of mitochondrial energetic functions and cell metabolism (Lemasters and Holmuhamedov 2006, Lemasters et al. 2012). The high abundance of VDAC in the mitochondrial outer membrane is usually thought to cause significant dissipation of the transmembrane potential, thus inciting the long-standing debates about the physiological relevance of the voltage-induced gating (Colombini 2004, 2012, Rostovtseva and Bezrukov 2012). However, the Donnan potential which arises due to the high concentration of non-permeable through VDAC charged macromolecules (e.g., cytochrome c of +9 charges) in the mitochondrial intermembrane space at the outer membrane surface could be a source of potentials estimated between 10 to 20 mV (Lemeshko 2006) or even as high as 46 mV (Porcelli et al. 2005). One of the new models even suggests generation of trans-outer-membrane potentials as high as 50 mV by VDAC complexes with hexokinase (Lemeshko 2014a, b). Moreover, VDAC gating in vivo could be significantly facilitated by significant osmotic effects arising from the crowded environment of the cell (Zimmerberg and Parsegian 1986).
VDAC gating is remarkably complex (Colombini 2012). Nevertheless, reproducible dependences of the gating on such environmental parameters as pH (Bowen et al. 1985, Ermishkin and Mirzabekov 1990, Teijido et al. 2014), osmotic pressure (Zimmerberg and Parsegian 1986), presence of poly-anions (Colombini 1989, Mangan and Colombini 1987), membrane lipid content (Rostovtseva et al. 2006), etc., has been reported, which called for some means of their empirical quantitative characterization.
Assuming that the channel is a two-state equilibrium system, gating is usually characterized by two parameters: gating charge and the characteristic voltage of equipartitioning (half-effect) between the open and closed states (Ehrenstein et al. 1970, Hille 2001). When voltage changes with time, such a description is still applicable if the voltage variation rate is low enough to ensure “instantaneous” equilibration of the channel. Colombini and colleagues (Schein et al. 1976, Zizi et al. 1998, Zizi et al. 1995) applied this simple description to VDAC gating based on the observation that at the decreasing voltages, corresponding to channel opening, the channels exhibit equilibrium-like behavior (Schein et al. 1976). In particular, the authors demonstrated that changing the frequency of the periodic triangular wave of voltage from 0.5 mHz to 5 mHz did not change the “opening” branches of the properly normalized multichannel current-voltage dependences, which were satisfactorily described by a two-state model of the channel voltage gating. Though this analysis was systematically used to study VDAC gating for the last four decades (see, e.g., a recent review article (Colombini 2012) and references therein), to our knowledge, the full hysteresis curves have never been reported in the literature.
The goal of this study is to examine VDAC conductance hysteresis in a wide frequency range in an attempt to reconcile the recognized complexity of VDAC gating with the simplicity of its well-accepted characterization in terms of a two-state equilibrium model for the opening branches of the hysteretic curves. In the discussion section we use a comparison to a two-state Markov model not only because of this quasi-equilibrium behavior, but also because analytical results for the hysteresis area are available only for this model (Pustovoit et al. 2006). We find that the hysteresis curves are characterized by a complex shape that can be interpreted as a result of very fast opening and very slow channel closure with a characteristic time that exceeds the longest period of the applied voltage ramp of 2000 s used in our experiments. This is in agreement with earlier findings (Colombini 2012, Schein et al. 1976), where the complexity of VDAC response to voltage was mentioned and, in particular, it was shown that the relaxation towards voltage-induced VDAC closure is much slower than the relaxation to its opening upon return to the virtual zero voltage. However, we point out that such a behavior can be expected even in the simplest possible case of a two-state Markov model, if the rate constants are functions of the voltage. We perform a crucial experiment on relaxation to the same voltage from two different initial voltages. In the case of a two-state Markov model, this relaxation is expected to be characterized by a single exponent with the relaxation time that is independent of initial conditions. The results of our experiment show that the relaxation times can be different by orders of magnitude and thus clearly demonstrate the failure of the two-state model to grasp the remarkable VDAC gating complexity. To rationalize rich gating behavior of VDAC, we speculate that the channels explore distinctly different regions of their free energy landscape: one region on the way to the voltage-induced closure and the other on the way to the opening, where the channels are close to equilibrium.
Materials and methods
Planar lipid membranes were formed on 70-90 μm diameter orifices in the 15 μm thick Teflon partition that separated two compartments (Rostovtseva et al. 2006). Briefly, the cis and trans compartments were filled with 1.2 mL aqueous 1M KCl (M = mol/l) buffered with 5 mM HEPES at pH 7.4. Lipid monolayers used for membrane formation were made from 5 mg/ml solution of asolectin/5% cholesterol (Avanti Polar Lipids, Inc. Albaster, AL) in pentane. Teflon orifices were pretreated with petroleum jelly. Channel insertion was achieved by adding 0.2-1 μg of VDAC isolated from rat liver mitochondria to the cis compartment while stirring. Potential was defined as positive when it was greater at the cis side. Channel incorporation into the membrane usually took 20 to 30 minutes, after which their conductance reached an acceptable steady-state level. Current recordings were performed as previously described (Rostovtseva et al. 2006) using an Axopatch 200B amplifier (Axon Instruments, Inc., Foster City, CA) in the voltage-clamp mode.
Hysteresis experiments were performed using periodic triangular waves from a Function Waveform Generator 33120A (Hewlett Packard) with voltage changing from 0 to −60 mV and back in the frequency range of 0.5 mHz – 0.2 Hz. Data were acquired with a Digidata 1322A board (Axon Instruments, Inc.) at the sampling frequencies ranging from 1 Hz to 5.0 kHz, with the low-pass Bessel filter set to 1.0 kHz, and analyzed using the pClamp 10.2 software (Axon Instruments, Inc.). Relaxation experiments used protocols described in the figure captions.
Results and discussion
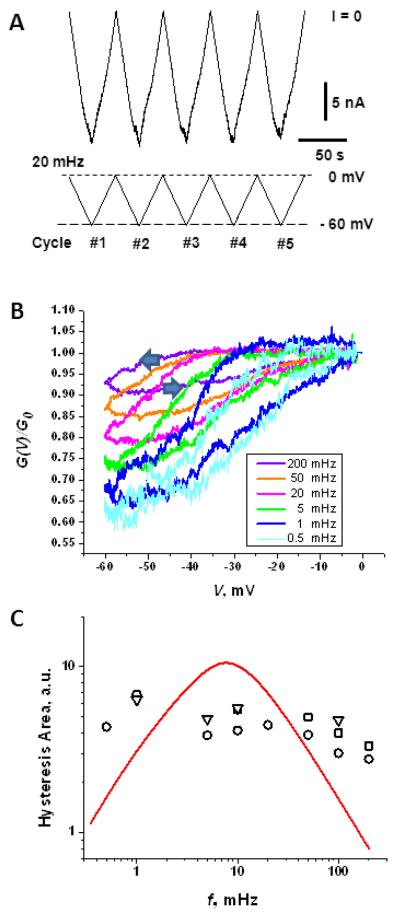
Though the response of the multichannel VDAC conductance to the decreasing branches of voltage ramps (channel opening) has been extensively studied (Colombini 1989, Mangan and Colombini 1987, Rostovtseva et al. 2006, Schein et al. 1976, Teijido et al. 2014, Zizi et al. 1998, Zizi et al. 1995), to our knowledge full hysteresis curves have never been published. To fill this void, we study the conductance of multichannel membranes in response to a voltage ramp (a piece-wise linear voltage vs. time protocol). An example of the 20 mHz ramp with voltage changing between 0 and −60 mV is given in the bottom panel of Figure 1A. The current response of the membrane containing ~ 70 VDAC channels is shown in the upper panel. The response is sub-linear, which is revealed by reproducible deviations of the current from the initial straight lines at small voltages.
Figure 1.
Conductance of the multichannel membrane with the voltage ramp frequency ranging from 0.5 mHz to 0.2 Hz shows sensitivity of the hysteresis curves to the ramp frequency. A: “Raw” data on the ion current through a multichannel system of about 70 VDAC channels (upper panel) in response to a 0 mV to −60 mV voltage ramp of 20 mHz frequency (lower panel). B: Conductance hysteresis curves for different frequencies of the ramp. The arrows at the 0.2 Hz trace show the direction of the voltage change in the parts of the hysteresis loop corresponding to the channel closing and opening. The data are averaged over several ramp periods. C: The area encircled by the hysteresis curves as a function of the ramp frequency, calculated from three independent experiments on multi-channel membranes containing 70-180 channels, is shown by different symbols. The area does not display the tendency to decrease at low frequencies, suggesting strong deviations from equilibrium and the existence of a broad spectrum of relaxation times, including times exceeding 1/(0.5 mHz) = 2000 s. The solid line through the data is the best fit by A(f) = A0/f / f0 + f0 / f) with A0 and f0 used as adjustable parameters (see text).
Figure 1B presents the relative conductance of a membrane with about hundred VDAC channels as a function of the instantaneous voltage of piece-wise linear ramps at 5 different ramp frequencies ranging from 0.5 mHz to 0.2 Hz. Each hysteresis loop is an average over several voltage cycles. The relative conductance is defined as the ratio G(V) / G(0), where G(V) is the instantaneous multichannel membrane conductance at a given voltage, G(V) = I(V)/V, and G(0) is the conductance at zero applied voltage corresponding to the beginning of each cycle. It is important to note here that the experiment shows that the value of G(0) is independent of the ramp frequency. The only goal of such normalization is to facilitate the comparison of the data obtained in different experiments and in the course of long experiments with multiple repetitive ramp applications by eliminating long-term variations due to gradual change in the number of VDAC channels in the bilayer. It is seen that the conductance response to a particular instantaneous voltage is frequency dependent, specifically, the slower the voltage change, the stronger the response. For example, the 0.2 Hz ramp leads to only about 10% reduction of the conductance from its value measured at zero voltage, whereas the 0.5 mHz ramp induces about 40% conductance reduction. Thus, the slowest ramp used in our experiment has about four-fold larger effect on the channel conductance at the voltages of about −60 mV to −50 mV than the fastest one. Interestingly, one of the features of VDAC channel response to the periodically varying piecewise linear voltage is that the system returns to the same initial “conductance of zero applied voltage” after each cycle for the entire frequency range, from 0.5 mHz to 0.2 Hz, so that G(0) is independent of the ramp frequency (data not shown).
Analysis of hysteretic behavior has proved to be a useful tool in the studies of ion channels (Andersson 2010, Banerjee 2015, Das et al. 2012, Flyvbjerg et al. 2012, Fologea et al. 2011, Juraszek et al. 2005, Kaestner et al. 2000, Mannikko et al. 2005, Mathes and Engelhardt 1998, Pustovoit et al. 2006, Zhou et al. 1998). One of the ways of hysteresis characterization is to examine the area encircled by the curves as a function of the ramp frequency. The symbols in Figure 1C are the loop areas calculated from the data in Fig. 1B (circles) and similar measurements performed on multichannel membranes (squares and triangles). It is seen that the change in the loop area does not exceed a factor of three in the whole range of the ramp frequencies.
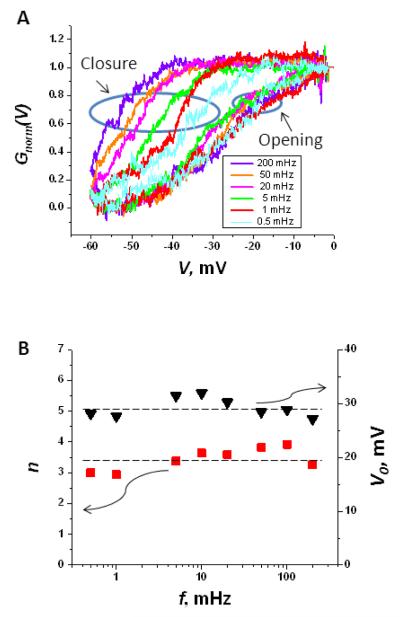
Figure 2A presents the hysteresis curves of Fig. 1B after the following transformation, traditionally used in VDAC gating analysis (Zizi et al. 1998):
| (1) |
where Gmin is the minimal conductance within a particular ramp cycle. Essentially, this transformation excludes the population of the channels which did not have enough time to close, so that the G(V(t)) – Gmin term mostly accounts for the channels that had “gated” to the closed states. It has an advantage that Gnorm(V) allows for a quantitative description of the voltage-induced gating. It is seen that while the descending, “closing” branches remain distinctly different from each other, depending on the voltage ramp frequency, the ascending, “opening” branches of the VDAC conductance response group together.
Figure 2.
Normalized hysteresis curves show that while the closure of the channels is highly frequency dependent, the normalized traces for the opening branches practically overlap. A: Conductance hysteresis curves of Fig. 1B after transformation according to Eq. (1). B: The gating parameters, the gating charge n and the voltage of the half-effect V0 corresponding to PO = 0.5, obtained from fitting the opening branches data to Eq. (2). The wavy arrows indicate that the triangles and squares give the values of V0 and n, respectively.
Quantitative analysis of equilibrium channel voltage gating is most often carried out within the framework of a two-state model. This model describes the voltage-dependent equilibrium between the two states using two parameters, the effective gating charge n and the voltage of channel equipartitioning between the open and closed conformations, or the “voltage of half-effect” V0 (Ehrenstein et al. 1970, Hille 2001). It is important that in the case of VDAC, only the opening branches of the hysteresis curves are used, assuming that Gnorm(V) is the equilibrium probability of finding the channel open (Zizi et al. 1998). The latter is given by the Boltzmann distribution:
| (2) |
where e is the elementary charge and kB and T have their usual meanings of the Boltzmann constant and absolute temperature, respectively. The gating parameters obtained by fitting the experimental data for the ascending branches in Fig. 2A to the voltage dependence in Eq. (2) are shown in Figure 2B. The values of the gating parameters turn out to be practically insensitive to the rate of the voltage change. Indeed, both the gating charge, n, and the characteristic potential, V0 , do not deviate by more than 15% from their average values of n = 3.4±0.4 and V0 = 29±3 mV over the whole range of ramp frequencies, from 0.5 mHz to 0.2 Hz. These values agree with those obtained by Zizi and coworkers (Zizi et al. 1998) who analyzed the opening branches at the ramp frequencies 0.5 and 5 mHz under similar conditions.
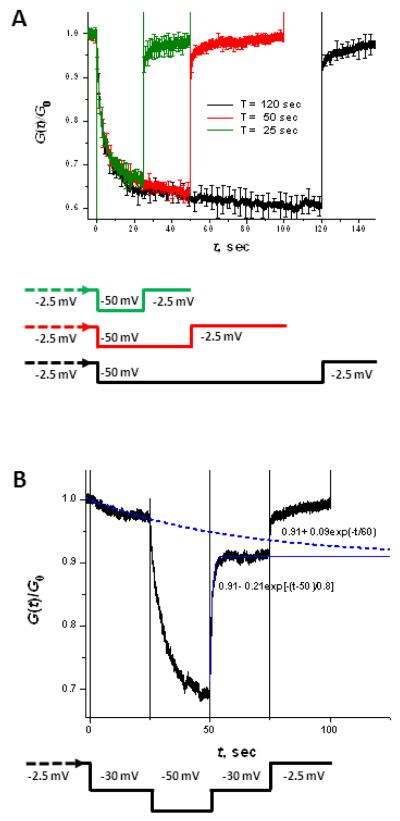
Universal quasi-equilibrium behavior of the channels on the opening branches of the hysteresis loops suggests “instantaneous” channel equilibration on these branches. Thus there is a huge difference in the relaxation rates of the channel closure and reopening, as was reported earlier (Colombini 2012, Schein et al. 1976). This drastic difference between the two rates is also evident in standard relaxation experiments on the conductance response to abrupt changes in the applied voltage. Figure 3A displays relaxation of the multi-channel membrane conductance after step-wise application of −50 mV for various periods of time (25, 50, and 120 s) followed by a step-wise return to the near-zero initial voltage of −2.5 mV. (This residual small potential is necessary to monitor the membrane “conductance at zero voltage” reliably.) In agreement with earlier findings (Schein et al. 1976), it is clearly seen that the rates of the channel closure and opening are quite different. Analysis of the data shows that the characteristic relaxation time, defined as the time necessary to reach 1/e level of the difference between the initial conductance and its long-term asymptote is about 3 s for the closure. For the opening, the relaxation time is about 7 ms. These numbers do not depend appreciably on the system preparation (e.g., on how long it was kept at a particular voltage), but are sensitive to the voltage step amplitude (data not shown).
Figure 3.
Two types of relaxation experiments. A: Conductance relaxation to two different voltages. The voltage protocol, shown at the bottom, is to start at −2.5 mV, then apply −50 mV for the three durations shown in the figure, and then return to −2.5 mV. Quite different relaxation rates towards closure and opening are clearly seen, as can be expected even in the case of a two-state model with voltage-dependent rate constants. B: Conductance relaxation to the same voltage. Experiments are started at −2.5 mV, then −30 mV is applied, in 25 seconds the voltage is switched to −50 mV, 25 seconds later the voltage is returned to −30 mV and then, in 25 seconds, to −2.5 mV. Dashed and solid lines are best fits by single exponentials with the equations displayed in the graph. They show about a two order of magnitude difference in the relaxation times. The data in panels A and B are averages over 3 and 4 separate experiments with membranes containing from 80 to 240 channels. The signal was filtered by a low-pass Bessel filter at 1.0 kHz and sampled at 5.0 kHz.
Though the major part of the relaxation, specifically, about 75% of the total amplitude, is well approximated by a single exponential function, a more thorough analysis of the curves reveals that they have more complex time dependences. In both channel closure and opening there are relaxation tails with additional slow components of at least hundreds of seconds. Considering the long known fact that the “closed” state of VDAC is actually represented by a broad distribution of sub-states with distinctly different conductances and selectivities (Zhang and Colombini 1990), it is natural to expect such multi-exponential behavior. Yet, as follows from Fig. 3A, for the voltage jumps to −50 mV and back the relaxation is mainly single-exponential, but occurs on the time scales that are about three orders of magnitude different.
It is worth noting that this large difference in the relaxation times for the channel closing and opening per se does not contradict the two-state model of gating. For a population of N identical, uncorrelated two-state channels that switch stochastically between two conductances gO and gC of the channel open and closed states, respectively, the time-dependent conductance is a linear function of the probability of finding the channel in the open state at time t, PO(t), that can be written as (e.g., (Pustovoit et al. 2006))
| (3) |
If the channels are Markovian, the probability PO(t) obeys the following rate equation
| (4) |
where kO(t) and kC(t) are the time-dependent rate coefficients for transitions between the open and closed states
| (5) |
The solution for the time-dependent open state probability is given by (Pustovoit et al. 2006)
| (6) |
where
| (7) |
When the time-dependent rate coefficients are the voltage-dependent rate constants, kO(V) and kC(V), for the channel opening and closing, in which the voltage changes with time, we have kO(t) = kO(V(t)) and kC(t) = kC(V(t)). In the case of voltage jump experiments, Eq. (6) leads to a single-exponential relaxation with the characteristic time τ(V*) that is a function of the voltage V* at which relaxation is observed, τ(V*)=1/[kO(V*)+kC(V*)]. It is important that this time is independent of the voltage at which the system was kept before the jump. In contrast, relaxation towards different applied voltages, let say to closure at −50 mV and to opening at −2.5 mV as shown in Fig. 3A, can differ by orders of magnitude, depending on the sensitivity of the rate coefficients on voltage.
As a particular example, consider the following voltage dependences of the rate coefficients
| (8) |
where and are the rate constants in the absence of voltage and positive constants αO and αC are inversely proportional to kBT. Such dependences can be interpreted as a consequence of interactions between the charged mobile voltage sensors on the channel-forming protein and the applied electric field (Hille 2001). Parameters , , αO, and αC in Eq. (8) are related to the usually reported gating parameters, the gating charge and the voltage of half-effect, by
| (9) |
This shows that the four parameters are not independent. Obeying the limitations imposed by the experiment (Fig. 2B), n ≃ 3 and V0 ≃ −30 mV, as an example, we choose , , αO=12V−1, and αC=108 V−1. Using Eqs. (7) and (8) it is easy to see that for this set of parameters the expected voltage-induced channel opening at V* = −2.5 mV is about 20 times faster than the closure at V* = −50 mV.
Thus, a crucial experiment to distinguish between the two-state and more complex system is to measure conductance relaxation at the same voltage in the case when the system was initially kept at different voltages. As discussed above, a “fingerprint” of the two-state system would be the independence of the relaxation times of the initial voltages. To perform such an experiment, we have chosen an intermediate voltage of −30 mV and studied relaxation of the channel conductance to its stationary value at this voltage from two different initial voltages −2.5 mV and −50 mV. Results in Figure 3B illustrate that the characteristic relaxation times of the multi-channel system to its “−30 mV conductance” are about hundred-fold different, depending on the relaxation direction. The relaxation time from −2.5 mV is about 60 s, while the relaxation time from the −50 mV is about 0.8 s. This huge difference in the relaxation times clearly demonstrates the failure of the two-state model.
Finally, we mention that for the two-state system described by Eq. (4) with the rate coefficients given by Eq. (8) there are analytical results for the area encircled by hysteresis curves (Pustovoit et al. 2006). In particular, it was shown that the hysteresis loop area A(f) vanishes as the ramp frequency f tends to zero or infinity, and its asymptotic behavior in the two limiting cases is given by A(f) ∝ f, as f → 0, and A(f) ∝1/f, as f → ∞. However, the experimental data for the loop area presented in Fig. 1C do not demonstrate a tendency to such asymptotic behavior both at low and high frequency. We explored the area frequency dependence at different values of the parameters entering Eqs. (8), which, through Eqs. (9), are compatible with the experimentally obtained values of n ≃ 3 and V0 ≃ −30 mV, and found that the area can be reasonably well approximated by an empirical dependence A(f) = A0/(f / f0 + f0 / f), where A0 and f0 are adjustable parameters, with an accuracy of 20% or better (data not shown). This dependence is given as a solid curve in Fig. 1C to demonstrate the discrepancy between the prediction of the two-state model and the experimental data, thus reflecting the complexity of VDAC gating.
Conclusions
We have studied hysteresis in VDAC conductance response to periodic triangular voltage ramps over a wide range of the ramp frequency, from 0.5 mHz to 0.2 Hz. The fast relaxation for the opening branches of the hysteresis loops ensures the quasi-equilibrium behavior of the channels along these branches and allows for a simple description of VDAC gating in terms of the two-state system. In the whole range of ramp frequencies, the obtained gating parameters do not deviate from their average values by more than 15%. At the same time, the relaxation-to-the-same-voltage experiment demonstrates conclusively that the gating cannot be described by a two-state Markov model even with the arbitrarily complex dependences of the rate coefficients on voltage. This suggests that VDAC gating is controlled by the dynamics on a multi-dimensional free energy landscape (Frauenfelder et al. 1991). Our tentative conclusion is that when closing and opening, the channels explore different regions of this landscape, so that on the way to the closed states the system is far from equilibrium, while during the opening it mostly follows quasi-equilibrium paths.
Acknowledgements
The study was supported by the Intramural Research Program of the National Institutes of Health (NIH), Eunice Kennedy Shriver National Institute of Child Health and Human Development and Center for Information Technology. D.P.H. held a National Research Council Research Associateship Award at the National Institute of Standards and Technology (NIST) and the NIH. Certain commercial materials, equipment, and instruments are identified in this work to describe the experimental procedure as completely as possible. In no case does such an identification imply a recommendation or endorsement by NIST, nor does it imply that the materials, equipment, or instrument identified are necessarily the best available for the purpose.
Footnotes
Conflict of interest
The authors declare they have no competing interests as defined by the European Biophysics Journal or other interests that might be perceived to influence the results and discussion reported in this paper.
References
- Andersson T. Exploring voltage-dependent ion channels in silico by hysteretic conductance. Mathematical Biosciences. 2010;226:16–27. doi: 10.1016/j.mbs.2010.03.004. [DOI] [PubMed] [Google Scholar]
- Arbing MA, Hanrahan JW, Coulton JW. Mutagenesis identifies amino acid residues in extracellular loops and within the barrel lumen that determine voltage gating of porin from Haemophilus influenzae type b. Biochemistry. 2001;40:14621–14628. doi: 10.1021/bi015611y. [DOI] [PubMed] [Google Scholar]
- Bainbridge G, Gokce I, Lakey JH. Voltage gating is a fundamental feature of porin and toxin beta-barrel membrane channels. Febs Letters. 1998a;431:305–308. doi: 10.1016/s0014-5793(98)00761-3. [DOI] [PubMed] [Google Scholar]
- Bainbridge G, Mobasheri H, Armstrong GA, Lea EJA, Lakey JH. Voltage-gating of Escherichia coli porin: A cystine-scanning mutagenesis study of loop 3. Journal of Molecular Biology. 1998b;275:171–176. doi: 10.1006/jmbi.1997.1474. [DOI] [PubMed] [Google Scholar]
- Banerjee K. Dynamic memory of a single voltage-gated potassium ion channel: A stochastic nonequilibrium thermodynamic analysis. Journal of Chemical Physics. 2015;142:185101. doi: 10.1063/1.4920937. [DOI] [PubMed] [Google Scholar]
- Bowen KA, Tam K, Colombini M. Evidence for Titratable Gating Charges Controlling the Voltage Dependence of the Outer Mitochondrial-Membrane Channel, Vdac. Journal of Membrane Biology. 1985;86:51–59. doi: 10.1007/BF01871610. [DOI] [PubMed] [Google Scholar]
- Bredin J, Saint N, Mallea M, De E, Molle G, Pages JM, Simonet V. Alteration of pore properties of Escherichia coli OmpF induced by mutation of key residues in anti-loop 3 region. Biochemical Journal. 2002;363:521–528. doi: 10.1042/0264-6021:3630521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunen M, Engelhardt H. Asymmetry of Orientation and Voltage Gating of the Acidovorax-Delafieldii Porin Omp34 in Lipid Bilayers. European Journal of Biochemistry. 1993;212:129–135. doi: 10.1111/j.1432-1033.1993.tb17642.x. [DOI] [PubMed] [Google Scholar]
- Colombini M. Voltage Gating in the Mitochondrial Channel, Vdac. Journal of Membrane Biology. 1989;111:103–111. doi: 10.1007/BF01871775. [DOI] [PubMed] [Google Scholar]
- — VDAC: The channel at the interface between mitochondria and the cytosol. Molecular and Cellular Biochemistry. 2004;256:107–115. doi: 10.1023/b:mcbi.0000009862.17396.8d. [DOI] [PubMed] [Google Scholar]
- — VDAC structure, selectivity, and dynamics. Biochimica Et Biophysica Acta-Biomembranes. 2012;1818:1457–1465. doi: 10.1016/j.bbamem.2011.12.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das B, Banerjee K, Gangopadhyay G. Entropy hysteresis and nonequilibrium thermodynamic efficiency of ion conduction in a voltage-gated potassium ion channel. Physical Review E. 2012;86:061915. doi: 10.1103/PhysRevE.86.061915. [DOI] [PubMed] [Google Scholar]
- Delcour AH, Martinac B, Adler J, Kung C. Voltage-Sensitive Ion Channel of Escherichia-Coli. Journal of Membrane Biology. 1989;112:267–275. doi: 10.1007/BF01870957. [DOI] [PubMed] [Google Scholar]
- Ehrenstein G, Lecar H, Nossal R. Nature of Negative Resistance in Bimolecular Lipid Membranes Containing Excitability-Inducing Material. Journal of General Physiology. 1970;55:119–133. doi: 10.1085/jgp.55.1.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermishkin LN, Mirzabekov TA. Redistribution of the Electric-Field within the Pore Contributes to the Voltage-Dependence of Mitochondrial Porin Channel. Biochimica Et Biophysica Acta. 1990;1021:161–168. doi: 10.1016/0005-2736(90)90029-n. [DOI] [PubMed] [Google Scholar]
- Flyvbjerg H, Gudowska-Nowak E, Christophersen P, Bennekou P. Modeling Hysteresis Observed in the Human Erythrocyte Voltage-Dependent Cation Channel. Acta Physica Polonica B. 2012;43:2117–2140. [Google Scholar]
- Fologea D, Krueger E, Mazur YI, Stith C, Okuyama Y, Henry R, Salamo GJ. Bi-stability, hysteresis, and memory of voltage-gated lysenin channels. Biochimica Et Biophysica Acta-Biomembranes. 2011;1808:2933–2939. doi: 10.1016/j.bbamem.2011.09.005. [DOI] [PubMed] [Google Scholar]
- Frauenfelder H, Sligar SG, Wolynes PG. The Energy Landscapes and Motions of Proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- Hille B. Ion Channels in Excitable Membranes. Sinauer Associates; Sunderland, MA: 2001. [Google Scholar]
- Juraszek J, Dybiec B, Gudowska-Nowak E. Hysteresis and synchronization in a two-level system driven by external noise. Fluctuation and Noise Letters. 2005;5:L259–L266. [Google Scholar]
- Kaestner L, Christophersen P, Bernhardt I, Bennekou P. The non-selective voltage-activated cation channel in the human red blood cell membrane: reconciliation between two conflicting reports and further characterisation. Bioelectrochemistry. 2000;52:117–125. doi: 10.1016/s0302-4598(00)00110-0. [DOI] [PubMed] [Google Scholar]
- Lemasters JJ, Holmuhamedov E. Voltage-dependent anion channel (VDAC) as mitochondrial governator - Thinking outside the box. Biochimica Et Biophysica Acta-Molecular Basis of Disease. 2006;1762:181–190. doi: 10.1016/j.bbadis.2005.10.006. [DOI] [PubMed] [Google Scholar]
- Lemasters JJ, Holmuhamedov EL, Czerny C, Zhong Z, Maldonado EN. Regulation of mitochondrial function by voltage dependent anion channels in ethanol metabolism and the Warburg effect. Biochimica Et Biophysica Acta-Biomembranes. 2012;1818:1536–1544. doi: 10.1016/j.bbamem.2011.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemeshko VV. Theoretical evaluation of a possible nature of the outer membrane potential of mitochondria. European Biophysics Journal with Biophysics Letters. 2006;36:57–66. doi: 10.1007/s00249-006-0101-7. [DOI] [PubMed] [Google Scholar]
- — VDAC electronics: 2. A new, anaerobic mechanism of generation of the membrane potentials in mitochondria. Biochimica Et Biophysica Acta-Biomembranes. 2014a;1838:1801–1808. doi: 10.1016/j.bbamem.2014.02.007. [DOI] [PubMed] [Google Scholar]
- — VDAC electronics: 1. VDAC-hexo(gluco)kinase generator of the mitochondrial outer membrane potential. Biochimica Et Biophysica Acta-Biomembranes. 2014b;1838:1362–1371. doi: 10.1016/j.bbamem.2014.01.001. [DOI] [PubMed] [Google Scholar]
- Mangan PS, Colombini M. Ultrasteep Voltage Dependence in a Membrane Channel. Proceedings of the National Academy of Sciences of the United States of America. 1987;84:4896–4900. doi: 10.1073/pnas.84.14.4896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mannikko R, Pandey S, Larsson HP, Elinder F. Hysteresis in the voltage dependence of HCN channels: Conversion between two modes affects pacemaker properties. Journal of General Physiology. 2005;125:305–326. doi: 10.1085/jgp.200409130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathes A, Engelhardt H. Voltage-dependent closing of porin channels: Analysis of relaxation kinetics. Journal of Membrane Biology. 1998;165:11–18. doi: 10.1007/s002329900416. [DOI] [PubMed] [Google Scholar]
- Nestorovich EM, Rostovtseva TK, Bezrukov SM. Residue ionization and ion transport through OmpF channels. Biophysical Journal. 2003;85:3718–3729. doi: 10.1016/S0006-3495(03)74788-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng S, Blachlydyson E, Forte M, Colombini M. Large-Scale Rearrangement of Protein Domains Is Associated with Voltage Gating of the Vdac Channel. Biophysical Journal. 1992;62:123–135. doi: 10.1016/S0006-3495(92)81799-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porcelli AM, Ghelli A, Zanna C, Pinton P, Rizzuto R, Rugolo M. pH difference across the outer mitochondrial membrane measured with a green fluorescent protein mutant. Biochemical and Biophysical Research Communications. 2005;326:799–804. doi: 10.1016/j.bbrc.2004.11.105. [DOI] [PubMed] [Google Scholar]
- Pustovoit MA, Berezhkovskii AM, Bezrukov SM. Analytical theory of hysteresis in ion channels: Two-state model. Journal of Chemical Physics. 2006;125:194907. doi: 10.1063/1.2364898. [DOI] [PubMed] [Google Scholar]
- Robertson KM, Tieleman DP. Molecular basis of voltage gating of OmpF porin. Biochemistry and Cell Biology-Biochimie Et Biologie Cellulaire. 2002;80:517–523. doi: 10.1139/o02-145. [DOI] [PubMed] [Google Scholar]
- Rostovtseva T, Colombini M. ATP flux is controlled by a voltage-gated channel from the mitochondrial outer membrane. Journal of Biological Chemistry. 1996;271:28006–28008. doi: 10.1074/jbc.271.45.28006. [DOI] [PubMed] [Google Scholar]
- — VDAC channels mediate and gate the flow of ATP: Implications for the regulation of mitochondrial function. Biophysical Journal. 1997;72:1954–1962. doi: 10.1016/S0006-3495(97)78841-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rostovtseva TK, Bezrukov SM. VDAC inhibition by tubulin and its physiological implications. Biochimica Et Biophysica Acta-Biomembranes. 2012;1818:1526–1535. doi: 10.1016/j.bbamem.2011.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rostovtseva TK, Kazemi N, Weinrich M, Bezrukov SM. Voltage gating of VDAC is regulated by nonlamellar lipids of mitochondrial membranes. Journal of Biological Chemistry. 2006;281:37496–37506. doi: 10.1074/jbc.M602548200. [DOI] [PubMed] [Google Scholar]
- Schein SJ, Colombini M, Finkelstein A. Reconstitution in Planar Lipid Bilayers of a Voltage-Dependent Anion-Selective Channel Obtained from Paramecium Mitochondria. Journal of Membrane Biology. 1976;30:99–120. doi: 10.1007/BF01869662. [DOI] [PubMed] [Google Scholar]
- Schindler H, Rosenbusch JP. Matrix Protein from Escherichia-Coli Outer Membranes Forms Voltage-Controlled Channels in Lipid Bilayers. Proceedings of the National Academy of Sciences of the United States of America. 1978;75:3751–3755. doi: 10.1073/pnas.75.8.3751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soares CM, Bjorksten J, Tapia O. L3 Loop-Mediated Mechanisms of Pore Closing in Porin - a Molecular-Dynamics Perturbation Approach. Protein Engineering. 1995;8:5–12. doi: 10.1093/protein/8.1.5. [DOI] [PubMed] [Google Scholar]
- Song JM, Midson C, Blachly-Dyson E, Forte M, Colombini M. The sensor regions of VDAC are translocated from within the membrane to the surface during the gating processes. Biophysical Journal. 1998;74:2926–2944. doi: 10.1016/S0006-3495(98)78000-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teijido O, Rappaport SM, Chamberlin A, Noskov SY, Aguilella VM, Rostovtseva TK, Bezrukov SM. Acidification Asymmetrically Affects Voltage-dependent Anion Channel Implicating the Involvement of Salt Bridges. Journal of Biological Chemistry. 2014;289:23670–23682. doi: 10.1074/jbc.M114.576314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas L, Blachlydyson E, Colombini M, Forte M. Mapping of Residues Forming the Voltage Sensor of the Voltage-Dependent Anion-Selective Channel. Proceedings of the National Academy of Sciences of the United States of America. 1993;90:5446–5449. doi: 10.1073/pnas.90.12.5446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanGelder P, Saint N, Phale P, Eppens EF, Prilipov A, vanBoxtel R, Rosenbusch JP, Tommassen J. Voltage sensing in the PhoE and OmpF outer membrane porins of Escherichia coli: Role of charged residues. Journal of Molecular Biology. 1997;269:468–472. doi: 10.1006/jmbi.1997.1063. [DOI] [PubMed] [Google Scholar]
- Watanabe M, Rosenbusch J, Schirmer T, Karplus M. Computer simulations of the OmpF porin from the outer membrane of Escherichia coli. Biophysical Journal. 1997;72:2094–2102. doi: 10.1016/S0006-3495(97)78852-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zachariae U, et al. beta-Barrel Mobility Underlies Closure of the Voltage-Dependent Anion Channel. Structure. 2012;20:1540–1549. doi: 10.1016/j.str.2012.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang DW, Colombini M. Group-Iiia-Metal Hydroxides Indirectly Neutralize the Voltage Sensor of the Voltage-Dependent Mitochondrial Channel, Vdac, by Interacting with a Dynamic Binding-Site. Biochimica Et Biophysica Acta. 1990;1025:127–134. doi: 10.1016/0005-2736(90)90089-7. [DOI] [PubMed] [Google Scholar]
- Zhou W, Cayabyab FS, Pennefather PS, Schlichter LC, DeCoursey TE. HERG-like K(+) channels in microglia. Journal of General Physiology. 1998;111:781–794. doi: 10.1085/jgp.111.6.781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmerberg J, Parsegian VA. Polymer Inaccessible Volume Changes during Opening and Closing of a Voltage-Dependent Ionic Channel. Nature. 1986;323:36–39. doi: 10.1038/323036a0. [DOI] [PubMed] [Google Scholar]
- Zizi M, Byrd C, Boxus R, Colombini M. The voltage-gating process of the voltage-dependent anion channel is sensitive to ion flow. Biophysical Journal. 1998;75:704–713. doi: 10.1016/S0006-3495(98)77560-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zizi M, Thomas L, Blachlydyson E, Forte M, Colombini M. Oriented Channel Insertion Reveals the Motion of a Transmembrane Beta-Strand during Voltage Gating of Vdac. Journal of Membrane Biology. 1995;144:121–129. doi: 10.1007/BF00232798. [DOI] [PubMed] [Google Scholar]