A study of the dynamics of seizure propagation across micro domains in the vicinity of the seizure onset zone

Abstract

Objective

The use of micro-electrode arrays to measure electrical activity from the surface of the brain is increasingly being investigated as a means to improve seizure onset zone localization. In this work, we used a multivariate autoregressive model to determine the evolution of seizure dynamics in the 70 – 110 Hz high frequency band across micro-domains sampled by such micro-electrode arrays.

Approach

We used 7 complex partial seizures recorded from 4 patients undergoing intracranial monitoring for surgical evaluation to reconstruct the seizure propagation pattern over sliding windows using a directed transfer function measure.

Main results

We showed that a directed transfer function can be used to estimate the flow of seizure activity in a set of simulated micro-electrode data with known propagation pattern. In general, depending on the location of the micro-electrode grid with respect to the clinical seizure onset zone and the time from seizure onset, ictal propagation changed in directional characteristics over a 2 to 10 seconds time scale, with gross directionality limited to spatial dimensions of approximately 9mm². It was also seen that the strongest seizure patterns in the high frequency band and their sources over such micro-domains are more stable over time and across seizures bordering the clinically determined seizure onset zone than inside.

Significance

This type of propagation analysis might in future provide an additional tool to epileptologists for characterizing epileptogenic tissue. This will potentially help narrowing down resection zones without compromising essential brain functions as well as provide important information about targeting anti-epileptic stimulation devices.

1. Introduction

Electrocorticography or intracranial EEG (iEEG), involves an invasive surgical procedure for implanting electrodes directly on the exposed surface and deep structures of the brain to record electrical activity from the cerebral cortex [1]. Since its development in the late 1940s as a diagnostic tool [2], iEEG has been used to localize epileptogenic zones and to perform mapping of cortical function during presurgical planning to ensure safe removal of epileptic tissue while sparing tissue involved in essential brain functions. The spatial resolution of iEEG is much higher than scalp EEG and can provide a critical advantage for presurgical planning for patients with medically intractable epilepsy [3]. iEEG signals are usually composed primarily of synchronized postsynaptic potentials (local field potentials), recorded directly from the exposed surface of the cortex. These potentials occur primarily in cortical pyramidal cells, and are conducted through several layers of tissue before reaching subdural recording electrodes placed just above the pia mater. Similarly, iEEG recorded from depth electrodes provide deeper field potential information [4]. iEEG is typically recorded over a narrow bandwidth (1–100Hz) from relatively large (2.3 mm diameter), widely spaced (5–10 mm) macro-electrodes. Although iEEG enables better seizure localization than scalp EEG, this technique sometimes fails to satisfactorily narrow down the seizure onset zone (SOZ) due to its inherent technological limitations (narrow bandwidth and 1 cm order electrode spacing) leading to long-term remission in only around 40–60 % of cases [5]. In some epilepsy centers, additional hybrid subdural recording arrays and depth electrodes are implanted for research purposes. These consist of standard subdural grid macro-electrodes mounted on the same flexible plastic substrate with micro-electrode recording elements (40–70µm diameter, with 1 mm center to center spacing) and depth electrodes with micro-contacts in between pairs of macro-elements (PMT Corporation, Chanhassen, MN; Ad-Tech Medical Instrument Corporation, Racine, WI).

Intracranial EEG recorded using micro-electrodes (micro-iEEG) in epileptic human hippocampus and neocortex has identified several new classes of electrographic activity localized to submillimeter scale tissue volumes, inaccessible to standard clinical iEEG technology [6]. Pathological high frequency oscillations have been localized to micro-domains in human epileptic hippocampus [7, 8]. Seizure like events not detectable on clinical macro-electrodes have been observed on sparsely distributed isolated micro-electrodes and these events were more frequent in brain regions that generated seizures, and sporadically evolved into large-scale clinical seizures [6]. Micro-electrode arrays embedded directly into human epileptic neocortex have shown microperiodic epileptiform discharges [9], high frequency oscillations [10] confined to 200 mm diameter tissue regions, and an ictal penumbra surrounding a core territory of recruited neurons during seizure buildup [11]. Such micro-electrode arrays have also captured a detailed view of early seizure propagation in a 4×4 mm cortical region [10, 12].

Accurate localization of the SOZ is of utmost importance not only for seizure management but also to avoid compromising essential brain functions. It has been shown in some studies [13, 14] that high frequency pre-ictal and ictal activity most closely correlates with improved post-surgical outcomes. Hence clinical evaluation which is mainly performed by visual analysis of iEEG in the low frequency (< 50 Hz) band might result in overestimation of the seizure core territory [15, 16]. In this work, we aim to characterize the epileptogenic zone by studying pathological evolution of seizures in higher frequency range(s) over millimeter scale spatial ranges and distinguish them from those arising in regions outside of the SOZ. We also compare high frequency micro propagation with those over the surrounding macro-electrodes in low and high frequency bands. A multivariate autoregressive model is fitted to simulated micro-electrode data to validate our modeling approach against known propagation patterns. Micro-iEEG recorded from epilepsy patients are then similarly modeled to calculate a spectral measure of causality in the Granger sense which in turn is used for estimating the seizure propagation pattern. We envision that a better understanding of the pathophysiology of seizures would not only contribute to a better seizure focus localization, but would also have profound implications for the early detection of seizures. A better spatial description and understanding of seizure propagation will help improve the efficacy of resection surgery as well as those of implantable anti-epileptic stimulation devices and possibly lead to improved seizure control [17].

The paper is organized as follows: Section 2 introduces the data simulation and collection along with data analysis methodology. Section 3 presents the results of propagation analysis. Section 4 discusses the results and concludes the work, pointing out interesting directions of future work.

2. Methods

2.1. Experimental setup

We used two types of data sets derived as follows:

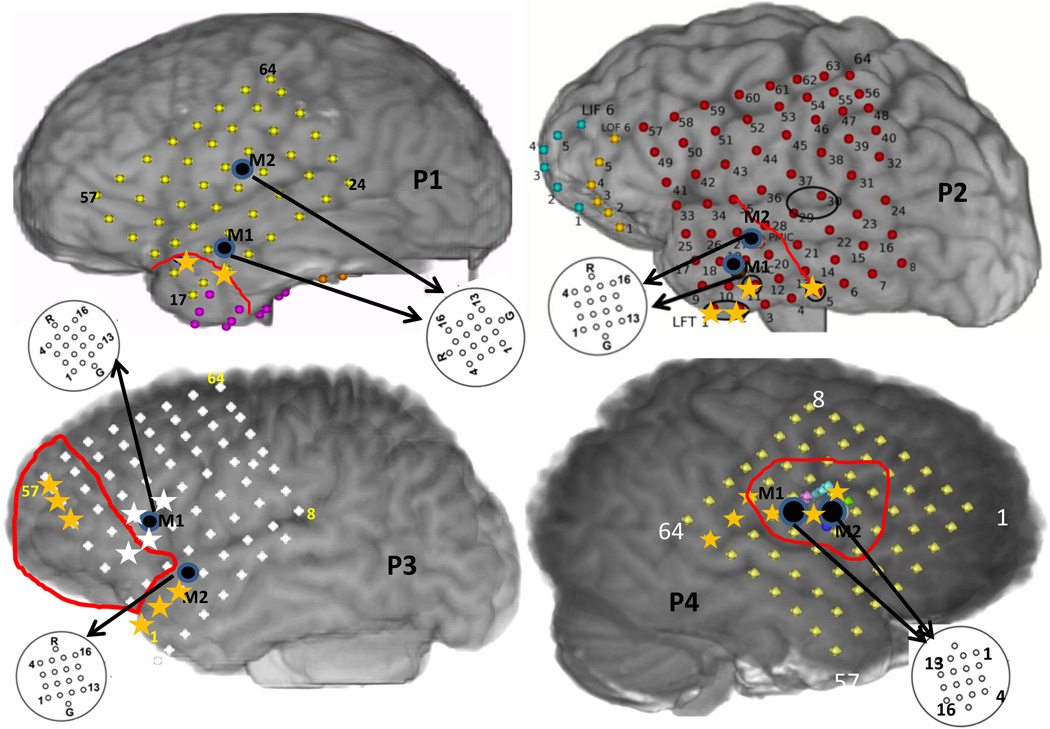
1. Multichannel micro-iEEG was recorded from adult patients (2 males, 2 females) with intractable epilepsy who were implanted with subdural grids, strips and depth electrodes for iEEG monitoring before surgical intervention in order to localize the seizure focus and essential functional brain areas. Such patients are generally monitored in the epilepsy monitoring unit for 7 days or more depending on seizure occurrence. During this period, iEEG is recorded continuously along with video monitoring which is reviewed by epileptologists for seizure localization by determining the macro-electrode(s) associated with earliest iEEG change. Some of these patients consent for additional micro-electrode (hybrid grids, strips, depths) implants currently used for research purposes. A 4 × 4 micro-electrode grid with 70µm diameter electrodes and 1mm spacing between them was used. The positioning of the micro-electrode array was determined by the treating epileptologist based on the hypothesized seizure focus. Signals from these micro-electrodes (micro-iEEG) were recorded continuously using a Blackrock Neuroport system (Blackrock Micro-systems, Salt Lake City, Utah) which can record up to 128 channels at a maximum bandwidth of 30 kHz. The details about these patients are provided in table 1 and Figure 1 shows reconstructed brain maps of these patients with the boundaries of the cortical surface overlying the resected region.

2. A realistic neural network simulator (GENESIS) was used to simulate a region of cortex [18, 19], to obtain extracellular local field potentials (LFP) from “virtual micro-electrodes” and produce test data for comparison with multisite micro-electrode recordings. A multi-compartmental neural network cortical model [20] was implemented in the Genesis neurosimulator. A simulated region of cortex was represented by layer of 2/3 pyramidal cells, spaced at 25 microns in each horizontal direction. The position of cells in a vertical direction was random within a range of 1.2 mm. Pyramidal cells received random afferent AMPA and NMDA input from neighboring cells at the basal and apical dendrites. The LFP data was generated by simulating five-site electrode array with the help of five GENESIS “efield” objects arranged at the predetermined positions with respect to the surface of the simulated network. The LFP for the model is derived from a weighted average of the current sources summed over the cellular compartments [21]:

   $$X(j,t)=\frac{1}{4\pi \sigma }\sum _{i=1}^n\frac{I_i(t)}{R_{i,j}}$$ (1)

   where I_i(t) represents an individual compartment’s current, R_i,j is the magnitude of distance from the i-th compartment to the j-th recording electrode, and σ is the homogeneous tissue conductivity (no capacitance is assumed for the intercellular medium). This includes synaptic currents, channel currents, and compartment currents. The cortical model used to simulate micro-iEEG corresponds to a square area of 0.8 × 0.8 mm sampled by 5 micro-electrodes. The distance between the micro-electrodes was 0.4 mm.

Table 1.

Patient details.

Patient#	electrodes	localization/ resection region	earliest involved macroelectrodes (SOZ)	distance of micro-electrode (M1, M2) from SOZ	# seizures analyzed	surgical outcome
P1(F)	Left temporal grid, strips, amygdala and hippocampal depths, 2 micros	left anterior temporal lobe including amygdala	LFT 19, 26	7 mm, 3.5 cm resected zone	1	seizure free
P2(M)	Left temporal grid, strips, amygdala and hippocampal depths, 2 micros	left anterior inferior temporal area including amygdala	LFT 1,2,11,15	7 mm, 1.5 cm resected zone	2	2–3 seizures per week
P3(M)	Left frontal grid, strips cingulate depths, 3 micros	left orbital frontal, left para hippocampal	early spikes on LFG 1–3, 9–10, 33, 42, 49, 57, ictal build up in 17–19, 27–28, 33–35	7 mm, 7 mm resected zone	2	seizure free
P4(F)	Right fronto-temporal grid, depths around cortical dysplasia, 2 micros	depths and part of grid, lesion and surrounding area resected	FTG 46,47,62,63	7 mm, 7 mm resected zone	2	seizure free

Figure 1.

The reconstructed brain maps of the 4 patients considered showing approximate positions of the macro-electrode and micro-electrode grids along with the boundaries of the resected region in red. The yellow asterisks in P1,P2,P4 indicate the SOZ macro-electrode contacts on the grid. The yellow and white asterisks in P3 denote SOZ macro-electrodes during seizures 1 and 2 respectively.

2.2. Data Analysis

We analyzed simulated micro-iEEG (with a known propagation pattern) and those recorded from 4 patients during the occurrence of 7 (1,2,2,2) symptomatic complex partial electrographic seizures used for determination of the SOZ. We also considered iEEG recorded from the macro-electrodes surrounding the micro-electrodes. The simulated and recorded data were sampled at 20 and 10 kHz, respectively and were down-sampled with a lowpass anti-aliasing filter to 1000 Hz. Each recorded data segment analyzed consisted of a period of 5 – 10 seconds before the clinical seizure onset and ended 10 – 40 s into the seizure. For the patient data, we used a Fourier transform based phase shuffling method [22] to estimate a null distribution for determining the zero threshold of causality calculated from the seizure data segment. The following subsections describe the methods used to calculate seizure propagation across the micro-electrode grid and neighboring macro-electrodes.

2.2.1. Multivariate autoregressive modeling

A multivariate autoregressive (MVAR) model for a set of M time series x_i(n), i = 1,…,M, n = 1, …, N of length N can be described as [23]:

$$\overline{x}(n)=\sum _{j=1}^p{A}_j\overline{x}(n-j)+ū(n)$$ (2)

where x̅(n) = [x₁(n), …, x_M(n)]^T is a vector of signal samples at time instant n over M channels and ū(n) = [u₁(n), …, u_M(n)]^T is an input vector of zero-mean white and uncorrelated noise processes with covariance matrix ${\sum }_U={\sigma }_{ij}^2$. A_j is an M × M matrix of the model coefficients at time lag j, and p is the MVAR model order.

An MVAR model was fitted to the simulated and recorded micro-iEEG data in the following way: Micro-electrode channels which were noisy or did not contain any signal were first rejected by visual inspection. The spectrogram of each micro-electrode channel was calculated to determine a frequency sub-band within the 70 – 110 Hz frequency band that visually showed a greater increase in spectral power with respect to that in the entire 70 – 110 Hz band, as compared to the other frequency sub-bands. The recorded micro-iEEG were filtered to retain signal components in the 70 – 110 Hz frequency band using a finite impulse response filter. The neighboring macro-iEEG were filtered to retain the 4 – 50 Hz and 70 – 110 Hz frequency bands. A time range of 10 – 50 seconds centered around the seizure onset was chosen. An MVAR model [23] was fitted to the filtered micro-iEEG and macro-iEEG data over windows of length N samples starting from a few seconds before the clinical seizure onset. The model order, p and the number of samples constituting each window, N were chosen to produce an optimal model fit. The model fit was considered over changing values of N. For each N > 500 and p > p₀ where p₀ was determined as the order thst minimized a Bayesian information criterion (BIC) [24], the goodness of model fit was determined by the predominance of off-diagonal elements in the noise covariance matrix ∑_U. This was quantified by calculating the ratio between the determinant of ∑_U and the product of the diagonal elements. When ∑_U is diagonal this ratio is 1 and hence, N and p were chosen as the ones that maximized this ratio. Since the MVAR model estimates are based on the assumption of a diagonal residual covariance matrix, using the model order p₀ is not sufficient to ensure that this assumption holds true. Hence, we looked into the covariance matrix structure to help us find a pair of N and p satisfying this assumption as well as minimized the BIC criterion (the BIC curve is mostly flat for p > p₀). The model parameters A_j, j = 1, …, p, for the simulated dataset were estimated using the Nuttall-Strand algorithm [25], whereas those for the recorded dataset were estimated using the arfit algorithm [26] implemented in MATLAB. Two different algorithms were used to account for the absence and presence of background noise in the simulated and recorded datasets respectively. This was also verified by a visual inspection of the BIC curves.

2.2.2. Propagation pattern from MVAR model

According to Granger’s definition of causality [27], a time series is called causal to another time series if the knowledge of the past of the first series significantly improves prediction of the second series. The MVAR model generalizes this aspect for more than two time series signals. In the frequency domain, (2) can be expressed as:

$$X(f)=A(f)X(f)+U(f)$$ (3)

where $A(f)={\sum }_{k=1}^p{A}_k{e}^{-j2\pi f\mathrm{\Delta }tk}$ and Δt is the sampling period. The main diagonal elements A_jj in the time domain describe the dependence of x_j(n) on its own p past points while the off-diagonal elements A_ij describe the dependence of x_i on the p past points of x_j. In the frequency domain, A_ij(f) represents “flow” or “propagation” at frequency f between channels j and i which is defined in more details in the following paragraph. Hence the presence of causal interactions between any two time series in this model is related to the presence of nonzero off-diagonal elements of the coefficient matrix A(f). The presence of direct interactions between two channels can be quantified by calculating the partial directed coherence (PDC) [28]. PDC is a frequency domain-measure of the directed influences between pairs of signals in a multivariate data set and quantifies the interactions from one channel to another that cannot be explained by any other observed time series. The PDC from x_j to x_i is defined as:

$${\pi }_{ij}(f)=\frac{{Ā}_{ij}(f)}{\sqrt{{\sum }_{m=1}^M|{Ā}_{mj}(f){|}^2}};Ā(f)=I-A(f)$$ (4)

The squared magnitude of the PDC function π_ij(f) quantifies the strength of direct flow from x_j → x_i at frequency f, being 0 in the absence of any flow and 1 when all causal influences originating from y_j are directed towards y_i. The calculation of PDC however does not take into account the differences in the noise variance ${\sigma }_{ij}^2$. To overcome this limitation, a generalized PDC (gPDC) can be defined as [29]:

$${\rho }_{ij}(f)=\frac{{Ā}_{ij}(f)/{\sigma }_{ii}}{\sqrt{{\sum }_{m=1}^M|{Ā}_{mj}(f){|}^2/{\sigma }_{mm}^2}}$$ (5)

where ${\sigma }_{ii}^2$ is the variance of the white noise process u_i. The gPDC is thus not affected by possible differences in the noise variance and quantifies direct flow of activity from x_j → x_i. (3) can be rewritten as:

$$X(f)=H(f)U(f);H(f)={(I-A(f))}^{-1}$$ (6)

where H(f) is the transfer matrix of the system and H_ij represents the connection between the j-th input and the i-th output of the system. The directed transfer function (DTF) can be calculated as [23]:

$${\gamma }_{ij}(f)=\frac{|H_{ij}(f)|}{\sqrt{{\sum }_{k=1}^N|H_{ik}(f){|}^2}}$$ (7)

The DTF measure does not distinguish between direct and indirect flows, i.e. it would produce similar results for a flow between channels i and j irrespective of the presence of other channel(s) mediating the flow between them. To overcome this limitation, the direct DTF (dDTF) was introduced [30] and is defined as:

$${\zeta }_{ij}(f)=\frac{|H_{ij}(f)||{\chi }_{ij}(f)|}{\sqrt{{\sum }_f{\sum }_{ij}|H_{ij}(f){|}^2|{\chi }_{ij}(f){|}^2}}$$ (8)

where χ_ij(f) is the partial coherence between channels i and j.

The 4 frequency dependent flow measures, PDC, gPDC, DTF and dDTF denoted as CM_k, k ∈ [pdc, gpdc, dtf, ddtf] were calculated for the MVAR model fitted to the simulated dataset. In this work, we are interested in finding a propagation measure and hence the measure which produced the most accurate propagation pattern for the simulated signals were then calculated for the iEEG signals.

2.3. Threshold for flow measures

All the 4 flow measures have values in the 0–1 range. In order to determine what value corresponds to a presence of causal interaction between two channels, a threshold has to be estimated such that all values less than the threshold can be treated as non-significant and set to zero. We refer to this threshold as the zero threshold of a particular measure. Classical statistical testing approaches to determine zero thresholds involving surrogates cannot be directly used for this case. This is because we do not have multiple trials of the same seizure event and we want to test the presence of significant causal interactions arising during seizure initiation and propagation with respect to a baseline devoid of ictal dynamics. However, it has been shown [15] that the baseline segments recorded during iEEG monitoring might not be devoid of ictal dynamics. On the other hand, in absence of any propagation within the micro-iEEG baseline segments, it might be difficult to fit a satisfactory MVAR model. This makes the determination of a zero threshold rather challenging. Considering that the objective is to test if the value of the flow measure between two channels is greater than zero, we propose to calculate a zero threshold based on surrogates generated by phase randomization [22].

In this method, a Fourier Transform (FT) surrogate method [22] is used to generate surrogate data over each time window. In brief, each channel data is first Fourier transformed, then keeping the absolute value fixed, the phase at each frequency point is substituted with a realization of a uniformly distributed random variable in the [02π] range and then an inverse Fourier transform is taken to obtain the surrogate data. The surrogate series preserves the power spectrum of the original series but the coupling among the channels is destroyed by the phase randomization. This method of surrogate generation has been widely used in connectivity analysis using causality measures [31, 32, 33, 34, 35, 36]. Using this method, 200 surrogate series were generated for each time window and CM_k were calculated for each of the surrogate dataset. The zero threshold T_α is then calculated as the α-th percentile of the 200 values of each CM_k, where α is set to a value in the 90 – 95 range.

2.4. Propagation analysis

The zero threshold calculated as outlined before is used to set those CM_k to zero which lie below the threshold. The top 4–5 percentile existing flows are plotted to have a visual representation of how the strongest propagation changes over the micro-electrodes as compared to the surrounding macro-electrodes. Additionally, the flow initiating from each micro-electrode contact is calculated by summing over the columns of the CM_k matrices as:

$$F_s(j)=\sum _{i=1}^{M}C{M}_k(i,j)$$ (9)

For each time window the following are calculated: i)the micro-electrode contact emanating the maximum outflow and ii)the coefficient of dispersion (COD) calculated as the ratio between inter-quartile range and median of outflow amongst all the micro-electrodes within a grid. A histogram is constructed from each of these two quantities. The COD quantifies the dispersion in the strength of outflow from each channel in a particular micro-array grid. A higher value would thus indicate a strong dominating source while a low value would mean similar strength outflows from multiple channels.

3. Results

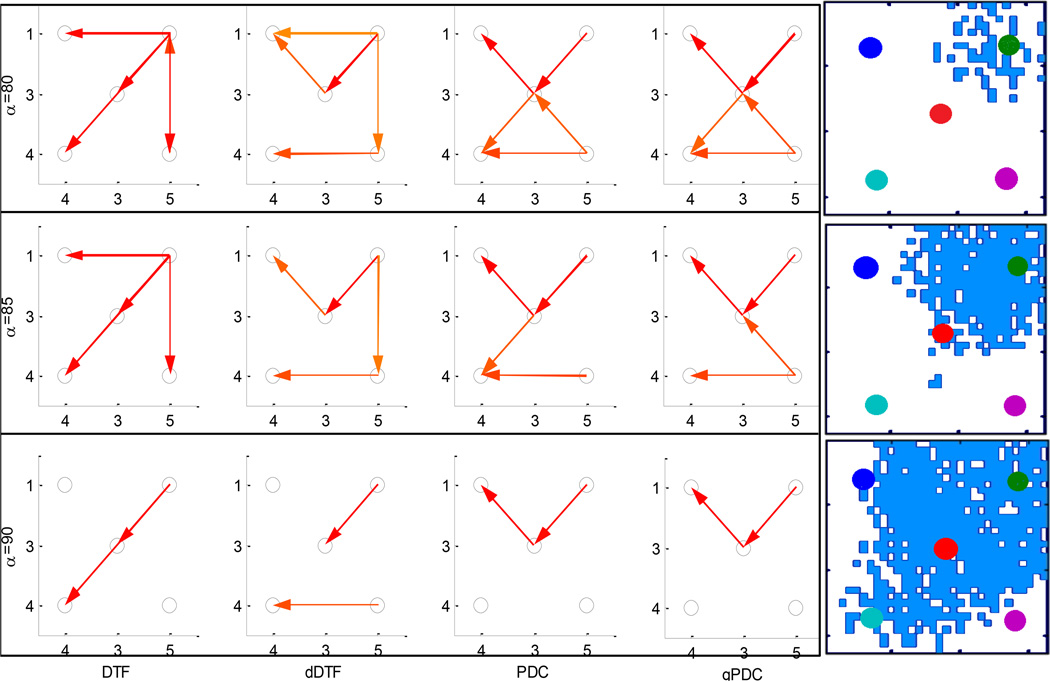
The simulated dataset consisting of micro-iEEG measured from 5 virtual micro-electrodes was fitted with an MVAR model with a model order 8 and window length of 0.5 seconds (500 samples). The DTF, dDTF, PDC and gPDC were calculated and the propagation pattern was determined over 2 – 30 Hz range using T_α, α = 80, 85, 90 as shown in figure 2. The actual propagation of the wave across the sampled region from the upper right corner to the lower left corner is shown on the right side of the figure. It can be seen that although all 4 measures produce similar flow patterns (initiating at right upper corner), DTF has the most accurate and robust estimation over all three values of T_α.

Figure 2.

Determination of known propagation (right top to bottom) in simulated 5 channel micro-iEEG data using DTF, dDTF, PDC and gPDC in the 2–30 Hz frequency band using three values of threshold T_α, α = 80, 85, 90.

The micro-iEEG recorded from 4 × 4 micro-electrode arrays which were placed within a centimeter of the clinical seizure foci in 4 patients with intractable epilepsy were used to determine the seizure propagation pattern. Each patient had at least 2 micro-electrode arrays, M1 and M2, M1 denoting the one closer to the clinically determined seizure focus than the other (M2) for most patients. Each set of micro-iEEG signals recorded from M1 and M2 were first filtered to retain the frequency band of 70 – 110 Hz and then the filtered signals were fitted with an MVAR model. Using the optimum model fit criteria as described in the previous section, we found that a time window of 2 s produced the most optimal model fit. Each window was shifted by 0.5 seconds to produce a time varying MVAR model over the entire duration of 40–100 seconds. The model order, p was determined for each time window as the order which produced the least off-diagonal elements in the input noise covariance matrix and was greater than the one that minimized BIC. For each time window, the fitted MVAR model was then used to calculate the propagation pattern within the frequency band that had maximum spectral power with respect to the power in the entire 70 – 110 Hz band.

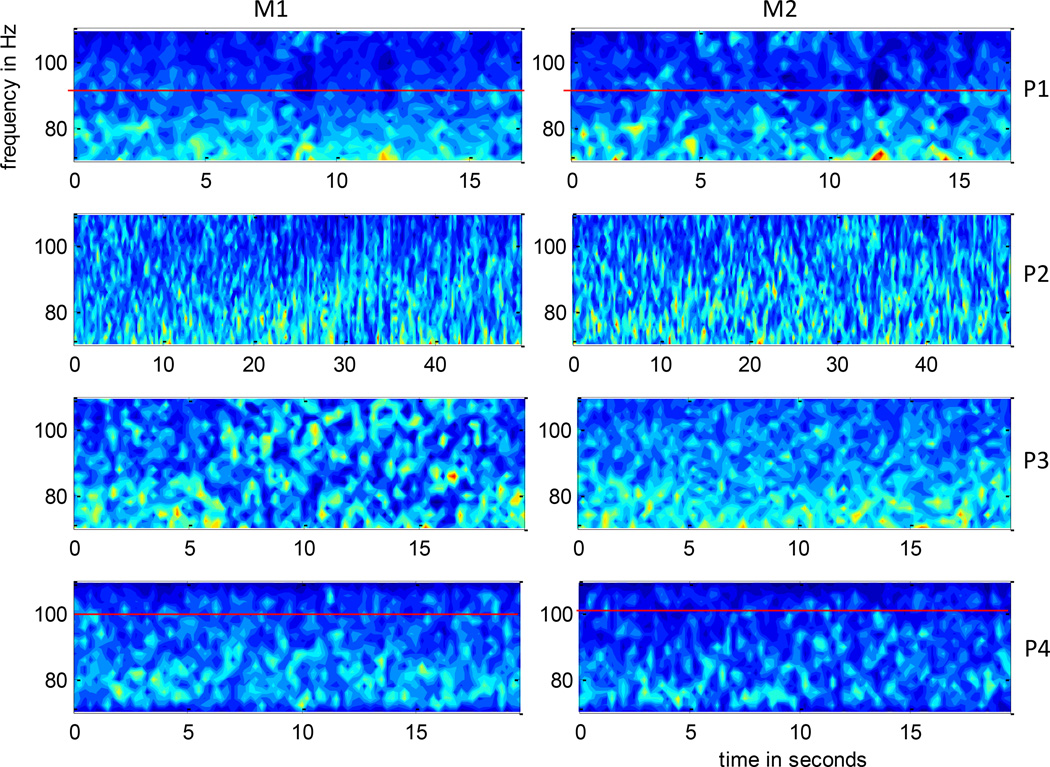
A time-frequency decomposition using short time Fourier Transform of each of the channels of M1 and M2 in the 70 – 110 Hz frequency band for each patient were visually inspected to determine a sub-band exhibiting a greater increase in spectral power as described in section 2. The DTF measure was summed over this sub-band to obtain a propagation pattern in this frequency band. The reasons for choosing the 70–110 Hz frequency band are: i) Lower frequency components (< 50 Hz) which are typically used for clinical evaluation are expected to be more synchronized over mm scale regions that is sampled by the micro-electrodes. In the absence of time-lagged interaction, they are thus not good candidates for MVAR kind of modeling. This was verified by fitting MVAR models to 2–50 Hz band and the model fit was not satisfactory as reflected by the presence of significant off-diagonal elements in the noise covariance matrix; ii) Incorporating higher frequency components (> 120 Hz) deteriorates the model fit. This might be due to the absence of propagation in these higher frequency ranges. Figure 3 shows them spectrogram averaged over all the channels as a ratio with respect to the total spectral power in the 70 – 110 Hz band, within each of M1 and M2 grids for patients P1–P4. Patients P1 and P4 had higher spectral power in the 70 – 90 and 70 – 100 Hz frequency sub-bands respectively, while P2 and P3 showed similar spectral contents throughout the 70 – 110 Hz range.

Figure 3.

Time frequency decomposition using short time Fourier Transform averaged over micro-electrode channels of M1 (left) and M2 (right) as a ratio with respect to total spectral power in 70–110 Hz, of the 4 patients P1–P4. The time interval for each patient shown here is the same as that considered for the propagation analysis. This figure gives the reader a sense of the distribution of spectral power in the 70 – 110 Hz band and the rationale behind choosing a frequency sub-band for estimating propagation. As indicated by a red horizontal line, P1 and P4 show a higher spectral power concentration in the 70–90 and 70–100 Hz ranges respectively while P2 and P3 have similar spectral power over the entire range.

We used the DTF measure to calculate propagation over the frequency band determined for each patient by summing over the DTF values in that frequency range. We chose the DTF measure primarily because in reconstructing patterns of propagation we were interested in identifying overall flows from the original source (focus), so both direct and indirect flows contribute. Thus by selecting DTF we make the primary source more clear than by using dDTF or PDC which may be more appropriate for causality investigations. Moreover, the simulations confirmed that patterns shown by DTF better reproduced simulated patterns of propagation. Early work [37] with application of DTF to intracranial EEG recordings have also shown relatively clear patterns of propagation from the source. A propagation pattern was similarly constructed across the 4 macro-electrodes encompassing M1 and M2.

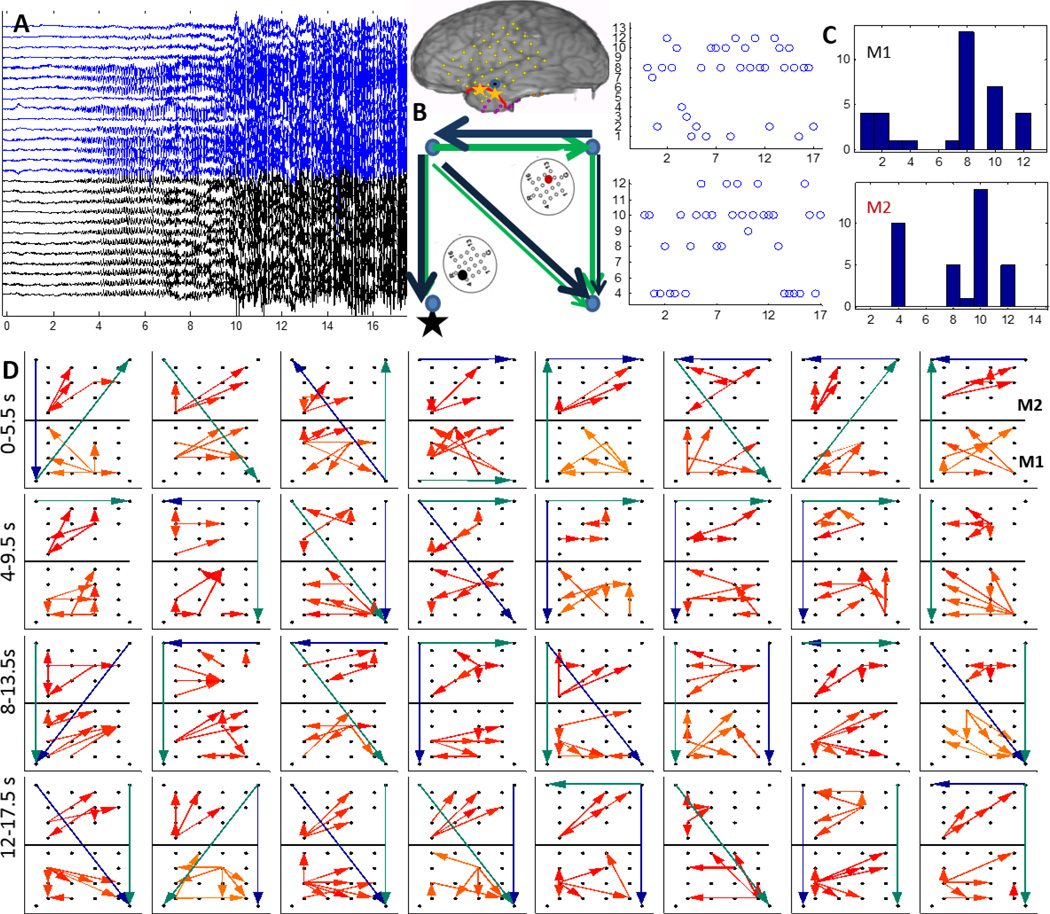
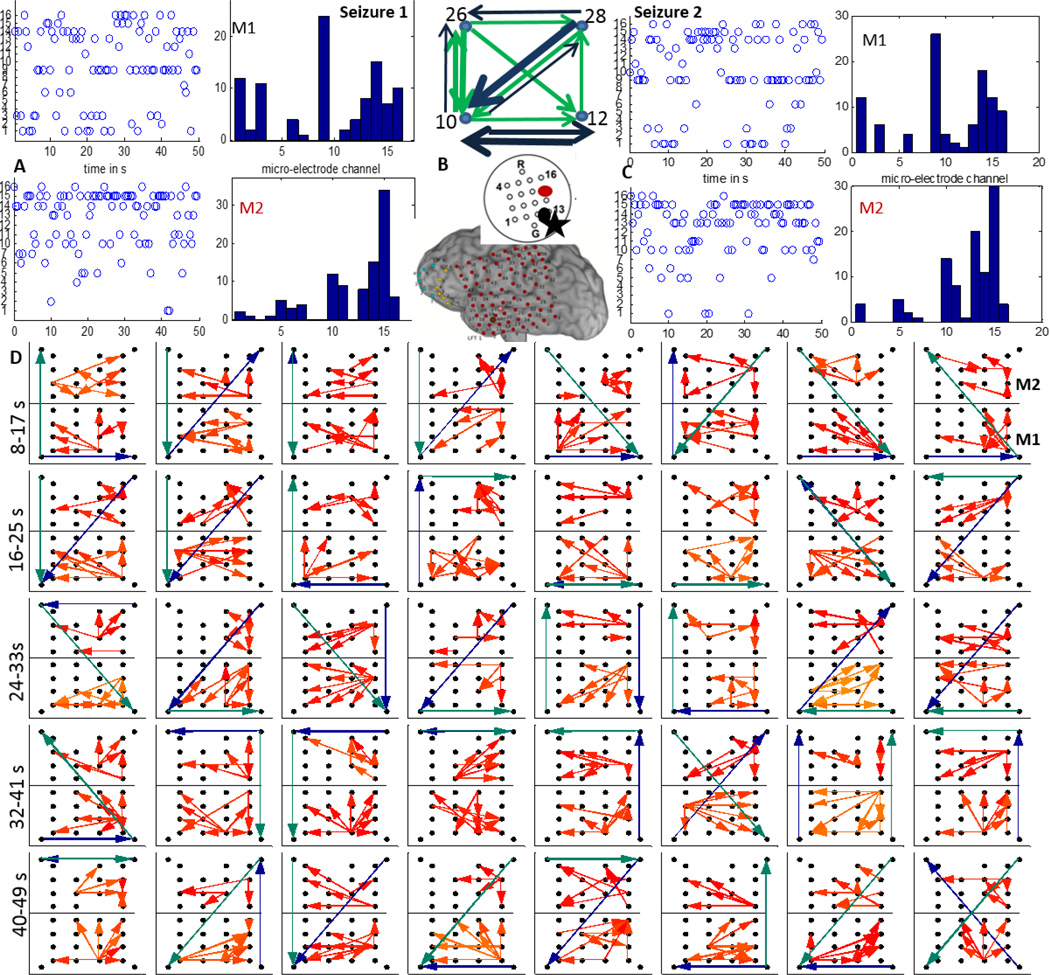
Patients P1 and P2 had left temporal grids (LFT) with two micro-arrays M1 and M2 as shown in figure 1. In P1, the earliest seizure onset on LFT were localized to contacts 19 and 26 as marked by yellow asterisks and the resection boundary with a red line as in figure 1. After removal of the noisy channels (15 in M1, 12 in M2), M1, M2 and LFT 19 (left corner), 22,43,46 were used to reconstruct the propagation across M1, M2 and the 4 macro-electrodes surrounding M1, M2 as shown in figure 4(A). As seen in figure 3, the 70–90 Hz frequency band was used to determine propagation across M1 and M2 using the DTF measure. A threshold for each frequency bin was determined using the FT surrogate measure as described before. Figure 4(D) shows the top 4 percentile of the thresholded DTF values plotted as propagation across M1 (left corner) and M2 (right corner) along with the strongest flows across the neighboring macro-electrodes in the 4–50 Hz range (green) and 70–110 Hz range (blue). The macro flow over each time window was aggregated and are plotted in figure 4 (B) with the thickness of the arrows being proportional to the number of flows across a pair of contacts. Both the frequency bands have similar dominant flows except for the top contact pair. Furthermore, the channel with the maximum outflow was calculated for M1 and M2 and are plotted over time (left) and as a histogram (right) in figure 4(C) which shows that in M1, channel 8 acts as the source for maximum number of time windows whereas in M2, channels 10 and 4 have the highest outflows. From figure 4(D), there seems to be a more stable one directional flow pattern in M2 although a single electrode (channel 8) dominates outflow in M1.

Figure 4.

A:15 channels of M1 (blue) and 12 channels of M2 (black) recorded from P1 during a clinical seizure, the inset shows a schematic of the implanted grid along with M1 and M2 with the black asterisk denoting the location of the SOZ macro-electrode contact with respect to M1; B: The 4–50 Hz (green) and the 70–110 Hz (blue) flows in the macro-channels surrounding M1 and M2. The thickness of the arrows is proportional to the number of times a particular direction of flow occurred in the entire interval considered as in D; C: time evolution and histogram of micro-electrode contact emanating the maximum outflow within grids M1 and M2 respectively. The channel having maximum outflow for the highest number of times over the entire seizure duration is marked in black and red for M1 and M2 respectively in the schematic in A ; D:Top 4 percentile of propagation in the 70–90 Hz frequency band across M1 (bottom) and M2 (top) along with the strongest flow across the neighboring macro-electrode contacts in the 4–50 Hz (green) and the 70–110 Hz (blue) frequency bands. Each square element corresponds to a time interval of 2 s and consecutive squares are separated by 0.5 s. The temporal evolution is from left to right. The 32 patterns shown thus correspond to a total duration of 16 s as shown in A.

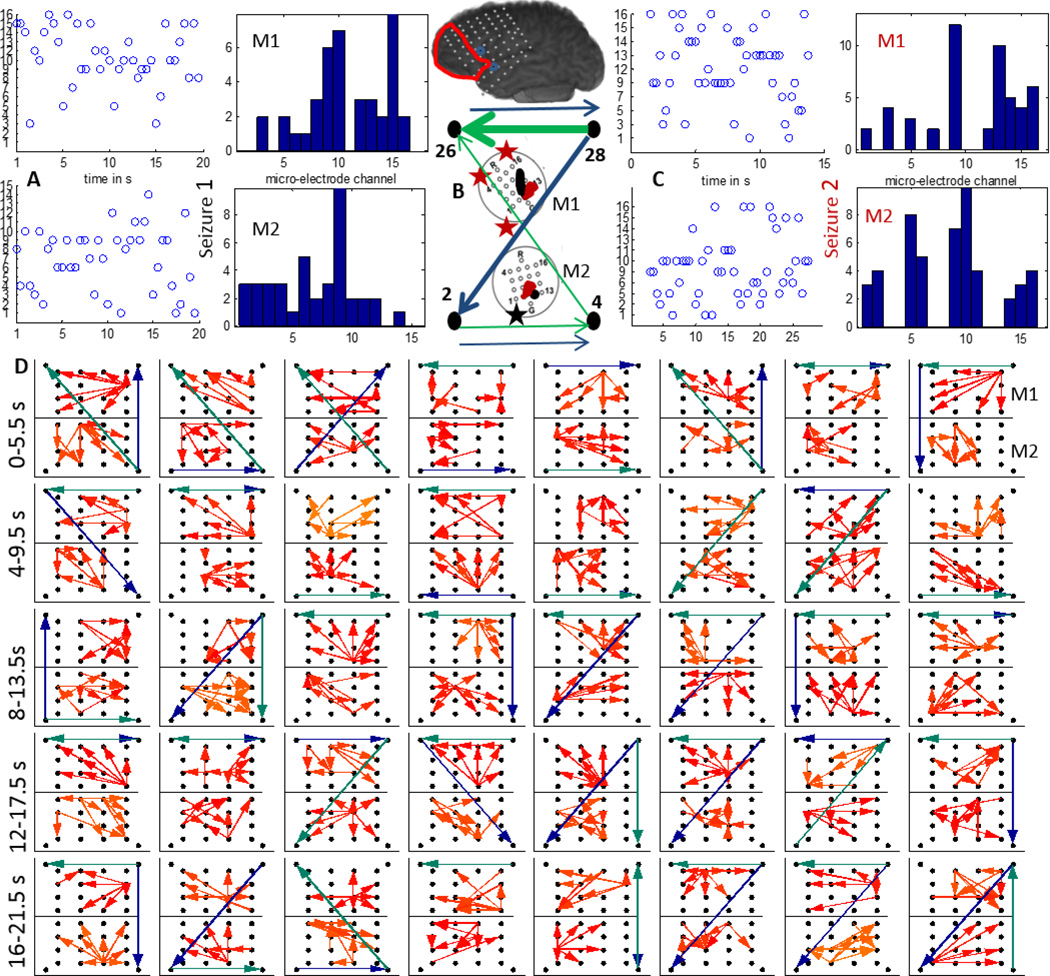
In P2, both M1 and M2 were in close proximity to the the LFT macro-electrodes (1,2,11) with earliest seizure onset and the region sampled by both were resected as shown by the red line in figure 1. We considered two clinical seizures which were separated by approximately 3 hours. In figure 5 (A) and (C), the time evolution and histograms of the channels in M1 and M2 with maximum outflow are plotted for seizures 1 and 2 respectively. It can be seen that both the time evolution and histogram of the strongest source in M1 (channel 9) is very similar for both seizures. M2 has channel 15 as the strongest source in both seizures. The strongest sources are marked with black (M1) and red (M2) on a schematic of the micro-array. Figure 5 (D) shows the propagation over time windows of 2 s shifted every 1 s across M1 (bottom) and M2 (top) in the 70–110 Hz band. The flow across the surrounding LFT electrodes 10(left corner),12,26,28 in the 4–50 Hz band (green) and 70–110 Hz band (blue) are also plotted. All the flows represent top 4 percentile of the thresholded DTF values. Note that LFT 10 and 12 (lower ones) are closer to the ones involved with early seizure detection. In M1, the propagation is mostly upward during the initial 10 s while in M2, there is not much consistent pattern. The flow across the macro-electrodes in the 70–110 Hz band is mostly originating from the bottom left corner (LFT10) for the first 7 s (10 windows) while that in the 4–50 Hz band is mostly downwards for the first 8 s. The aggregate macro flow during the first seizure as shown in figure 5(B) is more dominant and directional in the 70–110 Hz band than in the 4–50 Hz band.

Figure 5.

A:The time evolution and histogram of micro-electrode contact emanating the maximum outflow within grids M1 and M2 during a clinical seizure recorded from P2; B:The 4–50 Hz (green) and 70–110 Hz (blue) flows in the macro-channels surrounding M1 and M2. The thickness of the arrows is proportional to the number of times a particular direction of flow occurred in the entire interval considered as in D. The inset shows a schematic of the implanted grid along with M1 and M2 with the channels associated with maximum outflow marked in black (M1) and red (M2). The black asterisk shows the position of the SOZ macro-electrode closest to M1; C: Same as in A during a later seizure. D:Top 4 percentile of propagation in the 70–110 Hz frequency band during the seizure in A across M1(bottom) and M2(top) along with the strongest flow across the neighboring macro-electrode contacts in the 4–50 Hz (green) and the 70–110 Hz (blue) frequency bands. Each square element corresponds to a time interval of 2 s and consecutive squares are separated by 1 s. The temporal evolution is from left to right. The 40 patterns shown thus correspond to a total duration of 40 s.

Patient 3 (P3) was implanted with a left frontal grid (LFT) with M1 and M2 bordering the region resected (marked with a red line) as shown in figure 1. The macro-electrode contacts involved with early seizure onset are marked in yellow and white. We considered 2 complex partial seizures which did not generalize and were separated by over 24 hours. They had different patterns of initiation, the first one involving the macro-electrodes marked by yellow while the second one involving the ones marked in white in figure 1. From figure 6 (A) and (C), we can see that the two seizures differ in the strongest outflow channel both in M1 and M2. M1 does not exhibit a single strong source while M2 shows a strong source in channel 9 during seizure 1. Additionally, channel 9 in M1 as well as M2 seem to be a strong source for both the micro-electrodes during the seizures. The strongest sources during seizures 1 and 2 are marked in black and red respectively on schematics of M1 and M2 in figure 6. The evolution of seizure 1 propagation patterns (top 4 percentile of thresholded DTF values) in the 70–110 Hz over M1 (upper grid) and M2 (lower grid) along with those across LFT 2(left corner),4,26,28(right corner) in the 4–50 Hz (green) and 70–110 Hz (blue) ranges are plotted in figure 6(D). During the initial 10 s, the propagation direction across M1 is similar to that of the lower frequency components across the neighboring macro-electrodes, while later into the seizure it more closely follows the direction of the higher frequency macro-electrode propagation. Propagation across M2 on the other hand follows more closely the higher frequency components during the entire period considered. The aggregate macro flow during seizure 1 as shown in figure 6(B) has dominant flows from the upper right macro-electrode in both frequency bands for most of the time windows considered in (D).

Figure 6.

A:The time evolution and histogram of micro-electrode contact emanating the maximum outflow within grids M1 and M2 during a clinical seizure (seizure 1) recorded from P3; B:The 4–50 Hz (green) and 70–110 Hz (blue) flows in the macro-channels surrounding M1 and M2. The thickness of the arrows is proportional to the number of times a particular direction of flow occurred in the entire interval considered as in D. C:Same as in A during a later seizure (seizure 2). The inset shows a schematic of the implanted grid along with M1 and M2 with the channels associated with maximum outflow marked in black (M1) and red (M2). The black asterisk shows the position of the SOZ macro-electrode closest to M1; D:Top 4 percentile of propagation in the 70–110 Hz frequency band across M1 (top) and M2 (bottom) along with the strongest flow across the neighboring macro-electrode contacts in the 4–50 Hz (green) and the 70–110 Hz (blue) frequency bands. Each square element corresponds to a time interval of 2 s and consecutive squares are separated by 0.5 s. The temporal evolution is from left to right. The 40 patterns shown thus correspond to a total duration of 20 s.

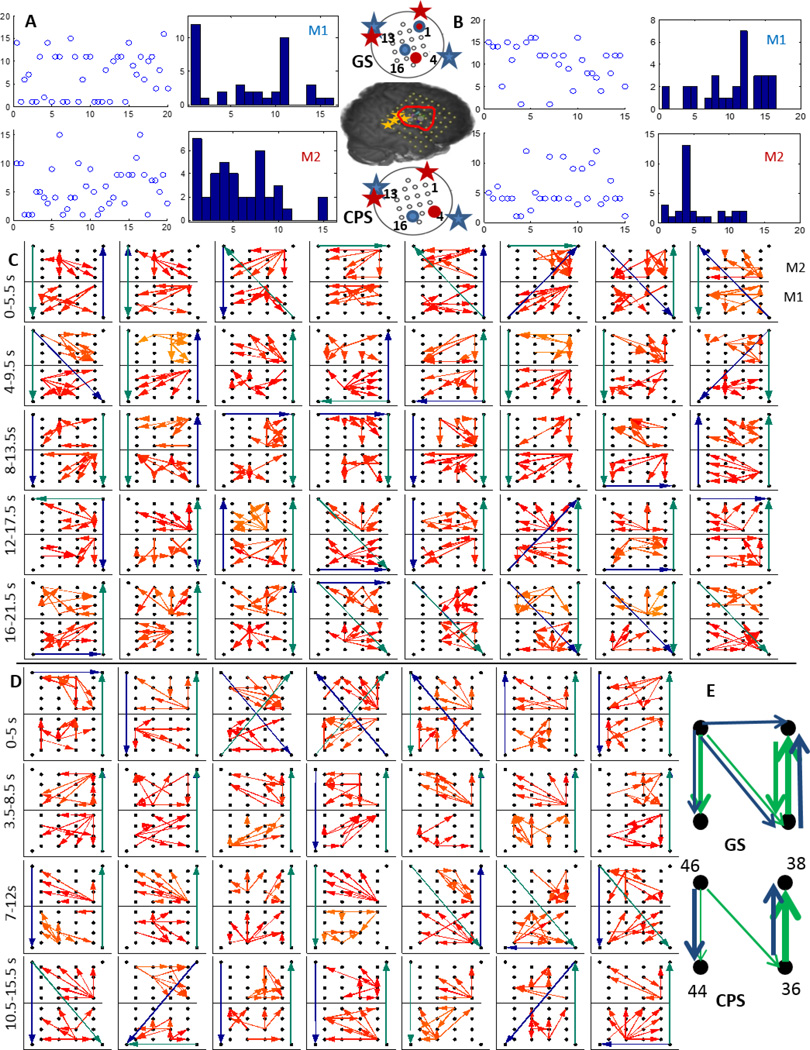
Patient 4 (P4) was implanted with a right frontal-temporal grid (RFT) with two micro-electrode grids M1 and M2 as shown in figure 1. Both M1 and M2 were inside the resected region (outlined in red) and adjacent to the macro-electrodes (marked with yellow asterisks) which were involved with early seizure onset. We considered two complex partial seizures, one that secondarily generalized (GS) and another that did not generalize (CPS). These seizures typically start in a small area of the temporal or frontal lobe of the brain and can quickly generalize, that is involve other areas of the brain that affect alertness and awareness. The propagation during the GS and the CPS were calculated using the thresholded DTF values and the top 4 percentile are shown in figure 7(C) and (D) respectively. During the GS neither M1 nor M2 exhibit any single dominating source of ictal outflow, while during the CPS, channel 12 in M1 and channel 4 in M2 show the strongest outflow. The position on the micro-electrode grid of these sources are however similar for GS and CPS as shown on the schematic in figure 7. The propagation in the 70–100 Hz band across M1 (bottom) and M2 (top) along with that across RFT 36,38,44 (bottom left corner),46 in the 4–50 Hz (green) and 70–110 Hz (blue) bands are shown in figure 7 during the GS (C) and the CPS (D). During the GS, M2 has a downward flow during the initial phase while an upward flow during the later phase, while during the CPS, its mostly directed downwards. M1 does not show a definite pattern during either GS or CPS. The aggregate macro flow during GS and CPS show similar dominant flows in both frequency bands as shown in figure 7(E).

Figure 7.

A:The time evolution and histogram of micro-electrode contact emanating the maximum outflow within grids M1 and M2 during a generalized clinical seizure (GS) recorded from P4; B:Same as in A during a complex partial seizure (CPS). The inset shows a schematic of the implanted grid along with M1 and M2 with the channels associated with maximum outflow marked in blue (M1) and red (M2)during GS (top) and CPS (bottom). The red asterisks indicate SOZ closest to M2 while the blue ones indicate those closest to M1; C:Top 4 percentile of propagation in the 70–100 Hz frequency band across M1 (bottom) and M2 (top) along with the strongest flow across the neighboring macro-electrode contacts in the 4–50 Hz (green) and the 70–110 Hz (blue) frequency bands. Each square element corresponds to a time interval of 2 s and consecutive squares are separated by 0.5 s. The temporal evolution is from left to right; D: Same as in C during CPS; E:The 4–50 Hz (green) and 70–110 Hz (blue) flows in the macro-channels surrounding M1 and M2 during GS and CPS over all the windows as in D.

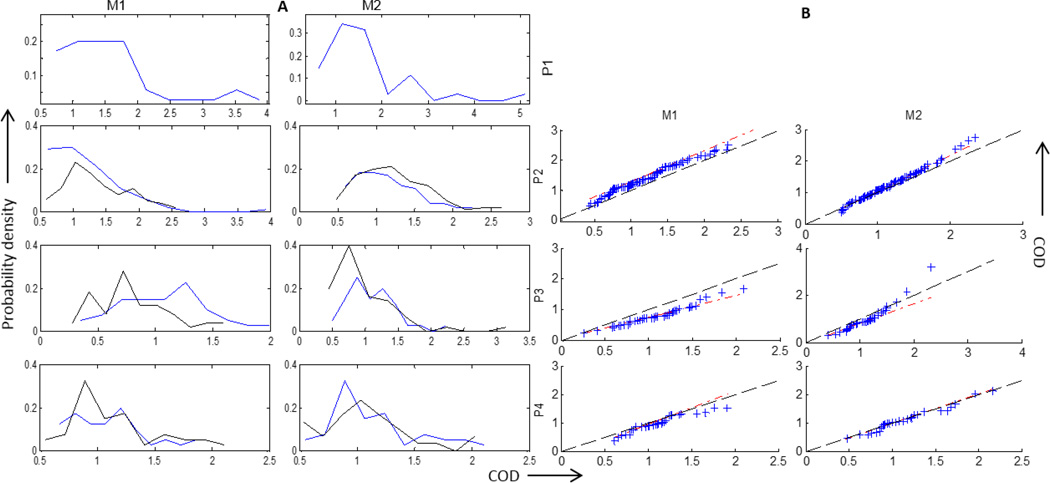
Finally, a comparison of the seizures considered in P2–P4 in terms of the coefficient of dispersion (COD) calculated for each of M1 and M2 are plotted in figure 8. A higher value of COD indicates a strong dominating source while a low value would mean similar strength outflows from multiple channels. A COD was calculated for M1 and M2 over each time window of 2 seconds. These COD values for each patient, each micro-array and each seizure were then used to construct a histogram for P1–P4 as shown in figure 8 A. The COD values are mostly concentrated in the range of 0.5 – 2. P1 has the highest COD values while P3 has the lowest. For P2–P4, a comparison between the seizures is depicted in terms of a qq-plot between the corresponding COD values as plotted in figure 8 B. The red line indicates the best straight line fit to the qq-plot while the (y=x) line is plotted in black. In other words, if the COD values calculated from both the seizures had the same underlying distribution, then the red and blue line would coincide. It can be seen that M2 in P4 has the most similar outflow pattern while M1 in P3 has the most different one in terms of the COD. A brief summary of the results are presented in table 2.

Figure 8.

Coefficient of dispersion (COD) calculated for M1 and M2 for each patients P1–P4 to construct A) histograms and B) QQ plots for P2–P4 using the values of COD for 2 seizures. The red line indicates the best straight line fit to the qq-plot while the (y=x) line is plotted in black. P1 is not included since there was one clinical seizure occurrence. The two seizures in P2–P4 are represented as blue and black in A.

Table 2.

Summary of results.

Patient	Electrode	General pattern	Relation with macro-electrode flow	Maximum outflow	COD
P1	M1 M2	Mostly away from SOZ for entire duration Away from left corner initially and towards the end, more structured flow than M1	Along 4–50 Hz from 9–12 s In the same direction as 4–50 Hz for initial 6s	dominating source near SOZ 2 strong sources	higher COD than other patients higher COD than other patients
P2	M1 M2	Upwards (away from SOZ) during initial 10 s No consistent pattern	Similar to 4–50 Hz flow during 6–10 s period similar to 4–50 Hz during initial and later period and that to 70–110 Hz in between	presence of a strong source near SOZ presence of a strong source similar sources across seizures for M1 and M2	Seizures are similar for both M1 and M2, most COD values are less than 1.5
P3	M1 M2	Structured flow but changes direction towards seizure 2 SOZ	follows 4–50 Hz initially and 70–110 Hz later mostly in the direction of 70–110 Hz	No strong source Strong source during seizure 1, similar sources during both seizures closer to seizure 1 SOZ	Seizures are different in terms of COD Seizure 1 has higher COD values than seizure 2 For lower values of COD, seizures are similar most COD are lesser than 1.5
P4	M1 M2	less structured flow During GS, downward flow initially and then upward flow, during CPS, mostly downward flow	Nothing in particular	A single dominant source absent Strong source during CPS	GS and CPS are similar wrt COD, most of the values are less than 1.5,

Note: SOZ refers to the macro-electrodes involved in early seizure onset

4. Discussion

An increasing number of studies are pointing to the importance of high frequency activity for localizing the SOZ [7, 38, 10, 12]. Some studies have localized pathological high frequency oscillations in micro-domains in human epileptic hippocampus [7, 8]. High frequency activity is generated locally by clusters of neurons [39] whose activity may be sampled with micro-electrode arrays. More invasive micro-electrode arrays with higher spatial resolution than ours have also captured early seizure propagation in a 4×4 mm cortical region [11, 12]. In [11], the seizure propagation is characterized by an increase in spiking of the multiunit activity (300Hz-3kHz) and an increase in amplitude of the low frequency 2 – 50 Hz components. This study demonstrated that the multiunit activity can distinguish the core territory of recruited neurons from an ictal penumbra as opposed to the low frequency activity. Hence it might be interesting to study the propagation of ictal activity in the high frequency range over localized regions of the epileptic cortex. However, ictal flow reconstruction using a threshold on band-passed local field potentials is not trivial, especially for multi-channel recordings.

Many different approaches exist to determine functional and pathological connectivity from time series data [40] which include use of distinct coupling measures (e.g., linear or nonlinear measures) and different strategies for assigning network edges. Dynamic Causal Modelling (DCM) has been used to estimate the seizure propagation pathway from fMRI data recorded in an epilepsy patient with hypothalamic hamartomas, by testing a set of clinically plausible network connectivity models of discharge propagation [41]. Ecog data from a population of male and female human patients with epilepsy were used to construct dynamic network representations using cross-correlation [42]. This study showed that these networks evolved through a distinct topological progression during the seizure. An information theoretic test for general Granger causality has been used to identify couplings and information transport between different brain areas during epileptic activities [43]. [44] used partial coherence to show that the anterior thalamus plays a role in the propagation of seizure activity between subcortex and cortex. Another study [45] used synchronization likelihood (SL) to characterize synchronization patterns in intracerebral EEG recordings from 7 epileptic patients for 5 periods of interictal, before, during and after seizure activity. A numerical approach to the multivariate linear discrimination of Fisher based on singular value decomposition was used to demonstrate that human seizures have distinct initiation and termination dynamics [46]. This approach is broadly applicable to a wide variety of neuronal data, from multichannel EEG or MEG, to sequentially acquired optical imaging data or fMRI. A study by [47] used an eigen value decomposition of the correlation matrix of multi-channel EEG recordings over short time intervals to demonstrate that during focal onset seizures this correlation structure shows a typical evolution, indicating an increase of overall zero lag correlations before seizure termination.

This work to the best of our knowledge is the first attempt at characterizing the epileptogenic regions by reconstructing seizure propagation patterns over highly localized cortical surfaces in the vicinity of clinically determined SOZ by fitting a model to simulated and recorded data. We used a linear MVAR model to fit simulated micro-electrode local field potentials and those recorded during symptomatic seizure occurrence in human patients. We were not able to obtain an MVAR model without dominating off-diagonal elements in the residual covariance matrix over few seconds of micro-electrode recordings, both for low (0 – 50Hz) and high frequencies (> 120Hz). However, MVAR models in the 70 – 110 Hz high gamma band could be estimated which produced residuals which had much lower off-diagonal contribution in their covariance matrix. Hence this frequency range was used as a reliable marker for illustrating propagation of seizures over micro-domains. In the following subsections, we discuss some interesting observations from the high gamma band propagation across the micro-electrode arrays in terms of general pattern, maximum outflow and comparison between seizures. We also briefly discuss implications for modeling studies.

4.1. Propagation pattern

The propagation patterns were constructed using the top 96 percentile of thresholded DTF values in the 70 – 110 Hz band for both M1 and M2. Additionally, propagation patterns across 4 neighboring macro-electrode channels were similarly constructed in the 4 – 50 Hz (LF) and 70 – 110 Hz (HF) frequency bands. In the 8 micro-electrode arrays studied, the propagation was either away from the closest macro-electrode channel involved in early seizure onset (SOZ), towards it or had no particular direction, i.e changed directions over time in no particular order. The pattern can be also be categorized as structured (figure 4 D, subplot 2), ie having a strong source and a directional flow or an unstructured (figure 4 D, subplot 30) flow where there are short range flows from multiple sources.

In P1, M1 showed a propagation away from the SOZ for most of the time windows considered while M2 had a similar flow during the initial and later parts of the time interval considered. Although M2 was spatially separated from M1, both of them showed a flow away from the SOZ for most parts. M1 in P2 also showed a flow away from the SOZ for most of the time windows during the initial 20 s (subplots 1–20). These observations suggest that the micro-electrode grids bordering and outside the SOZ, in general show a flow away from the SOZ. This might be a property of brain tissue that is not involved in seizure initiation. P3 had two main seizure onset patterns with M1 being in between the macro-electrodes involved in seizure 2 onset but not to the ones involved in seizure 1 onset. Unlike M2 in P1, M1 in P3 although being relatively far from the seizure 1 SOZ, showed a flow with less consistent directionality. This might be due to the fact that M1 was surrounded by the seizure 2 early onset macro-electrodes. This indicates that although clinically M1 was not close to the SOZ during seizure 1, the micro-flow still shows characteristics of being inside the SOZ. The micro-flows are more likely to be consistent across seizures. Similarly, M2 in P2, M2 in P3 and M1, M2 in P4 do not show any definite direction of flow. These were either very close to or inside the resected region and hence might be a characteristic of epileptogenic tissue.

The general direction of flow across the micro-electrode arrays were also compared with the strongest flow across the neighboring macro-electrode contacts. Both M1 and M2 in P4 did not show any particular relationship with the direction of flow in either LF or HF. M1 in P1 had a flow in the direction of LF towards the end of the time interval considered (9–12 s); M2 in P1, M1 in P3 and both M1, M2 in P2 had a propagation in the same direction as that in LF during the initial time period, while M2 in P3 showed a flow in the direction of HF across the macro-electrode channels. Thus we see that except for M1 and M2 in P4 which were placed right in between the macro-electrodes with early seizure involvement, strongest propagation were in the direction of either HF or LF during the entire or part of the interval considered. This might be indicative of the fact that micro seizure dynamics inside the SOZ is different from that observed on more macro scales. The LF and HF macro flows in P1, P3 and P4 which included one of the early onset macro-electrode contacts had similar and more consistent preferred directions over all the time windows considered. On the other hand, The LF macro flow in P2 which did not include any of the early onset macro-electrode contacts, did not show much preferred directionality. Thus propagation patterns across macro-electrodes which were not involved in seizure onset is less consistent. The lack of consistency in propagation across the macro-electrodes might also be due to the lack of spatial resolution to identify well localized micro seizure sources which can be identified using micro-electrodes. Moreover, the propagation was calculated over shorter moving time windows (2 s) which show a more dynamic temporal pattern even at the macro scale.

4.2. Outflow

The channel in each micro-electrode array having maximum outflow to other channels in terms of thresholded DTF values was calculated to examine if there is a particular channel that acts as a dominating source for most of the time windows considered. On the other hand, if the flow is more random, we would see multiple channels acting as sources over the entire time period considered for each patient. M1 in P1; M1, M2 in P2; M2 in P3 during seizure 1 and M2 in P4 during CPS showed a strong dominant source close to the focus. M1 in P3 and M1, M2 in P4 were the micro-electrode arrays which were surrounded by early seizure onset macro-electrode contacts and were also the ones which did not show a very dominant source during generalized seizures. This might indicate the presence of strong sources even over highly localized cortical regions bordering the epileptogenic region, while an absence would point toward no sources inside the seizure generating tissue.

The total outflow from each channel, calculated as the sum of thresholded DTF values for each micro-electrode array were used to calculate the COD as the ratio between the interquartile range and the median. The COD quantifies the dispersion among outflows form the different channels of an array over the sliding time windows considered. A lower value of COD would indicate that all the channels have similar outflows while a higher value would suggest fewer dominating channels. As shown in figure 8, P1 who had both M1 and M2 distinctly outside the resected region showed the highest values of COD. This might be a general property of cortical tissue which is not involved in seizure generation. P2 and P4 had the micro-electrode arrays inside the resection region while P3 had a conservative resection with M1, M2 bordering the resection boundary. Hence, the lower values of COD might be due to the location of M1 and M2 inside the epileptogenic region.

4.3. Comparing seizures

P2–P4 had multiple seizures during the intracranial monitoring period. We considered 2 seizures for each patient and compared them in terms of the existence of a dominating source and COD values. The 2 seizures in P2 were approximately 3 hours apart and hence clinically were a part of one seizure cluster. They show very similar sources and COD values across M1 and M2. P3 on the other hand had very dissimilar seizures clinically. The 2 seizures considered were separated by more than 24 hours and had different macro-electrodes that were involved in seizure onset as shown in figure 1. The channels acting as strongest sources were in similar locations in M1 and M2 for both the seizures and were closer to the focus as seen in figure 6 A, B. The COD values however did not have similar distributions, specifically in M1 as in figure 8. In P4, we considered two seizures one of which generalized and the other did not. M1 showed two dominant sources during GS while one during CPS and one of the two sources during the GS was located in the same region of M1 as the one during the CPS. M2 on the other hand showed a very dominant source during CPS but not during GS. Across patients, only P1 had a mesial-temporal seizure onset which spread very rapidly as compared to the other patients which had neocortical seizure onsets. This might account for the narrow high frequency band of seizure activity and a higher COD value (fewer stronger sources) as compared to the other patients.

4.4. Implications for realistic computational models

We used a realistic computational model to generate micro-electrode data with a known propagation pattern and the DTF measure accurately reconstructed the propagation pattern in the simulated data. The MVAR model estimation was done using a different algorithm than the one for measured data due to the difference in the level of noise between the two types of datasets. However the choice of MVAR algorithm is not very significant as long as the number of sample is not limited [48]. One of the major challenges of building a realistic computational model for local field potentials is calibration and comparison with a measured signal. Although we used a computational model here to validate our propagation reconstruction method, this could also provide a modeling framework for tuning such computational models to match real data in terms of propagation. Efforts focused on reconstruction of pattern of activity propagation between micro-electrodes will potentially play an important role in constructing and validating models of cortical activity, with a reliance on human recordings for calibration. Specifically, these reconstructed patterns from micro-electrodes will help quantify activity spread in lateral direction similar to current density analyses, which allow for studying the laminar pattern of neural activity in neocortex. Therefore details of reconstructed propagation pattern can help in estimation of some values of network parameters which are difficult to determine in situ. These might include selection of weights, numbers, and the range of synaptic contacts in the process of network model parameter tuning in order to reproduce the propagation pattern consistent with measurements of the propagation of epileptiform activity in neocortex [19, 49].

5. Conclusion

In this study, we showed that an MVAR model can be used to reconstruct propagation patterns between local field potentials measured over highly localized cortical surfaces in the high gamma frequency band range. In contrary, other frequency components of such signals such as those below 50Hz and above 110Hz over short time intervals do not exhibit such propagation and hence could not be satisfactorily modeled using such an approach. We also found that a DTF measure was the best among the 4 measures considered for reconstructing the propagation pattern as well as the sources of outflow in the gamma band using the fitted MVAR model. The propagation over 8 micro-electrode arrays during 7 symptomatic complex partial seizures reveal highly dynamic patterns with low COD and absence of a strong source in those that were inside the clinically determined epileptogenic region. Although the patient population studied is limited to 4 and has heterogeneous sampling of the cortical micro-domain (the placement of the micro-array is dictated by a presurgical prediction of SOZ location), we showed a more directed ictal pattern with strong sources across micro-domains bordering or at a few centimeters away from the seizure generating regions than those inside. This indicates that even if the micro-array does not target the focal point during surgery, the pattern of seizure propagation across it may still provide information guiding the consecutive resection. Hence, these features of microscopic seizure propagation can potentially be used in future clinical evaluation for determining resection regions. Additionally they might also reveal important information for targeting anti-epileptic stimulation systems. This would however require validation of such features on a bigger patient population.