Optimal Drug Prediction from Personal Genomics Profiles

Abstract

Cancer patients often show heterogeneous drug responses such that only a small subset of patients is sensitive to a given anti-cancer drug. With the availability of large-scale genomic profiling via next generation sequencing (NGS), it is now economically feasible to profile the whole transcriptome and genome of individual patients in order to identify their unique genetic mutations and differentially expressed genes, which are believed to be responsible for heterogeneous drug responses. Although subtyping analysis has identified patient subgroups sharing common biomarkers, there is no effective method to predict the drug response of individual patients precisely and reliably. Herein, we propose a novel computational algorithm to predict the drug response of individual patients based on personal genomic profiles, as well as pharmacogenomic and drug sensitivity data. Specifically, more than 600 cancer cell lines (viewed as individual patients) across over 50 types of cancers and their responses to 75 drugs were obtained from the Genomics of Drug Sensitivity in Cancer (GDSC) database. The drug-specific sensitivity signatures were determined from the changes in genomic profiles of individual cell lines in response to a specific drug. The optimal drugs for individual cell lines were predicted by integrating the votes from other cell lines. The experimental results show that the proposed drug prediction algorithm can be used to improve greatly the reliability of finding optimal drugs for individual patients and will thus form a key component in the precision medicine infrastructure for oncology care.

I. Introduction

Traditionally, cancer types have been defined by their anatomical origin. Molecular analysis now shows that cancers of different organs may share similar features while cancers from the same organ are often quite distinct, as evidenced by the observation that cancer patients with the same cancer type often show heterogeneous responses to the same therapy. It is believed that complex and distinct genomic instability is responsible for the diversity in drug response [1, 2]. For example, one non-small cell lung cancer (NSCLC) patient was found to be responsive to Dasatinib dramatically and remained cancer-free four years later [3]. In the consequent genomic analysis, an inactivating BRAF mutation (Y472C) was found in the patient's tumor while no inactivating BRAF mutations were found in the non-responding tumors [3]. The Pan-Cancer project [4], which aims to analyze the molecular aberrations in cancer cells across a range of tumor types, combines all of the data from different tumor types and enables researchers and scientists to find new patterns of genomic aberrations.

To support studies on uncovering the relationship between the genomic aberrations and diverse drug responses, many valuable large-scale genomic data sets funded by federal agencies have been generated for public access. For example, Cancer Cell Line Encyclopedia (CCLE) [5] and Genomics of Drug Sensitivity in Cancer (GDSC) [6] are two projects that generate such databases and aim to systemically study the causal correlations between drug sensitivity and genomic biomarkers in hundreds of cancer cell lines. Moreover, The Connectivity Map (CMAP) generated gene expression signature data of different cell lines under various perturbations by more than 1,000 small molecules [7]. These data have since been scaled over 1,000 times and is publicly available at the Library of Integrated Network-based Cellular Signatures (LINCS) (http://www.lincscloud.org/). These large-scale data sets have been used to enable drug repositioning [8, 9], predict drug combinations [10, 11] and delineate mechanisms of action (MoA) [12] and are becoming an important component in drug discovery [13, 14]. Meanwhile, Gene Expression Omnibus (GEO) [15], a public database repository, also archives millions of microarray data sets of various types of cancer under different treatments and perturbations.

Many approaches have been developed to reposition or repurpose known drugs to new indications [16, 17], based on the assumption that drugs sharing similar chemical structures would have same targets. With the advance of large-scale genomic profiling techniques, it is economically feasible to profile the whole transcriptome and genome (e.g., microarray, RNAseq, DNAseq and somatic copy number alterations (SCNAs)) [18-20] of individual patients and identify their unique genetic mutations and differentially expressed genes, which in turn can be used as biomarkers to predict drug sensitivity for those patients. For example, The Cancer Genome Atlas (TCGA) [21, 22] database repository has collected comprehensive genomics profiles of over ten thousand patient samples covering more than 30 types of cancer. Also, the International Cancer Genome Consortium (ICGC) [23] was formed to coordinate the generation and management of large-scale genomic data sets from over fifty cancer types or subtypes collected from all over the world. These large-scale and comprehensive genomic profiling data sets are invaluable in identifying predictive biomarkers of an individual's drug response, these unique biomarkers can be used for personalized medicine [15, 24-26].

Though subtyping analysis of cancer patients has identified patient subgroups sharing common biomarkers, the genomic instability patterns among the subtypes of a cancer are complex and not easily distinguishable [18, 22, 27-29]. Thus, these genomic patterns derived from the subtyping analysis often fail to offer insight into drug sensitivity and identify reliable predictive biomarkers of individual subtypes. Herein, we propose a novel computational algorithm to predict the optimal drugs for individual patients based on personal genomic profiles, as well as available pharmacogenomics and drug sensitivity information across cancer types. Specifically, 624 cancer cell lines (viewed as individual patients) and their responses to 75 drugs were obtained from GDSC. The drug-specific sensitivity signatures were obtained with the genomics profile changes of individual cell lines. Then, the optimal drug treatments for individual cell lines were predicted by integrating the drug response information from the other cell lines. To test the accuracy of our drug prediction algorithm, we performed two-fold cross-validation on GDSC dataset and further downloaded 480 cell lines and their responses to 11 drugs from CCLE for validation. The results show that our prediction algorithm can significantly improve the chance of finding sensitive drugs for individual patients.

II. Data and Methodology

2.1 Data

The simplified molecular-input line-entry system (SMILES) data that describe the structure of compounds using short ASCII strings were downloaded from PubChem (version 2.0.1, 17 Oct, 2011) [30]. Gene expression data of cell lines, and the IC50 data of drugs on the cell lines were downloaded from GDSC (release 4, march 2013) and CCLE (version 2.17, August 2014). Only drugs that have both SMILES and IC50 information, and cell lines that have both IC50 and gene expression profile data were used in our analysis. In summary, IC50 data of 75 drugs on 624 cell lines in GDSC and 24 drugs on 504 cell lines in CCLE were obtained.

2.2 Algorithm overview

Figure 1 shows an overview of the proposed drug prediction algorithm. Let D be the set of known drugs in GDSC, C be the cell line set, and G be the drug-related gene signature consisting of differentially expressed genes between the drug-specific resistant and sensitive cell lines, where n_d = |D|, n_c = |C|, n_g = |G| denoting the number of drugs, cell lines, and genes respectively. Let A = (a_ij) be the cell line expression matrix, where a_ij is the expression value of gene g_i ∈ G in cell line C_j ∈ C. Let B = (b_jk) be the IC50 value matrix, where b_jk is the normalized IC50 value of cell line C_j ∈ C treated by drug d_k ∈ D. For each drug-cell line pair, we first calculate similarity scores for pairwise drugs based on their chemical structures and then select most similar drugs to the given one. A gene signature is calculated based on the IC50 values of the selected drugs and gene expression profiles of the cell lines. A flexible similarity score between cell lines was calculated based on the gene signature and finally we assign a drug-cell line effect score by combining drug-similarity scores and cell line similarity scores. Using this method, we predicted the top candidate drugs that have the best sensitivity for the given cell line.

Fig. 1.

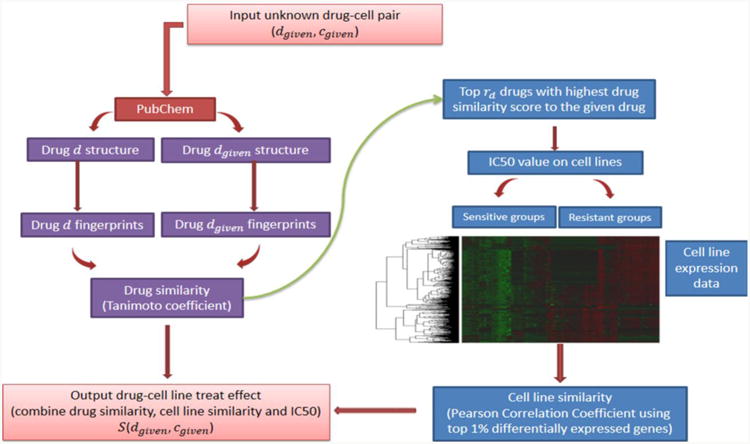
An overview of the drug prediction algorithm.

2.3 IC50 value normalization

As suggested by GDSC, cell lines with IC50 values greater than the maximum concentration of a drug are likely to be resistant to that drug while those with IC50 values smaller than maximum concentration are likely to be sensitive. So we divide the raw IC50 value by the maximum concentration of d_k ∈ D and then log2-transform it as normalized IC50 value. For drug-cell line pairs that lack IC50 values from GDSC, we set their normalized IC50 to 0. Cell lines with a normalized IC50 value greater than 0 are considered to be resistant cell lines to the drug while others with normalized IC50 value smaller than 0 were considered to be sensitive. As the range of IC50 values of sensitive cell lines differs from the range of resistant cells, we further scaled the normalized IC50 value to the range of [-1,1] for the following analysis.

2.4 Drug-drug similarity

Given two drugs d_k1 ∈ D and d_k2 ∈ D, the ‘rcdk’ R package [31] is used to retrieve their fingerprint information fp_k1 and fp_k2 from the SMILES data. The similarity between the two drugs, S(d_k1, d_k2), is calculated using Tanimoto coefficient:

$$\mathrm{S}({\mathrm{d}}_{{\mathrm{k}}_1},{\mathrm{d}}_{{\mathrm{k}}_2})=\frac{\mathrm{c}}{\mathrm{a}+\mathrm{b}+\mathrm{c}}$$

where c is the number of fingerprints that appear in both fp_k1 (figureprints of d_k1 by using the ‘fingerprint’ R package) and fp_k2 (figureprints of d_k2), a is the number of fingerprints that only appear in fp_k1, and b is the number of fingerprints that only appear in fp_k2.

2.5 Patient-patient genomics similarity

Even if two cell lines (or patient cells) share similar overall gene expression signatures, they might still have different drug-treatment response due to the variability in gene expressions of the drug-resistance related genes. Here, we propose a new method of calculating the cell line similarity scores based on drug-specific related genes, i.e., different similarity scores are given to each pair of cell lines for different drugs as follows.

For a given drug d_given ∈ D, to calculate cell line similarity, we first calculate the drug-drug similarities, S_k = S(d_given, d_k), between d_given and all other drugs d_k ∈ D. Then, we rank d_k in descending order S_k. Top r_d drugs, which show the most similarity to the given drug, are selected as D_dgiven. The next step is to find a gene signature for D_dgiven and calculate cell line similarity score based on this signature.

For each drug d_t ∈ D_dgiven, we separate cell lines into two groups according to their normalized IC50 values. If b_jt, which is the IC50 value of cell lines C_j treated by drug d_t, is greater than 0, C_j is assigned to group 1 (the resistant group); whereas the others with b_jt < 0 are assigned to group 2 (the sensitive group). For each gene g_i, we calculate its fold change between the mean expression levels of the two groups, $\text{Fold}({\mathrm{g}}_{\mathrm{i}})=\frac{\text{mean}\{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}|{\mathrm{b}}_{\mathrm{j}\mathrm{t}}>0,j=1,\dots ,{\mathrm{n}}_{\mathrm{c}}\}}{\text{mean}\{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}|{\mathrm{b}}_{\mathrm{j}\mathrm{t}}<0,j=1,\dots ,{\mathrm{n}}_{\mathrm{c}}\}}$. The top 1% genes with the largest or smallest fold change are selected as the gene signature of d_t, denoted by G_dt. Then, signatures of all drugs in D_dgiven are combined together as the signature of D_dgiven, denoted by G(d_given) = U _dt∈DdgivenG_dt.

Using the k signature genes in G(d_given) as the features, we define the similarity values S(c_j1, C_j2) between two cell lines c_j1, c_j2 ∈ C under drug d_given as the Pearson Correlation Coefficient between <a_i1j1,a_i2j1, …, a_ikj1>(a_ij1) and <a_i1j2,a_i2j2, …, a_ikj2>(a_ij2), where g_i ∈ G(d_given). To be consistent to the drug-drug similarity score, we scale S(c_j1, c_j2) to [0,1]. Given a cell line c_given, the top r_c cell lines that are most similar to it are selected as C_cgiven.

2.6 Drug-patient similarity

Given the gene expression profile of a patient, we rank the effects of all drugs in GDSC on this patient by defining the drug-patient effect score S(d_given, c_given). We first find D_dgiven to include top r_d drugs that are most similar to d_given and C_cgiven. to include top r_c cell lines that are most similar to c_given. Then the drug-patient effect score is defined by:

$$\mathrm{S}({\mathrm{d}}_{\text{given}},{\mathrm{c}}_{\text{given}})=\frac{1}{r_d{r}_c}{\sum }_{\begin{array}{c}{\mathrm{d}}_{\mathrm{k}}\in {\mathrm{D}}_{{\mathrm{d}}_{\text{given}}}\\ {\mathrm{c}}_{\mathrm{j}}\in {\mathrm{C}}_{{\mathrm{c}}_{\text{given}}}\end{array}}{\mathrm{b}}_{\mathrm{j}\mathrm{k}}\sqrt{\mathrm{S}({\mathrm{d}}_{\text{given}},{\mathrm{d}}_{\mathrm{k}})\times \mathrm{S}({\mathrm{c}}_{\text{given}},{\mathrm{c}}_{\mathrm{j}})}.$$

III. Results

The raw IC50 values for 75 drugs on 624 cell lines from GDSC and their cell line expression profiles were collected, and normalized as described in Method part. Figure 2 shows the heatmap of the normalized IC50 values (column scaled). The normalized IC50 values were further scaled to [-1,1] (-1 means the most sensitive, and 1 means the most resistant) for the subsequent analysis. We selected the top 1% genes (about 300 genes) with the largest or smallest fold change between the resistant group and sensitive group as the gene expression signature of individual drugs. Figure 3 shows the distinct gene expression signatures of AICAR and Dasatinib. To predict the effectiveness between a given cell line and a given drug, the top r_d most similar drugs and r_c cell lines were tested. Finally, we assigned a similarity score for each drug-cell line (patient) pair. Given a new cell line, the top ranked drugs were considered to be the best candidates.

Fig. 2.

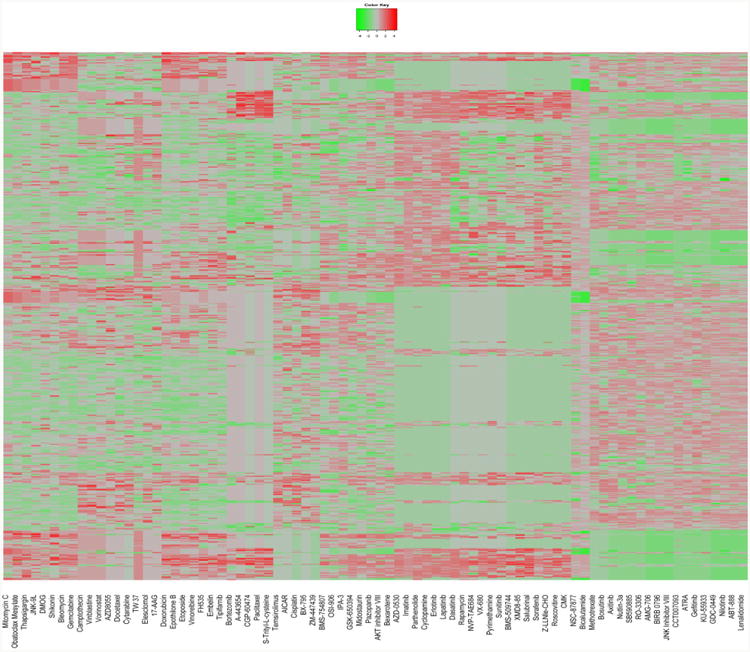
Heatmap for normalized IC50 values of 75 drugs (columns) on 624 cell lines (rows). Green means the most sensitive, red means the most resistant.

Fig. 3.

Heatmap for mRNA expression of gene signatures (rows) of two drugs (AICAR and Dasatinib) on 624 cell lines (columns).

We have conducted two new validation strategies to reduce the bias in validation and for selecting optimal values for r_d and r_c. The first one is to use two-fold cross-validation for modeling GDSC dataset, and the second one is to use GDSC dataset as the training set and CCLE dataset as the independent testing set.

First, we apply two-fold cross-validation on GDSC dataset, i.e., randomly divide the cell lines into two sub-groups, with equal size and each time use one as training set and the other as testing set. The testing results are then averaged for each r_d and r_c. The drug response on the testing set were estimated using drug treated IC50 values on the training set. Top ten prioritized drugs for each testing cell line were selected. All the drugs were ranked in increasing order based on their normalized IC50 values on the given cell line. We then calculated the enrichment score of the ten drugs in the ordered drug list using Gene Set Enrichment Analysis (GSEA) [32], denoted as ES_cl. The enrichment score, ES_cl, which ranges from -1 to 1, and would be close to 1 if the selected drugs were found at the top of the ranked drug list and vice versa. To test whether our selected drugs for the given cell line ranked higher than random selection, we randomly selected ten drugs for each cell line for five thousand times and recalculated the enrichment score, denoted by ES_i, i = 1,..,5000. The p value was calculated as: $\frac{{\sum }_{\mathrm{i}=1}^{5000}{\mathrm{f}}_{\mathrm{i}}}{5000}$, where ${\mathrm{f}}_{\mathrm{i}}=\{\begin{array}{c}1,{\text{ES}}_{\mathrm{i}}\ge {\text{ES}}_{\text{cl}}\\ 0,{\text{ES}}_{\mathrm{i}}<{\text{ES}}_{\text{cl}}\end{array}$. Small p value (here we set the threshold as p<0.05) means that the prediction can discover the more sensitive drugs to the given cell line, compared with the random selection. The percentage of cell lines with corresponding p value<0.05 were then averaged (two-fold cross-validation) to for each r_d = [1, …,4] and r_c = [1,…,10]. The results were shown in Figure 4. As can be seen, the prediction power of single drug (r_d=1) decreases when more similar cell lines being added (noise sensitive). Whereas, the prediction power with multiple similar drugs increases with more similar cell lines (noise robust). Especially, the parameter setting, r_d =3 and r_c =9, generates the best prediction power.

Fig. 4.

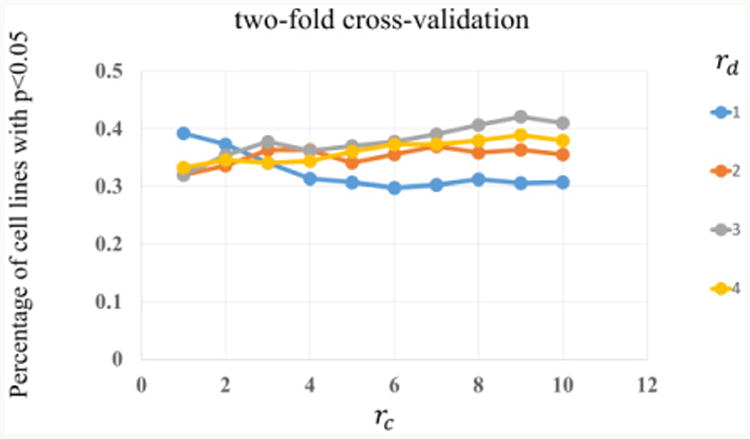
Two-fold cross-validation results for different r_d and r_c values.

Moreover, the CCLE data sets were also collected for the validation. There are 11 drugs in both GDSC and CCLE database. We use GDSC data as the training set, and download drug treated IC50 values for 480 cell lines of the 11 drugs from CCLE database as the testing dataset. We then predict the drug responses on 480 cell lines in CCLE for 11 drugs. Since there are only 11 drugs available, it is hard to find sensitive drugs for each cell line. We thus select top 10 drug-cell line pairs predicted using our model and compare their IC50 values in CCLE with all other drug-cell line IC50 values. Then p values were calculated for each r_d and r_c using GSEA as described above. The results were shown in Table 1. As we can see, the p values are smaller than 0.05 in almost all the cases, which means the top 10 drug-cell line pairs predicted by our model have a much lower IC50 value compared with random selection and thus the cell lines are more sensitive to these drugs. Note that the p value for r_d=3 and r_c =9 was smaller than 4e-04. By considering both validation method, we suggest to use r_d=3 and r_c=9 in our model.

Table. 1.

Prediction results using CCLE as testing set.

P_value		rd
		1	2	3	4
rc	1	0.013	0.2652	0.098	0.0054
	2	0.006	0.0226	0.1114	0.0932
	3	0.0006	0.0054	<4e-04	0.8668
	4	0.0024	0.0006	<4e-04	0.8668
	5	0.0008	0.043	0.0008	0.8668
	6	0.0008	0.0698	<4e-04	0.0384
	7	0.0028	0.0494	<4e-04	0.005
	8	<4e-04	0.0068	<4e-04	0.0384
	9	<4e-04	0.0068	<4e-04	0.0384
	10	<4e-04	0.0116	0.1858	0.0384

In summary, the proposed prediction algorithm can improve the effective drug selection significantly, and the evaluation results indicate the possibility of selecting the optimal drugs among all anti-cancer drugs based on their genomic profiles to achieve better therapeutic outcomes.

IV. Discussion

It is difficult to determine “sensitive” responses to drugs. We use normalized IC50 score to measure the cell line sensitivity based on the documents of GDSC which suggest that cell lines with acute drug response, IC50<max drug concentration and small confidence intervals are supposed to be sensitive to drugs. In the latest release of GDSC (release 5, June 2014), a Z-score is calculated for each cell line to define “sensitive” and “resistance” to drugs. Both measurements should be fine and people can also use other drug response data to replace the normalized IC50 values in our algorithm.

There also exist other algorithms to find differentially expressed genes between sensitive groups and resistant groups. We first tested if t test could be used to find drug signatures. We did Shapiro-Wilk test on the expression values of genes across cell lines and found that the expression value of most of the genes (over 10,000) did not form normal distribution. Thus t test and other similar methods such as SAMR were not suitable here. Then we tested Wilcoxon rank sum test which was a nonparametric statistic test followed by the Benjamini and Hochberg method (Journal of the Royal Statistical Society Series B 57, 289–300, 1995) to control false discovery rate. Genes with adjusted p value <0.05 were selected as drug signature. However, the number of differentially expressed genes varies significantly from tens to thousands; furthermore, the drug prediction result is worse than using the top 1% fold change genes. One possible reason is that the sample size of sensitive cell lines for each drug is usually too small (less than 10) to provide sufficient power for statistic testing.

V. Conclusion

Patients with the same type of cancer often respond differently to the same drug treatment, and only a small subset of patients has profound sensitivity to the given drugs. The complex and distinct genomic instability of individual cancer patients is believed to be responsible for that diversity in drug response. Due to recent advances made in the next generation sequencing, large-scale pharmacogenomic databases are now publicly available while genomic profiling of individual patients is becoming economically affordable. It is timely to leverage such information to predict the drug sensitivity for each patient in order to achieve optimal personalized treatment. However, computational analysis is the bottleneck in associating the complex genomic profiles reliably with heterogeneous drug responses.

Motivated by the public availability of informative data resources, this study contributed a computational algorithm for predicting the best drugs for individual cell lines (representing individual patients) based on their genomic profiles and drug response data. Our cross-validation showed that the best drug prediction results on over 40% cell lines are improved significantly compared to random selection. Moreover, the results from CCLE validation showed that the top ten most sensitive drug-cell line pairs predicted by our model using GDSC database have significant lower IC50 values than others. Our research finding suggests the potential of selecting optimal drugs among anti-cancer drugs for individual patients based on their genomic profiles, which will impact the cancer clinical regimen profoundly. Our ongoing work of integrating the drug prediction algorithm into the precision medicine framework being developed at Houston Methodist Cancer Center to investigate personal genomic profiles from patients, evaluate the prediction results on patient-derived xenograft models, and track the predictive performance on selected patients under treatment at Houston Methodist Hospital.