Abstract
Although traditional phase II cancer trials are usually single arm, with tumor response as endpoint, and phase III trials are randomized and incorporate interim analyses with progression-free survival or other failure time as endpoint, this paper proposes a new approach that seamlessly expands a randomized phase II study of response rate into a randomized phase III study of time to failure. This approach is based on advances in group sequential designs and joint modeling of the response rate and time to event. The joint modeling is reflected in the primary and secondary objectives of the trial, and the sequential design allows the trial to adapt to increase in information on response and survival patterns during the course of the trial and to stop early either for conclusive evidence on efficacy of the experimental treatment or for the futility in continuing the trial to demonstrate it, on the basis of the data collected so far.
Keywords: generalized likelihood ratio statistics, group sequential clinical trials, phase II–III designs, survival analysis
1. Introduction
Although randomized phase II studies are commonly conducted in other therapeutic areas, in oncology, the majority of phase II studies leading to phase III studies are single arm, as noted by El-Maraghi and Eisenhauer [1] and Chan et al. [2], and they typically measure the efficacy of a treatment by an early or short-term binary response, such as complete or partial tumor response or whether the disease has progressed at a predetermined time after treatment is initiated. If the results meet or exceed the efficacy target, the treatment is declared worthy of further investigation; otherwise, further development is stopped. The most commonly used phase II designs are Simon’s [3] single-arm two-stage designs, which allow early stopping of the trial if the treatment has not shown benefit. These two-stage designs, testing the null hypothesis H0: p ≤ p0 with significance level α and power 1 − β at a given alternative p1, choose the first-stage sample size n1 = m, the second-stage sample size n2 = M − m, and the acceptance thresholds of H0 at the end of the first and second stages to minimize the expected sample size at p0. Jung et al. [4] and Banerjee and Tsiatis [5], for example, have also introduced variations of this two-stage design.
Whether the new treatment is declared promising in a single-arm phase II trial, however, depends strongly on the prespecified p0 and p1. As noted in [6], uncertainty in the choice of p0 and p1 can increase the likelihood that (a) a treatment with no viable positive treatment effect proceeds to phase III, for example, if p0 is chosen artificially small to inflate the appearance of a positive treatment effect when one exists; or (b) a treatment with positive treatment effect is prematurely abandoned at phase II, for example, if p1 is chosen optimistically large. In their systematic review of phase II trials published in the Journal of Clinical Oncology or Cancer in the 3 years to June 2005, Vickers et al. [6] identified 70 of the 134 trials that were deemed to require historical data for design. Nearly half (32) of these studies did not cite the source for the control rate p0. No study accounted for sampling error in the control estimate or possible case-mix difference between the phase II sample and the historical cohort. Trials that failed to cite prior data appropriately were significantly more likely to declare an agent to be active (82% versus 33%; p = 0.005). They concluded that ‘more appropriate use of historical data in phase II design will improve both the sensitivity and specificity of phase II for eventual phase III success, avoiding both unnecessary definitive trials of ineffective agents and early termination of effective drugs for lack of apparent benefit.’ It is well known that the success rate of phase III cancer clinical trials is low [7]. This indicates that preliminary data at the end of phase II studies are inadequate for determining whether to launch phase III trials and how to design them.
To circumvent the problem of choosing p0, Vickers et al. [6], Ratain and Sargent [8], and Rubinstein et al. [9] have advocated randomized phase II designs. In particular, it is argued that randomized phase II trials are needed before proceeding to phase III trials when (a) there is not a good historical control rate, because of incomparable controls (bias), few control patients (large variance of the control rate estimate), or outcome that is not ‘antitumor activity’; and (b) the goal is to select one from several candidate treatments or several doses for use in phase III. However, although randomized phase II studies are commonly conducted in other therapeutic areas, few phase II cancer studies are randomized with internal controls. The major barriers to randomization include that randomized designs typically require a much larger sample size than single-arm designs and that there are multiple research protocols competing for a limited patient population. Being able to include the phase II study as an internal pilot for the confirmatory phase III trial may be the only feasible way for a randomized phase II cancer trial of such sample size and scope to be conducted.
In Section 2, we review two approaches to designing randomized phase II and phase II–III cancer trials that have been proposed in the past decade. One approach, which is limited to phase II, is frequentist and uses sequential generalized likelihood ratio (GLR) statistics to test differences in tumor response between two treatments. The other is Bayesian and uses a parametric mixture model that connects the tumor response endpoint in phase II to the survival endpoint in phase III in a Bayesian framework. In Section 3, we combine the idea of joint modeling of response and survival with that underlying group sequential GLR tests to develop a seamless phase II–III design that performs confirmatory testing by using commonly used likelihood ratio statistics for sample proportions and partial likelihood ratio statistics for censored survival data. Section 4 describes a prostate cancer study that has motivated the proposed design, gives a simulation study of its performance, and provides the implementation details. We provide further discussion of the design and some concluding remarks in Section 5.
2. Bivariate endpoints of tumor response and survival
2.1. Randomized phase II trial as an internal pilot to test response rates
In standard clinical trial designs, the sample size is determined by the power at a given alternative, and an obvious method to determine a realistic alternative at which sample size calculation can be based is to carry out a preliminary pilot study. Noting that the results from a small pilot study are often difficult to interpret and apply, Wittes and Brittain [10] proposed to use an adaptive design, whose first stage serves as an internal pilot from which the overall sample size of the study can be estimated. Bartroff and Lai [11, Section 3.2] have recently refined this idea to improve the two-stage randomized designs of Thall et al. [12] that extended Simon’s two-stage designs for single-arm trials. Ellenberg and Eisenberger [13] pointed out the dilemma that although most clinical investigators are aware of the ‘unreliability of data’ obtained in small single-arm phase II cancer trials, they cannot commit the resources needed for ‘comparative controlled trials or phase III trials’ that require much larger sample sizes until the new treatment has some promising results. Following Ellenberg and Eisenberger [13], Bartroff and Lai [11] focused on tumor response as the primary endpoint so that phase II–III designs for this endpoint can be embedded into group sequential designs, with the first group representing the phase II component. In particular, the design proposed by Thall et al. [12] is basically a group sequential design with two groups that correspond to the two stages of the design. Instead of a conventional group sequential design, Bartroff and Lai [11] used an adaptive design that allows stopping early for efficacy, in addition to futility, in phase II as an internal pilot and that also adaptively chooses the next group size on the basis of the observed data. Despite the data-dependent sample size and the inherent complexity of the adaptive design, the usual GLR statistics can still be used to test for differences in the response rates of the two treatments, as the Markov property can be used to compute error probabilities in group sequential or adaptive designs. We provide implementation details in Section 4.2.
2.2. Phase II–III designs with survival endpoint for phase III
Although tumor response is an unequivocally important treatment outcome, the clinically definitive endpoint in phase III cancer trials is usually time to event, such as time to death or time to progression. The go/no-go decision to phase III is typically based on tumor response because the clinical time-to-failure endpoints in phase III are often of long latency, such as time to bone metastasis in prostate cancer studies. These failure-time data, which are collected as censored data and analyzed as a secondary endpoint in phase II trials, can be used for planning the subsequent phase III trial. Furthermore, because of the long latency of the clinical failure-time endpoints, the patients treated in a randomized phase II trial carry the most mature definitive outcomes if they are also followed in the phase III trial. Seamless phase II–III trials with bivariate endpoints consisting of tumor response and time to event are an attractive idea, but up to now, only Bayesian statistical methodologies, introduced by Inoue et al. [14] and Huang et al. [15] for their design and analysis, have been developed.
2.3. A Bayesian model connecting response and survival
The aforementioned Bayesian approach is based on a parametric mixture model that relates survival to response. Let Zi denote the treatment indicator (0 = control, 1 = experimental), Ti denote survival time and Yi denote the binary response for patient i. Assume that the responses Yi are independent Bernoulli variables and the survival time Ti given Yi follows an exponential distribution, denoted Exp(λ) in which 1/λ is the mean:
| (1) |
| (2) |
Then, the conditional distribution of Ti given Zi is a mixture of exponentials:
| (3) |
The parametric relationship of response Y on survival T assumed by (1) and (2) enables one to use the Bayesian approach to update the parameters so that various posterior quantities can be used for Bayesian inference. Note that Y is a ‘causal intermediary’ because treatment may affect Y and then T through its effect on Y and may also have other effects on T. Models (1) and (2) reflect this nicely by considering the conditional distribution of Y given Z and that of T given (Y, Z).
Let μz = E(Ti | Zi = z) denote the mean survival time in treatment group z. Inuoe et al. [14] proposed the following Bayesian design, assuming independent prior gamma distributions for λz,0 and λz,1 (z = 0, 1) and beta distributions for π0 and π1. Each interim analysis involves updating the posterior probability p̂ = pr(μ1 > μ0 | data) and checking whether p̂ exceeds a prescribed upper bound pU or falls below a prescribed lower bound pL, which is less than pU. If p̂ > pU (or p̂ < pL), then the trial is terminated, rejecting (accepting) the null hypothesis that the experimental treatment is not better than the standard treatment; otherwise, the study continues until the next interim analysis or until the scheduled end of the study. The posterior probabilities are computed by Markov chain Monte Carlo, and simulation studies of the frequentist operating characteristics under different scenarios are used to determine the maximum sample size, study duration, and the thresholds pL and pU. Whereas Inuoe et al. [14] considered a more complex scenario in which Yi is observable only if Ti > t0, Huang et al. [15] introduced a more elaborate design that uses the posterior probability p̂ after an interim analysis for outcome-adaptive random allocation of patients to treatment arms until the next interim analysis. These Bayesian designs are called phase II–III because they involve a small number of centers for phase II after which ‘the decision of whether to stop early, continue phase II, or proceed to phase III with more centers is made repeatedly during a time interval.’
3. A seamless phase II–III design
Although model (3) provides a parametric approach to modeling the response–survival relationship using mixture of exponential survival times, semiparametric methods such as Cox regression are often preferred for reproducibility considerations and because of the relatively large sample sizes in phase III studies. Moreover, it would be valuable to complement the Bayesian framework described in the preceding section with a frequentist approach based on methods that are standard in cancer biostatistics, including logrank tests or more general Cox proportional hazards (PH) regression to analyze survival data and GLR tests for sample proportions. In this section, we develop an alternative seamless phase II–III design that uses a semiparametric model to relate survival to response and is directly targeted toward frequentist testing with GLR or partial likelihood statistics.
3.1. A semiparametric model for response and survival
Instead of assuming a stringent parametric model involving exponential distributions in (2), we develop here a semiparametric counterpart that generalizes the Inoue–Thall–Berry model. Let Y denote the response and Z denote the treatment indicator, taking the value 0 or 1. Consider the PH model
| (4) |
The Inoue–Thall–Berry exponential model is a special case of (4), with λ0(·) being the constant hazard rate of an exponential distribution. Let π0 = pr(Y = 1 | control) and π1 = pr(Y = 1 | treatment). Let a = eα, b = eβ, and c = eγ, and let S be the survival distribution and f be the density function associated with the hazard function λ0 so that λ0 = f/S. From (4), it follows that the survival distribution of T is
| (5) |
We note that the coefficients β, γ in (4) do not have direct causal interpretations as the effects of treatment because of the inclusion of the causal intermediary Y in the model. However, we propose an expression that is suitable for testing a causal null hypothesis, arguing as follows: If we assume that model (4) is correctly specified, then the hazard ratio of the treatment to control survival varies with t because of the mixture form in (5). Nevertheless, one might assume that a and c are close to 1, as in the case of contiguous alternatives. Then, the PH model approximately holds for the distribution of T given Z, with the hazard ratio of treatment (Z = 1) to control (Z = 0) well approximated by 1 − d(π, ξ), where π = (π0, π1), ξ = (a, b, c) and
| (6) |
as will be explained in Appendix A. Therefore, under this scenario of approximately time-invariant hazard ratio (indeed, such an assumption would typically be made by ignoring the response Y in a standard analysis of survival), treatment prolongs survival if d(π, ξ) > 0.
For more general parametric configurations (π, ξ), comparison of the survival distributions of the control and treatment groups entails also the survival distribution S. We can use (4) to obtain the Cox regression (partial likelihood) estimate of ξ and then the Breslow estimate of S from the data at each time of interim (or terminal) analysis; we provide details in the next section. In this way, we obtain estimates of the survival distributions of the control and treatment groups at each time of the data accumulated so far. The issue is how we should compare the survival distributions in (5) and test for significance of the observed difference. A standard method in the case of non-PH is to use some functional of the survival distributions. The functional used by Inoue et al. [14] is the difference of means of the two distributions that are mixtures of exponential distributions in their parametric model. Another functional that is associated with the Peto–Prentice extension of the Wilcoxon test to censored survival data is pr(TE > TC), in which TE denotes the survival time chosen at random from the experimental treatment group and TC denotes that chosen independently from the control group. A third functional, considered by Thall [16, Section 6], is to compare survival within a certain period, such as comparing the 1-year survival probabilities. Each of these choices reflects how one would measure the benefits of treatment over control on survival.
In practice, graphical plots of the estimated survival curves are examined in order to interpret a finding of statistical significance of any summary of the observed benefit of treatment. The two survival curves start at time 0 with the common value 1 and then grow apart if treatment is indeed beneficial, and eventually narrow in their difference and may even cross each other, with both curves approaching 0 if time is long enough. In view of this pattern for the survival difference
of the control from the treatment group, (6) provides a simple and yet effective measure because Δ(0) = 0 and
which implies that Δ is increasing in a neighborhood of 0 if d(π, ξ) > 0, noting that S(t) is a decreasing function and therefore has a negative derivative. Therefore, treatment prolongs (or shortens) survival at least up to a certain time if d(π, ξ) > 0 (or < 0). Thus, even for general parameter values, d(π, ξ) > 0 characterizes the treatment’s benefit on survival in the vicinity of t = 0.
A commonly adopted premise in the sequenced experiments to develop and test targeted therapies of cancer is that the treatment’s effectiveness on an early endpoint such as tumor response would translate into long-term clinical benefit associated with a survival endpoint such as progression free or overall survival and, conversely, that failure to improve that early endpoint would translate into lack of definitive clinical benefit. This explains why the go/no-go decision to phase III made in a conventional phase II cancer trial is based on the response endpoint. Under this premise, the complement of the set of parameter values defining an efficacious treatment leads to the null hypothesis
| (7) |
3.2. Time-sequential partial likelihood ratio and modified Haybittle–Peto tests of H0
Let t* denote the scheduled end of the clinical trial and 0 < t1 < ··· < tk−1 denote the calendar times of interim analyses, and let tk = t*. The trial can stop prior to t* if significant differences between the treatment and control groups are found in an interim analysis. Suppose n patients enter the trial and are randomized to either the experimental or the standard treatment upon entry. Because they do not enter the trial at the same time, there are two time scales to be considered, namely, calendar time t as measured from the time the study starts and age time s as measured for each patient from the time the patient enters the study. The data at calendar time t, therefore, consists of
| (8) |
for the i th subject, where ηi is the subject’s entry time and ξi is the subject’s withdrawal time,
| (9) |
In (9), Ti denotes the age time of i th subject, which is subject to two sources of censoring. One is ‘administrative censoring’, represented by (t − ηi)+, which is the duration between the subject’s entry time ηi and the calendar time t of interim analysis. The other is censoring due to withdrawal from the study at time ξi, which may be infinite.
Consider the PH model (4). Let θ = (α, β, γ)T, π = (π0, π1), Wi = (Yi, Zi, YiZi)T, 1 ≤ i ≤ n. In view of (4), we can decompose the log partial likelihood function lt(π, θ) on the basis of the observed data (8) at calendar time t as , where is the log likelihood of the observed responses Yi:
| (10) |
and is the (conditional) log partial likelihood of the observed failure-time data given the observed responses:
| (11) |
in which Ri(t) = {j: Tj(t) ≥ Ti(t)} is the ‘risk set’ consisting of subjects still ‘at risk’ (i.e., not having failed nor been censored) at calendar time t. The maximum partial likelihood estimator (π̂t, θ̂t) of (π, θ) can be computed by maximizing (10) to obtain π̂t and maximizing (11) to obtain θ̂t.
The commonly used logrank statistic to test the null hypothesis that the hazard ratio of treatment to control, which is assumed to be time invariant, is at least 1 considers only the Ti and ignores the Yi. Thall [16, Section 6] noted that ‘the rationale for using a phase 2 trial based on an early response indicator Y to decide whether to proceed to a phase 3 trial based on T is that the occurrence of response is likely to increase the value of T, that is, T increases stochastically with Y.’ Ignoring Y not only loses important information but also ‘ignore(s) the fact that the unconditional distribution of T is the mixture’ of distributions for responders and nonresponders, as pointed out by Thall [16]. The Bayesian approach relies on the assumed parametric (i.e., exponential) survival model to deal with the mixing. Our approach returns to the root of the logrank test, that is, the PH model that is intrinsically related to logistic regression, and modifies it by including the response indicator Yi as a covariate in (4).
As in the Bayesian approach, we consider the bivariate endpoint (Yi, Ti). However, because of the different information flow rates for Yi and Ti, we use a group sequential design that bears some resemblance to the conventional demarcation of Yi as a phase II endpoint and Ti as a phase III endpoint, as described in the following text. In contrast, the Bayesian approach uses the posterior distribution of the difference in mean lifetime to combine the information from Yi and Ti. Because the survival endpoint involves a relatively long study duration, periodic reviews of the data are mandatory, at least for safety monitoring. Therefore, we use a group sequential instead of an adaptive design; see Jennison and Turnbull [17] who have shown that group sequential tests with suitably chosen group sizes can be nearly as efficient as their optimal adaptive counterparts that are considerably more complicated.
The bivariate endpoint is incorporated in the null hypothesis (7). We next modify the group sequential GLR tests introduced by Lai and Shih [18, Section 3.4] to test H0. The initial interim analyses mainly focus on the response component of H0, and after this component is rejected, the remaining interim analyses switch to the survival component of H0. Specifically, we decompose H0 as
| (12) |
At each interim analysis, there is also a go/no-go decision on whether the trial should be stopped for futility. Thus, the trial can stop early not only to accept the alternative hypothesis in favor of the experimental treatment but also to accept the null hypothesis H0.
To test , we use the group sequential GLR tests introduced by Lai and Shih [18], who call these tests ‘modified Haybittle–Peto tests’ and have established their asymptotic optimality. Let
| (13) |
where is defined in (10) and π̂t is the maximum likelihood estimator of π at calendar time t. Whereas is the GLR statistic for testing π0 = π1, is the GLR statistic for testing the alternative hypothesis π1 = π0 + δ, with δ > 0 chosen to denote clinically significant alternatives, which will be used to guide futility stopping for the response endpoint. The stopping region of the group sequential GLR test of is the following:
| (14) |
Similarly, for η > 0, define
| (15) |
We can extend the modified Haybittle–Peto tests of Lai and Shih [18] and Gu and Lai [19] to test H0 after rejecting . Specifically, for the j th analysis at calendar time t = tj(k0 ≤ j < k), the test rejects (after has already been rejected) if
| (16) |
Note that k0 is fixed at the design stage and tk0 represents the calendar time of the first interim analysis of the phase III trial. During the execution of the trial, however, phase III testing is suspended at the j th analysis (k0 ≤ j ≤ k) if rejection of has not yet occurred. In addition, the trial can stop early for futility to accept H0 at calendar time t = tj (j < k) if
| (17) |
| (18) |
If is not rejected and futility stopping has not occurred at t = tk−1, reject at t = tk when (16) occurs but with bS replaced by cS. Noting that and partition H0 and that the preceding test rejects H0 only after has been rejected, we can choose bR, bS, cR, and cS to maintain a prescribed type I error probability constraint. We provide details in Section 4.2. The choice of b̃R and b̃S for the futility boundary is related to the power of the test at the alternatives π1 = π0 + δ and d(π, eα, eβ, eγ) = η; see Section 4.2 for details.
4. Implementation and examples
4.1. An application
The proposed group sequential design was motivated by a clinical trial to test a new combination therapy for castrate-resistant prostate cancer, also known as androgen-insensitive prostate cancer or hormone-refractory prostate cancer. With the exception of toxic docetaxel-based chemotherapy that elicits only modest survival benefit [20, 21], the treatment arsenal for castrate-resistant prostate cancer is limited and ineffective for improving survival. On the basis of preliminary studies, it is hypothesized that the new combination therapy, which is a standard-of-care therapy plus a c-Met inhibitor, can improve survival by delaying onset of bone metastasis and that this can be reflected in the early outcome of prostate-specific antigen (PSA) response. In fact, PSA response is usually chosen as the primary endpoint for phase II and time to bone metastasis as the primary endpoint for phase III.
A standard phase II design is Simon’s two-stage single-arm design that requires specification of π0 and π1. For the response rate of the standard-of-care therapy, experience and background literature suggest π0 = 0.3. However, there was little background to guide the guess of π1, and an adaptive design of a randomized trial, of the type proposed by Bartroff and Lai [11], was appealing to the clinical investigators who believed the combination therapy to be promising in improving survival. The possibility of including the survival outcomes of phase II patients in the subsequent phase III trial made it feasible to design a randomized instead of the usual single-arm phase II trial. In view of constraints on funding and patient accrual, a total sample size of 80 patients was planned. A 5% level one-sided test with fixed sample size 80 has 86% power to detect a PSA response rate π1 = 0.6. This means that the phase II trial has 86% chance of moving on to phase III if π1 = 0.6; the chance drops to 57% if π1 is 0.5 instead. The maximum sample size constraint of 80 is due to patient accrual at a single center and funding that can be realistically sought for the trial. However, if the trial shows promising results, then additional funding and centers can be anticipated. Although one can use trial extension or sample size re-estimation to incorporate this possibility in an adaptive design [11, Section 2.2], such design does not consider the eventual phase III trial, which is the ultimate objective of the clinical investigators.
Because the endpoint for the combination therapy is actually bivariate, consisting of the PSA response and time to bone metastasis, the maximum sample size for testing this bivariate endpoint should be formulated in terms of a combined phases II and III trials, especially if the combined trial follows those patients in phase II through phase III. With the results of Smith et al. [22], the 2-year bone metastasis rate in this patient population was anticipated to be 50%. Taking a 10% reduction (from 50% to 40%) in bone metastasis to be a clinically meaningful alternative hypothesis would require 368 events of bone metastasis for a one-sided 5% level logrank test to have 90% power at this alternative. Assuming 4 years of accrual with accrual rate 80, 120, 160, and 160 and 3 years of follow-up, this 7-year study would provide 385 events of bone metastasis, yielding 91% power.
In view of the uncertainties in the preceding guesses of the bivariate endpoint of the combination therapy relative to the standard-of-care therapy and the feasibility of the overall study, the clinical investigators recognized the need for innovative clinical trial designs. Subsequent research led to the following phase II–III design, which they found particularly attractive. With the use of the notation of the preceding section, the trial has maximum duration t* = 7 (years) and three interim analyses are planned at tj = 1, 3, 5 years. The first analysis involves only a single center and 80 patients randomized to the two treatments, which corresponds to the randomized phase II trial to test PSA response that was originally planned. Embedding it in a group sequential phase II–III design has the advantage that one does not have to arrive at a definitive conclusion on response (i.e., whether the combination therapy is significantly better than the standard therapy), using the somewhat questionable sample size of 80 patients, for the study to continue. If the results show enough promise to attract additional funding and centers, the study can continue even when a statistically significant improvement in response has not been demonstrated. Another attractive feature of the modified Haybittle–Peto design is its statistically efficient provision for early stopping due to futility, analogous to the go/no-go provision in the widely used Simon’s two-stage designs for single-arm phase II trials [11, 18].
4.2. Implementation details
Because H0 is the disjoint union of and , we can control the type I error probability of the proposed group sequential test by controlling it on and . The test of using the sequential GLR statistics is a special case of the modified Haybittle–Peto test introduced by Lai and Shih [18, Section 3.4], in which it is shown how the thresholds bR and cR can be chosen such that
| (19) |
where α is the prescribed type I error probability. In particular, letting nt denote the number of subjects who have response data at time t, Lai and Shih [18] used the fact that the signed-root likelihood ratio statistics have asymptotically independent increments and are asymptotically normal with mean 0 and variance nt under π0 = π1. Therefore, we can compute the probability in (19) using recursive numerical integration [23].
By using the theory of time-sequential partial likelihood ratio statistics [24, Section V.5; 25], it can be shown that analogous to under ,
| (20) |
where Γt is determined from the log partial likelihood function (11) as follows. First, rewrite (11) as a function lt (a, b, d) after reparameterizing θ = (α,β, γ) as (a, b, d), with a = eα, b = eβ, c = eγ, and d = d(π̂t, a, b, c) defined in (6). Note that this reparametrization conveniently expresses the constrained maximization problem in (15) associated with as the unconstrained problem supa,b lt (a, b, 0), with maximizer (ât, b̂t). Letting Ii,j denote the (i, j)th entry of the Hessian matrix of the second partial derivatives with respect to a, b, d evaluated at (ât, b̂t, 0), define
| (21) |
The type I error probability on can be maintained by choosing the thresholds bS and cS such that
| (22) |
In view of (20), we can compute the probability in (22) using the recursive numerical integration in the same way as that in (19) considered by Lai and Shih [18]. Because interim analyses are carried out at calendar times, one does not know Γt and may not even know nt until the time t of an interim analysis. In determining bR or bS in (19) or (22) before the study, we assume a random walk approximation to the signed-root likelihood (or partial likelihood) ratio statistics, with k − 1 (or k − k0) standard normal increments zi, to determine bR (or bS) by
| (23) |
where 0 < ε < 1 represents the fraction of type I error spent during the interim analyses prior to the prescheduled termination date t* of the trial. Note that is the signed-root likelihood ratio statistic for testing that the mean of zi (with known variance 1) is 0 in the normal case. We recommend choosing ε between 1/3 and 1/2, as in [18], and use ε = 1/3 in the simulation studies in the next section. The determination of cR or cS for the final analysis at tk, however, uses the actual ntj or Γtj to evaluate the probability (19) or (22).
Similarly, for a given type II error probability α̃, the futility boundaries b̃R and b̃S for early stopping can be determined by using the fact that is approximately a normal random walk with mean 0 and variance nt under π1 − π0 = δ and that is approximately a normal random walk with mean 0 and variance Γ̃t under d(π̂t, eα, eβ, eγ) = η, where Γ̃t is the same as Γt but evaluated at the constrained maximum partial likelihood estimate under the constraint d(π̂t, eα, eβ, eγ) = η. As in the preceding paragraph, b̃R and b̃S can be chosen at the design stage by assuming k − 1 (or k − k0) standard normal increments zi in the random walk approximations to the boundary crossing probabilities. A software package to design and analyze the proposed phase II–III trial has been developed using R and is available at http://med.stanford.edu/biostatistics/ClinicalTrialMethodology.html
4.3. Simulation study of proposed test
Motivated by application in Section 4.1, we consider a maximum-duration trial with 4 years of accrual and additional 3 years of follow-up, with 80, 120, 160, and 160 patients entering the study uniformly within years 1, 2, 3, and 4, respectively. We generate response and survival data according to (1) and (4) with λ0(t) ≡ 0.35 and different values of (π0, π1, α, β, γ). For the proposed phase II–III design, five analyses are planned at the end of years 1, 2, 3, 5, and 7. Because all the patients have entered the study by the end of year 4 and hence there are no additional response data between the interim analysis at year 5 and the final analysis at year 7, the last analysis of the response data is at year 5, whereas the last analysis of the survival data is at year 7, if no early stopping has occurred previously. A planned interim analysis of survival at time t is suspended if is not yet rejected at time t, if the observed number of events at time t is less than 20, or if the increase in Γt from its value in the previous interim analysis is less than 20%. The stopping boundaries, using α = 0.05, α̃ = 0.01 for response and α̃ = 0.1 for survival, ε = 1/3, δ = 0.3, and η = 0.25, are bR = 3.058 and b̃R = 4.565 for response, assuming interim analyses with nominal nt = 80, 200, 360, and bS = 3.171 and b̃S = 2.517 that use (23) with k = 5 and k0 = 1. Note that if the survival time T given Z were generated from a PH model with constant hazard λ0 = 0.35 in the control group (Z = 0) and λ1 = 0.35 × 0.75 = 0.26 in the treatment group (Z = 1), the fixed-duration 7-year trial that performs a one-sided logrank test at the end of year 7 with α = 0.05 would have 88% power to detect a hazard ratio of 0.75.
The proposed phase II–III design is compared with two conventional designs of separate phase II and III trials with the same maximum duration and same maximum number of patients: (a) Simon’s single-arm two-stage design for phase II, with 28 patients, followed by a phase III study of 492 patients (denoted by II1 and III) and (b) a randomized phase II trial of 80 patients followed by a phase III study of 440 patients (denoted by II2 and III). In the phase II1 and III design, the Simon’s two-stage design for phase II has 10 patients at stage 1, with possible early stopping for futility if the observed number of responses is less or equal to 3, and a total of 28 patients at stage 2. If the observed number of responses out of 28 patients is greater than 12, a phase III trial with 3.65 years of accrual and 3 additional years of follow-up (total 492 patients) is initiated immediately, with three interim and one final analyses at calendar times (measured from the start of phase II study) 2, 3, 5, and 7 years. If the observed number of responses is less than or equal to 12, the phase III trial is abandoned for futility. In the phase II2 and III design, the phase II trial randomizes 80 patients in a 1:1 ratio to the two treatment groups, which gives 86% power to test π0 = 0.3 versus π1 = 0.6 at level α = 0.05, as noted in Section 4.1. The phase III trial has 3 years of accrual and 3 additional years of follow-up, with three interim and one final analyses at calendar times 2, 3, 5, and 7 years. In this simulation study, we assume for simplicity that the phase III trial is initiated immediately after phase II, although in reality, there is often a gap for starting up phase III trial. Both of these phase III trials use the conventional partial likelihood
| (24) |
which assumes a PH model for the distribution of T given Z, to define the following analog of (15):
| (25) |
where . The stopping boundaries of the modified Haybittle–Peto test based on (25) are bS = 2.997, b̃S = 2.355 using (23).
Table I gives the type I error probabilities pr(RS) and expected study duration E(T) for these three designs. Each result is based on 2000 simulations. Besides pr(RS), the table also gives the probability pr(R) of rejecting and the probability pr(R1) of rejecting in the first interim analysis for the phase II–III design. Table I shows that the phase II–III design maintains the nominal type I error probability 0.05 for the parameter vectors considered. When the true response rate of the control group is 0.6 instead of the assumed rate 0.3 (cases F and G), the phase II1 and III design has over 90% probability of falsely claiming improvement in response, because the single-arm Simon’s two-stage design for phase II1 assumes π0 to be 0.3 (Section 4.1) and therefore satisfies the probability constraint on incorrectly rejecting only when π0 ≤ 0.3. Note that this results in a much longer study duration than the other two designs because rejection of leads to conducting the subsequent phase III trial. The phase II1 and III and phase II2 and III designs have inflated type I error probability for cases D and E, in which the experimental treatment group does not improve survival over the control group and they use the logrank test even though survival curves of the treatment and control groups cross each other and d(π, ξ) < 0 (see Figure 1 for case E). Note that, in case E, the question ‘which treatment is better?’ has an answer that depends on the functional used to compare the survival curves in Figure 1(b).
Table I.
Type I error probabilities and expected study duration of three clinical trial designs: Simon’s two-stage design followed by a phase III trial (denoted by II1 and III), randomized phase II trial followed by a phase III trial (denoted by II2 and III), and the proposed phase II–III design.
| Case | π0 | π1 | eα | eβ | eγ | d(π, ξ) | Phase II1 and III
|
Phase II2 and III
|
Phase II–III
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pr(RS) | pr(R) | E(T) | pr(RS) | pr(R) | E(T) | pr(RS) | pr(R) | pr(R1) | E(T) | |||||||
| A | 0.3 | 0.3 | 1.0 | 1.00 | 1.0 | 0 | 0.002 | 0.045 | 0.39 | 0.002 | 0.048 | 1.22 | 0.000 | 0.014 | 0.006 | 1.59 |
| B | 0.3 | 0.3 | 0.5 | 1.00 | 1.0 | 0 | 0.004 | 0.047 | 0.43 | 0.002 | 0.058 | 1.25 | 0.002 | 0.019 | 0.011 | 1.62 |
| C | 0.3 | 0.6 | 1.0 | 1.00 | 1.0 | 0 | 0.048 | 0.911 | 4.32 | 0.040 | 0.859 | 4.76 | 0.049 | 0.994 | 0.645 | 4.98 |
| D | 0.3 | 0.6 | 0.2 | 1.56 | 1.0 | −0.05 | 0.134 | 0.903 | 4.67 | 0.104 | 0.849 | 5.15 | 0.022 | 0.984 | 0.646 | 3.94 |
| E | 0.3 | 0.6 | 0.2 | 1.73 | 0.8 | −0.10 | 0.142 | 0.913 | 4.61 | 0.133 | 0.844 | 5.01 | 0.008 | 0.979 | 0.654 | 3.54 |
| F | 0.6 | 0.6 | 1.0 | 1.00 | 1.0 | 0 | 0.036 | 0.914 | 4.27 | 0.002 | 0.046 | 1.21 | 0.002 | 0.021 | 0.012 | 1.73 |
| G | 0.6 | 0.6 | 0.5 | 1.00 | 1.0 | 0 | 0.051 | 0.911 | 4.65 | 0.002 | 0.048 | 1.21 | 0.002 | 0.016 | 0.007 | 1.70 |
Figure 1.
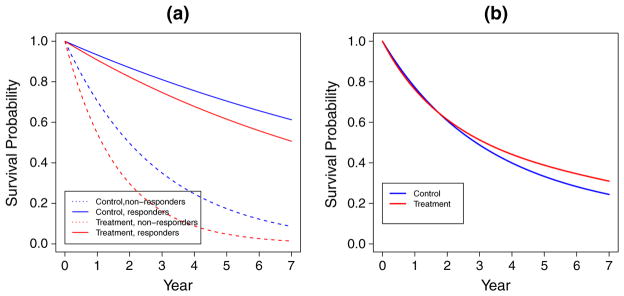
Survival curves for case E of Table I: (a) by treatment group and response status; (b) by treatment group.
Table II gives the power and expected study duration for the three designs under various parameter configurations that have a common d(π, ξ) value of 0.25. When the true response rates are equal to the assumed values (cases 1–6), the proposed phase II–III design generally has higher than or comparable power with the conventional designs and somewhat longer study duration. When the improvement in response is smaller than the assumed value (cases 7 and 8), the phase II1 and III and phase II2 and III designs have 35–45% probability of stopping the study prematurely at the end of the phase II1 or phase II2 trial, resulting in substantially lower power than the phase II–III design. In case 9, the phase II1 and III design has about 35% probability of failing to detect the improvement in response and hence stopping too early at the end of the phase II1 trial, the phase II2 and III design has 11% probability of not rejecting and therefore abandoning the phase III trial at the end of the phase II2 trial, whereas the phase II–III trial can continue testing for improvement in response throughout the course of the trial and has only 0.2% probability of not rejecting . This accounts for the substantially higher power of the phase II–III trial in case 9.
Table II.
Power and expected study duration of the three designs in Table I.
| Case | π0 | π1 | eα | eβ | eγ | d(π, ξ) | Phase II1 and III
|
Phase II2 and III
|
Phase II–III
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pr(RS) | pr(R) | E(T) | pr(RS) | pr(R) | E(T) | pr(RS) | pr(R) | pr(R1) | E(T) | |||||||
| 1 | 0.3 | 0.6 | 1.00 | 0.75 | 1.00 | 0.25 | 0.734 | 0.895 | 4.67 | 0.699 | 0.859 | 5.19 | 0.855 | 0.998 | 0.638 | 5.58 |
| 2 | 0.3 | 0.6 | 0.75 | 0.79 | 1.00 | 0.25 | 0.797 | 0.913 | 4.68 | 0.711 | 0.851 | 5.13 | 0.883 | 0.998 | 0.665 | 5.44 |
| 3 | 0.3 | 0.6 | 0.50 | 0.86 | 1.00 | 0.25 | 0.823 | 0.904 | 4.46 | 0.872 | 0.869 | 5.09 | 0.895 | 0.996 | 0.628 | 5.35 |
| 4 | 0.3 | 0.6 | 0.17 | 1.00 | 1.00 | 0.25 | 0.885 | 0.910 | 4.09 | 0.817 | 0.846 | 4.70 | 0.895 | 0.999 | 0.664 | 5.11 |
| 5 | 0.3 | 0.6 | 0.75 | 1.00 | 0.61 | 0.25 | 0.849 | 0.905 | 4.42 | 0.788 | 0.854 | 4.93 | 0.867 | 0.997 | 0.661 | 5.46 |
| 6 | 0.3 | 0.6 | 0.50 | 1.00 | 0.67 | 0.25 | 0.891 | 0.922 | 4.36 | 0.814 | 0.851 | 4.80 | 0.897 | 0.999 | 0.641 | 5.34 |
| 7 | 0.3 | 0.5 | 0.75 | 1.00 | 0.47 | 0.25 | 0.616 | 0.639 | 3.10 | 0.544 | 0.570 | 3.53 | 0.789 | 0.889 | 0.274 | 5.06 |
| 8 | 0.3 | 0.5 | 1.00 | 0.75 | 1.00 | 0.25 | 0.527 | 0.647 | 3.43 | 0.447 | 0.557 | 3.72 | 0.759 | 0.875 | 0.299 | 5.22 |
| 9 | 0.2 | 0.5 | 1.00 | 0.75 | 1.00 | 0.25 | 0.550 | 0.665 | 3.54 | 0.691 | 0.882 | 5.30 | 0.855 | 0.998 | 0.638 | 5.51 |
4.4. Comparison with Bayesian phase II–III design
There are three motivations for developing the proposed design as an alternative to the existing Bayesian versions. First, our method provides explicit control of the type I error rate. The Bayesian designs use simulations under certain assumed survival rates to control the type I error, but the assumptions may be too simplistic and unrealistic. Second, the functional used to compare the survival curves in the Bayesian method is the difference in mean lifetimes, which are not estimable in the presence of censoring without the parametric assumptions. Our method is semiparametric and involves the widely used PH model (4) for λ(· |Y, Z) that generalizes the parametric model in the Bayesian phase II–III design methodology. It uses another functional that involves the parameters π0, π1, α, β, γ and is estimable in the presence of censoring to compare the survival curves. Third, the Bayesian designs do not stop early due to futility in the binary response Y. Under the premise described in Section 2.2 that no effect on Y implies no effect on survival, considering futility stopping on the binary response Y yields much shorter trial durations under the response null. Thus, to compare our design with the Bayesian design under circumstances that favor the latter, we must depart from the central premise of our method and turn off futility stopping on Y.
To turn off futility stopping on Y, we consider instead of (7) the more restrictive null hypothesis
| (26) |
Note that is the same as in (12) but with the response constraint π0 < π1 removed. Therefore, the Haybittle–Peto–type test of in Section 3.2 can be readily modified by dropping the requirement of first rejecting before proceeding to test . To be more specific, we can again use the stopping criteria (16) and (18), but not (17), to test . We call this modified version of the design in Section 3.2 the ‘frequentist’ counterpart of the Bayesian design of Huang et al. [15]. Unlike the phase II–III design in Section 3.2, these two designs do not actually have a phase II component for testing the effect of treatment on the binary response. Strictly speaking, it is a phase III trial on the survival outcome, which involves the response rates via the parametric model (3) or the more general semiparametric model (4). Comparison of frequentist operating characteristics between the methods is complicated by this difference in what it means for one treatment to be ‘better than’ another. However, we can still compare our design with the Bayesian design when both functionals in the preceding paragraph identify the same treatment as the better one. We can then compare the designs on three figures of merit: the probability pr(S) of selecting the experimental treatment over the control, the expected study duration E(T), and the expected number of study subjects E(N). In particular, assuming exponential baseline survival, we perform the comparison for cases A–D, F, and G in Table I and cases 1–9 in Table II. Table III gives the values of pr(S), E(T), and E(N) in these cases, for the Bayesian phase II–III design of Huang et al. [15]. We compute these values from 2000 simulations using the R program available at the M.D. Anderson Cancer Center website (https://biostatistics.mdanderson.org/SoftwareDownload). We can compare pr(S) and E(T) with the corresponding values pr(RS) and E(T) of our phase II–III design in Tables I and II. The Bayesian phase II–III design has two options in the choice of randomization schemes. One uses the equal randomization (ER) that assigns equal probabilities to treatment and control. The other uses adaptive randomization (AR) whose assignment probabilities depend on past outcomes according to some Bayesian rule described in the program’s documentation. We consider both in Table III.
Table III.
Comparison of the Bayesian design of Huang et al. [15], using adaptive randomization (AR) or equal randomization (ER), with its frequentist counterpart.
| Case | Frequentist |
Bayesian AR |
Bayesian ER |
||||||
|---|---|---|---|---|---|---|---|---|---|
| pr(S) | E(T) | E(N) | pr(S) | E(T) | E(N) | pr(S) | E(T) | E(N) | |
| A | 0.047 | 5.00 | 453 | 0.040 | 6.73 | 508 | 0.039 | 6.76 | 510 |
| B | 0.046 | 4.57 | 458 | 0.049 | 6.65 | 505 | 0.036 | 6.77 | 511 |
| C | 0.049 | 5.00 | 454 | 0.039 | 6.75 | 507 | 0.064 | 6.62 | 501 |
| D | 0.025 | 3.94 | 399 | 0.436 | 5.20 | 426 | 0.169 | 6.33 | 488 |
| F | 0.052 | 5.14 | 458 | 0.030 | 6.78 | 510 | 0.059 | 6.61 | 502 |
| G | 0.045 | 4.13 | 416 | 0.067 | 6.56 | 501 | 0.040 | 6.69 | 508 |
| 1 | 0.852 | 5.52 | 482 | 0.674 | 5.22 | 439 | 0.812 | 4.63 | 415 |
| 2 | 0.878 | 5.50 | 483 | 0.787 | 4.60 | 404 | 0.860 | 4.34 | 398 |
| 3 | 0.906 | 5.32 | 477 | 0.855 | 3.97 | 367 | 0.862 | 4.25 | 395 |
| 4 | 0.898 | 5.15 | 476 | 0.976 | 2.50 | 258 | 0.831 | 4.00 | 372 |
| 5 | 0.868 | 5.50 | 484 | 0.945 | 3.61 | 352 | 0.969 | 3.48 | 351 |
| 6 | 0.879 | 5.39 | 481 | 0.977 | 3.03 | 308 | 0.979 | 3.46 | 349 |
| 7 | 0.853 | 5.45 | 479 | 0.987 | 3.21 | 332 | 0.991 | 3.28 | 347 |
| 8 | 0.855 | 5.51 | 482 | 0.686 | 5.15 | 438 | 0.803 | 4.63 | 418 |
| 9 | 0.864 | 5.53 | 480 | 0.701 | 4.81 | 410 | 0.812 | 4.38 | 397 |
The baseline survival distribution is Exponential with hazard rate λ0(t) = 0.35.
Table III shows that under the null cases (cases A–D, F, and G), the Bayesian ER and AR designs have approximately 0.05 probability of selecting the experimental treatment over the control except for case D, but both designs have longer expected study durations and larger expected sample sizes than the frequentist counterpart. As expected, the contrast is even more marked in the comparison with the proposed phase II–III design in Section 3.2 (Table I), which takes advantage of futility stopping on Y. Under the alternative cases (cases 1–9), the Bayesian ER and AR designs have smaller expected sample sizes and shorter expected durations than the frequentist counterpart, but except for cases 4–7, they have lower power than the frequentist counterpart whose power is over 85% in all the alternative cases.
Instead of using the same exponential baseline distribution as in Tables I, II, and III, Table IV provides parallel results when the baseline distribution is Weibull with hazard function λ0(t) = 0.45t0.8. Under the null cases, the Bayesian AR design fails to control the type I error. The Bayesian ER design has better control of the type I error, which, however, is still inflated to over 20% in case D. Moreover, the expected sample size and duration are considerably larger than the frequentist counterpart in all null scenarios.
Table IV.
Comparison of the Bayesian design of Huang et al. [15], using adaptive randomization (AR) or equal randomization (ER), with its frequentist counterpart.
| Case | Frequentist |
Bayesian AR |
Bayesian ER |
||||||
|---|---|---|---|---|---|---|---|---|---|
| pr(S) | E(T) | E(N) | pr(S) | E(T) | E(N) | pr(S) | E(T) | E(N) | |
| A | 0.049 | 4.97 | 462 | 0.221 | 5.23 | 446 | 0.018 | 6.90 | 517 |
| B | 0.050 | 4.48 | 445 | 0.220 | 5.37 | 450 | 0.015 | 6.95 | 518 |
| C | 0.050 | 4.87 | 456 | 0.368 | 5.07 | 431 | 0.027 | 6.84 | 514 |
| D | 0.018 | 3.88 | 407 | 0.900 | 3.09 | 318 | 0.231 | 6.36 | 503 |
| F | 0.040 | 4.99 | 460 | 0.197 | 5.54 | 463 | 0.021 | 6.84 | 514 |
| G | 0.033 | 4.06 | 424 | 0.205 | 5.61 | 466 | 0.016 | 6.95 | 519 |
| 1 | 0.909 | 5.45 | 489 | 0.995 | 2.68 | 286 | 0.981 | 4.82 | 451 |
| 2 | 0.932 | 5.28 | 487 | 0.998 | 2.51 | 273 | 0.988 | 4.55 | 440 |
| 3 | 0.938 | 5.10 | 482 | 1.000 | 2.39 | 257 | 0.958 | 4.54 | 439 |
| 4 | 0.927 | 5.02 | 481 | 0.997 | 2.27 | 242 | 0.857 | 4.52 | 441 |
| 5 | 0.918 | 5.09 | 487 | 1.000 | 2.34 | 254 | 1.000 | 3.91 | 418 |
| 6 | 0.934 | 5.10 | 481 | 0.999 | 2.32 | 251 | 0.999 | 3.93 | 421 |
| 7 | 0.914 | 5.35 | 487 | 0.998 | 2.69 | 298 | 1.000 | 4.07 | 434 |
| 8 | 0.908 | 5.41 | 488 | 0.990 | 3.00 | 321 | 0.982 | 4.89 | 456 |
| 9 | 0.912 | 5.43 | 487 | 0.995 | 2.85 | 306 | 0.986 | 4.82 | 453 |
The baseline survival distribution is Weibull with hazard function λ0(t) = 0.45t0.8.
5. Discussion
Treatments showing promise in single-arm phase II studies often do not show clinical benefit in subsequent phase III studies, which are carried out at great cost in patient exposure to side effects, time and money, and lost opportunity to pursue other treatments. Reasons for the failure to detect nonperforming treatments in single-arm phase II studies include inadequate and nonpredictive preclinical models, over-reliance on historical controls (despite questionable comparability of historical controls and uncertainty of control rate estimates), biomarkers that have not been validated, and the uncertain relationship of early response and long-term clinical outcomes. It has been suggested that randomized phase II trials, either after or instead of single-arm trials, should be an important intermediate step in the clinical development process, which culminates in randomized phase III trials. But the information value of the response outcome is discarded in the conventional phase III trials, and this has motivated the Bayesian approach [14–16] that combines the response and time-to-event data in a mixture model. In this article, we provide an alternative method on the basis of conventional survival analysis (Cox PH models) and GLR hypothesis testing in an optimal group sequential design. Our method does not require parametric modeling of the survival times and uses a natural summary of the data to describe departures from the null treatment effect. It offers another option for investigators who would prefer a semiparametric approach, which is perhaps more familiar to consumers of trial information (including regulatory agencies). We note that the PH assumption in our model could (and should) be checked in existing databases of treatment trials of the same tumor type and similar drugs to the one being tested, if such data are available. Furthermore, we emphasize that our approach (and also the Bayesian approach) is based on the knowledge of a binary early outcome that is suitable for the go/no-go decision because it carries information on the distribution of time to event on the two treatment arms.
As measurement of response improves, one can expect that the relationship between response and clinical outcome will strengthen. In particular, the science underlying targeted therapies promises great strides toward the goal of early biological markers of long-term success or failure. Thus, the utility of response indicators should only increase in the future. As they become more accurate, the value of modeling them with survival data in phase III trials will grow apace. The availability of mixture-based approaches, such as the Inoue–Thall–Berry Bayesian approach and the standard semiparametric approach described in this article, may encourage investigators to take advantage of the response information. In addition, we hope that it will encourage a more coherent approach to therapeutic development. Instead of waiting for success in a randomized phase II trial before designing a definitive phase III trial, investigators can propose a definitive trial that stops early for futility. Funding, recruitment of sites, and other logistical issues can be addressed ‘just in time’, as the interim milestones are achieved.
The availability of statistical methods to support such trials may encourage funding agencies and sponsors to think more strategically about planning trials. One way to speed up the clinical development process is to eliminate or shorten the ‘stop and start’ dead time between phases II and III. If investigators come to think that a randomized phase II–III trial that is progressing satisfactorily will likely be extended to its full size, they will be encouraged to begin randomizing earlier. We anticipate that such changes will be forced on the field by the inefficiencies of the current development process, which is breaking down in the face of the throng of targeted therapies that clamor for clinical testing.
The PH model (4) can be readily extended to include covariates Xi, or even more general time-varying covariates Xi(t) to account for possible time variations in (4), as follows:
An important special case related to the emerging field of biomarker-guided personalized therapies is binary Xi, taking the value 1 or 0 according to whether the ith patient belongs to the biomarker-positive subgroup. In this setting, π0 and π1 should be allowed to depend on Xi, leading to four parameters πj,x (j = 0, 1; x = 0, 1). These extensions and their applications are presented elsewhere, but we want to point out here the ubiquity of the mixture survival model and the versatility of the methodology to handle it (Section 3).
Acknowledgments
The National Cancer Institute grant 1 P30 CA124435-01 (T. L. Lai and P. Lavori), the National Science Foundation grant DMS-0805879 (T. L. Lai), the Clinical and Translational Science Award 1UL1 RR025744 for the Stanford Center for Clinical and Translational Education and Research (Spectrum) from the National Center for Research Resources, National Institute of Health, and the U.S. Department of Veterans Affairs Cooperative Studies Program (M-C. Shih) partly supported this research. The authors thank Balasubramanian Narasimhan of Stanford University for developing the software at the Center for Innovative Study Design website mentioned in Section 4. They also thank Johann Won and Pei He for the assistance and the comments.
APPENDIX A
First, consider the case where S(t) = e−λt, as in the Inoue–Thall–Berry model (1)–(3), with λ0,0 = λ. The log survival function for the control group given by (5) reduces to
| (A1) |
as a → 1, by a Taylor’s series expansion as a function of a around a = 1. Similarly, as ac → 1, the log survival function reduces to
| (A2) |
Therefore, as a → 1 and c → 1, the hazard ratio of treatment to control at every fixed t is
More generally, we can use Taylor’s theorem to obtain that at every fixed t with S(t) > 0, (S(t))a = ea log S(t) ≈ S(t) + (a − 1)(log S(t))S(t) as a → 1, and thereby generalize (A1) to
as a → 1. Similarly, as ac → 1, we can generalize (A2) to
It then follows from (5) that at every fixed t with S(t) > 0,
as a → 1 and c → 1. Moreover, b(π1ac + 1 − π1)/(π0a + 1 − π0) = 1 − d(π, ξ)(1 + o(1)).
References
- 1.El-Maraghi RH, Eisenhauer EA. Review of phase II trial designs used in studies of molecular targeted agents: outcomes and predictors of success in phase III. Journal of Clinical Oncology. 2008;26:1346–1354. doi: 10.1200/JCO.2007.13.5913. [DOI] [PubMed] [Google Scholar]
- 2.Chan JK, Ueda SM, Sugiyama VE, Starve CD, Shin JY, Monk BJ, Sikic BI, Osann K, Kapp DS. Analysis of phase studies on targeted agents and subsequent phase III trials: what are the predictors for success? Journal of Clinical Oncology. 2008;26:1511–1518. doi: 10.1200/JCO.2007.14.8874. [DOI] [PubMed] [Google Scholar]
- 3.Simon R. Optimal two-stage designs for Phase II clinical trials. Controlled Clinical Trials. 1989;10:1–10. doi: 10.1016/0197-2456(89)90015-9. [DOI] [PubMed] [Google Scholar]
- 4.Jung S-H, Lee T, Kim K, George SL. Admissible two-stage designs for phase II cancer clinical trials. Statistics in Medicine. 2004;23:561–569. doi: 10.1002/sim.1600. [DOI] [PubMed] [Google Scholar]
- 5.Banerjee A, Tsiatis AA. Adaptive two-stage designs in phase II clinical trials. Statistics in Medicine. 2006;25:3382–3395. doi: 10.1002/sim.2501. [DOI] [PubMed] [Google Scholar]
- 6.Vickers AJ, Ballen V, Scher HI. Setting the bar in Phase III trials: the use of historical data for determining “Go/No Go” decision for definitive Phase II trials. Clinical Cancer Research. 2007;13:972–976. doi: 10.1158/1078-0432. CCR-06-0909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kola I, Landis J. Can the pharmaceutical industry reduce attrition rates? Nature Reviews. 2004;3:711–715. doi: 10.1038/nrd1470. [DOI] [PubMed] [Google Scholar]
- 8.Ratain MJ, Sargent DJ. Optimising the design of phase II oncology trials: the importance of randomisation. European Journal of Cancer. 2009;45:275–280. doi: 10.1016/j.ejca.2008.10.029. [DOI] [PubMed] [Google Scholar]
- 9.Rubinstein L, Crowley J, Ivy P, LeBlanc M, Sargent D. Randomized phase II designs. Clinical Cancer Research. 2009;15:1883–1890. doi: 10.1158/1078-0432.CCR-08-2031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wittes J, Brittain E. The role of internal pilot studies in increasing efficiency of clinical trials. Statistics in Medicine. 1990;9:65–72. doi: 10.1002/sim.4780090113. [DOI] [PubMed] [Google Scholar]
- 11.Bartroff J, Lai TL. Efficient adaptive designs with mid-course sample size adjustment in clinical trials. Statistics in Medicine. 2008;27:1593–1611. doi: 10.1002/sim.3201. [DOI] [PubMed] [Google Scholar]
- 12.Thall PF, Simon R, Ellenberg SS. Two-stage selection and testing designs for comparative clinical trials. Biometrika. 1988;75:303–310. [Google Scholar]
- 13.Ellenberg SS, Eisenberger MA. An efficient design for Phase III studies of combination chemotherapies (with discussion) Cancer Treatment Reports. 1985;69:1147–1154. [PubMed] [Google Scholar]
- 14.Inoue LYT, Thall PF, Berry DA. Seamlessly expanding a randomized Phase II trial to Phase III. Biometrics. 2002;58:823–831. doi: 10.1111/j.0006-341x.2002.00823.x. [DOI] [PubMed] [Google Scholar]
- 15.Huang X, Ning J, Li Y, Estay E, Issa J-P, Berry DA. Using short-term response information to facilitate adaptive randomization for survival clinical trials. Statistics in Medicine. 2009;28:1680–1689. doi: 10.1002/sim.3578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Thall PF. A review of phase 2–3 clinical trial designs. Lifetime Data Analysis. 2008;14:37–53. doi: 10.1007/s10985-007-9049-x. [DOI] [PubMed] [Google Scholar]
- 17.Jennison C, Turnbull BW. Efficient group sequential designs when there are several effect sizes under consideration. Statistics in Medicine. 2006;25:917–932. doi: 10.1002/sim.2251. [DOI] [PubMed] [Google Scholar]
- 18.Lai TL, Shih MC. Power, sample size and adaptation considerations in the design of group sequential clinical trials. Biometrika. 2004;91:507–528. [Google Scholar]
- 19.Gu M, Lai TL. Repeated significance testing with censored rank statistics in interim analysis of clinical trials. Statistica Sinica. 1998;8:411–428. [Google Scholar]
- 20.Tannock IF, de Wit R, Berry WR, et al. Docetaxel plus prednisone or mitoxantrone plus prednisone for advanced prostate cancer. New England Journal of Medicine. 2004;351:1502–1512. doi: 10.1056/NEJMoa040720. [DOI] [PubMed] [Google Scholar]
- 21.Petrylak DP, Tangen CM, Hussain MH, et al. Docetaxel and estramustine compared with mitoxantrone and prednisone for advanced refractory prostate cancer. New England Journal of Medicine. 2004;351:1513–1520. doi: 10.1056/NEJMoa041318. [DOI] [PubMed] [Google Scholar]
- 22.Smith MR, Kabbinavar F, Saad F, et al. Natural history of rising serum prostate-specific antigen in men with castrate nonmetastatic prostate cancer. Journal of Clinical Oncology. 2005;23:2918–2925. doi: 10.1200/JCO.2005.01.529. [DOI] [PubMed] [Google Scholar]
- 23.Jennison C, Turnbull BW. Group Sequential Methods with Applications to Clinical Trials. Chapman and Hall/CRC; London: 2000. [Google Scholar]
- 24.Siegmund DO. Sequential Analysis: Tests and Confidence Intervals. Springer; New York: 1985. [Google Scholar]
- 25.Bilias Y, Gu M, Ying Z. Towards a general asymptotic theory for Cox model with staggered entry. Annals of Statistics. 1997;25:662–682. [Google Scholar]


