From one generation to the next: a comprehensive account of sympathetic receptor control in branching arteriolar trees

Abstract

The effect of the sympathetic nervous system on blood flow distribution within skeletal muscle microvasculature is conditional upon regional activation of receptors for sympathetic neurotransmitters. Previous studies have shown that proximal arterioles are largely governed by adrenergic activation, whereas it is speculated that distal branches are controlled by peptidergic and purinergic activation. However, no study has systematically evaluated the activation of adrenergic, peptidergic and purinergic receptors in continuously branching arteriolar trees of an individual skeletal muscle model. Therefore, in the present study, sympathetic agonists were used to evaluate the constriction responses along first to fifth order arterioles in continuously branching arteriolar trees of a in vivo rat gluteus maximus muscle preparation with respect to specific activation of receptors for sympathetic neurotransmitters (α1R, α2R, NPY1R and P2X1R). Constriction responses were incorporated into a mathematical blood flow model to estimate the total flow, resistance and red blood cell flow heterogeneity within a computationally reconstructed gluteus maximus arteriolar network. For the first time, the effects of activating receptors for sympathetic neurotransmitters on vasoconstrictor responses and the ensuing haemodynamics in continuously branching arteriolar trees of skeletal muscle were characterized, where proximal arterioles responded most to α1R and α2R adrenergic activation, whereas distal arterioles responded most to Y1R and P2X1R activation. Total flow and resistance changed with activation of all receptors, whereas red blood cell flow heterogeneity was largely affected by peptidergic and purinergic activation in distal arterioles. The reported data highlight the functional consequences of topologically-dependent sympathetic control and may serve as novel input parameters in computational modelling of network flow.

Key points

• The sympathetic nervous system increases skeletal muscle arteriolar resistance by activating adrenergic, peptidergic and purinergic receptors, which may depend on network topology.

• To date, there has been limited work conducted on topologically-dependent sympathetic nervous system control in continuously branching skeletal muscle microvascular networks.

• In the present study, we investigated how arterioles respond to activation of receptors for sympathetic neurotransmitters based on their location within continuously branching arteriolar trees in skeletal muscle.

• For the first time, we show differential order-dependent responses to adrenergic, peptidergic and purinergic agonists in continuously branching arteriolar trees.

• These results provide novel and detailed network data describing full-range sympathetic control in the skeletal muscle microcirculation. This work provides much needed experimental data, which can be applied to mathematical models of skeletal muscle blood flow and oxygen transport.

Introduction

The sympathetic nervous system) (SNS) promotes tonic vasoconstriction in skeletal muscle microvascular beds (Clifford & Hellsten, 2004; Segal, 2005) via neuronal release of noradrenaline (NA), neuropeptide Y (NPY) and ATP, which act on their respective receptors (i.e. α1R and α2R, Y1R and P2X1R) located extraluminally on arteriolar vascular smooth muscle cells (Kiowski et al. 1983; Ruffolo et al. 1991; Malmstrom et al. 1997; Burnstock, 2007). Vasoconstriction to SNS stimulation varies among arterioles as a result of arteriolar size and branch order (Marshall, 1982; Boegehold & Johnson, 1988; Dodd & Johnson, 1991). Arteriolar network geometry (i.e. topology) is a primary determinant of baseline network resistance (Pries et al. 1995); therefore, the acute control of arteriolar diameter must co-ordinate with topology to effectively regulate microvascular blood flow and red blood cell (RBC) distribution.

Past and recent investigators of α-adrenoreceptor (i.e. α1R and α2R) arteriolar control of the rat cremaster (Faber, 1988; Ohyanagi et al. 1991) and mouse gluteus maximus (GM) muscle (Moore et al. 2010) concluded that proximal arterioles, namely first order (1A) to third order (3A), are dominated by adrenergic control. This is in contrast to both NPY (Ekelund & Erlinge, 1997) and ATP (Gitterman & Evans, 2000), where peak responses have been reported to act at the distal pre-capillary terminal arterioles. However, the scope of such studies is limited because previous experimental approaches enabled the interrogation of partial networks (i.e. 1A to 3A arterioles at best) or discrete vessels. In an attempt to understand how the SNS regulates blood flow distribution in skeletal muscle microvasculature, the development of a preparation with access to complete branching arteriolar trees is necessary. To date, no studies have systematically and comprehensively defined the relationship between arteriolar order, differential activation of receptors for sympathetic neurotransmitters and haemodynamics in skeletal muscle networks.

We recently developed a novel rat GM preparation (Al-Khazraji et al. 2012) adapted from the mouse (Bearden et al. 2004) that enables the investigation of sympathetic control in complete branching arteriolar trees. The study aimed to characterize topologically-dependent SNS modulation along arteriolar trees in the rat GM and to investigate the consequent haemodynamics. Thus, the objectives were to: (1) systematically determine the arteriolar responses to activation of specific receptors for sympathetic neurotransmitters as a function of branch order (i.e. from 1A to 5A) and (2) input these responses into an in-house developed computational blood flow model to estimate the functional consequence(s) of order-dependent sympathetic control on total blood flow and red blood cell distribution within the arteriolar tree. We predict that adrenergic control will be greatest in proximal arterioles, with progressive attenuation with increasing arteriolar order. Conversely, we predict that peptidergic and purinergic control will be greatest in distal arterioles, with progressive attenuation with decreasing arteriolar order. Finally, we anticipate that theoretical estimates of haemodynamic consequences will differ based on predicted topologically-dependent SNS control.

Methods

Animal care and use

Experimental protocols were approved by The Council on Animal Care at the University of Western Ontario. Experiments were performed using 27 male Sprague–Dawley rats (aged 6–7 weeks; mean ± SD mass: 170 ± 12 g), purchased from Charles River Laboratories (Saint-Constant, Quebec, Canada) and housed on site for at least 1 week prior to the study. Rats were housed in animal care facilities of the University of Western Ontario under a 12:12 h light/dark cycle at 24°C with access to food and water ad libitum. At the end of the experiment, the anaesthetized rat was killed with an overdose of α-chloralose and urethane cocktail mix (i.p. injection) and cervical dislocation.

Anaesthesia and skeletal muscle preparation

A more detailed description is provided elsewhere (Al-Khazraji et al. 2012). Briefly, the rat was anaesthetized with a cocktail of α-chloralose (80 mg kg⁻¹) and urethane (500 mg kg⁻¹) using i.p. injection. The fur of the neck and lower back region was shaved, and the animal was tracheotomized and cannulated in both the jugular (for continuous i.v. drug delivery) and the carotid (for blood pressure recordings). Temperature was maintained at 37°C (rectal probe) using a customized temperature-controlled platform. With the animal shaved and the skin prepared, and under microscopic guidance, the GM muscle was cut from its origin along the spine and along its rostral and caudal borders. Taking great care taken to preserve its neurovascular supply, the muscle flap was gently reflected away from the rat, spread evenly onto a transparent (Sylgard 184; Dow Corning, Midland, MI, USA) pedestal to approximate in situ dimensions and pinned to secure edges. The exposed tissue was superfused continuously (4–5 ml min⁻¹) with bicarbonate-buffered PSS (35°C at tissue, pH 7.4) of composition (mm): 137 NaCl, 4.7 KCl, 1.2 MgSO₄, 2 CaCl₂ and 18 NaHCO₃ and then equilibrated with 5% CO₂ ⁄ 95% N₂ gas.

Intravital video microscopy (IVVM)

Upon completion of microsurgical procedures, the preparation was transferred to the stage of the intravital microscope (Olympus BX51; Olympus, Tokyo, Japan). The preparation was equilibrated for ∼30 min, during which time the arteriolar network was observed for experimental sites of observation (vasomotion was not observed). Microvessels were imaged under Kohler illumination using a long working distance condenser (NA = 0.80) and a long working distance water immersion objective (Olympus LUMPLFL: 10× NA = 0.30; depth of field ∼9 μm) with illumination from a 100 W halogen light source. The optical image was coupled to an EMCCD camera (Rolera EMC²; Qimaging, Surrey, BC, Canada), viewed using specialized imaging software (MetaMorph, version 7.6; Molecular Devices Inc., Sunnyvale, CA, USA) and stored on a hard drive for offline analysis. Following equilibration, the baseline internal vessel lumen diameter was recorded and arterioles were tested for oxygen sensitivity by elevating superfusate O₂ from 0% to 21% (5% CO₂, balance N₂) for 5 min and recording the arteriolar diameter (Table1). Equilibration with 5% CO₂–95% N₂ was restored for the duration of the experimental procedures. Bright-field video (tiff) images were collected (17 fps) under Kohler bright-field illumination for offline analysis of internal vessel lumen diameters using ImageJ (NIH, Bethesda, MD, USA) (Schneider et al. 2012).

Table 1.

Summary values (mean ± SEM) for luminal diameters at five arteriolar orders

Arteriolar	Baseline	O2 response	SNP
order	diameter (μm)	(μm)	response(μm)
1A	93 ± 2	–11 ± 1	24 ± 3
2A	70 ± 2	–9 ± 1	22 ± 3
3A	55 ± 1	–8 ± 1	22 ± 2
4A	42 ± 1	–7 ± 1	12 ± 1
5A	35 ± 1	–5 ± 1	11 ± 1

Responses are reported as change (O₂ response = D_O2 – D_Baseline; SNP response = D_SNP - D_Baseline) from baseline values.

Preparation and delivery of agonists and antagonists

All working solutions of drugs were prepared fresh daily and dissolved in the gassed and warmed PSS solution. The highest dose of drug was initially prepared, followed by preparation of the other concentrations of drug using a dilution series with logarithmic increments (dissolved in gassed PSS). Each concentration level was independently stored in its own tightly-sealed storage bottle, and placed in a heated water bath to maintain solution temperature of 37°C. Two water jacketed reservoir units (Radnoti LLC, CA, USA) were set up: (1) one provided warmed and gassed PSS that was gravity fed from a larger reservoir bottle and (2) the other was used only for drug delivery. Each solution was then poured into the heated reservoir unit, and was topically applied to the preparation via a gravity feed. Once the arteriolar responses for a given drug concentration were recorded, the solution in the reservoir was replaced with the next highest dose of drug solution. This procedure was repeated throughout concentration–response determinations. All solutions were pre-gassed prior to mixture and received continuous bubbling of gas within the chamber to ensure continuous and homogenous gassing of the solution. For treatment with antagonists, the desired concentration was similarly prepared as a combined solution of agonist and antagonist.

Experimental protocols

Protocol 1: regional activation of α1R, α2R, Y1R and P2X1R

Five groups of animals were used to evaluate arteriolar responses to phenylephrine (PE; α1R specific agonist; Sigma–Aldrich, St Louis, MO, USA), UK 14304 (α2R specific agonist; Tocris Biosciences, St Louis, MO, USA), neuropeptide Y (NPY; Tocris Biosciences) and ATP (Sigma-Aldrich). ATP has been shown to exhibit both vasoconstrictor (via P2X1R activation; Hopwood & Burnstock, 1987) and vasodilatator (Hellsten et al. 1998) effects; therefore, in an attempt to isolate ATP-mediated vasoconstriction (Buckwalter et al. 2004), we conducted a separate set of experiments with a fifth group of animals receiving α,β-methylene ATP (αβ-meATP; potent P2X1 receptor agonist; Sigma–Aldrich), a stable non-degradable ATP analogue. All experiments were conducted in the rat GM arteriolar network, with one agonist evaluated per animal. Arteriolar responses were recorded at log increments (PE: 10⁻⁹ to 10⁻⁴ m; UK 14304: 10⁻⁹ to 10⁻⁵ m; NPY: 10⁻¹³ to 10⁻⁸ m; ATP: 10⁻⁹ to 10⁻⁴ m; αβ-meATP: 10⁻⁹ to 10⁻⁵ m) and were evaluated when the diameter responses stabilized and remained static for a minimum of 5–10 min.

Protocol 2: selectivity of α1R, α2R, Y1R and P2X1R agonists

To confirm specific functional responses to agonists, agonist data were also collected in the face of specific receptor antagonist delivery (α1R antagonist: prazosin at 2 × 10⁻⁸ m; α2R antagonist: yohimbine at 10⁻⁶ m; Y1R antagonist: BIBP3226 at 2 × 10⁻⁸ m; and P2X1R antagonist: NF023 at 10⁻⁶ m). Concentrations of antagonists were selected based on pilot work conducted in our laboratory that showed the successful blockade at EC₅₀ values of agonist.

Selection of agonist concentrations

In all cases, the concentrations selected for each agonist application ranged from physiological resting levels to supraphysiological levels in an attempt to maximize constriction responses. The ranges selected for PE and UK 14304 were based on resting plasma levels of noradrenaline (1–4 nm; Mortensen et al. 2012) and high intensity exercise (∼50 nm; Stratton & Halter, 1985). The range selected for NPY concentrations were from resting conditions (∼1 pm) to high physiological stress such as high intensity exercise (10 pm) or vaginal birth delivery (∼10 nm) (Hirsch & Zukowska, 2012). In an attempt to characterize the baseline activity of ATP as a vasoconstrictor (Galligan et al. 2001; Gitterman & Evans, 2001; Erlinge & Burnstock, 2008), as well as its role in vasodilatation as seen in exercise concentrations (2 μm; Hellsten et al. 1998), we selected ATP concentrations that represented interstitial skeletal muscle levels ranging from resting conditions (∼100 nm; Mortensen et al. 2011) to those noted during heavy exercise (Hellsten et al. 1998). The range selected for αβ-meATP encompassed the above ATP range and is similar to the range employed in a previous study (Buckwalter et al. 2004).

Experimental data collection

Arteriolar responses at varying branch orders (from 1A to 5A) were recorded at each log increment of agonist concentration. The tissue was then superfused with PSS and arteriolar diameters were restored to that of baseline. Finally, maximal diameter responses to superfused sodium nitroprusside (SNP) (10⁻⁵ m) were recorded (Table1). At baseline and during all drug interventions, continuously branching sets of arteriolar trees were scanned and imaged from 1A to 5A. Next, the same arteriolar tree was scanned and imaged from 5A to 1A to confirm that vessel responses were stable and that there were no temporally-dependent alterations in responses during image scans. The total scanning/imaging time (1A to 5A, then from 5A to 1A) was under 30 s. In all cases, the responses at the beginning and end of imaging did not differ, indicating that there were no changes in responses over the scanning period.

Tissue viability and inclusion criteria

Preparations were evaluated for oxygen sensitivity as a means to test for vascular responsiveness. In addition, responses to oxygen and SNP were used as a metric (independent of the tested variables) to determine repeatability between preparations. Results from preparations that did not respond to either oxygen or SNP were not included in the data. All 27 animals used in the present study responded physiologically to both O₂ and SNP (Table1).

Arteriolar order classification

The arteriolar network was classified using the centrifugal arteriolar classification method (Ellsworth et al. 1987): 1A was set as the first bifurcation coming off the feed vessel that entered the proximal end of the tissue. Each subsequent large bifurcation was classified as the next generation of arterioles (e.g. 2A daughter vessels bifurcated off a 1A vessel, etc.) (Wiedemann, 1962; Boegehold & Johnson, 1988; Moore et al. 2010). To normalize arteriolar order classification across experiments and to avoid bias, the following criteria were used to define changes in branch order: (1) the branch angle between two arterioles at a bifurcation was less than 90° and greater than 15°; (2) bifurcations coming off of 1A to 3A did not bifurcate directly into a capillary bed but, instead, gave rise to another bifurcation (i.e. a bifurcation coming off a 3A is labelled as a 4A arteriole and should give rise to 5A vessels, instead of a capillary bed); and (3) the diameters of the two arterioles at a bifurcation were less than 80% of parent vessel diameter. As reported in other studies (Murrant & Sarelius, 2000), the larger bifurcations (1A to 3A) of the GM preparation were observed to be paired with the venular tree, whereas the smaller orders (4A to 5A) did not run alongside the venular tree.

In an attempt to ensure that only continuously branching arteriolar trees were analysed, we outlined the arteriolar tree considered for observation and subsequent analysis using the criteria: (1) each order must give rise to a subsequent interconnected series of bifurcations (i.e. a tree was outlined by selecting a 1A that is followed by 2A, etc., until 5A) and (2) similarly, each order, with the exception of 1A, must have bifurcated in line with a parent vessel that was within the same connected series of arterioles. For example, 4A vessel data were only accepted if the 4A bifurcation originated from a 3A vessel included in the original chosen arteriolar tree path.

Computational modelling

Computational modelling is useful for integrating measurements of diameter changes at various levels in the arteriolar tree when aiming to determine the resulting changes in overall network resistance and blood flow (Pries et al. 1994). This is particularly important when seeking to compare the overall effects of SNS receptor activation between proximal and distal arterioles. Modelling is also useful for determining how measured diameter changes co-ordinate to alter flow distribution within the arteriolar tree, which requires having an accurate representation of in vivo network geometry. Thus, in an attempt to estimate the haemodynamic consequences arising from SNS receptor activation along the branching arteriolar tree network, we incorporated our experimental findings into a computational flow model developed in-house.

We consistently observed high network homology across all rat GM preparations; thus, our model was developed from a single rat GM preparation that represented the topological mean of all experimental animals observed at baseline. Certainly, network homology has been reported in the mouse GM preparation (Bearden et al. 2004). For blood flow simulations, arteriolar tree geometry was determined from vascular reconstructions using IVVM image montages of the rat GM and consisted of 27 unbranched vessels. The arteriolar tree was discretized into 111 segments with a mean length of 33 μm and blood flow was calculated assuming a fixed pressure drop (18 mmHg) between the inlet segment (1A arteriole) and all the outlet segments (4A and 5A arterioles). At the inlet segment, the discharge haematocrit was set to 0.42 (the normal value for blood sample haematocrit). Arteriolar orders were mathematically determined to best represent the ordering scheme used in the experimental analysis (with order increasing at bifurcations when a vessel had a diameter <80% of parent, or a bifurcation angle >15°).

A previously described two-phase (RBCs and plasma) continuum blood flow model was used (Goldman & Popel, 2000, 2001). Based on the in vivo rheological model of Pries et al. (1990, 1994), the two-phase continuum flow model was used to calculate the steady-state distribution of total blood flow (Q) and discharge haematocrit (H_D) throughout the arteriolar tree. The flow model uses conservation equations for blood and RBC volume flow into each node j:

where each vessel segment ij is labelled by its end nodes and the sums are over all nodes i connected to node j. The flow in segment ij is given by the pressure difference (Δp_ij) along the segment divided by the hydrodynamic resistance of the segment. The pressure–flow relationship is described by:

where L and R are the length and radius of the vessel segment being considered, μ_pl is the viscosity of plasma, and μ_rel is the relative viscosity of blood in that segment, which depends on both radius and haematocrit (Fahraeus–Lindqvist effect; Pries et al. 1990). The non-linear relationship between RBC flow distribution at vessel bifurcations and overall blood flow distribution (plasma skimming effect; Pries et al. 1994; Goldman & Popel, 2000) is also included in the model. The non-linear rheological effects included in the model make it necessary to solve the steady-state equations using an iterative method (Pries et al. 1994; Goldman & Popel, 2000). For the arteriolar geometries considered, the Matlab (MathWorks Inc., Natick, MA, USA) flow simulation code typically required ∼30 steps and <10 s to converge to a fixed solution for all node pressures, segment flows and haematocrits.

For baseline blood flow calculations, the arteriolar diameters used in the model were those measured under control conditions (i.e. in the absence of any SNS agonists or antagonists in the superfusion solution). In a separate set of experiments (n = 39 vessels), the computational model was validated against in vivo blood flow measurements, using the ‘streak length’ method (Al-Khazraji et al. 2012), in continuously branching arteriolar trees from the rat GM preparation under baseline control conditions.

To computationally determine haemodynamic consequences from the experimental data, constriction levels for the various cases were input into the model as a function of both vessel order and drug concentration (evaluated from in vivo changes in constriction at PE, UK 14304, ATP at 10⁻⁹ to 10⁻⁶ m and NPY at 10⁻¹³ to 10⁻¹⁰ m). These data were used to alter diameters throughout the model arteriolar tree, based on a vessel ordering consistent with the experimental approach, and then the flow model described above was used to calculate the resulting haemodynamics. Total network flow, resistance and RBC flow heterogeneity (coefficient of variation of RBC volume flow; i.e. SD divided by the mean) at each order were calculated for the given reconstructed network.

Statistical analysis

Experimental data are presented as the mean ± SEM, except where stated. Summary data for baseline diameters, responses to O₂ (O₂ response = D_O2 – D_Baseline; in μm) and SNP (SNP response = D_SNP – D_Baseline; in μm) are summarized in Table1. For constriction responses, values were calculated as changes from baseline diameter: % constriction = (D_Baseline – D_Response)/D_Baseline × 100%. Reactivity between orders was expressed as percentage change differences: [(% constriction_A – % constriction_B)/% constriction_A] × 100%, where A and B correspond to two different arteriolar orders. At each concentration of agonist, a one-way ANOVA was conducted to observe the effect of arteriolar order on level of arteriolar constriction, with an α level of 0.05 for statistical significance. For each agonist–antagonist plot, individual t tests were conducted at each concentration of drug to evaluate the effect of the antagonist on constriction for each order. In the event of unequal variance, a Welsh correction was applied to the t test.

Data for each agonist treatment were fit to a variable-slope sigmoid and compared where sigmoidal convergence was possible. As a result of dichotomous (vasodilatatory and vasoconstrictor) responses to ATP application and variable responses among arteriolar orders to αβ-meATP application, the data did not converge and sigmoidal (logEC₅₀) analyses were not possible.

To compare concentration–response curves (logEC₅₀) with differing absolute maximum constriction responses (E_Max), data for PE, UK 14304 and NPY were transformed using Prism (GraphPad Software Inc., San Diego, CA, USA). Responses were normalized to their respective E_Max, where the minimum and maximum (y-axis) values were set to 0% and 100%, respectively, and the x-axis was converted to a logarithmic scale. LogEC₅₀ values were then compared across all orders using a one-way ANOVA with α level of 0.05 for statistical significance, followed by Tukey’s honestly significant difference post hoc test.

Results

Protocols 1 and 2: activation and selectivity of α1R, α2R, Y1R and P2X1R agonists

To confirm the receptor-mediated effects of the sympathetic agonists used in the present study, we conducted a subset of experiments in the face of antagonist delivery. In all cases, antagonism of receptors for sympathetic neurotransmitters abolished vasoconstriction to the respective sympathetic agonists.

Phenylephrine data

There was an order-dependent effect of PE on arteriolar constriction (Fig.1, top; n = 8 rats). Arteriolar constriction at maximum PE concentration (10⁻⁴ m) was greatest at 1A, which progressively decreased with increasing arteriolar order, such that 1A arterioles were 85% more reactive than 5A. Constriction to maximum PE concentration (10⁻⁴ m) was blocked by prazosin (P < 0.05), confirming that the responses were a result of α1R activation.

Figure 1.

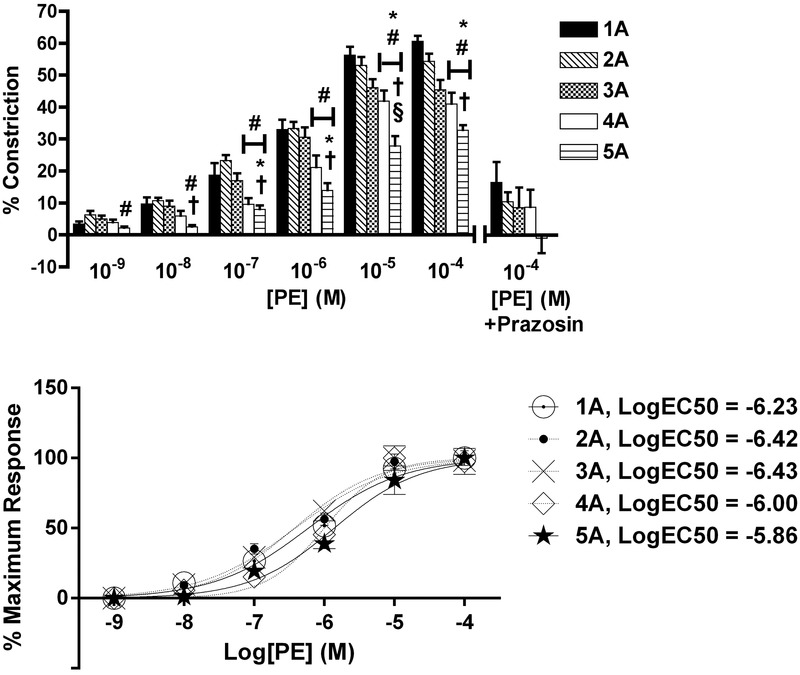
Arteriolar responses to α1R activation at five arteriolar orders

Top: percentage change in arteriolar constriction (from baseline) for five arteriolar orders (1A through 5A, n = 8–17 arterioles) at increasing concentrations (m) of PE. Data presented as the mean ± SEM. *Statistically different from 1A; #statistically different from 2A; †statistically different from 3A; §statistically different from 4A (all P < 0.05). Constriction responses to peak concentrations of PE were blocked by prazosin (% indicates the difference between responses with and without antagonist at PE 10⁻⁴ m, P < 0.05) for all orders. Bottom: normalized constriction responses fit to sigmoids. LogEC₅₀ values are reported for each arteriolar order. LogEC₅₀ values for 2A and 3A were greater than 4A and 5A (P < 0.05).

Phenylephrine logEC₅₀ values were different across arteriolar orders (Fig.1, bottom; P < 0.05), where the logEC₅₀ values (m) were: 1A, –6.23; 2A, –6.42; 3A, –6.43; 4A, –6.00; and 5A, –5.86. Specifically, logEC₅₀ for 2A was greater than 4A and 5A, and logEC₅₀ for 3A was greater than 4A and 5A (P < 0.05).

UK 14304 data

There was an order-dependent effect of UK 14304 on arteriolar constriction (Fig.2, top; n = 5 rats). Arteriolar constriction at maximum UK 14304 (10⁻⁵ m) was greatest at 1A, 2A and 3A, such that these arteriolar orders were up to 85% more reactive than 5A. Constriction to UK 14304 at 10⁻⁷ to 10⁻⁶ m was blocked by yohimbine at all orders, and UK 14304 at 10⁻⁵ m was blocked by yohimbine at 3A to 5A (P < 0.05), confirming that the responses to UK 14304 were a result of α2R activation.

Figure 2.

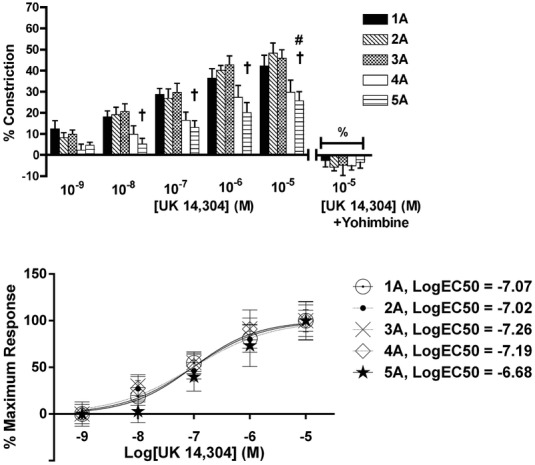
Arteriolar responses to α2R activation at five arteriolar orders

Top: percentage change in arteriolar constriction (from baseline) for five arteriolar orders (1A through 5A, n = 6–22 arterioles) at increasing logarithmic concentrations (m) of UK 14304. Data presented as mean the ± SEM. #Statistically different from 2A; †statistically different from 3A (both P < 0.05). Constriction responses to peak concentrations of UK 14304 were blocked by yohimbine (% indicates difference between responses with and without antagonist at UK 14304 10⁻⁵ m, P < 0.05) for all orders. Bottom: normalized constriction responses fit to sigmoids. LogEC₅₀ values are reported and were similar across arteriolar orders.

UK 14304 logEC₅₀ values were similar across arteriolar orders (Fig.2, bottom), where the logEC₅₀ values (m) were: 1A, –7.07; 2A, –7.02; 3A, –7.26; 4A –7.19; and 5A, –6.68.

Neuropeptide Y data

There was an order-dependent effect of NPY on arteriolar constriction (Fig.3, top; n = 8 rats). Arteriolar constriction at maximum NPY concentration (10⁻⁸ m) was greatest at 5A, which progressively decreased with decreasing arteriolar order, such that 5A arterioles were 121% more reactive than 1A. Constriction to NPY at maximum concentration (10⁻⁸ m) was blocked by BIBP3226 (P < 0.05), confirming that responses to NPY were a result of Y1R activation.

Figure 3.

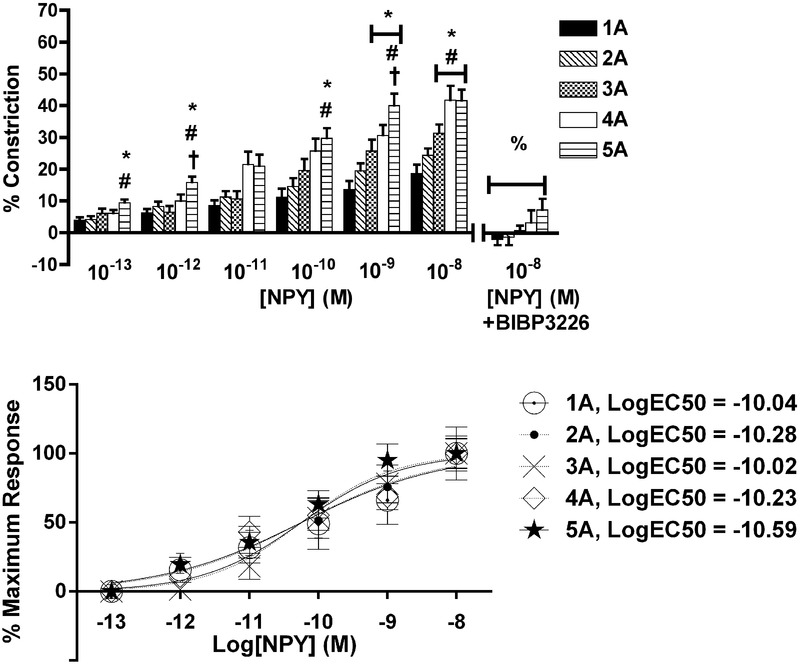
Arteriolar responses to Y1R activation at five arteriolar orders

Top: percentage change in arteriolar constriction (from baseline) for five arteriolar orders (1A through 5A, n = 8–17 arterioles) at increasing logarithmic concentrations (m) of NPY. Data presented as the mean ± SEM. *Statistically different from 1A; #statistically different from 2A; †statistically different from 3A (all P < 0.05). Constriction responses to peak concentrations of NPY were blocked by BIBP3226 (% indicates difference between responses both with and without antagonist, P < 0.05) for all orders. Bottom: mormalized constriction responses fit to sigmoids. LogEC₅₀ values are reported in legend, and were similar across arteriolar orders.

Neuropeptide Y logEC₅₀ values were similar across arteriolar orders (Fig.3, bottom), where the logEC₅₀ (m) values were: 1A, –10.04; 2A, –10.28; 3A, –10.02; 4A –10.23; and 5A, –10.59.

ATP data

ATP produced concentration-dependent dichotomous arteriolar responses (Fig.4). Lower ATP concentrations (10⁻⁹ to 10⁻⁷ m) evoked arteriolar constriction, with the following branch orders having the greatest level of constriction at each concentration: 10⁻⁹ m of ATP, 4A > 1A and 3A; 10⁻⁸ m, 4A > 1A; and 10⁻⁷ m, 4A > 1A and 2A (P < 0.05). ATP evoked maximum arteriolar constriction at 10⁻⁸ m, with the following constrictor responses: 1A, 3.5%; 2A, 8%; 3A, 9%; 4A, 15%; and 5A, 11%. These data indicate that 4A arterioles are the most responsive to the constrictor effects of ATP.

Figure 4.

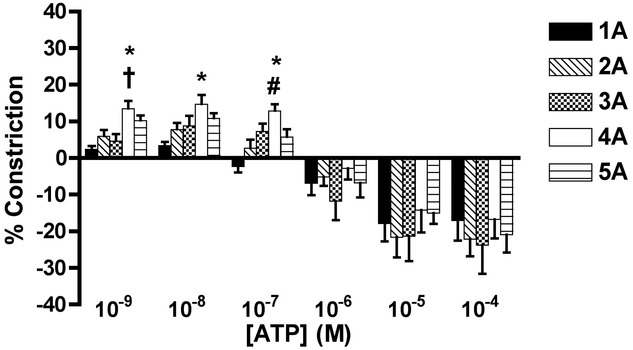
Arteriolar responses to ATP application at five arteriolar orders

Percentage change in arteriolar constriction (from baseline) for five arteriolar orders (1A through 5A, n = 6–22 arterioles) at increasing logarithmic concentrations (m) of ATP. Data presented as the mean ± SEM. A negative constriction is determined as a dilatatory response. *Statistically different from 1A; #statistically different from 2A; †statistically different from 3A (all P < 0.05).

At concentrations > 10⁻⁶ m, all orders dilated, with peak responses to maximal concentration of ATP 10⁻⁴ m as indicated: 1A, 18%; 2A, 22%; 3A, 24%; 4A, 17%; and 5A, 21% (Fig.4).

Constriction to ATP at 10⁻⁹ to 10⁻⁷ m was blocked by NF023 (Fig. 4B, P < 0.05) indicating that responses to ATP were a result of P2X1R activation.

Figure 5.

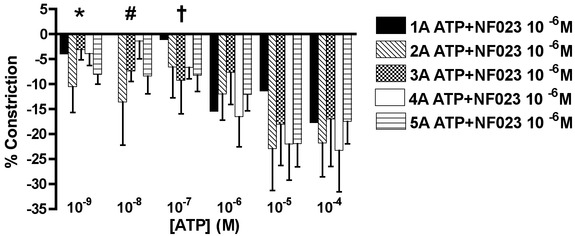
Arteriolar responses to ATP application with P2X1R blockade at five arteriolar orders

Percentage change in arteriolar constriction (from baseline) for five arteriolar orders (1A through 5A, n = 5–20 arterioles) at increasing logarithmic concentrations (m) of ATP in the face of NF023 (P2X1R antagonist). Data presented as the mean ± SEM. A negative constriction is determined as a dilatatory response. Data presented as the mean ± SEM. Constriction responses to ATP were blocked by NF023 for ATP concentrations of 10⁻⁹ m (statistical difference in constriction responses for 2A to 5A with and without antagonist, P < 0.05), 10⁻⁸ m (#statistical difference in constriction responses for 3A to 5A with and without antagonist, P < 0.05) and 10⁻⁷ m (†statistical difference in constriction responses for 4A to 5A with and without antagonist, P < 0.05).

αβ-meATP data

All arteriolar orders constricted for the full concentration range of αβ-meATP (Fig. 4C). Because αβ-meATP is P2X1R specific, these data show that the dilatation effects of ATP (shown in Fig. 4A) were not P2X1R mediated. Furthermore, constriction effects of αβ-meATP were blocked by NF023 (10⁻⁶ m) (P < 0.05, Fig. 4C).

Computational analysis: calculating haemodynamic consequences from spatially-dependent SNS receptor activation

An arteriolar tree was modelled from in vivo network geometry, with centrifugal branch orders mathematically determined in the same way and represented using the same nomenclature (1A to 5A) as in our experimental data analysis (Fig.7). Comparison between computational calculations for baseline blood flow did not differ from experimental blood flow calculations because there was no significant difference between slope and intercept between the two regression lines (Fig.8).

Figure 7.

Computational network reconstruction schematic

Schematic of digital reconstruction of arteriolar network from rat GM muscle photomontage (left, n = 1 rat). Numbers on reconstruction (right) indicate arteriolar order and represent in vivo observations, with largest vessel (inlet) as 1A and smallest vessels (outlets) as 5A. Network is colour-coded based on baseline (control) blood flow through vessel segments, with red indicating high flow and dark blue indicating low flow.

Figure 8.

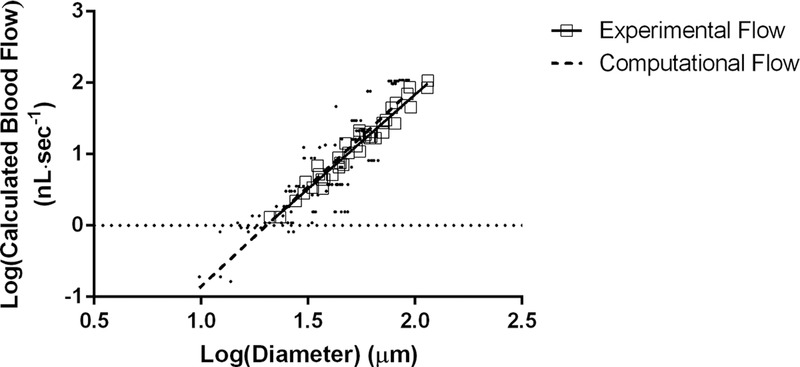
alidation of computational flow data with experimental flow data

Comparison of blood flow values calculated from the computational model versus blood flow values calculated from experimental protocol. There was no significant difference between the slopes or the intercepts for both linear regressions. Experimental flow: log (calculated blood flow) = [2.64 × log(diameter)] – 3.44; r² = 0.96, P < 0.05. Computational flow: log (calculated blood flow) = [2.79 × log(diameter)] – 3.65; r² = 0.76, P < 0.05.

This reconstructed arteriolar tree was used in our haemodynamic calculations to obtain network flow (Fig.6A), total resistance (Fig.6B) and RBC flow heterogeneity at 2A to 5A (Fig.7). There was a progressive decrease in total flow within the simulated network with increasing concentrations of PE, UK and NPY (Fig.6A). Correspondingly, there was a progressive increase in total network resistance within the simulated network with increasing concentrations of PE, UK and NPY (Fig.6B). In parallel to the complementary constriction data, ATP data exhibited an effect on total flow and network resistance, which was opposite to that of the other ligands: ATP increased total flow with an increasing concentration and decreased network resistance with an increasing concentration. It has been shown previously that these results are attributed to ATP acting as a dilatator at higher concentrations (Hellsten et al. 1998; Nyberg et al. 2013).

Figure 6.

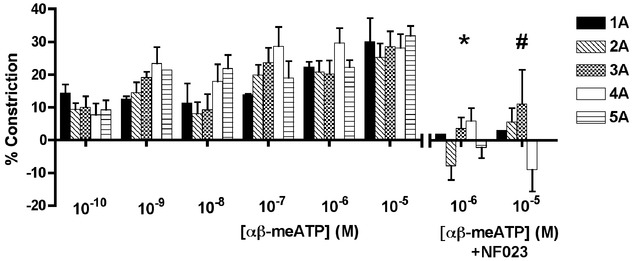
Arteriolar responses to αβ-meATP application at five arteriolar orders

Percentage change in arteriolar constriction (from baseline) for five arteriolar orders (1A through 5A, n = 5–15 arterioles) at increasing logarithmic concentrations (m) of αβ-meATP. Data presented as the mean ± SEM. Constriction responses to αβ-meATP were blocked by NF023 for αβ-meATP concentrations of 10⁻⁶ m (*statistical difference in constriction responses for 2A, 4A to 5A with and without antagonist, P < 0.05) and 10⁻⁵ m (#statistical difference in constriction responses for 4A with and without antagonist, P < 0.05).

Figure 9.

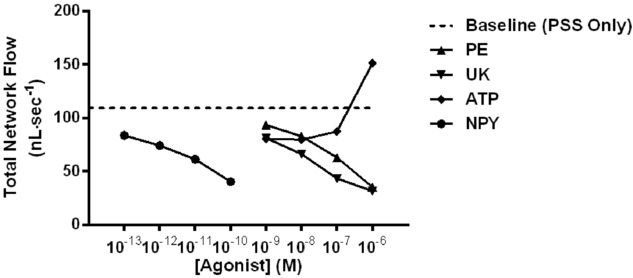
alculated total network flow during baseline and during activation of receptors for sympathetic neurotransmitters

Calculated total network flow for baseline; PE, UK 14304 (UK) and ATP from 10⁻⁹ to 10⁻⁶ m; NPY from 10⁻¹³ to 10⁻¹⁰ m. There was a progressive decrease in calculated total network flow with increasing concentration of agonist, with the exception of ATP because dilatation occurs at higher concentrations.

Figure 10.

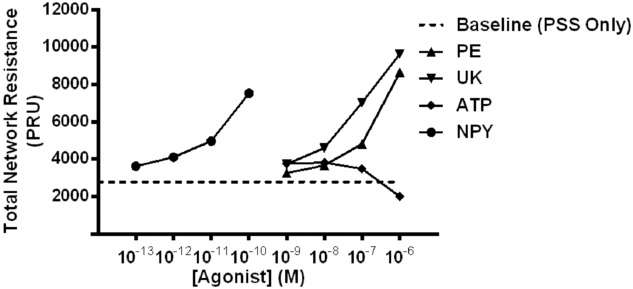
Calculated total network resistance during baseline and during activation of receptors for sympathetic neurotransmitters

Calculated total network resistance for baseline; PE, UK 14304 (UK) and ATP from 10⁻⁹ to 10⁻⁶ m; NPY from 10⁻¹³ to 10⁻¹⁰ m. There was a progressive increase in calculated total network resistance with increasing concentration of agonist, with the exception of ATP because dilatation occurs at higher concentrations.

Figure 11.

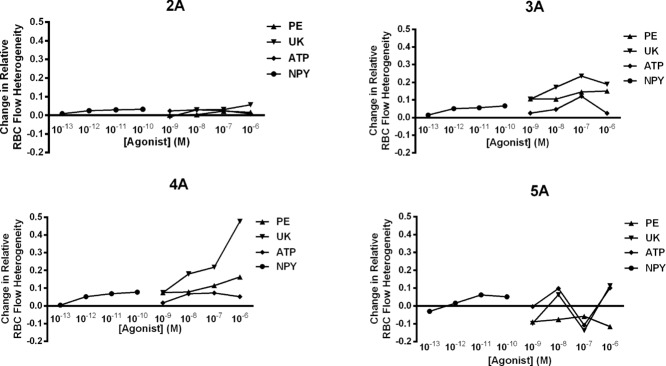
Change in RBC flow heterogeneity at 2A to 5A during activation of receptors for sympathetic neurotransmitters

Relative change (from baseline) in RBC flow heterogeneity at 2A to 5A vessels in the arteriolar network model of the GM muscle. The coefficient of variation of RBC flow heterogeneity as a function of agonist is normalized to baseline RBC flow heterogeneity. Heterogeneity is calculated for agonist concentrations: PE, UK 14304 (UK) and ATP from 10⁻⁹ to 10⁻⁶ m; NPY from 10⁻¹³ to 10⁻¹⁰ m. An increase in heterogeneity is shown as a positive value, whereas a decrease in heterogeneity is shown as a negative value.

To calculate changes in RBC flow heterogeneity, baseline heterogeneity was used as the reference value, and any changes from baseline heterogeneity were reflected as positive (increase in heterogeneity) or negative (decrease in heterogeneity) changes from baseline. This fractional change was calculated for each order (1A to 5A) of the reconstructed network (Fig.1). For 2A vessels, there was minimal change in RBC flow heterogeneity for all concentrations of the four ligands, with a maximum of 5% increase in heterogeneity exhibited by the addition of 10⁻⁶ m UK 14304. For 3A vessels, there was a 10–24% increase in RBC flow heterogeneity exhibited by PE and UK 14304 at all concentrations, with a smaller (∼1–12%) effect of ATP and especially NPY. For 4A vessels, there was a progressive increase in RBC flow heterogeneity with increasing concentrations of PE and UK 14304 and the greatest effect on heterogeneity (∼50% increase) with a 10⁻⁶ m concentration of UK 14304. The changes in heterogeneity for 5A vessels do not follow a distinct pattern for each of the concentrations of UK 14304 and ATP; however, Fig.1 highlights two important outcomes: (1) PE and NPY have opposing effects on heterogeneity at 5A (increasing PE decreases heterogeneity, whereas increasing NPY increases heterogeneity) and (2) although PE has a large impact on blood flow heterogeneity in the larger vessels (2A to 4A), it decreases heterogeneity at 5A vessels.

Discussion

In the present study, we provide a comprehensive topological evaluation of sympathetic modulation in branching skeletal muscle arteriolar networks. Our work provides much needed new data describing the concentration- and order-dependent vasoconstrictor effects of adrenergic (α1R and α2R), peptidergic (Y1R) and purinergic (P2X1R) receptor activation in complex skeletal muscle arteriolar trees. Furthermore, we have applied these experimental data to our computational blood flow model and described the haemodynamic consequences of heterogeneous modulation of receptors for sympathetic neurotransmitters across a skeletal muscle network. Our data support and build on the classic ‘adrenocentric’ view of sympathetic vascular control but, most importantly, illustrate equipotent roles for peptidergic and purinergic sympathetic components in skeletal muscle arteriolar haemodynamics.

Experimental findings: topologically-dependent sympathetic control along arteriolar trees

Visualization and imaging of arteriolar networks

One of the prominent features of the rat GM muscle is its two-dimensional planar geometry (Al-Khazraji et al. 2012), whereby complete arteriolar networks can be quickly scanned and imaged with minimal changes in focal depth. For the present study, this enabled the simultaneous and systematic evaluation of the topologically-dependent effects of activating receptors for sympathetic neurotransmitters along branching arteriolar trees (from 1A to 5A).

Topologically-dependent vasoconstrictor responses to adrenergic control

Previous studies describing differential α-adrenergic control in branching arterioles were limited to selected small groupings of arterioles in non-locomotive muscle (i.e. rat cremaster) (Faber, 1988; Ohyanagi et al. 1991) or locomotive skeletal muscle arteriolar networks of limited branch orders (Moore et al. 2010). In the rat cremaster, Faber (1988) binned groups of arterioles (based on luminal diameter) as either large or small. Where large arterioles were composed of 1A and 2A vessels (mean diameter of 100 μm) and small arterioles were composed of 3A vessels (mean diameter of 25 μm). Ohyanagi et al. (1991) also used binning but categorized large arterioles (mean diameter of 120 μm) as 1A and terminal arterioles (mean diameter of 13 μm) as 3A vessels. Although such an approach provided meaningful data, their binning approaches limited spatial resolution, which precludes topologically based analyses.

In the present study, arteriolar responses to PE were order-dependent, where 1A and 2A were 27% to 317% more reactive than 4A and 5A for the entire range of PE concentrations. In addition, arteriolar constriction elicited by the highest PE concentration (10⁻⁴ m) was completely blocked by prazosin (α1R antagonist; 2 × 10⁻⁸ m) (Fig.1, top). Although our data support many of the findings of Moore et al. (2010) obtained in mice, we observed that 1A were most responsive to PE application, whereas Moore et al. (2010) reported that 3A were most responsive to PE application. Although we cannot preclude species differences (i.e. rat versus mouse), such discrepancies are probably attributed to fundamental differences in the experimental protocols. Specifically, Moore et al. (2010) applied a narrow PE concentration range (10⁻⁹ to 10⁻⁶ m) that did not elicit plateaus in arteriolar response curves, suggesting that responses did not reach maximum constriction. By contrast, we employed a broader PE concentration range (10⁻⁹ to 10⁻⁴ m), resulting in maximum arteriolar constriction (i.e. plateau responses). Applying higher PE concentrations (10⁻⁵ and 10⁻⁴ m), we demonstrated that 1A and 2A constrict greater than 3A (Fig.1, top).

Because EC₅₀ represents the potency of ligands on arteriolar responses and because efficacy (E_Max) differed among arteriolar orders, arteriolar responses were normalized and plotted as concentration–response curves. In response to PE, logEC₅₀ differed among orders (Fig.1, bottom; P < 0.05), where logEC₅₀ values of 2A and 3A were greater than 4A and 5A. Our data show that PE has greater potency (i.e. logEC₅₀) and efficacy (E_Max) (Fig.1, top) in proximal versus distal arterioles. These data suggest that proximal arterioles may have either greater receptor density and/or binding affinity; however, any conclusions describing receptor density and/or binding affinity are beyond the scope of the present study.

Arteriolar responses to UK 14304 (α2R activation) (Fig.2, top) were order-dependent, where (at 10⁻⁸ to 10⁻⁵ m) 2A was 87% to 261% and 3A was 78% to 289% more reactive than 5A vessels (P < 0.05). E_Max values in 2A and 3A were 87% and 78% greater, respectively, than E_Max in 5A (Fig.2, top). Because all arteriolar orders received the same range of agonist concentrations and reached plateaus in responses, these E_Max data illustrate the profound efficacy of UK 14304 in proximal versus distal arterioles. By contrast, there were no differences in logEC₅₀ values across arteriolar orders in response to UK 14304 (Fig.2, bottom), demonstrating its similar potency among all arteriolar orders.

As noted previously, Faber (1988) and Ohyanagi et al. (1991) binned arterioles (based on luminal diameter), which is fundamentally different from the ordering scheme used in the present study. Despite differences in arteriolar nomenclature, and strictly comparing based on diameters instead of orders, our data are in alignment with Faber (1988) and Ohyanagi et al. (1991) in that we also found ‘larger’ arterioles (∼100 μm) responded more to α2R activation than ‘smaller’ arterioles (∼25 μm). However, in comparisons based on arteriolar orders, we were unable to resolve differences among 1A to 3A arterioles for α2R activation.

Recently, Moore et al. (2010) reported that 1A arterioles (versus 2A and 3A) were most responsive to α2R activation (via UK 14304) in the GM of the C57BL/6 mouse. This is in contrast to our current data where we observed the greatest responses to UK 14304 in 2A and 3A vessels in the GM of the rat. Nevertheless, our findings are in direct congruence with work conducted in the cremaster of the C57BL/6 mouse by Moore et al. (2010). These findings highlight the complexity in arteriolar control among different species and experimental preparations. Notably, topological differences in microvascular networks between different species may contribute to such comparative and interpretative discrepancies. To illustrate, our laboratory has recently reported that there are at least four orders of arterioles (from 1A to terminal arterioles) in the same C57BL/6 mouse (Novielli & Jackson, 2014). By contrast, we reported up to six orders of arterioles (from 1A to terminal arterioles) in the Sprague–Dawley rat GM (Al-Khazraji et al. 2012). The microvasculature is designed to provide adequate O₂ delivery to the muscle tissue, yet the geometry is constrained by the dimensions of the capillary bed (i.e. capillary size does not scale with species; West et al. 1997); therefore, the pre-capillary arterioles should behave the same despite the difference in species. Based on noted differences in network complexity, it could be argued that a 4A arteriole in the mouse should be similar haemodynamically to a 5A or 6A arteriole in the rat; however, this remains untested. If SNS control of arteriolar networks is order-dependent, then we would expect subtle differences in control among species and preparations with differing arteriolar network complexities.

Topologically-dependent vasoconstrictor response to peptidergic control

In the present study, arteriolar responses to NPY were order-dependent, where 5A was 70% to 151% more reactive than 1A and 2A (Fig.3, top panel; P < 0.05). In addition, arteriolar constriction elicited by the highest NPY concentration (E_Max;10⁻⁸m) was completely blocked by BIBP3226 (Y1R antagonist; 2 × 10⁻⁸ m) (Fig.3, top; P < 0.05). E_Max values in 4A and 5A were 124% and 71% greater than E_Max in 1A and 2A, respectively (Fig.3, top). Because all arteriolar orders received the same range of agonist concentrations and reached plateaus in responses, these E_Max data illustrate the profound efficacy of NPY in distal versus proximal arterioles. However, there were no differences in logEC₅₀ values across arteriolar orders in response to NPY (Fig.3, bottom), demonstrating its similar potency among all arteriolar orders.

Our data are the first to show differential responses to Y1R activation as a function of arteriolar order. To date, there have been few studies directly investigating the effects of NPY on branching skeletal muscle arteriolar trees (from 1A to pre-terminal arterioles). Although we consider ourselves to be the first to describe the effects of NPY in locomotive skeletal muscle arteriolar networks, Joshua (1991) was the first to examine NPY-induced arteriolar tree vasoconstriction in the rat cremaster muscle, as studied by IVVM. Despite fundamental differences in the approach employed, and despite the data obtained by Joshua (1991) being limited to only three generations of arterioles, the data from their study and the present study are in close agreement.

To test the effect of NPY on vascular resistance in the cat gastrocnemius muscle, Ekelund & Erlinge (1997) used arterially infused NPY and indirect estimations of resistance changes from pressure/bulk flow relationships. Although their data lacked spatial resolution (i.e. detailed topology) and simply indicated that NPY provided preferential vasoconstriction in small-bore (<25 μm) compared to large-bore (>25 μm) arterioles, our findings are in general agreement.

Our data further corroborate previous work showing the prominent role of NPY in regulating the distal microvasculature (Joshua, 1991; Jackson et al. 2004; Evanson et al. 2012). However, these previous studies were limited in scope and did not provide any information on network topology or order dependency. For example, Evanson et al. (2012) limited their investigation to isolated 1A vessels from rat gastrocnemius muscle, Jackson et al. (2004) made generalized inferences from bulk blood flow profiles measured at the femoral artery of rats, and Joshua (1991) limited their findings to three arteriolar orders in non-locomotive skeletal muscle (cremaster).

Topologically-dependent vasoconstrictor response to purinergic control: dichotomous effects of ATP

In the present study, arteriolar responses to ATP were order-dependent, where 4A arterioles were up to 333% more reactive than 1A (for 10⁻⁹ to 10⁻⁷ m), 285% more reactive than 2A (at 10⁻⁷ m) and 189% more reactive than 3A (at 10⁻⁹ m). ATP exhibited vasoconstriction (at low concentrations) and vasodilatation (at high concentrations) (Fig.4A). ATP-mediated vasoconstriction was primarily a result of P2X1R activation (Fig.4B) because vasoconstrictor effects were completely blocked by the application of NF023 (a specific P2X1R antagonist; 10⁻⁶ m) (Fig.4B, P < 0.05). Although ATP has been more commonly described as a vasodilatator (Hellsten et al. 1998; Clifford & Hellsten, 2004; Mortensen et al. 2009), the vasoconstriction elicited by ATP in the present study is in agreement with work reported from experiments in the rat tail and hindlimb (Johnson et al. 2001), as well as the rat heart (Hopwood & Burnstock, 1987).

ATP acts on P2X receptors, which are located on the abluminal smooth muscle of the vessel (Hirst & Jobling, 1989), as well as P2Y receptors (responsible for dilatation), which are located on the intraluminal endothelium (Burnstock, 1996). In the present study, ATP promoted vasoconstriction in all arteriolar orders at 10⁻⁹ and 10⁻⁸ m (Fig.4A, P < 0.05). However, with progressive increases in ATP concentration (10⁻⁶ and 10⁻⁵ m), we observed vasodilatation in all arteriolar orders (P < 0.05). Interestingly, similar ATP concentrations in exercising human skeletal muscle have been reported, where interstitial ATP levels (measured from i.m. microdialysate) ranged between 2 and 5 × 10⁻⁶ m, depending on exercise intensity (Hellsten et al. 1998).

During micropipette application of ATP to arterioles in the hamster cheek pouch preparation, the vasodilatator effect of interstitial ATP was suggested to be mediated (in part) by the formation of adenosine (from ATP degradation) via 5’-ectonucleotidase activity (Duza & Sarelius, 2003). This mechanism of ATP-mediated dilatation (via breakdown to adenosine) would then differ from intravascular ATP-mediated dilatation, which is solely based on ATP binding onto P2Y receptors residing on the endothelium (and is independent of the vasodilatatory effects of adenosine). Although Duza & Sarelius (2003) applied ATP at concentrations of 10⁻⁷  to10⁻³ m, we used lower concentrations of ATP (10⁻⁹ to 10⁻⁷ m), which elicited vasoconstriction. Our conditions correspond to the interstitial ATP concentrations measured with i.m. microdialysis at baseline in humans (Mortensen et al. 2011). The results from the present study together with those obtained in previous studies suggest that 5’ ectonucleotidase is either not active at low concentrations of ATP, or that the breakdown of ATP to adenosine does not override the vasoconstrictor effects of ATP at these concentrations.

We recently reported that vasodilatation, and the ensuing blood flow changes, in response to high ATP concentrations (10⁻⁶ and 10⁻⁵ m) can be completely abolished by l-NA and indomethacin in the rat GM. Thus, the vasodilatator effects of high abluminal ATP concentrations are best explained by nitric oxide and prostanoid formation, respectively (Nyberg et al. 2013). Certainly, ATP can diffuse from the interstitial space into the vessel lumen and invoke P2Y-mediated vasodilatation; however, a 50-fold difference in ATP concentration difference across the vessel wall is required for this cross-over to occur (Mo & Ballard, 2001). Notably, the whole blood concentration of ATP in the Sprague–Dawley rat is 3 to 5 × 10⁻⁶ m (Jagger et al. 2001), which would lead to no net flux of ATP from the interstitium to the blood in the present study. Thus, vasodilatation induced by 10⁻⁶ to 10⁻⁵ m [ATP] in the present study cannot be a result of diffusion and subsequent P2Y activation.

When applying ATP in the face of P2X1R blockade, ATP acted as a vasodilatator at all concentrations (Fig. 4B, P < 0.05). These data suggest that ATP-induced vasodilatation buffers its vasoconstrictor effects at all (physiologically relevant) concentrations. This was further corroborated by the pure vasoconstrictor effect of αβ-meATP (Fig. 4C) (also blocked by NF023, emphasizing that vasoconstriction was specific to P2X1R activation), an ATP analogue that does not degrade at the same rate as ATP with high affinity for P2X1R receptors.

Based on our findings and those of previous studies, we conclude that ATP acts as a vasoconstrictor in skeletal muscle so long as: (1) it is not degraded to adenosine; (2) it cannot cross-over into the lumen to act on P2Y receptors; and/or (3) it is available at low concentrations because high concentrations of ATP induce nitric oxide and prostacyclin formation (Nyberg et al. 2013) which masks the vasoconstricting capacity of ATP (Fig. 4B). The dichotomous roles of ATP may serve to optimize resistance and perfusion pressure in contracting muscle (in areas of lower concentration) and, in areas of high concentration, participate in localized exercise-induced functional sympatholysis (Kirby et al. 2011).

Computational experiments: total network resistance and flow changes as a result of a differential distribution of receptors for sympathetic neurotransmitters

The inlet, or 1A, vessel to the arteriolar network provides the bulk flow to the outlets (or all the 5A vessels); therefore, having access to tree geometry allows for calculation of ‘upstream’ and ‘downstream’ effects on haemodynamics as a result of topologically-dependent differential responses of arterioles to activation of receptors for sympathetic neurotransmitters. The ability to assess the ‘up/downstream’ effects is unique to network analysis, and highlights the benefit of analyzing networks of interconnected bifurcations, as opposed to acquiring data from single sites of observation (Pries et al. 1995).

In our previous work, we speculated that Y1R blockade (via BIBP3226) modulated downstream systemic vascular resistance, as shown by changes in the diastolic conductance of the rat hindlimb (Jackson et al. 2004). A remarkable outcome of our present haemodynamic calculations was that NPY greatly contributed to total network resistance. NPY decreased calculated network flow to the same degree as PE (Fig. 6A); however, NPY operated in a range of concentrations that were 1000-fold lower than PE. Per mole of concentration, it can be stated that NPY is a more potent vasoconstrictor, and therefore greatly contributes to resistance, compared to either PE or UK 14304 alone. As previously noted, this highlights the importance of understanding the consequent implications of neurotransmitter contribution, despite its concentration in the interstitial milieu. The microvascular surface area increases with progressively increasing arteriolar order, with the greatest level of surface area exhibited by the capillaries (Poole et al. 2013).

Order and diameter-dependent changes in RBC heterogeneity as a result of a differential distribution of receptors for sympathetic neurotransmitters

Progressing down the arteriolar network, there is an increase in the number of arteriolar bifurcations, and a progressive decrease in haematocrit of single vessels for a given order (compared to parent orders) (Pries et al. 1986). This assists in providing a baseline level of heterogeneous RBC delivery to capillary beds, where RBC flow preference is given to the daughter with the greater diameter (or path of lower resistance). Accordingly, small changes in resistance at the smaller (distal) arterioles will result in robust changes in haematocrit (Pries et al. 1990).

Traditionally, dilatatory mechanisms have been proposed as the primary means for RBC distribution within the microvasculature (Clifford & Hellsten, 2004). From our experimental data, we show that sympathetic ligands can promote differential and topologically-dependent changes in resistance for a wide range of ligand concentrations. We propose that this is carried out through differential SNS control across the microcirculation. A topologically-dependent arrangement of sympathetic control would enable the SNS to co-ordinate with intrinsic dilatatory mechanisms to precisely titrate RBC delivery throughout the network. With regard to the concept of phase separation, where blood flow fraction delivery is more sensitive to changes in resistance of smaller compared to larger arterioles (Pries et al. 1990), topologically-dependent SNS receptor activation warrants large haemodynamic consequences in terminal arterioles feeding into capillary beds.

Perspectives

Our theoretical model illustrates that, as a result of topologically-dependent modulation, the SNS affects RBC heterogeneity differentially at each arteriolar order (Fig.7). Under baseline healthy conditions, such control would contribute to setting baseline resistance and RBC distribution. At the onset of both healthy ageing (Narkiewicz et al. 2005) and cardiovascular diseases (Malpas, 2010), there exist concomitant increases in sympathetic nerve activity, which may then act to exaggerate blood flow heterogeneity (Jackson et al. 2010) and further exacerbate microvascular dysfunction, perhaps via upregulation of any (or all) of the receptors for sympathetic neurotransmitters. Certainly, under high stress conditions, Y1R is upregulated in microvessels of injured carotid arteries (Li et al. 2005); in addition, hypertensive patients have demonstrated increased P2X1R activation (Steinmetz et al. 2000; Hollah et al. 2001). Our model flow calculations show that (compared to PE and UK) NPY and ATP produced higher RBC flow heterogeneity (relative to baseline) in distal (5A) vessels (Fig.1), indicating that heightened SNS receptor activation, as in disease conditions, would elicit detrimental consequences to RBC delivery.

Conclusions

To conclude, we have comprehensively and systematically determined network responses to cumulative concentra-tions of specific sympathetic agonists among five arteriolar orders, and we have used these responses to mathematically determine the functional consequ-ence(s) of a heterogeneous distribution of receptors for sympathetic neurotransmitters on network haemodynamics. We have shown differential responses to sympathetic ligands along the arteriolar tree, such that proximal arterioles are largely under adrenergic control, whereas distal arterioles are largely under peptidergic and purinergic control. Using computational modelling, we calculated that the adrenergic component of blood flow regulation is mostly responsible for maintaining total flow to the tissue, whereas the peptidergic and/or purinergic component(s) contribute both to total network resistance/flow and to RBC flow distribution within the network. Finally, we have indicated that, alongside the noradrenergic system, the peptidergic and purinergic components of the SNS carry out integral roles in sympathetically-mediated microvascular control.

Glossary

αβ-meATP

α,β-methylene ATP

GM

gluteus maximus

IVVM

intravital video microscopy

NA

noradrenaline

NPY

neuropeptide Y

PE

phenylephrine

RBC

red blood cell

SNP

sodium nitroprusside

SNS

sympathetic nervous system

Additional information

Competing interests

The authors declare that they have no competing interests.

Author contributions

BKA, DG and DNJ contributed to the conception of the study, as well as the experimental design, analysis and interpretation of the data. BKA performed all of the experiments in the laboratory of DNJ at the University of Western Ontario and prepared the first draft of the article, which was edited by all of the co-authors. AS contributed to the computational modelling of network blood flow. All authors approved the version manuscript submitted for publication.

Funding

All research was supported by a Natural Sciences and Engineering Research Council (NSERC) grant (R4218A03) awarded to DNJ. BKA was a recipient of the Alexander Graham Bell Canada Graduate Scholarship-Doctoral (CGS-D). AS was a recipient of the Saudi Arabian King Abdullah Scholarship. Computational modelling was also supported by NSERC grant R4081A03 awarded to DG.