Efficient Multi-Atlas Abdominal Segmentation on Clinically Acquired CT with SIMPLE Context Learning

Abstract

Abdominal segmentation on clinically acquired computed tomography (CT) has been a challenging problem given the inter-subject variance of human abdomens and complex 3-D relationships among organs. Multi-atlas segmentation (MAS) provides a potentially robust solution by leveraging label atlases via image registration and statistical fusion. We posit that the efficiency of atlas selection requires further exploration in the context of substantial registration errors. The selective and iterative method for performance level estimation (SIMPLE) method is a MAS technique integrating atlas selection and label fusion that has proven effective for prostate radiotherapy planning. Herein, we revisit atlas selection and fusion techniques for segmenting 12 abdominal structures using clinically acquired CT. Using a re-derived SIMPLE algorithm, we show that performance on multi-organ classification can be improved by accounting for exogenous information through Bayesian priors (so called context learning). These innovations are integrated with the joint label fusion (JLF) approach to reduce the impact of correlated errors among selected atlases for each organ, and a graph cut technique is used to regularize the combined segmentation. In a study of 100 subjects, the proposed method outperformed other comparable MAS approaches, including majority vote, SIMPLE, JLF, and the Wolz locally weighted vote technique. The proposed technique provides consistent improvement over state-of-the-art approaches (median improvement of 7.0% and 16.2% in DSC over JLF and Wolz, respectively) and moves toward efficient segmentation of large-scale clinically acquired CT data for biomarker screening, surgical navigation, and data mining.

Graphical Abstract

1. Introduction

The human abdomen is an essential, yet complex body space. Computed tomography (CT) scans are routinely obtained for the diagnosis and prognosis of abdomen-related disease. Automated segmentation of abdominal anatomy may improve patient care by decreasing or eliminating the subjectivity inherent in traditional qualitative assessment. In large-scale clinical studies, efficient segmentation of multiple abdominal organs can also be used for biomarker screening, surgical navigation, and data mining.

Atlas-based segmentation provides a general-purpose approach to segment target images by transferring information from canonical atlases via registration. When adapting to abdomen, the variable abdominal anatomy between individuals (e.g., weight, stature, age, disease status) and within individuals (e.g., pose, respiratory cycle, clothing) can lead to substantial registration errors (Figures 1, 2). Previous abdominal segmentation approaches have used single probabilistic atlases constructed by co-registering atlases to characterize the spatial variations of abdominal organs (Park et al., 2003; Shimizu et al., 2007); statistical shape models (Okada et al., 2013; Okada et al., 2008) and / or graph theories (Bagci et al., 2012; Linguraru et al., 2012) have been integrated to refine the segmentation using probabilistic atlases. Multi-atlas segmentation (MAS), on the other hand, is a technique that has been proven effective and robust in neuroimaging by registering multiple atlases to the target image separately, and combining voxel-wise observations among the registered labels through label fusion (Sabuncu et al., 2010). Recently, Wolz et al. applied MAS to the abdomen using locally weighted subject-specific atlas (Wolz et al., 2013); yet the segmentation accuracies were inconsistent. We posit that the efficiency of atlas selection for abdominal MAS requires further exploration in the context of substantial registration errors, especially on clinically acquired CT.

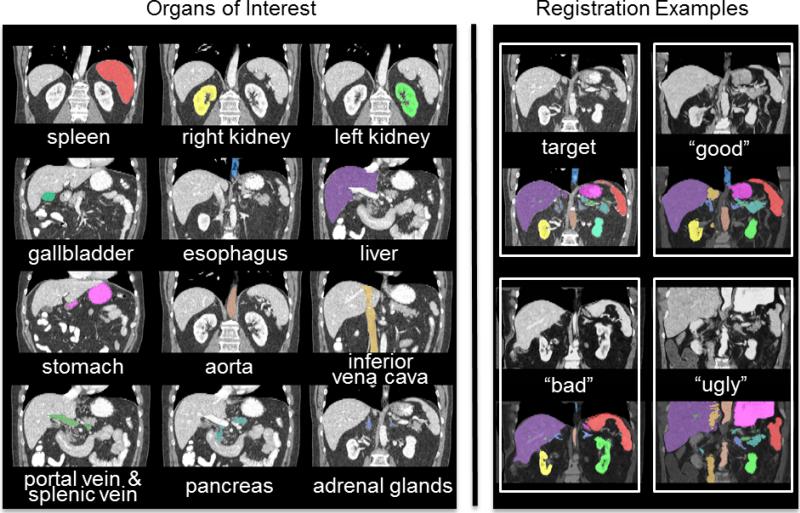
Figure 1.

Twelve organs of interest (left) and registration examples of variable qualities for one target image (right). Note that the “good”, “bad”, and “ugly” registration examples were selected regarding the organ-wise correspondence after the atlas labels were propagated to the target image.

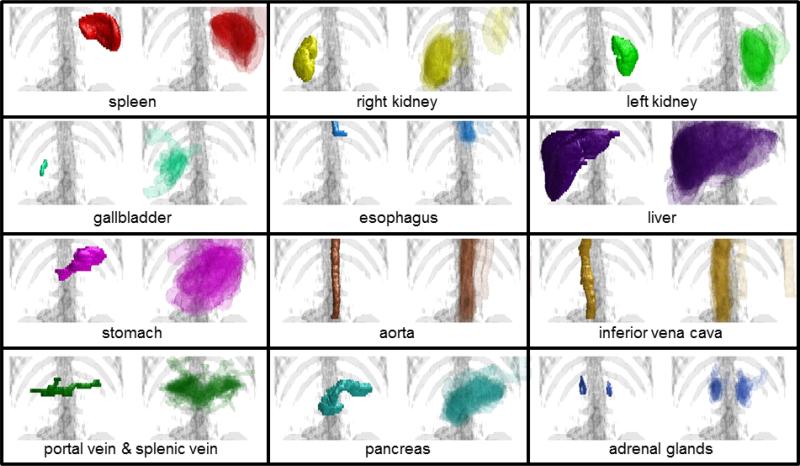
Figure 2.

Organ-wise examples of variations after non-rigid registrations. For each panel, the target manual segmentation is on the left, the 30 registered labels are semi-transparently overlaid on the right.

The selective and iterative method for performance level estimation (Langerak et al., 2010) (SIMPLE) algorithm raised effective atlas selection criteria based on the Dice similarity coefficient (Dice, 1945) overlap with intermediate voting-based fusion result, and addressed extensive variation in prostate anatomy to reduce the impact of outlier atlases. In (Xu et al., 2014), we generalized a SIMPLE theoretical framework to account for exogenous information through Bayesian priors – referred to as context learning; the newly presented model selected atlases more effectively for segmenting spleens in metastatic liver cancer patients. A further integration with joint label fusion (JLF) (Wang et al., 2012) addressed the label determination by reducing the correlated errors among the selected atlases, and yielded a median DSC of 0.93 for spleen segmentation.

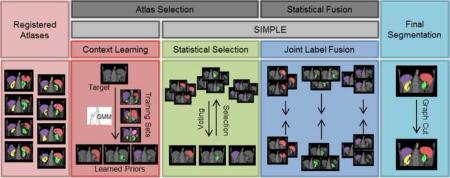
Herein, we propose an efficient approach for segmenting 12 abdominal organs of interest (Figure 1) in 75 metastatic liver cancer patients and 25 ventral hernia patients on clinically acquired CT. Based on the re-derived SIMPLE framework (Xu et al., 2014), we construct context priors, select atlases, and fuse estimated segmentation using JLF for each organ individually, and combine the fusion estimates of all organs into a regularized multi-organ segmentation using graph cut (Boykov et al., 2001) (Figure 3). The segmentation performances are validated with other MAS approaches, including majority vote (MV), SIMPLE, JLF, and the Wolz approach. This work is an extension of previous theoretical (Xu et al., 2014) and empirical (Xu et al., 2015) conference papers and presents new analyses of algorithm performance and parameter sensitivity.

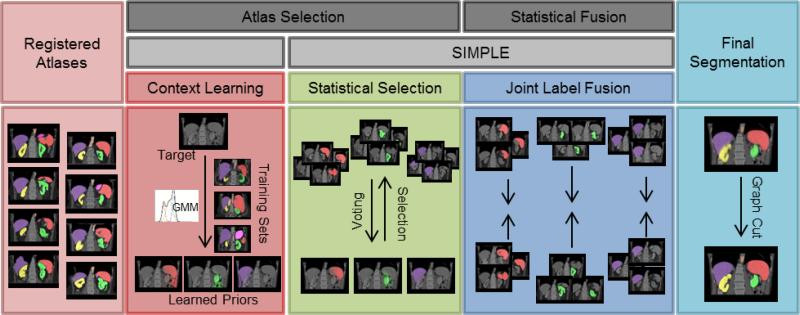
Figure 3.

Flowchart of the proposed method. Given registered atlases with variable qualities, atlas selection and statistical fusion are considered as two necessary steps to obtain a reasonable fusion estimate of the target segmentation. The SIMPLE algorithm implicitly combines these two steps to fusion selected atlases; however, more information can be incorporated to improve the atlas segmentation, and a more advanced fusion technique can be used after the atlases are selected. We propose to (1) extract a probabilistic prior of the target segmentation by context learning to regularize the atlas selection in SIMPLE for each organ, (2) use Joint Label Fusion to obtain the probabi listic fusion estimate while characterizing the correlated errors among the selected organ-specific atlases, and render the final segmentation for all organs via graph cut.

2. Theory

We re-formulate the SIMPLE algorithm from the perspective of Expectation-Maximization (EM) while focusing on the atlas selection step. In this principled likelihood model, the Bayesian prior learning from context features (e.g., intensity, gradient) is considered as exogenous information to regularize the atlas selection.

2.1 Statistical SIMPLE Model

Consider a collection of R registered atlases with label decisions, D ∈ L^N×R, where N is the number of voxels in each registered atlas, and L = {0,1,..., L – 1} represents the label sets. Let c ∈ S^R, where S = {0,1} indicates the atlas selection decision, i.e., 0 – ignored, and 1 – selected. Let i be the index of voxels, and j of registered atlases. We propose a non-linear rater model, $\theta \in {\mathbb{R}}^{R\times 2\times L\times L}$, that considers the two atlas selection decisions. Let the ignored atlases be no better than random chance, and the selected atlases be slightly inaccurate with error factors ε ∈ E^R×1, where $\mathbf{E}\in (0,\frac{L-1}{L})$. Thus

$${\theta }_{j0s^{\prime }s}=\frac{1}{L},\forall s^{\prime };{\theta }_{j1s^{\prime }s}=\{\begin{array}{cc}1-{∊}_j,\hfill & s^{\prime }=s\hfill \\ \frac{{∊}_j}{L-1},\hfill & s^{\prime }\ne s\hfill \end{array}\phantom{\}}$$ (1)

where each element θ_jns′s represents the probability that the registered atlas j observes label s′ given the true label is s and the atlas selection decision is n with an error factor ε_j if selected, – i.e., θ_jns′s ≡ f(D_ij = s′|T_i = s, c_j = n, ε_j).

Following (Warfield et al., 2004), let $\mathit{W}\in {\mathbb{R}}^{L\times N}$, where $W_{si}^{\left(k\right)}$ represents the probability that the true label associated with voxel i is label s at the k^th iteration. Using Bayesian expansion and conditional inter-atlas independence, the E-step can be derived as

$$W_{si}^{\left(k\right)}=\frac{f(T_i=s){\prod }_{j}f(D_{ij}\mid T_i=s,c_j^{\left(k\right)}=n,{∊}_j^{\left(k\right)})}{{\sum }_{s^{\prime }}f(T_i=s^{\prime }){\prod }_{j}f(D_{ij}\mid T_i=s^{\prime },c_j^{\left(k\right)}=n,{∊}_j^{\left(k\right)})}$$ (2)

where f(T_i = s) is a voxel-wise a priori distribution of the underlying segmentation. Note that the selected atlases contribute to W in a similar way as globally weighted vote given the symmetric form of θ_j1s′s as in the original SIMPLE.

In the M-step, the estimation of the parameters is obtained by maximizing the expected value of the conditional log likelihood function found in Eq. 2. For the error factor,

$$\begin{array}{cc}\hfill {∊}_j^{(k+1)}=& \arg \underset{{∊}_j}{\max }\sum _{i}E[\ln f(D_{ij}\mid T_i,c_j^{\left(k\right)},{∊}_j)\mid \mathit{D},c_j^{\left(k\right)},{∊}_j^{\left(k\right)}]\hfill \\ \hfill =& \arg \underset{{∊}_j}{\max }{\sum }_{s^{\prime }}{\sum }_{i:D_{ij}=s^{\prime }}{\sum }_s{W}_{si}^{\left(k\right)}\ln {\theta }_{j{c}_j^{\left(k\right)}{s}^{\prime }s}\equiv L_{{∊}_j}\hfill \end{array}$$ (3)

Consider the binary segmentation for simplicity, let $M_{TP}={\sum }_{i:D_{ij}=1}{W}_{1i}^{\left(k\right)}$, $M_{FP}={\sum }_{i:D_{ij}=1}{W}_{0i}^{\left(k\right)}$, $M_{FN}={\sum }_{i:D_{ij}=0}{W}_{1i}^{\left(k\right)}$, $M_{TN}={\sum }_{i:D_{ij}=0}{W}_{0i}^{\left(k\right)}$, and M_T = M_TP + M_TN, M_F = M_FP + M_FN. After taking partial derivative of L_εj,

$${∊}_j^{(k+1)}=\frac{M_F}{M_T+M_F},i.e.,1-{∊}_j^{(k+1)}=\frac{M_T}{M_T+M_F}$$ (4)

Then for the atlas selection decision

$$\begin{array}{cc}\hfill c_j^{(k+1)}=& \arg \underset{c_j}{\max }{\sum }_{i}E[\ln f(D_{ij}\mid T_i,c_j,{∊}_j^{(k+1)})\mid \mathit{D},{c_j}^{\left(k\right)},{∊}_j^{(k+1)}]\hfill \\ \hfill =& \arg \underset{c_j}{\max }{\sum }_{s^{\prime }}{\sum }_{i:D_{ij}=s^{\prime }}{\sum }_s{W}_{si}^{\left(k\right)}\ln {\theta }_{j{c}_j{s}^{\prime }s}.\hfill \end{array}$$ (5)

Given the intermediate truth estimate $W_{si}^{\left(k\right)}$, $c_j^{(k+1)}$ can be maximized by evaluating each 0/1 atlas selection separately. Note the selecting/ignoring behavior in Eq. 5 is parameterized with the error factor ε_j, and thus affected by the four summed values of True Positive (TP), False Positive (FP), False Negative (FN), and True Negative (TN) as in Eq. 4. Typical practice for a fusion approach might use the prior probability, f(T_i = s), to weight by expected volume of structure. With outlier atlases, one could reasonably expect a much larger region of confusion (i.e., non “consensus” (Asman and Landman, 2011)) than true anatomical volume. Hence, an informed prior would greatly deemphasize the TN and yield a metric similar to DSC. Therefore, we argue that SIMPLE is legitimately viewed as a statistical fusion algorithm that is approximately optimal for the non-linear rater model proposed in Eq. 1.

2.2 Context Learning

Different classes of tissues in CT images can be characterized with multi-dimensional Gaussian mixture models using intensity and spatial “context” features. On a voxel-wise basis, let $\mathit{v}\in {\mathbb{R}}^{d\times 1}$ represent a d dimensional feature vector, m ∈ M indicate the tissue membership, where M = {1, ... , M} is the set of possible tissues, and typically, a superset of the label types, i.e., $\mathit{M}\supseteq \mathit{L}$. The probability of the observed features given the tissue type is t can be represented with the mixture of N_G Gaussian distributions,

$$f(\mathit{v}\mid m=t)=\sum _{k=1}^{N_G}\frac{{\alpha }_{kt}}{{\left(2\pi \right)}^{\frac{d}{2}}{\mid {\mathit{C}}_{kt}\mid }^{\frac{1}{2}}}exp\left[-\frac{1}{2}{(\mathit{v}-{\mu }_{kt})}^T{\mathit{C}}_{kt}^{-1}(\mathit{v}-{\mu }_{kt})\right]$$ (6)

where ${\alpha }_{kt}\in {\mathbb{R}}^{1\times 1}$, ${\mu }_{kt}\in {\mathbb{R}}^{d\times 1}$, and ${\mathit{C}}_{kt}\in {\mathbb{R}}^{d\times d}$ are the unknown mixture probability, mean, and covariance matrix to estimate for each Gaussian mixture component k of each tissue type t by the EM algorithm following (Van Leemput et al., 1999). This context model can be trained from datasets with known tissue separations.

The tissue likelihoods on an unknown dataset can be inferred by Bayesian expansion and can use a flat tissue membership probability from extracted feature vectors.

$$f(m=t\mid \mathit{v})=\frac{f(\mathit{v}\mid m=t)f(m=t)}{{\sum }_{t^{\prime }}f(\mathit{v}\mid m=t^{\prime })f(m=t^{\prime })}=\frac{f(\mathit{v}\mid m=t)}{{\sum }_{t^{\prime }}f(\mathit{v}\mid m=t^{\prime })}$$ (7)

Consider a desired label s as one tissue type t, and thus f(T_i = s) ≡ f(m = t|v), the Bayesian prior learning from context features serves to regularize the intermediate fusion estimate in Eq. 3, and hence the atlas selection.

3. Methods and Results

3.1 Data

Under Institutional Review Board (IRB) supervision, the first-session of abdomen CT scans of 75 metastatic liver cancer patients were randomly selected from an ongoing colorectal cancer chemotherapy trial, and an additional 25 retrospective scans were acquired clinically from post-operative patients with suspected ventral hernias. The 100 scans were captured during portal venous contrast phase with variable volume sizes (512 × 512 × 33 ~ 512 × 512 × 158) and field of views (approx. 300 × 300 × 250 mm³ ~ 500 × 500 × 700 mm³). The in-plane resolution varies from 0.54 × 0.54 mm² to 0.98 × 0.98 mm², while the slice thickness ranges from 1.5 mm to 7.0 mm. Twelve abdominal organs were manually labeled by two experienced undergraduate students, and verified by a radiologist on a volumetric basis using the MIPAV software (NIH, Bethesda, MD (McAuliffe et al., 2001)). All images and labels were cropped along the cranio-caudal axis with a tight border without excluding liver, spleen, and kidneys before any processing (following (Wolz et al., 2013)).

3.2 General Implementation

We used 10 subjects to train context models for 15 tissue types, including twelve manually traced organs, and three automatically retrieved tissues (i.e., muscle, fat, and other) using intensity clustering and excluding the traced organ regions. Six context features were extracted, including intensity, gradient, and local variance, and three spatial coordinates with respect to a single landmark, which was loosely identified as the mid-frontal point of the lung at the plane with the largest cross-sectional lung area (see rendering in Figure 8). We specified the number of components of Gaussian mixture model, N_G = 3. For each organ, the foreground and background likelihoods were learned from the context models based on the context features on target images, and used as a two-fold spatial prior to regularize the organ-wise SIMPLE atlas selection. We constrained the number of selected atlases as no less than five and no larger than ten.

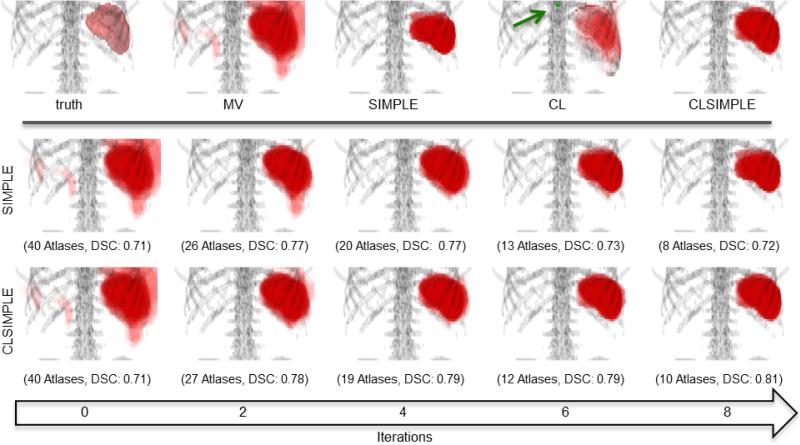
Figure 8.

(upper pane): The ground truth surface rendering and the probability volume rendering of different methods for spleen segmentation. Note that the transparencies of volume rendering were adjusted for visualization. CL indicates the posterior probability of spleen when applying the trained context learning model to the target. The green arrow points at the landmark used for deriving spatial context. (lower pane): Progressive results of SIMPLE and CLSIMPLE along iterations. Note that both methods reach the convergence within 8 iterations in this case.

When using JLF on the selected atlases for each organ, we specified the local search radii (in voxel) as 3 × 3 × 3, the local patch radii (in voxel) as 2 × 2 × 2, and set the intensity difference mapping parameter, and the regularization term as 2 and 0.1, respectively (i.e., default parameters).

Following (Song et al., 2006; Wolz et al., 2013), we regularized the final segmentation with graph cut (GC). The GC problem is solved by maximizing the following MRF-based energy function

$$E\left(p\right)=\lambda \sum _{i\in \mathbb{I}}{D}_i\left(p_i\right)+\sum _{\{i,i^{\prime }\}\in \mathcal{N}}{V}_{i,i^{\prime }}(p_i,p_{i^{\prime }})$$ (8)

where i and i′ are voxel indices, d835dc5d represents the labeling of the final segmentation for image $\mathbb{I}$. The data term D_i(p_i) characterize the probability of voxel i assigned to the label p_i; we define it as a combination of the probabilistic fusion estimate from JLF with the intensity likelihoods using 1-D context learning. The smoothness term V_i,i′ (p_i, p_i′) penalizes the discontinuities between the voxel pair {i, i′} in the specified neighborhood system $\mathcal{N}$; we define it as a combination of the intensity appearance with local boundary information. d835df06 is a coefficient that weights the data term over the smoothness term; we set it as 3.3. Note that we only applied GC smoothing to large organs (i.e., spleen, kidneys, liver, stomach), and kept the JLF results for the remaining organ structures.

For the direct JLF approach, the same parameters were used as above, except that it was conducted for all organs simultaneously. For the Wolz approach, we kept 30 atlases for the global atlas selection, adjusted the exponential decay for the organ level weighting to support 10 atlases, followed (Wolz et al., 2013) for voxel-wise weighting by non-local means, and used the same GC scheme as applied to our proposed method.

Note that we used the JLF (Wang et al., 2012) method in the Advanced Normalization Tools (ANTs) (Avants et al., 2009), all other algorithms, i.e., MV (Rohlfing et al., 2004), SIMPLE (Langerak et al., 2010), the Wolz approach (Wolz et al., 2013), and GC (Boykov et al., 2001; Song et al., 2006), were implemented based on the corresponding literature, and run on a 64-bit 12-core Ubuntu Linux workstation with 48G RAM.

3.3 Motivating Simulation

3.3.1 Experimental Setup

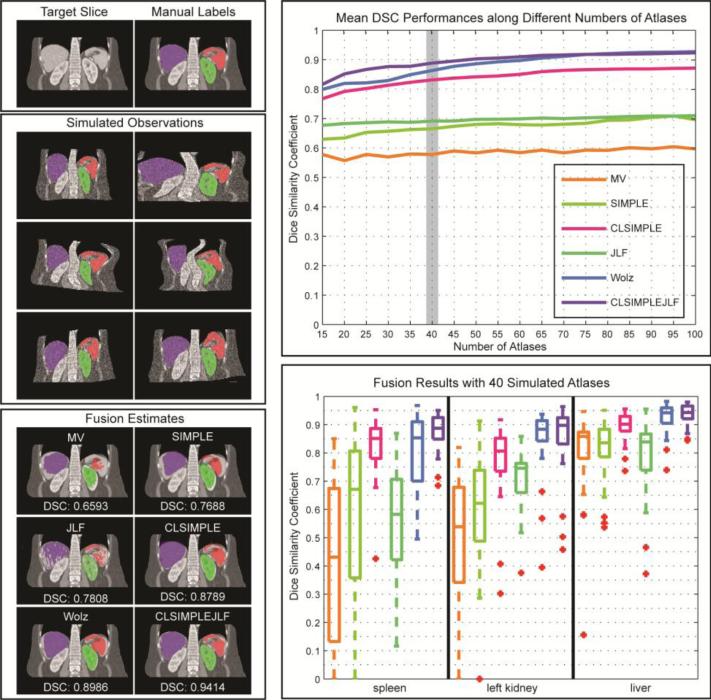
A simulation on 2-D CT slices was constructed to demonstrate and motivate the benefits of SIMPLE context learning for atlas selection and label fusion (see Figure 4). Forty CT scans were randomly selected from the 90 subjects not used for context learning. A representative slice with the presences of all three organs, i.e., spleen, left kidney, and liver, was extracted from each scan, and considered as a target image. A hundred simulated observations were estimated by applying a random transformation model to each target slice, and considered as the atlases with different degrees of registration errors for segmenting the target.

Figure 4.

(top left) Target slices and the associated manual labels. (middle left) Simulated observations drawn from an individual target slice with a randomly generated transformation model. (top right) The mean DSC (over 40 target slices and three organs) values evaluated for six label fusion approaches using different numbers (from 15 to 100) of atlases. (bottom right) Organ-wise DSC performances for the fusion results using 40 simulated atlases. (bottom left) Fusion estimates using 40 simulated atlases overlaid on a representative target slice, and annotated with the mean DSC value over the organs.

The simulation model involved an affine followed by a non-rigid transformation. The affine transformation consisted of a rotational component as well as two translational and two scaling components, with the effect of each component drawn from a zero-mean Gaussian distribution with standard deviations of 2 degrees for the rotational component, 5 mm for the translational components and 0.2 mm for the scaling components. The non-rigid transformation used a deformation field created by sextic Chebyshev polynomials. The Chebyshev coefficients for each grid location were randomly generated from a standard normal distribution, on the top of which, two additional factors to control the deformation effect on each dimension were drawn from a zero-mean Gaussian distribution with standard deviations of 3 mm. Voxel-wise Gaussian random noise (with a standard deviation of 100 Hounsfield units) was added to the simulated intensity images.

Six MAS methods, i.e., MV, SIMPLE, JLF, CLSIMPLE, CLSIMPLEJLF, and the Wolz approach were applied to 40 target slices using different numbers of atlases (from 15 to 100, with a step size of 5), and then evaluated based on the DSC values of spleen, left kidney, and liver. Note that (1) CLSIMPLE used MV, while CLSIMPLEJLF used JLF for label fusion after atlas selection; (2) We did not append GC to smooth the results of CLSIMPLEJLF and the Wolz approach since no surface distance error was assessed in this simulation. (3) The Wolz approach here used the simulated atlases for all three stages of subject-specific atlas construction given no other intermediate registered atlases.

3.3.2 Results

Under the tests using various numbers of atlases, CLSIMPLE, CLSIMPLEJLF, and the Wolz approach demonstrate consistently and substantially more accurate segmentations than MV, SIMPLE, and JLF. CLSIMPLEJLF and the Wolz approach yield similar accuracies when using larger than 70 atlases (p-value < 0.05, paired t-test), while CLSIMPLEJLF performs better with less atlases available.

Using 40 atlases, the spread of DSC values demonstrate significant improvement by incorporating context learning. CLSIMPLE achieves a median DSC improvement of 0.26 and 0.15 over MV and SIMPLE, respectively, while CLSIMPLEJLF outperforms JLF by 0.19. CLSIMPLEJLF also provides the least range of DSC values, and thus indicates its robustness to the outliers. A representative fusion result represents that CLSIMPLEJLF accurately captures the shape, location, and orientation of the spleen, left kidney, and liver.

3.4 Volumetric Multi-Organ Multi-Atlas Segmentation

3.4.1 Experimental Setup

Ten of the 100 subjects were randomly selected as training datasets for context learning (these ten subjects happen to be all within the 75 liver cancer datasets), thus the segmentations were validated on the remaining 90 subjects. From the same cohort, forty subjects were randomly selected (independent from the ten selections for context learning) as the atlases for validating five MAS approaches, including MV, SIMPLE, JLF, the Wolz approach, and our proposed method (CLSIMPLEJLFGC), on the segmentation of twelve abdominal organs against the manual labels using DSC, mean surface distance (MSD), and Hausdorff distance (HD).

The five approaches shared a common multi-stage registration procedure for each of the 90 target images (excluding the 10 context learning), where all atlases (except the target if it was selected in the set of atlases) were aligned to the target in the order of rigid, affine and a multi-level non-rigid registration using free-form deformations with B-spline control point spacings of 20, 10, and 5mm (Rueckert et al., 1999). In summary, (1) the 10 context learning datasets were never used as targets (but they were allowed to be atlases), and (2) an atlas image was never used as its own target. Randomization of selecting context learning datasets and atlas images was performed to maximize the available data subject to these constraints.

3.4.2 Results

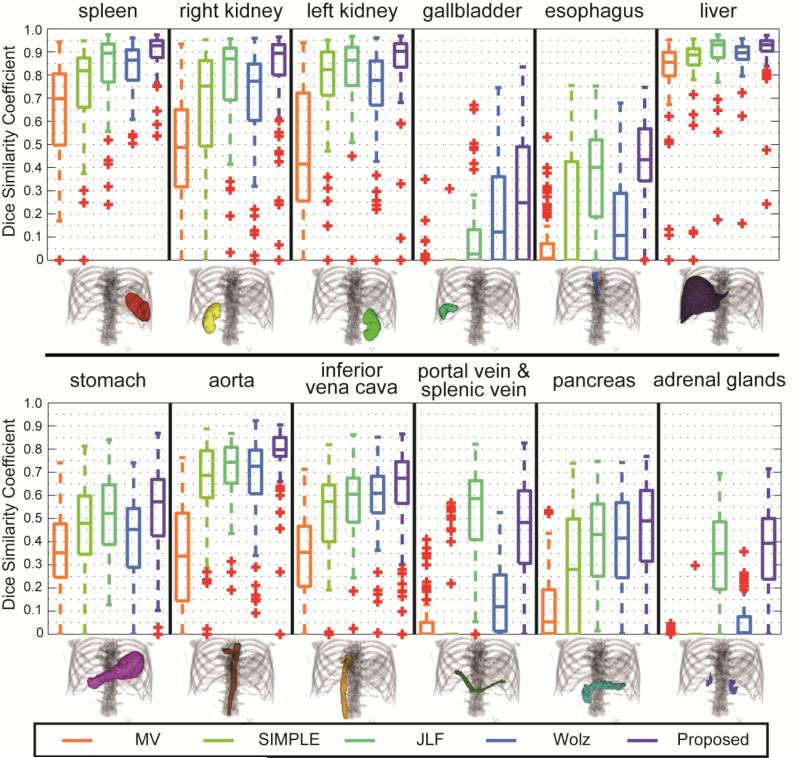
Compared to the other MAS approaches, the proposed method presents consistently improved segmentation in DSC on 11 of 12 organs of interest (Figure 5, Table 1). Based on the mean DSC of each organ, a median improvement of 7.0% and 16.2% were achieved over JLF and Wolz, respectively. The segmentations of spleen, gallbladder, esophagus, and aorta using the proposed method significantly outperformed those using the other approaches.

Figure 5.

Boxplot comparison among five tested methods for 12 organs.

Table 1.

Quantitative evaluation for five tested methods using dice similarity coefficient (mean ± std.).

	MV	SIMPLE	JLF	Wolz	Proposed
Spleen	0.63 ± 0.24	0.73 ± 0.22	0.84 ± 0.15	0.83 ± 0.10	0.90 ± 0.08**
R. Kidney	0.47 ± 0.26	0.65 ± 0.27	0.79 ± 0.19	0.70 ± 0.24	0.81 ± 0.20
L. Kidney	0.46 ± 0.27	0.74 ± 0.25	0.81 ± 0.17	0.72 ± 0.21	0.84 ± 0.20
Gallbladder	0.01 ± 0.04	0.00 ± 0.03	0.09 ± 0.15	0.19 ± 0.21	0.27 ± 0.26*
Esophagus	0.07 ± 0.11	0.20 ± 0.25	0.37 ± 0.21	0.18 ± 0.19	0.43 ± 0.18*
Liver	0.79 ± 0.20	0.84 ± 0.18	0.89 ± 0.11	0.88 ± 0.09	0.91 ± 0.09
Stomach	0.34 ± 0.18	0.46 ± 0.19	0.51 ± 0.17	0.41 ± 0.19	0.55 ± 0.18
Aorta	0.34 ± 0.22	0.64 ± 0.22	0.72 ± 0.13	0.67 ± 0.18	0.77 ± 0.13*
IVC	0.33 ± 0.18	0.50 ± 0.21	0.57 ± 0.15	0.58 ± 0.15	0.62 ± 0.19
PV & SV	0.05 ± 0.10	0.05 ± 0.15	0.52 ± 0.20**	0.16 ± 0.16	0.45 ± 0.21
Pancreas	0.11 ± 0.13	0.27 ± 0.25	0.40 ± 0.19	0.40 ± 0.19	0.45 ± 0.21
A. Glands	0.00 ± 0.01	0.00 ± 0.03	0.34 ± 0.20	0.05 ± 0.08	0.36 ± 0.19

^*indicates that the DSC value was significantly higher than the second best DSC across the methods for the organ segmentation as determined by a right-tail paired t-test with p<0.05.

^**indicates a p<0.01.

The serpentine labels of portal vein and splenic vein are barely captured by registration (0.06 in DSC by median), thus the intermediate voting-based fusion estimates had a good chance of missing the structure entirely (zero median in DSC for MV and SIMPLE). A MV fusion (instead of JLF) of the selected atlases by SIMPLE context learning identified this structure better (0.25 in DSC by median). While with limited atlases of catastrophic registration errors, our proposed method was outperformed by JLF with all available atlases.

On the other hand, in the context of reasonably substantial registration errors for other organs, our proposed method yields segmentation with better performances in not only accuracies, but also efficiencies. With much fewer atlases (while more target-alike than average) included for label fusion, our method (1.5 hours, 10G RAM) relieved massive computational time and memory required by JLF (22 hours, 30G RAM) and Wolz approach (30 hours, 10G RAM), and thus provides more efficient abdominal segmentations. As found in our previous study (Xu et al., 2014), the MV fusion of the registered atlases with the top five DSC achieves a median DSC of 0.9 for spleen. Therefore, we considered the global non-linear selection of the atlases as a necessary procedure in addition to the locally weighted label determination for MAS in abdomen.

With a closer look, our proposed method yielded the segmentation with at least 0.89 in DSC and less than 3.3 mm in MSD for the major organs of interest, i.e., spleen, kidneys, and liver. For other structures, the proposed method also provided successful identification over half of the subjects, even those that empirically considered difficult to capture, e.g., adrenal glands (Tables 2, 3). Qualitatively, the segmentation on a subject with median accuracy captures the organs from the perspective of both 3-D rendering and 2-D coronal slices (Figure 6). As a side note, applying GC for the five large organs (i.e., spleen, kidneys, liver, stomach) reduces the HD by 1.99 mm (p < 0.001, paired t-test), with similar the DSC values (Δ = –0.0038, p < 0.01, paired t-test).

Table 2.

Quantitative evaluation for five tested methods using mean surface distance (mean ± std.) in mm.

	MV	SIMPLE	JLF	Wolz	Proposed
Spleen	6.44± 4.30	4.42± 3.55	4.38± 7.44	3.06± 2.21	1.75± 1.71**
R. Kidney	7.81± 6.73	5.22± 5.85	4.81± 10.38	4.80± 5.66	2.99± 3.92**
L. Kidney	6.55± 4.63	2.92± 2.95	5.38± 11.12	3.85± 3.01	2.00± 2.80**
Gallbladder	12.88± 8.29	N/A†	21.84± 29.35	11.89± 10.53**	14.36± 20.34
Esophagus	7.59± 3.20	3.73± 1.73	7.61± 15.26	6.76± 3.70	4.16± 2.05
Liver	7.42± 9.21	5.03± 6.02	4.69± 7.01	4.86± 5.48	3.22± 4.43*
Stomach	16.06± 6.61	10.96± 5.18	8.75± 6.92*	16.91± 8.15	10.26± 6.36
Aorta	10.18± 7.43	4.26± 3.53	5.89± 12.83	4.68± 3.74	3.02± 2.27**
IVC	7.92± 5.35	4.32± 1.82	6.36± 13.77	4.41± 2.38	3.75± 1.84**
PV & SV	20.00± 5.54	6.37± 3.18	7.24± 11.61	17.46± 7.54	5.92± 5.08**
Pancreas	16.08± 8.81	6.51± 3.96	8.24± 12.52	7.82± 4.75	5.47± 3.51**
A. Glands	19.88± 6.43	N/A†	7.75± 15.12	13.30± 8.71	4.06± 3.56*

^†N/A was assigned when the segmentations were empty, and the MSD could not be computed for over 75 subjects (at least 15 subjects were not empty);

^*indicates that the MSD value was significantly lower than the second lowest MSD across the methods for the organ segmentation as determined by a left-tail paired t-test with p<0.05.

^**indicates a p<0.01.

Table 3.

Quantitative metrics of the proposed segmentation method.

Metrics	Dice Similarity Coefficient	Surface Distance (mm)
Organs	Median [Min, Max]	Sym. HD
Spleen	0.93 [0.54, 0.97]	17.27 ± 8.42
R. Kidney	0.89 [0.00, 0.96]	19.47 ± 11.37
L. Kidney	0.90 [0.00, 0.97]	16.13 ± 8.05
Gallbladder	0.25 [0.00, 0.84]	34.57 ± 22.87
Esophagus	0.43 [0.00, 0.75]	17.97 ± 5.46
Liver	0.93 [0.24, 0.97]	34.46 ± 15.03
Stomach	0.57 [0.00, 0.87]	49.48 ± 18.91
Aorta	0.80 [0.00, 0.90]	23.23 ± 10.98
IVC	0.67 [0.00, 0.87]	19.89 ± 5.60
PV & SV	0.48 [0.00, 0.83]	38.37 ± 17.18
Pancreas	0.49 [0.00, 0.77]	31.34 ± 8.92
A. Glands	0.39 [0.00, 0.72]	20.68 ± 8.68

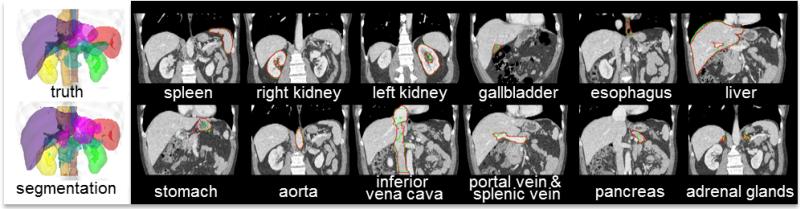
Figure 6.

Qualitative segmentation results on a subject with median DSC. On the left, the 3-D organ labels are rendered for the true segmentation, and the proposed segmentation. On the right, the truth (red) and the proposed segmentation (green) for each organ of interest are demonstrated on a representative coronal slice.

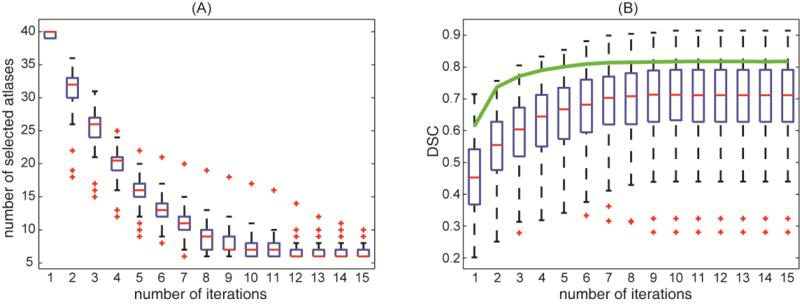
In a retrospective analysis, CLSIMPLE demonstrates effective atlas selection for spleen along iterations in terms of the mean DSC of the selected atlases and their MV fusion estimate (Figure 7). Comparing to the original SIMPLE on an example with median accuracy, CLSIMPLE keeps adjusting the atlas selection with learned context on the target image as opposed to yielding progressively biased intermediate fusion estimate if only the registered labels were used (Figure 8).

Figure 7.

Demonstration of the effectiveness of CLSIMPLE atlas selection for spleen segmentation on 90 subjects along number of iterations (A) number of selected atlases remaining along iterations. (B) mean DSC value of the selected atlases along iterations. Note the solid green line in (B) indicates the mean DSC of the majority vote fusion estimate using the selected atlases across all subjects.

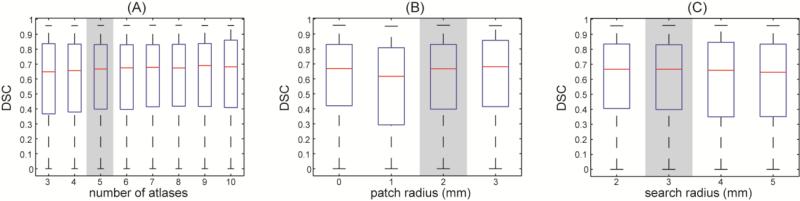
In a further test on the parameter sensitivity of the proposed method, ten subjects were randomly selected from the 90 subjects used for validation. The impact of using different values of three parameters, i.e., (1) number of atlases minimally allowed in CLSIMPLE, (2) patch radius in JLF, and (3) search radius in JLF, on the overall performances of the proposed method is shown in Figure 9. Comparing to the parameters values chosen for the validation of 90 subjects, potential improvement were observed with more atlases (9 atlases, Δ = 0.0231, p < 0.05, paired left-tail Wilcoxon signed rank test), and larger patch radius (3×3×3 voxels, Δ = 0.0143, p < 0.005, paired left-tail Wilcoxon signed rank test).

Figure 9.

Illustration of parameters sensitivity of the proposed method. The overall DSC values (including all twelve organs on ten subjects) are evaluated on different values of (A) number of atlases minimally allowed in CLSIMPLE; (B) patch radius in JLF; and (3) search radius in JLF. Note when testing on one parameter, the other two keep as the values the gray backgrounds; these values are also used for the segmentation of 90 subjects.

4. Discussion

The proposed method provides a fully automated approach to segment twelve abdominal organs on clinically acquired CT. The SIMPLE context learning reduces the impact of the vastly problematic registrations with appropriate atlas selection considering exogenous contexts in addition to intermediate fusion estimate, and thus enables more efficient abdominal segmentations. We note that proposed generative model naturally leads to an iterative atlas selection, which differs from the STEPS approach (Jorge Cardoso et al., 2013) that first locally ranks atlases, and uses the top local atlases for statistical fusion.

MAS has been widely used for segmenting brain structures; commonly accepted optimal number of the included atlases is approximately 10 to 15. While the registration errors for brains are well constrained within the cranial vault, the registrations for abdomens, on the other hand, have much more chances to fail in terms of both global alignment and internal correspondence. Thus an atlas selection procedure along with more included atlas images becomes essential to MAS for abdominal organs, where the effectiveness of atlas selection determines the segmentation robustness. It can be also expected that this atlas selection procedure can be beneficial for brain segmentation among subjects with substantial aging and pathological variations. The Wolz approach selects/weights atlases based on the similarity between the target and atlases in a hierarchical manner, which turns out to be more effective for the homogeneous datasets in the simulation than it is for the clinically acquired datasets. We posit that the inconsistent performances of the Wolz approach lie in the non-robust efficacy of similarity measure as discussed in the original SIMPLE literature (Langerak et al., 2010). Using the SIMPLE context learning framework, our proposed method yields consistently good performances in both datasets.

Some specific approaches for single organ segmentation, e.g., liver (Heimann et al., 2009) and pancreas (Shimizu et al., 2010), can provide higher performances, while our efforts in this study focus on the development of a generic approach for multiple organ segmentation. In addition, provided with adequate number (>20) of labeled atlases, we expect that our proposed method can be adapted to other thoracic (e.g., lungs), abdominal (e.g., psoas muscles), and pelvic (e.g., prostate) organs on CT, where the organs to segment have (1) consistent intensity-based and spatial appearance, (2) high contrast to the surrounding tissues, and (3) reasonable amount of overlap between the registered atlases and the target. Much caution should be taken when these three conditions are not satisfied. For example, intensity normalization would be required for applications on MR images, texture-based features can be included when structures with similar intensities but distinguishable textures are close to each other, pre-localization would be necessary for tiny, thin, and/or irregular structures so that registrations errors can be constrained within the region of interest. Our future work will focus on the cases above to further improve the segmentation performances, and enhance the generalization of the method.

The estimated segmentations could be used in large-scale trials to provide abdominal surgical navigation, organ-wise biomarker derivation, or volumetric screening. The method also enables explorative studies on the correlation the structural organ metrics with surgical/physiological conditions. We note that some organs (e.g., gallbladder, portal and splenic vein, adrenal glands) have low DSC and/or high MSD values despite the proposed method presents better segmentation over other tested MAS methods; their practice use can be limited. To our best knowledge, fully-automatic segmentation of these structures are essentially atlas-based (Gass et al., 2014; Shimizu et al., 2007). Although no ideal result has been accomplished so far, atlas-to-target registration remains the most effective approach to roughly capture these structures. Thus we present the segmentation performance for all twelve organs as a benchmark for further development. Other types of segmentation approaches, e.g., geodesic active contours (Caselles et al., 1997), graph cut (Boykov et al., 2001), and statistical shape models (Heimann and Meinzer, 2009), are sensitive to the surrounding environment; they are often incorporated with the atlas-based framework to provide complementary information and refine the results (Linguraru et al., 2012; Okada et al., 2013; Shimizu et al., 2007). Some semi-automatic approaches (Kéchichian et al., 2013) demonstrate the potential for fundamentally better results with the requirement of manual organ identification. MAS approach performs well on automatically identifying/localizing these organs, and thus can be used as an initialization for those semi-automatic methods, and make the whole process free from manual intervention.

Highlights.

• Represent the SIMPLE atlas selection criteria with principled likelihood models.

• Augment the SIMPLE framework with exogenous information learned from image context.

• Integrate SIMPLE context learning with joint label fusion and graph cut.

• Efficiently segment 12 abdominal organs on clinical CT of liver cancer patients.