MR Image Synthesis by Contrast Learning On Neighborhood Ensembles

Abstract

Automatic processing of magnetic resonance images is a vital part of neuroscience research. Yet even the best and most widely used medical image processing methods will not produce consistent results when their input images are acquired with different pulse sequences. Although intensity standardization and image synthesis methods have been introduced to address this problem, their performance remains dependent on knowledge and consistency of the pulse sequences used to acquire the images. In this paper, an image synthesis approach that first estimates the pulse sequence parameters of the subject image is presented. The estimated parameters are then used with a collection of atlas or training images to generate a new atlas image having the same contrast as the subject image. This additional image provides an ideal source from which to synthesize any other target pulse sequence image contained in the atlas. In particular, a nonlinear regression intensity mapping is trained from the new atlas image to the target atlas image and then applied to the subject image to yield the particular target pulse sequence within the atlas. Both intensity standardization and synthesis of missing tissue contrasts can be achieved using this framework. The approach was evaluated on both simulated and real data, and shown to be superior in both intensity standardization and synthesis to other established methods.

1. Introduction

Magnetic resonance (MR) imaging (MRI) is the preferred diagnostic and research imaging modality for soft tissue contrast. It is a very versatile modality in part because MR pulse sequences allow for diverse manipulations of the nuclear magnetic spins, thus providing a vast amount of complementary information in neuroimaging. For example, T₁-weighted (T₁-w) images are typically preferred for tissue segmentation (Styner et al., 2000; Prastawa et al., 2004; Roy et al., 2012) and cortical reconstruction (Dale and Fischl, 1999; Han et al., 2004; Shiee et al., 2014), whereas Double Spin Echo (DSE) and FLAIR (Fluid Attenuated Inversion Recovery) sequences are useful to delineate tissue abnormalities like white matter lesions (Shiee et al., 2010).

The versatility of MRI also poses a problem. Patient scanner time is finite and thus decisions are made about which subset of the many available pulse sequences to acquire. Another factor in this decision is the expense of scanning and the long scan time associated with various sequences, T₂-weighted (T₂-w) images for example. A confound in the acquired data is the inhomogeneous quality of the data due to the different imaging requirements of each sequence. For example, the DSE sequence is generally acquired at a much lower resolution than a T₁-w magnetization prepared rapid gradient echo (MPRAGE) sequence because of the longer repetition time (TR). Sequences like FLAIR suffer from artifacts that are not present in other sequences (Stuckey et al., 2007), contributing to problems with their use in multimodal analysis. More fundamentally, the imaging data can be corrupted due to patient motion or inappropriate parameter settings. Our work is focused on improving the utility of multimodal data through image synthesis, either by restoring corrupt data or by standardizing the intensity of existing data.

By image synthesis we mean learning and applying an intensity transformation to MR images in order to produce images that perform better in various image processing tasks. The resultant synthetic images could belong to any pulse sequence we choose to synthesize. Image synthesis, in the broadest sense, is already used in nearly every image processing pipeline—for example in intensity inhomogeneity correction or intensity scaling. Intensity standardization transforms the intensities of a given subject image to a reference image, typically of the same (or similar) pulse sequence. It is a special case of image synthesis, in which the synthesized image is of the same (or similar) pulse sequence. Synthesized images are not meant to be used for diagnostic purposes or to replace scanning subjects. Rather, they are intended to facilitate image analysis for the extraction of clinical or scientific information.

Intensity standardization has long been an important problem for MR image processing, and many solutions have been proposed. Unlike x-ray computed tomography (CT), MRI does not have a consistent image intensity scale for different tissues. Though this does not pose a problem for diagnostic purposes, automatic image processing algorithms such as segmentation algorithms are known to be inconsistent as a result (Nyúl and Udupa, 1999). Since there is no consistent anatomical meaning to the numerical value of an intensity, it is difficult to directly compare MR data acquired at different sites and on different scanners. Even data acquired in the same machine for the same subject can differ in intensity characteristics. Intensity standardization using ideas of image synthesis can assist in consistent processing of such data (Roy et al., 2013a).

Image synthesis of an alternative modality has been shown to be useful in many image analysis tasks. Iglesias et al. (2013) showed that it is better to register a T₂-w image to a synthetic T₂-w image created from a T₁-w image, than to directly register a T₂-w image to the T₁-w image. A similar application to correct geometric distortion in diffusion tensor images using synthetic T₂-w images was demonstrated by Roy et al. (2013a). In Jog et al. (2014a) it was shown that datasets with a missing FLAIR image could be augmented by creating a synthetic FLAIR image. Lesion segmentation using synthetic FLAIRs was shown to be equivalent to and more consistent than the lesion segmentation using real FLAIRs. The consistency was attributed to the fact that the synthetic FLAIRs were produced using a common set of atlas or training images. The lesion segmentation markedly improved when real FLAIR images with significant imaging artifacts were replaced with synthetic FLAIRs. In Jog et al. (2014b), a method to create super-resolution images using image synthesis ideas was presented. This significantly improved the image quality and resolution of inherent low resolution data acquired using the DSE or FLAIR pulse sequences.

Image synthesis in general has gained significant attention in the medical imaging community in the last seven years (Rousseau, 2008; Roy et al., 2010a,b; Rousseau, 2010; Roy et al., 2011; Roohi et al., 2012; Jog et al., 2013a; Rousseau and Studholme, 2013; Konukoglu et al., 2013; Burgos et al., 2013; Ye et al., 2013; Iglesias et al., 2013; Roy et al., 2013a,b, 2014). A classical registration-based solution to this problem was presented in (Miller et al., 1993): Given a subject image b₁ with contrast ₁ and a pair of co-registered atlas images a₁ and a₂ of contrasts ₁ and ₂, respectively, a₁ is registered to b₁ using a deformable registration algorithm, and the transformation is then applied to a₂ to produce the synthetic image b̂₂ with contrast ₂. The method demonstrated synthesis of positron emission tomography images from MR images. An extension of this approach, described by Burgos et al. (2013), uses multiple, aligned pairs of MR and CT images as atlases and performs multi-atlas deformable registration to the subject with intensity fusion to synthesize a subject CT image from a subject MR. This approach produces synthetic CT images from which the attenuation coefficients are learned and used for PET reconstruction. A more general, intensity transformation-based approach to image synthesis is described by Hertzmann et al. (2001), wherein an image transformation, which can be defined as an application of an image filter, was learned. Given training data the filtered image was synthesized from the unfiltered one by applying the learned transformation. This approach, known as image analogies, has seen use in MRI synthesis (Iglesias et al., 2013). More recently, the work by Roy et al. (2011, 2013a) handles image synthesis using a sparse reconstruction of a dictionary of atlas image patches.

While each of these methods produces a useful, synthetic image under different initial assumptions, they each have certain shortcomings. For instance, deformable registration may fail to yield an accurate registration throughout the whole brain. If the subject images show pathology in normal tissue regions and the atlas images do not, then registration is unable to recreate these differences. Methods based on intensity transformation like image analogies and the sparse reconstruction approach are dependent on the b₁ image being correctly intensity standardized with the training data (atlas image a₁). These methods also do not take into account the MR image formation process while synthesizing the new image. We would like to improve upon these approaches by using the atlas-based intensity transformation ideas while incorporating the MR image formation process.

Jog et al. (2013a) presented a patch-based regression approach using random forest regression for synthesizing MR images. The synthesis is modeled as a nonlinear regression in terms of a patch in a₁ transforming to the corresponding central voxel in a₂. This approach, though extremely fast, also requires the subject image to be intensity standardized to the atlas image prior to applying the learned regression and does not account for the MR physics of acquisition. In this paper, we have built upon this random forest regression by synthesizing a new subject image from the available subject image(s) and a set of atlas images. We create a preprocessing framework in which we synthesize images using knowledge of both the imaging physics and information in the atlas. Voxel intensity in MRI is primarily dependent on intrinsic nuclear magnetic resonance (NMR) parameters such as proton density (P_D), transverse relaxation time (T₂), longitudinal relaxation time (T₁) and on pulse sequence parameters such as scanner gain (G₀), repetition time (T_R), echo times (T_E), etc. Given an unseen subject image (and the pulse sequence) we estimate the pulse sequence parameters using information derived solely from the image intensities. We apply this pulse sequence with the estimated parameters to quantitative P_D, T₁, and T₂ images in our atlas. Thus, a new atlas image with the same imaging characteristics as the subject image is synthesized. We then learn a nonlinear regression (Jog et al., 2013a) between this standardized atlas image and the desired, target atlas contrast. This learned regression can then be applied to the subject image, thereby synthesizing a subject image with the desired contrast.

The core idea of estimating tissue parameters was previously used in Fischl et al. (2004). However, that approach required the acquisition of very specific pulse sequences—a requirement that our approach does not share. We refer to our method as Pulse Sequence Information-based Contrast Learning On Neighborhood Ensembles (PSI-CLONE)—which we stylize as Ψ-CLONE. We describe our four-step algorithm to perform image synthesis in Section 2. Results on phantom data are in Section 3 and on real data in Section 4; these experiments include scanner intensity standardization and synthesis of T₂-w images. In Section 5, we present additional synthesis applications: super-resolution and FLAIR synthesis. In Section 6, there is a discussion about the potential impact of this work and concluding remarks.

2. Method

Let 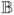= {b₁, b₂, … , b_m} be the given subject image set, imaged with pulse sequences Γ₁, … , Γ_m. This set can contain images from different pulse sequences such as MPRAGE, spoiled gradient recalled (SPGR), and DSE. Let 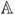= {a₁, a₂, … , a_n} be the atlas collection, with images of contrasts 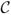₁, 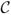₂, … , 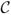_n, generated by pulse sequences Ψ₁, … , Ψ_n, respectively. By pulse sequence we mean particular, named procedures like MPRAGE. By contrast we mean the tissue contrast produced by a pulse sequence, say a T₁-weighted contrast or a T₂-weighted contrast. For instance, the MPRAGE pulse sequence produces a T₁-w contrast image. Since in most cases our data consists of specific pulse sequences producing specific contrasts, these terms can be used interchangeably.

The pulse sequence sets Γ₁, … , Γ_m and Ψ₁, … , Ψ_n need not intersect, which represents an important distinction between Ψ-CLONE and all other atlas-based image synthesis methods. The atlas also contains quantitative P_D, T₁, and T₂ maps, denoted a_PD, a_T1, and, a_T2. Our goal is to synthesize the subject image b̂_r, r ∈ {1 … , n}, which is how the subject brain would look had it been imaged with pulse sequence Ψ_r used to acquire the atlas image a_r. The steps of our algorithm are as follows: 1) Estimate the pulse sequence parameters used to acquire b_i, i ∈ {1, … , m}; 2) With this estimate, generate a_bi the atlas image with the same contrast, 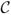_i, as b_i; 3) From the expanded atlas collection ∪ {a_bi} we learn the nonlinear intensity transformation between contrast _i and the target contrast image a_r (of contrast _r), using patch-based random forest regression; 4) The intensity transformation is then applied to b_i, generating the subject image b̂_r, of the desired contrast. These steps are outlined graphically in Fig. 1 and detailed in the following sections.

Figure 1.

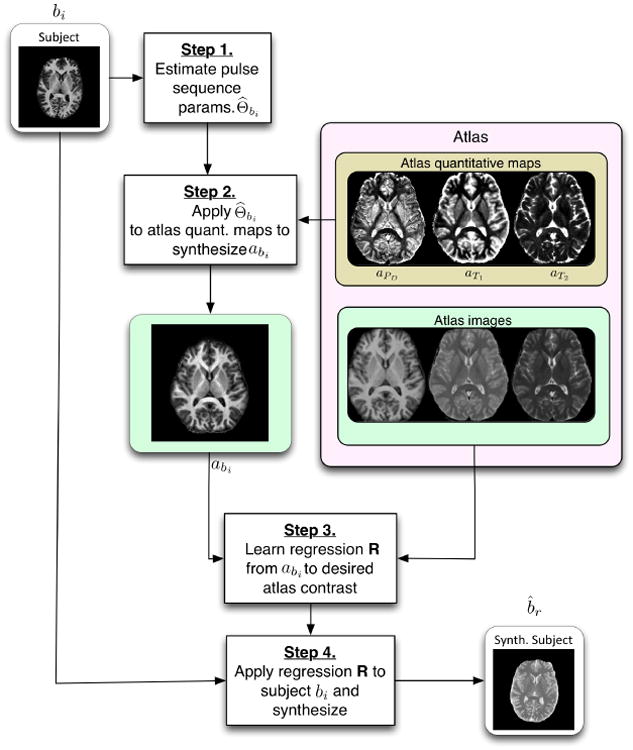
A flow chart of the Ψ-CLONE algorithm.

2.1. Estimation of Subject Pulse Sequence Parameters

The intensity observed at voxel location x in b_i is assumed to be a result of the underlying tissue parameters—proton density P_D, longitudinal relaxation time T₁, and transverse relaxation time T₂—denoted by β(x) = [P_D(x), T₁(x), T₂(x)]. The intensity is also a result of the pulse sequence used, Γ_i, and its imaging parameters denoted Θ_bi. Thus we denote the imaging equation as,

$$b_i(\mathbf{x})={\mathrm{\Gamma }}_i(\mathit{\beta }(\mathbf{x});{\mathrm{\Theta }}_{b_i}).$$ (1)

For the DSE pulse sequence, the equation is

$$b_{\mathit{\text{DSE}}}(\mathbf{x})={\mathrm{\Gamma }}_{\mathit{\text{DSE}}}(\mathit{\beta }(\mathbf{x});{\mathrm{\Theta }}_{\mathit{\text{DSE}}})=G_{\mathit{\text{DSE}}}{P}_D(\mathbf{x})(1-2e^{-\frac{\text{TR}-\frac{{\text{TE}}_1+{\text{TE}}_2}{2}}{T_1(\mathbf{x})}}+2e^{-\frac{\text{TR}-\frac{{\text{TE}}_1}{2}}{T_1(\mathbf{x})}}-e^{-\frac{\text{TR}}{T_1(\mathbf{x})}})e^{-\frac{{\text{TE}}_2}{T_2(\mathbf{x})}},$$ (2)

where Θ_DSE = {TR, TE₁, TE₂, G_DSE} consists of repetition time TR, two echo times TE₁ and TE₂ and scanner gain G_DSE (Glover, 2004). For the T₁-w SPGR sequence the imaging equation is

$$b_S(\mathbf{x})={\mathrm{\Gamma }}_S(\mathit{\beta }(\mathbf{x});{\mathrm{\Theta }}_S)=G_S{P}_D(\mathbf{x})sin\theta \frac{(1-e^{-\frac{\text{TR}}{T_1(\mathbf{x})}})}{1-cos\theta e^{-\frac{\text{TR}}{T_1(\mathbf{x})}}}{e}^{-\frac{\text{TE}}{T_2^{\ast }(\mathbf{x})}},$$ (3)

where Θ_S = {TR, TE, θ, G_S} consists of repetition time TR, echo time TE, and flip angle θ (Glover, 2004). The imaging equation for the MPRAGE sequence can be approximated from the mathematical formulation calculated by Deichmann et al. (2000) as

$$b_M(\mathbf{x}){\mathrm{\Gamma }}_M(\mathit{\beta }(\mathbf{x});{\mathrm{\Theta }}_M)=G_M{P}_D(\mathbf{x})(1-\frac{2e^{\frac{-\text{TI}}{T_1(\mathbf{x})}}}{1+e^{\frac{-(\text{TI}+\text{TD}+\tau )}{T_1(\mathbf{x})}}}),$$ (4)

where Θ_M = {TI, TD, τ, G_M} consists of inversion time TI, delay time TD, and the slice imaging time τ (Deichmann et al., 2000). We assume that we know one of these parameters from the image header and estimate the rest by fitting the imaging equation to average tissue intensities.

Given an input subject image, b_i, we want to estimate a subset (such as scanner gain, flip angle, echo times) of pulse sequence parameters Θ_bi of Γ_bi. We make certain assumptions about the tissues being imaged thereby simplifying the system of equations we need to solve. As the human brain is dominated by three primary tissues, cerebrospinal fluid (CSF), gray matter (GM), and white matter (WM), we can use the known average values of β to solve for the imaging parameters. The mean values of β for CSF, GM, and WM denoted by β̄_C, β̄_G, and β̄_W, respectively have been reported previously for 1.5 T (Kwan et al., 1999) and 3 T MRI (Wansapura et al., 1999). To identify the three tissue classes, we run a simple three-class fuzzy c-means (Bezdek, 1980) algorithm on the T₁-w image (b_S or b_M), and choose voxels with high class memberships (≥0.8) to compute the mean intensities of CSF, GM, and WM in b_i as b̄_iC, b̄_iG, and b̄_iW, respectively for i = 1, … , m.

We make the assumption that these mean intensities are a result of the mean tissue parameter values. This relationship is written as,

$${\overline{b}}_{iC}={\mathrm{\Gamma }}_i({\overline{\mathit{\beta }}}_C;{\mathrm{\Theta }}_{b_i}),{\overline{b}}_{iG}={\mathrm{\Gamma }}_i({\overline{\mathit{\beta }}}_G;{\mathrm{\Theta }}_{b_i}),{\overline{b}}_{iW}={\mathrm{\Gamma }}_i({\overline{\mathit{\beta }}}_W;{\Theta }_{b_i}).$$ (5)

The only unknown is Θ_bi, which for DSE type pulse sequences is parametrized by four terms. Similarly, MPRAGE and SPGR pulse sequences (Deichmann et al., 2000; Glover, 2004) have four parameters. Thus, we have three equations (Eqn. 5) and four unknowns, and we can solve this system of equations using Newton's method after assuming knowledge of one of the unknowns. For example, in the SPGR pulse sequence, we assume that the repetition time, TR is known from the image header and the unknowns that are often not well-calibrated in an MR scanner—e.g, flip angle and scanner gain—are estimated. For the given subject image set = {b₁, b₂, … , b_m}, we can thus estimate {Θ̂_b1, … , Θ̂_bm} for each of the subject images at the end of Step 1.

There are many factors that affect the accuracy of a pulse sequence equation, and more unknowns are likely to be actually involved than we may know about. To address this, we have simplified the problem by using theoretical equations or approximations of theoretical equations that describe the basic, functional relationship between the NMR parameters (P_D, T₁, T₂) and the signal intensity. For instance, the signal intensity equation for the MPRAGE pulse sequence, given in Eqn. 4, is an approximation derived from a complex theoretical derivation of a simple MPRAGE sequence by Deichmann et al. (2000). In practice, the MPRAGE sequence implemented on the scanner has many additional parameters that are not accounted for by this derivation. Therefore, in most cases, our estimates of the pulse sequence parameters are not particularly close to the parameters recorded in the image headers. It turns out that this is not important for the problem at hand, since we do not need to know the exact imaging parameters of any given pulse sequence. Instead, we need to be able to generate a realistic synthetic image from our atlas that has the same intensity characteristics as the subject image using the estimated parameters and approximate pulse sequence. Approximate imaging equations and their estimated parameters are sufficient for this purpose.

2.2. Synthesizing a New Atlas Image with Subject Pulse Sequence Estimates

Now we describe Step 2 of the process, as illustrated in Fig. 1. It is unlikely that our atlas would contain an image with the exact pulse sequence parameters Θ_bi estimated from b_i, which is why we synthesize an atlas image with the same parameters. Using the estimated imaging parameters, Θ̂_bi, we apply the pulse sequence to the atlas β. The atlas 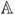= {a₁, a₂, … , a_n} consists of a set of co-registered brain MR images of a single brain with different pulse sequences. It also consists of a_PD, a_T1, and a_T2, the quantitative P_D, T₁, and T₂ maps for the atlas. Thus, we can directly apply the subject pulse sequence, Γ_i, and its estimated Θ̂_bi to synthesize a new atlas image a_bi. We thereby create an atlas image that looks as if the atlas brain was imaged with the pulse sequence Γ_i with parameters Θ̂_bi. We need this intermediate step so that we can learn the intensity transformation between the subject pulse sequence Γ_i and the reference pulse sequence Ψ_r in a common image space, which is the atlas image space.

In practice, the atlas collection 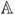may lack the quantitative P_D, T₁, and T₂ maps—the relaxometry sequence data is generally not available for most clinical data. We can approximately estimate these maps from the images present in the atlas collection by solving for P_D, T₁, and T₂ at each voxel. Since we are estimating three quantities in β(x) = [P_D(x), T₁(x), T₂(x)], we require at least three atlas images, a_u, a_v, and a_w. From the method described in Section 2.1, we can estimate Θ̂_au, Θ̂_av, and Θ̂_aw. For each voxel x, we have three intensity values from three images, thus leading to three equations,

$$\begin{array}{c}{\mathrm{\Psi }}_u(\mathit{\beta }(\mathbf{x});{\widehat{\mathrm{\Theta }}}_{a_u})=a_u(\mathbf{x}),\\ {\mathrm{\Psi }}_v(\mathit{\beta }(\mathbf{x});{\widehat{\mathrm{\Theta }}}_{a_v})=a_v(\mathbf{x}),\\ {\mathrm{\Psi }}_w(\mathit{\beta }(\mathbf{x});{\widehat{\mathrm{\Theta }}}_{a_w})=a_w(\mathbf{x}).\end{array}$$ (6)

This system of simultaneous nonlinear equations can be solved by Newton's method for each voxel to provide us with an estimate β̂(x). The component parts of β̂(x) are [β̂₁(x), β̂₂(x), β̂₃(x)] that are our estimates of [P_D(x), T₁(x), T₂(x)]. Thus, we add the images a_β̂1, a_β̂2, and a_β̂3 to our atlas to represent the P_D, T₁, and T₂ quantitative maps, respectively. This calculation needs to be done only once, during the construction of a suitable atlas. A variant of this approach was used in Jog et al. (2013b) as a step in intensity standardization.

2.3. Learning and Applying Nonlinear Regression on Image Patches

Having synthesized the atlas image a_bi that has the pulse sequence characteristics of the subject image b_i, we next learn the intensity transformation that will convert the intensities in a_bi to the corresponding intensities in the target atlas image a_r. We depict this as Step 3 in Fig. 1. This is achieved through a nonlinear regression by considering the image patches of a_bi together with the corresponding central voxel intensities in a_r. We extract p × q × r sized patches from a_bi, centered at the v^th voxel—in our experiments p = q = r = 3. We stack the 3D patch into a d × 1 = 27 × 1 vector and denote it by f_v ∈ ℝ^d, which we refer to as a feature vector of the v^th voxel. The corresponding intensity at the v^th voxel of a_r is denoted by y_v and acts as the dependent variable in our regression; we denote these training data pairs as 〈f_v, y_v〉. We use patches as intensity features to learn this transformation. A small patch captures the local context at a voxel and ensures spatial smoothness. We could use other synthesis methods like MIMECS (Roy et al., 2013a) to learn this transformation, however we chose to use the random forest regression as it was shown to produce better quality synthetic images at an order of magnitude lower computation time (Jog et al., 2013a).

We use a bagged ensemble of regression trees to learn this nonlinear regression (Breiman, 1996). This standalone regression ensemble for synthesis was previously explored in Jog et al. (2013a). A single regression tree learns a nonlinear regression by partitioning the d-dimensional space. This is done by performing binary comparison splits at each node of the tree, based on a particular attribute value which is compared to a threshold. The tree is built by minimizing the least squares criterion during training. The growth of the tree is limited by fixing the maximum number of vectors allowed at each leaf, in our experiments this was limited to five data vectors. This stops a tree from becoming too deep and hence over-fitting the training data. A single regression tree is considered a weak learner and in general has higher error (Breiman, 1996), therefore we use a bagged ensemble of regression trees (30 in our experiments), which reduces errors by bootstrap aggregation (Breiman, 1996). To create a bootstrapped data set, a training sample is picked at random with replacement N times, where N is the size of the training data, ∼10⁶ in our experiments.

Once the training is complete, the trained regression ensemble transforms intensities of a_bi to those of a_r. This ensemble is used to synthesize the subject image b̂_r by extracting image patches from b_i and applying the trained regression ensemble to each patch to synthesize the corresponding b̂_r voxel intensities, which is the last step, Step 4 in Fig. 1.

Thus, starting with a subject image and a set of atlas images, we estimate the pulse sequence parameters of the subject image, create an additional atlas image by applying those parameters to the atlas quantitative images, learn an intensity transformation from the additional atlas image to the target atlas contrast image using random forest regression, and lastly apply the regression to the given subject image to create a synthetic image of the required contrast. In the following sections, we will describe validation experiments and applications of Ψ-CLONE in different image analysis contexts.

3. Computational Phantom Experiments

The goal of our method is to produce synthetic images that are useful substitutes for real images for image processing tasks. Thus, one aspect of algorithm performance evaluation consists of using image quality metrics to compare synthetic images with known ground truth images. The ground truth images are simulated with known pulse sequence parameters on brain voxels with known NMR parameters. We compare our synthetic images with these known simulated images to validate our method in a controlled experimental setting. In this section, we used the Brainweb image phantom for intensity standardization and synthesis of T₂-w images from T₁-w images.

3.1. Brainweb SPGR: Estimating a_bi

In this validation experiment the atlas set 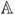consisted of images from the Brainweb (Cocosco et al., 1997) phantom, consisting of:

• a₁: SPGR image (1.5 T, TR = 18 ms, α = 30°, TE = 10 ms) with 0% noise,

• a_T1: Quantitative T₁ map derived from two different SPGR images, with two different flip angles (TR = 100 ms, TE = 15 ms, α₁ = 15°, and α₂ = 30°) using the dual flip angle method (Bottomley and Ouwerkerk, 1994),

• a_T2: Quantitative T₂ map derived from a DSE sequence (TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms) by the two point method (Landman et al., 2011),

• a_PD: Quantitative P_D map derived from the reference SPGR and the DSE images using the method described in Section 2.2.

The aim of this experiment is to validate Step 1 and Step 2 of Ψ-CLONE. We do this by taking several images as a potential subject image and carry out just the first two steps of Ψ-CLONE which results in the image a_bi. Specifically the subject images were:

• b₁: SPGR image (1.5 T, TR = 18 ms, α = {15°, 30°, 45°, 60°, 75°, 90°}, TE = 10 ms) with 0% noise. (Parameters, excepting TR, not provided to the algorithm)

We note that the subject imaging parameters are shown for the sake of the reader and are not provided to the algorithm (except TR).

The first step of Ψ-CLONE estimates the imaging parameters from the subject image. As both the atlas and subject images come from the same phantom—they have the same phantom anatomy and NMR parameters—this allows us to validate Step 2, in which we create a synthetic atlas image using the pulse sequence parameters of the subject image. Since the anatomy of subject and atlas is the same in this special case, we can directly compare the synthetic atlas image with the subject image to validate if the pulse sequence parameters are producing an identical image. We would prefer to compare the estimated pulse sequence parameters with the known true parameters. Unfortunately, this comparison is not suitable for all parameters because we use theoretical equations or their approximations to estimate the pulse sequence parameters and the actual simulation or scanner implementation can be more complex with a larger number of parameters. As a small example, we carried out an experiment on the Brainweb phantom data to measure the error between the true parameters and the estimated parameters. We simulated different SPGR images by keeping the repetition time TR = 18 ms fixed, and varying the flip angle. We next estimated the imaging parameters of these images by the method described above. The estimated flip angles for these images and the true flip angles used to simulate these images are recorded in Table 1. As can be seen, these estimates are close to but not equal to the truth. This error increases in realistic settings.

Table 1.

Flip angles used in Brainweb SPGR simulation vs estimated Flip angles after fitting.

True flip angle (°)	Estimated flip angle (°)
30	32.08
45	48.70
60	65.08
75	84.79
90	106.57

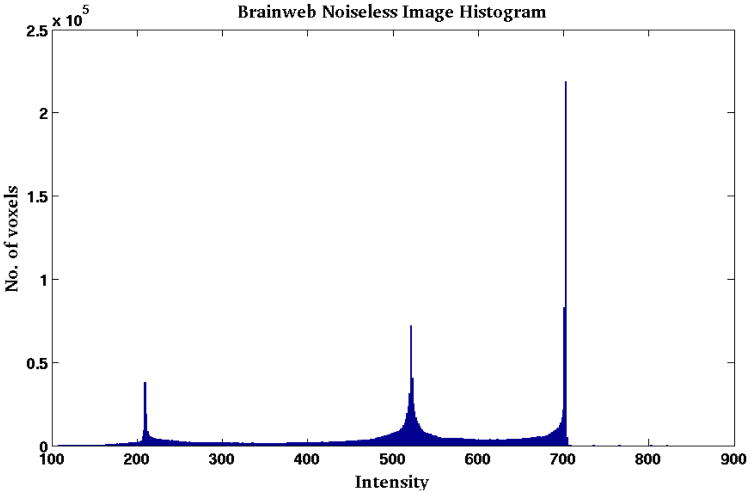
Hence we focus on the images that these parameter estimates create when applied to the estimated P_D, T₁, and T₂ values. We compute the root mean squared error (RMSE) and peak signal to noise ratio (PSNR) between the new atlas image (a_bi) and the subject image (b_i), as shown in Table 2. Figure 2 shows the input b₁ image and the estimated a_b1, along with the difference image for the case of α= 45° (third column of Table 2). The images are very similar to each other with small differences at tissue boundaries. The differences are only visible at the boundaries because, as the histogram in Fig. 4 shows, Brainweb phantom images with no noise typically have very homogenous intensity distribution in each of the tissue classes (WM, GM, CSF). Hence the error inside the tissues is very close to zero, but is slightly higher at the intermediate intensity voxels that are closer to the boundaries. We note that RMSE and PSNR are computed over the non-zero voxels in the image. RMSE is reported in terms of percentage error with respect to the maximum intensity in the image. The high PSNR values in Table 2 along with the visual result in Fig. 2 confirm that the theoretical pulse sequence equations and the underlying quantitative P_D, T₁, and T₂ maps produce images that are close to the ground truth images, thus validating the first two steps of our algorithm.

Table 2.

RMSE between a_b1 and b₁ (as a % w.r.t max intensity) and PSNR (dB) values for Brainweb T₁-w SPGR atlas synthesis for subject pulse sequences with varying flip angles.

Flip angle	15°	30°	45°	60°	75°	90°
RMSE %	5.09	2.49	1.63	1.18	0.88	0.68
PSNR	29.82	34.24	35.42	35.76	35.88	35.94

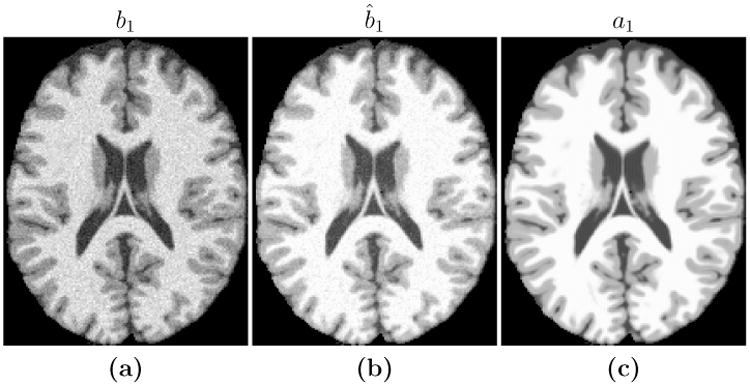
Figure 2.

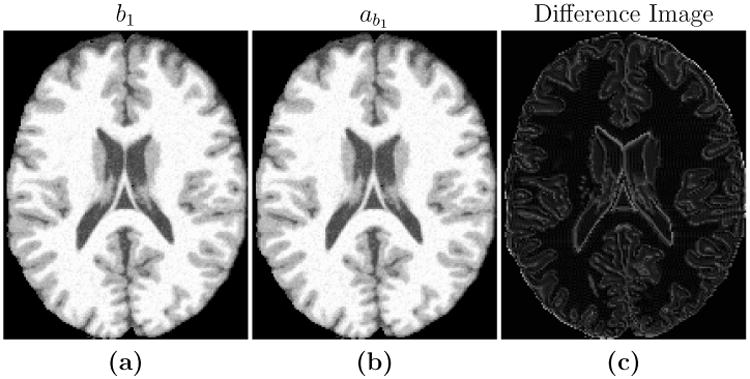
Shown are (a) an SPGR image (TR = 18 ms, TE = 10 ms, α= 45° with 0% additive noise) which we use as our subject image b₁, the maximum intensity value is 1080, the (b) new atlas image, a_b1, with pulse sequence parameters estimated from b₁, and (c) the difference image |a_b1 − b₁|, the maximum value is 5.

Figure 4. Histogram of a typical noiseless Brainweb phantom.

3.2. Brainweb SPGR Intensity Standardization

The goal of this experiment is to standardize a Brainweb SPGR subject image to an atlas target SPGR image. Different subject SPGR images were simulated using different input pulse sequence parameters. Using the same Brainweb atlas collection described in Section 3.1, we evaluated the results of Steps 3 and 4 of our method, the regression based image synthesis. Our subject images are:

• b₁: SPGR image (1.5 T, TR = 18 ms, α= {15°, 30°, 45°, 60°, 75°}, TE = 10 ms) with {0%, 3%} noise levels. (Parameters, excepting TR, not provided to the algorithm)

As the target atlas and subject images are both from the SPGR pulse sequence, this is a special case of synthesis, normally referred to as intensity standardization or normalization. We can compare the standardized subject image to the target atlas image directly as they have the same anatomy. We also compared the performance of our standardization with a landmark-based piecewise linear scaling method (UPL) (Nyúl et al., 2000), reporting PSNR for the input subject image in Table 3. UPL estimates the landmarks in the images for each of the three tissue classes (CSF, GM, & WM) and then uses a piecewise linear scaling between the target and subject histogram to normalize the images.

Table 3.

PSNR (dB) values between a₁ and b̂₁, for standardization of Brainweb phantoms with varying flip angles (°) and noise levels are shown for UPL and Ψ-CLONE. In the noise free case, UPL is better, however the introduction of noise causes UPL results to deteriorate.

	0% Noise		3% Noise
Flip Angle	UPL	Ψ-CLONE	UPL	Ψ-CLONE
15°	37.95	27.95	27.27	26.00
30°	62.66	35.90	28.93	30.96
45°	49.26	37.32	28.88	31.48
60°	46.94	37.67	28.81	31.39
75°	46.08	37.79	28.78	31.52

The histogram of a noise free Brainweb SPGR phantom is shown in Fig. 4. The histogram landmarks consist of very sharp peaks, indicating that a large number of voxels have very similar intensities. A piecewise linear transform can map exactly between two (subject and atlas) such histograms of noiseless Brainweb phantoms. This explains why the UPL method performs better than our method in the 0% noise case. However, with the introduction of noise our method outperforms UPL in four out of the five cases, as shown in Table 3.

3.3. Brainweb T₂-w Synthesis

Ψ-CLONE was next used to synthesize a T₂-w image from a subject SPGR image, using the Brainweb atlas collection described in Section 3.1 with the addition of:

• a₂: T₂-w image from the second echo of a DSE (1.5 T, TR = 3000 ms, TE₁ = 17 ms, TE₂ = 80 ms) with 0% noise.

We use the following input subject Brainweb SPGR images:

• b₁: SPGR image (1.5 T, TR = 18 ms, α= {15°, 30°, 45°, 60°}, TE = 10 ms) with {0%, 1%, 3%, 5%} noise levels. (Parameters, excepting TR, not provided to the algorithm)

The UPL method is unable to synthesize a T₂-w image from an SPGR, as it is primarily an intensity standardization approach; thus, for this experiment we compare Ψ-CLONE to MIMECS (Roy et al., 2011, 2013a). MIMECS is a state-of-the-art MR contrast synthesis approach that uses an example-based sparse reconstruction from image patches to perform intensity standardization and missing tissue contrast recovery. MIMECS, unlike Ψ-CLONE, is blind to the MR physics and solves the synthesis problem based on patch similarity between the subject and the atlases. As the atlas and the subject have the same phantom anatomy, an ideal synthesis would result in an image that is exactly equal to the atlas T₂-w image. Thus, we evaluate the quality of synthesis by calculating the PSNR between the atlas image and the synthesized subject image. We also evaluate the quality of synthesis using the universal quality index (UQI) (Wang and Bovik, 2002), which is an image quality metric that models how the human visual system would perceive the similarity of two images. If the images are perceptually identical, their UQI is 1; otherwise it lies between 0 and 1.

The results for this experiment are shown in Table 4. The top half of the table shows results for changing noise levels with a fixed flip angle (30°) for the input SPGR, while the bottom half shows the results for changing flip angles with 0% noise in the input SPGR. For both metrics, Ψ-CLONE outperforms MIMECS. An example of an input SPGR used in this experiment, the true T₂-w, image and the outputs of both MIMECS and Ψ-CLONE are shown in Fig. 5.

Table 4.

PSNR (dB) and UQI values for Brainweb T₂-w synthesis with varying noise levels (%) and flip angles (°) are shown for MIMECS and our algorithm (Ψ-CLONE).

Noise (%)		0	1	3	5
PSNR	MIMECS	26.25	19.96	19.09	19.21
	Ψ-CLONE	30.33	30.71	29.09	26.63
UQI	MIMECS	0.93	0.88	0.83	0.82
	Ψ-CLONE	0.95	0.94	0.91	0.88
Flip Angle (°)		15	30	45	60
PSNR	MIMECS	24.51	26.25	25.27	24.82
	Ψ-CLONE	25.99	30.33	30.94	31.06
UQI	MIMECS	0.90	0.93	0.92	0.92
	Ψ-CLONE	0.90	0.95	0.96	0.96

Figure 5.

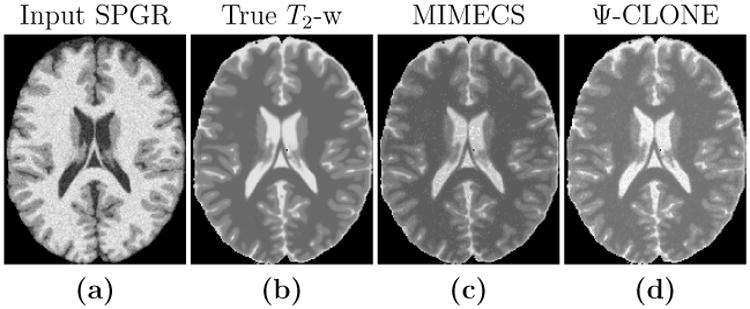
(a) An example input subject SPGR from which we synthesize a T₂-w image. (b) The true T₂-w image and the outputs of synthesis produced by (c) MIMECS and (d) Ψ-CLONE.

4. Real Data Experiments

In this section, we present intensity standardization and image synthesis experiments performed on real datasets.

4.1. Human Stability Data

A normal, healthy human subject was imaged at weekly intervals using the same scanner and pulse sequence for nine weeks. We demonstrate that image segmentation is more consistent on data which is intensity standardized using Ψ-CLONE. To do this we standardize each time point to an atlas consisting of:

• a₁: MPRAGE image (3 T, TR = 10.3 ms, TE = 6 ms, 0.82 × 0.82 × 1.17 mm³ voxel size),

• a_T1: Quantitative T₁ map computed as described in Section 2.2,

• a_T2: Quantitative T₂ map derived as described in Section 2.2,

• a_PD: Quantitative P_D map derived as described in Section 2.2,

and each of the nine subject images is:

• b₁: MPRAGE image (3 T, TR = 10.3 ms, TE = 6 ms, 0.82 × 0.82 × 1.17 mm³ voxel size. (Parameters, excepting TR, not provided to the algorithm)

We compare the segmentations of the images pre- and post-standardization using Ψ-CLONE, based on segmentations generated by TOADS (Bazin and Pham, 2007). We specifically compare the relative tissue volumes (relative to the intra-cranial volume (ICV)), over the nine weeks. Ideally, a normal healthy subject should not present any changes in tissue volumes over such a short period of time.

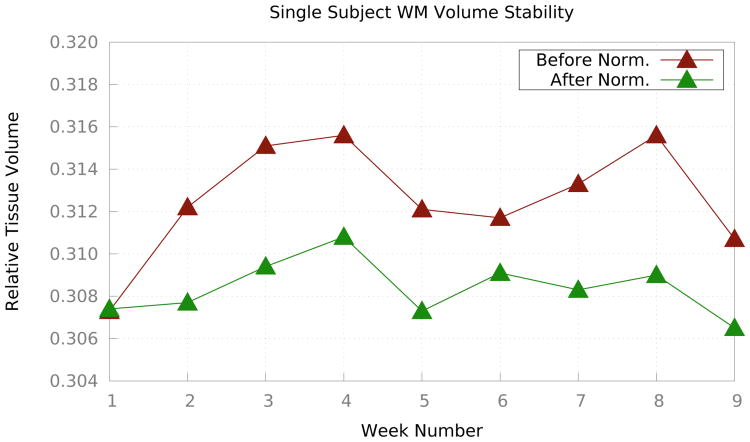
Fig. 6 shows the relative WM volumes before and after Ψ-CLONE was applied. Visually, it is apparent that the WM volumes change less when standardized images are segmented. Table 5 shows the coefficient of variation of relative tissue volumes for CSF, cortical GM, subcortical GM, ventricles, and cortical WM. The coefficients of variation from segmentation after standardization by Ψ-CLONE are smaller than those without standardization for cortical WM, cortical and subcortical GM, and ventricles, indicating that the segmentation is more stable. As there are only nine time-points there is insufficient data to determine significance.

Figure 6.

The brown plot illustrates relative WM volumes (with respect to the ICV) over nine weeks before any standardization while the green plot illustrates the same values after intensity standardization using Ψ-CLONE.

Table 5.

Coefficient of Variation (CV) of the relative tissue volumes (× 10⁻³) over the nine weeks on the original data and after intensity standardization with Ψ-CLONE for each of white matter (WM), cortical gray matter (Cort. GM), subcortical gray matter (Sub. GM), cerebrospinal fluid (CSF), and the ventricles (Vent.). Table 6 shows further breakdown of Sub. GM structures.

	Classes
Vol. CV	WM	Cort. GM	Sub. GM	CSF	Vent.
Original	8.6	6.4	20.4	11.9	30.7
Ψ-CLONE	4.3	5.7	19.4	12.0	23.1

The subcortical gray matter class consists of the thalamus, caudate and putamen structures. We compared the volumes of these structures before and after standardization and calculated the coefficient of variation in both cases. Results are shown in Table 6. The thalamus volumes for Ψ-CLONE standardized images are most stable as evinced by the reduced coefficient of variation. The coefficient of variation decreases slightly for putamen and increases slightly for caudate. However the accuracy of LesionTOADS segmentations for subcortical structures is not as high as it is for the cortical GM or WM, hence these numbers may not be reliable indicators of segmentation consistency. Additionally, these are only nine time-points of a single subject, so we cannot claim statistical significance in these measurements at this point.

Table 6.

Coefficient of Variation (CV) of the relative tissue volumes (× 10⁻³) over the nine weeks on the original data and after intensity standardization with Ψ-CLONE for each of caudate, putamen, and thalamus.

	Structures
Vol. CV	Caudate	Putamen	Thalamus
Original	9.9	9.9	51.9
Ψ-CLONE	10.3	9.7	45.3

4.2. MR Intensity Scale Standardization for MS Patients

To allow us to have statistical power in our exploration of MR intensity scale standardization, we employ a cohort of 15 Multiple Sclerosis (MS) patients with 57 scans. Each patient has at least three scans (mean # of scans per subject is 3.8) acquired approximately a year apart. Preprocessing of the images included skull-stripping (Carass et al., 2011) and bias field inhomogeneity correction (Sled et al., 1998). For this experiment our atlas consisted of:

• a₁: MPRAGE image (3 T, TR = 10.3 ms, TE = 6 ms, 0.82 × 0.82 × 1.17 mm³ voxel size),

• a₂: T₂-w image from the second echo of a DSE (3 T, TR = 4177 ms, TE₁ = 12.31 ms, TE₂ = 80 ms, 0.82 × 0.82 × 2.2 mm³ voxel size),

• a₃: P_D-w from the first echo of a DSE (3 T, TR = 4177 ms, TE₁ = 12.31 ms, TE₂ = 80 ms, 0.82 × 0.82 × 2.2 mm³ voxel size),

• a₄: FLAIR (3 T, TI = 11000 ms, TE = 68 ms, 0.82 × 0.82 × 2.2 mm³ voxel size)

• a_T1: Quantitative T₁ map computed as described in Section 2.2,

• a_T2: Quantitative T₂ map derived as described in Section 2.2,

• a_PD: Quantitative P_D map derived as described in Section 2.2,

and our subject image was:

• b₁: MPRAGE image (3 T, TR = 10.3 ms, TE = 6 ms, 0.82 × 0.82 × 1.17 mm³ voxel size). (Parameters, excepting TR, not provided to the algorithm)

We use an atlas MPRAGE as the target pulse sequence to which we standardize the 57 data sets. We treat each data set independently, handling the intensity standardization as a cross-sectional task. To validate the intensity standardization, we segmented (Shiee et al., 2010) the original MPRAGE datasets giving us ten labeled structures: ventricles, sulcal CSF, cerebellar GM (Cereb. GM), cortical GM (Cort. GM), thalamus, putamen, cerebellar WM (Cereb. WM), cortical WM (Cort. WM), and lesions. Using these structures as reference, we compared the mean intensity within these structures prior to standardization and after standardization with UPL—using the target MPRAGE in our atlas as a standardization target—and our method (Ψ-CLONE). We note that the atlas images did not have lesions. For applications like T₁-w intensity standardization, we observed that the presence or absence of lesion samples in the training data did not affect the synthesis result. The primary reason is that white matter lesion intensities are similar to GM (and rarely CSF) in T₁-w contrasts. Thus, the database has a large number of normal appearing GM and CSF samples available to reconstruct the lesion intensities.

Results are shown in Table 7. The mean intensity values of the original images and the Ψ-CLONE standardized images recorded in Table 7, demonstrate that our method is moving the MS data intensities closer to the atlas intensities, as desired by standardization. A one tailed F-test on the mean structure intensities after standardization shows that the standard deviation of the mean structure intensities across the 57 datasets for Ψ-CLONE is significantly smaller in comparison to UPL for seven of the ten structures. We also note that the statistical significance does not change if the segmentation is done on the original data or on the standardized versions.

Table 7.

The mean intensity value for the atlas used in the MS standardization experiment are shown for ten structures. We also show the mean (× 10⁴) and std (× 10⁴) (over 57 images) of the average intensity value for each structure, based on the original unnormalized data (Original) and after standardization with both UPL (Nyúl et al., 2000) and our method (Ψ-CLONE).

	Atlas	Original		UPL		Ψ-CLONE
	Mean	Mean	Std	Mean	Std	Mean	Std
Ventricles	3.92	5.41	1.815	4.25	0.664	4.11†	0.271*
Sulcal CSF	2.50	3.95	1.132	3.11	0.543	2.97	0.478
Lesions	—	18.54	5.880	14.62	1.293	14.51	1.516
Cereb. GM	12.27	15.86	5.295	12.68	1.013	12.27†	0.433*
Cort. GM	10.47	13.40	4.722	10.62	1.199	10.27†	0.260*
Caudate	12.93	16.98	5.866	13.53	1.130	13.10†	0.526*
Thalamus	14.99	21.20	7.036	16.96	1.010	16.63†	0.548*
Putamen	15.53	20.26	7.286	16.23	1.196	15.77†	0.485*
Cereb. WM	20.79	27.66	9.333	21.05	0.209	22.02	0.266
Cort. WM	20.53	25.77	8.778	20.22	0.266	20.41†	0.186*

^†Difference between atlas mean and normalized mean is significantly smaller than UPL (α level of 0.05) using a two-sample one-tailed T-test.

^*Standard deviation is significantly smaller than UPL (α level of 0.05) based on a two-sample F-test.

Next, we ran Lesion TOADS segmentation on images before and after standardization. These segmentations were used to calculate image contrast between neighboring structures to indicate the effect of synthesis-based standardization on subsequent segmentation. We looked at the following structure boundaries, Cortical CSF-Cortical GM, Cortical GM-WM, WM-lesions, WM-Ventricles, WM-Caudate, WM-Putamen, WM-Thalamus, Caudate-Ventricles, and Thalamus-Ventricles and have tabulated the results in Table 8. We can show that on average these contrast values for synthetic images are higher than the real images, significantly in most cases. The contrast values for synthetic images are also closer to the reference contrast values for the same structures, than the original images. We have defined contrast between two neighboring structures f and g as $\frac{\mu (f)-\mu (g)}{\mu (f)}$, where μ(f) is the mean intensity of the brighter structure f and μ(g) is the mean intensity of the structure g. The higher the contrast, the easier it is to differentiate structures.

Table 8.

Contrast values between neighboring structures for original, synthetic, and atlas images.

	Structure Boundary Contrasts
Struct. Boundaries	Original	Ψ-CLONE	Atlas
Cort CSF–Cort GM	0.594	0.604*	0.625
Cort GM–WM	0.480	0.482	0.489
WM–Lesions	0.279	0.300	—
WM–Caudate	0.341	0.367*	0.370
WM–Putamen	0.214	0.219	0.240
WM–Thalamus	0.176	0.208*	0.269
WM–Ventricles	0.846	0.863*	0.878
Ventricles–Caudate	0.765	0.784*	0.804
Ventricles–Thalamus	0.814	0.827*	0.834

^*indicates that the contrast in synthetic images higher than the original images (statistically significant using Student's one-tailed T test with p < 0.05).

4.3. T₂-w Synthesis from Real MPRAGE Data

To demonstrate T₂-w synthesis from MPRAGE on real data, we used the 21 subjects from the publicly available multimodal reproducibility data (Landman et al., 2011). We held out a single subject as the atlas:

• a₁: MPRAGE image (3 T, TR = 6.7 ms, TE = 3.1 ms, TI = 842 ms, 1.0 × 1.0 × 1.2 mm³ voxel size),

• a₂: T₂-w image from the second echo of a DSE (3 T, TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms, 1.5 × 1.5 × 1.5 mm³ voxel size),

• a₃: P_D-w image from the first echo of a DSE (3 T, TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms, 1.5 × 1.5 × 1.5 mm³ voxel size),

• a_T1: Quantitative T₁ map computed from two flip angles (3 T, TR = 100 ms, TE = 15 ms, α₁ = 15°, α₂ = 60°, 1.5 × 1.5 × 1.5 mm³ voxel size),

• a_T2: Quantitative T₂ map derived from a two-point method (3 T, TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms, 1.5 × 1.5 × 1.5 mm³ voxel size),

• a_PD: Quantitative P_D map derived from the MPRAGE and the DSE images using the method described in Section 2.2.

Our subject image is:

• b₁: MPRAGE image (3 T, TR = 6.7 ms, TE = 3.1 ms, TI = 842 ms, 1.0 × 1.0 × 1.2 mm³ voxel size). (Parameters, excepting TR, not provided to the algorithm)

We note that the atlas image did not have lesions. For an application like T₂-w synthesis, we again observed that the presence or absence of lesion samples in the training data did not affect the synthesis result. The primary reason is that white matter lesion intensities are similar to GM (and rarely CSF) in T₁-w and T₂-w contrasts. Thus, the database has a large number of normal appearing GM and CSF samples available to reconstruct the lesion intensities.

The remaining 20 available subjects each have two MPRAGE acquisitions and two corresponding DSE images which are co-registered to the MPRAGE. These images were acquired on the same scanner within a short duration of each other. For each of these 40 images (20 subjects × 2 MPRAGE scans) we synthesized a T₂-w image. As the atlas was imaged on the same scanner we directly compare the synthesized T₂-w image with the true T₂-w image from the same scanning session, using PSNR and UQI. We compared to MIMECS (Roy et al., 2011) and to a deformable registration-based synthesis.

To carry out synthesis using deformable registration, the atlas image is registered deformably to the subject image of the same contrast. The same deformation is then applied to the atlas image of the desired contrast to produce the synthetic subject image. We use the state-of-the-art registration method SyN (Avants et al., 2008) for this synthesis and refer to this method as D-SyN. Table 9 shows the PSNR and UQI for these three methods. We observe that our method (Ψ-CLONE) provides a significantly (α < 0.01, using the right-tailed two sample t-test) better quality synthesis in comparison to both MIMECS and D-SyN.

Table 9.

Mean and standard deviation (Std. Dev.) of the PSNR and UQI values for synthesis of T₂-w images from 40 MPRAGE scans.

	PSNR	UQI
	Mean (Std. Dev.)	Mean (Std. Dev.)
D-SyN	16.59 (1.35)	0.64 (0.06)
MIMECS	15.01 (0.84)	0.78 (0.03)
Ψ-CLONE	18.59 (1.09)*	0.79 (0.02)*

^*Statistically significantly better than either of the other two methods (α level of 0.01) using a right-tailed test.

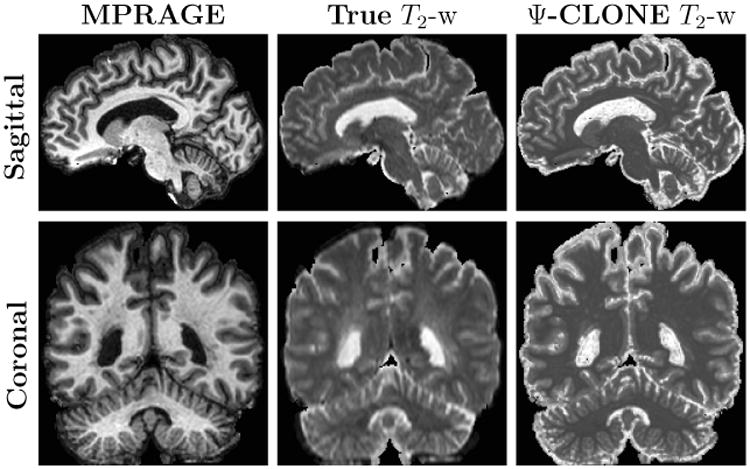
Figure 7 shows the results for each synthesis approach in comparison to the ground truth image. Though the PSNR values for D-SyN are better than MIMECS (see Table 9), the D-SyN synthesis result is anatomically incorrect—the ventricle boundary is incorrect and lesions posterior to the ventricles are not synthesized. As the output of D-SyN is based on deformably registering the atlas to the subject, if the atlas does not contain certain tissue features—lesions, for example—then the synthesized subject will not contain them as well. The lesion in Fig. 7 is a white matter lesion. We know that lesion boundaries appear slightly different in the MPRAGE than in the real T₂-w image, and hence it cannot be perfectly reproduced in the synthetic T₂-w image. However we aim to synthesize it as correctly as possible and do a better job than currently available synthesis algorithms. The result of MIMECS is quite noisy and Ψ-CLONE yields an image that is most visually similar to the true image.

Figure 7.

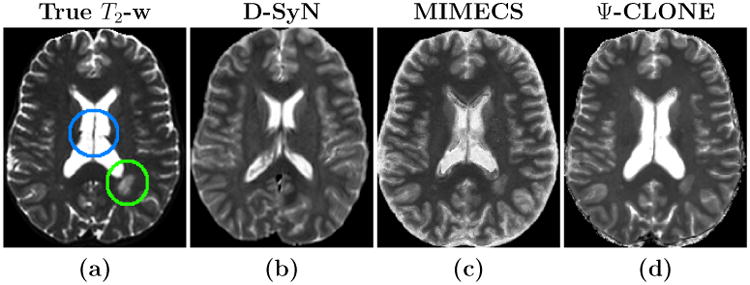
Shown are (a) the true T₂-w image, and the synthesis results from the MPRAGE for each of (b) D-SyN, (c) MIMECS, and (d) Ψ-CLONE (our method). The lesion (in the green circle) and the ventricles (in the blue circle) in the true image are synthesized by MIMECS and Ψ-CLONE, but not by D-SyN.

We also used the atlas images of this dataset to evaluate our estimation procedure for the intrinsic parameters T₂ and T₁. The median T₂ values calculated by the two point method (Landman et al., 2011) using the DSE images were 76 ms for WM, 85 ms for GM, and 175 ms for CSF. We used our estimation procedure (as described in Section 2.2) and the estimated median T₂ values obtained were 76 ms for WM, 91 ms for GM, and 762 ms for CSF. Both CSF distributions have a very large standard deviation (∼10⁴), due to numerical errors. The intensities determined by the imaging equations also plateau off after a certain T₂ value due to their inverse exponential nature (see Eq. 2). Thus the intensities produced for high enough T₂ values are very close to each other. The T₁ map was estimated via two flip angle spoiled gradient images, as mentioned in the atlas description. This is not an ideal approach as the images acquired were noisy and the flip angle calibration is not considered accurate enough. The median T₁ values thus calculated using the dual flip angle image were 775 ms for WM, 1074 ms for GM, and 1616 ms for CSF. Our estimation procedure returned the following median T₁ values of 779 ms for WM, 1151 ms for GM, and 2916 ms for CSF. As with T₂ values, the intensities produced by high T₁ values plateau off after a certain point due to the inverse exponential dependence on T₁ (see Eqs. 2, 3, 4). Thus, despite being slightly different from the expected values, our estimated T₂ and T₁ values are good enough to provide a realistic synthesis.

5. Further Synthesis Applications

In this final experimental section, we present additional results that demonstrate potential uses of Ψ-CLONE.

5.1. Synthesizing Higher Resolution T₂-w Data

Example-based synthesis of high resolution brain MR images has been explored in many recent works (Rousseau, 2008; Manjón et al., 2010a,b; Konukoglu et al., 2013). We applied Ψ-CLONE to synthesize higher resolution T₂-w images than those acquired on the scanner. Our atlas collection is:

• a₁: MPRAGE image (3 T, TR = 6.7 ms, TE = 3.1 ms, TI = 842 ms, 1.1 × 1.1 × 1.1 mm³ voxel size),

• a₂: T₂-w image from the second echo of a DSE (3 T, TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms, 1.1 × 1.1 × 1.1 mm³ voxel size),

and our subject images come from our MS cohort:

• b₁: MPRAGE image (3 T, TR = 10.3 ms, TE = 6 ms, 0.82 × 0.82 × 1.17 mm³ voxel size). (Parameters, excepting TR, not provided to the algorithm)

Pulse sequences like the DSE or FLAIR tend to have large TR or TI values to achieve the right contrast. To reduce the scan time while imaging patients, these pulse sequences are usually acquired at a lower resolution than a T₁-w sequence such as MPRAGE. Multimodal analysis of such datasets requires all images to exist in the same coordinate system at the same digital resolution. This is usually achieved by upsampling the low resolution scans to the high resolution ones using interpolation, which results in blurring of the image data. Using Ψ-CLONE, we can synthesize a T₂-w image from the high resolution MPRAGE. This synthetic image will have the same resolution as that of the MPRAGE and hence can replace the acquired low resolution image. As we have no ground truth for the higher resolution T₂-w image we visually compare it with the acquired T₂-w image. The acquired T₂-w image has a through-plane resolution of 2.2 mm whereas the subject MPRAGE, and consequently the synthetic T₂-w image have a through-plane resolution of 1.1 mm. Both are shown in Fig. 8. The quality and resolution of the newly synthesized image is visually superior to the original acquisition.

Figure 8.

The MPRAGE has a through-plane resolution of 1.1 mm, while the original T₂-w has through-plane resolution of 2.2 mm. This is evident as the true interpolated T₂-w image shows blurring while the Ψ-CLONE synthesized image is crisp.

5.2. FLAIR Synthesis

FLAIR is the pulse sequence of choice when identifying white matter lesions present in MS patients. The lesions appear hyperintense with respect to the rest of the tissue which makes delineating them easier. Most leading lesion segmentation algorithms rely on the FLAIR image to provide intensity information for accurate classification (Lecoeur et al., 2009; Shiee et al., 2010; Forbes et al., 2010). FLAIR images are prone to certain artifacts for a variety of reasons (Stuckey et al., 2007). The long inversion times make it difficult to acquire high resolution scans in a short time. We demonstrate that if we acquire T₁-w, P_D-w, and T₂-w images of a subject, we have enough information to generate a synthetic FLAIR using Ψ-CLONE. The lesion intensity signature in FLAIR images is very distinct from the rest of the tissues. Hence the presence of lesion samples in the atlas set is essential in order to learn to reproduce it correctly. For this experiment, the atlas brain we use has a moderate lesion load. The atlas contained the following images:

• a₁: MPRAGE image (3 T, TR = 6.7 ms, TE = 3.1 ms, TI = 842 ms, 1.0 × 1.0 × 1.2 mm³ voxel size),

• a₂: T₂-w image from the second echo of a DSE (3 T, TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms, 1.5 × 1.5 × 1.5 mm³ voxel size),

• a₃: P_D-w image from the first echo of a DSE (3 T, TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms, 1.5 × 1.5 × 1.5 mm³ voxel size),

• a_T1: Quantitative T₁ map computed as described in Section 2.2,

• a_T2: Quantitative T₂ map derived as described in Section 2.2,

• a_PD: Quantitative P_D map derived as described in Section 2.2.

Our subject images are:

• b₁: MPRAGE image (3 T, TR = 6.7 ms, TE = 3.1 ms, TI = 842 ms, 1.0 × 1.0 × 1.2 mm³ voxel size), (Parameters, excepting TR, not provided to the algorithm)

• b₂: T₂-w image from the second echo of a DSE (3 T, TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms, 1.5 × 1.5 × 1.5 mm³ voxel size), (Parameters, excepting TR, not provided to the algorithm)

• b₃: P_D-w image from the first echo of a DSE (3 T, TR = 6653 ms, TE₁ = 30 ms, TE₂ = 80 ms, 1.5 × 1.5 × 1.5 mm³ voxel size). (Parameters, excepting TR, not provided to the algorithm)

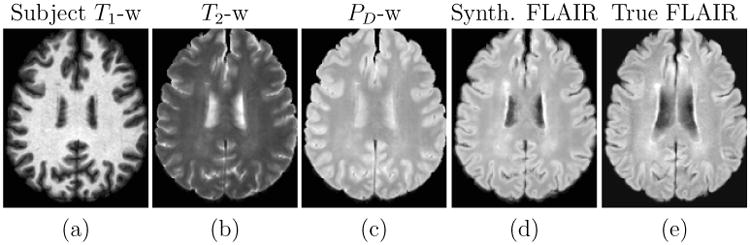
We would like to stress that the set of subject pulse sequence parameters (except TR) are unknown and these are extracted using the first step of Ψ-CLONE. Next, the new atlas T₁-w, P_D-w, and T₂-w atlas images are generated by applying the respective pulse sequence equations to the atlas P_D, T₁, and T₂ values. The following step of learning a patch-based regression is slightly different from the previous experiments. The feature vector b_i for a voxel i, is created by concatenating the corresponding 3 × 3 × 3-sized patches centered on voxel i, from all three images. The dependent variable r_i is the corresponding target atlas FLAIR intensity at voxel i. Thus, the training data consists of pairs of 〈b_i, r_i〉 from the extracted synthetic atlas images and the atlas FLAIR image. A nonlinear regression is learned using random forests and the trained regression is then applied to the extracted patches from the subject images to synthesize the subject FLAIR. Figure 9 displays the subject input images and synthetic FLAIR with the true FLAIR for visual comparison.

Figure 9.

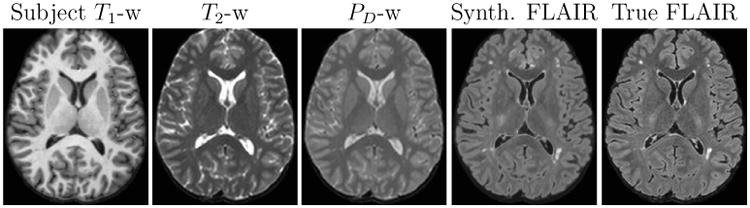
Subject input images along with the synthetic and true FLAIR images.

We ran LesionTOADS on the real and synthetic FLAIR images shown in Fig. 9. The resulting segmentations are shown in Fig. 10. The lesion volume obtained from the real FLAIR using LesionTOADS was 3107.5 mm³ whereas that obtained from a synthetic FLAIR was 5900.3 mm³. The excess seems to come from slightly enlarged regions with lesion-like intensities in the synthetic FLAIR. Our result, though visual in nature, is still a large improvement on the FLAIR synthesis result demonstrated in Roy et al. (2013a). Synthesizing FLAIR images is especially useful when the original FLAIR has artifacts, which can lead to erroneous tissue segmentation. In the next experiment, we looked at data where the acquired FLAIR was of bad quality due to motion artifacts and created a synthetic FLAIR image for visual comparison. The atlas brain for this experiment also has lesion voxels, which are essential for training. The atlas set was:

• a₁: MPRAGE image (3 T, TR = 10.3 ms, TE = 6 ms, 0.82 × 0.82 × 1.17 mm³ voxel size),

• a₂: T₂-w image from the second echo of a DSE (3 T, TR = 4177 ms, TE₁ = 3.41 ms, TE₂ = 80 ms, 0.82 × 0.82 × 2.2 mm³ voxel size),

• a₃: P_D-w from the first echo of a DSE (3 T, TR = 4177 ms, TE₁ = 3.41 ms, TE₂ = 80 ms, 0.82 × 0.82 × 2.2 mm³ voxel size),

• a₄: FLAIR (3 T, TI = 11000 ms, TE = 68 ms, 0.82 × 0.82 × 2.2 mm³ voxel size)

• a_T1: Quantitative T₁ map computed as described in Section 2.2,

• a_T2: Quantitative T₂ map derived as described in Section 2.2,

• a_PD: Quantitative P_D map derived as described in Section 2.2.

Figure 10.

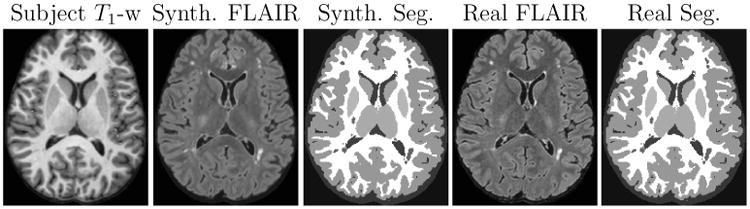
Real T₁-w image along with the corresponding real and synthetic FLAIR images and their resulting segmentations.

The subject set consisted of:

• b₁: MPRAGE image (3 T, TR = 10.3 ms, TE = 6 ms, 0.82 × 0.82 × 1.17 mm³ voxel size), (Parameters, excepting TR, not provided to the algorithm)

• b₂: P_D-w image from the first echo of a DSE (3 T, TR = 4177 ms, TE₁ = 3.41 ms, TE₂ = 80 ms, 0.82 × 0.82 × 2.2 mm³ voxel size), (Parameters, excepting TR, not provided to the algorithm)

• b₃: T₂-w image from the second echo of a DSE (3 T, TR = 4177 ms, TE₁ = 3.41 ms, TE₂ = 80 ms, 0.82 × 0.82 × 2.2 mm³ voxel size). (Parameters, excepting TR, not provided to the algorithm)

The results of this experiment are shown in Fig. 11. The synthetic FLAIR shown in Fig. 11(d) does not possess the motion artifacts present in the true FLAIR in Fig. 11(e), since these are not present in the input T₁-w, T₂-w, and P_D-w images.

Figure 11.

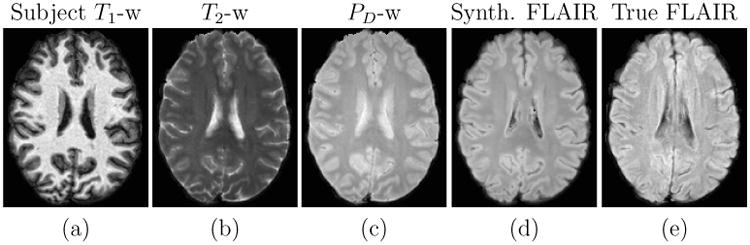
Input T₁-w, T₂-w, and P_D-w images followed by the synthetic FLAIR and the true FLAIR. The true FLAIR shows motion artifacts, which are not present in the synthetic FLAIR.

Segmentation errors can also stem from misalignment of multimodal images. In the next experiment we will demonstrate the potential benefit of using Ψ-CLONE generated synthetic FLAIR images in multimodal analysis. We use the same set of atlas and subject image sets as above, but for a different individual subject in this experiment. The original FLAIR image (Fig. 12(e)) for this experiment has a voxel size of 0.82 × 0.82 × 4.4 mm³, which is much larger than the MPRAGE voxel size of 0.82 × 0.82 × 1.17 mm³. Registering the original FLAIR to the MPRAGE requires an upsampling by a factor of four in the through-plane direction. Upsampling via interpolation (trilinear, in this case) results in blurring in the through-plane direction. This blurring is clearly visible in the original FLAIR image in Fig. 12(e), especially in the ventricles. It is also visible to some extent in right posterior ventricle region of Fig 11(e). The blurring is also a cause of gross misalignment between the high resolution images and the low resolution FLAIR images. Such misalignment has the potential to adversely affect segmentation results. The synthetic FLAIR image is created by applying Ψ-CLONE on a high resolution T₁-w image (1.17 mm slice thickness) and intermediate resolution P_D-w and T₂-w images (2.2 mm slice thickness). Thus, it is better aligned to the high resolution images and is at a higher resolution than the acquired FLAIR image. Fig. 12(d) shows the synthetic FLAIR along with the true FLAIR in Fig. 12(e). Visually it is apparent that it is better aligned to the rest of the images than the true FLAIR.

Figure 12.

Input T₁-w, T₂-w, P_D-w images with the synthetic FLAIR and the true FLAIR. The true FLAIR shows blurring because of interpolation in order to match the high resolution T₁-w

6. Discussion and Conclusion

We have proposed an MR image pre-processing framework, Ψ-CLONE, which allows us to perform MR image synthesis and scanner standardization. Ψ-CLONE represents a new direction in image synthesis. It works by estimating relevant information about the imaging parameters of a given image and incorporating these into a synthesis that respects MR image formation resulting in more correct synthetic images then previous synthesis methods. Prior work in MR image synthesis has ignored the image acquisition process when solving the synthesis problem. Our use of imaging equation approximations and the underlying NMR tissue parameters to construct atlases that are adaptive to the subject image is a unique feature. In Sections 3 and 4, we demonstrated the significantly higher quality of image standardization and synthesis than the existing state-of-the-art methods. In addition to this in Section 5, we showcased advanced capabilities of our synthesis approach—specifically FLAIR synthesis—which cannot be accomplished by other methods (Roy et al., 2013a).

Application of Ψ-CLONE for image synthesis can be used to enhance and expand multimodal datasets for better image processing. Improved resolution for modalities like FLAIR and DSE pulse sequences which are often acquired at a low resolution can prove useful for tasks such as segmentation and registration. In addition, the ability to replace an artifact-ridden image with a synthetic one for better and more consistent processing of the entire dataset will help in providing more usable subject data, which should in turn help improve the statistical power of any derived scientific results.

In addition to improving the quality and capabilities of MR image synthesis, Ψ-CLONE is also quite fast, taking less than five minutes to synthesize a new image. In comparison, state-of-the-art methods like MIMECS take around 2–3 hours on the same computational resources. This makes Ψ-CLONE well-suited as a quick pre-processing tool or as an MR intensity standardization that can be done on the scanner prior to any other processing. The nonlinear simultaneous equation solver can sometimes lead to local minima in the absence of a good initialization. The robustness of estimation is something we want to work on in the immediate future, by incorporating more accurate models of the pulse sequence equations. This will help improve the pulse sequence parameter estimation. The atlases used in the experiments are obviously of critical importance in the quality of the synthesis that can be performed. As such we are working to acquire high resolution data from a small cohort of subjects on multiple scanners to have a complete picture of the NMR properties at various field strengths as is technically feasible.

Ψ-CLONE has certain limitations which we would like to address in the future. First, it requires a segmentation of the input image(s) to estimate the imaging equation parameters. Specifically, the pulse sequence parameter estimation depends on tissue class means provided by a fuzzy k-means algorithm on T₁-w images. For typical T₁-w sequences like MPRAGE, the fuzzy k-means algorithm is fairly robust in providing the class mean intensities. In the rare case that the algorithm fails, the estimated imaging parameters tend to have very large errors, which results in the formation of inferior synthetic atlas images that can be easily spotted as inaccurate and rectified at the end of Step 2. Some of the earlier image synthesis methods (Rousseau, 2008; Roy et al., 2010b, 2011) had similar drawbacks that have since been overcome by dictionary selection techniques and use of a higher-dimensional space to normalize image patches (Roy et al., 2013a). Incorporation of these ideas is feasible, but we have yet to explore them. However, unlike Roy et al. (2013a) we do not require a WM peak normalization step.

Second, our pulse sequence parameter estimation method allows us to generate images of high quality and similar characteristics to the ground truth images (see Section 3 for experiments). However, the estimated parameters are not identical to the truth for various reasons including the use of theoretical and approximate pulse sequence equations. This is not ideal, as even though the metrics we use to measure the similarity of the images are commonplace; they may have a subtle deficiency that could only be revealed by a far larger and more rigorous study. Our estimation of P_D, T₁, and T₂ maps also requires (a) 3 different types of pulse sequence images, preferably T₁-w, P_D-w, and T₂-w images, of an acceptable resolution (the worst we have worked with is 1 × 1 × 5 mm³ voxel-size in experiments described in Jog et al. (2013b) for a different application), (b) known pulse sequence name (for example SPGR or DSE), and (c) known imaging equation or approximation for each of the three. These can be potentially restrictive in some clinical scenarios and we are working towards relaxing these requirements.

A third deficiency is our chosen regression model (random forests), it is being used because of it expediency and its ability to handle nonlinear intensity transformations. When predicting, random forest regression takes the mean of all the training data that accumulates in a leaf node during model training. In addition, when using the random forest the output value from each tree is averaged to give the final prediction from the regression. Clearly all these averages diminish the quality of the results, which can be seen in Fig. 11 where the synthetic result appears smoother than the truth. This could be addressed by modifying the random forest to do a linear fit of the data in the leaf nodes or through the use of a different regression approach. Finally, the influence of the patch size on the synthesis results has been explored—not reported here—though a complete understanding and rationale of the optimality of small patch size, i.e. 3 × 3 × 3, is not completely understood at present.

In summary, we have described a new MR synthesis approach which incorporates principles based on the pulse sequence equations. The framework is validated on synthetic and real data demonstrating its superior synthesis to state-of-the-art approaches. In addition, we have demonstrated the capability to synthesize the FLAIR pulse sequence, which is a noted deficiency of the MIMECS algorithm Roy et al. (2013a). Our estimation of pulse sequence parameters to generate a better atlas image could be used by any synthesis approach (Rousseau, 2008; Rousseau and Studholme, 2013; Roy et al., 2013a,b; Jog et al., 2014a,b) to help improve results immediately.

Figure 3.

Shown are (a) an SPGR image (TR = 18ms, TE = 10ms, α= 45° with 3% additive noise) which we use as our subject image b₁, the (b) reconstruction, b̂₁, of the subject image with the same pulse sequence as used to image (c) the atlas target image a₁ (TR = 18ms, α= 30°, TE = 10ms with 0% noise).

Highlights.

• We describe an MR image synthesis algorithm that works by estimating pulse sequence parameters of given image

• We create subject specific atlas (training) images to learn an intensity mapping using patch-based random forest regression

• We demonstrate superior image synthesis and intensity standardization and compare to the state-of-the-art

• We also demonstrate advanced capabilities of image synthesis via super-resolution and FLAIR synthesis experiments

• Our algorithm is computationally fast and is a powerful image preprocessing tool