Modeling fMRI signals can provide insights into neural processing in the cerebral cortex

Abstract

Every stimulus or task activates multiple areas in the mammalian cortex. These distributed activations can be measured with functional magnetic resonance imaging (fMRI), which has the best spatial resolution among the noninvasive brain imaging methods. Unfortunately, the relationship between the fMRI activations and distributed cortical processing has remained unclear, both because the coupling between neural and fMRI activations has remained poorly understood and because fMRI voxels are too large to directly sense the local neural events. To get an idea of the local processing given the macroscopic data, we need models to simulate the neural activity and to provide output that can be compared with fMRI data. Such models can describe neural mechanisms as mathematical functions between input and output in a specific system, with little correspondence to physiological mechanisms. Alternatively, models can be biomimetic, including biological details with straightforward correspondence to experimental data. After careful balancing between complexity, computational efficiency, and realism, a biomimetic simulation should be able to provide insight into how biological structures or functions contribute to actual data processing as well as to promote theory-driven neuroscience experiments. This review analyzes the requirements for validating system-level computational models with fMRI. In particular, we study mesoscopic biomimetic models, which include a limited set of details from real-life networks and enable system-level simulations of neural mass action. In addition, we discuss how recent developments in neurophysiology and biophysics may significantly advance the modelling of fMRI signals.

Toward Biomimetic Modeling in fMRI

During the last twenty years, functional magnetic resonance imaging (fMRI) (Kwong et al. 1992; Ogawa et al. 1990) has established a prominent role in the study of the human brain (for reviews, see Kim and Ogawa 2012; Kriegeskorte and Bandettini 2007; Logothetis 2008; Logothetis and Wandell 2004). A typical fMRI study measures blood oxygenation level-dependent (BOLD) hemodynamic signal, which has been solidly associated with neural activation (Goense and Logothetis 2008; Kim and Ogawa 2012; Logothetis et al. 2001; Magri et al. 2011, 2012; Mukamel et al. 2005; Nir et al. 2007; Shmuel et al. 2006).

While fMRI studies have been highly successful in mapping the human brain, it has remained uncommon to apply models to address the neural activity underlying fMRI signals. However, modeling is needed for advancing from description of brain states toward understanding the computational architecture of the brain. Models can be constructed at various conceptual levels, as defined in detail below. To understand neural-level signal processing in conjunction with BOLD data, neurons and their connections need to be included into biophysically meaningful neural network models, or biomimetic networks. Simulating a biomimetic network aims at actually reproducing some part of the neural computation before forward modeling the BOLD signal. Such a model-based systems neuroscience approach could facilitate basic neurosciences and sharpen clinical diagnostics and therapy. During the last decade a global systems' perspective has emerged in computational models (Frank 2005; Friston 2010; Friston et al. 2003), including emerging clinical applicability in psychiatry and neurology (Frank et al. 2004; Maia and Frank 2011; Stephan and Mathys 2014). However, the bridge between the established theoretical models of local activity, classically verified with electrophysiology, and the global systems perspective, as viewed from noninvasive brain imaging, has been missing.

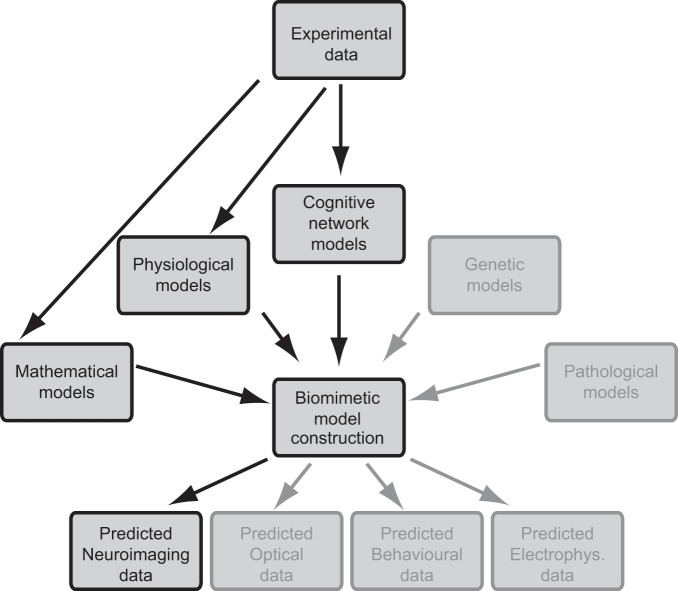
The principle of applying theoretical models to predict BOLD signals is straightforward (Fig. 1). Experimental data from various fields are combined to provide an explicit hypothesis at the neural level. This determines the architecture and appropriate level of detail for the model system, as well as the expected response. The biophysical simulation of neural response is transformed into hemodynamic response to predict the relative changes in BOLD signals, which can be tested experimentally. Deviations from the prediction provide seeds for further development of the hypothesis deployed at the beginning. Depending on the information used in the explicit neural models, fMRI could provide data to test hypotheses that incorporate variations in connectivity or physiological properties of neurons or neural system. Importantly, such simulations might also help to link apparently unrelated disciplines to fMRI data, such as pharmacology, molecular biology, or genetics, because any factor affecting membrane voltage build-up can be included in the simulations.

Fig. 1.

Schematics for theory-driven functional magnetic resonance imaging (fMRI). Recorded data (top) evoke preliminary models of brain function in various research areas. An explicit, physiologically meaningful mathematical model (center) can be modified according to hypotheses and can simulate nonexistent data. This prediction can be compared with new experimental data to validate or confront the hypotheses. The high-contrast boxes indicate areas that are most relevant for the fMRI.

The emerging potential to simulate fMRI BOLD signals with neural networks is based on achievements in theoretical and empirical neuroscience, as well as on the availability of increasingly powerful computational hardware. Theoretical neuroscience has firm roots in well-established mathematical models of single neuron function (Hodgkin and Huxley 1952; Lapicque 2007; Rall 1962), which have enabled a growing number of simulations of single neuron and network responses (for reviews, see Arbib 2003; Brette et al. 2007; Sejnowski et al. 1988). More recently, populations of neurons have been simulated with probability distributions of neural firing rates instead of detailed simulations of single neurons (for reviews, see Deco et al. 2008; Pinotsis and Friston 2011). Compared with exhaustive simulations including every single neuron of the system, such a model reduces the computational demands by a large factor and reduces the number of parameters able to affect the overall systems' behavior.

We first look into existing literature linking simulations with fMRI data at different levels of description. To aid transition from the global network approach to higher-resolution biomimetic networks, we then review recent evidence for the linkage between glutamate release and the BOLD signal. We also consider the input-output relationship of biological neurons, suggesting that dendrites retune the glutamate signals, which may partly explain the discrepancies between BOLD and spiking responses. Finally, we draw a blueprint for bridging the gap between neural models and fMRI experiments, concluding with a case study on primary visual cortex (V1), to qualitatively illustrate some of the discussed issues. In this article, we prefer to use the concept of data processing, instead of information processing, because neurons receive not only structured information but many types of input, including noise.

Biomimetic Modeling Requires Balancing between Modeling Power and Model Complexity

Below, we divide biomimetic neural models into three categories according to the size of the computational unit. Macroscopic models comprise computational nodes approximately corresponding to functional areas, with typically less than 100 computational neural units covering the whole brain. Mesoscopic models parcel functional or anatomical areas into explicit neuron-like subunits and comprise from hundreds to hundreds of thousands of computational units. Detailed models try to include as many details as possible from the real-life networks, and no single model of this type has yet tried to simulate any full-size mammalian cortex.

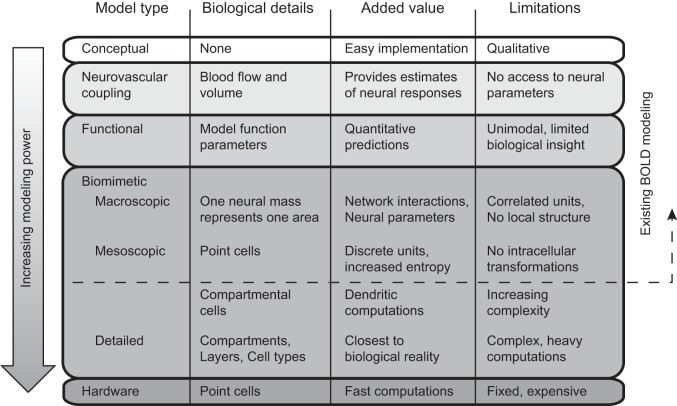
Biomimetic fMRI simulation is different from the more traditional conceptual, neurovascular, and functional modeling (Fig. 2). Conceptual modeling (e.g., in Goodale and Westwood 2004; Hari and Kujala 2009; Hickok and Poeppel 2007) includes no mathematical formulation of the theory. Instead, abstract models are presented as flowcharts or the imaging findings are simply discussed, often using concepts like “processing,” implicitly suggesting analogy to computational processes. Conceptual models are difficult to verify or falsify with new experiments, because there is no quantitative prediction to test.

Fig. 2.

Different types of theoretical models that can be associated with blood oxygenation level-dependent (BOLD) data. Modeling power, increasing downward, refers to the potential to estimate neural parameters from the data.

A necessary part of any quantitative fMRI model is the transfer function between neural activation and BOLD signal. This has been described with nonlinear biophysical models, such as the balloon model (Buxton et al. 1998), the delayed venous compliance model (Mandeville et al. 1999), or spatiotemporal hemodynamic response function (Aquino et al. 2014). In addition to blood flow, the neurovascular coupling models account for the temporal variations in cerebral blood volume, whose increase nonlinearly attenuates the positive BOLD signal. However, they contain no explicit model of neural function and provide no access to neural or network-level parameters. These models are commonly applied in conjunction with the temporal design of the experiment, to estimate BOLD signal changes related to a task or stimulus.

In one form of functional modeling, referred to as computational fMRI by Friston and Dolan (2010), the brain response to sensory input or cognitive task is associated with mathematical modeling. These formulations contain hidden variables that either are directly predicting the BOLD response without fitting or are fitted to the relative strength of BOLD response. Such computational models can provide insight into particular brain mechanisms, such as early visual transformations (Boynton et al. 1996; Kay et al. 2013; Nurminen et al. 2009), detection of stimulus statistics (Strange et al. 2005), classical conditioning (O'Doherty et al. 2003), or motor learning (Grafton et al. 2008). They do not, however, explicitly model the neural networks, although estimates of relative neural firing rates might be included. Multivariate models, classifying or decoding information from brain responses (Haxby et al. 2001; Kamitani and Tong 2005; Kay et al. 2008), can be viewed as another family of functional models. The functional models cannot simulate systems that were not targeted in the first place and thus are hard to generalize outside their scope.

The most widely used biomimetic BOLD models have targeted macroscopic networks, and in particular the connectivity between discrete nodes. They typically assume a set of active nodes, which correspond approximately to functional areas in the brain, as well as particular connectivity between the nodes. The BOLD data come from a cluster of fMRI voxels whose activation is averaged, increasing the signal-to-noise ratio.

The most prominent macroscopic network model is dynamic causal modeling (DCM) (Friston et al. 2003), where fMRI time series are extracted from regions of interest, and explicit hypotheses of causal interactions are tested between the time series from those regions. However, the need for an explicit hypothesis is a significant limitation because the direction of interaction, connectivity, or even areas involved in a particular task may be difficult to predict. Later development of DCM allowed for competition between few candidate causal interaction models, which were tested with Bayesian inference (Penny et al. 2004). Recently this has been expanded to Bayesian model selection, without a priori hypotheses about the network structure and thus searching the whole model space (Friston et al. 2011). This has, however, been criticized for being unable to actually select the model freely from all possible connections (Lohmann et al. 2012). The DCM has been incorporated into statistical parametric mapping toolbox, implemented in Matlab (Wellcome Department of Imaging Neuroscience, London, UK) (Friston et al. 2007).

The recently released The Virtual Brain toolbox (Sanz Leon et al. 2013) is a whole brain simulator using a macroscopic dynamical model, whose connectivity can be built based on individual diffusion imaging data. Moreover, it supports forward calculation from the neural model to EEG and fMRI data, as well as estimation of some neural-level variables. Such an approach is complementary to direct seeding of an electromagnetic source model with fMRI prior (Dale et al. 2000; Liu et al. 1998; Murray et al. 2002; Vanni et al. 2004), which in principle could help constraining timing of macroscopic nodes on the millisecond scale.

Resting-state fMRI data is the most common type of data simulated with macroscopic network models (reviewed in Deco et al. 2011). Following a network model at a macroscopic scale (Breakspear et al. 2003), Honey et al. (2009) studied how well individual structural connectivity in humans, assessed with diffusion MRI, matches the functional resting-state connectivity. They found that whereas structural connectivity predicted functional connectivity, the functional data were poor predictors of the structural connectivity. In particular, some areas with no measured structural connectivity showed strong functional connectivity. The same approach was replicated in a network simulation exploring the impact of lesions in network connectivity (Alstott et al. 2009). Lesions close to the cortical midline, frontal cortex, and temporoparietal junction were most disruptive. Lesions close to primary sensory cortices seemed to have mainly local effects. Interestingly, lesions could induce a decrease or increase of connectivity in seemingly unrelated parts of the network, suggesting that analysis of the clinical consequences of cortical lesion might benefit from such modelling in the future.

In mesoscopic models, the addition of discrete neural units enables the simulation of local dynamics and the use of single neuron parameters. Compared with macroscopic models, they allow for uncorrelated model neurons causing concomitant increase in entropy and capacity for information transfer in their population response. Early mesoscopic biomimetic models of imaging signals simulated neural firing rates together with positron emission tomography (Arbib et al. 1994; Tagamets and Horwitz 1998). Decreasing integration time and adding hemodynamic delays allowed Horwitz and Tagamets (1998) to modify the same rate-based model for working memory fMRI data. The first fMRI simulation with conductance-based spiking neurons studied resting-state networks. Deco and Jirsa (2012) constructed a model of 66 cortical areas, each housing biophysically meaningful attractor networks of 100 excitatory and 100 inhibitory integrate-and-fire (IF) cells. They explained resting-state BOLD signals as noise fluctuations at low-activity state, contributed by multistable attractors of a high-activity state. More recently Bonaiuto and Arbib (2014) studied a winner-take-all model with adaptive exponential leaky IF model neurons. Multiple types of synaptic activity (AMPA, NMDA, GABA-A, GABA-B) were summed up, and transformed, via a neurovascular coupling model, to a virtual BOLD signal. The network performance was measured in a decision-making task using a classification of the firing rates. The simulated BOLD signal increased linearly with stimulus contrast, i.e., was inversely related to task difficulty. This apparently counterintuitive result emphasizes the need for explicitly modeling the neural correlates of the BOLD signals for meaningful interpretation of the imaging data.

There are two important questions unanswered with the aforementioned BOLD modeling work. First, there are important differences in experimental BOLD signals and neural spiking responses, which have gone unexplained. For example, in the V1, BOLD data and their interactions can spread over significant distances (Fig. 3, adapted from Sharifian et al. 2013; see also Haak et al. 2012; Zuiderbaan et al. 2012). This is at odds with the small receptive fields in V1, as measured from action potentials. In addition, spatial frequency tuning functions in human visual cortex, measured with fMRI, are at much lower frequencies (Henriksson et al. 2008) than monkey single cell tuning functions (Foster et al. 1985), even though the visual performance of the two species is similar. This difference cannot be explained easily by averaging many neurons into single voxels because their means remain different. Finally, there can be a clear mismatch between BOLD and spiking activity (Logothetis et al. 2001; Maier et al. 2008) as well as different responses in many cognitive tasks (Boynton 2011). Without a single model explaining both neural and fMRI signals, we are left with uncertainty whether BOLD data are really useful for any quantitative studies or whether they are plagued with unknown sources of noise or biases that fundamentally preclude any quantitative model validation.

Fig. 3.

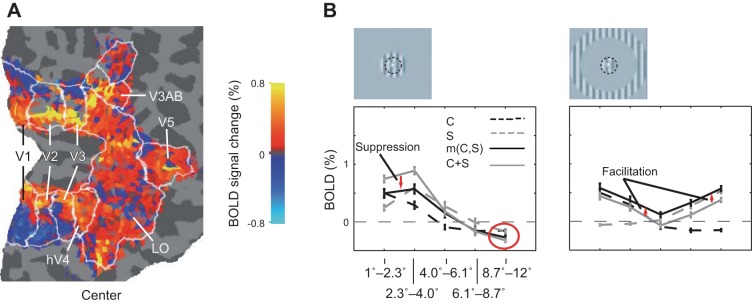
Spread of BOLD signal in the primary visual cortex (V1). A: the BOLD signal change without threshold calculated for a central ring (B, left). When no threshold is applied, it is apparent that the BOLD signal spreads first positive and then negative to cover the full extent of the low-level retinotopic areas V1, V2, and V3. B: stimuli consisted of rings containing gratings. The center stimulus is the innermost ring (denoted C, delineated with a black dashed line in the inset), whereas the near surround (S, on the left) and the far surround (right) are the more eccentric ones. Note the consistently negative BOLD at eccentricities several degrees off the primary representation for both C and S stimuli (red circle), the suppression [m(C,S) < C + S] with near surround (red arrows, left) and the trend for facilitation [m(C,S) > C + S] in the far surround condition (red arrows, right) at all eccentricities. C stands for center; S, for surround; m(C,S), for center and surround together; and C + S, for the summation of the BOLD signals measured separately for the C and S conditions. Adapted from Sharifian et al. (2013).

The second unanswered question is that if we want to understand how the cerebral cortex processes data, we need to have a model capable of similar data processing. While the models described above have many ingredients of physiology, none of them yet replicates cerebral functions in detail, nor has shown (or even aimed to show) any general purpose cortex-like data processing capabilities. While it is possible to include large amounts of details in a simulation (Traub et al. 2005), with concomitant increasing needs in computing power (Migliore et al. 2006), it is apparent that this approach provides limited benefits. We gain little by attempting to construct a model with maximally detailed biological realism, because we cannot yet efficiently compute such a model on a large scale. In addition, we do not know all the details of the target system. Such a model would thus have a large number of unknown parameters, affecting the model performance and biasing our interpretation. Hence the second question becomes: which pieces of cortical structures and functionality are essential for information processing, and how to efficiently capture them in a model?

We suggest that adding dendritic compartments to the mesoscopic models with discrete model neurons is a necessary next step for answering both questions. First, it might help to bridge BOLD to single unit electrophysiology, because a compartmental model allows complex transfer functions between neural input and output. Moreover, data from visual cortex have shown that single cell receptive fields are modulated by stimuli that fail to drive the neurons when presented alone (Angelucci et al. 2002; Knierim and Van Essen 1992; Sceniak et al. 1999). A compartmental model can capture these modulatory effects, which emerge from subthreshold postsynaptic events (see below, and Heikkinen et al. 2015). Second, below we discuss how dendrites seem to retune the neural input to much sparser output, with an unknown contribution to neural data processing. Recent biomimetic hardware implementations have been motivated by extreme speed and fault tolerance of computations. However, hardware is fixed and implement functionalities deemed necessary at the time of their planning. For example, both the SpiNNaker (Furber et al. 2012) and the Very Large Scale Integration system of the FACETS project (Millner et al. 2010) comprise point-like IF units, which might be a significant limitation if dendritic signal transfer function turns out to be important for neural data processing.

Insights from Cellular Neuroscience Call for an Update of BOLD Signal Modeling

Glutamate release as a substitute for the modeled BOLD response.

It has been suspected for some time that BOLD reflects more the synaptic input than the action potential output of neural activation (Logothetis et al. 2001). Overall, the fMRI signal has been reported to couple well with neural activity (Magri et al. 2011), both in anesthetized and in awake brains (Goense and Logothetis 2008). However, the correspondence has been consistently better with local field potentials (LFP) than with action potentials (Logothetis et al. 2001; Nir et al. 2007). Particularly gamma-band LFPs have been solidly associated with BOLD signals (Magri et al. 2012; Murayama et al. 2010). Interestingly, the alpha-band and other low-frequency LFPs (<12 Hz) have been reported to correlate inversely with the BOLD signal (Magri et al. 2011; Mukamel et al. 2005). It is technically difficult to isolate the contribution of action potentials to BOLD signals, because both BOLD signals and action potentials are highly correlated with gamma-band LFPs (Mukamel et al. 2005). In addition, it is counterintuitive why energetically expensive action potentials (Attwell and Laughlin 2001) would not contribute to neurovascular coupling.

The problem of neurovascular coupling unraveled when the role of astrocytes was understood (Attwell et al. 2010; Koehler et al. 2009; Lauritzen 2005; Zonta et al. 2003). In particular, the neurovascular coupling now appears best explained by glutamate release, which acts as a feedforward surrogate signal for the oxygen consumption (Gordon et al. 2011; Koehler et al. 2009; Petzold and Murthy 2011; see Lecrux et al. 2011 for a complementary view). The glutamate is sensed by the astrocytes, whose extensions touch local vascular smooth muscle and mediate the neurovascular coupling. The fact that vascular response may be triggered primarily by excitatory synaptic signaling is of importance for designing a successful computational model to predict and interpret the BOLD signal.

Neural input tuning may be different from output tuning: consequences for modelling the BOLD response.

The core element of any network-level data processing model of the brain is the signal transfer function within one neuron. In most computational models, this transfer function is a simple linear, nonlinear, or thresholded function of the summed input (reviewed e.g., in Rolls and Deco 2002). However, recent data suggest that the transfer function between neural input and output may be much more complex and actually relate to the structure of the neuron. Furthermore, inputs arriving to various parts of the dendritic tree could be integrated quite differently.

Indeed, subcellular processes, in particular the dendritic active and passive properties have been suggested to have an important role in cortical data processing (Branco and Häusser 2010; Gollo et al. 2009; Poirazi et al. 2003; Polsky et al. 2004; Sidiropoulou et al. 2006; Sjöström et al. 2008; Spruston 2008; Spruston et al. 1994). Jia and colleagues (2010) showed that in the mouse visual cortex synaptic spines form “hot spots,” each with their own orientation tuning. Such tunings seemed to land in a rather random fashion, and the inputs of visual neurons were, on average, not very well tuned. However, the action potential tuning for orientation was very specific and relatively narrow. Such intracellular transformations call for a distinction between the sensitivity function, i.e., the representation of parameter space at the synaptic input, and the classical tuning function, i.e., the representation of parameter space, measured from action potentials. BOLD, reflecting the input, may be best associated with the sensitivity function, in contrast to neural firing rates, which define the tuning function.

In addition, in the cerebral cortex, the position where a synapse lands in the dendritic tree may have a strong influence on the synaptic efficiency at the axon initial segment (Magee 2000; Williams and Stuart 2002).

If we combine the anisotropic mapping (Petreanu et al. 2012, 2009; Spruston 2008) of synaptic inputs with the decreased synaptic efficiency as a function of dendritic distance (Williams and Stuart 2003), we end up with a broader tuning in the fMRI signal than in the classical electrophysiological signals, as depicted in Fig. 4. This could explain the narrow tuning in extracellular recordings, as well as the much broader tuning in fMRI responses, and perhaps even account for other differences between the two methods in general.

Fig. 4.

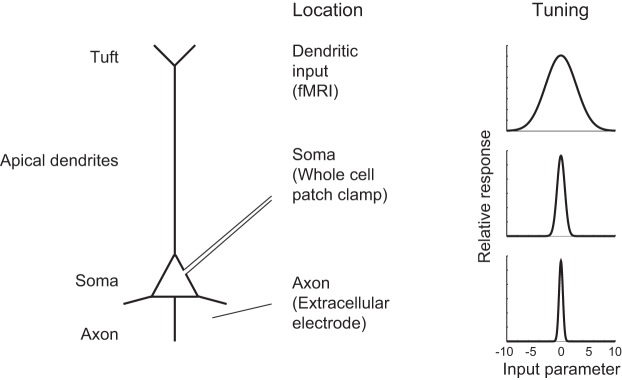
Hypothesized difference between tuning functions at different parts of single neuron. The BOLD signal is primarily reflecting glutamate release and is thus sensitive to dendritic input. This input may be much wider tuned than the output (Jia et al. 2010). Moreover, in the cerebral cortex, signal decay along the dendrites render the soma less sensitive to distal than to proximal dendritic inputs (Williams and Stuart 2002). In addition, distal inputs may come from a wider set of cortical sources (Petreanu et al. 2009, 2012; Spruston 2008) and thus be less selective than the proximal inputs. This may result in larger bandwidth, i.e., a wider tuning in the dendrites than in the soma, as depicted in the figure. The tuning function may further narrow, when the membrane depolarization at the axon initial segment is turned into an action potential firing probability with an exponential function (Anderson et al. 2000; Miller and Troyer 2002).

In summary, biomimetic BOLD models might need to account for the signal transformation between the neural input and output. As a consequence, the computational units in such models need to include dendrites, i.e., consist of multiple neural compartments. A similar conclusion was recently made with modeling of local field potentials (Einevoll et al. 2013), which further increase pressure to include compartmental neurons to large-scale models of neural systems in the future.

Constructing Biomimetic Neural Networks to Simulate BOLD Signals

In the following, we will concentrate on outlining the building blocks for a mesoscopic model of cortical functions. The same principle can be applied to more detailed or more abstract networks by increasing the biological realism and detail or by generalizing some features to more abstract representations of larger units, respectively.

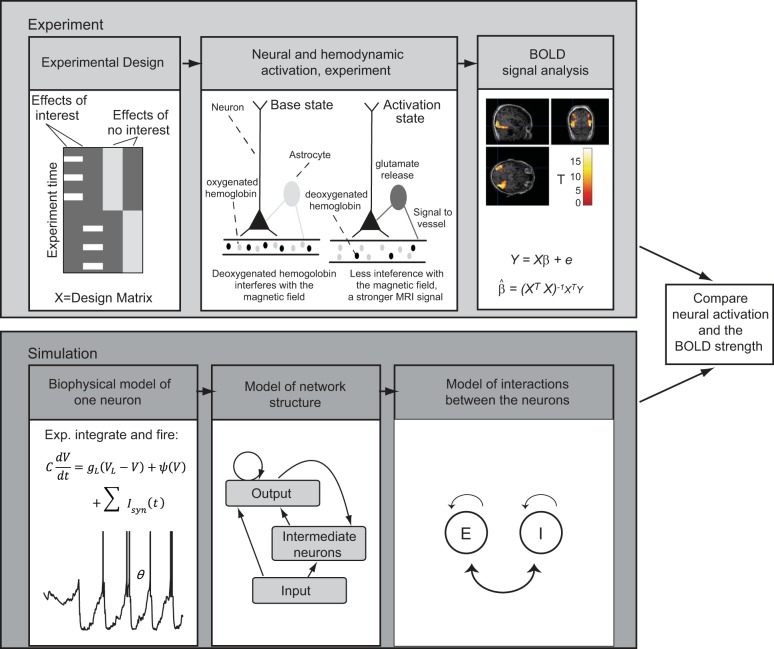
To simulate fMRI signals with a neural network, we need to implement a parallel experiment that can be conducted with both fMRI and a modeled neural network in silico, with the same experimental design (Fig. 5). For a given system under investigation, the process comprises the following steps: 1) choose the biological model for neurons, i.e., the computational units of the cortical network; 2) define the general architecture of the connections between the neurons in the network; 3) model the interaction between neurons; 4) simulate the network at a computationally feasible scale and transform the model output to a predicted hemodynamic signal; 5) compare the responses predicted by the simulated network with the observed fMRI BOLD signals. We will next discuss each of these steps and use the visual cortex as a representative and well-characterized hierarchical data processing system to elucidate selections that could be made at each stage. Finally, we will review an example on bridging spiking output of neurons and measured BOLD signals in V1.

Fig. 5.

Predicting BOLD response. Top frame: the fMRI experimental design should result in isolated activity, whose relative magnitude can be modeled using, e.g., the general linear model. Bottom: the neural model should simulate the experimental design, with assumed connectivity structure and neural interactions. The modelled population response can then be compared with the measured BOLD response.

Biological neuron models and synaptic transmission.

A neuron model for simulating neural computations underlying fMRI data should be robust to small differences in parameter initialization and computationally efficient in a large-scale network. Contemporary simulations of biomimetic neuronal networks are constructed either with firing rate models, which simulate mean spike rates without information on spike timing, or with somewhat more realistic spiking network models. The units in spiking network models are typically simplifications from full single-neuron models. They typically model the membrane potential dynamics, such as the spike-generating nonlinearity with phenomenological mathematical descriptions, bypassing the complex kinetics of voltage-gated channels. Such simplified models, such as the IF neuron model [based on Lapique's work from 1907, translated in Brunel and van Rossum (2007) and recently reviewed by Burkitt (2006)], its subsequent extensions as well as the more recent Izhikevich model (2003), provide computationally efficient analytical expressions for a neuron's spiking mechanism. They can also be augmented by explicitly modeled ionic conductances and synaptic currents. Our exemplary model for V1 uses an extension of the IF neuron, the exponential integrate and fire (EIF) neuron (Fourcaud-Trocme et al. 2003). In this model, the neuron's membrane voltage V is governed by the membrane capacitance C, the leakage conductance g_L and the synaptic inputs I_syn, until a depolarized regime is reached, where a depolarizing nonlinearity ψ(V) takes place.

$$C\frac{dV}{dt}=g_{\mathrm{L}}(V_{\mathrm{L}}-V)+\mathit{\psi }\left(V\right)+\mathrm{\Sigma }\hspace{0.17em}{\mathrm{I}}_{\text{syn}}(t).$$ (1)

where

$$\psi \left(V\right)=g_{\text{L}}{\Delta }_{\text{T}}\exp \left(\frac{V-V_{\text{T}}}{\Delta \text{T}}\right).$$

is the spiking current, which makes Eq. 1 unstable at membrane potentials close to the threshold V_T. When that threshold is crossed, spike generation is enabled. The slope factor Δ_T determines the voltage dependence of the spiking current. Conceptually, a spike is triggered at the time at which the voltage equation diverges toward infinity, after which the membrane potential is instantly reset to a hyperpolarized value, where it is clamped for a refractory period. Compared with the simple RC-circuit behavior of the original IF neuron, the spike-generating nonlinearity ψ(V) provides a better phenomenological description of the membrane potential dynamics preceding the action potential.

While basic spiking models can reproduce selected properties of neuronal output reasonably well, they generally consider a neuron as a single point-like isopotential compartment (i.e., without dendrites). These basic models can be extended into circuits with a number of isopotential compartments, connected to each other with resistances. This way, details of a neuron's morphology as well as spatially inhomogeneous distributions of ion channels can be implemented to any degree of detail [models with various levels of detail are compared e.g., by Herz et al. (2006)]. In our example model, the computational efficiency was a key limiting factor, and thus we chose to use only six compartments to model the cable properties of dendrites in pyramidal cells at the expense of compromising detail of data processing within individual cells.

Network structure and synaptic interactions.

The next step is to define a map of neural connections within the investigated region, were it the whole brain, a defined hierarchical system, or a single area. These connections can be classified into two major types: 1) connections between different types of neurons, such as inhibitory and excitatory ones and 2) connections of neurons between and within different cortical areas. Such parameters can be based on anatomical and physiological studies (Marino et al. 2005; Markov et al. 2014b; Schwabe et al. 2006). The relative number of axonal connections between cortical areas can follow anatomical studies in monkeys (Felleman and Van Essen 1991; Markov et al. 2014a; Markov et al. 2011) or, in the case of whole brain models, the relative structural connectivity between cortical areas, as shown in diffusion tractography in humans (Honey et al. 2009). However, the full connectivity profile of human brain is a work in progress and comprises a number unresolved issues both methodological and conceptual (Sporns 2014).

Implementation of synapses in a neural network varies from abstract descriptions transferring spike rates in the presynaptic unit directly into changes in the membrane potential of the postsynaptic neuron into explicit modeling of individual synaptic events, their dynamics, and plasticity. In addition, neural dendrites integrate inputs nonlinearly, so that summation of two events depends on the relative location of synapses (Spruston 2008). The amount of biological realism incorporated in the model depends again on the question asked of the model. To address interplay of multiple synaptic inputs and network states, conductance-based synapses are vital, as the currents driven by synaptic activation depend also on the membrane voltage. In the example we review below, the synapses were divided into two main groups for simplicity: excitatory glutamatergic (AMPA) and inhibitory (GABA_A) synapses. Segregation of dendritic inputs from various sources was implemented by their anisotropic landing to the dendritic tree with realistic decay of postsynaptic events. On the other hand, no attempt was made to address local processing through nonlinear interactions of the synaptic events or detailed modelling of the cellular morphology, as the purpose of the model was to study the mean population activity of large groups of neurons.

Network interactions.

All excitatory interactions in neural network simulations need to be accompanied by inhibition, both to avoid saturating the excitatory activation and because inhibition apparently modulates all processing of the network (Isaacson and Scanziani 2011). In addition, the brain network is very code efficient. In theory, to reach maximal capacity in information transmission, the network should be composed of mutually independent neurons, with similar response probability profiles (Shannon 1948). Correspondingly, correlation between neurons reduce information that is available in a neural network (reviewed in Averbeck et al. 2006), and thus some kind of mechanism capable of modifying correlated firing would be justified. Such mechanism can be implemented with a particular relation between excitation and inhibition (King et al. 2013; Renart et al. 2010; Vanni 2012).

Simulation.

Several toolboxes have become available to support cellular (Hines and Carnevale 2003) and network-level (Bower and Beeman 1998; Brette et al. 2007; Gewaltig and Diesmann 2007; Goodman and Brette 2008) simulations of neural activity. While increasingly realistic large-scale neural network simulations are becoming practical with supercomputer technology (Helias et al. 2012), efficient use of computational resources remains important, regardless of the scale of the simulation. For example, the average number of neurons in adult human V1 per hemisphere is ∼14 × 10⁷ (Leuba and Kraftsik 1994). To keep the complexity of such a network tractable, one approach is to build a simple visual system, where the network structure, spatial dimensions of connectivity between neurons, and cellular biophysics are borrowed from nature. The number of neurons is reduced in the model (e.g., in the reviewed example below it is about 74 × 10³), and the structure of the system simplified, including only parts that are considered necessary to replicate the modeled behavior.

Comparison between simulated neural network responses and fMRI signals.

When comparing neural and BOLD signals, we need to acknowledge the limitations of the fMRI method. These include larger measurement unit size than in invasive recordings, a low temporal resolution, and the indirect hemodynamic signal with its nonlinear association to neural activity. In addition, BOLD signal has no absolute baseline but is dependent on the level of both resting-state activity and blood flow. These limitations affect the questions asked, the reasonable scale of the model, and the interpretation of the results.

The large unit size is more or less unavoidable in fMRI. Today, most studies comprise voxel volumes of 8–30 mm³, (isotropic voxel with side length 2–3 mm), including 10⁵–10⁶ neurons, In the future, a plausible goal for spatial resolution is the size of a functional column, with volumes between 0.15 and 0.8 mm³, (radius 0.15–0.25 mm, height 2–4 mm). This resolution has already been achieved in a number of studies (Cheng et al. 2001; Kim et al. 2000; Menon et al. 1997; Moon et al. 2007; Sun et al. 2007; Yacoub et al. 2008, 2007), and hardware development will inevitably support smaller voxel volumes (Logothetis 2008). Simulated or experimental neural activation data need to be sampled to the fMRI resolution for comparison.

We need to take into account further the neurovascular coupling. In our example, the relevant output of the network is the glutaminergic conductance of the V1 pyramidal neurons. This glutaminergic conductance is then assumed to be linearly associated with local cerebral blood flow after a delay between neural and hemodynamic response. The blood flow, again, has a known nonlinear relationship with the BOLD signal (Buxton et al. 1998), which depends on blood volume at each instant.

The detailed spatial distribution of the BOLD signal is strongly affected by the data acquisition sequence. Most fMRI studies are conducted with gradient echo echo-planar imaging, which provides the best signal-to-noise ratio. Unfortunately, the strongest gradient-echo signals emerge not from the parenchyma or microvasculature in the cortex, but from the cortical surface, which houses the superficial veins (Mandeville and Marota 1999; Zhao et al. 2006), as depicted in Fig. 6. Yet, it is possible to improve the spatial accuracy by selecting the spin-echo sequence instead. While losing a significant portion of the signal, the spin-echo sequence is less sensitive to signals from the draining veins and thus less prone to localization inaccuracies (Parkes et al. 2005; Zhao et al. 2006). Optimization of spatial accuracy (micro- vs. macrovascular contribution) for spin-echo sequences is dependent both on echo-time and field strength (Uludag et al. 2009). Alternatively, the superficial veins can be detected from a separate resting state run, selected on the basis of a high variance, and masked away in the analysis (Olman et al. 2007).

Fig. 6.

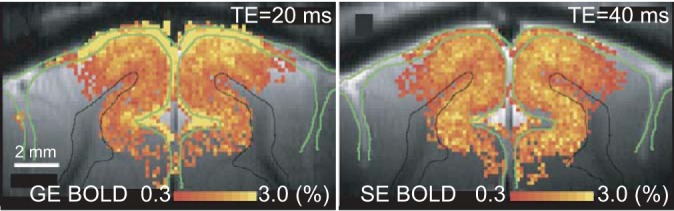
The BOLD signal with the typical gradient-echo (GE) sequence comes, to large extent, from the draining veins located at the cortical surface, reducing the spatial specificity of fMRI. Left: BOLD signal in GE data shows strongest signal at the cortical surface, which houses the large draining veins. Right: spin-echo (SE) data show strongest signal at the middle of the cortex and a lesser amount at the surface. Cat cortex. Reprinted from Zhao et al. (2006) with permission from Elsevier.

In our work we have discarded the temporal behavior of fMRI data and concentrate on the spatial distribution of the data, after modeling the BOLD signal changes with standard methods.

Once in possession of both the simulated neural response and the BOLD signal, we can assess the discrepancies between these outcomes and adjust model parameters iteratively when necessary. Unlike the neural field modeling, studied in, e.g., Deco et al. 2008; Pinotsis and Friston 2011; Pinotsis et al. 2012, the spiking network model with discrete neural units offers a simpler mathematical formalism (e.g., bypassing the field equations), while allowing for monitoring various patterns of neural responses. However, due to the intrinsic stochastic nature of the models, multiple trials may need to be performed, and robust estimates found through averaging over the found solutions, as in in vivo experiments. Another benefit of the proposed methodology is the modular nature of the models, which allows for an easy modification of the model structure, and the explicit testing of hypotheses. With rather simple manipulations, one can e.g., add neuronal compartments in a single neuron modelling, restructure the connectivity of the network, add ionic currents, or use different neuronal models.

Practical example: bridging neural activation and BOLD in the primary visual cortex.

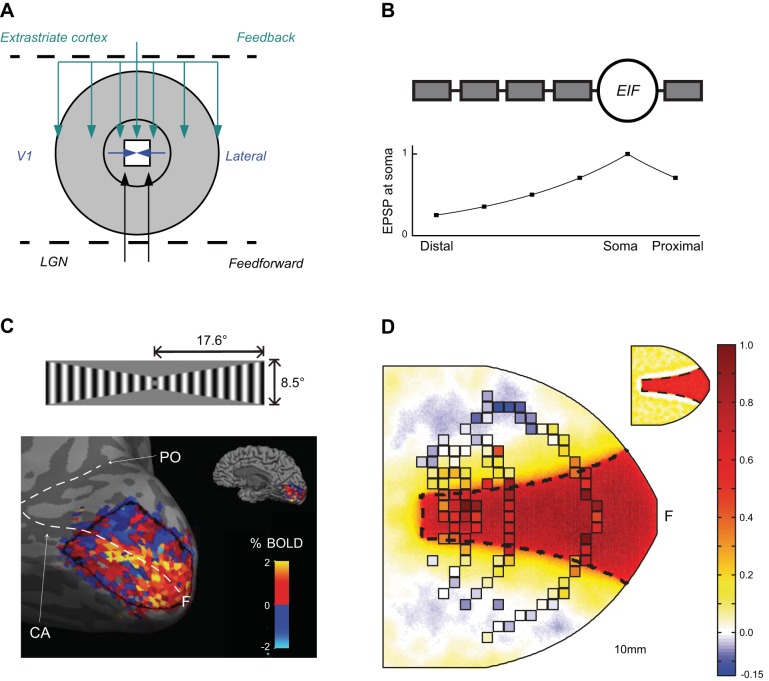
Recently, Heikkinen et al. (2015) simulated fMRI BOLD response with a spiking neural network model and compared the simulation results with real fMRI data from humans, as well as with the single cell response estimated from V1 cell receptive field data from the macaque monkey. The objective of the simulation was to bridge the difference between neural and BOLD responses by reproducing the spatial profile of the spin-echo BOLD response to a fixed-shape visual grating stimulus, while simultaneously providing a plausible neural substrate for this response. Based on published anatomical studies (Angelucci et al. 2002) and a spike-rate model of primate single unit recordings (Schwabe et al., 2006), they explored the possibility that the well-characterized long-range modulation of V1 neuronal signals could underlie also the substantial spread of BOLD responses outside the stimulated area. In this scheme, V1 neurons with characteristically narrow receptive fields receive feedback from higher-order extrastriate areas where the neurons have large receptive fields (Fig. 7A). Through such a feedback, each V1 neuron could receive subthreshold input representing a much larger proportion of the visual field than the one covered by their narrow summation fields. Schwabe et al. (2006) postulated that such cortico-cortical feedback can mediate long-distance interactions in V1 and successfully reproduced salient features of spatial interactions in the V1 neural spiking responses. Departing from their rate-based model, which distinguished “driving” and “modulatory” inputs, the two with distinct yet unspecified biological mechanisms, Heikkinen et al. (2015) implemented this network architecture onto a 2D spiking neuron network of compartmental EIF neurons. Decay of postsynaptic potentials (Williams and Stuart 2003) in the six-compartment neuron model (Fig. 7B) allowed for distinct tuning for the inputs to distal and to proximal parts of dendrites as well as in neuronal output, following the hypothesis illustrated in Fig. 4. Monitoring the excitatory conductance of the model neurons simultaneously with their spike response permitted evaluation of the hypothesis that the different spatial properties of BOLD and spike response stem from the differences between neuronal input and output.

Fig. 7.

Simulating the BOLD response in the primary visual cortex. A: the network architecture of the model is adapted from Schwabe et al. (2006): The spatially limited extent of minimal receptive field provided by feedforward inputs is complemented by the lateral connections on V1 and modulatory feedback (with large receptive fields) from the extrastriate cortex. B: the modulatory role of the extrastriate feedback was implemented through connecting the feedback to distal dendrites, where the individual inputs were ineffective in driving the firing of the cells. C: BOLD SE response in V1 of a representative subject. The corresponding signal changes in individual voxels were mapped without threshold into the model cortical space through separate multifocal localizer run (Vanni et al. 2005) and downsampled to a 2 × 2 mm grid (D). The cerebral blood flow response estimate derived from the population mean BOLD data (squared samples), superimposed as discrete samples on the glutamate-mediated conductance response of the spiking neuron model to the same stimulus, which is presented as continuous data in the main panel. The spike response of the model is shown in the inset. It was to a large extent confined to the primary retinotopic representation of the stimulus on the model cortex (depicted by dashed border in D) with narrow surrounding reduction from the baseline firing rate (arrows). The letter F in C and D indicates the approximate region of foveal representation. LGN, lateral geniculate nucleus; EIF, exponential integrate and fire; EPSP, excitatory postsynaptic potential; PO, parietooccipital sulcus; CA, calcarine sulcus. Modified from Heikkinen et al. 2015.

Figure 7C shows the BOLD response to a wedge-shaped grating stimulus in area V1 of a representative subject. There was moderate individual variability in the data, suggesting somewhat variable parameters across subjects. After exhaustive search of V1-extrastriate as well as excitatory-inhibitory connection strengths within V1, the model provided an excellent correspondence to the neural and fMRI data (Fig. 7D). Importantly, the total error was significantly lower for the network with compartmental neurons than for the one constructed from point-like neurons, in which the spread of the estimated BOLD signal was always accompanied with spread of the spike response. In particular, it was not possible to retain spike-frequency downmodulation close to stimulus representation, as the monkey data suggest, and simultaneously follow the widely spread BOLD response modulation.

The simulation was applied to a stationary, fixed-shape grating stimulus. This was considered an ideal contrast stimulus and was represented by spike generators at cortical locations corresponding to the primary retinotopic representation of the stimulus. Locations beyond this region were stimulated at a much lower rate. When applying more complex stimuli, such as natural images, they would first need to be processed by a filter representing the retinal signal processing.

Although a number of parameters in the model are specific to primate visual system, most are not. Thus such a model should in principle be applicable to other cortical systems as well. That said, the model is still very limited. It is restricted in targeting one sensory input and does not include intracortical communication utilizing several sources of information (such as multiple sensory modalities or attention). Neither does it include cortical layers or corticothalamic signaling. However, overcoming the aforementioned limitations and extending this approach to other functional areas and systems are clearly conceivable.

Conclusions

Rapid development in many subfields of neuroscience is enhancing the theoretical basis of systems neuroscience and supporting the modeling of fMRI data. First, the increasing resolution of fMRI together with better understanding of the BOLD signal generation mechanisms are advancing the role of fMRI in acquisition of fine-grained data. Simultaneously, methodological and conceptual advances in cellular neuroscience have provided detailed information on the single-neuron input-output transformation. Finally, increasing computational power and development of simulation environments have brought computational modeling of neural networks closer to biological reality. Together, these developments are enabling simulations of mesoscopic neural population responses, which can be verified experimentally.

Although derived from a practical need to bridge macroscopic measurements and neural functions, in principle a mesoscopic model can also aim at finding basic laws of network operation, while avoiding the complexity and immense computational needs of very detailed and biologically realistic simulation (Markram 2006). This enables easier experimentation with large-scale brain models. On the other hand, simulators, which are close to the biological reality, unlike mathematical abstractions, may help life scientists lacking a very strong mathematical background to work with theory-based experiments. The conceptual and computational simplicity of mesoscopic models may carry beyond brain imaging and provide strong explanatory power when trying to understand the principles of biological data processing in a hierarchical network.

GRANTS

This work has been supported by the Academy of Finland (grants 124698, 140726, 218054), the BRAHE neuroscience collaboration between the Aalto University and the University of Helsinki, the Finnish Society of Sciences and Letters, the Oskar Öflund Foundation, and the Otto A. Malm Foundation.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.V. and H.H. conception and design of research; S.V., F.S., and H.H. performed experiments; S.V., F.S., and H.H. analyzed data; S.V., F.S., H.H., and R.V. interpreted results of experiments; S.V., F.S., and H.H. prepared figures; S.V., F.S., H.H., and R.V. drafted manuscript; S.V., F.S., H.H., and R.V. edited and revised manuscript; S.V., F.S., H.H., and R.V. approved final version of manuscript.