Detecting Functional Connectivity During Audiovisual Integration with MEG: A Comparison of Connectivity Metrics

Abstract

In typical magnetoencephalography and/or electroencephalography functional connectivity analysis, researchers select one of several methods that measure a relationship between regions to determine connectivity, such as coherence, power correlations, and others. However, it is largely unknown if some are more suited than others for various types of investigations. In this study, the authors investigate seven connectivity metrics to evaluate which, if any, are sensitive to audiovisual integration by contrasting connectivity when tracking an audiovisual object versus connectivity when tracking a visual object uncorrelated with the auditory stimulus. The authors are able to assess the metrics' performances at detecting audiovisual integration by investigating connectivity between auditory and visual areas. Critically, the authors perform their investigation on a whole-cortex all-to-all mapping, avoiding confounds introduced in seed selection. The authors find that amplitude-based connectivity measures in the beta band detect strong connections between visual and auditory areas during audiovisual integration, specifically between V4/V5 and auditory cortices in the right hemisphere. Conversely, phase-based connectivity measures in the beta band as well as phase and power measures in alpha, gamma, and theta do not show connectivity between audiovisual areas. The authors postulate that while beta power correlations detect audiovisual integration in the current experimental context, it may not always be the best measure to detect connectivity. Instead, it is likely that the brain utilizes a variety of mechanisms in neuronal communication that may produce differential types of temporal relationships.

Introduction

In magnetoencephalography and/or electroencephalography (M/EEG) functional brain connectivity, the word connectivity can refer to many different mathematical methods used to measure relationships between brain regions, typically applied to oscillations in one of several frequency ranges. Most connectivity measures used to detect these relationships, with the exception of local gamma band phase coherence, do not have a complete bottom-up theory from neural circuitry to the measured electrical/magnetic relationships (for review, see Siegel et al., 2012). As a result, many connectivity measures are plausible methods for assessing functional connectivity, and indeed many different types of these measures are utilized, such as coherence, imaginary coherence, and correlation of power envelopes.

A large number of connectivity methods will use either the phase or the power of M/EEG oscillations. Regarding phase-based metrics, a theory termed communication through coherence predicts that effective neuronal communication is established through electromagnetic coherence, a phase-based connectivity measure (Fries, 2005). Under this theory, oscillations between communicating neuronal groups have a stable phase relationship, in which action potentials from a sending group of neurons arrive at a receiving group when the phase of the receiving group is at an optimal point to impact their responses and are thus functionally connected. Conversely, if the action potentials from the sending group arrive at the receiving neurons at phases where they cause minimal neuronal responses, they are not functionally connected.

It is less clear how neuronal communication could be facilitated by the temporal correlation of oscillatory power (Siegel et al., 2012). Instead, power correlations are selected as a connectivity measure not due to a connectivity theory, but because of the many known oscillatory power responses in cognitive states and tasks. For example, because it is known that the brain has a variety of beta band responses to stimuli and cognitive states, correlating these responses between areas can be done to determine connectivity. However, it is unknown how these covariations of power could impact effective communication between neurons.

The fact that researchers find realistic connectivity findings with a variety of techniques can have two possible interpretations. First, the analysis techniques could be measuring distinct aspects of the same underlying neuronal processes involved in communication. For instance, if two brain regions' communication produced phase coherent gamma bursts, both phase coherence and power correlations would increase. However, the authors feel a more likely scenario is that different metrics reflect different aspects of brain communication. For instance, working memory could be reflected through gamma coherence, while stimulus binding could be reflected in beta power correlations.

The current study investigates the ability of seven magnetoencephalography (MEG) connectivity techniques to detect neural audiovisual communication. The connectivity metrics are based on common linear techniques, which are easily directly compared, leaving nonlinear and directional methods for future investigation. Additionally, the authors excluded methods, which require a large exploration of parameter space.

M/EEG techniques are often developed and utilized without a reasonable amount of testing and verification (Gross et al., 2013). In this study, the authors developed a testing platform that involves very similar active and control periods, where a subject visually tracks a ball that does or does not correlate with an ongoing auditory tone. Three key aspects of this approach allow for a careful and systematic investigation of the differences in connectivity techniques. First, the stimulus involves spatial audiovisual integration, which allows the authors to view if metrics are sensitive to communication occurring during audiovisual processing; if a metric reflects underlying neuronal audiovisual communication, the authors expect it to detect higher connectivity during the audiovisual portion of this task between auditory and visual regions. This line of reasoning follows many studies in humans and nonhuman primates, which have shown LFP (Ghazanfar et al., 2005), ERP/ERF (Giard and Peronnet, 1999; Mishra et al., 2007; Molholm et al., 2002; Shams et al., 2005), and BOLD (Marchant et al., 2012; Noesselt et al., 2007; van Atteveldt et al., 2004; Watkins et al., 2006) -modulated responses in auditory and visual cortices during congruent audiovisual stimulation. Second, the stimulus provides large time periods where connectivity should be sustained, which are critical in establishing robust connectivity measurements. Last, the authors test the connectivity metrics on an all-to-all mapping of cortical voxels, which avoids the pitfalls of seed selection and typical region of interest (ROI) analyses, vastly expanding the scope of this investigation.

Materials and Methods

Hummingballs task

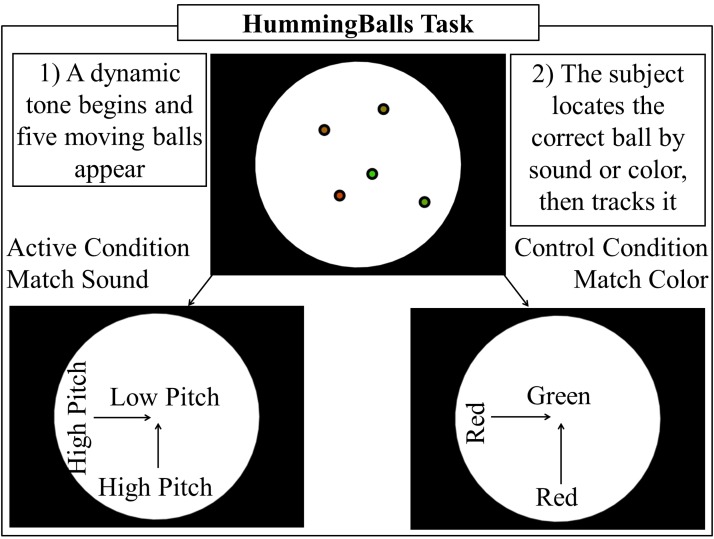
As part of a larger experimental design, subjects performed a task to locate and track a correct target ball from four distractor balls on a screen. The target ball is identified in two ways for two separate experimental conditions (Fig. 1). In the first condition, termed sound matching, a pitch varies depending on the target ball's distance from the center of the screen; as the ball moves toward the outside of the screen, the pitch increases. In the second condition, termed color matching, the target ball's color varies depending on its distance from the center of the screen; as the ball moves toward the outside of the screen, it changes from green to red. During sound matching, all balls change color randomly. During color matching, a varying tone is still present; however, it does not correlate with either the target or distractor balls' positions. In this way, the stimulus is similar for both conditions: a varying tone and five color changing balls are displayed, while the task performed by the subject varies. Examples of the hummingballs task can be seen in the Supplementary Video S1 (Supplementary Data are available online at www.liebertpub.com/brain).

FIG. 1.

Hummingballs task design. Eye tracker data and a visually inspected algorithm determine when a subject locates the correct target ball. Subjects are instructed to find the ball as quickly as possible and are given feedback on every trial detailing how long it took them to locate the correct ball. Only periods of time after the correct ball is located and the subject is tracking it are utilized in this report.

An infra-red eye tracker is used to identify when subjects locate the target ball. Only periods of time after the subject locates the correct target ball are utilized in this report. The contrast the authors will explore is sound tracking, as the active condition when the subject is tracking a ball whose position corresponds to an auditory pitch versus color tracking as the control condition, where the subject is tracking a ball whose position corresponds to the ball's color. Simply put, the subject is tracking a unified audiovisual sensory percept or a visual object accompanied by an uncorrelated tone. In both the active and control conditions, smooth pursuit of the tracked ball is present, resulting in contributions due to eye movements being canceled between conditions.

This stimulus is designed to first provide a clear separation where more audiovisual integration should be occurring during sound tracking compared with color tracking. Second, the time periods are long, on the order of several seconds. This gives the authors an advantage when investigating connectivity metrics since the longer the time period, the more the data to make a statistical inference with, resulting in more robust analysis. The stimuli employed here differ from a history of studies that use stimuli either comprising flashes and beeps, illusions, or brief congruent and incongruent stimuli, such as a cat producing a woof sound (Bischoff et al., 2007; Dhamala et al., 2007; Hein et al., 2007; Jones and Callan, 2003). While these studies are excellent at localizing areas that produce supra-additive responses to multimodal stimuli, they are not optimal for investigating connectivity due to the short time frame to determine a connectivity measurement. Additionally, utilizing short onset-based stimuli is likely to misidentify event-related coactivation as connectivity unless a proper illusion or experimental contrast is employed.

Twenty-one subjects (11 male, 10 female), aged 21–58 (mean age=32.6 years, SD=9.6), performed the hummingballs task, twice on day 1 and twice on a subsequent day within 4 days of the first. Several datasets were lost due to eye tracker failure or subject movement and were discarded from the analysis immediately after collection, leaving on average 3.29 runs per subject, for a total of 69 runs. Each run consisted of 16 active and control trials, which lasted 15 sec each. Informed written consent was obtained from all participants, and the study was conducted according to the guidelines approved by the National Institute of Mental Health Institutional Review Board, in accordance with the Declaration of Helsinki.

Derivation of time series and source techniques

Subjects underwent MEG scans during all hummingballs sessions. MEG signals were recorded at a rate of 600 Hz in a magnetically shielded room using a 275-channel whole-head magnetometer (CTF Systems, Inc., Coquitlam BC, Canada). An additional 3rd gradient spatial filter derived from 30 reference sensors was applied to reduce extracranial signals (Vrba et al., 1995).

For each subject, a volumetric MRI scan was coregistered with their MEG head coordinates obtained using fiducial coils at the nasion and two preauricular points, and a warping transform to a common Talairach subject space was created using AFNI (Cox, 1996). A 1-cm-spaced grid of points spanning the entire brain was generated in this common space and reverse warped to each individual subject's anatomy. Forward solutions generated through the CTF version 5.2 software using a multisphere model, which computes spheres for each sensor aligned to the curvature of the inner skull nearest the sensor, were then calculated for each voxel for each subject. Forward solutions that did not include at least ten channels in every subject with an absolute weighting of two standard deviations above the mean per subject were discarded. This was done to eliminate voxels not properly covered by the scanner in all subjects as well as voxels with poor signal-to-noise ratios. The remaining 528 voxels resembled a superficial cortical shell roughly 2 cm deep (Supplementary Fig. S1).

Only tracking segments of time starting 1 sec after the subject located the ball were used in the present investigation. Tracking periods under 2 sec were discarded to establish robust connectivity measurements. Due to beamformers/covariance matrices requiring a large amount of time to stabilize, runs where performance did not yield at least 20 sec of active and control tracking periods were discarded. Sound tracking and color tracking periods were evenly balanced on an overall run, and per trial level. For instance, if a sound tracking segment of 8.6 sec was selected, an equal 8.6 sec color tracking time segment was also selected from the same run. This resulted in a perfectly balanced active and control time frame per run, thus avoiding known temporal effects of some connectivity measures as well as beamformer bias. Connectivity values from each trial over 2 sec were averaged within each run, yielding a single connectivity value per run between each voxel pair.

Covariance matrices computed from band-passed time segments spanning the entire active and control periods were selected for each run and used to derive adaptive beamformers for each of the 528 voxels (Sekihara et al., 2001; Vrba and Robinson, 2001) regularized at a constant five femto Tesla per root Hz. Sensor data were band passed with a 4th-order zero phase-shift Butterworth IIR filter into a given frequency range before beamformer application, resulting in estimated virtual channel time series for each of the 528 voxels for every active and control time segment.

Connectivity metrics

While the number of connectivity metrics is still growing, the authors chose seven metrics to test (four based on power fluctuations and three that use phase information). Both power and phase-based methods have been previously used to deduce brain connectivity (for a review, see Siegel et al., 2012).

The phase-based metrics the authors tested were phase coherence (Coh), imaginary coherence (ICoh), and phase-locking index (PLI). Coh is a widely used measure, in which segments of time Δ are evaluated between two signals and the stability of the phase angle difference between the two time series is measured over many Δs (full mathematical description included in Nolte et al., 2004). ICoh, specifically developed for brain connectivity analysis (Nolte et al., 2004), is similar; however, only the nonzero phase-lagged components are utilized. The appeal of ICoh over Coh is that a zero phase-lagged delay between two neural sources measured through M/EEG can be influenced by a single source's signal spread. Therefore, ICoh, by only utilizing the nonzero phase relationships, discounts possible artificial inter-regional relationships. The PLI (Stam et al., 2007), also developed specifically for brain connectivity, computes an index of positive and negative phase values, discarding possible amplitude interactions that can bias ICoh. The PLI is thought to be advantageous as it is less impacted by amplitude effects present in Coh and ICoh (Stam et al., 2007).

Of these four power-based methods, two are derived from the Hilbert envelope. The Hilbert envelope, while mathematically complex (for full description, see Brookes et al., 2008), is theoretically simple and easy to understand visually as simply an envelope that surrounds a band-passed oscillatory signal (Supplementary Fig. S2). The first Hilbert-based method is Hilbert-R, which is simply a Pearson-R value between envelopes from two voxels. The second Hilbert method, the correlation of average envelope (CAE), introduces a Δ variable (Brookes et al., 2011) where the envelope is averaged across time length Δ, then windowed throughout the time signal. In this way, CAE is similar to Hilbert-R, with an effective low-pass filter that specifies the maximum rate of interaction between the two envelopes that can be detected. The CAE connectivity measure is thought to improve as Δ decreases from 10 to 0.5 sec or 0.1 to 2 Hz low-pass (Brookes et al., 2011); however, the given study did not go below 0.5 sec likely because it was attempting to imitate functional motor connectivity previously seen with functional magnetic resonance imaging, which cannot detect quicker interactions.

These two additional power-based methods are derived from the Stockwell transform (for full mathematical descriptions, see Stockwell et al., 1996). The Stockwell transform is similar to a continuous wavelet transform and is based on a moving and scalable localizing Gaussian window. The resulting time–frequency representation has the property that the integral over time is simply the ordinary Fourier spectrum wherein any point across the time axis can be resolved as an instantaneous power estimate. For the measure R of Stockwell power mean frequency (RSP-MF), the authors took the mean power value across the frequency band of interest (for instance, beta band) and then computed a Pearson-R value from the resulting time series. In contrast, R of Stockwell power per frequency (RSP-PF) computes the Pearson-R value for the power time series of each individual resolved frequency within the band of interest, and then calculates the average of the R values as the resulting connectivity (Supplementary Fig. S3).

As previously stated, the authors selected these seven metrics largely because they require no additional variables other than Δ and a frequency band; exploring how a variety of parameters affect results is outside the scope of this article.

Selection of parameters

For all of these connectivity techniques, a frequency range of interest needed to be specified. While a full analysis across the spectrum with all connectivity metrics would be ideal, to limit the scope of the investigation, the authors selected the beta band (15–30 Hz) for an in-depth analysis.

The authors focused on the beta band because it is known to be a physiological rhythm that responds to a wide variety of stimuli and cognitive processes (for review and one of the latest theories of beta oscillations, see Engel and Fries, 2010) and is known to be spatially coincident with hemodynamic responses in similar tasks (Singh et al., 2002). Additionally, the authors performed a more focused analysis in theta (4–8 Hz), alpha (8–13 Hz), and gamma (40–80 Hz) bands, which have all been reported to illustrate multimodal responses (for review, see Senkowski et al., 2008). It is noteworthy that as a general trend higher frequency brain rhythms occur at lower amplitudes, resulting in lower signal-to-noise ratios, which impact all oscillation-based findings, connectivity notwithstanding.

For each of the phase-based metrics, as well as CAE, a time window Δ was set as 1/3rd of a second and computed every 1/12th of a second (i.e., each Δ-sized window overlapped 3/4ths with the last). In this way, metrics were time-resolved over short highly overlapping windows. Ideally, a full analysis of Δ with all of the metrics it applies to would be optimal; however, the scope is vast. The authors used 1/3rd of a second to have an acceptable resolution across the frequency domain for phase-based metrics, while keeping the time frame short to detect interactions on fine temporal scales.

Multiple comparisons

When imaging an entire brain volume, a false discovery rate test (FDR; Genovese et al., 2002) is commonly utilized to correct for family-wise type I errors. Importantly, FDR correction is sensitive to the distribution of p values, that is, the percentage of tests that differ from the null hypothesis; as the fraction of nonsignificant tests (high p values) entered into the FDR increases, p values need to be lower to pass the q threshold. Because of this, areas which are not expected to differ from the null hypothesis should be removed before testing, for instance, CSF, air, and ventricles (Genovese et al., 2002).

Due to the audiovisual nature of the task, the authors hypothesize that they will detect connectivity differences between auditory and visual regions, thus expecting no connectivity differences in the majority of voxels included in the all-to-all mapping. Voxels not expected to show significant connectivity are typically not included in connectivity analyses (Palva and Palva, 2012; Schoffelen and Gross, 2009). The authors included all voxels in the volume to investigate the specificity of possible audiovisual connectivity differences, a component they feel is crucial when investigating connectivity metrics. For example, a metric which shows increased audiovisual connectivity during audiovisual integration would be interpreted differently if it additionally showed increased connectivity throughout the majority of the brain. Furthermore, by using all full grids of voxels, the authors can verify that connectivity is not a result of signal leakage between beamformers as they would be expected to show star-burst-like patterns with prominent connections to neighboring voxels, which would be excluded in seed selection.

Problematically, the distribution of significant and nonsignificant tests (low and high p values), which underlies the FDR, is vastly different between a single brain volume and an all-to-all connectivity mapping. For example, in the contrast, the authors expected to see no significant connectivity with a voxel in the hand knob area of motor cortex. In a brain volume, this voxel would add a single high p value to the FDR multiple comparisons computation. However, in an all-to-all mapping, tests are done with every other voxel, adding an entire brain volume of high p values to the FDR. This drastically affects the distribution of p values, resulting in extremely low p values being required to pass the q threshold. To clarify, a theoretical brain volume consisting of 5% real active and control differences can be compared with a theoretical connectivity volume, where 5% of the voxels have real active and control connectivity differences with 5% of the brain. In this case, real active and control differences in the data drive 5% of tests in the brain volume, producing low p values, but only 0.25% of the tests in the all-to-all mapping. To reach an equivalent distribution of p values as the brain volume, the 5% of voxels in the all-to-all analysis would need to have real active and control differences with the entire brain. As a specific example, because of the extremely low percent of low p values (as expected) in the all-to-all analysis in Figures 2 and 3, a p<7.2e-7 would be required to pass an overall FDR (q<0.1) of the entire connectivity volume.

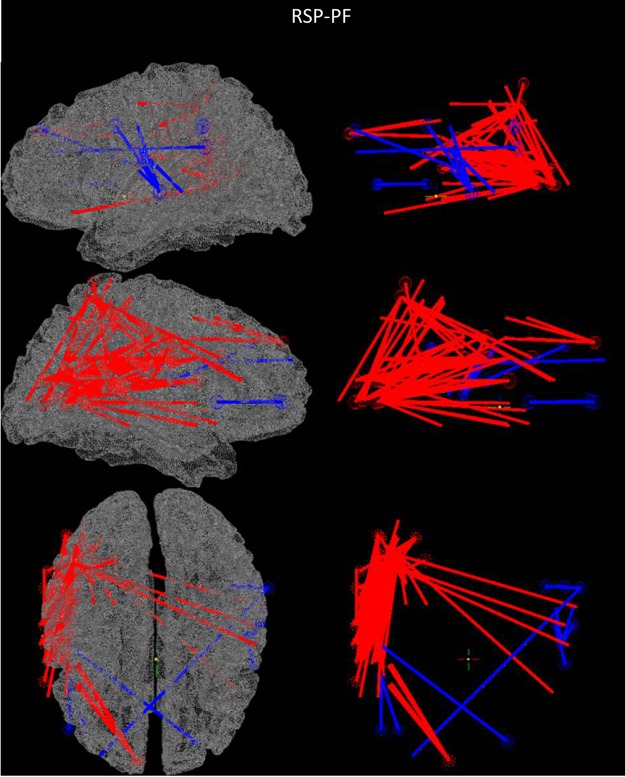
FIG. 2.

Beta band sound tracking minus color tracking R of Stockwell power mean frequency (RSP-PF) results; visualization of all connections q<0.1. Connections in red indicate active (sound tracking) is significantly larger than control (color tracking), and connections in blue indicate control is significantly larger than active.

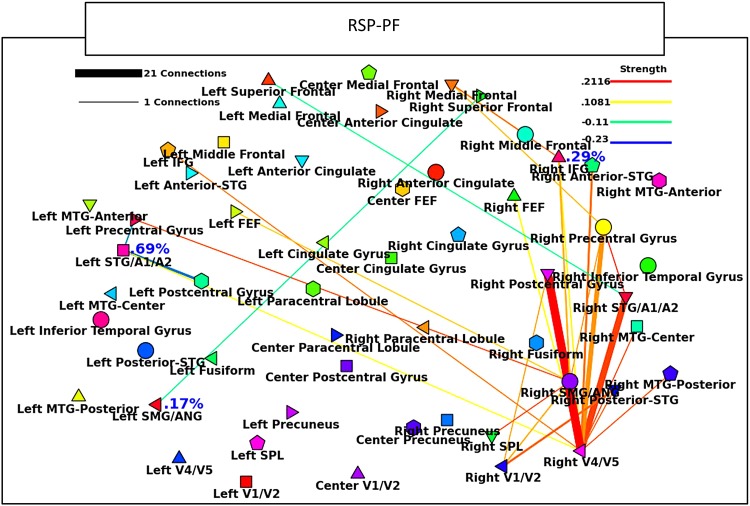
FIG. 3.

Beta band sound tracking minus color tracking RSP-PF results; region of interest (ROI) breakdown of the all-to-all connections in Figure 2. Thickness of the lines indicates the amount of significant connections between ROIs, shown in the legend at upper left. The color of the lines (legend upper right) indicates the average strength of all significant connections between the ROIs. Within ROI connectivity is shown by a percentage directly to the right of the ROI, colored red for active>control and blue for control>active. If any connections between two ROIs include significant positive and negative values, the line is colored black. If any significant within ROI connectivity has both positive and negative connections, the percentage to the right of the ROI is also colored black.

The authors are not the first to point out the limitations of FDR multiple comparisons testing in connectivity analyses (Gross et al., 2013; Zalesky et al., 2010). Indeed, alternative multiple comparisons tests have been developed to apply to all-to-all connectivity volumes. A high-dimensional statistical method utilizing neighborhood filters and nonparametric shuffling has been proposed (Hipp et al., 2011). While this technique is promising, it requires significant connections to have clusters of similar neighbors, which the authors are uncertain to expect at the spatial sampling size of 1 cm. Similarly, the authors do not utilize the random field theory (for introduction, see Brett et al., 2003) due to the required smoothness of the data, which they are again uncertain to expect from the metrics, especially at the large spatial sampling. Additionally, a graph metric-based approach, termed network-based statistics, has been proposed (Zalesky et al., 2010). However, graph metrics are also directly affected by spatial sampling (Antiqueira et al., 2010).

In light of this, the authors have opted to rely on the FDR due to its simplicity and its reliability over the last decade of publications. However, to account for the FDR limitations in all-to-all mappings, the authors separated the connectivity matrix into individual brain volumes, one connectivity volume per voxel. The authors then perform the FDR on single brain volumes where it has proven to be robust. Each brain volume comprises connectivity values between a single voxel and every other voxel in the brain. In this way, the authors investigated every connection regardless of its expected significance, while simultaneously avoiding massive skew in the distribution of p values.

The authors emphasize they are not using this multiple comparisons correction in the typical manner utilized in brain imaging, which is to deduce brain activity. The authors are testing the metrics themselves and are not attempting to prove that audio and visual areas communicate during audiovisual integration. Hence, they are simply utilizing statistics to limit the results to connections with stable differences between the active and control conditions, then viewing which metrics, if any, show connectivity between audio and visual regions, thus implicating that they are sensitive to audiovisual communication.

Data processing

In each of the seven connectivity metrics, the resulting correlation values are Fisher transformed at the appropriate stage, which is when they are bound between 0 and 1, before averaging (e.g., Fisher is applied in RSP-PF to the R values at each resolved frequency within the band of interest before the R values are averaged together across frequencies). Results are then averaged between all trials in the run, yielding an active and control connectivity metric between each voxel pair per subject per run. These are then normalized by their standard deviations. A linear mixed effects model is then applied through the NMLE package in R (Pinheiro et al., 2013) to generate p values while accounting for repeated measures within subjects.

These resulting p values are then FDR corrected through AFNI (Cox, 1996) with a Benjamini–Hochberg correction, on a brain volume basis as outlined above, and only results of q<0.1 are determined as significant and discussed below. This q threshold was selected because this study is a comparison of metrics not intending to prove that auditory and visual areas communicate during audiovisual integration. If a higher q threshold were employed, the authors are concerned that a metric may be prematurely deemed unable to detect the communication when only a slight statistical variance was present. Furthermore, the authors are interested in directly comparing connectivity patterns to determine similarity between metrics and thus are concerned that a strict threshold would result in extremely sparse networks that would de-emphasize similarity between metrics by not allowing much overlap.

For comparison, the authors additionally performed a traditional, nonconnectivity SAM power analysis in all frequency ranges. This analysis was performed as outlined above; however, the authors were able to use a finer spatial grid (0.5 cm) as well as typical statistics (FDR q<0.05) due to computational and statistical simplicity in comparison with connectivity.

All computations not specifically mentioned otherwise are performed in Python. AFNI and SUMA (Cox, 1996; Saad et al., 2004) are utilized for visualization. Due to the massive amount of computations involved, this study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health, Bethesda, MD (http://biowulf.nih.gov).

Network analysis

This analysis was done on two levels; first, the authors performed a direct connection-by-connection contrast between the methodologies, which are presented in table format. The authors have opted for this simple direct comparison of connections because the time series that go into each voxel-to-voxel connection are identical and only the methodology is varied. This leaves overlapping connections between methodologies as a direct comparison of the computational technique without anatomically blurring or clustering.

In addition to how similar connectivity metrics are, the authors are also interested in where these connections are. To make the results more concise, the authors performed a secondary analysis by clustering voxels into 54 ROIs and summarizing the connections between them. Neither averaging of time signals within ROI nor selecting seeds within each ROI was performed in this step. Visualizations are summary figures, indicating the number and strength of connections between voxel pairs grouped in the ROIs. Overall this ROI-based analysis adds human readability at the cost of additional spatial ambiguity.

Results

Behavioral results

Subjects took on average 6.36 sec to find the target ball and failed 30.07% of the trials. The time the ball was found was determined as a point when the target ball began to be reliably tracked until the end of the trial. The algorithm for determining this was visually inspected to verify its accuracy (an example can be seen in the Supplementary Video S2). Trials were considered failed if the subject was unable to continually track the correct ball from a time point until the end of the trial. Subjects were 0.62 sec faster at finding the ball based on sound than color (p=0.00227) and failed 1.88 fewer sound trials than color trials (p=3.76e-8).

Overall beta band results

Tracking a ball whose position correlated with a tone versus a color caused significant differences in connectivity with all methodologies (Tables 1, 2 and Figs. 2–4). Resulting networks with all methodologies are extremely sparse, below 1 in 1000 connections. The greatest number of statistically significant connections is seen through CAE, with 130 (0.0934%). The method of computing the FDR for each connectivity volume appears conservative as the largest p value that achieves q<0.1 is 0.005 (seen in the CAE methodology). In every case, over 94% of the voxels have no connections that pass the FDR (Table 1). The methodology that yields the fewest connections is the PLI, with 7 (0.00503%).

Table 1.

Overview of Results Per Methodology, Determined in the Beta Band Contrasting Sound Tracking Versus Color Tracking

	RSP-PF	RSP-MF	Hilbert-R	CAE	Coh	ICoh	PLI
Number of voxels with significant connections (q<0.1)	34 (6.43%)	12 (2.27%)	28 (5.30%)	26 (4.92%)	23 (4.35%)	31 (5.87%)	14 (2.65%)
Number of significant connections (q<0.1)	108 (0.077%)	21 (0.015%)	47 (0.034%)	130 (0.093%)	40 (0.016%)	26 (0.019%)	7 (0.005%)
Largest p value (q<0.1)	0.004	0.001	0.001	0.005	0.002	0.0005	0.0002
Smallest p value	6.63E-06	1.419E-05	8.31E-06	1.316E-05	1.08E-05	1.235E-05	1.97E-05
Largest significant connection strength active-control	0.211	0.105	0.218	0.394	0.134	0.314	0.374
Smallest significant connection strength active-control	−0.236	−0.087	−0.181	−0.338	−0.052	−0.319	−0.309
Number of connections sound>vision tracking	94 (.067%)	14 (0.010%)	28 (0.020%)	123 (0.088%)	16 (0.011%)	16 (0.011%)	5 (0.004%)
Number of connections vision>sound tracking	14 (.010%)	7 (0.005%)	19 (0.014%)	7 (0.005%)	24 (0.017%)	10 (0.007%)	2 (0.001%)

CAE, correlation of average envelope; Coh, phase coherence; ICoh, imaginary coherence; PLI, phase-locking index; RSP-MF, R of Stockwell power mean frequency; RSP-PF, R of Stockwell power per frequency.

Table 2.

Comparison of Overlapping Voxels and Connections Determined in the Beta Band When Contrasting Sound Tracking Versus Color Tracking

	RSP-PF	RSP-MF	Hilbert-R	CAE	Coh	ICoh	PLI
(A)
RSP-PF	108	14	12	20	0	0	0
RSP-MF	66.67%	21	8	8	0	0	0
Hilbert-R	25.53%	38.10%	47	7	1	0	0
CAE	18.52%	38.10%	14.89%	130	1	0	0
Coh	0.00%	0.00%	2.50%	2.50%	40	6	0
ICoh	0.00%	0.00%	0.00%	0.00%	23.1%	26	0
PLI	0.00%	0.00%	0.00%	0.00%	0.00%	0.00%	7
(B)
RSP-PF	85	11	21	32	7	1	3
RSP-MF	55.0%	20	11	11	1	0	1
Hilbert-R	44.7%	55.0%	47	14	9	2	1
CAE	40.5%	55.0%	29.8%	79	10	4	4
Coh	17.1%	5.00%	21.9%	24.4%	41	14	1
ICoh	2.63%	0.00%	5.26%	10.5%	36.8%	38	1
PLI	21.4%	7.14%	7.14%	28.6%	7.14%	7.14%	14

(A) Common (directly overlapping) connections between methodologies. The diagonal is the total amount of significant (q<0.1) connections for that methodology; the upper triangle is the number of significant common connections between two methodologies; the lower triangle is the percent of significant connections in common, determined by dividing the upper triangle by the diagonal. (B) Common voxels between methodologies. The diagonal is the number of voxels that have at least one significant connection. The upper and lower triangles are the same as A, but for voxels with significant connections instead of the connections themselves.

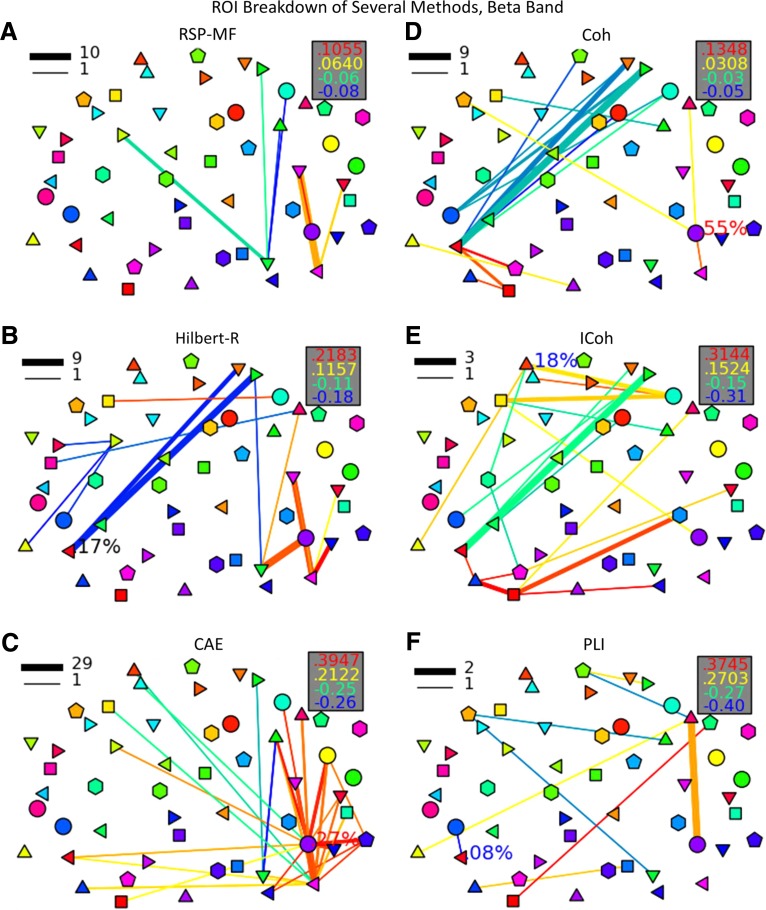
FIG. 4.

Beta band sound tracking minus color tracking results for the six other tested metrics aside from RSP-PF. Metrics are grouped via power (A–C) and phase (D–F) accordingly. Refer to Figure 3 for node and legend labeling.

Connection strength varies across the metrics; however, the largest range of strength is seen with CAE, which has the largest positive difference of .394 as well as the largest negative difference of −0.338 (Table 1). Notably, because this is a connectivity contrast, negative values indicate that connectivity is larger in the control condition.

Power-based metrics, which included RSP-PF, RSP-MF, Hilbert-R, and CAE, produced connectivity maps that largely do not overlap with the phase-based metrics, Coh, ICoh, and PLI (Table 2). Only one directly overlapping connection is present in both phase-based and power-based metrics: a connection between the right angular gyrus and right V5 seen with Coh, Hilbert-R, and CAE metrics.

Because power-based metrics yielded connectivity patterns separate from phase-based metrics, aside from the single aforementioned connection, the authors review their results separately.

Beta band results, power-based metrics

Power metric-based connectivity patterns are more similar to each other than those created with phase-based metrics (Table 2 and Supplementary Fig. S4).

All four power metrics show right hemisphere dominant increased connectivity between auditory, visual, and multimodal areas (Figs. 2–4 and Supplementary Fig. S4A). Importantly, all four metrics show right hemisphere increases between primary auditory and V4/V5, as well as between V4/V5 and the supramarginal/angular gyri (SMG/ANG). CAE and RSP-PF show the heaviest right side interconnectivity, including connections between R-V4/V5 and both the right frontal eye fields (FEF) and the right inferior frontal gyrus (IFG). RSP-MF and Hilbert-R show more limited increases in connectivity, although Hilbert-R shows an increase between the right superior parietal lobule (SPL) and R-IFG.

Beta band results, phase-based metrics

Coh and ICoh have 23.08% of their connections in common (Table 2 and Supplementary Fig. S4B). The majority of these connections are negative and between the left SMG/ANG and right frontal cortices. PLI shares no common connections with any other metric.

None of the phase-based metrics show audiovisual connectivity. Coh shows increased connectivity between right V4/V5 and the right SMG/AMG, as well as between left V1/V2 and the left SMG/ANG; however, no connectivity is seen between the auditory cortex and any visual or multimodal areas (Fig. 4D–F). It is additionally interesting to note the increased connectivity seen with Coh between right SMG/ANG and the bilateral IFG. ICoh additionally shows left side visual connectivity with the multimodal SMG/ANG. PLI shows connectivity between the right SMG/ANG and the R-IFG; however, like the other phase metrics, no connectivity is detected between audiovisual areas.

Gamma, alpha, and theta band results

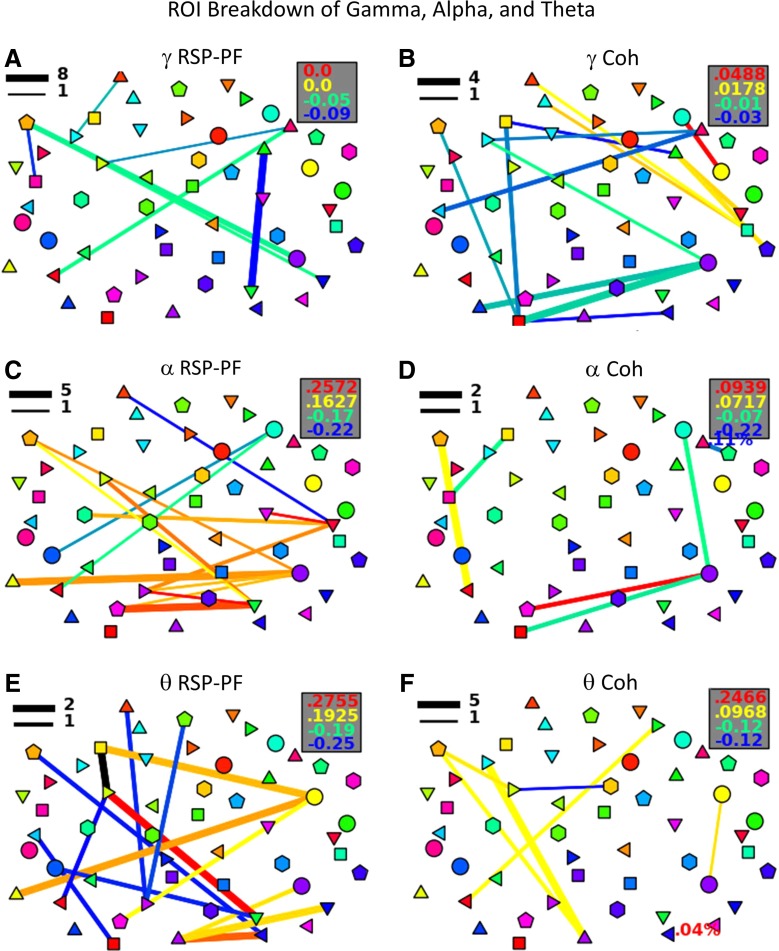
While the majority of the analysis is in the beta band (15–30 Hz), the authors also explored alpha, gamma, and theta bands. They used two metrics, Coh and RSP-PF, to limit the scope of the investigation. Coh was selected as a phase metric because of its similarity to ICoh and because Coh did not show the short range connectivity in the beta band contrast that ICoh is designed to compensate for. In addition, gamma Coh is a major tool used in connectivity literature. RSP-PF was selected because of its similarity to all the other power metrics, its lack of additional variables (Δ), and its ability to account for frequency-specific sub-band interactions.

Neither Coh nor RSP-PF connectivity patterns show connections between auditory and visual regions in gamma, alpha, or theta bands (Fig. 5). It is, however, interesting to note that gamma Coh between the primary auditory cortex and the right FEF is greater during audiovisual tracking than during visual tracking. Additionally, gamma RSP-PF shows large negative connectivity between the FEF and the SPL, as well as between the IFG and the SMG/ANG, signifying larger gamma power correlation during color tracking between these areas. Alpha RSP-PF shows auditory connectivity with the postcentral gyrus and the precuneus; however, no connectivity is seen with any segment of the visual cortex. Theta RSP-PF, theta Coh, and alpha Coh do not show any auditory connectivity.

FIG. 5.

Gamma (A, B), alpha (C, D), and theta (E, F) sound tracking minus color tracking for the RSP-PF (A, C, E) and coherence (B, D, F) metrics. Refer to Figure 3 for node and legend labeling.

Within ROI connectivity and signal spread

The largest within ROI connectivity (0.55%) is seen with Coh in the right SMG/ANG; however, further inspection of these connections indicates that they are between the intraparietal sulcus (IPS) and the SMG/ANG. The IPS, being on the border of the SPL and SMG/ANG, leads to ambiguity in the ROI separation on their border. Furthermore, even this highest within ROI connectivity is a very low percentage. The overall lack of within ROI connectivity provides evidence that these active and control contrasts are sufficient in dealing with signal spread in this experimental design. If this were not the case and signal spread were biasing these results, the authors would expect to see extensive connectivity with neighboring voxels, which would manifest as large percentages of within ROI connectivity. The authors stress that utilizing an active and control period will not always be sufficient to deal with signal spread. For instance, if the active and control periods are vastly different, such as when contrasting a task against a rest condition, it is plausible that large amounts of connectivity will be seen with neighboring voxels.

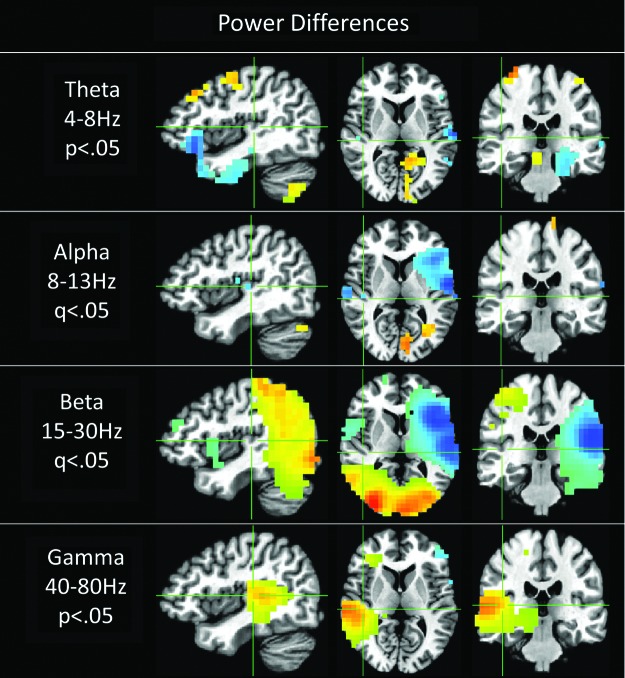
Power differences

Nonconnectivity power results show significant differences in both the alpha and beta frequency ranges, as well as trends in theta and gamma bands (Fig. 6). Beta power is larger during sound tracking throughout the visual/parietal cortex and inversely stronger during vision tracking in the left auditory cortex. Notably, there is no significant beta power difference detected with the right auditory cortex, which these beta power connectivity results implicate in audiovisual integration. Additionally, gamma power shows a strong localized trend (p<0.05) with the right auditory cortex, but not left auditory cortex.

FIG. 6.

Power differences between sound and vision tracking. Significant q<0.05 differences were seen in the beta and alpha bands. No significant differences were seen in the theta and gamma bands, trends p<0.05 are presented. Blue indicates power was greater in the vision condition, while red signifies higher power in the sound tracking condition. Crosshairs in all Figures are centered on right auditory cortex (−41, 25, 8).

Discussion

Many types of functional connectivity metrics have been utilized to determine functional brain connectivity in the past. In this study, the authors test several methods to investigate which are sensitive to audiovisual integration. These results show that beta power correlation-based connectivity strongly detects connectivity between auditory and visual regions. Specifically, all four beta power measures (RSP-PF, RSP-MF, CAE, and Hilbert-R) exhibit larger connectivity between V4/V5 and auditory cortices when tracking an audiovisual object than when tracking a visual object that does not correlate with the auditory tone.

In contrast, phase-based methods in the beta band as well as power and phase methods in the theta, alpha, and gamma bands do not show any connectivity between auditory and visual regions.

By investigating the subtle differences between power-based metrics, the authors can further illuminate aspects of functional connectivity. Because a similar, but larger, connectivity structure is seen with CAE (with Δ=1/3s) than Hilbert-R, the authors can conclude that the majority of these beta power interactions are taking place below 3 Hz (see Materials and Methods section). Additionally, because a larger connectivity structure is seen with RSP-PF than RSP-MF, the authors can conclude that these connections take place in particular sub-bands of beta, and not across frequencies. For instance, if one area's beta power at 25 Hz fluctuates during audiovisual connectivity, the area it is connected to cofluctuates at 25 Hz, and not 18 Hz, which is also within the beta band. This is potentially illuminating for understanding of the computational network mechanisms that underlie connectivity.

The present study directly investigated a subset of possible measures of neural interaction, however, only during audiovisual integration. It is possible, if not likely, that the brain utilizes separate network mechanisms to achieve communication during other tasks, which in turn could produce other types of inter-regional relationships in different frequency ranges. For instance, working memory may employ network and cellular mechanisms that produce gamma Coh between involved areas. The authors can begin to see these different types of brain connectivity even within the task design. For instance, stronger gamma RSP-PF connectivity was seen between the R-SPL and R-FEF during the visual control task. SPL activity could reflect lateral intraparietal (LIP) activity as the spatial resolution of 1 cm is unable to differentiate between them. LIP and FEF work together to drive decision making and execute eye movements in response to stimuli (for reviews, see Sugrue et al., 2005; Wardak et al., 2011). The higher gamma connectivity the authors see between R-SPL and R-FEF during visual tracking may reflect communication involved in coordinating the change in the color of the tracked ball and the production of eye movements; however, more investigation is required.

Additionally, the authors found IFG connectivity to be of special interest. The IFG is known to be involved in other rule-based tasks to identical stimuli, such as the well-known Stroop task as well as task switching (Derrfuss et al., 2005). Three beta power methods as well as beta Coh and PLI detected larger R-IFG connectivity with parietal cortices during audiovisual tracking. The authors suspect this connectivity to be reflective of the novel task rule set of the hummingballs stimulus; however, more investigation is required. Furthermore, connectivity between the left SMG/ANG and right frontal cortices is detected with several methods to be higher during color tracking with RSP-PF, Hilbert-R, Coh, and ICoh in the beta band. While these connections also require additional investigation, the authors believe they may reflect aspects of the novel task, which are more prominent in color tracking than sound tracking.

This study tested the ability of various metrics to detect connectivity between auditory and visual areas during audiovisual integration. However, the role of some areas in audiovisual integration, such as the primary visual cortex, is still under debate (Alais et al., 2010). While a detailed report of all significant connections is too vast in scope, the authors mostly detected increased audiovisual connectivity between higher-level visual cortices and primary/higher-level auditory cortices, as well as with the multimodal inferior parietal lobule (SMG/ANG). This indicates that audiovisual integration in this task largely does not utilize lower-level visual cortices, although this task is based in visual motion, so it is reasonable that most visual connectivity differences were seen with V4/V5. On the other hand, differences in local beta power are detected throughout the visual cortex, which may indicate involvement of the lower-level visual cortex.

Last, this study investigated what types of oscillatory correlations were present during audiovisual integration and thus the authors can apply these results to theories of how neurons communicate through oscillations, particularly during binding (Fries, 2005; Senkowski et al., 2008; Singer and Grey, 1995). These findings are overall supportive of the notion that temporal relationships underlie neuronal connectivity, notably detected here through power correlations. Interestingly, unlike Coh, it remains unclear how power correlations between areas impact communication between neurons (Siegel et al., 2012). The authors feel further investigation into the neural mechanisms, which underlie these relationships, is paramount to understanding this form of functional connectivity.

Conclusion

The authors believe that the brain has many complex and separate ways of processing different types of information, and these independent processing pathways likely manifest in a variety of statistical relationships and frequencies between areas. While much remains unknown about these interactions, these results show vast differences between power and phase-based connectivity results. Finally, the authors conclude that audiovisual integration when tracking an object is strongly reflected by correlations of beta power.

Acknowledgments

This research was supported by the Intramural Research Program of the National Institute of Mental Health, National Institutes of Health: http://intramural.nimh.nih.gov/(99-M-0172). Dr. Horwitz received funding from the Intramural Research Program of the National Institute on Deafness and Other Communication Disorders. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Author Disclosure Statement

Research was conducted in the absence of commercial or financial relationships that could be construed as a potential conflict of interest.