Spatial precision of population activity in primate area MT

Abstract

The middle temporal (MT) area is a cortical area integral to the “where” pathway of primate visual processing, signaling the movement and position of objects in the visual world. The receptive field of a single MT neuron is sensitive to the direction of object motion but is too large to signal precise spatial position. Here, we asked if the activity of MT neurons could be combined to support the high spatial precision required in the where pathway. With the use of multielectrode arrays, we recorded simultaneously neural activity at 24–65 sites in area MT of anesthetized marmoset monkeys. We found that although individual receptive fields span more than 5° of the visual field, the combined population response can support fine spatial discriminations (<0.2°). This is because receptive fields at neighboring sites overlapped substantially, and changes in spatial position are therefore projected onto neural activity in a large ensemble of neurons. This fine spatial discrimination is supported primarily by neurons with receptive fields flanking the target locations. Population performance is degraded (by 13–22%) when correlations in neural activity are ignored, further reflecting the contribution of population neural interactions. Our results show that population signals can provide high spatial precision despite large receptive fields, allowing area MT to represent both the motion and the position of objects in the visual world.

primates, including humans, use vision to guide movements (Dessing et al. 2013; Groh et al. 1997; Lisberger 2010). These tasks require knowledge of both the position and motion of the moving object, which are thought to be represented by a “where” pathway in the primate visual system, a dorsal stream of extrastriate cortical areas important in the analysis of space (Goodale and Milner 1992). Whereas areas in the where pathway, such as the middle temporal (MT) area, are better known for their sensitivity to object motion, position and motion are often perceptually intertwined (Burr and Thompson 2011) and may be encoded by the same populations of neurons. Yet, spatial receptive-field size increases substantially at each stage in the visual hierarchy, and receptive fields in extrastriate areas can cover 100 times more visual field than those in the primary visual cortex (V1) (Born and Bradley 2005; Britten 2003; Lennie 1998). The question we address here is the following: how are the signals provided by these areas capable of supporting high spatial precision in the absence of small receptive fields?

One hypothesis is that distributed encoding helps provide sufficient spatial precision (Baldi and Heiligenberg 1988; Eurich and Schwegler 1997; Hinton et al. 1986; Snippe and Koenderink 1992). A distributed code uses small differences in the activity of many neurons with wide but overlapping tuning curves. For example, in the retina, three broadly tuned photoreceptor classes support normal color vision, but humans and other animals can discriminate many thousands of colors. Similarly, neurons in the V1 area show wide- and overlapping-orientation tuning curves, and discrimination of pattern orientation is likely to rely on activity distributed across populations of neurons (Graf et al. 2011). Psychophysical (Regan and Beverley 1985) and theoretical work (Paradiso 1988; Pouget and Thorpe 1991; Seung and Sompolinsky 1993; Shadlen et al. 1996; Tzvetanov and Womelsdorf 2008) also suggest that distributed codes are important in the representation of visual features. Distributed codes are particularly useful when multiple dimensions of the visual image, such as both spatial position and object motion, need to be encoded in the same population of neurons (Hinton et al. 1986; Montemurro and Panzeri 2006).

The wide receptive fields of neurons in extrastriate areas are topographically organized (Sereno and Lehky 2011) and show extensive spatial overlap, such that each position in the visual field projects onto a large ensemble of neurons. Population activity may therefore be able to support fine spatial discriminations, but this has not been established. Here, we measure population activity in area MT, a highly conserved area of primate visual cortex. Area MT is a core component of the dorsal where pathway and is important in the representation of visual motion (Born and Bradley 2005; Britten 2003; Lennie 1998; Salzman and Newsome 1994; Solomon et al. 2011) and control of movements (Dessing et al. 2013; Groh et al. 1997; Lisberger 2010). In the marmoset monkey, extrastriate areas, including area MT, lie exposed on the cortical surface (Solomon and Rosa 2014; Solomon et al. 2014). We exploit this accessibility to implant multielectrode arrays, which allowed us to monitor populations of neurons working together to represent an object moving through visual space. We establish the precision with which population activity is able to track a moving object and derive how spatial information is distributed across individual neurons in the population. In addition, we identify a rich and dynamic structure of interneuronal correlations during object motion, which can provide a source of information about spatial position.

MATERIALS AND METHODS

Subjects and electrophysiological recordings.

The surgical and recording procedures have been detailed previously (McDonald et al. 2014; Solomon et al. 2014). All procedures were approved by the University of Sydney Animal Ethics Committee and conform to Australian National Health and Medical Research Council (NHMRC) policies on the use of animals in neuroscience research. Adult male marmosets (Callithrix jacchus, n = 3) were obtained from the NHMRC combined breeding facility. The animal was initially sedated with an intramuscular injection of 12 mg/kg Alfaxan (Jurox, New South Wales, Australia) and 3 mg/kg Diazepam (Roche, New South Wales, Australia). Postsurgical anesthesia was maintained by continuous intravenous infusion of sufentanil citrate (4–12 μg·kg⁻¹·h⁻¹; Sufenta Forte; Janssen Cilag, Beerse, Belgium). The animal was artificially ventilated with a 70:30 mix of N₂O and Carbogen. Rectal temperature was kept near 38°C with the use of a heating blanket. Vital signs (ECG, EEG, SpO₂, and rectal temperature) were monitored continuously. Dominance of low frequencies (1–5 Hz) in the EEG recording and absence of EEG changes under noxious stimulus (tail pinch) were used as the chief sign of an adequate level of anesthesia. At any sign of the reduced level of anesthesia, the dose of sufentanil citrate was increased. To suppress eye movements, muscular paralysis was then induced and maintained by continuous infusion of pancuronium bromide (0.3 mg·kg⁻¹·h⁻¹; AstraZaneca, New South Wales, Australia). High-permeability contact lenses remained in place for the duration of the experiment. No artificial pupils were used. At the end of the experiment, the animal was euthanized with an intravenous overdose of sodium pentobarbitone (500 mg/kg; Lethabarb; Verbac Australia, New South Wales, Australia).

A craniotomy was made over area MT in the left hemisphere and the dura reflected. Multichannel recordings were made with a 96-channel array (Blackrock Microsystems, Salt Lake City, UT; 1.5 mm length, 0.4 mm separation, average impedance 0.265 MΩ), band-pass filtered (0.3–5 kHz), and sampled by a PZ2/RZ2 at 24 kHz (Tucker-Davis Technologies, Alachua, FL). The array was inserted to a depth of ∼1 mm using a high-speed pneumatic device (Rousche and Normann 1992). The electrodes generally extended into or past layer 4, and slight curvature of the cortex means that the depth of the electrodes varies across the array. From the trajectory of receptive-field positions on each electrode (Rosa and Elston 1998), we were able to identify electrodes that were likely to be within area MT and others likely to be in area MTc [a thin area bordering the anterior of area MT; see Rosa and Elston (1998) and Solomon and Rosa (2014)]. For the current analyses, we have included neurons from electrodes in both areas.

Stimuli.

Visual stimuli were generated by a Power Mac G4 computer using custom software (EXPO; Peter Lennie, University of Rochester, Rochester, NY) and presented on a cathode ray tube monitor (Sony G500, 100 Hz refresh rate, width 40 cm, height 30 cm, mean luminance 45–55 cd/m²), viewed directly at 45 cm. Supplementary lenses were used to focus the eyes, and the contralateral eye was occluded during measurements. In one animal, we made an additional measurement with the ipsilateral eye instead occluded. The primary stimulus was a white disk of diameter 3° and intensity twice that of the background, moving across a gray screen at 20°/s. The disk traveled in a straight line along one of five paths, length 40°, at angular −18°, −6°, 0°, 6°, and 18° from the horizontal [throughout, we use the term “degrees” (°) to refer to spatial separations on the monitor and “angular degrees” (angular °) to refer to the angle of motion], and all crossing at the center of the screen (see Fig. 1B). Both directions of motion were sampled for each path; each direction of motion is referred to as one trajectory. Each of the 10 trajectories was presented 80 times in pseudorandom order.

Fig. 1.

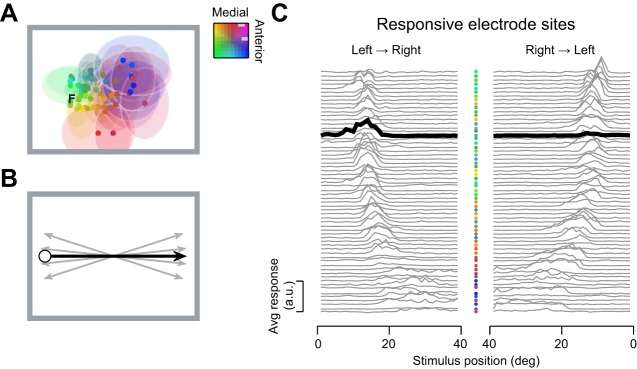
Population response to a moving stimulus in the middle temporal area (MT). A: receptive fields of neurons in area MT are large and highly overlapping. Estimated receptive-field center (dots) and extent (shaded regions; 1 SD) for multiunit activity obtained with a 10 × 10 electrode array implanted into area MT in the left hemisphere of 1 animal. Estimated position of the fovea is marked with “F.” For clarity, the extent of a subset of receptive fields is illustrated. Color of receptive fields specifies position in the recording array. B: the stimulus was a disc moving across the screen. Response was obtained to both directions of movement, along each of 5 paths arranged around the horizontal axis. C: average response at each recording site to a disc moving along the horizontal axis from left to right (left) and from right to left (right). Note the x-axis on the right is flipped to preserve the true temporal order of neural response. Electrode sites were arranged by the preferred stimulus position. Electrode position in the recording array is identified by the color of the dots between panels. One recording site is highlighted by the thick lines in both left and right and illustrates the directional sensitivity of neural responses in area MT.

Multiunit spiking activity.

Analyses were performed in MATLAB (R2012a; MathWorks, Natick, MA). The function “findpeaks” was used to identify waveforms with peak amplitude that exceeded 3 SD of the raw signal. Multiunit spike count at each site was estimated in nonoverlapping time bins of width 0.05 s or 0.01 s and transformed into z-scores for subsequent analysis. z-Scores were calculated independently for each electrode, using the mean and the SD of the binned spike counts across all trials of all trajectories.

For explication in the following, we call the position and direction of motion associated with each time bin a single “stimulus.” Not every pair of stimulus positions fell within the spatial receptive fields of the recorded population, and discrimination performance between these pairs is difficult to interpret. To focus on the pairs of positions that elicited response from the recorded population, we first calculated the mean z-score across electrodes and trials at each stimulus position. Pairs of positions were included for analysis if mean z-scores both exceeded zero. When analyzing pairs of positions on different motion trajectories, we included only pairs separated by >0.5°; this means that the central point, where all trajectories cross, was excluded from analysis.

Estimating spatial receptive fields.

Response latency (90 ms) was estimated as the delay that maximized the cross-correlation of each recording site's response to opposite directions of motion along the same stimulus path, collapsed across recording sites and paths within an animal. Spatial receptive fields for each trajectory were characterized by finding the best predictions of a one-dimensional Gaussian model, with four parameters defining maximum response, center position, SD, and maintained activity. Preferred motion direction of each site was determined separately for each stimulus path. Some sites obviously did not respond to the stimulus at any position along the trajectory(ies) of interest, such that the peak amplitude of the Gaussian that best predicted response did not reach significance (P < 0.05). Our primary aim is to understand how receptive fields contribute to spatial discrimination, and therefore, we excluded these sites from the analyses. Counterpart analyses that nevertheless included these sites generally resulted in poorer discrimination performance (not shown).

Support vector machine analysis.

Linear support vector machines (SVMs) (Graf et al. 2011; Joachims 1999; Vapnik 2000) were used to quantify the discriminability of population activity for pairs of stimuli. A leave-one-out cross-validation procedure was used: SVMs were trained on population activity, measured over 79 trials of each stimulus, and tested on the pair of left-out trials. The procedure was repeated for the 80 unique pairs of left-out trials. Support weights from each SVM (that is, for each pair of stimuli) were normalized to a unit vector and then averaged across the 80 cross-validated datasets. In each case, performance was estimated as d-prime (d′)

$$d\prime =\text{norminv}\left(\frac{100\cdot \text{HIT}+1}{102}\right)-\text{norminv}\left(\frac{100\cdot \text{fHIT}+1}{102}\right)$$ (1)

with the (100° k + 1)/102 adjustment to assign large, noninfinite values when the hit rate or false-alarm rate was 0 or 100%, and “norminv” is the inverse normal function with a mean of 0 and SD of 1. SVMs that were instead trained with 10 or 20 trials left out for cross-validation showed d′ performance and distribution of support weights that were consistent with that obtained in the leave-one-out approach (not shown), suggesting that the SVMs are identifying robust patterns of activity across the relevant populations.

To assess discrimination performance of a single site and randomly drawn subpopulations of 2, 5, 10, or 20 sites, we repeated the SVM analyses above. In each case, 80 randomly selected subpopulations of responsive sites were drawn and d′ performance calculated. In further analyses, a Gaussian weighting function (SD 6° of the visual field), centered on the discrimination target, was used to bias the subpopulation toward the locality of the target position; 80 weighted subpopulations of 10 sites were drawn and the SVM analyses repeated. Linear regression was used to compare performance for weighted and randomly selected subpopulations of the same size.

Compensation for cortical footprint.

The decoder performance depended on the fraction of the population recruited at each stimulus position. Two positions that are by larger sets of neurons or neurons with better signal to noise are inherently more discriminable than others. We used a general linear model (GLM), assuming normally distributed error, to estimate the variability in performance that could be attributed to stimulus position. Effectively, the GLM estimates d′_POS1 and d′_POS2

$$d\prime \hspace{0.17em}\left(\text{POS1, POS2}\right)=d{\prime }_{\text{POS1}}+d{\prime }_{\text{POS2}}+\widehat{d}\prime$$ (2)

yielding residuals $\widehat{d}\prime$, representing position-independent performance.

The position-independent performance was further modeled with an elliptical surface [parameters: A, r, spatial-direction ratio (SDR), and d′₀], with respect to separation in the stimulus position (ΔPOS) and motion direction (ΔDIR)

$$\widehat{d}\prime =A.\left(\exp \left(-\sqrt{\frac{1}{r^2}\left(\frac{\Delta {\text{POS}}^2}{{\text{SDR}}^2}+\Delta {\text{DIR}}^2\right)}\right)-1\right)+\widehat{d}{\prime }_0$$ (3)

from which we extract the SDR. SDR characterizes the difference in spatial position that is required to achieve the decoding performance observed for motion directions that are an angular 1° apart. Finally, the offset value $\widehat{d}\prime$₀ was removed so that the final “estimated d′” (see Fig. 6, C and D) is zero when both positional and directional separation are zero.

Fig. 6.

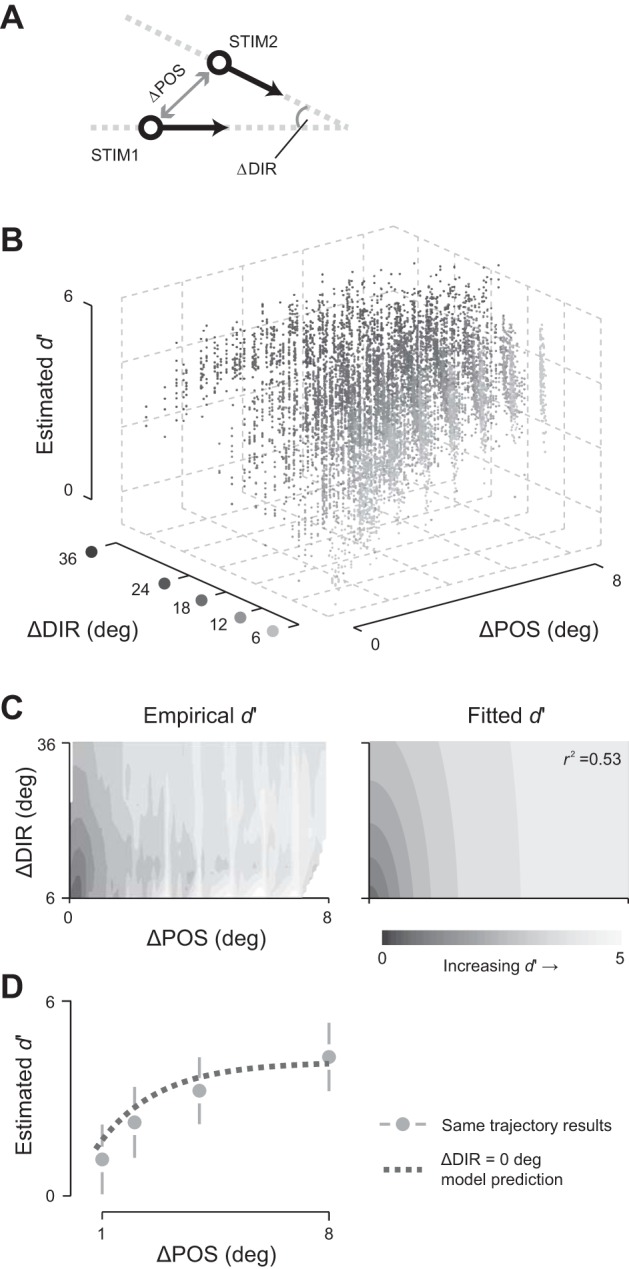
Comparison of discrimination performance for space and motion direction. A: schematic of the analysis. Population discrimination performance was measured for 2 stimuli (STIM1 and STIM2) from different motion trajectories. Each pair of stimuli is classified by the difference in spatial position (ΔPOS; analyses were confined to spatial separation of up to 8°) and the difference in motion direction (ΔDIR; between 6° and 36° angular difference). B: population discrimination performance depends on separation in space and motion direction. Performance estimates were corrected for biases arising from differences in the number of sites responsive at each spatial position. Only stimulus positions that were well represented in the population are included; data pooled across experiments (n = 9,824 pairs of stimuli). C: descriptive model of discrimination performance for space and motion direction. Left: “birds-eye” view of data in B; image shading represents mean discrimination performance. Right: descriptive model of the data on the left: an exponential incline of elliptical contours. r² indicates the goodness of fit. D: performance for spatial separations along the same motion trajectory. Discrimination performance along the same motion trajectory was corrected for biases arising from differences in the number of sites responsive at each spatial position (symbols). The dotted line shows predictions of the descriptive model, obtained using the separate measurements described in B and C for ΔDIR = 0°. Error bars show SD across spatial positions.

In additional analyses, we asked if the discrimination surface could be better explained by alternative descriptive models. Linear, separable functions in ΔPOS and ΔDIR failed to follow the elliptical contours in the data. Multiplicative, separable functions produced similar SDR values (∼1.2× greater than the inseparable model used in the main analyses) but showed larger fitting error at small values of ΔPOS and ΔDIR.

Influence of noise correlations on decoding performance.

To assess whether the performance of the SVM was dependent on having access to the structure of interneuronal correlations, we repeated the analyses above but after shuffling the order of the trials in the training dataset. As above, the decoder was cross-validated on “raw” trials that were left out of the training dataset; that is, the decoder is tested on actual brain activity, but training on shuffled data makes it incapable of using any correlations that may exist in the real dataset. Changes in the performance of the shuffled decoder therefore reflect the contribution of the information in the structure of interneuronal correlations to subsequent computations.

We recognized that there is a simple relationship between the performance from SVMs trained on the raw data (correlation-aware) and SVMs trained on shuffled data (correlation-blind) decoders. By definition, d′ measures the ratio between the difference of the mean responses to the SD of the noise. Since shuffling the training data does not change mean response, the impact of shuffling on d′ must be related to changes in SD of the noise in the population that is introduced by shuffling. The ratio of the d′ between the decoders can therefore be characterized by a simple gain/loss factor (G)

$$\frac{d{\prime }_2}{d{\prime }_1}=\frac{\frac{m}{{\sigma }_2}}{\frac{m}{{\sigma }_1}}=\frac{{\sigma }_1}{{\sigma }_2}=G$$ (4)

This allows us to use linear regression to characterize the change in performance (G) when using different decoders. In the relevant analyses (see Fig. 4), we used only d′ values <3.5 in the regression to avoid ceiling effects of near-perfect discrimination.

Fig. 4.

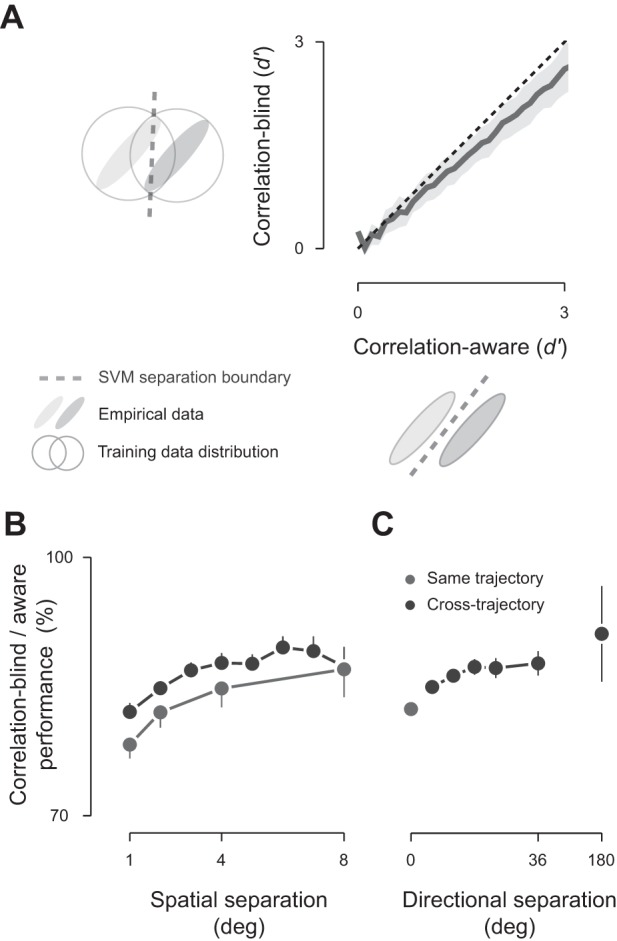
Population correlations are important for optimal decoding. A: two decoders were considered: the correlation-aware decoder was trained on the empirical data distribution containing noise correlation, and the correlation-blind decoder was trained on trial-shuffled data with the noise correlation destroyed. Data were pooled across animals for stimulus positions that were well represented by the underlying populations (n = 3,739 pairs of stimuli). Shaded regions show 1 SD around the mean. Relative performance of the correlation-blind decoder is the fractional change in performance across the stimuli under consideration. B: relative performance of the correlation-blind decoder as a function of spatial separation, collapsed across spatial separation (same trajectory: n = 257, 179, 119, and 65 pairs, respectively, for 1°, 2°, 4°, and 8°; cross-trajectory separation was rounded to the nearest integer: n = 546, 610, 540, 393, 329, 261, 197, and 82, respectively, for 1–8°). C: relative performance of the correlation-blind decoder as a function of direction separation, collapsed across directional separation (n = 620, 902, 998, 625, 361, 216, and 17 pairs, respectively, for 0°, 6°, 12°, 18°, 24°, 36°, and 180°). Error bars show 95% confidence interval from regression analysis for B and C. To avoid ceiling effects, in B and C, we include only data points in which d′ < 3.5.

Pearson's correlation coefficient was calculated for all possible pairing of responsive sites. To factor out site-by-site variations in correlation magnitude, GLMs were used to estimate the correlations $(\widehat{\rho })$ not attributable to the pairs of electrodes (MU1 and MU2) under consideration (applied as seen in Fig. 5)

$$\rho \left(\text{MU}1,\text{MU}2\right)=\widehat{\rho }+{\rho }_{\text{MU}1}+{\rho }_{\text{MU}2}$$ (5)

Fig. 5.

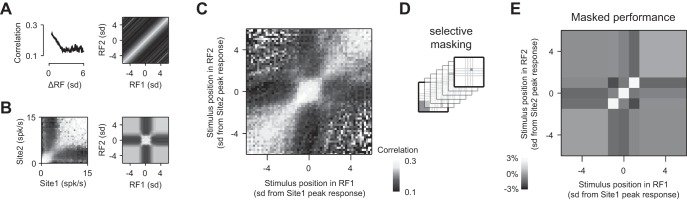
Structure of neural correlations depends on stimulus position. The structure of pairwise spike count correlations (“noise correlations”) from different perspectives. Data represent all pairs of responsive sites where the stimulus was moving in the preferred direction of both sites (n = 967,980). Receptive field (RF) positions are expressed in SD of a Gaussian fit to each site's spatial-response profile. Stimulus positions preceding the receptive-field center are indicated as negative values and vice versa for stimulus positions after passing through the receptive-field center. Shading of bar in C applies to A–C. A: noise correlation is higher for pairs of receptive fields with greater overlap. Left: average noise correlations collapsed across stimulus positions as a function of the distance between receptive fields (ΔRF), normalized by the geometric mean of their SD. Right: the correlation structure on the left can be projected into a joint space, defined by the position of a stimulus within 2 receptive fields (RF1 and RF2). The shading of the image indicates the strength of noise correlation that is predicted by the data on the left. B, left: noise correlation as a function of the response rate of each neuron. Average noise correlations were collapsed across stimulus positions. Right: the spiking rate was mapped to receptive-field positions using the average spatial response profile and the result projected onto the joint space, defined by the position of a stimulus within 2 receptive fields. The shading of the image indicates the strength of noise correlation that is predicted by the data on the left. C: joint space defined by the position of a stimulus within 2 receptive fields (RF1 and RF2). The shading of the image indicates the strength of noise correlation measured at each stimulus position. The rich structure is similar to that predicted by the combination of A and B. D: population activity was simulated multiple times using multivariate, normal distributions. In each simulation, the mean activity of neurons was that measured, and the correlation matrix was preserved everywhere except within 1 partition, where the correlation coefficient was halved. E: impact of decorrelation on spatial discrimination depends on the masked partition. Shading indicates the relative impact of decorrelation on capacity to discriminate 1° change in stimulus position: darker shades indicate where attenuating correlations reduced performance and lighter shades, where attenuating correlations improved performance.

Selective correlation masking.

We used synthetic data to investigate how decoding performance depends on noise correlations between pairs of electrode sites whose receptive fields are at different locations with respect to the stimulus. For each electrode, the position of each stimulus was expressed as distance from its receptive-field center in multiples of the SD of its receptive field. These normalized positions were then binned in five partitions (negative numbers imply the position is earlier in the trajectory than the receptive-field center): less than −1.5 SD; −1.5 to −0.5; −0.5 to 0.5; 0.5–1.5; >1.5. Responses of each pair of electrodes were collated for each pair of normalized positions. This created 25 datasets; for example, in one dataset, we have the responses of pairs of neurons, where one of the receptive fields is centered on the stimulus (−0.5 to 0.5 SD), and one is far ahead of the stimulus (>1.5 SD).

We calculated the correlation matrix for these datasets and then created two synthetic datasets (1,280 trials each), in which we preserved mean rate at each recording site but either retained or modified the covariances. We used MATLAB's multivariate normal random number generator “mvnrnd” to generate the synthetic datasets, providing it with the mean activity for each electrode site and the preserved or modified covariance matrix. In the modified set, we halved (rather than removed) the covariances and used the nearest “symmetric-positive definite” matrix to minimize side effects that can arise when altering the covariance matrix. SVMs were trained on the real datasets and tested on the two synthetic datasets; performance gain for each dataset was calculated as in Eq. 4.

RESULTS

In the following, we characterize the precision of spatial representations in area MT by recording from populations of neurons with planar multielectrode arrays implanted into three anesthetized marmosets; each implant yielded between 24 and 65 responsive sites for analysis. The arrays covered a large fraction of area MT, such that the underlying receptive fields occupied a wide swathe of the visual field (Fig. 1A). As expected, the receptive fields in area MT were retinotopically organized and highly overlapping (Born and Bradley 2005; Britten 2003; Rosa and Elston 1998). To understand how populations of motion-sensitive neurons might represent spatial position, we analyzed multiunit activity evoked by a single moving object (diameter 3°) that traveled smoothly across the visual field at moderate speed (20°/s; Fig. 1B). We analyzed four sessions obtained in three animals; in one animal, we had sufficient time to reposition the monitor and obtain a second recording.

The receptive fields of neurons in area MT are large, and the consequence is that neurons respond to a wide range of spatial positions (Fig. 1C). Receptive-field diameter (full width at half height) increased with eccentricity from a mean of 6.3° (±3.7 SD) in the parafoveal half of the stimulus trajectory to 11.7° (±4.6 SD) in the more peripheral half of the stimulus trajectory. Individual neurons will therefore be poorly capable of detecting small changes in position. By contrast, as an object moves across the screen, it evokes reliable responses in many neurons at each spatial position, and the moving object therefore creates a moving “hill” of activity in the MT population response. This distributed response is a potentially rich source of information for fine position judgements.

Spatial precision of area MT population response.

To characterize the spatial precision of population responses in area MT, we used linear SVMs, which allow us to estimate empirically the discriminability of population response at two spatial positions without requiring assumptions about the correlation structure of population responses or how they might be used to discriminate changes in spatial position. Here, we trained the SVMs to discriminate a change in the spatial position of the moving object along a single trajectory of motion (Fig. 2A). For each pair of spatial positions, we trained a new set of SVMs, using a “leave-one-out” cross-validation approach to establish how well the population response could be discriminated on a single trial. We obtained similar results in each of the four recordings and therefore, pooled across them.

Fig. 2.

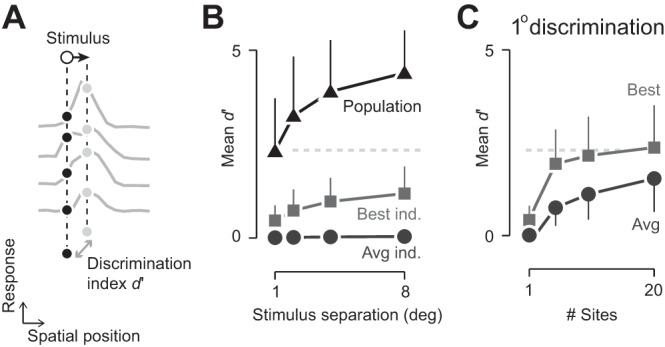
Area MT population response allows fine spatial discriminations along the trajectory of motion. A: schematic representation of the decoding task. Neural response at each electrode was binned according to stimulus position. For each pair of stimulus positions along a single trajectory, the d-prime (d′) discrimination performance was calculated. B: population response supports fine spatial discriminations; discrimination performance along the same trajectory. Triangles and line show performance with the full population (24–65 sites, depending on experiment). Circles and line show the average performance of individual recording sites (Avg ind.). Squares and line show performance of the optimal individual recording site for each spatial discrimination (Best ind.). Data were pooled across all experiments and all well-represented stimulus positions (n = 316, 308, 301, and 282 pairs, respectively, for 1°, 2°, 4°, and 8° spatial separation). Error bars represent 1 SD and for clarity, are shown on 1 side. Gray, dashed line shows average population performance for 1° spatial separation, extended to C. C: dependence of performance on population size. Each line shows performance for discrimination of 1° spatial separation. In each case, 80 randomly selected subpopulations (n = 5, 10, or 20) of responsive sites were analyzed and then collapsed across experiments. Circles and line show average performance across all randomly selected subpopulations. Squares and line show the best performing subpopulation. Conventions are the same as B.

Application of the SVM showed that population response was capable of fine spatial precision on individual trials, with robust performance for both small and large changes in the spatial position of the moving object (Fig. 2B). For a 1° change in object position, average d′ was 2.2 (±0.1 SE); that is, an unbiased observer, forced to choose between the two positions, would be correct on 86% of trials. Performance increased with spatial separation, and in all cases, the precision of population response exceeded that of the best individual site. To assess how performance depended on population size, we repeated the analysis, drawing on randomly sampled subpopulations (Fig. 2C). Performance increased with the number of sites included, and the performance of the 10 best sites approached that of an entire population of 24–65 sites.

The analyses above used a response window of 0.05 s, which parsed a trajectory into bins of 1°. To assess performance over finer spatial separations, we repeated the analyses with a response window of 0.01 s, thereby parsing the trajectories into bins of 0.2°. The smaller bin size naturally reduces spike count and in addition, may change covariances among neurons in the population, both of which may impair discrimination performance. Indeed, discrimination performance for spatial separations of 1° was impaired when using the narrower time windows to an average d′ of 1.5 (77% correct). Performance nevertheless remained above chance (d′ = 0) for spatial separations of 0.2° (d′ = 0.35 ± 0.01, SE; 57% correct) and 0.4° (d′ = 0.74 ± 0.01, SE; 64% correct).

Neuronal contributions to a distributed code.

How are the responses of neurons used to discriminate between alternative spatial positions? To address this question, we revisited the SVMs trained to discriminate pairs of positions (using time bins of 0.05 s) along a single motion trajectory and analyzed the weights that the SVMs applied to different recordings sites. The organization of our analyses means that the SVMs assign positive weights to neural activity that supports the hypothesis that the stimulus is at the target position and negative weights to neural activity that supports the hypothesis that the stimulus is at an earlier position in the trajectory, which can be 1°, 2°, 4°, or 8°. The SVMs give stronger weight to neurons that are more informative about the decision boundary, and the question here is how the weights relate to the spatial tuning of the underlying neurons.

We first investigated the coding strategy for fine position discriminations. Inspection of individual sites suggested that neurons were more likely to be informative when the peak of the receptive field was offset from the targets, such that the positions to be discriminated lay on one of the flanks (Fig. 3A). To represent the distribution of weights across the population of neurons, we aligned the position of each stimulus to each tuning curve and expressed stimulus position in units of that tuning curve's width. Projection of SVM weights into the same space (Fig. 3B) confirms that neurons are more likely to be informative when their receptive field was offset from the discrimination. By contrast, large position differences—spatial separations larger than the size of receptive fields—activated largely separate populations of neurons, and neurons were more likely to be informative if one of the targets was near the center of the tuning curve (Fig. 3B). Analyses over a range of target separations showed smooth transition in the distribution of weights between the two coding schemes (not shown).

Fig. 3.

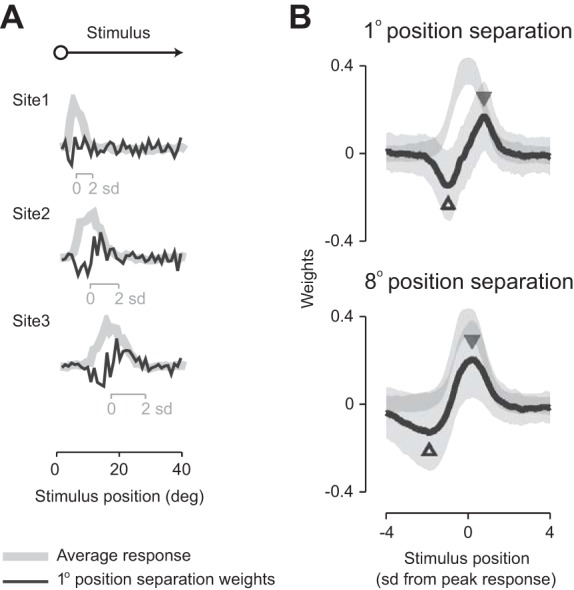
Neural activity supporting fine and coarse spatial discrimination. A: spatial response and support vector machine (SVM) weight profiles for individual sites. Gray lines show the spatial profile of receptive fields at each of 3 simultaneously recorded sites. Insets show the size of each receptive field, in units of the SD of a Gaussian fit to the spatial profile. Black lines show the weights applied by the SVM to each site during discrimination of positions, separated by 1° of the visual field, at each point along the trajectory. B: profile of SVM weights is different for discrimination of small (1°, top) and large (8°, bottom) differences in spatial position. Population average weights (black lines), plotted for stimuli moving in the preferred direction (n = 973). Weights are plotted as a function of the position of the stimulus within the aligned and scaled receptive fields (in SD of a Gaussian fit to each site's spatial profile). Positive weights indicate that neural activity provided evidence that the stimulus was at that position; negative weights indicate that neural activity provided evidence that the stimulus was at the comparison position. Triangles indicate the maxima and minima of the average SVM weights. As a reference, the correspondingly scaled spatial response (gray lines) is plotted in the background (in arbitrary y-axis units). Lightly shaded regions show 1 SD around the mean.

Given open access to population response, fine position discrimination was primarily supported by those neurons with receptive fields within 2 SD (∼6°) of the discrimination locus (Fig. 3B). This suggests that downstream areas may be able to recover spatial position with limited pooling over area MT output. To establish if limited pooling would be sufficient, we constructed SVMs where the probability of being included in the SVM was set by the centroid of the receptive field relative to the target positions. Specifically, subpopulations of 10 neurons were drawn from the population with probability given by a Gaussian distribution over visual space (SD 6°) and centered on the target positions. Discrimination performance of these localized subpopulations was, on average, 89% [±3%, 95% confidence interval (CI)] that of the random subpopulations shown in Fig. 2C. The reduction in performance implies that neurons farther away from the discrimination locus may provide useful signals, particularly when they have high signal to noise, and is consistent with the very large receptive fields of neurons in area MT. The high performance of the localized SVMs suggests that the spatial precision of population response can be “read out” with limited spatial pooling of its signals.

Impact of interneuronal correlations on fine spatial discriminations.

Receptive fields of neurons in area MT are highly overlapping and are therefore likely to receive input from overlapping sets of neurons. Neurons in area MT are therefore unlikely to provide independent analyses of the retinal image—some of their activity will be shared with other neurons (Bair et al. 2001; Cohen and Kohn 2011; Cohen and Newsome 2008; Huang and Lisberger 2009; Solomon et al. 2014). These interneuronal correlations will impose motifs on area MT population response that might be important for its targets and be used by our decoding machines.

To assess whether the SVMs had identified population motifs, we further trained SVMs on artificial datasets, where the patterns of neural correlations were destroyed by shuffling the order of trials in each recording site. Shuffling allowed us to test an alternate decoding framework, where the brain is blind to its interneuronal correlations. We therefore refer to this set of SVMs as “correlation-blind” SVMs and the original set as “correlation-aware” SVMs. We cross validated the performance of the correlation-blind SVMs on real data to establish how those decoders interpret real neural activity. If the correlation-blind decoders showed the same performance as the correlation-aware decoders, then this would imply that the structure of interneuronal correlations is not useful for spatial discriminations.

The removal of correlations from the training set did not change the pattern of weights that the SVM attributed to individual sites (not shown). We used linear regression to estimate the change in decoder performance (G; Eq. 4) that is brought about by removing correlations from the training set. This analysis showed that removing correlations substantially reduced performance, by 13–22% (Fig. 4B). This provides evidence for the presence of reproducible population motifs in the spiking activity. The performance reduction was more pronounced for fine discriminations (1° separation: 22 ± 2%, 95% CI; Fig. 4C) than coarse discriminations (8° separation: 13 ± 3%), implying that population motifs are most useful when two stimuli elicit similar population responses.

To understand the structure of these motifs, we calculated the correlation in spike counts (“noise correlations” over timescales of 0.05 s) between pairs of recording sites, using Pearson's correlation coefficient. Preliminary analyses indicated that individual recording sites could show consistently higher or lower levels of correlation with other sites: individual sites contributed 9.5–23.7% of the variance in correlation estimates in each recording. This may reflect differences in the number of neurons contributing to multiunit activity at each site (Cohen and Kohn 2011). To compensate for the overall differences in correlation at individual sites, we removed them (see Eq. 5). The resulting, adjusted correlation coefficients are plotted as a function of the object's position within the tuning curve of each site (Fig. 5C). As the object moves across the visual field, it traverses the receptive field of each neuron, and Fig. 5C shows that the magnitude of correlations depends on where the object is within each receptive field.

The population motifs that emerge in Fig. 5C are rich in structure, but they appear to be driven by two rules. The first rule is that correlation is highest in neurons that are near each other and therefore, have similar receptive fields (Huang and Lisberger 2009; Smith and Kohn 2008; Solomon et al. 2014); this provides a diagonal structure in the matrix (Fig. 5A). The second rule is that correlation depends on response amplitude. This provides a cross structure in the matrix (Fig. 5B). The shape of this cross arises from the inter-relationship of two factors: correlation increases with response amplitude when the stimulus is within the receptive fields of both neurons (Churchland et al. 2010; Gutnisky and Dragoi 2008; Kohn and Smith 2005), and correlation is also high when the stimulus is absent from both receptive fields (Smith and Kohn 2008). The result is that correlation is relatively low when the stimulus is within one receptive field but not the other, and this is what forms the centered vertical and horizontal bands of low correlation in the matrix.

We would like to know which aspects of the motifs in Fig. 5C might be exploited in decoding, but we cannot isolate them in real spiking activity. We therefore simulated population response using the original measurements of response amplitude and the correlation matrix in Fig. 5C to generate distributions of synthetic spiking activity. Selective attenuation of parts of the correlation matrix (Fig. 5D) allowed us to generate new distributions of spiking activity. We used changes in the performance of the SVM, implemented as above, to assess the importance of those correlations. The attenuation of all correlations reduced discrimination performance by, on average, 10% (±0.4%, 95% CI), similar to the reduction in performance that is brought about by shuffling training data above. Selective attenuation of parts of the correlation matrix revealed that this overall reduction in performance arises because the SVMs particularly rely on pairs of neurons in which the object lies on opposite flanks of the receptive field. In these pairs, changes in object position bring about an increase in spiking activity at one site and a decrease at the other, whereas interneuronal correlations either increase or decrease activity in both neurons. In these pairs, therefore, noise correlations distribute response along dimensions that are not aligned with the changes in response that are brought about by object motion. By contrast, the attenuation of correlations among neurons with similar receptive fields improved performance (Fig. 5E). This is because interneuronal correlations and changes in object position both increase or decrease activity in both neurons.

Comparison of spatial and direction discrimination.

We established a benchmark for our estimates of spatial precision by measuring discrimination performance for pairs of positions along different motion trajectories (Fig. 6A). Each combination of position and motion direction has a different cortical footprint. That is, each position in visual space is sampled differently—both in terms of the number of electrode sites that are active at each position of the moving object in visual space and the signal to noise at those electrode sites. Combinations of positions that project onto larger ensembles of neurons or neurons with better signals are inherently more discriminable. To assess its impact, we created a surrogate measure of cortical footprint for each pair of positions: the average of z-scored spike rates across all recording sites and all trials at the two positions. This measure was a strong predictor of the d′ performance (not shown): as average z-score increased from −0.1 to 0.1, discrimination increased by 1.8 d′ units.

To establish how discrimination depends on spatial and direction separation, we need to establish the variation in performance that does not reflect variation in cortical footprint. We therefore estimated the impact of the cortical footprint by incorporating the actual positions of the two stimuli as predictors of discrimination performance in a GLM (see materials and methods). Individual stimulus positions accounted for a substantial fraction of the variance in discrimination performance: this fraction ranged from 63.2% to 90.1% in the different recordings. We then subtracted out the position-dependent components, leaving a measure of relative performance ($\widehat{d}\prime$₀), which we used for further analysis and is independent of the cortical footprint. Indeed, $\widehat{d}\prime$₀ showed no dependence on average z-score (not shown).

Discrimination performance increased with spatial and directional separation and saturated at large separations along either dimension (Fig. 6B). The joint surface can be well described by elliptical contours with an exponential gradient (r² = 0.53), and the axes of this ellipse characterize the relative impact of spatial and direction separation on discrimination performance (Fig. 6C). To quantify performance, we calculated the ratio of the ellipses' length along the axis of spatial separation to that along the axis of direction separation. This index, which we call the SDR, was 0.056 (±0.001, 95% CI). This ratio implies that if area MT could support discrimination of an angular 2° difference in the motion direction of full-field dot patterns (Hol and Treue 2001; Purushothaman and Bradley 2005) and smooth pursuit targets (Osborne et al. 2007), then it should also be able to support discrimination of a 0.11° difference in visual space position.

To determine the impact of retinal eccentricity on discrimination performance, we conducted the same analysis on the parafoveal and peripheral halves of the stimulus trajectories: estimated discrimination resolution for the two halves was, respectively, 0.10° and 0.14° (SDR of 0.049 ± 0.002 and 0.071 ± 0.009, 95% CI, respectively). The reduced resolution in periphery reflects an increase in average receptive-field size from of 6.3° to 11.7°. In a separate recording from the same animals, we estimated the directional tuning of multiunit activity for a field of moving dots (McDonald et al. 2014). Full-width, half-maximum directional tuning bandwidth was an angular 130° (±54 SD) and was similar for neurons with parafoveal and peripheral receptive fields (P = 0.10, t-test); a commonly used index of directional selectivity (1 − resp_null/resp_pref) in the same recordings was 0.81 (±0.34 SD). These are comparable with that reported for single-unit activity in area MT of macaque and marmoset, in which tuning bandwidth is angular 100–120°, and the direction selectivity index is 0.85–1.0 (Britten 2003; Solomon et al. 2011).

In the analyses above, we excluded spatial discriminations for pairs of positions that lay on the same trajectory as a safeguard against effects arising from temporal correlations between these data points. We asked if the model could predict discrimination performance for these pairs of positions. We first factored out the impact of the cortical footprint (position-dependent performance) using the footprint that we estimated from the pairs of positions on different trajectories. The model's predicted discrimination performance for positions on the same trajectory is very similar to that observed (Fig. 6D), with slight overestimation for small spatial separations.

DISCUSSION

Visually guided behavior requires precise knowledge of both the position and motion of objects. The size of receptive fields of neurons in extrastriate areas of visual cortex, including area MT, means that individual neurons have limited capacity to signal the position of objects. By measuring the response of populations of these neurons, we have shown that the population signals of these areas allow high spatial precision and that these signals are accessible to simple decoders. Even our relatively small populations of neurons in area MT showed above-chance performance for targets separated by 0.2° of the visual field, and we inferred by comparison with capacity to discriminate motion direction that population acuity will be in the order of 0.1°. As a reference, the spatial acuity of marmoset reaches 30 cycles/degree (Ordy and Samorajski 1968), suggesting that although activity in area MT is unlikely to match the maximal acuity of activity in retina and area V1, it can provide a spatial representation with behaviorally relevant acuity. Yet, our estimates of spatial precision are difficult to relate to extant measurements of behavioral acuity, which can use form and motion signals, as well as positional signals (Morgan and Benton 1989; Verdon-Roe et al. 2006; Westheimer 1987), and are likely to be task dependent.

Discrimination of fine differences in orientation and motion direction is thought to rely on populations of neurons with broad tuning curves along the relevant dimension in the V1 [e.g., Graf et al. (2011)] or area MT [e.g., Purushothaman and Bradley (2005)]. Our analyses invoke a similar population representation of spatial position. Despite wide tuning curves for motion direction and spatial position, the same population of neurons is capable of fine discrimination of motion direction and spatial position (cf. Fig. 6), suggesting that area MT can represent the position, as well as the motion of objects, in the visual world. The breadth of spatial and direction tuning curves of neurons in area MT may, in part, reflect compromises that arise when populations of neurons need to encode more than one dimension of the visual image (Hinton et al. 1986; Montemurro and Panzeri 2006).

Population coding of spatial position.

Visual cortical areas are defined by the presence of a retinotopic map, but this inherent representation does not imply that the analysis of visual space is fundamentally different to the analysis of other features of objects and surfaces. The presence of retinotopic maps has driven the local sign hypothesis [e.g., Whitney and Bressler (2007)], whereby an object's position is assigned to the peak of activity in a retinotopic map. Our results are not in conflict with this hypothesis but place the analysis of space in the same framework as the analysis of derived visual features, such as form and motion. For coarse discriminations—spatial separations larger than the size of receptive fields—the most useful neurons are those with receptive fields centered on each position. For fine spatial discriminations, however, neurons with receptive fields centered on the spatial positions are less useful than those whose receptive fields flank the judgement. This is consistent with the distribution of likelihood (Graf et al. 2011; Jazayeri and Movshon 2006) or Fisher information (Tzvetanov and Womelsdorf 2008) across the neural population. Similar “flank-encoding” representations have been implicated in the discrimination of other visual features: spatial frequency (Bradley et al. 1987), orientation (Beaudot and Mullen 2006; Graf et al. 2011; Paradiso 1988; Pouget and Thorpe 1991), and motion direction (McDonald et al. 2014; Purushothaman and Bradley 2005; Seung and Sompolinsky 1993; Tzvetanov and Womelsdorf 2008).

The presence of robust visuotopic maps throughout visual cortex makes it difficult to dissect the contribution of each area to behavior, and many tasks may simply rely on the very fine scale representations that are provided by area V1. In macaque, microstimulation of area MT biases the end point of saccades (Groh et al. 1997), although the contribution of position, rather than velocity, signals remains unclear. In human perceptual work, flank encoding is best revealed during adaptation. Adaptation has its greatest impact on capacity to discriminate changes in pattern orientation, spatial frequency, or motion direction when the adapting stimulus is offset from the discrimination locus in the relevant dimension (Hol and Treue 2001; Regan and Beverley 1983, 1985; Tzvetanov and Womelsdorf 2008). By analogy, our observations predict that many aspects of spatial discrimination will be poorer during adaptation to displaced positions than during adaptation to overlapping positions. The most potent displacement should depend on the scale of the receptive fields engaged in the task, and this may help constrain which cortical regions are engaged in different forms of spatial vision.

Knowledge of noise correlations improves discrimination.

Our analyses show that moving objects impose a rich pattern of interneuronal correlations, which may be useful for spatial discriminations. Because a small moving object moves into and out of individual receptive fields, the structure of correlations is richer than that previously revealed during visual stimulation with large surfaces, which always cover the receptive fields of the neurons under study [e.g., Bair et al. (2001), Cohen and Kohn (2011), Rosa and Elston (1998), Smith and Kohn (2008), and Solomon et al. (2014)]. We were able to reveal this structure because we made measurements from large populations of neurons simultaneously: measurements from pairs of neurons would only provide single slices through the matrix in Fig. 5C. This rich structure emerges from simple principles. First, interneuronal correlations in the absence of a visual stimulus are likely to reflect intrinsic rhythms of cortical networks (Smith and Kohn 2008; Vidne et al. 2012), and introduction of a stimulus reduces the impact of these rhythms in neurons whose receptive fields cover the stimulus position (Churchland et al. 2010; Gutnisky and Dragoi 2008; Kohn and Smith 2005). Second, the presence of a stimulus brings neurons away from spike threshold and allows more of the shared membrane-potential fluctuations to be visible in spiking activity (Cohen and Kohn 2011)—spike correlations are stronger when the stimulus is within the receptive fields of the relevant neurons. Third, neurons with similar receptive fields, those close together in the cortical sheet, show stronger correlations [e.g., McDonald et al. (2014) and Smith and Kohn (2008)].

How interneuronal correlations affect population performance will depend on the functional properties of the relevant neurons. The most important neurons in fine spatial discriminations are those whose receptive fields flank the discrimination locus (cf. Fig. 3). In pairs of similarly tuned neurons, where the object lies on the same flank of the receptive field, noise correlations increase overlap in firing rates evoked by each of the two positions and impair neural performance. By contrast, where the object lies on opposing flanks of receptive fields, noise correlations can reduce overlap in responses to two positions and can thereby improve neural performance. This is because the change in stimulus position brings about opposite changes in mean response. Thus interneuronal correlations can help or hinder neural computations, as implied by theoretical work (Averbeck et al. 2006; Averbeck and Lee 2006; Cohen and Kohn 2011; Latham and Nirenberg 2005; Nirenberg and Latham 2003; Romo et al. 2003; Sompolinsky et al. 2001). Our observations further suggest that these different impacts of noise correlations do not “cancel out” when considered across populations of neurons. When we implemented decoders that ignored correlations, performance dropped by 13–22%, consistent with other work (Graf et al. 2011; Pillow et al. 2008). The performance loss is especially acute in fine spatial discriminations, where two stimuli elicit similar population responses.

Our observations predict that in spatial discrimination tasks that rely on the activity of similarly tuned neurons, reduced noise correlations should be associated with increased behavioral performance (Fig. 5C). This is in agreement with previous work that shows that attention-related improvements in a change-detection task are associated with reduction in correlations between neurons, in which the visual change generally increased mean firing rate (Cohen and Maunsell 2009). For tasks that instead rely on neurons with opposite changes in mean response, our observations predict that improvements in performance may be associated with increased neural correlations. This is in agreement with recent work that shows that attention-dependent improvements in a contrast-discrimination task can be associated with increased noise correlations between neurons that provide evidence for opposite choices (Ruff and Cohen 2014).

GRANTS

Support for this work was provided by National Health and Medical Research Council of Australia Grant 10005427 and the Australian Research Council Centre of Excellence in Vision Science.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: S.C.C., J.W.M., and S.G.S. conception and design of research; S.C.C., J.W.M., and S.G.S. performed experiments; S.C.C. and S.G.S. analyzed data; S.C.C., J.W.M., and S.G.S. interpreted results of experiments; S.C.C. prepared figures; S.C.C. and S.G.S. drafted manuscript; S.C.C., J.W.M., and S.G.S. edited and revised manuscript; S.C.C., J.W.M., and S.G.S. approved final version of manuscript.