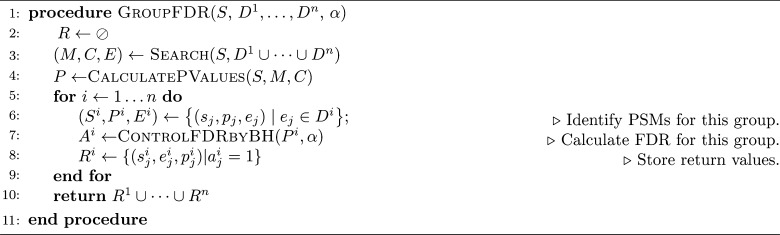Tandem Mass Spectrum Identification via Cascaded Search

Abstract

Accurate assignment of peptide sequences to observed fragmentation spectra is hindered by the large number of hypotheses that must be considered for each observed spectrum. A high score assigned to a particular peptide–spectrum match (PSM) may not end up being statistically significant after multiple testing correction. Researchers can mitigate this problem by controlling the hypothesis space in various ways: considering only peptides resulting from enzymatic cleavages, ignoring possible post-translational modifications or single nucleotide variants, etc. However, these strategies sacrifice identifications of spectra generated by rarer types of peptides. In this work, we introduce a statistical testing framework, cascade search, that directly addresses this problem. The method requires that the user specify a priori a statistical confidence threshold as well as a series of peptide databases. For instance, such a cascade of databases could include fully tryptic, semitryptic, and nonenzymatic peptides or peptides with increasing numbers of modifications. Cascaded search then gradually expands the list of candidate peptides from more likely peptides toward rare peptides, sequestering at each stage any spectrum that is identified with a specified statistical confidence. We compare cascade search to a standard procedure that lumps all of the peptides into a single database, as well as to a previously described group FDR procedure that computes the FDR separately within each database. We demonstrate, using simulated and real data, that cascade search identifies more spectra at a fixed FDR threshold than with either the ungrouped or grouped approach. Cascade search thus provides a general method for maximizing the number of identified spectra in a statistically rigorous fashion.

1. Introduction

A typical protein mass spectrometry experiment proceeds in two phases. The first, experimental, stage produces thousands to millions of peptide fragmentation spectra. The second, analytic, stage assigns a putative peptide to each fragmentation spectrum and reports those peptide–spectrum matches (PSMs) that are deemed to be significant. The matching is done using a peptide database search procedure, and the significance threshold is typically expressed in terms of the false discovery rate (FDR): the estimated percentage of accepted PSMs that are incorrect.¹ Estimating the FDR is critically important because it allows researchers to identify high-confidence PSMs for use in designing downstream experiments. Thus, in designing a mass spectrometry analysis pipeline, a primary consideration is whether we can guarantee that the reported collection of PSMs has a false discovery rate that is no greater than the reported FDR.

The flipside of controlling the FDR is maximization of statistical power. In this setting, statistical power is defined as the probability of accepting a correctly identified spectrum. When statistical power is low, many correctly identified spectra will be left out of our final set of high-confidence PSMs. The design of analysis procedures for mass spectrometry analysis can thus be seen as a tension between two desiderata: maximizing statistical power (i.e., identifying as many spectra as possible) while at the same guaranteeing that the reported false discovery rate estimates are accurate.

1.1. Standard Methods for Controlling the FDR

The FDR can be controlled using a variety of methods, which largely fall into two categories. The first category consists of methods requiring that we assign a p-value to each optimal PSM, i.e., to each PSM that achieves the highest score among all of the candidates for a given spectrum. Specifically, this p-value is defined as the probability that the optimal PSM for a given spectrum achieves a score at least as high as the observed PSM score when searching the same spectrum against a randomly drawn peptide database. This definition hinges on how we define our null, or random, database model, but it is commonly assumed that the peptides are generated independently of one another and that each random peptide is either a shuffled version of an original peptide or is generated according to an independent and identically distributed (IID) model. When optimal PSM p-values are available, they can be fed into well-developed methods that control the FDR, of which the first and most widely used is the Benjamini–Hochberg procedure.¹

There are several approaches to estimating the optimal PSM p-value, including parametric methods that use a relatively small sample of randomly drawn peptide databases to fit a parametric family of distributions² or a fully nonparametric approach that relies on a brute force Monte Carlo approach.³ A different approach is taken by methods that invest their efforts in estimating the probability that a single random candidate peptide (within the precursor mass tolerance) will match the given spectrum at least as well as the optimal PSM does. A variety of methods have been proposed to compute the latter tail probability, including empirical curve fitting procedures^4,5 and dynamic programming methods.⁶⁻⁸ To get from this computed tail probability to the optimal PSM p-value, these methods rely on the assumption that random candidate peptides are independently drawn.

The second category of methods for FDR control does not require computing optimal PSM p-values. For example, many methods evaluate the optimal PSM using an alternative expect value (E-value) instead of a p-value.^4,7,9,10 In such cases, the Benjamini–Hochberg procedure cannot be used. Therefore, the FDR is estimated using an approach based on target–decoy competition (TDC),¹¹ in which each spectrum is searched against a database containing real peptides (targets) and reversed or randomly shuffled peptides (decoys). The FDR is then directly estimated from the number of optimal PSMs that involve decoy peptides, thereby circumventing the need to estimate the p-value of the optimal PSMs.

1.2. Controlling the FDR with Peptide Groups

In typical mass spectrometry analysis, we consider a single flat database of peptides, which reflects an implicit prior belief that all peptides within a specified tolerance around the precursor m/z are equally likely to have generated a given spectrum. Unfortunately, this approach often leads to loss of statistical power because not all of the peptides are equally likely to have generated the given spectrum. For example, consider a case where an observed spectrum matches two distinct peptide sequences with exactly the same score. With no other information, we would be unable to decide which spectrum is more likely to have generated the spectrum. However, if we are told that the spectrum came from a sample digested with trypsin and if we are told that only one of the two peptides has tryptic cleavage sites on both termini, then we would reasonably prefer the match to the tryptic peptide over the match to the nontryptic peptide. A similar argument holds, for example, for peptides that harbor no post-translational modifications (PTMs) versus peptides that contain a PTM, although, in this case, the motivation for selecting the unmodified peptide is the knowledge that there many ways for a peptide to be modified but only one way for it to be unmodified.

In general, when the peptides in the database naturally fall into groups, an analysis that fails to take this grouping information into account will sacrifice statistical power.¹² Similar grouping phenomena have been considered, for example, in the context of hypothesis testing for genome-wide association studies.¹³ In our context, the loss of power can manifest itself in the database search procedure or in the ensuing statistical analysis. For example, if our database includes PTMs, then spectra generated by unmodified peptides will be scored against a larger number of irrelevant peptides than if the database did not include PTMs. Thus, for these spectra, adding PTMs to the database increases the risk of finding a random match whose score exceeds the score of the correct match. More insidiously, even if none of the random match scores exceeds the score of the correct match, the p-value of the same correct PSM will be much larger and hence less significant when computed relative to the augmented database than when computed relative to the unmodified peptide database. Indeed, the p-value computation takes into account the number of candidate peptides, which is directly related to the size of the database, and clearly the augmented database is much larger than the one containing only the unmodified peptides. In addition to the overall loss of power that we just discussed, ignoring the group structure leads to a somewhat undesirable situation where the actual FDR among some peptide groups exceeds the desired level.^12,14

In mass spectrometry analysis, by far the most widely used solution to this grouping problem is simply to discard most of the peptide groups and to focus on one or two small groups that are deemed most likely to be responsible for generating the observed spectra. For example, many analysis pipelines consider only the subset of peptides in the database that exhibit various enzymatic cleavage properties (enzymatic cleavage sites at one or both termini and a few or no missed cleavage sites internal to the peptide). PTMs, if they are considered at all, are typically limited to a few common modifications. One motivation for limiting the peptide set in this way is to reduce the amount of time spent in database search, but a more important motivation is to increase the statistical power as suggested above.

A variety of more nuanced approaches to the peptide grouping problem have been proposed in the literature. For example, the Iterative Search for PTMs (ISPTM) method was proposed in the context of PTM discovery but could be applied to any grouping of peptides.¹⁵ In this method, groups of peptides are arranged a priori in a series such that subsequent peptide groups contain peptides that are deemed to be increasingly less likely to occur in the sample. The ISPTM method iteratively searches a spectrum over the series of peptide groups, assigning to the spectrum the first peptide whose E-value is smaller than a predefined threshold.

Similarly, the stratified search method,⁷ which was proposed for handling peptides grouped based on enzymatic cleavage properties, could be applied to any grouping of peptides. Similar to ISPTM, the procedure uses an ordered series of peptide groups. However, in the stratified search approach, the spectrum is searched iteratively against the union of the current group and all previous groups in the series. At each stage, the E-value of the optimal PSM is computed, and at the end of the search, each spectrum is assigned the peptide with the smallest E-value.

Both ISPTM and stratified search have the drawback that they fail to control the FDR relative to the complete set of spectra being analyzed. More recently, Fu et al.¹⁴ pointed out that, in a set of PSMs with a correctly estimated FDR, the actual FDR associated with subsets of specific classes of PSMs, such as PSMs harboring post-translational modifications, will likely be much different from the global FDR. The authors therefore established a quantitative relationship, called transferred subgroup FDR, between the overall FDR and the separate FDRs calculated on groups. The proposed approach involves postprocessing PSMs identified using the standard methodology and separately estimating FDRs for each group of PSMs. The approach was evaluated on mass spectrometry data where peptides containing the same type of PTMs were grouped together.

1.3. Cascade Search

In this work, we generalize the ISPTM method to control the FDR. The resulting cascade search algorithm operates on an ordered series of peptide groups, similar to ISPTM and stratified search. However, whereas ISPTM treats each spectrum independently, thereby failing to control the FDR in the reported list of optimal PSMs, cascade search takes into account the entire collection of spectra to exert multispectrum FDR control. To evaluate cascade search, we perform empirical comparisons to two existing methods for controlling FDR at the spectrum level: the ungrouped approach and the group FDR method.¹⁴ We use simulated data and three real data sets, two analyzed using peptide groups based on enzymatic cleavage properties and the third analyzed using groups based on PTMs. We evaluate the statistical power of the three methods applied to real data based on the number of discoveries at a given FDR. The latter is estimated using the Benjamini–Hochberg procedure applied to optimal PSM p-values, which, in turn, are evaluated on the basis of tail probabilities computed via dynamic programming.⁸ To increase our confidence in this FDR estimation procedure, we confirm that the selected nominal FDR levels agreed with the corresponding FDR estimates derived using an independent target–decoy competition (TDC).¹¹ Independently of that, we also used TDC to control the FDR in lieu of the Benjamini–Hochberg procedure in all three search strategies we consider here in conjunction with two other search engines, MS-GF+¹⁶ and X!Tandem.¹⁷ Overall, our experiments show that cascade search yields more statistical power, i.e., the procedure identifies more spectra at a fixed FDR threshold, than either the ungrouped or grouped approach. An implementation of cascade search is available as part of the Crux mass spectrometry analysis toolkit (http://cruxtoolkit.sourceforge.net).¹⁸

2. Materials and Methods

2.1. Three Methods for Database Search and FDR Control

In this article, we consider three protocols for reporting a list of PSM discoveries when searching a set of spectra against a sequences of peptide databases: ungrouped, grouped, and cascade search. We assume that these databases are of increasing size and decreasing relevance. All three methods share the basic features of most such database searches, but they differ in how each component of the search is applied.

In general, the assignment of peptides and corresponding confidence estimates to a collection S of tandem mass spectra can be carried out in two steps: database search and FDR control.

Typically, in the first step, each spectrum s ∈ S is searched against a database D of peptide sequences. This step involves iteratively comparing the spectrum to candidate peptides d ∈ D whose masses lie within a specified tolerance of the spectrum precursor mass. Each such comparison yields a score that quantifies the quality of the PSM, and the spectrum s is assigned the best scoring peptide e. The first two protocols we consider, ungrouped FDR (Algorithm 1) and group FDR (Algorithm 2), apply an identical search procedure: each spectrum is searched against the union of the databases. The third method, cascade FDR (Algorithm 3), applies a different search strategy: initially, each spectrum is searched against the first (and presumably smallest) database, and only those spectra that, together with their assigned peptides, fail to achieve statistical significance are used for further searches against the subsequent database. The same principle applies iteratively to the remaining databases.

Scheme 1. Details of Algorithm 1: Controlling FDR with No Peptide Groups.

The input is a collection S of spectra, a peptide database D, and an FDR threshold α. The subroutine Search(S,D) returns a list of selected peptides E, the associated matching scores M, and the numbers of candidate peptides C, where |S| = |M| = |C| = |E|. The subroutine CalculatePValues(S,M,C) converts raw scores into p-values and then adjusts each p-value to account for the corresponding number of candidate peptides. The ControlFDRbyBH procedure takes as input a list P of p-values and a confidence threshold α and returns a list A of Booleans, each indicating whether the corresponding p-value is accepted or not. Note that, in general, we use an uppercase variable name to refer to a list of values and a lowercase variable with a subscript to refer to entries in that list, e.g., S = s₁, ..., s_|S|.

Scheme 2. Details of Algorithm 2: Controlling FDR with Peptide Groups.

The input is a collection S of spectra, a series D¹, ..., Dⁿ of peptide databases, and an FDR threshold α.

Scheme 3. Details of Algorithm 3: Controlling FDR with Cascaded Groups.

Like the group FDR algorithm, the input is a collection S₀ of spectra, a series D¹, ..., Dⁿ of peptide databases, an FDR threshold α, and a threshold k specifying the minimum number of identifications required per group.

In the second step, we need to estimate the FDR among the list of discoveries and report only those PSMs that score above a threshold at which the estimated FDR matches the desired level. Controlling the FDR can be done in several ways, the choice of which depends on whether or not one can estimate the p-values of each optimal PSM. If no such estimates are available, then one is forced to use target–decoy competition,¹¹ but if such p-values are available, then one can use a method like the Benjamini–Hochberg procedure¹ to achieve FDR control. Note that, although the following discussion is largely framed in terms of the latter p-value based FDR controlling procedure, it can be equivalently formulated using target–decoy competition. We have accordingly provided generalizations of the algorithms that can utilize p-values if they exist (employing the Benjamini–Hochberg procedure) or, in the absence of p-values, resort to using target–decoy competition (Supporting Information Algorithms S1–S4).

In Algorithms 1–3, we assume that we can compute p-values. Specifically, the algorithms assume that if the top-scoring (optimal) PSM for a given spectrum achieves a score of s, then we can compute p′ := p(X ≥ s), the statistical significance of the PSM score s assuming the unique candidate peptide was chosen at random according to an IID model. This probability is the same as the spectral probability of ref (6). Such probabilities can be assigned using approximate^4,5,9,10 or exact methods.⁶⁻⁸ However, because the score s is selected as the best from c candidates rather than using a unique candidate, the p-value of the optimal PSM (defined as the probability of seeing a match scoring s or better when searching against an entire null database) should be corrected for that fact. Empirical evidence suggests that it is reasonable to assume independence between the scores assigned to different random candidate peptides.⁸ Under such an independence assumption, it readily follows that the p-value of the optimal PSM is given by p = 1 – (1 – p′)^c. Note that this is often referred to as the Šidák correction in the context of hypothesis testing.¹⁹

Each of the three procedures we present here includes a step, or multiple steps, to control the FDR in its reported list of discoveries. All three rely on computing the relevant p-values as described above, followed by applying the Benjamini–Hochberg procedure,¹ which takes as input a collection of p-values and a desired FDR threshold α and produces as output a set of accepted p-values.

Our three methods, however, differ in how they compute the p-values and in how they apply the Benjamini–Hochberg procedure. The ungrouped FDR procedure (Algorithm 1), which corresponds to the case where we do not have information (or choose to ignore information) about peptide groups, estimates the FDR in a straightforward manner: the p-values are computed relative to the union database and we simply apply the Benjamini–Hochberg procedure to the set of all PSM p-values, P (line 4, Algorithm 1).

Alternatively, the group FDR procedure (Algorithm 2) uses information about the peptides to compartmentalize the PSMs into groups, as proposed by Fu et al.¹⁴ In this case, because the search is still done relative to the union of the databases, the p-values are computed, as in the group FDR procedure, relative to that union; however, the Benjamini–Hochberg procedure is executed separately on each group of PSMs, or each database, and the union of the resulting set of accepted PSMs is returned. Note that this procedure is a simplified form of the group FDR procedure used by Fu et al. in which we do not include the transferred subgroup FDR calculation. That calculation would decrease the variance of the FDR estimates for each group, particularly for groups with a small number of discoveries, but would not affect the overall conclusions of this work (a point that is given further evidence below).

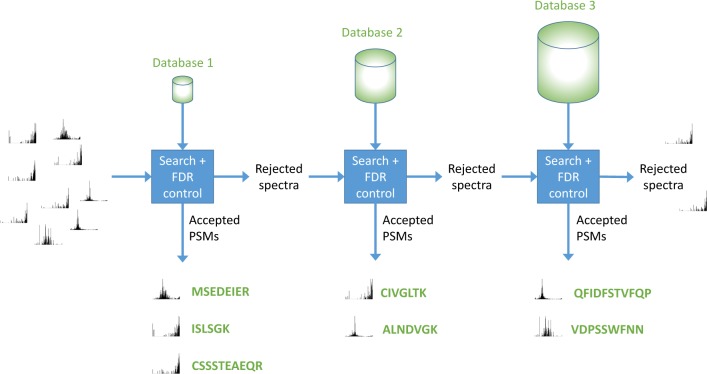
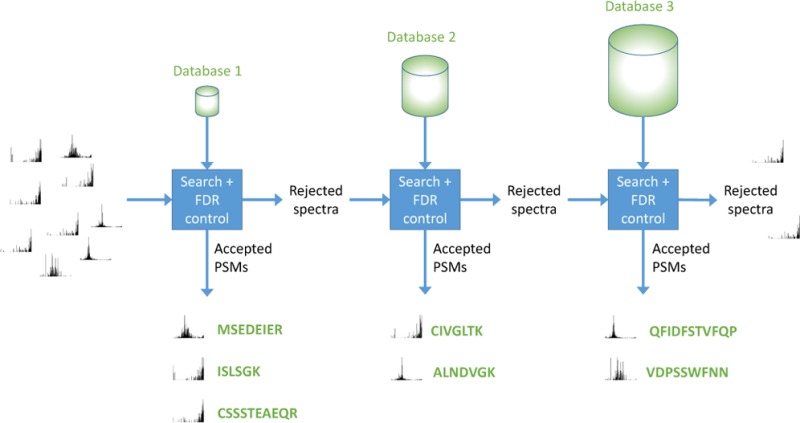
Finally, as mentioned above, in the cascade FDR procedure (Figure 1 and Algorithm 3), we interleave the database search and the FDR control. Specifically, we iteratively search each database, estimate the p-values relative only to the searched database, and apply the Benjamini–Hochberg procedure in that reduced context. Any spectrum that is identified with confidence better than the specified FDR threshold α is committed to be reported together with its matching peptide and, consequently, this spectrum is left out of all subsequent searches.

Figure 1.

Cascade search. Fragmentation spectra are searched against a series of peptide databases. After each search, spectra that are not matched according to a user-specified FDR threshold are passed on to the next search.

The minimal identifications threshold k, which is specific to the cascade FDR procedure (line 7, Algorithm 2), guards against situations where an unusually low number of identifications compromises our ability to control the FDR. As noted in a similar, although not identical, setup in ref (12), separate FDR analysis is legitimate if the expected number of identifications is reasonably large. In practice, we found that setting k ∼ 20 seems to guarantee control of the FDR.

2.2. Target–Decoy Estimation

For target–decoy analysis, we generated decoy peptides by shuffling each unique target peptide, leaving the N- and C-terminal amino acids in place. If the decoy peptide already appears either in the target database or in the previously generated set of decoys, then the peptide is reshuffled up to 10 times to attempt to generate a distinct decoy. Homopolymers for which decoys cannot be generated are left out of the decoy database. Hence, the procedure approximately doubles the number of the peptides in the database. After revealing the target/decoy labels for a set of PSMs, the FDR among the target PSMs is estimated as N_d/N_t, where N_d is the number of decoy PSMs and N_t is the number of target PSMs.¹¹

2.3. Data Sets

We analyze three previously described collections of shotgun proteomics fragmentation spectra.

The yeast data set consists of 35 236 low-resolution MS/MS spectra obtained on a trypsin-digested whole-cell membrane fraction from the yeast Saccharomyces cerevisiae using an LTQ ion trap mass spectrometer. This data set is fully described by Käll et al.²⁰

The yeast protein sequence database was obtained from http://noble.gs.washington.edu/proj/percolator/data/yeast.fasta.gz. It contains 6734 protein sequences. Three peptide data sets were generated, containing 146 034 fully tryptic, 2 424 546 semitryptic, and 42 859 931 nontryptic peptides. No missed cleavages were allowed. One static modification was included: carbamidomethylation (57.02146 Da) of cysteine. No variable modifications were used.

The human data set consists of 23 713 high-resolution MS/MS spectra derived from a lymphoblastoid cell line and stored in the file Linfeng_120110_HapMap29_6.RAW.²¹ Protein lysates were subjected to detergent cleanup, cysteine alkylation, trypsin digestion, and isobaric tandem mass tag (TMT) labeling. Digested peptides were labeled with sixplex TMT, and the six TMT-labeled samples were equally mixed to generate the final digest mixture. The mixture was analyzed on an LTQ Orbitrap Velos (Thermo Scientific) equipped with an online 2D nanoACQUITY UPLC System (Waters). Full MS scans were acquired in the Orbitrap in the range of 400–1800 m/z at a resolution of 60 000, followed by the selection of the 10 most intense ions for HCD-MS2 fragmentation using a precursor isolation window of 1.5 m/z. The normalized collision energy for HCD was set to 38% at 0.1 ms activation time. Ions with a singly charged state or unassigned charge states were rejected for MS2. Ions within a 10 ppm m/z window around ions selected for MS2 were excluded from further selection for fragmentation for 60 s.

The IPI.Human database, version 3.87, contains 91 491 protein sequences. Two static modifications were included: carbamidomethylation (57.02146 Da) of cysteine and TMT labeling (229.16293 Da) of N-terminal amino acids. No variable modifications were included. As in yeast, three peptide data sets were generated, containing fully tryptic, semitryptic, and nontryptic peptides. Two missed cleavages were allowed, and peptides ranged in length from 7 to 20 amino acids. The resulting databases contained 1 916 754, 29 226 648, and 155 553 742 peptides, respectively.

The Aurum data set is a publicly available collection of 9832 singly charged spectra, which were generated on an ABI 4700 MALDI-TOF/TOF instrument from 246 purified and trypsin-digested protein samples. This data set was explicitly designed for testing novel mass spectrometry algorithms and tools.²² The data were downloaded from ProteomeCommons.org.

This spectrum data set was searched against seven theoretical peptide databases, each generated from the IPI Human database, version 3.87,²³ containing 91 491 protein sequences. The initial database contains 647 650 unmodified tryptic peptides, and each subsequent database corresponds to a specific PTM:

• •353 539 oxidized peptides (2MW + 15.9949),
• •1 800 839 methylated peptides (2ED + 14.0156),
• •363 539 dioxidated peptides (2MW + 31.9898),
• •203 901 iodinated peptides (1Y + 125.897),
• •1 295 300 peptides with amonia or water loss on the N-terminus (−18.0106, −17.0265), and
• •647 650 peptides with acetylation on the N-terminus (+42.0106).

All peptide are fully tryptic without missed cleavages and carry at most two variable PTMs and one static modification: carbamidomethylation (57.02146 Da) of cysteine.

All three data sets were searched using Tide with exact p-values (--exact-p-value T), as implemented in Crux, version 2.1.¹⁸ The precursor mass tolerance was set to 3 Da for the yeast data, 10 ppm for the human data, and 1 Da for the Aurum data. All other parameters were left at their default values.

In addition, the yeast data was searched using MS-GF+, v10089,¹⁶ and X!Tandem, v10-12-01-1.¹⁷ To ensure consistency, both programs were provided with predigested peptides, rather than full-length protein sequences. MS-GF+ was run with “-e 10 -ignoreMetCleavage 1” to prevent enzymatic cleavage of the input peptides. Both programs were used with target–decoy search (“-tda 1” for MS-GF+ and “include reverse = yes” for X!Tandem), without any cleavages and without isotope errors. In both programs, the minimum and maximum charge states were specified to be 1 and 5, respectively, whereas precursor and fragment ion tolerances were specified to be 3 and 1 Da, respectively. X!Tandem was used without refinement search.

3. Results

3.1. The Cascade FDR Method Yields Improved Statistical Power on Simulated Data

To compare the performance of the three methods, ungrouped, grouped and cascade search, we performed a simulation experiment. In agreement with our presumed setup, we simulated grouping of the peptides into a sequence of three databases of increasing size and decreasing relevance. Specifically, in our simulations, peptides in the ith database (peptide group) generated a corresponding spectrum set of size proportional to 1/(i²). The total number of spectra thus generated was 10 000, so, for example, the first spectrum set that was generated by peptides from the first database had 7347 spectra, the second spectra set had 1837 spectra, and the third spectrum set had 816 spectra generated by peptides from the last group/database. We refer to those 10 000 spectra that were generated by peptides in our databases as native. We added to those spectra a set of 40 000 foreign spectra that correspond either to peptides outside of the database or to nonpeptide molecular species. Note that this native/foreign terminology is formally introduced as an integral part of a probabilistic model that we introduce in ref (24).

We next simulated searching our 50 000 spectra against our three databases according to the three protocols. In line with the assumption that the databases are increasing in size, we set the number of candidate PSMs per spectrum in the three databases according to the average number of tryptic, semitryptic, and nontryptic candidate peptides in the yeast database, yielding 358, 5936, and 107 407, respectively. Thus, every spectrum was matched with a total of 113 701 candidate PSMs.

Each PSM was assigned a label, true or false. Matching any candidate peptide against a foreign spectrum obviously yields a false PSM. Matching a native spectrum against the unique peptide that generated it yields a true PSM, whereas matching it against any other candidate peptide again yields a false PSM. The p-values of the false PSMs were randomly sampled from a uniform U(0,1) distribution, whereas the p-values of the true PSMs were generated U(0,1) × 10^–ξ, where ξ ∼ Poisson(a) . The parameter a determines how distinct the true and false PSMs are. We selected a = 8, which provided a realistic overlap (data not shown).

The final steps of the simulation differ for the three different search procedures. In the ungrouped FDR procedure, the minimum of all 113 701 p-values was assigned to the corresponding spectrum, yielding one PSM per spectrum. That assignment was marked as false if the corresponding p-value was generated by the uniform distribution; otherwise, it was marked as true. To account for the number of candidates, we adjusted this minimal p-value by the Šidák correction with factor n = 113 701. (This correction would normally be done in the CalculatePValues procedure in Algorithm 1.) To control the FDR, we used the Benjamini–Hochberg procedure on the full set of PSMs (step 4 in Algorithm 1). The grouped procedure is similar to the ungrouped except that each PSM was assigned to the group/database associated with the matched peptide. Benjamini–Hochberg was then carried out separately on each of the three groups of PSMs.

At the ith step of the cascade FDR procedure, for each of the remaining spectra we chose the smallest p-value from the matched candidate peptides of the ith group/database. This p-value was adjusted using the Šidák correction with the number of candidate PSMs (358, 5936, or 107 407), as would normally be done in the CalculatePValues procedure in Algorithm 3. The Benjamini–Hochberg procedure was then applied to the list of adjusted p-values (one per each remaining spectrum), and spectra identified at a specified FDR threshold α were then removed. The procedure was repeated iteratively on subsequent groups.

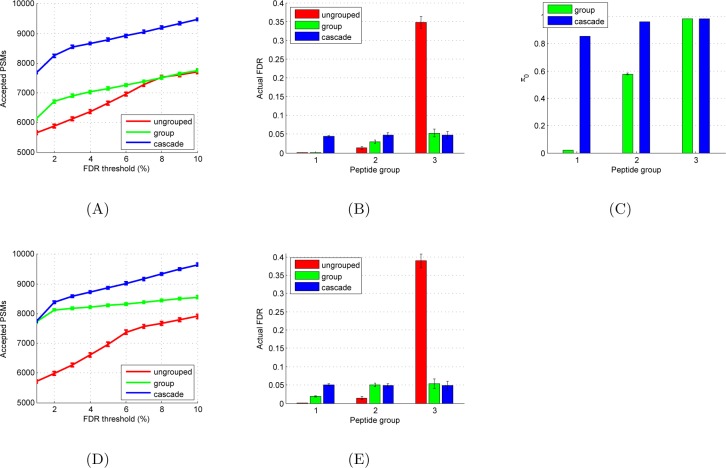
The simulation shows that the cascade FDR procedure yields better statistical power than either ungrouped or grouped FDR at thresholds from 1 to 10% FDR (Figure 2A). For example, at α = 0.01 (1% FDR), the ungrouped FDR procedure identifies 5662 PSMs, on average, across 100 simulations, whereas the grouped and cascade FDR procedures identify 6139 and 7690 PSMs, respectively. For lower FDR thresholds, the grouped procedure yields more PSMs, on average, than the ungrouped procedure, whereas for higher thresholds (FDR >8%), this difference disappears.

Figure 2.

Simulation of ungrouped, grouped, and cascade FDR procedures. (A) Plots, for each procedure, of the number of identified spectra as a function of FDR threshold. (B) Plots, for each of the three groups, of the actual FDR produced by each of the three procedures. (C) Proportion π₀ of PSMs that are marked false for each group. (D, E) Same as panels A and B but for a simulation in which the FDR estimates include the actual value of π₀. All simulations were repeated 100 times; means and standard deviations are indicated.

To better understand the relative performance of the three methods, we used the true and false PSM labels to measure the actual FDR within each of the three groups. This analysis was performed using an FDR threshold of 5% for each of the three methods. The overall actual FDRs for the ungrouped, grouped, and cascade FDR methods is, on average, 4.22, 0.91, and 4.51%, respectively. However, only the cascade approach shows a consistent FDR across all three groups (Figure 2B). In contrast, the ungrouped FDR procedure shows a striking upward trend in FDR as we move from early groups with fewer candidate peptides and a larger proportion of native PSMs (FDR far below 5%) to later groups containing many candidate peptides and few native spectra (FDRs >30%). This behavior, which has been pointed out previously,¹⁴ arises because the PSMs in the later groups are substantially more difficult to detect correctly. Indeed, this phenomenon motivated the estimation of group-specific FDRs.

Accordingly, the grouped FDR procedure successfully eliminates this tendency to enrich the results associated with the later groups in the series with more false PSMs; however, the procedure does not fully eliminate the trend toward low actual FDR rates for the first groups in the series. In particular, the average actual FDR for the first group is only 1%.

We hypothesized that the conservative behavior of the grouped FDR procedure for the initial groups is, at least in part, a result of using the Benjamini–Hochberg procedure. This procedure makes the implicit assumption that all of the p-values being analyzed are drawn according to the null distribution. Accordingly, a variety of subsequently described FDR estimation procedures (reviewed in ref (25)) improve upon the Benjamini–Hochberg procedure by explicitly estimating a mixture parameter π₀, which represents the proportion of hypotheses that are drawn according to the null. The Benjamini–Hochberg procedure corresponds to π₀ = 1, and for alternate values of π₀, the FDR can be estimated by multiplying the Benjamini–Hochberg estimate by π₀. In our simulation, we used the true/false labels to compute the actual values of π₀. The results (Figure 2C) show that, as expected, the proportion of false PSMs increases for later databases in the series. For reference, in the ungrouped case the unique value of π₀ is 0.86.

Because each method has at least one π₀ value that is less than 1, we could improve the power of each method by using one of these mixture model methods in place of Benjamini–Hochberg. To test whether this improvement would eliminate the observed differences in statistical power among the three methods, we modified our simulation accordingly: rather than using Benjamini–Hochberg to estimate FDR (which assumes π₀ = 1), we simulated the situation where we estimate π₀ from the data and incorporated this factor into the FDR control. However, to eliminate any variability due to the quality of the π₀ estimate, we simply provided each method with the actual value or values of π₀. In particular, during the simulation, in any call to the Benjamini–Hochberg procedure, which occurs once for UngroupedFDR and multiple times for GroupFDR and CascadeFDR, we provided the procedure with p-values that were corrected by the true π₀ associated with these p-values. This setting thus represents an optimal situation, where π₀ is estimated perfectly. These experiments show that the π₀ correction results in approximately uniform FDR estimates for the grouped procedure (Figure 2E). However, critically, although the difference in statistical power between the cascade FDR method and the grouped FDR method has grown smaller, we still see better power for the cascade FDR approach across a range of confidence thresholds (Figure 2D). Note that this modified simulation is unrealistic due to the use of the true value of π₀, which is unknowable in practice; our purpose is simply to demonstrate that the difference in power offered by the cascade approach cannot be explained away by differences in how π₀ is handled. Note that, to test for robustness, we repeated both of these simulations (with and without the π₀ correction) using a series of 50 databases and observed very similar trends (Supporting Information Figure S1).

Importantly, this last simulation shows that methods that improve the FDR estimation, such as the transferred subgroup FDR of ref (14), will still be inferior to the proposed cascade approach. Presumably these methods lose power at the search step, which is executed against the union database rather than sequentially as in the cascade approach.

3.2. The Cascade FDR Method Yields Improved Statistical Power on Real Data

Having established the utility of the cascade FDR method in simulation, we next applied the method, along with the ungrouped and grouped FDR procedures, to three real data sets. In this setting, we cannot distinguish between true and false positive identifications. However, the preceding simulations suggest that our method successfully controls the FDR. Hence, our analysis compares, across the three methods, the number of accepted PSMs at a fixed FDR.

For the first data set, composed of 35 236 low-resolution MS/MS spectra obtained form a whole-cell membrane fraction of the yeast S. cerevisiae, we grouped the peptides based upon their enzymatic cleavage properties. In this particular experiment, peptides were digested with trypsin. Accordingly, we expect most of the identified peptides to have tryptic cleavage sites on both ends (fully tryptic) and for semitryptic or nontryptic peptides to be increasingly rare. On the other hand, the total number of tryptic peptides in the database (146 034) is much smaller than the numbers of semitryptic (2 424 546) and nontryptic (42 869 931) peptides. Thus, in this case, we expect the three groups of peptides to exhibit very different rates of correct identifications.

Our results (Table 1) are consistent with this expectation. At a 1% FDR threshold, the standard, ungrouped procedure yields 4245 PSMs, of which 58 are semitryptic and 159 are nontryptic. The simulation results in Figure 2B suggest that the false positives among these 4245 PSMs are highly enriched in the semitryptic and nontryptic groups, and the group FDR analysis of the yeast data set supports this hypothesis: analyzed separately, the number of tryptic PSMs accepted at 1% FDR increases from 4028 to 5536, whereas the number of nontryptic PSMs decreases from 159 down to 61. The cascade FDR approach improves upon group FDR still further, yielding a total of 8947 PSMs at 1% FDR, an improvement of 110.8% over the ungrouped FDR approach and 58.5% over the group FDR approach. Interestingly, the cascade approach achieves this high statistical power without accepting a single nontryptic PSM. Analyses at FDR thresholds of 5 and 10% (Supporting Information Table S1) are consistent with this overall trend in statistical power. For reference, the distributions of p-values for target and decoy PSMs, respectively, are provided in Supporting Information Figure S2.

Table 1. Number of Accepted PSMs at 1% FDR in the Yeast Data Set.

	tryptic	semitryptic	nontryptic	total
ungrouped	4028	58	159	4245
group	5536	48	61	5645
cascade	8827	120	0	8947

Next, we repeated this experiment with a high-resolution data set, consisting of 23 713 spectra from a study of genetic control of protein abundance in humans.²¹ The results (Table 2) are consistent with the results from the yeast experiment. Switching from ungrouped to group FDR analysis yields 389 additional PSMs, corresponding to an increase in statistical power of 33.9%. Switching from ungrouped to cascade search yields an even larger improvement of 855 PSMs, or a 74.5% increase in power. Similar to the yeast analysis, cascade search fails to find any nonenzymatic identifications in the human data; instead, most of the gain in statistical power comes in the form of additional tryptic PSMs.

Table 2. Number of Accepted PSMs at 1% FDR in the Human Data Set.

	tryptic	semitryptic	nontryptic	total
ungrouped	1059	37	52	1148
group	1485	33	19	1537
cascade	1977	26	0	2003

The increase in tryptic identifications arises because of the difference in how p-values are adjusted in the two methods. In the group FDR case, the p-values of all the PSMs are corrected by the total number of candidate peptides, including tryptic, semitryptic, and nontryptic candidates. In practice, this means that, relative to the cascade search procedure, the tryptic PSM p-values are overcorrected. Specifically, in the group FDR case, the tryptic peptide p-values are corrected by, on average, a factor of 113 701, whereas in the cascade search case, the same p-values are corrected by a factor of only 358.

Next, we investigated the performance of the three approaches on a data set in which peptides are grouped according to post-translational modifications (PTMs). The data set was generated on a MALDI TOF/TOF instrument from a mixture of 246 purified human proteins and is known to contain a variety of different types of PTMs. Our modification series begins with unmodified peptides and then considers six different possible PTMs: oxidation, methylation, dioxidation, iodination, N-terminal ammonia or water loss, and N-terminal acetylation. The results of this analysis (Table 3 and Supporting Information Table S2) show the same relative performance of the three methods, with the ungrouped approach identifying 3458 PSMs, the grouped approach identifying 33 additional PSMs, and the cascade approach identifying an additional 125 PSMs. Overall, using the cascade approach on this data set boosts statistical power at FDR 1% by 3.6% relative to the ungrouped approach.

Table 3. Number of Accepted PSMs at 1% FDR in the Aurum Data Set.

	tryptic	oxidized	methyl	nt loss	dioxid	iodo	nt acetyl	total
ungrouped	2133	493	408	254	144	18	8	3458
group	2203	510	381	238	137	17	5	3491
cascade	2293	546	380	231	133	0	0	3583

Thus far, our analyses of the yeast, human, and Aurum data sets have relied upon the validity of the p-values computed by Tide using dynamic programming. To boost our confidence in our Benjamini–Hochberg FDR control based on these p-values, we repeated the comparison of the ungrouped, grouped, and cascade approaches on the Aurum data set, this time using a target–decoy approach to estimate FDR (Materials and Methods).¹¹ In this case, the size of the database was doubled to include one decoy for each target peptide, and the entire simulation was repeated. At the very end, the target/decoy labels were revealed, and the FDR was re-estimated based on these labels. Note that this is a different procedure from controlling the FDR using TDC: here, controlling the FDR is again done using the Benjamini–Hochberg procedure and only the actual FDR in the reported discovery list was estimated using TDC. The resulting estimates, for identifications with an initial FDR estimate of 1% (Table 4), are consistent with the estimates obtained using the Tide p-values. Similar results (Supporting Information Table S3) were obtained using an FDR threshold of 5% rather than 1%.

Table 4. Target–Decoy FDR Estimates for the Aurum Data Set^a.

	tryptic	oxidized	methyl	nt loss	dioxid	iodo	nt acetyl	total
ungrouped	0.09	0.41	0.98	1.97	1.39	11.11	75.0	0.66%
group	0.36	0.59	1.05	0.84	0.73	11.77	0.0	0.57%
cascade	1.08	0.73	0.79	0.43	1.53	0	0	0.97%

^aThe FDR was initially estimated at 1% using exact p-values, and then the target/decoy labels were revealed and the FDR was re-estimated for each group. The table reports the target–decoy FDR estimates, as percentages.

Finally, to demonstrate the generalizability of our approach, we repeated the analysis of the yeast data set using the MS-GF+ and X!Tandem search engines coupled with target–decoy competition (TDC) in lieu of the Benjamini–Hochberg p-value derived FDR estimation (employing Supporting Information Algorithms S1–S4). The results (Table 5) are consistent with our observations for Tide: relative to both the ungrouped and group FDR procedures, cascade search offers a boost in statistical power. Specifically, at 1% FDR, the total number of accepted PSMs increases by 70.74% for MS-GF+ and 81.94% for X!Tandem relative to that with the ungrouped FDR approach and by 16.07 and 31.61%, respectively, for the group FDR approach.

Table 5. Spectrum Annotation at 1% FDR in the Yeast Data Set Using MS-GF+ and X!Tandem.

		tryptic	semitryptic	nontryptic	total
MS-GF+	ungrouped	6186	160	71	6417
	group	9292	134	14	9440
	cascade	10 804	153	0	10 957
X!Tandem	ungrouped	3967	118	179	4264
	group	5476	66	70	5612
	cascade	7611	85	62	7758

3.3. The Cascade Approach Exhibits a Low Level of Early Commitments

One potential drawback to cascaded search is that the procedure might commit too early. For example, in an enzymatic cascade over tryptic, semitryptic, and nontryptic databases, a spectrum that is incorrectly assigned to a tryptic peptide and receives a good enough score in the initial, tryptic, search might receive an even better scoring semitryptic peptide in the subsequent search, even after correcting for the larger number of semitryptic candidate peptides.

We argue, on both intuitive and empirical grounds, that this type of early commitment is unlikely to be a significant problem for cascaded search, assuming that we are employing well-calibrated statistical confidence estimates and that we order our databases in a reasonable fashion. Consider the scenario described above, in which we search first a tryptic and then a semitryptic database. If we control the false discovery rate at, say, 5%, then, on average, a maximum of ∼5% of the matches produced during the tryptic search could potentially involve spectra produced by semitryptic peptides. This 5% is presumably composed of a mixture of spectra generated by (1) tryptic peptides that were incorrectly identified, (2) semitryptic peptides, (3) nontryptic peptides, and (4) nonpeptide species. Because tryptic peptides are far more common than semitryptic, we expect a priori that group (1) will comprise the bulk of the misidentifications.

To investigate the early commitment phenomenon empirically, we first revisited the simulations described in Section 3.1. In the simulation, we define an early commitment as an accepted PSM that is incorrect and that involves a native spectrum whose generating peptide belongs to one of the subsequent peptide groups. Note that this is a conservative definition of early commitment, since, in practice, an early commitment is problematic only if the above criteria are met and the spectrum would actually have been correctly identified in the subsequent search. However, even with this conservative approach, we find (Figure 3A) that the fraction of early commitments at an FDR threshold of 1% is less than 0.1% among all accepted PSMs. Not surprisingly, as we increase the FDR threshold, the proportion of early commitments rises.

Figure 3.

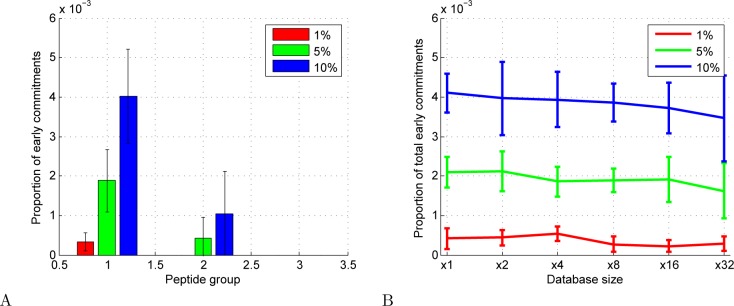
Early commitments in simulation. (A) The proportion of early commitments, as defined in the text, in the simulation described in Section 3.1. (B) The proportion of early commitments in the total set of accepted PSMs, plotted as a function of the size of the peptide database. In both panels, values are means and error bars represent standard deviation across 10 simulations.

To understand how the rate of early commitment varies as a function of the size of the database, we repeated the simulation experiment while varying the database size by factors of 2, 4, 8, 16, and 32 relative to that of the initial simulation. The results (Figure 3B) suggest that the overall rate of early commitments decreases as a function of database size. A decrease in the total number of early commitments as a function of database size is not surprising: as the database gets larger, the total number of accepted PSMs decreases due to a larger number of competing peptides that can generate incorrect PSMs. However, the observed decrease in the proportion of early commitments among the accepted PSMs is less easy to explain. We hypothesize that this trend occurs because the early commitment PSMs are false and hence are generally of lower quality than true PSMs. Thus, these PSMs are more susceptible to being dropped due to the increase in the number of candidates.

We then examined the results from the Aurum data set, searching for evidence of the early commitment phenomenon. To do so, we first searched the entire set of spectra separately against each peptide group and identified spectra using a given FDR threshold. Note that in this single group protocol the same spectrum may end up being accepted in multiple searches, but the procedure provides a useful upper bound on the total number of spectra that could be assigned to each group. We then defined an early commitment as a PSM that (1) is accepted by the cascade FDR procedure and (2) has an optimal p-value that is greater than the smallest optimal p-value for that same spectrum among all subsequent single group searches. The results (Table 6) show, not surprisingly, that the rate of early commitment depends strongly upon the FDR threshold but that, even using a loose FDR threshold of 20%, the proportion of early commitments among all accepted PSMs is still quite low (4.46%).

Table 6. Early Commitments in the Aurum Data Set.

FDR threshold	accepted PSMs	early commitments	percentage
1%	3583	26	0.73%
5%	3931	54	1.37%
10%	4180	91	2.18%
20%	4621	206	4.46%

4. Discussion

An important difference between the cascade search procedure and, say, the ungrouped approach is that cascade search requires a bit more work from the user. In particular, cascade search relies on an ordered series of databases. Requiring that the peptides be subdivided into separate databases in such a way that some databases are more likely than others to be enriched for generating peptides is somewhat demanding. Still, this much is also required to use the group FDR procedure. What really sets the cascade search approach apart is not only the requirement that the peptides be segregated into databases but also that the databases must be ordered in such a way that, a priori, we expect more identifications to come from the earlier databases in the series. This observation naturally leads to the following question: What happens if we get the order wrong? Unfortunately, it is easy to see that, in an extreme case, a misordering of peptide databases could be fatal to the cascade search procedure. Imagine, for example, a case in which the first database yields a very small number of identified spectra. In such a setting, cascade search will terminate (line 7 in Algorithm 3), even though the subsequent databases may contain many identifications. It is therefore important that the user employs a reasonable ordering of databases. If such an ordering is not possible, i.e., if there is no prior expectation for what classes of peptides are most likely to occur in the data set, then the ungrouped or grouped procedures should be used.

Our simulated and real experiments suggest that cascade search offers a much larger gain in statistical power in the context of a series of databases representing differences in enzymatic cleavage relative to that with a series of database representing different PTMs. This difference can be attributed primarily to the difference in the relative sizes of the databases in the series. The enzymatic cleavage series contains in total 45 430 511 peptides, including 146 034 tryptic, 2 424 546 semitryptic, and 42 859 931 nontryptic peptides. Among these, the tryptic PTMs are the most common, accounting for 98.7% of the identifications at 1% FDR in the cascade FDR approach. Critically, the cascade search procedure identifies these tryptic peptide PSMs while searching against the much smaller database that contains only the tryptic peptides. On the other hand, the group FDR and ungrouped methods carry out their searches in the cumulative peptide database and are thus more likely to encounter a random peptide match that eclipses the correct one while, at the same time, the p-value of any optimal PSM must take into account the much larger search space. Thus, in this case, the huge nontryptic data set is a significant burden. In contrast, the databases in the PTM series are less skewed, containing a total of 5 312 418 peptides distributed roughly evenly over the subdatabases. Furthermore, we observe empirically that each of these databases yields a significant number of PSMs; hence, in this setting, searching against each of the databases separately is roughly equivalent to searching the union of the databases.

While this article was under review, an analysis by Woo et al. was published that corroborates our primary conclusion.²⁶ That study discusses the special case of searching two databases in the context of a proteogenomic cancer analysis. The authors investigate three different methods of evaluating the FDR, which coincide with the ones we describe when the number of databases is two: their Combined-FDR is our ungrouped FDR, their Separate-FDR is our group FDR, and their Two-Stage-FDR is our cascade search. Note, however, that Woo et al.’s application is quite specialized, and they do not compare or validate their methods beyond the specific context in which they are described. In addition, as noted in the discussion of our cascade algorithm, the described Two-Stage-FDR might, in general, fail to control the FDR because it lacks some method, such as our abort condition (line 7, Algorithm 3), that guarantees FDR control when the number of discoveries is low.

An alternative approach to the one we have adopted here is to incorporate knowledge about peptide groups into a machine learning postprocessor. Such methods, instantiated in tools like PeptideProphet²⁷ and Percolator,²⁰ take as input PSMs produced by a search engine and then use a supervised classification algorithm to learn to discriminate between correct and incorrect PSMs. In addition to the primary PSM score, this learning procedure typically takes into account features of the spectrum, features that reflect the quality of the match, and features of the peptide, such as the number of tryptic termini and the number of missed cleaveages. In contrast, statistical analysis methods like cascade search, stratified search, ISPTM, and the group FDR method take into account only (1) the score produced by the database search engine and (2) the segregation of peptides into different groups. This direct approach is simpler than the postprocessor approach, removing the need for decoy PSMs or a hand-derived gold standard data set, for computation of a series of features for each PSM or for training of the classifier itself. More importantly, due to its relative simplicity, the direct approach allows us to make more precise statistical claims. Finally, in contrast to a postprocessor that must be adapted to each new search engine,^28,29 cascade search is a meta-analysis procedure that works with any search engine, without requiring any tweaking or redesign.

Another alternative approach would be to incorporate information about peptide groups directly into the score function rather than relying upon the postprocessor to incorporate this information. During review of this article, we learned about an undocumented feature of the MS-GF+ algorithm that follows this route. Specifically, the algorithm defines an efficiency for each enzyme and adds in a term, scaled by this efficiency, that differentially penalizes nonenzymatic peptides relative to enzymatic peptides. An interesting avenue for future work would be to explore how best to compute this enzymatic score term and to compare this type of approach to the ungrouped, grouped, and cascade search procedures outlined here.

An interesting direction for future work would involve inferring the proper ordering in a data-driven fashion. As noted previously, there exist a variety of methods that aim to estimate, on the basis of a collection of p-values, a mixture parameter π₀ that represents the proportion of hypotheses that are drawn according to the null.²⁵ An extended version of cascade search could employ such a method to attempt to automatically learn the proper ordering of databases. Such an approach might be particularly useful in the context of a metaproteomics study, where the size of the database may or may not be reflective of the prior probability that a given observed spectrum is generated by a given peptide. For example, an organism with a small genome might be very abundant in the analyte. In such settings, the ordering of the databases would have to be done either on the basis of prior knowledge about species abundance or by estimating π₀ separately for each database.

Another important avenue for future research is improving the power of the cascade algorithm by relaxing the abort condition (line 7, Algorithm 3). We again stress that some condition such as this one is necessary to control the FDR; however, we suspect that this particular condition is overly conservative and that alternative, more liberal conditions might still be able to guarantee the desired FDR control in the context of small discovery numbers.

In summary, cascade search provides a principled and flexible way to assign peptides to observed spectra with high statistical power, as long as the user is willing to provide in advance a statistical confidence threshold and a series of appropriately ordered peptide databases. Cascade search will be particularly valuable in studies that include increasingly diverse types of PTMs and particularly in the context of large proteogenomics studies where unexpected sequence variants must be considered.

Supporting Information Available

Figure S1: Simulation of ungrouped, group, and cascade FDR procedures using 50 peptide groups. Figure S2: Distribution of target and decoy p-values in the Aurum data set. Table S1: Number of accepted PSMs at 5 and 10% FDR in the yeast data set. Table S2: Number of accepted PSMs at 5 and 10% FDR in the Aurum data set. Table S3: Target–decoy FDR estimates for the Aurum data set. Algorithm S1: Controlling FDR using target–decoy analysis. Algorithm S2: Controlling FDR using TDC with no peptide groups. Algorithm S3: Controlling FDR using TDC with peptide groups. Algorithm S4: Controlling FDR using TDC with cascaded groups. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/pr501173s.

The authors declare no competing financial interest.