On the Estimation of Disability-Free Life Expectancy: Sullivan’ Method and Its Extension

Abstract

A rapidly aging population, such as the United States today, is characterized by the increased prevalence of chronic impairment. Robust estimation of disability-free life expectancy (DFLE), or healthy life expectancy, is essential for examining whether additional years of life are spent in good health and whether life expectancy is increasing faster than the decline of disability rates. Over 30 years since its publication, Sullivan’s method remains the most widely used method to estimate DFLE. Therefore, it is surprising to note that Sullivan did not provide any formal justification of his method. Debates in the literature have centered around the properties of Sullivan’s method and have yielded conflicting results regarding the assumptions required for Sullivan’s method. In this article we establish a statistical foundation of Sullivan’s method. We prove that, under stationarity assumptions, Sullivan’s estimator is unbiased and consistent. This resolves the debate in the literature, which has generally concluded that additional assumptions are necessary. We also show that the standard variance estimator is consistent and approximately unbiased. Finally, we demonstrate that Sullivan’s method can be extended to estimate DFLE without stationarity assumptions. Such an extension is possible whenever a cohort life table and either consecutive cross-sectional disability surveys or a longitudinal survey are available. Our empirical analysis of the 1907 and 1912 U.S. birth cohorts suggests that while mortality rates remain approximately stationary, disability rates decline during this time period.

1. INTRODUCTION

A rapidly aging population, such as the United States today, is characterized by the increased prevalence of chronic impairment, which is especially pronounced among the elderly. Robust estimation of disability-free life expectancy (DFLE), or healthy life expectancy, is essential for examining whether additional years of life are spent in good health and whether life expectancy is increasing faster than the decline of disability rates. DFLE represents the expected number of years of remaining disability-free life a member of the life table cohort would experience if cohort age-specific rates of mortality and disability prevailed throughout his/her lifetime.

In his seminal article, Sullivan (1971) developed a method for combining mortality and morbidity rates into a single summary measure of a population’s health status. Over 30 years after its publication, Sullivan’s method remains the most widely used method among applied researchers and government officials for estimating DFLE. The key idea of the method is to combine the period life table, which is the main method to calculate life expectancy, with the age-specific disability prevalence estimated from cross-sectional survey data. In particular, Sullivan’s method simply partitions the total number of person-year lived, which is obtained from the period life table, into the disability and disability-free life expectancy based on the proportion disabled, which is in turn measured from the cross-sectional disability survey.

Sullivan’s method is of prime methodological importance in the ongoing exploration of morbidity (e.g., Crimmins, Saito, and Ingeneri 1989, 1997). It has been used extensively to estimate DFLE in various populations (e.g., Iburg, Bronnum-Hansen, and Bjerregaard 2001) as well as differences in DFLE by socioeconomic status (e.g., Sihvonen, Kunst, Lahelma, Valkonen, and Mackenbach 1998; Molla, Madans, and Wagener 2004), educational levels (e.g., Minicuci 2005), occupational groups (e.g., Bronnum-Hansen 2000; Cambois, Robine, and Hayward 2001), and between time periods (e.g., Crimmins et al. 1989; Bronnum-Hansen, Andersen, Kjoller, and Rasmussen 2004; Graham, Blakely, Davis, Sporle, and Pearce 2004). The method has also been used to estimate the burden of disease from chronic conditions such as diabetes (e.g., Manuel and Schultz 2004) and the contribution of specific diseases to educational disparities in DFLE (e.g., Nusselder et al. 2005). Nusselder and Looman (2004) used Sullivan’s method to analyze the contribution of various causes of death and disability to differences healthy life expectancy among populations and over time. Murray and Lopez (1996) compared the disability-adjusted life expectancy, a quantity closely related to DFLE, across world regions using Sullivan’s method as part of their Global Burden of Disease Study. In addition to academic researchers, a number of governments and international health organizations employ Sullivan’s method. The U.S. National Center for Health Statistics uses Sullivan’s method as part of the Healthy People 2010 Study (Molla, Madans, Wagener, and Crimmins 2003). The Australian Institute of Health and Welfare used Sullivan’s method in its 1996 Burden of Disease Study (Mathers, Vos, Stevenson, and Begg 2001). The World Health Organization also used the method to estimate disability-adjusted life expectancy for 191 member states (Musgrove et al. 2000).

Robust estimation of DFLE is also vital to the theoretical understanding of morbidity. The existing research on DFLE of various populations and time periods has often reached contradictory conclusions regarding the competing nature of mortality and morbidity. For example, Gruenberg (1977) and Kramer (1980) argued that the decline in mortality rates only reflects a decline in the mortality rate of chronic diseases rather than a decline in their incidence. Greater life expectancy will result in more severe chronic diseases. Fries (1980), on the other hand, argued for the compression of morbidity. If the onset of the chronic condition can be postponed and adult life expectancy is relatively constant, morbidity will be compressed into a shorter period of time. Moreover, Manton (1982) offered an alternative theory of dynamic equilibrium in which the decline in mortality leads to an increase in the prevalence of milder chronic diseases. Therefore, the accurate estimation of DFLE is essential for the empirical evaluation of these competing theories.

Given the importance and popularity of Sullivan’s method, it is surprising to note that Sullivan (1971) did not provide any formal justification of his method. Debates in the literature have centered around the properties of Sullivan’s method and have yielded conflicting results regarding the assumptions required for Sullivan’s method to provide a valid estimate of DFLE (e.g., Rogers, Rogers, and Belanger 1990; Mathers 1991; Barendregt, Bonneux, and Van der Maas 1994, 1995; Van de Water, Boshuizen, Perenboom, Mathers, and Robine 1995). In this article, we establish a statistical foundation of Sullivan’s method. After defining DFLE and reviewing the period life table method in Section 2, we prove in Section 3 that under stationarity assumptions, Sullivan’s estimator is consistent and unbiased and that the standard variance estimator is consistent and approximately unbiased. Our theoretical results imply that Sullivan’s method requires no additional assumption other than stationarity assumptions. This resolves the debate in the literature, which has generally concluded that additional assumptions are necessary (e.g., Newman 1988; Palloni, Guillen, Monteverde, Ayuso, and White 2005). Our theoretical results appear to be consistent with the existing simulation and empirical studies that investigate the performance of Sullivan’s method under various conditions (e.g., Barendregt et al. 1994; Mathers and Robine 1997; Lievre, Brouard, and Heathcote 2003).

In Section 4 we demonstrate that Sullivan’s method can be extended to estimate DFLE without stationarity assumptions. Such an extension is possible whenever a cohort life table and either consecutive cross-sectional disability surveys or a longitudinal survey are available. The multistate life table method is a popular alternative in the literature (e.g., Rogers, Rogers, and Branch 1989a; Robine et al. 1995), but it requires longitudinal data as well as a number of theoretical and practical assumptions. In contrast, our extension of Sullivan’s method allows for unbiased and consistent estimation of DFLE without adhering to the assumptions and data requirement of the multistate life table method. The computer code that implements the methods proposed in this article is available at the first author’s website. In Section 5 we apply our proposed methodology to estimate DFLE for the 1907 and 1912 U.S. birth cohorts using mortality data from U.S. Vital Statistics and disability data from the U.S. Medicare Current Beneficiary Survey. Our empirical analysis suggests that while mortality rates remained approximately stationary, disability rates may have declined during this time period. Finally, in Section 6 we present conclusions.

2. DISABILITY–FREE LIFE EXPECTANCY AND PERIOD LIFE TABLE

Sullivan’s method utilizes the mortality data from a period life table and the disability prevalence data from a crosssectional survey. In this section, we introduce the standard notation of the period life table used in the field of demography (e.g., Chiang 1984; Preston, Heuveline, and Guillot 2001) and define the estimand (i.e., DFLE).

2.1 Theoretical Definitions of Life Expectancy and DFLE

Theoretically, mortality for a cohort (either real or hypothetical) can be considered as a continuous-time process, which is determined solely by the hazard function, μ(x,y), representing the instantaneous rate of death at age x ∈ [0,∞) for a cohort born at time y. Given the hazard function, one can derive life expectancy at age x for this cohort, denoted by e(x, y), which represents the expected remaining life of an individual at age x who is born at time y. Let l(0, y) represent the total number alive at age 0 for this cohort. Then, the number of survivors at age x is given by

$$l(x,y)=l(0,y)\exp \left[-{\int }_0^x\mu (t,y)dt\right].$$ (1)

If l(0, y) is set to 1, as we do for the remainder of this article, l(x, y) corresponds to the survival function of this cohort. Given the survival function l(x, y), life expectancy at age x can be written as

$$e(x,y)=\frac{1}{l(x,y)}{\int }_x^{\infty }l(t,y)dt.$$ (2)

Similarly, one can define DFLE, denoted by e^DF(x, y), which represents the expected remaining disability-free (DF) life of an individual age x born at time y. Let π(x, y) be the proportion disabled at exact age x for the cohort born at time y. In other words, π(x, y) represents the conditional probability that an individual of this cohort is disabled at age x given that he/she survived up to age x. Because the proportion of survivors who are disability-free at age x is equal to [1 − π(x, y)]l(x, y), DFLE is given by

$$e^{\mathrm{DF}}(x,y)=\frac{1}{l(x,y)}{\int }_x^{\infty }[1-\pi (t,y)]l(t,y)dt.$$ (3)

2.2 Calculation of Life Expectancy From a Period Life Table

Although the theoretical definition of life expectancy is given within the continuous-time framework, the data are typically recorded in a discrete form. A period life table is a common source of discrete data and is often analyzed in order to approximate the continuous-time mortality process. Sullivan’s method also requires the use of a period life table. A main purpose of a period life table is to calculate the life expectancy of a hypothetical cohort that experiences the currently observed cross-sectional mortality rates.

Let 𝚨 be a set of the starting ages for the age intervals of a period life table. We use ω to denote the starting age of the oldest age interval. Let n_x represent the width (years) of an age interval starting at age x ∈ 𝚨. Typically, the width of age intervals is the same for all but the oldest age interval [ω, ∞), that is n_x = n for all x ∈ 𝚨 \{ω} and n_ω = ∞. When n = 1, a period life table is said to be unabridged, whereas it is called abridged if n > 1. In this article we allow for a more general setting where each age interval may have a different width.

A period life table is created by first observing the midinterval population, denoted by _nxP_x, and the total number of deaths, denoted by _nxDx, for each interval [x, x + n_x). Then, the observed mortality rate for each interval, denoted by _nxMx, is calculated as _nxDx/_nxPx. Keeping with the standard demographic notation, we use prescripts to indicate the width of the interval under consideration. A period life table relies on the following stationarity assumptions of the population (e.g., Chiang 1984; Preston et al. 2001):

1. The age-specific hazard rate is constant over time, that is, μ(x, y) = μ(x) for all y.

2. The birth rate is constant over time.

3. The net migration rates are 0 at all ages.

The assumptions imply that the survival function is also constant over time, that is, l(x, y) = l(x), and that the crude death rate, that is, ${\sum }_{x\in \mathcal{𝒜}}{}_{n_x}{D}_x∕{\sum }_{x\in \mathcal{𝒜}}{}_{n_x}{P}_x$, equals the crude birth rate, that is, $B∕{\sum }_{x\in \mathcal{𝒜}}{}_{n_x}{P}_x$ where B is the total number of births to members of the population in the period. Therefore, the total size of the hypothetical cohort is assumed to remain constant over time. Another important consequence of stationarity assumptions is that the age distribution of the hypothetical cohort in any given interval, [x, x + n_x), is constant over time and is proportional to the survival function. Formally, for all s ∈ [x, x + n_x), the age distribution is defined by the following density function:

$$\frac{l\left(s\right)}{{\int }_x^{x+n_x}l\left(t\right)dt}.$$ (4)

For example, a common departure from stationarity occurs in many developing countries today, where annual births have been growing relative to deaths. As we see in Section 5, a violation of the stationarity assumptions is also possible in developed countries where the death rates are declining due to the advance of medical technologies.

Because _nxP_x and _nxD_x are directly obtained from the Census data and vital statistics, they are typically large. Thus, in the literature, the sampling variability about the mortality rate of the hypothetical cohort, denoted by _nxm_x, is considered to be small and, hence, typically ignored. That is, _nxM_x is assumed to equal _nx m_x, which is given by

$${}_{n_x}{m}_x=\frac{{\int }_x^{x+n_x}l\left(t\right)\mu \left(t\right)dt}{{\int }_x^{x+n_x}l\left(t\right)dt}$$ (5)

for all x ∈ 𝚨. Nevertheless, we later show how our results apply to the case where _nx m_x is consistently estimated by _nx M_x (see Sec. 3.4).

Furthermore, it can be shown that the conditional probability of death within an interval [x, x + n_x) given that an individual of the hypothetical cohort survived up to age x, which is denoted by _nx q_x, is equal to n_{x nx} m_x/[1 + (n_x − _nxa_x)_nx m_x], where _nxa_x represents the average person-years lived in a given interval [x, x + n) among those who are alive at age x but die within the interval. The values of _nxa_x are obtained from complete life tables and used in subsequent calculations as a known quantity (e.g., Molla, Wagener, and Madans 2001; Preston et al. 2001).

Within this framework, the total number of person-years lived in an interval, [x, x + n_x), is given by

$${}_{n_x}{L}_x=n_x{l}_{x+n_x}+l_{x{n}_x}{q}_{x{n}_x}{a}_x,$$ (6)

where the members of the l_x+nx proportion who survive the entire interval each contribute n_x years, and the members of the l_{x nx}q_x proportion who die in the interval contribute _nxa_x years, on average. Finally, life expectancy at age x is equal to the total number of person-years for subsequent age intervals:

$$e_x=\frac{1}{l_x}{\sum _{i\in {\mathcal{𝒜}}_x}}_{n_i}{L}_i,$$ (7)

where 𝚨_x = {i ∈ 𝚨 : x ≤ i}. Under stationarity assumptions for the unbounded last age interval [ω, ∞), life expectancy at age ω is equal to the inverse of the death rate, that is, $e_{\omega }{=}_{\infty }{m}_{\omega }^{-1}$. The equality follows from the fact that all those alive at age ω must die in the interval, that is, _∞qω = 1.

We now show that under the stationarity assumptions discussed previously, e_x, which is the life expectancy calculated from a period life table in (7), equals e(x), which is the theoretical definition of life expectancy given in (2). Although in common demographic notation, l(x) is used in continuous notation and l_x in discrete, both refer to the proportion alive at exact age x and, hence, are numerically identical. Given the hazard function, μ(x), the conditional probability of death for an age interval, [x, x + n_x), is equal to the number of deaths in an age interval divided by the proportion alive at the beginning of the age interval:

$$n_x{q}_x=\frac{{\int }_x^{x+n_x}l\left(t\right)\mu \left(t\right)dt}{l\left(x\right)}.$$ (8)

Next, the average number of years lived in an interval among those who die in the interval is equal to the total number of person-years lived among those who will die divided by the proportion who will die in the interval:

$$n_x{a}_x=\frac{{\int }_x^{x+n_x}l\left(t\right)\mu \left(t\right)(t-x)dt}{{\int }_x^{x+n_x}l\left(t\right)\mu \left(t\right)dt}.$$ (9)

Substituting (8) and (9) into (6) and integrating it by parts yield

$$n_x{L}_x={\int }_x^{x+n_x}l\left(t\right)dt.$$ (10)

Therefore, it follows that e_x equals e(x).

Table 1 shows the 1999 U.S. unabridged period life table for selected ages (Arias 2002). In keeping with common demographic notation, the left prescript, n = 1, is not written. The radix, l₀, is set at 1 so that l_x represents the survival probability. At age 20 years, 98.6% of the hypothetical life table cohort remains. From age 20 to ω = 85, the remaining 98.6% of the cohort will live ${\sum }_{i=20}^{85}{L}_i=54.9$ person-years. Hence, a 20-year-old member of the hypothetical cohort will live, on average, 55.9 years given he/she experiences the prevailing period age-specific conditional probabilities of death. For the last age group, _∞a₈₅ = e₈₅ because everyone who is alive at age ω = 85 dies within the last interval.

Table 1.

The 1999 U.S. period life table and life expectancy for selected ages

Age	lx	qx	ax	Lx	ex
20	.986	.001	.506	.986	55.851
25	.982	.001	.500	.981	51.101
30	.977	.001	.495	.976	46.338
35	.971	.001	.500	.970	41.597
40	.963	.002	.500	.962	36.916
45	.952	.003	.500	.950	32.323
50	.935	.004	.500	.933	27.853
55	.911	.007	.499	.908	23.516
60	.875	.011	.501	.870	19.391
65	.820	.016	.500	.813	15.499
70	.743	.025	.500	.733	11.839
75	.638	.038	.500	.626	8.356
80	.505	.059	.500	.490	4.873
85+	.345	1.000	.951	.328	.951

NOTE: The unabridged period life table (n_x = 1 for all x ∈ 𝚨 \ {85}) is created from the conditional probability of death, q_x, and the average person-years lived in the age interval by those dying in the interval, a_x. l_x is the proportion of survivors at age x, whereas L_x represents the total number of person-years lived within the age interval [x, x + 1) for those who were alive at age x. The last age interval is [85, ∞). The final column gives the life expectancy e_x at each age.

3. STATISTICAL FOUNDATION OF SULLIVAN’ METHOD

Unlike life expectancy, DFLE cannot be estimated from a period life table alone without obtaining additional information about disability prevalence. Sullivan (1971) proposed a measure of DFLE by combining mortality information from a period life table and disability information from a cross-sectional disability survey. However, he did not offer any formal justification of his method. In this section, we provide a statistical foundation of Sullivan’s method by deriving the assumptions under which Sullivan’s method yields a valid estimate of DFLE. We also discuss how our theoretical findings relate to the previous investigations of Sullivan’s method in the literature.

3.1 Sullivan’s Method

Sullivan’s method estimates DFLE by partitioning the person-years lived in a given age interval into the proportion with and without disability. Formally, Sullivan’s estimator is defined by

$${\widehat{e}}_x^{\mathrm{DF}}=\frac{1}{l_x}\sum _{i\in \mathcal{𝒜}x}{\left(1{-}_{n_i}{\widehat{\pi }}_i\right)}_{n_i}{L}_i,$$ (11)

where ${}_{n_i}{\widehat{\pi }}_i$ is the sample fraction of the disabled survey respondents within the age interval [i, i + n_i). If simple random sampling is used for the disability survey, ${}_{n_i}{\widehat{\pi }}_i$ is given by

$${}_{n_i}{\widehat{\pi }}_i=\frac{1}{{}_{n_i}{N}_i}\sum _{j=1}^{{}_{n_i}{N}_i}{Y}_{ij}\left(t_{ij}\right),$$ (12)

where _niN_i represents the total number of survey respondents in the age interval, [i, i + n_i) and Y_ij(t_ij) is the disability indicator variable for the jth respondent of that interval whose age is t_ij ∈ [i, i + n_i) at the time of survey. Depending on one’s sampling scheme, ${}_{n_i}{\widehat{\pi }}_i$ may be computed as a weighted average with appropriate sampling weights. In this article, for notational simplicity, we assume simple random sampling, but all the results can be easily generalized to other sampling schemes. Note that in the original article Sullivan (1971) proposed and applied an invalid estimator of disability prevalence, which is different from the estimator of (12) used by subsequent researchers (see Sec. 3.3).

In the literature, the standard way to obtain the variance of Sullivan’s estimator is to assume that the total number of the disabled within each age interval, x, x + n_x, follows an independent binomial process with a constant probability, which is estimated by ${}_{n_x}{\widehat{\pi }}_x$ (e.g., Mathers 1991; Montpellier 1997; Molla et al. 2001). Given this distributional assumption, the variance of Sullivan’s estimator can be estimated by

$${\widehat{\sigma }}_x^{\mathrm{DF}}=\frac{1}{l_x^2}\sum _{i\in {\mathcal{𝒜}}_x}\frac{{}_{n_i}{\widehat{\pi }}_i{\left(1{-}_{n_i}{\widehat{\pi }}_i\right)}_{n_i}{L}_i^2}{{}_{n_i}{N}_i},$$ (13)

where the sampling weights can be incorporated by calculating ${}_{n_i}{\widehat{\pi }}_i$ as a weighted average.

We illustrate Sullivan’s method with the 1999 U.S. period life table of Table 1. We estimate the disability prevalence from the 1999 National Health Interview Survey (NHIS) and the 1999 National Nursing Home Survey (NNHS), both of which are conducted by U.S. Department of Health and Human Services. The NHIS is a multipurpose health survey conducted by the National Center for Health Statistics and is the principal source of information on the health of the civilian, noninstitutionalized population of the United States, which included a sample of 97,059 in 1999. The NNHS is a survey of the residents of nursing homes and related care facilities in the United States also conducted by the NCHS with 8,215 observations in 1999. The use of the two surveys gives a complete picture of disability prevalence among the noninstitutionalized and institutionalized populations.

The second column of Table 2 shows the estimated disability prevalence in each interval, ${\widehat{\pi }}_x$, where the sampling weights are incorporated so that respondents from the two surveys are appropriately weighted. Following the literature (e.g., Crimmins et al. 1997; Crimmins and Saito 2001; Molla et al. 2004), a respondent was considered disabled if he/she responded affirmatively to the following question: “Because of a physical, mental, or emotional problem, do you need the help of other persons with personal care needs, such as…?” where “…” represents various activities of daily living (ADL). ADL includes bathing and showering, dressing, eating, getting in/out of bed or chair, using the toilet, and getting around in home. The third column of Table 2 presents the point estimates of DFLE based on Sullivan’s method, while the next four columns show their 95% confidence intervals. The “_nxm_x known” 95% confidence intervals (fourth and fifth columns) are based on the standard variance in (13). The “_nxm_x estimated” 95% confidence intervals (sixth and seventh columns) account for additional variability in the estimation of _nxm_x based on the large-sample variance of ê^DF in (A.6) and is discussed further in Section 3.4.

Table 2.

Estimated DFLE based on Sullivan’s method for selected ages of the 1999 U.S. population

Age	Estimated disability prevalence	Estimated DFLE	nxmx known 95% CI		nxmx estimated 95% CI
			Lower	Upper	Lower	Upper
20	.01	54.47	54.40	54.53	54.37	54.56
25	.00	49.73	49.67	49.79	49.64	49.82
30	.00	44.98	44.91	45.04	44.89	45.07
35	.00	40.25	40.19	40.32	40.16	40.34
40	.01	35.59	35.53	35.66	35.51	35.68
45	.01	31.02	30.96	31.09	30.94	31.10
50	.01	26.58	26.52	26.64	26.50	26.66
55	.02	22.26	22.19	22.32	22.18	22.34
60	.01	18.17	18.11	18.24	18.10	18.25
65	.03	14.31	14.24	14.37	14.24	14.38
70	.05	10.70	10.64	10.77	10.64	10.77
75	.08	7.30	7.24	7.37	7.24	7.37
80	.15	4.05	3.99	4.11	3.99	4.11
85	.20	.77	.75	.78	.74	.79

NOTE: The first column shows the estimated disability prevalence using the sample (weighted) averages from the 1999 National Health Interview Survey and the 1999 National Nursing Home Survey. The definition of disability is based on activities of daily living. The remaining five columns present the point estimates of DFLE and their 95% confidence intervals using Sullivan’s method, without and with accounting for the sampling variability in the estimation of _nxm_x.

3.2 Assumptions and Statistical Properties of Sullivan’s Method

Sullivan’s method inherits three stationarity assumptions discussed in Section 2.2 because it relies on a period life table. The following proposition shows that the stationarity of age-specific disability prevalence is the only additional assumption required for Sullivan’s estimator to be unbiased and consistent for DFLE. The stationarity assumption about the disability prevalence is needed for the exact same reason as the other stationarity assumptions. It guarantees that cross-sectional data from different cohorts can be used to infer the age-specific disability prevalence of a hypothetical cohort.

Proposition 1

Suppose that three stationary assumptions of period life tables hold. In addition, suppose that the age-specific disability prevalence is constant over time, that is, π(x, y = π(x) for all y. Then, Sullivan’s method estimates DFLE without bias, that is, $E\left({\widehat{e}}_x^{\mathrm{DF}}\right)=e^{\mathrm{DF}}\left(x\right)$, and is also consistent, that is ${\widehat{e}}_x^{\mathrm{DF}}\stackrel{p}{\to }{e}_x^{\mathrm{DF}}$ for $e_x^{\mathrm{DF}}$ for all x ∈ 𝚨.

A proof is given in the Appendix. The result does not depend on the interval widths and, hence, applies to both abridged and unabridged period life tables. It also does not require researchers to know the exact age of survey respondents, so long as one knows the age interval to which they belong.

Next, we show that under the same stationarity assumptions, the standard variance estimator of (13) is consistent and approximately unbiased. Furthermore, these properties do not depend on the assumption of the constant disability prevalence in each interval, which is unlikely to hold when the age interval is wide, as in many applications of Sullivan’s method to abridged period life tables. Indeed, no additional assumption is required for the functional form of π(x).

Proposition 2

Under the four stationarity assumptions of Proposition 1, the variance of Sullivan’s estimator is given by

$${\sigma }_x^{\mathrm{DF}}=\frac{1}{l_x^2}\sum _{i\in \mathcal{𝒜}x}\frac{{}_{n_i}{p}_i{\left(1{-}_{n_i}{p}_i\right)}_{n_i}{L}_i^2}{{}_{n_i}{N}_i},$$

where ${}_{n_i}{P}_i={\int }_i^{i+n_i}\pi \left(t\right)l\left(t\right)dt∕{\int }_i^{i+n_i}l\left(t\right)dt$. The standard variance estimator of (13) is consistent and approximately unbiased for ${\sigma }_x^{\mathrm{DF}}$ for all x ∈ 𝚨.

A proof is given in the Appendix. As is the case of Proposition 1, the statistical validity of Sullivan’s method does not depend on the way the age is partitioned into intervals. The proof of Proposition 2 can also be used to derive the following alternative variance estimator that is both (exactly) unbiased and consistent:

$$\frac{1}{l_x^2}\sum _{i\in {\mathcal{𝒜}}_x}\frac{{}_{n_i}{L}_i^2\sum _{j=1}^{{}_{n_i}{N}_i}{\left(Y_{ij}\left(t_{ij}\right){-}_{n_i}{\widehat{\pi }}_i\right)}^2}{{}_{n_i}{N}_i{(}_{n_i}{N}_i-1)}.$$ (14)

3.3 Discussion

Proposition 1 shows that four stationarity assumptions are sufficient to establish the unbiasedness and consistency of Sullivan’s estimator, whereas Proposition 2 shows that, under these assumptions, the standard variance estimator is consistent and approximately unbiased. Because three out of four stationarity assumptions are needed for any analysis based on period life tables, the only additional assumption required is the stationarity of disability prevalence. This assumption may be reasonable once the stationarity of mortality rates is invoked if morbidity and mortality are closely related in a given population. However, it is also possible that mortality rates remain approximately stationary while disability rates depart from stationarity (see Sec. 5).

In his original article, Sullivan (1971) briefly touched on the requirement of mortality and disability stationarity, which corresponds to the assumptions in Propositions 1 and 2,

This expectation of disability [DFLE] can be interpreted as the number of years of disability a member of the life table cohort would experience if current agespecific rates of mortality and disability prevailed throughout the cohort’s lifetime (p. 351).

Sullivan did not, however, give a formal proof of this stationarity requirement. Our results establish both finite-sample and large-sample statistical properties of Sullivan’s method and, consequently, provide a formal justification of his claim.

Furthermore, Sullivan incorrectly suggested the use of the following estimator of disability prevalence, which was also used in his own application:

$${}_{n_x}{\widehat{\pi }}_x=\frac{1}{{}_{n_x}{N}_x}\sum _{j=1}^{{}_{n_x}{N}_x}\frac{W_{ij}\left(t_{ij}\right)}{365},$$ (15)

where W_ij(t_ij) is the self-reported number of days the jth respondent of the ith age interval spent in disability during the previous year. The proof of Proposition 1 in the Appendix implies that the equality, ${\int }_x^{x+n_x}\frac{W\left(t\right)}{365}l\left(t\right)dt={\int }_x^{x+n_x}\pi \left(t\right)l\left(t\right)dt$, must hold for each x ∈ 𝚨 in order for ${}_{n_x}{\widehat{\pi }}_x$ given in (15) to estimate DFLE without bias, where W(t) represents the population average days spent in disability during the past year at age t. The equality is unlikely to hold because π(t) measures the disability prevalence at age t, while W(t) corresponds to the disability prevalence over the one-year period. Fortunately, with the exception of few studies (e.g., Newman 1988), most applications of Sullivan’s method used the valid disability prevalence estimator of (12) rather than that of (15).

Since the publication of Sullivan (1971), the literature has generated controversies over Sullivan’s method. For example, Rogers et al. (1990) argued that Sullivan’s method underestimates DFLE because of bias in the estimation of disability prevalence. Yet, Mathers (1991) argued the observed bias actually results from a nonstationary population that has not reached equilibrium associated with the given transition rates. Another controversy has taken place over the question of whether Sullivan’s method allows for transitions from disabled status to healthy status (e.g., Barendregt et al. 1994, 1995; Van de Water et al. 1995; Laditka and Hayward 2003). However, the arguments presented in these studies are informal and are often based on simulation studies rather than theoretical results.

The lack of formal results has prompted some theoretical investigations about the required assumptions of Sullivan’s method. Nevertheless, these studies yielded conflicting results on what, if any, additional assumptions are required for Sullivan’s method. Some have argued that even with a stationary population, Sullivan’s method requires additional strong assumptions about the probability of the transitions between healthy and disabled status. For example, Newman (1988) argued that if the probability of transition from disabled state to healthy state (i.e., the “recovery” probability) is large, Sullivan’s method provides a consistent estimator of DFLE. Conversely, Palloni et al. (2005) maintained that Sullivan’s method assumes this recovery probability to be negligible and further argued that Sullivan’s method requires another assumption about the homogeneity in the mortality risks of the disabled and healthy populations.

In contrast, Propositions 1 and 2 imply that Sullivan’s method does not make any assumption about the hazard function and disability prevalence rate other than that they must be stationary. They also show that Sullivan’s method does not make any assumption regarding the homogeneity of mortality risk between the healthy and disabled populations. Note that the stationarity of transition probabilities implies that of prevalence rates, but the latter do not necessarily imply the former. For example, although perhaps rare, it is possible that more disabled people are dying at a certain age over (calendar) time but more people are transitioning into the disabled state over time such that the proportion of the disabled among those who are alive remains constant.

In addition to formal investigations, numerous simulation and empirical studies have been conducted to examine the performance of Sullivan’s method under various conditions. These studies in general confirm our theoretical results. For example, Mathers and Robine (1997) found that, under stationarity assumptions, Sullivan’s method provides a consistent estimator of DFLE. A number of studies also suggest that Sullivan’s method performs poorly when the assumption of stationarity is grossly violated, especially with respect to disability prevalence (e.g., Barendregt et al. 1994; Mathers and Robine 1997; Lievre et al. 2003).

3.4 Incorporating Additional Uncertainty About _nxm_x

As briefly mentioned in Section 2.2, the standard use of Sullivan’s method assumes stationarity and ignores the sampling variability about _nxm_x by simply setting n_xm_x = n_xM_x. Here, we discuss how Propositions 1 and 2 extend to the situation where _nxm_x is unknown but consistently estimated by _nxM_x. First, although ${\widehat{e}}_x^{\mathrm{DF}}$ is no longer an unbiased estimate of e^DF(x), the former is still consistent for the latter because l(x) can be consistently estimated by l_x and, hence, ${\int }_x^{x+n_x}l\left(t\right)dt$ can also be consistently estimated by n_xL_x.

Second, because the standard variance estimator of (13) ignores this additional source of uncertainty, it generally leads to underestimation of the true variance. In the Appendix we derive the large-sample variance of ${\widehat{e}}_x^{\mathrm{DF}}$, which incorporates the uncertainty about n_xm_x, and show that this variance can be consistently estimated. The sixth and seventh columns of Table 2 present the 95% confidence intervals based on the large-sample variance of (A.6). These confidence intervals are slightly wider than the confidence intervals based on the standard variance estimator of (13). For example, at age 50, allowing for additional variability about the estimation of n_xm_x, the 95% confidence widens by .04 years from (26.52, 26.64) to (26.50, 26.66).

4. ESTIMATION OF DFLE WITHOUT STATIONARITY ASSUMPTIONS

The assumption of stationary mortality and disability required for Sullivan’s method may be tenuous, especially in developed countries over the 20th century where mortality rates for the oldest ages have declined. Therefore, it is often of interest to estimate DFLE without stationarity assumptions. A popular approach in the literature has been the multistate life table method, which models the transition probabilities among the healthy state, disabled state, and death (e.g., Rogers et al. 1989b, 1990). This approach, however, requires a large-scale longitudinal disability survey, which is rarely available. Moreover, as discussed later, the multistate life table method makes assumptions about the transition probabilities that are often strong and untestable.

In this section we show that if DFLE is the quantity of interest, Sullivan’s method can be used to estimate DFLE without stationarity and other assumptions by using a cohort life table. The unbiased estimation of DFLE is also possible with consecutive cross-sectional disability surveys, which are often easier to obtain than longitudinal data.

4.1 Cohort Life Table

A cohort life table describes the mortality experience of a real cohort of individuals from birth of the first to death of the last member of the group (e.g., Chiang 1984). An important advantage of cohort life tables over period life tables is that the three assumptions of stationarity discussed in Section 2.2 are not invoked. A main purpose of cohort life tables is to calculate the life expectancy of a real birth cohort using cohort-specific birth and mortality rates for each age. Cohort life tables are created by first observing the midinterval population of the cohort born in year y, denoted by _nxP_x,y, and the total number of deaths in this cohort, denoted by n_xD_x,y, for each interval [x, x + n_x). Other quantities such as l_x,y and n_xL_x,y are defined analogously as done for period life tables. Calculation of cohort life expectancy also follows the methods identical to the ones described in Section 2.2.

There are two common ways to close a cohort life table. First, an ideal way is to observe the birth cohort until the last member dies. If a birth cohort cannot be observed until the last member dies, as is often the case, then the last age interval, [ω, ∞) is unbounded, and an assumption must be made about the hazard function within the last age interval. For example, Horiuchi and Coale (1982) derived an expression for e_ω by assuming that the proportion of the last age group relative to the overall population remains constant. Another commonly invoked assumption is the stationarity of mortality in the last age group, which will yield negligible error if the proportion of the birth cohort alive at age ω is sufficiently small (e.g., Wilmoth, Andreev, Jdanov, and Glei 2005).

4.2 Estimation of Cohort DFLE Using Sullivan’s Method

Next, we show that cohort DFLE can be estimated using Sullivan’s method. Specifically, Sullivan’s estimator of DFLE for the cohort born in year y is defined by

$${\widehat{e}}_{x,y}^{\mathrm{DF}}=\frac{1}{l_{x,y}}\sum _{i\in {\mathcal{𝒜}}_x}{\left(1{-}_{n_i}{\widehat{\pi }}_{i,y}\right)}_{n_i}{L}_{i,y},$$ (16)

where ${}_{n_i}{\widehat{\pi }}_{i,y}$ is the sample fraction of the disabled survey respondents within the age interval [i, i + n_i) for the cohort born in year y. Thus, ${}_{n_x}{\widehat{\pi }}_{x,y}$ can be computed for each x either from consecutive cross-sectional surveys, which follow the cohort born in year y, or from a longitudinal survey, which follows the same individuals of that cohort over time. Proposition 1 applies directly to Sullivan’s estimator of (16) except that stationarity assumptions are no longer necessary. The variance of this estimator can be calculated in the exact same way as before, and Proposition 2 also holds without stationarity assumptions. The use of Census data and vital statistics implies that sampling variability about n_xm_x can be ignored because a cohort life table directly summarizes the cohort of interest rather than a random sample from a hypothetical cohort. Thus, Sullivan’s method, if applied to a cohort life table and either consecutive cross-national disability surveys or longitudinal data, requires no assumption.

When consecutive cross-sectional surveys are available, it is possible to model π(x, y) as a function of y by assuming that the disability prevalence does not experience a sudden change of large magnitude across different cohorts. One may then estimate π(x, y), for example, using the generalized additive models (GAMs) (Hastie and Tibshirani 1990) or a random-walk model similar to the approach used by Lee and Carter (1992). Borrowing the information across cohorts in this way may increase the efficiency of estimation (see also Sec. 5).

So far, we have assumed that disability surveys cover all the age intervals. However, it is possible that the starting age of the oldest age group surveyed for disability prevalence, denoted by ω* ∈ 𝚨, is less than the starting age of the last age interval for the cohort life table, that is, ω* < ω. In this case, we can bound DFLE by considering the maximum and minimum values of the contribution of disability-free person-years within the last age intervals that are not covered by disability surveys. Because disability prevalence is bounded between 0 and 1, the bounds for disability-free person-years for these intervals are given by

$$0\le {\int }_{{\omega }^{\ast }+n_{{\omega }^{\ast }}}^{\infty }[1-\pi (t,y)]l(t,y)dt\le {}_{\infty }{L}_{{\omega }^{\ast }+n_{{\omega }^{\ast }},y}.$$ (17)

The preceding bounds do not impose any assumption, but may not be informative in practice.

In order to further narrow the bounds, we entertain a monotonicity assumption regarding the nature of disability for older ages. In particular, we may assume that the disability prevalence of a given birth cohort in the last interval of interest, [ω* + n_ω*, ∞), is greater than or equal to the average disability prevalence of the previous age interval, [ω*, ω* + n_ω*). Formally, we assume

$$\pi (t,y)\ge E\left[\pi (s,y)\right]=\frac{{\int }_{{\omega }^{\ast }}^{{\omega }^{\ast }+n_{{\omega }^{\ast }}}\pi (s,y)l(s,y)ds}{{\int }_{{\omega }^{\ast }}^{{\omega }^{\ast }+n_{{\omega }^{\ast }}}l(s,y)ds},$$ (18)

for all t ∈ [ω* + n_ω*, ∞). Then, the new bounds for disability free person-years in the last interval are given by

$$\begin{array}{cc}\hfill 0& \le {\int }_{{\omega }^{\ast }+n_{{\omega }^{\ast }}}^{\infty }[1-\pi (t,y)]l(t,y)dt\hfill \\ \hfill & \le {\left\{1-E\left[\pi (s,y)\right]\right\}}_{\infty }{L}_{{\omega }^{\ast }+n_{{\omega }^{\ast }},y},\hfill \end{array}$$ (19)

which are more informative than those in (17). Indeed, the new upper bound is almost always more informative. The proof of Proposition 1 in Appendix 1 shows that ${}_{n_{{\omega }^{\ast }}}{\widehat{\pi }}_{{\omega }^{\ast },y}$ is an unbiased and consistent estimator of E[π(s, y)], and, hence, the new upper bound can be estimated without bias and consistently.

Similarly, if disability surveys do not cover earlier age intervals, one can obtain the bounds of DFLE using the monotonicity assumption. Suppose that disability surveys start at age x and we wish to bound the total number of disability-free years for the preceding age interval, [x − n_x−, x), with some n_x− > 0, where n_x− indicates the length of the interval ending at age x. The bounds are given by

$$\begin{array}{cc}\hfill {\left\{1-E\left[\pi (s,y)\right]\right\}}_{n_{x-}}{L}_{x-n}& \le {\int }_{x-n_{x-}}^x[1-\pi (t,y)]l(t,y)dt\hfill \\ \hfill & {\le }_{n_{x-}}{L}_{x-n_{x-},y},\hfill \end{array}$$ (20)

where s ∈ [x, x + n_x) and the expectation is taken with respect to s and over the region, [x, x + n_x). We can use ${}_{n_x}{\widehat{\pi }}_{x,y}$ to estimate the lower bound without bias and consistently.

4.3 Confidence Intervals for the Bounds

When the bounds in (17) do not involve ${}_{n_x}{\widehat{\pi }}_{x,y}$, they can be estimated without sampling variability. This implies that the upper (lower) confidence bound for the bounds of the DFLE equals the usual upper (lower) confidence band separately obtained for the upper (lower) bound of the DFLE based on its estimated variance. The resulting confidence interval covers the true bounds with exact (finite sample) probability.

Under the monotonicity assumption, the estimated upper bound in (19) and the lower bound in (20) have sampling variability. Thus, if we estimate the confidence interval for the bounds of DFLE in the same way as before, the coverage probability of the resulting confidence intervals can be greater than its nominal level, yielding wider confidence intervals than necessary. Formally, let B^L and B^U be true lower and upper bounds of DFLE. Then, applying the Bonferroni inequality, we see that $\mathrm{Pr}([B^L,B^U]\subset [{\widehat{B}}_{\alpha }^L,{\widehat{B}}_{\alpha }^U])\ge \mathrm{Pr}(B^L\ge {\widehat{B}}_{\alpha }^L)+\mathrm{Pr}(B^U\le {\widehat{B}}_{\alpha }^U)-1=1-\alpha$, where ${\widehat{B}}_{\alpha }^U$ and ${\widehat{B}}_{\alpha }^L$ represent the estimated lower and upper (1 − α) confidence intervals and are found such that $\mathrm{Pr}(B^L\ge {\widehat{B}}_{\alpha }^L)=\mathrm{Pr}(B^U\le {\widehat{B}}_{\alpha }^U)=1-\alpha ∕2$.

It is possible to obtain the balanced confidence interval for the bounds with asymptotically exact coverage probability (e.g., Cheng and Small 2006). Beran (1988) provided such a method based on the bootstrap method. To apply the method, we choose ${\tilde{c}}_{\alpha }^L={\widehat{F}}_L^{-1}\left[{\widehat{F}}^{-1}(1-\alpha )\right]$ and ${\tilde{c}}_{\alpha }^U={\widehat{F}}_U^{-1}\left[{\widehat{F}}^{-1}(1-\alpha )\right]$, where ${\widehat{F}}_L$ and ${\widehat{F}}_U$ are the empirical distribution functions of ${\tilde{B}}^L-{\widehat{B}}^L$ and ${\widehat{B}}^U-{\tilde{B}}^U$, and $\widehat{F}$ is the empirical distribution functions of $\max \{{\widehat{F}}_L({\tilde{B}}^L-{\widehat{B}}^L),{\widehat{F}}_U({\widehat{B}}^U-{\tilde{B}}^U)\}$. The resulting confidence interval, $[{\widehat{B}}^L-{\tilde{c}}_{\alpha }^L,{\widehat{B}}^U+{\tilde{c}}_{\alpha }^U]$, asymptotically covers the true bounds by the fixed probability 1 − α. Moreover, these confidence intervals are balanced in a sense that they treat upper and lower bounds fairly; that is, $\mathrm{Pr}({\widehat{B}}^L-{\tilde{c}}_{\alpha }^L\le B^L)=\mathrm{Pr}({\widehat{B}}^U+{\tilde{c}}_{\alpha }^U\ge B^U)$ hold asymptotically. In contrast, the bootstrap confidence intervals proposed by Horowitz and Manski (2000) have asymptotically exact coverage probability but are not balanced.

4.4 Comparison With the Multistate Life Table Method

The multistate life table method is another popular approach to estimating the DFLE in the literature. Here, we compare this alternative method with the proposed extension of Sullivan’s method described previously. The multistate life table method models transitions among different states over age by assuming the continuous-time first-order Markov process (e.g., Land and Rogers 1982; Schoen 1988). Newman (1988) and Rogers et al. (1989b) were among the first to apply the multistate life table method to estimate DFLE. These authors modeled the transitions of individuals of a specific cohort among nonabsorbing states (e.g., disabled and disability-free) and an absorbing state (e.g., death). The assumption of the first-order Markov process implies that all individuals of the life table cohort who are found in a given state at the same age will have the same transition probabilities regardless of their previous paths. Some researchers have raised a concern that this assumption may be tenuous because past history of disability is likely to affect the probability of future disability (e.g., Nour and Suchindran 1983; Laditka and Wolf 1998).

The multistate life table method is similar to the period life table method discussed in Section 2.2, but is based on transition probabilities, τ^(ij)(x, x + t), which represent the probability that a person in state i at age x is in state j at exact age x + t for t > 0. The estimation of these transition probabilities requires the availability of longitudinal data. Ordinarily, researchers estimate transition probabilities using either sample fractions (e.g., Rogers et al. 1990; Crimmins, Hayward, and Saito 1994) or parametric models (e.g., Mathers and Robine 1997). Given τ^(ij)(x, x + t), one can recursively define the proportion of survivors at age x who are in state i, which we denote by $l_x^{\left(i\right)}$, as $l_{x+t}^{\left(i\right)}=l_x^{\left(i\right)}+{\sum }_{j\ne i}{\tau }^{\left(ji\right)}(x,x+t)l_x^{\left(j\right)}-{\sum }_{j\ne i}{\tau }^{\left(ij\right)}(x,x+t)l_x^{\left(i\right)}$ for t < 0.

Next, let ${}_{n_x}{L}_x^{\left(i\right)}$ represent the number of person-years spent in state i in a given age interval, [x, x + n_x), that is, formally, ${}_{n_x}{L}_x^{\left(i\right)}={\int }_x^{x+n_x}{l}^{\left(i\right)}\left(t\right)dt$. To estimate this quantity, researchers must make assumptions about the average number of personyears spent in each state for the interval given that a person starts in state j at age x and ends up in state k at age x + n_x for all j and k (e.g., Land and Rogers 1982; Schoen 1988). There are four common methods to estimate this quantity within a given age interval. They are based on the assumption that within each age interval, the survival functions are linear (e.g., Schoen 1975; Mathers 1991; Crimmins et al. 1994), quadratic (e.g., Schoen 1979), exponential (e.g., Krishnamoorthy 1979), or cubic (e.g., Schoen and Nelson 1974; Schoen and Urton 1979). Finally, the expected number of remaining years spent in state i can be computed by $e_x^{\left(i\right)}={\sum }_{j\in {\mathcal{𝒜}}_x}{}_{n_j}{L}_j^{\left(i\right)}∕l_x$, where l_x represents the survival function evaluated at age x as before.

In addition to these theoretical assumptions, typical applications of the multistate life table method invoke several other assumptions. First, the stationarity of age-specific mortality rates is often assumed because of limited observation of a birth cohort (e.g., Rogers et al. 1989b, 1990; Crimmins et al. 1994; Albarran, Ayuso, Guillen, and Monteverde 2005). While Mathers and Robine (1997) did not assume the stationarity of mortality rates, the lack of historical records forced the same researchers to make the stationarity assumption about disability rates.

Second, because of limited data availability, the vast majority of studies estimate transition probabilities from just a handful of panels from longitudinal disability surveys (e.g., Newman 1988; Rogers et al. 1989a, b, 1990; Crimmins et al. 1994; Albarran et al. 2005). Consequently, these studies assume the stationarity of transition probabilities beyond the period covered by longitudinal surveys. Even in the United States, few nationally representative and long-term longitudinal studies of disability exist, due to the inherent difficulty in following the same cohort of individuals during a long period of time. A notable exception is the National Long Term Care Survey, but its panel waves are five years apart. In contrast, nationally representative cross-sectional studies are conducted every year in the United States, including the National Health Interview Survey, the American Community Survey, the Medicare Current Beneficiary Survey, and the National Health and Nutrition Examination Survey. As shown in Section 5, Sullivan’s method can exploit the availability of these large-scale consecutive crosssectional disability surveys and estimate DFLE without stationarity and other assumptions.

Finally, Davis, Heathcote, and O’Neil (2001) described the estimation of cohort DFLE using the notation of multistate life tables. However, as the authors correctly pointed out, it is not possible to estimate transition probabilities from consecutive cross-sectional surveys. Instead, Davis et al. (2001) proposed a method that is similar to the one described in Section 4.2 by estimating the marginal probabilities of various states of health and death. Unlike the method proposed in this article, however, the approach of Davis et al. (2001) requires numerical integration and the calculation of standard errors is more complex.

In sum, the multistate life table method provides valuable information about transitions among different states and, hence, allows researchers to conduct a richer analysis of mortality and morbidity than Sullivan’s method. However, the method also requires a number of assumptions about transition probabilities and the functional form of hazard function, none of which is necessary for Sullivan’s method. Numerous studies investigate the performance of the multistate life table method when its required assumptions are violated (Hoem and Jensen 1982; Nour and Suchindran 1984; Liu, Liang, Jow-Ching, and Whitelaw 1997; Manton and Land 2000; Schoen 2001; Yi, Danan, and Land 2004). If DFLE is the quantity of interest, Sullivan’s method yields a valid estimate of DFLE with minimal assumptions and data requirement. If quantities other than DFLE are of interest, on the other hand, the multistate life table method may be useful.

5. AN EMPIRICAL ANALYSIS OF THE 1907 AND 1912 U.S. BIRTH COHORTS

In this section we apply our extension of Sullivan’s method to the 1907 and 1912 U.S. birth cohorts. We also compare cohort DFLE estimated from the 1907 birth cohort with period DFLE estimated from the 1991 to 2002 U.S. populations. Our analysis is based on the mortality rates of the 1907 and 1912 birth cohorts and the cross-sectional mortality rates from 1991 to 2002, all of which are obtained from the Human Mortality Database and are based on annual U.S. vital statistics. The data were downloaded on April 1, 2006, from http://www.mortality.org, the website maintained by the University of California, Berkeley, and the Max Planck Institute for Demographic Research.

We estimate the disability prevalence using consecutive cross-sectional surveys. In particular, we use the 1991 Medicare Current Beneficiary Survey (MCBS) [available through the Inter-university Consortium for Political and Social Research (ICPSR)], 1992 and 1993 MCBS Access to Care (available through the ICPSR), and 1994 to 2002 MCBS Cost and Use (available through the U.S. Department of Health and Human Services). The MCBS is a continuous, multipurpose survey of a representative national sample of the Medicare population, which includes both the noninstutitionalized and the institutionalized populations, and is conducted by the Centers for Medicare and Medicaid Services. Medicare is the largest health insurance program in the United States, which covered over 95% of the U.S. population age 65 and older between the years 1991 and 2002 (DeNavas-Walt, Proctor, and Hill Lee 2005). Thus, the use of this survey gives us a complete picture of disability status for the overall U.S. population for each year. We use the MCBS rather than the NHIS and NNHS discussed in Section 3.1 because while the NHIS is administered annually from 1991 to 2002, the NNHS was only administered in 1995, 1997, and 1999 during the period of interest.

As in Section 3.1, a respondent was considered disabled if he or she reported at least one activity of daily living limitation. In all the analyses presented in this section, the survey weights are incorporated so that respondents are appropriately weighted according to their population size. We estimate disability prevalence for the 1907 (1912) birth cohort from age 81 (76) to 90 (90) using the first MCBS survey in 1991 to the 2002 MCBS. We estimate DFLE for ages 81 (76) to 83 (78) using the monotonicity assumption and estimate the bounds shown in (20). For the sake of a comparison between the 1907 and 1912 birth cohorts, we close both cohort life tables by assuming a stationary population at age ω = 90 and beyond. We use only the first 7 years of mortality and disability (1991–1997) for the 1907 birth cohort, while all 12 years of the data are used for the 1912 birth cohort.

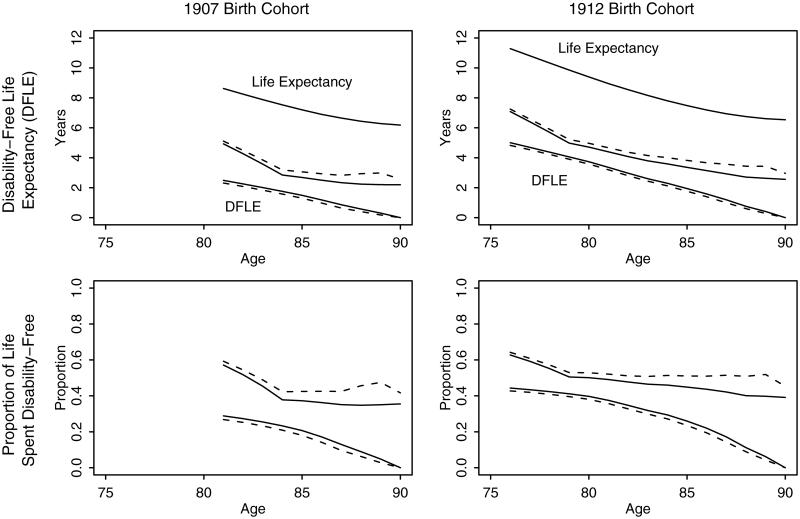
The upper left (right) panel of Figure 1 shows the estimated bounds of DFLE for the 1907 (1912) birth cohort along with life expectancy. Based on the mortality experience of the 1907 birth cohort, for example, individuals who are alive at age 85 lived, on average, 7.20 years, and they spent between 1.30 and 3.06 years without disability. The lower left (right) panel of the figure shows another quantity of interest, the estimated bounds of the proportion of remaining life spent disability-free, ${\widehat{e}}_x^{\mathrm{DF}}∕e_x$ for the 1907 (1912) birth cohort. For example, at age 85, members of the 1907 birth cohort are expected to spend between 18.0% and 42.5% of their remaining life without disability. The estimated proportion decreases gradually with age. For both DFLE and the proportion, the 95% balanced confidence intervals are estimated using the bootstrap procedure alluded to in Section 4.3 with 10,000 replications.

Figure 1.

Estimated bounds of disability-free life expectancy (DFLE) and proportion of life spent disability-free for the 1907 and 1912 U.S. birth cohorts. The upper left (right) panel shows the estimated bounds of DFLE along with life expectancy for the 1907 (1912) birth cohort from age 81 (76) to 90 (90). The lower panels show the estimated bounds of the proportion of remaining life spent disability-free. The 95% confidence intervals are shown as dashed lines. For the 1907 (1912) birth cohort, DFLE and proportion of remaining life spent disability-free are calculated using the monotonicity assumption for ages from 81 (76) to 83 (78).

The comparison of the two birth cohorts shows that while life expectancy increased slightly over the two birth cohorts, the estimated proportion of remaining life spent disability-free does not show clear differences between the two cohorts due to the wide confidence intervals. For example, life expectancy at age 85 increases by .28 years between the two birth cohorts. Yet, the 95% balanced confidence intervals of DFLE overlap significantly, that is, (1.30, 3.06) for the 1907 birth cohort and (1.76, 3.82) for the 1912 birth cohort. Consequently, the 95% balanced confidence interval of the proportion of remaining life spent disability-free for the 1907 birth cohort (.18, .42) overlaps with that of the 1912 birth cohort (.24, .51). The wide confidence intervals are in part due to the fact that the mortality and disability data are available only up to 90 years of age for the 1912 birth cohort (i.e., year 2002). If the additional years of data become available in the future, the bounds may become substantially narrower and exhibit statistically significant differences between the two cohorts.

As described in Section 4.2, we also use a model-based adjustment and estimate π(x,y) as a smooth function of y. In particular, we modeled π(x,y) using the GAM with binomial family and logistic link. The estimated DFLE based on GAM is between .05 (.10) and .30 (.29) years smaller for the 1907 (1912) birth cohort than those based on the observed disability prevalence. The 95% balanced confidence intervals of DFLE are also slightly narrower for both birth cohorts using GAM. For example, at age 93 for the 1907 birth cohorts, the confidence interval for DFLE was (.18, 1.62) using sample weighted averages and (.19, 1.51) using GAM.

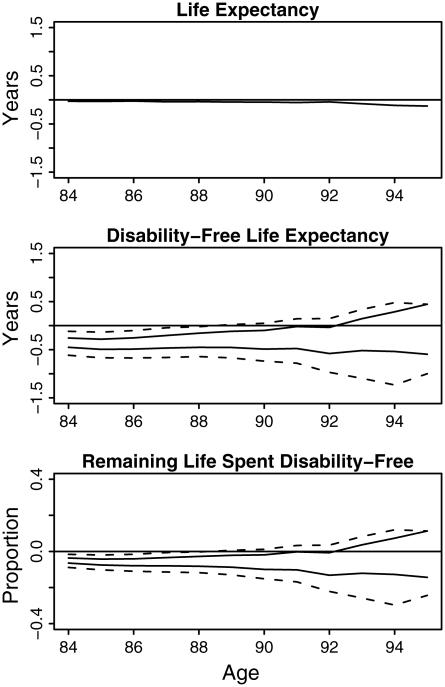
For the purpose of comparison, we also estimate life expectancy, DFLE, and the proportion of remaining life spent disability-free for the 1991 hypothetical period cohort using the standard Sullivan method and compare the results with those of the 1907 birth cohort. In this case, we use the full mortality and disability information available, 1991 to 2002, corresponding to ages 84 to 95. We begin our analysis at age 84, the age of the 1907 birth cohort in 1991, and examine the differences between the period and cohort estimates for subsequent ages. The upper panel of Figure 2 plots the difference between the 1991 period and 1907 birth cohort life expectancy, that is, 1991 period estimate minus 1907 cohort estimate. Age-specific life expectancy is nearly identical for the birth cohort than for the hypothetical period cohort from age 84 to 95, which indicates virtually stationary age-specific mortality rates.

Figure 2.

Comparison between the 1991 period and 1907 U.S. birth cohorts. The upper, middle, and lower panels compare the difference in life expectancy, DFLE, and the proportion or remaining life spent disability-free (i.e., 1991 period minus 1907 birth cohort). The estimated bounds of the differences are shown. The 95% balanced confidence intervals are calculated from the bootstrap method and shown as dashed lines.

The middle panel plots the estimated bounds for the same differences for DFLE. The 1907 birth cohort DFLE is significantly higher than the 1991 period cohort DFLE from age 84 (the age of the 1907 birth cohort in 1991) to 88 as seen from the fact that the 95% confidence intervals for the bounds of the differences do not contain 0 in this range. Given the near stationarity of mortality rates, this nonstationarity of DFLE is possible only with the nonstationarity of age-specific disability rates. The lower panel plot shows that for the proportion of remaining life spent disability-free is also significantly higher for the birth cohort than the hypothetical period cohort from age 84 to 88. The evidence shows that while mortality rates remain approximately stationary, disability rates may have declined during this time period.

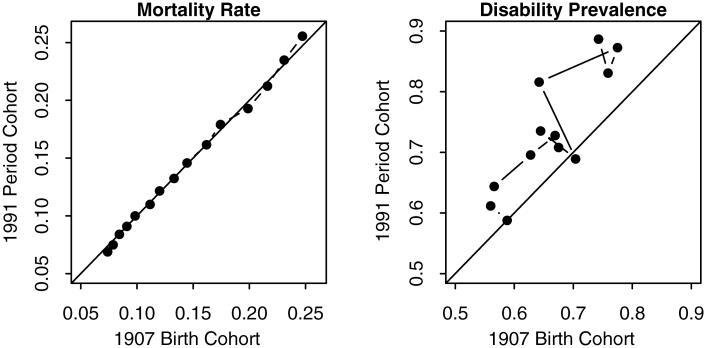
Indeed, as shown in Figure 3, mortality rates remained nearly stationary while disability rates did not between the 1991 period and 1907 birth cohorts. The upper panel plots 1991 period and 1907 birth cohort mortality rates for ages 81 to 95. Mortality rates for this age range are approximately stationary as shown by the equality of period and cohort rates. As shown in the lower panel of Figure 3, however, age-specific disability rates are nonstationary and decrease over time. The disability rate for each age of the hypothetical cohort in the 1991 period is uniformly greater than the corresponding disability rate experienced by the birth cohort of 1907.

Figure 3.

Comparison of the 1991 period cohort with the 1907 birth cohort. The left panel compares the 1991 period cohort mortality rate (vertical axis) with the 1907 birth cohort mortality rate (horizontal axis) from age 81 to 95. The right panel compares the 1991 period disability prevalence (vertical axis) with the 1907 birth cohort disability prevalence (horizontal axis) from age 84 to 95. The 45° solid line represents equality.

6. CONCLUDING REMARKS

Robust estimation of DFLE is vital to testing the competing theories of morbidity and mortality. Over the last 30 years, Sullivan’s method has been the most widely used method for estimating DFLE. Academic researchers and government officials use this method because of the relative ease of obtaining mortality data from a period life table and disability data from a cross-sectional survey. Yet, the statistical properties of Sullivan’s method have not been understood. In this article we establish a statistical foundation of Sullivan’s method by proving that, under stationarity assumptions, Sullivan’s estimator is unbiased and consistent and the standard variance estimator is also consistent and approximately unbiased. Our results resolve methodological debates in the literature, which generally concluded that Sullivan’s method requires additional assumptions.

Finally, we show how to extend Sullivan’s method to cohort life tables so that the valid estimation of DFLE is possible without stationarity assumptions. When compared with the multistate life table method, which is popular among applied researchers, this extension of Sullivan’s method avoids the strong assumptions about transition probabilities and can be applied even with consecutive cross-sectional disability surveys, which are often easier to obtain than a longitudinal survey. While the multistate life table method allows for a richer analysis of morbidity and mortality, if DFLE is the quantity of interest, Sullivan’s method is easier to implement and can estimate DFLE with fewer assumptions and less stringent data requirement. Our empirical analysis of the 1907 and 1912 U.S. birth cohorts suggests that while mortality rates remain approximately stationary, disability rates may have declined during this time period.

APPENDIX: PROOFS

A.1. PROOF OF PROPOSITION 1

Under the assumptions, DFLE may be expressed as

$$e^{\mathrm{DF}}\left(x\right)=\frac{1}{l\left(x\right)}\sum _{i\in {\mathcal{𝒜}}_x}\left[{}_{n_i}{L}_i-{\int }_i^{i+n_i}\pi \left(t\right)l\left(t\right)dt\right],$$ (A.1)

where the equality follows from the fact that, under the stationarity assumptions, (10) holds for all x ∈ 𝚨. Moreover, under the stationarity assumptions, the age distribution is given by (4) and is proportional to the probability that an individual of exact age x being sampled. Therefore, for any age interval, [x, x + n_x), if t ∈ [x, x + n_x), then we have

$$E{(}_{n_x}{\widehat{\pi }}_x)=E\left[\pi \left(t\right)\right]=\frac{{\int }_x^{x+n_x}\pi \left(t\right)l\left(t\right)dt}{{\int }_x^{x+n_x}l\left(t\right)dt},$$ (A.2)

where the first equality follows from (12) and E[Y(t)|t] = π(t). Equally (A.2) implies ${}_{n_x}{L}_{x}E{(}_{n_x}{\widehat{\pi }}_x)={\int }_x^{x+n_x}\pi \left(t\right)l\left(t\right)dt$ for any age interval, [x, x + n_x). Together with (A.1), we have the desired result:

$$E\left({\widehat{e}}_x^{DF}\right)=\frac{1}{l_x}\sum _{i\in {\mathcal{𝒜}}_x}{\left[1-E\left({}_{n_i}{\widehat{\pi }}_i\right)\right]}_{n_i}{L}_i=e^{\mathrm{DF}}\left(x\right).$$ (A.3)

To prove the consistency, observe that the variance of Y(t) is bounded from above by 1 because Y(t) is binary. Therefore, as n_xN_x goes to ∞, the variance of ${}_{n_x}{\widehat{\pi }}_x$ goes to 0, which together with its unbiasedness implies that ${}_{n_x}{\widehat{\pi }}_x$ converges in probability to E[π(t) for any age [x, x + n_x). Thus, Sullivan’s estimator is consistent for $e_x^{\mathrm{DF}}$.

A.2. PROOF OF PROPOSITION 2

We first derive the variance of Sullivan’s estimator. Given any age interval, [x, x + n_x), we can write the variance of Y(t) as follows:

$$\mathrm{var}\left[Y\left(t\right)\right]=E\left[Y\left(t\right)\right]-{\left\{E\left[Y\left(t\right)\right]\right\}}^2{=}_{n_x}{p}_x\left(1{-}_{n_x}{p}_x\right),$$ (A.4)

where the first equality follows from the fact that Y(t) is binary and the second equality follows from E[Y(t)] = E[π(t)], the expression of which is given in (A.2). Together with the definition of Sullivan’s estimator in (11), this implies that the variance equals ${\sigma }_x^{\mathrm{DF}}$.

To prove the consistency of ${\widehat{\sigma }}_x^{\mathrm{DF}}$, note that the proof of Proposition 1 shows that, under the stationarity assumptions, for any age interval, [x, x + n_x), _nxp_x can be estimated by ${}_{n_x}{\widehat{\pi }}_x$ consistently. Thus, it follows that ${\widehat{\sigma }}_x^{\mathrm{DF}}$ in (13) is a consistent estimator of ${\sigma }_x^{\mathrm{DF}}$. To prove the approximate unbiasedness of ${\widehat{\sigma }}_x^{\mathrm{DF}}$, we note that

$$E\left[{}_{n_i}{\widehat{\pi }}_i\left({}_{n_i}{\widehat{\pi }}_i\right)\right]=E\left[\frac{1}{{}_{n_i}{N}_i}\sum _{j=1}^{{}_{n_i}{N}_i}{\left(Y_{ij}\left(t_{ij}\right){-}_{n_i}{\widehat{\pi }}_i\right)}^2\right]$$ (A.5)

for any age interval, [i, i + n_i), where the equality follows from the fact that Y_ij(t_ij) is binary. Then, the right side of this equation approximates n_xP_x(1−n_xP_x) = var[Y(t)] if and only if n_iN_i ≈ n_iN_i − 1.

A.3. LARGE–SAMPLE VARIANCE OF ${\widehat{e}}_x^{\mathrm{DF}}$ WHEN _nxm_x IS ESTIMATED

Because _nxL_x = _nxa_xl_x + (n_x − _nxa_x)l_x+nx, we rewrite ${\widehat{e}}_x^{\mathrm{DF}}$ as

$${\widehat{e}}_x^{\mathrm{DF}}={\left(1{-}_{n_x}{\widehat{\pi }}_x\right)}_{n_x}{a}_x+{\left(1{-}_{\infty }{\widehat{\pi }}_{\omega }\right)}_{\infty }{a}_{\omega }{\widehat{p}}_{x\omega }+\sum _{i\in {\mathcal{𝒜}}_{x+n_x}\backslash \left\{\omega \right\}}\left(1{-}_{n_i}{\widehat{\pi }}_i\right)c_i{\widehat{p}}_{xi},$$

where c_i = (n_i− − _ni−a_i−) + _nia_i is a constant and i− indexes the age interval ending at age i and _njp̂_xi = l_i/l_x. Recall that p̂_xi = ∏_{j∈𝚨x \{i} nj}p̂_j, where _njp̂_j = 1 − _njq̂_j. Because _nxM_x is a consistent estimate of _nxM_x is a consistent estimate of _nxm_x, p̂_xi also converges to p_xi in probability. Then, following Chiang (1984, chap. 4), we expand the variance of $e_x^{\mathrm{DF}}$ around $E\left({}_{n_x}{\widehat{\pi }}_x\right)$ and p_xi, which is true value of p̂_xi, using Taylor’s theorem to obtain the large-sample variance:

$$\begin{array}{cc}\hfill \mathrm{Var}& \left({\widehat{e}}_x^{\mathrm{DF}}\right)\hfill \\ \hfill & {=}_{n_x}{a}_x^2\mathrm{Var}{(}_{n_x}{\widehat{\pi }}_x)\hfill \\ \hfill & +\mathrm{Var}\left({\left(1{-}_{\infty }{\widehat{\pi }}_{\omega }\right)}_{\infty }{a}_{\omega }{\widehat{p}}_{x\omega }+\sum _{i\in {\mathcal{𝒜}}_{x+n_x}\backslash \left\{\omega \right\}}\left(1{-}_{n_i}{\widehat{\pi }}_i\right)c_i{\widehat{p}}_{xi}\right)\hfill \\ \hfill & {\approx }_{n_x}{a}_x^2\mathrm{Var}{(}_{n_x}{\widehat{\pi }}_x)\hfill \\ \hfill & +\sum _{i\in {\mathcal{𝒜}}_x\backslash \left\{\omega \right\}}{p}_{xi}^2{\left[\left\{1-E\left({}_{n_i}{\widehat{\pi }}_{i+n_i}\right)\right\}\left(n_i{-}_{n_i}{a}_i\right)+e_{i+n_i}^{\mathrm{DF}}\right]}^2\mathrm{Var}\left({}_{n_i}{\widehat{p}}_i\right)\hfill \\ \hfill & +{{(}_{\infty }{a}_{\omega }{p}_{x\omega })}^2\mathrm{var}{(}_{\infty }{\widehat{\pi }}_{\omega })\hfill \\ \hfill & +\sum _{i\in {\mathcal{𝒜}}_{x+n_x}\backslash \left\{\omega \right\}}{\left(c_i{p}_{xi}\right)}^2\mathrm{Var}\left({}_{n_i}{\widehat{\pi }}_i\right),\hfill \end{array}$$ (A.6)

where

$$\mathrm{Var}\left({}_{n_i}{\widehat{p}}_i\right)=\frac{{\left[E{(}_{n_i}{\widehat{q}}_i)\right]}^2[1-E{(}_{n_i}{\widehat{q}}_i)]}{{}_{n_i}{D}_i}$$

and

$$\mathrm{Var}\left({}_{n_i}{\widehat{\pi }}_i\right)=\frac{E{(}_{n_i}{\widehat{\pi }}_i)[1-E{(}_{n_i}{\widehat{\pi }}_i)]}{{}_{n_i}{N}_i^2}.$$

Note that the independence of ${}_{n_x}{\widehat{\pi }}_x$ across age groups and between ${}_{n_x}{\widehat{\pi }}_x$ and p̂_x′ for any x ≠ x́ as well as the independence of p̂_x across age groups are assumed. (These independence assumptions are reasonable if the cross-sectional disability survey is conducted separately from the construction of the period life table, as is often the case.) Finally, the large-sample variance in (A.6) can be consistently estimated by replacing $E{(}_{n_x}{\widehat{\pi }}_x)$ and p_xi with their consistent estimates, that is, ${}_{n_x}{\widehat{\pi }}_x$ and p̂_xi, respectively.