Abstract
Gjedde–Patlak graphical analysis (GPGA) has commonly been used to quantify the net accumulations (Kin) of radioligands that bind or are taken up irreversibly. We suggest an alternative approach (MLAIR: multiple linear analysis for irreversible radiotracers) for the quantification of these types of tracers. Two multiple linear regression model equations were derived from differential equations of the two-tissue compartment model with irreversible binding. Multiple linear analysis for irreversible radiotracer 1 has a desirable feature for ordinary least square estimations because only the dependent variable CT(t) is noisy. Multiple linear analysis for irreversible radiotracer 2 provides Kin from direct estimates of the coefficients of independent variables without the mediation of a division operation. During computer simulations, MLAIR1 provided less biased Kin estimates than the other linear methods, but showed a high uncertainty level for noisy data, whereas MLAIR2 increased the robustness of estimation in terms of variability, but at the expense of increased bias. For real [11C]MeNTI positron emission tomography data, both methods showed good correlations, with parameters estimated using the standard nonlinear least squares method. Multiple linear analysis for irreversible radiotracer 2 parametric images showed remarkable image quality as compared with GPGA images. It also showed markedly improved statistical power for voxelwise comparisons than GPGA. The two MLAIR approaches examined were found to have several advantages over the conventional GPGA method.
Keywords: neuroreceptor imaging, parametric images, positron emission tomography, tracer kinetic modeling
Introduction
Parameter estimations using nonlinear least square (NLS) methods are not suitable for generating images of kinetic parameters (parametric images) from dynamic positron emission tomography (PET) data, mainly because of the high level of noise in the time–activity curves of individual PET voxels. The extensive computation time required for iterative parameter estimation is another important reason for this unsuitability. Therefore, several graphical methods have been devised to estimate kinetic parameters based on linear regression analysis, and have been used to generate parametric images, because they are computationally simple and independent of any particular model structure (Gjedde, 1981, 1982; Patlak et al, 1983; Logan et al, 1990, 1996; Yokoi et al, 1993).
However, these graphical approaches may provide biased estimates if there are regional differences between the times required to reach tissue–plasma equilibrium of radiotracer concentrations and/or noise levels in tissue time–activity curves are high (Carson, 1993; Slifstein and Laruelle, 2000). Although several methods have been proposed to reduce such bias and improve the accuracy of parameter estimations for radiotracers with reversible uptake or binding (Carson, 1993; Ichise et al, 2002, 2003; Logan et al, 2001; Varga and Szabo, 2002), little has been done to quantify kinetic parameters of irreversible tracers (Blomqvist, 1984).
In this study, therefore, we focused on the multiple linear analysis method to effectively calculate the net accumulation rate (Kin) of radiotracer with an irreversible specific binding and to generate its parametric images. Two different formulas (MLAIR: multiple linear analysis for irreversible radiotracers) were used for this purpose, which were derived from the differential equations for the irreversible two-tissue compartment model. The statistical properties of these methods were explored by Monte Carlo simulation. These methods were applied to the dynamic PET data of N1′-([11C]methyl)naltrindole (MeNTI) to assess the usefulness of these methods for volume of interest (VOI) analysis and parametric image generation. Their plausibilities for voxelwise statistical analysis based on Kin parametric images were also investigated. The properties of these methods were compared with those of the NLS method and Gjedde–Patlak graphical analysis (GPGA), the latter of which is most commonly used to estimate Kin for irreversible tracers. Finally, the results of the preliminary applications of these methods to [18F] flurodeoxyglucose ([18F]FDG) are presented.
Materials and methods
Theory
Compartment model
The three-compartment model (two-tissue compartment model) for irreversibly binding radiotracers was assumed. Each compartment represents the concentration of the unmetabolized radiotracer in plasma (Ca, μCi/mL), free or nonspecifically bound radiotracer (Cf, μCi/g), and specifically bound radiotracer (Cb, μCi/g), respectively. Differential equations for two-tissue compartments (Cf and Cb) with irreversible binding can be described by
| (1) |
| (2) |
where the rate constants K1, k2, and k3 are defined as those of delivery (mL/min/g), washout (per minute), and forward uptake (i.e., phosphorylation of 18F-flurodeoxyglucose, forward receptor–ligand reaction for radioligands; per minute). The total tracer concentration in tissue VOI or region of interest can be obtained using the following equation:
| (3) |
where Va is the blood volume fraction in tissue (mL/g). It should be noted that the factor Ca(t) in the above equation stands for radiotracer concentration in whole blood, although Ca(t) in Equation (1) is the concentration of unmetabolized radiotracer in plasma. If the metabolite-corrected input function is used to determine the blood volume fraction, estimation errors associated with this simplification should be considered.
Gjedde–Patlak graphical analysis
Although the graphical methods are independent of particular model structures, if a model structure describes the transfer of a tracer, the slope of the linear equation may be related to combinations of model parameters (Logan, 2000). Gjedde–Patlak graphical analysis is the most widely used conventional graphical method for irreversibly binding tracers (Gjedde, 1981, 1982; Patlak et al, 1983). In GPGA, the Equations (1) and (2) are rearranged as to yield:
| (4) |
Assuming that Cf(t) and Ca(t) reach equilibrium after some time (equilibrium time t*) following tracer injection, the second term on the right of the above equation is constant and Kin can be estimated from the slope of a straight line. One disadvantage of this method is that the time range for the line fitting must be determined to estimate Kin. This is especially undesirable when generating Kin parametric images for radiotracers, which have regional differences in terms of the time required to reach equilibrium.
Multiple linear analysis for irreversible radiotracer 1
Changes in tissue concentration, dCT(t)/dt, are given by adding (1), (2), and VadCa(t)/dt.
| (5) |
By rearranging Equation (5)
| (6) |
Substituting Equation (6) into Equation (3) and differentiating yields
| (7) |
Therefore, Equation (2) can be written as Equation (8) by substituting Equation (6) and (7) into Equation (2)
| (8) |
By integrating the above equation twice, the following linear equation can be obtained (MLAIR1):
| (9) |
where the macro parameters P1~P4 are given by
| (10) |
This equation is an extended version of the linear equation developed by Blomqvist (1984). The incorporation of a vascular volume term in the above equation is an additional feature. The generalized version of this equation, which is applicable to both reversible and irreversible tracers, can be found in the literature (Evans, 1987; Feng et al, 1996; Gjedde, 1995). The series of Equation (9) for each sampling time point (t1, t2,…, tn) can be arranged into the following matrix:
| (11) |
where y is a vector for the dependent variable, X the matrix for the independent variables, θ a vector for the parameters to be estimated, and ε is the equation error term.
| (12) |
| (13) |
| (14) |
The estimate of θ based on the linear least squares criterion is given by the following equation:
| (15) |
The net accumulation rate Kin can then be acquired using the following equation:
| (16) |
The MLAIR1 Equation (9) has a desirable feature of ordinary least squares estimations because only the dependent variable CT(t) is noisy and the correlation of the noise in the independent variables is minimal.
Multiple linear analysis for irreversible radiotracer 2
Multiple linear analysis for irreversible radiotracer 1 would be a useful alternative to the GPGA because the determination of a linear interval is not necessary. However, the error propagation associated with the division calculation on the macro parameters (Equation (16)), to obtain Kin, is a possible limitation of MLAIR1 for the voxelwise estimations of Kin for the generation of parametric images because of the high noise level in the individual time–activity curves of each voxel. Therefore, we also used a formula in which Kin could be directly estimated from the coefficient of an independent variable. By dividing both sides of Equation (9) by k2 + k3 and rearranging the equation, we obtained the following equation, which allows direct estimations of Kin from a macro parameter without unstable division calculation.
| (17) |
where the macro parameters are given by the following equations and can also be obtained by linear least squares estimation (MLAIR2).
| (18) |
A general version of this formula for reversible tracers has been suggested, as outlined in an abstract by Blomqvist (1987), and derivations of similar equations have been published in book form (equation 7.221 in Gjedde, 2003). In the cases of MLAIR1 and MLAIR2, it is not necessary to determine the period of linear fitting (as is required for GPGA), because the entire dataset is used for parameter estimation. Although MLAIR2 has the desirable feature that the division calculation is not required to obtain Kin, it is questionable how accurate and precise Kin estimation by this method is, because one of the independent variables, CT(t), may be noisy. This should be avoided, if possible, because estimation by linear regression analysis requires that all independent variables be nonnoisy or nonrandom to obtain unbiased estimates. Therefore, considering the pros and cons of these methods, critical assessments of their statistical properties in the Kin estimation should be performed to understand the possible sources of erroneous results produced using these methods and misinterpretation of them, and to determine their possible application fields. The following computer simulations and applications to real PET data were performed for these reasons.
Computer Simulations
Noiseless total tissue time–activity curves (Equation (3)) were generated using the following analytic solution of the irreversible two-tissue compartment model.
| (19) |
A metabolite-corrected plasma input function obtained from a human [11C]MeNTI PET study involving intermittent arterial blood sampling for 90 mins was used. K1, k2, and Va were fixed at 0.24 mL/min/g, 0.028 per minute, and 5%, respectively. Binding parameter k3 was varied between 0.5 and 1.5 times the value of k2 (Kin = 0.08 to 0.144 mL/min/g). Ratios of k3/k2 above 1.5 were not considered because the net uptake of radiotracer does not increase linearly with k3, the parameter of interest, and is proportional to K1 (Koeppe et al, 1994). Gaussian noise with zero mean and following variance was added to the ith frame of CT in order to simulate noisy measurements (Feng et al, 1993; Logan et al, 2001; Lee et al, 2005).
| (20) |
where CT(ti) and Δti are the radioactivity concentration (μCi/g) and the duration (second) of the ith frame, respectively. The scaling factor α that determines the noise level varied from 0 (noiseless) to 1.0. For all possible pairs of k3 and α, 10,000 realizations of noisy CT were produced. Kin values were then estimated using NLS, GPGA, MLAIR1, and MLAIR2, respectively, and coefficients of variation (CV), biases and errors of estimations were calculated. Coefficients of variation, bias, and error were defined as follows:
| (21) |
| (22) |
| (23) |
where K̂in is an estimated parameter, Kin is a true value, K̄in is the mean of estimates, and N is the number of realizations. The initial values for unknown variables in NLS were set equal to the true values of rate constants to provide the most favorable condition for the NLS estimation. Nonnegative constraints on estimates were also used for the NLS estimation. In the high noise condition, the division performed to obtain Kin in NLS and MLAIR1 sometimes resulted in the physiologically irrelevant estimate (i.e., a negative or excessive value). Therefore, negative results were set to zero and values higher than 0.5 mL/min/g were set to 0.5 to reduce the adverse effects of values that deviated excessively from the relevant range when assessing general statistical properties.
Application to [11C]MeNTI Positron Emission Tomography Data
Positron emission tomography data acquisition and volume of interest analysis
To show the feasibility of the proposed method, 90-min dynamic [11C]MeNTI PET data were acquired from 15 extensively alcohol-dependent subjects (before and after naltrexone, a nonselective opioid receptor antagonist, treatment) and 8 healthy volunteers, as described in a previous study (Weerts et al, 2008), were retrospectively analyzed. [11C]MeNTI is a specific δ-opioid receptor agonist developed for PET imaging (Lever et al, 1992; Madar et al, 1996), and it has been shown that the irreversible two-tissue compartment model is suitable for the kinetic modeling analysis of this radioligand (Smith et al, 1999). Arterial blood concentrations corrected for labeled metabolites were used as the input function for kinetic analysis (Smith et al, 1999; Weerts et al, 2008).
Regional time–activity curves for kinetic analysis were obtained using an automated VOI method (Lee et al, 2004; Lee and Lee, 2005). Static PET images were composed by summing all frames in dynamic data and were spatially normalized to the standard template of [11C]MeNTI PET (Weerts et al, 2008) using SPM2 (Statistical Parametric Mapping). To remove confounding effects caused by mismatched anatomical variations within subjects, PET data of same subjects were coregistered before spatial normalization and the spatial normalization parameters obtained from averaged coregistered images were applied identically. By applying the transformation parameters obtained using static images, all dynamic frames were also spatially normalized into standard brain space. Predefined probabilistic VOIs on brain regions of interest with high or intermediate δ-opioid receptor density (basal ganglia, cingulate cortex, inferior and middle frontal gyri, superior temporal gyrus, angular gyrus, amygdala, hippocampus) and reference regions with low receptor density (thalamus, cerebellum) were applied to the dynamic images to extract regional time–activity curves.
These curves were then analyzed using NLS, GPGA, MLAIR1, and MLAIR2 to estimate Kin values. Whole-frame data were used for NLS and MLAIR (MLAIR1 and MLAIR2), but only the data obtained after t* was used for GPGA. For GPGA, various t* values (10, 20, and 30 mins) were tried, and correlation analyses were performed to explore the relationships between these Kin values estimated using different methods. Regional distribution of Kin values estimated using each method was also compared.
Voxel-based statistical analysis
Parametric images of Kin were generated by the voxelwise applications of GPGA and MLAIR to dynamic PET data. The parametric images obtained were spatially normalized using the transformation parameters obtained above. Only Kin images by MLAIR2 were used for voxel-based statistical analysis, because MLAIR1 was not suitable for voxelwise computations, as shown in the next section. Voxelwise mean and percent CV of Kin parametric images of eight healthy volunteers were compared in terms of the image quality and magnitude of variance.
The plausibilities of voxelwise statistical analysis of Kin parametric images using GPGA and MLAIR2 were also compared in terms of their compatibility with the established results and statistical power to detect the changes of Kin. Spatially normalized parametric images were smoothed using an isotropic 3D Gaussian filter with a 16mm full width at half-maximum. To remove the effects of global differences in Kin among individuals, each voxel value of parametric images was normalized versus regional mean value in the thalamus or cerebellum, which showed the lowest specific biding of [11C]MeNTI PET (Smith et al, 1999; Weerts et al, 2008). Changes in regional Kin after naltrexone treatment in alcohol-dependent subjects were then assessed by voxelwise paired t-testing and compared with published results based on VOI analysis (Weerts et al, 2008).
Preliminary Application to [18F]FDG Positron Emission Tomography Data
To show the feasibility of the proposed method for [18F]FDG, the most commonly used 18F-labed PET tracer, parametric images of Kin were generated from the dynamic brain PET data of a 22-year-old male volunteer acquired during our previous study (Kim et al, 2000).
Results
Computer Simulation
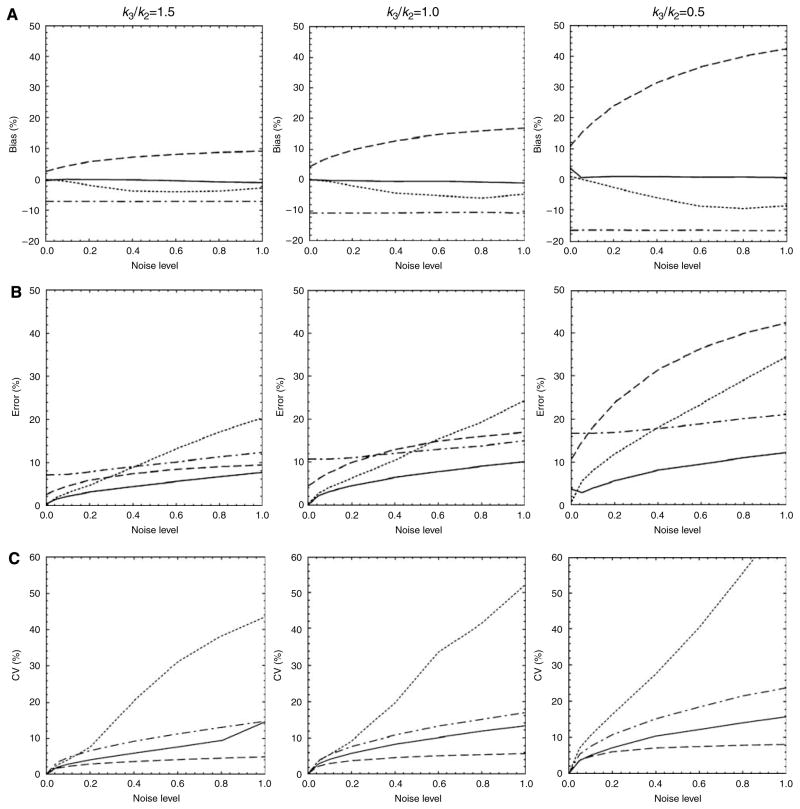
In Figure 1, the bias, error, and CV of the estimation of Kin for simulated noiseless and noisy tissue time–activity curves, with different levels of receptor availability (k3/k2 = 0.5~1.5), were plotted versus noise level (α = 0 to 1.0). As GPGA results were dependent on the assumed equilibrium time (or the range of line fitting), we used data that produced best results (fitting range: 10 to 90 mins).
Figure 1.
Plots of (A) biases, (B) errors, and (C) coefficients of variation (CV) for the estimation of Kin versus noise level (α) from simulated time–activity curves for high (left column), intermediate (middle), and low (right) receptor density regions (k3/k2=1.5, 1.0, and 0.5, respectively). NLS: solid line; MLAIR1: dotted; MLAIR2: dashed; GPGA: dash-dot.
Generally, NLS (solid line in Figure 1) showed good statistical properties: almost no bias, smallest errors, and moderate CV levels. However, it should be noted that initial values for NLS estimation were set equal to true estimates to provide the most favorable condition for the NLS estimation. Thus, we focus on comparisons of simulation results for MLAIR and GPGA in the following paragraphs.
MLAIR1 (dotted line) showed almost no bias for Kin estimations for noiseless data (Figure 1A). As the noise level increased, receptor density decreased and bias became larger in the negative direction. However, degree of bias was smaller than those of the other linear methods. Multiple linear analysis for irreversible radiotracer 2 (dashed line) showed positive bias, which also increased with noise level and decreased with receptor density. The degree of bias in the low noise condition was smaller than that for GPGA (dash-dot line), which showed a consistent negative bias regardless of noise level, but higher than that for GPGA under high noise conditions.
Both MLAIR1 and MLAIR2 showed negligible percent errors for Kin estimations for noiseless data (Figure 1B). Multiple linear analysis for irreversible radiotracer 1 had a smaller error than the other linear methods under low noise conditions, but this error increased rapidly as noise levels increased. Although MLAIR2 had lesser errors than the other linear methods for high receptor density, errors increased as receptor density decreased. Gjedde–Patlak graphical analysis showed relatively consistent errors regardless of noise level.
Coefficients of variation for Kin estimations were highest for MLAIR1 and lowest for MLAIR2 (Figure 1C). Coefficient of variationV values obtained by MLAIR2 were less than 10% regardless of the receptor density and noise level, whereas those obtained by MLAIR1 increased rapidly as the noise level increased.
Application to [11C]MeNTI Positron Emission Tomography Data
Volume of interest analysis
Figure 2 shows correlations between Kin values estimated using each linear method and using NLS for regional time–activity curves on 10 VOIs. All data obtained from healthy volunteers and alcohol-dependent subjects (before and after naltrexone treatment) were included to examine the consistencies of correlations across a wide range of Kin. Although Kin values estimated using GPGA were well correlated with NLS values (r = 0.92 to 0.97), the slope of the regression line was dependent on the duration of line fitting and increasing the start time of fitting diminished the correlation (Figure 2A).
Figure 2.
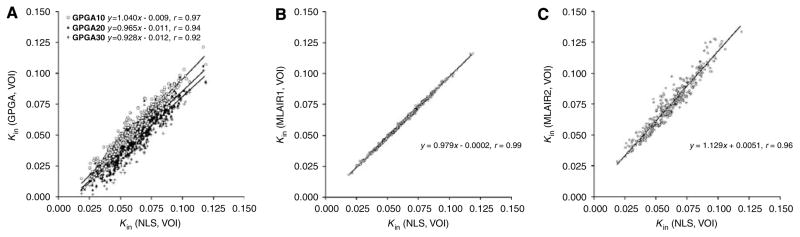
Correlations between regional Kin values as determined using different methods and VOI data. (A) GPGA (GPGA10, GPGA20, and GPGA30: t*=10, 20, and 30 mins, respectively) versus NLS. (B) MLAIR1 versus NLS. (C) MLAIR2 versus NLS.
Figure 2B shows that Kin values estimated using MLAIR1 were almost identical to those estimated using NLS (r = 0.99). This result shows that MLAIR1 can provide an unbiased solution relative to NLS estimations for data with low noise levels without requiring initial estimates of rate constants and without the risk of falling into the local minima of the cost function for parameter estimation. Although the correlation for NLS was poorer with MLAIR2 than with MLAIR1, correlation coefficient was similar to best GPGA results (Figure 2C). The small value of the y-intercept of the regression line (0.005mL/min/g) also shows that the bias of Kin in the low receptor density region was minimal.
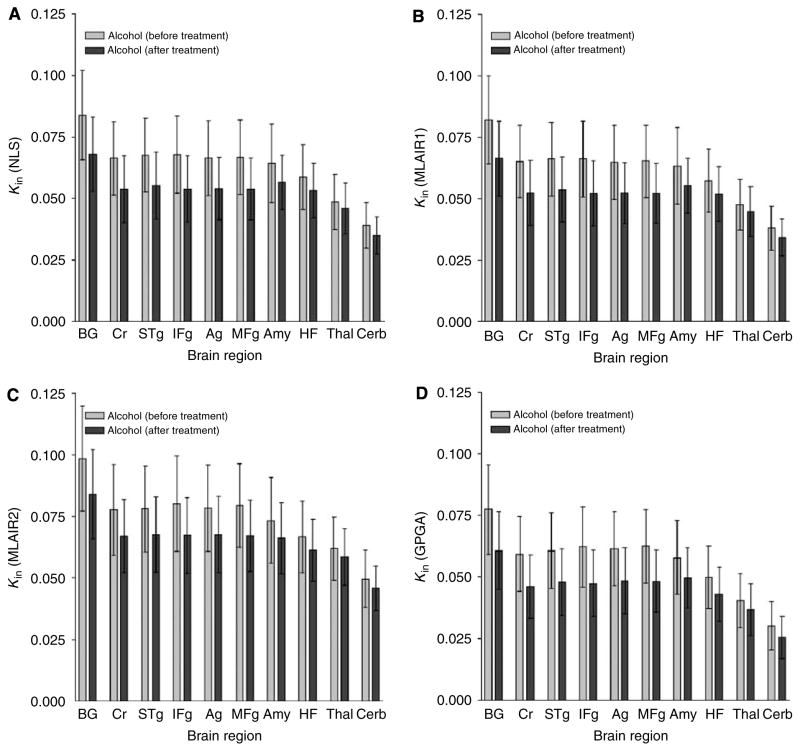
Figure 3 shows the regional distributions of the Kin estimates in the alcohol-dependent subjects before and after treatment. Higher regional Kin estimates by MLAIR2 than for the other methods were observed in all regions included in the VOI analysis. However, all methods led to identical findings, that is, Kin values were reduced by naltrexone, which reflected the displacement of δ-opioid receptors by naltrexone.
Figure 3.
Means and s.d. of regional Kin values of [11C]MeNTI estimated using the various methods: distribution across brain regions and comparison between different conditions. (A) NLS; (B) MLAIR1; (C) MLAIR2; (D) GPGA (range: 10 to 90 mins). BG: basal ganglia, Cr: cingulate cortex, STg: superior temporal gyrus, IFg: inferior middle frontal gyrus, Ag: angular gyrus, MFg: middle frontal gyrus, Amy: amygdala, HF: hippocampal formation, Thal: thalamus, Cerb: cerebellum.
The ranking of mean regional Kin estimates using MLAIR1 across brain regions (Figure 3B) was almost identical to those using the NLS (BG >Cr >…> Th > Cerb; Figure 3A). Although MLAIR2 showed ranking alternations between some regions of intermediate receptor density (STg~MFg; Figure 3C), an identical trend was observed for GPGA (Figure 3D). In addition, differences between the Kin values of these regions were not significant relative to variances in regional Kin values.
Parametric images
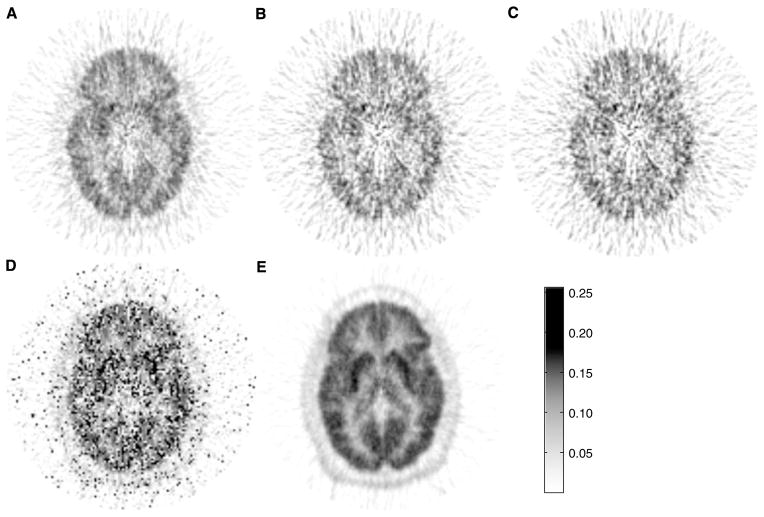
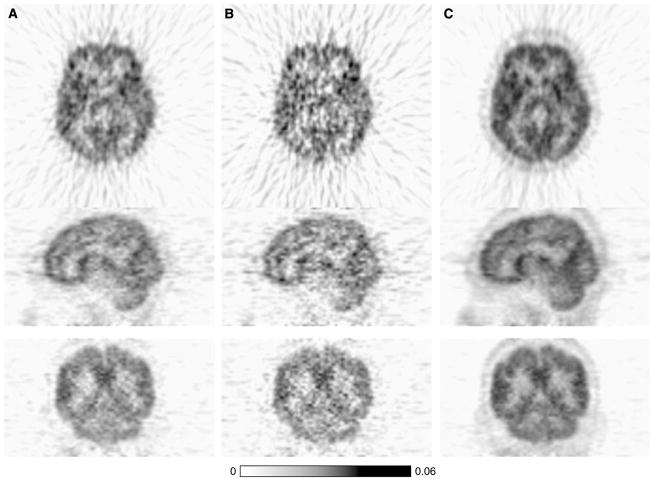
The parametric images of Kin values generated using GPGA or MLAIR are shown in Figure 4. Voxels with Kin values of < 0 or > 0.25 (much higher than those obtained by VOI analysis) were reset to marginal values that corresponded to physiologically relevant ranges. Gjedde–Patlak graphical analysis parametric images with different fitting ranges showed different image qualities (Figures 4A–4C). Figure 4D shows a MLAIR1 parametric image. Many voxels both inside and outside the brain showed extremely high Kin values, which resulted in significant salt-and-pepper noise in parametric images displayed using a relevant dynamic range of Kin. However, MLAIR2 parametric images (Figure 4E) showed remarkable image quality as compared with GPGA and MLAIR1 parametric images. No voxel showing an abrupt intensity change was observed and regional differences in Kin values shown by VOI analysis were illustrated well. Moreover, contrast between gray and white matter was also much better than those of the other methods.
Figure 4.
Kin parametric image of [11C]MeNTI obtained from a healthy volunteer using the various methods. (A) GPGA (range: 10 to 90 mins). (B) GPGA (range: 20 to 90 mins). (C) GPGA (range: 30 to 90 mins). (D) MLAIR1. (E) MLAIR2.
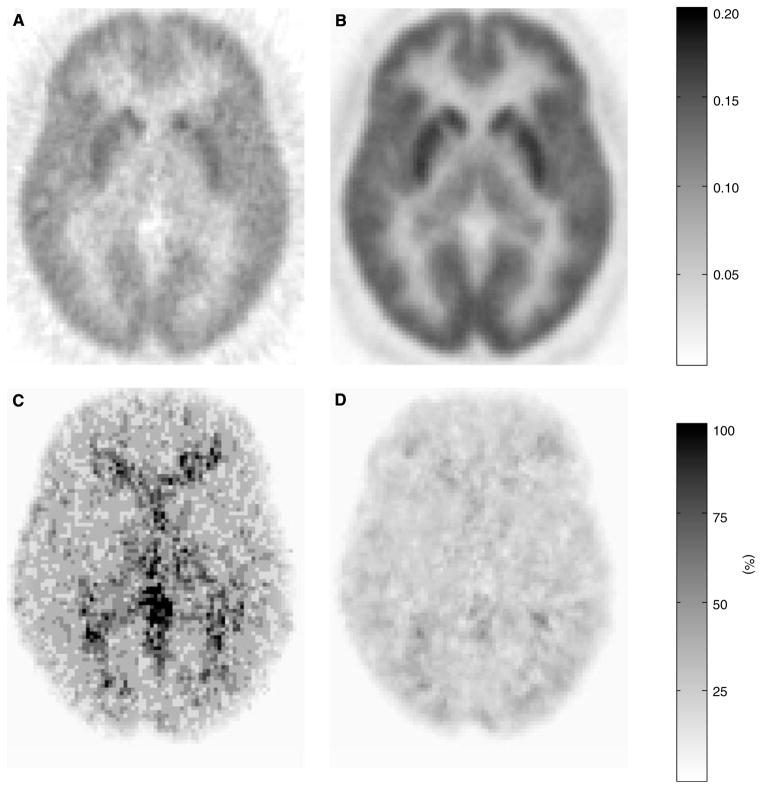
The images in Figure 5 are voxelwise representations of mean (A: GPGA 10 to 90 mins, B: MLAIR2) and percent CV (C: GPGA, D: MLAIR2) of Kin parametric images obtained from eight healthy volunteers. Multiple linear analysis for irreversible radiotracer 2 data showed less noisy intensity distribution in mean image (Figure 5B) and lower levels of inter-subject variability (Figure 5D). These superior properties of MLAIR2 over GPGA were most distinct in the thalamus and cerebellum which have the low level of receptor density.
Figure 5.
Voxelwise representation of mean (A, B) and % coefficients of variation (C, D) of Kin parametric images of [11C]MeNTI obtained from eight healthy volunteers. (A, C) GPGA (range: 10 to 90 mins). (B, D) MLAIR2.
Voxel-based statistical analysis
The improved properties of MLAIR2 (shown in Figures 4 and 5) led to greater statistical power for voxelwise comparisons than the GPGA method. Figure 6 shows brain regions showing significant decreases of Kin after nalrexone in alcohol-dependent subjects in the voxelwise paired t-testing. The analyses were conducted using the Kin parametric images composed using GPGA (A) or MLAIR2 (B), respectively, and after normalization to the thalamus. Clusters of > 100 voxels at the level of P < 0.001 (uncorrected for multiple comparisons) and P < 0.05 (corrected based on familywise error) are illustrated in this figure. Multiple linear analysis for irreversible radiotracer 2 clearly shows a significant decrease of Kin in wide cortical regions even after applying the strict significant criterion. No voxel with significant increase after treatment was found with the same thresholds. Analyses using normalized parametric images to the cerebellum produced equivalent results.
Figure 6.
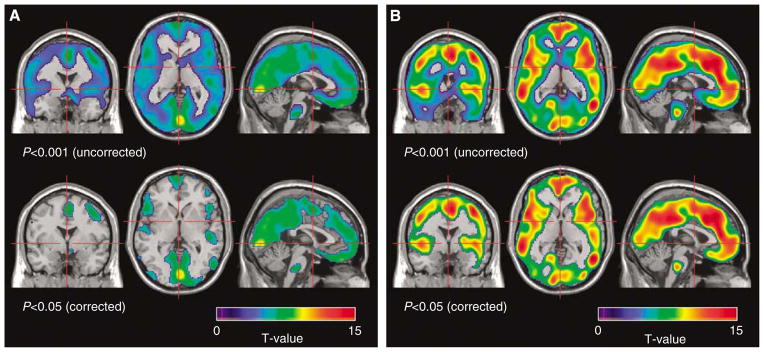
Brain areas with decreased Kin of [11C]MeNTI during naltrexone treatment relative to baseline in alcohol-dependent subjects (n=15): voxelwise paired t-test (upper row: uncorrected P<0.001, lower row: corrected P<0.05). (A) GPGA (range: 10 to 90 mins). (B) MLAIR2.
Application to [18F]FDG Positron Emission Tomography Data
Figure 7 shows the parametric images of Kin values of [18F]FDG data generated using GPGA and MLAIR2, and also shows the improved noise properties of MLAIR2 over GPGA.
Figure 7.
Kin parametric image of [18F]FDG of a healthy volunteer using (A) GPGA (range: 10 to 60 mins), (B) GPGA (range: 20 to 60 mins), and (C) MLAIR2.
Discussion
Graphical methods have been commonly used to generate parametric images because of their computational simplicity and model independence. Logan graphical analysis (Logan et al, 1996) is renowned for estimating distribution volumes or the binding potentials of reversibly binding radioligands. However, this method has a recognized problem concerning biased parameter estimations for noisy data (Logan et al, 2001), and resultantly, several approaches have been proposed to reduce this bias. These approaches include generalized linear least squares (Logan et al, 2001), total least squares (Varga and Szabo, 2002), linear integration (Carson, 1993), and multiple linear regression (Ichise et al, 2002). Another weakness of simple graphical analysis concerns the uncertainty of estimated parameters associated with arbitrary determinations of equilibrium periods. Considerations of the interindividual and interregional variabilities in equilibrium time (or period) are particularly irksome when calculating parametric images, because of the huge number of data sets that must be analyzed.
GPGA is the analog of Logan graphical analysis for the irreversibly binding radiotracers, and has similar limitations. However, few systematic investigations have been undertaken to overcome these limitations of GPGA, although various compensational approaches are available for Logan graphical analysis. Therefore, in this study, we used two MLAIR methods and investigated their properties and utilities, and we finally reached the conclusion that they have several strengths over GPGA.
As whole-data samples are used for MLAIR estimations, no equilibrium time or linear region must be imposed on data. They require similar amounts of computation time as GPGA, but have better bias properties than GPGA. By computer simulation, bias levels for Kin estimations using MLAIR1 for high or intermediate receptor density regions were compatible to those of NLS estimations performed with ideal initial values, although GPGA and MLAIR2 showed nonzero bias even with noiseless data. Biases for low receptor density regions also did not exceed 10%. In addition, MLAIR1 estimates for real PET data showed a strong correlation with NLS estimates (Figure 2B). This method has excellent bias properties mainly because all independent variables are almost noise-less (Ca and the single or double integrals of Ca and CT), and only the dependent variable (CT) is noisy (Equation (9)).
However, MLAIR1 showed a high level of uncertainty for Kin estimations for highly noisy data, mainly because a division operation on estimated macro parameters is required to obtain the Kin value. Therefore, we suggest that MLAIR1 is the method of choice for the VOI analysis of noiseless or low-noise data, but that it is inadequate for the analysis of noisy time–activity curves from individual voxels. In addition, it should be noted that MLAIR1 can provide a parametric map of tracer delivery K1 if the blood volume fraction is negligible (P2≈K1; Blomqvist, 1984). This information is valuable for many tracers, for example, labeled compounds with transport mechanism.
The results of this study indicate that MLAIR2 is more relevant for parametric image generation rather than MLAIR1, and that it has better statistical properties than the GPGA. The MLAIR2 equation (Equation (17)) was derived so that Kin is obtained directly from macro parameters estimated by multiple linear regression, which leads to a stable and robust estimation of Kin (in terms of its variability) even in noisy environments. In fact, its CV was < 6% even for highly noisy data from low receptor density regions in the computer simulation.
However, the inclusion of CT in independent variables could not be avoided in this modification (MLAIR2), which resulted in increased bias of Kin estimations. Nevertheless, despite this bias shown in computer simulations and real PET data, MLAIR2 estimates correlated well with NLS estimates (Figure 2C). Furthermore, the relative distributions of Kin values estimated using MLAIR2 under different conditions and across different regions were not different from those estimated using the other methods (Figure 3), indicating that MLAIR2 is a valid quantification method for comparative studies based on VOI data and/or parametric images.
The merits of the improved parametric images obtained using MLAIR2 were well illustrated by voxel-based statistical analyses. Regional changes of Kin values after naltrexone treatment in the alcohol-dependent subjects well matched the results obtained using VOI data. Multiple linear analysis for irreversible radiotracer 2 also showed much higher statistical power for voxelwise comparisons than GPGA (Figure 6). Further investigations of methods of regularization to improve the bias property of MLAIR2 without compromising its robustness for parameter estimation will undoubtedly augment the advantageous features of MLAIR2 when parametric images are used. A possible approach might be to use the total least squares method, which provides more consistent estimates in linear models, with the presence of errors in both dependent and independent variables than ordinary least squares (Varga and Szabo, 2002). Noise reduction in tissue time–activity curves using wavelet filtering or principle component analysis would also be useful (Millet et al, 2000; Joshi et al, 2008).
Multicollinearity is a common problem when multiple linear analysis methods are applied to tracer kinetics, because all dependent and independent variables used are derived from the tissue time–activity curve or arterial input function. In this situation, some of these variables are so highly correlated that the reliable estimations of individual regression coefficients are difficult. Variances of parameter estimates are usually inflated by this linear dependency (Myers, 1990). Further investigations on the covariance structure of MLAIR methods and possible ways of overcoming this problem using sophisticated statistical methods, such as, ridge regression, are required (Hoerl and Kennard, 1970).
Although radiolabeled ligands that bind reversibly to certain receptors during scan periods are preferred for in-vivo receptor–ligand assay based on PET or single photon emission computed tomography (SPECT), irreversible [11C]MeNTI, which selectively binds to δ-opioid receptors, is currently the only approved PET tracer for human administration. [11C]MeNTI has a desirable property as an irreversible tracer concerning the simplicity of quantifying receptor–ligand binding, that is, the lumped parameter Kin is approximately proportional to k3 (Bmaxkon), the rate constant of primary interest when kinetics are irreversible, because it has moderate k3/k2 ratio (Koeppe et al, 1994; Smith et al, 1999). However, voxelwise calculations of Kin in [11C]MeNTI PET studies using conventional methods suffer from severe noise levels in parametric images (Figure 4), because of regional differences between times required to reach equilibrium and a short radioisotope half-life (Smith et al, 1999). Nevertheless, MLAIR2 showed much better properties than GPGA for voxelwise parameter estimations and statistical analyses using [11C]MeNTI PET data, and should be useful for investigations on central δ-opioid receptor systems.
Improvements in parametric image quality are not limited to noisy dynamic 11C PET data. Although we have not accumulated a sufficient amount of data yet, our preliminary studies on [18F]FDG brain (Figure 7) and 18F skeletal PET (Kim et al, 2007) data show that efficient and robust parametric imaging of glucose and fluoride influx rates is also possible using MLAIR2. Further investigations using other radiotracers with irreversible binding or uptake are warranted.
Although Kin is proportional to k3 given suitable k3/k2 ratios, it is also dependent on the blood–flow-mediated parameter K1. Therefore, direct assessments of k3 are also important for kinetic studies on irreversible tracers. Because the division operation must be performed to obtain k3 from both MLAIR1 and MLAIR2 macro parameters, there may be a similar problem of uncertainty concerning parameter estimations using the present versions of the MLAIR algorithms. Therefore, modification of the model equations for the direct measurement of k3 without the division operation should also be explored.
Wong et al (1986, 1997) presented a graphical means of estimating k3 for irreversibly binding dopamine D2 ligand 3-N-[11C]methylspiperone in a similar manner to GPGA. According to this approach, tissue and plasma ratios are fitted to a combination of linear and mono-exponential functions of normalized time integral of plasma input function. This approach has the advantage of using entire time–activity curves and of providing a graphical representation of binding rate, but requires nonlinear curve fitting and combinations of multiple parameters to obtain k3.
In summary, the characteristics of multiple linear analyses of radiotracers with irreversible kinetics were explored by simulation and using real PET data. The devised MLAIR1 and MLAIR2 methods were found to be computationally efficient and showed good correlations with parameters estimated using the standard NLS method. Multiple linear analysis for irreversible radiotracer 1 showed unbiased parameter estimations but high levels of uncertainty for noisy data, and thus, would be useful for VOI-based data analysis. In addition, we suggest that MLAIR2, which showed lowest parameter estimating variabilities, is suitable for voxel-based data analysis.
Acknowledgments
This work was supported by a Korea Research Foundation Grant (KRF-2005-041-E00321) funded by the Korean Ministry of Education & Human Resources Development, Brain Research Center of the 21st Century Frontier Research Program (M103KV010016-08K2201-01610) funded by the Korean Ministry of Science and Technology, and a Seoul R&BD Program Grant (10550) funded by the Seoul Development Institute.
References
- Blomqvist G. On the construction of functional maps in positron emission tomography. J Cereb Blood Flow Metab. 1984;4:629–32. doi: 10.1038/jcbfm.1984.89. [DOI] [PubMed] [Google Scholar]
- Blomqvist G. On the construction of functional maps in positron emission tomography-genaralizations. J Cereb Blood Flow Metab. 1987;7:S447. doi: 10.1038/jcbfm.1984.89. [DOI] [PubMed] [Google Scholar]
- Carson RE. PET parameter estimation using linear integration methods: bias and variability consideration. In: Uemura K, Lassen NA, Jones T, et al., editors. Quantification of Brain Function. Tracer Kinetics and Image Analysis in Brain PET. Amsterdam: Elsevier Science Publishers B.V; 1993. pp. 81–9. [Google Scholar]
- Evans AC. A double integral form of the three-compartmental, four-rate-constant model for faster generation of parametric maps. J Cereb Blood Flow Metab. 1987;7:S453. [Google Scholar]
- Feng D, Huang SC, Wang ZZ, Ho D. An unbiased parametric imaging algorithm for nonuniformly sampled biomedical system parameter estimation. IEEE Trans Med Imaging. 1996;15:512–8. doi: 10.1109/42.511754. [DOI] [PubMed] [Google Scholar]
- Feng D, Wang Z, Huang S-C. A study on statistically reliable and computationally efficient algorithms for generating local cerebral blood flow parametric images with positron emission tomography. IEEE Trans Med Imaging. 1993;12:182–8. doi: 10.1109/42.232247. [DOI] [PubMed] [Google Scholar]
- Gjedde A. High- and low-affinity transport of D-glucose from blood to brain. J Neurochem. 1981;36:1463–71. doi: 10.1111/j.1471-4159.1981.tb00587.x. [DOI] [PubMed] [Google Scholar]
- Gjedde A. Calculation of cerebral glucose phosphorylation from brain uptake of glucose analogs in vivo: a re-examination. Brain Res. 1982;257:237–74. doi: 10.1016/0165-0173(82)90018-2. [DOI] [PubMed] [Google Scholar]
- Gjedde A. Glucose metabolism. In: Wagner HN Jr, Szabo Z, Buchanan JW, editors. Principles of Nuclear Medicine. Vol. 2. Philadelphia, PA: Saunders; 1995. pp. 54–71. [Google Scholar]
- Gjedde A. Modelling metabolite and tracer kinetics. In: Feinendegen LE, Shreeve WW, Eckelman WC, Bahk Y-W, Wagner HN Jr, editors. Molecular Nuclear Medicine: The Challenge of Genomics and Proteomics to Clinical Practice. Berlin: Springer-Verlag; 2003. pp. 121–70. [Google Scholar]
- Hoerl AE, Kennard RW. Ridge regression: biased estimation for non-orthogonal problems. Technometrics. 1970;12:55–67. [Google Scholar]
- Ichise M, Liow JS, Lu JQ, Takano A, Model K, Toyama H, Suhara T, Suzuki K, Innis RB, Carson RE. Linearized reference tissue parametric imaging methods: application to [11C] DASB positron emission tomography studies of the serotonin transporter in human brain. J Cereb Blood Flow Metab. 2003;23:1096–112. doi: 10.1097/01.WCB.0000085441.37552.CA. [DOI] [PubMed] [Google Scholar]
- Ichise M, Toyama H, Innis RB, Carson RE. Strategies to improve neuroreceptor parameter estimation by linear regression analysis. J Cereb Blood Flow Metab. 2002;22:1271–81. doi: 10.1097/01.WCB.0000038000.34930.4E. [DOI] [PubMed] [Google Scholar]
- Joshi A, Fessler JA, Koeppe RA. Improving PET receptor binding estimates from Logan plots using principal component analysis. J Cereb Blood Flow Metab. 2008;28:852–65. doi: 10.1038/sj.jcbfm.9600584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim DE, Park SH, Kim SK, Nam HW, Lee YS, Chung JK, Roh JK. Hypoglycemia-induced cerebellar dysfunction and quantitative positron emission tomography study. Neurology. 2000;55:418–22. doi: 10.1212/wnl.55.3.418. [DOI] [PubMed] [Google Scholar]
- Kim SJ, Lee JS, Lee WW, Kim YK, Jang S-J, Son KR, Kim H-C, Chung JW, Lee DS. Multiple linear analysis for generating parametric images of irreversible radiotracer. Korean J Nucl Med. 2007;47:78–84. [Google Scholar]
- Koeppe RA, Frey KA, Mulholland GK, Kilbourn MR, Buck A, Lee KS, Kuhl DE. [11C]tropanyl benzilate-binding to muscarinic cholinergic receptors: methodology and kinetic modeling alternatives. J Cereb Blood Flow Metab. 1994;14:85–99. doi: 10.1038/jcbfm.1994.13. [DOI] [PubMed] [Google Scholar]
- Lee JS, Lee DS. Analysis of functional brain images using population-based probabilistic atlas. Curr Med Imaging Rev. 2005;1:81–7. [Google Scholar]
- Lee JS, Lee DS, Ahn JY, Yeo JS, Cheon GJ, Kim SK, Park KS, Chung JK, Lee MC. Generation of parametric image of regional myocardial blood flow using dynamic PET and a linear least-squares method. J Nucl Med. 2005;46:1687–95. [PubMed] [Google Scholar]
- Lee JS, Lee DS, Kim YK, Kim JS, Lee JM, Koo BB, Kim JJ, Kwon JS, Yoo TW, Chang KH, Kim SI, Kang H, Kang E, Chung JK, Lee MC. Quantification of brain images using Korean standard templates and structural and cytoarchitectonic probabilistic maps. Korean J Nucl Med. 2004;38:241–52. [Google Scholar]
- Lever JR, Scheffel U, Kinter CM, Ravert HT, Dannals RF, Wagner HN, Jr, Frost JJ. In vivo binding of N1′-([11C]methyl)naltrindole to delta-opioid receptors in mouse brain. Eur J Pharmacol. 1992;216:459–460. doi: 10.1016/0014-2999(92)90448-d. [DOI] [PubMed] [Google Scholar]
- Logan J. Graphical analysis of PET data applied to reversible and irreversible tracers. Nucl Med Biol. 2000;27:661–70. doi: 10.1016/s0969-8051(00)00137-2. [DOI] [PubMed] [Google Scholar]
- Logan J, Fowler JS, Volkow ND, Ding YS, Wang GJ, Alexoff DL. A strategy for removing the bias in the graphical analysis method. J Cereb Blood Flow Metab. 2001;21:307–20. doi: 10.1097/00004647-200103000-00014. [DOI] [PubMed] [Google Scholar]
- Logan J, Fowler JS, Volkow ND, Wang GJ, Ding YS, Alexoff DL. Distribution volume ratios without blood sampling from graphical analysis of PET data. J Cereb Blood Flow Metab. 1996;16:834–40. doi: 10.1097/00004647-199609000-00008. [DOI] [PubMed] [Google Scholar]
- Logan J, Fowler JS, Volkow ND, Wolf AP, Dewey SL, Schlyer DJ, MacGreor RR, Hitzemann R, Bendriem B, Gatley SJ, Christman DR. Graphical analysis of reversible radioligand binding from time-activity measurements applied to [N-11C-methyl]-(−)-Cocaine PET studies in human subjects. J Cereb Blood Flow Metab. 1990;10:740–7. doi: 10.1038/jcbfm.1990.127. [DOI] [PubMed] [Google Scholar]
- Madar I, Lever JR, Kinter CM, Scheffel U, Ravert HT, Musachio JL, Mathews WB, Dannals RF, Frost JJ. Imaging of delta opioid receptors in human brain by N1′-([11C]methyl)naltrindole and PET. Synapse. 1996;24:19–28. doi: 10.1002/(SICI)1098-2396(199609)24:1<19::AID-SYN3>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- Millet P, Ibáñez V, Delforge J, Pappata S, Guimón J. Wavelet analysis of dynamic PET data: application to the parametric imaging of benzodiazepine receptor concentration. Neuroimage. 2000;11:458–72. doi: 10.1006/nimg.2000.0563. [DOI] [PubMed] [Google Scholar]
- Myers RH. Classical and Modern Regression with Applications. Pacific Grove, CA: Duxbury; 1990. pp. 368–423. [Google Scholar]
- Patlak CS, Blasberg RG, Fenstermacher JD. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake. J Cereb Blood Flow Metab. 1983;3:1–7. doi: 10.1038/jcbfm.1983.1. [DOI] [PubMed] [Google Scholar]
- Slifstein M, Laruelle M. Effects of statistical noise on graphic analysis of PET neuroreceptor studies. J Nucl Med. 2000;41:2083–8. [PubMed] [Google Scholar]
- Smith JS, Zubieta JK, Price JC, Flesher JE, Madar I, Lever JR, Kinter CM, Dannals RF, Frost JJ. Quantification of delta-opioid receptors in human brain with N1′-([11C]methyl) naltrindole and positron emission tomography. J Cereb Blood Flow Metab. 1999;19:956–66. doi: 10.1097/00004647-199909000-00003. [DOI] [PubMed] [Google Scholar]
- Varga J, Szabo Z. Modified regression model for the Logan plot. J Cereb Blood Flow Metab. 2002;22:240–4. doi: 10.1097/00004647-200202000-00012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weerts EM, Kim YK, Wand GS, Dannals RF, Lee JS, Frost JJ, McCaul ME. Differences in delta- and mu-opioid receptor blockade measured by positron emission tomography in naltrexone-treated recently abstinent alcohol-dependent subjects. Neuropsychopharmacology. 2008;33:653–65. doi: 10.1038/sj.npp.1301440. [DOI] [PubMed] [Google Scholar]
- Wong DF, Gjedde A, Wagner HN., Jr Quantification of neuroreceptors in the living human brain. I. Irreversible binding of ligands. J Cereb Blood Flow Metab. 1986;6:137–46. doi: 10.1038/jcbfm.1986.27. [DOI] [PubMed] [Google Scholar]
- Wong DF, Young D, Wilson PD, Meltzer CC, Gjedde A. Quantification of neuroreceptors in the living human brain: III. D2-like dopamine receptors: theory, validation, and changes during normal aging. J Cereb Blood Flow Metab. 1997;17:316–30. doi: 10.1097/00004647-199703000-00009. [DOI] [PubMed] [Google Scholar]
- Yokoi T, Iida H, Itoh H, Kanno I. A new graphic plot analysis for cerebral blood flow and partition coefficient with Iodine-123-Iodoamphetamine and Dynamic SPECT validation studies using Oxygen-15-water and PET. J Nucl Med. 1993;34:498–505. [PubMed] [Google Scholar]