On being the right (cell) size

Abstract

Different animal cell types have distinctive and characteristic sizes. How a particular cell size is specified by differentiation programs and physiology remains one of the fundamental unknowns in cell biology. In this review we explore the evidence that individual cells autonomously sense and specify their own size. We discuss possible mechanisms by which size sensing and size specification may take place. Finally, we explore the physiological implications of size control. Why is it important that particular cell types maintain a particular size? We develop these questions by examination of current literature and pose the questions that we anticipate will guide this field in the upcoming years.

Introduction

Early cytologists found that, within a species, it is the number of cells, rather than the size of the cells that makes one individual larger than another; cell size is relatively constant (1). While this seems to downgrade the question of cell size in favor of proliferative potential, it raises the curious question of how cells of a common cell type achieve such a uniform size, yet are capable of changing their size by orders of magnitude during differentiation or in response to physiological stimuli. For example, pancreatic beta cells are surrounded by acinar cells that are roughly twice their size, and chondrocytes increase their volume by 10 to 20 fold during hypertrophic bone growth (2). These examples, among others (figure 1), demonstrate that a cell’s size is not the result of physical constraints, but rather it is adaptively regulated. What, then, specifies a particular cell’s size?

Figure 1.

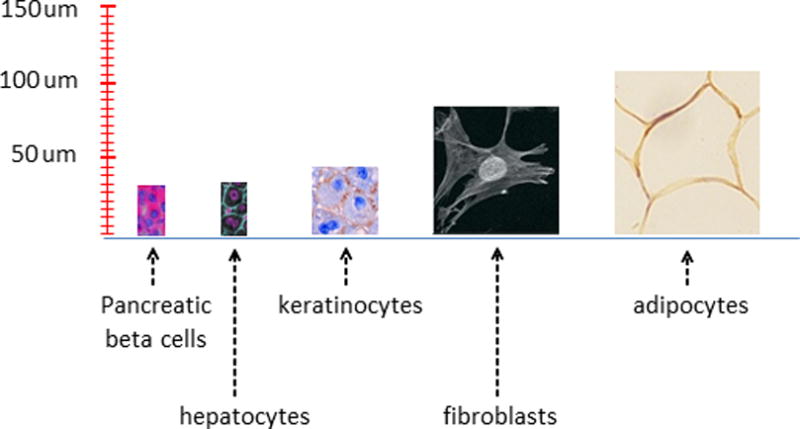
Sizes of different human cell types. Cells are shown to scale. Pancreatic beta cells (insulin and DNA stained) (76), hepatocytes (β-catenin and DNA stained) (77), keratinocyes from oral tissue (78), fibroblasts (79), adipocytes from subcutaneous tissue (80).

Much work on this subject has focused on identifying extracellular factors (and their intracellular responsive pathways) that elicit changes in cell size. These studies found that the size of a cell of is largely controlled by its cell surface receptors and the combinations of growth factors, mitogens and cytokines in its environment. In the 1980s (3, 4), Zetterberg and coworkers distinguished between factors, such as insulin-like growth factor 1 (IGF-1) and insulin, that primarily initiate cell growth and factors such as epidermal growth factor (EGF) that primarily drive cell cycle progression even in the absence of growth. In Schwann cells, for example, IGF-1 functions primarily as a growth factor increasing cell mass, while glial growth factor (GGF) acts as a mitogen inducing proliferation (5, 6). Consequently, Schwann cell size can be manipulated by adjustment of the relative concentrations of IGF-1 and GGF in their environment. These findings caused some to conclude that, in proliferating animal cells, growth and cell cycle progression are independent processes, each governed by extracellular cues. According to this view, size itself is not actively controlled, but merely results from the independent control of the rates of cell growth and cell division.

Although it is clear that extracellular growth factors and mitogens can trigger changes in cell size, such cues do not account for how cell size variance is constrained, to achieve the uniformity in cell size typically seen in tissues (figure 2). These extracellular signals can dictate the mean size of cells, but individual cells will still deviate from that mean. Variability in cell size can arise from variability in growth rate and cell cycle length, or asymmetry in cell division. These sources of inevitable variation raise the question of whether there are cellular mechanisms that might act to increase size homogeneity. Size variation can only be reduced with processes that differentially affect cells of different sizes, despite the fact that they share the same environment. Such a process could reduce heterogeneity by eliminating cells that deviate widely from the mean, through cell death or differentiation. Alternatively, a size-discriminatory process could force large cells to accumulate less mass than small ones, in response to identical extracellular signals. This kind of control requires a mechanism whereby individual cells measure their own size and adjust their cell cycle length, growth rate, or both, as necessary to achieve a common target size. In this review, we will discuss a growing body of evidence that such mechanisms exist and address the following questions:

1. Do animal cells have mechanisms to autonomously measure and adjust their individual sizes?

2. Does the presence of such mechanisms indicate that there is an optimal cell size for a particular cell’s function?

Figure 2.

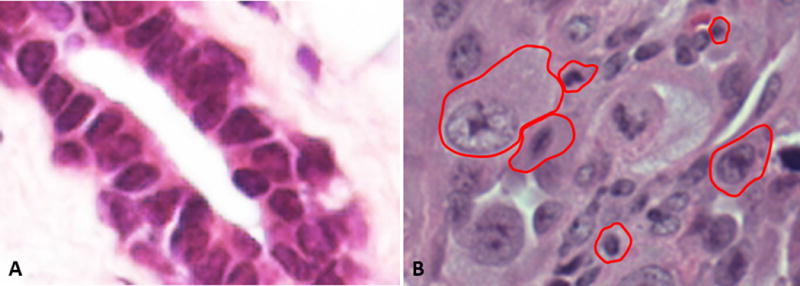
Cell size uniformity in healthy tissues contrasts with cell size heterogeneity in pleomorphic tumors. (A) A section of epidermal stratum spinosum is used to illustrate uniformity in cell size that is typical of epithelial tissues. (B)This uniformity is contrasted with the extreme disparities in cell size in a typical pleomorphic melanoma. Stratum spinosum image was taken from http://www.studyblue.com/ while melanoma section was taken from Pathpedia (http://www.pathpedia.com/).

Our discussion of cell size control will focus on proliferating populations of cells, which have been more extensively studied in this context, although many of the issues raised are relevant in non-proliferating tissues as well.

Ways to limit heterogeneity in cell size

In proliferating cells, size variability can be constrained if cells progress through the cell cycle in a size-dependent manner (figure 4A). Cells that are born small would have more time to grow before their next division, as compared to oversized cells which would divide more quickly. Several groups have suggested that mammalian cells have a size threshold for exit from G1 phase of the cell cycle (7–9), as has been observed in budding yeast (10). In order for a size threshold to work, cell size must be reported to the processes regulating the cell cycle. The “signal” could be the amount of a particular protein or protein modification, the distance between cytoskeletal features, or even the number or size of the cell’s neighbors.

Figure 4.

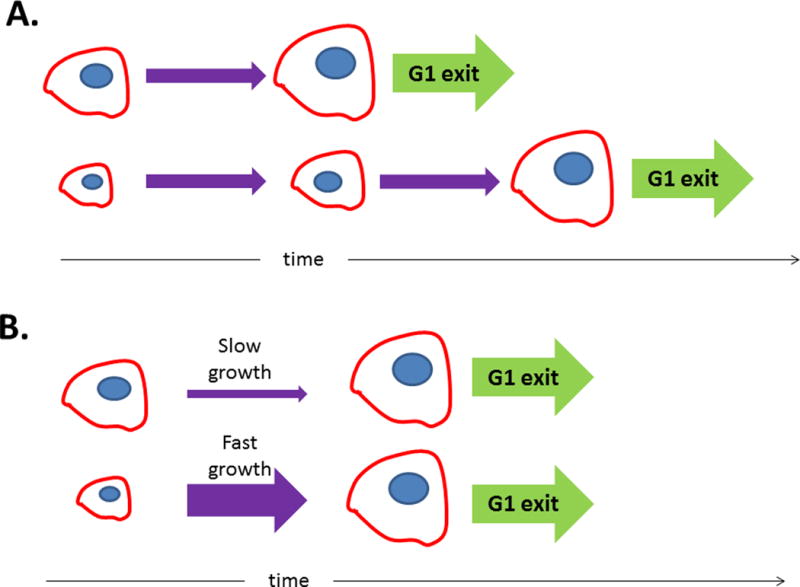
To exit G1 with the appropriate size, cells can either adjust the amount of time spent in G1 (A) or the rate at which they grow (B).

Instead of (or in addition to) changing their cell-cycle length in a size-dependent manner, cells could also reach their target size by adjusting their growth rate, so that small cells grow quickly, while large cells grow slowly (figure 4B). This growth rate adjustment could be modulated by the sort of signals described above. Alternatively, the growth rate, and the final cell size, could be determined by a “balance point” of synthesis and degradation. If, for example, cells synthesize proteins at a fixed rate but degrade them at a rate that is proportional to their total cell size, net growth would slow as cell size increases. Note that this is not a trivial condition, because it requires that degradation depend on the total amount of protein in the cell, rather than the protein concentration.

Evidence for cell autonomous size measurement

There is increasing evidence that cells autonomously regulate their size to reduce cell size variation. In 1965, Killander and Zetterberg used interferometric microscopy to measure the dry mass of individual fibroblasts as a function of time since division. They reported that cells that had recently entered S-phase were less variable in size than those in early G1 (8). S-phase entry appeared to be more heavily dependent on a cell’s size than its age, as cells entered S-phase at similar sizes, whereas their age at S-phase entry varied widely. These results suggested that there might be a cell-size threshold gating G1-exit in animal cells. Killander et al. also showed that cells split into separate culture dishes often displayed slight difference in phenotypes, including cell size (7). When comparing cell size and cell cycle distributions of different cultures, they noticed that populations with smaller average birth sizes had longer average G1 lengths, such that cells exited G1 at a similar size in all populations. They concluded that a critical cell mass is required for S-phase entry (figure 3).

Figure 3.

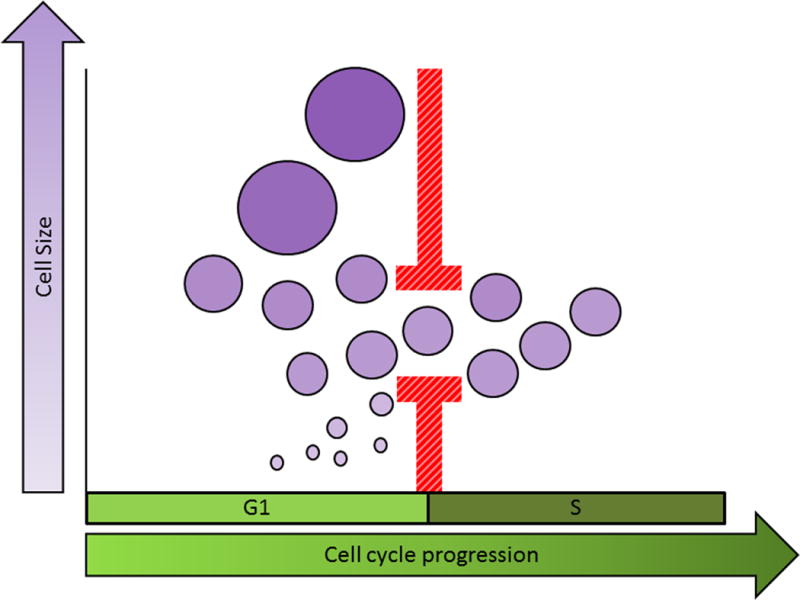
In populations of proliferating cells, size uniformity may be ensured by linking the processes of growth and cell cycle progression. One way this can be accomplished is by restricting progress through a particular cell cycle stage (for example, the G1/S transition) to cells that have reached a specific “target” size.

A dependence of G1 length on cell size was also observed by Dolznig, et al. (9). They engineered avian erythroblasts to proliferate in the absence of cytokines, under control of a viral constitutively active EGF-R1, v-ErbB. When v-ErbB signaling was blocked with an EGF-R inhibitor, and the cells were supplied with the appropriate cytokines, they proliferated under the control of their physiological receptors, c-Kit and EpoR. Cells were significantly larger when driven by v-ErbB than they were during c-Kit/EpoR-driven proliferation. Dolznig et al. monitored the cell cycle distribution after switching cells from v-ErbB- to c-Kit/EpoR-driven proliferation. They reasoned that if there is a size threshold which is lowered in c-Kit/EpoR-driven proliferation, the first cell cycle following the switch should be shorter than subsequent cycles. This expectation was fulfilled, suggesting that there is a size threshold at G1 exit that is influenced by extracellular conditions. While the results of Killander and Zetterberg can be explained by a correlation between G1 length and size at any point in G1, Dolznig’s work suggests that a true size threshold restricts G1 exit. Notably, Echave et al. (11) transferred Schwann cells from 3% serum (in which they maintain a large size) to serum-free medium (in which they are small) and failed to see a shortening of the first cell cycle. This discrepancy may be attributable to differences in experimental conditions or cell type.

Kafri et al. provided evidence of a size-discriminatory process that reduces variability in cell mass (assayed by protein staining) at G1-exit in several normal and transformed cell lines (12). To reveal the coordination of growth and cell cycle progression, using fixed unsynchronized cell preparations, they applied a fundamental statistical principle: In an unsynchronized population of cells, the proportion of cells characterized by a certain property or phenotype is a function of the duration of the events during the cell cycle where that phenotype is expressed. Specifically, if cells of a given size and cell cycle position are underrepresented in the population, those cells must either grow or progress through that stage of the cell cycle more rapidly. Based on this “ergodic rate analysis” (ERA) of large populations captured in a single image, they detected a prominent fingerprint of feedback regulation. In late G1, large cells are distinguished from small cells in a process that causes large cells to accumulate less mass than smaller ones, thereby decreasing size heterogeneity in the population. Their conclusions were consistent with either of two possibilities: a faster growth rate or a longer duration of G1 for smaller cells.

A major source of variation in size is variation in the rates at which individual cells grow. Growth rates of individual cells are very hard to measure, requiring methods for resolving small differences in mass (a fraction of the mass of a single cell). To address this problem, Scott Manalis and colleagues developed a microfluidic resonator that measures the buoyant mass of single cells with exquisite accuracy, enabling measurement of the instantaneous growth rate of a cell with a resolution of about 3 minutes (13). Their experiments on mouse lymphocyte precursors provided the first highly accurate, direct measurements of growth curves of single cells (14). They observed a convergence of the variable growth rates of individual cells, as they approach the end of G1. At birth there are large disparities in growth rate among individual cells in the population, and, as cells progress through the cell cycle, their growth rates continuously increase, creating more disparity. However, in these cells, G1 length is inversely proportional to a cell’s initial rate of growth, not size. Slower-growing cells are held in G1, allowing them more time to accelerate their growth, so that all cells exit G1 with similar growth rates. These results suggest that a growth rate threshold gates G1 exit. Such a mechanism would reduce the rate at which variation builds up during cell growth, by both allowing slower-growing cells more time to grow between divisions and reducing growth rate disparities. An alternative possibility consistent with these observations is that cells measure not their rate of growth, but the amount of mass accumulated since birth.

For many investigators in the past few decades, the question of whether cells regulate their own size was tied to another, more abstract question: do cells grow with linear or exponential kinetics (15–19)? At first glance, the latter question may seem to have little biological relevance. But, upon closer examination, a distinction between these models carries significant implications. With exponential growth, larger cells grow faster than smaller cells, amplifying any existing size disparities in proliferating populations. Therefore, evidence that cells grow exponentially, and are expected to diverge in size, would suggest that regulatory mechanisms exist to counterbalance this effect and maintain size homeostasis.

Despite the elegance of this claim, to actually distinguish exponential from linear kinetics requires measurements of cell size with an error smaller than 6% (20), a resolution that was technologically unavailable until recently. Ingeniously circumventing this challenge, in 1963 Collins and Richmond (21) published a method to calculate growth kinetics from three static size distributions: a distribution of newborn cells, dividing cells, and an unsynchronized population. Intuitively, if one observes very few cells in the unsynchronized population with a particular size, this might be because (i) cells of this size grow very quickly (and spend very little time at this volume), (ii) most newborn cells are larger than this, or (iii) most cells divide before reaching this size. By comparing the three size distributions in the Collins-Richmond relation, the effects of (ii) and (iii) can be estimated, and one can infer the average growth rate for cells of any given size. The most difficult aspect of applying the Collins-Richmond method is measuring the sizes of newborn and dividing cells. This challenge was overcome in 2009 (20), by culturing mouse lymphoblasts that were loosely attached to a membrane, such that one daughter cell from every mitosis was released, and the volumes of these newborn cells were measured via Coulter counter. The size distribution of dividing cells was inferred, by assuming that the volume of a cell just before division is the same as the total volume of the two resulting newborns.

Applying the Collins-Richmond equation to the measured cell volume distributions revealed that growth kinetics are more complex than either the linear or the exponential models. Overall, lymphoblast growth rates do increase with cell size, upholding the exponential growth model, although this trend is reversed in the very largest of cells. Additionally, during early G1, the growth of all cells accelerates faster than predicted by either model. The extent of this complexity was further revealed by the newly-developed methods described above (12, 14), which detailed how growth kinetics vary over the course of the cell cycle.

The finding that growth is size-dependent during much of the cell cycle suggested that lymphoblasts must have a robust size-control mechanism. To investigate this possibility, the authors tracked the size distribution of a synchronized population of cells over several cycles. They found that for cells of equal age, the larger is more likely to divide. Similarly, for two cells of equal size, the older cell is more likely to divide. This implies that lymphoblast division is regulated by both cell size and age—that both a “sizer” and a “timer” are involved.

How can a cell measure its own size?

While changes in cell size are easily induced by extracellular conditions, such as growth factor levels, cells of different types in a common environment display characteristic and distinctive sizes. It is clear that different cell types respond to the same signals in different ways, such that their size distinction is preserved. The combination of a cell’s differentiation state and the composition of its environment specify the particular target size it will maintain. The uniformity in cell size of most cell types suggests that single cells sense their individual size in relation to this target size. Perhaps the most intriguing aspect of such a regulatory mechanism is that both the cell’s target size and its actual size must be evaluated on absolute rather than relative scales. This type of absolute size measurement has been proposed to occur in keratinocytes, which differentiate only at a diameters between 12 and 14 um (22).

How can individual cells assess their size on an absolute, rather than a relative, scale? Researchers studying size control in the fission yeast, Schizosaccharomyces pombe, proposed that a physical basis for size sensing is an intracellular gradient of the mitotic inhibitor Pom1, whose concentration is high at the cell ends and decreases towards the cell center (23–25). As the S. pombe cell grows by elongation, a Pom1-depleted region is established at its center and plays a role in triggering mitosis. The concentration profile of intracellular Pom1 was proposed to serve as a ruler marking the distance between the cell tips. More recent work, showing that cells maintain size homeostasis even in the absence of Pom1, led others to conclude that the Pom1 gradient is not the direct size sensor responsible for the negative correlation between cell size at birth and cell cycle length (26). However, Pom1 does modulate the absolute size for mitotic entry, possibly by preventing mitosis near cell ends, thereby ensuring a minimum cell length. In this example, the link between cell cycle progression and cell size is thought to be the kinetics of a reaction-diffusion system. Despite the fact that most cells lack the morphological simplicity of the rod-shaped S. pombe, it is possible that such intracellular gradients serve as cellular “rulers” in many contexts.

The observation that growth rates of lymphocyte precursors converge at G1-exit raises the possibility that a target growth rate, and not a target size, is required for cell cycle progression, and that individual cells measure their own rates of growth. There is evidence that this type of mechanism is active in the budding yeast Saccharomyces cerevisiae, where cells must achieve a threshold protein synthesis rate before progressing through G1 to S-phase. There is a well-established link between growth and G1/S progression in S. cerevisiae (see (27) for a comprehensive review), which is reflected in the negative correlation between cell size at birth and G1 duration (28). Di Talia et al. showed that size control is imposed during the earlier part of G1 and depends on the G1 cyclin Cln3, while the late events of G1 are size-independent (28). In small cells, G1 is lengthened, allowing cells to approach a “size threshold” before passing Start and subsequently exiting G1. In S. cerevisiae cells, growth rate is proportional to size (28), so a growth rate threshold gating G1 exit would give the appearance of a size threshold.

Cln3 has been implicated as a sensor of the rate of protein synthesis (29, 30). Cln3 is a rate-limiting determinant of G1 exit; mutants with highly abundant Cln3 have a shorter G1 and smaller size than wild-type cells (31). The link between cell growth and G1 exit may lie in the CLN3 5′ untranslated region, where an open reading frame allows appreciable Cln3 synthesis only when there are sufficient ribosomes to bypass the block. Because this leaky scanning mechanism is inefficient, Cln3 synthesis requires a minimium rate of protein translation (29). As Cln3 is highly unstable (31), its abundance at any given time is indicative of the current translation rate. This work suggests that, in budding yeast, cell cycle entry is regulated by a threshold on the overall rate of protein synthesis. A similar threshold has been proposed to regulate mitotic entry. Both cdc25 (a dosage dependent activator of mitosis) and the G2/M cyclin cdc13 mRNAs have long 5′ untranslated regions containing open reading frames, rendering their levels particularly sensitive to the rate of translation initiation (32).

Cln3 promotes cell cycle progression by relieving inhibition of the transcription factor SBF, activating the transcription of many cell cycle genes, including downstream G1 cyclins Cln1 and Cln2. These cyclins further activate SBF, triggering a positive feedback loop which ensures an irreversible commitment to the cell cycle (“Start”) (33–35). Among its other modes of action, Cln3 localizes to SBF binding sites in the CLN2 promoter, where it releases SBF inhibitor Whi5 (30). Titration of Cln3 against the fixed number of SBF binding sites in the genome may be the means by which the cell senses the total amount of Cln3, despite the increasing volume of the cell that is expected to stabilize Cln3 concentration (30).

In vertebrate systems, cyclin E is functionally homologous to the yeast Cln3. Expression of human cyclin E can compensate for loss of Cln3 in yeast lacking all G1 cyclins (Keyomarsi K. personal communication). Active cyclin E activates CDK2, thereby promoting G1 exit and the onset of the cell division cycle. In line with is roles in cell cycle, cyclin E overexpression shortens G1 resulting in a decreased cell size (36, 37).

The idea that cyclin E might serve as sensor of protein translation rate, analogous to Cln3, was first proposed by Edgar and Nuefeld (37), in their work on growth of the drosophila wing disc. Like Cln3, the drosophila cyclin E contains several open reading frames in its 5′ untranslated region (38). Ras activation, which increases cell size and growth rates, was found to cause a posttranscriptional increase in cyclin E levels, promoting G1/S progression (39).

Similarly, in mammalian hepatocytes, cyclin E abundance correlates more strongly with cell growth than with cell cycle progression (40–42). Transfecting hepatocytes with cyclin D causes proliferation one day after treatment. Six days later, hepatocytes show little proliferation but increased growth. Though the amount of cyclin E mRNA is highly increased during the earlier proliferative phase, a large increase in the cyclin E protein abundance occurs only later, with cell growth. The fact that translation, but not transcription, of cyclin E is correlated with cell growth suggests that it might serve as a translation rate sensor. However, due to the correlative nature of these findings, further investigation is still needed to determine whether cyclin E truly links cell growth to cell cycle progression. Another potential translation rate sensor is the E2F1 transcription factor. E2F1 drives endocycles in drosophila salivary cells, by promoting cyclin E expression and S-phase entry, and translational control of E2F1 was found to couple rates of endocycle progression to cellular growth rates (43).

Physiological consequences of cell size

Why would cells need a mechanism to specify and fine-tune their individual sizes? For certain cells, there is an obvious association between a cell’s function and its physical dimensions. Neurons, for example, must span the distance across which they relay information. Yet, for the majority of cell types, whether epithelial or mesenchymal, the advantage of a specific size is not obvious. A famous 1945 study by Gerhard Fankhauser documents the effects of the increased cell size in polyploid salamander larvae on the formation of various multicellular structures, such as pronephric tubules (44). In many organs, the shape and dimensions of these structures are unchanged, with a decrease in cell number compensating for the increase in cell size. In pentaploid larvae, this compensation meant that the circumference of pronephric tubules and ducts was often spanned by just a single cell! The fact that normal structures could be formed even with large alterations in cell size suggested that, for many cell types, a cell’s size is not imposed by its role as the structural unit of the organism. Notable exceptions to this trend include the observation that cell size influences the size and morphological complexity of the brain (45).

There is some indication that a cell’s size is commonly related to its physiology, since some cells change their size in response to external cues. For example, kidney epithelial cells modulate their size in response to rates of fluid flow in the nephron ducts, sensed by mechanical shear on the primary cilium (46). Cell size also often changes during differentiation. Lymphocytes, for instance, rapidly grow to a larger size after exposure to cytokines or TLR stimulation (47). However, in these cases, it is not clear whether size is the target of regulation or a by-product of some other adaptation.

A change in organ size, when demanded by physiology, can be accomplished through a change in cell number, a change in cell size, or both. The choice of modulating organ growth through cell growth or proliferation is often context-dependent. Pancreatic beta cells, for example, increase their size by over 25% during pregnancy, in response to increased insulin demand (48). However, the insulin demand resulting from beta cell death leads to increased proliferation of beta cells, without changing their size (48). Similarly, liver size increases during pregnancy through hepatocyte hypertrophy, whereas liver regeneration after surgical resection occurs by increased hepatocyte proliferation. These examples suggest that, under particular physiological conditions, it might be advantageous for a specific cell to have a specific size. This raises the question: do cells function most efficiently when at the ‘right’ size?

Because cells have multiple roles, a cell’s “function” is hard to define and its functional efficiency hard to quantify. Another difficulty is, for most cell types, size has not been a primary focus of investigation. Consequently, literature that systematically quantifies cell size and relates it to cell behavior is sparse. An exception to this rule is the case of the pancreatic beta cell. Insulin secretion is associated with beta cell mass, so the size of beta cells has been the subject of much research. To a simple approximation, a beta cell may be described as a device that performs one main function- secretion of insulin in response to increases in blood glucose-and this process can be measured quantitatively. For these reasons, we will examine the evidence of a size-function relationship in beta cells, with the hope that this discussion will stimulate similar investigations of other cell types.

Giordano et al. found that the rate of insulin production of individual rat beta cells is more strongly correlated with cell size than with metabolic activity as assayed by NAD(P)H fluorescence (49). In fact, in cultured rat beta cells, insulin secretion, metabolic activity, and global rates of protein production are all correlated with cell size. These correlations are further reinforced in transgenic mice harboring mutations that affect cell size. For example, beta cells of mice lacking S6K1 are reduced in size (50, 51). These small beta cells secrete less insulin per cell than normal beta cells, possibly due to the reduction in membrane surface available, leading to hypoinsulinemia. By contrast, rapamycin treatment of wild-type beta cells, which reduces S6K1 activity but does not change beta cell size, does not affect insulin secretion, indicating that the reduced insulin secretion results from a size defect rather the absence of S6K1 (50).

Additional studies suggest that there is an optimal size for maximum efficiency of insulin secretion. Like S6K1 knockouts, mice expressing only a mutant, non-phosphorylatable ribosomal protein S6 have small beta cells (52–54). However, in these mutants, the cell size defect is compensated by increased cell number so that their total beta cell mass is similar to that of wild-type mice. Despite this rough conservation of bulk mass, these mutants are still hypoinsulinemic, suggesting that small cells are disproportionately less efficient insulin producers than normal-sized cells. Furthermore, mice expressing constitutively active protein kinase Akt1 have larger beta cells than wild-type mice and an increased rate of insulin secretion (55). However, insulin secretory capacity per unit of beta cell mass is lower. A persistent hyperinsulinemia in these transgenic mice may indicate inefficiency in hormone secretion. These results suggest that beta cell function may be impaired in cells that are either larger or smaller than their target size. A caveat to this interpretation comes from the pleiotrophic effects of pathways like mTOR, MAPK and PI3K, pathways which, in addition to affecting cell size, can also regulate many other functions. Hence, it is hard to know whether a change in size actually causes a change in function or is simply correlated with it.

Another case where evidence may suggest an optimal cell size criterion is that of mammalian adipocytes. Clear differences in gene expression between large and small adipocytes suggest that cell size influences adipocyte biology (56, 57). One explanation for this effect is that cellular enlargement, by increasing cell surface area and modifying interactions between the cell and its extracellular matrix, activates the β₁-integrin/ERK signaling pathway that modulates several transcription factors (57). Large adipocytes display a marked increase in the activity of fatty acid synthase and lipoprotein lipase. These changes are further manifested in the altered metabolic activity of large adipocytes. For example, Smith et. al. compared large and small adipocytes isolated from the same specimen of human adipose tissue (58, 59) and found that large adipocytes have higher rates of lipid synthesis. This increase in lipogenesis rate is still evident when measurements are normalized to cell size, meaning that large cells are disproportionally more productive than small cells. Changes in cell size have also been linked to transcriptional and metabolic changes in other cell types, including hepatocytes and erythrocytes (60–63).

However, the increased metabolic efficiency of large adipocytes comes at a price. Larger cells are less sensitive to the stimulating effects of insulin on glucose uptake, the oxidation of glucose to CO2 (64), and the uptake of triglyceride fatty acids (65). These defects may result from the stress of adipocyte enlargement against the physical constraints imposed by collagen and the extracellular matrix (66). The balance between metabolic capacity that scales positively with adipocyte size and insulin sensitivity that scales negatively with size implies an optimal adipocyte size. Supporting this idea, increased adipocyte size, rather than total body fat, is associated with insulin resistance in obesity and is a risk factor for development of type II diabetes mellitus (67).

Several lines of research have suggested an interesting link between the regulation of cell size variability and the pathology of cancer, although the systematic studies needed to confirm this link are still lacking. While cancer is a disease of deregulated proliferation, in clinical histology it is the size of cancer cells that renders their appearance distinct from the surrounding tissue (68). Malignant tumor cells are both larger and more variable in size than normal cells. Pleomorphism, the increased variability in cell size and shape, is a histological characteristic of many malignant lesions (69–71) and is sometimes used as a criterion for the determination of histologic grade. The loss of cell size regularity in cancer cells also occurs when cell lines of normal and neoplastic origin are grown in matching culture conditions, indicating that the increased size variability in cancer is cell-autonomous and not a product of the tumor microenvironment (72). Furthermore, when epidermoid carcinoma cell lines were classified based on cell size variability, only the highly heterogeneous lines initiated tumors upon heterotransplatation into mice (72). These experiments raise the question of whether aberrant regulation of cell size has a role in tumorigenesis, although increased cell size variability may also be a mere correlate of tumor biology (perhaps the result of aneuploidy), and further experiments are warranted to resolve this conflict.

Questions, challenges, suggestions

Early cell cycle research featured a debate over whether the cell cycle was the result of a linear cascade of interdependent events, with early events providing substrates essential for later ones, or whether there was an independent master regulator of cell cycle – a cell cycle clock (73). Investigations of cell size now face a similar dilemma. Is the size of a cell simply the byproduct of its rate of growth and frequency of division? Or is there a master regulator that independently specifies cell size on the basis of a cell’s function and physiological needs? The evidence reviewed above, suggests that there is a separate and at least partially independent pathway for cell size regulation.

Almost exclusively, studies of size regulation have focused on the possibility of a size checkpoint, an event that regulates either G1 exit or cell division based on cell size. The checkpoint model posits that the size of a cell is specified by adjusting the amount of time during which it grows. Lengthening G1 would increase the amount of time in which a cell grows, resulting in an increased cell size. This possibility is grounded in observations from yeast biology (10). Yet, there is also an alternative class of mechanisms that can just as easily dictate cell size. Instead of regulating the amount of time during which they grow, cells may regulate the rate at which they accumulate mass. To limit size disparity, small cells could accelerate their growth rate, or large cells could decelerate it. This alternative has remained unexplored, largely because of the difficulty of making precise measurements of cell growth.

If individual cells were to specify their size by modulating their growth rates rather than their cell cycle length, a cell’s overall synthetic machinery would have to be fine-tuned to reflect its size. In other words, there would have to be feedback linking a cell’s physical dimensions to its anabolic control. The identification of such a mechanism would significantly alter the way we understand growth control. We would need to expand the simple and intuitive model of a discrete size checkpoint to include the continuous modulation of growth rates.

It has been over 150 years since Virchow wrote, “omnis cellula e cellula”, giving us a very modern concept of the cell; since that time, the problem of how cell size is regulated has been staring us in the face. Today we have only achieved a partial phenomenological explanation of cell size homeostasis. Why has it been so difficult? Despite the simplicity of size as a phenotype, its study is inherently challenging. The specific size of a cell is an outcome of numerous and diverse processes. Accumulation of cell mass is directly related to a cell’s metabolic and anabolic activity, as well as protein turnover and autophagy. In proliferating populations, cell size reflects a balance between growth and division. In some cases, size is also affected by a cell’s state of differentiation and physiological conditions. For this reason, it is hard to establish whether a mutation or chemical perturbation that affects cell size is associated with size control per se. In a screen for cell size mutants, Jorgenson et al pointed out this problem, stating that an increase in the mean cell size in a population could reflect a shift to later cell cycle stages, rather than abnormal growth (74). Additionally, a change in rates of cell division could increase or decrease cell size, even if growth rates remain unchanged. In retrospect, anatomical structure has been easier to study than physiological process. Chemical composition yielded to biochemical investigation more readily than integrated mechanisms like growth, shape, motility, and behavior. Whereas genetics could point us to processes that affect size, it could not easily disentangle contributions from nutrition, biogenesis, differentiation, and cell division. But, most importantly, we had only the crudest quantitative measures for the very processes we wished to study at the single cell level: growth and size.

The advances in recent years, summarized above, have provided evidence that growth and cell cycle progression are coordinated in proliferating cells. Confident that we are not merely studying the wake behind the boat, but that real circuits exist to precisely specify cell size, we can confront the underlying molecular circuitry and explore its biological consequences. We have interesting questions to address. How is the mean cell size established for each lineage? How do cells adapt to external stimuli to change the set point for their size? How does each cell measure its size and assess its deviation from the mean? By what mechanism do proliferating cells alter their rates of growth or passage through the cell cycle to prevent the natural accumulation of size variability? How do size changes affect cell function and do certain cells function best at a given size? What role does cell size play in pathology and senescence? JBS Haldane reminded us of the importance of size at the organism level in his lively essay, “On being the right size.” (75) Biologists who have reveled in the qualitative complexity of cells might take new inspiration from the simple process of size control; it is certain to have deep consequences and fascinating explanations.