Alfred J. Lotka and the origins of theoretical population ecology

Ecology, being an interdisciplinary subject, has often advanced by borrowing perspectives and methods from numerous other disciplines. Of the many cross-disciplinary transfers that have contributed to the science of ecology, one unusual source of inspiration has been physical chemistry, which in a round-about way served to stimulate the development of population ecology in the 1920s. This transfer from physical chemistry into biology was the brainchild of Alfred James Lotka (1880–1949), a man of exceptional creativity and one of the fathers of what would later become theoretical population ecology.

Alfred James Lotka, 1880–1949. Image courtesy of MetLife Archives.

Lotka’s story has an ironic twist because he did not intend to contribute to the discipline of ecology. His goal was to create a new biological discipline called “physical biology,” by which he meant the “broad application of physical principles and methods in the contemplation of biological systems” (1). The analogy between physical chemistry and physical biology lay in the idea that the same basic laws governed both kinds of systems. In both systems, all processes could be reduced to two kinds of changes: those involving exchanges of matter between the components of the system, and those involving exchanges of energy. In the chemical system the components were molecules. In the biological system the components were organisms plus the raw materials in their environment, and the exchanges of matter and energy took place through the web of food relationships, growth, and reproduction. Understanding these relationships mathematically was the goal of physical biology. Because of his attention to systems, Lotka’s approach was strongly ecological, but when he started his project in the early 20th century, ecology barely existed as a discipline and he did not think, even two decades later, that ecologists would be his main audience.

Lotka received his undergraduate education in physics and chemistry at the University of Birmingham in the United Kingdom, where he was influenced by John Henry Poynting, a student of James Clerk Maxwell. After graduation in 1901 Lotka spent a year at the Physical-Chemical Institute at Leipzig, where Wilhelm Ostwald was advancing the idea that energy was the central organizing concept of the physical and biological sciences. Ostwald’s lectures prompted Lotka to explore the idea of developing a new discipline, which would be a biological analog to physical chemistry. After moving to the United States in 1902, Lotka started publishing articles on various aspects of physical biology while working at short-term jobs, completed a master’s degree at Cornell University in 1909, and on the basis of 12 publications earned a Doctorate of Science from Birmingham in 1912 (2).

As time passed, Lotka perceived growing interest in the application of mathematics to biology. One sign was D’Arcy Wentworth Thompson’s 1917 study, On Growth and Form, which applied methods commonplace in the physical sciences to problems of morphology and growth (3). Lotka, working in isolation, was frustrated that his own work had failed to gain recognition. That situation changed in 1920 when his publications came to the attention of Raymond Pearl, a biostatistician at the Johns Hopkins University’s School of Hygiene and Public Health. Pearl had noticed a connection between some of Lotka’s articles and Pearl’s own interests in population growth in single species. Pearl contacted Lotka, started communicating his articles to PNAS, and eventually invited him to Johns Hopkins for an extended stay so that he could gather his ideas into a book.

The first article that Pearl communicated to PNAS in 1920, “Analytical note on certain rhythmic relations in organic systems,” typified Lotka’s approach by opening with discussion of chemical systems and then moving to biological examples (4). The biological case was a hypothetical interaction between two species (a plant and an herbivore feeding on the plant). Lotka arrived at the unexpected result that their interaction would produce undamped or indefinitely continued oscillations in the two populations. Lotka developed this analysis into a general study of predator–prey (or host–parasite) interactions in his subsequent book, Elements of Physical Biology (1925), written in Pearl’s laboratory. That book was reprinted posthumously in 1956 as Elements of Mathematical Biology (1). It is now considered an ecological classic.

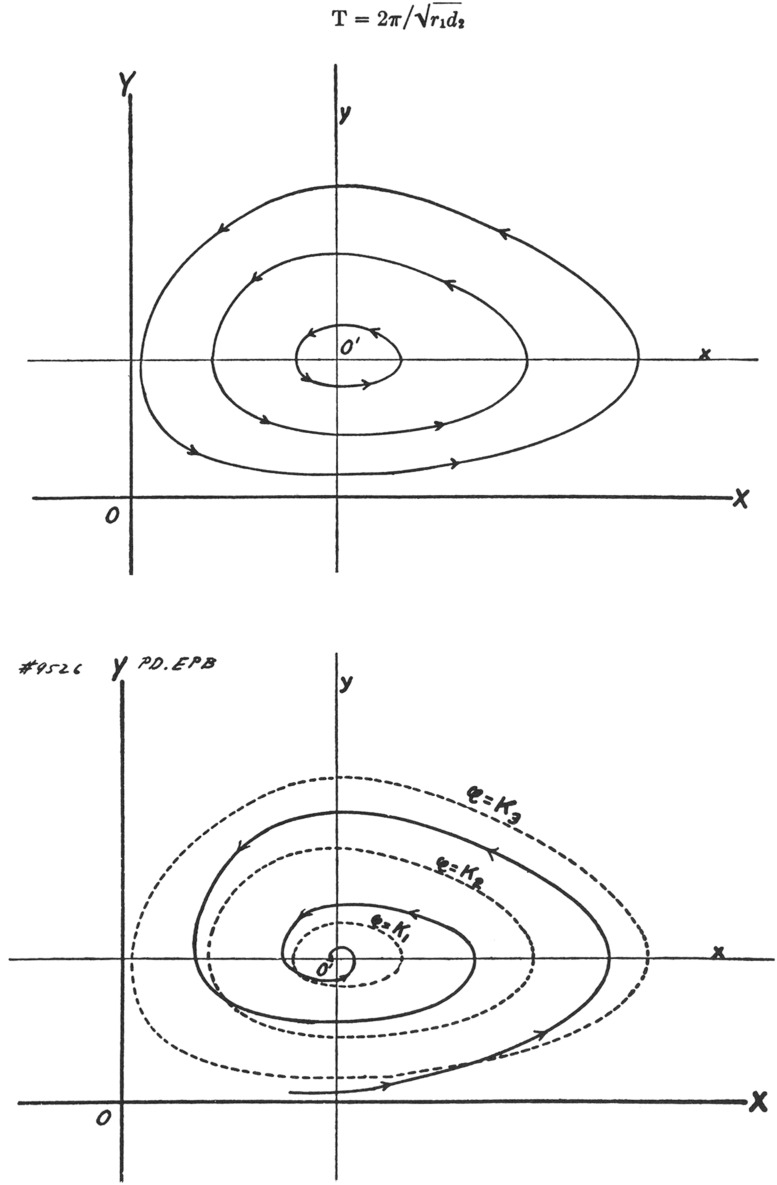
In the expanded treatment in Elements, Lotka fleshed out the analysis by building on research in entomology and epidemiology that dealt with host–parasite interactions. His elementary treatment of the problem resulted in undamped oscillations of the two populations, but a more exact treatment led to a damped oscillation (Fig. 1). Later, Lotka revisited the “mathematical theory of capture” to explore how the interaction of predator and prey populations would be affected by refuges that enabled prey to escape capture (5).

Fig. 1.

Lotka’s illustrations of (Upper) undamped population oscillations in host-parasite interactions, the classic Lotka-Volterra equations, and (Lower) his more exact treatment showing a damped oscillation. Reproduced from ref. 1.

In 1925 Vito Volterra, an eminent Italian mathematician, independently took up the analysis of predator–prey interactions, publishing a short discussion in 1926 (6). Volterra also concluded that populations would oscillate as a result of the interaction between them. Volterra pursued this theory and related ecological problems over the next few years, and biologists began to take note of these ideas. The equations describing the predator–prey interaction eventually became known as the “Lotka–Volterra equations,” which served as the starting point for further work in mathematical population ecology. Charles Elton later explained why this model had such deep impact (7). Ecologists normally thought in terms of entire food chains, which might have five stages, as the means of controlling populations: each species at a higher level was thought to control the species lower down the chain. Lotka and Volterra, however, skipped the complication of thinking in terms of five stages and showed how interactions between only two species resulted in regulation, with each species controlling the population of the other in a cyclical manner. Theories that used the food chain to explain population regulation were hence oversimplified.

Lotka’s interests focused on species preying on or being parasitic on other species. He recognized that species competing for a common food supply would form another category, but he devoted relatively little attention to competitive interactions and published only one later article on the topic (8). Here Lotka differed greatly from Volterra, who was more interested in exploring competitive interactions. G. F. Gause, a Russian ecologist, tested Volterra’s conclusions experimentally in the 1930s (9, 10). Because of this difference between Lotka and Volterra, the term “Lotka–Volterra equations” strictly applies only to predator-prey interactions, but the ecological literature often uses the same label for the competition model (see ref. 11, for example). Hutchinson’s practice of referring to the competition model as the “Volterra–Gause equations” is more accurate (12).

Lotka’s book contained more than discussions of two-species interactions. He was especially keen to explore the energetics of evolution: that is, how to understand evolution broadly as a process involving the capture and transmission of energy. Lotka envisioned systems as giant machines or energy transformers that changed over time. For him, natural selection could be understood as a physical principle with the same level of generality as the laws of thermodynamics (13). Lotka argued that natural selection would tend to favor an increase in the rate of circulation of matter through the system, and would also favor more efficient use of energy. Seeking to derive a general law expressing this idea, Lotka proposed the principle that “evolution proceeds in such direction as to make the total energy flux through the system a maximum compatible with the constraints” (14). In a manner of speaking, the evolving “world engine,” as he conceived it, accomplished the remarkable achievement of improving itself as it went along.

Volterra’s entry into population ecology helped to draw attention to Lotka’s work, but Lotka worried about being overshadowed by the more famous mathematician, although he claimed priority based on his 1920 article (4). After his book appeared, Lotka accepted a job at the Metropolitan Life Insurance Company, where he worked as a statistician and demographer until retirement in 1947. His publications on ecological topics fell off and Lotka later became known for his work on stable population theory.

Given his extraordinary vision of how to combine biology with the physical sciences while envisioning a new discipline focused on biological systems, it is little wonder that readers were puzzled by Lotka’s book. Although he never created his new discipline, people who were open to interdisciplinary thinking found Lotka’s work to be stimulating. D’Arcy Thompson referred to Lotka’s work in the new edition of On Growth and Form, while admitting that the work of Lotka and Volterra lay outside the scope of his book (15). Economist Herbert A. Simon lauded Elements and praised Lotka’s ability to open up new lines of inquiry (16). In ecosystem ecology, H. T. Odum picked up on Lotka’s ideas about how systems evolve but modified his approach by relating efficiency to power, proposing that “systems perform at an optimum efficiency for maximum power output” (17). Lotka’s work had many different impacts because of his synthetic, systems orientation and unique vision, yet he completely failed to achieve his original goal.