Impact of fossil fuel emissions on atmospheric radiocarbon and various applications of radiocarbon over this century

Significance

A wide array of scientific disciplines and industries use radiocarbon analyses; for example, it is used in dating of archaeological specimens and in forensic identification of human and wildlife tissues, including traded ivory. Over the next century, fossil fuel emissions will produce a large amount of CO₂ with no ¹⁴C because fossil fuels have lost all ¹⁴C over millions of years of radioactive decay. Atmospheric CO₂, and therefore newly produced organic material, will appear as though it has “aged,” or lost ¹⁴C by decay. By 2050, fresh organic material could have the same ¹⁴C/C ratio as samples from 1050, and thus be indistinguishable by radiocarbon dating. Some current applications for ¹⁴C may cease to be viable, and other applications will be strongly affected.

Abstract

Radiocarbon analyses are commonly used in a broad range of fields, including earth science, archaeology, forgery detection, isotope forensics, and physiology. Many applications are sensitive to the radiocarbon (¹⁴C) content of atmospheric CO₂, which has varied since 1890 as a result of nuclear weapons testing, fossil fuel emissions, and CO₂ cycling between atmospheric, oceanic, and terrestrial carbon reservoirs. Over this century, the ratio ¹⁴C/C in atmospheric CO₂ (Δ¹⁴CO₂) will be determined by the amount of fossil fuel combustion, which decreases Δ¹⁴CO₂ because fossil fuels have lost all ¹⁴C from radioactive decay. Simulations of Δ¹⁴CO₂ using the emission scenarios from the Intergovernmental Panel on Climate Change Fifth Assessment Report, the Representative Concentration Pathways, indicate that ambitious emission reductions could sustain Δ¹⁴CO₂ near the preindustrial level of 0‰ through 2100, whereas “business-as-usual” emissions will reduce Δ¹⁴CO₂ to −250‰, equivalent to the depletion expected from over 2,000 y of radioactive decay. Given current emissions trends, fossil fuel emission-driven artificial “aging” of the atmosphere is likely to occur much faster and with a larger magnitude than previously expected. This finding has strong and as yet unrecognized implications for many applications of radiocarbon in various fields, and it implies that radiocarbon dating may no longer provide definitive ages for samples up to 2,000 y old.

Radiocarbon is produced naturally in the atmosphere and decays with a half-life of 5,700 ± 30 y (1–3). Fossil fuels, which are millions of years old, are therefore devoid of ¹⁴C, and their combustion adds only the stable isotopes ¹²C and ¹³C to the atmosphere as CO₂. First observed by Hans Suess in 1955 using tree ring records of atmospheric composition (4), the dilution of ¹⁴CO₂ by fossil carbon provided one of the first indications that human activities were strongly affecting the global carbon cycle. The apparent “aging” of the atmosphere—i.e., the decreasing trend in the ratio ¹⁴C/C of CO₂ (reported as Δ¹⁴CO₂) (5)—was interrupted in the 1950s when nuclear weapons testing produced an immense amount of “bomb” ¹⁴C that approximately doubled the ¹⁴C content of the atmosphere. Direct atmospheric observations began in the 1950s, capturing the rapid rise of Δ¹⁴CO₂ and its subsequent quasi-exponential decay as the bomb ¹⁴C mixed into oceanic and biospheric reservoirs (6–9) (Fig. 1).

Fig. 1.

Model predictions of atmospheric radiocarbon for the RCPs. (Left) Atmospheric CO₂ concentration (Top), CO₂ emissions from fossil fuel combustion (Middle), and CO₂ emissions from land use change (Bottom) in the RCP scenarios (11, 34). (Middle) Fossil fuel CO₂ emitted to the atmosphere is shown with solid lines; dashed lines show net fossil fuel CO₂ emitted, including “negative emissions” from biomass energy with carbon capture and storage. (Right) Observed (7, 10, 18, 35, 36) (1940–2012) and projected (2005–2100) radiocarbon content of atmospheric CO₂ (Δ¹⁴CO₂) (Table S2). The right axis shows the conventional radiocarbon age of a carbon-containing specimen with the same radiocarbon content, calculated by 8033 * ln (Δ¹⁴C/1,000 + 1). Filled areas indicate the range simulated for different sets of model parameters, each consistent with 20th-century atmospheric and oceanic Δ¹⁴C and CO₂ observations, within their uncertainties (10) (SI Text).

Now that several decades have passed since the Partial Nuclear Test Ban Treaty and the peak in atmospheric Δ¹⁴CO₂, fossil fuel emissions are once again the main influence on the long-term trend in Δ¹⁴CO₂ (7, 10). The growth or decline of fossil fuel emissions over the coming century determines to what extent Δ¹⁴CO₂ will be diluted further by fossil carbon. Also important is how atmospheric Δ¹⁴CO₂ dilution is moderated by natural exchanges of CO₂ with the ocean and the terrestrial biosphere. Future dynamics of carbon and ¹⁴C are simulated here using the Representative Concentration Pathways (RCPs) developed for the Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report (11, 12), and a simple carbon cycle model with parameters constrained by 20th-century atmospheric and oceanic Δ¹⁴C and CO₂ observations (10, 13) (SI Text).

The simple carbon cycle model includes a one-dimensional box diffusion model of the ocean and represents the atmosphere and the biosphere as one-box carbon reservoirs (10, 13, 14). Exchanges of carbon and ¹⁴C are governed by a small number of model parameters (Table S1). Multiple simulations were run using various parameter sets selected by their representation of Δ¹⁴C and inventories of CO₂ and bomb ¹⁴C (15–17). Atmospheric CO₂ concentration and fossil fuel and land use fluxes were prescribed by the RCPs, which include historical data through 2005. To match the prescribed atmospheric CO₂ concentration, the residual of carbon emissions and atmospheric and oceanic accumulation was added to the biospheric reservoir (single deconvolution). Atmospheric Δ¹⁴CO₂ was prescribed by observations until 2005, then predicted by model fluxes from 2005 to 2100 (SI Text).

Table S1.

Parameter sets used in the carbon cycle model simulations

Keddy, m2⋅y−1	τam, y	τab, y	τba, y	β
3,000	9	25	30	0
3,000	9	25	30	0.2
3,000	9	25	35	0
3,000	9	25	35	0.2
3,000	9	25	35	0.4
3,000	10	18	35	0
3,000	10	25	28	0
3,000	10	25	28	0.2
3,000	10	25	28	0.4
3,000	10	25	30	0
3,000	10	25	30	0.2
3,000	10	25	30	0.4
3,000	10	25	35	0
3,000	10	25	35	0.2
3,000	10	25	35	0.4
3,000	11	18	30	0
3,000	11	18	30	0.2
3,000	11	18	35	0
3,000	11	18	35	0.2
3,000	11	18	35	0.4
3,000	11	25	35	0
3,000	11	25	35	0.2
3,000	11	25	35	0.4
4,000	9	25	20	0
4,000	9	25	20	0.2
4,000	9	25	25	0
4,000	9	25	25	0.2
4,000	9	25	25	0.4
4,000	9	25	30	0
4,000	9	25	30	0.2
4,000	9	25	30	0.4
4,000	9	25	35	0
4,000	9	25	35	0.2
4,000	9	25	35	0.4
4,000	10	18	28	0
4,000	10	18	28	0.2
4,000	10	18	30	0
4,000	10	18	30	0.2
4,000	10	18	35	0
4,000	10	25	23	0
4,000	10	25	23	0.2
4,000	10	25	23	0.4
4,000	10	25	25	0
4,000	10	25	25	0.2
4,000	10	25	25	0.4
4,000	10	25	28	0
4,000	10	25	28	0.2
4,000	10	25	28	0.4
4,000	10	25	30	0
4,000	10	25	30	0.2
4,000	10	25	30	0.4
4,000	10	25	35	0
4,000	10	25	35	0.2
4,000	10	25	35	0.4
4,000	11	18	28	0
4,000	11	18	28	0.2
4,000	11	18	28	0.4
4,000	11	18	30	0
4,000	11	18	30	0.2
4,000	11	18	30	0.4
4,000	11	18	35	0
4,000	11	18	35	0.2
4,000	11	18	35	0.4
4,000	11	25	28	0
4,000	11	25	28	0.2
4,000	11	25	28	0.4
4,000	11	25	30	0
4,000	11	25	30	0.2
4,000	11	25	30	0.4
4,000	11	25	35	0.4
5,000	9	25	20	0
5,000	9	25	20	0.2
5,000	9	25	25	0
5,000	9	25	25	0.2
5,000	9	25	25	0.4
5,000	9	25	30	0
5,000	9	25	30	0.2
5,000	9	25	30	0.4
5,000	9	25	35	0
5,000	10	18	28	0
5,000	10	18	28	0.2
5,000	10	18	28	0.4
5,000	10	18	30	0
5,000	10	18	30	0.2
5,000	10	25	20	0
5,000	10	25	20	0.2
5,000	10	25	20	0.4
5,000	10	25	23	0
5,000	10	25	23	0.2
5,000	10	25	23	0.4
5,000	10	25	25	0
5,000	10	25	25	0.2
5,000	10	25	25	0.4
5,000	10	25	28	0
5,000	10	25	28	0.2
5,000	10	25	28	0.4
5,000	10	25	30	0.2
5,000	10	25	30	0.4
5,000	10	25	35	0.4
5,000	11	18	28	0
5,000	11	18	28	0.2
5,000	11	18	28	0.4
5,000	11	18	30	0
5,000	11	18	30	0.2
5,000	11	18	30	0.4
5,000	11	18	35	0
5,000	11	18	35	0.2
5,000	11	18	35	0.4
6,000	10	25	20	0.4
6,000	10	25	23	0.4
6,000	10	25	25	0.4
6,000	11	18	28	0
6,000	11	18	28	0.2
6,000	11	18	28	0.4
6,000	11	18	30	0
6,000	11	18	30	0.2
6,000	11	18	30	0.4

Results

From its present value of ∼20‰ (18), which signifies a 2% enrichment in ¹⁴C/C of CO₂ above preindustrial levels, Δ¹⁴CO₂ is certain to cross below the preindustrial level of 0‰ by 2030, but potentially as soon as 2019 (Fig. 1, Table S2). After 2030, simulated Δ¹⁴CO₂ trends diverge according to the continued growth, slowing, or reversal of fossil fuel CO₂ emissions in the RCP scenarios. Distinct patterns are simulated for different RCPs despite the range of model parameters used, indicating the fossil fuel emissions scenario is the determining factor for long-term Δ¹⁴CO₂ trends in these simulations rather than the rates of carbon cycling.

Table S2.

Tabulated annual midrange (Mid), maximum (Max), and minimum (Min) Δ¹⁴CO₂ simulated for each RCP, 2005–2100 (in ‰)

Year	RCP2.6			RCP4.5			RCP6.0			RCP8.5
	Mid	Min	Max	Mid	Min	Max	Mid	Min	Max	Mid	Min	Max
2005	66.3	64.8	67.7	66.3	64.8	67.7	66.3	64.8	67.7	66.3	64.8	67.7
2006	62.0	60.5	63.4	62.0	60.5	63.4	62.0	60.5	63.4	62.0	60.5	63.4
2007	57.2	55.4	59.0	57.3	55.5	59.1	57.3	55.5	59.1	57.2	55.4	59.0
2008	52.9	50.4	55.3	53.0	50.6	55.5	53.1	50.6	55.5	52.8	50.3	55.2
2009	48.5	45.3	51.6	48.8	45.6	51.9	48.9	45.7	52.1	48.3	45.2	51.5
2010	44.1	40.3	48.0	44.6	40.7	48.4	44.8	40.9	48.6	43.9	40.1	47.7
2011	39.9	35.4	44.3	40.5	36.0	44.9	40.8	36.3	45.2	39.5	35.1	44.0
2012	35.8	30.8	40.8	36.4	31.4	41.4	36.9	31.9	41.9	35.1	30.1	40.1
2013	31.9	26.3	37.4	32.5	27.0	38.1	33.2	27.7	38.8	30.7	25.1	36.2
2014	28.2	22.1	34.3	28.7	22.6	34.7	29.7	23.7	35.8	26.3	20.2	32.4
2015	24.7	18.1	31.2	25.0	18.4	31.5	26.3	19.8	32.9	22.0	15.4	28.6
2016	21.3	14.2	28.3	21.3	14.3	28.3	23.1	16.0	30.1	17.6	10.5	24.7
2017	18.0	10.5	25.4	17.7	10.2	25.2	19.9	12.4	27.3	13.3	5.7	20.8
2018	14.8	6.9	22.6	14.2	6.3	22.0	16.8	9.0	24.7	8.9	1.0	16.9
2019	11.6	3.4	19.9	10.7	2.4	18.9	13.8	5.6	22.0	4.6	−3.7	12.9
2020	8.6	0.0	17.2	7.2	−1.4	15.8	10.9	2.3	19.5	0.3	−8.4	9.0
2021	5.7	−3.2	14.6	3.8	−5.1	12.7	8.0	−0.9	16.9	−4.0	−13.0	5.0
2022	3.0	−6.2	12.3	0.4	−8.8	9.7	5.2	−4.0	14.3	−8.3	−17.6	1.1
2023	0.6	−8.9	10.1	−2.8	−12.4	6.7	2.3	−7.2	11.8	−12.5	−22.1	−2.8
2024	−1.6	−11.3	8.2	−6.1	−15.8	3.7	−0.5	−10.3	9.2	−16.6	−26.5	−6.7
2025	−3.6	−13.6	6.4	−9.3	−19.3	0.8	−3.4	−13.3	6.6	−20.7	−30.9	−10.6
2026	−5.4	−15.7	4.8	−12.4	−22.6	−2.1	−6.2	−16.4	4.0	−24.8	−35.2	−14.4
2027	−7.1	−17.5	3.3	−15.5	−25.9	−5.0	−9.0	−19.4	1.4	−28.8	−39.4	−18.3
2028	−8.7	−19.3	1.9	−18.5	−29.1	−7.9	−11.8	−22.3	−1.2	−32.8	−43.6	−22.0
2029	−10.1	−20.9	0.7	−21.5	−32.3	−10.7	−14.5	−25.3	−3.8	−36.8	−47.7	−25.8
2030	−11.4	−22.3	−0.5	−24.4	−35.4	−13.5	−17.3	−28.2	−6.3	−40.7	−51.8	−29.6
2031	−12.6	−23.7	−1.5	−27.3	−38.5	−16.2	−20.0	−31.1	−8.9	−44.6	−55.8	−33.3
2032	−13.6	−24.9	−2.4	−30.1	−41.4	−18.9	−22.8	−34.1	−11.6	−48.5	−59.8	−37.1
2033	−14.6	−25.9	−3.2	−32.9	−44.3	−21.5	−25.6	−37.0	−14.2	−52.4	−63.9	−40.9
2034	−15.4	−26.8	−3.9	−35.5	−47.0	−24.0	−28.4	−40.0	−16.9	−56.3	−67.9	−44.7
2035	−16.1	−27.6	−4.5	−38.1	−49.7	−26.5	−31.3	−42.9	−19.6	−60.2	−71.9	−48.5
2036	−16.7	−28.3	−5.0	−40.6	−52.3	−28.9	−34.1	−45.9	−22.3	−64.1	−75.9	−52.3
2037	−17.2	−28.9	−5.5	−43.0	−54.8	−31.2	−37.0	−48.9	−25.1	−68.0	−79.9	−56.1
2038	−17.6	−29.4	−5.8	−45.4	−57.3	−33.5	−39.8	−51.8	−27.8	−71.9	−83.9	−59.9
2039	−17.9	−29.8	−6.1	−47.7	−59.7	−35.8	−42.7	−54.8	−30.6	−75.8	−87.8	−63.7
2040	−18.2	−30.1	−6.2	−50.0	−62.0	−38.0	−45.5	−57.7	−33.4	−79.6	−91.7	−67.6
2041	−18.4	−30.4	−6.4	−52.2	−64.3	−40.2	−48.4	−60.6	−36.1	−83.5	−95.6	−71.4
2042	−18.6	−30.6	−6.5	−54.4	−66.5	−42.3	−51.2	−63.5	−38.9	−87.3	−99.4	−75.2
2043	−18.8	−30.8	−6.7	−56.4	−68.6	−44.3	−54.0	−66.4	−41.7	−91.2	−103.3	−79.1
2044	−19.0	−31.1	−6.9	−58.4	−70.6	−46.2	−56.9	−69.3	−44.4	−95.0	−107.2	−82.9
2045	−19.2	−31.3	−7.1	−60.3	−72.5	−48.1	−59.6	−72.1	−47.2	−98.9	−111.0	−86.8
2046	−19.4	−31.6	−7.3	−62.1	−74.3	−49.9	−62.4	−74.9	−49.9	−102.8	−114.9	−90.6
2047	−19.7	−31.8	−7.5	−63.9	−76.1	−51.7	−65.2	−77.7	−52.6	−106.6	−118.7	−94.4
2048	−19.9	−32.0	−7.7	−65.6	−77.8	−53.4	−67.9	−80.5	−55.3	−110.4	−122.5	−98.2
2049	−20.0	−32.2	−7.9	−67.2	−79.5	−55.0	−70.6	−83.2	−58.0	−114.1	−126.3	−101.9
2050	−20.2	−32.4	−8.1	−68.9	−81.0	−56.7	−73.3	−85.9	−60.7	−117.9	−130.1	−105.7
2051	−20.4	−32.5	−8.2	−70.4	−82.6	−58.2	−76.0	−88.6	−63.4	−121.6	−133.8	−109.4
2052	−20.5	−32.7	−8.4	−71.8	−84.0	−59.6	−78.7	−91.3	−66.1	−125.3	−137.6	−113.1
2053	−20.6	−32.7	−8.5	−73.1	−85.2	−61.0	−81.4	−94.0	−68.8	−129.1	−141.5	−116.8
2054	−20.7	−32.8	−8.6	−74.3	−86.4	−62.1	−84.1	−96.6	−71.5	−132.9	−145.3	−120.4
2055	−20.7	−32.8	−8.6	−75.3	−87.5	−63.2	−86.7	−99.3	−74.2	−136.6	−149.1	−124.1
2056	−20.7	−32.8	−8.7	−76.3	−88.4	−64.1	−89.4	−101.9	−76.8	−140.3	−152.9	−127.7
2057	−20.7	−32.7	−8.7	−77.2	−89.3	−65.0	−92.0	−104.6	−79.4	−144.0	−156.7	−131.3
2058	−20.7	−32.7	−8.6	−78.0	−90.1	−65.8	−94.6	−107.2	−82.1	−147.6	−160.4	−134.9
2059	−20.6	−32.6	−8.6	−78.7	−90.8	−66.6	−97.2	−109.8	−84.7	−151.3	−164.1	−138.4
2060	−20.5	−32.4	−8.5	−79.4	−91.5	−67.3	−99.8	−112.3	−87.3	−154.9	−167.8	−142.0
2061	−20.3	−32.3	−8.4	−80.0	−92.1	−67.9	−102.4	−114.9	−89.9	−158.4	−171.4	−145.4
2062	−20.2	−32.1	−8.3	−80.5	−92.6	−68.5	−105.0	−117.4	−92.5	−161.9	−174.9	−148.9
2063	−20.1	−31.9	−8.3	−81.0	−93.0	−68.9	−107.5	−120.0	−95.0	−165.3	−178.4	−152.2
2064	−19.9	−31.7	−8.1	−81.4	−93.3	−69.4	−110.0	−122.4	−97.6	−168.6	−181.8	−155.5
2065	−19.8	−31.5	−8.0	−81.7	−93.6	−69.7	−112.5	−124.9	−100.1	−171.9	−185.1	−158.7
2066	−19.6	−31.3	−7.9	−81.9	−93.8	−70.0	−115.0	−127.4	−102.7	−175.1	−188.4	−161.8
2067	−19.4	−31.1	−7.8	−82.1	−94.0	−70.2	−117.5	−129.9	−105.2	−178.3	−191.6	−165.0
2068	−19.2	−30.8	−7.7	−82.2	−94.1	−70.4	−120.0	−132.3	−107.7	−181.4	−194.7	−168.0
2069	−19.0	−30.5	−7.5	−82.3	−94.2	−70.5	−122.5	−134.8	−110.2	−184.4	−197.8	−171.0
2070	−18.8	−30.3	−7.3	−82.4	−94.2	−70.6	−124.9	−137.2	−112.6	−187.4	−200.9	−174.0
2071	−18.6	−30.0	−7.2	−82.4	−94.2	−70.6	−127.4	−139.7	−115.1	−190.4	−203.9	−176.9
2072	−18.4	−29.7	−7.0	−82.3	−94.1	−70.6	−129.8	−142.2	−117.4	−193.3	−206.8	−179.8
2073	−18.2	−29.4	−6.9	−82.2	−93.9	−70.5	−132.2	−144.6	−119.8	−196.1	−209.6	−182.6
2074	−18.0	−29.2	−6.8	−82.0	−93.7	−70.3	−134.5	−146.9	−122.0	−198.9	−212.4	−185.3
2075	−17.8	−29.0	−6.7	−81.7	−93.4	−70.1	−136.7	−149.2	−124.3	−201.5	−215.1	−188.0
2076	−17.7	−28.8	−6.6	−81.4	−93.0	−69.8	−138.9	−151.4	−126.4	−204.2	−217.7	−190.6
2077	−17.6	−28.6	−6.6	−81.0	−92.6	−69.4	−141.1	−153.6	−128.6	−206.7	−220.3	−193.2
2078	−17.4	−28.3	−6.5	−80.6	−92.1	−69.0	−143.2	−155.8	−130.6	−209.3	−222.9	−195.7
2079	−17.3	−28.1	−6.4	−80.1	−91.6	−68.6	−145.3	−157.9	−132.7	−211.8	−225.4	−198.1
2080	−17.1	−27.9	−6.4	−79.5	−91.0	−68.1	−147.3	−160.0	−134.7	−214.2	−227.8	−200.6
2081	−17.0	−27.7	−6.3	−79.0	−90.4	−67.6	−149.3	−161.9	−136.7	−216.6	−230.2	−203.0
2082	−16.9	−27.6	−6.3	−78.5	−89.9	−67.2	−151.1	−163.7	−138.4	−219.0	−232.6	−205.3
2083	−16.8	−27.4	−6.3	−78.2	−89.5	−66.9	−152.6	−165.3	−140.0	−221.3	−234.9	−207.6
2084	−16.8	−27.3	−6.3	−77.9	−89.1	−66.6	−154.0	−166.7	−141.3	−223.5	−237.1	−209.9
2085	−16.7	−27.1	−6.3	−77.7	−88.9	−66.5	−155.2	−167.9	−142.5	−225.7	−239.4	−212.1
2086	−16.6	−27.0	−6.3	−77.5	−88.7	−66.4	−156.2	−168.9	−143.5	−227.9	−241.5	−214.3
2087	−16.6	−26.9	−6.3	−77.4	−88.5	−66.4	−157.1	−169.8	−144.4	−230.0	−243.6	−216.4
2088	−16.6	−26.8	−6.4	−77.4	−88.4	−66.4	−157.9	−170.6	−145.1	−232.1	−245.7	−218.5
2089	−16.5	−26.7	−6.4	−77.4	−88.4	−66.5	−158.5	−171.3	−145.8	−234.1	−247.8	−220.5
2090	−16.5	−26.6	−6.5	−77.5	−88.3	−66.6	−159.1	−171.9	−146.3	−236.1	−249.8	−222.4
2091	−16.5	−26.5	−6.5	−77.5	−88.4	−66.7	−159.6	−172.4	−146.8	−238.1	−251.8	−224.3
2092	−16.5	−26.4	−6.6	−77.7	−88.4	−66.9	−160.1	−172.9	−147.4	−240.0	−253.8	−226.2
2093	−16.5	−26.3	−6.7	−77.8	−88.5	−67.1	−160.7	−173.4	−147.9	−241.9	−255.8	−228.0
2094	−16.5	−26.3	−6.8	−77.9	−88.5	−67.4	−161.3	−174.0	−148.5	−243.8	−257.9	−229.8
2095	−16.6	−26.2	−6.9	−78.1	−88.6	−67.6	−161.9	−174.6	−149.1	−245.7	−259.8	−231.5
2096	−16.6	−26.2	−7.0	−78.3	−88.8	−67.9	−162.5	−175.2	−149.8	−247.5	−261.8	−233.3
2097	−16.7	−26.2	−7.1	−78.5	−88.9	−68.1	−163.1	−175.8	−150.4	−249.3	−263.7	−235.0
2098	−16.7	−26.2	−7.3	−78.8	−89.2	−68.4	−163.8	−176.4	−151.1	−251.1	−265.5	−236.6
2099	−16.8	−26.2	−7.4	−79.1	−89.4	−68.7	−164.4	−177.1	−151.8	−252.8	−267.4	−238.3
2100	−16.8	−26.2	−7.5	−79.3	−89.6	−69.0	−165.1	−177.7	−152.5	−254.5	−269.2	−239.9

In the low-emission RCP2.6 simulation where fossil fuel emissions decrease after 2020, Δ¹⁴CO₂ remains nearly constant around −15‰ through the end of the century (Fig. 1). Fossil fuel emissions in the RCP4.5 and RCP6.0 scenarios continue to rise and then peak later, around 2040 and 2080, reducing Δ¹⁴CO₂ to a level of −80‰ (RCP4.5) or −150‰ (RCP6.0) in 2100.

The business-as-usual emissions in RCP8.5 reduce Δ¹⁴CO₂ more rapidly and more dramatically than the other RCPs: Δ¹⁴CO₂ is less than −100‰ by 2050 and reaches −250‰ in 2100, which means that atmospheric CO₂ in 2100 is as depleted in ¹⁴C as the “oldest” part of the ocean (19) (Fig. 2).

Fig. 2.

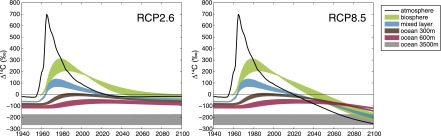
Simulation of radiocarbon in various carbon reservoirs for the low-emission and business-as-usual RCPs. Simulated Δ¹⁴C in biospheric and four ocean carbon reservoirs, surface mixed layer, 300, 600, and 3,500 m in RCP2.6 (Left) and RCP8.5 (Right). The black line shows the midrange value of simulated atmospheric Δ¹⁴CO₂ (full simulated range of Δ¹⁴CO₂ is shown in Fig. 1).

The simulated trends in atmospheric Δ¹⁴CO₂ propagate to other carbon reservoirs through natural carbon exchanges (Fig. 2). Reduction of fossil fuel emissions in RCP2.6 leads to nearly steady Δ¹⁴C in atmospheric, biospheric, and upper ocean carbon in 2100, slightly elevated above preindustrial levels.

As atmospheric Δ¹⁴CO₂ decreases strongly in the higher-emission scenarios, it becomes much more depleted in ¹⁴C than actively overturning carbon in the oceanic and biospheric reservoirs (shown for RCP8.5 in Fig. 2). After 2050, the simulated air–sea gradient of Δ¹⁴C in RCP8.5 is −50‰, opposite of the preindustrial gradient, and by 2100 atmospheric Δ¹⁴CO₂ is 150‰ lower than Δ¹⁴C at midthermocline depths of 600 m. Reversal of Δ¹⁴C gradients causes natural exchanges to transfer ¹⁴C from the ocean to the atmosphere (Fig. S1), as shown by Caldeira et al. (20). Caldeira et al. (20) used a similar carbon cycle model with the IS92-A scenario from the IPCC Third Assessment Report (21), which is comparable to RCP6.0. Emissions over the past 10 y have outpaced the IS92-A and RCP6.0 scenarios, and are currently on track to follow RCP8.5 (22). Δ¹⁴CO₂ is nearly 50‰ lower in 2050 and 100‰ lower in 2100 in RCP8.5 compared with RCP6.0 (Fig. 1), suggesting that fossil fuel emissions are likely to reduce Δ¹⁴CO₂ much faster than expected from the IS92-A scenario used by Caldeira et al. (20). As a result, the atmospheric inventory of ¹⁴C could approach the peak ¹⁴C inventory from the early 1960s later this century (Fig. S1).

Fig. S1.

Simulated radiocarbon inventories, relative to 1950, in atmospheric, oceanic, and biospheric reservoirs for the simulations shown in Figs. 1 and 2. The atmospheric radiocarbon inventory over 1950–2005 is shown in each panel.

Discussion

Though these simulations indicate tremendous changes to the global radiocarbon cycle and the use of radiocarbon in earth science and biogeochemical research, the potential impacts of future trends in Δ¹⁴CO₂ are much broader. Radiocarbon is currently used in a wide array of scientific and industrial applications, many of which exploit its radioactive decay to determine the age of carbon-containing specimens through radiocarbon dating.

Atmospheric CO₂ is presently aging at a rate of ∼30 y⋅y⁻¹, and by 2050 the atmosphere could appear to be 1,000 y old in conventional radiocarbon age (Fig. 1). In 2100, atmospheric CO₂ in RCP8.5 has the same radiocarbon content as a specimen that has undergone 2,000 y of radioactive decay—i.e., a specimen originating around AD 100. The aging of the atmosphere predicted by these simulations has the potential to severely impact the use of radiocarbon dating. Within the next 85 y, the atmosphere may experience Δ¹⁴CO₂ corresponding to conventional ages from within the historical period encompassing the Roman, Medieval and Imperial Eras. For archaeological or other items that are found without sufficient context to rule out a modern origin, radiocarbon dating will give ambiguous results.

Radiocarbon has various applications in isotope forensics (23). Some applications use the presence of elevated Δ¹⁴C in a sample to distinguish its origin to be subsequent to 1950, whereas other applications use the rapid changes in Δ¹⁴CO₂ after 1963 (the so-called “bomb curve”) to distinguish the year of origin of a sample more precisely. These techniques have been used to test vintages of wine and whisky, identify the age of human remains, and detect illegal ivory trading (23–25). As with radiocarbon dating, forthcoming Δ¹⁴CO₂ changes are likely to introduce ambiguity into these techniques, and the presence of elevated Δ¹⁴CO₂ will not identify samples with recent origins beyond ∼2030.

If the lower-emission RCPs 2.6 or 4.5 were followed instead of business-as-usual RCP8.5, the simulated stabilization of Δ¹⁴CO₂ (Fig. 1) would hinder the use of radiocarbon in fields such as ecology and physiology. These applications take advantage of the decreasing trend in Δ¹⁴CO₂ since the 1960s to evaluate the decadal-scale rate of turnover of carbon in soil compounds (26) or human cells (27), for example. Annual changes in Δ¹⁴CO₂ could become undetectable in two to three decades if CO₂ emissions are rapidly reduced, thereby limiting the use of these applications.

Another prominent application for radiocarbon involves the identification of CO₂ emitted by fossil fuel combustion in urban or continental regions (28, 29). Here too, the projected atmospheric changes will have a major impact. The sensitivity of Δ¹⁴CO₂ to local additions of fossil fuel-derived CO₂ depends on the concentration of atmospheric CO₂ and the Δ¹⁴C disequilibrium between atmospheric CO₂ and fossil carbon (being ¹⁴C-free, the Δ¹⁴C of fossil fuels is −1,000‰). Neglecting other effects, the sensitivity of Δ¹⁴CO₂ to fossil fuel-derived CO₂ is approximated by α ∼ (−1,000‰ − Δ¹⁴CO₂)/CO₂. The ratio α is presently −2.6‰ ppm⁻¹, but it drops to −1.6‰ ppm⁻¹ by 2050 and to −0.8‰ ppm⁻¹ by 2100 in RCP8.5; this suggests that measurement precision will have to increase by approximately a factor of 2 in the next few decades simply to maintain current detection capabilities for fossil fuel-derived CO₂.

Simulated trends in Δ¹⁴CO₂ therefore motivate new efforts to improve precision in radiocarbon measurements and to develop ancillary measurements that can help resolve ambiguity in radiocarbon analyses. The development of accelerator mass spectrometry (AMS) in the 1980s dramatically reduced the amount of time and the amount of carbon needed for analysis, compared with traditional decay counting techniques (30, 31). Further improvement in the precision of ¹⁴C detection by AMS is needed, as well as reductions in other sources of uncertainty (32), which may change as atmospheric Δ¹⁴CO₂ decreases. Ever-higher requirements in precision will also need to be met by alternative measurement techniques currently in development (33).

Fossil fuel emissions are now increasing faster than ever before. Continued business-as-usual growth in emissions will cause the atmosphere to approach a 1,000-y-old radiocarbon age by 2050 and a 2,000-y-old age by 2100. The application of radiocarbon in a wide array of disciplines implies that changing atmospheric radiocarbon content will have far-reaching impacts.

SI Text

A simple model based on Oeschger et al. (10, 13) was used to simulate carbon cycling in atmospheric, oceanic, and biospheric reservoirs. The model includes one atmospheric box, one biospheric box, and a one-dimensional box diffusion ocean model with 43 ocean boxes. The one-box atmosphere does not resolve horizontal gradients or gradients between the troposphere and stratosphere. The model was run in single deconvolution mode using RCP-specified CO₂ and emissions from 1765 to 2100 (34) after a 30,000-y spin-up time.

For Δ¹⁴C, spatially averaged tropospheric observations were used to specify atmospheric Δ¹⁴C up to 2005 (10). After 2005, atmospheric Δ¹⁴C was simulated by model fluxes. Radioactive decay was included, and natural ¹⁴C production was specified by the simulated total ¹⁴C inventory after model spin-up, specific to the model parameters. Production of ¹⁴C by the nuclear industry was assumed to remain constant at 2008 values (37) for 2005–2100. Negative emissions occur by biomass energy with carbon capture and storage (BECCS) (11), such that carbon with the isotopic composition of that entering the biospheric reservoir was removed from the system. Data on BECCS in the RCPs was provided by the RCP Task Group. To calculate fossil fuel CO₂ emitted to the atmosphere (Fig. 1), BECCS fluxes were added to net fossil fuel emissions. Since the BECCS data is based on nonharmonized emissions, there may be some discrepancy with net fossil fuel emissions before 2040 in RCP2.6, however this is unlikely to have a significant impact on the simulations.

Separate simulations were run using 117 sets of model parameters. The parameter sets were selected to explore carbon cycle dynamics across a range of parameter space that is consistent with CO₂ and Δ¹⁴C observations, within the context of the simple model running in single deconvolution mode. Parameter sets were chosen from a larger ensemble by examining the simulated oceanic Δ¹⁴C and oceanic bomb ¹⁴C and anthropogenic CO₂ inventories and the simulated total bomb ¹⁴C inventories, and selecting those sets that matched 20th-century observations, within their uncertainties (10). The parameter sets include values for the eddy diffusivity (K_eddy) of 3,000–6,000 m²⋅y⁻¹, atmospheric CO₂ residence time with respect to exchange with the mixed layer of 9–11 y (τ_am, corresponding to piston velocities of 14.8–18.1 cm⋅h⁻¹), atmospheric CO₂ residence time with respect to biospheric exchange (τ_ab) of 18–25 y, biospheric residence time (τ_ba) of 20–35 y, and CO₂ fertilization factor (β) of 0–0.4 (10). The model neglects the rapidly overturned biospheric carbon that is returned to the atmosphere within 1–3 y, one-third or more of net primary productivity (10, 14).

The governing equations of the model follow Oeschger et al. (13), and a brief presentation is included here. The single deconvolution residual (S) is given by the difference between the prescribed atmospheric growth rate (dC_a/dt) and the sum of net fossil fuel (F) and land use (L) emissions and the simulated oceanic and biospheric uptake:

$$S=\left[\frac{1}{2.12}\left(F+L+\frac{1}{{\tau }_{ba}}{C}_b\right)-\frac{1}{{\tau }_{am}}\left(C_a-C_{eq}\right)-\frac{1}{{\tau }_{ab}}\left(C_a+\beta \left(C_a-C_a^{PI}\right)\right)\right]-\frac{d{C}_a}{dt},$$

where C_a is the atmospheric CO₂ concentration (in ppm) and C^PI_a is the preindustrial CO₂ concentration, C_b is the total carbon in the biospheric reservoir in PgC, C_eq is the pCO₂ of the mixed layer box of the box diffusion model, calculated following Peng et al. (38) using temperature of 18 °C and salinity of 35 per mille. Units of mol⋅m⁻³ are used for carbon in ocean boxes. The factor 2.12 converts between ppm and PgC units. S is added to the biospheric reservoir.

The model simulates ¹⁴C using the following equations for the atmosphere, biosphere, ocean mixed layer, and a representative ocean subsurface box. The atmospheric equation shows the prognostic ¹⁴C simulation used after 2005; atmospheric ¹⁴C (C¹⁴_a) was prescribed by observations before 2005. B is carbon removed by BECCS. The model also simulates ¹³C using similar equations, and simulated δ¹³C is used to calculate Δ¹⁴C in each reservoir (5).

Atmosphere:

$$\begin{array}{c}\frac{d{C}_a^{14}}{dt}=\frac{1}{{\tau }_{am}}\left({\alpha }_{ma}^{14}{R}_m^{14}{C}_{eq}-{\alpha }_{am}^{14}{C}_a^{14}\right)-\frac{1}{{\tau }_{ab}}{\alpha }_{ab}^{14}{R}_a^{14}\left(C_a+\beta \left(C_a-C_a^{PI}\right)\right)+\frac{1}{2.12}\left(\frac{1}{{\tau }_{ba}}\hspace{0.17em}{C}_b^{14}+L{R}_b^{14}\right)\\ -S{\alpha }_{ab}^{14}{R}_a^{14}-\lambda C_a^{14}+P_{nat}+P_{nuc}\mathrm{-}\frac{1}{2.12}{\mathit{\alpha }}_{\mathit{ab}}^{\mathit{14}}{R}_a^{14}B\end{array}$$

Biosphere:

$$\frac{d{C}_b^{14}}{dt}=2.12\left(\frac{1}{{\tau }_{ab}}{\alpha }_{ab}^{14}{R}_a^{14}\left(C_a+\beta \left(C_a-C_a^{PI}\right)\right)+S{\alpha }_{ab}^{14}{R}_a^{14}\right)-\frac{1}{{\tau }_{ba}}\hspace{0.17em}{C}_b^{14}-L{R}_b^{14}-\lambda C_b^{14}$$

Mixed layer, subscripts m − 1 and m − 2 denote the two ocean boxes below the mixed layer:

$$\frac{d{C}_m^{14}}{dt}=k_{ma}\left({\alpha }_{am}^{14}{C}_a^{14}-{\alpha }_{ma}^{14}{R}_m^{14}{C}_{eq}\right)+K_m\left(-3C_m^{14}+4C_{m-1}^{14}-C_{m-2}^{14}\right)-\lambda C_m^{14}$$

Representative subsurface box s, subscripts s + 1 and s − 1 denote ocean boxes above and below box s:

$$\frac{d{C}_s^{14}}{dt}=K_s\left(C_{s-1}^{14}-2C_s^{14}+C_{s+1}^{14}\right)-\lambda C_s^{14}$$

R¹⁴ denotes the ratio ¹⁴C/C. The decay constant of ¹⁴C is represented with λ, and P_nat and P_nuc denote production by natural cosmic radiation and by nuclear power plants. Fractionation factors are given by α. The parameter k_ma is related to τ_am, accounting for the mixed layer thickness and unit conversion. The exchange coefficients between ocean boxes (K_m, K_s) are determined by the eddy diffusivity parameter (K_eddy) and the thickness of the boxes, 75 m in the mixed layer, 25 m in the thermocline, and 546 m in the deep ocean (13). In the form of the equations given above, the single deconvolution residual and the land use emissions are positive; slightly different forms are used if these terms are negative, relating to uptake or release from the biosphere and the associated fractionation.

The model was run in MATLAB R2013b using the ode23tb routine with default settings. An annual time step was used in the model output, although the ode23tb routine uses variable time steps in calculating the solution.

Simulated Δ¹⁴C are plotted in Figs. 1 and 2, including the range across different parameter sets. Fig. S1 shows the simulated inventory of radiocarbon atoms, relative to 1950, in atmospheric, biospheric, and oceanic reservoirs. Table S2 lists midrange values for simulated Δ¹⁴CO₂ in addition to upper and lower bounds of the simulated ranges. Table S1 lists the 117 parameter sets that were used in the simulations.