Force generation by the growth of amyloid aggregates

Significance

Force generation by active biological materials, in particular through native protein polymerization, is a key feature of cellular function and motility. Protein polymerization to form amyloid fibrils is associated with a number of devastating and currently incurable protein misfolding diseases. Unlike the polymerization of actin and tubulin driving cell motility, little is known about the mechanical properties of amyloid fibril growth. Here, we present direct experimental measurements of the force generated by growing amyloid fibrils. These measurements demonstrate that amyloid growth can release comparable forces to actin and tubulin polymerization. This conclusion is remarkable as actin and tubulin, unlike proteins forming amyloid fibrils, have evolved to generate force.

Abstract

The generation of mechanical forces are central to a wide range of vital biological processes, including the function of the cytoskeleton. Although the forces emerging from the polymerization of native proteins have been studied in detail, the potential for force generation by aberrant protein polymerization has not yet been explored. Here, we show that the growth of amyloid fibrils, archetypical aberrant protein polymers, is capable of unleashing mechanical forces on the piconewton scale for individual filaments. We apply microfluidic techniques to measure the forces released by amyloid growth for two systems: insulin and lysozyme. The level of force measured for amyloid growth in both systems is comparable to that observed for actin and tubulin, systems that have evolved to generate force during their native functions and, unlike amyloid growth, rely on the input of external energy in the form of nucleotide hydrolysis for maximum force generation. Furthermore, we find that the power density released from growing amyloid fibrils is comparable to that of high-performance synthetic polymer actuators. These findings highlight the potential of amyloid structures as active materials and shed light on the criteria for regulation and reversibility that guide molecular evolution of functional polymers.

The formation and accumulation of amyloid fibrils is a hallmark of a wide range of fatal disorders including neurodegenerative conditions (1–4). In addition to such links with pathology, a small but diverse range of proteins has been observed to adopt the generic β-sheet–rich supramolecular arrangement characteristic of amyloid fibrils as a part of their native function (5, 6), providing inspiration for their use in the context of artificial functional nanomaterials (7–10).

As a result of their prominent role in biology and medicine, a significant effort has been focused on the characterization of amyloid fibrils, including elucidation of their structural properties, mechanism of formation, and material properties (11–14). However, unlike the forces generated by the polymerization of native proteins, such as those undergone by cytoskeletal proteins (15–21), the forces generated as a result of amyloid growth have not been explored. The lack of information on this key dynamic property of an active material is in large part due to the difficulty of achieving spatial control of protein aggregation, compounded by the depletion of amyloidogenic precursor molecules that can limit the force generated in bulk solution experiments.

To address these challenges, we have designed microfluidic devices for measuring the force generated by the growth of amyloid aggregates (Fig. 1A). These devices contain arrays of microcantilevers that act as micrometer-scale dynamometers for the measurement of small forces, and include a supply channel to ensure that the concentration of the precursor monomer solution remains constant during the experiment, thus preventing growth from stalling due to monomer depletion (Fig. 1 A–C). An upper limit to the force generated by the motion of biological systems is set by the available free energy. Thus, for events with a step length, l, on the nanometer scale, such as the addition of a monomer to a biopolymer, the upper bound to the force generated would, from dimensionality arguments, be expected to scale with ${\mathrm{k}}_{\mathrm{B}}T/l$, and therefore to result in force on the piconewton scale. To achieve the mechanical forces on the order of micronewton, that are required to deflect the microcantilevers, we therefore measured the cumulative force generated by the growth of a large number of amyloid fibrils pushing against each cantilever face.

Fig. 1.

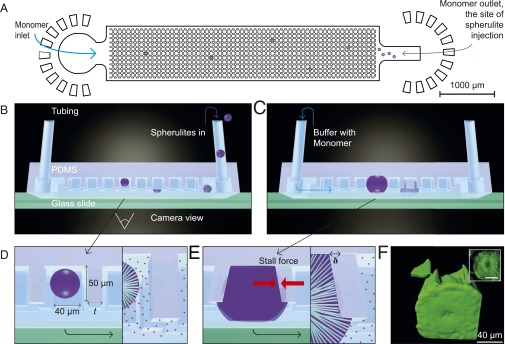
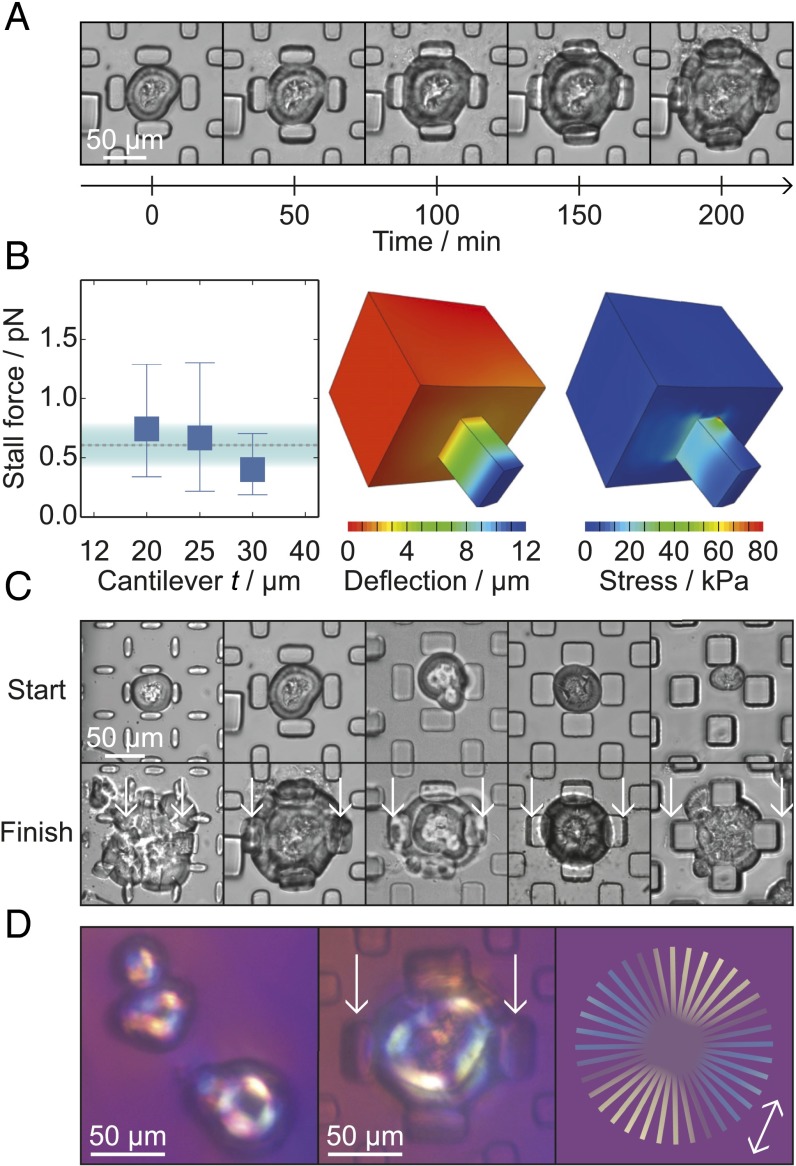
Experimental overview. (A) Design of the microfluidic device used in the present experiments. (B) Schematic diagram showing the introduction of preformed spherulites into the microfluidic device. To monitor the cantilever deflection, images were acquired through the glass slide at the bottom of the device. (C) Schematic diagram of spherulites growing within the device. (D) Illustration of a spherulite trapped between the microcantilevers, indicating the microcantilever dimensions for t = 20–40 μm. (E) Schematic diagram of a spherulite at the stall point, with red arrows indicating the opposing pressure and the measured deflection, δ. The Inset illustrates how radially arranged fibrils push against the cantilever. (F) Three-dimensional reconstruction of confocal fluorescence images of a ThT-stained spherulite within the microfluidic device. The Inset shows the corresponding inverted optics image of the spherulite fluorescence.

We focused initially on the polymerization of bovine insulin, one of the first proteins observed to undergo a conversion to the amyloid form in vitro (22), and a system commonly used to explore the phenomenon of amyloid assembly (22–25). Insulin has furthermore been observed to form amyloid deposits in vivo at injection sites of diabetic patients (26). Insulin self-assembly also has the propensity to result in the formation of spherical aggregate clusters, known as spherulites, with amyloid fibrils growing radially from a central core (22, 24, 25).

Results

We formed spherulite aggregates in bulk solution and introduced them into the microfluidic device so as to trap individual spherulites between polydimethylsiloxane (PDMS) cantilevers as shown schematically in Fig. 1 B–E. We observed that the clusters continued to grow when incubated under a continuous flow of fresh monomer solution (Fig. 2 and Supporting Information) and that growth ceased when the flow of monomer solution was stopped (Supporting Information). Analysis by polarization microscopy revealed that the spherulites consisted of ordered amyloid fibrils oriented in a radial manner (Fig. 2D), in agreement with earlier studies (24). Thus, the increase in the diameter of the spherulites originates from a well-defined ordered self-assembly process leading to the elongation of the component amyloid fibrils.

Fig. 2.

Microcantilever measurements. (A) Time course showing the gradual deflection of cantilevers with t = 20 μm. (B, Left) The force per fibril against cantilever depth, showing the mean and the range of forces measured for each value of t. For $t\hspace{0.17em}=$ 20, 25, and 30 μm, the numbers of stall points measured were $n\hspace{0.17em}=$ 15, 7, and 12, respectively. The mean force measured and the SD are shown by the dashed line and the shaded area. (Center) Schematic of a cantilever with t = 20 μm and δ = 11.8 μm as used in the finite element calculations. (Right) Diagram of the cantilever showing the local stresses calculated using the finite element method. (C) Images from the beginning (Top) and end (Bottom) of time courses with the five cantilever dimensions. (D) Images of spherulites placed between crossed polarizers and a wave plate. (Left) Preformed spherulites before injection into the microfluidic device. (Center) Trapped spherulite after incubation and growth between the cantilevers. (Right) Schematic figure showing the color of the polarized light depending on the orientation of the fibrils. The arrow indicates the orientation of the fast optical axis.

From the time courses acquired by bright-field optical microscopy of spherulites growing within the microfluidic devices, we observed that the force generated by the growing amyloid structures was sufficient to deflect the microcantilevers (Fig. 2 A and C). The mechanism of force generation is likely to be analogous to the ratcheting process underlying force generation by actin polymerization, where thermal fluctuations allow for the insertion of further protein molecules at the end of an elongating filament despite the presence of an opposing mechanical force (18, 20).

During incubation, the spherulites grew to contact the entire cantilever face, as revealed by bright-field and confocal microscopy (Fig. 1F), creating a uniformly loaded beam, as shown in Fig. 1E. Experiments were performed with microcantilevers with the dimensions shown in Fig. 1D and a varying thickness, t, of 12–40 μm. For cantilevers with t = 20–30 μm, we observed that the growth was arrested, and a stall point was reached, when the pressure exerted by the growing fibrils equaled that of the reaction force from the deflected cantilever (Fig. 2 A–C). The spherulites continued to grow in areas that were not experiencing a reaction force from the cantilevers (Figs. 1F and 2 A and C), indicating that the arrest of growth at the observed stall points was not caused by monomer depletion, but by stalling through the action of a mechanical force.

To probe the effect of an external load from the cantilevers on the growth kinetics of the insulin fibrils, we measured the rates of spherulite growth into free solution, where they did not encounter a cantilever, and the rates of cantilever deflection, which reflected the rate of growth against the cantilever face (Supporting Information). When growing against the cantilever face, the apparent rate of elongation was reduced compared with that for unimpeded spherulite growth (Supporting Information). This observation is analogous to the decrease in growth rate observed for native force-generating systems, for instance, actin in the presence of an opposing force (21). A comparison of the birefringence images in Fig. 2D of spherulites with and without incubation within the microfluidic devices did not reveal any change in the fibril arrangement in response to growth against the microcantilevers. The mature spherulites continued to show the birefringence pattern characteristic of a radial fibril arrangement.

To evaluate the force generated as a result of amyloid growth, we calibrated the observed cantilever deflections to the corresponding mechanical loading on the surface of the cantilevers by detailed material characterization. We performed compression tests and stress relaxation measurements to characterize the elastic behavior of the PDMS composing the cantilevers (Supporting Information). Using the measured shear relaxation modulus, we then performed finite element model (FEM) calculations to determine the forces required to obtain the observed cantilever deflections. The cantilevers were meshed with fully integrated second-order elements, using 10 elements through the thickness of the beam. Comparison of these values with the experimental findings thus yields the total force exerted by the ensemble of growing amyloid fibrils. Unlike many classical beam-bending models, FEM calculations fully balance the forces and moments of a given beam or cantilever. They are therefore not inherently limited to certain regimes of cantilever dimensions. However, they do require the use of an optimum type and number of elements in the simulation. These parameters were optimized through a mesh convergence study before the FEM calculations.

We then divided the cumulative force by the number of fibril ends at the cantilever face to find the force generated by a single filament. The number of filaments was estimated by making use of the knowledge of the density of the network (25) and the area of a fibril end, $a=3\times 4\hspace{0.17em}\text{nm}$ (23), to be 1.6 × 10⁷. This analysis revealed a mean force of $0.60\hspace{0.17em}\pm \hspace{0.17em}0.2$ pN per fibril for the three values of t, with an observed range of 0.2–1.3 pN (Fig. 2B). This mean value for the force generated by insulin amyloid growth was within the observed range for all three cantilever thicknesses.

From the FEM calculations, we were able to determine the overall mechanical force exerted by the amyloid fibrils on each cantilever, providing insight into the mean force generated by each fibril. In previous studies, the material properties of individual amyloid fibrils under compressive stress have been investigated (11, 27), and computational studies have revealed that for long amyloid fibrils the compressive stress required to induce fibril buckling decreased to a plateau of 10 MPa (11, 27). For fibrils with the cross-sectional area of insulin (23), this buckling stress would correspond to a force of several piconewtons on the fibril ends. This value is higher than the maximum reaction force from the cantilever, indicating that the insulin fibrils within the spherulites are unlikely to buckle under the back pressure from the microcantilevers. Furthermore, the close packing of the fibrils within the insulin spherulites would be expected to confer additional stability against buckling.

At the stall point, the pressure of the amyloid fibril growth was equal to the opposing pressure from the deflected cantilever. This pressure prevented further fibril elongation against the cantilevers. From the mechanical force generated by insulin amyloid growth, we were able to estimate the change in free energy of monomer addition and found this value to be of the same order of magnitude as reported in previous studies (28) (see Supporting Information for the calculation).

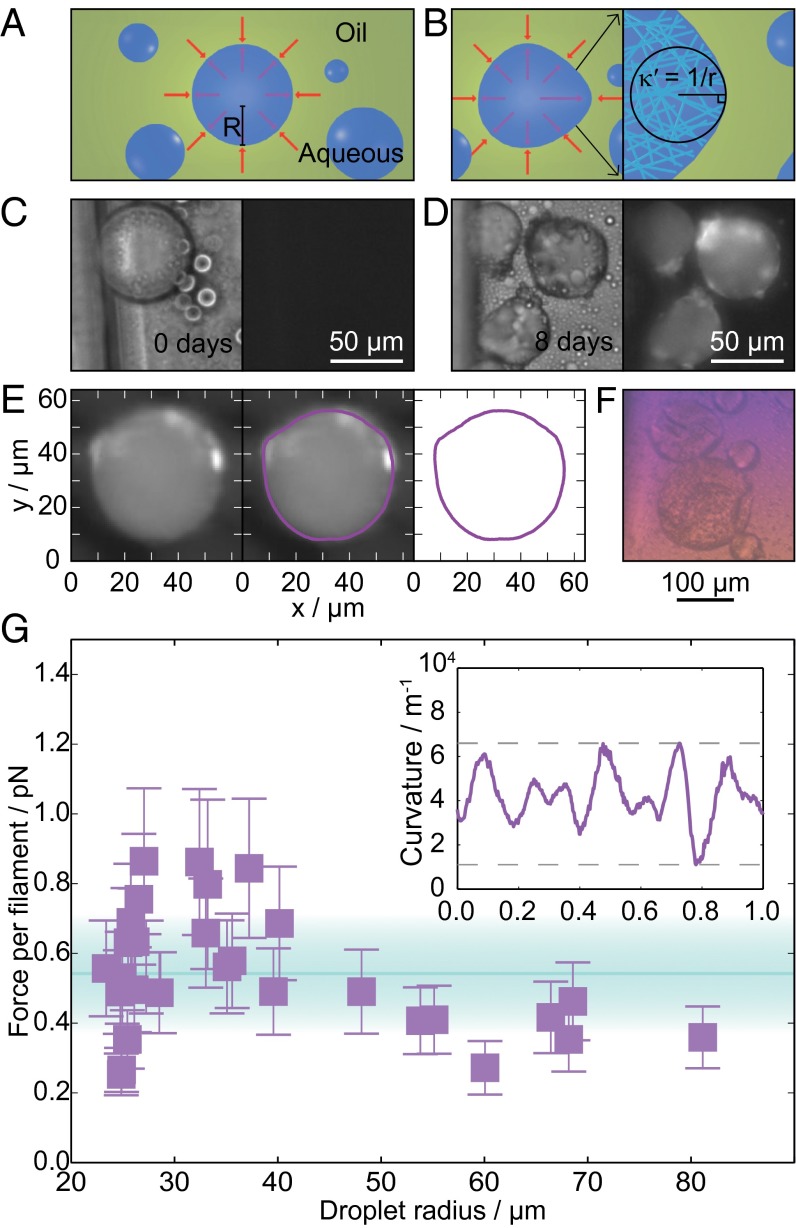
To investigate whether amyloid formation by other proteins generates comparable levels of force, we next focused on lysozyme. Amyloid formation by lysozyme is associated with a form of systemic amyloidosis in which significant quantities of aggregated material are deposited in vital organs such as the liver and the spleen (29). Lysozyme does not readily form the well-characterized clusters needed for the microcantilever measurements; however, this protein is very soluble in aqueous solution, enabling us to create an aqueous emulsion of highly concentrated protein in a continuous phase of fluorinated oil and surfactant, as shown in Fig. 3. This emulsion was incubated in sealed glass capillaries to prevent evaporation of the aqueous phase during the aggregation process. After incubation, as described in Materials and Methods, we observed deformation of the droplet interface that coincided with the appearance of Thioflavin T (ThT)-positive amyloid aggregates within the droplet (Fig. 3 C and D).

Fig. 3.

Forces from microdroplet deformation. (A) Diagram of aqueous lysozyme droplets (blue) with radius, R, in a continuous phase of oil and surfactant (green). Red arrows illustrate the normal stress balance before aggregation. (B) Diagram illustrating differences in the normal stress and curvature of droplets deformed by lysozyme amyloid formation (Left). Illustration of the random fibril orientation within the droplet (Right). (C) Bright-field (Left) and ThT fluorescence (Right) images of lysozyme droplets before aggregation. (D) Bright-field (Left) and ThT fluorescence (Right) images of lysozyme droplets after amyloid formation. (E) Tracing the droplet outline: fluorescence image of a deformed droplet; the droplet outline in magenta superimposed on the image; the droplet outline was then used to calculate the local curvature as a function of contour length. (F) Color image of deformed lysozyme droplets placed between crossed polarizers and a wave plate rotated at an angle of $45°$. (G) Force per filament against droplet radius (number of droplets = 30). The area shaded in cyan represents the mean value found $\pm$ SD. The Inset shows a plot of the local curvature against the normalized contour length for the droplet in E.

The force generated by the growth of lysozyme amyloid fibrils was obtained by calculating the difference in the Laplace pressure between the spherical and deformed droplets. For a spherical interface between two static fluids in the absence of external applied forces, the normal stress balance is described by Laplace’s law, which relates the difference between internal, $p_i$, and external, $p_e$, hydrostatic pressures to the curvature of the interface $p_i-p_e=2\gamma \kappa$, where γ is the surface tension, and $R=1/\kappa$ is the droplet radius. When fibrils push against the droplet surface, they introduce an additional normal stress component, ${\sigma }_{nn}$, which is balanced by the curvature pressure associated with droplet deformation $p_i-p_e=2\gamma {\kappa }^{\prime }-{\sigma }_{nn}$, where ${\kappa }^{\prime }$ is the curvature of the deformed interface. The maximum normal stress resulting from fibril formation was calculated by measuring the maximum curvature difference, $\mathrm{\Delta }\kappa$, of the droplet outline and multiplying this value by the surface tension, ${\sigma }_{nn}^{\text{M}}=\gamma \mathrm{\Delta }\kappa$, following an approach reported previously (30). The corresponding maximum total forces on the droplet interfaces were then obtained through integration of the normal pressure over the area of the droplet interface.

The lysozyme fibrils within the droplets were found to be randomly oriented from the lack of polarization when the droplets were placed between cross polarizers and a wave plate (compare Figs. 3F and 2D) (25). For each droplet, the number of molecules at the oil/water interface was calculated as described in Materials and Methods (31). A lower bound for the force per filament can thus be found from division of the total force for each droplet by the number of filaments, yielding a value of $0.54\pm 0.2\hspace{0.17em}\text{pN}$ per monomer addition for the force generated by lysozyme aggregation and an observed range of 0.3–0.9 pN (Fig. 3G).

Due to the random orientation of the amyloid fibrils, the droplet assay did not provide the same level of information about the fibril growth kinetics as did the microcantilever assay. The bounds for the magnitude of forces that can be assessed through this approach are defined by the force required to exceed the level of thermal fluctuations of the interface as a lower limit (32). The upper bound is set by the force that would disrupt the integrity of the droplet interface, or the opposing pressure, which would induce morphological changes in the fibrils, for instance through buckling. Adjusting the surface tension enables the detection of different ranges of forces.

Discussion

The forces generated by the growth of amyloid fibrils, determined here by different methods for two well-characterized protein systems, are of a closely similar magnitude; $0.60\pm 0.2$ pN for insulin and $0.54\pm 0.2$ pN for lysozyme. This similar level of mechanical force generation is likely to reflect the generic features of the amyloid structure, irrespective of the differences between the proteins in their native states (13).

The results presented here demonstrate further that, under the experimental conditions used, amyloid growth generates sufficient forces to deform soft interfaces with elastic moduli comparable to that of the cell membrane (33) and tissues with low moduli, such as those of the brain (34). In the light of this observation, it is interesting to note that the formation of large quantities of aggregates, such as occurs in a number of systemic amyloidoses, is associated with the deformation of the affected tissues (35). The results from the present study suggest that the buildup of mechanical forces during the growth process is a factor that is likely to contribute to this phenomenon.

Amyloid-based structures are not exclusively found in nature in the context of pathology, as a range of diverse functional materials, including bacterial coatings and catalytic scaffolds, has been shown to rely on the functional formation of amyloid. This observation has provided inspiration for the development of artificial protein-based nanomaterials (7, 9, 10). Such applications have to-date been largely static, exploiting the highly stable amyloid structure as a scaffold. However, the present results reveal that amyloid growth has significant potential as an actuator on the nanometer and micrometer scale. Indeed, the power density released as a result of the growth of insulin amyloid fibrils is of the order of milliwatts per kilogram (Supporting Information), a value comparable to high-performance microactuators (36). The measured growth rates for insulin spherulites in solution and within the microfluidic devices are on the order of micrometer per minute (25). Amyloid fibril growth possesses features that could make it well suited for actuation in solution, for instance, within fluidic systems. Depending on the protein involved and solution conditions used, the rates of amyloid growth could be further optimized for faster actuation, the rates of cantilever deflection by amyloid growth observed here are already similar to those achieved by chemical actuators (36).

To compare the elongation of amyloid fibrils to engineered chemomechanical force transducers, we calculated the surface stress exerted by the insulin fibrils on the PDMS microcantilevers using Stoney’s equation (Fig. 4) (see Supporting Information for the calculation). We found amyloid growth to induce a similar surface stress to engineered synthetic actuators (36–38). This result highlights the potential of amyloid structures for optimization as high-performance microactuators. Force generation by fibril growth is directional and, as demonstrated in this study, the combined force of multiple fibrils can be exploited to generate a targeted force several orders of magnitude larger than that of an individual fibril. For native force-generating polymers, force generation on the nanometer scale is exploited to perform mechanical work on the macroscale, for instance, by actin and myosin in muscle cells (39). As an active material, amyloid might therefore offer possibilities for direct actuation on the nanometer or micrometer scales.

Fig. 4.

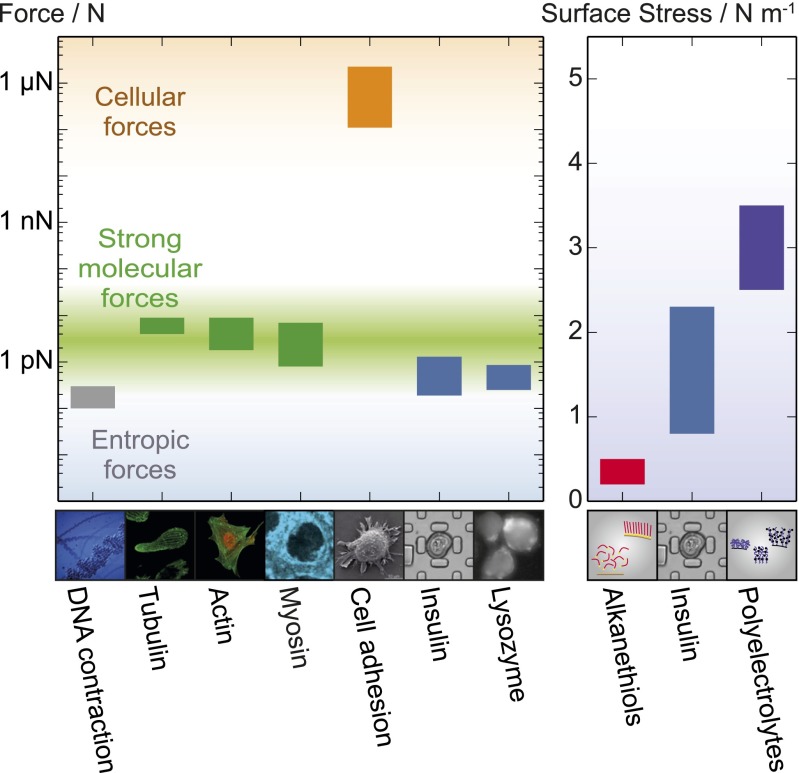
Force generation in a cellular context. (Left) Graph showing the range of forces associated with cellular processes; images of the different systems are shown below. (From Left to Right) The entropic force of DNA contraction (gray) (44); the force generated per polymer by the self-assembly of two types of native proteins: actin and tubulin (green) (16, 17, 19, 20), showing the range of values reported in the literature; myosin force generation with ATP hydrolysis (green) (15, 17); the concerted force generation at the level of entire cells, represented by Caulobacter crescentus substrate adhesion (orange) (45); growth of insulin and lysozyme amyloid fibrils (blue). (Right) The surface stress exerted by polymer assemblies on cantilever faces: alkanethiols on a gold surface (37, 38); insulin spherulites, containing 9.5% (vol/vol) protein (blue); synthetic polyelectrolyte actuators (purple) (36).

Finally, we consider the forces found here to result from the propagation of the amyloid state in the context of forces generated by functional processes at the cellular level. Our results reveal that the forces generated by amyloid growth can reach the same order of magnitude as those resulting from the polymerization of cytoskeletal proteins (Fig. 4) (15–20). This finding is remarkable given the fact that actin and tubulin have evolved to generate mechanical force via self-assembly as a part of their native functions. Amyloid fibrils, by contrast, are generally found as pathological species where force generation is simply a consequence of the nature of the fibril structure (13, 28). In contrast to the formation of persistent amyloid structures, however, the polymerization of cytoskeletal proteins must be reversible in a controllable manner under physiological conditions. Indeed, once formed, amyloid structures generally represent an energetically favorable conformation and are generally very persistent under physiological conditions. They do therefore not possess the dynamic properties required for cytoskeletal protein self-assembly. Despite the stringent criteria for control and reversibility of polymerization imposed on cytoskeletal protein systems, actin and tubulin have evolved to generate mechanical forces on the piconewton scale and can moreover generate additional force by exploiting associated proteins and the hydrolysis of nucleotides as a source of energy (15, 17). The findings presented here, therefore, give insight not only into the nature of the amyloid state in disease but also highlight some of the selection criteria that bias molecular evolution to favor and tune the properties of active materials for functional purposes. Moreover, the magnitude of force generation by amyloid growth illuminates the potential and ultimate performance limits of artificial protein-based active materials.

Materials and Methods

Microfluidic Device Fabrication.

Microfluidic devices were fabricated using soft lithography into PDMS using a 1:10 ratio of cross-linker to elastomer (184 Sylgard; Dow Corning) (40). Lithography masters were prepared in two photolithography steps: a 25-μm layer with the design for the gap below the free cantilever ends, followed by a 50-μm layer with the pillar design (Fig. 2) to create integrated cantilevers.

Spherulite Measurements.

Insulin spherulites were formed by incubating 100 μL of 1 mM (5.8 mg/mL) bovine insulin and 20 mM NaCl in HCl, pH 1.9, at 65 °C for 25 min. Experiments were performed in devices with t = 12, 20, 25, 30, and 40 μm, respectively.

Preformed spherulites were trapped between the cantilevers and then incubated on a microscope heating stage at 65$°\text{C}$, while supplied with monomeric insulin solution at a sufficient concentration to saturate the fibril growth rate, >1 mg/mL (20 mM NaCl, HCl pH 1.9, filtered) (25). The monomer solution was passed through the device at a flow rate of 150 $\pm$ 0.53 μL/h (Hamilton glass syringe; Harvard Apparatus).

Microscopy.

Aggregate growth and cantilever deflection were monitored at 30-s intervals using a CCD camera operated through long working distance inverted optics (Zeiss; Metamorph Software).

For the confocal fluorescence microscopy experiments, spherulites were incubated between the cantilevers in the presence of ThT, which selectively stained the amyloid fibrils. The insulin spherulites were analyzed using a confocal microscope (Laser Scan Confocal; Leica Microscope) with a tunable argon laser 458/477/488/514 nm at 30 mW. The 3D images were reconstructed using the Imaris image analysis software (on average 383 z-stack slices per protein spherulite).

The birefringence measurements were carried out using an uncoated quartz zero-order wave plate for 550 nm (United Crystals) and two linear polarizers (Thorlabs; LPVISE2X2). The samples were illuminated with linearly polarized light. The transmitted light was then passed through the green wave plate with its optical axis aligned at 45$°$ to the direction of polarization. This left the green light unchanged, whereas red- and blue-shifted light were elliptically polarized. A second polarizer, perpendicular to the first, filtered out the green light. In the absence of a birefringent sample, the transmitted light had a purple hue, which was recorded using a color camera (Thorlabs; DCC1645C).

A birefringent analyte, such as aligned amyloid fibrils, either effectively increases or decreases the thickness of the wave plate, depending on whether the fast optical axes of analyte and wave plate are parallel or perpendicular. Parallel fast optical axes result in longer wavelengths being filtered out by the detector system and consequently yielded a blue color, whereas perpendicular fast axes lead to a decrease of shorter wave spectral components and thus a yellowish color. It has been shown that amyloid fibrils have their slow optical axis along the growth direction (41–43); the Maltese cross-shaped pattern with the yellow colored diagonal in parallel to the fast optical axis of the wave plate resulting from the spherulites shown in Fig. 2D therefore demonstrates the radial growth of the insulin fibrils.

Finite Element Modeling.

The material properties of the PDMS devices were characterized as described in Supporting Information. From stress relaxation experiments, the shear relaxation modulus was calculated and normalized by the instantaneous shear modulus (0.54 MPa) (Supporting Information). Elasticity was modeled using the Marlow strain energy density potential and the uniaxial compression data shown in Supporting Information. The volumetric response was defined using a Poisson’s ratio of 0.49. The viscoelastic response was modeled using the time-dependent normalized shear relaxation modulus shown in Supporting Information [the viscoelastic Prony series parameters that characterize the viscoelastic behavior are calculated automatically by ABAQUS (Dassault Systèmes) using these data].

A mechanical displacement δ was specified as a boundary condition at a reference node positioned in the center of the beam. The reference node was linked to the surface of the beam using multipoint constraints in ABAQUS. The value of δ was altered iteratively until the predicted maximum tip deflection was equal to the value measured experimentally, for instance, 11.8-μm maximum tip deflection for t = 20 μm. The reaction force at the reference node was calculated as an output of the model. The reaction forces for cantilevers with t = 20, 25, and 30 μm were used to calculate the forces per insulin fibril shown in Fig. 2B.

Droplet Deformation Measurements.

Droplet deformation by hen egg lysozyme fibrils was measured for two sets of aggregation conditions: 60 mg/mL lysozyme in 50 mM HCl and 20 mM NaCl, with 20 μM ThT as a reporter of fibril formation, n = 12, and 100 mg/mL hen egg lysozyme in 133 mM HCl and 50 mM NaCl, with 20 μM ThT, n = 18. Droplets were prepared either mechanically, by mixing the relevant protein solution with an equivalent volume of fluorinert FC-40 (Sigma) containing 2% (vol/vol) surfactant or through a T-junction on chip. Glass capillaries (VitroCom) were filled with the emulsion by capillary action, sealed, fixed on a microscope glass slide, and incubated at 65 °C. Bright-field and fluorescence images were obtained using a CCD camera and inverted optics as above.

The droplet outlines were traced and the curvature at each point determined using scripts written in Python (open source). We then used the method published by Campàs et al. (30) to determine the pressure difference across the interface of the deformed droplets. The radius of the corresponding spherical droplet, R, was estimated as the mean radius of the deformed droplet, and from this value the surface area of the droplet, A, was calculated. In combination with the volume fraction of protein in the solution, $f_p$, and the radius of a monomer, r = 2.5 nm (31), the number of molecules at the droplet interface, $N_f$, were found. The filaments were found to be randomly oriented with respect to the droplet interface (Fig. 3F) to account for the random direction of the force generated a prefactor of 1/3 was added to the $N_f$ calculation: $N_f=\left(1/3\right)\cdot f_p\cdot \left(4R^2/r^2\right)$, resulting in a range of 4.6 × 10⁶ to 1.0 × 10⁸, varying with the droplet size. This enabled us to estimate the force per filament $F={\sigma }_{nn}\hspace{0.17em}A\hspace{0.17em}{N}_f^{-1}$.