Sparse and dense coding of natural stimuli by distinct midbrain neuron subpopulations in weakly electric fish

Katrin Vonderschen; Maurice J Chacron

doi:10.1152/jn.00588.2011

. Author manuscript; available in PMC: 2015 Aug 13.

Published in final edited form as: J Neurophysiol. 2011 Sep 21;106(6):3102–3118. doi: 10.1152/jn.00588.2011

Sparse and dense coding of natural stimuli by distinct midbrain neuron subpopulations in weakly electric fish

Katrin Vonderschen ¹, Maurice J Chacron ¹

PMCID: PMC4535167 CAMSID: CAMS4950 PMID: 21940609

Abstract

While peripheral sensory neurons respond to natural stimuli with a broad range of spatiotemporal frequencies, central neurons instead respond sparsely to specific features in general. The nonlinear transformations leading to this emergent selectivity are not well understood. Here we characterized how the neural representation of stimuli changes across successive brain areas, using the electrosensory system of weakly electric fish as a model system. We found that midbrain torus semicircularis (TS) neurons were on average more selective in their responses than hindbrain electrosensory lateral line lobe (ELL) neurons. Further analysis revealed two categories of TS neurons: dense coding TS neurons that were ELL-like and sparse coding TS neurons that displayed selective responses. These neurons in general responded to preferred stimuli with few spikes and were mostly silent for other stimuli. We further investigated whether information about stimulus attributes was contained in the activities of ELL and TS neurons. To do so, we used a spike train metric to quantify how well stimuli could be discriminated based on spiking responses. We found that sparse coding TS neurons performed poorly even when their activities were combined compared with ELL and dense coding TS neurons. In contrast, combining the activities of as few as 12 dense coding TS neurons could lead to optimal discrimination. On the other hand, sparse coding TS neurons were better detectors of whether their preferred stimulus occurred compared with either dense coding TS or ELL neurons. Our results therefore suggest that the TS implements parallel detection and estimation of sensory input.

Keywords: information theory, neural coding, electrocommunication

How neural populations encode sensory information changes at each processing stage in the brain. In particular, neurons located in more peripheral sensory areas tend to use a dense code in order to represent the external environment in that they respond to a wide range of stimuli. In contrast, neurons located in more central areas tend to use a sparse code in that they respond selectively to particular stimulus features (Barlow 1972) such as faces (Rolls and Tovee 1995; Young and Yamane 1992), persons and/or objects (Quiroga et al. 2005), places (Thompson and Best 1989), odors (Hromádka et al. 2008; Perez-Orive et al. 2002), or sounds (DeWeese et al. 2003; Olshausen and Field 2004). Sparse neural codes are thought to be advantageous as they are easier to read out by downstream neurons and are more energy efficient (Attwell and Laughlin 2001; Földiák and Young 1995). However, the nature of the mechanisms by which a dense code is converted into a sparse one is poorly understood and remains an important problem in systems neuroscience.

Here we focus on the transition from dense to sparse coding across two subsequent sensory processing stages in the weakly electric fish Apteronotus leptorhynchus. These fish actively generate a quasi-sinusoidal electric field through the electric organ discharge (EOD). Electroreceptors on the skin monitor EOD amplitude modulations (AMs) caused by prey or conspecifics and relay this information to pyramidal cells within the electrosensory lateral line lobe (ELL). Pyramidal cells then synapse onto cells within the midbrain torus semicircularis (TS), which is homologous to the mammalian inferior colliculus (see Chacron et al. 2011 for review). While ELL pyramidal cells tend to respond to a broad range of electrosensory stimuli (Bastian 1981; Chacron et al. 2005), TS neurons instead display much more selectivity in their responses (Fortune and Rose 1997a, 2000) and the mechanisms leading to this selectivity are largely unknown (but see Chacron et al. 2009; Chacron and Fortune 2010).

The spatiotemporal characteristics of natural stimuli in these fish are well known (Zakon et al. 2002). In particular, two fish that come into close contact will experience a sinusoidal AM of their field (i.e., a beat) whose frequency is equal to the difference frequency between the fields and ranges between 0 and 400 Hz (Benda et al. 2005; Zakon et al. 2002). Moreover, these fish display communication stimuli (i.e., chirps) during agonistic and courtship encounters that consist of transient increases in their EOD frequency that occur on top of the beat (Bastian et al. 2001; Hupé and Lewis 2008; Zakon et al. 2002). Although the responses of ELL pyramidal cells to beats and chirps are well characterized (Krahe et al. 2008; Marsat et al. 2009; Marsat and Maler 2010), the responses of TS neurons to these stimuli are largely unknown.

To better understand the mechanisms by which TS neurons become more selective than ELL neurons, we investigated the responses of ELL and TS neurons to a wide range of behaviorally relevant stimuli. While a significant fraction (19%) of TS neurons were highly selective in their responses, the remainder (81%) displayed dense coding similar to that of ELL neurons. Our results therefore indicate that the transition from a dense code in ELL to a sparse code in TS does not involve making every TS neuron more selective than its afferent input. Rather, our results show that it involves making a subpopulation of TS neurons display sparse responses in order to better detect the presence of relevant stimuli in the environment and making a distinct subpopulation display dense responses in order to better discriminate between different stimuli. We suggest that combining the information streams from these two subclasses allows the animal to both optimally detect and distinguish between different natural stimuli. A short report of part of our results has been published previously in abstract form (Vonderschen and Chacron 2009).

METHODS

Experimental preparation

Forty-six adult specimens of either sex of the weakly electric fish A. leptorhynchus were used in this study. The fish were housed in groups (2–8) at controlled water temperature (26–29°C) and water conductivity (300–600 μS/cm) in 150-liter tanks according to published guidelines (Hitschfeld et al. 2009). For experiments animals were transferred to a Plexiglas tank (30 cm × 30 cm × 10 cm) supplied with water from the animal’s home tank. Animals were paralyzed with an intramuscular injection of tubocurarine chloride hydrate (100 μl of a 0.2% solution; Sigma, St. Louis, MO) and artificially respirated with water flowing through their gills at a rate of ~10 ml/min. All surgical methods have been described previously (Chacron and Bastian 2008; Chacron et al. 2009; Chacron and Fortune 2010; Krahe et al. 2008; Toporikova and Chacron 2009). Briefly, the animal’s head was locally anesthetized (5% lidocaine ointment). Subsequently, the skull was partly exposed and a small fenestra was carved over the recording region. All procedures were approved by McGill University’s animal care committee.

Recordings

Extracellular recordings from pyramidal cells in the hindbrain ELL were obtained with Carbostar electrodes (Kation Scientific). Recordings were limited to pyramidal cells within the lateral and centrolateral segments of ELL that respond most strongly to communication signals (Marsat et al. 2009; Marsat and Maler 2010). Pyramidal cells within these segments can be distinguished from cells within the centromedial segment based on recording depth, the medio-lateral and rostro-caudal positions of the recording electrode with respect to surface landmarks such as the “T0” vein and its afferent veins (Maler et al. 1991), and their responses to sensory input as previously described (Krahe et al. 2008; Marsat et al. 2009; Marsat and Maler 2010). Using these criteria, we found that n = 6 ELL neurons were located in the centrolateral segment while the remaining n = 20 were located in the lateral segment. As response selectivity as quantified in this study (see below) did not differ significantly between ELL neurons recorded in the centrolateral and the lateral segments (Kolmogorov-Smirnov test, P = 0.52), the data were pooled.

ELL pyramidal cells provide excitatory input to the midbrain torus semicircularis dorsalis (TS) (Fig. 1A). Recordings from TS neurons were obtained with patch electrodes (Chacron et al. 2009; Chacron and Fortune 2010; Rose and Fortune 1996). Briefly, electrodes were pulled on a horizontal electrode puller (Sutter Instruments P-97) with borosilicate glass capillaries (OD 1 mm, ID 0.58 mm; AM Systems) and filled with patch solution (in mM: 100 KAc, 43 D-mannitol, 20 KOH, 10 HEPES, 2 KCl, 1 MgCl₂ anhydrous, pH 7–7.3); impedances ranged between 10 and 30 MΩ. Extracellular recordings were obtained in the “loose patch” configuration (n = 128). Some neurons (n = 59) were also recorded from intracellularly. As the response properties of these neurons were not significantly different from those of neurons that were recorded from extracellularly, the data were pooled. Furthermore, some of these intracellularly recorded neurons (n = 14) were filled with neurobiotin (Rose and Fortune 1996). Subsequent histological analysis revealed that these were distributed in layers II–VIIID (data not shown), which suggests that our recordings came from most if not all TS layers.

Recordings were amplified (AM Systems 1700, Axoclamp 2B with HS2A × 0.1 headstage, respectively), digitized at 10-kHz sampling rate (CED 1401 hardware plus Spike2 software; Cambridge Electronic Design, Cambridge, UK), and stored on a computer for later analysis.

Stimulation

A detailed description of the stimulation protocol was given by Bastian et al. (2002). As A. leptorhynchus possesses a neurogenic electric organ during adulthood, its EOD is unperturbed by injection of paralytic agents. To obtain AMs of the fish’s own EOD, the desired AM waveform was first multiplied (MT 3; Tucker Davis Technologies) with a sinusoidal carrier wave that was phase-locked to the animal’s own EOD. The resulting signal was then attenuated (Leader LAT-45; Leader Electronics), isolated from ground (WPI A395 linear stimulus isolator), and delivered to the experimental tank via a pair of silver-silver chloride electrodes located on each side of the animal. Such stimuli will primarily activate p-type tuberous electroreceptors on the animal’s skin that respond to such modulations through changes in firing rate (Scheich et al. 1973). However, it has been shown previously in other species of weakly electric fish that AMs of the EOD will also cause latency shifts in the firing of t-type electroreceptors (Carlson and Kawasaki 2006b, 2008; Heiligenberg and Bastian 1980; Heiligenberg and Rose 1985; Kawasaki and Guo 1996; Mathieson et al. 1987; Rose and Heiligenberg 1985). Since the p- and t-unit pathways display anatomical convergence at the levels of the ELL and TS (Mathieson et al. 1987; Rose and Heiligenberg 1985), we cannot fully exclude that the activation of the t-unit pathway contributes to the observed responses of ELL and TS neurons.

The AM stimuli used in this study consisted of steps (250-ms duration, 1-Hz repetition), zero mean low-pass filtered (120-Hz cutoff frequency, 8th order Butterworth filter) Gaussian white noise (5 repetitions of a 20-s-long segment), beats, and the AMs that are associated with chirps (Fig. 1D). Beats are sinusoidal AMs that naturally result from the interference of two fishes’ EODs and signal sex or social status (Hagedorn and Heiligenberg 1985). We used different beat frequencies (1, 2, 4, 8, 16, 32, 64, 128, 256 Hz).

Chirps are considered communication signals and occur when one fish transiently increases its EOD frequency in a stereotyped fashion (Fig. 1, B and C). The two major chirp types are distinct by their duration, chirp frequency excursion and amplitude modulation, and associated beat frequencies (Bastian et al. 2001; Hagedorn and Heiligenberg 1985; Zupanc and Maler 1993; Zupanc et al. 2006): small chirps (type II, frequency excursion 30–180 Hz, duration ~15 ms) have been associated with agonistic behaviors that are mostly observed during male-male encounters. As males tend to produce higher EOD frequencies (800–1,000 Hz) than females (600–800 Hz) (Zakon et al. 2002), the EOD frequency differences between same-sex con-specifics tend to be smaller than those between opposite-sex conspecifics. As a consequence, small chirps tend to occur on top of a lower (<100 Hz)-frequency beat. In contrast, big chirps (type I, frequency excursion 300–900 Hz, duration ~25 ms, amplitude reduction) have been associated with courtship (Bastian et al. 2001). They commonly occur during male-female encounters and occur on top of a higher-frequency beat. Both big and small chirps occur randomly at any phase of the beat (Hupé and Lewis 2008).

This frequency excursion can be simulated as a Gaussian function and leads to an accelerated phase progression of the beat (Benda et al. 2005). To obtain a beat signal with an embedded chirp S(t) = cos[ϕ(t)], we model the phase as a linear sum of the phase progression due to the beat and the phase progression due to the chirp: ϕ(t) = Δϕ_Beat(t) + Δϕ_hirp(t), where Δϕ_Beat(t) = 2π bf t with bf being the beat frequency in Hz.

The phase advance due to the chirp Δϕ_Chirp is defined by the integral over time of the Gaussian function that describes the frequency excursion during a chirp:

Δ ϕ_{chirp} (t) = cf \int_{- \infty}^{t} e^{- {(\frac{x - σ - t_{c}}{σ})}^{2}} d x

where $σ = Δ t / 2 \sqrt{ln (10)}$ , with Δt being the chirp duration equivalent to the width of the Gaussian function at 10% height; cf is the maximum of the frequency excursion during the chirp; t_c is the chirp onset time expressed relative to the beat phase and is given by

t_{c} = \frac{n + cp}{bf}

with n being the number of beat cycles preceding the chirp and cp being the phase of the beat at which the chirp occurs. For small chirps we used a chirp duration of 14 ms. We varied three parameters: the beat frequency (bf: 5, 10, 20, 30, 60 Hz), the maximum frequency of the chirp frequency excursion [i.e., the chirp frequency (cf): 30, 60, 90, 123.2, 153 Hz], and the chirp onset phase of the beat [i.e., the chirp phase (cp): 0, 25, 50, 75% of the beat period]. Note that, because of limited recording times, we could not test all possible combinations of these parameters for a given neuron. Different chirp phases were presented with chirp excursion frequency fixed to 60 Hz and beat frequency to 5 Hz as default values; the different chirp frequencies were presented with the beat frequency set to 5 Hz and the chirp phase chosen to be the one that elicited the best responses for that neuron. Finally, beat frequency was varied with the chirp frequency fixed to 60 Hz, and the chirp phase was fixed to the one that elicited the best responses.

Big chirps were generated with a duration of 24 ms and the onset phase fixed to cp = 0%. The default settings were a beat frequency of 100 Hz and a chirp frequency of 600 Hz. In addition, big chirps were characterized by a Gaussian amplitude reduction to 25% of the peak-to-peak amplitude during the beat, whose time course mirrored that of the frequency excursion. We also varied some big chirp attributes such as the beat frequency (bf: 100, 200, 300, 400 Hz), the chirp frequency (cf: 0, 300, 600 Hz), and the amplitude reduction (100%, 75%, 50%, 25%). As with small chirps, only one parameter was varied while the others were held at their default value. A specific chirp was presented sequentially at least 10 times at a fixed rate. The interval between two successive small chirps was either 5 beat cycles, 10 beat cycles, or 1 s. Big chirps were presented at a rate of 1/s.

Since the rate of small chirp production is much higher than that of big chirps even in male-female encounters (Bastian et al. 2001; Hupé and Lewis 2008) and it was impossible to present every stimulus to every neuron given the finite recording times, we decided to concentrate on varying small chirp attributes more than big chirp attributes for most of our data set. As such, the standard stimulus protocol comprised 24 stimuli (1 step, 1 noise, 9 beats, 1 big chirp, 12 small chirps). However, for three ELL and five TS neurons, we presented big chirps with varying attributes as described above.

Data analysis

All off-line analysis routines were custom written in Matlab (MathWorks, Natick, MA). Spike waveforms were detected by band-pass filtering the recorded trace (low cutoff frequency 20 Hz, high cutoff frequency 4 kHz, 8-pole Butterworth filter) and setting an appropriate threshold. Suprathreshold events (i.e., events that crossed the threshold from below) were sorted and identified by semiautomatic cluster analysis based on the minimum and maximum peaks of the waveform corresponding to each event. Single-unit recordings were confirmed by standard criteria such as the consistency of the action potential shape and the presence of an absolute refractory period.

Testing response significance

Responses to all stimuli were accumulated as peristimulus time histograms (PSTHs) across 10 or more trials and were smoothed with a 6-ms-wide rectangular window. Depending on the stimulus, the PSTHs were triggered on the start of identical noise segments, the step onset, the chirp onset, or phase zero of the beat. Whether a neuron responded significantly to a given stimulus was tested based on the entropy of the PSTH (Kajikawa and Hackett 2005) computed over a time window starting at stimulus onset and lasting 250 ms. For chirp stimuli the response window was set to a quarter of the time between two chirps and was resampled such as to have 20 bins in all cases. The entropy was then computed as

H = - \sum_{i = 1}^{n} p (i) {log}_{2} p (i)

with p(i) being the probability of a spike falling into bin i.

The entropy contained in the PSTH was compared with the entropy of PSTHs generated from surrogate data sets. One thousand surrogate data sets were generated by shuffling the spike times randomly in each trial of the original PSTH, and the entropy was computed for each surrogate data set. We considered the response significant if the entropy in the original PSTH was lower than in 95% of the simulations (P < 0.05 level). We note that we could have also compared the entropy of the baseline activity to that computed during stimulation in order to determine whether the response was significant or not (Chacron et al. 2003). However, the entropy computed from the surrogate data sets is equal, in theory, to that computed from the baseline activity, as both would give rise to uniform PSTHs because they are not correlated with the stimulus. Computing the entropy from the baseline activity would, however, have severely restricted the set of stimuli from which we could record neural activity, as it would have then become necessary to record baseline activity for at least as long as we could record driven activity.

Chirp selectivity index

For chirp stimuli, the response to the chirp itself also had to be stronger than the response to the beat as well as satisfying the criterion described above. This was necessary in order to exclude neurons that actually responded similarly to the beat and chirp. We quantified the response to the chirp by computing the chirp selectivity index:

CSI = | \frac{R_{chirp} - R_{beat}}{R_{chirp} + R_{beat}} |

where R_chirp is the maximum firing rate obtained in a PSTH during a time window starting with chirp onset; R_beat is the maximum rate obtained during the ongoing beat in a time window ending on chirp onset. The time window was set to a quarter of the time between consecutive chirps, i.e., 250 ms for chirp presentation at 1 Hz; | … | denotes the absolute value. A neuron for which the CSI value was >0.1 was taken as responding significantly to the chirp.

Movement selectivity index

Moving stimuli were presented by a small electric dipole with an interelectrode distance of ~1 mm moved back and forth alongside the fish by a programmable robotic arm at velocities of 10 cm/s. The dipole emitted a constant positive AM as in previous studies (Chacron et al. 2009; Chacron and Fortune 2010; Khosravi-Hashemi et al. 2011). The movement selectivity index was defined as

MSI = | \frac{R_{max} - R_{φ_{max - Δ φ}}}{R_{max} + R_{φ max - Δ φ}} |

R_max is the maximal response rate; R_φ_max−Δ_φ is the response rate at a phase Δφ = 1/4 away from φ_max, the movement cycle phase that elicited the maximal rate. A response for which both the MSI value was >0.1 and the entropy criterion described in the above section was fulfilled was taken as significant.

Specificity of neural responses

To test whether neurons would respond specifically to a given stimulus category that consisted of either small chirps, big chirps, or moving objects, we built two-dimensional histograms over the best detection index obtained in each stimulus category. If a neuron responds to one category but not at all to another, then we would expect that all data points would lie on the y = 0 and x = 0 axes. The fraction of data points that fell on the axes was considered significant if it was different at the 0.05 level from the fraction obtained by surrogate data sets. These were generated by 5,000 runs of Monte Carlo simulations in which the data points are distributed uniformly within the range occupied by the data.

Response latency

The response latency was defined as the time between the step onset or, in a few cases, the step offset and the point where the PSTH reaches half of its maximum value.

Sparseness measures

The sparseness of a neural code can be quantified either at the population level or at the single-neuron level. At the population level, the sparseness is inversely proportional to the fraction of neurons within a given population that respond to a given stimulus. At the single-neuron level, the sparseness would be inversely proportional to the number of stimuli out of a given set of stimuli that the neuron responds to, the so-called lifetime sparseness (Perez-Orive et al. 2002). We note that lifetime and population sparseness can be independent and as such give different information about the sparseness of a given neural code (Willmore and Tolhurst 2001). We computed sparseness at the population level, using the population sparseness index SI_p defined by

{SI}_{p} = \frac{1 - A_{p}}{1 - 1 / n}

SI_p takes values between 0 and 1, and A_p is the activity fraction defined by Rolls and Tovee (1995):

A_{p} = \frac{{(\sum_{i = 1}^{n} \frac{r_{i}}{n})}^{2}}{\sum_{i = 1}^{n} \frac{r_{i}^{2}}{n}}

where r_i is the response of neuron i to a given stimulus, i.e., the maximum firing rate obtained during the response time window (cf. Chirp selectivity index). In a sparse coding population only a few neurons will fire strongly in response to a given stimulus. The respective firing rate distribution will consequently display a long tail for high values of the firing rate. We note that the activity fraction A_p is inversely proportional to the length of the tail of the firing rate distribution.

We also computed the lifetime sparseness, using the lifetime sparseness index SI_l defined by Vinje and Gallant (2002):

{SI}_{1} = \frac{1 - A_{1}}{1 - 1 / n}

where A_l is the activity fraction defined by

A_{1} = \frac{{(\sum_{i = 1}^{n} \frac{R_{i}}{n})}^{2}}{\sum_{i = 1}^{n} \frac{R_{i}^{2}}{n}}

where R_i is the response of a given neuron to a stimulus i. In practice, we took R_i and r_i as the maximum firing rates from the PSTH during the response window. We note that the response window length was typically 250 ms, although it was shorter for some chirp stimuli as described above.

Mutual information and spike metrics

If a neuron always fires the same spike train in response to the same stimulus but different stimuli elicit different spike trains, an ideal observer would be able to identify each stimulus just by looking at the neural response. Therefore, the mutual information, i.e., the information contained in a set of responses about a set of stimuli, can be measured by assessing the variability of the responses elicited by one stimulus versus the variability of the response across different stimuli (Borst and Theunissen 1999).

To quantify the similarity between spike trains we used a nonparametric approach introduced by Victor and Purpura (1996). Briefly, the similarity is measured as distance d between two spike trains, which corresponds to the cost of transforming one spike train into the other. Each elementary step needed to transform a spike train is associated with a fixed cost. Elementary steps consist of inserting a spike, deleting a spike, or shifting a spike. The cost of inserting and deleting is 1. The cost q for shifting ranges from 1 to 500 s⁻¹. The value assigned to q is important as it sets the temporal precision in comparing spike trains: With q = 0 spike trains are compared under the assumption of a pure spike count code (i.e., a rate code), whereas high values of q assume a high precision code (i.e., a temporal code). To find which temporal precision led to the most successful encoding, we used q ranging from 0 s⁻¹ to 500 s⁻¹ in steps of 50 s⁻¹. For a given q, we found the sequence of elementary steps that leads to the minimal cost by using the algorithm provided by Victor and Purpura (1996). We then computed the distance $d_{i}^{α}$ between a given spike train $t_{i}^{α}$ and a set of n other spike trains ${t_{j}^{α}}^{n}_{j = 1}$ recorded in response to the same stimulus α ∈ {1,2, … k} (k being the number of stimuli) as the average cost c to transform this spike train into each of the others:

d_{i}^{α} = \frac{1}{n - 1} \sum_{j = 1, j \neq i}^{n} c (t_{i}^{α}, t_{j}^{α})

Each spike train $t_{i}^{α}$ was then allocated to the response category β that elicited a set of spike trains to which it had a minimum distance:

t_{i}^{α} \to β = {min}_{β} (d_{i}^{β}), with β = {1, 2, .., k}

The frequency of finding a spike train $t_{i}^{α}$ elicited by stimulus α and associated with response category β was represented in a k * k confusion matrix N(α, β), with k being the number of stimuli. Whenever a spike train had an equal minimal average distance to a number m of response categories, each corresponding element of N(α, β) was increased by 1/m. A set of stimuli is optimally encoded if exclusively the values on the diagonal of the matrix differ from zero. Values off the diagonal correspond to incorrectly associating a response with a stimulus that did not give rise to it. We then computed the mutual information between the set of responses and the set of stimuli as follows:

\begin{array}{l} MI = \sum_{β = 1}^{k} \sum_{α = 1}^{k} p (β ∣ α) {log}_{2} [\frac{p (β ∣ α)}{p (β) p (α)}] \\ = \frac{1}{N_{tot}} \sum_{β = 1}^{k} \sum_{α = 1}^{k} N (β ∣ α) [{log}_{2} N (β ∣ α) - {log}_{2} \sum_{b = 1}^{k} N (b ∣ α) - {log}_{2} \sum_{a = 1}^{k} N (β ∣ a) + {log}_{2} N_{tot}] \end{array}

The MI encoded by a set of different neurons z for a fixed set of k stimuli was obtained by extending the distance measure d from a single to a multidimensional array with each cell representing one dimension. For each neuron an equal number of spike trains was included by randomly choosing out of the set of spike trains (a minimum of 10 and a maximum of 100 trials per stimulus). Using large numbers of trials reduces an overestimation of MI that will result from insufficient assessment of the trial-to-trial response variability (Abbott et al. 1996). However, allowing different trial numbers introduces redundancy in the stimulus set and limits the maximum value of MI that can be obtained. To correct for this, we express MI as percentage of the maximum obtainable MI for a given stimulus set. The maximal obtainable MI is equal to the entropy H in the stimulus set

H_{Stimulus} = - \sum_{i}^{k} p (α) {log}_{2} p (α)

with p(α) being the fraction of trials in which stimulus α was presented.

The allocation of the ith set of spike trains to a response category followed this rule:

{{{}^{cell1}t}_{i}^{α}, {{}^{cell 2}t}_{i}^{α}, .., {{}^{cell z}t}_{i}^{α}} \to β = {argmin}_{β} (\sum_{h = 1}^{z} {{}^{{cell}_{h}}d}_{i}^{β}),

where ${{}^{{cell}_{h}}d}_{i}^{β}$ refers to the average distance of the ith spike train measured in cell h to all spike trains elicited from cell h by stimulus β. The sum of average distances is then built across cells. The response category that has the minimal sum of distances across cells is assigned to the ith set of spike trains. Although the spike trains were restricted to a 100-ms response window starting with stimulus onset, analysis with different window length (200 ms) led to similar results (data not shown).

Receiver-operator characteristic curves

The area under the receiver-operator characteristic (ROC), a measure derived from signal detection theory (Green and Swets 1966), was used to quantify how well a given chirp could be detected based on the spike trains obtained in response to it. To do so, we built the distribution of spike counts in a 100-ms window before and after the chirp onset. Spike count distributions were obtained from responses elicited with an equal number of trials (at least 10) with different chirp stimuli. We obtained the probability of false alarm [p(FA)] from the distribution of spike counts in the window before chirp onset and the probability of correct detection [p(CD)] from the distribution of spike counts in the window starting with chirp onset. Different spike count criteria (ranging from 0 to the maximum spike count in steps of 1) were used to assess a ROC curve. Detection performance was quantified by the area under the ROC curve, which is 0.5 for random performance and 1 for perfect detection. For detectability based on the combined activity of several neurons we built joint spike count distributions by summing spike counts for each trial elicited in each neuron. To check for the robustness of our results time windows of 100 and 200 ms were used, and similar results were obtained for both values.

RESULTS

Sparse coding in torus semicircularis

To quantify the set of transformations by which information from more peripheral brain areas is decoded by more central areas, we compared the responses of ELL neurons and their postsynaptic targets, TS neurons, to a wide range of stimuli.

Figure 2 shows the responses of example ELL (Fig. 2A) and TS (Fig. 2, B and C) neurons to the set of stimuli used in this study. The example ELL neuron responded to almost all stimuli presented (Fig. 2A) and displayed a strong phase-locking response to the beat, chirp, and noise stimuli. One example TS neuron, in contrast, responded almost exclusively to three types of small chirp stimuli (Fig. 2B), while the other example TS neuron tended to respond to a larger stimulus set that included beats as well as small and big chirps (Fig. 2C).

These differences in the responses of TS and ELL neurons were seen across our data set. While ELL neurons tended to respond to all stimuli, TS neurons instead tended to only respond to a fraction of the stimuli presented (Fig. 3, A and B). We quantified this by computing the response probability (i.e., the fraction of stimuli a neuron responds to) for ELL and TS neurons. As expected, the response probability of TS neurons was on average smaller than that of ELL neurons (ELL: 0.64 ± 0.18, TS: 0.44 ± 0.27; U-test, P < 0.01, n = 26 and 71, respectively) and was furthermore distributed over a range that exceeded that of ELL neurons (ELL: 0.25–0.92, TS: 0.04–0.92; minimum-maximum value) (Fig. 3C). Moreover, the shapes of the distributions differed between ELL and TS: the ELL distribution of response probability was consistent with data drawn from a Gaussian distribution (Lilliefor test, P = 0.5) but was inconsistent with a uniform distribution (χ²-test, P < 0.01). In contrast, the response probability distribution for TS neurons was not consistent with data drawn from a normal distribution (Lilliefor test, P = 0.048). This and the fact that the TS data were consistent with data drawn from a uniform distribution (χ²-test, P = 0.23) suggest that the response profiles of TS neurons are more diverse than that of ELL neurons.

Fig. 3 — Comparing sparse coding in ELL and TS. A and B: population activity for a set of 24 stimuli measured in 17 ELL neurons (A) and 29 TS neurons (B). Black squares mark stimuli for which a significant response was obtained. Cells were sorted as a function of their response probability. C: response probabilities for TS (black bars) and ELL (gray bars) neurons computed as the fraction of the stimuli each cell responded to. Response probabilities were included from neurons tested with a minimum of 12 different stimuli. The response probability of TS neurons was significantly lower than that of ELL neurons (U-test, P < 0.01). Response probability was distributed normally in ELL (Lilliefor test, ELL: P = 0.5, TS: P = 0.04) and uniformly in TS (χ²-test, ELL: P < 0.01, TS: P = 0.23). D: baseline (i.e., in the absence of stimulation) firing rates were correlated with response probability for TS neurons (r = 0.5, P < 0.01), not for ELL neurons (r = 0.34, P = 0.09). Note that spontaneous firing rates reached much lower values in TS neurons than in ELL neurons (U-test, P < 0.01). Different markers label sparse TS neurons with lifetime sparseness index > 0.5 (triangles), dense TS neurons with lifetime sparseness index ≤ 0.5 (black filled circles), and dense ELL neurons with lifetime sparseness index ≤ 0.5 (gray filled circles). E: lifetime sparseness indices were consistent with data drawn from a normal distribution in ELL (Lilliefor test, P = 0.37) but were significantly different than data drawn from a unimodal distribution in TS neurons (Hartigan’s dip test, P = 0.017). On average TS neuron responses were sparser than ELL neuron responses (U-test, P < 0.01). The sparseness is quantified based on the firing rate distribution (see METHODS). *Insets*: firing rate distributions corresponding to the same neurons as in Fig. 2, A and B. L_S, lifetime sparseness. F: population sparseness was higher across TS neurons than across ELL neurons (U-test, P < 0.01). *Insets*: firing rate distributions for responses to a small chirp (bf = 5 Hz, cf = 60 Hz, cp = 75) for ELL and TS. P_S, population sparseness.

Since TS neurons had lower spontaneous firing rates on average than ELL neurons (ELL: 17.4 ± 7.2 Hz, TS: 6 ± 8 Hz; U-test, P < 0.001, n = 27 and 187, respectively), we next tested whether this might help explain their lower response probability. Our results suggest that this is the case, as there was a significant positive correlation between the baseline firing rate and response probability for TS neurons (r = 0.5, P < 0.01; Fig. 3D). In contrast, this correlation was not significant for ELL neurons (r = 0.34, P = 0.09; Fig. 3D).

High response selectivity in neurons has been associated with sparse coding (Perez-Orive et al. 2002). In a sparse code, a small fraction of neurons would be activated by any given stimulus, with each neuron responding to a small set of stimuli. The former aspect can be quantified by the population sparseness index, while the latter aspect can be quantified by computing the lifetime sparseness index (Willmore and Tolhurst 2001). As previous studies have shown that the population sparseness and lifetime sparseness indices can be independent (Willmore and Tolhurst 2001), we computed both indices for ELL and TS neurons. Our results show that the lifetime sparseness index was rather low on average in ELL neurons (0.23 ± 0.08, n = 26) and was distributed over a narrow range (0.14–0.47) (Fig. 3E). In contrast, the lifetime sparseness index was significantly larger in TS neurons (0.46 ± 0.2; n = 71, U-test, P < 0.001) and varied over a broad range (0.11–0.83) that contained the range of values found for ELL neurons (Fig. 3E). Moreover, TS neurons with high (>0.5) lifetime sparseness displayed lower baseline firing rates than TS neurons with low (<0.5) lifetime sparseness (Fig. 3D). Similar to the response probability, the distribution for lifetime sparseness for ELL neurons was consistent with data drawn from a Gaussian distribution (Lilliefor test, P = 0.37) but not with data drawn from a uniform distribution (χ²-test, P < 0.01). Interestingly, the lifetime sparseness distribution for TS was not consistent with data drawn either from a normal or from a uniform distribution (Lilliefor test, P = 0.048; χ²-test, P < 0.01). Moreover, the distribution was not consistent with data drawn from a unimodal distribution (Hartigan’s dip test compared with random uniform data, 1,000 bootstrap runs, P = 0.017, bins = 10). Furthermore, we investigated whether lifetime sparseness was correlated to response latency. TS neurons displayed variable first spike latencies in response to steps with median 11 ms and with 50% of the data falling within the range of 9–20 ms. The first spike latency was not significantly correlated with lifetime sparseness (r = 0.08, P = 0.64, n = 35). Moreover, TS neurons with lifetime sparseness > 0.5 and TS neurons with lifetime sparseness ≤ 0.5 displayed latencies that were not significantly different from one another (P > 0.05, U-test).

We next quantified population sparseness in ELL and TS neurons and found that TS neurons displayed significantly higher values than ELL neurons (TS: 0.53 ± 0.1, ELL: 0.25 ± 0.1; U-test, P < 0.01; Fig. 3F). However, the distributions for ELL and TS neurons were both unimodal in nature (Fig. 3F). This can be explained by the fact that, unlike the lifetime sparseness measure, the population sparseness measure is plotted for different stimuli and not for different neurons. As such, the population sparseness measure confirms the fact that TS neurons are, as a population, more selective than ELL neurons. This is consistent with our previous results, since some TS neurons are more selective in their responses than ELL neurons.

To verify that our results were not a direct consequence of the fact that not all stimuli were tested for all neurons, we took the subset of neurons for which all 24 stimuli were presented (17 ELL and 29 TS neurons). We found that the distributions of response probability, lifetime sparseness, and population sparseness were not significantly different for this subset of neurons compared with the full data set for both ELL and TS (U-tests, P > 0.05 in all cases). Second, in order to verify that our results were not an artifact of the particular stimulus set used in this study, we randomly took n stimuli out of the possible 24 (8 ≤ n ≤ 24) and recomputed the response probability, lifetime sparseness, and population sparseness indices for this stimulus subset. For each stimulus number we repeated this process using up to 100 different stimulus subsets. Irrespective of the subset and the stimulus number, we obtained qualitatively similar results: TS neurons had significantly smaller response probabilities than ELL neurons. Both lifetime and population sparseness were larger in TS than in ELL (U-test and Kolmogorov-Smirnov test, P < 0.01 in all cases). As such, it is extremely unlikely that our results are an artifact of the stimulus ensemble used in this study.

To summarize our results so far, we have shown that TS neurons are more selective than ELL neurons on average and as a population. However, this is because some TS neurons are quite selective while other TS neurons display response properties similar to those of ELL neurons. The bimodal distribution of lifetime sparseness across TS neurons, with one mode largely overlapping with the unimodal distribution of lifetime sparseness in ELL neurons, suggests that there are two sub-populations in TS and strongly speaks against the hypothesis that all TS neurons are more selective than ELL neurons.

Response selectivity between different stimulus categories

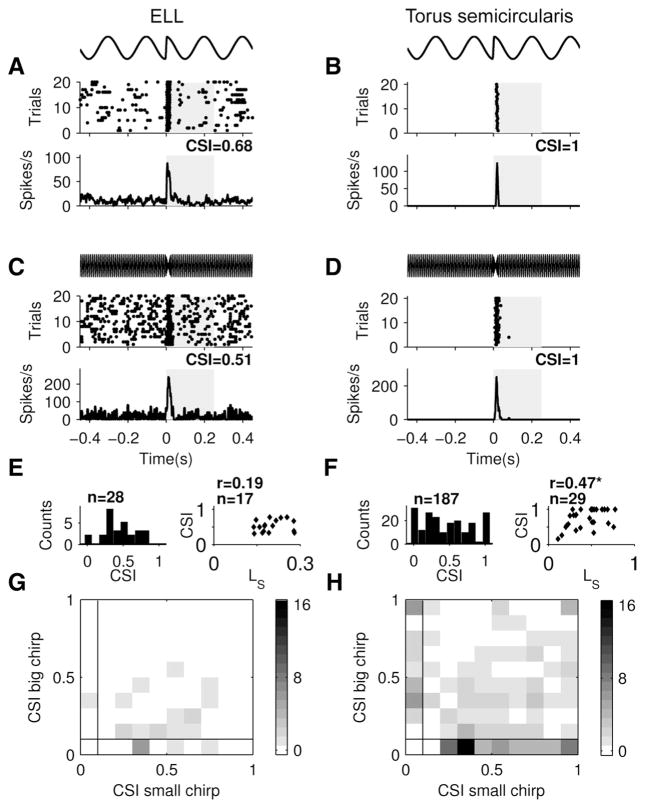
To better characterize response selectivity for different stimulus categories, we next quantified the selectivity in the responses of ELL and TS neurons to natural communication stimuli (i.e., chirps). Our data show that ELL neurons could fire a burst of spikes reliably in response to either small chirps (Fig. 4A) or big chirps (Fig. 4C) while also firing spikes during the beat. TS neurons, in contrast, could be highly selective to chirp stimuli: some neurons responded exclusively to small chirps (Fig. 4B) or big chirps (Fig. 4D). Typically, these neurons displayed no spiking activity during the beat and responded to small chirps with a single spike (Fig. 4B) and to big chirps with a burst of spikes (Fig. 4D). We quantified these responses, using a chirp selectivity index (CSI) ranging between 0 and 1 (0 means that the neuron responds equally well to the chirp and the beat, and 1 means that the neuron responds exclusively to the chirp and not to the beat). While both example TS neurons had CSI = 1, the most chirp-responsive neurons in ELL displayed less selective chirp responses and had lower CSI values for both small and big chirps (Fig. 4, A and C). This is mostly due to their ongoing spiking activity during the beat.

TS neurons displayed a significantly larger range of CSI values than ELL neurons (Ansari-Bradley test, P < 0.01, n = 187, 28; Fig. 4, E and F, left). Some responded equally well to chirps and beats, while others responded exclusively to chirps. In contrast, ELL neurons tended to respond to the presented chirps in a more consistent manner that is similar to that previously described by Marsat et al. (2009) and Marsat and Maler (2010). While we observed no significant correlation between CSI and lifetime sparseness for ELL neurons (r = 0.19, P = 0.48; Fig. 4E, right), these measures were significantly correlated for TS neurons (r = 0.47, P = 0.01; Fig. 4F, right). This indicates that TS neurons that are selective to chirps also tend to not respond to other stimuli.

As big and small chirps are preferentially elicited in different behavioral contexts, we first tested whether selective responses to big and small chirps were mutually exclusive. To do so, we plotted the maximum CSI obtained for each neuron for small chirps as a function of the CSI obtained for big chirps. Neurons with mutually exclusive responses to either small or big chirps will appear as data points on either x = 0 or y = 0 axes, respectively. We found a significant proportion of data points on the x = 0 and y = 0 axes for TS (Fig. 4H; Monte Carlo simulation, 5,000 runs, P < 0.01, n = 146) but not for ELL (Fig. 4G; P = 0.08, n = 24) neurons. We conclude that a significant fraction (33%) of TS neurons respond selectively to either big or small chirps.

Previous studies have shown that TS neurons can also respond strongly to moving object stimuli (Chacron et al. 2009; Chacron and Fortune 2010; Khosravi-Hashemi et al. 2011). Therefore, we next tested for selectivity between responses to chirps and to moving objects. Our results show that TS neurons that responded strongly to moving objects (Fig. 5A) did not respond selectively to chirp stimuli (Fig. 5B). Moreover, neurons that did respond selectively to chirp stimuli tended not to respond to moving objects (Fig. 5, C and D). As above, we tested whether the selective responses to chirps and moving objects were mutually exclusive by plotting the maximum CSI as a function of the MSI. We found a significant proportion of data points (43%) on the x = 0 and y= 0 axes (Fig. 5E; Monte Carlo simulation, 5,000 runs, P < 0.01, n = 27), indicating that neurons that were selective for moving objects tended not to be selective to chirps and vice versa. However, their nonselective response to chirps could occur because these neurons respond nonselectively to beats and chirps (i.e., display a dense code) or because they respond selectively to moving objects and do not respond to other stimuli. To test this, we quantified the responses of 27 TS neurons to six stimuli (a moving object, 3 chirp stimuli, and 2 beat stimuli) (Fig. 5F). We found that the coding properties for these neurons were similar to those described for TS neurons tested with a different stimulus set (compare Figs. 5F and 3A). Indeed, they displayed similar response probabilities (U-test, P = 0.24) as well as population sparseness (U-test, P = 0.86). The lifetime sparseness for these neurons was slightly but significantly larger than that obtained for TS neurons tested with a different stimulus set (U-test, P < 0.001). Furthermore, 4 of these 27 neurons responded exclusively to moving objects (Fig. 5F). As such, our data indicate that sparse coding in TS neurons applies to moving object stimuli as well.

Fig. 5 — TS neurons are selective to moving objects and communication signals. A: example TS neuron that was responsive to a small dipole moved alongside the fish when the dipole was at a specific location on the animal’s rostro-caudal axis. The movement selectivity index (MSI) was defined in analogy to the CSI. The gray rectangle marks the window of movement cycle to which the maximal firing rate is being compared. B: this same example neuron was not responsive to small chirps (nor to big chirps, CSI = 0; not shown). C: example TS neuron that was not responsive to the moving dipole. D: this same neuron responded to big chirps (best CSI for small chirps was 0). E: the maximum value of MSI as a function of maximum value of CSI for TS neurons (n = 27) showed a strong trend for selectivity for either chirps or moving objects. This is a consequence of the data points falling significantly more often on the axes than expected from random data (Monte Carlo test, P < 0.01). F: response profiles for a set of 6 stimuli including the moving object sorted as a function of response probability. Note that most neurons responded to ≤2 stimuli.

Do chirp attributes determine TS and ELL neural responses?

We next tested whether the responses of ELL and TS neurons could be used to discriminate between chirps with different attributes. Such discrimination can be quantified by comparing the response variability to different stimuli to that measured from repeated presentations of the same stimulus. We used a distance metric between responses and an automatic decision algorithm (Victor and Purpura 1996) to assign a given response as being generated by a given stimulus based on both sources of variability. The performance of the algorithm was assessed by computing the confusion matrix whose element (β,α) gives the probability that a response was assigned as being generated by stimulus β given that it was actually generated by stimulus α. As such, the sum of the diagonal elements in the confusion matrix indicates the average probability that a response was correctly assigned, whereas the sum of the off-diagonal elements indicates the average probability that a response was incorrectly assigned.

The results for an example ELL neuron are shown in Fig. 6A. The neuron responded differentially to most chirps with different attributes. Its responses varied greatly for chirps with different attributes but displayed little trial-to-trial variability overall (Fig. 6A). These responses allow for increased chirp discrimination performance, as can be seen from confusion matrices that displayed relatively low numbers of nonzero off-diagonal elements (Fig. 6A). We quantified the performance by computing the mutual information normalized by its maximum value. A mutual information value of log₂(N) bits implies that the system can discriminate between N stimuli. For each neuron, we expressed the mutual information as a percentage of the maximum mutual information that can be obtained for the set of stimuli used for that neuron. The discrimination performance for the example ELL neuron scored high mutual information (>40%).

Our results obtained from two representative TS neurons are shown in Fig. 6, B and C. While one neuron was highly selective in its responses and responded to only a few chirp stimuli (Fig. 6B), the other tended to respond differentially to most chirp stimuli (Fig. 6C), which was reminiscent of the ELL neuron. As such, the responses from the first TS neuron were unreliable signals when used to discriminate between chirps with different attributes, as can be seen from the confusion matrices that displayed significant nonzero off-diagonal elements (Fig. 6B). However, the confusion matrix from the second TS neuron displayed relatively fewer nonzero off-diagonal elements (Fig. 6C). Accordingly, this was quantified by a small amount of information obtained for the first example TS neuron (<20%), while the second encoded more information (>60%). This is mostly due to the fact that the former did not respond to a significant fraction of the stimuli used in this study while the latter did so with differential responses.

On the basis of the strong positive correlation between the lifetime sparseness index and maximal CSI in TS neurons (Fig. 4E) and the bimodal distribution of lifetime sparseness values (Fig. 3E), we segregated the TS data into two groups: one with low lifetime sparseness and CSI < 0.8 (dense group) and one with high lifetime sparseness and CSI ≥ 0.8 (sparse group). Of the 187 TS neurons for which CSI was obtained, we found that 152 (~81%) belonged to the dense group while the remaining 35 (~19%) belonged to the sparse group. We then compared the mutual information obtained from all three groups for a restricted stimulus set (the same chirp delivered at 4 phases) and our full stimulus set. Sparse TS neurons had MI = 23 ± 18% and MI = 13 ± 8% for the restricted and full stimulus sets, respectively. In contrast, dense TS neurons had MI = 44 ± 30% and MI = 36 ± 24% for the restricted and full stimulus sets, respectively. Finally, ELL neurons had MI = 37 ± 22% and MI = 27 ± 19% for the restricted and full stimulus sets, respectively. Although these differences were statistically significant only between sparse and dense TS neurons for the full stimulus set (multiple comparison test, P ≤ 0.05), we observed the trend that dense TS neurons encoded the largest amount of information, followed by ELL neurons, followed by sparse TS neurons. As such, we conclude that chirp discrimination persists at the level of TS. While dense TS neurons displayed larger mutual information than sparse TS neurons or ELL neurons in absolute terms, sparse TS neurons actually transmitted significantly more information per spike (1 ± 0.5 bits/spike) than dense TS neurons (0.68 ± 0.52 bits/spike) and ELL neurons (0.22 ± 0.13 bits/spike) (multiple comparison tests, P < 0.05). This is primarily because sparse TS neurons displayed significantly lower spontaneous firing rates (3.3 ± 3.5 spikes/s) than both dense TS (10.6 ± 9.3 spikes/s) and ELL (19.6 ± 8 spikes/s) neurons (multiple comparison tests, P < 0.05).

We next tested whether combining the activities of multiple TS and ELL neurons in response to chirp stimuli might improve their discrimination performances. In particular, if different sparse TS neurons were selective to disjoint sets of chirps, then it is expected that such a procedure would lead to large improvements in discrimination performance as quantified by the mutual information.

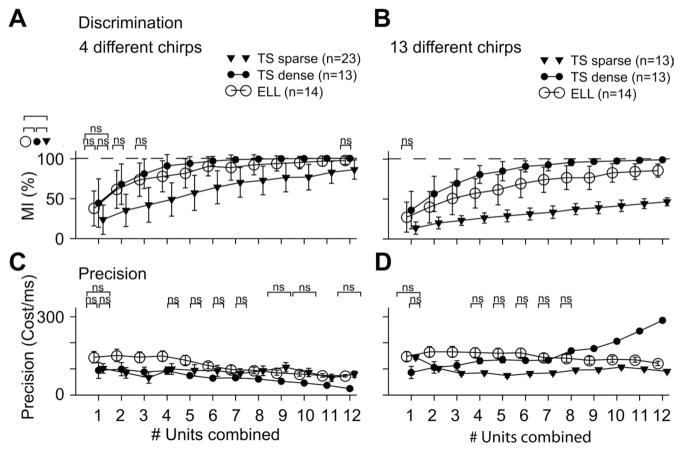
Our results show that combining the activities of multiple neurons led to large improvements in the mutual information for all three groups for both the restricted (Fig. 7A) and full stimulus (Fig. 7B) sets (Kruskal-Wallis test, P < 0.01). Combining the activities of as few as 12 dense TS neurons led to optimal (MI = 100%) discrimination for the restricted set and almost optimal (MI = 99 ± 1%) discrimination for the full stimulus set. In contrast, combining the activities of 12 ELL neurons gave rise to MI values of 97 ± 5% and 85 ± 8% for the restricted and full stimulus sets, respectively. Finally, combining the activities of 12 sparse TS neurons gave rise to MI = 86 ± 12% and MI = 46 ± 5% for the restricted and full stimulus sets, respectively. We note that the mutual information for the full stimulus set obtained by combining the activities of sparse TS neurons was always significantly lower than that obtained from a group of ELL neurons with the same size, which in turn was lower than that obtained for dense TS neurons (multiple comparison tests, P < 0.05). As such, the differences in discrimination performance observed between dense TS neurons, ELL neurons, and sparse TS neurons remained when we pooled neural activities. We note in passing that there were no synergistic effects for the stimuli used here when we considered either TS neurons that are excited by increases in EOD amplitude (E type) or TS neurons that are inhibited by increases in EOD amplitude (I type) (data not shown). This is because many stimuli used here can elicit excitatory responses from both E- and I-type TS neurons.

Fig. 7 — Discrimination of chirps based on pooling of the activities of sparse TS, dense TS, and ELL neurons. A: average mutual information (error bars represent SD) as a function of population size for the restricted stimulus set. Chirp discrimination was enhanced by combining the activities of multiple neurons for all 3 groups (analysis as in Fig. 6; Kruskal-Wallis test, P < 0.01 for all groups). It is seen that all 4 chirps can be optimally discriminated by the dense coding TS population. B: mutual information as a function of population size for the full stimulus set. The discrimination performance of dense TS neurons was significantly greater than that of ELL neurons. Moreover, the discrimination performance of ELL was significantly greater than that of sparse TS neurons. C: cost values indicating the precision that led to the maximal mutual information for the restricted stimulus set. D: cost values for the full stimulus set. Precision decreased with increasing group size in ELL and sparse TS neurons but increased for dense TS neurons (Kruskal-Wallis test, P < 0.01 for all groups). Brackets labeled “ns” indicate pairs that were not significantly different based on pairwise group comparisons; all other groups displayed significant differences (Kruskal-Wallis test with Tukey-Kramer correction for multiple comparisons, P < 0.05).

Precision of spike timing in response to chirp stimuli

We note that the spike metric we are using depends on a cost factor that is indicative of the temporal precision of the code. Our results show that this cost factor was similar for individual neurons of all three groups for the restricted and full stimulus sets, but a significant difference was observed between dense TS and ELL neurons (Fig. 7, C and D). For increasing population size, the average cost factor tended to decrease in all groups for the restricted stimulus set (Kruskal-Wallis test, P < 0.01). For the full stimulus set, precision decreased with increasing population size in sparse TS neurons and ELL but increased in dense TS neurons (Kruskal-Wallis test, P < 0.01). Moreover, the average cost factor for dense TS neurons tended to be higher than that of both sparse TS and ELL neurons for population sizes > 7 units (multiple comparison test, P < 0.05). This suggests that spike timing is important mainly for dense TS neurons.

Chirp detection

The poor performances of sparse TS neurons at discriminating between chirps suggest that they might be more apt at detecting their occurrence. Since the precision of spike timing was the lowest for this neuron group, we used signal detection theory (Green and Swets 1966) to quantify an ideal observer’s performance at discriminating the spike count obtained before and after chirp stimuli irrespective of chirp attributes. The performance of an example sparse TS neuron is shown in Fig. 8A. It is seen that this neuron was mostly silent before the chirp and responded to most small chirps strongly, giving rise to spike count distributions that were discriminable for both the restricted (Fig. 8B) and full stimulus (Fig. 8C) sets. We then quantified discriminability by computing the ROC curve and quantified the area under it (an area of 0.5 implies chance discrimination, whereas an area of 1 implies optimal discrimination) and obtained 0.69 and 0.64 for the restricted and full stimulus sets, respectively.

To provide a comparison, we also quantified detection in example dense TS (Fig. 8, D–F) and ELL (Fig. 8, G–I) neurons. It is seen that both neurons responded both before and after the chirp. For the restricted stimulus set, the response after the chirp was stronger than that before the chirp, resulting in discriminability of the spike count distributions (Fig. 8, E and H). In contrast, for the full stimulus set the spike count distributions before and after the chirp had limited discriminability and ROC curves were closer to the identity line (Fig. 8, F and I). While both neurons had ROC areas that were similar to that of the sparse TS neuron for the restricted stimulus set (~0.65), their ROC areas were barely above chance level for the full stimulus set (~0.54). These differences in detection performance were, however, not statistically significant for single neurons in both stimulus sets (multiple comparison test, P > 0.05).

While combining the activities of multiple TS and ELL neurons is expected to lead to improvement in detectability, it is not clear how this will affect all three neuron groups. Therefore, we summed the activities of multiple neurons when computing the spike count distributions. Our results show that this gave rise to significant improvements in detectability as quantified by the area under the ROC curve for all three groups (Kruskal-Wallis test, P < 0.01) (Fig. 8, J and K). However, the improvement was much greater for sparse TS neurons than either dense TS or ELL neurons. Indeed, the area under the ROC curve was significantly larger for sparse TS neurons than for ELL neurons (multiple comparison test, P < 0.05). The area under the ROC curve for dense TS neurons was furthermore significantly greater than for ELL neurons when considering the restricted stimulus set (multiple comparison test, P < 0.05). In contrast, for the full stimulus set the area under the ROC curve was similar in dense TS and ELL neurons when combining <8 units (multiple comparison test, P > 0.05) and showed small but significant differences for larger population sizes (multiple comparison test, P < 0.05).

While we have used the CSI to define the groups of sparse and dense TS neurons, we note that lifetime sparseness was significantly different between the groups (sparse TS neurons: 0.48 ± 0.16, dense TS neurons: 0.29 ± 0.14; U-test, P < 0.01, n = 19, 13), as expected from the correlation between CSI and lifetime sparseness. When regrouping neurons based on lifetime sparseness index ≥ 0.5 (sparse group) and < 0.5 (dense group), we obtained qualitatively similar performances in the encoding of stimulus attributes, time precision, and chirp detection (data not shown).

Finally, we note that similar results were found when testing discrimination and detection performance for a set of 9 big chirps with different attributes on 3 ELL and 5 TS neurons (data not shown). All neurons included displayed a maximal CSI for big chirps ≥ 0.4. Mutual information for both ELL and TS populations did not exceed 40%, with discriminability being slightly higher for ELL. In contrast, detectability of big chirps was much higher based on TS neurons (ROC area > 0.85) than on ELL neurons. We thus conclude that sparse TS neurons are more apt at detecting the occurrence of either big or small chirps irrespective of their attributes than either dense TS or ELL neurons. However, dense TS neurons are more apt at discriminating between chirps of differing attributes than either sparse TS or ELL neurons.

DISCUSSION

Summary

The purpose of this study was to characterize the transformations of the neural code along successive stages in the electrosensory system. While ELL neurons displayed dense responses, TS neurons displayed sparser responses. Interestingly, sparsening in the TS population was based on two subpopulations of neurons. Despite significant overlap between their response probabilities and sparseness indices, one sub-population tended to display sparse coding while the other tended to display dense coding. Sparse coding neurons were highly selective to either communication signals such as big chirps and small chirps or moving objects. Moreover, spike trains of sparse TS neurons provided no basis for the discrimination of chirp attributes within a given class (i.e., big or small). Instead, their spike trains could be used for chirp detection. In contrast, information about chirp attributes could be decoded from the spike trains of dense coding TS as well as ELL neurons.

Parallel processing in the midbrain

The dense and sparse coding subpopulations in TS might correspond to parallel information processing streams. This is supported by anatomical results showing that TS, which is the homolog midbrain structure of the mammalian inferior colliculus, consists of 12 laminae of which all but the most dorsal one give rise to parallel streams of processing that feed into different brain areas such as the optic tectum (OT) and the diencephalic nucleus electrosensorius (nE) (Carr et al. 1981; Carr and Maler 1985; Heiligenberg and Rose 1985; Metzner and Heiligenberg 1991). In particular, both upper and deeper laminae receive direct projections from ELL. Neurons in the deeper TS laminae then project to nE, while neurons from both upper and deeper laminae project to OT (Carr et al. 1981).

Some TS neurons receive direct input from ELL, whereas others receive this input indirectly via other TS neurons through inter- and intralaminar connections (Carr and Maler 1985). Therefore, as an alternative interpretation of our data, dense TS neurons could represent those that receive direct inputs from ELL and the sparse neurons might represent later stages of processing within TS that receive only indirect input from ELL. However, our results showed that sparse TS neurons did not display first spike latencies that were significantly larger than those of dense TS neurons, which speaks against this alternative hypothesis. On the other hand, response latency is not solely a consequence of the number of synapses away from the periphery and can be influenced by the interplay of excitatory and inhibitory kinetics at the cell membrane and neuromodulators (Faure et al. 2003; Heil 2004; Hurley and Pollak 2005). Therefore the absence of a correlation between latency and sparseness may not be sufficient to exclude that the two subpopulations in TS represent different stages in a serial processing line. Preliminary histological data from this study indicate that we recorded from TS neurons across most laminae (II–IX, n = 13). While dense neurons (lifetime sparseness ≤ 0.5, n = 7) that tended to respond to both beats and chirps were found in various laminae (II–IX), sparse neurons (lifetime sparseness > 0.5, n = 6) that tended to be chirp selective seemed to be confined to layers VII and VIII. This is in line with TS neurons recorded in the related genus Eigenmannia, in which neurons sensitive to beat stimuli, i.e., similar to our dense neurons, have been reported in layers V, VII, and VIIIA-C, while neurons selective for communication stimuli, i.e., similar to our sparse neurons, have mostly been associated with lamina VIIID (Metzner and Heiligenberg 1991; Rose and Heiligenberg 1985).

However, we note that the hypothetical case in which dense TS neurons actually project to sparse TS neurons is not necessarily inconsistent with both TS subpopulations giving rise to parallel projections to upstream targets outside TS. This is because, in Eigenmannia, neurons of both response types have been identified to project to OT, to nE, or to both (Metzner and Heiligenberg 1991; Rose and Heiligenberg 1985). If we assume homologous projections for Apteronotus, this speaks strongly in favor of the hypothesis that sparse and dense TS neurons give rise to parallel processing streams that project to both OT and nE. Interestingly, neurons in distinct areas of nE respond preferentially to either communication signals or beats (Heiligenberg et al. 1991), suggesting that information from sparse and dense TS neurons is decoded in nE and continues to give rise to parallel processing streams. Further studies are needed, however, to verify these predictions.

Mechanisms underlying dense and sparse responses

How do the coding properties such as the dense or the sparse coding emerge in TS?

The midbrain TS receives purely excitatory inputs from ELL neurons (Carr and Maler 1985). Pyramidal cells in the hind-brain ELL, the first stage of electrosensory processing, are known to respond to a wide range of EOD amplitude modulations including beats and chirps (Bastian et al. 2002; Krahe et al. 2002; Maler 2009a, 2009b; Marsat et al. 2009; Marsat and Maler 2010; Saunders and Bastian 1984). We verified with a large stimulus set that ELL responses comply with a dense coding scheme. Because dense TS neurons showed response properties similar to ELL neurons, the simplest explanation is that their response properties are inherited from their afferent neurons.

To explain the highly selective responses observed in sparse TS neurons, nonlinear mechanisms are likely necessary. If a neuron’s membrane potential crosses spiking threshold only in response to strong synaptic input currents, it behaves nonlinearly because of the spiking threshold’s rectifying effect.

Neurons that displayed high lifetime sparseness also featured extremely low spontaneous firing rates (<1 Hz), suggesting that strong synaptic currents were needed to elicit spiking. Low baseline activity (<1 Hz) was also reported from neurons highly selective to odors (Perez-Orive et al. 2002; Poo and Isaacson 2009). In both studies the selective spiking was explained by selective excitatory input combined with nonselective feedforward inhibition driven by oscillatory activity from the first-order nucleus. Interestingly, responses to chirps comprised usually between zero and two spikes or a burst of spikes. Such transient responses in sparse coding neurons have been attributed to a precisely tuned interplay of excitation and inhibition in other electric fish species (Carlson 2009; Pluta and Kawasaki 2010) and other systems (Covey et al. 1996; Faure et al. 2003; Higley and Contreras 2006; Leary et al. 2008; Rosen and Mooney 2003; Wehr and Zador 2003; Zhang et al. 2003). Alternatively, other mechanisms such as temporal filtering mediated by active subthreshold conductances have been shown to enhance selectivity (Carlson and Kawasaki 2006a; Chacron and Fortune 2010; Fortune and Rose 1997a, 1997b, 2003; Haag and Borst 1996).

Discrimination and detection of chirps

We found that chirp attributes could be discriminated based on combined spike activity of a rather low number (12) of ELL neurons and dense TS neurons. However, Marsat and Maler (2010) found that small chips are not discriminable from ELL spike trains. These conflicting results can most likely be explained by different assumptions made on the decoder. As a major difference, Marsat and Maler (2010) assumed a specific decoder since they used a short response window (10–50 ms) adjusted in time to contain the maximum response after the chirp, averaged away trial-to-trial variability, and filtered the neural response. In contrast, our analysis made less stringent assumptions on the decoder: We used a larger time window (100 ms), which increases the potential discriminability of the spike trains as they contained the response to the chirp and parts of the beat. Furthermore, our methodology accounted for trial-to-trial variability and therefore represents an estimate of the available information and precision contained in the spike trains.

How reliably neurons respond to stimuli clearly contributes to the ability of an observer to discriminate between these stimuli. Such reliability can take the form of synchronization to specific times during the beat or chirp, such that the small differences in temporal structure of chirps with different attributes could be resolved from the spike trains. The use of high-precision decoders resulted in the maximum mutual information (i.e., best discriminability) when the activity of eight or more dense TS neurons was combined (Fig. 7, B and D). This suggests that dense neurons use high temporal precision in order to transmit information. We note that the low decoding precision obtained when only a few neurons were combined does not necessarily contradict this, as these few neurons then do not provide a complete representation of the stimulus set. A decoder with high temporal precision thus becomes essential when information on small timing differences in the responses of several neurons can help distinguish between stimuli given that spike timing is reliable from trial to trial in the first place. Our data further indicate that spike timing was on average more precise and reliable in dense TS neurons than in ELL. This might be due to the fact that TS neurons obtain higher temporal precision from averaging over convergent inputs from ELL pyramidal cells.

In contrast, chirps with different attributes could not be discriminated based on spike trains from sparse TS neurons. This was surprising: If each chirp with given attributes were encoded by a distinct group of sparse neurons, it would suffice to know which neurons are active in order to identify the stimulus from the population activity. Our analysis of population activity aimed at quantifying the information contained in such a labeled-line code. This code requires that 1) each stimulus evokes responses from at least one neuron; 2) these responses are reliable; and 3) different stimuli activate disjoint sets of neurons. While conditions 1 and 3 were observed in sparse TS neurons (data not shown), their large trial-to-trial variability in response to chirps was detrimental to discrimination. It thus appears that sparse TS neurons do not transmit information about specific chirp attributes within a given category but instead respond selectively to a particular stimulus category (e.g., small, big chirps, moving objects). This selectivity was the basis for these neurons showing better chirp detection than either ELL or dense TS neurons.

Thus the processing of electrosensory stimuli may segregate into different streams that allow either detection or discrimination within TS. Given the fact that the lifetime sparseness index distribution was bimodal, we suggested that these two processing streams are carried by two distinct neural subpopulations. While it is possible that TS neurons instead form a continuum in terms of their response selectivity, this does not affect the qualitative nature of our conclusions. Such segregation is reminiscent of the “what” and “where” processing streams in the visual system (reviewed in, e.g., Ungerleider and Haxby 1994) that have also been proposed for the auditory system (Rauschecker and Tian 2000). While it is known that these fish respond behaviorally to chirps (Bastian et al. 2001; Hagedorn and Heiligenberg 1985; Hupé and Lewis 2008), further studies are needed to uncover whether they use the information contained in different chirp attributes.

Preserving sensory information in sparse coding populations

Numerous studies of higher-order neurons in different sensory modalities support the doctrine of a transition from dense to sparse coding along the sensory processing chain (Barlow 1972; DeWeese et al. 2003; Hromádka et al. 2008; Olshausen and Field 2004; Perez-Orive et al. 2002). In the visual system as the classic example, ganglion cells feature simple center-surround receptive fields (Kuffler 1953), while neurons in V1 function as edge detectors (Hubel and Wiesel 1959), and finally neurons in higher cortical areas such as MT can be selective to individual faces or objects (Quiroga et al. 2005; Rolls and Tovee 1995; Young and Yamane 1992).

Does transitioning from a dense code to a sparse code preserve sensory information?

Recent work suggests that information from the retina is preserved in thalamus while at the same time leading to a sparse representation (Rathbun et al. 2010; Sincich et al. 2009; Wang et al. 2010). Such sparsening involves the fact that thalamic neurons have lower firing rates than retinal ganglion cells. Thus sparse codes seem to be an energy-efficient way (Attwell and Laughlin 2001; Földiák and Young 1995) to represent information about the sensory world once the categories, objects, or filters are well matched to relevant sensory patterns. As such, the information on the occurrence of a chirp was recovered from the sparse TS population. However, the attributes of the chirp, i.e., its timing within the beat and frequency excursion, could only be recovered from spike trains of the dense TS neurons that had high firing rates and displayed the highest spike time precision. Hence preserving both categorical information about a sensory object as well as descriptive information on the time-varying stimulus features through parallel dense and sparse subpopulations seems advantageous, as it allows for discrimination of behaviorally relevant stimuli without compromising their detection.

Most studies have reported sparse responses only in a small percentage (<15%) of recorded neurons (Quiroga et al. 2005; Young and Yamane 1992), leaving the possibility open that a parallel dense coding population is present as well. Other studies explicitly state that beneath the sparse coding neurons a small subpopulation of auditory and olfactory cortical neurons displayed dense responses (Hromádka et al. 2008; Poo and Isaacson 2009). Even in the insect olfactory system, which displays an impressive degree of sparsening between the first-order projection neurons and the second-order Kenyon cells, ~10% of the Kenyon cells had lifetime sparseness indices <0.3 and thus displayed dense coding (Perez-Orive et al. 2002).

Preserving energy-costly descriptive stimulus information through dense coding may allow an animal to form selectivity to new sensory patterns through learning mechanisms possibly implemented in higher brain structures. In starlings, which acquire new song sequences throughout their life span, selectivity to new sequences emerges in forebrain neurons after a period of exposure (Gentner and Margoliash 2003). Alternatively, the preservation of dense coding subpopulations may be important, if behavioral output needs to be synchronized to the time-varying features of a sensory stimulus. This could be the case in echo chirping (Hupé and Lewis 2008; Zupanc et al. 2006), concerted signal production during group hunting in electric fish (Arnegard and Carlson 2005), or chorus-singing birds (Mann et al. 2006).

We suggest that dense coding may be sustained in small parallel subpopulations to help preserve sensory information. Our results suggest that parallel sparse and dense subpopulations give rise to rapid detection and estimation of incoming behaviorally relevant sensory input. Further studies carried out in higher-order brain areas are needed to understand the decoding of these parallel information streams.

Acknowledgments

We thank Oscar Ávila-Åkerberg, Jacob Engelmann, and Eric S. Fortune for helpful comments on the manuscript. We thank Ana Catarina Casari Giassi for the processing of brain tissue and help with the interpretation of the histological data.

GRANTS

This research was supported by the Canadian Institutes of Health Research, the Natural Sciences and Engineering Research Council, the Canada Foundation for Innovation, and the Canada Research Chairs program (M. J. Chacron).

Footnotes

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

K.V. performed experiments; K.V. analyzed data; K.V. and M.J.C. interpreted results of experiments; K.V. prepared figures; K.V. and M.J.C. drafted the manuscript; K.V. and M.J.C. edited and revised the manuscript; K.V. and M.J.C. approved the final version of the manuscript; M.J.C. conception and design of research.

References

Abbott LF, Rolls ET, Tovee MJ. Representational capacity of face coding in monkeys. Cereb Cortex. 1996;6:498–505. doi: 10.1093/cercor/6.3.498. [DOI] [PubMed] [Google Scholar]
Arnegard ME, Carlson BA. Electric organ discharge patterns during group hunting by a mormyrid fish. Proc Biol Sci. 2005;272:1305–1314. doi: 10.1098/rspb.2005.3101. [DOI] [PMC free article] [PubMed] [Google Scholar]
Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab. 2001;21:1133–1145. doi: 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]
Barlow HB. Single units and sensation: a neuron doctrine for perceptual psychology? Perception. 1972;1:371–394. doi: 10.1068/p010371. [DOI] [PubMed] [Google Scholar]
Bastian J. Electrolocation. I. How the electroreceptors of Apteronotus albifrons code for moving objects and other electrical stimuli. J Comp Physiol A. 1981;144:465–479. [Google Scholar]
Bastian J, Chacron MJ, Maler L. Receptive field organization determines pyramidal cell stimulus encoding capability and spatial stimulus selectivity. J Neurosci. 2002;22:4577–4590. doi: 10.1523/JNEUROSCI.22-11-04577.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bastian J, Schniederjan S, Nguyenkim J. Arginine vasotocin modulates a sexually dimorphic communication behavior in the weakly electric fish Apteronotus leptorhynchus. J Exp Biol. 2001;204:1909–1923. doi: 10.1242/jeb.204.11.1909. [DOI] [PubMed] [Google Scholar]
Benda J, Longtin A, Maler L. Spike-frequency adaptation separates transient communication signals from background oscillations. J Neurosci. 2005;25:2312–2321. doi: 10.1523/JNEUROSCI.4795-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Borst A, Theunissen FE. Information theory and neural coding. Nat Neurosci. 1999;2:947–957. doi: 10.1038/14731. [DOI] [PubMed] [Google Scholar]
Carlson BA, Kawasaki M. Stimulus selectivity is enhanced by voltage-dependent conductances in combination-sensitive neurons. J Neurophysiol. 2006a;96:3362–3377. doi: 10.1152/jn.00839.2006. [DOI] [PubMed] [Google Scholar]
Carlson BA, Kawasaki M. Ambiguous encoding of stimuli by primary sensory afferents causes a lack of independence in the perception of multiple stimulus attributes. J Neurosci. 2006b;26:9173–9183. doi: 10.1523/JNEUROSCI.1513-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Carlson BA, Kawasaki M. From stimulus estimation to combination sensitivity: encoding and processing of amplitude and timing information in parallel, convergent sensory pathways. J Comput Neurosci. 2008;25:1–24. doi: 10.1007/s10827-007-0062-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Carlson BA. Temporal-pattern recognition by single neurons in a sensory pathway devoted to social communication behavior. J Neurosci. 2009;29:9417–9428. doi: 10.1523/JNEUROSCI.1980-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Carr CE, Maler L. A Golgi study of the cell types of the dorsal torus semicircularis of the electric fish Eigenmannia—functional and morphological diversity in the midbrain. J Comp Neurol. 1985;235:207–240. doi: 10.1002/cne.902350206. [DOI] [PubMed] [Google Scholar]
Carr CE, Maler L, Heiligenberg W, Sas E. Laminar organization of the afferent and efferent systems of the torus semicircularis of gymnotiform fish: morphological substrates for parallel processing in the electrosensory system. J Comp Neurol. 1981;203:649–670. doi: 10.1002/cne.902030406. [DOI] [PubMed] [Google Scholar]
Chacron MJ, Longtin A, Maler L. The effects of spontaneous activity, background noise, and the stimulus ensemble on information transfer in neurons. Network. 2003;14:803–824. [PubMed] [Google Scholar]
Chacron MJ, Maler L, Bastian J. Electroreceptor neuron dynamics shape information transmission. Nat Neurosci. 2005;8:673–678. doi: 10.1038/nn1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chacron MJ, Bastian J. Population coding by electrosensory neurons. J Neurophysiol. 2008;99:1825–1835. doi: 10.1152/jn.01266.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chacron MJ, Fortune ES. Subthreshold membrane conductances enhance directional selectivity in vertebrate sensory neurons. J Neurophysiol. 2010;104:449–462. doi: 10.1152/jn.01113.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chacron MJ, Toporikova N, Fortune ES. Differences in the time course of short-term depression across receptive fields are correlated with directional selectivity in electrosensory neurons. J Neurophysiol. 2009;102:3270–3279. doi: 10.1152/jn.00645.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chacron MJ, Longtin A, Maler L. Efficient computation via sparse coding in electrosensory neural networks. Curr Opin Neurobiol. 2011 Jun 15; doi: 10.1016/j.conb.2011.1005.1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
Covey E, Kauer JA, Casseday JH. Whole-cell patch-clamp recording reveals subthreshold sound-evoked postsynaptic currents in the inferior colliculus of awake bats. J Neurosci. 1996;16:3009–3018. doi: 10.1523/JNEUROSCI.16-09-03009.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
DeWeese MR, Wehr M, Zador AM. Binary spiking in auditory cortex. J Neurosci. 2003;23:7940–7949. doi: 10.1523/JNEUROSCI.23-21-07940.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Faure PA, Fremouw T, Casseday JH, Covey E. Temporal masking reveals properties of sound-evoked inhibition in duration-tuned neurons of the inferior colliculus. J Neurosci. 2003;23:3052–3065. doi: 10.1523/JNEUROSCI.23-07-03052.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Földiák P, Young MP. Sparse coding in the primate cortex. In: Arbib MA, editor. The Handbook of Brain Theory and Neural Networks. Cambridge, MA: MIT Press; 1995. [Google Scholar]
Fortune ES, Rose GJ. Passive and active membrane properties contribute to the temporal filtering properties of midbrain neurons in vivo. J Neurosci. 1997a;17:3815–3825. doi: 10.1523/JNEUROSCI.17-10-03815.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fortune ES, Rose GJ. Temporal filtering properties of ampullary electrosensory neurons in the torus semicircularis of Eigenmannia: evolutionary and computational implications. Brain Behav Evol. 1997b;49:312–323. doi: 10.1159/000113000. [DOI] [PubMed] [Google Scholar]
Fortune ES, Rose GJ. Short-term synaptic plasticity contributes to the temporal filtering of electrosensory information. J Neurosci. 2000;20:7122–7130. doi: 10.1523/JNEUROSCI.20-18-07122.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fortune E, Rose G. Voltage-gated Na+ channels enhance the temporal filtering properties of electrosensory neurons in the torus. J Neurophysiol. 2003;90:924–929. doi: 10.1152/jn.00294.2003. [DOI] [PubMed] [Google Scholar]
Gentner TQ, Margoliash D. Neuronal populations and single cells representing learned auditory objects. Nature. 2003;424:669–674. doi: 10.1038/nature01731. [DOI] [PMC free article] [PubMed] [Google Scholar]
Green D, Swets J. Signal Detection Theory and Psychophysics. Oxford: Wiley; 1966. [Google Scholar]
Haag J, Borst A. Amplification of high-frequency synaptic inputs by active dendritic membrane processes. Nature. 1996;379:639–641. [Google Scholar]
Hagedorn M, Heiligenberg W. Court and spark: electric signals in the courtship and mating of gymnotoid electric fish. Anim Behav. 1985;33:254–265. [Google Scholar]
Heil P. First-spike latency of auditory neurons revisited. Curr Opin Neurobiol. 2004;14:461–467. doi: 10.1016/j.conb.2004.07.002. [DOI] [PubMed] [Google Scholar]
Heiligenberg W, Bastian J. The control of Eigenmannia’s pacemaker by distributed evaluation of electroreceptive afferences. J Comp Physiol. 1980;136:113–133. [Google Scholar]
Heiligenberg W, Keller CH, Metzner W, Kawasaki M. Structure and function of neurons in the complex of the nucleus electrosensorius of the gymnotiform fish Eigenmannia: detection and processing of electric signals in social communication. J Comp Physiol A. 1991;169:151–164. doi: 10.1007/BF00215862. [DOI] [PubMed] [Google Scholar]
Heiligenberg W, Rose G. Phase and amplitude computations in the midbrain of an electric fish: intracellular studies of neurons participating in the jamming avoidance response of Eigenmannia. J Neurosci. 1985;5:515–531. doi: 10.1523/JNEUROSCI.05-02-00515.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
Higley MJ, Contreras D. Balanced excitation and inhibition determine spike timing during frequency adaptation. J Neurosci. 2006;26:448–457. doi: 10.1523/JNEUROSCI.3506-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hitschfeld EM, Stamper SA, Vonderschen K, Fortune ES, Chacron MJ. Effects of restraint and immobilization on electrosensory behaviors of weakly electric fish. ILAR J. 2009;50:361–372. doi: 10.1093/ilar.50.4.361. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hromádka T, DeWeese MR, Zador AM. Sparse representation of sounds in the unanesthetized auditory cortex. PLoS Biol. 2008;6:e16. doi: 10.1371/journal.pbio.0060016. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hubel DH, Wiesel TN. Receptive fields of single neurones in the cat’s striate cortex. J Physiol. 1959;148:574–591. doi: 10.1113/jphysiol.1959.sp006308. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hupé GJ, Lewis JE. Electrocommunication signals in free swimming brown ghost knifefish, Apteronotus leptorhynchus. J Exp Biol. 2008;211:1657–1667. doi: 10.1242/jeb.013516. [DOI] [PubMed] [Google Scholar]
Hurley LM, Pollak GD. Serotonin shifts first-spike latencies of inferior colliculus neurons. J Neurosci. 2005;25:7876–7886. doi: 10.1523/JNEUROSCI.1178-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kajikawa Y, Hackett TA. Entropy analysis of neuronal spike train synchrony. J Neurosci Methods. 2005;149:90–93. doi: 10.1016/j.jneumeth.2005.05.011. [DOI] [PubMed] [Google Scholar]
Kawasaki M, Guo YX. Neuronal circuitry for comparison of timing in the electrosensory lateral line lobe of the African wave-type electric fish Gymnarchus niloticus. J Neurosci. 1996;16:380–391. doi: 10.1523/JNEUROSCI.16-01-00380.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
Khosravi-Hashemi N, Fortune ES, Chacron MJ. Coding movement direction by burst firing in electrosensory neurons. J Neurophysiol. 2011;106:1954–1968. doi: 10.1152/jn.00116.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Krahe R, Bastian J, Chacron MJ. Temporal processing across multiple topographic maps in the electrosensory system. J Neurophysiol. 2008;100:852–867. doi: 10.1152/jn.90300.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Krahe R, Kreiman G, Gabbiani F, Koch C, Metzner W. Stimulus encoding and feature extraction by multiple sensory neurons. J Neurosci. 2002;22:2374–2382. doi: 10.1523/JNEUROSCI.22-06-02374.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kuffler SW. Discharge patterns and functional organization of mammalian retina. J Neurophysiol. 1953;16:37–68. doi: 10.1152/jn.1953.16.1.37. [DOI] [PubMed] [Google Scholar]
Leary CJ, Edwards CJ, Rose GJ. Midbrain auditory neurons integrate excitation and inhibition to generate duration selectivity: an in vivo whole-cell patch study in anurans. J Neurosci. 2008;28:5481–5493. doi: 10.1523/JNEUROSCI.5041-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Maler L. Receptive field organization across multiple electrosensory maps. I. Columnar organization and estimation of receptive field size. J Comp Neurol. 2009a;516:376–393. doi: 10.1002/cne.22124. [DOI] [PubMed] [Google Scholar]
Maler L. Receptive field organization across multiple electrosensory maps. II. Computational analysis of the effects of receptive field size on prey localization. J Comp Neurol. 2009b;516:394–422. doi: 10.1002/cne.22120. [DOI] [PubMed] [Google Scholar]
Maler L, Sas E, Johnston S, Ellis W. An atlas of the brain of the electric fish Apteronotus leptorhynchus. J Chem Neuroanat. 1991;4:1–38. doi: 10.1016/0891-0618(91)90030-g. [DOI] [PubMed] [Google Scholar]
Mann NI, Dingess KA, Slater PJB. Antiphonal four-part synchronized chorusing in a Neotropical wren. Biol Lett. 2006;2:1–4. doi: 10.1098/rsbl.2005.0373. [DOI] [PMC free article] [PubMed] [Google Scholar]
Marsat G, Maler L. Neural heterogeneity and efficient population codes for communication signals. J Neurophysiol. 2010;104:2543–2555. doi: 10.1152/jn.00256.2010. [DOI] [PubMed] [Google Scholar]
Marsat G, Proville RD, Maler L. Transient signals trigger synchronous bursts in an identified population of neurons. J Neurophysiol. 2009;102:714–723. doi: 10.1152/jn.91366.2008. [DOI] [PubMed] [Google Scholar]
Mathieson WB, Heiligenberg W, Maler L. Ultrastructural studies of physiologically identified electrosensory afferent synapses in the gymnotiform fish, Eigenmannia. J Comp Neurol. 1987;255:526–537. doi: 10.1002/cne.902550405. [DOI] [PubMed] [Google Scholar]
Metzner W, Heiligenberg W. The coding of signals in the electric communication of the gymnotiform fish Eigenmannia—from electroreceptors to neurons in the torus-semicircularis of the midbrain. J Comp Physiol A. 1991;169:135–150. doi: 10.1007/BF00215861. [DOI] [PubMed] [Google Scholar]
Olshausen BA, Field DJ. Sparse coding of sensory inputs. Curr Opin Neurobiol. 2004;14:481–487. doi: 10.1016/j.conb.2004.07.007. [DOI] [PubMed] [Google Scholar]
Perez-Orive J, Mazor O, Turner GC, Cassenaer S, Wilson RI, Laurent G. Oscillations and sparsening of odor representations in the mushroom body. Science. 2002;297:359–365. doi: 10.1126/science.1070502. [DOI] [PubMed] [Google Scholar]
Pluta SR, Kawasaki M. Temporal selectivity in midbrain electrosensory neurons identified by modal variation in active sensing. J Neurophysiol. 2010;104:498–507. doi: 10.1152/jn.00731.2009. [DOI] [PubMed] [Google Scholar]
Poo C, Isaacson JS. Odor representations in olfactory cortex: “sparse” coding, global inhibition, and oscillations. Neuron. 2009;62:850–861. doi: 10.1016/j.neuron.2009.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
Quiroga R, Reddy L, Kreiman G, Koch C, Fried I. Invariant visual representation by single neurons in the human brain. Nature. 2005;435:1102–1107. doi: 10.1038/nature03687. [DOI] [PubMed] [Google Scholar]
Rathbun DL, Warland DK, Usrey WM. Spike timing and information transmission at retinogeniculate synapses. J Neurosci. 2010;30:13558–13566. doi: 10.1523/JNEUROSCI.0909-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rauschecker JP, Tian B. Mechanisms and streams for processing of “what” and “where” in auditory cortex. Proc Natl Acad Sci USA. 2000;97:11900–11806. doi: 10.1073/pnas.97.22.11800. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rolls ET, Tovee MJ. Sparseness of the neuronal representation of stimuli in the primate temporal visual cortex. J Neurophysiol. 1995;73:713–726. doi: 10.1152/jn.1995.73.2.713. [DOI] [PubMed] [Google Scholar]
Rose GJ, Heiligenberg W. Structure and function of electrosensory neurons in the torus semicircularis of Eigenmannia—morphological correlates of phase and amplitude sensitivity. J Neurosci. 1985;5:2269–2280. doi: 10.1523/JNEUROSCI.05-08-02269.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rose GJ, Fortune ES. New techniques for making whole-cell recordings from CNS neurons in vivo. Neurosci Res. 1996;26:89–94. doi: 10.1016/0168-0102(96)01074-7. [DOI] [PubMed] [Google Scholar]
Rosen MJ, Mooney R. Inhibitory and excitatory mechanisms underlying auditory responses to learned vocalizations in the songbird nucleus HVC. Neuron. 2003;39:177–194. doi: 10.1016/s0896-6273(03)00357-x. [DOI] [PubMed] [Google Scholar]
Saunders J, Bastian J. The physiology and morphology of 2 types of electrosensory neurons in the weakly electric fish Apteronotus leptorhynchus. J Comp Physiol [A] 1984;154:199–209. [Google Scholar]
Scheich H, Bullock TH, Hamstra RH. Coding properties of two classes of afferent nerve fibers: high frequency electroreceptors in the electric fish, Eigenmannia. J Neurophysiol. 1973;36:39–60. doi: 10.1152/jn.1973.36.1.39. [DOI] [PubMed] [Google Scholar]
Sincich LC, Horton JC, Sharpee TO. Preserving information in neural transmission. J Neurosci. 2009;29:6207–6216. doi: 10.1523/JNEUROSCI.3701-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Thompson LT, Best PJ. Place cells and silent cells in the hippocampus of freely-behaving rats. J Neurosci. 1989;9:2382–2390. doi: 10.1523/JNEUROSCI.09-07-02382.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
Toporikova N, Chacron MJ. SK channels gate information processing in vivo by regulating an intrinsic bursting mechanism seen in vitro. J Neurophysiol. 2009;102:2273–2287. doi: 10.1152/jn.00282.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ungerleider LG, Haxby JV. “What” and “where” in the human brain. Curr Opin Neurobiol. 1994;4:157–165. doi: 10.1016/0959-4388(94)90066-3. [DOI] [PubMed] [Google Scholar]
Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol. 1996;76:1310–1326. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]
Vinje WE, Gallant JL. Sparse coding and decorrelation in primary visual cortex during natural vision. Science. 2000;287:1273–1276. doi: 10.1126/science.287.5456.1273. [DOI] [PubMed] [Google Scholar]
Vonderschen K, Chacron MJ. Sparse coding of natural communication signals in midbrain neurons (Abstract) BMC Neurosci. 2009;10:O3. [Google Scholar]
Wang X, Hirsch JA, Sommer FT. Recoding of sensory information across the retinothalamic synapse. J Neurosci. 2010;30:13567–13577. doi: 10.1523/JNEUROSCI.0910-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wehr M, Zador AM. Balanced inhibition underlies tuning and sharpens spike timing in auditory cortex. Nature. 2003;426:442–446. doi: 10.1038/nature02116. [DOI] [PubMed] [Google Scholar]
Willmore B, Tolhurst DJ. Characterizing the sparseness of neural codes. Network. 2001;12:255–270. [PubMed] [Google Scholar]
Young MP, Yamane S. Sparse population coding of faces in the inferotemporal cortex. Science. 1992;256:1327–1331. doi: 10.1126/science.1598577. [DOI] [PubMed] [Google Scholar]
Zakon HH, Oestreich J, Tallarovic S, Triefenbach F. EOD modulations of brown ghost electric fish: JARs, chirps, rises, and dips. J Physiol (Paris) 2002;96:451–458. doi: 10.1016/S0928-4257(03)00012-3. [DOI] [PubMed] [Google Scholar]
Zhang LI, Tan AYY, Schreiner CE, Merzenich MM. Topography and synaptic shaping of direction selectivity in primary auditory cortex. Nature. 2003;424:201–205. doi: 10.1038/nature01796. [DOI] [PubMed] [Google Scholar]
Zupanc G, Maler L. Evoked chirping in the weakly electric fish Apteronotus leptorhynchus: a quantitative biophysical analysis. Can J Zool. 1993;71:2301–2310. [Google Scholar]
Zupanc G, Sirbulescu R, Nichols A, Ilies I. Electric interactions through chirping behavior in the weakly electric fish, Apteronotus leptorhynchus. J Comp Physiol A. 2006;192:159–173. doi: 10.1007/s00359-005-0058-5. [DOI] [PubMed] [Google Scholar]

[R1] Abbott LF, Rolls ET, Tovee MJ. Representational capacity of face coding in monkeys. Cereb Cortex. 1996;6:498–505. doi: 10.1093/cercor/6.3.498. [DOI] [PubMed] [Google Scholar]

[R2] Arnegard ME, Carlson BA. Electric organ discharge patterns during group hunting by a mormyrid fish. Proc Biol Sci. 2005;272:1305–1314. doi: 10.1098/rspb.2005.3101. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab. 2001;21:1133–1145. doi: 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]

[R4] Barlow HB. Single units and sensation: a neuron doctrine for perceptual psychology? Perception. 1972;1:371–394. doi: 10.1068/p010371. [DOI] [PubMed] [Google Scholar]

[R5] Bastian J. Electrolocation. I. How the electroreceptors of Apteronotus albifrons code for moving objects and other electrical stimuli. J Comp Physiol A. 1981;144:465–479. [Google Scholar]

[R6] Bastian J, Chacron MJ, Maler L. Receptive field organization determines pyramidal cell stimulus encoding capability and spatial stimulus selectivity. J Neurosci. 2002;22:4577–4590. doi: 10.1523/JNEUROSCI.22-11-04577.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] Bastian J, Schniederjan S, Nguyenkim J. Arginine vasotocin modulates a sexually dimorphic communication behavior in the weakly electric fish Apteronotus leptorhynchus. J Exp Biol. 2001;204:1909–1923. doi: 10.1242/jeb.204.11.1909. [DOI] [PubMed] [Google Scholar]

[R8] Benda J, Longtin A, Maler L. Spike-frequency adaptation separates transient communication signals from background oscillations. J Neurosci. 2005;25:2312–2321. doi: 10.1523/JNEUROSCI.4795-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] Borst A, Theunissen FE. Information theory and neural coding. Nat Neurosci. 1999;2:947–957. doi: 10.1038/14731. [DOI] [PubMed] [Google Scholar]

[R10] Carlson BA, Kawasaki M. Stimulus selectivity is enhanced by voltage-dependent conductances in combination-sensitive neurons. J Neurophysiol. 2006a;96:3362–3377. doi: 10.1152/jn.00839.2006. [DOI] [PubMed] [Google Scholar]

[R11] Carlson BA, Kawasaki M. Ambiguous encoding of stimuli by primary sensory afferents causes a lack of independence in the perception of multiple stimulus attributes. J Neurosci. 2006b;26:9173–9183. doi: 10.1523/JNEUROSCI.1513-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] Carlson BA, Kawasaki M. From stimulus estimation to combination sensitivity: encoding and processing of amplitude and timing information in parallel, convergent sensory pathways. J Comput Neurosci. 2008;25:1–24. doi: 10.1007/s10827-007-0062-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] Carlson BA. Temporal-pattern recognition by single neurons in a sensory pathway devoted to social communication behavior. J Neurosci. 2009;29:9417–9428. doi: 10.1523/JNEUROSCI.1980-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] Carr CE, Maler L. A Golgi study of the cell types of the dorsal torus semicircularis of the electric fish Eigenmannia—functional and morphological diversity in the midbrain. J Comp Neurol. 1985;235:207–240. doi: 10.1002/cne.902350206. [DOI] [PubMed] [Google Scholar]

[R15] Carr CE, Maler L, Heiligenberg W, Sas E. Laminar organization of the afferent and efferent systems of the torus semicircularis of gymnotiform fish: morphological substrates for parallel processing in the electrosensory system. J Comp Neurol. 1981;203:649–670. doi: 10.1002/cne.902030406. [DOI] [PubMed] [Google Scholar]

[R16] Chacron MJ, Longtin A, Maler L. The effects of spontaneous activity, background noise, and the stimulus ensemble on information transfer in neurons. Network. 2003;14:803–824. [PubMed] [Google Scholar]

[R17] Chacron MJ, Maler L, Bastian J. Electroreceptor neuron dynamics shape information transmission. Nat Neurosci. 2005;8:673–678. doi: 10.1038/nn1433. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] Chacron MJ, Bastian J. Population coding by electrosensory neurons. J Neurophysiol. 2008;99:1825–1835. doi: 10.1152/jn.01266.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] Chacron MJ, Fortune ES. Subthreshold membrane conductances enhance directional selectivity in vertebrate sensory neurons. J Neurophysiol. 2010;104:449–462. doi: 10.1152/jn.01113.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Chacron MJ, Toporikova N, Fortune ES. Differences in the time course of short-term depression across receptive fields are correlated with directional selectivity in electrosensory neurons. J Neurophysiol. 2009;102:3270–3279. doi: 10.1152/jn.00645.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] Chacron MJ, Longtin A, Maler L. Efficient computation via sparse coding in electrosensory neural networks. Curr Opin Neurobiol. 2011 Jun 15; doi: 10.1016/j.conb.2011.1005.1016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] Covey E, Kauer JA, Casseday JH. Whole-cell patch-clamp recording reveals subthreshold sound-evoked postsynaptic currents in the inferior colliculus of awake bats. J Neurosci. 1996;16:3009–3018. doi: 10.1523/JNEUROSCI.16-09-03009.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] DeWeese MR, Wehr M, Zador AM. Binary spiking in auditory cortex. J Neurosci. 2003;23:7940–7949. doi: 10.1523/JNEUROSCI.23-21-07940.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R24] Faure PA, Fremouw T, Casseday JH, Covey E. Temporal masking reveals properties of sound-evoked inhibition in duration-tuned neurons of the inferior colliculus. J Neurosci. 2003;23:3052–3065. doi: 10.1523/JNEUROSCI.23-07-03052.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] Földiák P, Young MP. Sparse coding in the primate cortex. In: Arbib MA, editor. The Handbook of Brain Theory and Neural Networks. Cambridge, MA: MIT Press; 1995. [Google Scholar]

[R26] Fortune ES, Rose GJ. Passive and active membrane properties contribute to the temporal filtering properties of midbrain neurons in vivo. J Neurosci. 1997a;17:3815–3825. doi: 10.1523/JNEUROSCI.17-10-03815.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] Fortune ES, Rose GJ. Temporal filtering properties of ampullary electrosensory neurons in the torus semicircularis of Eigenmannia: evolutionary and computational implications. Brain Behav Evol. 1997b;49:312–323. doi: 10.1159/000113000. [DOI] [PubMed] [Google Scholar]

[R28] Fortune ES, Rose GJ. Short-term synaptic plasticity contributes to the temporal filtering of electrosensory information. J Neurosci. 2000;20:7122–7130. doi: 10.1523/JNEUROSCI.20-18-07122.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Fortune E, Rose G. Voltage-gated Na+ channels enhance the temporal filtering properties of electrosensory neurons in the torus. J Neurophysiol. 2003;90:924–929. doi: 10.1152/jn.00294.2003. [DOI] [PubMed] [Google Scholar]

[R30] Gentner TQ, Margoliash D. Neuronal populations and single cells representing learned auditory objects. Nature. 2003;424:669–674. doi: 10.1038/nature01731. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] Green D, Swets J. Signal Detection Theory and Psychophysics. Oxford: Wiley; 1966. [Google Scholar]

[R32] Haag J, Borst A. Amplification of high-frequency synaptic inputs by active dendritic membrane processes. Nature. 1996;379:639–641. [Google Scholar]

[R33] Hagedorn M, Heiligenberg W. Court and spark: electric signals in the courtship and mating of gymnotoid electric fish. Anim Behav. 1985;33:254–265. [Google Scholar]

[R34] Heil P. First-spike latency of auditory neurons revisited. Curr Opin Neurobiol. 2004;14:461–467. doi: 10.1016/j.conb.2004.07.002. [DOI] [PubMed] [Google Scholar]

[R35] Heiligenberg W, Bastian J. The control of Eigenmannia’s pacemaker by distributed evaluation of electroreceptive afferences. J Comp Physiol. 1980;136:113–133. [Google Scholar]

[R36] Heiligenberg W, Keller CH, Metzner W, Kawasaki M. Structure and function of neurons in the complex of the nucleus electrosensorius of the gymnotiform fish Eigenmannia: detection and processing of electric signals in social communication. J Comp Physiol A. 1991;169:151–164. doi: 10.1007/BF00215862. [DOI] [PubMed] [Google Scholar]

[R37] Heiligenberg W, Rose G. Phase and amplitude computations in the midbrain of an electric fish: intracellular studies of neurons participating in the jamming avoidance response of Eigenmannia. J Neurosci. 1985;5:515–531. doi: 10.1523/JNEUROSCI.05-02-00515.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Higley MJ, Contreras D. Balanced excitation and inhibition determine spike timing during frequency adaptation. J Neurosci. 2006;26:448–457. doi: 10.1523/JNEUROSCI.3506-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] Hitschfeld EM, Stamper SA, Vonderschen K, Fortune ES, Chacron MJ. Effects of restraint and immobilization on electrosensory behaviors of weakly electric fish. ILAR J. 2009;50:361–372. doi: 10.1093/ilar.50.4.361. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] Hromádka T, DeWeese MR, Zador AM. Sparse representation of sounds in the unanesthetized auditory cortex. PLoS Biol. 2008;6:e16. doi: 10.1371/journal.pbio.0060016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] Hubel DH, Wiesel TN. Receptive fields of single neurones in the cat’s striate cortex. J Physiol. 1959;148:574–591. doi: 10.1113/jphysiol.1959.sp006308. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Hupé GJ, Lewis JE. Electrocommunication signals in free swimming brown ghost knifefish, Apteronotus leptorhynchus. J Exp Biol. 2008;211:1657–1667. doi: 10.1242/jeb.013516. [DOI] [PubMed] [Google Scholar]

[R43] Hurley LM, Pollak GD. Serotonin shifts first-spike latencies of inferior colliculus neurons. J Neurosci. 2005;25:7876–7886. doi: 10.1523/JNEUROSCI.1178-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R44] Kajikawa Y, Hackett TA. Entropy analysis of neuronal spike train synchrony. J Neurosci Methods. 2005;149:90–93. doi: 10.1016/j.jneumeth.2005.05.011. [DOI] [PubMed] [Google Scholar]

[R45] Kawasaki M, Guo YX. Neuronal circuitry for comparison of timing in the electrosensory lateral line lobe of the African wave-type electric fish Gymnarchus niloticus. J Neurosci. 1996;16:380–391. doi: 10.1523/JNEUROSCI.16-01-00380.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] Khosravi-Hashemi N, Fortune ES, Chacron MJ. Coding movement direction by burst firing in electrosensory neurons. J Neurophysiol. 2011;106:1954–1968. doi: 10.1152/jn.00116.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] Krahe R, Bastian J, Chacron MJ. Temporal processing across multiple topographic maps in the electrosensory system. J Neurophysiol. 2008;100:852–867. doi: 10.1152/jn.90300.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] Krahe R, Kreiman G, Gabbiani F, Koch C, Metzner W. Stimulus encoding and feature extraction by multiple sensory neurons. J Neurosci. 2002;22:2374–2382. doi: 10.1523/JNEUROSCI.22-06-02374.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] Kuffler SW. Discharge patterns and functional organization of mammalian retina. J Neurophysiol. 1953;16:37–68. doi: 10.1152/jn.1953.16.1.37. [DOI] [PubMed] [Google Scholar]

[R50] Leary CJ, Edwards CJ, Rose GJ. Midbrain auditory neurons integrate excitation and inhibition to generate duration selectivity: an in vivo whole-cell patch study in anurans. J Neurosci. 2008;28:5481–5493. doi: 10.1523/JNEUROSCI.5041-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] Maler L. Receptive field organization across multiple electrosensory maps. I. Columnar organization and estimation of receptive field size. J Comp Neurol. 2009a;516:376–393. doi: 10.1002/cne.22124. [DOI] [PubMed] [Google Scholar]

[R52] Maler L. Receptive field organization across multiple electrosensory maps. II. Computational analysis of the effects of receptive field size on prey localization. J Comp Neurol. 2009b;516:394–422. doi: 10.1002/cne.22120. [DOI] [PubMed] [Google Scholar]

[R53] Maler L, Sas E, Johnston S, Ellis W. An atlas of the brain of the electric fish Apteronotus leptorhynchus. J Chem Neuroanat. 1991;4:1–38. doi: 10.1016/0891-0618(91)90030-g. [DOI] [PubMed] [Google Scholar]

[R54] Mann NI, Dingess KA, Slater PJB. Antiphonal four-part synchronized chorusing in a Neotropical wren. Biol Lett. 2006;2:1–4. doi: 10.1098/rsbl.2005.0373. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] Marsat G, Maler L. Neural heterogeneity and efficient population codes for communication signals. J Neurophysiol. 2010;104:2543–2555. doi: 10.1152/jn.00256.2010. [DOI] [PubMed] [Google Scholar]

[R56] Marsat G, Proville RD, Maler L. Transient signals trigger synchronous bursts in an identified population of neurons. J Neurophysiol. 2009;102:714–723. doi: 10.1152/jn.91366.2008. [DOI] [PubMed] [Google Scholar]

[R57] Mathieson WB, Heiligenberg W, Maler L. Ultrastructural studies of physiologically identified electrosensory afferent synapses in the gymnotiform fish, Eigenmannia. J Comp Neurol. 1987;255:526–537. doi: 10.1002/cne.902550405. [DOI] [PubMed] [Google Scholar]

[R58] Metzner W, Heiligenberg W. The coding of signals in the electric communication of the gymnotiform fish Eigenmannia—from electroreceptors to neurons in the torus-semicircularis of the midbrain. J Comp Physiol A. 1991;169:135–150. doi: 10.1007/BF00215861. [DOI] [PubMed] [Google Scholar]

[R59] Olshausen BA, Field DJ. Sparse coding of sensory inputs. Curr Opin Neurobiol. 2004;14:481–487. doi: 10.1016/j.conb.2004.07.007. [DOI] [PubMed] [Google Scholar]

[R60] Perez-Orive J, Mazor O, Turner GC, Cassenaer S, Wilson RI, Laurent G. Oscillations and sparsening of odor representations in the mushroom body. Science. 2002;297:359–365. doi: 10.1126/science.1070502. [DOI] [PubMed] [Google Scholar]

[R61] Pluta SR, Kawasaki M. Temporal selectivity in midbrain electrosensory neurons identified by modal variation in active sensing. J Neurophysiol. 2010;104:498–507. doi: 10.1152/jn.00731.2009. [DOI] [PubMed] [Google Scholar]

[R62] Poo C, Isaacson JS. Odor representations in olfactory cortex: “sparse” coding, global inhibition, and oscillations. Neuron. 2009;62:850–861. doi: 10.1016/j.neuron.2009.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] Quiroga R, Reddy L, Kreiman G, Koch C, Fried I. Invariant visual representation by single neurons in the human brain. Nature. 2005;435:1102–1107. doi: 10.1038/nature03687. [DOI] [PubMed] [Google Scholar]

[R64] Rathbun DL, Warland DK, Usrey WM. Spike timing and information transmission at retinogeniculate synapses. J Neurosci. 2010;30:13558–13566. doi: 10.1523/JNEUROSCI.0909-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] Rauschecker JP, Tian B. Mechanisms and streams for processing of “what” and “where” in auditory cortex. Proc Natl Acad Sci USA. 2000;97:11900–11806. doi: 10.1073/pnas.97.22.11800. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] Rolls ET, Tovee MJ. Sparseness of the neuronal representation of stimuli in the primate temporal visual cortex. J Neurophysiol. 1995;73:713–726. doi: 10.1152/jn.1995.73.2.713. [DOI] [PubMed] [Google Scholar]

[R67] Rose GJ, Heiligenberg W. Structure and function of electrosensory neurons in the torus semicircularis of Eigenmannia—morphological correlates of phase and amplitude sensitivity. J Neurosci. 1985;5:2269–2280. doi: 10.1523/JNEUROSCI.05-08-02269.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] Rose GJ, Fortune ES. New techniques for making whole-cell recordings from CNS neurons in vivo. Neurosci Res. 1996;26:89–94. doi: 10.1016/0168-0102(96)01074-7. [DOI] [PubMed] [Google Scholar]

[R69] Rosen MJ, Mooney R. Inhibitory and excitatory mechanisms underlying auditory responses to learned vocalizations in the songbird nucleus HVC. Neuron. 2003;39:177–194. doi: 10.1016/s0896-6273(03)00357-x. [DOI] [PubMed] [Google Scholar]

[R70] Saunders J, Bastian J. The physiology and morphology of 2 types of electrosensory neurons in the weakly electric fish Apteronotus leptorhynchus. J Comp Physiol [A] 1984;154:199–209. [Google Scholar]

[R71] Scheich H, Bullock TH, Hamstra RH. Coding properties of two classes of afferent nerve fibers: high frequency electroreceptors in the electric fish, Eigenmannia. J Neurophysiol. 1973;36:39–60. doi: 10.1152/jn.1973.36.1.39. [DOI] [PubMed] [Google Scholar]

[R72] Sincich LC, Horton JC, Sharpee TO. Preserving information in neural transmission. J Neurosci. 2009;29:6207–6216. doi: 10.1523/JNEUROSCI.3701-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] Thompson LT, Best PJ. Place cells and silent cells in the hippocampus of freely-behaving rats. J Neurosci. 1989;9:2382–2390. doi: 10.1523/JNEUROSCI.09-07-02382.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R74] Toporikova N, Chacron MJ. SK channels gate information processing in vivo by regulating an intrinsic bursting mechanism seen in vitro. J Neurophysiol. 2009;102:2273–2287. doi: 10.1152/jn.00282.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R75] Ungerleider LG, Haxby JV. “What” and “where” in the human brain. Curr Opin Neurobiol. 1994;4:157–165. doi: 10.1016/0959-4388(94)90066-3. [DOI] [PubMed] [Google Scholar]

[R76] Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol. 1996;76:1310–1326. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]

[R77] Vinje WE, Gallant JL. Sparse coding and decorrelation in primary visual cortex during natural vision. Science. 2000;287:1273–1276. doi: 10.1126/science.287.5456.1273. [DOI] [PubMed] [Google Scholar]

[R78] Vonderschen K, Chacron MJ. Sparse coding of natural communication signals in midbrain neurons (Abstract) BMC Neurosci. 2009;10:O3. [Google Scholar]

[R79] Wang X, Hirsch JA, Sommer FT. Recoding of sensory information across the retinothalamic synapse. J Neurosci. 2010;30:13567–13577. doi: 10.1523/JNEUROSCI.0910-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R80] Wehr M, Zador AM. Balanced inhibition underlies tuning and sharpens spike timing in auditory cortex. Nature. 2003;426:442–446. doi: 10.1038/nature02116. [DOI] [PubMed] [Google Scholar]

[R81] Willmore B, Tolhurst DJ. Characterizing the sparseness of neural codes. Network. 2001;12:255–270. [PubMed] [Google Scholar]

[R82] Young MP, Yamane S. Sparse population coding of faces in the inferotemporal cortex. Science. 1992;256:1327–1331. doi: 10.1126/science.1598577. [DOI] [PubMed] [Google Scholar]

[R83] Zakon HH, Oestreich J, Tallarovic S, Triefenbach F. EOD modulations of brown ghost electric fish: JARs, chirps, rises, and dips. J Physiol (Paris) 2002;96:451–458. doi: 10.1016/S0928-4257(03)00012-3. [DOI] [PubMed] [Google Scholar]

[R84] Zhang LI, Tan AYY, Schreiner CE, Merzenich MM. Topography and synaptic shaping of direction selectivity in primary auditory cortex. Nature. 2003;424:201–205. doi: 10.1038/nature01796. [DOI] [PubMed] [Google Scholar]

[R85] Zupanc G, Maler L. Evoked chirping in the weakly electric fish Apteronotus leptorhynchus: a quantitative biophysical analysis. Can J Zool. 1993;71:2301–2310. [Google Scholar]

[R86] Zupanc G, Sirbulescu R, Nichols A, Ilies I. Electric interactions through chirping behavior in the weakly electric fish, Apteronotus leptorhynchus. J Comp Physiol A. 2006;192:159–173. doi: 10.1007/s00359-005-0058-5. [DOI] [PubMed] [Google Scholar]

PERMALINK

Sparse and dense coding of natural stimuli by distinct midbrain neuron subpopulations in weakly electric fish

Katrin Vonderschen

Maurice J Chacron

Abstract

METHODS

Experimental preparation

Recordings

Fig. 1.

Stimulation

Data analysis

Testing response significance

Chirp selectivity index

Movement selectivity index

Specificity of neural responses

Response latency

Sparseness measures

Mutual information and spike metrics

Receiver-operator characteristic curves

RESULTS

Sparse coding in torus semicircularis

Fig. 2.

Fig. 3.

Response selectivity between different stimulus categories

Fig. 4.

Fig. 5.

Do chirp attributes determine TS and ELL neural responses?

Fig. 6.

Fig. 7.

Precision of spike timing in response to chirp stimuli

Chirp detection

Fig. 8.

DISCUSSION

Summary

Parallel processing in the midbrain

Mechanisms underlying dense and sparse responses

Discrimination and detection of chirps

Preserving sensory information in sparse coding populations

Does transitioning from a dense code to a sparse code preserve sensory information?

Acknowledgments

Footnotes

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases