A hydrodynamic mechanism for attraction of undulatory microswimmers to surfaces (bordertaxis)

Abstract

Although small nematodes significantly impact human and animal health, agriculture, and ecology, little is known about the role of hydrodynamics in their life cycles. Using the nematode Caenorhabditis elegans as a model undulatory microswimmer, we have observed that animals are attracted to and swim along surfaces. The attraction to surfaces does not require mechanosensory neuron function. In dilute swarms, swimmers aggregate near surfaces. Using resistive force-based theory, symmetry arguments, and direct hydrodynamic simulations, we demonstrate that forces resulting from the interaction between the swimmer-induced flow field and a nearby surface cause a short-range hydrodynamic torque that stirs the swimmers towards the surface. When combined with steric forces, this causes locomotion along the surface. This surface attraction may affect nematode mate and food finding behaviour and, in the case of parasitic nematodes, may facilitate host penetration. Surface attraction must be accounted for when studying animals' responses to various stimuli, and suggests means of controlling undulatory microswimmers.

1. Introduction

Animals that swim with undulating anterior-to-posterior waves, such as nematodes, annelids and flat worms, are ubiquitous, inhabiting ecosystems such as soils, fresh water, marine water, vegetation and in the case of parasitic worms, mammalian intestinal tracts and bloodstreams [1,2]. Over a billion humans and numerous livestock and plants are infected with parasitic worms that cause morbidity as well as severe economic damage [1–4]. On the positive side, worms play an important role in medical research. A non-parasitic worm, the nematode Caenorhabditis elegans (C. elegans), is used to study the genetic mechanisms that govern animal physiology and development. Although undulatory swimmers significantly impact human and animal health, agriculture, ecology and, in the case of C. elegans, medical research, little is known about the role of hydrodynamics in their life cycles. When migrating through their various habitats, undulating swimmers often encounter and interact with surfaces such as the epithelia of hosts [5,6]; the walls of rocks, soil and plants and, in laboratory settings, the walls of microfluidic devices [7–9]. In this paper, we focus on a particular, as yet, unexplained trait of undulatory swimmers, the attraction to surfaces (bordertaxis) and comment on its role in the animals' life cycles and in man-made devices. Recently, we have shown that, in the presence of external flow, bordertaxis plays a role in the orientation of undulatory swimmers to face against the flow (positive rheotaxis) [10]. Here, we delineate the mechanisms responsible for bordertaxis.

When placing C. elegans in a liquid-filled conduit, we have observed that the animals migrated towards and aggregated next to the conduit's walls, spending a considerable time swimming along the surfaces. Previously, experimenters reported that undulatory swimmers such as infective hookworm larvae in a water-filled glass box and in a drop [11] and C. elegans in a drop [12] aggregated next to surfaces. On other occasions, although surface aggregation was evident and likely interfered with stimuli such as chemotaxis, its existence went unrecognized ([8], electronic supplementary material, video S3).

It is likely that maintaining proximity to surfaces is beneficial to the animals. Regions close to surfaces are often rich in food such as bacteria [13], a major food source for free-living nematodes [14]. Animal aggregation could favour mate finding. Movement close to a surface may assist in navigation, such as the migration of the hookworm through the host's bloodstream [15]. Regions close to a surface are subject to slower fluid velocities, enabling upstream swimming. For example, the plant pathogenic nematode Aphelenchoides ritzemabosi swims along the surface of a stem, against the current, to invade the host [16]. Proximity to surfaces increases the probability of host penetration by parasitic nematodes. When propelling themselves along the host epidermis, both Aphelenchus avenae and Meloidogyne javanica's heads undergo frequent collisions with the epidermis, probing for penetration sites [17,18]. Despite the significant role that attraction to surfaces plays in nematodes' life cycles and their interactions with hosts, little is known about the mechanisms that cause undulatory swimmers to ‘attract’ to, swim along and aggregate next to surfaces.

In contrast, the interactions between surfaces and motile cells have attracted considerable attention [19]. Self-propelling bacteria, such as Escherichia coli (E. coli) [20], and mammalian cells, such as spermatozoa [21–23], accumulate next to and swim along surfaces. Often, self-propelled bacteria and cells are modelled as force dipoles (stresslets), in which the flagella motion provides forward thrust that is opposed, for the most part, by the relatively large cell body-induced drag [19,20]. Force-dipole-based, hydrodynamic theories predict surface attraction in certain types of motile cells. It has been proposed, however, that contact (steric) interactions between the cell's flagella and the surface dominate the behaviour of motile cells next to surfaces, whereas hydrodynamics plays a secondary role [21,24–27]. Because undulatory swimmers lack flagella and cilia, and the thrust and drag are nearly uniformly distributed along the animal's body, the force dipole model is not appropriate for undulatory swimmers and fails to describe faithfully the flow field in close proximity to the swimmer's body [24]. Moreover, because undulatory swimmers possess a nervous system, the question arises as to whether surface attraction in undulatory swimmers is active or passive. In this paper, we delineate for the first time the mechanisms of surface attraction in undulatory swimmers.

We use C. elegans as a model of an undulatory, low Reynolds number swimmer [28]. In the case of adult C. elegans, the Reynolds number ρva/μ ∼ 0.02, where ρ = 1000 kg m⁻³ is the fluid density, v = 300 µm s⁻¹ is the mean velocity of the swimmer, a = 70 µm is the body diameter, and μ = 0.001 Ns m⁻² is the fluid's dynamic viscosity. Our conclusions are relevant, however, to all low Reynolds number undulatory swimmers. In the first part of the paper, we report on experiments that demonstrate the attraction of swimmers to surfaces. In the second part of the paper, we use resistive force theory (RFT) to estimate the hydrodynamically induced rotational velocity and support our calculations with qualitative symmetry arguments and direct hydrodynamic simulations. In the third part of the paper, we demonstrate that surface attraction is responsible for the aggregation of swimmers next to surfaces in dilute swarms. Lastly, based on our experimental observations and theoretical considerations, we present a simple surface attraction-based method for automated high-throughput sorting of undulatory swimmers out of a flow stream.

2. Results and discussions

2.1. Experimental observations of individual Caenorhabditis elegans swimmers' surface attraction

We experimented with wild-type (n = 10) animals as well as with mechanosensation-defective mec-4 (n = 9) and mec-3 (n = 9) mutant, young adult C. elegans. The animals were 2a = 69 ± 1 µm in diameter and l = 1077 ± 9 µm in length (mean ± standard deviation). When suspended in water, the animals swam with an undulatory gait with a frequency f = 2.22 ± 0.02 Hz, an amplitude b = 170 ± 3 µm and a velocity of approximately 300 µm s⁻¹. The animal's radius-based Reynolds number is about 0.02.

To study the interactions between swimmers and surfaces, we moulded a conduit L = 30 mm long, W = 2.6 mm wide and 100 µm tall in a polydimethylsiloxane (PDMS) slab. The conduit's height was small enough to accommodate just one animal in the vertical direction, but tall enough for unhindered motion. The conduit was capped with a glass slide, placed horizontally (i.e. perpendicular to the gravity vector) and filled with water (electronic supplementary material, figure S1). Animals were introduced into the conduit one at a time and their trajectories were viewed with a stereomicroscope, recorded with a digital camera and processed with a custom Matlab program to obtain the position and orientation of each animal as functions of time in the absence of any externally induced fluid motion. Our custom Matlab program performs two-dimensional tracking using a combination of various build-in functions in Matlab's image processing toolbox.

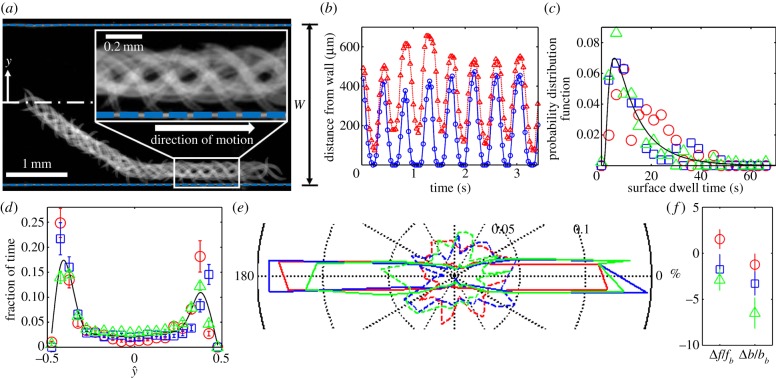
Figure 1a and electronic supplementary material, video S1 depict the trajectory of a wild-type animal. The image is composed of superposed individual video frames, spaced 0.15 s apart. This particular animal, initially close to the conduit's mid-width, progressed at an angle of θ ∼−37° with respect to the conduit's axis, along a trajectory that eventually brought it into proximity to the conduit's side wall. Once the animal's head contacted the surface, the animal turned to swim parallel to the surface, maintaining an average distance of approximately 200 µm (∼(b + a)) between its centre of mass and the surface. During the animal's motion, its head periodically contacted the surface. The inset in figure 1a provides an amplified view of the nematode–surface interactions. Figure 1b depicts the distance of the animal's head (blue line, hollow circles) and the distance of its tail's tip (red line, upright triangles) from the surface as functions of time. While the animal was swimming along the surface, its head collided with the surface at a frequency of 2.20 ± 0.08 Hz, the same as its gait frequency. In contrast, the animal's tail made only occasional contacts with the surface.

Figure 1.

Surface attraction of individual C. elegans. (a) Superposed video frames (6.6 frames per second) of 19 swimming cycles of one worm with an initial position in the centre of the conduit. The blue dashed lines represent the conduit's side walls. The magnified inset shows periodic contacts between the animal's head and the side wall. (b) The position of the individual nematode's head (blue line) and tail's tip (red line) are depicted as functions of time. (c) The probability distribution functions of surface dwell times of wild-type animals (n = 10, red circles), mec-3 mutants (n = 9, blue squares) and mec-4 mutants (n = 9, green triangles). The solid line is the Binbaum–Saunders (fatigue life) distribution. (d) The fraction of residence time of the centre of mass of the wild-type animals (n = 10, red circles), mec-3 mutants (n = 9, blue squares) and mec-4 mutants (n = 9, green triangles) as functions of position 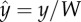along the conduit's width. The solid line is the average of all the data. The error bars correspond to 1 s2.d. (e) The fraction of time that the wild-type animals (n = 10, red), mec-3 mutants (n = 9, blue) and mec-4 mutants (green) swim in direction θ when |ŷ| ≥ 0.3 (solid contours) and |ŷ| < 0.3 (dashed contours). (f) The relative difference (%) of the gait frequency Δf/f_b and amplitude Δb/b_b between near-surface (|ŷ| ≥ 0.3) and distant (|ŷ| < 0.3) swimmers. The subscript ‘b’ denotes a swimmer far from the surface. Red circles denote data of wild-type animals, blue squares denote data from mec-3 mutants, and green triangles denote data from mec-4 mutants.

Once the animal had started swimming along the surface, its centre of mass maintained, on average, a constant distance approximately (b + a) from the surface for a significant time span. The propulsion parallel to the surface was occasionally interrupted by the animal executing a turn (electronic supplementary material, video S2). Subsequent to the turn, the animal resumed swimming along the surface in its original direction, swam along the surface in the opposite direction, or swam away from the surface (electronic supplementary material, video S2). Figure 1c depicts the probability distribution function (red hollow circles) of the animal's dwelling time t_d of continuous swimming along the surface. The Birnbaum–Saunders probability distribution function [29]

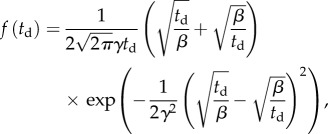is often used to model time to failure, and more generally lifetimes. The distribution with β = 10.26 s, γ = 0.79 and R² = 0.98 (solid line) fits well our experimental data. The average dwell time 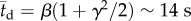and the standard deviation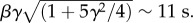

Overall, the animals spent most of their time swimming next to one of the surfaces. Figure 1d (red circles) depicts the fraction of time that the animal's centre of mass resided at a (normalized) transverse position 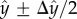along the conduit's width (W), where 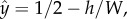h is the distance of the animal's centre of mass from the surface, Δy = 130 µm, and 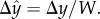Most of the time, the animals' centre of mass was approximately at h = (b + a). What then are the mechanisms responsible for the animals' prolonged retention time near the surface?

Figure 1e (red curves) is a polar plot depicting the fraction of time that the nematode swims in a direction θ ± Δθ/2 as a function of θ. The angle θ is measured with respect to the conduit's axis and Δθ =10°. The solid and dashed red lines correspond, respectively, to nematodes with centre of mass located far from the surface (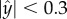) and close to the surface (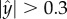). When the nematodes were far from the surface (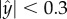), all the directions of motion were nearly equally likely and the existence of the surface did not affect the direction of propulsion. In contrast, most of the nematodes proximate to the surface swam nearly parallel to the surface (with small deviations Δθ < 10°). As a result, once proximate to the surface, the nematode swam along the surface for lengthy time intervals with a dwell time of 14 s ± 11 s.

When the animal swam along and close to the surface, its body rotated towards the surface, which resulted in the animal's head touching (colliding with) the surface (electronic supplementary material, video S3). Despite frequent contacts with the surface, the nematode preserved its far-field gait. In a frame of reference that moves with the animal, the animal's head (blue solid line and hollow circles in figure 1b) performed a bobbing motion with periodic head contacts with the surface. Because the head's motion is smooth and the retracting motion mirrors the approaching motion, the head's motion away from the surface appears to be part of the animal's normal undulating gait. Indeed, the gait frequency and amplitude of an animal swimming next to the surface and occasionally touching the surface was nearly the same (within 2% difference, p > 0.1) as that of an animal far away from the surface (red hollow circles, figure 1f). Although when close to a surface, the animals experienced a greater drag than in the bulk [30], this increased drag did not alter the animals' swimming gaits. Our observation is consistent with prior work [31], demonstrating that the swimming gait remains unaltered when the viscosity of the suspending medium is increased, as long as the increase in the viscosity does not exceed that of water by more than 100-fold. The available experimental data suggest that when in water, the animal's swimming gait is controlled by neurological signals, and not by hydrodynamic resistance [32].

Because C. elegans possesses a nervous system, one wonders whether the animal senses the presence of the surface and adjusts its orientation deliberately. The fact that the gait of the surface-following animal that occasionally collides with the surface remains nearly identical with that of an animal swimming far from the surface suggests that the animals' interactions with the surface were not deliberate. We hypothesize that as a result of the collisions with the surface, the animal was pushed away (repelled) from the surface just enough to enable it to sustain its far-field, normal gait. In prior work, we have observed that a similar ‘repulsion’ mechanism plays a major role in interactions among nematode pairs [33].

To further examine the role of the nervous system in the animal's locomotion next to surfaces, we repeated our experiments with touch-insensitive mutants, lacking mec-3 (n = 9) or mec-4 (n = 9) gene function. The mec-4 null mutants are insensitive to weak mechanical stimuli to the body [34], whereas mec-3 null mutants are insensitive to both weak and harsh mechanical stimuli to the body [35]. Both genes are required for the function of the six mechanoreceptor neurons (MRNs) that sense gentle touch along the animal's body [36]. If MRN function were required for surface interactions, we should observe differences in the behaviours of the mec-3 and mec-4 null mutants when compared with the touch-sensitive, wild-type animals. The data for mec-3 (blue hollow squares and lines in figure 1c–f) and mec-4 (green hollow triangles and lines in figure 1c–f) null mutants are similar to that of the wild-type animals. Therefore, we conclude that sensitivity to touch is not needed for the observed interactions with the surface. This provides further support to the hypothesis that steric hindrance repels the animals away from the surface, allowing them to maintain their normal, far-field gait.

Because the animal spends a considerable amount of time in close proximity to the surface, the repulsive steric hindrance cannot be the only interaction between the nematode and the surface. A mechanism that ‘attracts' the animals to the surface is also needed. We hypothesize that short-range hydrodynamic torque rotates the animals towards the surface (electronic supplementary material, video S3) and we support this claim in the theoretical section of the paper.

2.2. Experimental observations of surface attraction in swarms of Caenorhabditis elegans

Because individual animals are attracted to surfaces, we surmise that when in suspension, a larger number of animals will be present next to the surface than far from the surface. To test this hypothesis, we placed animals at various concentrations in our apparatus (figure 2) and tracked their positions in space and time. When the suspension was relatively dilute (figure 2a,b), most of the animals, indeed, aggregated next to surfaces. In support of our pervious observations [33], when two or more swimmers came close to each other, they synchronized their gaits to better use available space (electronic supplementary material, video S4).

Figure 2.

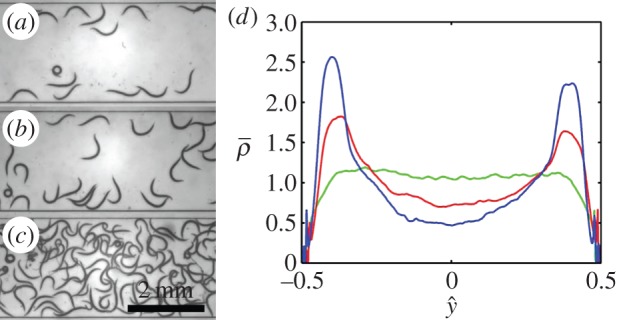
Surface attraction of C. elegans when in a swarm. Images of swarms of animals in a conduit when the area fraction occupied by the animals is Φ = 0.04 (a), 0.07 (b) and 0.28 (c). (d) The time-averaged, probability distribution function 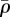of finding an animal at 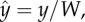transverse to the surface, as a function of 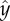when Φ = 0.04 (blue line), 0.07 (red line) and 0.28 (green line).

To quantify the nematode concentration distribution in the suspension, we consider the fraction of the imaged plane (figure 2) occupied by nematodes. We use the binary variable ρ to specify whether an image pixel centred at {x_i, y_j} contains a portion of the nematode's body at time t (ρ(x_i, y_j, t) = 1) or not (ρ(x_i, y_j, t) = 0). The Cartesian coordinates x (0 < x < L_R) and y (−W/2 < y < W/2) are aligned, respectively, along the conduit's length and width. The average animal density in the conduit is 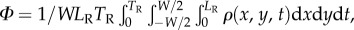where T_R = 75 s is the duration of the video recording and L_R = 5.9 mm is the length of the conduit within the camera's field of view. The fractions of the areas occupied by the animals in figure 2a,b and c are, respectively, Φ = 0.04, 0.07 and 0.28.

The steady-state (electronic supplementary material, S3) probability distribution function of finding an animal at any position y along the conduit's width is 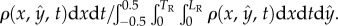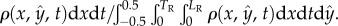Figure 2d depicts 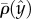as a function of 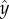when Φ = 0.04 (blue), 0.07 (red) and 0.28 (green). When the suspension is dilute (Φ = 0.04 and 0.07), the nematodes segregated with most of the animals close to the surfaces at 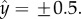Segregation did not occur, however, at high animal concentrations (Φ = 0.28, figure 2c). At this high concentration, overcrowding and inter-animal interactions prevented the animals from aggregating next to the surfaces, and the animal's density distribution was nearly uniform along the conduit's width. We conclude that in a sufficiently dilute suspension of undulatory swimmers, one would find a higher concentration of animals next to surfaces than far from the surfaces. Next, we explore the origins of the surface attraction.

2.3. Theoretical calculation of surface-induced rotation

We studied the hydrodynamic forces that act on a low Reynolds number, undulating swimmer proximate to a solid surface. To estimate the angular velocity of an undulatory swimmer close to a surface, we use RFT [37]. Briefly, the swimmer's body is divided into small segments of length Δs each, such that 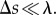Each segment is approximated as a rigid, straight cylinder of radius a. The transverse and tangential drag coefficients of each segment are approximated with those of an infinitely long, straight cylinder. In contrast to the classical RFT [37], which uses uniform drag coefficients of cylinders submerged in an infinite medium, we employ drag coefficients that vary with the distance from the surface. See equations S2 and S3 in the electronic supplementary material.

We consider a model swimmer moving parallel to a surface at a distance h from the surface in otherwise unbounded liquid (figure 3a). The model approximates circumstances encountered in nature, but not in our experimental apparatus. To image the animals in the experiment, we confined them to the focal plane of the microscope, equipping the apparatus (electronic supplementary material, figure S1) with a floor and a ceiling. The floor and ceiling increased the drag on the swimmers above the magnitude experienced by swimmers in an unconfined medium. This effect was not accounted for in our theory. Because the vertical spacing between floor and ceiling is constant, the presence of the floor and ceiling does not qualitatively affect the bordertaxis phenomenon, and it is reasonable to expect our theory to appropriately explain our experimental observations.

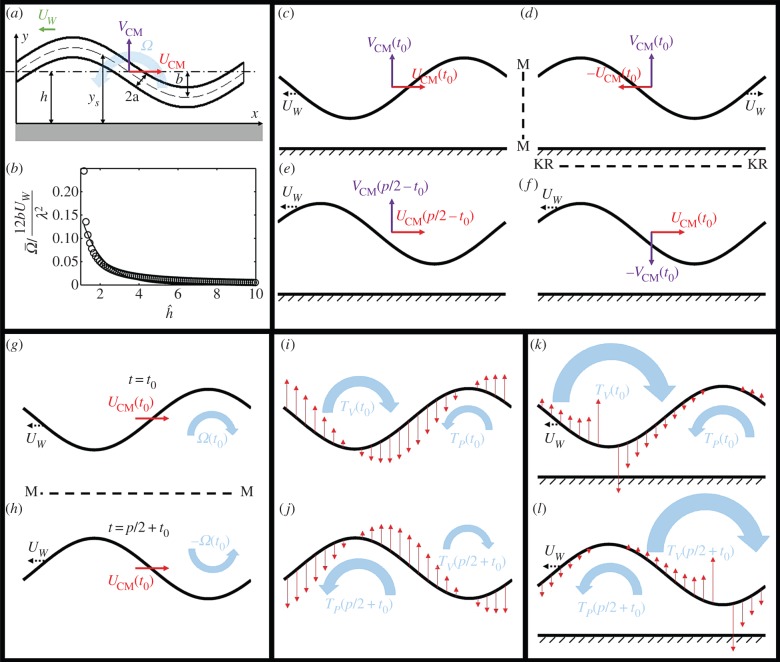
Figure 3.

(a) The instantaneous shape of a model, undulatory swimmer next to a non-slip surface. (b) The calculated (hollow circles) and correlated (solid line) normalized, time-averaged swimmer's angular velocity as a function of the distance from the surface 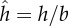. (c–f) Symmetry arguments determine that the swimmer's centre of mass does not have a velocity component normal to the surface. (g–h) Symmetry arguments demonstrate that, in the absence of a surface, there is no time-averaged rotation. (i–j) Resistive force theory arguments demonstrate that, in the absence of a surface, there is no time-averaged rotation. (k–l) Resistive force theory provides a mechanism to rotate the swimmer towards the surface when the swimmer is close to the surface. (Online version in colour.)

The distance between any point along the swimmer's skeleton and the surface is

2.1

where U_W is the wave speed in the –x-direction, λ is the wavelength and x (0 < x < λ) is a coordinate along the direction of motion. The velocity components in the x- and y-directions at any point along the swimmer's body are, respectively,

2.2

and

2.3

In the above, U and V correspond, respectively, to the velocity components in the x- and y-directions, Ω is the angular velocity, V_w is the vertical velocity and the subscript CM denotes the centre of mass. At low Reynolds numbers, the net forces and the torque vanish. The detailed calculation of the velocities is given in electronic supplementary material, S3.

When the swimmer is far from the surface 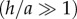and the ratio between the gait amplitude and wavelength is small 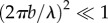, the equations of motion yield

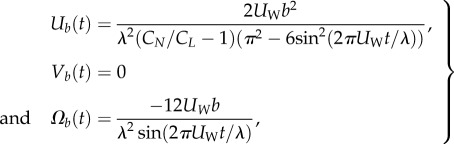2.4

where C_N and C_L are, respectively, the normal and tangential drag coefficients. The expressions in (2.4) are identical to the ones derived by Shack et al. [38] for a finite-length, undulatory swimmer in an unbounded domain. Unfortunately, closed-form expressions cannot be derived when the animal is close to a surface. For brevity, we consider only swimmers swimming in parallel to the surface. We obtained the time-averaged swimmer's velocities (electronic supplementary material, S3) 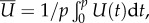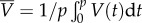and 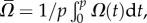where 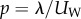is the gait's period. All the data presented here correspond to the characteristic dimensions of an adult, wild-type C. elegans swimming in water with a = 30 µm, b = 180 µm, λ = 1000 µm, p = 0.5 s and μ = 1 mPa s⁻¹.

We predict that the nematode's average velocity in the direction normal to the surface is always zero (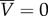), independent of the distance (h) from the surface. We will show in §2.4 that the same conclusion results from symmetry arguments. In contrast to flagellated cells that experience a vertical velocity component normal to, either towards (attraction) or away from (repulsion), the surface, depending on the relative positions of the cell and flagella [19], the centre of mass of the undulating swimmer does not experience any such transverse velocity.

Next, we examine the angular velocity averaged over a gait period 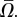Figure 3b depicts 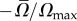(hollow circles) as a function of the amplitude-normalized distance 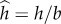from the surface. In the above, 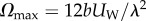is the maximum instantaneous angular speed of a swimmer far from the surface. The data were fitted well (R² = 0.87) with 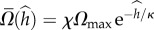(solid line in figure 3b), where χ = 0.35. The decay length κ = 1.14. When the swimmer is far from any surface (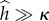), consistent with symmetry arguments, 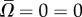. The rotational velocity decays exponentially as the distance of the animal from the surface increases with an approximate decay length that is slightly larger than the nematode's gait amplitude b. Animals swimming close to the surface tilt towards the surface, causing the animal to collide with the surface, as we observed in our experiments (figure 1a,b and electronic supplementary material, video S3).

2.4. Theoretical considerations based on symmetry arguments

The results of our numerical calculations can be anticipated from symmetry considerations. First, we argue that an undulating swimmer swimming parallel to a surface does not have an average velocity component in the direction normal to the surface. Figure 3c depicts a swimmer swimming to the right at a time instant t = t₀ with a wave propagating to the left with a speed U_w. The swimmer's centre of mass has instantaneous velocity components U_CM(t₀) and V_CM(t₀). The location of the surface is indicated with the textured region. Figure 3d is a mirror image of figure 3c (reflected across the vertical line M–M). The swimmer in figure 3d has velocities −U_CM(t₀) and V_CM(t₀). Next, in figure 3f, we reverse the direction of the wave (kinematic reversal KR). The kinematically reversed swimmer (figure 3f) has velocities U_CM(t₀) and −V_CM(t₀) while retaining the same body shape as the swimmer in figure 3d. Finally, we depict in figure 3e the swimmer of figure 3c at time p/2 − t₀. As before, p is the period of the swimming gait. The swimmer of figure 3e has velocities U_CM(p/2 − t₀) and V_CM(p/2 − t₀). Because the swimmer in figure 3e has the same body shape, same position with respect to the surface, and same wave speed as the swimmer in figure 3f, it must possess the same instantaneous velocities, i.e. U_CM(p/2 − t₀) = U_CM(t₀) and V_CM(p/2 − t₀) = −V_CM(t₀). Thus, 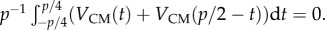An undulating swimmer that swims parallel to a flat surface has zero period-averaged transverse velocity. This is consistent with the results of our numerical calculations.

Next, using similar symmetry arguments, we examine the angular velocity far from the surface. Figure 3g depicts an undulating swimmer in an unbounded domain at time t = t₀ with an instantaneous velocity U_CM(t₀), an angular velocity Ω(t₀), and a wave propagating to the left with speed U_w. Figure 3h is a mirror image of the swimmer of figure 3g, mirrored across the horizontal plane M′ = M′. We refer to the body shape of the mirrored swimmer as S_M′(t₀). The swimmer in figure 3h has angular velocity −Ω(t₀) and linear velocity U_CM(t₀). The body shape of the swimmer in figure 3h has the same shape as the swimmer of figure 3g one half period later, S(t₀ + p/2) at t = t₀ + p/2. Such a swimmer will have angular velocity Ω(t₀ + p/2) and linear velocity U_CM(t₀ + p/2). Because S(t₀ + p/2) = S_M′(t₀) and both swimmers have the same wave speed, U_CM(t₀ + p/2) = U_CM(t₀) and Ω(t₀ + p/2) = − Ω(t₀). Consistent with our numerical calculations, the period-averaged angular velocity of the swimmer in an unbounded domain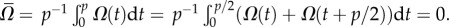

How does the presence of a nearby surface affect the swimmer's angular velocity? In the presence of a surface, the conclusion of the last paragraph is no longer valid, because the mirrored image of figure 3h differs from the configuration of the swimmer of figure 3g at t₀ + p/2. Thus, in the presence of a nearby surface, 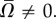To gain further insights into what causes the rotational motion, we consider the distribution of the resistive force along the swimmer's body.

Figure 3i–l depicts the shape of the swimmer (black solid lines) at time t₀ (figure 3i,j) and half a period later at t₀ + p/2 (figure 3k,l) in the absence (figure 3i,k) and the presence (figure 3j,l) of a nearby surface. The red arrows indicate the corresponding distribution of the resistive force in the direction that is normal to the direction of motion. The direction of the resistive force is opposite to the direction of the body's velocity and proportional to the product of the local body velocities and the drag coefficients. Based on the force distribution, we can qualitatively estimate the directions of the torques T_V and T_P. T_V is centred at the trough and directed clockwise (towards the surface) and T_P is centred at the peak and acting anticlockwise. The terms trough and peak are used with reference to the surface. When the swimmer is in an unbounded domain, owing to symmetry, T_V(t₀) + T_V(t₀ + pi/2) = T_P(t₀) + T_P(t₀ + pi/2) = 0, and on average, there is no net torque acting on the swimmer, as we have concluded in the previous paragraph based on a symmetry argument. In the presence of the surface, the resistive force is greater along the portions of the swimmer's body that are closest to the surface, as we indicated qualitatively by the length of the arrows in the figure. As a result, both at times t₀ and t₀ + p/2, |T_V(t₀) + T_V(t₀ + pi/2) | > |T_P(t₀) + T_P(t₀ + pi/2)| and a net angular velocity is produced by this imbalanced torque to steer the swimmer towards the surface. The net angular velocity becomes significant only when the animal is close to the surface (h ∼ b) when there are large variations in the drag coefficients along the swimmer's length. This is consistent with both our experimental observations and the numerical calculations.

2.5. Finite-element simulations of a swimmer next to a boundary

If, indeed, bordertaxis is solely induced by hydrodynamic effects, we should be able to reproduce the experimentally observed behaviour in computer simulations that account only for passive mechanical forces. Because three-dimensional simulations are time-consuming and the essence of bordertaxis can be captured with a two-dimensional model, we solve the two-dimensional Stokes equations for an undulatory swimmer in a conduit. The simulation differs from the experiment in the absence of the conduit's floor and ceiling. The vertical confinement in the experiment increases the drag forces acting on the swimmer [30]. The two-dimensional model does include, however, the key features responsible for bordertaxis such as the interaction between the flow field induced by the swimmer and the side wall. The details of the mathematical model and code validation were previously described [10]. Briefly, we approximate the C. elegans as a sinusoidal, undulating object with a uniform width. The animal's size and gait are selected to approximate an adult C. elegans [33]. The swimmer's projected length along its direction of motion is 1005 µm, its body width is 69 µm, its wavelength is 1005 µm, its amplitude is 112.5 µm and the frequency of bends is 2.2 Hz. The conduit's width is 2600 µm. The liquid is water.

Because the swimmer's velocity and rotational speed are not a priori known, we take advantage of the linearity of the Stokes equation and superpose solutions of auxiliary problems, comprised a swimmer with a unit velocity in the x-direction, a swimmer with a unit velocity in the y-direction, a swimmer with a unit rotational velocity, and a stationary swimmer with a surface velocity distribution consistent with the nematode's undulatory gait. The instantaneous x-direction velocity, the y-direction velocity and the rotational velocity are obtained by requiring that no net forces and torque act on the swimmer. To account for the repulsive forces resulting from the collisions between the swimmer and the surface, the force balance equations are augmented with short-range Lennard–Jones-like repulsive terms.

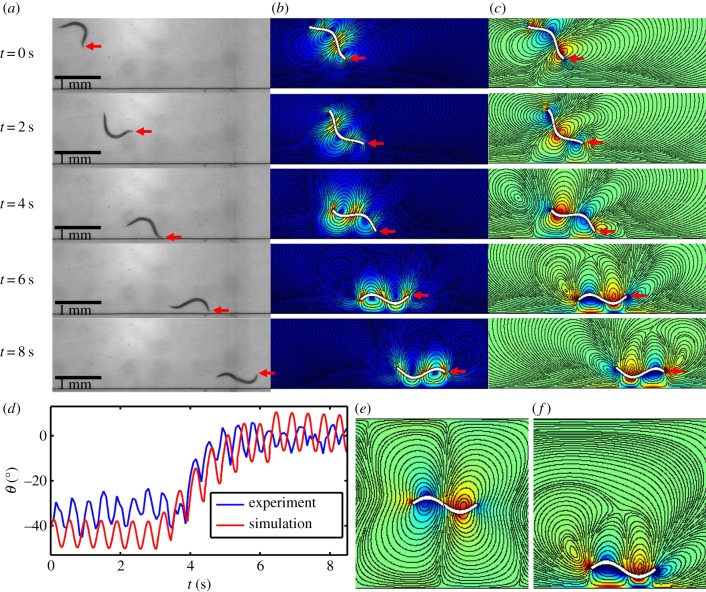
Figure 4 and electronic supplementary material, video S5 compare our numerical simulation results with the experimental data. Figure 4a depicts from top-to-bottom video frames of an experiment, recording the position of the swimmer at various times. Initially (t = 0), the swimmer's centre of mass is distance y(0) = 1300 µm from the solid surface and θ(0) ∼ −37°. As time goes by, the swimmer approaches the boundary and rotates to orient itself parallel to the surface. Figure 4b,c depicts the computed positions and orientations of the theoretical swimmer with initial conditions similar to the ones in the experiment. Figure 4b depicts the colour-coded, instantaneous velocity field and streamlines (solid lines). Figure 4c depicts the colour-coded, instantaneous vorticity field and streamlines. The predicted counter-rotating vortex pair agrees well with previously published flow visualization experiments [6,28]. The computer-simulated trajectories of the animal are in qualitative agreement with our experimental observations. Electronic supplementary material, video S5 provides a vivid comparison of the computer animations and experimental observations. Figure 4d depicts the experimentally observed (blue) and the predicted (red) instantaneous inclination angle θ as functions of time. The striking resemblance between the theoretical predictions and experimental observations reinforces the notion that boundary attraction is caused by hydrodynamic effects. To better appreciate the influence of the proximate surface on the flow pattern generated by the swimmer, snapshots of the computer-simulated flow field of an undulatory swimmer near and far away from a surface are depicted, respectively, in figure 4e and f. When the swimmer is far away from the surface (figure 4e), the flow pattern generated by the swimmer consists of pairs of symmetric counter-rotating vortexes, resembling previous experimental data [6,28]. In contrast, when the swimmer is swimming in close proximity to the solid surface (figure 4f), the structure of the counter-rotating vortexes is altered owing to the presence of the nearby surface, resulting in a net angular velocity that rotates the swimmer towards the surface.

Figure 4.

Comparison of the experimental observations (a) and computer-simulated (b,c) of the position and orientation of an undulatory swimmer approaching a surface. Red arrows denote the position of the swimmer's head. (d) The swimmer's measured (blue) and predicted (red) orientation (θ) as functions of time. The computer-simulated flow field of an undulatory swimmer away (e) and near (f) a surface. The colour in b represents velocity magnitude. The colour in c, e and f represents vortex magnitude. The solid lines in b, c, e and f are streamlines.

In summary, both symmetry arguments and numerical calculations indicate that a swimmer located far from the surface is subject to a time varying rotation with a zero average rotational speed. This predicted yawing motion of the animal was observed in many different species of nematodes [6]. When proximal to a surface, the swimmer is subject to a net angular velocity that rotates it towards the surface, causing it to swim into the surface and manifesting as surface attraction. The magnitude of this net angular velocity decays rapidly, on the length scale of the swimmer's amplitude, as the distance from the surface increases. Thus, boundary following in undulatory swimmers is the result of the combined action of short-range hydrodynamic attraction and steric repulsion. An understanding of the mechanisms involved in boundary attraction of undulatory swimmers is not only important from a scientific point of view, but can also be exploited in a variety of applications.

2.6. An example of an application—a skimmer/sorter for undulatory swimmers

In some circumstances, it is desirable to reduce parasitic worm concentration in a flow stream. On other occasions, one may desire to sort animals based on their mobility. Bordertaxis can assist in both tasks. As a proof of this concept, we constructed a simple embodiment of such a device (figure 5 and electronic supplementary material, video S6). The three-dimensional-printed device is comprised of a long, uniform conduit that bifurcates into three branches at its downstream end: a central branch and two side branches. The dimensions and a photograph of the device are given in electronic supplementary material, figure S5. When a suspension of worms is pumped through the long conduit, active (motile) worms attract to its side walls and aggregate along these walls, leaving the central stream with a reduced concentration of motile worms. Because boundary attraction affects only motile worms, the side branches are enriched with active worms while paralysed worms, if any, stay in the central flow. This is a flow fractionation device with bordertaxis providing the transverse separation.

Figure 5.

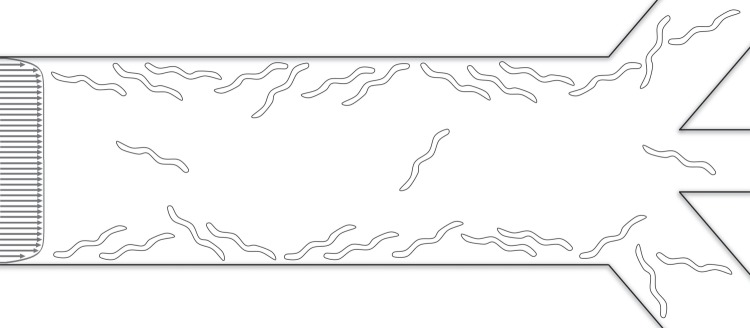
A schematic drawing of the device that uses bordertaxis to sort motile animals. Motile animals migrate to the side walls and are mostly cleared through the side branches. Inactive animals stay in the main stream and are cleared through the central branch.

We pumped a dilute suspension (volume fraction of the animals approx. 1%) containing mostly (95% ± 3%) active C. elegans through the device. We measured the liquid volume and counted the number of active and paralysed animals exiting through the various branches (electronic supplementary material, video S6). An animal was defined as paralysed if it did not deform its body during an 8-s time interval. Approximately 10% ± 1% of the active animals that entered the device exited through the central branch. The number of active animals per unit volume at the central branch normalized by the number of entering, active animals per unit volume was 0.41 ± 0.05. The number of inactive animals per unit volume exiting the central branch normalized by the number of paralysed animals per unit volume entering the device was 1.41 ± 0.28. The sorting efficiency of the device can be improved by optimizing its dimensions and operating conditions and by repeating the separation process. Our experiments suggest that bordertaxis can be effectively used for a continuous, high-throughput depletion of live worms from a flow stream and for sorting out of motile worms.

The isolation of motile worms may be of interest for genetic screening. We provide two examples. Widespread use of anthelmintics in livestock has resulted in the emergence of drug-resistant worms. Chemotherapy paralyses drug-susceptible worms. When pumping a drug-treated suspension of worms through our device, the drug-resistant worms would migrate to the conduit boundaries and exit through the side branches, enabling their isolation for further molecular–genetic analysis. In another application, C. elegans is used as a model organism to study the genetic basis of sleep [39–42]. Heat shock induces sleep-like quiescence in wild-type animals. By separating animals that remain active after heat treatment, the device can isolate heat-shock-resistant animals, so that the genes responsible for abnormal sleep behaviour can be identified. Currently, this process is done manually and is laborious and time-consuming.

Importantly, bordertaxis must also be considered when designing and experimenting with sorters using other taxing mechanisms such as chemotaxis. Bordertaxis may obscure and stealthily bias the performance of such devices as is strikingly evident in a recent publication ([8], electronic supplementary material, video S3).

3. Conclusion

We studied both experimentally and theoretically the effect of a surface on the swimming dynamics of C. elegans, an undulatory, low Reynolds number swimmer [28]. The experimental data demonstrate that the presence of the surface does not affect the swimming patterns of animals located far from the surface. Such swimmers randomly select their direction of motion, eventually arriving close to a surface. However, once close to the surface, the animal stays next to the surface and swims parallel to it for significant time intervals, periodically touching the surface with its anterior. The surface following is occasionally interrupted by the animal deliberately turning in a direction that takes it away from the surface.

Our experimental observations indicate that once it is sufficiently close to the surface, the animal tends to tilt towards the surface, which causes it to swim towards the surface and eventually contact the surface. Theoretical calculations, based on RFT, suggest that this rotation towards the surface is caused by a short-range hydrodynamic torque, resulting from the interaction between the flow field induced by the swimmer and the surface. The magnitude of the surface-induced rotation decays exponentially as the swimmer's distance from the surface increases.

As a result of the hydrodynamically induced rotation, the swimmer follows a trajectory that brings it into contact with the surface. Owing to the collision with the surface, the animal's centre of mass shifts away (is repelled) from the surface just to a sufficient distance to allow the swimmer to maintain its far-field gait. Once repelled, the swimmer does not migrate far from the surface, because the hydrodynamic torque provides a restoring mechanism to change the animal's direction of motion back towards the surface. The experimentally observed phenomenon is duplicated closely with finite-elements simulations. In summary, the animals' long residence times next to the surface are the result of the interplay between short-range attractive hydrodynamic forces and repulsive steric forces. This mechanism for surface following does not require mechanosensory neuron function as animals incapable of touch sensation behaved similarly to the touch-sensitive wild-type animals. Our ability to reproduce the behaviour observed in experiments with numerical simulations that account only for hydrodynamic forces provides further evidence that surface attraction is driven solely by hydrodynamics.

In the presence of a dilute suspension of motile animals, surface attraction causes concentration gradients with the animals tending to aggregate next to surfaces. In other words, one observes a higher concentration of animals next to the surface than far from the surface. This concentration imbalance diminishes as the average concentration of the suspension increases, and it disappears altogether once a certain concentration threshold, at which near neighbours undergo frequent collisions, is exceeded. In the presence of externally induced flow, attraction to surfaces facilitates yet another hydrodynamically induced trait in undulatory swimmers, the tendency to orient to face the flow and to swim against the flow (rheotaxis) [10]. In the presence of external flow parallel to a stationary surface, surface attraction rotates the swimmer towards the surface, exposing its tail to a higher velocity than its head. The combined action of surface attraction and the external flow velocity gradient rotate the swimmer to orient it to face the flow.

Is the tendency to aggregate next to and swim along surfaces beneficial to nematodes? Because the boundary region is rich in motile bacteria [13], a source of food for free-living nematodes such as C. elegans [14], the surface ‘attraction’ positions the animals in regions abundant in food. Aggregation next to surfaces increases interactions among animals, favours mating, and enhances the probability of parasitic nematodes penetrating the host body [17,18]. Surface following may also assist the animals in navigation, both in the wild and in a host's body. Although bordertaxis is involuntary and hydrodynamically induced, it appears to play an important role in animals' life cycles. Our work suggests that multicellular organisms, such as worms, possessing a small nervous system, exploit passive hydrodynamic mechanisms for survival and reproduction.

Our findings suggest methods to control undulatory swimmers. We demonstrate this with a simple high-throughput sorter that uses bordertaxis to skim animals out of a flow stream and to separate motile and paralysed animals. With the increased use of microfluidic devices in research, a good understanding of bordertaxis is essential when designing devices such as sorters, because surface attraction may alter behavioural response to sensory stimuli, such as chemotaxis, and may adversely and stealthily impact the performance of sorting devices [9].

4. Material and methods

A microfluidic channel was formed with PDMS using standard soft photolithography techniques and bonded to an oxygen plasma-treated glass slide. The sorting device was fabricated in optically transparent polycarbonate-like material with a high-resolution three-dimensional printer (ProJet 6000 HD, 3D Systems) and attached to a glass slide with double-sided adhesive tape (9500PC, 3M). Images were recorded with a digital camera (1600, PCO) through a microscope (20×, Olympus BX51) and processed with a custom Matlab program. The numbers of animals passing through each branch of the sorting device were counted manually.

Authors' contributions

J.Y. and H.H.B. designed research; J.Y. performed research; J.Y., D.M.R., and H.H.B. analysed data; and J.Y., D.M.R., and H.H.B. wrote the paper.

Competing interests

We have no competing interests.

Funding

This research was supported in part by National Institutes of Health (NIH) NIA grant no. 5R03AG042690-02 and by National Science Foundation NSEC DMR08-32802 through the University of Pennsylvania Nano-Bio Interface Center (NBIC). D.M.R. was supported by NIH R01NS064030 and 5R03AG042690-02. Strains of C. elegans were obtained from the Caenorhabditis Genetics Center, which is funded by the NIH Office of Research Infrastructure Programmes (P40 OD010440).