Directional, passive liquid transport: the Texas horned lizard as a model for a biomimetic ‘liquid diode’

Abstract

Moisture-harvesting lizards such as the Texas horned lizard (Iguanidae: Phrynosoma cornutum) live in arid regions. Special skin adaptations enable them to access water sources such as moist sand and dew: their skin is capable of collecting and transporting water directionally by means of a capillary system between the scales. This fluid transport is passive, i.e. requires no external energy, and directs water preferentially towards the lizard's snout. We show that this phenomenon is based on geometric principles, namely on a periodic pattern of interconnected half-open capillary channels that narrow and widen. Following a biomimetic approach, we used these principles to develop a technical prototype design. Building upon the Young–Laplace equation, we derived a theoretical model for the local behaviour of the liquid in such capillaries. We present a global model for the penetration velocity validated by experimental data. Artificial surfaces designed in accordance with this model prevent liquid flow in one direction while sustaining it in the other. Such passive directional liquid transport could lead to process improvements and reduction of resources in many technical applications.

1. Introduction

Directed transport of liquids such as water and lubricants is a common requirement in technical systems. Alongside forced transport by active pumping, passive transport or the so-called ‘secondary active transport’—that is, liquid flow resulting from a motion not primarily intended for transport—is often needed or at least desired. One example is the transport of lubricant in a bearing due to the rotary motion of the shaft. In general, one can think of a variety of applications where passive directed transport of liquids is desired. A device that allows a liquid to flow in one direction but inhibits flow in the other could be considered a ‘liquid diode’.

Capillary tubes or channels are used in various fields, for example, in microfluidics for autonomous capillary pumps [1]. Although primarily passive, fluid transport often has a secondary energy source such as mechanical vibration energy, electrical energy and radiation. In such case, directionality of liquid transport is achieved by microstructures: in tubular capillaries [2], half-open channels [3] or by chemical surface modifications [4].

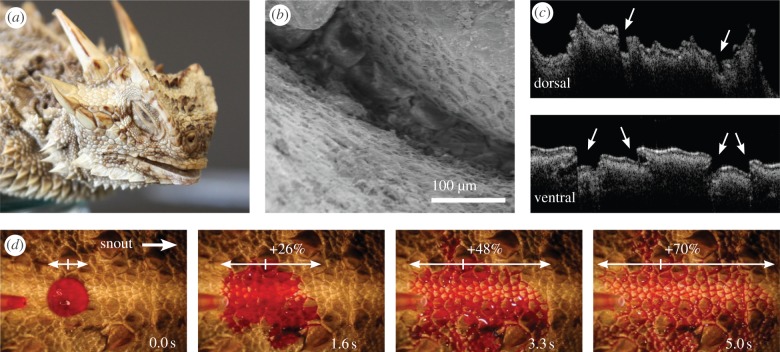
Some lizards survive in arid environments, because they have the extraordinary ability to collect water with their skin [5–11]: a special microstructure enhances collection efficiency, and after accumulation in small capillary channels between the scales, water is transported towards the snout, where it is ingested [5,6,9]. One such moisture-harvesting lizard is the Texas horned lizard Phrynosoma cornutum (figure 1a), which inhabits arid regions of North America. In the case of P. cornutum, this passive transport mechanism also has a pre-determined flow direction towards the snout [5]. In more detail, the integument¹ of P. cornutum provides a network of capillary channels between the overlapping scales (figure 1b,c) [5,9,11]. These capillaries are about 100–250 µm in width, with a smaller opening towards the surface of up to 100 µm [9,11]. Transportation of water to the snout is necessary because the integument is almost waterproof to minimize water loss by evaporation [12]. It has to be emphasized that the collection and transport of water in the case of P. cornutum is achieved by microstructures of the homogeneous scale material, mainly keratins. This is in contrast to other moisture-harvesting animals such as the tenebrionid beetle Stenocara sp., where a mosaic of hydrophilic and hydrophobic structures is used to achieve the special wetting properties [13].

Figure 1.

Phenomenon of directed water transport on the integument of Phrynosoma cornutum. (a) Phrynosoma cornutum. (b) SEM-image of capillary opening between the dorsal scales. (c) Skin cross section analysed by optical coherence tomography (OCT). Capillaries are indicated by arrows. (d) Image sequence of a coloured water droplet (7 µl, dye: Ponceau S red), which is transported on the dorsal integument. The direction towards the snout (rostral) is indicated. (Online version in colour.)

In this study, we used a biomimetic approach to design artificial surfaces that are capable of directed liquid transport, based on the principles found in the Texas horned lizard. For this purpose, we analysed the morphology of the capillary network of P. cornutum and characterized the material properties of the animal's surface. We then developed a theoretical model of the liquid transport in the capillary system that explains the physical principles of the observed passive directed liquid transport. This model allows parameters critical to this effect to be identified and suitable parameter ranges to be determined. Finally, the abstracted principles were transferred to technically relevant materials suitable for aqueous liquids. These artificial surfaces behave like ‘liquid diodes', which means that directed passive liquid transport through them is observed. This might be of interest, for example, in context of microfluidics or medical applications, where small amounts of liquid need to be transported directionally towards a component that is difficult to access.

2. Results and discussion

2.1. Functional analysis of the biological model Phrynosoma cornutum

When a droplet of water is applied to the integument of the Texas horned lizard (figure 1a), it immediately spreads into a network of interconnected capillary channels between the scales (figure 1b,c) and is transported preferentially towards the snout. As a typical example, figure 1d depicts the water transport on the central part of the upper body (dorsal). Owing to variations in the three-dimensional structure between body regions, transport velocities differ. However, we found the same results as those found dorsally on other body parts such as the underside of the body (ventral), as well as on the head and the tail: independent of body region, the transport velocity is higher towards the snout (rostral) than tailwards (caudal). On the dorsal side, for example, the asymmetry in transport amounts to a factor of about two: water flows approximately twice as fast to the snout (forwards) as to the tail (backwards) [5]. This holds as long as water from the droplet is available. Within the first 333 ms, the average velocities to the snout and to the tail are 3.15 ± 0.94 mm s⁻¹ and 1.61 ± 0.45 mm s⁻¹, respectively. The velocity was measured at various positions on the lizard's body, with n ≥ 6 independent measurements at each position. The velocity of the liquid front decreases with time t approximately proportionally to t^−0.5. In the forward direction, the liquid front travels 4.1 mm in 1.6 s and 8.6 mm in 5 s. By contrast, the liquid front advances more slowly in the backward direction, covering a distance of only 3.5 mm in 1.6 s and 5.1 mm in 5 s.

The capillary water transport mechanism appears to be highly useful for the animal for two reasons: first, according to our observation, the low water content of the lizard's diet leads to a greater need for additional water (P.C. and W.B. 2014, unpublished data). Therefore, the ability to collect water with the skin appears to be a successful adaptation. Secondly, waterproof skin diminishes water loss by evaporation but also inhibits transcutaneous water absorption. Thus, transport of collected water via capillary channels seems itself to be an adaptation to the lizard's arid habitat. Directed transport towards the snout represents a further specialization that enables exploitation of even smaller amounts of water. In this way, further reduction of water loss takes place, allowing the animal to populate more arid environments.

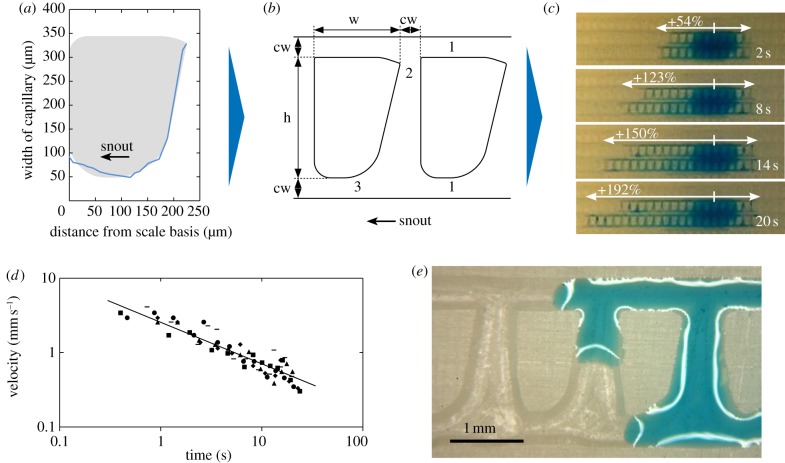
The capillary system was first analysed by means of optical coherence tomography (OCT; figure 2a,b), from which a model of the capillary system was derived that consists of longer half-open capillaries in the longitudinal direction than in the lateral direction (figure 2d). For a more detailed view on single capillary channels, we examined their dimensions by histological slice series (figure 2c) of up to 300 slices over a distance of up to 2 mm. Our examination revealed mainly longitudinal capillary channels with a width varying from 26.3 to 327.8 µm and a depth from 36.8 to 63.8 µm. In our histological analysis of dorsal capillary channels, we found that the capillaries narrow mainly in width towards the snout along each scale (figure 3a). An abrupt widening of the capillaries follows the narrowing. The narrowing in depth was much less pronounced and in many cases even indeterminable. From the entire network of channels, we derived a model consisting of (laterally) interconnected capillaries that periodically narrow (longitudinally; figures 2d and 3).

Figure 2.

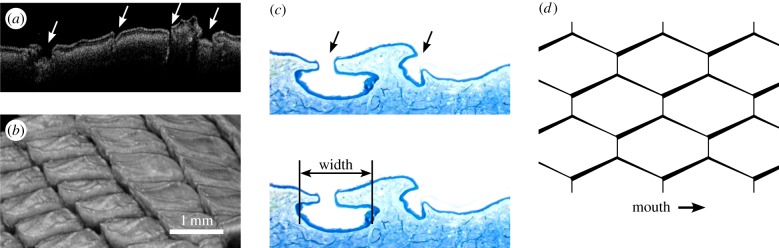
Analyses of capillary structure. (a) Skin cross section of Phrynosoma cornutum from single OCT slide. Longitudinal capillaries are indicated by arrows. (b) OCT rendering of skin topography. (c) Histological slices of the integument (stained with methylene blue and azur II), illustrating the cross-sectional view of longitudinal capillary channels (arrows) between dorsal scales, here 194 µm from scale basis. (d) Model of skin capillary network. Longitudinal capillaries are longer than lateral capillaries, i.e. interconnections. (Online version in colour.)

Figure 3.

Abstraction process of capillary structure for technical surfaces. (a) Exemplary capillary width along a single dorsal scale of P. cornutum (graph), based on analysis of histological slice series in figure 2c. That course of width was fit with a scale-like form (grey) to get a technically feasible scale surrounded by assumed channels of the capillary network. The minimal width was set to 50 µm. (b) Scale fits (from (a)) were arranged in arrays to design a structure for manufacturing (sketched in top view). To mimic the observed capillary network, longitudinal capillaries (1) were created that were interconnected (2). The course of capillary width (from (a)) is found below each subnatural fit (3). For manufacturing with use of a 0.3 mm cutter head the structure was constructed at 6 : 1 scale defined by scale fits with height h (1519 µm), width w (1086 µm) and a channel width cw (300 µm). (c) Sequence of a video analysis. The capillary structure was micro-milled into the surface of plain grinded epoxy resin at 6 : 1 scale for use of a 0.3 mm cutter head. They were analysed with 10 µl water droplets (stained with blue ink). (d) Measured velocities in the forward direction as a double logarithmic plot with fit according to the analytical model. Symbols indicate single measurements, n = 5. (e) Water flow on a microscopic scale. (Online version in colour.)

2.2. Abstraction and modelling

Our morphological analysis of the biological model leads us to assume that two essential functional principles of the structure are (i) the periodically and asymmetrically changing shape of the capillaries (gradual narrowing and abrupt widening) and (ii) the interconnections between the capillary channels. Hence, in a first step, we manufactured an abstracted subnatural structure to verify these two geometric principles as the reason for directed liquid transport. After a detailed analysis of these underlying geometric principles, we present mathematical models for the liquid transport.

2.2.1. Abstracted subnatural structure

We sought to reproduce the effect of the natural antetype as closely as possible. To this end, a material with surface properties similar to those of the lizard's scales was chosen and structured. It has recently been shown that the contact angle of water on Phrynosoma scales is about 70° when the material is unstructured [5]. We found an epoxy resin with similar wettability and a contact angle of about 60°–70°. In order to manufacture the abstracted subnatural structure (figure 3b) by micro-milling, the material had capillary channels with a square cross-section and a constant depth of about 150 µm. The channel width varied according to an abstraction of the narrowing found in P. cornutum (figure 3a). The structure was cut into a plain grinded epoxy resin, and its functionality was tested by video analysis of coloured water droplets applied to it. We observed not only a directed transport of water comparable to that found for P. cornutum, but even more pronounced directionality (figure 3c). Straight capillaries, by contrast, showed symmetric water transport, i.e. the same transport velocity in both directions (data not shown). The strong pronounced directionality proved that functionality was preserved despite the natural structure being scaled up by a ratio of 6 : 1 so that a 300 µm cutter head could be used. This can be verified theoretically by estimating the ratios of gravitational and viscous forces to the capillary forces, captured by the Bond number (Bo = Δρ g R²/γ) and the capillary number (Ca = η v/γ) [14]. Here, Δρ denotes the volumic mass difference between liquid and air, g the gravitational acceleration, R the characteristic length for a fluid subject, γ the surface tension, η the dynamic viscosity and v the characteristic velocity of the transported liquid. For the natural scale, these characteristic numbers were calculated as Bo_1:1 ≈ 3.0 × 10⁻³ and Ca_1:1 ≈ 4.3 × 10⁻⁵, and for the scaled-up structures as Bo_6:1 ≈ 1.7 × 10⁻¹ and Ca_6:1 ≈ 6.0 × 10⁻⁵, respectively. As they are found to remain well below one for both systems, the up-scaling preserves the dominance of the capillary forces over gravitational and viscous forces. Therefore, mainly capillary forces provoke fluid transport in the structures.

While in the forward direction (towards the snout) a sustained, albeit decelerating, transport was observed, the liquid front in the backward direction stopped after a short distance of about 2.6 mm. By contrast, the liquid front in the forward direction covered a distance of about 19 mm within 23 s. Both, the velocities in the forward and in backward directions decreased with time. In the forward direction, the velocity decreased from 2.9 ± 0.3 mm s⁻¹ after 2 s to 0.57 ± 0.15 mm s⁻¹ after 10 s, whereas the liquid front in the backward direction started with a velocity of 0.63 ± 0.32 mm s⁻¹ after 2 s and stopped for most samples after 10 s. Five videos were analysed for these measurements, and all tested samples showed a continuous volume flow in the forward direction, whereas the liquid transport in the backward direction was blocked.

2.2.2. The functional principle of ‘longitudinal asymmetry’

The saw-tooth shape is the simplest periodic, asymmetrically narrowing and widening capillary structure with respect to the longitudinal axis. If a droplet is applied to such a channel, the liquid develops a meniscus at each free liquid–air interface, mainly depending on the surface tension γ between liquid and air (resulting in the contact angle θ) and the geometry (angle α of the capillary side wall; figure 4). Passive transport of this liquid requires a positive pressure difference Δp across the liquid interface. The pressure difference Δp can be described by the Young–Laplace equation

2.1a

where r₁, r₂ denote the principal radii of curvature. If we assume a capillary channel with infinite depth (r₂ → ∞, r₁ = r), the equation can be simplified to

2.1b

Figure 4.

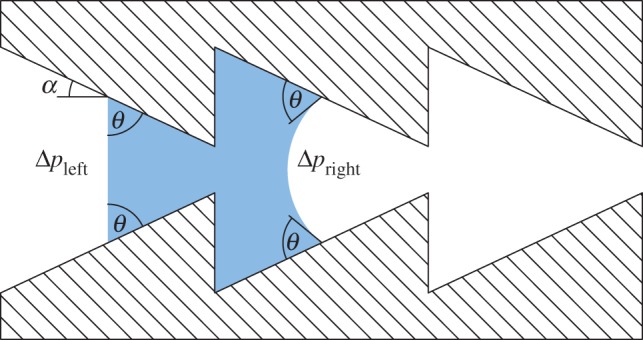
Saw-tooth-shaped horizontal capillary channel with an infinite depth in top view. Each curvature of the liquid–air interface in longitudinal direction is determined by the tilt angle α of the capillary side walls and the contact angle θ within the capillary. Pressure differences Δp across the liquid surface result from these curvatures. A concave curvature (Δp > 0) causes the liquid front to advance, whereas a convex curvature (Δp < 0) causes the liquid front to recede. Here, the left meniscus illustrates a special case where Δp = 0. (Online version in colour.)

In the case of a saw-tooth-shaped capillary channel, as shown in figure 4, the principal radius r can be calculated for narrowing sections (positive angle α) and widening sections (negative angle α), if determined based on an inside-to-outside perspective of the droplet

2.2

where d(x) denotes the capillary width at position x. Inserting equation (2.2) into equation (2.1b) yields

2.3

For a concave curvature (Δp > 0), the capillary provides energy for transport in the direction of narrowing, whereas a convex curvature (Δp < 0) leads to retardation of flow. When considering a liquid slug in a horizontal capillary channel, the curvatures of the liquid–air interfaces at the two sides (1 and 2, i.e. “right” and “left” in figure 4) must be taken into account. Here, the liquid is transported in direction 1 as long as Δp₁ > 0 and Δp₂ ≤ 0. For the more general case of asymmetric transport, a liquid is transported faster in direction 1 if Δp₁ > 0 and Δp₁ > Δp₂.

Since the contact angle θ is constant for a given liquid–solid combination, the meniscus curvature is influenced mainly by the geometry (d(x), α) of the capillary. To achieve a pre-determined directional flow in a capillary channel, particular angles α for narrowing and widening sections must be used depending on the contact angle. (A calculation of the pressures according to equation (2.3) is provided in the electronic supplementary material.)

2.2.3. The functional principle of ‘interconnections'

The model of a saw-tooth-shaped capillary channel, as illustrated in figure 4, allows only a local description of liquid transport, because the liquid would stop at one of the sharp edges (i.e. singularities) at the end of each narrowing section.

Phrynosoma cornutum has lateral channels that are much shorter than those in the longitudinal direction. We found that these lateral capillaries form interconnections between longitudinal capillaries, and elucidated their role in water transport: the interconnected capillaries provide a means of overcoming the stopping points mentioned above. In an abstraction of this interconnection principle, the transport of liquid can be continued with the help of interconnections between at least two asymmetric (e.g. saw-tooth-shaped) capillaries, as shown in figure 5.

Figure 5.

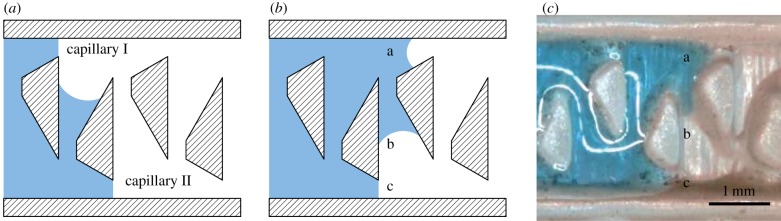
Principle of ‘interconnection’ for two saw-tooth-shaped capillary channels. (a) An applied droplet is soaked into the structure by capillary forces. The liquid front stops at the sharp edges in capillary I, while it is transported farther into capillary II. As the liquid front in capillary II reaches the nearby interconnection the liquid is transported into capillary I. (b) The liquid coming through the interconnection picks up the stopped liquid in capillary I and forms a new free liquid front. Thereafter, the liquid is transported through a second interconnection into capillary II, where the stopped liquid is picked up. (c) Advancing water droplet on a biomimetic prototype laser engraved into PMMA. Characters indicate the same situations as in (b). (Online version in colour.)

The advancing liquid front of a droplet stops at positions in capillary I that have an abrupt widening (figure 5a), because there the meniscus radius becomes infinite. As soon as the liquid front in capillary II reaches the nearby interconnection, it is transported into capillary I (figure 5b). Now the liquid passing through the interconnection picks up the liquid that has halted. This leads to the formation of a new, advancing liquid front (figure 5b,c). While the liquid in capillary II stops, liquid is transported through a second interconnection from capillary I into capillary II (figure 5c), where it picks up the halted liquid. Again, it will form a new meniscus and will be transported through the third interconnection, and so on. Based on this mechanism of overcoming sections of abrupt widening, the capillary transport of liquid may become alternating or pulsating, but always remains asymmetrical. In the backward direction, liquid transport stops at the widening sections, and no interconnection can pick up the halted liquid front.

2.2.4. Modelling

In the previously described structure, a sub-unit (i.e. one period) consists of two channels of varying diameter and their interconnections. Linking a large number of sub-units leads to a directional liquid transport at macroscopic scale. For a large number of sub-units, the structure details are averaged spatially, and therefore velocity fluctuations due to singularities vanish. A system of two saw-tooth-shaped capillaries with interconnections can thus be described by an averaged channel width d_m and an averaged angle of slope α_m. The abstracted subnatural structure described in §2.2.1 can be modelled accordingly. In the extreme case of a large number of capillaries with infinite depth, this approach allows the system to be described by the model of a porous body [15]. Here, the velocities in the forward and backward directions, v_forward(t) and v_backward(t), respectively, are

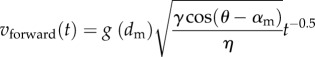2.4a

and

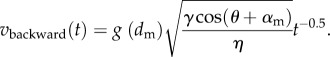2.4b

In the above equations, t denotes the observation time, η the dynamic viscosity of the applied fluid, and g (d_m) = 0.5 (d_m/3)^0.5 denotes a factor that depends only on the geometry of the capillary system. (See also electronic supplementary material, §2 for the derivation of the equations above from the plane Poiseuille flow profile [16].) Note that the term cos(θ ± α_m) might be equal to zero, describing a halted liquid front. If (θ + α_m) > 90° and 0° < (θ − α_m) < 90°, the absolute value of cos(θ + α_m) has to be taken and a positive pressure difference at the meniscus in the forward direction will force the liquid onwards, while the pressure difference in the backward direction will be negative. In this case, additional hydrostatic pressure would be needed to force the liquid in the backward direction, while a steady capillary flow in the forward direction is sustained. For example, depositing a droplet on the lizard's skin would provide such an additional pressure head. This drop would exhibit positive Laplace pressure and a slight gravitational head, both of which would provide additional pressure to the liquid front, thereby reducing inhibition of transport in the reverse direction. Estimates of the additional hydrostatic pressure of example drops on the tested structures indicate that the gravitational head is negligible for the applied droplet volumes, but that the Laplace pressure can have a measurable influence. However, the above equations would need to be extended in order to fully capture this situation. For the designed and tested subnatural structure, the Laplace pressure and the gravitational pressure have been calculated to be below 5% of the capillary pressure; therefore, they are neglected.

The magnitude of the total volumetric flow rate (electronic supplementary material, figure S3A) through the biomimetic capillary structure results from the sum of flows in both directions

2.5

where A_m is the mean cross-sectional area of the structure. Inserting equations (2.4a,b) into equation (2.5), gives the following relationship:

2.6a

which defines a characteristic function for the volumetric flow rate Vol(θ, α_m). This characteristic function allows us to analyse the volumetric flow rate with respect to the contact angle θ and to the mean angle of slope α_m. The characteristic function of total volumetric flow rate Vol takes its minimal and maximal values of 0 and 2 for symmetric flows in hydrophobic and hydrophilic capillaries with θ = 90° and θ = 0°, respectively. At a given contact angle θ, an increase in the mean angle of slope α_m leads to a decrease in the characteristic function and therefore to a decrease of the total volumetric flow rate as well.

The ratio of forward and backward velocity is a measure of the flow asymmetry with respect to the contact angle θ and the mean angle of slope α_m (electronic supplementary material, figure S3B). We define a characteristic function of asymmetry As(θ, α_m) by the following expression:

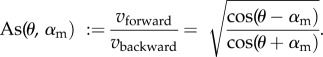2.6b

The characteristic function of asymmetry As(θ, α_m) can take values between 1 and ∞, 1 being symmetric capillary flow, i.e. equal flow in both directions in conventional straight capillaries, and ∞ meaning maximal asymmetry, i.e. a stopping liquid front in one direction and maintained flow in the other.

Analysing the characteristic functions of volumetric flow rate and asymmetry depicted in electronic supplementary material, figure S3, reveals that high asymmetry represented by high values of As can only be achieved at the expense of the total volumetric flow rate Vol. The graphical representation reveals that the highest asymmetry value As of ∞, results in the lowest values of the volumetric flow rate Vol. This result shows that the most advantageous behaviour—the highest possible volumetric flow rate coupled with the highest possible asymmetry—underlies some fundamental limitations which can be described by the characteristic functions Vol(θ, α_m) and As(θ, α_m).

2.2.5. Verification of the model

In order to verify the model, we manufactured the abstracted subnatural structure. The velocity of the liquid front was measured over time (figure 3d) and showed the desired asymmetry: the liquid advanced in the forward direction and stopped completely in the backward direction after 1–2 s.

Assuming an average capillary width of 480 µm, the model describes the observed behaviour. This width is well within the range of the manufactured free capillary widths ranging from 300 to 500 µm throughout the structure. Note that the average width is the only free parameter that was fitted to the data. All other parameters (see the electronic supplementary material, §2) were either given by geometry or were material parameters determined by independent measurements. Thus, all essential aspects of the directional liquid transport were considered.

Most importantly, a negative pressure in the backward direction is well described by the theoretical model. This means that capillaries can be designed which transport liquid in the forward direction but—and this is the crucial aspect—decelerate and stop the liquid front in the backward direction, even if a small hydrostatic pressure is applied. The pressure for which the structure can compensate depends on the contact angle and geometry. Analysis of the equations above clearly shows that the desired transport behaviours have some limitations. For instance, high directionality requires no or very slow transport in the backward direction, which can only be achieved at the cost of lower velocity in the forward direction and smaller volumes transported per time unit.

The transport model in equations (2.4a,b) shows that the velocity in the forward direction is highest for liquids with low viscosities and high surface tensions with air or another ambient gas. Since the terms under the square roots in equations (2.4a,b) must be positive, the possible combinations of contact angles θ and mean angles of slope α_m are limited. Therefore, the liquid used should exhibit a contact angle well below 90°. Further limitations arise from the achievable volume flow rates. The ratio of volume flow rates is given by the characteristic function of asymmetry As(θ, α_m) = (cos(θ − α_m) (cos(θ + α_m))⁻¹)^0.5 defined in equation (2.6b), if the averaged cross-sectional area of the capillaries is constant. Hence, the best choice for maximum directionality in fluid transport is θ = 45° and α_m = 45°. However, asymmetry is increased at the expense of the total transport volume described by Vol(θ, α_m) (see equation (2.6a)), which is reduced compared to a conventional capillary transport with α_m = 0° and θ = 45°. We recommend a contact angle between θ = 60° and θ = 80° in combination with suitable mean angles of slopes to obtain devices with moderate asymmetries and comparably high transport volumes.

2.3. Technical transfer

To show that the principles described can be applied to a technically interesting liquid–material combination, we designed and fabricated a prototype. For this purpose, an interconnected capillary structure for transport of aqueous liquids (figure 5) was engraved into the surface of plain polymethyl methacrylate (PMMA) by means of laser structuring (figure 5c). We chose a saw-tooth shape of the interconnected capillaries such that the liquid front stops in the backward direction. Applying soapy water droplets (0.16% soap concentrate) of 50 µl to the prototype resulted in asymmetric liquid transport (figure 5c), which accords well with the theory described. A video of liquid flow in the PMMA prototype is provided in the electronic supplementary material.

Analysis of individual pictures of transported droplets (figure 5c) and comparison with our model (figure 5a,b) showed a precise analogy for (i) transportation in a capillary, (ii) transportation via interconnections and (iii) halting of the liquid front at a singularity. The experimental results therefore demonstrate three processes in the transport mechanism:

• (1) transport of a liquid in one capillary and halting in the other;

• (2) transport via an interconnection to the other capillary and

• (3) picking up of the halted liquid and formation of a new advancing liquid front.

These results verify the basic physical principles responsible for directional, passive liquid transport on the Texas horned lizard’s skin. Furthermore, we abstracted the subnatural structure fabricated in epoxy resin and applied the principle to PMMA, which is a common polymer in microfluidics. In contrast to other technologies for microfluidic diodes, movable parts like flaps [17] or cylindrical discs [18] are avoided. Conventional bulk material is applied and there is no need for superhydrophobic treatment or the application of porous substrates such as in [19]. In addition to the structure for one-way wicking presented in [20], the fabricated biomimetic structures allow for a complete halting of the liquid front in one direction. In general, the application spectrum of such a directional liquid transport is broad and ranges from microfluidics, medical applications, distilleries and heat exchangers to lubrication or e-ink displays.

3. Conclusion

Based on the Texas horned lizard as a model for passive directional liquid transport, we have employed a biomimetic approach that revealed the functional geometric principles of ‘asymmetry’ and ‘interconnection’. Asymmetric capillaries enable directional liquid transport, while interconnections help the liquid to overcome singularities and thus extend the transport distance. The Young–Laplace equation was used to calculate the pressure difference Δp across the fluid–air interface, which allows structures to be constructed for directional transport of a wide range of liquid–solid combinations. Using the example of aqueous liquids in microfluidics or medical devices, we have demonstrated the potential of surfaces with structural modifications for passive directed liquid transport, which might lead to process improvements and reduced resource requirements. Undoubtedly, there is comparable potential in practically all applications that require directed passive transport of liquids. The transport mechanism we have presented provides free access over the entire transport distance. As part of future work, further validation will be necessary to make these principles suitable for specific product assemblies.

4. Experimental section

For histological slices, tissue samples (approx. 1 × 3 mm) were taken from different body regions of alcohol-fixed specimens (Zoological Research Museum Alexander Koenig (ZFMK) in Bonn, Germany) of P. cornutum (ZFMK, 21313). These samples were fixed overnight in 4% (v/v) glutardialdehyde in 70% ethanol, followed by dehydration in an ascending alcohol series (90%, 60 min; 96%, 60 min; twice: 99.8%, 60 min; 100%, 2 days).

After the alcohol was substituted by propylene oxide (2 × 30 min), samples were put in a 1 : 1 alloy of propylene oxide and epon overnight. On the following day, epon was exchanged (2 × 2 h). The samples were transferred to moulds and arranged such that the cut slices were perpendicular to the longitudinal axis of the lizard and were then hardened at 60°C for 48 h.

The 0.75 µm thick slices were cut with a microtome (Om U3, C. Reichert Optische Werke AG, Vienna, Austria) and stained with methylene blue-azure II. Photographs were taken with a Canon Power Shot A70 (Canon Deutschland GmbH, Krefeld, Germany). For the slice series we used pictures of about every 10th slice. Height and width were measured using the GIMP freeware (v. 2.6.8).

To obtain three-dimensional information of the capillary network, we used OCT—a purely optical, non-destructive, non-invasive and contactless high-resolution imaging method applicable to semi-transparent and turbid media [21]. The OCT system employed was a commercially available Telesto SD-OCT system from Thorlabs (Lübeck, Germany) using a centre wavelength of 1325 nm. The axial resolution is less than 7.5 µm in air, and the lateral resolution is approximately 15 µm. The images were obtained from alcohol-preserved lizard specimens without further treatment.

For SEM imaging, tissue samples were taken from different body regions of alcohol-fixed museum specimens (ZFMK in Bonn, Germany) of P. cornutum. These samples were fixed overnight in 4% (v/v) glutardialdehyde in 70% ethanol, followed by dehydration in an ascending alcohol series (90%, 60 min; 96%, 60 min; twice: 99.8%, 60 min; 100%, 2 days). After washing three times for 20 min with hexamethyldisilazane, the samples were dried at room temperature for 3 days. The samples were sputter-coated without further treatment with gold and examined using a Stereoscan S604 SEM (Cambridge Instruments, UK). Images were digitally recorded with an attached i-scan digitizer (ISS Group Services Ltd, Manchester, UK) with an image acquisition time of 50 s.

To obtain the subnatural structure, 3 mm thick plates of epoxy resin were produced. The epoxy resin (10 : 4 resin to hardener; toolcraft, Conrad Electronic, Hirschau, Germany) was hardened at room temperature for 48 h, then removed from the mould and plain grinded with a 3-axis CAD cutter. Structures were milled with a 0.3 mm cutter head. The video analysis was conducted using a binocular microscope (Olympus SZ, Olympus Deutschland GmbH, Hamburg, Germany) on which a digital camera (Canon Power Shot A70, Canon Deutschland GmbH, Krefeld, Germany) was mounted.

PMMA structures with interconnected saw-tooth-shaped capillaries were manufactured using laser ablation. The ablation was done with a Trotec Speedy 300 TM laser cutter/engraver. This device has a 95 W CO₂ laser source with a main wavelength of 10.6 µm. The laser beam was focused with a spot size diameter of 100 µm on the surface of the demonstrator plates using a Trotec lens with a focal length of 1.5 inch (3.81 cm). The plate material was 6 mm Evonik industries Plexiglas^® extruded acrylic sheet according to ISO 7823–2. This PMMA was laser structured at a pulse energy of 2.26 mJ achieved by selecting an average laser power of 95 W and a pulse repetition rate of 42 kHz. The active feed rate of the laser beam was 1.065 m s⁻¹ (42 inch s⁻¹) leading to a pulse density of 1000 ppi. The effective ablation depth per single laser cycle was 964 µm.

Videos of the advancing liquid front served as an optical method for velocity measurement. Video analysis was conducted using a digital high-speed microscope (Keyence VW-9000, Keyence Deutschland GmbH, Neu-Isenburg, Germany) mounted on a pipetting robot (Hamilton STARlet, Hamilton AG, Bonaduz, Switzerland).

Data accessibility

Refer to electronic supplementary material videos and request any further data from the corresponding author.

Authors' contribution

P.C. performed acquisition of biological data, identification and analyses of functional principles, design of prototypes, velocity measurements on prototypes, data analysis and interpretation, drafting the article, final approval. G.B. designed prototypes, performed physical modelling and calculations, data analysis and interpretation, drafting the physical part of the article as well as electronic supplementary material, final approval. A.B. performed OCT measurements and drafting corresponding parts of article, final approval. Both R.B. and A.K. performed laser structuring of PMMA-prototypes and drafting corresponding parts of the article, final approval. S.B. revised the manuscript with special emphasis on the physical part, style and structure, final approval. W.B. had the idea for the scientific project, conceived and designed experiments, identified functional principles, was involved in data interpretation, revising the manuscript, final approval.

Competing interests

We declare we have no competing interests.

Funding

 Financial support from the German Federal Ministry of Education and Research (BMBF) is acknowledged within the ‘BioLas.exe’ project in the scope of the VIP program, from Kimberly-Clark within the ‘Reptile’ project and from the European Research Council within the Advanced Investigators Grant SoftMap (Soft Matter Physics Team). RECENDT acknowledges financial support by the European Regional Development Fund (EFRE) in the framework of the EU-program REGIO 13, and the Federal State of Upper Austria is acknowledged.