Abstract
Cities are characterized by concentrating population, economic activity and services. However, not all cities are equal and a natural hierarchy at local, regional or global scales spontaneously emerges. In this work, we introduce a method to quantify city influence using geolocated tweets to characterize human mobility. Rome and Paris appear consistently as the cities attracting most diverse visitors. The ratio between locals and non-local visitors turns out to be fundamental for a city to truly be global. Focusing only on urban residents' mobility flows, a city-to-city network can be constructed. This network allows us to analyse centrality measures at different scales. New York and London play a central role on the global scale, while urban rankings suffer substantial changes if the focus is set at a regional level.
Keywords: networks, human mobility, city–city interaction, geolocated data, epidemiology
1. Introduction
Ever since Christaller proposed the central place theory in the 1930s [1], researchers have worked to understand the relations and competition between cities leading to the emergence of a hierarchy. Christaller envisioned an exclusive area surrounding each city at a regional scale to which it provided services such as markets, hospitals, schools, universities, etc. The services display different level of specialization, inducing thus a hierarchy among urban areas according to the type of services offered. In addition, this idea naturally brings an equidistant distribution of urban centres of similar category as long as no geographical constraints prevent it. Still, in the present globalized world relations between cities go beyond mere geographical distance. In order to take into account this fact, it was necessary to introduce the concept of world city [2]. These are cities that concentrate economic warehouses such as the headquarters of large multinational companies or global financial districts, of knowledge and innovation as the cutting edge technological firms or universities, or political decision centres, and that play an eminent role of dominance over smaller, more local, counterparts. The concept of global city is, nevertheless, vague and in need of further mathematical formalization. This is attained by means of so-called world city networks, in which each pair of cities is linked whether they share a common resource or interchange goods or people [3–7]. For instance, a link can be established if two cities share headquarters of the same company [7–9], if both are part of good production chains [10], interchange finance services [11], Internet data [12] or if direct flights or boats connect them [4,13–15]. Centrality measures are then applied to the network and a ranking of the cities naturally emerges. Due in great part to their geographical locations and traditional roles as trans-Atlantic bridges, New York and London are typically the top rankers in many of these studies [5,9,14]. There are, however, inconsistencies in terms of the meaning and stability of the results obtained from different networks or with different centrality measures [14,16] and a more organic and stable definition is needed.
Here, we use information and communication technologies (ICT) to approach the problem from a different perspective. How long would information originating from a given city reach any other city if it were to pass from person to person only through face to face conversations? Or, in other words, what is the likelihood that information reaches a certain distance away after a given time period. In this experiment, the most central place in the world would simply be the place from which a message could reach everywhere else in the shortest amount of time. This view allows us to easily define a temporal network of influence.
We perform this analysis by empirically observing how people travel worldwide and using that as a proxy for how quickly our message would be able to spread. The recent popularization and affordability of geolocated ICT services and devices such as mobile phones, credit or transport cards generates a large quantity of real-time data on how people move [17–25]. This information has been used to study questions such as interactions in social networks [26–29], information propagation [30], city structure and land use [23,31–40], or even road and long-range train traffic [41]. It is bringing a new era in the so-called science of cities by providing a basis for systematic comparison of the structure of urban areas of different sizes or in different countries [37,38,40,42–47]. Data from credit cards and mobile phones are usually constrained to a limited geographical area such as a city or a country, whereas those generated from online social media as Twitter, Flickr or Foursquare can refer to the whole globe. This is the reason we focus here on geolocated tweets, which have already proven to be an useful tool to analyse mobility between countries [48] and provide the ideal framework for our analysis.
In particular, we select 58 of the most populated cities in the world and analyse their influence in terms of the average radius travelled and the area covered by Twitter users visiting each of them as a function of time. Differences in the mobility for local residents and external visitors are taken into account, in such a way that cities can be ranked according to the extension covered by the diffusion of visitors and residents, taken both together and separately, and by the attractiveness they exhibit towards visitors. Finally, we also consider the interaction between cities, forming a network that provides a framework to study urban communities and the role cities play within their own community (regional) versus a global perspective.
2. Material and methods
2.1. Twitter dataset
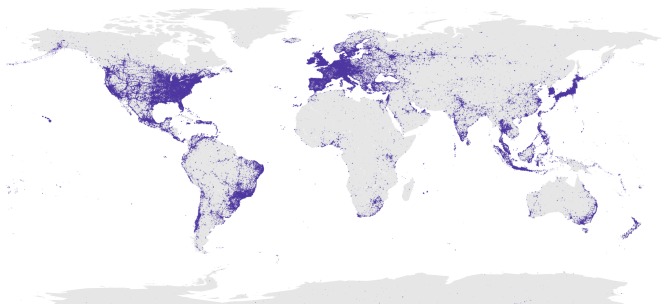
Our database contains 21 017 892 tweets geolocated worldwide written by 571 893 users in the temporal period ranging from October 2010 to June 2013 (1000 days). There are on average 36 tweets per user. Non-human behaviour or collective accounts have been excluded from the data by filtering out users travelling faster than a plane (750 km h−1). For this, we have computed the distance and the time spent between two successive geolocated tweets posted by the same user. The geographical distribution of tweets is plotted in figure 1. The distribution matches population density in many countries, although it is important to note that some areas are under-represented such as, for example, most of Africa and China.
Figure 1.
Positions of the geolocated tweets. Each tweet is represented as a point on the map from where it was posted. (Online version in colour.)
We take as reference 58 cities around the world (see electronic supplementary material, table S1, for a detailed account) that are both highly populated (most are among the 100 most populated cities in the world) and have a sufficiently large number of geolocated Twitter users. To avoid distortions imposed by different spatial scales and urban area definitions that can be problematic [49,50], we operationally defined each city to be a circle of radius 50 km around the respective city hall.
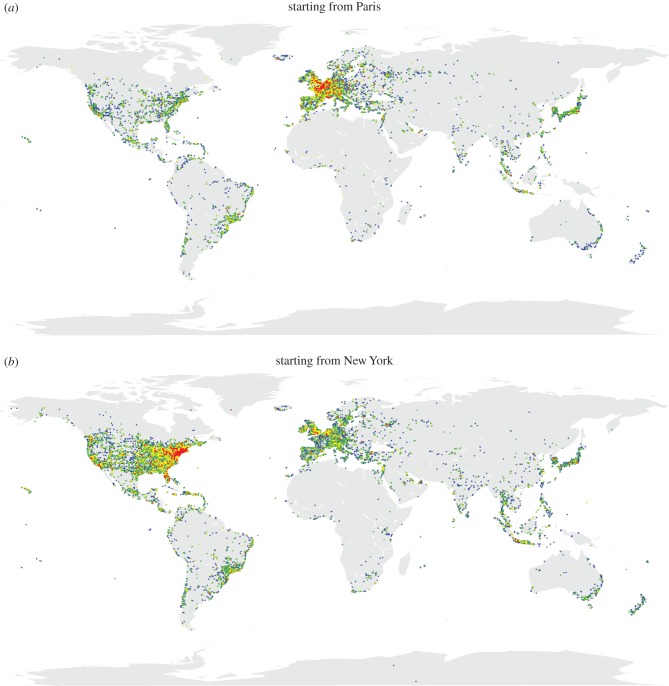
In order to assess the influence of a city, we need to characterize how users travel after visiting it. To do so, we consider the tweets posted by user υ Δt days after visiting city c. In figure 2, the locations of geolocated tweets are plotted according to the number of days since the first visit in Paris and New York as an example. Not surprisingly, a large part of the tweets are concentrated around these cities but one can observe how users eventually diffuse worldwide.
Figure 2.
Geolocated tweets of users who have been at least once in Paris (a) and New York (b). The colour changes according to the number of days Δt since the first passage in the city. In red, 1 day; in yellow, between 1 and 10 days; in green, between 10 and 100 days; and in blue, more than 100 days.
2.2. Definition of the user's place of residence
To identify the Twitter users' place of residence, we start by discretizing the space. To do so, we divide the world using a grid composed of 100 × 100 km2 cell in a cylindrical equal-area projection. In total, there are approximately 5000 inhabited cells in our dataset. The place of residence of a user is a priori given by the cell from which he or she has posted most of his/her tweets. However, to avoid selecting users who did not show enough regularity, we consider only those users who posted at least one-third of their tweets form the place of residence (representing more than 95% of the overall users). For each city, the number of valid users as well as the number of tweets posted from their first passage in the city are provided in electronic supplementary material, table S1.
We can now determine for each city whether a user is resident (local user) or a visitor (non-local user). To do so, we compute the average position of the tweets posted from his/her cell of residence. If this position falls within the city boundaries (circle of radius 50 km around the city hall), the user is considered as a local and as a non-local user otherwise.
2.3. Metrics to assess city influence
We select a fixed number of users u in each city at random and track their displacements in a given period of time Δt as their first tweet from it. As the results might depend on the specific set of users chosen, we average over 100 independent user extractions. As shown in electronic supplementary material, figure S2, the longer Δt is, the lower the population of users who remain active, so we must establish a trade-off between number of users and activity time. Unless otherwise stated, we set u = 300 and Δt = 350 days in the discussion that follows.
2.3.1. Average radius
There are different aspects to take into account when trying to define how to properly measure the influence of a city due to human mobility. We start our discussion by considering the average radius travelled by Twitter users since their first tweet from a city c. We tracked for each user the positions from which he or she tweeted after visiting c, and compute the average distance from these locations to the centre of c. The average radius, R, is then defined as the average over all the u users of their individual radii.
The average radius is informative but can be biased by the geography. Cities that are in relatively isolated positions such as islands may have a high average radius just because a long trip is the only option to travel to them. To avoid this effect, we define the normalized average radius 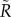 of a city c as the ratio between R(c) and the average distance of all the Twitter users' places of residence to c (electronic supplementary material, figure S4).
of a city c as the ratio between R(c) and the average distance of all the Twitter users' places of residence to c (electronic supplementary material, figure S4).
2.3.2. Coverage
One possible way to overcome the limitation of the average ratio defined above is to discard geographical coherence all together and simply measure the area covered by those users, regardless of the distance at which it might be located from the originating city. In order to estimate the area cover by the users, the world surface has been divided into cells of 100 × 100 km2 as we have done to identify the users' place of residence. By tracking the movements of the set of users passing through each city, we count the number of cells from which at least a tweet has been posted and define coverage as this number. This metric has the clear advantage of not being sensitive to isolated locations but it still does not consider how specific cells, specifically those corresponding to other important cities, are visited much more often than others.
3. Results
3.1. Comparing the influence of cities
We start by taking the perspective from the city to the world and compare how effective the cities are as starting points for the Twitter users' diffusion. The evolution of the average radius as a function of the time is plotted in figure 3 for the 58 cities. The curves of the log–log plot show an initial fast increase followed by a much slower growth after approximately 15–20 days. The presence of these two regimes is mainly due to the presence of non-local users as it can be observed in electronic supplementary material, figure S5. In the initial phase, the radius grows for all the cities at a rhythm faster than the square root of time, which is the classical prediction for 2D Wiener diffusion [51]. This is not fully surprising as the users' mobility is better described by Levy flights than by a Wiener process. Still the differences between cities are remarkable. There are two main behaviours: the radius for cities such as Detroit grows slowly, whereas others like Paris show an increase that is close to linear. After this initial transient, the average radius enters in a regime of slow growth for all the cities that is even slower than 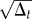 . This implies that the long displacements by the users are concentrated in the first month, period during which the non-local users come back home, after which the exploration becomes more localized. Even though the curves of different cities may cross in the first regime, they reach a relatively stable configuration in the second one. We can see that the top ranker in terms of capacity of diffusion is Hong Kong for the whole time window considered and the bottom one is Bandung (West Java, Indonesia).
. This implies that the long displacements by the users are concentrated in the first month, period during which the non-local users come back home, after which the exploration becomes more localized. Even though the curves of different cities may cross in the first regime, they reach a relatively stable configuration in the second one. We can see that the top ranker in terms of capacity of diffusion is Hong Kong for the whole time window considered and the bottom one is Bandung (West Java, Indonesia).
Figure 3.
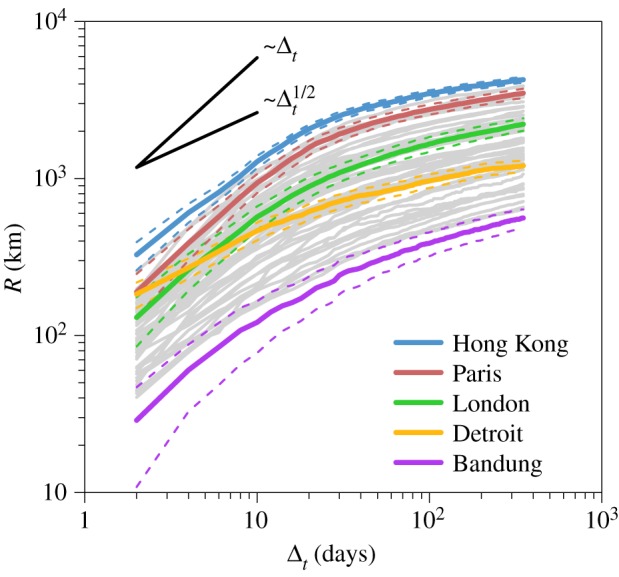
Evolution of the average radius. Each curve represents the evolution of the average radius R averaged over 100 independent extractions of a set of u = 300 users as a function of the number of days Δt since the first passage in the city. In order to show the general trend, each grey curve corresponds to a city. The evolution of the radius for several cities is highlighted, such as the top and bottom rankers or representatives of the two main detected behaviours. Curves with a linear and square root growth are also shown as a guide for the eye. The dashed lines represent the standard deviation.
The top 10 cities according to the average radius are plotted in figure 4a. It is worth noting that New York only appears in the last position, in contrast to previously published rankings based on different approaches [5,9,14]. Many cities on the top are in the Pacific Basin (Hong Kong, Sydney, Beijing, Taipei, San Francisco and Shanghai), which is clear evidence for the impact of geography on R. We take geographical effects into account by calculating the normalized radius 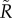 as shown in figure 4b. With this correction, the top cities are Rome, Paris and Lisbon. These cities are located in densely populated Europe but still manage to send travellers further away than any other, proof of their aptitude as sources for the spread of information as described in the introduction. Actually, all cities in the top 10 set are also able to attract visitors at a worldwide scale, some are relatively far from other global cities and/or they may be the gate to extensive hinterlands (China). The same ranking for the coverage is shown in figure 4c. Even though these two metrics are strongly correlated (see electronic supplementary material, figure S6), there are still some significant differences indicating that they are able to capture different information. The top cities, however, are again Rome, Paris and Lisbon probably due to a combination of the factors explained above. It should also be noted that even though the users extraction is stochastic and the rankings can vary slightly from one realization to another (see electronic supplementary material, figure S7), the ranking is stable when averaged over several realizations (electronic supplementary material, figure S8).
as shown in figure 4b. With this correction, the top cities are Rome, Paris and Lisbon. These cities are located in densely populated Europe but still manage to send travellers further away than any other, proof of their aptitude as sources for the spread of information as described in the introduction. Actually, all cities in the top 10 set are also able to attract visitors at a worldwide scale, some are relatively far from other global cities and/or they may be the gate to extensive hinterlands (China). The same ranking for the coverage is shown in figure 4c. Even though these two metrics are strongly correlated (see electronic supplementary material, figure S6), there are still some significant differences indicating that they are able to capture different information. The top cities, however, are again Rome, Paris and Lisbon probably due to a combination of the factors explained above. It should also be noted that even though the users extraction is stochastic and the rankings can vary slightly from one realization to another (see electronic supplementary material, figure S7), the ranking is stable when averaged over several realizations (electronic supplementary material, figure S8).
Figure 4.
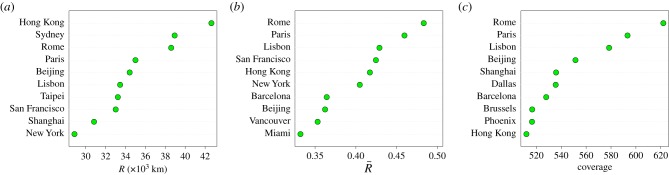
Rankings of the cities according to the average radius and the coverage. (a) Top 10 cities ranked by the average radius R. (b) Top 10 cities ranked by the normalized average radius  . (c) Top 10 cities ranked by the coverage (number of visited cells). All the metrics are averaged over 100 independent extractions of a set of u = 300 users. (Online version in colour.)
. (c) Top 10 cities ranked by the coverage (number of visited cells). All the metrics are averaged over 100 independent extractions of a set of u = 300 users. (Online version in colour.)
3.2. Local versus non-local Twitter users
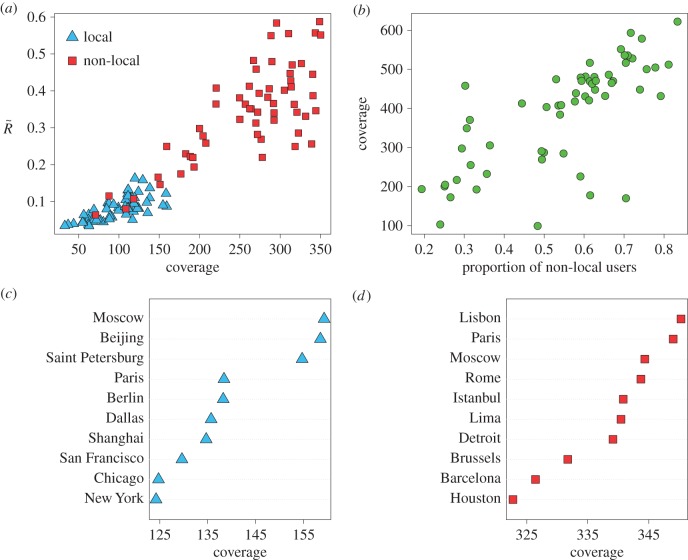
We have yet to take into account that individuals residing in a city might behave differently from visitors. We consider a user to be a resident of a city if most of his/her tweets are posted from it. Otherwise, he/she is seen as an external visitor. Residents of the 58 cities we consider have a significantly lower coverage (about 96) than visitors (about 260). This means that the locals move towards more concentrated locations, such as places of work or the residences of family and friends, while visitors have a comparatively higher diversity of origins and destinations.
The difference between locals and non-locals is even more dramatic when the normalized radius,  , for each city is plotted as a function of the coverage for both types of users in figure 5a. Two clusters clearly emerge showing that the locals tend to move less than the visitors. This difference between users is likely to be behind the change of behaviour in the temporal evolution of the average radius detected in figure 3, and introduces the ratio of visitors over local users as a relevant parameter to describe the mobility from a city. Indeed, visitors contribute the most to the radius and the area covered (see figure 5b for the coverage) while residents contribute most to the local relevance of a city (figure 5c for the coverage and electronic supplementary material, figure S10a, for
, for each city is plotted as a function of the coverage for both types of users in figure 5a. Two clusters clearly emerge showing that the locals tend to move less than the visitors. This difference between users is likely to be behind the change of behaviour in the temporal evolution of the average radius detected in figure 3, and introduces the ratio of visitors over local users as a relevant parameter to describe the mobility from a city. Indeed, visitors contribute the most to the radius and the area covered (see figure 5b for the coverage) while residents contribute most to the local relevance of a city (figure 5c for the coverage and electronic supplementary material, figure S10a, for  ). The top rankers in this classification are Hong Kong and San Francisco in
). The top rankers in this classification are Hong Kong and San Francisco in 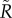 and Moscow and Beijing in the coverage. All of them are cities that may act as gates for quite extensive hinterlands. The rankings based on non-locals (figure 5d for the coverage and electronic supplementary material, figure S10b, for
and Moscow and Beijing in the coverage. All of them are cities that may act as gates for quite extensive hinterlands. The rankings based on non-locals (figure 5d for the coverage and electronic supplementary material, figure S10b, for 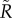 ) get us back the more common top rankers such as Paris, New York and Lisbon.
) get us back the more common top rankers such as Paris, New York and Lisbon.
Figure 5.
Relation between local and non-local users. (a) Scatter-plot of 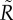 as a function of the coverage for locals (blue triangles) and non-locals (red squares). (b) Coverage as a function of the proportion of non-local Twitter users. (c) Top 10 ranking cities based only on local users according to the coverage. (d) The same ranking but based only on the movements of non-local users. In all the cases, the number of local and non-local users extracted is u = 100 for every city and all the metrics are averaged over 100 independent extractions. (Online version in colour.)
as a function of the coverage for locals (blue triangles) and non-locals (red squares). (b) Coverage as a function of the proportion of non-local Twitter users. (c) Top 10 ranking cities based only on local users according to the coverage. (d) The same ranking but based only on the movements of non-local users. In all the cases, the number of local and non-local users extracted is u = 100 for every city and all the metrics are averaged over 100 independent extractions. (Online version in colour.)
3.3. City attractiveness
Thus far, we have considered a city as an origin and analysed how people visiting it diffuse across the planet. We now consider the attractiveness of a city by taking the opposite point of view and analysing the origins of each user seen within the confines of a city. We modify the two metrics defined above to consider the normalized average distance of the users' residences (represented by the centroid of the cell of residence) to the centre of the considered city c and the number of different cells where these users come from. In this case, the two metrics are averaged over 100 independent extractions of u = 1000 Twitter users per city. The resulting rankings depict the attractiveness of each city from the perspective of external visitors: how far are people willing to travel to visit this city? The top 10 cities are shown in figure 6 for the coverage (see electronic supplementary material, figure S11, for the normalized average radius). Rome, Paris and Lisbon are also quite consistently the top rankers in terms of attractiveness to external visitors.
Figure 6.
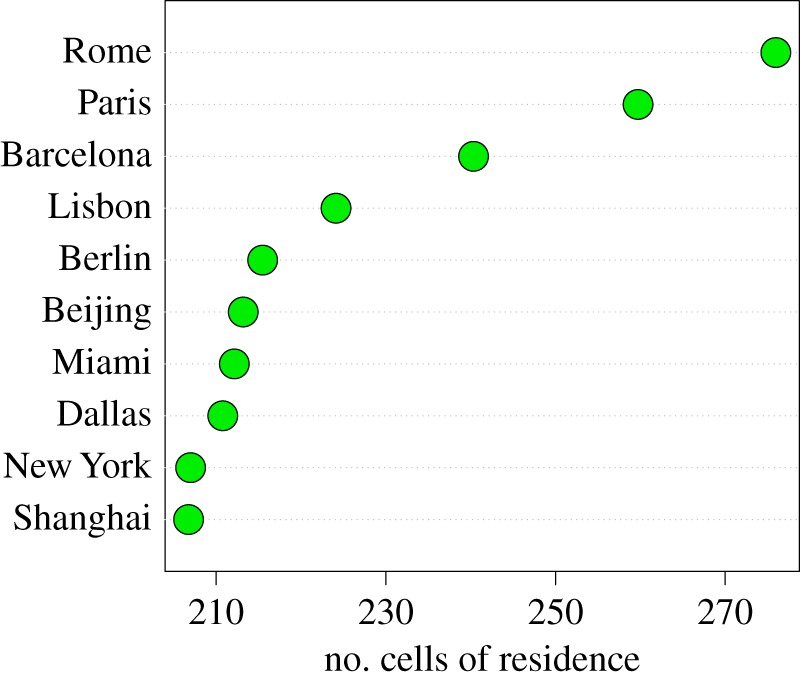
City attractiveness. Top 10 cities ranked by the number of distinct cells of residence for u = 1000 Twitter users drawn at random. The metric is averaged over 100 independent extractions. (Online version in colour.)
3.4. A network of cities
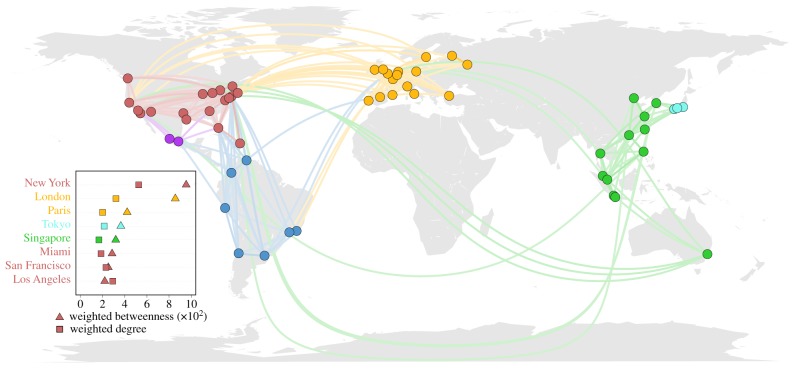
Finally, we complete our analysis by considering travel between the 58 selected cities. We build a network connecting the 58 cities under consideration where the directed edge from city i to city j has a weight given by the fraction of local Twitter users in the city i which were observed at least once in city j. For simplicity, in what follows, we consider only local users who left their city at least once. This network captures the strength of connections between cities allowing us to analyse the communities that naturally arise due to human mobility. Using the OSLOM clustering detection algorithm [52,53], we find six communities as shown in figure 7. These communities follow approximately the natural boundaries between continents: two communities in North and Central America, one community in South America, another in Europe, two communities in Asia (Japan and rest of Asia plus Sydney), indicating that they correspond to economic, cultural and geographical proximities. Similar results were obtained using the Infomap [54] cluster detection algorithm, confirming the robustness of the communities detected.
Figure 7.
Mobility network. Local Twitter users’ mobility network between the 58 cities. Only the flows representing the top 95% of the total flow have been plotted. The flows are drawn from the least to the greatest. The inset shows the top eight cities ranked by weighted betweenness and weighted degree.
With these empirical communities in hand, we can now place each city into a local as well as a global context. In a network context, the importance of each node can be measured in different ways. Two classical measures are the strength of a node [55] and the weighted betweenness [56,57]. Given the way we defined our network above, these correspond, roughly, to the fraction of local users that travel out of a city and how important that city is in connecting travellers coming from other cities to their final destinations. In the inset of the figure 7, we analyse the ranking resulting from these two metrics and identify New York and London as the most central nodes in terms of degree and betweenness and, particularly, New York for the weighted degree at a global scale. However, when we restrict our analysis to just the regional scene of each community, the relative importance of each city quickly changes. The rankings for the regional weighted degree are similar to the global ones as this metric depends only on the population of each city and not on who it is connected to. The most central cities occupy the same positions except for San Diego, which slipped down three places. On the other hand, the weighted betweenness is a property that depends strongly on the network topology, a property that can be seen by the dramatic shifts we observe when considering only the local community of each city with most cities moving several positions up or down (see details in table 1 and electronic supplementary material, table S2). For example, San Diego went down nine places meaning that this city has a global influence due to the fact that San Diego is a communication hub between United States and Central America. Dallas went up six places, indicating that its influence is higher at the regional scale rather than in the international arena. In the same way, Madrid went down four places, whereas Barcelona stayed at the same place, this means that Madrid is more influential than Barcelona on a global scale as an international bridge connecting Europe and Central and South America but not on a regional (European) scale.
Table 1.
Comparison of the regional and the global betweenness rankings. In parenthesis the total global ranking position of each city.
| global ranking | regional ranking |
|---|---|
| North America | |
| 1. New York (1) | 1. New York |
| 2. Miami (6) | 2. Los Angeles |
| 3. San Francisco (8) | 3. Chicago |
| 4. Los Angeles (9) | 4. Toronto |
| 5. Chicago (18) | 5. Detroit |
| 6. Toronto (19) | 6. Miami |
| 7. San Diego (23) | 7. Dallas |
| 8. Detroit (25) | 8. San Francisco |
| 9. Montreal (26) | 9. Washington |
| 10. Atlanta (27) | 10. Atlanta |
| Europe | |
| 1. London (2) | 1. London |
| 2. Paris (3) | 2. Paris |
| 3. Madrid (10) | 3. Moscow |
| 4. Barcelona (11) | 4. Barcelona |
| 5. Moscow (16) | 5. Berlin |
| 6. Berlin (20) | 6. Rome |
| 7. Rome (21) | 7. Madrid |
| 8. Amsterdam (24) | 8. Lisbon |
| 9. Lisbon (38) | 9. Amsterdam |
| 10. Milan (40) | 10. Saint Petersburg |
4. Discussion
The study of competition and interactions between cities has a long history in fields such as geography, spatial economics and urbanism. This research has traditionally been based on information from finance exchanges, sharing of firm headquarters, number of passengers transported by air or tons of cargo dispatched from one city to another. One can define a network relying on these data and identify the so-called world cities, those with a higher level of centrality as the global economic or logistic centres. Here, we have taken a radically different approach to measure quantitatively the influence of a city in the world. Nowadays, geolocated devices generate a large quantities of real-time and geolocated data permitting the characterization of people mobility. We have used Twitter data to track users and classify cities according to the mobility patterns of their visitors. Top cities as mobility sources or attraction points are identified as central places at a global scale for cultural and information exchanges. This definition of city influence makes possible its direct measurement instead of using indirect information such as firm headquarters or direct flights. Still, the quality of the results depends on the capacity of geolocated tweets to describe local and global mobility. Indeed, observing the World through Twitter data can lead to possible distortions, economic and sociodemographic biases, the Twitter penetration rate may also vary from country to country leading to an under-representation of the population, for example, from Africa and from China. The cities selected for this work are those that, on one hand, concentrate large populations and, on the other, have sufficient tweets to be part of the analysis. There are biases acting against our work, such as the lack of coverage in some areas of the world, and others in favour, such as the fact that younger and wealthier individuals are more likely to both travel and use Twitter. The estimated mobility patterns are naturally partial as they only refer to selected cities. Still, as long as the users provide a significant sample of the external urban mobility, the flow network is enough for the performed analysis. Furthermore, several recent works have proven the capacity of geolocated tweets to describe human mobility, comparing different data sources as information collected from cell phone records, Twitter, traffic measure techniques and surveys [23,24,41].
More specifically and assuming data reliability, we consider the users' displacements after visiting each city. The urban areas are ranked according to the area covered and the radius travelled by these users as a function of time. These metrics are inspired by the framework developed for random walks and Levy flights, which allows us to characterize the evolution of the system with well-defined mathematical tools and with a clear reference baseline in mind. Previous literature rankings usually find a hierarchy captained by New York and London as the most central world cities. The ranks dramatically change when one has taken into account users' mobility. A triplet formed by Rome, Paris and Lisbon consistently appear on the top of the ranking by extension of visitor's mobility but also by their attractiveness to travellers of very diverse origin. A combination of economic activity appealing to tourism and diversity of links to other lands, in some cases the product of recent history, can explain the presence of these cities on the top. These three cities are followed by others such as San Francisco, which without being one of the most populated cities in the US extends it influence over the large Pacific basin, or Hong Kong, Beijing and Shanghai, which replicates that on the other side of the Pacific region. These cities are in some cases gates to broad hinterlands. This is relevant as our metrics have into account the diversity in the visitors' origins.
These results rely on the full user population, discriminating only by the place of residence between locals and non-locals to each city. The influence of cities measured in this way includes their impact on rural as well as on other urban areas. However, the analysis can be restricted to users residing in an urban area and to their displacements towards other cities. In this way, we obtain a weighted directed network between cities, whose link weights represent the (normalized) fluxes of users travelling from one city to another. This network provides the basis for a more traditional centrality analysis, in which we recover London and New York as the most central cities on a global scale. The match between our results and those from previous analysis brings further confidence on the quality of the flow measured from online data. The network framework permits clustering techniques to be performed and divides the world city network into communities or areas of influence. When the centrality is studied only within each community, we obtain a regional perspective that induces a new ranking of cities. The comparison between the global and the regional ranking provides important insights into the change of roles of cities in the hierarchies when passing from global to regional.
In summary, we have introduced a new method to measure the influence of cities based on Twitter user displacements as proxies for mobility flows. The method, despite some possible biases due to the population using online social media, allows for a direct measurement of a city's influence in the World. We proposed three types of rankings capturing different perspectives: rankings based on ‘city-to-world’ and ‘world-to-city’ interactions and rankings based on ‘city-to-city’ interaction. It is interesting to note that the most influential cities are very different according to the perspective and the scale (regional and global). This introduces the possibility of studying relations among cities and between cities and rural areas with unprecedented detail and scale.
Supplementary Material
Authors' contributions
M.L. designed the study, analysed the data and wrote the manuscript. B.G., A.T. and J.J.R. designed the study and wrote the manuscript. All authors read, commented and approved the final version of the manuscript.
Competing interests
We declare we have no competing interests.
Funding
Partial financial support has been received from the Spanish Ministry of Economy (MINECO) and FEDER (EU) under project INTENSE@COSYP (FIS2012–30634), and from the EU Commission through projects LASAGNE and INSIGHT. The work of M.L. has been funded under the PD/004/2013 project, from the Conselleria de Educación, Cultura y Universidades of the Government of the Balearic Islands and from the European Social Fund through the Balearic Islands ESF operational programme for 2013–2017. J.J.R. acknowledges funding from the Ramón y Cajal program of MINECO. B.G. was partially supported by the French ANR project HarMS-flu (ANR-12-MONU-0018).
References
- 1.Christaller W. 1966. Die Zentralen Orte in Süddeutschland: eine Ökonomisch-Geographische Untersuchung Über die Gesetz Massigkeit der Verbreitung und Entwicklung der Siedlungen mit Städtischen Funktionen, Fischer Verlag, Jena (1933). (English translation: Christaller W, Baskin CW. Central places in Southern Germany, Prentice Hall, Englewood Cliffs, NJ).
- 2.Friedmann J, Wolff G. 1982. World city formation: an agenda for research and action. Int. J. Urban Reg. Res. 6, 309–344. ( 10.1111/j.1468-2427.1982.tb00384.x) [DOI] [Google Scholar]
- 3.Berry B. 1964. Cities as systems within a systems of cities. Papers Reg. Sci. Assoc. 13, 147–163. ( 10.1111/j.1435-5597.1964.tb01283.x) [DOI] [Google Scholar]
- 4.Knox PL, Taylor PJ. 1995. World cities in a world-system. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 5.Rimmer P. 1998. Transport and telecommunications among world cities. In Globalization and the world of large cities (eds Lo FC, Yeung YM), pp. 433–470. Tokyo, Japan: United Nations University Press. [Google Scholar]
- 6.Pumain D. 2000. Settlement systems in the evolution. Geografiska Ann. 82B, 73–97. ( 10.1111/j.0435-3684.2000.00075.x) [DOI] [Google Scholar]
- 7.Taylor JP. 2001. Specification of the world city network. Geogr. Anal. 33, 181–194. ( 10.1111/j.1538-4632.2001.tb00443.x) [DOI] [Google Scholar]
- 8.Derudder B, Taylor PJ, Witlox F, Catalano G. 2003. Hierarchical tendencies and regional patterns in the world city network: a global urban analysis of 234 cities. Reg. Stud. 37, 875–886. ( 10.1080/0034340032000143887) [DOI] [Google Scholar]
- 9.Derudder B, Witlox F. 2004. Assessing central places in a global age: on the networked localization strategies of advances producer services. J. Retail. Consum. Serv. 11, 171–180. ( 10.1016/S0969-6989(03)00023-7) [DOI] [Google Scholar]
- 10.Brown E, Derudder B, Parnreiter C, Pelupessy W, Taylor PJ, Witlox F. 2010. World city networks and global commodity chains: towards a world-systems’ integration. Glob. Netw. 10, 1470–2266. ( 10.1111/j.1471-0374.2010.00272.x) [DOI] [Google Scholar]
- 11.Bassens D, Derudder B, Witlox F. 2010. Searching for the Mecca of finance: Islamic financial services and the world city network. Area 42, 35–46. ( 10.1111/j.1475-4762.2009.00894.x) [DOI] [Google Scholar]
- 12.Neal Z. 2011. Differentiating centrality and power in the world city network. Urban Stud. 48, 2733–2748. ( 10.1177/0042098010388954) [DOI] [Google Scholar]
- 13.Zook MA, Brunn SD. 2005. Hierarchies, regions and legacies: European cities and global commercial passenger air travel. J. Contemp. Eur. Stud. 13, 203–220. ( 10.1080/14782800500212459) [DOI] [Google Scholar]
- 14.Derudder B, Witlox F. 2005. On the use of inadequate airline data in mappings of a global urban system. J. Air Transp. Manage. 11, 231–237. ( 10.1016/j.jairtraman.2005.01.001) [DOI] [Google Scholar]
- 15.Derudder B, Witlox F. 2008. Mapping world city networks through airline flows: context, relevance, an problems. J. Transp. Geogr. 16, 305–312. ( 10.1016/j.jtrangeo.2007.12.005) [DOI] [Google Scholar]
- 16.Allen J. 2010. Powerful city networks: more than connections, less than domination and control. Urban Stud. 47, 2895–2911. ( 10.1177/0042098010377364) [DOI] [Google Scholar]
- 17.Brockmann D, Hufnagel L, Geisel T. 2006. The scaling laws of human travel. Nature 439, 462–465. ( 10.1038/nature04292) [DOI] [PubMed] [Google Scholar]
- 18.Gonzalez MC, Hidalgo CA, Barabasi A-L. 2008. Understanding individual human mobility patterns. Nature 453, 779–782. ( 10.1038/nature06958) [DOI] [PubMed] [Google Scholar]
- 19.Balcan D, Colizza V, Gonçalves B, Hu H, Ramasco JJ, Vespignani V. 2009. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl Acad. Sci. USA 106, 21 484–21 489. ( 10.1073/pnas.0906910106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Noulas A, Scellato S, Lambiotte R, Pontil M, Mascolo C. 2012. A tale of many cities: universal patterns in human urban mobility. PLoS ONE 7, e37027. ( 10.1371/journal.pone.0037027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bagrow JP, Lin Y-R. 2012. Mesoscopic structure and social aspects of human mobility. PLoS ONE 7, e37676. ( 10.1371/journal.pone.0037676) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Grabowicz PA, Ramasco JJ, Goncalves B, Eguiluz VM. 2014. Entangling mobility and interactions in social media. PLoS ONE 9, e92196. ( 10.1371/journal.pone.0092196) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lenormand M, Picornell M, Garcia Cantú O, Tugores A, Louail T, Herranz R, Barthelemy M, Frías-Martínez E, Ramasco JJ. 2014. Cross-checking different source of mobility information. PLoS ONE 9, e105184. ( 10.1371/journal.pone.0105184) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tizzoni M, Bajardi P, Decuyper A, Kon Kam King G, Schneider CM, Blondel V, Smoreda Z, González MC, Colizza V. 2014. On the use of human mobility proxy for the modeling of epidemics. PLoS Comput. Biol. 10, e1003716. ( 10.1371/journal.pcbi.1003716) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jurdak R, Zhao K, Liu J, AbouJaoude M, Cameron M, Newth D.2014. Understanding human mobility from Twitter. (http://arxiv.org/abs/1412.2154. ) [DOI] [PMC free article] [PubMed]
- 26.Java A, Song X, Finin T, Tseng B. 2007. Why we twitter: understanding microblogging usage and communities. In Proc. 9th ACM WebKDD and 1st SNA-KDD 2007 Workshop on Web Mining and Social Network Analysis, 12–15 August, San Jose, CA, pp. 56–65. New York, NY: ACM.
- 27.Krishnamurthy B, Gill P, Arlitt M. 2008. A few chirps about twitter. In WOSP ‘08: ACM Proc. First Workshop on Online Social Networks, 23–26 June, Princeton, NJ, pp. 19–24. New York, NY: ACM.
- 28.Huberman BA, Romero DM, Wu F. 2009. Social networks that matter: Twitter under the microscope. First Monday 14, pp. 1–5 ( 10.5210/fm.v14i1.2317) [DOI] [Google Scholar]
- 29.Grabowicz PA, Ramasco JJ, Moro E, Pujol JM, Eguiluz VM. 2012. Social features of online networks: the strength of intermediary ties in online social media. PLoS ONE 7, e29358. ( 10.1371/journal.pone.0029358) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ferrara E, Varol O, Menczer F, Flammini A. 2013. Traveling trends: social butterflies or frequent fliers? In Proc. First ACM Conf. on Online Social Networks COSN ‘13,New York, NY, USA, 7–8 October, Boston, MA, pp. 213–222. New York, NY: ACM.
- 31.Reades J, Calabrese F, Sevtsuk A, Ratti C. 2007. Cellular census: explorations in urban data collection. Pervasive Comput. 6, 30–38. ( 10.1109/MPRV.2007.53) [DOI] [Google Scholar]
- 32.Reades J, Calabrese F, Ratti C. 2009. Eigenplaces: analysing cities using the space–time structure of the mobile phone network. Environ. Plan. B Plan. Des. 36, 824–836. ( 10.1068/b34133t) [DOI] [Google Scholar]
- 33.Cheng Z, Caverlee J, Lee K. 2010. You are where you tweet: a content-based approach to geo-locating Twitter users. In Proc. 19th ACM Int. Conf. on Information and Knowledge Management, 26–30 October, Toronto, ON, vol. 17, pp. 759–768. New York, NY: ACM. [Google Scholar]
- 34.Soto V, Frías-Martínez E. 2011. Automated land use identification using cell-phone records. In HotPlanet’11 Proc. 3rd ACM Int. Workshop on MobiArch,New York, NY, USA, 28 June, Bethesda, MD, pp. 17–22. New York, NY: ACM.
- 35.Frías-Martínez V, Soto V, Hohwald H, Frías-Martínez E. 2012. Characterizing urban landscapes using geolocated tweets. In SOCIALCOM-PASSAT ‘12 Proc. 2012 ASE/IEEE Int. Conf. on Social Computing and 2012 ASE/IEEE Int. Conf. on Privacy, Security, Risk and Trust, 3–5 September, Amsterdam, The Netherlands, pp. 239–248. Piscataway, NJ: IEEE Computer Society.
- 36.Noulas A, Mascol C, Frías-Martínez E. 2013. Exploiting foursquare and cellular data to infer user activity in urban environments. In Proc. MDM ‘13, 3–6 June, Milan, Italy, pp. 167–176. Piscataway, NJ: IEEE Computer Society.
- 37.Louail T, Lenormand M, Garcia Cantú O, Picornell M, Herranz R, Frías-Martínez E, Ramasco JJ, Barthelemy M. 2014. From mobile phone data to the spatial structure of cities. Sci. Rep. 4, 5276 ( 10.1038/srep05276) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Grauwin S, Sobolevsky S, Moritz S, Godor I, Ratti C. 2015. Towards a comparative science of cities: using mobile traffic records in New York, London and Hong Kong. In Computational approaches for urban environments 13 (eds Helbich M, Jokar Arsanjani J, Leitner M), pp. 363–387. Springer International Publishing. [Google Scholar]
- 39.França U, Sayama H, McSwiggen C, Daneshvar R, Bar-Yam Y.2014. Visualizing the ‘heartbeat’ of a city with Tweets. (http://arxiv.org/abs/1411.0722. )
- 40.Louail T, Lenormand M, Picornell M, Garcia Cantú O, Herranz R, Frías-Martínez E, Ramasco JJ, Barthelemy M. 2015. Uncovering the spatial structure of mobility networks. Nat. Commun. 6, 6007 ( 10.1038/ncomms7007) [DOI] [PubMed] [Google Scholar]
- 41.Lenormand M, Tugores A, Colet P, Ramasco JJ. 2014. Tweets on the road. PLoS ONE 9, e105407. ( 10.1371/journal.pone.0105407) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bettencourt L, Lobo J, Helbing D, Kuhnert C, West G. 2007. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl Acad. Sci. USA 104, 7301–7306. ( 10.1073/pnas.0610172104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Batty M. 2008. The size, scale, and shape of cities. Science 319, 769–771. ( 10.1126/science.1151419) [DOI] [PubMed] [Google Scholar]
- 44.Bettencourt L, West G. 2010. A unified theory of urban living. Nature 467, 912–913. ( 10.1038/467912a) [DOI] [PubMed] [Google Scholar]
- 45.Bettencourt L. 2013. The origins of scaling in cities. Science 340, 1438–1441. ( 10.1126/science.1235823) [DOI] [PubMed] [Google Scholar]
- 46.Adnan A, Leak A, Longley P. 2014. A geocomputational analysis of Twitter activity around different world cities. Geo-spatial Inform. Sci. 17, 145–152. ( 10.1080/10095020.2014.941316) [DOI] [Google Scholar]
- 47.Batty M. 2013. The new science of cities. Cambridge, MA: The MIT Press. [Google Scholar]
- 48.Hawelka B, Sitko I, Beinat E, Sobolevsky S, Kazakopoulos P, Ratti C. 2014. Geo-located twitter as a proxy for global mobility patterns. Cartogr. Geogr. Inform. Sci. 41, 260–271. ( 10.1080/15230406.2014.890072) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Oliveira EA, Andrade JS Jr, Makse HA. 2014. Large cities are less green. Sci. Rep. 4, 4235 ( 10.1038/srep04235) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Arcaute E, Hatna E, Ferguson P, Youn H, Johansson A, Batty M. 2015. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 12, 20140745 ( 10.1098/rsif.2014.0745) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Weiss GH. 1994. Aspects and applications of the random walk. Amsterdam: North-Holland Publishing Co. [Google Scholar]
- 52.Lancichinetti A, Radicchi F, Ramasco JJ. 2010. Statistical significance of communities in networks. Phys. Rev. E 81, 046110 ( 10.1103/PhysRevE.81.046110) [DOI] [PubMed] [Google Scholar]
- 53.Lancichinetti A, Radicchi F, Ramasco JJ, Fortunato S. 2011. Finding statistically significant communities in networks. PLoS ONE 6, e18961. ( 10.1371/journal.pone.0018961) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Rosvall M, Bergstrom CT. 2008. Maps of random walks on complex networks reveal community structure. Proc. Natl Acad. Sci. USA 105, 1118–1123. ( 10.1073/pnas.0706851105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Barrat A, Barthelemy M, Pastor-Satorras R, Vespignani A. 2004. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA 101, 3747–3752. ( 10.1073/pnas.0400087101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Newman MEJ. 2001. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys. Rev. E 64, 016132 ( 10.1103/PhysRevE.64.016132) [DOI] [PubMed] [Google Scholar]
- 57.Brandes U. 2001. A faster algorithm for betweenness centrality. J. Math. Soc. 25, 163–177. (doi:10.1.1.11.2024) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.