Bayesian Methods for Examining Hardy–Weinberg Equilibrium

Summary

Testing for Hardy–Weinberg equilibrium is ubiquitous and has traditionally been carried out via frequentist approaches. However, the discreteness of the sample space means that uniformity of p-values under the null cannot be assumed, with enumeration of all possible counts, conditional on the minor allele count, offering a computationally expensive way of p-value calibration. In addition, the interpretation of the subsequent p-values, and choice of significance threshold depends critically on sample size, because equilibrium will always be rejected at conventional levels with large sample sizes. We argue for a Bayesian approach using both Bayes factors, and the examination of posterior distributions. We describe simple conjugate approaches, and methods based on importance sampling Monte Carlo. The former are convenient because they yield closed-form expressions for Bayes factors, which allow their application to a large number of single nucleotide polymorphisms (SNPs), in particular in genome-wide contexts. We also describe straightforward direct sampling methods for examining posterior distributions of parameters of interest. For large numbers of alleles at a locus we resort to Markov chain Monte Carlo. We discuss a number of possibilities for prior specification, and apply the suggested methods to a number of real datasets.

1. Introduction

The testing of Hardy–Weinberg equilibrium (HWE) is an important step in many analyses of genetic data. Frequentist methods are popular for testing HWE, with χ² and exact tests providing the usual implementations. There are a number of important complications that require consideration when such approaches are used. A first problem is that the discreteness of the sample space leads to nonuniformity of p-values under the null (Rohlfs and Weir, 2008). An additional major problem with frequentist tests is how to decide upon a threshold for significance, in particular as a function of the sample size. When the exact test is used, computation is an issue when the number of alleles at the locus is not small (Guo and Thompson, 1992; Huber et al., 2006). Recently, there has been great interest in testing for HWE in genome-wide association studies (GWAS) in which departure from HWE may indicate problems with quality control for the SNP in question (Wigginton, Cutler, and Abecasis, 2005).

We describe Bayesian approaches to examination of HWE based on Bayes factors for testing, and scrutiny of posterior distributions for interpretation. The discreteness of the sample space causes no complications for the Bayesian approach because all inference is conditional on the configuration of observed counts so there is no need to consider hypothetical data realizations.

The structure of this article is as follows. In Section 2, we state the Hardy–Weinberg law, and describe frequentist approaches to its testing. Section 3 describes the Bayesian approach to testing and estimation based on conjugate analysis and Monte Carlo methods, and Section 4 applies the approaches to a number of previously considered datasets. We provide a discussion in Section 5, while an appendix contains mathematical details.

2. Background

2.1 Diallelic Markers

We first consider a diallelic marker with alleles A₁ and A₂ and population frequencies of p₁ and 1 – p₁. For genotypes A₁A₁, A₁A₂, A₂A₂ the population frequencies are denoted p₁₁, p₁₂, p₂₂. Let n₁₁, n₁₂, n₂₂ denote the observed genotype frequencies which, under independent sampling, follow the multinomial distribution:

$$\mathrm{Pr}(\mathit{n}\mid \mathit{p})=\frac{n!}{n_{11}!n_{12}!n_{22}!}{p}_{11}^{n_{11}}{p}_{12}^{n_{12}}{p}_{22}^{n_{22}},$$ (1)

where n = (n₁₁, n₁₂, n₂₂), p = (p₁₁, p₁₂, p₂₂), and $n={\sum }_{i,j=1\ge i}^k{n}_{ij}$. In a large random-mating population, in the absence of migration, mutation, natural selection, and assortative mating, HWE corresponds to the frequencies of A₁ homozygotes, heterozygotes, and A₂ homozygotes being $p_1^2$, 2p₁(1 – p₁), and (1 – p₁)². Hence the HWE model and the saturated model have one and two parameters, respectively. There are various ways in which the saturated model space can be parameterized (Weir, 1996). We will consider the fixation index parameter (also called the inbreeding coefficient), f, whose use gives

$$p_{11}=p_1^2+p_1(1-p_1)f,p_{12}=2p_1(1-p_1)(1-f),p_{22}={(1-p_1)}^2+p_1(1-p_1)f,$$

so that f = 0 recovers the HWE model. Examining point and interval estimates for f yields insight into departures from HWE: positive values are manifested in an excess of homozygotes (and may indicate inbreeding) while negative values correspond to an excess of heterozygotes. Defining p_min = min(p₁, 1 – p₁), the range of f is ($\frac{-p_{\min }}{1-p_{\min }},1$), and so depends on the allele frequencies, which complicates inference. In a GWAS, f > 0 may indicate population stratification, while f < 0 may occur if there are regions of low-copy repeats, leading to an increase in the number of apparent heterozygotes (Wigginton et al., 2005).

2.2 Multiallelic Markers

The generalization to k alleles, A₁ , . . . , A_k, is relatively straightforward. In an obvious notation let p_ij be the frequency of genotype A_iA_j , and n_ij be the observed count, i, j = 1 , . . . , k, j ≥ i. The likelihood is again multinomial:

$$\mathrm{Pr}(\mathit{n}\mid \mathit{p})=\frac{n!}{\prod _{i,j=1,j\ge i}^k{n}_{ij}!}\prod _{i,j=1,j\ge i}^k{p}_{ij}^{n_{ij}},$$ (2)

where n = (n₁₁, n₁₂ , . . . , n_kk), and p = (p₁₁, p₁₂ , . . . , p_kk) are k(k + 1)/2-dimensional vectors and $n={\sum }_{i,j=1,j\ge i}^k{n}_{ij}$ Under HWE $p_{ii}=p_i^2,i=1,\dots ,k$, and p_ij = 2p_ip_j , i, j = 1 , . . . , k, j ≥ i. We can parameterize the saturated model as $p_{ii}=p_i^2+p_i{\sum }_{j\ne i}{p}_j{f}_{ij},p_{ij}=2p_i{p}_j(1-f_{ij})$ so that we have introduced a set of fixation indices f_ij (Weir, 1996; Ayres and Balding, 1998); f_ij = 0 for all i ≠ j recovers the HWE model. Again we may examine estimates of f_ij to discover the reasons for departure from HWE; a positive/negative f_ij indicates a deficiency/excess of heterozygotes of type A_iA_j. A disadvantage of this model is that the fixation indices are on awkward ranges: $1-\frac{1}{2p_i{p}_j}\le f_{ij}\le 1$ (so that the lower bound can extend below −1, which is not true for the model with a single f), which can produce difficulties for inference.

An interesting submodel corresponds to f_ij = f, and is known as the inbreeding model because all pairs of allele frequencies are assumed to be equally perturbed. Under this model: $p_{ii}=p_i^2+p_i(1-p_i)f$, $p_{ij}=2p_i{p}_j(1-f)$, and $\frac{-p_{\min }}{1-p_{\min }}\le f\le 1$, where p_min is the minimum of the allele frequencies. Under HWE the multinomial likelihood (2) takes the form

$$\mathrm{Pr}(\mathit{n}\mid \mathit{p})=\frac{{}_2\sum _{i=1,j>i}^k^{n_{ij}}n!}{\prod _{i,j=1,j\ge i}^k{n}_{ij}!}\prod _{i=1}^k{p}_i^{2n_{ii}+{\sum }_{j>i}{n}_{ij}}.$$ (3)

2.3 Frequentist Approaches

Frequentist asymptotic χ² and exact tests provide the most common approaches to the testing of HWE (Weir, 1996). The exact test is recommended (Balding, 2006) because it does not depend on large sample sizes, and the χ² test can have inaccurate type I errors as documented by Wigginton et al. (2005). We concentrate on the exact test. For two alleles, one proceeds by considering the distribution of the counts conditional on the observed numbers of A₁ alleles, n₁ = 2n₁₁ + n₁₂, to give, under the null

$$\mathrm{Pr}(n_{12}\mid n_1)=\frac{n!}{[(n_1-n_{12})∕2]!n_{12}![(n-n_1-n_{12})∕2]!}\times \frac{2^{n_{12}}{n}_1!(n-n_1)!}{\left(2n\right)!}.$$

The null of HWE is rejected if the observed data fall into the tails of this distribution, with the tail defined by the specified significance level. In the multiallelic case the enumeration of the counts in the tails may be computationally expensive and a number of Monte Carlo algorithms have been proposed (Guo and Thompson, 1992; Huber et al., 2006). In general the distribution of the p-value under the null is not uniform due to the discreteness of n₁₂ and so enumeration of all possible tables consistent with n₁ is advised to obtain the empirical p-value distribution (Rohlfs and Weir, 2008).

Maximum likelihood estimates (MLEs) of the allele frequencies and parameters of interest are readily available from the multinomial likelihood, though inference requires asymptotic arguments, and the awkward constraints on the inbreeding coefficient/fixation indices make the construction of intervals that obey the constraints difficult.

3. Bayesian Approaches

Bayesian approaches have been described by a number of authors. Altham (1971) showed the close link between the exact test and a posterior tail area under a Dirichlet prior, while Pereira and Rogatko (1984) considered the two allele case with estimation and testing via Bayes factors being carried out with Dirichlet priors. Lindley (1988) also considered this case and parameterized in terms of $\alpha =\frac{1}{2}\log \frac{4p_{11}{p}_{22}}{p_{12}^2}$ and $\beta =\frac{1}{2}\log \frac{p_{11}}{p_{22}}$. HWE corresponds to $4p_{11}{p}_{22}=p_{12}^2$, or equivalently α = 0. When α = 0, $\beta =\log \frac{p_1}{1-p_1}$, where p₁ is the frequency of allele A₁. An advantage of this parameterization is that α and β are defined over the whole real line, which simplifies inference. A disadvantage is the lack of interpretability of the parameters, which makes prior specification difficult. Shoemaker, Painter, and Weir (1998) considered estimation for the two allele case and placed prior distributions on either the allele frequencies or on the disequilibrium parameter $D=p_{11}-p_1^2$, which (as with f) is subject to awkward constraints; these authors used numerical integration to obtain the posterior distribution. Ayres and Balding (1998) considered estimation for the fixation indices model, with inference carried out using Markov chain Monte Carlo (MCMC). Montoya-Delgado et al. (2001) use the Bayes factor as a test statistic. Consonni, Gutierrez-Pena, and Veronese (2008) discuss various methods for choosing “compatible” priors for nested models, with particular reference to the HWE model.

3.1 Bayes Factors

The Bayesian approach to hypothesis testing requires consideration of the Bayes factor (Kass and Raftery, 1995), which is the probability of the data under the null divided by the probability of the data under the alternative. In the HWE context the Bayes factor (BF) is given by

$$\mathrm{BF}=\frac{\mathrm{Pr}(\mathit{n}\mid H_0)}{\mathrm{Pr}(\mathit{n}\mid H_1)}=\frac{\int \mathrm{Pr}(\mathit{n}\mid \theta )\pi \left(\theta \right)d\theta }{\int \int \mathrm{Pr}(\mathit{n}\mid \theta ,\lambda )\pi (\theta ,\lambda )d\theta d\lambda },$$ (4)

where θ represent a vector of parameters under the null and λ an additional set of parameters under the alternative hypothesis, with prior distribution π(θ) under the null and joint prior π(θ, λ) under the alternative. A conjugate choice for the parameters under both the null and saturated hypotheses is the Dirichlet distribution. In the k allele case, for the saturated model, let Dir(v) with v = (v₁₁, v₁₂ , . . . , v_kk) denote the Dirichlet distribution with parameters v and density:

$$\pi \left(\mathit{p}\right)=\frac{\Gamma \left(\sum _{i,j=1,j\ge i}^k{v}_{ij}\right)}{\prod _{i,j=1,j\ge i}^k\Gamma \left(v_{ij}\right)}\prod _{i,j=1,j\ge i}^k{p}_{ij}^{v_{ij}-1},$$

where p_ij > 0 and ${\sum }_{i,j=1,j\ge i}^k{p}_{ij}=1$. Combining this prior on genotype frequencies with the multinomial likelihood gives the Dirichlet posterior Dir(v + n), in an obvious notation. The conjugate prior under the null, Dir(w) with w = (w₁ , . . . w_k) follows in an analogous fashion (and is a prior on allele frequencies) to give the posterior Dir(w + m), where m = (m₁ , . . . , m_k) and $m_i=2n_{ii}+{\sum }_{j>i}{n}_{ij}$.

In the diallelic case the conjugate priors Dir(w₁, w₂) and Dir(v₁₁, v₁₂, v₂₂) under the null and alternative lead to the Bayes factor:

$$\mathrm{BF}=\frac{2^{n_{12}}\Gamma \left(w\right)\Gamma (2n_{11}+n_{12}+w_1)\Gamma \left(v_{11}\right)\Gamma \left(v_{12}\right)\Gamma \left(v_{22}\right)\Gamma (n_{12}+2n_{22}+w_2)\Gamma (n+v)}{\Gamma \left(w_1\right)\Gamma \left(w_2\right)\Gamma (2n+w)\Gamma \left(v\right)\Gamma (n_{11}+v_{11})\Gamma (n_{12}+v_{12})\Gamma (n_{22}+v_{22})},$$ (5)

where w = w₁ + w₂ and v = v₁₁ + v₁₂ + v₂₂ (Consonni et al., 2008). For k alleles and under conjugate priors the normalizing constants for the HWE and saturated models are available in closed form and are given by:

$$p(\mathit{n}\mid H_0)=\frac{{}_{n!2}\sum _{i,j=1,j>i}^k{n}_{ij}}{\prod _{i,j=1,j\ge i}^k{n}_{ij}!}\frac{\Gamma \left(w\right)}{\prod _{i=1}^k\Gamma \left(w_i\right)}\times \frac{\prod _{i=1}^k\Gamma \left(w_i+2n_{ii}+\sum _{j>i}{n}_{ij}\right)}{\Gamma \left(w+\sum _{i=1}^{k}2n_{ii}+\sum _{i=1}^k\sum _{j>i}{n}_{ij}\right)},$$ (6)

$$p(\mathit{n}\mid H_1)=\frac{n!}{\prod _{i,j=1,j\ge i}{n}_{ij}!}\frac{\Gamma \left(v\right)}{\prod _{i,j=1,j\ge i}\Gamma \left(v_{ij}\right)}\times \frac{\prod _{i,j=1,j\ge i}\Gamma (v_{ij}+n_{ij})}{\Gamma (v+n)},$$ (7)

where $w={\sum }_{i=1}^k{w}_i$ and $v={\sum }_{i,j=1,j\ge i}^k{v}_{ij}$. The ratio of equation (6) to equation (7) gives the Bayes’ factor, of which (2) is the special case when k = 2.

With nested models, as in the HWE context, an appealing specification is one under which π(θ | H₀) = π(θ | H₁), so that when comparing the data under the null and alternative models we are examining whether the addition of the extra set of parameters that define the alternative leads to a better explanation of the data. This relationship does not hold under conjugate specifications for the null and alternative, but does hold for the following specification for k = 2. Under the alternative suppose we assume π₁(p₁₁, p₁₂, p₂₂) is Dir(1,1,1). To obtain a consistent prior under the null we reparameterize from (p₁₁, p₁₂, 1 – p₁₁ – p₁₂) to (p₁, p₁₂, 1 – p₁ p₁₂/2) and then integrate over p₁₂ to give:

$${\pi }_0\left(p_1\right)=\{\begin{array}{cc}4p_1\hfill & 0<p_1\le 0.5\hfill \\ 4(1-p_1)\hfill & 0.5<p_1<1.\hfill \end{array}\phantom{\}}$$ (8)

For these priors the Bayes factor is again available in easily computable form with the denominator as in the conjugate case, i.e., equation (7) with k = 2 and v = (1, 1, 1), and

$$p(\mathit{n}\mid H_0)=\frac{n!2^{n_{12}+2}}{n_{11}!n_{12}!n_{22}!}[\mathrm{IBe}(0.5,2n_{11}+n_{12}+2,n_{12}+2n_{22}+1)+\mathrm{Be}(2n_{11}+n_{12}+1,n_{12}+2n_{22}+2)-\mathrm{IBe}(0.5,2n_{11}+n_{12}+1,n_{12}+2n_{22}+2)],$$

where Be(a, b) = Γ(a)Γ(b)/Γ(a + b) and $\mathrm{IBe}(x,a,b)={\int }_0^x{z}^{a-1}{(1-z)}^{b-1}dz$ is the incomplete beta function (which is straightforward to calculate). Under the Dir(1,1,1) prior the probability that the inbreeding coefficient f is greater than 0 is 0.67, showing that the implications of innocuous looking priors should be carefully examined.

Often we will wish to specify nonconjugate priors, for increased flexibility. For example, in the inbreeding single f model, prior information may exist on the coefficient f for which, recall, f_min ≤ f ≤ 1, where $f_{\min }=\frac{-p_{\min }}{1-p_{\min }}$. We require a joint prior for p,f and we assume π(p,f) = π(p) × π(f|p), with an $N({\mu }_{\lambda },{\sigma }_{\lambda }^2)$ prior for $\lambda =\log \left(\frac{f-f_{\min }}{1-f}\right)$, which gives

$${\pi }_f(f\mid \mathit{p})={\left(2\pi {\sigma }_{\lambda }^2\right)}^{-1∕2}\exp \left[-\frac{1}{2{\sigma }_{\lambda }^2}{\left\{\log \left(\frac{f-f_{\min }}{1-f}\right)-{\mu }_{\lambda }\right\}}^2\right]\times \frac{1-f_{\min }}{(f-f_{\min })(1-f)},$$ (9)

as a prior for f, where the final term corresponds to the Jacobian |dλ/df| (see Appendix). For prior specification we choose two probabilities, along with their corresponding quantiles, for f, and then solve for μ_λ , σ_λ. Much data are available on the possible sizes of f. For example, Table 7.3 of Cavalli-Sforza and Bodmer (1971) gives estimates of f for a range of human populations. It is possible that f < 0, for example, due to avoidance of mating relatives, and through selection for heterozygozity.

For the single f model, and with the prior p = (p₁ , . . . , p_k) ~ Dir(w) under the null, we may use importance sampling to evaluate the denominator of the Bayes factor (4). To obtain an efficient proposal we parameterize in terms of the set (θ, λ), where θ = (θ₁ , . . . , θ_k–1) with θ_i = log(p_i/p_k), i = 1 , . . . , k – 1. Under this parameterization the restrictions on p and the awkward constraints on f|p are automatically satisfied, and (θ, λ) are defined on ${\mathbb{R}}^k$, which is desirable for finding an efficient importance sampling proposal. Under the alternative we have p ~ Dir(w) multiplied by equation (9) and so require

$$p(\mathit{n}\mid H_1)=\int p(\mathit{n}\mid \mathit{p},f){\pi }_p\left(\mathit{p}\right){\pi }_{f\mid p}(f\mid \mathit{p})d\mathit{p}df=E_{{\pi }_p{\pi }_{f\mid p}}\left[p(\mathit{n}\mid \mathit{p},\lambda )\right]$$ (10)

$$=\int \frac{p(\mathit{n}\mid \theta ,\lambda ){\pi }_p\left(s\left(\theta \right)\right){\pi }_{f\mid p}(t(\theta ,\lambda )\mid \mathit{p})\mid \mathit{J}\mid }{g_{\theta ,\lambda }(\theta ,\lambda )}\times g_{\theta ,\lambda }(\theta ,\lambda )d\theta d\lambda =E_{g_{\theta },\lambda }\left[\frac{p(\mathit{n}\mid \theta ,\lambda ){\pi }_p\left(h\left(\theta \right)\right)\mid \mathit{J}\mid {\pi }_{\lambda }(\lambda \mid \mathit{p})}{g_{\theta ,\lambda }(\theta ,\lambda )}\right],$$ (11)

where p = s(θ) and f = t(θ, λ) are the reverse transformations and J is the Jacobian for the transformation from (p, f) → (θ, λ). Details are contained in the Appendix. For small numbers of alleles, we sample directly from the prior as in (10), which is a computationally simple approach (because the estimator is simply the likelihood averaged with respect to the prior). This strategy is computationally expensive if either the number of alleles or the sample size is large, however, because the likelihood will be relatively peaked and so the majority of the points will provide essentially zero contribution. As an alternative we may take g(·, ·) in equation (11) as a k-dimensional normal distribution. We run an MCMC sampler (coded in the WinBUGS software, Spiegelhalter, Thomas, and Best, 1998) and take the posterior mean vector and the posterior variance–covariance matrix of (θ, λ) as the moments of g(·, ·).

Once the Bayes factor is evaluated a decision theory approach to testing requires the specification of the prior odds (PO) on H₀, PO = π₀/(1 – π₀), where π₀ = Pr(H₀), and the ratio of costs of type II to type I errors, R = C_II/C_I. The decision theory solution is to accept H₁ if BF × PO < R. In contrast, frequentist hypothesis testing must specify the significance threshold α. The choice of PO and R is not straightforward, but at least it is clear what is being specified rather than having the implicit choices in a p-value threshold (Wakefield, 2009). To inform the choices, one may carry out simulations to examine the type I and type II errors associated with particular values of PO and R.

If only the ranking of discrepancies from HWE is required (for example in a GWAS in which HWE is examined in controls for a large number of SNPs) then if PO and R are constant across SNPs the ranking can be based on the Bayes factors alone, and there is no need to specify PO and R.

3.2 Estimation

Exploitation of conjugate prior distributions allows closed form inference for allele frequencies under HWE, and under the saturated alternative model for the genotype frequencies, but such closed form inference is not available for the fixation indices. However, it is straightforward to obtain samples for these indices, by simple transformation of the samples for p. Specifically, if p^(s), s = 1 , . . . , S represent samples from the posterior for the collection of geno-type frequencies, p_ij, then $f_{ij}^{\left(s\right)}=1-p_{ij}^{\left(s\right)}∕2p_i^{\left(s\right)}{p}_j^{\left(s\right)}$ with $p_i^{\left(s\right)}=2p_{ii}^{\left(s\right)}+{\sum }_{i,j=1,i\ne j}^k{p}_{ij}^{\left(s\right)}$, $p_j^{\left(s\right)}=2p_{jj}^{\left(s\right)}+{\sum }_{i,j=1,i\ne j}^k{p}_{ji}^{\left(s\right)}$.

For the f model we cannot exploit conjugacy but may use a rejection algorithm with sampling from the prior if the number of alleles is small, with MCMC being used otherwise.

4. Examples

4.1 Four Group Data

We first analyze the four class genotype data that have been previously analyzed by a number of authors (Louis and Dempster, 1987; Guo and Thompson, 1992). The data are given by

$$(A_1{A}_1,A_2{A}_1,A_2{A}_2,A_3{A}_1,A_3{A}_2,A_3{A}_3,A_4{A}_1,A_4{A}_2,A_4{A}_3,A_4{A}_4)=(0,3,1,5,18,1,3,7,5,2).$$

The exact p-value for these data is 0.01744, which under conventional levels would be deemed as showing mild evidence of departure from HWE. These data are described in Thomson et al. (1986) and concern the antigen class of 45 French type 1 diabetes patients, with the classes being DR1, DR3, DR4, and Y, a fourth class corresponding to all other antigens. In our notation these classes correspond to (A₁, A₂, A₃, A₄). The interest here is in the mode of inheritance of type 1 diabetes, with a hypothesized recessive model being equivalent to the HWE model (Thomson, 1983). The translation into the HWE framework is as follows. Assume a hypothetical two-locus model with k = 4 alleles at one (antigen) locus along with a second disease locus. Under a recessive model of inheritance we require two disease alleles, D, and among cases we may consider the probabilities of obtaining the different antigen combinations under the recessive model:

$$\mathrm{Pr}(A_{i}D∕A_{j}D\mid \text{Disease})=\frac{\mathrm{Pr}(\text{Disease}\mid A_{i}D∕A_{j}D)\mathrm{Pr}(A_{i}D∕A_{j}D)}{\mathrm{Pr}\left(\text{Disease}\right)},$$

where A_iD/A_jD are the possible genotypes of diseased individuals, for i, j = 1 , . . . , k. Thomson (1983) parameterized the model in terms of k_i = Pr (A_i | D), and let f₂ be the probability of disease given two copies of the disease allele, and p_D the frequency of the disease allele. Under the recessive model two disease alleles are required and so

$$\mathrm{Pr}\left(\text{Disease}\right)=\sum _{i,j,i\ne j}\mathrm{Pr}(\text{Disease}\mid A_{i}D∕A_{j}D)\mathrm{Pr}(A_{i}D∕A_{j}D)=f_2{p}_D^2\left[\sum _{i=1}^k{k}_i^2+\sum _{i,j=1,i\ne j}^k{k}_i{k}_j\right]=f_2{p}_D^2,$$

where the summations within the square brackets equal 1 because we have added over the set of conditional allele probabilities. Hence

$$\mathrm{Pr}(A_{i}D∕A_{j}D\mid \text{Disease})=\{\begin{array}{cc}{k}_i^2\hfill & i=j\hfill \\ 2k_i{k}_j\hfill & i\ne j\hfill \end{array}\phantom{\}},$$

which is equivalent to HWE. Deviations from this model suggest that the recessive model does not hold. In particular we may interpret, for example, negative f₃₄ as an excess of A₃A₄ genotypes among diseased individuals. The single f model is more difficult to interpret in this context but corresponds to a general excess (negative f) or deficit (positive f) of heterozygotes.

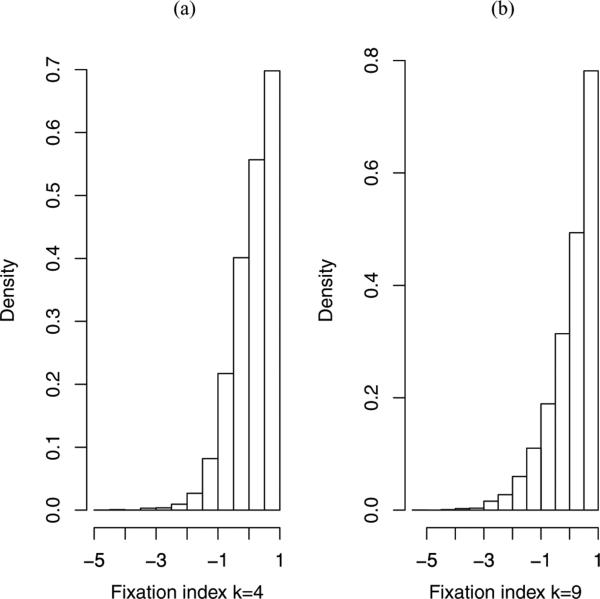
For these data we fit the HWE (recessive) model, along with the single f and saturated models. For the HWE and saturated models we assume conjugate Dirichlet priors with all parameters set to 1. This prior is flat over the simplex of probabilities, but is far from uninformative on each of the fixation indices. Figure 1a gives the marginal prior density for a generic fixation index; the prior probability that this fixation index is greater than 0 is 0.64. For the single f model we assume the transformed normal prior model described in Section 3.1, and fix prior probabilities Pr(f < 0) = 0.5 and Pr(f < 0.26) = 0.95 to give μ_λ = −2.95, σ_λ = 1.07. The normalizing constants for the recessive and saturated models are given by equations (6) and (7) and are 1.39 × 10⁻¹¹ and 1.88 × 10⁻¹⁰, respectively, to give a Bayes factor of 0.074. Hence the data are 14 times more likely under the saturated model. The probability of the data under the single f model is 1.36 × 10⁻¹⁰ so that the data are 10 times more likely under this model when compared to the recessive (HWE) model, but slightly less likely than under the saturated model. The normalizing constant under the single f model was evaluated using importance sampling Monte Carlo, with sampling from both the prior, and from a four-dimensional normal (as described in Section 3.1), both being computationally feasible for these data.

Figure 1.

Prior distribution for a generic fixation index with (a) k = 4 alleles, (b) k = 9 alleles, given a Dirichlet prior with parameters 1, on the 10 (k = 4) and 45 (k = 9) allele frequencies.

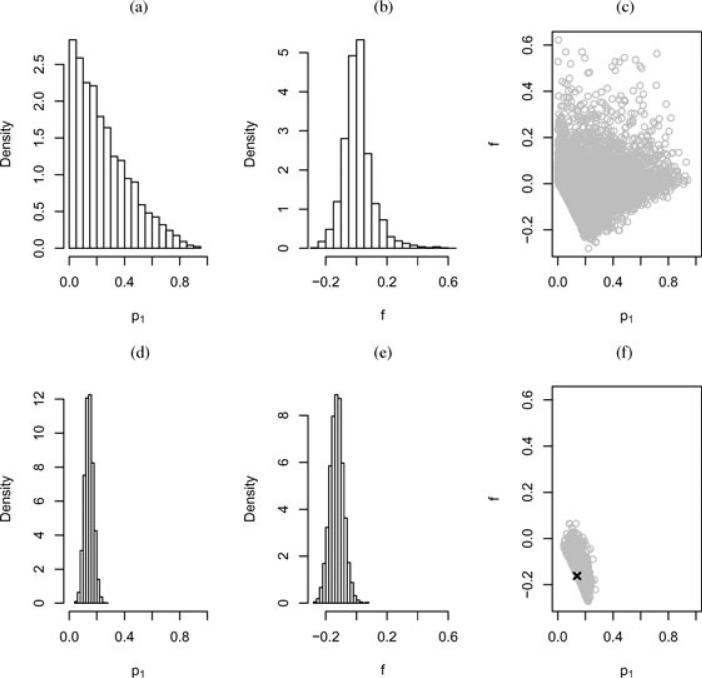
Figure 2 gives prior (top row) and posterior (bottom row) distributions from the single f model. We provide the prior/posterior for f and the single allele frequency p₁ (for illustration). Under the single f model Pr(f < 0 | n) = 0.994. The MLE is indicated as the cross on the scatterplot in panel (f). The MLE $\widehat{f}$ for the single f model lies on the lower boundary of its range, which led to instability in attempting to derive a standard error. Figure 2f illustrates this problem with the posterior density concentrated near the boundary. When a parameter lies close to its boundary, it is often indicative of model inadequacy and here we interpret f close to its boundary as reflecting an inadequacy of the single f model. Examination of posterior interval estimates under the general fixation model is revealing in this respect.

Figure 2.

Prior (top row) and posterior (bottom row) distributions based on 5000 samples, for the four group data and the single inbreeding coefficient f model. The MLE is indicated as the cross in (f). We examine p₁ for illustration, and could just as easily have picked p₂, p₃, or p₄.

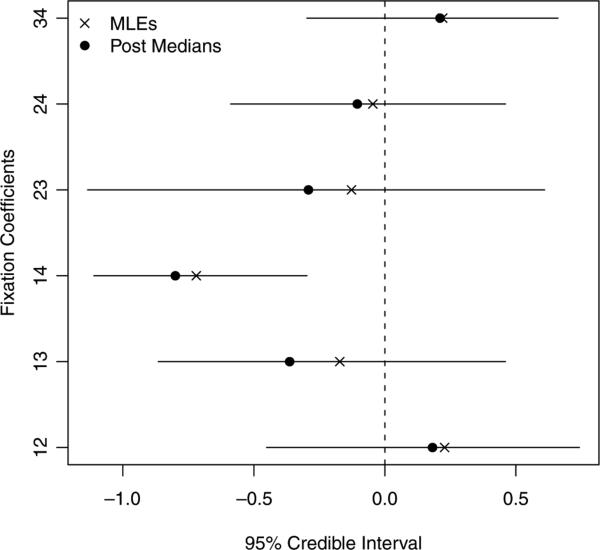
In Figure 3, we give posterior intervals along with posterior medians and MLEs for each of the fixation indices. The posterior medians are all pulled toward 1, relative to the MLEs, due to the prior, see Figure 1a. We see that the fixation index associated with the A₁A₄ combination is furthest from zero and negative, and most responsible for the negative estimate of f in the single inbreeding coefficient model. The heterogeneity of the fixation indices explains why the data are slightly more consistent with the saturated model than the single f model. It is interesting to observe that the A₁A₄ combination was not noteworthy in these data using the method implemented in Thomson et al. (1986). However, they comment that in the German population that they also examined (and in a Caucasian population investigated in Winnearls et al., 1984) there was an excess of A₁A₄ individuals, which is consistent with the posterior interval observed in Figure 3.

Figure 3.

Posterior summaries and MLEs for the fixation coefficients, in the four group example.

4.2 Nine Group Data

Our second example was also analyzed by Guo and Thompson (1992) and consists of rhesus data on 8297 individuals with nine groups. The (exact) p-value for these data is 0.71. Under the HWE null we assume the Dirichlet prior with w = (1, 1, 1, 1, 1, 1, 1, 1, 1) so that this prior is uniform on the simplex of allele frequencies. Under the single f alternative we use the information in Table 7.3 of Cavalli-Sforza and Bodmer (1971), which contains estimates of f that are predominantly less than 0.03. Consequently, under the single f model we assume a prior on f that has 50% and 95% points of 0 and 0.03. We obtain normalizing constants for the HWE and the single f model 1.3 × 10⁻⁵³ and 5.1 × 10⁻⁵⁴ so that the data are 2.5 times more likely under the HWE model, as compared to the single f model. For these data, sampling from the prior was not feasible, so instead importance sampling Monte Carlo was implemented using a nine-dimensional normal distributed with moments estimated from an MCMC run. For illustration, the probability of the data under the saturated model with conjugate Dirichlet prior with a vector of 45 1's is 8.7 × 10⁻¹¹⁹, emphatically ruling out this model. The “model” being summarized by the normalizing constant consists of the likelihood and the prior, and the conjugate prior assumed here is very unappealing for these data because it gives priors on the fixation indices that are not realistic. Figure 1b gives the induced marginal prior on a generic fixation index and shows that the distribution is not concentrated close to zero as is reasonable in this context.

Under the single f model the (2.5%, 50%, 97.5%) posterior quantiles are (−0.0001, 0.0002, 0.0106) so that the 95% credible interval contains zero (the MLE is 0.01). For these data we would conclude that there is not a genetically significant departure from HWE.

4.3 Genome-Wide Data

We illustrate the use of Bayes factors for examination of HWE in GWAS. In this context, testing for HWE is used as a method for carrying out quality control, and in particular to detect SNP specific genotyping errors. Fisher's exact test is the recommended frequentist procedure (Wigginton et al., 2005; Balding, 2006), but there are a number of difficulties in implementation. In a multiple testing situation one must select a criterion to control in order to specify a significance threshold, and by far the most common approach is a Bonferroni correction. However, the rationale for control of the family-wise error rate (FWER) is not obvious in a genome-wide quality context when one would not expect all nulls to be true. Even if one accepts that this is the correct quantity to control, the choice of a specific threshold is difficult. There is no agreed threshold in the literature, as Wittke-Thompson, Pluzhnikov, and Cox (2005, p. 967) state, “. . . there is little consensus on the correct thresholds for identifying DHW (departure from HWE) in the context of large-scale studies” (I have added the expression in italics). In practice a range of thresholds have been used: Easton et al. (2007) use a threshold of 10⁻⁵ for breast cancer (227,876 SNPs, with 400 controls); Libioulle et al. (2007) use 10⁻³ for Crohn's disease (317,5497 SNPs, with 928 controls); Zeggini et al. (2007) use 10⁻⁴ for type 2 diabetes (459,448 SNPs, with 2938 controls); Stacey et al. (2007) use 10⁻¹⁰ (317,503 SNPs, with 11,563 controls). It would seem desirable to have a p-value threshold that decreases with increasing sample size (because in the limit we would not want to make any type I errors), but this does not seem to be exercised in practice, because power is not considered when a threshold is determined. Extending this idea suggests that the threshold should be minor allele frequency (MAF) specific also, as power is a function of the MAF. The Bayes factor approach explicitly considers power (i.e., sample size and MAF) in its calculation because the denominator is the probability of the data under the alternative. The threshold is a function of the prior odds and the costs of the two types of error. Using the Bayes factor as a test statistic gives a procedure by which the type I and type II errors decrease to zero with increasing sample size (Wakefield, 2009).

A common practice in GWAS is to plot the observed –log₁₀ p-value versus that expected under the null, where the latter are derived assuming uniformity of the p-value. Due to the discreteness of the test statistic p-values derived from an exact test are not uniform under the null, however. The correct MAF-specific distribution can be derived by enumerating all counts under the null for that MAF in the sample. In this context it is also difficult to use the q-value methodology (Storey, 2003) due to the nonuniformity of the null distribution.

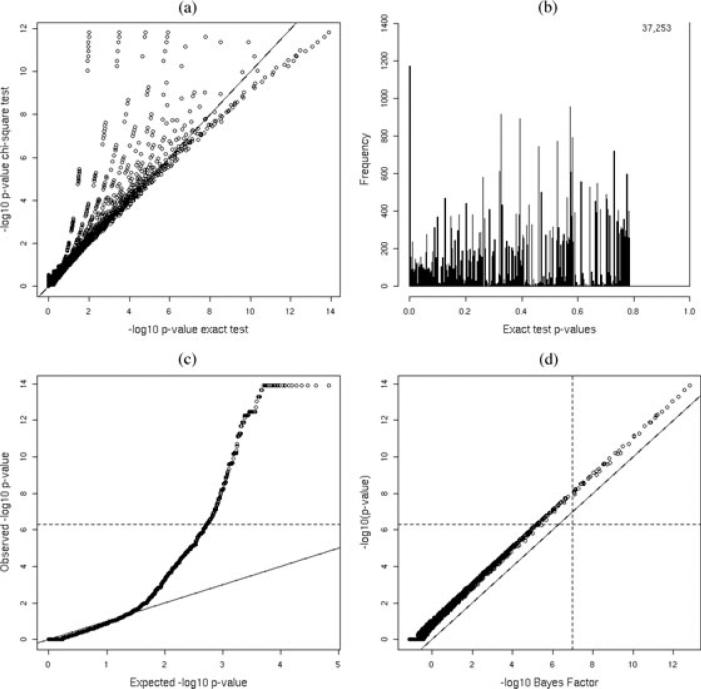
We examine data from Klein et al. (2005), who reported a GWAS for age-related macular degeneration; being one of the first GWAS there were just 96 cases and 50 controls. We examine HWE for 116,212 SNPs in controls. We first carried out a number of quality control measures, and for comparison purposes use the same criteria as Klein et al. (2005). Specifically, SNPs were removed if they were called in less than 85% of individuals or if the MAF was less than 1%; this left 102,640 SNPs. In Klein et al. (2005), a Bonferroni correction was applied to control the FWER at 5%, to give a p-value threshold of 4.9 × 10⁻⁷. Figure 4 displays various summaries for these data. In panel (a) we plot –log₁₀ p-values from the χ² test versus their exact test counterparts and we see a large degree of dissimilarity, which is not surprising given the small sample sizes here. The discreteness of the p-values from the exact test is apparent also, and the distribution away from zero (which corresponds principally to null SNPs) is far from uniform. To reinforce this point we plot the histogram of exact p-values in panel (b), the most probable configuration of genotypes has probability 1 and for these data more than a third (consisting of 37,253 SNPs) have a p-value of 1. This plot shows a great similarity to Figure 2 of Rohlfs and Weir (2008) (except that we have truncated the vertical axis so that more detail in the bulk of the distribution can be revealed). In panel (c), we plot the observed –log₁₀ p-values versus those expected under a uniform null. A plot containing this information is almost universally presented in GWAS, but it is not strictly valid because it assumes uniformity under the null. The Bonferroni threshold is indicated on this plot and leads to HWE being rejected for 191 SNPs.

Figure 4.

Bayes factor and p-value summaries for the GWAS for age-related macular degeneration data: (a) –log₁₀ p-values from a χ² test versus those from the exact test; (b) histogram of exact p-values (vertical axis truncated, the count at a p-value of 1 is indicated); (c) QQ-plot of observed versus expected –log₁₀ p-values, assuming uniformity of p-values under the null; and (d) –log₁₀ p-values against –log₁₀ Bayes factors. The dashed lines corresponds to the Bonferroni threshold (p-value axes) and Bayes factor thresholds (Bayes factor axes).

Turning now to a Bayesian approach we assume Dir(1,1,1) priors under the alternative and compare results based on two priors under the null, namely Dir(1,1) and the triangular distribution, equation (8). In terms of computation time, the Bayes factor calculations took approximately half the time of the exact p-values (which were calculated using the hwexact function in R). In Figure 4d, we plot –log₁₀ Bayes factors (under the conjugate prior) versus –log₁₀ p-values (from the exact test), and we see a very close correspondence, particularly for the SNPs that deviate from HWE.

To pick a threshold for rejection of HWE using Bayes factors we need to specify the PO of H₀, and the ratio of costs of type II to type I errors. In this context we would expect π₁ = 1 – π₀ to be very close to 0 (though not as close as the prior on a SNP being associated with disease), while we would not want to unnecessarily exclude a SNP from an association analysis, which suggests $R\ll 1$ (if in the association stage a signal is found, then clearly one would closely examine the control data from such a SNP). We choose π₀ = 0.999 and R = 1/1000, which leads to a Bayes factor threshold of 10⁻⁷, so that the data have to be 10⁷ times more likely under the alternative than under the null before HWE is rejected. This leads to 112 rejections under the conjugate prior Bayes factor and 100 under the triangular prior Bayes factor (we do not plot the latter as they are in close agreement with those under the conjugate prior).

In a GWAS context, another approach to prior specification is to recognize that under the alternative there may be an excess of heterozygotes, which could be reflected in the Dir(v₁₁, v₁₂, v₂₂) prior under the alternative by taking v₁₁ = v₂₂ < v₁₂.

5. Discussion

In this article, we have described a Bayesian approach to examination of HWE, using a variety of approaches to implementation. Depending on one's perspective the Bayesian need for prior specification may be judged a blessing or a curse. Certainly, great care is required in the specification of a prior distribution, as illustrated in the nine-allele example in which the “uniform over the simplex” prior under the saturated alternative was seen to be grossly inappropriate. However, under a particular prior, Bayes factors may be produced with the same ordering as asymptotic p-values, as we now briefly discuss.

For illustration, consider the two allele case and suppose we have a p-value based on the Wald statistic for f with MLE

$$\widehat{f}=\frac{4n_{11}{n}_{22}-n_{12}^2}{(2n_{11}+n_{12})(2n_{22}+n_{12})}$$

and asymptotic variance

$$V\left(f\right)=\mathrm{var}\left(\widehat{f}\right)=\frac{1}{2n{p}_1{p}_2}(1-f)[2p_1{p}_2(1-f)(1-2f)+f(2-f)].$$ (12)

The χ² statistic is given by ${\widehat{f}}^2∕V\left(0\right)=n{\widehat{f}}^2$. As shown elsewhere (Wakefield, 2007, 2009) an asymptotic Bayes factor (ABF) may be obtained by combining the “likelihood” $\widehat{f}\mid f\sim N\{f,V\left(0\right)\}$ with prior f ~ N(0, W) to give

$$\mathrm{ABF}=\sqrt{\frac{V\left(0\right)+W}{V\left(0\right)}}\exp \left(-\frac{z^2}{2}\frac{W}{V\left(0\right)+W}\right),$$ (13)

where $z=\widehat{f}∕\sqrt{V\left(0\right)}$ and W is the prior variance for f. If we take W independent of n then ABF tends to ∞ and 0 under the null and alternative respectively, as n → ∞, as desired. The ABF (13) is dependent on z only, and hence the Wald p-value (or equivalently the χ² statistic), when we take the prior variance W = K × V(0) = K/n, where K is a constant that does not depend on the data. This p-value prior gives

$${\mathrm{ABF}}_p={(1+K)}^{1∕2}\exp \left(-\frac{n{\widehat{f}}^2}{2}\frac{K}{1+K}\right)$$

and under this prior identical rankings of significance will be achieved between ABF_p and the χ² statistic. The dependence of the prior on n is troubling and leads to the p-value Bayes factor being inconsistent under the null because ABF_p tends to (1 + K)^1/2 as n → ∞, and not ∞ required. This indicates why p-value thresholds should decrease with increasing sample size, see Wakefield (2009) for further discussion.

R and WinBUGS codes to implement the methods presented here are available from http://faculty.washington.edu/jonno/cv.html. The supplementary material contains the WinBUGS code for the single f model.

Appendix

For simplicity we consider the case of two alleles. We have

$${\pi }_{p,f}(p,f)={\pi }_p\left(p\right)\times {\pi }_f(f\mid p),$$

where p ~ Beta(1, 1) and $\frac{-\min (p,1-p)}{1-\min (p,1-p)}=f_{\min }\le f\le 1$. Now consider the transformation (p, f ) → (θ, λ), where θ = log{p/(1 − p) and λ = log {(f − f_min/(1 − f)}. We wish to find the prior for θ, λ. We have p = s(θ) = e^θ/(1 + e^θ) and

$$f=t(\lambda ,\theta )=\{\begin{array}{cc}\frac{{\mathrm{e}}^{\lambda }-{\mathrm{e}}^{\theta }}{{\mathrm{e}}^{\lambda }+1}\hfill & \text{if}p<1-p\hfill \\ \frac{{\mathrm{e}}^{\lambda }-{\mathrm{e}}^{-\theta }}{{\mathrm{e}}^{\lambda }+1}\hfill & \text{if}1-p<p.\hfill \end{array}\phantom{\}}$$

The prior for θ, λ is given by

$${\pi }_{\theta }\left(\theta \right)\times {\pi }_{\lambda }(\lambda \mid \theta )={\pi }_p\left(s\left(\theta \right)\right)\times {\pi }_f(t(\lambda ,\theta )\mid \theta )\mid \mathit{J}\mid ,$$

where

$$\mid \mathit{J}\mid =\mid \begin{array}{cc}\hfill \frac{\partial p}{\partial \theta }\hfill & \hfill \frac{\partial p}{\partial \lambda }\hfill \\ \hfill \frac{\partial f}{\partial \theta }\hfill & \hfill \frac{\partial f}{\partial \lambda }\hfill \end{array}\mid ={\mid \begin{array}{cc}\hfill \frac{\partial \theta }{\partial p}\hfill & \hfill \frac{\partial \theta }{\partial f}\hfill \\ \hfill \frac{\partial \lambda }{\partial p}\hfill & \hfill \frac{\partial \lambda }{\partial f}\hfill \end{array}\mid }^{-1}$$

and

$$\frac{\partial \theta }{\partial p}=\frac{1}{p}+\frac{1}{1-p}$$ (A.1)

$$\frac{\partial \theta }{\partial f}=0$$ (A.2)

$$\frac{\partial \lambda }{\partial p}=\{\begin{array}{cc}\frac{1}{(1-p)[f(1-p)+p]}\hfill & \text{if}p<1-p\hfill \\ \frac{1}{p[fp+(1-p)]}\hfill & \text{if}1-p<p\hfill \end{array}\phantom{\}}$$ (A.3)

$$\frac{\partial \lambda }{\partial f}=\frac{1}{f-f_{\min }}+\frac{1}{1-f}$$ (A.4)

so that we can ignore $\frac{\partial \lambda }{\partial p}$. Hence

$$\mid \mathit{J}\mid =\frac{{\mathrm{e}}^{\theta }}{{(1+{\mathrm{e}}^{\theta })}^2}\times \frac{{\mathrm{e}}^{\lambda }(1-f_{\min })}{{(1+{\mathrm{e}}^{\lambda })}^2},$$

where f_min is a function of θ. This is the form that appears (in the general k allele case) in equations (10) and (11).